Mixed Navier-layerwise differential quadrature three-dimensional static and free vibration analysis of functionally graded carbon nanotube reinforced composite laminated plates

Abstract

The three-dimensional free vibration and static analysis of the laminated plates with functionally graded (FG) carbon nanotube reinforced composite (CNTRC) layers is presented using a semi-analytical approach. The individual layers are assumed to be made from a mixture of aligned and straight single-walled carbon nanotubes (CNTs) with volume fractions graded in the thickness direction, and an isotropic matrix. The effective material properties of the resulting FG-CNTRC layers are estimated through a micromechanical model. The through-the-thickness variations of the displacement components are accurately modeled using a layerwise-differential quadrature method, and their in-plane variations are approximated using the trigonometric series. After demonstrating the convergence and accuracy of the method, the effects of geometrical parameters, type of CNTs distribution and volume fractions, and also lamination scheme on the natural frequencies, displacement and stress components of the FG-CNTRC layered plates are investigated.

1 Introduction

Due to high strength and stiffness to weight ratios and other improved mechanical properties, reinforced composite materials have been increasingly used in many modern industries like automobile, aeronautic and astronautic technology. Usually micro-fibers such as micro-sized glass, Kevlar and carbon fibers have been used as reinforcement phases in a matrix medium to build up the conventional reinforced composite materials. But the exceptional mechanical and physical properties of carbon nanotubes (CNTs) over the micro-sized carbon fibers [1, 2] have stimulated a great deal of interest in replacing the conventional micro-sized carbon fibers with CNTs to produce carbon nanotube reinforced polymer composites with low density, high strength and elastic modulus, in recent years [1–9].

It is evident that the production of nanocomposites with either uniformly or randomly distributed CNTs through the matrix is easier than those with functionally graded (FG) distribution. However, the previous studies showed that the uniform distribution of CNTs as the reinforcements in the matrix can only achieve moderate improvement of the mechanical properties [8, 9]. On the other hand, since only a low percentage of the CNTs (2–5 % by weight) is used in making these advanced composites [1–9], effective use of the CNTs becomes essential. In this regards, Shen [10] introduced the idea of using functionally graded nanotube reinforced composite (FG-CNTRC) materials. He showed that by using the graded distribution through the matrix of CNTs, the nonlinear bending behavior of CNTs reinforced composite plates can be considerably improved [10].

For the purpose of their engineering design and manufacture, accurate prediction of the global behaviors of structural elements made of FG-CNTRC materials such as buckling, static response and vibrational characteristics is essential. In this regards, some studies were conducted by researchers in recent years; see for example [10–30]. However, there exist only few studies that concerned with the vibration and static analysis of FG-CNTRC plates [13–20], which are briefly reviewed in the following.

Wang and Shen [13] examined the large amplitude vibration of single layered CNTRC plates reinforced by SWCNTs resting on an elastic foundation in thermal environments. In another work, they studied the large amplitude vibration and the nonlinear bending of a sandwich plate with carbon nanotube-reinforced composite (CNTRC) face sheets resting on an elastic foundation in thermal environments [14]. Also, they presented the nonlinear dynamic response of single layered CNTRC plates resting on elastic foundations in thermal environments [15]. Shen and Zhang [16, 17] investigated the large amplitude vibration, non-linear bending and postbuckling behaviors of FG-CNTRC cross-ply and/or antisymmetric angle-ply laminated plates resting on Pasternak elastic foundations under different hygrothermal environments conditions. In all of these interesting works, the governing differential equations were obtained using the higher-order shear deformation plate theory, which were solved for simply supported plates using a two-step perturbation technique.

Zhu et al. [18] analyzed the bending and free vibration of thin-to-moderately thick single layered FG-CNTRC plates based on the first order shear deformation plate theory (FSDT) and using the finite element method (FEM). Lei et al. [19–21] employed the element-free kp-Ritz method in conjunction with the FSDT to study the linear free vibration, the nonlinear bending and the buckling characteristics of single layered FG-CNTRC plates. More recently, Liew and coauthors applied the element-free kp-Ritz method to investigate the linear and nonlinear mechanical behaviors of carbon nanotube-reinforced functionally graded cylindrical panels [22–26]. It should be mentioned that this method can abolish mesh distortion due to large deformation, avoid the need for remeshing, smooth and continuous shape functions and evaluate more accurate stress in comparison with the conventional finite element method [19–30].

All of these valuable studies are based on the two-dimensional theories. To the authors’ best of knowledge, the three-dimensional behavior of laminated plates with FG-CNTRC layers is not investigated yet. In this study, the three-dimensional static and free vibration analysis of multi-layered plates with FG-CNTRC layers are presented. It is assumed that the individual layers are composed of the aligned and straight SWCNTs, which are graded in the thickness direction, and an isotropic matrix. The extended rule of mixture as a simple and convenient micromechanical model for predicting the overall properties of the CNTRC materials [10–17, 31–34] is employed to estimate the effective material properties of the CNTRC layers. Due to the intrinsic complexity of the three-dimensional formulation of laminated plates with FG-CNTRC layers, the layerwise-differential quadrature method (LW-DQM) as an efficient and accurate numerical tool [33–39] is applied to approximate the variations of the displacement fields in the thickness direction. The governing differential equations of the layers, the related external boundary conditions and the compatibility conditions at the interface of two adjacent layers are clearly stated. Using the DQM enables one to accurately and efficiently discretize the governing differential equations along the graded direction and also implement the related boundary and compatibility conditions. Also, the in-plane variations of the displacement components are approximated using the trigonometric series. The present formulation and method of solution are validated through the convergence and accuracy studies. Then, a detailed parametric study is carried out to investigate the effects of types of CNTs distributions, CNTs volume fractions and also the lamination scheme on the natural frequencies, displacement and stress components of the FG-CNTRC layered plates.

2 Mathematical modeling

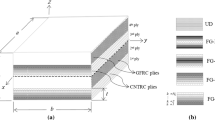
Consider a multi-layered plate composed of $N_{L}$ perfectly bonded FG-CNTRC layers (Fig. 1). The distribution of CNTs is graded along the thickness direction of the layers. The material properties and thickness of each layer of the plate are assumed to be arbitrary. The rectangular plate has the length a, width b and total thickness $h$ as shown in Fig. 1. Also, the Cartesian coordinate system with coordinate variables $\left( {x,y,z} \right)$, which are shown in Fig. 1, is used to label the material points of the laminated plate in the undeformed reference configuration. The displacement components of an arbitrary material point of the plate are denoted as u, v and w along the x, y and z-directions, respectively.

Fig. 1

The geometry of the laminated plate with FG-CNTRC layers

2.1 Effective material properties and the 3D constitutive relations

It is assumed that the individual layers are made of a mixture of SWCNTs and an isotropic matrix. On the other hand, the behavior of CNTs strongly influences the overall properties of the resulting materials. Hence, the layers become two-phase composite materials. Consequently, the micromechanical models usually used for the two-phase composite materials such as the Mori–Tanaka model [9] and the Voigt model as the rule of the mixture [3, 4] can be employed to evaluate their effective material properties. However, these models should be extended to include the small scale effect of SWCNTs to become applicable at the nanoscale [3, 4, 9]. In this work, the extended rule of mixture as a simple and convenient micromechanic model [10–17, 31–34], which includes the small scale effect by introducing the CNT efficiency parameters, is used.

The volume fractions of the CNTs are assumed to vary continuously and smoothly in the thickness direction of the individual layers. Therefore, the effective material properties of layers become graded in their thickness direction, i.e. z-direction. According to the extended rule of mixture, the effective Young’s modulus and shear modulus of the $k{\text{th}}$ physical FG-CNTRC layer in its principal material coordinate directions can be estimated as [32],

$$ E_{11}^{\left( k \right)} = \eta_{1} V_{CN}^{\left( k \right)} E_{11}^{CN} + V_{M}^{\left( k \right)} E^{M} ,\quad \frac{{\eta_{2} }}{{E_{22}^{\left( k \right)} }} = \frac{{V_{CN}^{\left( k \right)} }}{{E_{22}^{CN} }} + \frac{{V_{M}^{\left( k \right)} }}{{E^{M} }},\quad \frac{{\eta_{3} }}{{G_{12}^{\left( k \right)} }} = \frac{{V_{CN}^{\left( k \right)} }}{{G_{12}^{CN} }} + \frac{{V_{M}^{\left( k \right)} }}{{G^{M} }} $$

(1a-c)

where $E_{11}^{CN}$, $E_{22}^{CN}$ and $G_{12}^{CN}$ are the Young’s and shear moduli of the CNTs, $E^{M}$ and $G^{M}$ are the corresponding properties for the matrix, and $\eta_{j} \left( {j = 1, \, 2, \, 3} \right)$ are the CNTs efficiency parameters, respectively. In addition, $V_{CN}^{\left( k \right)}$ and $V_{M}^{\left( k \right)}$ are the volume fractions of the CNTs and the matrix of the $k{\text{th}}$ physical layer, which satisfy the relationship of $V_{CN}^{\left( k \right)} + V_{M}^{\left( k \right)} = 1$.

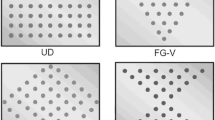
In order to study the effect of different CNTs distributions on the vibration and static behavior of the FG-CNTRC layered plates, in addition to uniformly distributed (UD) CNTs (Fig. 2a), three other types of material profiles through the layer thickness is considered. In this work, only linear distribution of the CNTs volume fraction that can readily be achieved in practice is considered [18],

Fig. 2

a–d Different types of CNTs distributions through the CNTRC layer

FG-V (Fig. 2b):

$$ V_{CN}^{\left( k \right)} = \,\left( {\frac{{2z^{\left( k \right)} + h^{\left( k \right)} }}{{h^{\left( k \right)} }}} \right)\left( {V_{CN}^{ * } } \right)^{\left( k \right)} $$

(2)

FG-Λ (Fig. 2i):

$$ V_{CN}^{\left( k \right)} = - \,\left( {\frac{{2z^{\left( k \right)} - h^{\left( k \right)} }}{{h^{\left( k \right)} }}} \right)\left( {V_{CN}^{ * } } \right)^{\left( k \right)} $$

(3)

FG-X (Fig. 2d):

$$ V_{CN}^{\left( k \right)} = \,\left( {\frac{{4\left| {z^{\left( k \right)} } \right|}}{{h^{\left( k \right)} }}} \right)\left( {V_{CN}^{ * } } \right)^{\left( k \right)} $$

(4)

in which,

$$ z^{\left( k \right)} = z - \frac{{h^{\left( k \right)} }}{2} - \sum\limits_{i = 1}^{k - 1} {h^{\left( i \right)} } ,\,\;\left( {V_{CN}^{ * } } \right)^{\left( k \right)} = \frac{{w_{CN}^{\left( k \right)} }}{{w_{CN}^{\left( k \right)} + \frac{{\rho^{CN} }}{{\rho^{M} }} - \left( {\frac{{\rho^{CN} }}{{\rho^{M} }}} \right)w_{CN}^{\left( k \right)} }} $$

(5a, b)

where $h^{\left( k \right)}$ is the $k{\text{th}}$ layer thickness and $w_{CN}^{\left( k \right)}$ is the mass fraction of CNTs in the $k{\text{th}}$ physical layer; also,$\rho^{CN}$ and $\rho^{M}$ are the densities of CNTs and matrix, respectively. Note that $V_{CN}^{\left( k \right)} = \left( {V_{CN}^{ * } } \right)^{\left( k \right)}$ corresponds to the CNTRC layer with uniformly distributed CNTs (UD-CNTRC). It is assumed that in all cases the FG-CNTRC layers have the same CNTs mass fraction.

According to the rule of mixture, Poisson’s ratio $\nu_{ij}^{\left( k \right)}$ $\left( {i, \, j = 1, \, 2, \, 3; \, i \ne j} \right)$ and the mass density $\rho^{\left( k \right)}$ of the $k{\text{th}}$ layer can be calculated as [32], respectively,

$$ \nu_{ij}^{\left( k \right)} = V_{CN}^{\left( k \right)} \nu_{ij}^{CN} + V_{M}^{\left( k \right)} \nu^{M} ,\,\;\rho^{\left( k \right)} = V_{CN}^{\left( k \right)} \rho^{CN} + V_{M}^{\left( k \right)} \rho^{M} $$

(6a, b)

where $\nu_{ij}^{CN}$ and$\nu^{M}$ are Poisson’s ratios of CNTs and matrix, respectively.

Based on the 3D linear theory of elasticity, the constitutive relations at an arbitrary material point of the$k{\text{th}}$ physical layer can be summarized as [40],

$$ \left\{ {\begin{array}{*{20}c} {\sigma_{xx}^{\left( k \right)} } \\ {\sigma_{yy}^{\left( k \right)} } \\ {\sigma_{zz}^{\left( k \right)} } \\ {\sigma_{yz}^{\left( k \right)} } \\ {\sigma_{xz}^{\left( k \right)} } \\ {\sigma_{xy}^{\left( k \right)} } \\ \end{array} } \right\} = \left[ {\begin{array}{*{20}c} {C_{ 1 1}^{\left( k \right)} } & {C_{ 1 2}^{\left( k \right)} } & {C_{ 1 3}^{\left( k \right)} } & 0 & 0 & 0 \\ {C_{ 1 2}^{\left( k \right)} } & {C_{ 2 2}^{\left( k \right)} } & {C_{ 2 3}^{\left( k \right)} } & 0 & 0 & 0 \\ {C_{ 1 3}^{\left( k \right)} } & {C_{ 2 3}^{\left( k \right)} } & {C_{ 3 3}^{\left( k \right)} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{ 4 4}^{\left( k \right)} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{ 5 5}^{\left( k \right)} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{ 6 6}^{\left( k \right)} } \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\partial u^{\left( k \right)} /\partial x} \\ {\partial v^{\left( k \right)} /\partial y} \\ {\partial w^{\left( k \right)} /\partial z} \\ {\frac{{\partial v^{\left( k \right)} }}{\partial z} + \frac{{\partial w^{\left( k \right)} }}{\partial y}} \\ {\frac{{\partial u^{\left( k \right)} }}{\partial z} + \frac{{\partial w^{\left( k \right)} }}{\partial x}} \\ {\frac{{\partial u^{\left( k \right)} }}{\partial y} + \frac{{\partial v^{\left( k \right)} }}{\partial x}} \\ \end{array} } \right\} $$

(7)

where $\sigma_{ij}^{\left( k \right)} \,\left( {i,j = x,\;y,\;z} \right)$ are the stress tensor components and $C_{ij}^{\left( k \right)}$ are the material elastic coefficients at an arbitrary material point of the $k{\text{th}}$ physical layer [40].

2.2 Three-dimensional semi-analytical modeling

In order to accurately represent the variation of the field variables across the thickness of the laminated plates based on the three-dimensional elasticity theory, the plate is divided into $N_{m} \,\left( { {\ge} N_{L} } \right)$ mathematical layers in the thickness direction. In the following, the governing differential equations of the $e{\text{th}}$ mathematical layer together with the related external boundary conditions and also the compatibility conditions at the interface of layers (e) and (e + 1) are presented.

The boundary conditions at the top and bottom surfaces of the laminated plates are as follows,

$$ {\text{At}}z = - h/ 2:\sigma_{xz}^{\left( e \right)} = 0,\,\;\sigma_{yz}^{\left( e \right)} = 0,\;\,\sigma_{zz}^{\left( e \right)} = 0,\quad \,{\text{for}}\;\,e = 1 $$

(8a-c)

$$ {\text{At}}\;z = h/ 2:\sigma_{xz}^{\left( e \right)} = 0,\,\;\sigma_{yz}^{\left( e \right)} = 0,\,\;\sigma_{zz}^{\left( e \right)} = \left\{ \begin{aligned}& - q\left( {x,y} \right)&&\,\,{\text{ for static}}\,{\text{analysis}} \hfill \\ &0&&\,\,{\text{for free}}\,{\text{vibration}}\,{\text{analysis}} \hfill \\ \end{aligned} \right.,\,\quad {\text{for}}\;e = N_{m} $$

(9a-c)

Hereafter, the superscript ‘e’ is used to denote the material properties and field variables of the eth mathematical layer.

In the present study, simply supported boundary conditions at the edges of the laminated rectangular plate is assumed,

$$ {\text{At}}\;x = 0,\;a:\sigma_{xx}^{\left( e \right)} \left( {x,y,z,t} \right) = 0,\;\,v^{\left( e \right)} \left( {x,y,z,t} \right) = 0,\,\;w^{\left( e \right)} \left( {x,y,z,t} \right) = 0 $$

(10a-c)

$$ {\text{At}}\; \, y = 0,\;b:\sigma_{yy}^{\left( e \right)} \left( {x,y,z,t} \right) = 0,\,\;u^{\left( e \right)} \left( {x,y,z,t} \right) = 0,\,\;w^{\left( e \right)} \left( {x,y,z,t} \right) = 0 $$

(11a-c)

where $e = 1, \, 2, \ldots , \, N_{m}$.

For the 3D analysis of plates with simply supported edges, the displacement components of the eth mathematical layer can be expanded in terms of the trigonometric sin and cosine functions in the x and y-directions as,

$$ \begin{gathered} u^{\left( e \right)} \left( {x,y,z,t} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {e^{{I\omega_{mn} t}} U_{mn}^{\left( e \right)} \left( z \right)\cos \left( {\alpha_{m} x} \right)} } \sin \left( {\beta_{n} y} \right) \hfill \\ v^{\left( e \right)} \left( {x,y,z,t} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {e^{{I\omega_{mn} t}} V_{mn}^{\left( e \right)} \left( z \right)\sin \left( {\alpha_{m} x} \right)} } \cos \left( {\beta_{n} y} \right) \hfill \\ w^{\left( e \right)} \left( {x,y,z,t} \right) = \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {e^{{I\omega_{mn} t}} W_{mn}^{\left( e \right)} \left( z \right)\sin \left( {\alpha_{m} x} \right)} } \sin \left( {\beta_{n} y} \right) \hfill \\ \end{gathered} $$

(12a-c)

where $\alpha_{m} = \frac{{m\pi {\kern 1pt} }}{a}$ and $\beta_{n} = \frac{{n\pi {\kern 1pt} }}{b}$; m and n are the half wave numbers along the x- and y-direction, respectively; $\omega_{mn}$ is the natural frequency associated to the half wave numbers m and n and has a zero value for the static analysis; also, $I\left( { = \sqrt { - 1} } \right)$ is the imaginary unit number. It should be noted that for the case of static analysis, one should insert $\omega_{mn} = 0$ in Eq. (12).

Using Eqs. (7) and (12), the three-dimensional equations of motion at an arbitrary material point of the $e{\text{th}}$ mathematical layer in terms of the displacement components can be obtained as,

$$ \begin{aligned} &C_{55}^{\left( e \right)} \frac{{d^{2} U_{mn}^{\left( e \right)} }}{{dz^{2} }} + \frac{{dC_{55}^{\left( e \right)} }}{dz}\frac{{dU_{mn}^{\left( e \right)} }}{dz} - \left( {\alpha_{m}^{2} C_{11}^{\left( e \right)} + \beta_{n}^{2} C_{66}^{\left( e \right)} } \right)U_{mn}^{\left( e \right)} - \alpha_{m} \beta_{n} \left( {C_{12}^{\left( e \right)} + C_{66}^{\left( e \right)} } \right)V_{mn}^{\left( e \right)} \\ &+ \;\alpha_{m} \left( {C_{13}^{\left( e \right)} + C_{55}^{\left( e \right)} } \right)\frac{{dW_{mn}^{\left( e \right)} }}{dz} + \alpha_{m} \frac{{dC_{55}^{\left( e \right)} }}{dz}W_{mn}^{\left( e \right)} + \rho^{\left( e \right)} \omega_{mn}^{2} U_{mn}^{\left( e \right)} = 0 \hfill \\ \end{aligned} $$

(13)

$$ \begin{aligned}& - \alpha_{m} \beta_{n} \left( {C_{12}^{\left( e \right)} + C_{66}^{\left( e \right)} } \right)U_{mn}^{\left( e \right)} + C_{44}^{\left( e \right)} \frac{{d^{2} V_{mn}^{\left( e \right)} }}{{dz^{2} }} + \frac{{dC_{44}^{\left( e \right)} }}{dz}\frac{{dV_{mn}^{\left( e \right)} }}{dz} - \left( {\alpha_{m}^{2} C_{66}^{\left( e \right)} + \beta_{n}^{2} C_{22}^{\left( e \right)} } \right)V_{mn}^{\left( e \right)} \hfill \\ &+ \;\beta_{n} \left( {C_{23}^{\left( e \right)} + C_{44}^{\left( e \right)} } \right)\frac{{dW_{mn}^{\left( e \right)} }}{dz} + \beta_{n} \frac{{dC_{44}^{\left( e \right)} }}{dz}W_{mn}^{\left( e \right)} + \rho^{\left( e \right)} \omega_{mn}^{2} V_{mn}^{\left( e \right)} = 0 \hfill \\ \end{aligned} $$

(14)

$$ \begin{gathered} - \alpha_{m} \left( {C_{13}^{\left( e \right)} + C_{55}^{\left( e \right)} } \right)\frac{{dU_{mn}^{\left( e \right)} }}{dz} - \alpha_{m} \frac{{dC_{13}^{\left( e \right)} }}{dz}U_{mn}^{\left( e \right)} - \beta_{n} \left( {C_{23}^{\left( e \right)} + C_{44}^{\left( e \right)} } \right)\frac{{dV_{mn}^{\left( e \right)} }}{dz} - \beta_{n} \frac{{dC_{23}^{\left( e \right)} }}{dz}V_{mn}^{\left( e \right)} \hfill \\ + C_{33}^{\left( e \right)} \frac{{d^{2} W_{mn}^{\left( e \right)} }}{{dz^{2} }} + \frac{{dC_{33}^{\left( e \right)} }}{dz}\frac{{dW_{mn}^{\left( e \right)} }}{dz} - \left( {\alpha_{m}^{2} C_{55}^{\left( e \right)} + \beta_{n}^{2} C_{44}^{\left( e \right)} } \right)W_{mn}^{\left( e \right)} + \rho^{\left( e \right)} \omega_{mn}^{2} W_{mn}^{\left( e \right)} = 0 \hfill \\ \end{gathered} $$

(15)

where Eqs. (13)–(15) are the equations of motion along the x, y and z-directions, respectively.

Also, the external boundary conditions on the lowermost and uppermost surfaces of the laminated plate$\left( {{\text{i}} . {\text{e}} . , { }z = - h/2,\;h/2} \right)$ reduce to,

$$ \begin{aligned}& {\text{At}}\,\,z = - h/2:\frac{{dU_{mn}^{\left( e \right)} }}{dz} + \alpha_{m} W_{mn}^{\left( e \right)} = 0,\,\frac{{dV_{mn}^{\left( e \right)} }}{dz} + \beta_{n} W_{mn}^{\left( e \right)} = 0, \\ & \alpha_{m} C_{13}^{\left( e \right)} U_{mn}^{\left( e \right)} + \beta_{n} C_{23}^{\left( e \right)} V_{mn}^{\left( e \right)} - C_{33}^{\left( e \right)} \frac{{dW_{mn}^{\left( e \right)} }}{dz} = 0 \\ \end{aligned} $$

(16a-c)

$$ \begin{aligned} &{\text{At}}\; \, z = h/2:\,\frac{{dU_{mn}^{\left( e \right)} }}{dz} + \alpha_{m} W_{mn}^{\left( e \right)} = 0,\,\;\frac{{dV_{mn}^{\left( e \right)} }}{dz} + \beta_{n} W_{mn}^{\left( e \right)} = 0 \\ & \alpha_{m} C_{13}^{\left( e \right)} U_{mn}^{\left( e \right)} + \beta_{n} C_{23}^{\left( e \right)} V_{mn}^{\left( e \right)} - C_{33}^{\left( e \right)} \frac{{dW_{mn}^{\left( e \right)} }}{dz} = \left\{ \begin{aligned}& 0&&\quad {\text{for free}}\,{\text{vibration}}\,{\text{analysis}}\,\, \hfill \\ &q_{mn} &&\, \quad {\text{for static}}\,{\text{analysis}} \hfill \\ \end{aligned} \right. \\ \end{aligned} $$

(17a-c)

where

$$ q_{mn} = - \frac{4}{ab}\sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\int_{0}^{b} {\int_{0}^{a} {q(x,y)\sin (\alpha_{m} x)\sin (\beta_{n} y)dxdy} } } } $$

(18)

The geometrical and natural compatibility conditions at the interface of two adjacent mathematical layers ‘e’ and ‘e + 1’ of the laminated plate are as follows,

$$ \begin{gathered} U_{mn}^{\left( e \right)} \left( {z_{2}^{\left( e \right)} } \right) = U_{mn}^{{\left( {e + 1} \right)}} \left( {z_{1}^{{\left( {e + 1} \right)}} } \right),\,V_{mn}^{\left( e \right)} \left( {z_{2}^{\left( e \right)} } \right) = V_{mn}^{{\left( {e + 1} \right)}} \left( {z_{1}^{{\left( {e + 1} \right)}} } \right),\,W_{mn}^{\left( e \right)} \left( {z_{2}^{\left( e \right)} } \right) = W_{mn}^{{\left( {e + 1} \right)}} \left( {z_{1}^{{\left( {e + 1} \right)}} } \right) \hfill \\ \left. {\left( {\alpha_{m} C_{13}^{\left( e \right)} U_{mn}^{\left( e \right)} + \beta_{n} C_{23}^{\left( e \right)} V_{mn}^{\left( e \right)} - C_{33}^{\left( e \right)} \frac{{dW_{mn}^{\left( e \right)} }}{dz}} \right)} \right|_{{z = z_{2}^{\left( e \right)} }} = \left( {\alpha_{m} C_{13}^{{\left( {e + 1} \right)}} U_{mn}^{{\left( {e + 1} \right)}} + \beta_{n} C_{23}^{{\left( {e + 1} \right)}} V_{mn}^{{\left( {e + 1} \right)}} } \right. \hfill \\ \left. {\left. { - C_{33}^{{\left( {e + 1} \right)}} \frac{{dW_{mn}^{{\left( {e + 1} \right)}} }}{dz}} \right)} \right|_{{z = z_{1}^{{\left( {e + 1} \right)}} }} \hfill \\ \left. {C_{55}^{\left( e \right)} \left( {\frac{{dU_{mn}^{\left( e \right)} }}{dz} + \alpha_{m} W_{mn}^{\left( e \right)} } \right)} \right|_{{z = z_{2}^{\left( e \right)} }} = \left. {C_{55}^{{\left( {e + 1} \right)}} \left( {\frac{{dU_{mn}^{{\left( {e + 1} \right)}} }}{dz} + \alpha_{m} W_{mn}^{{\left( {e + 1} \right)}} } \right)} \right|_{{z = z_{1}^{{\left( {e + 1} \right)}} }} \hfill \\ \left. {C_{44}^{\left( e \right)} \left( {\frac{{dV_{mn}^{\left( e \right)} }}{dz} + \beta_{m} W_{mn}^{\left( e \right)} } \right)} \right|_{{z = z_{2}^{\left( e \right)} }} = \left. {C_{44}^{{\left( {e + 1} \right)}} \left( {\frac{{dV_{mn}^{{\left( {e + 1} \right)}} }}{dz} + \beta_{m} W_{mn}^{{\left( {e + 1} \right)}} } \right)} \right|_{{z = z_{1}^{{\left( {e + 1} \right)}} }} \hfill \\ \end{gathered} $$

(19a-f)

where $z_{1}^{\left( k \right)}$ and $z_{2}^{\left( k \right)}$ $\left( {k = e, \, e + 1} \right)$ are the thickness coordinate of the lower and upper surfaces of the kth mathematical layer, respectively.

Due to coupling of the obtained system of equations and also since their coefficients are variable, it is very difficult to solve the above system of equations analytically. Hence, an approximate method should be employed to solve this system of equations. On the other hand, the differential quadrature method (DQM) as a simple, efficient and accurate numerical technique has been established for solving different structural problems in recent years; see for example Refs. [33–39]. It should be mentioned that this method has the advantages that discretize the strong forms of the governing equations and boundary and compatibility conditions. In addition, the boundary conditions are exactly satisfied at the boundary grid points. Thus, in this work, this numerical tool is employed to discretize the governing differential equations of motion and the related boundary and compatibility conditions of the mathematical layers in the thickness direction. According to this method, each mathematical layer is discretized into a set of $N_{z}$ grid points along the thickness direction. Using the DQM, the governing partial differential equations and the related boundary and compatibility conditions are converted into a system of algebraic equations. For brevity purpose, only the discretized form of equations of motion (13)–(15) are presented here, Eq. (13):

$$ \begin{gathered} \left( {C_{55}^{\left( e \right)} } \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {B_{ij}^{z} U_{mnj}^{\left( e \right)} } + \left( {\frac{{dC_{55}^{\left( e \right)} }}{dz}} \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} U_{mnj}^{\left( e \right)} } - \left( {\alpha_{m}^{2} C_{11}^{\left( e \right)} + \beta_{n}^{2} C_{66}^{\left( e \right)} } \right)_{i} U_{mni}^{\left( e \right)} - \alpha_{m} \beta_{n} \left( {C_{12}^{\left( e \right)} + C_{66}^{\left( e \right)} } \right)_{i} V_{mni}^{\left( e \right)} \hfill \\ + \alpha_{m} \left( {C_{13}^{\left( e \right)} + C_{55}^{\left( e \right)} } \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} W_{mnj}^{\left( e \right)} } + \alpha_{m} \left( {\frac{{dC_{55}^{\left( e \right)} }}{dz}} \right)_{i} W_{mni}^{\left( e \right)} + \rho_{i}^{\left( e \right)} \omega_{mn}^{2} U_{mni}^{\left( e \right)} = 0 \hfill \\ \end{gathered} $$

(20)

Equation (14):

$$ \begin{aligned} &- \alpha_{m} \beta_{n} \left( {C_{12}^{\left( e \right)} + C_{66}^{\left( e \right)} } \right)_{i} U_{mni}^{\left( e \right)} + \left( {C_{44}^{\left( e \right)} } \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {B_{ij}^{z} V_{mnj}^{\left( e \right)} } + \left( {\frac{{dC_{44}^{\left( e \right)} }}{dz}} \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} V_{mnj}^{\left( e \right)} } - \left( {\alpha_{m}^{2} C_{66}^{\left( e \right)} + \beta_{n}^{2} C_{22}^{\left( e \right)} } \right)_{i} V_{mni}^{\left( e \right)} \hfill \\ & + \;\beta_{n} \left( {C_{23}^{\left( e \right)} + C_{44}^{\left( e \right)} } \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} W_{mnj}^{\left( e \right)} } + \beta_{n} \left( {\frac{{dC_{44}^{\left( e \right)} }}{dz}} \right)_{i} W_{mni}^{\left( e \right)} + \rho_{i}^{\left( e \right)} \omega_{mn}^{2} V_{mni}^{\left( e \right)} = 0 \hfill \\ \end{aligned} $$

(21)

Equation (15):

$$ \begin{gathered} - \alpha_{m} \left( {C_{13}^{\left( e \right)} + C_{55}^{\left( e \right)} } \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} U_{mnj}^{\left( e \right)} } - \alpha_{m} \left( {\frac{{dC_{13}^{\left( e \right)} }}{dz}} \right)_{i} U_{mni}^{\left( e \right)} - \beta_{n} \left( {C_{23}^{\left( e \right)} + C_{44}^{\left( e \right)} } \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} V_{mnj}^{\left( e \right)} } - \beta_{n} \left( {\frac{{dC_{23}^{\left( e \right)} }}{dz}} \right)_{i} V_{mni}^{\left( e \right)} \hfill \\ + \left( {C_{33}^{\left( e \right)} } \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {B_{ij}^{z} W_{mnj}^{\left( e \right)} } + \left( {\frac{{dC_{33}^{\left( e \right)} }}{dz}} \right)_{i} \sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} W_{mnj}^{\left( e \right)} } - \left( {\alpha_{m}^{2} C_{55}^{\left( e \right)} + \beta_{n}^{2} C_{44}^{\left( e \right)} } \right)_{i} W_{mni}^{\left( e \right)} + \rho_{i}^{e} \omega_{mn}^{2} W_{mni}^{\left( e \right)} = 0 \hfill \\ \end{gathered} $$

(22)

where $i = 2, \ldots ,N_{z} - 1$; $A_{ij}^{z}$ and$B_{ij}^{z}$ represent the weighting coefficients of the first and second order derivatives along the z-direction, respectively [33–39]; also, $\left( {\frac{{dC_{13}^{\left( e \right)} }}{dz}} \right)_{i}$ means the function value at the grid point $z = z_{i}$. In a similar manner, the DQ discretized form of the boundary and compatibility conditions can be obtained. In this study, the cosine-type grid generation rule is used in the thickness direction [33–39].

After completing the DQ discretization procedure, one obtains a system of algebraic equations in the case of the static analysis, which can be solved using the conventional system of algebraic equations solver. But for the free vibration analysis, one achieves a system of algebraic eigenvalue problem. In order to reduce the computational efforts for solving this system of eigenvalue problem, the boundary and domain degrees of freedom are separated. In vector forms, they are denoted as $\left\{ {\delta_{b} } \right\}$ and $\left\{ {\delta_{d} } \right\},$ respectively. Based on these definitions, the DQ discretized form of the equations of motion and the related boundary and compatibility conditions can be represented in the matrix form as, respectively,

$$ \left[ {K_{db} } \right]\left\{ {\delta_{b} } \right\} + \left[ {K_{dd} } \right]\left\{ {\delta_{d} } \right\} - \omega_{mn}^{2} \left[ M \right]\,\left\{ {\delta_{d} } \right\} = \left\{ 0 \right\} $$

(23)

$$ \left[ {K_{bb} } \right]\left\{ {\delta_{b} } \right\} + \left[ {K_{bd} } \right]\left\{ {\delta_{d} } \right\} = \left\{ 0 \right\} $$

(24)

The elements of the stiffness matrixes $\left[ {K_{di} } \right]$ (i = b, d) and the mass matrix $\left[ M \right]$ are obtained from the discretized form of the equations of motion and those of the stiffness matrixes $\left[ {K_{bi} } \right]$ (i = b, d) are obtained from the discretized form of the related boundary and compatibility conditions.

Eliminating the boundary degrees of freedom from Eq. (24) using Eq. (23), the result reads

$$ {\kern 1pt} \left( {\,\left[ {\bar{K}} \right] - \omega_{mn}^{2} \left[ M \right]\,} \right)\,\left\{ {\delta_{d} } \right\} = \left\{ 0 \right\} $$

(25)

where $\left[ {\bar{K}} \right] = \left[ {K_{dd} } \right] - \left[ {K_{db} } \right]\left[ {K_{bb} } \right]^{ - 1} \left[ {K_{bd} } \right]$.

Solving the system of eigenvalue Eq. (25), the natural frequencies are obtained. Also, in the case of static analysis, after solving the corresponding system of algebraic equations and evaluating the displacement components, the stress components at the material points of each mathematical layer can be obtained. For this purpose, by considering$\omega_{mn} = 0$ in Eq. (12) and after substituting for the displacement components from this equation into Eq. (7) and using the DQM rule for the spatial derivative discretization, the stress component at the grid point $z = z_{i}$ of eth mathematical layer are obtained as,

$$ \begin{gathered} \left\{ {\begin{array}{*{20}c} {\sigma_{xx}^{\left( e \right)} } \\ {\sigma_{yy}^{\left( e \right)} } \\ {\sigma_{zz}^{\left( e \right)} } \\ {\sigma_{yz}^{\left( e \right)} } \\ {\sigma_{xz}^{\left( e \right)} } \\ {\sigma_{xy}^{\left( e \right)} } \\ \end{array} } \right\}_{{z = z_{i} }} = \left[ {\begin{array}{*{20}c} {C_{ 1 1}^{\left( e \right)} } & {C_{ 1 2}^{\left( e \right)} } & {C_{ 1 3}^{\left( e \right)} } & 0 & 0 & 0 \\ {C_{ 1 2}^{\left( e \right)} } & {C_{ 2 2}^{\left( e \right)} } & {C_{ 2 3}^{\left( e \right)} } & 0 & 0 & 0 \\ {C_{ 1 3}^{\left( e \right)} } & {C_{ 2 3}^{\left( e \right)} } & {C_{ 3 3}^{\left( e \right)} } & 0 & 0 & 0 \\ 0 & 0 & 0 & {C_{ 4 4}^{\left( e \right)} } & 0 & 0 \\ 0 & 0 & 0 & 0 & {C_{ 5 5}^{\left( e \right)} } & 0 \\ 0 & 0 & 0 & 0 & 0 & {C_{ 6 6}^{\left( e \right)} } \\ \end{array} } \right]_{{z = z_{i} }} \hfill \\ \quad \times\,\left\{ {\begin{array}{*{20}c} { - \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\alpha_{m} U_{mni}^{\left( e \right)} \sin \left( {\alpha_{m} x} \right)} } \sin \left( {\beta_{n} y} \right)} \\ { - \sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\beta_{n} V_{mni}^{\left( e \right)} \sin \left( {\alpha_{m} x} \right)} } \sin \left( {\beta_{n} y} \right)} \\ {\sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} W_{mnj}^{\left( e \right)} } \sin \left( {\alpha_{m} x} \right)} } \sin \left( {\beta_{n} y} \right)} \\ {\sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left( {\sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} V_{mnj}^{\left( e \right)} } + \beta_{n} W_{mni}^{\left( e \right)} } \right)\sin \left( {\alpha_{m} x} \right)} } \cos \left( {\beta_{n} y} \right)} \\ {\sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left( {\sum\limits_{j = 1}^{{N_{z} }} {A_{ij}^{z} U_{mnj}^{\left( e \right)} } + \alpha_{m} W_{mni}^{\left( e \right)} } \right)\cos \left( {\alpha_{m} x} \right)} } \sin \left( {\beta_{n} y} \right)} \\ {\sum\limits_{m = 1}^{\infty } {\sum\limits_{n = 1}^{\infty } {\left( {\beta_{n} U_{mni}^{\left( e \right)} + \alpha_{m} V_{mni}^{\left( e \right)} } \right)\cos \left( {\alpha_{m} x} \right)} } \cos \left( {\beta_{n} y} \right)} \\ \end{array} } \right\} \hfill \\ \end{gathered} $$

(26)

3 Numerical results

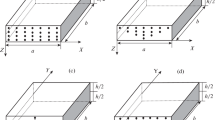
In this section, as a first step, the formulation and method of solution is validated by studying their fast rate of convergence for the static and free vibration analysis of single and multilayered laminated plates with FG-CNTRC layers. In addition, the accuracy of the approach is exhibited by performing the comparison studies with the other available solutions in the limit cases. Then, parametric study for plates with the single FG-CNTRC layer and two common types of sandwich plates, namely, the sandwich plates with FG-CNTRC lower/upper face sheets and UD-CNTRC core (model I, see Fig. 3a) and the sandwich plates with UD-CNTRC lower/upper face sheets and FG-CNTRC core (model II, see Fig. 3b) are presented. For the static analysis, the following mechanical load is considered [41],

Fig. 3

a, b Two models of sandwich plates. a Sandwich plates with FG-CNTRC lower/upper face sheets and UD core (model I), b sandwich plates with UD lower/upper face sheets and FG-CNTRC core (model II)

$$ q\left( {x,y} \right) = q_{0} \sin \left( {\frac{{\pi {\kern 1pt} x}}{a}} \right)\sin \left( {\frac{{\pi {\kern 1pt} y}}{b}} \right) $$

(27)

Also, otherwise specified, the material properties of the FG-CNTRC layers vary through the thickness according to Eqs. (2)–(4). Also, the following non-dimensional parameters are used through the numerical studies [41, 42],

$$ \xi = \frac{2z + h}{2h},\,(U,V,W) = (u,v,w)\frac{{E^{M} }}{{q_{0} h}},\,\varSigma_{ij} = \frac{{\sigma_{ij} }}{{q_{0} }}\left( {i,j = x,y,z} \right),\,\lambda_{mni} = \omega_{mni} h\sqrt {\frac{{\rho^{M} }}{{E^{M} }}} $$

(28a-d)

The material properties of FG-CNTRC layers and CNTs efficiency parameters $\eta_{j}$ (j = 1, 2, 3) are chosen from the work of Shen and Xiang [32], which are,

$$ \begin{gathered} E_{11}^{CN} = 5.6466\,{\text{TPa, }}E_{22}^{CN} = 7.0800\,{\text{TPa}},\,G_{12}^{CN} = 1.9445\,{\text{TPa}},\,\rho^{CN} = 1400\,{\text{kg/m}}^{ 3} \hfill \\ \nu_{12}^{CN} = 0.175,\,E^{M} = 2.5\,{\text{GPa}},\,\nu^{M} = 0. 3 4\hfill \\ \end{gathered} $$

For the three different values of $V_{CNT}^{*}$, the values of $\eta_{j}$ are presented in Table 1. In addition, it is assumed that $G_{13} = \,G_{12}$, $G_{23} = \,1.2G_{12}$ and$E_{33} = \,E_{22}$.

Table 1 The CNTs efficiency parameters [32]

As a first example, the convergence behavior of the present approach for the static and free vibration analysis of a single FG-CNTRC layer plate against the number of DQ grid points along the z-direction are studied in Tables 2 and 3, respectively. The influences of different types of CNTs distributions on the convergence behavior of the approach are also investigated in these tables. In Table 2, the results for the non-dimensional displacement and stress components are presented. In Table 3, the variation of the first five non-dimensional natural frequencies associated to the half wave numbers (m, n = 1, 1) of the FG-CNTRC plates verses the DQ number of grid points are given. In Table 4, the convergence behaviors of the approach against the number of mathematical layers are shown. In this table, the results for the static analysis of a single layer plate with uniformly distributed CNTs are presented. In addition, the convergence behaviors of the approach for the static and free vibration analysis of the both types of sandwich plates (i.e., models I and II) are exhibited in Tables 5 and 6, respectively. It is noticeable that in all cases, the results converge rapidly without any numerical instability by increasing the number of DQ grid points or the number of mathematical layers.

Table 2 Convergence of the results for the single layered CNTRC plates subjected to sinusoidal pressures $(a/b = 1,\;a/h = 5,\;N_{m} = 1)$

Table 3 The convergence behavior of the non-dimensional natural frequency parameters of the single layered CNTRC plates with different CNTs distribution $(a/b = 1,\;a/h = 5,\;N_{m} = 1)$

Table 4 Convergence of the results against the number of mathematical layer for the CNTRC (UD) plates $\left( {a/b = 1,\;a/h = 5,\;V_{CN}^{ * } = 0.12} \right)$

Table 5 Convergence of the results for the three layered CNTRC plates subjected to sinusoidal pressures $(a/b = 1,\;a/h = 5,\;N_{m} = 3)$

Table 6 The convergence behavior of the non-dimensional natural frequency parameters of the sandwich plates $(a/b = 1,\;a/h = 5,\;N_{m} = 3)$

In order to verify the accuracy of the formulation and the method of solution, the results for the static and free vibration analysis of the conventional FG plates, i.e. functionally graded plates with ceramic–metal constituents, are compared with those of the higher-order shear deformation theory (HSDT) of Matsunaga [41, 42] in Tables 7 and 8. He assumed that all the material properties vary according to the power law distribution as [41, 42],

$$ P\left( z \right) = P^{M} + \left( {P^{C} - P^{M} } \right)\,\left( {\frac{2z + h}{2z}} \right)^{p} $$

(29)

where P denotes a generic material property,$P^{C}$ and $P^{M}$ are the corresponding values at the top surface (ceramic rich) and bottom surface (metal rich) of the plate; p is the power law index (or the material property graded index), which is a positive real number. The material properties of the constituents are as follows [42],

$$ E^{M} = 70\;{\text{GPa}},\rho^{M} = 2 7 0 2\,\,{\text{kg/m}}^{ 3} ,\nu^{M} = 0.3,E^{C} = 380\;{\text{GPa}},\rho^{C} = 3 8 0 0\,\,{\text{kg/m}}^{ 3} ,\nu^{C} = 0.3 $$

Table 7 Accuracy of the results for the static analysis of the FG plates $\left( {a/b = 1,N_{m} = 1,N_{z} = 17} \right)$

Table 8 Comparison of the fundamental non-dimensional natural frequency parameter $\left( {\lambda_{111} } \right)$ of a FG plate $\left( {a/b = 1,\;N_{m} = 1,\;N_{z} = 11} \right)$

The non-dimensional transverse displacement W and transverse shear stress$\varSigma_{xz}$ for the two different values of the length-to-thickness ratio and also for the different values of the material graded index ‘p’ are compared with those of HSDT [41] in Table 7. Also, the non-dimensional fundamental natural frequency parameters of the FG plates for the different values of the material graded index ‘p’ and the length-to-thickness ratio of the FG plates are compared with those of the HSDT [42] in Table 8. In all cases, excellent agreement between the results of the two approaches is obvious.

In order to further verify the presented approach, in Table 9, comparison between the fundamental natural frequency parameter of the simply supported rectangular plates with single FG-CNTRC layer is made with those obtained by Zhu et al. [18] using FEM and ANSYS software. The values of $V_{CNT}^{*}$ and CNT efficiency parameter $\eta_{j}$ (j = 1, 2) are as follows [18]:

$$ \left\{ \begin{array}{llll} \eta_{1} = 0.149, &\eta_{2} = 0.934&{\text{ if }}&V_{CN}^{ * } = 0.11\, \hfill \\ \eta_{1} = 0.150,&\eta_{2} = 0.941&{\text{ if }}&V_{CN}^{ * } = 0.14 \hfill \\ \eta_{1} = 0.149,&\eta_{2} = 1.381&{\text{if }}&V_{CN}^{ * } = 0.17 \hfill \\ \end{array} \right. $$

(30)

Table 9 Comparison of the fundamental non-dimensional natural frequency parameter $\left( {\lambda_{111} = (\omega_{111} a^{2} /h)\sqrt {\rho^{M} /E^{M} } } \right)$ of FG-CNTRC plates $\left( {a/b = 1,\;N_{m} = 1,\;N_{z} = 19} \right)$

In addition, they assumed that $\eta_{3} = \eta_{2}$ and $G_{13} = \,G_{12} = G_{23}$.

The results are compared for different thickness-to-length ratio of the plate, CNTs distribution through the plate thickness and CNTs volume fraction. It can be observed that in all cases excellent agreement exists between the results of the present study and those of Zhu et al. [18], which once more validate the present approach (Table 9).

After validating the presented approach, some parametric studies are carried out to exhibit the influences of the CNTs volume fraction, different profiles of CNTs distribution through the layer thickness, lamination scheme and thickness-to-length ratio on the static and free vibration behaviors of the laminated plates with CNTRC layers.

The effects of the type of CNTs distributions on the static response of the CNTRC plates are studied by comparing the results for the single layered CNTRC plates with the different profiles of CNTs distributions in Fig. 4a–f. It can be seen that the plates with symmetric CNTs distributions (i.e., UD and FG-X cases) have lower overall stiffness than plates with asymmetric distributions ones (i.e., FG-V and FG-Λ). Both the maximum displacement and stress components of the plates with symmetric distributions are greater than those of the corresponding field variables of the plates with the asymmetric distributions ones. Also, for the cases of asymmetric distributions of the CNTs through the plate thickness (i.e., FG-V, FG-Λ), the transverse shear stresses $\left( {\varSigma_{xz} } \right)$ are also asymmetric with respect to middle surface of the plate.

Fig. 4

a–f The influence of the profile of CNTs distribution on the static response of the single layer plates $(a/h = 5,\;a/b = 1,\;N_{m} = 1,\;N_{z} = 2 5,\;\;V_{CN}^{*} = 0.12)$

The effects of the CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$ on the static response of plates with single FG-CNTRC layer (FG-X) are shown in Fig. 5a–f. One can observe from the data presented in these figures that, compromise to the other the studies on the CNTRC plate (see for example Ref. [14]), increasing the CNTs volume fraction causes increasing of the overall plate stiffness.

Fig. 5

a–f The influence of the CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$ on the static response of the single layered plates (FG-X) $(a/h = 5,\;a/b = 1,\;N_{m} = 1,\;N_{z} = 25)$

The influences of the length-to-thickness ratio on the static responses of the plates with single UD-CNTRC layer are presented in Fig. 6a–f. It is obvious that this geometrical parameter significantly changes the variation of the displacement and stress components (except the transverse normal component, $\varSigma_{zz}$) through the plate thickness. However, its effect on the transverse normal component of the stress $\left( {\varSigma_{zz} } \right)$ is small and can be ignored. It is also interesting to note that, in spite of the results based on the two-dimensional classical and the first-order shear deformation theories, the through-the-thickness variations of the in-plane normal and shear stress components $\left( {{\text{i}} . {\text{e}} . , { }\varSigma_{xx} {\text{and }}\varSigma_{xy} } \right)$ for the case of moderately thick plates is not linear. However, for the thin plates, these parameters have almost linear variations.

Fig. 6

a–f The influence of the length-to-thickness ratio on the static response of the single layered plates with uniformly distributed CNTs $(a/b = 1,\;N_{m} = 1,\;N_{z} = 25,\;V_{CN}^{*} = 0.12)$

In Fig. 7a–c, the influences of CNTs distribution through the plate thickness and also the CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$ on the first ten non-dimensional natural frequency parameters of the plates with single CNTRC layer are studied. It can be observed that in the all cases, the fundamental frequency parameters of the CNTRC plates with symmetric distributions of the CNTs are less than those of plates with asymmetric distribution ones. This again indicates that the overall stiffness of the plates with symmetric distributions of the CNTs is less than those of plates with asymmetric distributions ones, which was previously found in the static analysis. However, the higher order modes have not a regular trend and their variations depend on the value of the CNTs volume fraction. In these figures, it is obvious that both FG-V and FG-Λ distribution have the same effects on the natural frequency parameters. Also, it can be seen that increasing the values of the CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$, the non-dimensional natural frequency parameters increase, which is in agreement with those reported by other researchers [13, 14].

Fig. 7

a–c The influence of the types of CNTs distribution and volume fraction $\left( {V_{CN}^{ * } } \right)$ on the frequency parameters of the single layered plates $(m = n = 1,\;a/h = 5,\;a/b = 1,\;N_{m} = 1,\;N_{z} = 23)$

Comparison between the variation of the non-dimensional displacement and stress components along the thickness direction of the sandwich plates of models I and II and also UD-CNTRC plates are presented in Fig. 8a–f. It is obvious that the sandwich plates of model I are more stiffen than the two other types of plates.

Fig. 8

a–f Comparison between the static response of the sandwich plates and also plates with uniformly distributed CNTs $(a/h = 5,\;a/b = 1,\;N_{m} = 3,\;N_{z} = 11,\;V_{CN}^{*} = 0.12)$

The influence of the CNTs volume fraction$\left( {V_{CN}^{ * } } \right)$ on the static response of the sandwich plates of models I and II are studied in Figs. 9a–f and 10a–f, respectively. One can see that the CNTs volume fraction considerably affect the non-dimensional displacement components of the both models but the stress components of the model I are more exaggerated than those of model II.

Fig. 9

a–f The influence of the CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$ on the static response of the sandwich plates (model I) $(a/h = 5,\;a/b = 1,\;N_{m} = 3,\;N_{z} = 11)$

Fig. 10

a–f The influence of the CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$ on the static response of the sandwich plates (model II) $(a/h = 5,\;a/b = 1,\;N_{m} = 3,\;N_{z} = 11)$

The effects of the length-to-thickness ratio as an important geometrical parameter on the static response and the frequency parameters of the sandwich plates of models I and II are shown in Figs. 11a–f, Figs. 12a–f, and Table 10, respectively. It is evident from these figures that this parameter has significant effect on the non-dimensional displacement and stress components of the both types of sandwich plates. Also, the unsymmetrical nature of the transverse shear stress $\left( {\varSigma_{xz} } \right)$ for the case of thick plates (a/h = 2), specially for model I, is obvious. This is due to unsymmetrical transverse loading with respect mid-plane of the plate and for the thin-to-moderately thick plates its influence becomes negligible.

Fig. 11

a–f The influence of the length-to-thickness ratio on the static response of the sandwich plates (model I) $(a/b = 1,\;N_{m} = 3,\;N_{z} = 11,\;V_{CN}^{*} = 0.12)$

Fig. 12

a–f The influence of the length-to-thickness ratio on the static response of the sandwich plates (model II) $(a/b = 1,\;N_{m} = 3,\;N_{z} = 11,\;V_{CN}^{*} = 0.12)$

Table 10 The fundamental non-dimensional natural frequency parameters$\left( {\lambda_{mn1} } \right)$ of the sandwich plates $(a/h = 5,\;N_{m} = 3)$

Comparison between the first ten non-dimensional natural frequency parameters associated to the half wave numbers (m, n = 1, 1) of the sandwich plates and also plates with uniformly distributed CNTs (i.e., UD-CNTRC plates) are made in Fig. 13. The results are prepared for the two different values of the CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$. As one can concluded based on the results of the static analysis, since the overall stiffness of the sandwich plates of model I is greater than those of the two other types of plates, its fundamental natural frequency is also greater than those of the two other plates. But, the higher order modes of the sandwich plates of model I are less than those of the two other plates. It is interesting to note that the plates with uniformly distributed CNTs and the sandwich plate of model II, which has the uniformly distributed CNTs face sheets, have almost the same frequency parameters. It is also noticeable that the non-dimensional natural frequency parameters increase with increasing CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$ in all cases.

Fig. 13

Comparison between the frequency parameters of the sandwich plates and plates with uniformly distributed CNTs $(a/b = 1,\;m = n = 1,\;a/h = 5,\;N_{z} = 13)$

The influence of the length-to-thickness ratio on the first ten non-dimensional natural frequency parameters associated to the half wave numbers (m, n = 1, 1) of the sandwich plates are exhibited in Fig. 14. This study is conducted for the two different values of the CNTs volume fraction $\left( {V_{CN}^{ * } } \right)$. One can see that the length-to-thickness ratio has a contrary effect on the frequency parameters, i.e., the frequency parameters increase by reducing this geometrical parameter.

Fig. 14

a, b The influence of the length-to-thickness ratio on the frequency parameters of the sandwich plates $(a/b = 1,\;m = n = 1,\;a/h = 5,\;N_{m} = 3,\;N_{z} = 13)$

4 Conclusion

The three-dimensional the free vibration and static analysis of the laminated plates with FG-CNTRC layers was carried out. The effective material properties of the individual layers, which were assumed to be build up from a mixture of aligned and straight SWCNTs and an isotropic matrix, were estimated through the extended rule of mixture as a simple and convenient micromechanical model. A semi-analytical approach composed of the layerwise-differential quadrature method and the series solution was employed to accurately model the 3D variations of the displacement components in the plate thickness and in-plane directions, respectively. After studying the convergence behavior and accuracy of the method, firstly, the influences of different types of CNTs distributions through the layer thickness were examined by analyzing and comparing the results for single layer plates. Then, the static and vibration behavior of two types of sandwich plates, i.e. the sandwich plates with FG-CNTRC lower/upper face sheets (model I) and UD-CNTRC core and the sandwich plates with UD-CNTRC lower/upper face sheets and FG-CNTRC core (model II) were studied. From the obtained results, one can conclude that

• The maximum displacement and stress components of the single layered plates with symmetric CNTs distributions are greater than those of the corresponding field variables of the plates with the asymmetric CNTs distributions. But their fundamental frequency parameters are less than those of these types of plates. Hence, the plates with symmetric CNTs distributions (i.e., UD and FG-X cases) have lower overall stiffness than plates with asymmetric distributions ones. However, in all cases, by increasing the CNTs volume fraction, the overall stiffness of the plates increases.

• The length-to-thickness ratio significantly changes the variation of the displacement and stress components through the plate thickness,

• The sandwich plates with FG-CNTRC lower/upper face sheets and UD-CNTRC core (model I) are more stiffen than the sandwich plates with UD-CNTRC lower/upper face sheets and FG-CNTRC core (model II) and also plates with single UD-CNTRC layer,

• The CNTs volume fraction considerably affect the non-dimensional displacement components of the both types of sandwich plates under consideration, but its effect on the stress components of the sandwich plates of model I are more observable than those of model II,

• The through-the-thickness unsymmetrical variation of the transverse shear stress $\left( {\varSigma_{xz} } \right)$ for the case of thick plates (a/h = 2) under transverse loading, especially for the sandwich plates of model I, becomes apparent, but for the thin-to-moderately thick plates it has almost a symmetric variation,

• The fundamental natural frequency of the sandwich plates of model I is greater than those of the sandwich plates of model II and also single layered plates with uniformly distributed CNTs. But, the higher-order modes of the sandwich plates of model I are less than those of the two other types of plates,

• The sandwich plates of model II, which have the uniformly distributed CNTs face sheets, have nearly the same frequency parameters as the single layered plates with uniformly distributed CNTs.

In addition, owing to the practical significance of the 3D analysis of laminated plates with FG-CNTRC layers, and also lack of information in the open literature in this regards, the obtained results can be used as benchmark in the future researches.