Free vibration analysis of hybrid laminated plates containing multilayer functionally graded carbon nanotube-reinforced composite plies using a layer-wise formulation

Abstract

This paper studies the free vibration behavior of hybrid laminated plates using a layer-wise formulation. The laminated structures are made of graphite fiber-reinforced composite (GFRC) and multilayer functionally graded carbon nanotube-reinforced composite (FG-CNTRC) plies. The internal single-walled carbon nanotubes (SWCNTs) are distributed in layer-wise form along the ply thickness direction either uniformly or functionally graded according to four separate patterns. Both the linear and nonlinear of the CNTs distributions form are considered. Theatrical formulations are based on the first-order shear deformation theory (FSDT), and finite element method is employed to obtain the nondimensional natural frequency. The elastic modulus of both GFRC and CNTRC plies composed the hybrid laminated plate is obtained by a micromechanics model. Initially, the provided results are validated by comparing it with the literature; thereafter, a parametric study is carried out the influences of laminates configuration, number of CNTRC plies layers, CNT volume fraction, CNT distribution patterns, linear and nonlinear distribution of CNTs, plate width-to-thickness ratio, plate aspect ratio, boundary conditions, stacking sequences, and number of plies on the free vibration behavior of hybrid laminated plates. Some final remarks considering the laminated plate configuration and the distribution form of the CNT fillers are presented in order to provide a useful observation on the design criteria of the laminated composite plate structures.

1 Introduction

Due to their extremely attractive thermal, mechanical, and electrical properties, carbon nanotubes (CNTs) have been progressively introduced as an excellent reinforcement for composite materials instead of ordinary fibers [1,2,3,4,5]. The combination of a polymer matrix and CNTs or in other words carbon nanotube-reinforced composite (CNTRC), leads the nanocomposites structures to have high stiffness and high strength with a lighter weight of about four times compared to the metal material structures [6, 7]. Owing to these excellent properties, many researchers considered CNTs to be an outstanding reinforcement for advanced performance composite [8,9,10]. Qian et al. [11] revealed that only 1 % of CNTs weight fraction is able to enhance the mechanical properties of the polystyrene carbon nanotube-reinforced composite by 36–42%. Moreover, it has been noted from many published papers that dispersing the CNTs in a nonuniform way through the thickness direction can considerably enhance the mechanical behavior of the nanocomposite structures. A literature review on the recent progress of functionally graded carbon nanotube (FG-CNT)-reinforced composites and structures was reported recently by Liew et al. [12].

Inspired by the concept of functionally graded materials (FGMs) [13,14,15,16,17], Shen examined the carbon nanotubes successfully in terms of functionally graded dispersion in a polymer matrix across the thickness direction [18]. Recently, many researchers in diverse field such as science and engineering give great interest in the functionally graded CNTRC concept, as this interest has been translated into several publications over the past few years, with the aim of studying many influencing parameters, including CNT volume fraction and CNT distribution patterns for static analysis [19], forced vibration analysis [20, 21], free vibration analysis [22,23,24], buckling analysis [25,26,27], and postbuckling analysis [28, 29]. Owing to its geometrical shape, composite plate structures are very essential structural components, and they support various external forces applied to them with all efficiency and effectiveness. The plates structures are extensively used in diverse fields such as marine, civil, architectural, and aeronautical engineering, they are often subjected to varying dynamic loads that produce vibrations, so investigate the vibration behavior of those structures is an essential task for a successful application. Many investigations are reported to study the vibration behavior of CNTRC square plate [30], skew plates [31, 32], triangular plates [33], quadrilateral plates [34, 35], arbitrarily shaped plates [36], sandwich plates [37], and laminated plates [38].

Composite laminated plate structures are largely used in several structural applications due to their high mechanical performance compared to a single-layer structure. In this regard, numerous work has been carried the performance of CNTRC laminated plates. Based on the first-order shear deformation theory Lei et al. [39] investigated the bending responses of perfectly bonded FG-CNT-reinforced composite plates using the element-free kp-Ritz method. Based on the same approach Lei et al. [40] studied the buckling behavior of FG-CNT-reinforced composite laminated plate using the meshless kp-Ritz method. Shen and Xiang [41] employed the Reddy’s third-order shear deformation shell theory including the effects of the temperature change to examine the postbuckling behavior of the FG graphene platelet-reinforced composite laminated cylindrical shells subjected to thermo-mechanical load using an analytical approach. Employing the element-free kp-Ritz method, Lei et al. [42] analyzed the vibration behavior of perfectly bonded rotating laminated cylindrical panels with FG-CNT-reinforced composite layers. Malekzadeh and Zarei [43] employed the FSDT to study the free vibration characteristics of thin-to-moderately thick quadrilateral laminated plates with CNTRC layers. The authors concluded that, for both thin and moderately thick plate, the distribution of CNTs across the thickness direction corresponding to FG-X patterns leads to a stiffer composite plate then in comparison with other distribution patterns. Using a semi-analytical approach Malekzadeh and Heydarpour [44] presented the static and three-dimensional free vibration analysis of perfectly bonded laminated plates with FG-CNT-reinforced composite layers. Studying two different sandwich plates models, the authors found that the stiffness of the laminated plate affected by the plate configuration. Employing the FSDT Lei et al. [38] investigated the vibration behavior of perfectly bonded thin-to-moderately thick laminated FG-CNT-reinforced composite rectangular plates, the effect of CNT distributions patterns, CNT volume fraction, number of plate layers, and geometrical parameters were discussed. Employing a simple four-variable FSDT, Huang et al. [45] studied the free vibration and bending problems of antisymmetrically laminated FG-CNT-reinforced composite plates. The authors concluded that each of CNT volume fraction, CNT distribution types, number of layer, and geometrical parameters have a remarkable influence on the dynamic characterizations of CNTRC laminated plates.

Moreover, Fan and Wang [46] investigated the large amplitude vibration and thermal postbuckling of thermally postbuckled hybrid laminated plates containing conventional fibers and FG-CNT layers. Lei et al. [47] presented a mathematical model for nonlinear vibration analysis of a hybrid laminated plate composed of CNTRC layers and GFRC layers. In their investigation, the different distribution types of CNTs, matrix cracks density, CNT volume fraction, number of layers, and geometry parameters were considered. Lei et al. [48] studied the banding and vibration behavior of both cracked and un-cracked hybrid laminated plates containing graphite fiber-reinforced composite layers and FG-CNT-reinforced composite layers. The authors presented a detailed parametric study to investigate the influence of material parameters, boundary condition, and geometrical parameters on banding and vibration responses of the laminated hybrid plate. Using the FSDT, Pan et al. [49] proposed a model for geometrically nonlinear large deformation behaviors of matrix cracked hybrid composite double-curved deep shell composed of graphite fiber-reinforced composite layers and FG-CNT-reinforced composite layers. Comparing the two models of sandwich plates the authors concluded that for the design process it is important to take into consideration crack influence in the matrix for the nonlinear deflection response. In addition, comparing between two plate structure types the authors found that the laminated shell configuration can improve the resisting of deformation under external loadings.

The present paper aims to study the free vibration behavior of hybrid laminated plates that contain multilayer CNTRC and GFRC plies, with multiple plate configuration employing a layer-wise formulation. The FSDT is employed to characterize the displacement fields in the hybrid composite plate. The elastic modulus of both GFRC and CNTRC plies is estimated based on micromechanics model. The parametric investigations are examined to exhibit the effect of plate configuration, CNT volume fraction, CNT destruction patterns, linear and nonlinear distribution of CNTs, number of CNTRC ply’ layers, boundary condition, and the number of plate’ plies on the free vibration behavior of hybrid laminated plate.

2 Problem formulation

2.1 Geometrical and CNT distribution pattern characterization

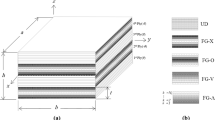
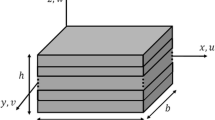
A perfectly bonded hybrid laminated plate with length (a), width (b), and total thickness (h) is taken under consideration in the current study. The hybrid laminated plate is defined in a three-dimensional coordinate system (x, y, z) in which x-, y-, and z-axes are, respectively, parallel to the length, width, and thickness direction, as depicted in Fig. 1a. It is assumed that the hybrid laminated plates consist of $(P_{t})$ plies in which each ply is either made of CNTRC or GFRC. The CNTRC plies are divided into $(N_{L})$ layers in which each layer has the same thickness $(\Delta h=t \big / {N_{L} })$ where t is the CNTRC ply thickness. It is assumed that each individual layer of the CNTRC plies has a uniform dispersion of CNT fillers in the plane (x, y) embedded in a polymer matrix and a different amount of it from layer to layer across the ply thickness. So far, five different distributions patterns, denoted by UD, FG-V, FG-$\Lambda$, FG-O, and FG-X are considered in the present study as depicted in Fig. 1b. The CNT volume fraction shows a layer-wise change in order to shape the functionally graded structure; accordingly, the CNT volume fraction of the kth CNTRC ply’ layer $(f_\mathrm{CNT}^{(k)} )$ for the five CNT distribution patterns is given as follows [50]:

$$\begin{aligned} \hbox {UD}: f_\mathrm{CNT}^{(k)}= & {} f_\mathrm{CNT}^{*} \end{aligned}$$

(1)

$$\begin{aligned} \hbox {FG-V}: f_\mathrm{CNT}^{(k)}= & {} f_\mathrm{CNT}^{*} (\text{ P}_{\text{ in }} +1)\left( {\frac{k-0.5}{N_{L} }} \right) ^{\text{ P}_{\text{ in }} } \end{aligned}$$

(2)

$$\begin{aligned} \hbox {FG-}\Lambda : f_\mathrm{CNT}^{(k)}= & {} f_\mathrm{CNT}^{*} (P_\mathrm{in} +1)\left( {\frac{0.5-k+N_{L} }{N_{L} }} \right) ^{P_\mathrm{in} } \end{aligned}$$

(3)

$$\begin{aligned} \hbox {FG-O} : f_\mathrm{CNT}^{(k)}= & {} f_\mathrm{CNT}^{*} (P_{\text{ in }} +1)\left( {\frac{1-\left| {2k-N_{L} -1} \right| }{N_{L} }} \right) ^{P_{\text{ in }} } \end{aligned}$$

(4)

$$\begin{aligned} \hbox {FG-X}~: f_\mathrm{CNT}^{(k)}= & {} f_\mathrm{CNT}^{*} (P_\mathrm{in} +1)\left( {\frac{\left| {2k-N_{L} -1} \right| }{N_{L} }} \right) ^{P_\mathrm{in} } \end{aligned}$$

(5)

in which $k=1,2,3 \ldots N_{L} ,$ $\hbox {P}_{\mathrm {in}}$ denote the power-law index or (the index that controls the distribution form of the CNT fillers) and $f_\mathrm{CNT}^{*}$is the total volume fraction, which is given as follows:

$$\begin{aligned} f_\mathrm{CNT}^{*} =\frac{w_\mathrm{CNT} }{w_\mathrm{CNT} +({\rho ^\mathrm{CNT}} \big / {\rho ^{m}})(1-w_\mathrm{CNT} )} \end{aligned}$$

(6)

where $w_\mathrm{CNT}$ is the mass fraction of CNTs ; and $\rho ^\mathrm{CNT}$ and $\rho ^{m}$ denote, respectively, the mass density of the CNT fillers and polymer matrix. It should be noted that for all five distribution patterns the total volume fraction is the same.

Figure 2 shows the variation of the CNT volume fraction ratio $({f_\mathrm{CNT}^{(k)} }\big / {f_\mathrm{CNT}^{*} })$ along the thickness direction of a single ply of CNTRC plate with different CNT distribution patterns and power-law indexes. As can be seen the plates with UD pattern represent a special case, where the CNT fillers are distributed homogeneously across the thickness direction of the plate, which leads to an unchanged ${f_\mathrm{CNT}^{(k)} } \big / {f_\mathrm{CNT}^{*} }$ for all values of z/h. As for the nonuniform distribution types, which are FG-$\Lambda$, FG-V, FG-O, and FG-X patterns the CNT fillers dispersed in linear ($\hbox {P}_{\mathrm {in}}=1$) and nonlinear ($\hbox {P}_{\mathrm {in}}= 0.4, 0.8, 1.4, and 1.8$) form, respectively, either from the plate’ bottom surface to the top, from the plate’ top surface to the bottom, from the mid-plane of the plate to the top, and bottom surfaces or from the top and bottom surfaces to the mid-plane of the plate. In addition, one can see that the CNT volume fraction ratios ${f_\mathrm{CNT}^{(k)} } \big / {f_\mathrm{CNT}^{*} }$ change in a symmetrical way for the plates with UD, FG-O, and FG-X patterns and unsymmetrical way for the plates with FG-V and FG-$\Lambda$ patterns.

It is noteworthy that the combined plates are named by meeting the letter of the CNT distribution type denoted by ($\Lambda$, V, O, X, and UD) or GFRC denoted by (F) of each ply. For example, the laminate configuration shown in Fig. 1 [$\Lambda$-F-V-F], means that the first ply from the bottom surface of the laminated plate to the top has FG-$\Lambda$ distribution pattern, the second ply is made with GFRC, the third ply is made with FG-V distribution pattern, and the fourth ply is made with GFRC.

Since the under consideration composite hybrid laminated plates contain plies of CNTRC and GFRC, in the following, we will consider two different micromechanics models to describe the mechanical properties of each of these two compounds.

2.2 Mechanical priorities of the GFRC plies

Employing the micromechanical model, the material properties of GFRC plies can be expressed as [51]:

$$\begin{aligned} E_{11}= & {} f_{F} E_{11}^{F} +f_{m} E^{m} \end{aligned}$$

(7)

$$\begin{aligned} \frac{1}{E_{22} }= & {} \frac{f_{F} }{E_{22}^{F} }+\frac{f_{m} }{E^{m}}-f_{F} f_{m} \frac{{f_{F}^{^{2}} E^{m}} \big / {E_{22}^{F} +{f_{m}^{^{2}} E_{22}^{F} } \big / {E^{m}}-2\nu ^{F}\nu ^{m}}}{f_{F} E_{22}^{F} +f_{m} E^{m}} \end{aligned}$$

(8)

$$\begin{aligned} \frac{1}{G_{12} }= & {} \frac{f_{F} }{G_{12}^{F} }+\frac{f_{m} }{G^{m}} \end{aligned}$$

(9)

$$\begin{aligned} \rho= & {} f_{F} \rho ^{F}+f_{m} \rho ^{m} \end{aligned}$$

(10)

$$\begin{aligned} \nu _{12}= & {} f_{F} \nu ^{F}+f_{m} \nu ^{m} \end{aligned}$$

(11)

where $E, \quad G,$ and $\nu$ are, respectively, Young’s modulus, shear modulus, and Poisson’s ratio.

And (m) denotes matrix, while (F) denotes graphite fiber.

Related by the following relationship $f_{m} +f_{F} =1$, $f_{m}$ and $f_{F}$ are, respectively, the volume fractions of the matrix and graphite fibers.

Fig. 1

a Coordinate system and geometry of perfectly bounded hybrid laminated plate composed of GFRC and CNTRC plies; b different distribution types of the CNT fillers

Fig. 2

Variation of the CNT volume fraction ratio $({f_\mathrm{CNT}^{(z)} } \big / {f_\mathrm{CNT}^{*} })$ across the CNTRC plate thickness for different CNT distribution patterns

3 Mechanical properties of the CNTRC plies

According to the extended rule of mixture [52] the effective proprieties of the kth CNTRC ply’ layer are given by [18]:

$$\begin{aligned} E_{11}^{(k)}= & {} \eta _{1} f_\mathrm{CNT}^{(k)} E_{11}^\mathrm{CNT} +f_{m}^{(k)} E_{m} \end{aligned}$$

(12)

$$\begin{aligned} \frac{\eta _{2} }{E_{22}^{(k)} }= & {} \frac{f_\mathrm{CNT}^{(k)} }{E_{22}^\mathrm{CNT} }+\frac{f_{m}^{(k)} }{E_{m} } \end{aligned}$$

(13)

$$\begin{aligned} \frac{\eta _{3} }{G_{12}^{(k)} }= & {} \frac{f_\mathrm{CNT}^{(k)} }{G_{12}^\mathrm{CNT} }+\frac{f_{m}^{(k)} }{G_{m} } \end{aligned}$$

(14)

$$\begin{aligned} \nu _{12}^{(k)}= & {} f_\mathrm{CNT}^{*} \nu _{12}^\mathrm{CNT} +f_{m}^{(k)} \nu _{m} \end{aligned}$$

(15)

$$\begin{aligned} \rho ^{(k)}= & {} f_\mathrm{CNT}^{(k)} \rho ^\mathrm{CNT}+f_{m}^{(k)} \rho _{m} \end{aligned}$$

(16)

where (m) and (CNT) denote, respectively, the polymer matrix and carbon nanotubes. The parameter $\eta _{j} (j=1, 2, 3)$ represents the CNT efficiency parameters, which are used in order to deal with the small-scale effect [18]. Related by $f_\mathrm{CNT} +f_{m} =1$, $f_{m}$ and $f_\mathrm{CNT}$ are, respectively, the volume fraction of the matrix and the CNT.

3.1 Governing equations for laminated plate

Based on the first-order shear deformation plate theory FSDT [53] the displacement field at an arbitrary point M(x, y, z) in the ply is expressed as follows:

$$\begin{aligned} u(x,y,z)= & {} u_{0} (x,y)+z\theta _{x} (x,y) \nonumber \\ v(x,y,z)= & {} v_{0} (x,y)+z\theta _{y} (x,y) \nonumber \\ w(x,y,z)= & {} w_{0} (x,y) \end{aligned}$$

(17)

where $u_{0} (x,y)$, $v_{0} (x,y)$, and $w_{0} (x,y)$ denote the displacements component of a point on the mid-plane of the ply and $\theta _{x} \theta _{y}$ are, respectively, the rotations of the cross section of the ply about y- and x-axes.

According to the FSDT, the strain–displacement relations are expressed as follows:

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{y} } \\ {\varepsilon _{xy} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{(0)} } \\ {\varepsilon _{y}^{(0)} } \\ {\gamma _{xy}^{(0)} } \\ \end{array} }} \right\} +z\left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{(1)} } \\ {\varepsilon _{y}^{(1)} } \\ {\gamma _{xy}^{(1)} } \\ \end{array} }} \right\} , \quad \left\{ {{\begin{array}{*{20}c} {\gamma _{yz} } \\ {\gamma _{xz} } \\ \end{array} }} \right\} =\gamma ^{(0)} \end{aligned}$$

(18)

where

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{(0)} } \\ {\varepsilon _{y}^{(0)} } \\ {\gamma _{xy}^{(0)} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\frac{\partial u_{0} }{\partial x}} \\ {\frac{\partial v_{0} }{\partial y}} \\ {\frac{\partial u_{0} }{\partial y}+\frac{\partial v_{0} }{\partial x}} \\ \end{array} }} \right\} , \left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{(1)} } \\ {\varepsilon _{y}^{(1)} } \\ {\gamma _{xy}^{(1)} } \\ \end{array} }} \right\} =\left\{ {{\begin{array}{*{20}c} {\frac{\partial \theta _{x} }{\partial x}} \\ {\frac{\partial \theta _{y} }{\partial y}} \\ {\frac{\partial \theta _{x} }{\partial y}+\frac{\partial \theta _{y} }{\partial x}} \\ \end{array} }} \right\} , \gamma ^{(0)}=\left\{ {{\begin{array}{*{20}c} {\frac{\partial w_{0} }{\partial y}+\theta _{y} } \\ {\frac{\partial w_{0} }{\partial x}+\theta _{x} } \\ \end{array} }} \right\} \end{aligned}$$

(19)

Then, the stress–strain constitutive relations of the ply can be expressed as:

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\sigma _{x} } \\ {\sigma _{y} } \\ {\sigma _{xy} } \\ {\sigma _{yz} } \\ {\sigma _{xz} } \\ \end{array} }} \right\} =\left[ {{\begin{array}{*{20}c} {Q_{11} } &{}\quad {Q_{12} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {Q_{12} } &{}\quad {Q_{22} } &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {Q_{44} } &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {Q_{55} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {Q_{66} } \\ \end{array} }} \right] \left\{ {{\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{y} } \\ {\gamma _{xy} } \\ {\gamma _{yz} } \\ {\gamma _{xz} } \\ \end{array} }} \right\} \end{aligned}$$

(20)

where

$$\begin{aligned} Q_{11} =\frac{E_{11} }{1-\upsilon _{12} \upsilon _{21} }, Q_{12} =\frac{\upsilon _{21} E_{11} }{1-\upsilon _{12} \upsilon _{21} }, Q_{22} =\frac{E_{22} }{1-\upsilon _{12} \upsilon _{21} }, Q_{66} =G_{13} , Q_{55} =G_{23} , Q_{44} =G_{12} , \end{aligned}$$

(21)

The strains–stress relationships are defined as:

$$\begin{aligned}&\left\{ {{\begin{array}{*{20}c} {N_{x} } \\ {N_{y} } \\ {N_{xy} } \\ \end{array} }} \right\} =[A]\left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{(0)} } \\ {\varepsilon _{y}^{(0)} } \\ {\gamma _{xy}^{(0)} } \\ \end{array} }} \right\} +[B]\left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{(1)} } \\ {\varepsilon _{y}^{(1)} } \\ {\gamma _{xy}^{(1)} } \\ \end{array} }} \right\} , \end{aligned}$$

(22)

$$\begin{aligned}&\left\{ {{\begin{array}{*{20}c} {M_{x} } \\ {M_{y} } \\ {M_{xy} } \\ \end{array} }} \right\} =[B]\left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{(0)} } \\ {\varepsilon _{y}^{(0)} } \\ {\gamma _{xy}^{(0)} } \\ \end{array} }} \right\} +[D]\left\{ {{\begin{array}{*{20}c} {\varepsilon _{x}^{(1)} } \\ {\varepsilon _{y}^{(1)} } \\ {\gamma _{xy}^{(1)} } \\ \end{array} }} \right\} , \end{aligned}$$

(23)

$$\begin{aligned}&\left\{ {{\begin{array}{*{20}c} {Q_{y} } \\ {Q_{x} } \\ \end{array} }} \right\} =k_{s} [F]\left\{ {{\begin{array}{*{20}c} {\gamma _{yz} } \\ {\gamma _{xz} } \\ \end{array} }} \right\} , \end{aligned}$$

(24)

where

N, M,  and Q are respectively the total in plane forces, moment resultants and shear forces,

taken to be 5/6, $k_{s}$ is the shear correction coefficient.

And

$A_{ij} , \quad B_{ij} , \quad D_{ij}$, and $F_{ij}$ are the stiffness elements given as:

$$\begin{aligned}&\begin{array}{l} (A_{ij} ,B_{ij} ,D_{ij} )=\sum \limits _{k=1}^{P_{t} } {\int \limits _{z_{k} }^{z_{k+1} } {Q_{_{ij} }^{(k)} (1,z,z^{2}) } } dz, (i,j=1,2,6) \\ \\ \end{array} \end{aligned}$$

(25)

$$\begin{aligned}&F_{ij} =k_{s} \sum \limits _{k=1}^{P_{t} } {\int \limits _{z_{k} }^{z_{k+1} } {Q_{_{ij} }^{(k)} } } dz, (ij=4,5) \end{aligned}$$

(26)

$$\begin{aligned}&\qquad =k_{s} \sum \limits _{k=1}^{P_{t} } {\int \limits _{z_{k} }^{z_{k+1} } {Q_{_{ij} }^{(k)} } } dz, (j=4,5) \end{aligned}$$

(27)

3.2 Finite element formulation

A nine-noded isoperimetric element based on the Mindlin–Reissner plate theory was employed in the current study. It is noteworthy that the approach takes into consideration the effect of transverse shear deformation. Each node of the element has five degrees of freedom $(u_{i} ,v_{i} ,w_{i} ,\theta _{yi} ,\theta _{xi} )$, and the generalized displacement through the element can be expressed as:

$$\begin{aligned} u_{0} =\sum \limits _{i=1}^9 {N_{i} u_{0i} } , \quad v_{0} =\sum \limits _{i=1}^9 {N_{i} v_{0i} } , \quad w_{0} =\sum \limits _{i=1}^9 {N_{i} w_{0i} } , \quad \theta _{x} =\sum \limits _{i=1}^9 {N_{i} \theta _{x\,i} } , \quad \theta _{y} =\sum \limits _{i=1}^9 {N_{i} \theta _{y\,i} } \end{aligned}$$

(28)

where $N_{i}$ is the shape function

Based on the standard finite element procedure the governing equations for the free vibration of the hybrid laminated plate take the following form [54]:

$$\begin{aligned} K\delta +M\ddot{{\delta }}=0 \end{aligned}$$

(29)

where K denotes the stiffness matrix and M is the mass matrix , $\ddot{{\delta }}$ and $\delta$ are, respectively, the global acceleration and displacement vectors,

and

$$\begin{aligned}{}[k_{e} ]= & {} \int \limits _{\Lambda _{e} } {[B]}^{T}[C][B]d\Lambda _{e} \end{aligned}$$

(30)

$$\begin{aligned}{}[M_{e} ]= & {} \int \limits _{\Lambda _{e} } {[N]}^{T}[\bar{{m}}][N]d\Lambda _{e} \end{aligned}$$

(31)

where

$$\begin{aligned} C= & {} \left[ {{\begin{array}{*{20}c} A &{}\quad B &{}\quad 0 \\ B &{}\quad D &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad F \\ \end{array} }} \right] ,\bar{{m}}=\left[ {{\begin{array}{*{20}c} {I_{0} } &{}\quad 0 &{}\quad 0 &{}\quad {I_{1} } &{}\quad 0 \\ 0 &{}\quad {I_{0} } &{}\quad 0 &{}\quad 0 &{}\quad {I_{1} } \\ 0 &{}\quad 0 &{}\quad {I_{0} } &{}\quad 0 &{}\quad 0 \\ {I_{1} } &{}\quad 0 &{}\quad 0 &{}\quad {I_{2} } &{}\quad 0 \\ 0 &{}\quad {I_{1} } &{}\quad 0 &{}\quad 0 &{}\quad {I_{2} } \\ \end{array} }} \right] \end{aligned}$$

(32)

$$\begin{aligned}{}[B_{i} ]= & {} \left[ {{\begin{array}{*{20}c} {\frac{\partial N_{i} }{\partial x}} &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad {\frac{\partial N_{i} }{\partial y}} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ {\frac{\partial N_{i} }{\partial y}} &{}\quad {\frac{\partial N_{i} }{\partial y}} &{}\quad 0 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {\frac{\partial N_{i} }{\partial x}} &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad 0 &{}\quad {\frac{\partial N_{i} }{\partial y}} \\ 0 &{}\quad 0 &{}\quad 0 &{}\quad {\frac{\partial N_{i} }{\partial x}} &{}\quad {\frac{\partial N_{i} }{\partial x}} \\ 0 &{}\quad 0 &{}\quad {\frac{\partial N_{i} }{\partial x}} &{}\quad {N_{i} } &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad {\frac{\partial N_{i} }{\partial y}} &{}\quad 0 &{}\quad {N_{i} } \\ \end{array} }} \right] \end{aligned}$$

(33)

in which $\Lambda _{e}$ is the elementary surface, and $C\bar{{m}}$,,B are, respectively, the elasticity, the inertia, and the strain interpolation matrices.

The inertia-associated terms are defined by:

$$\begin{aligned} I_{i} =\sum \limits _{k=1}^{P_{t} } {\int \limits _{z_{k} }^{z_{k+1} } {z^{i}\rho ^{(k)}dz} } ,(i=0,1,2) \end{aligned}$$

(34)

Assuming that the composite plate undergoes a harmonic motion (given that we dealing with a free vibration analysis), Eq. (29) turns into a generalized eigenvalue problem, where the dynamic properties, frequencies $({\omega })$, and mode shapes $(\bar{{\delta }})$ can be obtained by solving the following relation:

$$\begin{aligned} (K-{\omega }^{2}M)\bar{{\delta }}=0 \end{aligned}$$

(35)

The following homogeneous boundary conditions (BCs) are employed to analyze the present investigation:

• I. Simply supported edge (S):

  • Cross-ply laminate:

At $x \quad =$ 0, a:$v_{0} =w_{0} =\theta _{y} =0$.

At $y=$ 0, b: $u_{0} =w_{0} =\theta _{x} =0.$

• Angle-ply laminate:

At $x \quad =$ 0, a :$u_{0} =w_{0} =\theta _{y} =0$,

At $y=$ 0, b: $v_{0} =w_{0} =\theta _{x} =0.$

• II. Clamped edge (C):

On all edges $u_{0} =v_{0} =w_{0} =\theta _{x} =\theta _{y} =0$, for both cross-ply and angle-ply laminate.

Table 1 Comparisons of the fundamental nondimensional frequency $({\bar{{\omega }}}={\omega }\sqrt{{\rho _{c} } \big / {E_{c} }} )$ of SSSS $\hbox {AL}/\hbox {AL}_{\mathrm {2}}\hbox {O}_{\mathrm {3}}$ FGM plate with different power-law index, width-to-thickness ratio, and mesh sizes

Table 2 Comparisons of the first six nondimensional frequency $({\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}}/0^{\mathrm {0}}/90^{\mathrm {0}}/0^{\mathrm {0}})$ laminated CNTRC plates with two type of boundary conditions for $a/b=1$, $b/h=10$, $N_{L}=20$ and $f_\mathrm{CNT}^{*} =0.11$

Table 3 Comparisons of the fundamental nondimensional frequency $({\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}})_{\mathrm {n}}$ and angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}})_{\mathrm {n}}$ laminated CNTRC plates with different number of lyres for $a/b=$1, $b/h=$50, $N_{L}=20$, and $f_\mathrm{CNT}^{*} =0.11$

Fig. 3

Effect of number of layers on the nondimensional frequency ${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}}$ for single ply of CNTRC plate

Table 4 Fundamental nondimensional frequency (${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of cross-ply $(0^{\mathrm {C}}/90^{\mathrm {F}})_{\mathrm {n}}$ hybrid laminated composite plates with various values of CNT volume fraction ($a/b=1$, $b/h=10$)

Table 5 Fundamental nondimensional frequency $({\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of cross-ply $(0^{\mathrm {C}}/90^{\mathrm {F}})_{\mathrm {n}}$ hybrid laminated composite plates with various values of plate width-to-thickness ratio ($a/b=1$, $f_\mathrm{CNT}^{*} =0.11)$

Table 6 Fundamental nondimensional frequency (${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of cross-ply $(0^{\mathrm {C}}/90^{\mathrm {F}})_{\mathrm {n}}$ hybrid laminated composite plates with various values of plate aspect ratio ($b/h=10$, $f_\mathrm{CNT}^{*} =0.11)$

Table 7 Fundamental nondimensional frequency (${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of angle-ply ($45^{\mathrm {C}}/-45^{\mathrm {F}})_{\mathrm {n}}$ hybrid laminated composite plates with various values of CNT volume fraction ($a/b=1$, $b/h=10$)

Table 8 Fundamental nondimensional frequency $({\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of angle-ply ($45^{\mathrm {C}}/-45^{\mathrm {F}})_{\mathrm {n}}$ hybrid laminated composite plates with various values of plate width-to-thickness ratio ($a/b=1$, $f_\mathrm{CNT}^{*} =0.11$)

Table 9 Fundamental nondimensional frequency (${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of angle-ply ($45^{\mathrm {0}}/-45^{\mathrm {0}})_{\mathrm {n}}$ hybrid laminated composite plates with various values of plate aspect ratio ($b/h=10$, $f_\mathrm{CNT}^{*} =0.11$)

Table 10 First six nondimensional frequency $({\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}})$ hybrid laminated composite plates with various plate configuration ($a/b=1$, $b/h=10$, and $f_\mathrm{CNT}^{*} =0.11$ )

Table 11 First six nondimensional frequency (${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}})$ hybrid laminated composite plates with various plate configuration ($a/b=1$, $b/h=10$ and $f_\mathrm{CNT}^{*} =0.11$ )

Table 12 First six nondimensional frequency (${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}})$ CNTRC laminated composite plates with various plate configuration ($a/b=1$, $b/h=50$, and $f_\mathrm{CNT}^{*} =0.11$ )

Table 13 First six nondimensional frequency (${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}})$ CNTRC laminated plates with various plate configuration ($a/b=1$, $b/h=50$ and $f_\mathrm{CNT}^{*} =0.11$ )

Table 14 Fundamental nondimensional frequency (${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of cross-ply $(0^{\mathrm {C}}/90^{\mathrm {F}}/0^{\mathrm {C}}/90^{\mathrm {F}})$ hybrid laminated composite plates with various values of power-law index and CNT volume fraction ($a/b=1$, $b/h=10$)

Table 15 Fundamental nondimensional frequency $({\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} )$ of angle-ply $(45^{\mathrm {C}}/-45^{\mathrm {F}}/45^{\mathrm {C}}/-45^{\mathrm {F}})$ hybrid laminated composite plates with various values of power-law index and CNT volume fraction ($a/b=1$, $b/h=10$)

Fig. 4

The percentage increase in the fundamental frequency(${\Delta \bar{{\omega }}=}{\text{100 }\times {(\bar{{\omega }}}_{\text{ p }} \text{- } {\bar{{\omega }}}_{\text{ u }} \text{) }} \big / {{\bar{{\omega }}}_{\text{ u }} })$ of cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}}/0^{\mathrm {0}}/90^{\mathrm {0}})$ hybrid laminated plate verses the power-law index $\hbox {P}_{\mathrm {in}}$ with different boundary conditions and plate configurations ($b/h=10$, $a/b=1.0$)

Fig. 5

The percentage increase in the fundamental frequency(${\Delta \bar{{\omega }}=}\text{100 }\times (\bar{{\omega }}_{\text{ p }} \text{- } {\bar{{\omega }}}_{\text{ u }} ) \big / {{\bar{{\omega }}}_{\text{ u }} })$ of angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}}/45^{\mathrm {0}}/-45^{\mathrm {0}})$ hybrid laminated plate verses the power-law index $\hbox {P}_{\mathrm {in}}$ with different boundary conditions and plate configurations ($b/h=10$, $a/b=1.0$)

Fig. 6

Effect of orientation angle $\theta$ on the fundamental frequency ${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}}$ of SSSS angle-ply $(\theta /- \quad \theta / \quad \theta /- \quad \theta )$ hybrid laminate plates with different values of CNT volume fraction and plate configuration ($a/b=1$ and $b/h=10$)

Fig. 7

Effect of orientation angle $\theta$ on the fundamental frequency ${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}}$ of CCCC angle-ply $(\theta /- \quad \theta / \quad \theta /- \quad \theta )$ hybrid laminate plates with different values of CNT volume fraction and plate configuration ($a/b=1$ and $b/h=10$)

Fig. 8

Effect of orientation angle $\theta$ on the fundamental frequency ${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}}$ of SSSS angle-ply $(\theta /- \quad \theta / \quad \theta /- \quad \theta )$ hybrid laminate plates with different width-to-thickness ratio and plate configuration ($a/b=1$ and $f_\mathrm{CNT}^{*} =0.11)$

Fig. 9

Effect of orientation angle $\theta$ on the fundamental frequency ${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}}$ of CCCC angle-ply $(\theta /- \quad \theta / \quad \theta /- \quad \theta )$ hybrid laminate plates with different width-to-thickness ratio and plate configuration ($a/b=1$ and $f_\mathrm{CNT}^{*} =0.11)$

Fig. 10

Effect of orientation angle $\theta$ on the fundamental frequency ${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}}$ of SSSS angle-ply $(\theta /- \quad \theta / \quad \theta /- \quad \theta )$ hybrid laminate plates with different length-to-width ratio and plate configuration ($b/h=10$ and $f_\mathrm{CNT}^{*} =0.11)$

Fig. 11

Effect of orientation angle $\theta$ on the fundamental frequency ${\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}}$ of CCCC angle-ply $(\theta /- \quad \theta / \quad \theta /- \quad \theta )$ hybrid laminate plates with different length-to-width ratio and plate configuration ($b/h=10$ and $f_\mathrm{CNT}^{*} =0.11$)

Fig. 12

The first six three-dimensional mode shapes of angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}}/45^{\mathrm {0}}/-45^{\mathrm {0}})$ hybrid laminated plate with SSSS boundary condition and [$\Lambda$-F-V-F] configuration. a Mode 1, b Mode 2, c Mode 3, d Mode 4, e Mode 5, f Mode 6

Fig. 13

The first six three-dimensional mode shapes of angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}}/45^{\mathrm {0}}/-45^{\mathrm {0}})$ hybrid laminated plate with CCCC boundary condition and [$\Lambda$-F-V-F] configuration. a Mode 1, b Mode 2, c Mode 3, d Mode 4, e Mode 5, f Mode 6

4 Numerical results and discussion

A detailed parametric analysis is conducted to study the effect of the laminated plate configuration and the CNT fillers distribution form on the free vibration behavior of hybrid laminated plates. In the current study, different level of CNT volume fraction, power-law index, geometry parameter, as well as plates stacking sequence, boundary conditions and ply’ number, are taken into account as a parameter under investigation. Before performing the numerical examples, it is required to determine the material properties of both CNTRC and GFRC plies. It is assumed that the poly(m-phenylenevinylene)-co-[(2,5-dioctoxy-p-phenylene) vinylene] (PmPV) polymer is chosen as a matrix for both CNTRC and GFRC plies, and the properties of the polymer matrix are taken to be $E^{m}=2.1 \text{ GPa },\nu ^{m}=0.34,\rho ^{m}=1150\text{ kg/m}^{\text{3 }}$. As a reinforcement in the CNTRC plies, the (10, 10) single-walled carbon nanotubes (SWCNTs) are chosen, whose properties are: $E_{11}^\mathrm{CNT} =5646.6 \text{ GPa, }E_{22}^\mathrm{CNT} =7080.0 \text{ GPa, }G_{22}^\mathrm{CNT} =1944.5 \text{ GPa, }\nu _{12}^\mathrm{CNT} =0.175,\rho ^\mathrm{CNT}=1400 \text{ kg/m}^{\text{3 }}$. The CNTs efficiency parameters corresponding to the CNT volume fraction ($=$0.11, 0.14, and 0.17) are $\eta _{1} =0.149, \eta _{2} =0.934, \eta _{3} =0.934,$for the case of $f_\mathrm{CNT}^{*} =0.11,$and $\eta _{1} =0.150, \eta _{2} =0.941, \eta _{3} =0.941,$for the case of $f_\mathrm{CNT}^{*} =0.14,$and $\eta _{1} =0.149, \eta _{2} =1.381, \eta _{3} =1.381,$for the case of $f_\mathrm{CNT}^{*} =0.17$. It is assumed that $G_{12} =G_{13} =G_{23}$ for the plies made with CNTRC$_{\mathrm {.}}$ Meanwhile, the graphite fibers are selected to be the reinforcement phase for the GFRC plies, whose properties are: $E_{11}^{F} =233.05 \text{ GPa, } \quad E_{22}^{F} =23.1 \text{ GPa, }G_{12}^{F} =8.96 \text{ GPa, }\nu ^{F}=0.2,\rho ^{F}=1750 \text{ kg/m}^{\text{3 }}$. It is assumed that $G_{12} =G_{13} \text{ and } G_{23} =1.2G_{12}$ for the plies made with GFRC. The volume fraction of the graphite fibers and the polymer matrix is, respectively, 0.6 and 0.4. In the following numerical applications, the ith nondimensional frequency parameter is given by [38]

$$\begin{aligned} {\bar{{\omega }}}={\omega } ({b^{2}} \big / h)\sqrt{{\rho ^{m}} \big / {E^{m}}} \end{aligned}$$

(36)

It should be noted that the power-law index $\hbox {P}_{\mathrm {in}}$ is taken to be 1.0 in the current paper unless otherwise specified.

4.1 Comparison studies

For the purpose of evaluating the accuracy and the reliability of the present approach, three test examples are performed. All of them are tested for the free vibration of composite plate structure.

The fundamental nondimensional frequency $({\bar{{\omega }}}={\omega }\sqrt{{\rho _{c} } \big / {E_{c} }} )$ of square SSSS functionally graded material (FGM) plate is compared in Table 1 with the results reported by Matsunaga [55] through the higher-order shear deformation theory and by Song et al. [56] employing the FSDT. The results are compared with respect to different width-to-thickness ratio b/h, power-law index $\hbox {P}_{\mathrm {in}}$, and mesh division. The constituent materials of the FGM plate are ceramic $\hbox {AL}_{\mathrm {2}}\hbox {O}_{\mathrm {3}}\,(c)$ and metal AL (m), whose properties are:

$E_{c} =380.0\hbox {Gpa}$, $\nu _{c} =0.3$, $\rho _{c} =3800\hbox {kg}/\hbox {m}^{\mathrm {3}}$.

$E_{m} =70.0\hbox {Gpa}$, $\nu _{m} =0.3$, $\rho _{m} =2702\hbox {kg}/\hbox {m}^{\mathrm {3}}$.

The elastic modulus and the Poisson’s ratio of the FGM plate are estimated using a layer-wise formulation, given as follows [50]:

$$\begin{aligned} E^{(k)}= & {} (E_{c} -E_{m} )\left( {\frac{k-0.5}{N_{L} }} \right) ^{\text{ P}_{\text{ in }} }+E_{m} \end{aligned}$$

(37)

$$\begin{aligned} \rho ^{(k)}= & {} (\rho _{c} -\rho _{m} )\left( {\frac{k-0.5}{N_{L} }} \right) ^{\text{ P}_{\text{ in }} }+\rho _{m} \end{aligned}$$

(38)

$$\begin{aligned} \nu ^{(k)}= & {} 0.3 \end{aligned}$$

(39)

where $N_{L}$ is the total number of plate layers and $k=1,2,3\cdots N_{L}$

It is observed that the present numerical results are in good agreement with those of the literature. Besides, the $8\times 8$ mesh has produced reasonably converted results. Therefore, for all the following numerical results, the mesh size of $8\times 8$ is used.

Table 2 compares the first six nondimensional frequency parameters of square cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}}/0^{\mathrm {0}}/90^{\mathrm {0}}/0^{\mathrm {0}})$ CNTRC laminated plates with the results reported by Lei et al. [38]. Two kinds of boundary conditions which are all edges are simply supported (SSSS) or all edges are clamped (CCCC) and four CNT distribution patterns (FG-O, FG-V, UD, and FG-X) are considered in this comparison. In the modeling, the CNT volume fraction and width-to-thickness ratio are selected to be, respectively, 0.11 and 10. The present paper used the same theory used by Lei et al. [38] which is the FSDT, which in turn led to a good agreement between our results and those reported by Lei et al. [38].

The last comparison test concerns the nondimensional fundamental frequency parameter of square simply supported CNTRC laminated plates. The achieved results are compared in Table 3 with the results of Huang et al. [45]. In the analysis, the CNT volume fraction and width-to-thickness ratio are selected to be, respectively, 0.11 and 10. Three levels of the number of layers (${n}=1$, 2, and 4) and two kinds of stacking sequences which are cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}})$ and angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}})$ are considered. As can be seen from Table 3, the obtained results are in good agreement with those of Huang et al. [45] for all four CNTs distribution patterns (FG-O, FG-V, UD, and FG-X).

4.2 Free vibration of hybrid laminated plates

Figure 3 shows the effect of number of ply’ layers $N_{L}$ on the fundamental nondimensional frequencies $({\bar{{\omega }}})$ parameter of a single ply of CNTRC plate with different CNT distribution patterns. It can be observed that the ${\bar{{\omega }}}$ parameter of the plates with UD pattern is not affected by the increment of $N_{L}$, and the main physical reason for this circumstance is that the plates with UD pattern have a homogeneous distribution of CNT fillers. For the case where the CNTs are nonuniformly distributed, an increase in $N_{L}$ leads to an increase in the ${\bar{{\omega }}}$ parameter for the plates with FG-X pattern and a decrease for the plates with FG-$\Lambda$ and FG-O patterns. However, this trend is more obvious when $N_{L}$ changes from 2 to 20; on the other hand, when $N_{L} > 20$, the fundamental nondimensional frequency parameter tends to converge to a constant value. Moreover, it is evident that the ${\bar{{\omega }}}$ parameter corresponding to FG-$\Lambda$ pattern is least influenced by the variation of $N_{L}$ among all three nonuniform distribution types. In the following numerical application, $N_{L}$ is selected to be 20 layers $(N_{L}=20)$.

Tables 4, 5, and 6 present, respectively, the effect of volume fraction, width-to-thickness, and aspect ratios on the ${\bar{{\omega }}}$ parameter of cross-ply $(0^{\mathrm {C}}/90^{\mathrm {F}})_{\mathrm {n}}$ hybrid laminated plates with different number of plies ($n=1$ ,2, and 4), distribution types of CNTs (FG-O, FG-$\Lambda$, UD, and FG-X), and boundary condition (SSSS and CCCC). The superscripts C and F denote, respectively, the CNTRC and GFRC plies. Results indicate that under both SSSS and CCCC boundary conditions the ${\bar{{\omega }}}$ parameter increases with an increase in the CNT volume fraction (owing to the fact that the effective elastic properties of the CNT fillers are higher than the polymer matrix). In addition the ${\bar{{\omega }}}$ parameter increases and decreases, respectively, as the width-to-thickness ratio and aspect ratio increase. It can be also observed that the number of plies has a significant effect on the ${\bar{{\omega }}}$ parameter of the laminated plates, where the ${\bar{{\omega }}}$ parameter shows a rapid increase as the number of plies increases for all four CNT distribution patterns. Due to the fact that the FG-X pattern has much more CNTs near to both bottom and top surfaces, and that the FG-O pattern has much more CNTs near to the middle surface, the $[\hbox {X}-\hbox {F}]_{\mathrm {n}}$ and $[\hbox {O}-\hbox {F}]_{\mathrm {n}}$ configurations have, respectively, the largest and the smallest ${\bar{{\omega }}}$ parameter.

The fundamental nondimensional frequency ${\bar{{\omega }}}$ parameter of angle-ply ($45^{\mathrm {C}}/-45^{\mathrm {F}})_{\mathrm {n}}$ hybrid laminated plates under the effects of CNT volume fraction, width-to-thickness ratio, and length-to-width ratio is, respectively, listed in Tables 7, 8, and 9. The influence of SSSS and CCCC boundary conditions and geometrical parameter including b/h ratio and a/b ratio on the ${\bar{{\omega }}}$ parameter is investigated. Similar observation to those obtained from the cross-ply hybrid laminated plates for CNT volume fraction, plies numbers, h/b and a/b ratios is found for both simply supported and clamped edges. For the same reasons mentioned in the previous case, the $[\hbox {O}-\hbox {F}]_{\mathrm {n}}$ configuration has the smallest ${\bar{{\omega }}}$ parameter, while the $[\hbox {X}-\hbox {F}]_{\mathrm {n}}$ configuration has the largest ${\bar{{\omega }}}$ parameter. It is also found that for all four CNT patterns and both stacking sequences, the ${\bar{{\omega }}}$ parameters corresponding to the plates with fully clamped edges are higher than those corresponding to the plates with fully simply supported edges.

Square hybrid laminated plates with different boundary conditions, number of layers, and laminate configuration (depending on different types of CNTs patterns) are investigated in this part. In the modeling, the CNT volume fraction and the width-to-thickness ratio are set to be 0.11 and 10, respectively. The first six nondimensional frequency ${\bar{{\omega }}}$ parameters of hybrid laminated plates are presented in Tables 10 and 11, respectively, for cross-ply and angle-ply staking sequences. It can be seen that all the first six ${\bar{{\omega }}}$ parameters corresponding to the laminated plate that containing the FG-V patterns in its upper half and the FG-$\Lambda$ patterns in its lower half produce the highest frequency even higher than the plate that contains FG-X patterns; this is for both boundary conditions and cross-ply and angle-ply stacking sequences.

The combined influences of laminate configuration types, number of plies, and boundary condition on the first six nondimensional frequency ${\bar{{\omega }}}$ parameters of CNTRC laminated plates are examined in Tables 12 and 13, respectively, for cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}}/0^{\mathrm {0}}/90^{\mathrm {0}})$ and angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}}/45^{\mathrm {0}}/-45^{\mathrm {0}})$ stacking sequences. In the analysis, the CNT volume fraction, b/h, and a/b are set to be 0.11, 10, and 1, respectively. From both Tables 12 and 13 results indicate that for $(n=1)$ the plates with [X-X] configuration have the largest frequencies, while the plates with $[\hbox {V}-\Lambda ]$ configuration yield the smallest frequencies in comparison with $[\Lambda -\hbox {V}]$ configuration, but for the case where n=(4 and 8) the laminated plate that contains each of FG-V and FG-$\Lambda$ patterns, respectively, in the upper and lower half of the laminated plate provides the largest frequencies, which leads in turn to a high improvement in the stiffness of the plate, suggesting a laminated plate of four or eight plies in which FG-V and FG-A patterns are puttied-up, respectively, in its upper and lower half can provide the best structural performance for both SSSS and CCCC boundary conditions and cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}})$ and angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}})$ stacking sequences.

Moreover, the combined effects of the power-law index, CNT volume fraction, and plate configuration on the nondimensional fundamental frequency ${\bar{{\omega }}}$ parameter of hybrid laminated plates are presented in Tables 14 and 15, respectively, for cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}}/0^{\mathrm {0}}/90^{\mathrm {0}})$ and angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}}/45^{\mathrm {0}}/-45^{\mathrm {0}})$ staking sequences. Results indicate that an increase in the power-law index $\hbox {P}_{\mathrm {in}}$ leads to a higher ${\bar{{\omega }}}$ parameter for [X-F-X-F] and [$\Lambda$-F-V-F] laminated plate configurations. However, this phenomenon is more obvious with the [$\Lambda$-F-V-F] configuration where the corresponding ${\bar{{\omega }}}$ parameter rapidly increases with the increasing $\hbox {P}_{\mathrm {in}}$. Thus, one can say that the plates with [$\Lambda$-F-V-F] configuration are more affected by $\hbox {P}_{\mathrm {in}}$ than those with [X-F-X-F] configuration. The same behavior is observed for both SSSS and CCCC boundary conditions, and cross-ply and angle-ply staking sequences. Again, these results indicate that the [$\Lambda$-F-V-F] configuration can provide plates with higher performance, especially if the CNT fillers are concentrate on the outer surfaces of each of FG-$\Lambda$ and FG-V plies. For further explanations, Figs. 4 and 5 show the percentage increase in the nondimensional fundamental frequency $(\Delta {\bar{{\omega }}})$ verses the power-law index $\hbox {P}_{\mathrm {in}}$, respectively, for cross-ply $(0^{\mathrm {0}}/90^{\mathrm {0}}/0^{\mathrm {0}}/90^{\mathrm {0}})$ and angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}}/45^{\mathrm {0}}/-45^{\mathrm {0}})$ hybrid laminated plates with different CNT volume fraction. Herein, ${\Delta \bar{{\omega }}=}\text{100 }\times {(\bar{{\omega }}_{\text{ p }} \text{- } {\bar{{\omega }}}_{\text{ u }} )} \big / {{\bar{{\omega }}}_{\hbox {u}} }$, where the ${\bar{{\omega }}}_{\text{ u }}$ and ${\bar{{\omega }}}_{\text{ p }}$ are, respectively, the nondimensional frequency with $\text{ P}_{\text{ in }} \text{=0 }$ and $\text{ P}_{\text{ in }} \ne \text{0 }$. As can be seen, the largest variation in the percentage increase of the nondimensional fundamental frequency $\Delta {\bar{{\omega }}}$ is reached for higher values of CNT volume fraction. Besides, these results also provide an overview of the main advantage that the FG reinforcement can add to the field of nanocomposite materials, where the overall stiffness of the structure can tune by adjusting the distribution of the nanofillers across the ply thickness.

Figures 6 and 7 show the effect of CNT volume fraction and CNTs orientation angle $\theta$ on the ${\bar{{\omega }}}$ parameter of hybrid laminated plates under SSSS and CCCC boundary conditions, respectively. The width-to-thickness ratio and aspect ratio are set to be 10 and 1, respectively. As can be seen, the ${\bar{{\omega }}}$ parameter increases when the orientation angle $\theta$ varies from $15^{\mathrm {0}}$ to $45^{\mathrm {0}}$, and decreases as the orientation angle $\theta$ varies from $45^{\mathrm {0}}$ to $75^{\mathrm {0}}$. It can be also found that the ${\bar{{\omega }}}$ parameter is symmetric under the orientation angle $\theta =45^{0}$ for all CNTs distribution patterns and SSSS and CCCC boundary conditions.

The effect of the width-to-thickness ratio together with the fillers orientation angle $\theta$ on the ${\bar{{\omega }}}$ parameter of hybrid laminated plates is illustrated in Figs. 8 and 9, respectively, for SSSS and CCCC boundary conditions. In the modeling, the plate aspect ratio and

CNT volume fraction are set to be 1 and 0.11, respectively. It is evident that the observation of the previous study can be sensed again, except the case corresponding to CCCC thin $(b/h=50)$ plate, where the ${\bar{{\omega }}}$ parameter decreases when the orientation angle $\theta$ varies from $15^{\mathrm {0}}$ to $45^{\mathrm {0}}$, and increases as the orientation angle $\theta$ varies from $45^{\mathrm {0}}$ to $75^{\mathrm {0}}$ as depicted in Fig. 9.

Figures 10 and 11 give the variation of the ${\bar{{\omega }}}$ parameter of hybrid laminated plates due to the influence caused by different length-to-width ratio and the CNT fillers orientation angle $\theta$ for SSSS and CCCC boundary conditions, respectively. In the analysis, the width-to-thickness ratio and CNT volume fraction are set to be 10 and 0.11, respectively. The frequency curve corresponding to square plate $(a/b=1)$ is symmetric under the orientation angle $\theta =45^{0}$, while the frequency curve corresponding to $a/b=1.5$ and $a/b=2.0$ keeps increasing when the orientation angle $\theta$ varies from $15^{\mathrm {0}}$ to $75^{\mathrm {0}}$. It is also found from Figs. 6, 7, 8, 9, 10, and 11 that the [$\Lambda$-F-V-F] configuration gained the largest values of ${\bar{{\omega }}}$ parameter for various width-to-thickness ratios, CNT volume fractions, aspect ratios, and two types of staking sequences and boundary conditions. Next, the first six three-dimensional mode shapes of angle-ply $(45^{\mathrm {0}}/-45^{\mathrm {0}}/45^{\mathrm {0}}/-45^{\mathrm {0}})$ hybrid laminated plate with width-to-thickness ratio of 10, CNTs volume fraction of 0.11, and [$\Lambda$-F-V-F] configuration are illustrated in Figs. 12 and 13, respectively, for SSSS and CCCC boundary conditions.

5 Conclusion

In order to enrich the existing research that investigates the mechanical behavior of laminated nanocomposite structures, this paper presents a study on free vibration behavior of hybrid laminated composite plates made with GFRC and CNTRC plies using a layer-wise formulation. The mechanical properties are determined by means of the extended rule of mixture micromechanics model. Self-made finite element code based on first-order shear deformation plate theory has been employed to carry out the numerical studies. Firstly, a comparison studies were performed to demonstrate the effectiveness and the accuracy of the present approach. Thereafter, focusing on the influence of different plate configuration and linear and nonlinear distribution of nanofillers, various numerical tests were conducted in order to investigate the effect of CNT distribution patterns, the number of CNTRC ply’ layers, CNT volume fraction, geometrical parameter, number of plies, and boundary conditions. Overall, the main findings of the present study are outlined as follows:

• Results reveal that CNTRC plies that divided into 20 layers $(N_{L}=20)$ can provide sufficiently accurate results.

• Increases in the number of plies cause to increase the fundamental frequency of the hybrid laminated plates.

• It was discovered that the configuration of the laminated plate structures with special layout arrangement using the CNT distribution types can remarkably enhance its performance. For instance, the plates with configuration [A-F-V-F] produced the highest fundamental frequency.

• It was also revealed that the accumulation of the CNT fillers on the outer surfaces of the FG-$\Lambda$ and FG-V distribution patterns can lead to a large enhancement on the performance of the hybrid laminated plate that has [$\Lambda$-F-V-F] configuration.

• Results show that the fundamental frequency increases as the orientation angle $\theta$ varies from $15^{\mathrm {0}}$ to $45^{\mathrm {0}}$ and decreases as the orientation angle $\theta$ varies from $45^{\mathrm {0}}$ to $75^{\mathrm {0}}$ for different values of CNTs volume fraction and width-to-thickness ratio, while keeps increasing for different values of the length-to-width ratio.

• A small increase in the CNT volume fraction can lead to a rapid and more remarkable variation in the fundamental frequency.

• The fundamental frequencies of the hybrid laminated structure increase and decrease, respectively, as the width-to-thickness and the length-to-width ratios of the plate increase.

• The fundamental frequency of the hybrid laminated strongly depends on the boundary conditions case, where the plates with clamped edges produce the highest frequency compared to the plates that are simply supported.