Hitting Time Problems of Sticky Brownian Motion and Their Applications in Optimal Stopping and Bond Pricing

Abstract

This paper investigates the hitting time problems of sticky Brownian motion and their applications in optimal stopping and bond pricing. We study the Laplace transform of first hitting time over the constant and random jump boundary, respectively. The results about hitting the constant boundary serve for solving the optimal stopping problem of sticky Brownian motion. By introducing the sharpo ratio, we settle the bond pricing problem under sticky Brownian motion as well. An interesting result shows that the sticky point is in the continuation region and all the results we get are in closed form.

1 Introduction

We denote by ($\Omega$, $\mathcal {F}$, $\mathbf {P}$) a complete probability space throughout this paper and the filtration $\{\mathcal {F}_t\}_{t\ge 0}$ is assumed to satisfy the usual conditions¹. For a Markov process $X=\{X_t\}_{t\ge 0}$, the notation ($X_t$, $\mathcal {F}_t$) signifies that $X=\{X_t\}_{t\ge 0}$ is adapted to the filtration $\{\mathcal {F}_t\}_{t\ge 0}$. For parameter (sticky coefficient) $\kappa \ge 0$, we define the sticky Brownian motion ($X_t$, $\mathcal {F}_t$) as a weak solution to

$$\begin{aligned} \left\{ \begin{array}{ll} X_t=x+\int _0^t1_{\{X_s\ne 0\}}W_s, \\ \int _0^t1_{\{X_s=0\}}ds=\kappa \hat{L}_t^X(0), \end{array} \right. \end{aligned}$$

(1)

where W is a standard Brownian motion on the probability space ($\Omega$, $\mathcal {F}$, $\mathbf {P}$) and $\hat{L}^X(0)$ is the symmetric local time of X at 0 (for symmetric local time, we refer the readers to Revuz and Yor (1999)). The aim of this paper is to investigate hitting time problems of sticky Brownian motion and the its application to optimal stopping problem.

Since the sticky boundary behaviour of diffusion processes was discovered by Feller in his 1952 paper Feller (1952) (see also Feller (1954, 1957)), many researchers have been interested in sticky diffusions satisfying certain stochastic differential equations (SDEs) that has a sticky point. Skorokhod conjectured that the SDE has no strong solution and Chitashvili published a technical report Chitashvili (1997) in 1989 claiming a proof (the paper was published after his death in 1997). In the same year, Warren (1997, 1999) further investigated solutions to (1) demonstrating that the process X is not adapted to the filtration generated by W and has some “extra randomness”. More general results on the non-cosiness of filtrations appeared in Watanabe (1999). Recently, Engelbert and Peskir (2014) and Bass (2014) proved that weak existence and weak uniqueness hold, but that pathwise uniqueness does not hold nor does a strong solution exist, respectively. In addition, Engelbert and Peskir considered the system of sticky Brownian motion with one-sided reflection boundary, and their results thus provide a new proof of those of Chitashvili. Besides, Nie and Linetsky (2020) focused on the sticky reflecting Ornstein-Uhlenbeck diffusions. It is worth noticing that Salins and Spiliopoulos (2017) proposed delayed process to study the sticky boundary and corresponding occupation times. Actually, the process with spatial delay in their paper seems to be similar to sticky process. The extension is that the authors studied a general class of Markov process where both skew and sticky behaviors exist. Besides, a most recent work by Zhang and Jiang (2020) studied the construction, time change and transition densities of sticky skew Brownian motion but with no applications.

From the definition on Chapter VII in Revuz and Yor (1999), we know that the sticky point is slowly reflecting. Here we emphasize the slowly reflecting, i.e. $0\ne \int _0^t1_{\{X_s=0\}}ds=\kappa \hat{L}_t^X(0)$. Consider a standard Brownian motion W and define $\tau ^W_{\delta }:=\inf \{t>0:|W_t|>\delta \},$ then we know

$$\mathop {\lim }\limits _{\delta \downarrow 0}E_0(\tau ^W_{\delta })=0.$$

But for the sticky Brownian motion X, again define $\tau ^X_{\delta }:=\inf \{t>0:|X_t|>\delta \}$, it follows that

$$\begin{aligned} \mathop {\lim }\limits _{\delta \downarrow 0}\frac{1}{\delta }E_0(\tau ^X_{\delta })=\kappa , \end{aligned}$$

which means that the sticky Brownian motion spends much more time in a $\delta$-neighborhood of 0 than standard Brownian motion. In particular, the sticky Brownian motion reduces to standard Brownian motion when $\kappa =0$.

By the seminal work of Feller (1957), we know that virtually any one dimensional, homogeneous, continuous Markov process can be uniquely characterized via its infinitesimal generator and the definition domain of the generator, and vice versa. We remark two recent optimal stopping work by Mordecki and Salminen (2019a, b) based on generalized Brownian motion, being oscillating Brownian motion and Brownian motion with broken drift, respectively. To our knowledge, there exists some of classical papers concerned with the construction and basic properties of sticky Brownian motion which are significant to be explored. In our paper, we first compute some meaningful properties of first hitting time over a constant boundary and a random jump boundary, respectively. Laplace transform and strong Markov property play an important role when dealing with these problems. Second, we turn to investigating the applications in optimal stopping and bond pricing of sticky Brownian motion. The results of first hitting time over constant boundary and sharpo ratio are essential.

The rest of our paper is organized as follows. In Section 2, we focus on the first hitting time problems over two kinds of boundaries: a constant boundary and a random jump boundary, respectively. Section 3 studies the applications in optimal stopping and bond pricing under sticky Brownian motion. By the results about hitting the constant boundary, we solve the optimal stopping problem; By introducing the sharpo ratio, we get the bond price. All the results we get are closed-form. Section 4 concludes.

2 First Hitting Time of Sticky Brownian Motion

In this section, we explore the basic first hitting time problems for sticky Brownian motion X defined by (1) over a constant boundary and a random jump boundary, respectively.

2.1 First Hitting Time Over the Constant Boundary

Set a constant level $l\ge 0$ and define the first hitting time of X for touching l by

$$\begin{aligned} \tau _l:=\inf \{t\ge 0; X_t=l\}. \end{aligned}$$

(2)

The Laplace transform of $\tau _l$ is

$$\begin{aligned} L(\theta ;x,l):=\mathbf {E}_x[e^{-\theta \tau _l}], \end{aligned}$$

(3)

where $X_0=x\ge 0$ is the initial point of X and $\theta >0$. Then we have the following theorem about the Laplace transform of the first hitting time.

Theorem 1

The Laplace transform of the first hitting time of sticky Brownian motion X is

$$\begin{aligned} L(\theta ;x,l)=\left\{ \begin{array}{ll} \displaystyle \frac{f(x)}{f(l)}, &{}x\le l, \\ \displaystyle \frac{g(x)}{g(l)}, &{}x>l, \end{array}\right. \end{aligned}$$

(4)

where

$$\begin{aligned} f(y)=\left\{ \begin{array}{ll} e^{y\sqrt{2\theta }}, &{} y\le 0,\\ a_1e^{y\sqrt{2\theta }}+a_2e^{-y\sqrt{2\theta }}, &{}y>0, \end{array}\right. \end{aligned}$$

(5)

and

$$\begin{aligned} g(y)=\left\{ \begin{array}{ll} b_1e^{y\sqrt{2\theta }}+b_2e^{-y\sqrt{2\theta }}, &{}y\le 0,\\ e^{-y\sqrt{2\theta }}, &{}y>0, \end{array}\right. \end{aligned}$$

(6)

with the coefficients $a_i$ and $b_i$ $(i=1,2)$ given by

$$\begin{aligned} a_1=b_2=1+\frac{\kappa }{2}\sqrt{2\theta },\ \ \ a_2=b_1=-\frac{\kappa }{2}\sqrt{2\theta }. \end{aligned}$$

(7)

Proof

It is easy to show that f is an increasing continuous function satisfying the boundary conditions

$$\begin{aligned} f\in C^2(\mathbb {R})\setminus \{0\},\ f^{'}(0+)=f^{'}(0-)+2\kappa \theta f(0), \end{aligned}$$

(8)

and g is a descreasing continuous function satisfying the boundary conditions

$$\begin{aligned} g\in C^2(\mathbb {R})\setminus \{0\},\ g^{'}(0+)=g^{'}(0-)+2\kappa \theta g(0). \end{aligned}$$

(9)

The boundary conditions come from the infinitesimal generator and the definition domain of the generator of sticky Brownian motion. Furthermore, for arbitrary $z\ne 0$, both f and g satisfy the Sturm-Liouville equation (h represents f or g)

$$\begin{aligned} \mathcal {A}h(z)=\frac{1}{2}h^{''}(z)=\theta h(z). \end{aligned}$$

(10)

Applying Itô-Tanaka formula (see, Revuz and Yor (1999)) to $e^{-\theta t}h(X_t)$, we have

$$\begin{aligned} e^{-\theta t}h(X_t)=&h(x)+\int _0^te^{-\theta s}(\frac{1}{2}h^{''}(X_s)-\theta h(X_s))ds+\int _0^te^{-\theta s}h^{'}(X_s)1_{\{X_s\ne 0\}}dW_s \nonumber \\&+\frac{1}{2}[h^{'}(0+)-h^{'}(0-)-\kappa h^{''}(0)]\int _0^te^{-\theta s}d\hat{L}_s^X(0)\\ =&h(x)+\int _0^te^{-\theta s}h^{'}(X_s)1_{\{X_s\ne 0\}}dW_s. \nonumber \end{aligned}$$

(11)

By the optional stopping theorem, for any $t>0$

$$\begin{aligned} \mathbf {E}_x[e^{-\theta (\tau _l\wedge t)}h(X_{\tau _l\wedge t})]=h(x). \end{aligned}$$

Then, we get

$$\begin{aligned} h(x)&=\mathbf {E}_x[e^{-\theta (\tau _l\wedge t)}h(X_{\tau _l\wedge t})]\\&=\mathbf {E}_x[e^{-\theta (\tau _l\wedge t)}h(X_{\tau _l\wedge t})1_{\{\tau _l<\infty \}}]+\mathbf {E}_x[e^{-\theta (\tau _l\wedge t)}h(X_{\tau _l\wedge t})1_{\{\tau _l=\infty \}}]. \end{aligned}$$

When $h:=f$ (case $x\le l$), we have $X_{\tau _l\wedge t}\le l$. Since f is increasing, it implies that

$$\begin{aligned} |f(X_{\tau _l\wedge t})|\le f(l). \end{aligned}$$

As a result, both

$$\begin{aligned} \mathbf {E}_x[e^{-\theta (\tau _l\wedge t)}f(X_{\tau _l\wedge t})1_{\{\tau _l<\infty \}}]\rightarrow \mathbf {E}_x[e^{-\theta \tau _l}f(X_{\tau _l})1_{\{\tau _l<\infty \}}] \end{aligned}$$

and

$$\begin{aligned} \mathbf {E}_x[e^{-\theta (\tau _l\wedge t)}f(X_{\tau _l\wedge t})1_{\{\tau _l=\infty \}}]\rightarrow 0 \end{aligned}$$

hold as $t\rightarrow \infty$ by the dominated convergence theorem. A similar argument for the case when $h=g$ leads to

$$\begin{aligned} g(x)=\mathbf {E}_x[e^{-\theta \tau _l}g(X_{\tau _l})1_{\{\tau _l<\infty \}}]=g(l)\mathbf {E}_x[e^{-\theta \tau _l}] \end{aligned}$$

and we end this proof.

Remark 1

It should be noted that the definition domain of function h in (10) is actually $z\in (-\infty ,\infty )$ containing 0 which is explained by (11). Intuitively, the construction of sticky Brownian motion can be viewed as a combination of continuous part and discontinuous part (symmetric local time, in our paper). Naturally, $h^{''}(z)$ makes sense at 0 and takes the form of $h^{''}(0)=2\theta h(0)$ according to (11). This fact can also come from the definition domain of infinitesimal generator of delayed process appeared in Salins and Spiliopoulos (2017), i.e., $\mathcal {A}h\in C(\mathbb {R})$ but $h\in C(\mathbb {R})\cap C^2(\mathbb {R})\setminus \{0\}$.

By virtue of the above theorem, we have the following corollary describing the mean time of sticky Brownian motion for first hitting l.

Corollary 1

The mean time of sticky Brownian motion for first hitting l are $\infty$, i.e.

$$\begin{aligned} \mathbf {E}_x[\tau _l]=\infty . \end{aligned}$$

Proof

Because

$$\begin{aligned} \mathbf {E}_x[\tau _l]=\mathop {\lim }\limits _{\theta \rightarrow 0+}\frac{1-L(\theta ;x,l)}{\theta }=\mathop {\lim }\limits _{\theta \rightarrow 0+}\frac{h(l)-h(x)}{\theta h(l)}, \end{aligned}$$

then a straightforward calculation by using the L’Hôpital’s rule produces the result.

Remark 2

It is obvious that $\mathbf {E}_x[\tau _l]=\infty$, because there exists no limited boundaries which guarantees the trajectory of sticky Brownian motion not far away from the hitting level l.

In addition, if we set $a\le x\le l$ and define

$$\begin{aligned} \phi _1(\theta ;x,a,l):=\mathbf {E}_x[e^{-\theta \tau _a}1_{\{\tau _a<\tau _l\}}]\ \ and \ \ \phi _2(\theta ;x,a,l):=\mathbf {E}_x[e^{-\theta \tau _l}1_{\{\tau _l<\tau _a\}}], \end{aligned}$$

we acquire the next useful corollary.

Corollary 2

The two-sided exit identities are

$$\begin{aligned} \phi _1(\theta ;x,a,l)=\frac{g(x)f(l)-f(x)g(l)}{g(a)f(l)-f(a)g(l)},\ \ \phi _2(\theta ;x,a,l)=\frac{f(x)g(a)-g(x)f(a)}{g(a)f(l)-f(a)g(l)}. \end{aligned}$$

Proof

By the strong Markov property, we adopt

$$\begin{aligned} \mathbf {E}_x[e^{-\theta \tau _a}]&=\mathbf {E}_x[e^{-\theta \tau _a}1_{\{\tau _a<\tau _l\}}]+ \mathbf {E}_x[e^{-\theta \tau _a}1_{\{\tau _l<\tau _a\}}]\\&=\phi _1(\theta ;x,a,l)+\mathbf {E}_x[\mathbf {E}_x[e^{-\theta \tau _a}1_{\{\tau _l<\tau _a\}}|\mathcal {F}_{\tau _l}]]\\&=\phi _1(\theta ;x,a,l)+\phi _2(\theta ;x,a,l)\mathbf {E}_l[e^{-\theta \tau _a}], \end{aligned}$$

and

$$\begin{aligned} \mathbf {E}_x[e^{-\theta \tau _l}]=\phi _2(\theta ;x,a,l)+\phi _1(\theta ;x,a,l)\mathbf {E}_a[e^{-\theta \tau _l}]. \end{aligned}$$

Then, the proof is finished by solving the equations.

Next, we provide a direct result for the Laplace transform representation of first exit time which follows from the above corollary. In addition, the proof of next corollary parallels with Corollary 3.7 in Li and Zhou (2013), hence we omit it. Suppose that $a<0<l$, then we provide the following corollary.

Corollary 3

The Laplace transform of the occupation time of X satisfies

$$\begin{aligned} \mathbf {E}_a[e^{-\theta \int _0^\infty 1_{\{a\le X_s\le l\}}ds}]=\frac{M(a,l,\theta )}{N(a,l,\theta )}\ \ and\ \ \mathbf {E}_b[e^{-\theta \int _0^\infty 1_{\{a\le X_s\le l\}}ds}]=\frac{2a_1}{N(a,l,\theta )}, \end{aligned}$$

where

$$\begin{aligned} M(a,l,\theta )=&b_1a_1\sqrt{2\theta }e^{(a+l)\sqrt{2\theta }}+(1-b_1a_2)\sqrt{2\theta }e^{(a-l)\sqrt{2\theta }}\\&+b_2a_1\sqrt{2\theta }e^{-(a-l)\sqrt{2\theta }}+(1-b_2a_2)\sqrt{2\theta }e^{-(a+l)\sqrt{2\theta }} \end{aligned}$$

and

$$\begin{aligned} N(a,l,\theta )=&b_1a_1(1-\sqrt{2\theta })e^{(a+l)\sqrt{2\theta }}+[1-a\sqrt{2\theta }-(1-\sqrt{2\theta })b_1a_2]e^{(a-l)\sqrt{2\theta }}\\&+b_2a_1(1+\sqrt{2\theta })e^{-(a-l)\sqrt{2\theta }}+[1+a\sqrt{2\theta }-(1+\sqrt{2\theta })b_2a_2]e^{-(a+l)\sqrt{2\theta }} \end{aligned}$$

with the coefficients specified in Theorem 1.

2.2 First Hitting Time Over the Random Jump Boundary

In this subsection, we explore the joint Laplace transform problem for first hitting time over a random jump boundary, which is associated with an exponential random variable. Let us first introduce some notations and definitions used in this subsection.

Define a random jump boundary by

$$\begin{aligned} J_t:=l+H1_{\{\eta \le t \}}, \end{aligned}$$

where $l>0$, H denotes a positive jump with distribution function F, and $\eta$ is an exponential random variable with parameter $\lambda$. In addition, H, $\eta$ and the sticky Brownian motion X are independent. Now define

$$\begin{aligned} \tilde{\tau }_l:=\inf \{t\ge 0; X_t=J_t\}. \end{aligned}$$

Obviously, $\tilde{\tau }_l=\tau _l$ when $t<\eta$, and $\tilde{\tau }_l=\tau _{l+H}$ when $t\ge \eta$. We focus on the joint Laplace transform

$$\begin{aligned} \eta (\theta _1,\theta _2;x):=\mathbf {E}_x[e^{-\theta _1X_{\tilde{\tau }_l}-\theta _2\tilde{\tau }_l}], \end{aligned}$$

where $x<l$.

Proposition 1

The joint Laplace transform $\eta (\theta _1,\theta _2;x)$ admits the following decomposition:

$$\begin{aligned} \eta (\theta _1,\theta _2;x)=e^{-\theta _1l}L(\theta _2+\lambda ;x,l)+e^{-\theta _1l}\mathbf {E}_x[e^{-\theta _1 H-\theta _2\eta }1_{\{\tilde{\tau }_l\ge \eta \}}L(\theta _2;X_\eta ,l+H)], \end{aligned}$$

(12)

where $L(\theta ;x,l)$ is defined in (3).

Proof

We decompose $\eta (\theta _1,\theta _2;x)$ as

$$\begin{aligned} \eta (\theta _1,\theta _2;x)&= \mathbf {E}_x[e^{-\theta _1X_{\tilde{\tau }_l}-\theta _2\tilde{\tau }_l}1_{\{\tilde{\tau }_l<\eta \}}] +\mathbf {E}_x[e^{-\theta _1X_{\tilde{\tau }_l}-\theta _2\tilde{\tau }_l}1_{\{\tilde{\tau }_l\ge \eta \}}]\\&=:I_1+I_2. \end{aligned}$$

Recalling the definitions (2) and (3), we have

$$\begin{aligned} I_1&=\mathbf {E}_x(e^{-\theta _1X_{\tilde{\tau }_l}-\theta _2\tilde{\tau }_l}1_{\{\tilde{\tau }_l<\eta \}})\\&=e^{-\theta _1l}\mathbf {E}_x[e^{-\theta _2\tau _l}1_{\{\tau _l<\eta \}}]\\&=e^{-\theta _1l}\mathbf {E}_x[e^{-\theta _2\tau _l}(\int _{\tau _l}^\infty \lambda e^{-\lambda \eta }d\eta )]\\&=e^{-\theta _1l}\mathbf {E}_x[e^{-\theta _2\tau _l}\cdot e^{-\lambda \tau _l}]\\&=e^{-\theta _1l}L(\theta _2+\lambda ;x,l) \end{aligned}$$

and

$$\begin{aligned} I_2&=\mathbf {E}_x[e^{-\theta _1X_{\tilde{\tau }_l}-\theta _2\tilde{\tau }_l}1_{\{\tilde{\tau }_l\ge \eta \}}]\\&=e^{-\theta _1l}\mathbf {E}_x[e^{-\theta _1H-\theta _2\tilde{\tau }_l}1_{\{\tilde{\tau }_l\ge \eta \}}]\\&=e^{-\theta _1l}\mathbf {E}_x[\mathbf {E}_x(e^{-\theta _1H-\theta _2(\eta +\tilde{\tau }_l-\eta )}1_{\{\tilde{\tau }_l\ge \eta \}}|\mathcal {F}_\eta )]\\&=e^{-\theta _1l}\mathbf {E}_x[e^{-\theta _1H-\theta _2\eta }1_{\{\tilde{\tau }_l\ge \eta \}}\mathbf {E}_x[e^{-\theta _2(\tilde{\tau }_l-\eta )} | \mathcal {F}_\eta ]]\\&=e^{-\theta _1l}\mathbf {E}_x[e^{-\theta _1H-\theta _2\eta }1_{\{\tilde{\tau }_l\ge \eta \}}\mathbf {E}_{X_\eta }[e^{-\theta _2\tau _{l+H}}]]\\&=e^{-\theta _1l}\mathbf {E}_x[e^{-\theta _1H-\theta _2\eta }1_{\{\tilde{\tau }_l\ge \eta \}}L(\theta _2;X_\eta ,l+H)]. \end{aligned}$$

Noticing that $\mathbf {E}_x[e^{-\theta _2(\tilde{\tau }_l-\eta )} | \mathcal {F}_\eta ]=\mathbf {E}_{X_\eta }[e^{-\theta _2\tau _{l+H}}]$ holds for the strong Markov property of X and the memoryless property of $\eta$, we finish the proof.

3 Applications: Optimal Stopping and Bond Pricing Under Sticky Brownian Motion

3.1 Optimal Stopping

Throughout this subsection, $\theta$ is replaced with r in the expressions (5) and (6). We will show that the sticky point is in continuation region and we also obtain the value of optimal stopping problem for sticky Brownian motion. For an excellent exposition on optimal stopping problem, see for instance Taylor (1968), Salminen (1985), Christensen and Irle (2011), Crocce and Mordecki (2014), Alvarez and Salminen (2017) and references therein. Optimal stopping problem is to look for a stopping time $\tau ^*$ such that

$$\begin{aligned} V(x):=\mathop {\sup }\limits _{\tau }\mathbf {E}_x[e^{-r\tau }G(X_\tau )]=\mathbf {E}_x[e^{-r\tau ^*}G(X_{\tau ^*})], \end{aligned}$$

where $r>0$ denotes the prevailing discount rate and $G:\mathbb {R}\rightarrow \mathbb {R}_+$ is the pay-off function satisfying that G is continuous, twice differentiable, non-decreasing, non-negative, and has finite left and right derivatives.

As is known from the literature on optimal stopping, V is the smallest r-excessive majorant of G (Theorem 1 on pp. 124 of Shiryaev (1978)). As usual, we call $\mathcal {S}:=\{x:V(x)=G(x)\}$ the stopping region and $\mathcal {C}:=\{x:V(x)>G(x)\}$ the continuation region.

Theorem 2

Assume that $G^{''}(0)>0$, i.e. G is convex. Then for sticky Brownian motion X defined by (1), the sticky point 0 is in the continuation region $\mathcal {C}$.

Proof

Denote by $(dG^{-}/dS)$ and $(dG^{+}/dS)$ the left and the right scale derivatives of G, respectively. Thanks to the fact $(dG^{+}/dS)(0)-(dG^{-}/dS)(0)=m(\{0\})\mathcal {A}G(0)$ in Engelbert and Peskir (2014), we obtain $(dG^{+}/dS)(0)-(dG^{-}/dS)(0)=\kappa \mathcal {A}G(0)$ in our paper, where $\mathcal {A}G(0)=(1/2)G^{''}(0)$ and m is the speed measure.

Assume that $0\in \mathcal {S}$. Then following the results in Alvarez and Salminen (2017), we obtain

$$\begin{aligned} \frac{d^{-}V}{dS}(0)-\frac{d^{+}V}{dS}(0)\le \frac{d^{-}G}{dS}(0)-\frac{d^{+}G}{dS}(0)=-\kappa \frac{1}{2}G^{''}(0)<0. \end{aligned}$$

On the other hand, according to Corollary 3.7 in Shiryaev (1978), for any r-excessive function H it follows that

$$\begin{aligned} \frac{d^{-}H}{dS}(0)\ge \frac{d^{+}H}{dS}(0). \end{aligned}$$

Because V is the smallest r-excessive majorant of G, we get the contradiction. Hence, $0\in \mathcal {C}$.

Recalling the result on speed measure m of sticky Brownian motion X in Bass (2014), the scale function for X is computed by

$$\begin{aligned} S(x)=x. \end{aligned}$$

Moreover, the so-called Wronskian

$$\begin{aligned} \omega _\theta :=\frac{g(x)f^{'}(x)}{S^{'}(x)}-\frac{f(x)g^{'}(x)}{S^{'}(x)}, \end{aligned}$$

(13)

is independent of x.

Now introduce for a differential function F

$$\begin{aligned} (L_fF)(x)&:=\frac{f^2(x)}{S^{'}(x)}\frac{d}{dx}[\frac{F(x)}{f(x)}]\\&=\left\{ \begin{array}{ll} \displaystyle \frac{1}{S^{'}(x)}[a_1e^{x\sqrt{2r}}(F^{'}(x)-\sqrt{2r}F(x))\\ \quad \quad \quad +a_2e^{-x\sqrt{2r}}(F^{'}(x)+\sqrt{2r}F(x))], &{}x>0,\\ \displaystyle \frac{1}{S^{'}(x)}[e^{x\sqrt{2r}}(F^{'}(x)-\sqrt{2r}F(x))], &{}x<0, \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} (L_gF)(x)&:=\frac{g^2(x)}{S^{'}(x)}\frac{d}{dx}[\frac{F(x)}{g(x)}]\\&=\left\{ \begin{array}{ll} \displaystyle \frac{1}{S^{'}(x)}[e^{-x\sqrt{2r}}(F^{'}(x)+\sqrt{2r}F(x))], &{}x>0,\\ \displaystyle \frac{1}{S^{'}(x)}[a_1e^{-x\sqrt{2r}}(F^{'}(x)+\sqrt{2r}F(x))\\ \quad \quad \quad +a_2e^{x\sqrt{2r}}(F^{'}(x)-\sqrt{2r}F(x))], &{}x<0, \end{array}\right. \end{aligned}$$

where the coefficients $a_1$ and $a_2$ are defined by (7). Let

$$\begin{aligned} \mathcal {M}:=\mathop {\text {argmax}}\limits _{x\in \mathbf {R}}\{\frac{G(x)}{f(x)}\} \end{aligned}$$

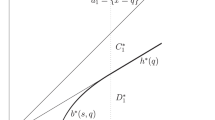
be the set of points at which the ratio G/f is maximized. Next we introduce a useful lemma which provides a candidate strategy to verify the optimization in the optimal stopping problem. This is exactly a corollary in Shiryaev (1978), and the proof also appears in Alvarez and Salminen (2017).

Lemma 1

Let $A\subset B$ be a nonempty Borel subset of B and $\tau _A:=\{t\ge 0:X_t\in A\}$. Assume that the function

$$\begin{aligned} \widehat{V}(x):=\mathbf {E}_x[e^{-r\tau _A}g(X_{\tau _A})] \end{aligned}$$

is r-excessive and dominates g. Then $V=\widehat{V}$ and $\tau _A$ is an optimal stopping time. Morever, $\tau _A$ is finite almost surely.

Then we state the main theorem.

Theorem 3

(A) Let $x^{*}\in \mathcal {M}$. Then, $(-\infty ,x^{*})\setminus \mathcal {M}\subset \mathcal {C}$.

(B) Assume that $\mathcal {M}=\{x^{*}\}$, where $x^{*}>0$, and the pay-off function G satisfies the property $G^{''}-2r G(x)\le 0$ for all $x\ge x^{*}$.

Then, $\tau _{x^{*}}:=\inf \{t\ge 0:X_t\ge x^{*}\}$ is an optimal stopping time and the value reads as

$$\begin{aligned} V(x)=\mathbf {E}_x[e^{-r\tau _{x^*}}G(X_{\tau _{x^*}})] =\left\{ \begin{array}{ll} G(x), &{}x>x^{*},\\ \displaystyle f(x)\frac{G(x^{*})}{f(x^{*})}, &{}x<x^{*}. \end{array}\right. \end{aligned}$$

(14)

Proof

Let $\widehat{V}$ denote the proposed value function on the right hand side of (14). Clearly, $V\ge \widehat{V}$. To show that $V=\widehat{V}$, we apply Lemma 1 and proof that $\widehat{V}$ is an r-excessive majorant of G. Since $x^{*}\in \mathcal {M}$, it follows that $\widehat{V}(x)\ge G(x)$ for all $x\in \mathbb {R}$. Select $x_0>x^{*}$ such that $G(x_0)>0$ and define $H(x):=\widehat{V}(x)/\widehat{V}(x_0)=\widehat{V}(x)/G(x_0)$. To show that H is r-excessive, let for $x\ge x_0$

$$\begin{aligned} \sigma _{x_0}^H((x,\infty ]):=\frac{f(x_0)}{\omega _\theta G(x_0)S^{'}(x)}(\widehat{V}^{'}(x)g(x)-\widehat{V}(x)g^{'}(x))=\frac{f(x_0)}{\omega _\theta G(x_0)}(L_g G)(x), \end{aligned}$$

and for $x\le x_0$

$$\begin{aligned} \sigma _{x_0}^H([-\infty ,x)):&=\frac{g(x_0)}{\omega _\theta G(x_0)S^{'}(x)}(\widehat{V}(x)f^{'}(x)-\widehat{V}^{'}(x)f(x))\\&= \left\{ \begin{array}{ll} -\frac{g(x_0)}{\omega _\theta G(x_0)}(L_f G)(x), &{} x^{*}<x\le x_0, \\ 0, &{} x\le x^*. \end{array} \right. \end{aligned}$$

Firstly, the monotonicity and the non-negativity of G imply that $(L_g G)(x)\ge 0$ for $x\ge x^{*}$, i.e. $\sigma _{x_0}^H((x,\infty ])\ge 0$ for $x\ge x_0$. Moreover, the property of G in (B) guarantees

$$\begin{aligned} (L_g G)^{'}(x)=\frac{G^{''}(x)g(x)-G(x)g^{''}(x)}{S^{'}(x)}\le 0 \end{aligned}$$

for all $x\ge x^{*}$ implying that $x\mapsto \sigma _{x_0}^H((x,\infty ])$ is non-increasing. Secondly, Since $x^{*}\in \mathcal {M}$, then $(L_f G)(x^{*})=0$. Again by the property of G in (B), we have

$$\begin{aligned} (L_f G)^{'}(x)=\frac{G^{''}(x)f(x)-G(x)f^{''}(x)}{S^{'}(x)}\le 0, \end{aligned}$$

and thus $(L_f G)(x)\le 0$ for $x\ge x^{*}$, i.e. $\sigma _{x_0}^H([-\infty ,x))\ge 0$ for $x\le x_0$, and $x\mapsto \sigma _{x_0}^H([-\infty ,x))$ is non-decreasing. Thirdly, it follows, recalling the definition (13) of the Wronskian, that

$$\begin{aligned} \sigma _{x_0}^H&([-\infty ,x_0))+\sigma _{x_0}^H((x_0,\infty ])\\ =&\frac{f(x_0)}{\omega _\theta G(x_0)}(\frac{G^{'}(x_0)}{S^{'}(x_0)}g(x_0)-\frac{g^{'}(x_0)}{S^{'}(x_0)}G(x_0))\\&- \frac{g(x_0)}{\omega _\theta G(x_0)}(\frac{G^{'}(x_0)}{S^{'}(x_0)}f(x_0)-\frac{f^{'}(x_0)}{S^{'}(x_0)}G(x_0))\\ =&\frac{1}{\omega _\theta }(\frac{g(x_0)f^{'}(x_0)}{S^{'}(x_0)} -\frac{f(x_0)g^{'}(x_0)}{S^{'}(x_0)})\\ =&1. \end{aligned}$$

Based on the calculation above and setting $\sigma _{x_0}^H(\{x_0\})=0$ lead that $\sigma _{x_0}^H$ constitutes a probability measure on $[-\infty ,\infty ]$. Then, $\sigma _{x_0}^H$ induces via the Martin representation an r-excessive function (Salminen (1985) and Shiryaev (1978)) which coincides with H. Since $\widehat{V}(x)=\widehat{V}(x_0)H(x)$ the proposed $\widehat{V}$ is excessive as well. Combining Lemma 1 finishes the proof.

Remark 3

In our paper, the increasing fundamental solution f satisfies the sticky boundary condition (see, (8)). Differently, the increasing fundamental solution $\psi _r(x)$ satisfies the skew boundary condition $(\beta \psi _r^{'}(0+)=(1-\beta )\psi _r^{'}(0-))$ in Alvarez and Salminen (2017).

3.2 Bond Pricing

In this subsection, we study the bond pricing problem under sticky Brownian motion $X_t$. Suppose that the financial market is arbitrage-free and the default-free bond price at time t is denoted by $B(X_t, \tau )$ or $B(t, T, X_t)$, where T is the maturity and $\tau =T-t$ is the bond’s term. Let $B(t, T, X_t)$ be the bond price based on $X_t$ with the maturity T at time t. By Itô formula (see Revuz and Yor (1999)), we have for $X_t\ne 0$,

$$\begin{aligned} {\mathrm {d}}B(t, T, X_t)&=\frac{\partial B}{\partial t}{\mathrm {d}}t+\frac{\partial B}{\partial X}{\mathrm {d}}X+\frac{1}{2}\frac{\partial ^2 B}{\partial X^2}{\mathrm {d}}t \\&=\mu _{B}(t,X_t)B{\mathrm {d}}t+\sigma _B(t,X_t)B{\mathrm {d}}W_t, \end{aligned}$$

where

$$\begin{aligned}&\mu _{B}(t,X_t)B:=\frac{\partial B}{\partial t}+\frac{1}{2}\frac{\partial ^2 B}{\partial X^2}, \end{aligned}$$

(15)

$$\begin{aligned}&\sigma _B(t,X_t)B:=\frac{\partial B}{\partial X}. \end{aligned}$$

(16)

What follows next is our main result about the bond price under sticky Brownian motion.

Theorem 4

Suppose that the underlying zero coupon interest rate satisfies (1) and $\lambda$ is the sharpe index in the modern market which is arbitrage-free. Then the bond price $B(t,T,X_t)$ of the zero coupon interest rate with the maturity time T is represented by

$$\begin{aligned} B(t,T,X_t)&=\exp \{\alpha (\tau )+\beta ^{+}(\tau )1_{\{X_t>0\}}X_t+\beta ^{-}(\tau )1_{\{X_t<0\}}X_t+\beta (\tau )1_{\{X_t=0\}}X_t\}\\&{=\exp \{\alpha (\tau )+\beta ^{+}(\tau )1_{\{X_t>0\}}X_t+\beta ^{-}(\tau )1_{\{X_t<0\}}X_t\}} \end{aligned}$$

with the coefficients

$$\begin{aligned} \alpha (\tau )=&\frac{1}{6}\tau ^3+\frac{1}{2}\lambda \tau ^2,\\ \beta (\tau )=&-\tau ,\\ \beta ^{+}(\tau )=&-\frac{1}{2}\tau +\frac{1}{2}\kappa \tau ^2,\\ \beta ^{-}(\tau )=&-\frac{1}{2}\tau -\frac{1}{2}\kappa \tau ^2. \end{aligned}$$

Proof

In the bond pricing theory, if a bond market is arbitrage-free, the sharpe ratio of trading bonds with different terms should be equal. Thanks to Vasicek (1997), we let sharpo ratio be $\lambda$ for $X_t\ne 0$, and derive the same pricing problem by

$$\begin{aligned} \frac{\mu _B(t,X_t)-X_t}{\sigma _B(t,X_t)}=\lambda . \end{aligned}$$

(17)

With the displays of (15), (16) and (17), we establish

$$\begin{aligned} \frac{1}{2}\frac{\partial ^2 B}{\partial X^2}+\frac{\partial B}{\partial t}-\lambda \frac{\partial B}{\partial X}-BX=0. \end{aligned}$$

(18)

To solve the pricing problem, we suppose that the solution to (18) takes the form of

$$\begin{aligned} B(t,T,X_t)=\exp \{\alpha (\tau )+\beta ^{+}(\tau )1_{\{X_t>0\}}X_t+\beta ^{-}(\tau )1_{\{X_t<0\}}r_t+\beta (\tau )1_{\{X_t=0\}}X_t\}, \end{aligned}$$

with $\alpha (0)=\beta ^{+}(0)+\beta ^{-}(0)=0.$ Taking the partial derivatives for B results in

$$\begin{aligned}&\frac{\partial B}{\partial \tau }=\big (\alpha ^{'}(\tau )+(\beta ^{+}(\tau )+\beta ^{-}(\tau ))^{'}X_t\big )B,\\&\frac{\partial B}{\partial X}=\big (\beta ^{+}(\tau )+\beta ^{-}(\tau )\big )B,\\&\frac{\partial ^2 B}{\partial X^2}=\big (\beta ^{+}(\tau )+\beta ^{-}(\tau )\big )^2B. \end{aligned}$$

Substitute them into (18), then we obtain

$$\begin{aligned}&X_t(-(\beta ^{+}(\tau )+\beta ^{-}(\tau ))^{'}-1)\\&+[\frac{1}{2}(\beta ^{+}(\tau )+\beta ^{-}(\tau ))^2-\lambda (\beta ^{+}(\tau )+\beta ^{-}(\tau ))-\alpha ^{'}(\tau )]\\&=0, \end{aligned}$$

which holds for arbitrary $X_t\ne 0$. It suggests that

$$\begin{aligned} \left\{ \begin{array}{ll} -(\beta ^{+}(\tau )+\beta ^{-}(\tau ))^{'}-1=0, \\ \frac{1}{2}(\beta ^{+}(\tau )+\beta ^{-}(\tau ))^2-\lambda (\beta ^{+}(\tau )+\beta ^{-}(\tau ))-\alpha ^{'}(\tau )=0. \end{array} \right. \end{aligned}$$

Recalling the infinitesimal generator and its domain for B in Remark 1, it follows that

$$\begin{aligned} \frac{1}{2}\frac{\partial B}{\partial X}\bigg |_{X_t=0+}-\frac{1}{2}\frac{\partial B}{\partial X}\bigg |_{X_t=0-}&=\kappa \mathcal {A} B\big |_{\{X_t=0\}}\\&=\kappa \bigg [\lambda \frac{\partial B}{\partial X}\bigg |_{\{X_t=0\}}+\frac{\partial B}{\partial \tau }\bigg |_{\{X_t=0\}}\bigg ], \end{aligned}$$

where the last equation comes from (18). Obviously, we get

$$\begin{aligned} \alpha (\tau )=&\frac{1}{6}\tau ^3+\frac{1}{2}\lambda \tau ^2,\\ \beta ^{+}(\tau )+\beta ^{-}(\tau )=&-\tau =:\beta (\tau ),\\ \beta ^{+}(\tau )-\beta ^{-}(\tau )=&\kappa \tau ^2. \end{aligned}$$

After solving the equations, we complete this proof.

Next, we will provide some numerical results for the bond price under sticky Brownian motion with different sticky coefficients $\kappa$. More precisely, we set $\lambda =0.5$ as the common parameter. Noted that 0 is the sticky point which later causes some interesting analysis for sticky phenomenon. In addition, in the following three figures, the bond’s $\tau$ is considered with respect to three different conditions, respectively. In each of three figures, different sticky coefficients are further discussed.

Fig. 1

Bond price under sticky CIR process with different sticky coefficients $\kappa$ when $\tau =0.3$. The red, blue, green lines represent $\kappa =0$, $\kappa =0.5$, $\kappa =1$, respectively

Fig. 2

Bond price under sticky CIR process with different sticky coefficients $\kappa$ when $\tau =0.5$. The red, blue, green lines represent $\kappa =0$, $\kappa =0.5$, $\kappa =1$, respectively

Fig. 3

Bond price under sticky CIR process with different sticky coefficients $\kappa$ when $\tau =0.7$. The red, blue, green lines represent $\kappa =0$, $\kappa =0.5$, $\kappa =1$, respectively

Figure 1 shows the displays of the bond price in the case of $\tau =0.3$. Usually, bond price decreases as underlying interest rate increases. The red line represents the classical bond price with respect to sticky coefficient $\kappa =0$. It is interesting to see that around sticky point 0, the bond prices exhibit different behaviors. With a bigger sticky coefficient $\kappa$, the underlying interest rate will spend more time at 0, leading to an aggregation phenomenon and such phenomenon obviously influences the bond price which decreases weakly with respect to the “aggregated” interest rate.

As Bass (2014) said that for a corporation having a takeover offer at 10. The stock price is then likely to spend a great deal of time precisely at 10 but is not constrained to stay at 10. Thus 10 would be a sticky point for the solution of the stochastic differential equation that describes the stock price. For interest rate, we also take sticky phenomenon into consideration. Suppose an interest rate is modelled by the sticky Brownian motion. Then it is possible for bond price to have more choice at the sticky point because the underlying interest rate will spend more time at such fascinating point. But once interest rate passing sticky point, the bond price will exhibit normal principle immediately regardless of the sticky phenomenon. Similar analysis applies to Figs. 2 and 3 for $\tau =0.5$ and $\tau =0,7$, respectively.

For different bond’s term $\tau$, we can learn from Figs. 1, 2 and 3 that the bond price decreases as the bond’s term increases. This coincides with the classical results in bond pricing theory.

4 Conclusion

In this work, we have studied the Laplace transform of the first hitting time of sticky Brownian motion and their applications in optimal stopping and bond pricing. The first hitting time problems and related properties of sticky Brownian motion have been acquired by Laplace transform, strong Markov properties and the definition domain of its generator. It should be noticed that our method for solving first hitting time problems is applicable to other models (different boundary conditions). In optimal stopping application, we have solved the problem about which region sticky point belongs to, and as a corollary of result in Alvarez and Salminen, we have obtained the value function of the optimal stopping problem. To derive the bond price under sticky Brownian motion, by introducing the sharpo ratio, we calculate the closed-form solution. More explanations about the sticky phenomenon are shown by the numerical results. In the future study, it is significant for us to pursue: (1) Investigate the explicit value of optimal stopping based on sticky Brownian motion under more weak assumptions; (2) Extend our results under other sticky processes like sticky OU, sticky CIR; (3) Consider the option pricing of American styles, which needs to find the exact stopping time to maximize the value function.