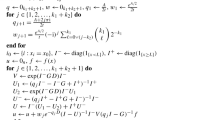1 Introduction

Parisian options were introduced by Chesney, Jeanblanc-Picqué and Yor [8] in 1997. They are similar to path-dependent barrier options where the contract is defined in terms of staying above or below a certain level for a fixed period of time, instead of just touching the barrier. The so-called excursion time denotes the time spent between two crossovers of the fixed barrier. On the other hand, one can also add up all excursion times and consider the so-called occupation time, which leads to the examination of cumulative Parisian options. This has been studied by Chesney et al. [8], Dassios and Wu [13], Cai et al. [6] and Zhang [22]. One motivation of introducing Parisian options lies in their insensitivity to influential agents; it is significantly more expensive to manipulate these kind of options. Variations of the Parisian option can be found in the double-sided Parisian option by Anderluh and Weide [2] or the double-barrier Parisian option by Dassios and Wu [12]. American-style Parisian options have been studied by Haber et al. [16] and Chesney and Gauthier [7]. Schröder [20, 21] studies Parisian excursions and finds a convolution representation for the Brownian minimum-length excursion law. Hedging strategies for Parisian options are developed as consequences of these results.

Even though Parisian options are not exchange-traded, they are used as building blocks in structured products, such as convertible bonds, which offer the holder the right but not the obligation to convert the bond at any time to a pre-specified number of shares. Most convertible bonds contain a call provision, allowing the issuer to buy back the bond at the so-called call price, in order to manage the company’s debt-equity ratio. Upon the issuer’s call, the holder either redeems at call price or converts. Apart from the hard call constraint, which protects the conversion privilege to be called away too early, the soft call constraint requires the stock price to be higher than a certain price level. This is sensitive to market manipulation by the issuer, which can be counteracted with the Parisian feature. The Parisian feature requires the stock price to stay above a level for a certain time. These callable convertible bonds with Parisian feature are commonly traded in the OTC market in Hong Kong; see [3, 18].

We introduce a new type of option, the so-called ParisianHit option, which in contrast to the Parisian option takes both the excursion time and the hitting time of a pre-specified barrier into account. One version of this modification, called MinParisianHit option, is triggered if either the age of an excursion above a level reaches a certain time or another barrier is hit before maturity. The MaxParisianHit on the other hand gets activated when both the excursion age exceeds a certain time and a barrier is hit. The key for pricing these kind of options lies in deriving the joint law of excursion and hitting time. Here, we study excursion and hitting time using a three-state semi-Markov model indicating whether the process is in a positive or negative excursion and above or below a fixed barrier. This will allow us to compute the double Laplace transform of these two stopping times, which can be inverted numerically using techniques as in Labart and Lelong [17]. Gauthier [14, 15] studies the first instant when a standard Brownian motion either spends consecutively more than a certain time above a certain level or reaches another level, that is, the minimum of Parisian and hitting time. Gauthier’s results are presented as Laplace transforms and coincide with our Lemmas 4.2 and 4.4 by setting \(\mu = 0\) and \(\tilde{h} \equiv 0\). In this paper, we generalise these results and the concept of the Parisian time by deriving the joint probability of the Parisian and hitting time. This allows us to also find the distribution of the maximum of Parisian and hitting time.

The paper is structured as follows. In Sect. 2, we motivate this paper with the financial application of pricing ParisianHit options. The pricing problem reduces to finding the joint distribution of Parisian and hitting time. We use the approach of a three-state semi-Markov model on a perturbed Brownian motion with drift, which has been introduced by Dassios and Wu [10], and present it in Sect. 3. This perturbed Brownian motion has the same behaviour as a drifted Brownian motion, except that it moves towards the other side of the barrier by a jump of size \(\epsilon\) each time it hits zero, disposing of the difficulty of the origin being regular. The semi-Markov process allows us to define an infinitesimal generator where the solution of the martingale problem provides us with the single Laplace transform of excursion and hitting time in Sect. 4. Dividing into the two possible cases in Sects. 4.1 and 4.2, we derive an explicit form of the double Laplace transform of hitting and Parisian time for drifted Brownian motion. Section 5 is devoted to the application to option pricing and explains the MinParisianHit and MaxParisianHit options in detail. Using results about the double Laplace transform, we are now able to price ParisianHit options.

2 Motivation

Following the Black–Scholes framework, let \((S_{t})_{t\geq 0}\) be the stock price process following a geometric Brownian motion, that is, solving the stochastic differential equation

$$ dS_{t} = \mu S_{t}\, dt + \sigma S_{t}\, dW_{t} $$

and fix a level \(L\). We define the times

$$\begin{aligned} &g_{L,t}(S)=\sup\{s\leq t: S_{s}=L\} ,\\ &d_{L,t}(S)=\inf\{s\geq t: S_{s}=L\} . \end{aligned}$$

The trajectory of \(S\) between \(g_{L,t}(S)\) and \(d_{L,t}(S)\) is the excursion of \(S\) at level \(L\) which straddles time \(t\). The variables \(g_{L,t}(S)\) and \(d_{L,t}(S)\) are called the left and right ends of the excursion. Assuming that the interest rate \(r\) is constant, the process representing the risk-neutral asset price is given by

$$ S_{t} = S_{0} e^{(r - \frac{\sigma ^{2}}{2}) t + \sigma W_{t}}, $$

solving the stochastic differential equation \(dS_{t} = r S_{t}\, dt + \sigma S_{t}\, dW_{t}\). We denote the equivalent martingale measure by \(\bar{\mathbb{Q}}\).

We define \(\tau_{L,d}^{+}(S)\) as the first time the age of an excursion above \(L\) for the price process is greater than or equal to \(d\), and \(H_{B}(S)\) as the first hitting time of a barrier \(B>L\), that is,

$$\begin{aligned} &\tau_{L,d}^{+} (S) = \inf\big\{ t\geq 0 : \mathbf{1}_{\{S_{t} >L\}}(t-g_{L,t}^{S}) \geq d\big\} ,\\ &H_{B}(S) = \inf \{ t \geq 0 : S_{t} = B\}. \end{aligned}$$

We introduce the notation

$$ m = \frac{1}{\sigma} \bigg(r - \frac{\sigma^{2}}{2} \bigg), \qquad \ell = \frac{1}{\sigma} \ln \frac{L}{S_{0}}, \qquad b = \frac{1}{\sigma} \ln \frac{B}{S_{0}} $$

and define the process \((Z_{t} )_{t \geq 0}= (W_{t} +mt)_{t \geq 0}\). This process \(Z\) contains a drift making it impossible for us to calculate the probabilities relating to the two stopping times exactly. Our strategy is now to tilt the sloped line back to a horizontal line. We write \(S_{t} = S_{0} e^{\sigma Z_{t}}\) with \(Z_{t} = W_{t} + mt\). The condition \(S_{t} \leq L \) becomes \(Z_{t} \leq \ell\). Using Girsanov’s theorem, we introduce a new probability measure ℚ that makes \(Z\) a ℚ-Brownian motion. The Radon–Nikodým derivative is given by

$$ \frac{d\mathbb{Q}}{d\mathbb{\bar{Q}}} \bigg|_{\mathcal{F}_{T}} = e^{mZ_{T} - \frac{m^{2}}{2}T} . $$
(2.1)

We define the first time at which the age of an excursion above the level \(\ell\) for the process \((Z_{t})_{t \geq 0}\) is greater than or equal to \(d\), that is,

$$\begin{aligned} & \tau_{\ell,d}^{+} (Z) = \inf\big\{ t\geq 0 : \mathbf{1}_{\{Z_{t}>\ell\}}(t-g_{\ell,t}) \geq d\big\} ,\\ & g_{\ell,t}(Z) = \sup \{u\leq t : Z_{u} =\ell \}. \end{aligned}$$

In the case where \(\ell=0\), we use the shortcuts \(\tau_{d}^{+}(Z)\) and \(g_{t}(Z)\).

Our so-called MinParisianHit option is triggered either when the age of an excursion above \(L\) reaches time \(d\) or a barrier \(B>L\) is hit by the underlying price process \(S\). More precisely, a MinParisianHit Up-and-In is activated at the minimum of both stopping times, that is, at \(\min ( \tau_{L,d}^{+}(S), H_{B}(S) )\). So a MinParisianHit Up-and-In call option has the payoff

$$ (S_{T} - K)^{+} \mathbf{1}_{\{\min ( \tau_{L,d}^{+}(S), H_{B}(S)) \leq T\}}, $$

where \(K\) denotes the strike price.

Using risk-neutral valuation and Girsanov’s change of measure (2.1), the price of this option can be written as

$$\begin{aligned} &\mathrm{minPHC}_{i}^{u} (S_{0},T,K,L,d,r) \\ & = e^{-(r+\frac{1}{2}m^{2})T} \\ &\quad{} \times \int_{\frac{1}{\sigma} \ln \frac{K}{S_{0}}}^{\infty}(S_{0} e^{\sigma z} - K) e^{m z} \mathbb{Q}_{0} \big[ Z_{T} \in dz, \min \big( \tau_{d}^{+}(Z), H_{b}(Z)\big) \leq T \big]. \end{aligned}$$
(2.2)

Hence, finding the fair price for a MinParisianHit option reduces to finding the joint distribution of the position at maturity and the minimum of Parisian and hitting times.

Our so-called MaxParisianHit option, on the other hand, is triggered when both the barrier \(B\) is hit and the excursion age exceeds duration \(d\) above \(L\). The payoff becomes

$$ (S_{T} - K)^{+} \mathbf{1}_{ \{ \max \{ \tau_{L,d}^{+}(S) , H_{B}(S) \} \leq T \} }, $$

and the option pricing problem can be reduced in a similar way, that is,

$$\begin{aligned} \begin{aligned} &\mathrm{maxPHC}_{i}^{u} (S_{0},T,K,L,d,r) \\ & = e^{-(r+\frac{1}{2}m^{2})T} \\ &\quad{} \times \int_{\frac{1}{\sigma} \ln \frac{K}{S_{0}}}^{\infty}(S_{0} e^{\sigma z} - K) e^{mz} \mathbb{Q}_{0} \big[Z_{T} \in dz, \max \big( \tau_{d}^{+}(Z), H_{b}(Z) \big) \leq T\big]. \end{aligned} \end{aligned}$$

This will be discussed in further detail in Sect. 5.2.

We can see from (2.2) and in further detail in Sect. 5 that both pricing problems can be solved by determining the joint distribution of hitting and Parisian time of a drifted Brownian motion. This is our focus for the next Sects. 3 and 4, where our main results are presented in Propositions 4.3 and 4.6.

Instead of finding a closed-form solution for the joint density of hitting and Parisian time, we focus on deriving the double Laplace transform, which uniquely determines the probability distribution.

3 Perturbed Brownian motion and the martingale problem

This section is the most technical one, and we give a brief outline of the steps that we follow. The property of the sample paths of Brownian motion of being regular around the origin zero results in the occurrence of infinitely many small excursions. In order to counteract this problem, we perturb the Brownian motion by a small jump at the origin. The construction can be found in (3.5), (3.6) below and follows Dassios and Wu [10]. Next, we construct a continuous-time finite-state Markov process in (3.7), which tracks whether the process is below 0, above a positive barrier \(b\), or between 0 and \(b\). This Markov process has an associated infinitesimal generator, and we formulate the corresponding martingale problem in (3.13). We construct a martingale of the form \(f (U_{t}(X),t) = e^{-\beta t} h(U_{t}(X))\). This function \(f\) looks arbitrary at first sight; however, it is chosen in such a way that after applying Doob’s optional sampling theorem in (3.15), it yields the Laplace transform of the desired stopping times.

It is important to note that this outlined procedure is not limited to ParisianHit option pricing within the Black–Scholes framework, but can be used to solve similar problems where the stochastic process does not follow a Brownian motion.

3.1 Definitions

For any stochastic process \(Y\), we define for fixed \(t>0\) the times

$$\begin{aligned} g_{t} (Y)& = \sup \{s \leq t : \text{sgn}(Y_{s}) \neq \text{sgn}(Y_{t})\}, \end{aligned}$$
(3.1)
$$\begin{aligned} d_{t} (Y)& = \inf \{s \geq t : \text{sgn}(Y_{s}) \neq \text{sgn}(Y_{t})\}, \end{aligned}$$
(3.2)
$$\begin{aligned} \tau_{d}^{+} (Y)& = \inf \big\{ t>0: \big(t-g_{t}(Y)\big) \mathbf{1}_{\{Y_{t} > 0\}} \geq d\big\} , \end{aligned}$$
(3.3)
$$\begin{aligned} H_{b}(Y) & = \inf \{t \geq 0 : Y_{t} = b \}. \end{aligned}$$
(3.4)

The time interval \(\left(d_{t}(Y), g_{t}(Y) \right)\) is the excursion interval straddling time \(t\), the time \(g_{t}(Y) - d_{t}(Y)\) is called the excursion time, and \(\tau_{d}^{+}(Y)\) denotes the first time the process \(Y\) spends time \(d\) above zero, the so-called Parisian time above zero.

Let \(W^{\mu}\), with \(W_{t}^{\mu}= W_{t} + \mu t\), be a Brownian motion with drift \(\mu \geq 0\) and \(W_{0}^{\mu}= 0\), where \(W\) is a standard Brownian motion under the probability measure ℚ. We notice that the origin zero is a regular point of the process, resulting in the occurrence of infinitely many small excursions. In order to counteract this problem, the perturbed Brownian motion \(W^{\epsilon, \mu}\) has been introduced by Dassios and Wu [10] as follows. Define the sequence of stopping times for \(\epsilon > 0\) and \(n \in \mathbb{N}_{0}\) by

$$\begin{aligned} \delta_{0} & = 0, \\ \sigma_{n} & = \inf \{ t > \delta_{n} : W_{t}^{\mu}= -\epsilon\}, \\ \delta_{n+1} & = \inf \{ t > \sigma_{n} : W_{t}^{\mu}= 0 \}. \end{aligned}$$
(3.5)

Define the perturbed drifted Brownian motion

$$ W_{t}^{\epsilon, \mu} =\textstyle\begin{cases} W_{t}^{\mu}+ \epsilon & \text{if } \delta_{n} \leq t < \sigma_{n},\\ W_{t}^{\mu}& \text{if } \sigma_{n} \leq t < \delta_{n+1}. \end{cases} $$
(3.6)

By introducing the jumps of size \(\epsilon\) towards the other side of zero whenever zero is hit by \(W^{\mu}\) we get a process \(W^{\epsilon, \mu}\) with a very clear structure of excursions above and below zero, making zero an irregular point. This construction has been introduced by Dassios and Wu [10]. See Fig. 1 for illustration. With the superscript \(\epsilon\) we denote quantities based on the perturbed process \(W^{\epsilon,\mu}\), for example, \(H_{b}(W^{\epsilon, \mu}) = \inf \{t \geq 0 : W_{t}^{\epsilon,\mu} = b \}\). By construction, we have \(P\)-a.s. that \(W_{t}^{\epsilon,\mu} \to W_{t}^{\mu}\) for all \(t\geq 0\) as \(\epsilon\) approaches zero. The quantities defined based on \(W^{\epsilon,\mu}\) also converge to those of the drifted Brownian motion \(W^{\mu}\). This has been proved in Dassios and Wu [10, 11] and Lim [19].

Fig. 1
figure 1

Sample paths of \(W^{\mu}\) and \(W^{\epsilon,\mu}\); see Dassios and Wu [10]

Full size image

3.2 Markov process construction

It is clear from the definition above that we are actually considering two states, namely the state when the stochastic process \(W^{\epsilon, \mu}\) is below zero and the state when it is above zero. Our final goal is to find the joint density of the Parisian time above or below zero and the hitting time \(H_{b}(W^{\mu})\) of a specified barrier \(b\). Hence, we construct an artificial absorbing state for the time the process \(W^{\epsilon, \mu}\) spends above the barrier \(b>0\). For each state above and below zero, we are now interested in the time it spends in it. We introduce a new process based on \(W^{\epsilon, \mu}\) by

$$ X_{t}= \textstyle\begin{cases} 2 & \text{if } W_{t}^{\epsilon,\mu} \geq b,\\ 1& \text{if } 0 < W_{t}^{\epsilon,\mu} < b,\\ -1 & \text{if } W_{t}^{\epsilon,\mu} \leq 0 . \end{cases} $$
(3.7)

Clearly, definitions (3.1)–(3.4) hold similarly for the process \(X\). We define state 2 to be an absorbing state, that is, once \(b\) is hit, the process does not return to state 1 any more.

Define \(U_{t}(X) := t - g_{t}(X)\) to be the time elapsed in the current state, for either state −1 or state 1 and 2 combined. Note that \(U_{t}(X)\) only distinguishes between above or below zero and converges to \(U_{t}(W^{\mu})= t - g_{t}(W^{\mu})\), the time elapsed above or below zero in the current excursion of the drifted Brownian motion \(W^{\mu}\). If the notation is unambiguous, then we abbreviate the definition of the time elapsed for the Brownian motion; so \(U_{t} = U_{t}(W^{\mu})\). \((X_{t}, U_{t}(X))\) becomes a Markov process. Hence, \(X\) is a three-state semi-Markov process with state space \(\{2, 1, -1 \}\). The transition intensities \(\lambda_{i,j}(u)\) for \(X\) satisfy

$$\begin{aligned} \mathbb{Q} [ X_{t+\Delta t} = j, i \neq j | X_{t} = i, U_{t}(X) = u ] &= \lambda_{i,j}(u)\Delta t + o(\Delta t), \\ \mathbb{Q} [ X_{t+\Delta t} = i | X_{t} = i, U_{t}(X) = u ] &= 1 - \sum\limits_{j \neq i} \lambda_{i,j}(u)\Delta t + o(\Delta t), \end{aligned}$$
(3.8)

for \(i , j = 2, 1, -1\). Define the survival probability and transition density by

$$\begin{aligned} & \bar{Q}_{i} (t) = e^{-\int_{0}^{t} \sum\limits_{j \neq i} \lambda_{i,j}(v)\, dv}, \end{aligned}$$
(3.9)
$$\begin{aligned} & q_{i,j}(t) = \lambda_{i,j}(t) \bar{Q}_{i}(t). \end{aligned}$$
(3.10)

In order to simplify notations, we define \(\hat{Q}_{i,j}(\beta)\) and \(\tilde{Q}_{i,j}(\beta)\) to be

$$\begin{aligned} & \hat{Q}_{i,j}(\beta) = \int_{0}^{d} e^{-\beta s} q_{i,j}(s)\, ds, \end{aligned}$$
(3.11)
$$\begin{aligned} & \tilde{Q}_{i,j}(\beta) = \int_{0}^{\infty}e^{-\beta s} q_{i,j}(s)\, ds. \end{aligned}$$
(3.12)

3.3 Martingale problem

Having constructed the process \(X\) and its time elapsed in the current state, we now consider a bounded function \(f: \{2,1,-1\} \times \mathbb{R}^{2} \rightarrow \mathbb{R}\). The infinitesimal generator \(\mathcal{A}\) is an operator making

$$ f\big(X_{t},U_{t}(X), t\big) - \int_{0}^{t} \mathcal{A} f\big(X_{s}, U_{s}(X), s\big)\, ds $$
(3.13)

a martingale. We use in the sequel the shortcuts \(\mathcal{A}f_{X_{t}}(U_{t}(X), t) = \mathcal{A} f(X_{t}, U_{t}(X), t) \) and \(f_{i}(z,u) = f(i,z,u)\). Hence, solving \(\mathcal{A} f = 0\) subject to certain conditions will provide us with martingales of the form \(f_{X_{t}}(U_{t}(X), t)\), to which we can apply the optional sampling theorem to obtain the Laplace transforms of interest. We have for the generator

$$\begin{aligned} \mathcal{A}f_{1} (u,t)& = \frac{ \partial f_{1}}{\partial t}(u,t) + \frac{ \partial f_{1}}{\partial u}(u,t) + \lambda_{1,1}(u) \big( f_{-1} (0,t) - f_{1}(u,t) \big) \\ & \quad{}+ \lambda_{1,2}(u) \big( f_{2}(u,t) - f_{1} (u,t) \big),\\ \mathcal{A}f_{-1} (u,t) &= \frac{ \partial f_{-1}}{\partial t} (u,t)+ \frac{ \partial f_{-1}}{\partial u}(u,t) + \lambda_{-1,1}(u) \big( f_{1} (0,t) - f_{-1}(u,t) \big) . \end{aligned}$$

Since we are not interested in what happens after the absorbing state 2 has been reached, we do not define \(\mathcal{A}f_{2}\), the generator starting from state 2.

We assume the function \(f\) to have the form \(f_{i} (u,t) = e^{-\beta t} h_{i}(u)\), where \(\beta \in \mathbb{R}_{+}\) is a positive constant, and solve \(\mathcal{A}f \equiv 0\) with the constraints \(h_{1}(d) = B\) and \(h_{-1}(\infty) = 0\) with constant \(B\). Since state 2 is an absorbing state, we may assign any bounded function to it. We choose \(h_{2}(u) = A \tilde{h}(u)\), where \(A\) is an arbitrary constant. The function \(\tilde{h}\) will be motivated and defined in the proof of Proposition 4.3. The intuition behind choosing the constraint \(h_{-1}(\infty) = 0\) is that since we are not concerned with the time elapsed below zero, we let the excursion window below zero approach infinity. \(A\) and \(B\) on the other hand are constants, indicating different scenarios and clarified in Lemma 3.3.

The reason for choosing the above form for the function \(f\) is our objective to derive the Laplace transform of stopping times.

Lemma 3.1

Using the conditions above, the initial value \(f_{1}(0,0) = h_{1}(0)\) is given by

$$ h_{1}(0) = \frac{ B e^{-\beta d}\bar{Q}_{1} (d) + A \int_{0}^{d} e^{-\beta w} \tilde{h}(w) q_{1,2}(w)\, dw }{ 1 - \tilde{Q}_{-1,1}(\beta) \hat{Q}_{1,-1}(\beta)}. $$

Proof

\(\mathcal{A}f \equiv 0\) transforms into

$$\begin{aligned} & \frac{dh_{1}(u)}{du} - \big(\beta + \lambda_{1,-1}(u) + \lambda_{1,2}(u)\big) h_{1}(u) +\lambda_{1,-1}(u) h_{-1}(0)+ A \lambda_{1,2}(u) \tilde{h}(u) = 0,\\ & \frac{dh_{-1}(u)}{du} - \big(\beta +\lambda_{-1,1}(u)\big) h_{-1}(u) + \lambda_{-1,1}(u) h_{1}(0) = 0. \end{aligned}$$

Using the integrating factor method for ordinary differential equations and the constraints, we find

$$\begin{aligned} h_{1}(u)& = B e^{-\int_{u}^{d} \beta \lambda_{1,-1}(v) + \lambda_{1,2}(v) dv} + \int_{u}^{d} \big( \lambda_{1,-1}(w) h_{-1}(0) + A \lambda_{1,2}(w) \tilde{h}(w) \big) \\ &\quad{}\times e^{-\int_{u}^{w} \beta \lambda_{1,-1}(v) + \lambda_{1,2}(v)\, dv}\, dw, \quad 0 \leq u \leq d\\ h_{-1}(u) &= h_{1}(0) \int_{u}^{\infty}\lambda_{-1,1}(w) e^{-\int_{u}^{w} \beta + \lambda_{-1,1}(v)\, dv}\, dw, \quad u \geq 0. \end{aligned}$$

Setting \(u=0\) and solving the system of equations give us

$$\begin{aligned} &h_{1}(0)\\ &= \frac{ B e^{-\int_{0}^{d} \beta + \lambda_{1,-1}(v) +\lambda_{1,2}(v)\, dv} + A \int_{0}^{d} \lambda_{1,2}(w) \tilde{h}(w) e^{-\int_{0}^{w} \beta + \lambda_{1,-1}(v) +\lambda_{1,2}(v)\, dv}\, dw }{ 1 - \int_{0}^{\infty}\lambda_{-1,1}(w) e^{-\int_{0}^{w} \beta + \lambda_{-1,1}(v) \,dv}\, dw \int_{0}^{d} \lambda_{1,-1} (w) e^{-\int_{0}^{w} \beta + \lambda_{1,-1}(v) + \lambda_{1,2}(v) \,dv}\, dw }\\ & = \frac{ B e^{-\beta d}\bar{Q}_{1} (d) + A \int_{0}^{d} e^{-\beta w} \tilde{h}(w) q_{1,2}(w)\, dw }{ 1 - \tilde{Q}_{-1,1}(\beta) \hat{Q}_{1,-1}(\beta)}, \end{aligned}$$

where \(\bar{Q}_{i}(t)\), \(q_{1,2}(t)\), \(\lambda_{i,j}(u)\), \(\hat{Q}_{i,j}(\beta)\) and \(\tilde{Q}_{i,j}(\beta)\) have been defined in (3.9), (3.10), (3.8), (3.11) and (3.12). □

For the transition densities, we use results from Borodin and Salminen [5, formulae (2.0.2), (3.0.2) and (3.0.6)]. Without loss of generality, we assume that \(b> \epsilon > 0\). Therefore, it is not possible to go straight from state −1 to state 2 and vice versa, that is, \(q_{-1,2} (t) = q_{2,-1}(t) = 0\). With \(H_{a,b}(Y) = \inf \{t \geq 0 : Y_{t} = a \text{ or } Y_{t} = b \}\) being the first exit time of the interval \((a,b)\) with \(a,b \in \mathbb{R}\) and \(a < b\) by a general stochastic process \(Y\), and the function

$$ \ss_{t}(x,y) = \sum\limits_{k=-\infty}^{\infty}\frac{(2k+1)y-x}{\sqrt{2\pi t^{3}}} e^{-\frac{((2k+1)y-x)^{2}}{2t}} $$

(see e.g. Borodin and Salminen [5, Appendix 2, Theta functions of an imaginary argument and related functions]), the quantities \(q_{i,j}(t)\), \(\hat{Q}_{i,j}(\beta)\), \(\tilde{Q}_{i,j}(\beta)\) and \(\bar{Q}_{i}(d)\) can be calculated as

$$\begin{aligned} q_{1,-1}(t) &= \frac{1}{dt}\mathbb{P}_{\epsilon}[H_{0,b}(W^{\epsilon, \mu}) \in dt, W_{H_{0,b}}^{\epsilon,\mu} = 0] \\ &= e^{- \mu \epsilon - \frac{\mu^{2} t}{2}} \mathrm{ss}_{t}(b-\epsilon, b)\\ & = e^{- \mu \epsilon - \frac{\mu^{2} t}{2}} \sum\limits_{k = - \infty}^{\infty} \frac{\epsilon + 2 k b}{\sqrt{2 \pi t^{3}}} e^{-\frac{ (\epsilon + 2 k b)^{2}}{2t}}\\ &= e^{-\mu \epsilon - \frac{\mu^{2} t}{2}} \sum\limits_{k=0}^{\infty}\bigg( \frac{2kb+\epsilon}{\sqrt{2 \pi t^{3}}} e^{-\frac{(2kb+ \epsilon)^{2}}{2t}} - \frac{2kb -\epsilon}{\sqrt{2 \pi t^{3}}} e^{-\frac{(2kb -\epsilon)^{2}}{2t}} \bigg) \\ &\quad{}- \frac{\epsilon}{\sqrt{2\pi t^{3}}} e^{-\frac{(\epsilon+\mu t)^{2}}{2t}}, \\ q_{-1,1}(t) &= \frac{ \epsilon}{\sqrt{2 \pi t^{3}}} e^{-\frac{(\epsilon - \mu t)^{2}}{2t}}, \\ q_{1,2}(t)& = \frac{1}{dt}\mathbb{P}_{\epsilon}[H_{0,b}(W^{\epsilon, \mu}) \in dt, W_{H_{0,b}}^{\epsilon,\mu} = b] \\ &= e^{\mu(b- \epsilon) - \frac{\mu^{2} t}{2}} \mathrm{ss}_{t}(\epsilon, b)\\ & = e^{\mu(b- \epsilon) - \frac{\mu^{2} t}{2}} \sum\limits_{k = - \infty}^{\infty} \frac{b - \epsilon + 2 k b}{\sqrt{2 \pi t^{3}}} e^{-\frac{( b- \epsilon + 2 k b)^{2}}{2t}}\\ & = e^{\mu(b- \epsilon) - \frac{\mu^{2} t}{2}} \\ &\quad{}\times \sum\limits_{k = 0}^{\infty} \bigg(\frac{(2k+1)b - \epsilon}{\sqrt{2\pi t^{3}}} e^{-\frac{((2k+1)b- \epsilon)^{2}}{2t}} - \frac{(2k+1)b + \epsilon}{\sqrt{2\pi t^{3}}} e^{-\frac{((2k+1)b+\epsilon)^{2}}{2t}}\bigg), \\ \hat{Q}_{1,2}(\beta) & = \sum\limits_{k = 0}^{\infty} \Bigg(e^{(\mu - (2k+1)\sqrt{2\beta + \mu^{2}}) b} \\ &\quad{} \times \bigg( e^{\epsilon(\sqrt{2\beta + \mu^{2}}-\mu)} \mathcal{N} \Big({ -} \frac{(2k+1)b - \epsilon}{\sqrt{d}} + \sqrt{(2\beta+ \mu^{2})d} \Big) \\ & \qquad\quad{}- e^{-\epsilon(\sqrt{2\beta + \mu^{2}}+\mu)} \mathcal{N} \Big( {-} \frac{(2k+1)b + \epsilon}{\sqrt{d}} + \sqrt{(2\beta+ \mu^{2})d} \Big) \Bigg) \\ &\quad {}+ e^{(\mu + (2k+1)\sqrt{2\beta + \mu^{2}}) b} \\ &\quad {}\times \Bigg( e^{-\epsilon(\sqrt{2\beta + \mu^{2}}+\mu)} \mathcal{N} \Big( {-} \frac{(2k+1)b - \epsilon}{\sqrt{d}} - \sqrt{(2\beta+ \mu^{2})d} \Big) \\ & \qquad\quad{} - e^{\epsilon(\sqrt{2\beta + \mu^{2}}-\mu)} \mathcal{N} \Big( {-} \frac{(2k+1)b + \epsilon}{\sqrt{d}} - \sqrt{(2\beta+ \mu^{2})d} \Big) \bigg)\Bigg), \\ \tilde{Q}_{-1,1}(\beta) &= e^{(\mu -\sqrt{2 \beta+\mu^{2}}) \epsilon},\\ \hat{Q}_{1,-1}(\beta) &= \int_{s = 0}^{d} \Bigg(e^{-\beta s} e^{-\mu \epsilon - \frac{\mu^{2} s}{2}} \sum\limits_{k=0}^{\infty}\bigg( \frac{2kb+\epsilon}{\sqrt{2 \pi s^{3}}} e^{-\frac{(2kb+\epsilon)^{2}}{2s}} - \frac{2kb -\epsilon}{\sqrt{2 \pi s^{3}}} e^{-\frac{(2kb -\epsilon)^{2}}{2s}} \bigg) \\ & \qquad\qquad{} - e^{-\beta s } \frac{\epsilon}{\sqrt{2\pi s^{3}}} e^{-\frac{(\epsilon+\mu t)^{2}}{2s}}ds\Bigg)\\ & = e^{-\mu \epsilon} \Bigg( \sum\limits_{k = 0}^{\infty}\bigg( e^{-\sqrt{2\beta +\mu^{2}}(2kb + \epsilon) } \mathcal{N} \Big({-} \frac{2kb + \epsilon}{\sqrt{d}}+ \sqrt{(2 \beta + \mu^{2}) d} \Big) \\ & \qquad\qquad\qquad{} + e^{\sqrt{2\beta +\mu^{2}}(2kb + \epsilon) } \mathcal{N} \Big({-} \frac{2kb + \epsilon}{\sqrt{d}} - \sqrt{(2 \beta + \mu^{2}) d} \Big) \\ & \qquad\qquad\qquad{} - e^{-\sqrt{2\beta +\mu^{2}}(2kb - \epsilon) } \mathcal{N} \Big( {-} \frac{2kb - \epsilon}{\sqrt{d}} + \sqrt{(2 \beta + \mu^{2}) d} \Big) \\ & \qquad\qquad\qquad{} - e^{\sqrt{2\beta +\mu^{2}}(2kb - \epsilon) } \mathcal{N} \Big( {-} \frac{2kb - \epsilon}{\sqrt{d}}- \sqrt{(2 \beta + \mu^{2}) d} \Big)\bigg) \\ & \qquad\qquad{} - e^{-\sqrt{2\beta +\mu^{2}}\epsilon} \mathcal{N} \Big( {-}\frac{\epsilon}{\sqrt{d}} +\sqrt{(2\beta + \mu^{2})d} \Big)\\ &\qquad\qquad{}- e^{\sqrt{2\beta +\mu^{2}}\epsilon} \mathcal{N} \Big( {-}\frac{\epsilon}{\sqrt{d}} -\sqrt{(2\beta + \mu^{2})d} \Big) \Bigg), \\ \bar{Q}_{1}(d) &= \mathbb{P}_{\epsilon}[H_{0}(W^{\epsilon, \mu})>d, H_{b}(W^{\epsilon, \mu})>d] \\ & = \int_{d}^{\infty}e^{-\frac{\mu^{2}t}{2}} \big( e^{-\mu \epsilon} \mathrm{ss}_{t}(b-\epsilon, b) +e^{\mu(b- \epsilon)} \mathrm{ss}_{t}(\epsilon, b) \big) dt\\ & = \sum\limits_{k = 0}^{\infty}\Bigg( e^{-\mu (2kb + 2\epsilon) } \mathcal{N} \Big( \frac{2kb + \epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big) - e^{2kb\mu } \mathcal{N} \Big( {-}\frac{2kb + \epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big) \\ & \qquad\quad{} - e^{-2kb\mu } \mathcal{N} \Big( \frac{2kb - \epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big) \\ & \qquad\quad{} + e^{\mu(2kb - 2\epsilon) } \mathcal{N} \Big( {-}\frac{2kb - \epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big) \\ & \qquad\quad{} + e^{-2kb\mu} \mathcal{N}\Big( \frac{(2k+1)b-\epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big) \\ & \qquad\quad{}- e^{2kb\mu + 2\mu(b-\epsilon)} \mathcal{N}\Big( {-}\frac{(2k+1)b-\epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big)\\ &\qquad\quad{} - e^{-2kb\mu - 2 \mu \epsilon} \mathcal{N}\Big( \frac{(2k+1)b+\epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big) \\ &\qquad\quad{}+ e^{2kb\mu + 2 \mu b} \mathcal{N}\Big( {-}\frac{(2k+1)b+\epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big) \Bigg) \\ &\quad{} - e^{-2\mu \epsilon} \mathcal{N} \Big( \frac{\epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big) + \mathcal{N}\Big( {-} \frac{\epsilon}{\sqrt{d}} - \mu \sqrt{d} \Big). \end{aligned}$$

Remark 3.2

With the subscript behind the expected value, we denote the starting position of any stochastic process \(Y\), that is, for any function \(f\),

$$ \mathbb{E}_{x} [f(Y)] = \mathbb{E}[f(Y); Y_{0} = x]. $$

In the case of no subscript, we assume the process to start at zero. The superscript announces under which probability measure we take the expectation, that is,

$$ \mathbb{E}^{\mathbb{P}} [f(Y)] = \int_{-\infty}^{\infty}f(x)\, \mathbb{P}[Y \in dx]. $$

If not specified, the notation should be clear.

3.4 An important lemma

In the following, we present an important lemma, which is the main building block in pricing ParisianHit options.

Lemma 3.3

For the perturbed Brownian motion with drift, we find the Laplace transform to be

$$\begin{aligned} &A \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\epsilon, \mu})} \tilde{h}\big(U_{H_{b}}(W^{\epsilon,\mu})\big) \mathbf{1}_{\{H_{b}(W^{\epsilon, \mu}) < \tau_{d}^{+}(W^{\epsilon,\mu})\}} \Big] \\ &\quad{} + B \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\epsilon,\mu})} \mathbf{1}_{\{\tau_{d}^{+}(W^{\epsilon,\mu}) < H_{b}(W^{\epsilon, \mu})\}} \Big] \\ &= \frac{ B e^{-\beta d}\bar{Q}_{1} (d) + A \int_{0}^{d} e^{-\beta w} \tilde{h}(w) q_{1,2}(w)\, dw }{ 1 - \tilde{Q}_{-1,1}(\beta) \hat{Q}_{1,-1}(\beta)}, \end{aligned}$$
(3.14)

where \(A\) and \(B\) are arbitrary constants.

Proof

Solving \(\mathcal{A} f \equiv 0\) with the constraints \(h_{1}(d) = B\) and \(h_{-1}(\infty)=0\) provides us with a martingale of the form \(\hat{M}_{t} := f_{X_{t}} (U_{t}(X), t) = e^{-\beta t} h_{X_{t}} (U_{t}(X))\). Recall that state 2, indicating the perturbed Brownian motion to be above the barrier \(b\), is an absorbing state. Hence, we may choose \(h_{2}\) to be any arbitrary bounded function. We assign \(h_{2}\) to be \(h_{2}(u) = A \tilde{h}(u)\), where \(A\) is a constant, and \(\tilde{h}\) is a bounded function, which will be specified in the proof of Proposition 4.3.

Let \(\tau(W^{\epsilon, \mu}) = \min ( H_{b}(W^{\epsilon, \mu}), \tau_{d}^{+}(W^{\epsilon,\mu}) )\). Then the optional sampling theorem on the martingale \(\hat{M}\) with the stopping time \(\tau(W^{\epsilon, \mu}) \wedge t\) yields

$$ \mathbb{E}_{\epsilon}^{\mathbb{Q}}[\hat{M}_{\tau(W^{\epsilon, \mu}) \wedge t} ] = \mathbb{E}_{\epsilon}^{\mathbb{Q}}[\hat{M}_{0}]. $$
(3.15)

The function \(h_{1}\) is continuous and therefore bounded on the compact interval \([0,d]\). Hence, there exists a constant \(K\) such that \(| h_{1}(U_{t}(X)) | \leq K\) for all \(U_{t}(X) \in [0,d]\). Furthermore, we have assumed that \(h_{2}\) is bounded. Therefore, Lebesgue’s dominated convergence theorem applies, yielding for the left-hand side of (3.15) that

$$\begin{aligned} &\lim\limits_{t \rightarrow \infty} \mathbb{E}_{\epsilon}^{\mathbb{Q}}[ \hat{M}_{\tau(W^{\epsilon, \mu}) \wedge t} ] \\ &= \mathbb{E}_{\epsilon}^{\mathbb{Q}}[\hat{M}_{\tau(W^{\epsilon, \mu})} ] \\ & = \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\epsilon, \mu})} h_{2} \big(U_{H_{b}(W^{\epsilon, \mu})}(W^{\epsilon, \mu})\big) \mathbf{1}_{\{H_{b}(W^{\epsilon, \mu}) < \tau_{d}^{+}(W^{\epsilon,\mu})\}} \Big] \\ & \phantom{=:}{} + \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\epsilon,\mu})} h_{1}\big(U_{\tau_{d}^{+}(W^{\epsilon,\mu})}(W^{\epsilon, \mu})\big)\mathbf{1}_{\{\tau_{d}^{+}(W^{\epsilon,\mu}) < H_{b}(W^{\epsilon, \mu})\}} \Big] \\ & = A \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\epsilon, \mu})} \tilde{h}\big(U_{H_{b}(W^{\epsilon, \mu})}(W^{\epsilon, \mu})\big) \mathbf{1}_{\{H_{b}(W^{\epsilon, \mu}) < \tau_{d}^{+}(W^{\epsilon,\mu})\}} \Big] \\ & \phantom{=:}{} + B \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\epsilon,\mu})} \mathbf{1}_{\{\tau_{d}^{+}(W^{\epsilon,\mu}) < H_{b}(W^{\epsilon, \mu})\}}\Big]. \end{aligned}$$

For the right-hand side of (3.15), we have \(\mathbb{E}_{\epsilon}^{\mathbb{Q}}[\hat{M}_{0}] = h_{1}(0)\), and the claim follows from Lemma 3.1. □

4 Double Laplace transform of Parisian and hitting times

This section is the main part of the paper and devoted to finding the double Laplace transform of Parisian and hitting times. We first derive the limiting Laplace transform through results on the perturbed process and distinguish between the two possible scenarios \(H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\) and \(\tau_{d}^{+}(W^{\mu}) < H_{b}(W^{\mu})\).

Proposition 4.1

The Laplace transform of the hitting and Parisian times for a drifted Brownian motion \(W^{\mu}\) is given by

$$\begin{aligned} &A \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\mu})} \tilde{h}(U_{H_{b}}) \mathbf{1}_{\{H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\}} \Big] + B \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\mu})} \mathbf{1}_{\{\tau_{d}^{+}(W^{\mu}) < H_{b}(W^{\mu})\}}\Big] \\ &= \Bigg( Be^{-\beta d} \bigg(\sum\limits_{k = 0}^{\infty} 2 \Big(z(k,0,\mu) - e^{\mu b} z(k+\frac{1}{2},0,\mu) \Big) - z(0,0,\mu) \bigg) \\ &\qquad{}+ A \int_{0}^{d} e^{-\beta w} \tilde{h}(w) \sqrt{\frac{2}{\pi w^{3}}} e^{\mu b - \frac{\mu^{2}w}{2}} \sum\limits_{k = 0}^{\infty} \bigg( \frac{(2k+1)^{2}b^{2}}{w} - 1 \bigg) e^{-\frac{(2k+1)^{2}b^{2}}{2w}}\,dw \Bigg) \\ &\quad{}\times \!\Bigg( \! \sum\limits_{k=0}^{\infty}2\Big( z(k,\beta,\mu) + \sqrt{2\beta + \mu^{2}} e^{-\sqrt{2\beta + \mu^{2}}2kb}\! \Big) - z(0,\beta,\mu) - 2\sqrt{2 \beta + \mu^{2}} \Bigg)^{-1}, \end{aligned}$$

where the function \(z\) is defined as

$$\begin{aligned} z(k,\beta,\mu ) & = \sqrt{\frac{2}{\pi d}} e^{-\frac{(2\beta + \mu^{2})d}{2} - \frac{2 (kb)^{2}}{d}} \\ &\quad{} - \sqrt{2 \beta + \mu^{2}} \Bigg( e^{\sqrt{2 \beta + \mu^{2} }2kb} \mathcal{N} \Big( {-} \frac{2kb}{\sqrt{d}} - \sqrt{(2 \beta+ \mu^{2}) d} \Big) \\ &\qquad\qquad\qquad\quad{}+ e^{- \sqrt{2 \beta + \mu^{2}}2kb} \mathcal{N} \Big( \frac{2kb}{\sqrt{d}} - \sqrt{(2 \beta + \mu^{2}) d} \Big) \Bigg). \end{aligned}$$
(4.1)

Proof

In order to find the Laplace transform for the drifted Brownian motion, we take the limit from the results about \(W^{\epsilon,\mu}\) and therefore let \(\epsilon\) approach zero in (3.14). In particular, notice that by construction we have \(P\)-a.s. that \(W_{t}^{\epsilon,\mu} \to W_{t}^{\mu}\) for all \(t\geq 0\) as \(\epsilon\) approaches zero. The quantities defined based on \(W^{\epsilon,\mu}\) also converge to those of the drifted Brownian motion \(W^{\mu}\). Furthermore, \(e^{-\beta H_{b}(W^{\mu})} \tilde{h}(U_{H_{b}})\) and \(e^{-\beta \tau_{d}^{+}(W^{\mu})}\) are both bounded functions. Recall that \(U_{H_{b}}\) is the abbreviation for \(U_{H_{b}(W^{ \mu})}(W^{\mu})\). Thus, dominated convergence applies to get the result for \(W^{\mu}\), that is,

$$\begin{aligned} & A \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\mu})} \tilde{h}(U_{H_{b}}) \mathbf{1}_{\{H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\}}\Big] + B \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\mu})} \mathbf{1}_{\{\tau_{d}^{+}(W^{\mu}) < H_{b}(W^{\mu})\}} \Big] \\ & = \lim\limits_{\epsilon \rightarrow 0}\Big( A \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\epsilon, \mu})} \tilde{h}\big(U_{H_{b}(W^{\epsilon, \mu})}(W^{\epsilon, \mu})\big) \mathbf{1}_{\{H_{b}(W^{\epsilon, \mu}) < \tau_{d}^{+}(W^{\epsilon,\mu})\}} \Big] \\ & \qquad\qquad{} + B \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\epsilon,\mu})} \mathbf{1}_{\{\tau_{d}^{+}(W^{\epsilon,\mu}) < H_{b}(W^{\epsilon, \mu})\}} \Big]\Big) \\ & = \lim\limits_{\epsilon \rightarrow 0} \frac{ B e^{-\beta d}\bar{Q}_{1} (d) + A \int_{0}^{d} e^{-\beta w} \tilde{h}(w) q_{1,2}(w)\, dw }{ 1 - \tilde{Q}_{-1,1}(\beta) \hat{Q}_{1,-1}(\beta)}. \end{aligned}$$
(4.2)

We refer to Dassios and Wu [10, 11] and Lim [19] for further details. Therefore, letting \(\epsilon\) go to zero in (3.14) will provide us with the Laplace transform for the drifted Brownian motion. In order to apply L’Hôpital’s rule, we take the derivative with respect to \(\epsilon\) and find for the denominator of (3.14) that

$$\begin{aligned} & \frac{\partial}{\partial \epsilon} \big( 1 - \tilde{Q}_{-1,1}(\beta) \hat{Q}_{1,-1}(\beta)\big) \\ & \underset{\epsilon \rightarrow 0}{\longrightarrow}\sum\limits_{k = 0}^{\infty} \ \Bigg( 2 \sqrt{2 \beta + \mu^{2}} \bigg(e^{-\sqrt{2 \beta + \mu^{2} }2kb} \mathcal{N} \Big( {-} \frac{2kb}{\sqrt{d}} + \sqrt{(2 \beta+ \mu^{2}) d} \Big) \\ &\qquad\qquad\qquad\qquad\qquad{}- e^{\sqrt{2 \beta + \mu^{2}}2kb} \mathcal{N} \Big( {-} \frac{2kb}{\sqrt{d}} - \sqrt{(2 \beta + \mu^{2}) d} \Big) \bigg) \\ &\qquad\qquad{}+ 2 \sqrt{\frac{2}{\pi d}} e^{-\frac{(2\beta + \mu^{2})d}{2} - \frac{2 (kb)^{2}}{d}}\Bigg) \\ &\qquad{}- 2\sqrt{2 \beta + \mu^{2}} \mathcal{N}\Big( \sqrt{(2 \beta + \mu^{2})d} \Big) - \sqrt{\frac{2}{\pi d}}e^{-\frac{(2\beta + \mu^{2})d}{2}} \\ &= \sum\limits_{k = 0}^{\infty} \Bigg( 2 \sqrt{2 \beta + \mu^{2}} \bigg(e^{-\sqrt{2 \beta + \mu^{2} }2kb} - e^{-\sqrt{2 \beta + \mu^{2} }2kb} \mathcal{N} \Big( \frac{2kb}{\sqrt{d}} - \sqrt{(2 \beta+ \mu^{2}) d} \Big) \\ &\qquad\qquad\qquad\qquad\quad{}- e^{\sqrt{2 \beta + \mu^{2}}2kb} \mathcal{N} \Big( {-} \frac{2kb}{\sqrt{d}} - \sqrt{(2 \beta + \mu^{2}) d} \Big) \bigg) \\ &\qquad\qquad{}+ 2 \sqrt{\frac{2}{\pi d}} e^{-\frac{(2\beta + \mu^{2})d}{2} - \frac{2 (kb)^{2}}{d}}\Bigg) \\ &\quad{}- 2\sqrt{2 \beta + \mu^{2}} \mathcal{N}\Big( \sqrt{(2 \beta + \mu^{2})d} \Big) - \sqrt{\frac{2}{\pi d}}e^{-\frac{(2\beta + \mu^{2})d}{2}}. \end{aligned}$$
(4.3)

For the numerator, we find

$$\begin{aligned} &\frac{\partial}{\partial \epsilon} \bar{Q}_{1}(d) \\ &\underset{\epsilon \rightarrow 0}{\longrightarrow}\sum\limits_{k=0}^{\infty}\Bigg( 2 \sqrt{\frac{2}{\pi d}} e^{-\frac{(2kb)^{2}}{2d} - \frac{\mu^{2} d}{2}} - 2 \sqrt{\frac{2}{\pi d}} e^{-\frac{(2k+1)^{2} b^{2}}{2d} - \frac{\mu^{2} d}{2} + \mu b} \\ &\qquad\qquad{}+ 2 \mu \bigg( e^{(2k+1) \mu b + \mu b} \mathcal{N} \Big( {-} \frac{(2k+1)b}{\sqrt{d}} - \mu \sqrt{d} \Big) \\ &\qquad\qquad\qquad\quad{}+ e^{-(2k+1) \mu b + \mu b} \mathcal{N} \Big( \frac{(2k+1)b}{\sqrt{d}} - \mu \sqrt{d} \Big) \\ &\qquad\qquad\qquad\quad{}- e^{2k\mu b} \mathcal{N} \Big( {-} \frac{2kb}{\sqrt{d}} - \mu \sqrt{d} \Big) - e^{-2k\mu b} \mathcal{N} \Big( \frac{2kb}{\sqrt{d}} - \mu \sqrt{d} \Big)\bigg) \Bigg) \\ &\qquad{}- \sqrt{\frac{2}{\pi d}} e^{-\frac{\mu^{2} d}{d}} + 2 \mu \mathcal{N} \big( {-} \mu \sqrt{d} \big) \end{aligned}$$
(4.4)

and

$$ \frac{\partial}{\partial \epsilon} q_{1,2}(t) \underset{\epsilon \rightarrow 0}{\longrightarrow} \sqrt{\frac{2}{\pi t^{3}}} e^{\mu b - \frac{\mu^{2}t}{2}} \sum\limits_{k = 0}^{\infty} \left( \frac{(2k+1)^{2}b^{2}}{t} - 1 \right) e^{-\frac{(2k+1)^{2}b^{2}}{2t}}. $$
(4.5)

Inserting (4.3)–(4.5) into (4.2) yields the proposition. □

4.1 Case \(H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\)

In the case where the barrier \(b\) is hit before the excursion above zero of length \(d\) is completed, we have found the single Laplace transform of the hitting time of the drifted Brownian motion in Proposition 4.1.

Lemma 4.2

$$\begin{aligned} &\mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\mu})} \tilde{h}(U_{H_{b}}) \mathbf{1}_{\{H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\}}\Big] \\ &= \frac{ \int_{0}^{d} e^{-\beta w} \tilde{h}(w) \sqrt{\frac{2}{\pi w^{3}}} e^{\mu b - \frac{\mu^{2}w}{2}} \sum_{k = 0}^{\infty} ( \frac{(2k+1)^{2}b^{2}}{w} - 1 ) e^{-\frac{(2k+1)^{2}b^{2}}{2w}}\,dw }{ \sum_{k=0}^{\infty}2( z(k,\beta,\mu) + \sqrt{2\beta + \mu^{2}} e^{-\sqrt{2\beta + \mu^{2}}2kb} ) - z(0,\beta,\mu) - 2\sqrt{2 \beta + \mu^{2}} }, \end{aligned}$$

where \(z\) is defined as in (4.1).

We are now interested in finding the double Laplace transform of hitting and Parisian times in the case that \(b\) is hit before the excursion exceeds \(d\). We make an appropriate choice of the bounded function \(\tilde{h}\), where the intuition will become clear in the proof of the following proposition.

Proposition 4.3

The double Laplace transform of the hitting and Parisian times of a drifted Brownian motion \(W^{\mu}\), where \(H_{b}(W^{\mu})<\tau_{d}^{+}(W^{\mu})\), is

$$\begin{aligned} &\mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\mu}) -\gamma \tau_{d}^{+}(W^{\mu})} \mathbf{1}_{\{H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\}} \Big] \\ &=\int_{0}^{d} e^{-\beta w} \Bigg( e^{-\gamma d} \bigg(1 - e^{-2 \mu b} \mathcal{N} \Big( \frac{\mu (d - w) - b}{\sqrt{d - w}} \Big) - \mathcal{N} \Big( \frac{ - \mu(d - w) - b}{\sqrt{d - w}} \Big) \bigg) \\ &\qquad{}+ \mathbb{E}_{0}^{\mathbb{Q}}\big[ e^{-\gamma \hat{\tau}_{d}^{+}}\big] \bigg( e^{-(\sqrt{ 2 \gamma + \mu^{2} } + \mu) b} \mathcal{N} \Big( \sqrt{ (2 \gamma + \mu^{2}) (d- w)} - \frac{b}{\sqrt{d-w}} \Big) \\ &\qquad{}+ e^{(\sqrt{ 2 \gamma + \mu^{2} } - \mu) b} \mathcal{N} \Big( {-} \sqrt{ (2 \gamma + \mu^{2}) (d- w)} - \frac{b}{\sqrt{d-w}} \Big) \bigg) \Bigg) \\ &\quad{}\times \sqrt{\frac{2}{\pi w^{3}}} e^{\mu b - \frac{\mu^{2}w}{2}} \sum\limits_{k = 0}^{\infty} \bigg( \frac{(2k+1)^{2}b^{2}}{w} - 1 \bigg) e^{-\frac{(2k+1)^{2}b^{2}}{2w}}\,dw \\ &\quad{}\times \bigg( \sum\limits_{k=0}^{\infty}2\Big( z(k,\beta,\mu) + \sqrt{2\beta \!+ \mu^{2}} e^{-\sqrt{2\beta + \mu^{2}}2kb}\! \Big) - z(0,\beta,\mu) - 2\sqrt{2 \beta + \mu^{2}} \bigg)^{\!-1}\!\!, \end{aligned}$$

where

$$\begin{aligned} \mathbb{E}_{0}^{\mathbb{Q}}\big[ e^{-\gamma \hat{\tau}_{d}^{+}(W^{\mu})}\big] &= \frac{ 2 \mu e^{-\gamma d} \mathcal{N} ( \mu \sqrt{d} ) + \sqrt{ \frac{2}{\pi d}} e^{-\gamma d - \frac{ \mu^{2} d}{2}} }{ 2 \sqrt{ 2 \gamma + \mu^{2}} \mathcal{N} ( \sqrt{(2\gamma + \mu^{2})d} ) + \sqrt{ \frac{2}{\pi d}} e^{-\frac{(2 \gamma + \mu^{2}) d}{2}}} \\ & = \frac{ e^{-\gamma d} (z(0,0,\mu) + 2\mu)}{z(0,\gamma, \mu) + 2 \sqrt{2 \gamma + \mu^{2}}}, \end{aligned}$$

and the function \(z\) is defined in (4.1).

Proof

In order to find the double Laplace transform

$$ \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\mu})} e^{-\gamma \tau_{d}^{+}(W^{\mu})} \mathbf{1}_{\{H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\}} \Big] $$

in the case where \(H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\), we define our previously generic function \(\tilde{h}\) to be

$$ \tilde{h}(U_{H_{b}}) = \mathbb{E}_{0}^{\mathbb{Q}}\big[ e^{-\gamma \tau_{d}^{+}(W^{\mu})} \big| \mathcal{F}_{H_{b}(W^{\mu})} \big], $$

where \((\mathcal{F}_{t} )_{t \geq 0}\) denotes the standard filtration associated with the Brownian motion. Hence, the left-hand side of Lemma 4.2 becomes

$$\begin{aligned} &\mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\mu})} \tilde{h}(U_{H_{b}}) \mathbf{1}_{\{H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\}} \Big] \\ & = \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\mu})} \mathbb{E}_{0}^{\mathbb{Q}}\big[ e^{-\gamma \tau_{d}^{+}(W^{\mu})} | \mathcal{F}_{H_{b}(W^{\mu})}\big] \mathbf{1}_{\{H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\}} \Big] \\ & = \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta H_{b}(W^{\mu})} e^{-\gamma \tau_{d}^{+}(W^{\mu})} \mathbf{1}_{\{H_{b}(W^{\mu}) < \tau_{d}^{+}(W^{\mu})\}} \Big] \end{aligned}$$

with our choice of \(\tilde{h}\). On the other hand, we have

$$\begin{aligned} \tilde{h}(U_{H_{b}}) &= \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\gamma( H_{b}(W^{\mu}) + d - U_{H_{b}})} \mathbf{1}_{\{\tilde{H}_{0}(W^{\mu}) > d - U_{H_{b}}\}} \Big|\mathcal{F}_{H_{b}(W^{\mu})} \Big]\\ & \quad{} + \mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\gamma( H_{b}(W^{\mu}) + \tilde{H}_{0}(W^{\mu}) + \hat{\tau}_{d}^{+}(W^{\mu}))} \mathbf{1}_{\{\tilde{H}_{0} < d - U_{H_{b}}\}} \Big|\mathcal{F}_{H_{b}(W^{\mu})}\Big]\\ & = e^{-\gamma H_{b}(W^{\mu})} \Big( e^{-\gamma ( d - U_{H_{b}})} \mathbb{P}_{b} [ \tilde{H}_{0}(W^{\mu}) > d - U_{H_{b}}] \\ & \qquad\qquad\qquad{} + \mathbb{E}_{b}^{\mathbb{Q}}\Big[ e^{-\gamma \tilde{H}_{0}(W^{\mu}) } \mathbf{1}_{\{\tilde{H}_{0}(W^{\mu}) < d - U_{H_{b}}\}} \Big]\mathbb{E}_{0}^{\mathbb{Q}}\big[ e^{-\gamma \hat{\tau}_{d}^{+}(W^{\mu})}\big] \Big) , \end{aligned}$$

where \(\tilde{H}_{0}(W^{\mu})\) is the first hitting time of zero of Brownian motion restarted at time \(H_{b}(W^{\mu})\) and hence independent of \(H_{b}(W^{\mu})\), and \(\hat{\tau}_{d}^{+}(W^{\mu})\) is the first time the excursion lasts time \(d\) above zero with Brownian motion restarted at time \(\tilde{H}_{0}(W^{\mu})\) and therefore also independent of \(H_{b}(W^{\mu})\). For the derivation of the Laplace transform of \(\hat{\tau}_{d}^{+}(W^{\mu})\), we set \(A = 0\), \(B=1\) and let \(b\) approach \(\infty\) in Proposition 4.1. Notice that \(\hat{\tau}_{d}^{+}(W^{\mu})\) and \(\tau_{d}^{+}(W^{\mu})\) are identically distributed due to the strong Markov property of Brownian motion. Therefore,

$$ \mathbb{E}_{0}^{\mathbb{Q}}\big[e^{-\gamma \tau_{d}^{+}(W^{\mu})} \big] = \frac{ e^{-\gamma d} (z(0,0,\mu) + 2\mu)}{z(0,\gamma, \mu) + 2 \sqrt{2 \gamma + \mu^{2}}}, $$

where the \(2\mu\) in the numerator comes in from the odd case in (4.4).

For the other quantities, straightforward calculations yield

$$\begin{aligned} \mathbb{P}_{b} [ \tilde{H}_{0} (W^{\mu})> d - U_{H_{b}}] &= \int_{d-U_{H_{b}}}^{\infty}\frac{b}{\sqrt{2 \pi t^{3}}} e^{-\frac{(b + \mu t)^{2}}{2t}}\, dt \\ &= 1 - e^{-2 \mu b} \mathcal{N} \bigg( \frac{\mu (d - U_{H_{b}}) - b}{\sqrt{d - U_{H_{b}}}} \bigg) \\ &\quad{}- \mathcal{N} \bigg( \frac{ - \mu(d - U_{H_{b}}) - b}{\sqrt{d - U_{H_{b}}}} \bigg) \end{aligned}$$

and

$$\begin{aligned} &\mathbb{E}_{b}^{\mathbb{Q}}\Big[ e^{-\gamma \tilde{H}_{0}(W^{\mu}) } \mathbf{1}_{\{\tilde{H}_{0} < d - U_{H_{b}}\}} \Big] \\ &= e^{-(\sqrt{ 2 \gamma + \mu^{2} } + \mu) b} \mathcal{N} \bigg( \sqrt{ (2 \gamma + \mu^{2}) (d- U_{H_{b}})} - \frac{b}{\sqrt{d-U_{H_{b}}}} \bigg) \\ &\quad{}+ e^{\sqrt{ 2 \gamma + \mu^{2} } - \mu) b} \mathcal{N} \bigg( {-} \sqrt{ (2 \gamma + \mu^{2}) (d- U_{H_{b}})} - \frac{b}{\sqrt{d-U_{H_{b}}}} \bigg). \end{aligned}$$

Inserting these calculations into Lemma 4.2 yields the proposition. □

4.2 Case \(\tau_{d}^{+}(W^{\mu}) < H_{b}(W^{\mu})\)

In the case where the excursion has exceeded length \(d\) before hitting the barrier \(b>0\), we obtain from Proposition 4.1 the following result.

Lemma 4.4

$$\begin{aligned} &\mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\mu})} \mathbf{1}_{\{\tau_{d}^{+}(W^{\mu}) < H_{b}(W^{\mu})\}} \Big] \\ &= \frac{ e^{-\beta d} ( \sum_{k = 0}^{\infty} 2 ( z(k,0,\mu) - e^{\mu b} z(k+\frac{1}{2},0,\mu) ) - z(0,0,\mu) )}{ \sum_{k=0}^{\infty}2 ( z(k,\beta,\mu) + \sqrt{2\beta + \mu^{2}} e^{-\sqrt{2\beta + \mu^{2}}2kb} ) - z(0,\beta,\mu) - 2\sqrt{2\beta + \mu^{2}} }, \end{aligned}$$

where the function \(z\) is defined in (4.1).

This lemma allows us to compute the probability that the Parisian time happens before the hitting time of \(b\) by setting \(\beta=\mu=0\), as outlined in the following corollary.

Corollary 4.5

For the standard Brownian motion \(W\), the probability that the excursion exceeds time \(d\) before hitting the barrier \(b\) is given by

$$ \mathbb{Q} [ \tau_{d}^{+}(W) < H_{b}(W) ] = 1 - \frac{ 2\sum_{k=0}^{\infty}e^{-\frac{(2k+1)^{2} b^{2}}{2d}}-1}{2\sum_{k=0}^{\infty}e^{-\frac{(2kb)^{2}}{2d}}-1}. $$

Now, the double Laplace transform of the hitting and Parisian times in the case where the excursion has exceeded length \(d\) before hitting \(b\) can be derived.

Proposition 4.6

The double Laplace transform of the hitting and Parisian times for a drifted Brownian motion \(W^{\mu}\) in the case where \(\tau_{d}^{+}(W^{\mu})< H_{b}(W^{\mu})\) is given by

$$\begin{aligned} &\mathbb{E}_{0}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\mu}) -\gamma H_{b}(W^{\mu})} \mathbf{1}_{\{\tau_{d}^{+}(W^{\mu}) < H_{b}(W^{\mu})\}}\Big] \\ &=\Bigg( e^{-\beta d} \bigg( e^{-b(\sqrt{2\gamma + \mu^{2}} - \mu)} \mathcal{N} \Big( \frac{b}{\sqrt{d}} - \sqrt{(2 \gamma + \mu^{2}) d} \Big) \\ & \qquad\qquad\quad{}- e^{b(\sqrt{2\gamma + \mu^{2}} - \mu)} \mathcal{N} \Big( {-} \frac{b}{\sqrt{d}} - \sqrt{(2 \gamma + \mu^{2}) d} \Big) \bigg) \\ &\qquad{}\times \sum\limits_{k = 0}^{\infty} 2 \Big( z(k,0,\mu) - e^{\mu b} z(k+\frac{1}{2},0,\mu) \Big) - z(0,0,\mu) \Bigg) \\ &\quad{}\times \Bigg( \bigg( \sum\limits_{k=0}^{\infty}2\Big( z(k,\beta+\gamma,\mu) + \sqrt{2(\beta+\gamma) + \mu^{2}} e^{-\sqrt{2(\beta+\gamma) + \mu^{2}}2kb} \Big) \\ &\qquad\qquad{}- z(0,\beta+\gamma,\mu) - 2 \sqrt{2(\beta+\gamma) +\mu^{2}} \bigg)\\ &\qquad\qquad{}\times \bigg(1- \mathcal{N} \Big( \frac{\mu d - b}{\sqrt{d} }\Big) - e^{2\mu b} \mathcal{N} \Big( \frac{-\mu d - b}{\sqrt{d}} \Big) \bigg) \Bigg)^{-1}, \end{aligned}$$

where the function \(z\) is defined by (4.1).

Proof

In order to find the double Laplace transform in this case, we define a new infinitesimal generator for the perturbed Brownian motion \(W^{\epsilon,\mu}\) starting at the stopping time \(\tau_{d}^{+}(W^{\epsilon,\mu})\). We can do this due to the strong Markov property of Brownian motion. State 2, which stands for \(W^{\epsilon,\mu}\) being above the barrier \(b\), is an absorbing state, hence nothing comes back from there. Also, we are not concerned with state −1, meaning that \(W^{\epsilon,\mu}\) is below zero, because our excursion has already exceeded time \(d\) and we are now only interested in hitting \(b\). With this motivation, the generator becomes

$$ \mathcal{A}f_{1}(u,t) = \frac{ \partial f_{1}}{\partial t} (u,t)+ \frac{ \partial f_{1}}{\partial u}(u,t) + \lambda_{1,2}(u) \big(f_{2}(u,t) - f_{1}(u,t) \big), $$

where we choose \(f_{2}\) to be \(f_{2}(u,t) = e^{-\gamma t}\). Since state 2 is absorbing, the function \(f_{2}\) can be assigned arbitrarily. Note that our choice of \(f_{2}\) is a bounded function.

Furthermore, at time \(\tau_{d}^{+}(W^{\epsilon,\mu})\), we are in state 1. Similarly to the proof of Lemma 3.3, we solve \(\mathcal{A} f \equiv 0\) in order to derive a martingale of the form

$$\hat{M}_{t} := f_{X_{t}} \big(U_{t}(X), t\big) = e^{-\beta t} h_{X_{t}} \big(U_{t}(X)\big). $$

However, notice that we have \(f_{1}(d,0)=h_{1}(d)\) because by definition our time elapsed at starting time \(\tau_{d}^{+}(W^{\epsilon,\mu})\) is \(d\). This is a stopping time that denotes the first time the excursion reaches a length \(d\), so the time since the last 0 is exactly \(d\). Since we have already achieved an excursion above zero of length \(d\), we are not concerned about any excursions any longer; hence, we choose the constraint \(h_{1}(\infty) = 0\). Solving \(\mathcal{A} f \equiv 0\) yields

$$ h_{1}(u) = \int_{u}^{\infty}\lambda_{1,2} (w) e^{-\int_{u}^{w} \gamma + \lambda_{1,2}(v)\, dv}\, dw , \qquad 0\leq u \leq \infty, $$

where

$$ \lambda_{1,2} (t) e^{-\int_{0}^{t} \lambda_{1,2}(v)\, dv} = p_{12}(t) = \mathbb{P}_{\epsilon}[H_{b}(W^{\mu}) \in dt] = \frac{b-\epsilon}{\sqrt{2\pi t^{3}}} e^{-\frac{(b-\epsilon - \mu t)^{2}}{2t}}. $$

Hence,

$$\begin{aligned} h_{1}(d) & = \frac{ e^{\gamma d} \int_{d}^{\infty}e^{-\gamma w} p_{12}(w)\, dw}{ 1- \int_{0}^{d} p_{12}(s)\, ds} \\ & = \Bigg( e^{\gamma d} \bigg( e^{-(b-\epsilon)(\sqrt{2\gamma + \mu^{2}} - \mu)} \mathcal{N} \Big( \frac{b-\epsilon}{\sqrt{d}} - \sqrt{(2 \gamma + \mu^{2}) d} \Big) \\ & \quad {} - e^{(b-\epsilon)(\sqrt{2\gamma + \mu^{2}} - \mu)} \mathcal{N} \Big( {-} \frac{b-\epsilon}{\sqrt{d}} - \sqrt{(2 \gamma + \mu^{2}) d} \Big) \bigg) \Bigg) \\ & \quad{} \times \bigg(1- \mathcal{N} \Big( \frac{\mu d - (b-\epsilon)}{\sqrt{d} }\Big) - e^{2\mu(b-\epsilon)} \mathcal{N} \Big( \frac{-\mu d - (b-\epsilon)}{\sqrt{d}} \Big) \bigg)^{-1}\\ & \overset{\epsilon \rightarrow 0}{\longrightarrow} \Bigg( e^{\gamma d} \bigg( e^{-b(\sqrt{2\gamma + \mu^{2}} - \mu)} \mathcal{N} \Big( \frac{b}{\sqrt{d}} - \sqrt{(2 \gamma + \mu^{2}) d} \Big) \\ &\quad{} - e^{b(\sqrt{2\gamma + \mu^{2}} - \mu)} \mathcal{N} \Big( {-} \frac{b}{\sqrt{d}} - \sqrt{(2 \gamma + \mu^{2}) d} \Big) \bigg) \Bigg) \\ & \quad{}\times \bigg( 1- \mathcal{N} \Big( \frac{\mu d -b}{\sqrt{d} }\Big) - e^{2\mu b} \mathcal{N} \Big( \frac{-\mu d -b}{\sqrt{d}} \Big) \bigg)^{-1}. \end{aligned}$$

As a result, we have found a martingale \(\hat{M}_{t} := f_{X_{t}} (U_{t}(X),t)\) that satisfies

$$\hat{M}_{0} = f_{1}(d,0) = h_{1} (d). $$

Also, with \(\hat{\hat{H}}_{b}(W^{\epsilon,\mu})\) being the first hitting time of \(b\) of our process restarted at \(\tau_{d}^{+}(W^{\epsilon,\mu})\), we have \(H_{b}(W^{\epsilon,\mu}) = \tau_{d}^{+}(W^{\epsilon,\mu}) + \hat{\hat{H}}_{b}(W^{\epsilon,\mu})\). Furthermore, note that

$$ \hat{M}_{\hat{\hat{H}}_{b}(W^{\epsilon,\mu})} = f_{2}\Big(U_{\hat{\hat{H}}_{b}(W^{\epsilon,\mu})}(X), \hat{\hat{H}}_{b}(W^{\epsilon,\mu})\Big) = e^{-\gamma \hat{\hat{H}}_{b}(W^{\epsilon,\mu})}. $$

Notice that at the hitting time of \(b\), the process \(W^{\epsilon,\mu}\) is in state 2. Hence, using the optional sampling theorem on the martingale \(\hat{M}\) with the stopping time \(\hat{\hat{H}}_{b}(W^{\epsilon,\mu}) \wedge t\) yields

$$ \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ \hat{M}_{\hat{\hat{H}}_{b}(W^{\epsilon,\mu}) \wedge t}\Big] = \mathbb{E}_{\epsilon}^{\mathbb{Q}}[\hat{M}_{0}]. $$

Notice that, by construction,

$$ \mathbb{E}_{\epsilon}^{\mathbb{Q}}[\hat{M}_{0}] = h_{1}(d). $$

Furthermore, \(h_{1}\) is continuous and decreasing. Hence, there exists a constant \(K\) such that \(| h_{1}(U_{t}(X)) | \leq K\) for all \(U_{t}(X)\). We then apply Lebesgue’s dominated convergence theorem and derive

$$ \lim\limits_{t \rightarrow \infty} \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ \hat{M}_{\hat{\hat{H}}_{b}(W^{\epsilon,\mu}) \wedge t} \Big] = \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ \hat{M}_{\hat{\hat{H}}_{b}(W^{\epsilon,\mu})}\Big] = \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[e^{-\gamma \hat{\hat{H}}_{b}(W^{\epsilon,\mu})} \Big]. $$

Hence, \(h_{1}(d) = \mathbb{E}_{\epsilon}^{\mathbb{Q}}[e^{-\gamma \hat{\hat{H}}_{b}(W^{\epsilon,\mu})} ]\), and the double Laplace transform becomes

$$\begin{aligned} &\mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{-\beta \tau_{d}^{+}(W^{\epsilon,\mu})} e^{-\gamma H_{b}(W^{\epsilon,\mu})} \mathbf{1}_{\{\tau_{d}^{+} (W^{\epsilon,\mu})< H_{b}(W^{\epsilon,\mu})\}}\Big] \\ &= \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{- \beta \tau_{d}^{+}(W^{\epsilon,\mu})}\mathbf{1}_{\{\tau_{d}^{+}(W^{\epsilon,\mu}) < H_{b}(W^{\epsilon,\mu})\}} \mathbb{E}_{\epsilon}^{\mathbb{Q}}\big[ e^{-\gamma H_{b}(W^{\epsilon,\mu})} \big| \tau_{d}^{+}(W^{\epsilon,\mu}) \big]\Big] \\ & = \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{- \beta \tau_{d}^{+}(W^{\epsilon,\mu})}\mathbf{1}_{\{\tau_{d}^{+}(W^{\epsilon,\mu}) < H_{b}(W^{\epsilon,\mu})\}} \mathbb{E}_{\epsilon}^{\mathbb{Q}}\big[ e^{-\gamma (\tau_{d}^{+}(W^{\epsilon,\mu}) + \hat{\hat{H}}_{b}(W^{\epsilon,\mu}))} \big| \tau_{d}^{+}(W^{\epsilon,\mu}) \big]\Big] \\ & = h_{1}(d) \mathbb{E}_{\epsilon}^{\mathbb{Q}}\Big[ e^{- (\beta +\gamma) \tau_{d}^{+}(W^{\epsilon,\mu})}\mathbf{1}_{\{\tau_{d}^{+} (W^{\epsilon,\mu})< H_{b}(W^{\epsilon,\mu})\}} \Big]. \end{aligned}$$

Together with Lemma 4.4, we conclude the proposition. □

5 Pricing Parisian hit options

Let \((S_{t})_{t\geq 0}\) be the stock price process following a geometric Brownian motion and recall all definitions from Sect. 2.

5.1 Option triggered at minimum of Parisian and hitting times

Our so-called MinParisianHit option is triggered either when the age of an excursion above \(L\) reaches time \(d\) or a barrier \(B>L\) is hit by the underlying price process \(S\). More precisely, a MinParisianHit Up-and-In is activated at the minimum of both stopping times, that is, \(\min ( \tau_{L,d}^{+}(S), H_{B}(S) )\). This time is illustrated by the blue line in Fig. 2. To simplify calculations, we assume from now on that the underlying process starts at the barrier, that is, \(S_{0} = L\) or equivalently \(\ell = 0\); hence, we can use the results from our three-state semi-Markov model. The more general case, where \(S_{0} \neq L\) and the strong Markov property of Brownian motion applies, is discussed in the Appendix.

Fig. 2
figure 2

Minimum of Parisian and hitting times (Color figure online)

Full size image

The MinParisianHit Up-and-In call option has the payoff

$$ (S_{T} - K)^{+} \mathbf{1}_{\{\min ( \tau_{L,d}^{+}(S), H_{B}(S)) \leq T\}}, $$

where \(K\) denotes the strike price. Using risk-neutral valuation and Girsanov’s change of measure (2.1), the price of this option can be written as

$$\begin{aligned} &\mathrm{minPHC}_{i}^{u} (S_{0},T,K,L,d,r ) \\ &= e^{-rT} \mathbb{E}_{S_{0}}^{\bar{\mathbb{Q}}}\Big[ (S_{T} - K)^{+} \mathbf{1}_{\{\min ( \tau_{L,d}^{+}(S), H_{B}(S)) \leq T \}}\Big] \\ & = e^{-(r+\frac{1}{2}m^{2})T} \mathbb{E}_{0}^{\mathbb{Q}}\Big[ (S_{0} e^{\sigma Z_{T}} - K)^{+} e^{m Z_{T}} \mathbf{1}_{\min \{ \tau_{d}^{+}(Z), H_{b}(Z)\} \leq T} \Big] \\ & = e^{-(r+\frac{1}{2}m^{2})T} \int_{\frac{1}{\sigma} \ln \frac{K}{S_{0}}}^{\infty}(S_{0} e^{\sigma z} - K) e^{m z} \mathbb{Q}_{0} \big[ Z_{T} \in dz, \min \big( \tau_{d}^{+}(Z), H_{b}(Z)\big) \leq T \big]. \end{aligned}$$
(5.1)

Hence, finding the fair price for a MinParisianHit option reduces to finding the joint distribution of the position at maturity and the minimum of Parisian and hitting times.

Remark 5.1

We fix the notation for inverse Laplace transforms. Given a function \(F(\beta)\), the inverse Laplace transform of \(F\), denoted by \(\mathcal{L}^{-1} \{F(\beta)\}\), is the function \(f\) whose Laplace transform is \(F\), that is,

$$ f(t) = \mathcal{L}^{-1}_{\beta}\{F(\beta)\}(t) \quad \Longleftrightarrow \quad \mathcal{L}_{t} \{f(t) \}(\beta) := \int_{0}^{\infty}e^{-\beta t} f(t)\, dt = F(\beta). $$

Note that we consider the inverse Laplace transform with respect to the transformation variable \(\beta\) at the evaluation point \(t\). If not otherwise stated, we take from now on \(\mathcal{L}^{-1}_{\beta}\{F(\beta)\}(t)\) as a function of the time variable \(t\).

Proposition 5.2

The joint density of the position at maturity and the minimum of hitting and Parisian times for standard Brownian motion is

$$\begin{aligned} &\mathbb{Q}_{0} \big[Z_{T} \in dz, \min \big( \tau_{d}^{+}(Z), H_{b}(Z)\big) \leq T\big] \\ & = \int_{t=0}^{T} \int_{w = -\infty}^{b} \frac{1}{\sqrt{2 \pi (T-t)}} e^{-\frac{(z-w)^{2}}{2(T-t)}} \\ &\qquad\qquad\qquad\quad{}\times \Bigg( \frac{ \sum_{k= -\infty}^{\infty}\frac{w+2kb}{d} e^{-\frac{(w+2kb)^{2}}{2d}} }{ 2 \sum_{k= 0}^{\infty}( e^{-\frac{(2kb)^{2}}{2d}} - e^{-\frac{(2k+1)^{2} b^{2}}{2d}} )} \mathcal{L}^{-1}_{\beta}\{H_{1} (\beta) \}(t) \\ &\qquad\qquad\qquad\qquad\quad{}+ \delta_{(w-b)} \mathcal{L}^{-1}_{\beta}\{ H_{2} (\beta) \}(t) \Bigg)\, dw \, dt \end{aligned}$$

with

$$\begin{aligned} & H_{1} (\beta) = \frac{ e^{-\beta d} (2\sum_{k = 0}^{\infty} (z(k,0,0) - z(k+\frac{1}{2},0,0) ) - z(0,0,0) ) }{ 2\sum_{k=0}^{\infty}( z(k,\beta,0) + \sqrt{2\beta } e^{-\sqrt{2\beta }2kb} ) - z(0,\beta,0) - 2\sqrt{2 \beta } },\\ & H_{2} (\beta) = \frac{ 2 \sum_{k = 0}^{\infty}z(k+\frac{1}{2},\beta,0) + \sqrt{2\beta} e^{-(2k+1)\sqrt{2\beta }b} }{ 2\sum_{k=0}^{\infty}( z(k,\beta,0) + \sqrt{2\beta } e^{-\sqrt{2\beta }2kb} ) - z(0,\beta,0) - 2\sqrt{2 \beta } }, \end{aligned}$$

with \(z\) defined by (4.1) and \(\delta_{x}\) being the Dirac delta function.

Proof

Let \(Z\) denote a standard Brownian motion, and \(\tau(Z) := \min ( \tau_{d}^{+}(Z), H_{b}(Z) )\). The joint distribution of the position at maturity and the minimum of Parisian and hitting times can be decomposed as

$$\begin{aligned} &\mathbb{Q}_{0} \big[Z_{T} \in dz, \min \big( \tau_{d}^{+}(Z), H_{b}(Z)\big) \leq T\big]\\ &= \int_{t=0}^{T} \int_{w = -\infty}^{b} \mathbb{Q}_{0}[Z_{T} \in dz, \tau(Z) \in dt, Z_{\tau} \in dw] \\ & = \int_{t=0}^{T} \int_{w = -\infty}^{b} \mathbb{Q}_{0}[Z_{T} \in dz | \tau(Z)= t, Z_{\tau} \in dw] \,\mathbb{Q}_{0}[\tau(Z)\in dt, Z_{\tau} \in dw]\\ & = \int_{t=0}^{T} \int_{w = -\infty}^{b} \frac{1}{\sqrt{2 \pi (T-t)}} e^{-\frac{(z-w)^{2}}{2(T-t)}}\, dz \, \mathbb{Q}_{0}[\tau(Z)\in dt, Z_{\tau} \in dw] \\ & = \int_{t=0}^{T} \int_{w = -\infty}^{b} \frac{1}{\sqrt{2 \pi (T-t)}} e^{-\frac{(z-w)^{2}}{2(T-t)}}\, dz\\ &\quad{}\times \big( \mathbb{Q}_{0}[\tau(Z) \in dt, Z_{\tau} \in dw | H_{b}(Z) < \tau_{d}^{+}(Z)] \, \mathbb{Q}_{0}[H_{b} (Z)< \tau_{d}^{+}(Z)] \\ &\qquad\quad{} + \mathbb{Q}_{0}[\tau(Z) \in dt, Z_{\tau} \in dw| \tau_{d}^{+}(Z) < H_{b}(Z)] \, \mathbb{Q}_{0}[\tau_{d}^{+}(Z) < H_{b}(Z)] \big). \end{aligned}$$

We find

$$\begin{aligned} &\mathbb{Q}_{0} [\tau(Z)\in dt, Z_{\tau} \in dw | \tau_{d}^{+}(Z) < H_{b}(Z)] \, \mathbb{Q}_{0}[\tau_{d}^{+}(Z) < H_{b}(Z)] \\ & = \mathbb{Q}_{0} \big[ Z_{\tau_{d}^{+}} \in dw | \tau(Z) = t , \tau_{d}^{+}(Z) < H_{b}(Z)\big]\, \mathbb{Q}_{0}[ \tau(Z) \in dt| \tau_{d}^{+}(Z) < H_{b}(Z)] \\ & \quad{} \times \mathbb{Q}_{0}[\tau_{d}^{+}(Z) < H_{b}(Z)] \\ & = \mathbb{Q}_{0} \big[ Z_{\tau_{d}^{+}} \in dw | \tau(Z) = t , \tau_{d}^{+}(Z) < H_{b}(Z)\big] \,\mathbb{Q}_{0}[ \tau(Z) \in dt, \tau_{d}^{+}(Z) < H_{b}(Z)]. \end{aligned}$$
(5.2)

For the first term on the right-hand side, we notice that

$$\begin{aligned} &\mathbb{Q}_{0} \big[ Z_{\tau_{d}^{+}} \in dw \big| \tau(Z) = t , \tau_{d}^{+}(Z) < H_{b}(Z)\big] \\ &= \lim\limits_{\epsilon \rightarrow 0} \mathbb{Q}_{\epsilon}\Big[ Z_{d} \in dw \Big| \inf\limits_{0< s< d} Z_{s} > 0, \sup\limits_{0< s< d} Z_{s} < b\Big] \\ & = \lim\limits_{\epsilon \rightarrow 0} \frac{ \mathbb{Q}_{\epsilon}[ Z_{d} \in dw , \inf_{0< s< d} Z_{s} > 0, \sup_{0< s< d} Z_{s} < b]}{ \mathbb{Q}_{\epsilon}[ \inf_{0< s< d} Z_{s} > 0, \sup_{0< s< d} Z_{s} < b]} \\ & = \lim\limits_{\epsilon \rightarrow 0} \frac{ \sum_{k = -\infty}^{\infty}(e^{-\frac{(w-\epsilon+2kb)^{2}}{2d}} - e^{-\frac{(w+\epsilon+2kb)^{2}}{2d}}) }{ \sum_{k = -\infty}^{\infty}\int_{0}^{b} (e^{-\frac{(z-\epsilon+2kb)^{2}}{2d}} - e^{-\frac{(z+\epsilon+2kb)^{2}}{2d}} )\,dz}\, dw \\ & = \frac{ \sum_{k= -\infty}^{\infty}\frac{w+2kb}{d} e^{-\frac{(w+2kb)^{2}}{2d}} }{ 2 \sum_{k= 0}^{\infty}( e^{-\frac{(2kb)^{2}}{2d}} - e^{-\frac{(2k+1)^{2} b^{2}}{2d}} )}\, dw. \end{aligned}$$
(5.3)

Notice that the first equality results from the position \(Z_{\tau_{d}^{+}}\) at the Parisian time being independent of the time \(\tau_{d}^{+}(Z) = t\); see Chesney et al. [8, Sect. 8.3.1] for further details. The formulae for the third line can be found in Borodin and Salminen [5, Chapter 1, formulae (1.15.4) and (1.15.8)]. The second term on the right-hand side of (5.2) can be calculated via inverting the Laplace transform of the minimum of the hitting and Parisian times. The Laplace transform has been found in Lemma 4.4. With \(\mu = 0\), we derive

$$\begin{aligned} &\mathbb{Q}_{0}\big[ \tau(Z) \in dt, \tau_{d}^{+}(Z) < H_{b}(Z)\big] =\mathcal{L}^{-1}_{\beta}\big\{ \mathbb{E}_{0}^{\mathbb{Q}}\big[ e^{-\beta \tau_{d}^{+}(Z)} \mathbf{1}_{\{\tau_{d}^{+}(Z) < H_{b}(Z) \}}\big] \big\} (t) \, dt \\ & =\mathcal{L}^{-1}_{\beta}\left\{ \frac{ e^{-\beta d} (\sum_{k = 0}^{\infty} 2 (z(k,0,0) - z(k+\frac{1}{2},0,0) ) - z(0,0,0) ) }{ \sum_{k=0}^{\infty}2( z(k,\beta,0) + \sqrt{2\beta } e^{-\sqrt{2\beta }2kb} ) - z(0,\beta,0) - 2\sqrt{2 \beta } } \right\} (t) \, dt, \end{aligned}$$

where \(z(k,\beta,\mu)\) is defined in (4.1). We also have in the case \(H_{b}(Z) < \tau_{d}^{+}(Z)\) that

$$\begin{aligned} &\mathbb{Q}_{0}[\tau(Z) \in dt, Z_{\tau} \in dw | H_{b}(Z) < \tau_{d}^{+}(Z)]\,\mathbb{Q}_{0}[H_{b}(Z) < \tau_{d}^{+}(Z)] \\ &=\mathbb{Q}_{0}[Z_{H_{b}} \in dw| \tau(Z) = t , H_{b}(Z) < \tau_{d}^{+}(Z)]\, \mathbb{Q}_{0}[\tau(Z) \in dt, H_{b}(Z) < \tau_{d}^{+}(Z)]. \end{aligned}$$

Since \(Z_{H_{b}}\) conditionally on \(H_{b}(Z)\) is deterministic, the conditional probability on the right-hand side above becomes the Dirac delta function at the point \(b\); hence,

$$ \mathbb{Q}_{0}[Z_{H_{b}} \in dw| \tau(Z) = t , H_{b}(Z) < \tau_{d}^{+}(Z)] = \delta_{w-b}\, dw, $$

where the Dirac delta function is defined for all \(x \in \mathbb{R}\) as

$$ \delta_{x} = \textstyle\begin{cases} 0 & \text{if } x \neq 0,\\ \infty &\text{if } x = 0, \end{cases} $$

and also satisfying the identity

$$ \int_{-\infty}^{\infty}\delta_{x} \, dx = 1. $$

By inversion of the Laplace transform in Lemma 4.2 with \(h \equiv 1\), we firstly derive for the numerator

$$\begin{aligned} \frac{\partial}{\partial \epsilon}\hat{Q}_{1,2}(\beta) &\longrightarrow \sum\limits_{k = 0}^{\infty}\Bigg(2 \sqrt{ \frac{2}{\pi d}} e^{\mu b - \frac{(2k+1)^{2} b^{2}}{2d} - \frac{(2\beta + \mu^{2})d}{2}} + 2 \sqrt{2\beta + \mu^{2}} e^{\mu b} \\ &\qquad\qquad{} \times \bigg( e^{-(2k+1)\sqrt{2\beta + \mu^{2}}b} \mathcal{N}\Big( {-} \frac{(2k+1)b}{\sqrt{d}} + \sqrt{(2\beta + \mu^{2})d} \Big) \\ &\qquad\qquad\qquad{}- e^{(2k+1)\sqrt{2\beta + \mu^{2}}b} \mathcal{N}\Big( {-} \frac{(2k+1)b}{\sqrt{d}} - \sqrt{(2\beta + \mu^{2})d} \Big) \!\bigg)\!\Bigg)\\ & \quad= 2 e^{\mu b} \sum\limits_{k = 0}^{\infty}\Big(z(k+\frac{1}{2},\beta,\mu) + \sqrt{2\beta + \mu^{2}} e^{-(2k+1)\sqrt{2\beta + \mu^{2}}b} \Big). \end{aligned}$$

Setting \(\mu=0\), we obtain

$$\begin{aligned} &\mathbb{Q}_{0}[\tau(Z)\in dt, H_{b}(Z) < \tau_{d}^{+}(Z)] = \mathcal{L}^{-1}_{\beta}\big\{ \mathbb{E}_{0}^{\mathbb{Q}}\big[ e^{-\beta H_{b}(Z)} \mathbf{1}_{\{H_{b}(Z) < \tau_{d}^{+}(Z)\}} \big] \big\} (t) \, dt \\ & = \mathcal{L}^{-1}_{\beta}\bigg\{ \frac{ 2 \sum_{k = 0}^{\infty}(z(k+\frac{1}{2},\beta,0) + \sqrt{2\beta} e^{-(2k+1)\sqrt{2\beta }b}) }{ 2\sum_{k=0}^{\infty}( z(k,\beta,0) + \sqrt{2\beta } e^{-\sqrt{2\beta }2kb} ) - z(0,\beta,0) - 2\sqrt{2 \beta } } \bigg\} (t) \, dt. \end{aligned}$$

Putting things together, the proposition follows. □

We are now able to price a MinParisianHit option by combining Proposition 5.2 and (5.1). In particular, the fair price of a MinParisianHit Up-and-In call option can be calculated via evaluating the integral

$$\begin{aligned} &\mathrm{minPHC}_{i}^{u} (S_{0},T,K,L,d,r) \\ &= e^{-(r+\frac{1}{2}m^{2})T} \int_{\frac{1}{\sigma} \ln \frac{K}{S_{0}}}^{\infty}(S_{0} e^{\sigma z} - K) e^{m z} \mathbb{Q}_{0} \big[ Z_{T} \in dz, \min \big\{ \tau_{d}^{+}(Z), H_{b}(Z)\big\} \leq T \big], \end{aligned}$$
(5.4)

where the joint probability has been derived in Proposition 5.2.

5.2 Option triggered at the maximum of Parisian and hitting times

Our so-called MaxParisianHit option is triggered when both the barrier \(B\) is hit and the excursion age exceeds the duration \(d\) above \(L\). Hence, the payoff of a call option with strike \(K\) becomes

$$ (S_{T} - K)^{+} \mathbf{1}_{ \{ \tau_{L,d}^{+}(S) \leq T, H_{B}(S) \leq T \}} = (S_{T} - K)^{+} \mathbf{1}_{ \{ \max ( \tau_{L,d}^{+}(S) , H_{B}(S) ) \leq T \} }. $$

The maximum of Parisian and hitting times is illustrated by the blue line in Fig. 3.

Fig. 3
figure 3

Maximum of Parisian and hitting times (Color figure online)

Full size image

As in the previous case, the problem reduces to finding the joint density of the hitting and Parisian times and the position for a drifted Brownian motion, which then can be related to the joint density of the hitting and Parisian time for a standard Brownian motion due to Girsanov. We also assume that \(S_{0}=L\), thus \(\tau_{\ell,d}^{+}(Z) = \tau_{d}^{+}(Z)\), and discuss the more general case \(S_{0} \neq L\) in the Appendix. The fair price becomes

$$\begin{aligned} &\mathrm{maxPHC}_{i}^{u} (S_{0},T,K,L,d,r) \\ &= e^{-rT} \mathbb{E}_{S_{0}}^{\bar{\mathbb{Q}}}\Big[ (S_{T} - K)^{+} \mathbf{1}_{\{ \tau_{L,d}^{+}(S) \leq T, H_{B}(S) \leq T \}} \Big] \\ & = e^{-(r+\frac{1}{2}m^{2})T} \mathbb{E}_{0}^{\mathbb{Q}}\Big[ (S_{0} e^{\sigma Z_{T}} - K)^{+} e^{m Z_{T}} \mathbf{1}_{ \{ \tau_{d}^{+}(Z) \leq T, H_{b}(Z) \leq T\}} \Big] \\ & = e^{-(r+\frac{1}{2}m^{2})T} \int_{\frac{1}{\sigma} \ln \frac{K}{S_{0}}}^{\infty}(S_{0} e^{\sigma z} - K) e^{mz} \mathbb{Q}_{0} \big[Z_{T} \in dz, \max \big( \tau_{d}^{+}(Z), H_{b}(Z)\big) \leq T\big]. \end{aligned}$$
(5.5)

Hence, finding the fair price of a MaxParisianHit option reduces to finding the joint distribution of the position at maturity and the maximum of Parisian and hitting times.

Proposition 5.3

The joint distribution of the position at maturity and the maximum of hitting and Parisian times of standard Brownian motion is

$$\begin{aligned} &\mathbb{Q}_{0} \big[Z_{T} \in dz, \max \big( \tau_{d}^{+}(Z), H_{b}(Z) \big) \leq T\big] \\ &= \int_{t=0}^{T} \int_{w = -\infty}^{\infty}\frac{1}{\sqrt{2 \pi (T-t)}} e^{-\frac{(z-w)^{2}}{2(T-t)}} \\ &\quad{} \times\Bigg( \frac{|w|}{\pi \sqrt{(t-d) d^{3}}} e^{-\frac{w^{2}}{2d}} - \frac{ \sum_{k= -\infty}^{\infty}\frac{w+2kb}{d} e^{-\frac{(w+2kb)^{2}}{2d}} }{ \sum_{k= -\infty}^{\infty}( e^{-\frac{(2kb)^{2}}{2d}} - e^{-\frac{(2k+1)^{2} b^{2}}{2d}} )} \mathcal{L}^{-1}_{\beta}\{H_{1} (\beta) \}(t) \, dt \\ &\qquad\quad{}+ \delta_{(w-b)} \mathcal{L}^{-1}_{\gamma}\{ H_{3}(\gamma)\}(t) \Bigg)\, dw \, dt \, dz, \end{aligned}$$

where

$$\begin{aligned} H_{1} (\beta) &=\frac{ e^{-\beta d} (2\sum_{k = 0}^{\infty} (z(k,0,0) - z(k+\frac{1}{2},0,0) ) - z(0,0,0) ) }{ 2\sum_{k=0}^{\infty}( z(k,\beta,0) + \sqrt{2\beta } e^{-\sqrt{2\beta }2kb} ) - z(0,\beta,0) - 2\sqrt{2 \beta } },\\ H_{3}(\gamma) &= \Bigg( \bigg( e^{-\sqrt{2\gamma}b} \mathcal{N} \Big( \frac{b}{\sqrt{d}} - \sqrt{2 \gamma d} \Big) - e^{\sqrt{2\gamma} b} \mathcal{N} \Big( {-} \frac{b}{\sqrt{d}} - \sqrt{2 \gamma d} \Big) \bigg) \\ &\qquad{}\times\sum\limits_{k = 0}^{\infty} 2 \Big( z(k,0,0) - z(k+\frac{1}{2}, 0 ,0) \Big) - z(0,0,0) \Bigg) \\ &\quad{}\times \Bigg( \bigg( \sum\limits_{k=0}^{\infty}2\Big( z(k,\gamma,0) + \sqrt{2\gamma } e^{-\sqrt{2\gamma}2kb} \Big) - z(0,\gamma,0) - 2 \sqrt{2\gamma} \bigg) \\ & \qquad\qquad{}\times \bigg(1- 2 \mathcal{N} \Big(- \frac{ b}{\sqrt{d} }\Big) \bigg) \Bigg)^{-1}, \end{aligned}$$

with \(z\) defined by (4.1) and \(\delta_{x}\) denoting the Dirac delta function.

Proof

Let \(\bar{\tau}(Z) = \max (\tau_{d}^{+}(Z), H_{b}(Z) )\). We again have the decomposition

$$\begin{aligned} &\mathbb{Q}_{0} \big[Z_{T} \in dz, \max \big( \tau_{d}^{+}(Z), H_{b}(Z) \big) \leq T\big] \\ &= \int_{t = 0}^{T} \int_{w = -\infty}^{\infty}\mathbb{Q}_{0}[ Z_{T} \in dz, \bar{\tau}(Z) \in dt, Z_{\bar{\tau}} \in dw] \\ & = \int_{t = 0}^{T} \int_{w = -\infty}^{\infty}\mathbb{Q}_{0}[Z_{T} \in dz | \bar{\tau}(Z) = t, Z_{\bar{\tau}} \in dw] \,\mathbb{Q}_{0}[\bar{\tau}(Z) \in dt, Z_{\bar{\tau}} \in dw] \\ & = \int_{t=0}^{T} \int_{w = -\infty}^{\infty}\frac{1}{\sqrt{2 \pi (T-t)}} e^{-\frac{(z-w)^{2}}{2(T-t)}} \mathbb{Q}_{0}[ \bar{\tau}(Z) \in dt, Z_{\bar{\tau}} \in dw]\, dz \\ & = \int_{t=0}^{T} \int_{w = -\infty}^{\infty}\frac{1}{\sqrt{2 \pi (T-t)}} e^{-\frac{(z-w)^{2}}{2(T-t)}} \big( \mathbb{Q}_{0}[\bar{\tau}(Z)\in dt, Z_{\bar{\tau}} \in dw , H_{b}(Z) < \tau_{d}^{+}(Z)] \\ & \qquad\qquad\qquad{}+ \mathbb{Q}_{0}[\bar{\tau}(Z) \in dt, Z_{\bar{\tau}} \in dw , \tau_{d}^{+}(Z) < H_{b}(Z)] \big)\, dz. \end{aligned}$$
(5.6)

For the second part of the right-hand side of (5.6), we have

$$\begin{aligned} &\mathbb{Q}_{0}[\bar{\tau}(Z) \in dt, Z_{\bar{\tau}} \in dw , \tau_{d}^{+}(Z) < H_{b}(Z)] \\ & = \mathbb{Q}_{0}[Z_{H_{b}} \in dw | H_{b}(Z) = t, \tau_{d}^{+}(Z) < H_{b}(Z)]\\ &\quad{}\times \mathbb{Q}_{0}[H_{b}(Z) \in dt, \tau_{d}^{+}(Z) < H_{b}(Z)] \\ & = \delta_{w-b} \, \mathcal{L}^{-1}_{\gamma}\{H_{3}(\gamma)\}(t)\, dw, \end{aligned}$$

where we know from Proposition 4.6 with \(\mu = 0\) and \(\beta = 0\) that

$$\begin{aligned} H_{3}(\gamma) &= \mathbb{E} \Big[e^{ -\gamma H_{b}(Z)} \mathbf{1}_{\{\tau_{d}^{+}(Z) < H_{b}(Z)\}}\Big]\\ &=\Bigg( \bigg( e^{-\sqrt{2\gamma}b} \mathcal{N} \Big( \frac{b}{\sqrt{d}} - \sqrt{2 \gamma d} \Big) -e^{\sqrt{2\gamma} b} \mathcal{N} \Big( {-} \frac{b}{\sqrt{d}} - \sqrt{2 \gamma d} \Big) \bigg) \\ &\qquad\times\sum\limits_{k = 0}^{\infty} 2 \Big( z(k,0,0) - z(k+\frac{1}{2}, 0 ,0) \Big) - z(0,0,0) \Bigg) \\ &\quad{}\times \Bigg( \bigg( \sum\limits_{k=0}^{\infty}2\Big( z(k,\gamma,0) + \sqrt{2\gamma } e^{-\sqrt{2\gamma}2kb} \Big) - z(0,\gamma,0) - 2 \sqrt{2\gamma} \bigg) \\ &\qquad\quad{}\times \bigg(1- 2 \mathcal{N} \Big(- \frac{ b}{\sqrt{d} }\Big) \bigg) \Bigg)^{-1}. \end{aligned}$$

Notice the Dirac delta function, which is due to the deterministic behaviour of \(Z_{H_{b}}\) conditioned on \(H_{b}(Z) = t\). For the first part of the right-hand side of (5.6), we have

$$\begin{aligned} &\mathbb{Q}_{0}[\bar{\tau}(Z) \in dt, Z_{\bar{\tau}} \in dw , H_{b}(Z) < \tau_{d}^{+}(Z)] \\ &= \mathbb{Q}_{0}\big[\tau_{d}^{+}(Z) \in dt, Z_{\tau_{d}^{+}} \in dw , H_{b}(Z) < \tau_{d}^{+}(Z)\big]\\ & = \mathbb{Q}_{0}\big[ Z_{\tau_{d}^{+}} \in dw , \tau_{d}^{+}(Z) \in dt \big] - \mathbb{Q}_{0}\big[ Z_{\tau_{d}^{+}} \in dw , \tau_{d}^{+}(Z) \in dt , \tau_{d}^{+}(Z) < H_{b}(Z)\big]. \end{aligned}$$

We have found in Sect. 5.1 that with (5.2) and (5.3) combined, we derive

$$\begin{aligned} &\mathbb{Q}_{0}\big[ Z_{\tau_{d}^{+}} \in dw , \tau_{d}^{+}(Z) \in dt , \tau_{d}^{+}(Z) < H_{b}(Z)\big]\\ &= \frac{ \sum_{k= -\infty}^{\infty}\frac{w+2kb}{d} e^{-\frac{(w+2kb)^{2}}{2d}} }{ 2\sum_{k= 0}^{\infty}( e^{-\frac{(2kb)^{2}}{2d}} - e^{-\frac{(2k+1)^{2} b^{2}}{2d}} )} \mathcal{L}^{-1}_{\beta}\{H_{1} (\beta) \}(t) \, dw \, dt. \end{aligned}$$

Also, [9, Theorem 1] provides us with

$$ \mathbb{Q}_{0}\big[ Z_{\tau_{d}^{+}} \in dw , \tau_{d}^{+}(Z) \in dt \big] = \frac{|w|}{\pi \sqrt{(t-d) d^{3}}} e^{-\frac{w^{2}}{2d}}\, dw \, dt. $$

Hence, putting terms together, we derive the proposition. □

Proposition 5.3 allows us to derive the price of a MaxParisianHit option. In particular, with (5.5) we find the fair price of a MaxParisianHit Up-and-In call to be

$$\begin{aligned} &\mathrm{maxPHC}_{i}^{u} (S_{0},T,K,L,d,r) \\ &= e^{-(r+\frac{1}{2}m^{2})T} \int_{\frac{1}{\sigma} \ln \frac{K}{S_{0}}}^{\infty}(S_{0} e^{\sigma z} - K) e^{mz} \mathbb{Q}_{0} \big[Z_{T} \in dz, \max \big( \tau_{d}^{+}(Z), H_{b}(Z) \big) \leq T\big] , \end{aligned}$$
(5.7)

where the joint probability has been found in Proposition 5.3. In Propositions 4.3 and 4.6, we have derived the double Laplace transform of the hitting and Parisian times for drifted Brownian motion. This main result leads to finding the joint distribution of the final position of Brownian motion and the minimum or maximum of hitting and Parisian time. We have established pricing formulae for MinParisianHit and MaxParisianHit options. These fair prices contain single Laplace transforms, which need to be inverted numerically using techniques as in Labart and Lelong [17], Abate and Whitt [1] and Bernard et al. [4].