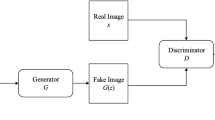
Abstract
In this paper, an innovative approach for enhancing fluid transport modeling in porous media is presented, which finds application in various fields, including subsurface reservoir modeling. Fluid flow models are typically solved numerically by addressing a system of partial differential equations (PDEs) using methods such as finite difference and finite volume. However, these processes can be computationally demanding, particularly when aiming for high precision on a fine scale. Researchers have increasingly turned to machine learning to explore solutions for PDEs in order to improve simulation efficiency. The proposed method combines an adaptive multi-scale strategy with generative adversarial networks (GAN) to increase simulation efficiency on a fine scale. The devised model, called simulation enhancement GAN (SE-GAN), takes coarse-scale simulation results as input and generates fine-scale results in conjunction with the provided petrophysical properties. With this new approach, a deep learning model is trained to map coarse-scale results to fine-scale outcomes, rather than directly solving the fluid flow model. Case studies reveal that SE-GAN can achieve a significant improvement in accuracy while reducing computational time compared to the original fine-scale simulation solver. A comprehensive evaluation of numerical experiments is conducted to elucidate the benefits and limitations of this method. The potential of SE-GAN in accelerating the numerical solver for reservoir simulations is also demonstrated.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Subsurface flow modeling is critical for addressing various contemporary technological challenges (Lie 2019). Achieving accurate and reliable numerical simulations of subsurface flow is essential for overcoming these challenges, particularly in petroleum engineering, where the focus is on the flow of oil, gas, and water through porous media due to pressure differentials. The efficiency of these simulations depends on the choice of numerical solver and the geological and petrophysical characteristics of subsurface reservoirs. In long-term oil recovery processes, operations rely heavily on simulation outcomes for aspects such as downhole rate control, well allocation, and production strategy optimization. Consequently, reservoir simulation models are widely used to determine objective functions, which require forward models to be executed numerous times (Brown et al. 2017; Olalotiti-Lawal et al. 2019; Salehi et al. 2019; Shirangi and Durlofsky 2016), thus posing computational challenges.
Efficiently and accurately solving fluid flow governing equations, typically a system of partial differential equations (PDEs), has been a longstanding challenge for simulation methodologies. Among numerical solvers, the finite-volume approach, which is derived from conservation principles applied to specific domains, has been widely adopted (Karimi-Fard and Durlofsky 2012). The approximations in finite-volume methods are based on averaged quantities, making them more physically grounded than the finite-difference method employed in many commercial software applications. To meet accuracy demands, a refined grid system is necessary, particularly in near-well regions (Cao et al. 2019a, b), where pressure changes are more pronounced than in areas farther from wells. However, computational costs increase significantly with larger grid systems, especially when the flow domain is highly heterogeneous and anisotropic (Cao et al. 2019a, b).
Recently, deep learning methods have been developed to address PDEs in various application fields, demonstrating significant progress and innovation. Despite many unanswered fundamental questions, deep learning as an emerging research direction has shown considerable potential and promising results. This background section focuses on the related work of deep learning concerning the numerical solutions of PDEs, which can be broadly divided into three main categories.
The first strategy is to solve directly PDEs using deep learning. Numerous studies have utilized deep learning networks to directly estimate PDE solutions. The majority of these works employ a data-driven strategy under supervised learning. These data-driven methods necessitate training procedures with existing data and have been shown to outperform physics-driven models in various tasks, particularly in solving high-dimensional PDEs (Brown et al. 2017; Bukharev et al. 2018; Nabian and Meidani 2018). Raissi et al. (2019) combined the classical implicit Runge–Kutta method and investigated the inverse problem of the equation. The Deep Ritz method (Weinan and Yu 2018) uses an energy minimization formulation as the loss function of artificial neural networks (ANNs) to solve PDEs, and recent studies (Xu et al. 2020; Li and Chen 2020) have employed deep learning to solve the Fokker–Planck equation and several nonlinear evolution equations. Wang et al. (2021) developed a pore-scale imaging and modeling workflow based on deep learning, spanning from image processing to physical processing. Wang et al. (2022a, b) proposed a methodology for constructing approximate solutions for stochastic partial differential equations (SPDEs) in groundwater flow by combining two deep convolutional residual networks. Chen et al. (2022) presented a numerical framework for deep neural network modeling of time-dependent PDEs using their trajectory data. A framework integrating deep learning and integral form has been proposed to address the challenges of PDEs with high order, data sparsity, noise, and simultaneous discovery of heterogeneous parameters (Xu et al. 2021).
The second strategy is to use deep learning to enhance and accelerate simulations. Many efforts have been made to deploy deep learning to reduce the complexity and improve the computational efficiency of existing numerical algorithms. For example, Bhalla et al. (2020) used neural networks to replace the flamelet look-up tables and reduced the memory it requires. In the study by Tompson et al. (2017), convolutional neural networks (CNN) were used to solve the large linear system derived from the discretization of incompressible Euler equations. Suzuki (2019) developed a neural network-based discretization scheme for the nonlinear differential equation using the regression analysis technique. A deep-learning-based approach was developed for the efficient evaluation of thermophysical properties in the numerical simulation of complex real-fluid flows (Milan et al. 2021). Ryu et al. (2022) formalized a deep-learning-based fast simulation model of thermal–hydraulic code and proposed a novel deep learning model, the ensemble quantile recurrent neural network (eQRNN).
In addition, an adaptive collocation strategy was proposed by Anitescu et al. (2019), while Raissi et al. (2019) employed latent variable models to construct probabilistic representations for the system states and put forth an adversarial inference procedure to train them. Wang et al. (2022a, b) proposed the theory-guided convolutional neural network (TgCNN), which incorporates the discretized governing equation residuals into CNN training, and extends it to the two-phase porous media flow problems, obtaining adequate inversion accuracy. The premise underlying all these efforts is to constrain their predictions to satisfy the given physical laws expressed by partial differential equations. Despite the improvement over classical numerical methods, however, these methods still suffer from exponentially increasing problems and are unsuitable for high-dimensional PDEs.
The third strategy is to upscale reservoir simulation using machine learning. Santos et al. (2022) proposed an artificial intelligence approach that achieved accurate upscaling, surpassing the reference method, with predicted production similar to the fine-scale model. Moreover, when considering multiple geological realizations, it also demonstrated fast computation speed, as it reduced the required numerical simulations to a fraction of the total. Trehan and Durlofsky (2018) introduced a machine-learning-based post-processing framework to model errors in the coarse model results under uncertainty quantification. The corrected coarse-grained solution demonstrated significantly improved accuracy in predicting oil production and quantifying uncertainty in important statistical measures compared to the uncorrected solution. Rios et al. (2021) focused on improving the representation of small-scale heterogeneity in coarse models. They extended the scale-up technique for dual porosity and dual permeability to apply to three-dimensional highly heterogeneous systems. Compared to traditional flow-based scale-up methods, this approach can provide more accurate results.
The existing research collectively demonstrates that deep learning can effectively characterize the numerical solution of a PDE. However, it is crucial to note that the primary challenge with current numerical simulations lies in the trade-off between simulation accuracy and computational cost. As the number of grid blocks in a reservoir model increases, computational costs can rise dramatically, potentially approaching exponential growth. As shown in Table 1, the computational time and memory requirements for numerical simulation significantly increase with the increase in the number of model grids. The challenge, therefore, is not with the simulation approaches—many of which are robust and efficient—but with the computational expenses associated with large model sizes.
In this study, we introduce an indirect method that maps coarse-grid simulation results to fine-grid simulation outcomes based on fine-scale geological models using deep learning techniques. The main objective is to improve and enhance the simulation process with deep learning while preserving engineering comprehension. Unlike direct solutions to PDEs using deep learning, the indirect approach capitalizes on both coarse-scale simulation results and fine-scale geological models, both of which are physically fundamental to the final fine-scale simulation results. This method aligns with the reservoir engineering workflow, where both coarse- and fine-scale models and results are generated for various purposes.
The remainder of the paper is structured as follows: First, we present the methodology as an integrated workflow, incorporating a numerical reservoir simulation method, fine-scale geological models, and a simulation enhancement GAN (SE-GAN) structure. The structural details of the SE-GAN, including the generator, discriminator, and loss function, are discussed. Next, we implement the workflow in a classical quarter-five-spot well pattern of a heterogeneous reservoir to train and evaluate the proposed method. Numerical case studies are investigated through a series of simulation experiments, where the accuracy and efficiency of the results are assessed and compared with fine-scale numerical simulations. Finally, we present the conclusions drawn from the case study, along with a discussion of limitations and future work.
2 Methodology
The conventional workflow for reservoir engineers involves generating models on both coarse and fine scales, as illustrated in Fig. 1. A geological model is typically represented numerically through discretization in a grid system with estimated petrophysical properties. The level of discretization can be chosen according to different requirements, and any simulation method can be used, yielding results with varying degrees of approximation. Finer discretization levels yield more accurate results but at the expense of higher computational costs. The discrepancies between simulation results arise from the numerical simulation approximations of different discretization grids. The primary objective is to bridge these gaps without numerically solving the problem on a fine scale while achieving high accuracy in results with lower memory and central processing unit (CPU) time costs.
To achieve this objective, we employ a deep learning approach, a subfield of machine learning, to estimate the deviations between approximations from simulation results of different discretization levels. However, this estimation is a multi-solution problem with considerable uncertainty. Therefore, we use the fine grid representing petrophysical properties as physics-informed data to reduce uncertainty and increase reliability on a large scale. These combined features have the potential to overcome the abovementioned limitations by improving the simulation results.
To address this challenge, we propose an adaptive multi-scale simulation method using the GAN structure. By employing deep learning methods and incorporating additional physics-informed data to reduce uncertainty, coarse-scale results can be enhanced. Ultimately, this approach can overcome the inherent limitations of general deep-learning-based solutions by improving simulation outcomes. The method uses the simulation results from a coarse grid as prior knowledge and physics-informed data to generate enhancement results comparable to those obtained from a fine-grid simulation. This implies that with the time and memory costs of a coarse-grid simulation, we can achieve results similar to those of a fine-grid simulation. Furthermore, the petrophysical data on fine grids are used as additional information to ensure improved simulation-enhanced results accuracy and a low level of uncertainty.
2.1 Applied Methodological Sequence
The sequence of this method consists of three main steps, as illustrated in Fig. 2. The initial step involves preparing the training datasets for our SE-GAN. The training dataset comprises several two-dimensional permeability grids and their corresponding pressure simulation results. These result matrices are simulated using finite-volume methods on randomly generated permeability grids. The grid sizes are divided into two groups: the coarse grid group and the fine grid group. For instance, in the first experiment, we use 50 × 50 (coarse) and 200 × 200 (fine) grids. The coarse grid is obtained by upscaling the fine grid using the arithmetic mean of its permeability values.
During the subsequent training phase, the coarse and fine pressure simulation results and the fine permeability grids are fed into the SE-GAN. Through the iterative process, SE-GAN gradually learns the relationship between the corresponding simulation results from coarse and fine grids, aided by the fine permeability grid. Enhancing the coarse results is a multi-solution problem, which leads to unavoidable uncertainty. To further improve the enhancement results and reduce uncertainty, the petrophysical property in the fine grid, namely permeability, serves as a physics-informed network in this training procedure. This offers additional information for the model, helping generate more reliable results without incurring any significant computational costs.
In the final step, the trained SE-GAN generator model can be used to enhance other random simulation results when simulating pressure distribution with a given petrophysical grid of permeability. The input grid size can be upscaled to 1/16 or lower, and the finite-volume simulation process is executed on this coarse grid. This approach requires less than 10% of the computational effort compared to simulations using the original grid, as shown in Table 4. Ultimately, SE-GAN can enhance this result using the original grid as input, requiring virtually no additional computational resources.
2.2 SE-GAN Generator
The generator of our SE-GAN, which incorporates the residual dense block (RDB) and residual channel attention block (RCAB), is capable of efficiently extracting and utilizing features from different layers to reconstruct the simulation matrix. The structure of the SE-GAN generator is shown in Fig. 3. It consists of three main steps: shallow numerical feature extraction, deep numerical feature extraction, and numerical simulation reconstruction. The details of these steps are introduced in the following.
2.2.1 Shallow Numerical Feature Extraction
The input \({P}_{{\text{coarse}}}\) matrix must be scale-adjusted (SA) to match the size of \({P}_{{\text{fine}}}\) and \({K}_{{\text{reference}}}\). In our first experiment, \({P}_{{\text{coarse}}}\) is 50 × 50 and should be adjusted to 200 × 200 as \({\widetilde{P}}_{{\text{coarse}}}\) by simply assigning every value from \({P}_{{\text{coarse}}}\) into each element of a 4 × 4 matrix. Once this SA preprocessing is complete, \({\widetilde{P}}_{{\text{coarse}}}\) and \({K}_{{\text{reference}}}\) are combined into the matrix \(X \in {R}^{M \cdot N \cdot {C}_{X}}\). First, a 3 × 3 CNN layer \({F}_{{\text{S}}}(\cdot )\) is used to extract the shallow features \({f}_{S}\in {R}^{M \cdot N \cdot {C}_{im}}\) from \(X\), where \({f}_{S}\) can be expressed as Eq. (1).
Here, \({\varvec{M}}\) and \({\varvec{N}}\) are the input matrix size, and \({{\varvec{C}}}_{{\varvec{X}}}\) and \({{\varvec{C}}}_{{\varvec{i}}{\varvec{m}}}\) represent the channel number of \({\varvec{X}}\) and the intermediate feature. In our numerical experiment, \({\varvec{M}}\) = \({\varvec{N}}\) = 200, \({{\varvec{C}}}_{{\varvec{X}}}\) = 2, and \({{\varvec{C}}}_{{\varvec{i}}{\varvec{m}}}\) = 64. \({{\varvec{F}}}_{\mathbf{S}}(\cdot )\), as the first CNN layer, can map matrix \({\varvec{X}}\) from low-dimensional to high-dimensional to extract potential features for subsequent processing steps. Furthermore, it helps our model learn the simulation matrix representation and produce stable optimization results.
2.2.2 Deep Numerical Feature Extraction
From the first shallow layer, we obtain \({{\varvec{f}}}_{{\varvec{S}}}\) as the output. In this step, model \({{\varvec{F}}}_{\mathbf{D}}(\cdot )\) consists of \({\varvec{K}}\) residual channel attention dense blocks (RCADB) and one CNN layer, which is used to extract deep features from \({{\varvec{f}}}_{{\varvec{S}}}\). RCADB is a composite module, and its detailed structural design is shown in Fig. 3. This procedure can be represented as Eq. (2).
The CNN layer \({{\varvec{F}}}_{{\varvec{C}}}(\cdot )\) is the last layer of the entire feature extraction process. After the RCADB layers have extracted numerous high-dimensional features, \({{\varvec{F}}}_{{\varvec{C}}}(\cdot )\) is then prepared to introduce the bias of the convolution operation into our network and provide a better foundation for the later aggregation of features from shallow and deep networks. This deep feature extraction step can be described in detail as Eq. (3), where K represents the number of RCADB blocks.
2.2.3 Numerical Simulation Reconstruction
Through the previous two steps, shallow feature \({f}_{S}\) and deep feature \({f}_{D}\) are extracted. \({f}_{S}\) contains information from low-frequency and \({f}_{D}\) contains relatively high-frequency information. The main objective of this step is to use the aggregation of these features to produce a complete simulation matrix. Therefore, we propose a global residual-based skip connection network to aggregate shallow and deep features together. The key network here is \({F}_{{\text{R}}}(\cdot )\), which consists of four 3 × 3 CNN layers and three leaky rectified linear unit (ReLU) activation layers arranged alternately in a series. This structure enables \({F}_{{\text{D}}}(\cdot )\) to transmit low-frequency information directly to the reconstruction model and make the training procedure more stable. After that, the global residual connection can fuse shallow features and deep features.
2.3 Discriminator
The discriminator of our SE-GAN is a U-Net with spectral normalization, as shown in Fig. 4. U-Net is an encoder–decoder structure suitable for dense prediction. Spectral normalization can stabilize the U-Net training procedure. Altogether, this structure can precisely evaluate the quality of the generator's results.
2.4 Loss Function
The simulation enhancement loss \({L}_{{\text{SE}}}\) is used to describe the L1 norm distance between the generated matrix \({G}_{{\text{SE}}}(X)\) and real simulated matrix \(Y\). Our generator benefits from the gradients of these two factors. The loss can be written as Eq. (4), where \({\xi }_{{\text{SE}}}\) represents the weight of \({L}_{{\text{SE}}}\).
Adversarial loss \({L}_{{\text{adversarial}}}\) is produced by the discriminator. When \({G}_{{\text{SE}}}(X)\) has been generated, \({L}_{{\text{adversarial}}}\) can be computed by Eq. (5) with the output of discriminator \({D}_{{\text{SE}}}({G}_{{\text{SE}}}(X))\), where \(\varphi \) is the sigmoid function, and \({\xi }_{{\text{adversarial}}}\) represents the weight loss of \({L}_{{\text{adversarial}}}\).
The total loss \({L}_{{\text{total}}}\) is used in each iteration during training and is computed by adding the above two loss values as expressed in Eq. (6), and in our experiment, the weight used in each formula is \({\xi }_{{\text{SE}}}\) = 1 and \({\xi }_{{\text{adversarial}}}\) = 0.1.
3 Comprehensive Numerical Analysis of Pressure Field Predictions with SE-GAN
Section 3.1 introduces the datasets employed in our experiments. Section 3.2 presents the training process for three distinct SE-GAN networks. The enhancement results for 16-times upscaled grid examples are thoroughly evaluated and analyzed in Sect. 3.3. Section 3.4 assesses the general effectiveness of SE-GAN for various upscaling factors using 64-times and 256-times upscaled grids. Lastly, the three trained networks are applied to larger-scale example cases to enhance simulation results with SE-GAN. All results shown in the figures and tables of Sect. 3 are derived from the testing dataset.
3.1 Simulation-Based Datasets
In this study, the training and testing datasets are generated from the simulation results obtained using the finite-volume method, implemented with the MATLAB Reservoir Simulation Toolbox (MRST) (Lie 2019) for a two-dimensional case. A well-established two-dimensional quarter-five-spot case is chosen, featuring one water injector and one oil producer, situated in the top left and bottom right grids, respectively, as illustrated in Fig. 5. The permeable grid is two-dimensional, generated by randomly assigned values, with a representative distribution depicted in Fig. 5. In this scenario, approximately 50% of the values are assigned below 0.1D, a majority of other values fall between 0.1 and 0.6D, and a mere 5% of values exceed 0.6D. The reservoir contains two fluid phases, water and oil, with identical viscosity of 10−3 Pa·s and density of 1,000 and 750 kg/m3, respectively. A bottom hole pressure difference of 1 Mpa is set between the injection well and production well. Initial oil and water saturation values are 0.8 and 0.2, respectively. The external boundary is considered a no-flow boundary condition, and the influence of gravity is disregarded.
In the numerical experiments, three datasets are designed to assess our SE-GAN from various perspectives. Here, we define the enhancement case using the ratio of the number of fine grids (\({N}_{f}*{N}_{f}\)) to the number of coarse grids (\({N}_{c}*{N}_{c}\)). It should be noted that a trained model has a constant ratio \(\frac{{{\text{N}}}_{{\text{f}}}}{{{\text{N}}}_{{\text{c}}}}\). The input coarse grid size \({N}_{c}\) can be random, and the fine grid size \({N}_{f}\) is determined accordingly.
The details of these data sets are listed below and also summarized in Table 2:
-
(A)
Dataset A is used to train and test the ×16 SE-GAN model. The fine grid is 200 × 200, and the corresponding coarse grid is 50 × 50. Dataset A comprises 5,000 samples each for fine and coarse results (each sample pair contains input data and output label data, with the input data containing unique permeability grid data randomly generated at random times during simulations). Among them, 4,500 sample pairs are used for training, and the other 500 pairs are used for testing the trained SE-GAN.
-
(B)
Dataset B aims to quantitatively evaluate the accuracy deviation affected by different discretization scales between fine and coarse grids. We choose 8-times and 16-times grids to simulate dataset B, divided into two independent groups, the 8-times group and the 16-times group, with the same sample number as dataset A for each group. The ratio of the training and testing pair is also 4,500:500. The size of the fine grid is changed to 256 × 256, and the coarse grid sizes in the 64-times and 256-times groups are 32 × 32 and 16 × 16, respectively. Other parameters and simulation settings remain the same as for dataset A.
-
(C)
Dataset C involves generating numerous simulation results with a larger grid system and testing the generalizability of the SE-GAN model by evaluating the enhancement performance based on various coarse grid size models. This process is purely for testing, meaning that it deploys the trained models from datasets A and B without requiring any additional training. It should also be noted that although the model size of the coarse grid can be chosen randomly, the corresponding refinement grid number can only be in specific multiples, which are 16, 64, and 256 for this research.
3.2 Training of SE-GAN
All the training procedures in our experiments share the same hyperparameters, as shown in Table 3.
The results for pressure distribution, a two-dimensional matrix, are evaluated. The relative difference between the coarse- and fine-grid simulation results for all training data is displayed in Fig. 6a, while the generator's loss value is presented in Fig. 6b. From Fig. 6a, it can be observed that the relative difference converges rapidly to a level below 2% as the iteration number increases. A similar phenomenon can be seen in Fig. 6b. The convergence of both the relative difference and the generator's loss value to lower levels during the training procedure provides direct evidence that our SE-GAN model can learn the correlation between coarse- and fine-grid simulation results and subsequently produce improved outcomes based on coarse input. It should be noted that the deep mapping relationship between coarse grid and fine grid is highly complex, and it is very challenging to train the model to obtain optimal network weight parameters. Figure 6 is presented to illustrate that the loss value at higher iteration numbers is smaller and tends towards zero compared to lower iteration numbers, and its variation is relatively more stable.
3.3 Enhancement Experiment Analysis
Sample no. 4,553 from the testing dataset of dataset A is randomly selected to demonstrate SE-GAN's capability in enhancing simulation results. As illustrated in Fig. 10, the fine-scale result (Fig. 7d) is simulated by the fine permeable grid (Fig. 7b) for comparison. Our SE-GAN requires the coarse simulation result (Fig. 7c), simulated from a coarse grid (Fig. 7a), and the fine permeable grid (Fig. 7b) as input to generate the enhanced result (Fig. 7e). From a human visual perspective, the enhanced result appears nearly identical to the real simulation result. In numerical terms, the average relative difference between them is only 0.0157%. The detailed distribution of relative error for each pixel is shown in Fig. 7f. The largest error, 2.7%, occurs in the right corner where the production well is located. The largest errors are found in the near-well regions of both the producer and the injector, where the pressure changes drastically. When the matrix values change rapidly between adjacent elements, the SE-GAN cannot fully capture the underlying patterns. However, even in the worst sample in the test dataset, SE-GAN still achieves over 99.7% accuracy on average after enhancement.
The other four randomly chosen samples are shown in Fig. 8. In most cases, SE-GAN demonstrates a powerful ability to enhance finite-volume simulation results, with stable and high prediction accuracy. The average accuracy for all testing sample results is 99.9235% in these samples.
We also calculated the average relative error interval distribution based on the 500 samples in the testing dataset of dataset A, as shown in Fig. 9. In our assessments, we observed that SE-GAN exceeds accuracy of 99.9% in over 80% of the evaluated instances. Furthermore, a distinct 13% of the total samples exhibited enhanced accuracy, surpassing 99.97%, when benchmarked against the original simulation results derived from the fine grid. It is noteworthy that a mere 6% of the samples fell below the 99.83% accuracy threshold. From Fig. 9, we can conclude that SE-GAN is capable of providing stable and accurate enhancement results for finite-volume simulations.
Figure 10 illustrates the dynamic changes in pressure at the injection well location, as derived from both coarse- and fine-grid simulations and SE-GAN, over the course of the injection process. The distinct trajectories underscore the model’s precision and its alignment with the fine grid data, offering insights into SE-GAN's capability to bridge the disparity in pressure readings between coarse and fine grids.
3.4 Other Discretization Scale in SE-GAN
In the previous section, we used the 16-times upscaled grid as the coarse grid. To fully evaluate the influence of the upscale size, we provide 64-times and 256-times upscaled grids in this section for experimental examples. All the hyperparameters used in the training procedure in this section are the same as in Table 2. Compared with ×16 results in Fig. 8, the ×64 sample enhancement in Fig. 11 is relatively blurred in pressure details, and the relative error is correspondingly higher but still occurs within the two corners where the injection well and production well are located. The average accuracy of the SE-GAN in the ×64 samples is 99.8553%.
From the relative error distribution of the 8-times SE-GAN in Fig. 12, we can observe that relative errors above 0.13% have increased from less than 6% (×16) to more than 25% (×64). The recovery ability of the SE-GAN has been significantly affected by the upscale size of the input coarse grid.
When the upscale level of the coarse grid is up to 256 times, the overall trend of pressure distribution can still be recovered, as shown in Fig. 13. However, many detailed changes are missing, which makes the image less distinct.
When the discretization scale of the coarse grid was upscaled to 256 times, the relative error also increased. The average relative error in the test dataset increased from 0.0765% (×16) and 0.1447% (×64) to 0.2603% (×256). From the distribution figure (Fig. 14), the relative error of all samples is greater than 0.1%, and more than 22% of the sample experiments resulted in an error between 0.25 and 0.3%.
3.5 Practical Application Analysis
When SE-GAN is produced for practical application, it is hard to guarantee that the size of the input grid will be the same as our training dataset. Hence, in this section, we use dataset C to test whether the SE-GAN is applicable for any given grid system size, and then move on to discuss its generalizability. The SE-GAN generation model was trained as described in Sects. 3.3 and 3.4. Here, the fine-scale grid is set as 2,000 × 2,000 as shown in Tables 2 and 4, and various coarse-scale grids with 1/16, 1/64, and 1/256 of the fine grids are upscaled. To reduce the uncertainty of different samples and validate this experiment, we build a dataset with 10 scenarios in this experiment, and the whole analysis index is based on their average values in Table 4. The simulation process is executed on a PC with an Intel Core i7-9700K processor and 32 GB memory.
To demonstrate the performance of SE-GAN in extremely challenging cases, we extract the data from the right corner for additional reference. The right corner is where the production well is located, and the pressure drops rapidly within the fluid recovery, which creates difficulty in the following enhancement process. For this, 3 × 3 grid data from the right corner of each coarse grid are extracted to represent the extreme conditions for comparison and analysis.
As demonstrated in Table 4, the benefits of using SE-GAN are more pronounced in the context of large grid enhancement. Compared to direct simulation of the fine grid, the overall time consumption in dataset 3o. 3 of dataset C can be decreased to 1/18th of the original time, while reducing the memory cost to approximately 1/1,000. This is achieved with only a 2.4% error in corner parts and a 0.1% error for the total grid.
In the case of large grids, the differences in simulation results are not easily discernible from a visual perspective, as shown in I of Figs. 15, 16, and 17; these discrepancies can only be observed upon closer examination of the details. Therefore, we focus on the corner part of the grids, with the results displayed in II. The enhancement results for the SE-GAN in large grids are similar to those in smaller grids, as presented in Sects. 3.3 and 3.4. Compared to the ×16 and ×64 results, the ×256 results lose some detail, causing the output to appear somewhat blurred. Taking into account both accuracy and computational costs, the ×64 enhancement is recommended due to its balance between these two factors.
Enhancement comparison based on the first sample (16-times) in dataset no.1 of dataset C: I, whole grid; II, bottom right corner part of I as shown in the yellow rectangle in I; a coarse grid pressure simulation result; b enhancement of coarse grid pressure simulation; c fine grid pressure simulation result; d relative error between b and c
Enhancement comparison based on the first sample (64-times) in dataset no. 2 of dataset C: I, whole grid; II, bottom right corner part of I as shown in the yellow rectangle in I; a coarse grid pressure simulation result; b enhancement of coarse grid pressure simulation; c fine grid pressure simulation result; d relative error between b and c
Enhancement comparison based on the first sample (256-times) in dataset no. 3 of dataset C: I, whole grid; II, bottom right corner part of I as shown in the yellow rectangle in I; a coarse grid pressure simulation result; b enhancement of coarse grid pressure simulation; c fine grid pressure simulation result; d relative error between b and c
3.6 Role of RCAB and GAN Structure
The inclusion of the RCAB in the SE-GAN model resulted in higher accuracy at every stage of training compared to the model without RCAB. The introduction of RCAB during the SE-GAN training process helps to improve the accuracy of the generated results and stabilize the model training process, as shown in Table 5.
As for the GAN structure, the main difference lies in the addition of a discriminator network and an extra loss term, the adversarial loss. The primary purpose of the discriminator network is to complement the traditional pixel-based loss computation method. This is particularly beneficial for enhancing the learning capability of the model when dealing with rapid pressure changes at well locations.
In summary, the incorporation of RCAB and the GAN structure contributes to improving the performance of the SE-GAN model. The RCAB enhances the accuracy and stability of the training process, while the discriminator network, along with the adversarial loss, helps capture rapid pressure changes at well locations more effectively. This combination results in a more robust and accurate model for subsurface problems.
3.7 The Physics-Informed Effect of Permeability
In order to evaluate the role of permeability in reducing the multi-solution problem in enhanced models, this subsection presents an experiment to demonstrate the physics-informed ability of permeability data. We conducted experiments on several groups of test cases, and the results of one group are shown in Fig. 18. From these images and comparisons, we can conclude that introducing permeability data in the model input can significantly improve the enhancement accuracy. Integrating \({K}_{{\text{reference}}}\) into the input of SE-GAN effectively guides the model to learn the deep mapping relationship between the coarse grid and the target fine grid simulation results, reducing the impact of multiple solutions during the enhancement process. These cases all present obvious improvements with \({K}_{{\text{reference}}}\). Specifically, in the relative error plots, \({K}_{{\text{reference}}}\), which is the physics-informed data, significantly reduces their errors by almost 20-fold.
The introduction of permeability in the input imposes physics-informed data on the enhancement results of SE-GAN: a permeable fine grid; b coarse grid pressure simulation result; c fine grid pressure simulation result; d relative error between c and e; e coarse grid pressure simulation enhancement result using input \({K}_{{\text{reference}}}\) and \({P}_{{\text{coarse}}}\); f relative error between c and g; g coarse grid pressure simulation enhancement result using only input \({P}_{{\text{coarse}}}\)
3.8 Evaluation of SE-GAN in Highly Heterogeneous Permeability Model
On the other hand, SE-GAN also demonstrated satisfactory enhancement results on highly heterogeneous permeability data with increased challenges. One representative height heterogeneity permeability matrix data example is shown in Fig. 19, with a wider range of permeability and closer resemblance to the scenarios encountered in actual reservoir engineering applications. We evaluated the performance of SE-GAN on simulated data with highly nonuniform permeability at ×16, ×64, and ×256 scales. It is worth noting that in this set of experiments, we increased the number of training iterations to 10,000 and the training set size to 9,000. The comparative results are shown in Table 6. In the scenario of highly nonuniform permeability simulation, due to the significant differences in numerical distribution and high randomness inherent in the simulated data, the enhancement effect of SE-GAN is slightly inferior to the results in Table 3. However, it still achieves a high level of enhancement accuracy.
4 Extending SE-GAN Applications: Oil Saturation Time Series Prediction and Analysis
Seeking to harness the transformative power of SE-GAN, we directed our efforts towards the time series diffusion modeling of oil saturation. This venture was influenced considerably by the intricacies of the permeability field, especially given our reservoir's detailed simulation setup.
4.1 Reservoir and Simulation Configuration
Our simulation adapted to a 128 × 128 × 128 two-dimensional grid, marking a distinct shift in spatial resolution. In contrast, the generation of the permeability field remained consistent with the methodology outlined in Sect. 3.1. The nuanced interplay between permeability and porosity was captured through a Gaussian field, a strategy anchored in predefined specific parameters, ensuring coherence in the reservoir’s physical characterization while accommodating the refined grid scale.
The fluid dynamics were governed by a biphasic system, characterized by distinct viscosities and densities, aligning with the parameters detailed in Sect. 3.1. Similarly, the simulation incorporated two pivotal wells, an injector and a producer, positioned at the top left and bottom right of the grid, respectively. This arrangement, consistent with the well configuration in Sect. 3.1, exemplifies a standard reservoir operation, ensuring uniformity in simulation conditions across different scales and models.
The bedrock of our simulation rested upon the incompressible two-point flux approximation (TPFA) method. Initiating from a predetermined reservoir state, our approach was iteratively time-stepped, where each phase updated the saturation profile. An outcome of interest, the oil in place (OIP), was methodically calculated after each iteration, capturing the progressive essence of oil saturation within the reservoir.
4.2 SE-GAN Network Structure and Simulation Strategy for Saturation Prediction
In our pursuit of refined oil saturation predictions, both the structure and operational strategy of the SE-GAN were meticulously adapted to accommodate the complex dynamics and data intricacies inherent to this specific application, all of which are comprehensively detailed in Fig. 20. These can be summarized as follows:
-
(1)
Network structure adaptations
While the foundational SE-GAN structure was preserved, the intricate nature of oil saturation modeling necessitated several critical modifications. A key focus was on the integration of permeability and fluid pressure data. These elements were strategically assimilated into the numerical reconstruction module, enhancing the model's ability to generate nuanced, accurate predictions that are deeply rooted in the actual physical and operational conditions of the reservoir.
-
(2)
Simulation and prediction strategy
Diverging from the direct generation strategy employed in pressure predictions, our approach for oil saturation leveraged an enhanced strategy. SE-GAN was tasked with utilizing coarse-grid data from the initial six time steps to predict fine-grid oil saturation across 24 time steps. This approach allowed us to evaluate SE-GAN's capability in a more dynamic, temporally extended context, effectively benchmarking its performance against complex, real-world scenarios where data may be limited. The integration of this enhanced generation strategy within the SE-GAN’s modified structure, as depicted in Fig. 20, presents a comprehensive viewof our approach, combining structural adaptability with strategic innovation to optimize oil saturation predictions.
4.3 Results and Comparative Analysis
Our tailored SE-GAN model yielded intriguing insights, with Figs. 21 and 22 providing a visual representation of the results at select time steps—1, 5, 7, 9, 13, 17, 21, and 24. These milestones in the simulation process were critical in assessing the model’s performance under varying conditions and complexities. They are summarized as follows:
-
(1)
Early-stage insights
In the early stages, the integration of coarse data constraints provided a foundational guide, establishing an initial benchmark for evaluating the predictive fidelity of the SE-GAN. The model demonstrated remarkable precision, offering insights into its capability to navigate and represent complex oil saturation dynamics.
-
(2)
Extended predictions
Transitioning into the latter stages, SE-GAN exhibited an innate ability to extrapolate data and predict future states with a significant degree of accuracy. Even in the absence of immediate coarse data guides, the model maintained its predictive integrity, illuminating its potential application in real-world scenarios where data can often be sparse.
-
(3)
Key observations
A detailed examination revealed that major discrepancies were localized in regions of pronounced saturation gradients, aligning with observations noted in pressure predictions. These insights are instrumental in understanding the model’s strengths and potential areas for further refinement, marking a significant step towards the optimization of SE-GAN for comprehensive reservoir simulations.
4.4 Numerical Experiment Result Discussion
The above experiments confirm the ability of the SE-GAN model to characterize the correlation between different discretization scales in reservoir simulation results. From the numerical experiments, even though the input simulation result is from a coarse grid system that has been upscaled to 1/256 of the fine-scale grid, SE-GAN achieves 99.7397% accuracy on average. The generalizability of the SE-GAN was also demonstrated for the reservoir model with various coarse grids. Once this model has been trained, it can be used in other grids of any size. Less difference between coarse and fine grid size leads to higher enhancement accuracy and recovery of more detail but with more computation time and memory cost. Therefore, the SE-GAN provides a flexible choice of grid numbers.
However, the limitations of SE-GAN applied here must also be noted, as follows:
-
(1)
Limitations of specific size proportions
Although the model is generally applicable to any input coarse grid size, the refined grid size (\({N}_{f}\)) is limited to specific multiples of the coarse grid size (\({N}_{c}\)). In this study, we trained models for three cases: ×16, ×64, and ×256. This means that the enhancement model is inherently designed for a constant ratio \({N}_{f}\)/\({N}_{c}\) between the total grid numbers of coarse- and fine-scale models.
-
(2)
Special location of injection well and production well
While SE-GAN can be adapted to grids of any size, it is sensitive to the locations of injection and production wells. Changes in their location or bottom pressure may cause the enhancement to fail, limiting the generalizability of the SE-GAN. However, well locations are usually fixed in a reservoir, and retraining a new model might only be considered when a new infill well is added to the reservoir.
-
(3)
Specific numerical solver
SE-GAN's performance is based on a specific numerical solver in structured grid systems. The conclusions and recommendations are also limited to the simulation solver, specifically for water flooding cases in a quarter-five-spot case.
-
(4)
Extension of model
The current simulation case is based on a two-dimensional model, and extending the development to three-dimensional models is considered for future work.
The experiments presented above demonstrate SE-GAN's ability to characterize the correlation between different discretization scales in reservoir simulation results. The numerical experiments show that even when the input simulation result comes from a coarse grid system that has been upscaled to 1/256 of the fine scale, SE-GAN achieves average accuracy of 99.7397%. The generalizability of the SE-GAN for reservoir models with various coarse grids is also evident. Once trained, the model can be used with grids of any size. A smaller difference between coarse and fine grid sizes results in greater enhancement accuracy and more detailed recovery, albeit with increased computation time and memory cost. As a result, SE-GAN offers a flexible choice of grid numbers.
5 Conclusions
To expedite reservoir simulation processes and reduce computational costs, we have proposed a deep learning method for enhancing simulation results from upscaled discretization grids. The designed model maps coarse-scale simulation results together with petrophysical properties to the fine-scale results. The results of numerical experiments demonstrate that the method produces enhanced results with high accuracy while incurring minimal computational expenses. Specifically, the enhancement results for 1/16, 1/64, and 1/256 upscaled grids were produced, analyzed, and evaluated. In the quarter-five-spot case study, the 64-times upscaled grid is recommended for practical application of our SE-GAN to strike a balance between computational accuracy and cost. In summary, SE-GAN can significantly reduce the time and memory requirements for numerical simulation at the cost of minor precision loss. The comprehensive evaluation and analysis of the numerical experiment results verify the ability of the SE-GAN to notably accelerate the reservoir simulation process, showing great potential for numerical simulation applications.
Data Availability
The associated data and source code for this manuscript can be accessed at our public repository on GitHub: https://github.com/ShuopengYang/SEGAN.
References
Anitescu C, Atroshchenko E, Alajlan N, Rabczuk T (2019) Artificial neural network methods for the solution of second order boundary value problems. Comput Mater Continua 59(1):345–359
Bhalla S, Yao M, Hickey JP, Crowley M (2020) Compact representation of a multi-dimensional combustion manifold using deep neural networks. In: Brefeld U, Fromont E, Hotho A, Knobbe A, Maathuis M, Robardet C (eds) Machine learning and knowledge discovery in databases. Springer International Publishing, Cham, pp 602–617. https://doi.org/10.1007/978-3-030-46133-1_36
Brown JB, Salehi A, Benhallam W, Matringe SF (2017) Using data-driven technologies to accelerate the field development planning process for mature field rejuvenation. In: SPE western regional meeting, Bakersfield, California, SPE-185751-MS. https://doi.org/10.2118/185751-MS
Bukharev A, Budennyy S, Lokhanova O (2018) The task of instance segmentation of mineral grains in digital images of rock samples (thin sections). In: International conference on artificial intelligence applications and innovations, Nicosia, Cyprus. https://doi.org/10.1109/IC-AIAI.2018.8674449
Cao J, Gao H, Dou L, Zhang M, Li T (2019a) Modeling flow in anisotropic porous medium with full permeability tensor. J Phys Conf Ser 1324(1):012054
Cao J, Zhang N, Johansen TE (2019b) Applications of fully coupled well/near-well modeling to reservoir heterogeneity and formation damage effects. J Petrol Sci Eng 176:640–652
Chen Z, Churchill V, Wu K, Xiu D (2022) Deep neural network modeling of unknown partial differential equations in nodal space. J Comput Phys 449:110782. https://doi.org/10.1016/j.jcp.2021.110782
Karimi-Fard M, Durlofsky L (2012) Accurate resolution of near-well effects in upscaled models using flow-based unstructured local grid refinement. SPE J 17(4):1084–1095. https://doi.org/10.2118/141675-PA
Li J, Chen Y (2020) A deep learning method for solving third-order nonlinear evolution equations. Commun Theor Phys 72(11):115003
Lie KA (2019) An introduction to reservoir simulation using MATLAB/GNU octave: user guide for the MATLAB reservoir simulation toolbox (MRST). Cambridge University Press, Cambridge. https://doi.org/10.1017/9781108591416
Milan PJ, Hickey JP, Wang X, Yang V (2021) Deep-learning accelerated calculation of real-fluid properties in numerical simulation of complex flowfields. J Comput Phys 444:110567. https://doi.org/10.1016/j.jcp.2021.110567
Nabian MA, Meidani H (2018) A deep neural network surrogate for high-dimensional random partial differential equations. Preprint arXiv:180602957. https://doi.org/10.48550/arXiv.1806.02957
Olalotiti-Lawal F, Salehi A, Hetz G, Castineira D (2019) Application of flow diagnostics to rapid production data integration in complex geologic grids and dual permeability models. In: SPE western regional meeting, San Jose, California, SPE-195253-MS. https://doi.org/10.2118/195253-MS
Raissi M, Perdikaris P, Karniadakis GE (2019) Physics-Informed neural networks: a deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J Comput Phys 378:686–707
Rios V, Schiozer DJ, Santos LOSD, Skauge A (2021) Improving coarse-scale simulation models with a dual-porosity dual-permeability upscaling technique and a near-well approach. J Petrol Sci Eng 198(1):108132
Ryu S, Kim H, Kim SG, Jin K, Cho J, Park J (2022) Probabilistic deep learning model as a tool for supporting the fast simulation of a thermal–hydraulic code. Expert Syst Appl 200:116966. https://doi.org/10.1016/j.eswa.2022.116966
Salehi A, Hetz G, Olalotiti F, Sorek N, Darabi H, Castineira D (2019) A comprehensive adaptive forecasting framework for optimum field development planning. In: SPE reservoir simulation conference, Galveston, Texas. https://doi.org/10.2118/193914-MS
Santos A, Scanavini HFA, Pedrini H, Schiozer DJ, Munerato FP, Barreto CEAG (2022) An artificial intelligence method for improving upscaling in complex reservoirs. J Petrol Sci Eng 211(7553):110071
Shirangi MG, Durlofsky LJ (2016) A general method to select representative models for decision making and optimization under uncertainty. Comput Geosci 96:109–123. https://doi.org/10.1016/j.cageo.2016.08.002
Suzuki Y (2019) Neural network-based discretization of nonlinear differential equations. Neural Comput Appl 31:3023–3038
Tompson J, Schlachter K, Sprechmann P, Perlin K (2017) Accelerating Eulerian fluid simulation with convolutional networks. In: Proceedings of the 34th international conference on machine learning, vol. 70, pp. 3424–3433
Trehan S, Durlofsky LJ (2018) Machine-learning-based modeling of coarse-scale error, with application to uncertainty quantification. Comput Geosci 22(3):1093–1113
Wang YD, Blunt MJ, Armstrong RT, Mostaghimi P (2021) Deep learning in pore scale imaging and modeling. Earth Sci Rev 215:103555. https://doi.org/10.1016/j.earscirev.2021.103555
Wang J, Pang X, Yin F, Yao J (2022a) A deep neural network method for solving partial differential equations with complex boundary in groundwater seepage. J Petrol Sci Eng 209:109880. https://doi.org/10.1016/j.petrol.2021.109880
Wang N, Chang H, Zhang D (2022b) Surrogate and inverse modeling for two-phase flow in porous media via theory-guided convolutional neural network. J Comput Phys 466:111419
Weinan E, Yu B (2018) The deep Ritz method: a deep learning-based numerical algorithm for solving variational problems. Commun Math Stat 6(1):1–12
Xu Y, Zhang H, Li Y, Zhou K, Kurths J (2020) Solving fokker–planck equation using deep learning. Chaos 30(1):013133. https://doi.org/10.1063/1.5132840
Xu H, Zhang D, Wang N (2021) Deep-Learning based discovery of partial differential equations in integral form from sparse and noisy data. J Comput Phys 445:110592. https://doi.org/10.1016/j.jcp.2021.110592
Acknowledgements
This study was supported by the National Natural Science Foundation of China (no. 52004214), the Natural Science Foundation of Shaanxi Province (2022JM-301, 2022JM-171), and the Postgraduate Innovation and Practice Ability Development Fund of Xi’an Shiyou University (YCS22211012).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Liu, Y., Yang, S., Zhang, N. et al. Simulation Enhancement GAN for Efficient Reservoir Simulation at Fine Scales. Math Geosci (2024). https://doi.org/10.1007/s11004-024-10136-7
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11004-024-10136-7