Finite Difference Implicit Structural Modeling of Geological Structures

Abstract

We introduce a new method for implicit structural modeling. The main developments in this paper are the new regularization operators we propose by extending inherent properties of the classic one-dimensional discrete second derivative operator to higher dimensions. The proposed regularization operators discretize naturally on the Cartesian grid using finite differences, owing to the highly symmetric nature of the Cartesian grid. Furthermore, the proposed regularization operators do not require any special treatment on boundary nodes, and their generalization to higher dimensions is straightforward. As a result, the proposed method has the advantage of being simple to implement. Numerical examples show that the proposed method is robust and numerically efficient.

1 Introduction

Structural implicit modeling, in this paper, is defined as the interpolation of randomly distributed, and possibly sparse, structural data. For simplicity, structural data, also referred to as structural constraints, will be limited to the following.

$$\begin{aligned}&\text {value constraints}: \phi ({\mathbf {x}}_j)=a_j, \end{aligned}$$

(1)

$$\begin{aligned}&\text {orientation constraints}: \nabla \phi ({\mathbf {x}}_j)=||\nabla \phi ({\mathbf {x}}_j)||{\mathbf {u}}_j; \end{aligned}$$

(2)

where $\phi ({\mathbf {x}})$ is the unknown function to be interpolated, ${\mathbf {x}}$ is a point in space, a is some given scalar, and ${\mathbf {u}}$ is some given unit vector. We refer to Eq. (2) as the normal form of an orientation constraint, which informs both about the direction and the norm of $\phi$, as opposed to the tangential form, which informs only about the orientation of $\phi$. Let ${\mathbf {u}}^1$ be a given unit vector, then there are $N-1$ unit vectors $\{{\mathbf {u}}^l\}_{l=2}^{l=N}$ such that $\{{\mathbf {u}}^l\}_{l=1}^{l=N}$ forms an orthogonal basis in $N\ge 2$ dimensions. In that case, the tangential form of the normal orientation constraint $\nabla \phi ({\mathbf {x}})=||\nabla \phi ({\mathbf {x}})||{\mathbf {u}}^1$ is

$$\begin{aligned} {\mathbf {u}}^l\cdot \nabla \phi ({\mathbf {x}})=0,\quad \text {for}\quad l=2,\ldots ,N . \end{aligned}$$

(3)

In implicit structural modeling, the object being modeled is obtained by extracting a hypersurface along an iso-value of the interpolated function $\phi ({\mathbf {x}})$ (Newman and Yi 2006). This principle can be distinguished from explicit structural modeling, where geological interfaces defined by a two-dimensional planar graph are embedded in three-dimensional space (Caumon et al. 2009).

Implicit structural modeling has extensively been used in geosciences for contour mapping (Briggs 1974; Mallet 1984; Smith and Wessel 1990; Wessel and Bercovici 1998), and for three-dimensional geological modeling (Lajaunie et al. 1997; Mallet 2004). The method presented here was developed mainly for geological modeling applications, but it is suited for contour mapping as well. Most of the groundwork of modern structural implicit modeling were developed in the 2000’s (Cowan et al. 2002; Ledez 2003; Chilès et al. 2005; Moyen 2005; Tertois 2007), starting with the pioneering work of Lajaunie et al. (1997), to the theoretical framework developed by Mallet (2004), all the way to the more application-ready works of Chilès et al. (2005) and Frank (2007). Structural implicit models can be separated into two main classes (Caumon et al. 2013): (1) methods based on dual Kriging and radial basis interpolation (Lajaunie et al. 1997; Cowan et al. 2002; Chilès et al. 2005; Calcagno et al. 2008), which yield a dense linear system whose size is mainly controlled by the number of data, (2) and methods based on domain discretization (Mallet 2004; Frank 2007; Caumon et al. 2013; Souche et al. 2013), which yield a sparse linear system whose size is mainly controlled by size of discretization grid. Domain, in this paper, refers to the volume of interest under investigation. Domain discretization methods are collectively referred to as Discrete Smooth Interpolation (DSI) methods hereafter (Mallet 1989, 1992, 1997). The principle of DSI methods is to discretize all structural constraints on a discrete domain, and assemble them into a least-squares system of linear equations supplemented with smoothing regularization constraints (Mallet 1989, 1992, 1997).

Implicit geological modeling is still an active area of research. Some authors have shown that existing methods still present limitations caused by the smoothing approaches and the discretization schemes currently used (Laurent 2016; Renaudeau et al. 2017b). In addition, recent work started investigating stochastic modeling approaches of geological structures geometry (Jessell et al. 2014; Cherpeau and Caumon 2015; Godefroy et al. 2017) for which structural interpolation is becoming a bottleneck. Computation times that used to be acceptable for building a single “best model” are becoming far too long when considering stochastic approaches for sampling uncertainty. Other recent research and advances in implicit modeling include better modeling of folds (Laurent et al. 2016; Grose et al. 2017), automated building of models that conform to seismic data (Wu 2017), more numerically efficient discretization schemes (Renaudeau et al. 2018), and many more (Mallet 2014; Hillier et al. 2014; Gonçalves et al. 2017; Martin and Boisvert 2017; Renaudeau et al. 2019). As we move towards an era of multi-realization structural modeling (Caumon 2010), new challenges continuously emerge and motivate the quest for more robust and more efficient structural implicit modeling schemes.

In this paper, we introduce a new approach based on finite differences; this method belongs to the DSI class of methods. Most DSI methods, as applied in geological modeling, rely on simplices (triangles in two-dimensions, tetrahedra in three-dimensions) for domain discretization due to their geometrical flexibility. Because simplicial meshes are unstructured and irregular, it is customary to discretize structural constraints and smoothing constraints using a piecewise linear approach (Frank 2007; Caumon et al. 2013). The method we introduce is based on discretizing the domain on Cartesian grids, and on discretizing structural constraints and smoothing constraints using finite differences. Cartesian gridding and finite differences are arguably the simplest discretizations possible for structural interpolation; as a result, the proposed method is also easy to implement. Modern computing capabilities, particularly general purpose GPU computing, make the method numerically efficient as well. A three-dimensional implicit structural modeling example using the proposed method is shown in Fig. 1.

Implicit structural interpolation on Cartesian grids using finite differences is not new. Briggs (1974) solves the biharmonic equation in two-dimensions directly on the Carstesian grid using finite differences. In Briggs (1974)’s formulation, assignment constraints (Eq. (1)) are treated as internal boundary conditions. He also shows the equivalence between the biharmonic equation and the minimization of the global curvature of the implicit function. Wu and Hale (2015) use finite differences operators on Cartesian grids to create implicit functions on seismic images. Assuming that (1) the normal of reflectors can be estimated at each point of the seismic image, and that (2) the implicit function increases monotonically with seismic traveltime (or depth), they use the normal form of orientation constraints (Eq. (2)) to assemble an overdetermined system solved using least-squares. However, it is usually challenging to make an accurate estimation of reflector dips at each grid point due to coherent noise in seismic data (Chauris et al. 2002; Fehmers and Höcker 2003). As for the second assumption, it is not always valid; the section from the Ribaute model (Caumon et al. 2009) in Fig. 2 is an example of where this assumption does not hold. Wu (2017) addresses this problem by first unfaulting and unfolding the seismic image before computing the implicit function. Mallet (1989) also proposed an interpolation method on Cartesian grids using finite differences; the method proposed here resolves some issues raised by Mallet (1989), as discussed in the section about discontinuities (Sect. 6). Furthermore, unlike Mallet (1989), the method proposed here does not require input data to be located at grid points.

Fig. 1

Implicit structural modeling workflow. a Interpolation of input data to build a stratigraphic function using the proposed method. b Extraction of implicit horizons from the isovalues of the stratigraphic function. Data courtesy of total

Fig. 2

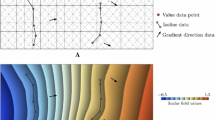
Implicit stratigraphic modeling of a section from the Ribaute model of Caumon et al. (2009). a Input data, three faults and three horizons. b Resulting stratigraphic field. Only value constraints were used in this experiment

We propose an alternative approach. Briggs (1974) noted that the one-dimensional interpolation problem had well defined properties; his strategy was then to extend these properties in two-dimensions by solving the equivalent continuous problem (partial differential equation). Here, we notice that the one-dimensional discrete interpolation problem has inherent properties that we wish to extend to high dimensional discrete interpolation problems. The main new elements of our method are the regularization operators we introduce. These operators discretize naturally on Cartesian grids: they do not require any special treatment at boundary nodes, and their generalization to higher dimensions is straightforward.

This paper is organized as follows. In Sects. 2 and 3 we present the basic theoretical aspects of our method. We apply our method in two-dimensions in Sect. 4, and then in three-dimensions in Sect. 5. We discuss how to handle discontinuities in Sect. 6 before concluding with a discussion on the shortcomings of the proposed method in Sect. 7.

Fig. 3

a One-dimensional domain discretization. b Two-dimensional domain discretization. The red nodes are external nodes, the blue nodes are boundary nodes, and the black nodes are internal nodes.

2 Domain and Problem Discretization

2.1 Domain Discretization

Let $\varOmega$ be the domain of definition of $\phi ({\mathbf {x}})$. $\varOmega$ is discretized on a Cartesian grid, therefore $\varOmega$ can be seen as a collection of N grid points $\{{\mathbf {x}}_l\}_{l=1}^{l=N}$. We distinguish three subdomains in $\varOmega$,

$$\begin{aligned} \varOmega =\{\varOmega _E\cup \varOmega _B\cup \varOmega _I\}, \end{aligned}$$

where $\varOmega _E$ is the set of external grid points, $\varOmega _B$ is the set of boundary grid points, and $\varOmega _I$ is the set of internal grid points. An example of this discretization is illustrated in Fig. 3. A more formal definition of these subdomains will be given shortly. The computational domain $\varOmega _C$ is defined as

$$\begin{aligned} \varOmega _C=\{\varOmega _B\cup \varOmega _I\}. \end{aligned}$$

(4)

Each point in ${\mathbf {x}}_j$ in $\varOmega _I$ has neighbors in $\varOmega _C$, these neighbors define the neighborhood ${\mathcal {N}}({\mathbf {x}}_j)$ of ${\mathbf {x}}_j$. Figure 4a and b illustrate the notion of neighborhoods in one and two-dimensions; this figure also introduces directional vectors. For example, the one-dimensional point $x_j$ has two neighbors

$$\begin{aligned} {\mathcal {N}}(x_j)=\{x_{j-1},x_{j+1}\}:=\{x_{j-d_1},x_{j+d_1}\}; \end{aligned}$$

that is, by definition, the one-dimensional directional vector $d_1$ is [1]. In general, a point ${\mathbf {x}}_j$ always has two neighbors along a given direction: one neighbor in front, and one neighbor behind. For example in two-dimensions the two neighbors of the point ${\mathbf {x}}_{i,j}={\mathbf {x}}_k$ along the direction ${\mathbf {d}}_4=[1 \; 1]$ are

$$\begin{aligned} \{{\mathbf {x}}_{i-1,j-1},{\mathbf {x}}_{i+1,j+1}\}:=\{{\mathbf {x}}_{k-{\mathbf {d}}_4},{\mathbf {x}}_{k+{\mathbf {d}}_4}\} . \end{aligned}$$

(5)

In N dimensions, there are $M_n=3^{N}-1$ points in the neighborhood ${\mathcal {N}}({\mathbf {x}}_j)$ of ${\mathbf {x}}_j\in \varOmega _I$, and there are $M_d=\frac{M_n}{2}$ directions such that

$$\begin{aligned} {\mathcal {N}}({\mathbf {x}}_j)=\Big \{{\mathbf {x}}_{j\pm {\mathbf {d}}_k} \,\big |\quad \text {for}\quad k=1,\ldots ,M_d\Big \}, \end{aligned}$$

(6)

where ${\mathbf {d}}_k$ is the kth directional vector, as illustrated for example in Fig. 4.

Fig. 4

Notion of neighborhoods and directional vectors in one and two-dimensions. a One-dimensional neighborhood: the neighborhood of the black node is made of the two (green) points that can be reached from it by taking one step (one forward and one backward) along the one-dimensional directional vector. b Two-dimensional neighborhood: the neighborhood of the black node is made of the eight (green) points that can be reached from it by taking one step (one forward and one backward) along the four two-dimensional directional vectors

Let us come back to the discretization $\varOmega =\{\varOmega _E\cup \varOmega _B\cup \varOmega _I\}$. Given a set of points in $\varOmega _E$, we formally define

$$\begin{aligned} \varOmega _I= & {} \Big \{{\mathbf {x}}_j\,|\, {\mathcal {N}}({\mathbf {x}}_j)\cap \varOmega _E=\emptyset \Big \} . \end{aligned}$$

(7)

$$\begin{aligned} \varOmega _B= & {} \Big \{{\mathbf {x}}_j\,|\, {\mathcal {N}}({\mathbf {x}}_j)\cap \varOmega _E\ne \emptyset \, \wedge \, {\mathcal {N}}({\mathbf {x}}_j)\cap \varOmega _I\ne \emptyset \Big \} . \end{aligned}$$

(8)

That is, a grid point that does not have a neighbor in $\varOmega _E$ is by definition a point in $\varOmega _I$, and a grid point that has at least one neighbor in $\varOmega _I$ and at least one neighbor in $\varOmega _E$ is by definition a point in $\varOmega _B$. Points in $\varOmega _E$ will usually be specified as inputs. It should be noted that an internal grid point is never in contact with an external grid point, there is always at least one boundary point between them.

2.2 Problem Discretization

The implicit function $\phi ({\mathbf {x}})$ is evaluated on the discrete computational domain $\varOmega _C$ by expansion into the series

$$\begin{aligned} \phi ({\mathbf {x}})=\sum _{{\mathbf {x}}_j\in \varOmega _C}B({\mathbf {x}},{\mathbf {x}}_j)\phi ({\mathbf {x}}_j)=\sum _{{\mathbf {x}}_j\in \varOmega _C}B({\mathbf {x}},{\mathbf {x}}_j)\phi _j, \end{aligned}$$

(9)

where $B({\mathbf {x}},{\mathbf {x}}_j)$ are some basis functions, and $\phi _j$ are the unknown coefficients at grid points. The basis functions $B({\mathbf {x}},{\mathbf {x}}_j)$ are assumed to satisfy the Kronecker delta property, that is for ${\mathbf {x}}_i,{\mathbf {x}}_j \in \varOmega _C$,

$$\begin{aligned} B({\mathbf {x}}_i,{\mathbf {x}}_j)= \left\{ \begin{array}{ll} 1&{}\quad \text {if}\quad i=j\\ 0&{}\quad \text {if}\quad i\ne j \end{array} \right. . \end{aligned}$$

Let $B({\mathbf {x}},{\mathbf {x}}_j)$ be 1st-order Lagrange basis functions, simplifying Eq. (9) to

$$\begin{aligned} \phi ({\mathbf {x}})=\sum _{{\mathbf {x}}_j\in {\mathcal {N}}'({\mathbf {x}}_i)}B({\mathbf {x}},{\mathbf {x}}_j) \phi _j , \end{aligned}$$

(10)

where ${\mathbf {x}}_i\in \varOmega _I$ is the closest internal grid point to ${\mathbf {x}}$, and

$$\begin{aligned} {\mathcal {N}}'({\mathbf {x}}_i):=\{{\mathcal {N}}({\mathbf {x}}_i)\cup {\mathbf {x}}_i\} ; \end{aligned}$$

it follows from the definitions in Eqs. (7) and (8) that ${\mathbf {x}}_j\in \varOmega _C$. Using Eq. (10), the first derivative along the kth direction is given by

$$\begin{aligned} \partial _k\phi ({{\mathbf {x}}})=\sum _{{\mathbf {x}}_j\in {\mathcal {N}}'({\mathbf {x}}_i)}\partial _kB({\mathbf {x}},{\mathbf {x}}_j) \phi _j. \end{aligned}$$

(11)

The constraints in Eqs. (1) and (3) can therefore be discretized in $N\ge 2$ dimensions as

$$\begin{aligned} \phi ({\mathbf {x}})=\sum _{{\mathbf {x}}_j\in {\mathcal {N}}'({\mathbf {x}}_i)}B({\mathbf {x}},{\mathbf {x}}_j) \phi _j=a , \end{aligned}$$

(12)

and

$$\begin{aligned} {\mathbf {u}}^l\cdot \nabla \phi ({{\mathbf {x}}})= & {} \sum _k^N u^l_k\partial _k \phi ({\mathbf {x}}) \nonumber \\= & {} \sum _k^N u^l_k\bigg (\sum _{{\mathbf {x}}_j\in {\mathcal {N}}'({\mathbf {x}}_i)}\partial _kB({\mathbf {x}},{\mathbf {x}}_j) \phi _j\bigg ) =0,\quad \text {for}\quad l=2,\ldots ,N. \end{aligned}$$

(13)

Some constraints may involve second derivatives; this is typically the case for smoothing regularization constraints. However, second derivatives of Eq. (10) cannot be computed directly, as was the case for first derivatives, because of the use of 1st-order Lagrange basis functions. The second derivative at a given point ${\mathbf {x}}$ is therefore approximated by the finite-difference second derivative at ${\mathbf {x}}_i\in \varOmega _I$, the closest internal grid point to ${\mathbf {x}}$. In particular, let $\text {d}_k$ denote the distance between two neighboring points along the directional vector ${\mathbf {d}}_k$; then, using the notation in the definition in Eq. (5), the second derivative along the kth direction is given by

$$\begin{aligned} \partial _k^2\phi ({{\mathbf {x}}})\approx \partial _k^2\phi ({{\mathbf {x}}_i})=\frac{-2\phi _i+\phi _{i+{\mathbf {d}}_k}+\phi _{i-{\mathbf {d}}_k}}{\text {d}_k^2} , \end{aligned}$$

(14)

and the mixed derivative along two orthogonal directions k, l is given by

$$\begin{aligned} \partial _k\partial _l\phi ({{\mathbf {x}}}) \approx \partial _k\partial _l\phi ({{\mathbf {x}}_i}) = \frac{ \phi _{i+{\mathbf {d}}_k+{\mathbf {d}}_l} + \phi _{i-{\mathbf {d}}_k-{\mathbf {d}}_l} - \phi _{i-{\mathbf {d}}_k+{\mathbf {d}}_l} - \phi _{i+{\mathbf {d}}_k-{\mathbf {d}}_l} }{4\text {d}_k\text {d}_l}. \end{aligned}$$

(15)

In this paper, all constraints involving second derivatives are imposed strictly on grid points; therefore, the approximation symbol $\approx$ in Eqs. (14) and (15) can be replaced by the equality symbol $=$.

2.3 Solving the Discrete Problem

The system of Eqs. (12)–(13), can be written in the more compact matrix form

$$\begin{aligned} \bar{\bar{{\mathbf {A}}}} {\bar{\varPhi }}= & {} \bar{{\mathbf {f}}}_a. \end{aligned}$$

(16)

$$\begin{aligned} \bar{\bar{{\mathbf {U}}}} {\bar{\varPhi }}= & {} \bar{{\mathbf {0}}}. \end{aligned}$$

(17)

In practice, the system above is usually underdetermined and we have to regularize it with some smoothing constraints of the form $\bar{\bar{{\mathbf {R}}}}{\bar{\varPhi }}=\bar{{\mathbf {0}}}$. That is, the solution ${\bar{\varPhi }}$ is obtained by solving

$$\begin{aligned} \begin{bmatrix} \bar{\bar{{\mathbf {A}}}}\\ \bar{\bar{{\mathbf {U}}}}\\ \bar{\bar{{\mathbf {R}}}} \end{bmatrix} \begin{bmatrix} {\bar{\varPhi }} \end{bmatrix} = \begin{bmatrix} \bar{{\mathbf {f}}_a}\\ \bar{{\mathbf {0}}}\\ \bar{{\mathbf {0}}} \end{bmatrix} \end{aligned}$$

(18)

in a least-squares sense. Convenient choices for $\bar{\bar{{\mathbf {R}}}}$ will be proposed later in the paper. The matrices involved in Eq. (18) are very sparse, making it possible to efficiently solve the least-squares system with sparse conjugate gradient solvers.

3 Interpolation in One-dimension: Problem Formulation

3.1 Interpolation in One-dimension

The structural interpolation problem can be described as a problem of finding a smooth function $\phi ({\mathbf {x}})$ that interpolates a given set of structural data. The smoothness is typically achieved by minimizing the function’s roughness ${\mathcal {R}}(\phi )$ (Mallet 1989). It is unclear what the definition of roughness is, precisely; roughness is usually understood to be related to the notion of curvature. In one-dimension, a widely accepted definition of roughness is the second derivative operator (Mallet 1997)

$$\begin{aligned} {\mathcal {R}}(\phi ):=\partial ^2_x\phi ({\mathbf {x}}); \end{aligned}$$

(19)

Minimizing the second derivative in one-dimension minimizes the curvature of the function; this statement is unambiguous because there is only one way to define curvature in one-dimension. The one-dimensional smoothing constraint, defined only on grid points, can therefore be discretized using Eq. (14) to give

$$\begin{aligned} {\mathcal {R}}(\phi _j)=\frac{-2\phi _j+\phi _{j+1}+\phi _{j-1}}{|dx|^2}=0 , \end{aligned}$$

(20)

for every grid point $x_j\in \varOmega _I$.

3.2 Problem Formulation

In higher dimensions, minimizing the roughness of a function becomes ambiguous: there are infinitely many candidate roughness operators in higher dimensions that reduce to Eq. (19) in one-dimension. The standard way of overcoming this ambiguity is to explicitly give a physical meaning to Eq. (19). For example, Briggs (1974) and Levy (1999) explicitly look for a function $\phi ({\mathbf {x}})$ that minimizes the global (mean) curvature; in that case, it becomes clear that the extension of Eq. (19) in higher dimensions is

$$\begin{aligned} {\mathcal {R}}(\phi )=\varDelta \phi ({\mathbf {x}}), \end{aligned}$$

(21)

which is unambiguous since the Laplacian operator $\varDelta$ has a precise definition in all dimensions. Another common choice is to seek for a function $\phi ({\mathbf {x}})$ that minimizes the bending energy (see for example Renaudeau et al. 2019, and references therein).

In this paper, we take a different approach to determine the equivalent of Eq. (19) in higher dimensions. We find inherent properties of the one-dimensional discrete Eq. (20) that we consider to be practical, from an implementation point of view, then we look for an equivalent discrete equation in higher dimensions which has the same properties. The resulting discrete operator in higher dimensions can then be transformed back to the continuous version if needed.

A very practical property of sparse data interpolation using Eq. (20) is that it does not require boundary conditions. We define a boundary condition as any constraint imposed on a grid point ${\mathbf {x}}\in \varOmega _B$. In the absence of discontinuities, a regularization matrix $\bar{\bar{{\mathbf {R}}}}$ built by imposing Eq. (20) on all grid points ${\mathbf {x}}\in \varOmega _I$, has a $\text {rank}(\bar{\bar{{\mathbf {R}}}})=M-2$, for a one-dimensional problem with M degrees of freedom (i.e. M grid points in $\varOmega _C$). The property $\text {rank}(\bar{\bar{{\mathbf {R}}}})=M-2$ highlights the fact that a minimum of two independent points are required to define a function in one-dimension. In general, ${\mathcal {R}}(\phi _j)$ will be said to satisfy the maximum-rank property if, in the absence of discontinuities, $\text {rank}(\bar{\bar{{\mathbf {R}}}})=M-(N+1)$; where $\bar{\bar{{\mathbf {R}}}}$ is the regularization matrix built by imposing ${\mathcal {R}}(\phi _j)=0$ for all grid points ${\mathbf {x}}_j\in \varOmega _I$, for a problem with M degrees of freedoms in N dimensions. Our aim is to look for roughness operators ${\mathcal {R}}(\phi _j)$ that satisfy the maximum-rank property in higher dimensions.

The maximum-rank property can be extended to higher dimensions if the high dimensional equivalent of Eq. (20) has the following properties:

Property 1

${\mathcal {R}}(\phi _j)$ should include all grid points in the neighborhood of ${\mathbf {x}}_j$, and ${\mathbf {x}}_j$ itself.

Property 2

${\mathcal {R}}(\phi _j)$ should smooth independently along all directional vectors at ${\mathbf {x}}_j$.

The two properties above are inherent in the one-dimensional discrete problem, as it can be observed by looking at Eq. (20) and Fig. 4a. Therefore, we propose to generalize these two properties to higher dimensions. As we increase dimensions, the first property will guarantee that every degree of freedom is taken into account, and the second property will guarantee that there are “enough” equations to constrain all the degrees of freedom.

3.3 Towards Interpolation in Higher Dimensions

We propose two strategies for extending Eq. (20) to higher dimensions. The first one is to generalize the one-dimensional smoothing constraint

$$\begin{aligned} {\mathcal {R}}(\phi _j)=\partial _x^2\phi _j=0 \end{aligned}$$

as a minimization of second directional derivatives of $\phi _j$ along all directional vectors, that is:

$$\begin{aligned} {\mathcal {R}}(\phi _j)=\partial _k^2\phi _j=0, \forall \text { directional vectors }{\mathbf {d}}_k \text { at } {\mathbf {x}}_j. \end{aligned}$$

(22)

The second approach is to generalize the one-dimensional smoothing constraint

$$\begin{aligned} {\mathcal {R}}(\phi _j)=\partial _x^2\phi _j=\partial _x(\partial _x\phi _j)=0 \end{aligned}$$

as a minimization of mixed derivatives of $\phi _j$ as follows

$$\begin{aligned} {\mathcal {R}}(\phi _j)=\partial _k(\partial _l\phi _j)=0, \left| \begin{array}{rl} &{} \forall \text { axis-aligned directional vectors }{\mathbf {d}}_k\text {, and}\\ &{} \forall \text { directional vectors }{\mathbf {d}}_l\text { s.t. }{\mathbf {d}}_l={\mathbf {d}}_k\text { or }{\mathbf {d}}_l\perp {\mathbf {d}}_k. \end{array} \right. \end{aligned}$$

(23)

Both Eqs. (22) and (24) satisfy the properties imposed in the last paragraph; these two equations lead to different roughness operators.

Fig. 5

Implicit stratigraphic modeling of a modified section from one of the two-dimensional benchmark models of Renaudeau et al. (2017a). a Input data, two horizons. b Resulting stratigraphic field using the proposed regularization operator. c Resulting stratigraphic field using the Laplacian operator. Only value constraints were used in this experiment

4 Interpolation in Two-dimensions

Let us introduce the two-dimensional Cartesian-axes matrix $\bar{\bar{{\mathbf {C}}}}_2$ and the two-dimensional diagonal-axes matrix $\bar{\bar{{\mathbf {D}}}}_2$ defined as

$$\begin{aligned} \bar{\bar{{\mathbf {C}}}}_2= \begin{bmatrix} 1 &{} 0 \\ 0 &{} 1 \end{bmatrix}, \quad \bar{\bar{{\mathbf {D}}}}_2=\frac{1}{\sqrt{2}} \begin{bmatrix} 1 &{} -1 \\ 1 &{} 1 \end{bmatrix}. \end{aligned}$$

(24)

Each row of these matrices is a directional vector on the two-dimensional grid as defined in Fig. 4b. The two-dimensional full direction matrix is defined as

$$\begin{aligned} \bar{\bar{{\mathbf {F}}}}_2= \begin{bmatrix} \bar{\bar{{\mathbf {C}}}}_2 \\ \bar{\bar{{\mathbf {D}}}}_2 \end{bmatrix}, \end{aligned}$$

(25)

its rows give all the directions available, locally, on a two-dimensional grid.

4.1 Directional Second Derivatives

From the directional second derivative point of view (Eq. (22)), the two-dimension version of Eq. (20) is

$$\begin{aligned} {\mathcal {R}}(\phi _j)=\partial _k^2\phi _j = \frac{-2\phi _j+\phi _{j+{\mathbf {d}}_k}+\phi _{j-{\mathbf {d}}_k}}{\text {d}_k^2} = 0, \; \forall \; {\mathbf {d}}_k\text { rows of }\bar{\bar{{\mathbf {F}}}}_2. \end{aligned}$$

(26)

Each of these directional derivatives $\partial _k^2\phi _j$ can be written analytically using the two-dimensional Hessian matrix

$$\begin{aligned} \bar{\bar{{\mathbf {H}}}}_2= \begin{bmatrix} \partial _x(\partial _x\phi ) &{} \partial _x(\partial _z\phi ) \\ \partial _z(\partial _x\phi ) &{} \partial _z(\partial _z\phi ) \end{bmatrix} \end{aligned}$$

as $\partial _k^2\phi ={\mathbf {d}}_k\bar{\bar{{\mathbf {H}}}}_2{\mathbf {d}}_k^T$. It follows that a two-dimension version of the roughness operator (19) that satisfies the maximum-rank property is

$$\begin{aligned} {\mathcal {R}}(\phi )= \left\{ \begin{array}{l} \partial ^2_{[1\;0]}\phi =\begin{bmatrix} 1 &{} 0 \end{bmatrix}\bar{\bar{{\mathbf {H}}}}_2\begin{bmatrix} 1 \\ 0 \end{bmatrix}=\partial _x^2\phi \\ \partial ^2_{[0\;1]}\phi =\begin{bmatrix} 0 &{} 1 \end{bmatrix}\bar{\bar{{\mathbf {H}}}}_2\begin{bmatrix} 0 \\ 1 \end{bmatrix}=\partial _z^2\phi \\ \partial ^2_{[1\;-1]}\phi =\frac{1}{2}\begin{bmatrix} 1 &{} -1 \end{bmatrix}\bar{\bar{{\mathbf {H}}}}_2\begin{bmatrix} 1 \\ -1 \end{bmatrix}=\frac{1}{2}(\partial _x^2+\partial _z^2-2\partial _x\partial _z)\phi \\ \partial ^2_{[1\;1]}\phi =\frac{1}{2}\begin{bmatrix} 1 &{} 1 \end{bmatrix}\bar{\bar{{\mathbf {H}}}}_2\begin{bmatrix} 1 \\ 1 \end{bmatrix}=\frac{1}{2}(\partial _x^2+\partial _z^2+2\partial _x\partial _z)\phi \\ \end{array} \right. . \end{aligned}$$

(27)

The roughness operator (27) is discretized exactly as the one-dimensional version. Let $\bar{\bar{{\mathbf {R}}}}$ denote the regularization matrix resulting from Eqs. (26)/(27), then the jth row of the least-squares matrix $\bar{\bar{{\mathbf {R}}}}^t\bar{\bar{{\mathbf {R}}}}$ is a finite-difference approximation of

$$\begin{aligned} \Big [\big (\partial ^2_{[1\;0]}\big )^2+\big (\partial ^2_{[0\;1]}\big )^2+\big (\partial ^2_{[1\;-1]}\big )^2+\big (\partial ^2_{[1\;1]}\big )^2\Big ]\phi _j. \end{aligned}$$

(28)

It is interesting to note that Eq. (28) equates to

$$\begin{aligned} \Big [\big (\partial _x^2\big )^2+\big (\partial _z^2\big )^2+2\big (\partial _x\partial _z)^2\Big ]\phi _j + \frac{1}{2}\Big [\big (\partial _x^2\big )^2+\big (\partial _z^2\big )^2+2\partial _x^2\partial _z^2\Big ]\phi _j, \end{aligned}$$

(29)

where the first term is the bending energy of Enriquez et al. (1983); Turk and O’Brien (2002); Renaudeau et al. (2019), and the second term is half the squared (mean) curvature of Briggs (1974), also known as the squared Laplacian (Levy 1999). Figure 5b shows an example using the roughness operator (26)/(27) to a modified version of a two-dimensional benchmark model proposed by Renaudeau et al. (2017a). For comparison, Fig. 5c shows the implicit function obtained using the Laplacian operator (Eq. (21)); note the saddle point in Fig. 5c, which is physically impossible from a stratigraphic modeling point of view.

4.2 Mixed Derivatives

From the mixed derivative point of view (Eq. (24)), another roughness operator ${\mathcal {R}}(\phi )$ that satisfies the maximum-rank property is

$$\begin{aligned} {\mathcal {R}}(\phi )= \left\{ \begin{array}{rcl} \partial _{[1\;0]}\big (\partial _{[1\;0]}\phi \big )=&\begin{bmatrix} 1 &{} 0 \end{bmatrix}\bar{\bar{{\mathbf {H}}}}_2\begin{bmatrix} 1 \\ 0 \end{bmatrix}=&{}\partial _x\big (\partial _x\phi \big )\\ \partial _{[0\;1]}\big (\partial _{[0\;1]}\phi \big )=&{}\begin{bmatrix} 0 &{} 1 \end{bmatrix}\bar{\bar{{\mathbf {H}}}}_2\begin{bmatrix} 0 \\ 1 \end{bmatrix}=&{}\partial _z\big (\partial _z\phi \big )\\ \partial _{[1\;0]}\big (\partial _{[0\;1]}\phi \big )=&{}\begin{bmatrix} 1 &{} 0 \end{bmatrix}\bar{\bar{{\mathbf {H}}}}_2\begin{bmatrix} 0 \\ 1 \end{bmatrix}=&{}\partial _x\big (\partial _z\phi \big )\\ \partial _{[0\;1]}\big (\partial _{[1\;0]}\phi \big )=&{}\begin{bmatrix} 0 &{} 1 \end{bmatrix}\bar{\bar{{\mathbf {H}}}}_2\begin{bmatrix} 1 \\ 0 \end{bmatrix}=&{}\partial _z\big (\partial _x\phi \big )\\ \end{array} \right. , \end{aligned}$$

(30)

which, using $\partial _x(\partial _z)=\partial _z(\partial _x)$, becomes

$$\begin{aligned} {\mathcal {R}}(\phi )= \left\{ \begin{array}{l} \partial _{[1\;0]}\big (\partial _{[1\;0]}\phi \big )=\partial ^2_x\phi \\ \partial _{[0\;1]}\big (\partial _{[0\;1]}\phi \big )=\partial ^2_z\phi \\ \sqrt{2}\partial _{[1\;0]}\big (\partial _{[0\;1]}\phi \big )=\sqrt{2}\partial _x\big (\partial _z\phi _i\big ) \end{array} \right. . \end{aligned}$$

(31)

The factor $\sqrt{2}$ comes from noticing that

$$\begin{aligned} \Big (\partial _{[1\;0]}\big (\partial _{[0\;1]}\big )\Big )^2\phi _j+\Big (\partial _{[0\;1]}\big (\partial _{[1\;0]}\big )\Big )^2\phi _j=\Big (\sqrt{2}\partial _{[1\;0]}\big (\partial _{[0\;1]}\big )\Big )^2\phi _j; \end{aligned}$$

as in the previous paragraph, the reason for equating squares of operators is because the problem is solved by least-squares. The complete sum of squares of terms in this operator equates to the first term on the right hand side of Eq. (29). The first two terms of Eq. (30) are discretized using Eq. (14) and the remaining terms are discretized using Eq. (15).

5 Interpolation in Three-Dimensions

The three-dimensional Cartesian-axes matrix $\bar{\bar{{\mathbf {C}}}}_3$ and diagonal-axes matrix $\bar{\bar{{\mathbf {D}}}}_3$ are

$$\begin{aligned} \bar{\bar{{\mathbf {C}}}}_3= \begin{bmatrix} 1 &{}\quad 0 &{}\quad 0 \\ 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \end{bmatrix}, \quad \bar{\bar{{\mathbf {D}}}}_3=\frac{1}{\sqrt{3}} \begin{bmatrix} 1 &{}\quad -1 &{}\quad -1 \\ 1 &{}\quad -1 &{}\quad 1 \\ 1 &{}\quad 1 &{}\quad -1 \\ 1 &{}\quad 1 &{}\quad 1 \end{bmatrix}. \end{aligned}$$

(32)

We also introduce the three-dimensional extended-diagonal-axes matrix $\bar{\bar{{\mathbf {E}}}}_3$ defined as

$$\begin{aligned} \bar{\bar{{\mathbf {E}}}}_3=\frac{1}{\sqrt{2}} \begin{bmatrix} 0 &{}\quad 1 &{}\quad -1 \\ 0 &{}\quad 1 &{}\quad 1 \\ 1 &{}\quad 0 &{}\quad -1 \\ 1 &{}\quad 0 &{}\quad 1 \\ 1 &{}\quad -1 &{}\quad 0 \\ 1 &{}\quad 1 &{}\quad 0 \end{bmatrix} . \end{aligned}$$

(33)

The three-dimensional extended-diagonal matrix $\bar{\bar{{\mathbf {E}}}}_3$ is obtained by inserting an extra zero at different positions of each row of the two-dimensional diagonal matrix $\bar{\bar{{\mathbf {D}}}}_2$. The full three-dimensional direction matrix is defined as

$$\begin{aligned} \bar{\bar{{\mathbf {F}}}}_3= \begin{bmatrix} \bar{\bar{{\mathbf {C}}}}_3 \\ \bar{\bar{{\mathbf {D}}}}_3 \\ \bar{\bar{{\mathbf {E}}}}_3 \end{bmatrix}, \end{aligned}$$

(34)

and its rows give all the directions available, locally, on a three-dimensional grid.

Following the same reasoning as in Sect. 4, we use the direction matrix $\bar{\bar{{\mathbf {F}}}}_3$ to propose the following choices for the roughness operators

$$\begin{aligned} {\mathcal {R}}(\phi )= \left\{ \begin{array}{l} \partial ^2_{[1\;0\;0]}\phi \\ \partial ^2_{[0\;1\;0]}\phi \\ \partial ^2_{[0\;0\;1]}\phi \\ \partial ^2_{[0\;1\;-1]}\phi \\ \partial ^2_{[0\;1\;1]}\phi \\ \partial ^2_{[1\;0\;-1]}\phi \\ \partial ^2_{[1\;0\;1]}\phi \\ \partial ^2_{[1\;-1\;0]}\phi \\ \partial ^2_{[1\;1\;0]}\phi \\ \partial ^2_{[1\;-1\;-1]}\phi \\ \partial ^2_{[1\;-1\;1]}\phi \\ \partial ^2_{[1\;1\;-1]}\phi \\ \partial ^2_{[1\;1\;1]}\phi \end{array} \right. , \end{aligned}$$

(35)

and

$$\begin{aligned} {\mathcal {R}}(\phi )= \left\{ \begin{array}{l} \partial ^2_{[1\;0\;0]}\phi _i\big )\\ \partial ^2_{[0\;1\;0]}\phi _i\big )\\ \partial ^2_{[0\;0\;1]}\phi _i\big )\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;1\;0]}\phi \big )\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;0\;1]}\phi \big )\\ \sqrt{2}\partial _{[0\;1\;0]}\big (\partial _{[0\;0\;1]}\phi \big )\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;1\;1]}\phi \big )\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;1\;-1]}\phi \big )\\ \sqrt{2}\partial _{[0\;1\;0]}\big (\partial _{[1\;0\;1]}\phi \big )\\ \sqrt{2}\partial _{[0\;1\;0]}\big (\partial _{[1\;0\;-1]}\phi \big )\\ \sqrt{2}\partial _{[0\;0\;1]}\big (\partial _{[1\;1\;0]}\phi \big )\\ \sqrt{2}\partial _{[0\;0\;1]}\big (\partial _{[1\;-1\;0]}\phi \big ) \end{array} \right. . \end{aligned}$$

(36)

Equation (35) comes from the directional second derivative approach (Eq. (22)) and Eq. (36) comes the mixed derivatives approach (Eq. (23)). It is also possible to combine these two approaches to get a third hybrid operator that satisfies the maximum-rank property (Sect. 3.2); in particular

$$\begin{aligned} {\mathcal {R}}(\phi )=\left\{ \begin{array}{l} \partial ^2_{[1\;0\;0]}\phi \\ \partial ^2_{[0\;1\;0]}\phi \\ \partial ^2_{[0\;0\;1]}\phi \\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;1\;0]}\phi \big )\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;0\;1]}\phi \big )\\ \sqrt{2}\partial _{[0\;1\;0]}\big (\partial _{[0\;0\;1]}\phi \big )\\ \partial ^2_{[1\;-1\;-1]}\phi \\ \partial ^2_{[1\;-1\;1]}\phi \\ \partial ^2_{[1\;1\;-1]}\phi \\ \partial ^2_{[1\;1\;1]}\phi \end{array} \right. . \end{aligned}$$

(37)

The analytic expressions of each term in these operators are given in the Appendix. While these operators may look complex as we increase dimensions, their discretizations remain straightforward: all the second derivative terms are discretized using Eq. (14), and all the mixed derivatives terms are discretized using Eq. (15). This means that the operator in Eq. (35) is implemented exactly as its two-dimensional (Eq. (26)), and its one-dimensional (Eq. (20)) version. The only thing that changes is the number of directional vectors and their dimension. Figure 6 shows an example using this smoothing operator to the Balzes model of Ramón et al. (2015).

Fig. 6

Implicit stratigraphic modeling of the Balzes fold model of Ramón et al. (2015). a Input data consisting of horizon points picked along two horizons. b Solid view of the resulting stratigraphic field. c Section view of the resulting stratigraphic field. Only value constraints were used in this experiment

6 Handling Discontinuities

Discontinuities are often encountered in geological structural modeling. They usually consist of faults, unconformities and intrusive bodies. We propose a simple way to handle discontinuities: grid points affected by a discontinuity, after its rasterization, are tagged as external grid points (grid points in $\varOmega _E$). Consider for example the illustration in Fig. 7: the discontinuity represented by the red line is rasterized to obtain the red external grid points, then boundary grid points are obtained from the definition in Eq. (8). In fact, handling discontinuities in this manner was the main motivation for most of the formalism presented earlier such as the definitions in Eqs. (6), (7), (8), and the maximum-rank property of Sect. 3.2. This formalism resolves some issues raised by Mallet (1989), Mallet (1989) cautioned that the discretization of the roughness operator ${\mathcal {R}}(\phi )$ may require special attention at model boundaries and near discontinuities. No special treatment is required at boundaries here, since the roughness operator is only discretized on internal grid points. For the illustration in Fig. 7, the solution would be obtained everywhere except at the red grid points, which belong to $\varOmega _E$. Values at the red grid points may be estimated by extrapolation as a post-processing step. As an example, tagging grid points rasterized by the fault in Fig. 8a as points in $\varOmega _E$, changes the stratigraphic field from Fig. 5b to the stratigraphic field in Fig. 8b. This straightforward approach has proven capable of handling quite complex fault networks as shown in Fig. 9. It also generalizes to higher dimensions as demonstrated by the three-dimensional example in Fig. 10.

Fig. 7

Domain discretization in the presence of a discontinuity. The red line and nodes represent a discontinuity and its rasterization. Red nodes are tagged as external nodes. Blue nodes are boundary nodes, and black nodes are internal nodes

Fig. 8

Implicit stratigraphic modeling of model in Figure 5, in the presence a discontinuity. a Input data, two horizons and one fault. b Resulting stratigraphic field. Only value constraints were used in this experiment

Fig. 9

Implicit stratigraphic modeling in a highly faulted model. a Input data, 1400 data points and 50 faults. b Resulting stratigraphic field. Only value constraints were used in this experiment. Synthetic data courtesy of ExxonMobil

Fig. 10

Implicit stratigraphic modeling of the three-dimensional sandbox model of Chauvin et al. (2018). a Input data consisting of 27 fault surfaces and horizon points picked along 6 horizons. b Solid view of the resulting stratigraphic field. c Section view of the resulting stratigraphic field. Only value constraints were used in this experiment. Initial CT data courtesy of IFPEN and C&C Reservoirs

Fig. 11

Implicit modeling of the large thickness variation benchmark model of Renaudeau et al. (2017b). a Resulting implicit function using value constraints. b Estimation of stratigraphic orientation vectors. c Resulting implicit function using value and orientation constraints

7 Limitations and Discussion

7.1 Large Thickness Variations

When a layer exhibits large thickness variations, the resulting implicit field can have strong artifacts. For example, Fig. 11a shows an implicit function obtained using Eq. (27) when stratigraphic layers have strong thickness variations; the resulting function contains loops, which is physically impossible from a stratigraphic modeling point of view. A more stratigraphically admissible implicit function is shown in Fig. 11c. Handling such large thickness variations automatically, as done in Fig. 11c, is still an active area of research (Laurent 2016; Renaudeau et al. 2017b); we defer that discussion for further investigation. The problem highlighted by Fig. 11a is common to most implicit modeling techniques. According to Smith and Wessel (1990), this problem seems to come from our need to look for functions with continuous second derivatives everywhere.

7.2 Discontinuities

The method proposed to handle discontinuities in Sect. 6 can be numerically inefficient in some cases. If two faults are very close to one another, and there are some data between them, we are forced to use a fine grid in order to take into account those points. This can dramatically increase both the computational time and the computer memory required to solve the system depending on how close the faults are. One strategy to address this resolution limitation in finite difference implicit modeling would be to use additional degrees of freedoms on nodes adjacent to faults as done for example in the extended finite element method (Moes and Belytscheko 2002), and also recently used in structural modeling (Renaudeau et al. 2018).

Fig. 12

Interpolation of a complex surface using value constraints and gradient constraints (i.e. $\nabla \phi =\frac{{\mathbf {g}}}{||{\mathbf {g}}||}$, for a gradient vector ${\mathbf {g}}$). a Input data: 3400 points (black) and 675 gradient vectors (red). b Resulting stratigraphic field. c The running time is a quasi-linear function of grid size

7.3 Performance

We use a multi-grid conjugate gradient solver running on GPU on a computer equipped with a 3.5 GHz core and a Quadro M4000 GPU. The two-dimensional problem takes about a second for a problem with 250 K grid points, and 3–4 s for a problem with 1M grid points. The three-dimensional problem takes about 10–12 s for a problem with 1M grid points, and about 50 s for a problem with 5M grid points. Figure 12 suggests that the running time is a quasi-linear function of the grid gize. Future research may include trying to improve performance by preconditioning our solver; some preconditioners for such a problem can be found in Wu and Hale (2015). One limitation of the proposed method is the high memory requirement for three-dimensional problems; if the first roughness operator from Eq. (35) is used, each grid point has a memory cost of at least

$$\begin{aligned}&13 \text { equations} \times 3 \text { nonzeros} \\&\quad \times (1 \text { row id} + 1 \text { column id} + \text {1 value } )\\&\quad \times 4\text { bytes}=468\text { bytes}. \end{aligned}$$

7.4 Beyond Three-Dimensions

Sections 4 and 5 gave particular applications of Eqs. (22) and (24) in two and three-dimensions. While the formulas for the roughness operator ${\mathcal {R}}(\phi )$ appeared to become more complex as we went from one, to two, to three-dimensions, the discrete version of the roughness operator did not change. The only change was in the size of the full directional matrix $\bar{\bar{{\mathbf {F}}}}$. It is reasonable to expect that this remains true for all higher dimensions $\text {N}>3$. That is, all we need for an N-dimensional interpolation problem is to determine the N-dimensional directional matrix $\bar{\bar{{\mathbf {F}}}}_\text {N}$. In general, the directional matrix is given by

$$\begin{aligned} \bar{\bar{{\mathbf {F}}}}_\text {N}= \begin{bmatrix} \bar{\bar{{\mathbf {C}}}}_\text {N} \\ \bar{\bar{{\mathbf {D}}}}_\text {N} \\ \bar{\bar{{\mathbf {E}}}}_\text {N} \end{bmatrix}, \end{aligned}$$

with the understanding that the diagonal-axis matrix $\bar{\bar{{\mathbf {D}}}}_\text {N}$ only exists for $\text {N}>1$, and the extented-diagonal-axis matrix $\bar{\bar{{\mathbf {E}}}}_\text {N}$ only exists for $\text {N}>2$. The Cartesian-axis and diagonal-axis matrices are given by

$$\begin{aligned} \bar{\bar{{\mathbf {C}}}}_\text {N}(i,j)= & {} \delta _{ij}.\\ \bar{\bar{{\mathbf {D}}}}_\text {N}(i,j)= & {} (-1)^{\text {f}(i,j)} \text {, with } \text {f}(i,j)=(2\cdot i)^{(j+1-\text {N})}. \end{aligned}$$

The extended-diagonal-axis matrix $\bar{\bar{{\mathbf {E}}}}_\text {N}$ is obtained by inserting a zero at different positions of each row of the matrix

$$\begin{aligned} \begin{bmatrix} \bar{\bar{{\mathbf {D}}}}_\text {N-1} \\ \bar{\bar{{\mathbf {E}}}}_\text {N-1} \end{bmatrix}, \end{aligned}$$

in a similar way that we obtained $\bar{\bar{{\mathbf {E}}}}_\text {3}$ from $\bar{\bar{{\mathbf {D}}}}_\text {2}$ in Sect. 5. $\bar{\bar{{\mathbf {F}}}}_\text {N}$ has $\frac{3^\text {N}-1}{2}$ rows and N columns.

8 Conclusions

We have introduced a new technique for implicit modeling on Cartesian grids. We identified inherent practical properties of the well behaved one-dimensional discrete second derivative operator classically used to regularize interpolation in one-dimension, and then we designed higher dimensional discrete regularization operators with the same properties. In doing so, we obtained regularization operators that discretize naturally on the Cartesian grid: the operators do not require special treatment on boundary nodes, and they generalize to higher dimensions easily. Discarding boundary conditions allowed us to handle discontinuities by simply surrounding them with boundary nodes. As a result, our method is easy to implement, even in the presence of discontinuities. Numerical experiments demonstrate the robustness and numerical efficiency of the proposed method.

Appendix

The analytic expressions of terms appearing in the formulas for ${\mathcal {R}}(\phi )$, as proposed in Sect. 5, are given below

$$\begin{aligned} \begin{array}{rcl} \partial ^2_{[1\;0\;0]}\phi &{}=&{}\partial _x^2\phi ,\\ \partial ^2_{[0\;1\;0]}\phi &{}=&{}\partial _y^2\phi ,\\ \partial ^2_{[0\;0\;1]}\phi &{}=&{}\partial _z^2\phi ,\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;1\;0]}\phi \big )&{}=&{}\sqrt{2}\partial _x\big (\partial _y\phi \big ),\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;0\;1]}\phi \big )&{}=&{}\sqrt{2}\partial _x\big (\partial _z\phi \big ),\\ \sqrt{2}\partial _{[0\;1\;0]}\big (\partial _{[0\;0\;1]}\phi \big )&{}=&{}\sqrt{2}\partial _y\big (\partial _z\phi \big ),\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;1\;1]}\phi \big )&{}=&{}\partial _x\big (\partial _y\phi +\partial _z\phi \big ),\\ \sqrt{2}\partial _{[1\;0\;0]}\big (\partial _{[0\;1\;-1]}\phi \big )&{}=&{}\partial _x\big (\partial _y\phi -\partial _z\phi \big ),\\ \sqrt{2}\partial _{[0\;1\;0]}\big (\partial _{[1\;0\;1]}\phi \big )&{}=&{}\partial _y\big (\partial _x\phi +\partial _z\phi \big ),\\ \sqrt{2}\partial _{[0\;1\;0]}\big (\partial _{[1\;0\;-1]}\phi \big )&{}=&{}\partial _y\big (\partial _x\phi -\partial _z\phi \big ),\\ \sqrt{2}\partial _{[0\;0\;1]}\big (\partial _{[1\;1\;0]}\phi \big )&{}=&{}\partial _z\big (\partial _x\phi +\partial _y\phi \big ),\\ \sqrt{2}\partial _{[0\;0\;1]}\big (\partial _{[1\;-1\;0]}\phi \big )&{}=&{}\partial _z\big (\partial _x\phi -\partial _y\phi \big ),\\ \partial ^2_{[0\;1\;-1]}\phi &{}=&{}\frac{1}{2}\big (\partial _y^2+\partial _z^2-2\partial _y\partial _z\big )\phi ,\\ \partial ^2_{[0\;1\;1]}\phi &{}=&{}\frac{1}{2}\big (\partial _y^2+\partial _z^2+2\partial _y\partial _z\big )\phi ,\\ \partial ^2_{[1\;0\;-1]}\phi &{}=&{}\frac{1}{2}\big (\partial _x^2+\partial _z^2-2\partial _x\partial _z\big )\phi ,\\ \partial ^2_{[1\;0\;1]}\phi &{}=&{}\frac{1}{2}\big (\partial _x^2+\partial _z^2+2\partial _x\partial _z\big )\phi ,\\ \partial ^2_{[1\;-1\;0]}\phi &{}=&{}\frac{1}{2}\big (\partial _x^2+\partial _y^2-2\partial _x\partial _y\big )\phi ,\\ \partial ^2_{[1\;1\;0]}\phi &{}=&{}\frac{1}{2}\big (\partial _x^2+\partial _y^2+2\partial _x\partial _y\big )\phi ,\\ \partial ^2_{[1\;-1\;-1]}\phi &{}=&{}\frac{1}{3}\big (\partial _x^2+\partial _y^2+\partial _z^2-2\partial _x\partial _y-2\partial _x\partial _z+2\partial _y\partial _z\big )\phi ,\\ \partial ^2_{[1\;-1\;1]}\phi &{}=&{}\frac{1}{3}\big (\partial _x^2+\partial _y^2+\partial _z^2-2\partial _x\partial _y+2\partial _x\partial _z-2\partial _y\partial _z\big )\phi ,\\ \partial ^2_{[1\;1\;-1]}\phi &{}=&{}\frac{1}{3}\big (\partial _x^2+\partial _y^2+\partial _z^2+2\partial _x\partial _y-2\partial _x\partial _z-2\partial _y\partial _z\big )\phi ,\\ \partial ^2_{[1\;1\;1]}\phi &{}=&{}\frac{1}{3}\big (\partial _x^2+\partial _y^2+\partial _z^2+2\partial _x\partial _y+2\partial _x\partial _z+2\partial _y\partial _z\big )\phi . \end{array} \end{aligned}$$