Introduction

The initial force affecting a structural element and even its inherent weight has a significant influence on the fatigue phenomenon. These types of stresses are called initial or mean stresses and are often overlooked by designers in the process of design of connections or components due to fatigue. In numerous branches of industry the adequate consideration of the mean stress plays a significant role due to the prevalence of time-varying external forces, as well as internal forces in structures and machine components [9]. We can also mention an especially important and difficult case involving the correct analysis of the mean stress, i.e., the case of multiaxial load with nonzero value of the mean stress [3, 4, 6, 7]. In this case, no one has been able to propose an efficient and reliable computation model so far. Steels belong to the most common groups of structural materials used for the construction of machines, mainly due to their availability, cost, and good mechanical properties [10] or corrosion resistance [2]. The literature review shows that the fatigue tests of S355JR steel studied in our work are rare. Therefore, the main aim of the present work is to verify the developed algorithm [12] used to determine the fatigue life on the basis of the original experimental results. The case of tension-compression of unnotched round specimens with different levels of mean stresses is analyzed. The computational algorithm is constructed with regard for the state of knowledge in the evaluation of fatigue life in a random uniaxial stress state. The Rainflow cycle counting procedure used together with the linear cumulative damage hypothesis by Palmgren–Miner [16] and six selected models that take into account the effect of mean stresses on the fatigue have been used in the proposed algorithm. The effect of mean stresses on the fatigue life was taken into account by transforming the stress amplitude specified for each cycle by the Rainflow method. The coefficient K [4, 14] was found for six models in order to perform this task.

Description of Fatigue Tests

We present the results of the original research performed for S355JR steel on the SHM250 fatigue testing bench for tension-compression. The research was carried out both for constant and random loads. The experiments were carried out with two stress ratios R = − 1 and R = 0 in the case of constant amplitude and for R = 0 in the case of random loading.

The basic strength properties of S355JR steel are summarized in Table 1. Its chemical composition is as follows: 0.18 C; 1.3 Mn; 0.45 Si; 0.04 P; 0.03 S; 0.3 Cr; 0.2 Cu; 0.2 Ni; balance Fe. The test samples used in the research are shown in Fig. 1.

Table 1 Strength Properties of S355JR Steel
Full size table
Fig. 1.
figure 1

Shape and dimensions of fatigue test samples.

Full size image

The test samples were prepared according to the ASTM E466-07 [1] standard. Under the conditions of random loading, the tests were performed with the help of a special stochastic loading module added to the existing driving software. A cross section of the applied signal is shown in Fig. 2. The signal has a narrow-band characteristic with a predominant frequency of 20 Hz. The characteristics of signals correspond to the stresses observed in the selected structural elements, although they are generated by noise-band filtering with normal distribution. The random tests are performed under random loading with a stress ratio R = 0, which means that the samples have been preloaded with a stress equal to the maximum global stress amplitude of the course. The indicated stress ratio is given by the formula:

Fig. 2.
figure 2

Record of sample random stresses used in the experiment prior to scaling to the appropriate ratio R.

Full size image
$$ R=\frac{\sigma_{\mathrm{min}}}{\sigma_{\mathrm{max}}}, $$
(1)

where σmin and σmax are the minimum and maximum stresses, respectively. The results of constant- and random-amplitude tests are shown in Fig. 3 in the form of Wöhler fatigue-life curves.

Fig. 3.
figure 3

Experimental results presented in the form of Wöhler curves for S355JR steel: (a) tension-compression with constant amplitude for R = –1 (○) and R = 0 (□); (b) random-amplitude tension for R = 0 (○).

Full size image

The crack shape obtained from the experiments is characteristic for the high-cycle fatigue, although it does not reveal the formation of a significant narrowing in the diameter of the sample, thus indicating a significant influence of strains.

Mean Stress Correction Equations

In the literature, there is a large variety of equations taking into account the mean stress. These are the socalled correction equations specifying the material with the use of certain strength parameters and then applied for the scaling of a nonzero mean stress signal (transform) to an equivalent zero mean signal.

In the present work, we use the following equations:

the Gerber equation:

$$ \frac{\sigma_a}{\sigma_{aT}}=1-{\left(\frac{\sigma_m}{R_m}\right)}^2; $$
(2)

the Kwofie equation:

$$ \frac{\sigma_a}{\sigma_{aT}}=\exp \left(-{\upalpha}_K\frac{\sigma_m}{R_m}\right); $$
(3)

the Morrow equation:

$$ \frac{\sigma_a}{\sigma_{aT}}=1-\frac{\sigma_m}{\sigma_f^{\prime }}; $$
(4)

the Goodman equation:

$$ \frac{\sigma_a}{\sigma_{aT}}=1-\frac{\sigma_m}{R_m}; $$
(5)

the Oding equation:

$$ {\sigma}_{aT}={\sigma}_a^2+{\sigma}_m{\sigma}_a={\sigma}_a{\sigma}_{\mathrm{max}}, $$
(6)

and the Niesłony–Böhm equation:

$$ {\sigma}_{aT}={\sigma}_a+\left({\sigma}_{a,R=-1}-{\sigma}_{a,R=0}\right)\frac{\sigma_m}{\sigma_{a,R=0}}, $$
(7)

where

σa is the stress amplitude,

σaT is the transformed stress amplitude,

σm is the mean stress value,

Rm is the ultimate strength of the material,

σ′f is the fatigue-strength coefficient,

α is the mean stress sensitivity coefficient of the material [5],

σaf is the fatigue limit in tension-compression,

and

σa,R = – 1 and σa,R = 0 are the amplitudes obtained from the Wöhler tension curves for the ratios R = − 1 and R = 0.

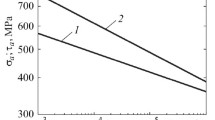
A diagram explaining the above models is presented in Fig. 4. In the present paper, we make an attempt to verify these classical empirical formulas and the formula presented by the authors in [12] on the example of the experimental results obtained for S355JR steel.

Fig. 4.
figure 4

Diagram explaining the characteristics of some mean-stress compensation models according to Kluger and Łagoda [3]: (1) Goodman; (2) Gerber; (3) Kwofe (α = 0.2); (4) NB; (5) Morrow; (6) Oding.

Full size image

An explanation of the generation of the test signal was presented in the previous section [8]. Nevertheless, the algorithm of evaluation of the fatigue life can be split into several main parts, e.g., cycle and half-cycle counting from the random course according to the Rainflow method [11]. At present, this is the most reliable cycle-counting method recommended (among other things) by the ASTM society.

As already indicated, our research deals with the verification of the compensation models of equivalent transformed amplitudes due to the mean stress. Five literature proposals and a model developed by the authors were chosen for verification. It was assumed that the stress course subjected to transformation was stationary with a constant value of the mean stress σm . In [7], it was proved that, for this type of stress courses, the mean stress can be found in a global way. These assumptions enable us to use the following transformation formula:

$$ {\sigma}_{ai T}={\sigma}_{ai}K, $$
(8)

where σaiT is the transformed stress amplitude, σai is the stress amplitude determined from the equivalent course with the use of a cycle-counting algorithm, K is a coefficient that depends on the transformation method as a function of the strength parameters and the mean-stress value σm .

For the coefficients K, the appropriate functions used in the procedure of calculations are obtained from the models proposed by Oding, Goodman, Morrow, Gerber, and Kwofie [4, 11, 13] and presented in Table 2.

Table 2 Formulas for the Coefficient K Used in the Process of Calculations
Full size table

A model developed by the authors in [12] is also used. This model employs the fatigue parameters of the material obtained for two limit states: tension-compression with the ratio R = – 1 and one-way tension with R = 0. These parameters have been taken from the the appropriate Wöhler curves. It is assumed that the intermediate state between the states of material effort can be described by a linear function. The results obtained for the case of random loading R = – 1 have been taken from the previous experiments carried out for this material.

The coefficient KNB is as follows:

$$ {K}_{NB}=1+\left({\sigma}_{a,R=-1}-{\sigma}_{a,R=0}\right)\frac{\sigma_m}{{\left({\sigma}_{a,R=0}\right)}^2}. $$
(9)

In the cumulative damage process, we use the Palmgren–Miner [16] hypothesis:

$$ D(N)=\left\{\begin{array}{c}{\sum}_{i=1}^j\frac{n_i}{N_0{\left({\sigma}_{af}/{\sigma}_{aiT}\right)}^m}\kern1.5em \mathrm{for}\kern1em {\sigma}_{aiT}\ge {a}_{PM}{\sigma}_{af},\\ {}\kern6.5em 0\kern9em \mathrm{for}\kern1em {\sigma}_{aiT}\ge {a}_{PM}{\sigma}_{af},\end{array}\right. $$
(10)

where D(N) is the degree of damage for N cycles, aPM is the coefficient taking into account the amplitudes beneath σaf , m is the slope of the Wöhler curve in tension-compression, ni is the number of stress cycles with the amplitude σaiT , and N0 is the number of cycles corresponding to the fatigue limit σaf .

The last step of the algorithm is the evaluation of fatigue life. It becomes possible after the determination of the degree of damage D(N) for a number of cycles performed in a loading unit. The durability in the number of cycles is given by the following formula:

$$ {N}_{\mathrm{cal}}=\frac{N}{D(N)}, $$
(11)

where Ncal is the calculated fatigue life, N is the number of cycles in the unit, and D(N) is the total degree of damage for the period of observations.

Conclusions

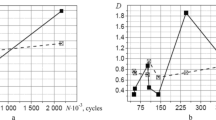
Mean-stress compensation models are verified under the conditions of random loading. For this purpose, we use a computation that consists of the rainflow cycle counting procedure and the linear Palmgren–Miner cumulative damage hypothesis. The numerical results are compared with the experimental data for six mean stress compensation models as presented in Fig. 5. It is easy to see that the numerical results obtained by using the Goodman model differ from the experimental data to the greatest degree. Note that two models, namely, the model proposed by Morrow and the model developed by the authors of the present paper, give satisfactory results in most cases.

Fig. 5.
figure 5

Comparison of the experimental and computed fatigue lives of S355JR steel for random loading with R = 0 determined by Niesłony with: (○) Gerber; (□) Kwofe; (◊) Morrow; (○) Goodman; (▽) Oding; (▷) Niesłony–Böhm.

Full size image

Some detailed observations are also formulated: If we subject S355JR steel to a random loading with nonzero mean stress, then we get the shorter fatigue life as compared with the case of zero mean value. The results accumulated for the uniaxial stress state in tension-compression and obtained by using the transformation models proposed by Gerber, Kwofie, Morrow, and the authors of the present paper lie within the value of scatter equal to 3. Most of the comparison results obtained by using the Oding model are located in the unacceptable scattering area. However it is important to note that this model is very conservative and does not overestimate the fatigue life after amplitude correction. The results obtained by the Goodman model do not lie in the accepted scatter area. In view of this fact, the indicated model is not suitable for the predictions of fatigue life for the analyzed type of steel.