The paper deals with the prediction of the fatigue life of 35NCD16 (36NiCrMo16) steel under random loading. This material is a high-strength alloy steel characterized by the absence of mutual parallelism of the fatigue characteristics for extension and torsion. It is shown that the fatigue life should not be estimated by using standard models because they do not take into account the variability relative to the tangential and normal stresses. The comparison of the experimental data with the numerical results obtained by using the proposed model gives satisfactory results.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
The 35NCD16 material is a high-strength alloy steel that takes its name from the French industry designation. The combination of high strength, high fracture toughness, and superior cleanliness identifies it as a good candidate for aerospace structural applications [1, 2]. In the present paper, we propose an algorithm for the determination of the fatigue life of materials in which there is no parallelism of the fatigue characteristics for extension and pure torsion. The verification of the proposed algorithm has been performed for 35NCD16 steel.
Materials and Fatigue Tests
We consider the test results obtained for 35NCD16 steel and presented in [3,4,5]. The chemical composition of the material is as follows (%):
In Fig. 1, we show the fatigue graph for extension and two-sided torsion of the considered material. As for 35NCD16 steel, the fatigue characteristics are not parallel (see Fig. 1). Variable values of the ratio of normal and shear stresses coming from extension and torsion, respectively, make it impossible to use a constant value of this ratio in the fatigue criteria including this ratio. The latest review of multiaxial fatigue criteria is presented in [6, 7].
The ratio of the fatigue limits from extension σ af and torsion τ af is usually assumed for the evaluation of
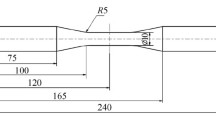
Cylindrical specimens subjected to cyclic and random loadings were used for the tests [3]. Cyclic and random tests were completed with proportional extension and torsion (τ a = 0.5σ a ).
In the case of random loading, the standard course CARLOS Car Loading Sequence-lateral [8] of 95,180 cycles in the block was applied. After the reduction of low-amplitude cycles, two kinds of blocks were obtained: f 1 = 46,656 extrema and f 2 = 13,568 extrema
Model of Evaluation of the Fatigue Life
Different stages of the algorithm of determination of the fatigue life are presented in Fig. 2. The previous models did not include the variability of the parameter k(N f ), which takes into account the out-of-parallelism fatigue characteristics for extension and pure torsion. A constant value of Eq. (1) has been usually assumed so far, e.g., in [9], for 35NCD16 steel, this value was assumed to be 3·105 cycles. A similar algorithm for cyclic loading was presented and used in [10]. In this paper, the authors took into account the variability of the parameter k(N f ) as follows:
where σ a is the amplitude of normal stresses under bending and τ a is the amplitude of shear stresses under torsion.
The presented model can be used for the analysis of the fatigue tests under cyclic and random loads in extension and torsion. The first block includes recording the components of the stress state within the range of long-lasting fatigue strength.
In the next stage, the initial number of cycles necessary for the calculation of the first cycle of operation of the algorithm is assumed to be N i = 106 cycles. The next block includes the determination of the critical plane orientation angle corresponding to the maximum effort of the material.
In the present paper, the position of the critical plane is determined by the method of damage accumulation, which is reduced to finding the angle of orientation of the critical plane for the maximum possible degree of damage (minimum durability) by using shear stress.
The expression for normal and shear stresses was complemented with the correction function with regard for the fatigue limits for extension and torsion Eq. (2):
where σ xx (t) are the stresses caused by bending; τ xy (t) are the stresses caused by torsion, and α is the critical plane orientation angle.
Note that Eqs. (3) and (4) contain a parameter k taking into account the out-of-parallelism of the fatigue characteristics for extension and pure torsion.
The authors of the present paper applied the criterion of maximum shear stresses [11]. In [12], they demonstrated that the expression for the equivalent value of stresses should be a linear function including normal and shear stresses. Based on this fact, the criteria were formulated and verified for cyclic [13,14,15] and random [16,17,18] loads.
The authors applied the criterion of maximum shear stresses [11]. This is directly connected with the orientation of the critical plane angle. The history of the equivalent stresses was written as
The degree of damage should be found prior to the fatigue life calculations. For the considered material, if we accept the hypothesis of fatigue damage accumulation according to Palmgren and Miner, then we get incorrect estimates of the fatigue life.
Thus, for the process of damage accumulation, the Serensen–Kogayev hypothesis [19] was used. This hypothesis is based on the Palmgren–Miner hypothesis [20, 21] and the coefficient b used to characterize the history:
where
is the frequency of particular levels σ ai in the realization of T 0, and σ a1 is the maximum stress amplitude.
In Fig. 3, we present the comparison of the computed and experimental fatigue lives for different values of the coefficient a in Eq. (5). The calculations were performed for the coefficient a = 0.5; 0.6; 0.8 and 1.
In the case of 35NCD16 steel, the coefficient a = 0.6 was used for subsequent analysis because this guaranteed the best possible agreement of the compared numerical results and the experimental fatigue lives. The computed life for the analysis of the method of modified amplitudes [22]
and the fatigue life were found from the modified Basquin equation
The mean relative errors of the computed fatigue lives for different values of the coefficient a are obtained from the following equation:
Here, for a = 1, R is equal to 1016%; for a = 0.8, it is equal to 151%; for a = 0.6, it is equal to 102%, and for a = 0.5, to 123%.
After the evaluation of the degree of damage S(T 0) according to Eq. (5), the next stage of the algorithm includes the determination of the fatigue life:
In the case of fatigue testing of the analyzed material, the time of observation (T 0) is a single block and the computed life is the sum of blocks. Under cyclic loads, after finding the equivalent stress history, it is necessary to compute the fatigue life according to the following equation [similar to Eq. (8)]:
The presented algorithm is based on the iterative method. Hence, later, it is necessary to find the ratio of the assumed and obtained lives:
This procedure is repeated for successively computed lives up to the time when the following condition is satisfied:
i.e. the assumed error is close to 1%, which is sufficient for the fatigue calculations.
Recall that the life given by Eq. (9) is the life in a single block. If condition (13) is satisfied, then the obtained fatigue life is just the required quantity.
Verification of the Proposed Criterion
The aim of our analysis is to check the efficiency of the proposed criterion not only for 35NCD16 steel but also for similar materials [23, 24] with special attention given to the variations of the parameter k(N f ). In Fig. 4, we present the comparison of the numerical and experimental lives under the conditions of extension and pure torsion. The analysis was carried out for two cases: for k = const determined for the ratio of the fatigue limits (k = 0.86), and k(N f ) within the scatter band of the coefficient 3.5 typical of the analyzed steel.
We also note that, in the case where k = const, the obtained results are less conforming than the results obtained for k(N f ). In Fig. 5, we present the comparison of the fatigue life with the experimental fatigue life for k = const (a) and k(N f ) (b).
In the case where k = const, the major part of the results are not contained in the scatter band of the coefficient 3.5 computed for the case of extension.
Conclusions
The analysis of the results of fatigue tests enables us to make the following conclusions: The proposed model can be used for the evaluation of the fatigue life under cyclic and random loadings of materials without parallelism of characteristics under the conditions of extension and pure torsion. The verification of the model gives satisfactory results. The analysis of the numerical results leads to the conclusion that the dependence of coefficient k on the number of cycles to damage N f gives better results than for k = const. The subsequent analysis of the proposed model for other materials and loads seems to be necessary.
References
O. I. Balyts’kyi, L. M. Ivaskevich, and V. M. Mochylskii, “Mechanical properties of martensitic steels in gaseous hydrogen,” Strength Mater., 44, No. 1, 64–73 (2012).
A. I. Balitskii, V. I. Vytvytskyi, and L. M. Ivaskevich, “The low-cycle fatigue of corrosion-resistant steels in high pressure hydrogen,” Proc. Eng, 2, No. 1, 2367–2371 (2010).
F. Morel, Fatigue Multiaxiale Sous Chargement d’Amplitude Variable, Docteur de L’Universite de Poitiers, Futuruscope (1996).
F. Morel, “A fatigue life prediction method based on a mesoscopic approach in constant amplitude multiaxial loading,” Fatigue Fract. Eng. Mat. Struct., 21, 241–256 (1998).
F. Morel, T. Palin-Luc, and C. Froustey, “Comparative study and link between mesoscopic and energetic approaches in high cycle multiaxial fatigue,” Int. J. Fatigue, 23, 317–327 (2001).
A. Niesłony, “Comparison of some selected multiaxial fatigue failure criteria dedicated for spectral method,” J. Theor. Appl. Mech., 48, No. 1, 233–254 (2010).
D. Skibicki and Ł. Pejkowski, “Integral fatigue criteria evaluation for life estimation under uniaxial combined proportional and nonproportional loadings,” J. Theor. Appl. Mech., 50, No. 4, 1073–1086 (2012).
M. Huck, W. Schutz, R. Fischer, and H. Kobler, A Standard Random Load Sequence of Gaussian Type Recommended for General Application in Fatigue Testing, LBF, Darmstadt Report No. 2909, IABG, Report No. TF-570, München (1976).
T. Łagoda, E. Macha, A. Niesłony, and F. Morel, “Estimation of the fatigue life of high-strength steel under variable-amplitude tension with torsion with use of the energy parameter in the critical plane,” in: A. Carpinteri, M. DeFreitas, and A. Spagnoli (editors), Biaxial/Multiaxial Fatigue Fract., Elsevier (2003), pp. 183–202.
M. Kurek and T. Łagoda, “Fatigue life estimation under cyclic loading including out-of-parallelism of the characteristics,” Appl. Mech. Mat., 104, 125–132 (2012).
P. Ogonowski and T. Łagoda, “Criteria of multiaxial random fatigue based on stress, strain, and energy parameters of damage in the critical plane,” Materialwissenschaft Werkstofftechnik, 36, No. 9, 429–437 (2005).
J. Grzelak, T. Łagoda, and E. Macha, “Spectral analysis of the criteria for multiaxial random fatigue,” Materialwissenschaft Werkstofftechnik, 22, 85–98 (1991).
K. Walat and T. Łagoda, “The equivalent stress on the critical plane determined by the maximum covariance of normal and shear stresses,” Materialwissenschaft Werkstofftechnik, 41, No. 4, 218–220 (2010).
K. Walat, M. Kurek, Ogonowski, and T. Łagoda, “The multiaxial random fatigue criteria based on strain and energy damage parameters on the critical plane for low cycle range,” Int. J. Fatigue, 37, 100–111 (2012).
K. Kluger and T. Łagoda, “Fatigue life of metallic material estimated according to selected models and load conditions,” J. Theor. Appl. Mech., 51, No. 3, 581–592 (2013).
T. Łagoda and E. Macha, “Estimated and experimental fatigue life of 30CrNiMo8 steel under in- and out-of-phase combined bending and torsion with variable amplitudes,” Fatigue Fract. Eng. Mat. Struct., 17, No. 11, 1307–1318 (1994).
T. Łagoda, E. Macha, and A. Niesłony, “Fatigue life calculation by means of the cycle counting and spectra methods under multiaxial random loading,” Fatigue Fract. Eng. Mat. Struct., 28, 409–420 (2005).
E. Macha, T. Łagoda, A. Niesłony, and D. Kardas, “Fatigue life variable amplitude loading according to the cycle counting and spectral methods,” Mater. Sci., 42, No. 3, 416–425 (2006).
S. V. Serensen, V. P. Kogaev, and P. M. Shneiderovich, Load-Bearing Ability and the Strength Analysis of Machine Parts [in Russian], Mashinostroenie, Moscow (1975).
A. Palmgren, “Die Lebensdauer Von Kugellagern,” VDI-Z, 68, 339–341 (1924).
M. A. Miner, “Cumulative damage in fatigue,” J. Appl. Mech., 12, 159–164 (1945).
T. Łagoda and C. M. Sonsino, “Comparison of different methods for presenting variable amplitude loading fatigue results,” Materialwissenschaft Werkstofftechnik, 35, No. 1, 13–19 (2004).
S. Mroziński, “The influence of loading program on the course of fatigue damage cumulation,” J. Theor. Appl. Mech., 49, No. 1, 83–95 (2011).
A. Karolczuk, K. Kluger, and T. Łagoda, “A correction in the algorithm of fatigue life calculation based on the critical plane approach,” Int. J. Fatigue, 83, 174–183 (2015).
Acknowledgments
The project is financed from the funds of the National Centre of Science (Decision No. 2011/01/B/ST8/06850) “Estimation of the fatigue life of 35NCD16 alloy steel under random loading.”
Author information
Authors and Affiliations
Corresponding author
Additional information
Published in Fizyko-Khimichna Mekhanika Materialiv, Vol. 52, No. 4, pp. 46–51, July–August, 2016.
Rights and permissions
About this article
Cite this article
Kurek, M., Łagoda, T. & Morel, F. Estimation of the Fatigue Life of 35NCD16 Alloy Steel Under Random Loading. Mater Sci 52, 492–499 (2017). https://doi.org/10.1007/s11003-017-9981-1
Received:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s11003-017-9981-1


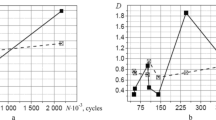





 ) σ = 0 for k = const.
) σ = 0 for k = const.
 ) τ = 0.5σ.
) τ = 0.5σ.