Stressed State of a Quasiorthotropic Half Plane with Curvilinear Edge

By the method of singular integral equations, we consider a plane periodic problem of the theory of elasticity for a quasiorthotropic half plane containing an infinite row of edge angular rounded notches. By using the unified approach to the solution of the problems of stress concentration near notches with sharp and rounded vertices, we determine the stress intensity factors at the sharp tips of the corresponding edge notches. The same method is used for the solution of the problem of stress distribution in a quasiorthotropic half plane with sinusoidal edge.

Introduction

The influence of free surface of the body on the stress distribution near edge notches is mainly studied for the elastic half plane. A two-dimensional periodic problem for an elastic isotropic half plane was, as a rule, analyzed for the case where the half plane contains a system of cracks, holes, or inclusions [1, 2].

In the present work, we consider a periodic problem for a quasiorthotropic half plane with curvilinear edge. As in the isotopic case [1,2,3,4,5], the boundary-value problem for this domain is reduced to a singular integral equation (SIE) with Hilbert kernel on a part of the boundary of the half plane located in the main band of periods. By using the numerical method of quadrature, we find the solution of integral equation for the half plane with sinusoidal and sawtooth edges.

Quasiorthotropic Plane with Periodic System of Curvilinear Cracks

Consider an elastic quasiorthotropic plane [6,7,8,9] referred to a Cartesian coordinate system xOy . The plane is weakened by a periodic system of cracks along smooth curvilinear contours. A single crack is located in a band of periods of width d. The Ox- and Oy-axes are directed along the principal axes of orthotropy. The contour of the crack located in the main band of periods (|x|≤d, −∞ < y < ∞) is denoted by L. We assume that the faces of all cracks are subjected to the action of the same self-balanced load as the contour L:

$$ {N}^{\pm }(t)+i{T}^{\pm }(t)={p}_0(t),\kern0.6em t=x+ iy\in L, $$

(1)

where N^±(t) and T^±(t) are the normal and tangential components of the stress vector. Moreover, at infinity, the plane is subjected to the action of uniaxial tensile stresses σ_x^∞=q.

The stress-strain state of the plane satisfies the conditions of periodicity (the stresses are periodic functions of x with a period d).

The posed problem is solved by the method of SIE [1, 2]. We apply the method of superposition and seek the complex stress potentials for the quasiorthotropic body in the form

$$ {\varphi}_1^{\ast}\left({z}_1\right)={\varphi}_1^0\left({z}_1\right)+{\varphi}_1\left({z}_1\right),\kern0.6em {\psi}_1^{\ast}\left({z}_1\right)={\psi}_1^0\left({z}_1\right)+{\psi}_1\left({z}_1\right), $$

where

$$ {\varphi}_1^0\left({z}_1\right)={\gamma}^{-2}q/4\kern0.72em and\kern1.2em {\psi}_1^0\left({z}_1\right)=-{\gamma}^{-2}q/2. $$

Here and in what follows, subscript “1” always means that the corresponding complex quantities are related to the plane z₁=x+iγy, where γ is the parameter of orthotropy (for the plane stressed state $\gamma =\sqrt[4]{E_x/{E}_y}$ , where E_x and E_y are the moduli of elasticity along the Ox- and Oy-axes, respectively). The integral images of the Kolosov–Muskhelishvili complex stress potentials Φ₁^*(z₁) and Ψ₁^*(z₁) for the analyzed problem have the form similar to their form in the isotropic case [10]:

$$ {\displaystyle \begin{array}{c}\begin{array}{l}{\varPhi}_1^{\ast}\left({z}_1\right)=\frac{q}{4{\upgamma}^2}+\frac{1}{2d}\underset{L_1}{\int }{g}_1^{\hbox{'}}\left({t}_1\right)\cot \frac{\pi }{d}\left({t}_1-{z}_1\right)d{t}_1,\\ {}{\psi}_1^{\ast}\left({z}_1\right)=-\frac{q}{2{\gamma}^2}+\frac{1}{2d}\underset{L_1}{\int}\left\{\overline{g_1^{\hbox{'}}\left({t}_1\right)}\;\cot \right.\frac{\pi }{d}\left({t}_1-{z}_1\right)\overline{d{t}_1}\end{array}\\ {}\left.-\left[\cot \frac{\pi }{d}\left({t}_1-{z}_1\right)+\frac{\pi }{d}\left(\overline{t_1}-{t}_1+{z}_1\right){\csc}^2\frac{\pi }{d}\left({t}_1-{z}_1\right)\right]\kern0.24em {g}_1^{\hbox{'}}\left({t}_1\right)d{t}_1\right\},\end{array}} $$

(2)

where g₁′(t₁) is the unknown density expressed via the derivative of the jump of vector of displacements u, v in passing through the contour L associated with the contour L₁ in the plane z₁ = x + iγy.

By using the expressions for the components of stress tensor σ x , σ y, τxy via the complex potentials Φ₁^*(z₁) and Ψ₁^*(z₁) and satisfying the boundary condition (1) with the help of potentials (2), we obtain the SIE in the form [2, 7]

$$ \underset{L_1}{\int}\left[{K}_1\left({t}_1,{t}_1^{\hbox{'}}\right){g}_1^{\hbox{'}}\left({t}_1\right)d{t}_1+{L}_1\left({t}_1,{t}_1^{\hbox{'}}\right)\overline{g_1^{\hbox{'}}\left({t}_1\right)}\overline{d{t}_1}\right]=\pi {\overline{P}}_1\left({t}_1^{\hbox{'}}\right),\kern0.36em {t}_1^{\hbox{'}}\in {L}_1, $$

(3)

where the kernels and the right-hand side are given by the formulas

$$ {\displaystyle \begin{array}{c}{K}_1\left({t}_1,{t}_1^{\hbox{'}}\right)\frac{\pi }{2d}\left[\cot \frac{\pi }{d}\left({t}_1-{t}_1^{\hbox{'}}\right)+\cot \frac{\pi }{d}\left(\overline{t_1}-\overline{t_1^{\hbox{'}}}\right)\frac{\overline{d{t}_1^{\hbox{'}}}}{d{t}_1^{\hbox{'}}}\right],\\ {}{L}_1\left({t}_1,{t}_1^{\hbox{'}}\right)\frac{\pi }{2d}\left[\left(1-\frac{\overline{d{t}_1^{\hbox{'}}}}{d{t}_1^{\hbox{'}}}\right)\cot \frac{\pi }{d}\left({t}_1-{t}_1^{\hbox{'}}\right)+\cot \frac{\pi }{d}\left({t}_1-\overline{t_1^{\hbox{'}}}-\overline{t_1}\right){\csc}^2\frac{\pi }{d}\left(\overline{t_1}-\overline{t_1^{\hbox{'}}}\right)\frac{\overline{d{t}_1^{\hbox{'}}}}{d{t}_1^{\hbox{'}}}\right],\\ {}{\tilde{P}}_1\left({t}_1\right)=\frac{1}{2\gamma}\left[\left(1-\gamma \right)p\left({t}^{\hbox{'}}\right)-\left(1-\gamma \right)\overline{p\left({t}^{\hbox{'}}\right)}\frac{\overline{d{t}^{\hbox{'}}}}{d{t}^{\hbox{'}}}\right]\frac{d{t}^{\hbox{'}}}{d{t}_1^{\hbox{'}}},\end{array}} $$

where $p\left({t}^{\hbox{'}}\right)={p}_0\left({t}^{\hbox{'}}\right)-q\left(1-\overline{d{t}^{\hbox{'}}}/d{t}^{\hbox{'}}\right)/2{\gamma}^2.$

For any continuous right-hand side p(t′), the integral equation (3) possesses a unique solution in the class of functions with integrable singularity at the ends of the contour L under the additional condition

$$ \underset{L}{\int }{g}^{\hbox{'}}(t) dt={a}_0-0 $$

(4)

guaranteeing the uniqueness of displacements in traversing the contour L.

Periodic Boundary-Value Problem of the Theory of Elasticity for a Half plane with Curvilinear Edge

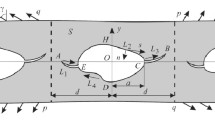
Consider an elastic half plane with smooth periodic curvilinear edge. A part of the contour of this edge located in the main band of periods (x ≤ d ) is denoted by L . We also assume that a periodic load

$$ N+ iT={p}_0(t),\kern0.36em t\in L $$

acts upon the edge of the half plane.

The complex stress potentials and the integral equation of the posed problem are obtained from the results, presented above for the periodic system of curvilinear cuts in the elastic plane under the assumption that the contour L intersects the entire main band of periods and the boundaries of the obtained half planes are smooth lines. This enables us to reduce Eq. (3) to a complete SIE with Hilbert kernel [11]. This equation has a solution that depends on an arbitrary constant only under the condition

$$ \underset{L}{\int }{p}_0(t) dt=0 $$

(5)

guaranteeing the equality of the resultant vector of external forces acting on the contour L to zero. In what follows, we assume that the external load satisfies condition (5). A unique solution of Eq. (3) is obtained under the additional condition (4), which has a different physical interpretation in this case. Indeed, this condition now guarantees the periodicity of the vector of jump of displacements with respect to the variable x .

By analogy with the integral equation for a multiply connected domain [7], we add a regularizing operator to the left-hand side of Eq. (3). As a result, we arrive at the following modified integral equation:

$$ \underset{L_1}{\int}\left[{K}_1\left({t}_1,{t}_1^{\hbox{'}}\right){g}_1^{\hbox{'}}\left({t}_1\right)d{t}_1+{L}_1\left({t}_1,{t}_1^{\hbox{'}}\right)\overline{g_1^{\hbox{'}}\left({t}_1\right)d{t}_1}\right]+\frac{\delta }{d}\frac{d{s}_1^{\hbox{'}}}{d{t}_1^{\hbox{'}}}{a}_0=\pi {\tilde{P}}_1\left({t}_1^{\hbox{'}}\right),\kern0.36em {t}_1^{\hbox{'}}\in L, $$

(6)

which has a unique solution for any right-hand side ${\tilde{P}}_1\left({t}_1^{\hbox{'}}\right)$ If the external load satisfies condition (5), then the operator a₀ in (4) is equal to zero and Eq. (6) gives the solution of the posed problem. Here, s1′ is the arc abscissa corresponding to a point t1′ on the contour L₁ and δ ≠ 0 is an arbitrary real number.We represent the parametric equation of the contour L₁ in the form

$$ {t}_1=l{\omega}_1\left(\xi \right)=\frac{\left(1+\gamma \right)t+\left(1-\gamma \right)\overline{t}}{2},\kern0.84em -\pi \le \xi \le \pi, $$

where l is a chosen parameter with dimension of length and the equation

$$ t= l\omega \left(\xi \right),\kern0.6em \pi \le \xi \le \pi $$

(7)

describes the contour L in the plane z = x + iy.

We now represent the integral equation (9) in the dimensionless form:

$$ \frac{1}{\pi}\underset{-\pi }{\overset{\pi }{\int }}\left[{M}_1\left(\xi, \eta \right)u\left(\xi \right)+{N}_1\left(\xi, \eta \right)\overline{u\left(\xi \right)}\right] d\xi ={\tilde{P}}_1\left(\eta \right),\kern0.6em -\pi \le \eta \le \pi, $$

(8)

where

$$ {\displaystyle \begin{array}{c}{M}_1\left(\xi, \eta \right)=l{K}_1\left(l{\omega}_1\left(\xi \right),l{\omega}_1\left(\eta \right)\right)+\frac{\delta l}{d}\frac{\left|{\omega}_1^{\hbox{'}}\left(\eta \right)\right|}{\omega_1^{\hbox{'}}\left(\eta \right)},\kern0.6em {N}_1\left(\xi, \eta \right)=l{L}_1\left(l{\omega}_1\left(\xi \right),l{\omega}_1\left(\eta \right)\right),\\ {}u\left(\xi \right)={g}_1^{\hbox{'}}\left(l{\omega}_1\left(\xi \right)\right)\frac{\omega_1^{\hbox{'}}\left(\xi \right)}{q},\kern0.72em {\tilde{P}}_1\left(\eta \right)=\frac{{\tilde{P}}_1\left(l{\omega}_1\left(\eta \right)\right)}{q}.\end{array}} $$

Hence, we have reduced our problem to finding a 2π -periodic continuous function of the SIE (8), which has a unique solution for any right-hand side. The numerical solution of this equation can be found by the method of quadratures.

Quasiorthotropic Half Plane with Sinusoidal Edge

Consider the problem tension of an elastic load-free [ p₀(t) = 0] half plane with sinusoidal edge at infinity. Here and in what follows, we choose the maximum depth of edge notches as the parameter l (Fig. 1). We represent the function ω(ξ) in the parametric equation (7) for a sinusoid in the form

Fig. 1.

Quasiorthotropic half plane with periodic curvilinear edge.

$$ \omega \left(\xi \right)=\frac{\xi }{\pi \tilde{\gamma}}-\frac{i\left(1+\cos \kern0.24em \xi \right)}{2},\kern0.84em -\pi \le \xi \le \pi, $$

where the parameter $\tilde{\gamma}=2l/d.$

The stresses acting on the edge of the half plane are given by the formula [13]

$$ {\sigma}_s^{\ast}\left(t\hbox{'}\right)=4\kern0.24em \operatorname{Re}\left[\frac{q}{4{\gamma}^2}+{\varphi}_1^{-}\left({t}_1^{\hbox{'}}\right)\right],\kern0.6em {t}_1^{\hbox{'}}\in L, $$

where

$$ {\varphi}_1^{-}\left({t}_1^{\hbox{'}}\right)=-\frac{i}{2}{g}_1^{\hbox{'}}\left({t}_1^{\hbox{'}}\right)+\frac{1}{2d}\underset{L_1}{\int }{g}_1^{\hbox{'}}\left({t}_1\right)\cot \frac{\pi }{d}\left({t}_1-{t}_1^{\hbox{'}}\right)d{t}_1. $$

For the stress concentration factor (SCF) kt = σ_s^* /q at the notch tip, we get

$$ {k}_t=4\kern0.24em \operatorname{Re}\left\{\frac{1}{4{\gamma}^2}-\frac{i}{2}\frac{u(0)}{\omega_1^{\hbox{'}}(0)}+\frac{l\pi}{nd}\sum \limits_{k=1}^{2n}u=\left({t}_k\right)\cot \frac{\pi }{d}l\left[{\omega}_1\left({\xi}_k\right)-{\omega}_1(0)\right]\right\}. $$

(9)

Here,

$$ {\xi}_k=\pi \left(2k-1\right)/(2n)-\pi, \kern0.48em k=\overline{1,2n}. $$

The value of u(0) is determined by using the Lagrange interpolation formula on uniform nodes:

$$ u(t)=\frac{1}{2n}\sum \limits_{k=1}^{2n}u\left({\xi}_k\right)\sin \left[n\left(t-{\xi}_k\right)\right]\cot \left(\frac{t-{\xi}_k}{2}\right). $$

The numerical analysis of the SCF (9) was carried out for the parameter $\tilde{\gamma}=2l/d$ within the range $0.01\le \tilde{\gamma}\le 100$(Fig. 2).

Fig. 2.

Stress concentration factor kt at the notch tip as a function of the parameter 2l/d for the quasiorthotropic half plane with sinusoidal edge.

As the radius of curvature approaches zero, the SCF k_t tends to infinity and, as the distance between the notch tips increases, i.e., as the parameter $\tilde{\gamma}$ decreases, the value of k_t approaches 1 (the case of a half plane with rectilinear edge).

Rounded Edge Angular Notches

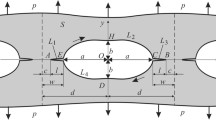
Assume that an elastic half plane is weakened by periodically arranged angular notches with rounded vertices. The edge of the half plane is free of loads [ p₀(t) = 0] and a tensile stress σ x = q is assigned at infinity. The contour of the notch consists of rectilinear domains oriented at an angle 2β joined by a circular arc of radius ρ₁ = ρ and also smoothly connected with the rectilinear edge of the half plane by a circular arc of radius ρ₂. The length of the rectilinear part of the edge of half plane located between the neighboring notches is equal

to 2a (Fig. 3).

Fig. 3.

Quasiorthotropic half plane weakened by a periodic system of rounded angular notches.

We now introduce dimensionless parameters

$$ {\varepsilon}_1=\varepsilon =\rho /l,\kern0.84em {\varepsilon}_2={\rho}_2/l,\kern0.72em {\varepsilon}_3=a/l,\kern0.6em and\kern0.6em \tilde{\gamma}=2l/d $$

satisfying the following relation:

$$ \tilde{\gamma}=\frac{1}{\left[1-\left({\varepsilon}_1+{\varepsilon}_2\right)\left(1-\sin\;\beta \right)\right]\tan \beta +\left({\varepsilon}_1+{\varepsilon}_2\right)\cos \beta +{\varepsilon}_3}. $$

In view of the symmetry of contour L about the Oy-axis, we can represent its parametric equation in the form

$$ t= l\omega \left(\xi \right)=l\left\{\begin{array}{l}-\overline{\omega_0\left(-\xi \right),}\kern0.6em -\pi \le \xi <0,\\ {}{\omega}_0\left(\xi \right),\kern2.04em 0\le \xi \le \pi .\end{array}\right. $$

Here, we have the following function:

$$ {\omega}_0\left(\xi \right)=\left\{\begin{array}{cc}{\varepsilon}_1\sin \left(\frac{\xi c}{\varepsilon_1}\right)+i\left[\left({\varepsilon}_1-1\right)-{\varepsilon}_1\cos \left(\frac{\xi c}{\varepsilon_1}\right)\right],& 0\le \xi <{\xi}_B,\\ {}{\varepsilon}_1\cos \beta +c\left(\xi -{\xi}_B\right)\sin \beta +i\left\{\left[{\varepsilon}_1\left(1-\sin \beta \right)-1\right]+c\left(\xi -{\xi}_B\right)\cos \beta \right\},& {\xi}_B\le \xi <{\xi}_C,\\ {}\left(\frac{1}{\gamma }-{\varepsilon}_3\right)-{\varepsilon}_2\cos \left[\frac{c\left(\xi -{\xi}_C\right)}{\varepsilon_2}+\beta \right]+i\left\{-{\varepsilon}_2+{\varepsilon}_2\sin \left[\frac{c\left(\xi -{\xi}_C\right)}{\varepsilon_2}+\beta \right]\right\},& {\xi}_C\le \xi <{\xi}_D,\\ {}\left(\frac{1}{\gamma }-{\varepsilon}_3\right)+c\left(\xi -{\xi}_D\right),& {\xi}_D\le \xi <\pi, \end{array}\right. $$

where

$$ {\displaystyle \begin{array}{c}{\xi}_B=\frac{\varepsilon_1\left(\pi /2-\beta \right)}{c},\kern0.84em {\xi}_C={\xi}_B+\frac{1-\left({\varepsilon}_1+{\varepsilon}_2\right)\left(1-\sin \beta \right)}{c\cos \beta}\\ {}{\xi}_D={\xi}_C+\frac{\varepsilon_2\left(\pi /2-\beta \right)}{c},\\ {}c=\frac{\varepsilon_3+\left({\varepsilon}_1+{\varepsilon}_2\right)\left(\pi /2-\beta \right)+\left[1-\left({\varepsilon}_1+{\varepsilon}_2\right)\left(1-\sin \beta \right)\right]/\cos \beta }{\pi }.\end{array}} $$

We performed the numerical analysis of the SCF for different values of the parameters ε₁ and ε₃ and the angle β as ε₂ → 0. Setting β = 0, we obtain a periodic system of U-shaped edge notches (Fig. 4).

Fig. 4.

Stress concentration factor at the vertex of a U-shaped notch (β = 0) as a function of the dimensionless distance between the notches for their different relative depths and the values of parameter ε = 1 (a) and ε = 0.5 (b).

We also consider the case of a half plane with sawtooth edge in which the rounded angular notches are connected (ε₃ = 0). We computed the dependences of SCF on the opening angle 2β (Fig. 5) for different relative radii of curvature at the notch tips. It is easy to see that the SCF take their maximum values at the inner points of the interval 0 < 2β < π.

Fig. 5.

Dependences of the SCF for a quasiorthotropic half plane with sawtooth edge on the opening angle of the notch 2β for the relative rounding radius ρ/l = 0.5.

The stress concentration factors at the tips of rounded angular notches in the quasiorthotropic plane take higher values when the parameter of orthotropy γ > 1, i.e., the SCF is higher if the axis of higher modulus of elasticity coincides with the axis of tension of the plane.

Sharp Angular Notches in the Quasiorthotropic Half Plane

To calculate the generalized stress intensity factors (SIF) at the tips of sharp edge angular notches, we use the dependence [1, 2]

$$ {\tilde{K}}_I^V={\frac{1}{R_1}}_{\rho \to 0}^{\mathrm{lim}}\left[{\left(2\pi \rho \right)}^{\lambda 1}{\sigma}_s^{\ast }(0)\right]. $$

For this purpose, at the tip of a sharp angular notch, it is necessary to know both the coefficient of influence of rounding of the notch R_I and the parameter of stress singularity λ_Ι . Thus, for the quasiorthotropic material, we have [10, 11]

$$ {\lambda}_I=1.247\cos {\beta}_1\left(\alpha \right)-1.312{\cos}^2{\beta}_1\left(\alpha \right)+0.8532{\cos}^3{\beta}_1\left(\alpha \right)-0.2882{\cos}^4{\beta}_1\left(\alpha \right), $$

where β1(α) = π + arctan (γ tan α), and α = π − β. In Fig. 6, we present the obtained dependences of the dimensionless SIF ${\tilde{F}}_I^V={\tilde{K}}_I^V/\left(p{\left(\pi l\right)}^{\lambda I}\right)$on the opening angle of the notch 2β.

Fig. 6.

Dimensionless stress intensity factor ${\tilde{F}}_I^V$ as a function of the opening angle 2β for relative distances between the edge angular notches a/l = 0 (a) and a/l = 2 (b) in the quasiorthotropic half plane.

If 2β = 180°, then the singularity of stress field at the notch tip disappears and, therefore,

${\tilde{F}}_I^V=1,$ which is a consequence of the accepted definition of generalized SIF.

Conclusions

We considered a periodic problem of the theory of elasticity for a quasiorthotropic half plane with curvilinear edge of periodic form. The boundary-value problem for this domain is reduced to SIE. We determined the SCF at the vertices of sinusoidal, U-shaped, and rounded angular notches in the quasiorthotropic half plane subjected to uniaxial tension at infinity. We computed the SIF at the sharp tips of edge angular notches in the quasiorthotropic half plane as functions of the opening angle of the notch.