Plane Problem of the Theory of Elasticity for a Quasiorthotropic Body with Cracks

We write basic relations of the plane problem of the theory of elasticity for a quasiorthotropic body. The integral representations for the complex stress potentials are constructed for a quasiorthotropic plane in terms of the jumps of displacements on open curvilinear contours. The first basic problem for a plane with cracks is reduced to singular integral equations. We find the asymptotic distribution of stresses near the tip of a curvilinear crack. The analytic solution of the problem is obtained for an arbitrarily oriented rectilinear crack. We numerically compute the stress intensity factors for a parabolic crack and analyze the influence of the ratio of the basic moduli of elasticity of the material on their behavior.

The plane problems of the theory of elasticity for anisotropic and orthotropic bodies with cracks were considered in [1–6] and the roots of the characteristic equation were assumed to be different. A degenerate anisotropic material, i.e., the case where the roots of the characteristic equation are multiple, was also studied [7]. A degenerate orthotropic material is called quasiorthotropic [8–10]. Isotropic materials and various kinds of composite materials based on ceramic, fibrous and layered composites, etc. belong to this class of materials [11]. In the literature [12], these bodies are also called pseudoisotropic and, in the problems of the theory of orthotropic shells with rectilinear cracks, they are called specially orthotropic [13–16].

In what follows, by the method of singular integral equations, we consider the plane problem of the theory of elasticity for a quasiorthotropic plane with curvilinear cracks. We obtain the stress intensity factors (SIF) for an arbitrarily located rectilinear and parabolic cracks.

Basic Relations of the Plane Problem of the Theory of Elasticity for Quasiorthotropic Media

The linear relations between the components of the stress tensors σ _x , σ _y , τ _xy and strain tensors ε _x , ε _y , ε _xy (Hooke's law) under the conditions of plane stressed state for an orthotropic body in a Cartesian coordinate system xyz in the case where the coordinate axes x and y are directed along the principal axes of orthotropy take the form [17]:

$$ {\upvarepsilon}_x={a}_{11}{\upsigma}_x+{a}_{12}{\upsigma}_y,\kern1em {\upvarepsilon}_y={a}_{12}{\upsigma}_x+{a}_{22}{\upsigma}_y,\kern1em {\upvarepsilon}_{xy}=2{a}_{66}{\uptau}_{xy} $$

where a ₁₁ = 1/E _x ; a ₂₂ = 1/E _y , a ₁₂ = − v _xy /E _x , and a₆₆ = 1/G. Here, E _x  = E ₁ and E _y  = E ₂(E _x  = E ₂, E _y  = E ₂) are the elasticity moduli in tension–compression along the x - and y-axes, ν _xy  = ν₁₂(ν _xy  = ν₂₁ = v ₁₂ E ₂/E ₁) is Poisson’s ratio in the case of compression of the plane in the direction of the y(x)-axis if tension is realized along the x(y)-axis, and G = G₁₂ = Gxy = G ₂₁ = G _yx is the shear modulus, which characterizes the variations of the angles between the principal axes.

We assume that the elastic constants a _ij satisfy the relation

$$ {a}_{66}=2\left(\sqrt{a_{11}{a}_{22}}-{a}_{12}\right), $$

(1)

or

$$ G={E}_1/2\left(\sqrt{E_1/{E}_2}+{\upnu}_{12}\right) $$

for the plane stressed state. Relation (1) may serve as an indication of the quasiorthotropic body.

For the plane deformation of the orthotropic body, it is necessary to replace the elastic constants a _ij in Hooke's law by the quantities a ^' _ij  = a _ij  − (a _i3 a _j3)/a ₃₃, where a ₁₃ = − ν₁₃/E ₁, a ₂₃ = − ν₂₃/E ₂, a ₃₃ = 1/E ₃ are the corresponding elastic characteristics of the material.

We introduce the function of stresses F(x, y) by the following formulas [17]:

$$ {\upsigma}_x=\frac{\partial^2F}{\partial {y}^2},\kern1em {\upsigma}_y=\frac{\partial^2F}{\partial {x}^2},\kern1em {\upsigma}_z=-\frac{\partial^2F}{\partial x\partial y}. $$

(2)

In the absence of mass forces, the function F(x, y) for the quasiorthotropic body satisfies the elliptic differential equation of the fourth order

$$ \frac{\partial^4F}{\partial {y}^4}+2{\upgamma}^2\frac{\partial^4F}{\partial {x}^2\partial {y}^2}+{\upgamma}^4\frac{\partial^4F}{\partial {x}^4}=0. $$

(3)

Its characteristic equation has the form

$$ {\upmu}^4+2{\upgamma}^2{\upmu}^2+{\upgamma}^4=0. $$

(4)

Here, $\upgamma = \sqrt[4]{a_{22}/{a}_{11}}$ is the parameter of orthotropy. For the plane stressed state, we have $\upgamma = \sqrt[4]{E_x/{E}_y}$. Equation (4) has multiple complex conjugate roots μ₁ = μ₂ = iγ and ${\overline{\upmu}}_1={\overline{\upmu}}_2=-i\upgamma$. For the isotropic materials, γ = 1.

The general solution of Eq. (3) for the quasiorthotropic body can be represented via the analytic functions φ₁(z ₁) and χ₁(z ₁) of the complex argument z ₁ = x + iγy in the form [17]

$$ F\left({z}_1\right)=\mathrm{R}\mathrm{e}\left[\overline{z_1}\upvarphi {}_1\left({z}_1\right)+{\upchi}_1\left({z}_1\right)\right]. $$

(5)

In view of relations (2) and (5), we express the components of stresses via the complex potentials

$$ {\varPhi}_1\left({z}_1\right)={\upvarphi}_1^{\prime}\left({z}_1\right)\kern1em \mathrm{and}\kern1em {\varPsi}_1\left({z}_1\right)={\varPsi}_1^{\prime}\left({z}_1\right)={\upchi}_1^{\prime \prime}\left({z}_1\right) $$

by the following formulas:

$$ \left\{\begin{array}{l}{\upsigma}_x\left({z}_1\right)=-{\upgamma}^2\mathrm{R}\mathrm{e}\left\{{\varPsi}_1\left({z}_1\right)+{\overline{z}}_1{\varPhi}_1^{\hbox{'}}\left({z}_1\right)-2{\varPhi}_1\left({z}_1\right)\right\},\hfill \\ {}{\upsigma}_y\left({z}_1\right)=\mathrm{R}\mathrm{e}\left\{{\varPsi}_1\left({z}_1\right)+{\overline{z}}_1{\varPhi}_1^{\hbox{'}}\left({z}_1\right)+2{\varPhi}_1\left({z}_1\right)\right\},\hfill \\ {}{\uptau}_{xy}\left({z}_1\right)=\upgamma \mathrm{I}\mathrm{m}\left\{{\varPsi}_1\left({z}_1\right)+{\overline{z}}_1{\varPhi}_1^{\hbox{'}}\left({z}_1\right)\right\}.\hfill \end{array}\right. $$

The Cartesian components of the vector of displacements u and v can also be represented via the complex potentials φ₁(z ₁) and ψ₁(z ₁) = χ ^'₁ (z ₁) as follows [18]:

$$ 2G\left[u+\left(\frac{i}{\upgamma}\right)\upnu \right]={\upkappa \upvarphi}_1\left({z}_1\right)-{z}_1\overline{\upvarphi_1^{\hbox{'}}\left({z}_1\right)}-\overline{\uppsi_1\left({z}_1\right)}, $$

(6)

where

$$ \upkappa = \frac{3\sqrt{a_{22}/{a}_{11}}+{a}_{12}/{a}_{22}}{\sqrt{a_{22}/{a}_{11}-{a}_{12}/{a}_{22}}}. $$

For the plane stressed state, κ = (3γ² − ν _xy )/(γ² + ν _xy ).

It follows from equality (6) that

$$ \begin{array}{cc}\hfill 2G\frac{d}{d{t}_1}\left(u+\left(\frac{i}{\gamma}\right)v\right)=\kappa {\varPhi}_1\left({t}_1\right)-\overline{\varPhi_1\left({t}_1\right)}-\frac{d{\overline{t}}_1}{d{t}_1}\left({t}_1\overline{\varPhi_1^{\hbox{'}}\left({t}_1\right)}+\overline{\varPsi_1\left({t}_1\right)}\right),\hfill & \hfill {t}_1=x+i\gamma y\in {L}_1,\hfill \end{array} $$

(7)

where L ₁ is the contour in the auxiliary plane z₁ = x + iγy corresponding to a curvilinear contour L in the complex plane z = x + iy.

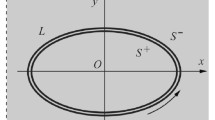
Let X _n and Y _n be the Cartesian components of the stress vector acting from the side of positive normal n on the curvilinear contour L (Fig. 1). They are connected with the normal and the tangential component of stresses N and T by the formula [19]

Fig. 1

Parabolic crack in a quasiorthotropic plane.

$$ {X}_n+i{Y}_n=-i\frac{dt}{ds}\left(N+ iT\right)=\frac{d}{ds}\left(\frac{\partial F}{\partial y}-i\frac{\partial F}{\partial x}\right), $$

(8)

where s is the arc abscissa on the contour L corresponding to a point t = x + iy ∈ L.

By using representations (5) and (8), we find

$$ \begin{array}{cc}\hfill \left(\left(\frac{i}{\gamma}\right){X}_n-{Y}_n\right)\frac{ds}{d{t}_1}={\varPhi}_1\left({t}_1\right)+\overline{\varPhi_1\left({t}_1\right)}+\frac{d{\overline{t}}_1}{d{t}_1}\left({t}_1\overline{\varPhi_1^{\hbox{'}}\left({t}_1\right)}+\overline{\varPsi_1\left({t}_1\right)}\right),\hfill & \hfill {t}_1\in {L}_1.\hfill \end{array} $$

(9)

Relations (7) and (9) enable us to reduce the basic problems of the theory of elasticity to the boundary-value problems of the theory of functions of a complex variable.

Integral Representations of Complex Potentials

We now find the solution of the auxiliary problem in the case where the stresses are continuous and the displacements are discontinuous on the open curvilinear contour L in the quasiorthotropic plane:

$$ \begin{array}{cc}\hfill {\left[\left(\frac{i}{\upgamma}\right){X}_n-{Y}_n\right]}^{+}-{\left[\left(\frac{i}{\upgamma}\right){X}_n-{Y}_n\right]}^{-}=0,\hfill & \hfill t\in L\hfill \end{array}, $$

(10)

$$ \begin{array}{cc}\hfill {\left[u+\left(\frac{i}{\gamma}\right)v\right]}^{+}-{\left[u+\left(\frac{i}{\gamma}\right)v\right]}^{-}=\frac{4i{\upgamma}^2}{E_x}g(t),\hfill & \hfill t\in L\hfill \end{array}, $$

(11)

and, at infinity, stresses and rotation are absent. Here, the superscripts “+” and “–” indicate the limit values of the corresponding values if z → t ∈ L, respectively, from the left (+) or from the right (–) relative to the chosen positive direction of tracing of the contour L (Fig. 1).

After differentiation, equality (11) takes the form

$$ \begin{array}{cc}\hfill \frac{d}{d{t}_1}\left[{\left(u+\left(\frac{i}{\upgamma}\right)v\right)}^{+}-{\left(u+\left(\frac{i}{\upgamma}\right)v\right)}^{-}\right]=\frac{4i{\upgamma}^2}{E_x}{g}_1^{\hbox{'}}\left({t}_1\right)\hfill & \hfill {t}_1=x+i\upgamma y\hfill \end{array}\in {L}_1, $$

(12)

where

$$ {g}_1\left({t}_1\right)=g(t). $$

Using relations (7), (9), (10), and (12), we arrive at the boundary-value problem

$$ \begin{array}{c}\hfill {\varPhi}_1^{+}\left({t}_1\right)-{\varPhi}_1^{-}\left({t}_1\right)=i{g}_1^{\hbox{'}}\left({t}_1\right),\hfill \\ {}\hfill \begin{array}{cc}\hfill {\left[\overline{t_1}{\varPhi}_1^{\hbox{'}}\left({t}_1\right)+{\varPsi}_1\left({t}_1\right)\right]}^{+}-{\left[\overline{t_1}{\varPhi}_1^{\hbox{'}}\left({t}_1\right)+{\varPsi}_1\left({t}_1\right)\right]}^{-}=i\left[\overline{g_1^{\hbox{'}}\left({t}_1\right)}-{g}_1^{\hbox{'}}\left({t}_1\right)\right]\frac{d{\overline{t}}_1}{d{t}_1}\hfill & \hfill {t}_1\in \hfill \end{array}{L}_1.\hfill \end{array} $$

The solution of this problem is known [20]

$$ \begin{array}{cc}\hfill {\varPhi}_1\left({z}_1\right)=\frac{1}{2\pi }{\displaystyle \underset{L_1}{\int}\frac{g_1^{\hbox{'}}\left({t}_1\right)d{t}_1}{t_1-{z}_1}},\hfill & \hfill {\varPsi}_1\left({z}_1\right)\hfill \end{array}=\frac{1}{2\pi }{\displaystyle \underset{L_1}{\int}\left[\frac{\overline{g_1^{\hbox{'}}\left({t}_1\right)}d{\overline{t}}_1}{t_1-{z}_1}-\frac{{\overline{t}}_1{g}_1^{\hbox{'}}\left({t}_1\right)d{t}_1}{{\left({t}_1-{z}_1\right)}^2}\right]}. $$

(13)

Relations (13) can be regarded as integral representations of the complex stress potentials Φ₁(z ₁) and Ψ₁(z ₁) via the derivative of the jump of the vector of displacements on the curvilinear contour L in the case where the stresses acting on the contour are continuous.

Integral Equation

By using the representation of complex potentials (13), we can consider various boundary-value plane problems for elastic quasiorthotropic bodies with holes and cracks [20]. Assume that the balanced stresses

$$ \begin{array}{ll}{N}^{+}+i{T}^{+}={N}^{-}+i{T}^{-}=p(t),\hfill & t\in L\hfill \end{array} $$

(14)

are given on the crack lips L (first basic problem) in the absence of stresses at infinity.

The boundary condition (14) can also be represented in the form

$$ \left[\left(\frac{i}{\upgamma}\right){X}_n^{\pm }-{Y}_n^{\pm}\right]\frac{ds}{d{t}_1}=\tilde{P}(t)={\tilde{P}}_1\left({t}_1\right)=\frac{1}{2\upgamma}\left[\left(1+\upgamma \right)p(t)-\left(1-\upgamma \right)\overline{p(t)}\frac{d\overline{t}}{dt}\right]\frac{dt}{d{t}_1}. $$

(15)

By using relation (9) and satisfying condition (14) with the help of potentials (13), we obtain the following singular integral equation for the unknown function g ^'₁ [9]:

$$ \frac{1}{\pi }{\displaystyle \underset{L_1}{\int}\left[{K}_1\left({\tau}_1,{t}_1\right){g}_1^{\hbox{'}}\left({\tau}_1\right)d{\tau}_1+{L}_1\left({\tau}_1,{t}_1\right)\overline{g_1^{\hbox{'}}\left({\tau}_1\right)}d\overline{\tau_1}\right]}={\tilde{P}}_1\left({t}_1\right), $$

(16)

where

$$ K{}_1\left({\tau}_1,{t}_1\right)=\frac{1}{2}\left[\frac{1}{\tau_1-{t}_1}+\frac{1}{{\overline{\tau}}_1-{\overline{t}}_1}\frac{d{\overline{t}}_1}{d{t}_1}\right],\kern1em {L}_1\left({\tau}_1,{t}_1\right)=\frac{1}{2}\left[\frac{1}{{\overline{\tau}}_1-{\overline{t}}_1}+\frac{1}{{\left({\overline{\tau}}_1-{\overline{t}}_1\right)}^2}\frac{d{\overline{t}}_1}{d{t}_1}\right]. $$

(17)

Note that the integral equation (16) agrees with the well-known equation for a degenerate anisotropic body [13] obtained by the limit transition from the general case of an anisotropic plane with curvilinear cracks.

Its solution must satisfy the following condition:

$$ {\displaystyle \underset{L_1}{\int }{g}_1^{\hbox{'}}}\left({t}_1\right)d{t}_1=0, $$

(18)

which guarantees the single-valuedness of displacements in traversing the contour of the crack L .

The complex stress potentials (13) and singular integral equation (16) also take place for a system of curvilinear cracks in the quasiorthotropic plane in the case where the symbol L denotes the collection of contours of the cracks but the auxiliary condition of single-valuedness of displacements (18) must be satisfied for each crack separately.

Distribution of Stresses Near the Crack Tip

The asymptotic distribution of stresses formed near the crack tip located on the x -axis in a two-dimensional quasiorthotropic body is described by the following dependences [7, 8]:

$$ \left\{\begin{array}{l}{\sigma}_x\simeq \frac{K_{\mathrm{I}}}{\sqrt{2\pi r}}\mathrm{R}\mathrm{e}\left[\frac{\upgamma^2\left(2\kern0.5em \cos \kern0.5em \uptheta \hbox{-} i\upgamma \kern0.5em \sin \kern0.5em \uptheta \right)}{2\kern0.5em {\left( \cos \kern0.5em \uptheta +i\upgamma \kern0.5em \sin \kern0.5em \uptheta \right)}^{3/2}}\right]-\frac{K_{\mathrm{I}\mathrm{I}}}{\sqrt{2\pi r}}\mathrm{R}\mathrm{e}\left[\frac{4i{\upgamma}^2\left(2\kern0.5em \cos \kern0.5em \uptheta \hbox{-} 3{\upgamma}^2\kern0.5em \sin \kern0.5em \uptheta \right)}{2\kern0.5em {\left( \cos \kern0.5em \uptheta +i\upgamma \kern0.5em \sin \kern0.5em \uptheta \right)}^{3/2}}\right],\hfill \\ {}{\sigma}_y\simeq \frac{K_{\mathrm{I}}}{\sqrt{2\pi r}}\mathrm{R}\mathrm{e}\left[\frac{2\kern0.5em \cos \kern0.5em \uptheta +3i\upgamma \kern0.5em \sin \kern0.5em \uptheta}{2\kern0.5em {\left( \cos \kern0.5em \uptheta +i\upgamma \kern0.5em \sin \kern0.5em \uptheta \right)}^{3/2}}\right]-\frac{K_{\mathrm{I}\mathrm{I}}}{\sqrt{2\pi r}}\mathrm{R}\mathrm{e}\left[\frac{\kern0.5em \sin \kern0.5em \uptheta}{2\kern0.5em {\left( \cos \kern0.5em \uptheta +i\upgamma \kern0.5em \sin \kern0.5em \uptheta \right)}^{3/2}}\right],\hfill \\ {}{\tau}_{xy}\simeq \frac{K_{\mathrm{I}}}{\sqrt{2\pi r}}\mathrm{R}\mathrm{e}\left[\frac{\upgamma^2\kern0.5em \sin \kern0.5em \uptheta}{2\kern0.5em {\left( \cos \kern0.5em \uptheta +i\upgamma \kern0.5em \sin \kern0.5em \uptheta \right)}^{3/2}}\right]-\frac{K_{\mathrm{I}\mathrm{I}}}{\sqrt{2\pi r}}\mathrm{R}\mathrm{e}\left[\frac{2\ \cos \kern0.5em \uptheta +i\upgamma \kern0.5em \sin \kern0.5em \uptheta}{2\kern0.5em {\left( \cos \kern0.5em \uptheta +i\upgamma \kern0.5em \sin \kern0.5em \uptheta \right)}^{3/2}}\right],\hfill \end{array}\right. $$

(19)

where K _I and K _II are the SIF at the crack tip, r is the distance from the crack tip, and θ is the angle measured from the crack line. Hence, we get the following formulas for the determination of the SIF via the stresses acting on the continuation of the crack:

$$ {K}_{\mathrm{I}}-i{K}_{\mathrm{I}\mathrm{I}}{=}_{r\to 0}^{\lim}\sqrt{2\pi r}\left[{\sigma}_y\left(r,0\right)-i{\tau}_{xy}\left(r,0\right)\right]. $$

(20)

Relations (19) and (20) hold for an arbitrarily oriented crack and, in particular, for a curvilinear crack if x , y and r , θ are local Cartesian and polar coordinates connected with the direction of tangent at the crack tip and with the crack tip itself.

By using the corresponding results obtained for an anisotropic body containing a curvilinear crack [7], we get the following expressions for the SIF in a quasiorthotropic body both at the beginning ((K ⁻_I , K ⁻_II )

and at the end (K ⁺_I , K ⁺_II ) of the crack as a result of the solution of the singular integral equation:

$$ \begin{array}{c}\hfill {K}_{\mathrm{I}}^{\pm }=\pm \sqrt{\pi}\mathrm{I}\mathrm{m}\frac{u_1\left(\pm 1\right)\overline{\omega_1^{\hbox{'}}}\left(\pm 1\right)}{i\left|\omega \hbox{'}\left(\pm 1\right)\right|\sqrt{\left|\omega \hbox{'}\left(\pm 1\right)\right|}},\hfill \\ {}\hfill {K}_{\mathrm{I}\mathrm{I}}^{\pm }+\pm \sqrt{\pi}\mathrm{R}\mathrm{e}\frac{u_1\left(\pm 1\right)\left[\left(1+\upgamma \right)\overline{\omega \hbox{'}}\left(\pm 1\right)-\left(1-\upgamma \right)\omega \hbox{'}\left(\pm 1\right)\right]}{2i\left|\omega \hbox{'}\left(\pm 1\right)\right|\sqrt{\left|\omega \hbox{'}\left(\pm 1\right)\right|}}\hfill \end{array} $$

(21)

where

$$ \begin{array}{c}\hfill {t}_1={\omega}_1\left(\xi \right)=x\left(\xi \right)+i\upgamma y\left(\xi \right);\kern1em t=\omega \left(\xi \right)=x\left(\xi \right)+iy\left(\xi \right),\kern1em -1\le \xi \le 1;\hfill \\ {}\hfill \frac{u_1\left(\xi \right)}{\sqrt{1-{\xi}^2}}={g}_1^{\hbox{'}}\left({t}_1\right){\omega}_1^{\hbox{'}}\left(\xi \right).\hfill \end{array} $$

The quantities u ₁ (±1) are found from the solution of the integral equation (16) [20].

Rectilinear Crack of Arbitrary Orientation in the Quasiorthotropic Plane

In the quasiorthotropic plane, we consider a rectilinear crack L of length 2l inclined at an angle α to the x -axis whose lips are subjected to the action of given self-balanced stresses

$$ {N}^{+}+i{T}^{+}={N}^{-}+i{T}^{-}=p(t),\kern1em t\in L. $$

Moreover, the stresses and rotation are absent at infinity. We also assume that the crack lips are not in contact.

We represent the parametric equations of the contours L and L ₁ in the form

$$ \begin{array}{cccc}\hfill \tau =\upomega \left(\xi \right)=\xi l{e}^{ia},\hfill & \hfill t=\upomega \left(\eta \right),\hfill & \hfill {\tau}_1\hfill & \hfill {\upomega}_1\left(\xi \right)=\frac{\xi l\varGamma }{2}\hfill \end{array},\kern1em {t}_1={\upomega}_1\left(\eta \right), $$

where

$$ \varGamma =\left(1+\upgamma \right){e}^{ia}+\left(1-\upgamma \right){e}^{-ia},\xi, \eta \in \left[-1;1\right]. $$

Then the kernels (17) and the right-hand side of Eq. (16) have the form

$$ \begin{array}{ccc}\hfill {K}_1\left(\xi, \eta \right)=\frac{2}{\left(\xi, \eta \right)/\varGamma },\hfill & \hfill {L}_1\left(\xi, \eta \right)=0,\hfill & \hfill \tilde{P_1}\left(\eta \right)\hfill \end{array}=\frac{1}{\upgamma \varGamma }{\widehat{P}}_1\left(\eta \right), $$

where

$$ {\widehat{P}}_1\left(\eta \right)=\left(1+\eta \right)=p\left(\eta \right)-\left(1-\upgamma \right)\overline{p\left(\eta \right)}e{-}^{2ia}. $$

We represent the integral equation of the problem in the dimensionless form

$$ \begin{array}{cc}\hfill \frac{1}{\pi }{\displaystyle \underset{-1}{\overset{1}{\int }}\frac{u_1\left(\xi \right)d\xi }{\sqrt{1-{\xi}^2\left(\xi -\eta \right)}}}=\frac{1}{2\gamma}\widehat{P_1}\left(\eta \right),\hfill & \hfill -1\le \eta \le \hfill \end{array}1. $$

The solution of this equation under condition (18) is given by the following formulas (see, e.g., [20]):

$$ \begin{array}{cc}\hfill {u}_1\left(\xi \right)=\frac{1}{2\upgamma \pi },\hfill & \hfill {u}_1\left(\pm 1\right)=\pm \hfill \end{array}\frac{1}{2\upgamma \pi }{\displaystyle \underset{-1}{\overset{1}{\int }}\frac{\sqrt{1\pm \upeta}}{\sqrt{1\mp \upeta}}}\widehat{P_1}\left(\upeta \right)d\upeta . $$

In view of expressions (21), we get the SIF in the form

$$ {K}_{\mathrm{I}}^{\pm }-i{K}_{\mathrm{I}\mathrm{I}}^{\pm }=-2\sqrt{\frac{l}{\pi }}\mathrm{R}\mathrm{e}{\displaystyle \underset{-1}{\overset{1}{\int }}\frac{\sqrt{1\pm \upeta}}{\sqrt{1\mp \upeta}}}p\left(\upeta \right)d\upeta . $$

If the crack lips are loaded by constant normal (σ) and tangential (τ) stresses ( p(η) = -σ-iτ = const),

then we get

$$ {K}_{\mathrm{I}}^{\pm }-i{K}_{\mathrm{I}\mathrm{I}}^{\pm }=2\sqrt{\pi l}\left(\sigma -i\tau \right). $$

If the infinite plane containing a crack free of loads is subjected to tension by external stresses σ ^∞ _y  = p and σ ^∞ _x  = q at infinity, then we can write

$$ {K}_{\mathrm{I}}^{\pm }-i{K}_{\mathrm{I}\mathrm{I}}^{\pm }=\sqrt{\pi l}\left(p+q-\left(p-q\right)e{2}^{ia}\right). $$

Thus, the SIF formed at the tip of an arbitrarily oriented crack in the quasiorthotropic body in the case where self-balanced loads are applied to the crack lips are identical to the SIF in the isotropic body, although the stresses formed on the continuation of the crack are different.

Crack Along the Parabolic Arc

Consider a plane problem of the theory of elasticity for a quasiorthotropic plane weakened by an arbitrarily located parabolic crack. The parametric equation of the contour L of this crack has the form

$$ \begin{array}{cc}\hfill t=\upomega \left(\xi \right)=l\left[\xi +i\varepsilon \left({\xi}^2-1\right)\right]{e}^{ia},\hfill & \hfill -1\le \xi \le 1,\hfill \\ {}\hfill t={\upomega}_1\left(\xi \right)=\frac{1}{2}\left[\left(\xi +i\varepsilon \left({\xi}^2-1\right)\right)\left(1+\upgamma \right){e}^{ia}+\left(\xi +i\varepsilon \left({\xi}^2-1\right)\right)\left(1-\upgamma \right){e}^{-ia}\right],\hfill & \hfill -1\le \xi \le 1,\hfill \end{array} $$

where ε =δ/l is the relative deflection of the crack and α is the angle of its orientation (Fig. 1).

The numerical solution of the integral equation (16) was obtained by the quadrature methods [20] in the case where the crack lips are free of loads and the stresses σ ^∞ _y  = p and σ ^∞ _x  = p are given at infinity.

We compared the relative SIF ${F}_{\mathrm{I}}={K}_{\mathrm{I}}^{+}/p\sqrt{\pi l}$ and ${F}_{\mathrm{II}}={K}_{\mathrm{II}}^{+}/p\sqrt{\pi l}$in the case where the angle α = 0 and the stresses q = p for the quasiorthotropic and orthotropic materials with the same ratio of the moduli of elasticity (see Table 1).

Table 1 Values of the Relative SIF F _I and F _II at the Tips of Parabolic Cracks in the Quasiorthotropic (Numerator) and Orthotropic (Denominator) Planes

The numerical results are presented for the following orthotropic materials: CF2 glass-reinforced plastic (E _x = 15, Ey = 232, Gxy = 5.02, v _xy = 0.28, and v _yx = 0.0181), Lu-1 carbon-reinforced plastic (Ex = 96, E _y = 10.8, G _xy = 2.61, and v _xy = 0.21), and EF carbon-reinforced plastic (E _x = 32.8, E _y = 21, G _xy = 5.7, and v _xy = 0.21) [5].

The obtained relative values of the SIF for the quasiorthotropic plane are close to the values obtained for the orthotropic body for equal ratios of the moduli of elasticity of these materials. Earlier, by comparing the powers of singularities of stresses at the vertices of orthotropic and quasiorthotropic wedges, the authors of [21] made a conclusion that the ratio of the moduli of elasticity is the main mechanical parameter of the orthotropic materials. This justifies the term “quasiorthotropic material” accepted in the present work.

We computed the relative SIF F _I and F _II for the arbitrarily oriented parabolic crack in the quasiorthotropic plane subjected to uniaxial tension at infinity (q = 0) for different values of the orthotropy parameter γ (Fig. 2). The dashed line describes the SIF for the isotropic material (γ = 1).

Fig. 2

Dependences of the relative SIF F _I (a, c) and F _II (b, d) for a parabolic crack with relative deflection ε = 0.25 (a, b) and 2.0 (c, d) on the angle α for different values of the parameter of orthotropy γ .

In the quasiorthotropic body, the SIF at the tip of an arbitrarily oriented rectilinear crack under the action of self-balanced load on its lips are identical to the SIF in the isotropic body, although the stresses formed on the continuation of the crack are different.

Conclusions

We deduce the basic relations of the plane problem of the theory of elasticity for a quasiorthotropic body. The first basic problem for a plane with cracks is reduced to singular integral equations. The asymptotic distribution of stresses near the crack tip is presented. We establish the analytic expressions for the SIF at the tip of an arbitrarily oriented rectilinear crack in the quasiorthotropic body. We compute the SIF for a curvilinear crack along the parabola for different values of the parameter of orthotropy and compare their values with the values of SIF obtained for the orthotropic body with the same ratio of the moduli of elasticity. The difference between the obtained results is insignificant, which means that the ratio of the moduli of elasticity in the orthotropic material is the main mechanical parameter. In the quasiorthotropic plane, the SIF at the tip of an arbitrarily oriented crack are the same as in the isotropic plane. At the tip of the curvilinear crack, the value of the SIF depends on the orthotropy parameter and this dependence becomes stronger as the deviation of the crack contour from the rectilinear contour becomes more pronounced.

The present work was performed within the framework of the Project No. 2011/03/B/ST8/06456 financed by the National Science Center (Poland).