1 Introduction

Mechanical structures are commonly an assembly composed of several components for achieving the required functions, which will make the contact inevitable in practical applications. The guarantee of high-performance contact behavior plays a vital role in ensuring the realization of the specified functions of the mechanical structures. Among others, the magnitude and distribution of the contact stress are two factors strongly influencing the performance of the involved structures (Chen et al. 2019; Collins JA 2010). For example, the magnitude of the contact stress along the contact interface determines the leakproofness reliability of a contact seal (Zhang and Niu 2018). Besides, the fatigue resistance is deeply affected by the contact stress distribution (Nakazawa et al. 2003). As the attainment of a uniform contact stress distribution is beneficial for the wear reduction and the prolongation of the fatigue life, numerous efforts have been devoted to optimizing the contact stress distribution.

Three pioneers, Klarbring, Strömberg and Hilding have supplied the basis for the applications of size, shape and topology optimization to the class of contact problems throughout the years (Hilding and Klarbring 2012; Hilding et al. 1999; Klarbring 1992; Strömberg and Klarbring 2009). Methods based on the mathematical programming methods (Conry and Seireg 1971; Haug and Kwak 1978), heuristic-based approaches (Li et al. 2003; Ou et al. 2013) and sensitivity analysis method (Hilding et al. 2001) were adopted for contact shape design. As for contact topology design, the traditional SIMP (Solid Isotropic Material with Penalization) model-based density method (Jeong et al. 2018; Niu et al. 2019, 2020; Strömberg and Klarbring 2009) and the emerging level set method (Lawry and Maute 2018, 2015; Myslinski 2008, 2015) and phase field method (Myśliński and Wróblewski 2017) have been extended to include the contact conditions. Recently, Kristiansen et al. (Kristiansen et al. 2020) performed a density-based topology optimization of contact problems for controlling the contact pressure distribution by proposing and utilizing a p-norm based objective function. Fernandez et al. (Fernandez et al. 2020) presented a topology optimization of multiple deformable three-dimensional bodies in contact with large deformations and maximized the total contact forces.

Considering that the multiple load cases exist widely in mechanical systems and are a very common phenomenon in practical engineering, many scholars have extended the optimization to the problem of bearing multiple load cases. Topology optimization dominates the literatures in problems with multiple load cases until now. Several methods including homogenization algorithm (Bendsøe et al. 1995), evolutionary topology optimization method (Young et al. 1999), material replacement method (Cai et al. 2013), meshless smoothed particle hydrodynamics (SPH) method (Li et al. 2020) have been proposed and applied to the topology optimization of the structures subjected to multiple load cases.

However, when it comes to the optimization problems under multiple loading conditions, relatively few publications involve the existence of contact. A few early papers addressed the optimization problem of minimizing the potential energies with introducing the multiple unilateral contact conditions (Ben-Tal et al. 2000; Kočvara et al. 1998). Another work worth mentioning is the work of Li et al. (Li et al. 2005), in which an evolutionary shape optimization algorithm was introduced to optimize the contact structures subjected to multiple load cases. This work defines the uniformity of the contact stress under multiple load cases as the objective function, through which the contact stress distribution could be reflected directly. It differs from many other works related with multiple load cases, because the objective functions considered in those works are in an indirect relation with the contact stress distribution such as the compliance, potential energies, etc.

With the development of the material science and inspired by the emerging engineered materials such as functionally graded materials, 3D printed materials and fiber-reinforced cement-based composites, materials with inhomogeneous properties, such as the Young’s modulus, have begun to attract designers’ attention. Researches showed that an appropriate inhomogeneous Young’s modulus distribution could do favors to stress concentration reduction (Goyat et al. 2018, 2019) and compliance minimization (Czarnecki and Lewiński 2017a, 2014), and the optimal Young’s modulus distribution has also been extended to consider multiple loading conditions (Czarnecki and Lewiński 2017b; Smyl 2018).

Nevertheless, there was no contact condition involved in those works, while this study focuses on the optimization design of the material stiffness in the considered elastic contact problems. Moreover, compared with the shape or topology optimization, little progress has been made towards the material stiffness optimization despite its significant influences on the contact stress distribution (Johnson 1987).

Regarding now the material stiffness optimization with contact condition and multiple loading conditions, to the authors’ best knowledge, literature focusing on the optimization of material stiffness in the frictional contact problems subjected to multiple load cases is scarce. In those work from the aforementioned literatures where contact conditions or multiple loading conditions are introduced, the optimization either refers to the shape or the topology of the structures. On the other hand, cases considering the Young’s modulus design or the material stiffness design are involved with no contact. In this paper, we consider the material stiffness design, where both the contact conditions and multiple loading conditions are involved. We proposed a heuristic-based material stiffness optimization algorithm, and extended it to the frictional contact problems with multiple load cases, where different objective function and different design criterion were proposed.

The aim of this paper was to realize the material stiffness optimization for attaining a uniform contact stress distribution in the frictional elastic contact problems subjected to multiple load cases, as illustrated in Fig. 1. Each of the multiple loads is independent and all loads are applied on the structure non-simultaneously. Thus, in a certain sense, an optimum compromise of these multiple loads is perused in this work. Building upon the existing literatures, the weighted objective function (Diaz and Bendsøe 1992; Li et al. 2005; Marler and Arora 2009) and the worst case design criterion (Li et al. 2005) are adopted.

Fig. 1
figure 1

Illustration of the material stiffness optimization of a two-body contact problem subjected to two load cases for the contact stress distribution

Full size image

The rest of this paper is organized as follows. Section 2 simply describes the frictional elastic contact problems subjected to multiple load cases. Section 3 focuses on the weighting criterion for the objective function with multiple load cases, and the individual criterion for the contact system with multiple contact regions is also addressed. Section 4 details the material stiffness optimization design algorithm. In Sect. 5, we present three contact problems subjected to multiple load cases, where multiple contact regions are considered in the third contact problem, to demonstrate the feasibility and effectiveness of the proposed material stiffness optimization under multiple load cases. Finally, Sect. 6 summarizes all the substantial findings.

2 Frictional elastic contact problems with multiple load cases

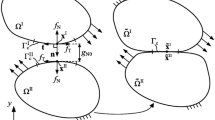
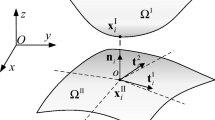
Without loss of generality, a frictional linear elastic contact problem is illustrated in Fig. 2. Domains \(\Omega^{I}\) and \(\Omega^{II}\) are two contact bodies and \(\Gamma_{c}\) is the real contact region. \({\text{F}}_{1}\) and \({\text{F}}_{2}\) are two loads that act independently at different time. We used finite element analysis (FEM) to solve the contact problem. Figure 3 depicts the finite element form of the contact problem, which is discretized with the quadrilateral elements. The pairs of boundary nodes \(i^{{\text{I}}}\) and \(i^{{{\text{II}}}}\) \((i = 1,2, \ldots ,n_{{\text{p}}} )\) are the points where contact may occur during the contact process with \(n_{{\text{p}}}\) being the number of the potential contact node pairs. Once the contact status of these defined contact nodes are classified, the contact stresses existing in these contact nodes under each load cases are obtained by a non-linear finite element analysis.

Fig. 2
figure 2

Frictional elastic contact problem between two bodies

Full size image
Fig. 3
figure 3

Finite element form of the contact problem at undeformed condition

Full size image

3 Weighting criterion of objective function with multiple load cases

In a system with multiple load cases, though it is highly desirable that the design would be suitable for all the load cases under the prescribed criteria, it is often extremely difficult to realize. Thus, compromises of these multiple loads are made.

Consider that P different load cases Fj \((j = 1,2, \ldots ,P)\) are applied to the contact system. Each will produce a different contact stress distribution \(\sigma ({\text{F}}_{j} )\). The corresponding variance of the contact stress is \(\delta_{j}\), which is a measure to the uniformity of the contact stress distribution \(\sigma ({\text{F}}_{j} )\). Regarding that different load cases may lead to totally different values of the variance, the decrease level of the variance of the contact stress is introduced and defined as

$$ g_{j} (\Gamma ) = \frac{{\delta_{j}^{0} - \delta_{j} }}{{\delta_{j}^{0} }}, $$
(1)

where \(g_{j} (\Gamma )\) is the decrease level of the variance for contact region \(\Gamma\) at jth load case; \(\delta_{j}^{0}\) and \(\delta_{j}\) stand for the variance before and after the optimization respectively.

Owing to its conceptual simplicity and numerical efficiency, a commonly used weighted function (Diaz and Bendsøe 1992; Li et al. 2005; Marler and Arora 2009) on each load case is adopted. It is assumed that the weight coefficient corresponding to jth load is wj, and is defined in a constrained form of

$$ \sum\limits_{j} {w_{j} = 1} , \, w_{j} \ge 0. $$
(2)

A weighted sum of the decrease levels under all load cases is constructed as the objective function, which can be given as

$$ f\left( {\Gamma } \right) = \sum\limits_{j} {w_{j} g_{j} (\Gamma )} . $$
(3)

With the purpose of achieving a uniform contact stress distribution and from the definition of the objective function in Eq. (3), we pursue maximizing the value of the objective function in the following work.

For systems consisting of \(m \, (m \ge 2)\) contact regions as \(\Gamma { = } \cup_{r} \Gamma_{r}\) \((r = 1,2, \ldots ,m)\), a multi-criteria optimization form can be formulated as

$$ \begin{gathered} \max \, f\left( {{\Gamma }_{1} } \right) = \max \, \sum\limits_{j} {w_{j} g_{j} (\Gamma_{1} )} , \hfill \\ \, \vdots \hfill \\ \max \, f\left( {{\Gamma }_{r} } \right) = \max \, \sum\limits_{j} {w_{j} g_{j} (\Gamma_{r} )} , \hfill \\ \, \vdots \hfill \\ \max \, f\left( {{\Gamma }_{m} } \right) = \max \, \sum\limits_{j} {w_{j} g_{j} (\Gamma_{m} )} , \hfill \\ \end{gathered} $$
(4)

which means each contact region is optimized individually. This so-called individual criteria, which shows good capabilities in homogenizing the contact stress field in contact shape optimization (Li et al. 2003), is adopted.

4 Material stiffness optimization design algorithm

Owing to the merits of ease in implementation and free from gradient information, the heuristic-based design approach has been successfully applied to the contact shape design problems (Li et al. 2005, 2003; Ou et al. 2013). Here, for material stiffness optimization design, the modifications of the Young’s modulus are based on the relative differences of the contact stress at different positions. According to the contact stress distribution of the design domain, the changes of the Young’s modulus can be expressed as a function \(f_{n} ( \cdot )\) as

$$ \Delta (\Phi_{t} ) = E(\Phi_{t} ) \times [f_{n} (\tilde{\sigma }(\Phi_{t} )) - 1], \, t = 1,2, \ldots ,N, $$
(5)

where \(\Phi_{t}\) is the sub design domain to be modified, \(\Delta (\Phi_{t} )\) the current Young’s modulus modification of sub design domain \(\Phi_{t}\), \(E(\Phi_{t} )\) the current Young’s modulus of domain \(\Phi_{t}\), \(\tilde{\sigma }(\Phi_{t} )\) the equivalent contact stress of domain \(\Phi_{t}\).

As shown in Fig. 4, the calculation of equivalent contact stress \(\tilde{\sigma }(\Phi_{t} )\) is the same as that in literature (Zhou et al. 2020) and is also presented here as

$$ \tilde{\sigma }(\Phi_{t} ) = \frac{1}{{n \, _{{\Phi_{t} }} }}\sum\limits_{{i \in \Phi_{t} }} {\sigma^{i} } , $$
(6)
Fig. 4
figure 4

Calculation of the equivalent contact stress of each sub design domain

Full size image

Considering the multiple loading conditions, we take the worst case design (Ben-Tal et al. 2000; Li et al. 2005). A stress \(\tilde{\sigma }_{ref}^{t}\) named extreme reference stress is introduced, which is defined as the highest stress level of subdomain \(\Phi_{t} \, (t = 1,2, \ldots ,N)\) among \(P\) load cases. This could be expressed as

$$ \tilde{\sigma }_{ref}^{t} { = }\mathop {\text{max }}\limits_{j} [\tilde{\sigma }_{1} (\Phi_{t} ),\tilde{\sigma }_{2} (\Phi_{t} ), \ldots ,\tilde{\sigma }_{j} (\Phi_{t} ), \ldots ,\tilde{\sigma }_{P} (\Phi_{t} )], $$
(7)

in which \(\tilde{\sigma }_{j} (\Phi_{t} )\) denotes the equivalent contact stress of subdomain \(\Phi_{t}\) under jth load case.

A relative stress level factor reflecting the ratio of the maximum stress and extreme reference stress of the subdomain to be modified is introduced. And Eq. 5 is re-expressed as

$$ \Delta (\Phi_{t} ) = E(\Phi_{t} ) \times (f_{n} \left( {\frac{{\tilde{\sigma }_{\max }^{t} }}{{\tilde{\sigma }_{ref}^{t} }}} \right) - 1), $$
(8)

where \(\tilde{\sigma }_{\max }^{t}\) is the maximal one among N extreme reference stresses and is calculated by

$$ \tilde{\sigma }_{\max }^{t} {\text{ = max }}[\tilde{\sigma }_{ref}^{1} ,\tilde{\sigma }_{ref}^{2} , \ldots ,\tilde{\sigma }_{ref}^{t} , \ldots ,\tilde{\sigma }_{ref}^{N} ]. $$
(9)

It is worth pointing out that different stress levels used in Eq. 8 may lead to different optimized results. There are other stress levels we could use, i.e. the weighted reference stress (Li et al. 2005), which is calculated by averaging the contact stresses under each load case instead of taking the maximum equivalent contact stress as this work dose.

For simplicity, the modification process is adjusted by a power law function with a constant coefficient STI as

$$ \Delta (\Phi_{t} ) = E(\Phi_{t} ) \times (STI \times \left( {\frac{{\tilde{\sigma }_{\max }^{t} }}{{\tilde{\sigma }_{ref}^{t} }}} \right)^{\gamma } - 1) $$
(10)

which is of a similar form of the typical evolutionary shape optimization procedure (Li et al. 2005, 2003).

A upper Young’s modulus limit Emax and a lower Young’s modulus limit Emin are defined, and the value of Young’s modulus (i.e., design variable) will be replaced by the limit value once it goes beyond the given range of variation. A convergence tolerance \(\rho\) is designated to check the convergence condition as

$$ \left| {\frac{{f\left( {\Gamma } \right)^{k} - f\left( {\Gamma } \right)^{{k{ - }1}} }}{{f\left( {\Gamma } \right)^{{k{ - }1}} }}} \right| \le \rho , $$
(11)

where subscript k stands for the number of iterations of the optimization process, and \(f\left( {\Gamma } \right)^{k}\) is the objective function at kth iteration.

Figure 5 outlines the material stiffness optimization procedure, which mainly consists of the following four steps.

Fig. 5
figure 5

Flowchart of the material stiffness optimization procedure

Full size image

Step 1 Set up models. Create the geometrical and finite element model, and set initial values for the optimization driven parameters.

Step 2 Carry out contact analysis. Perform finite element analysis for individual load cases. Then calculate the extreme reference stress \(\tilde{\sigma }_{ref}^{t}\) and the maximum value \(\tilde{\sigma }_{\max }^{t}\) according to Eqs. 6, 7 and 9.

Step 3 Check convergence condition. Compute objective function \(f\left( {\Gamma } \right)\) as Eq. 3. For a system with multiple contact regions, calculate objective functions \(f\left( {{\Gamma }_{r} } \right)\) for each contact region with the same manner. If the convergence condition is satisfied, terminate the iteration and output the results of the optimization. Otherwise, go to Step 4.

Step 4 Update models. Calculate the new values of design variable for subdomain \(\Phi_{t}\), and update the models with these new values. Regarding that none of the geometrical situations are changed, no remeshes are needed. Set \(k = k + 1\) and go back to Step 3.

5 Numerical examples

To demonstrate how the proposed material stiffness optimization influences the contact stress distribution in contact problems subjected to multiple load cases, three numerical examples are investigated here. The validation of the numerical simulation has been conducted in published literature (Zhou et al. 2020). Single contact region is considered in the first two examples and the system with multiple contact regions is addressed in the third example.

Plane stress state is adopted for all these three examples, and the model has a Young’s modulus of 200 GPa and a friction coefficient of 0.1. The upper Young’s modulus limit Emax and the lower Young’s modulus limit Emin are set as 300 GPa and 0.2 GPa respectively. Power law index \(\gamma\) is set as 1/2 for all following examples.

5.1 Elastic-to-rigid contact problem

An elastic-to-rigid contact model subjected to two symmetrically applied load cases is presented in Fig. 6. The deep gray area at the bottom represents a rigid body, the cyan area is an elastic body of 10 mm height, and the purple area denotes a 2 mm height design domain. The orange solid line denotes the contact region. The bottom of the rigid body is fully fixed and the left and right sides are constrained in the X-direction. The elastic body is discretized with 120 × 40 quadrilateral elements, and 121 contact node pairs exist at the contact interface. The coefficient STI is given as 0.95 and the convergence tolerance \(\rho\) is set as 0.1%.

Fig. 6
figure 6

The elastic-to-rigid contact model

Full size image

Considering the symmetry of these two loads, the decrease levels of the variance of the contact stress for these two load cases during the optimization process are always consistent. Thus, whatever the allocation scheme of the weight coefficients of these two loads is, the convergence condition will not be affected.

The contact stress distributions under two load cases are presented in Figs. 7 and 8. Compared with the contact stress distribution before the optimization as shown in Figs. 7a and 8a, a significant improvement on the uniformity of the contact stress, which is a decrease of 99.18% on the variance of the extreme reference stress specifically, can be observed in Figs. 7b and 8b.

Fig. 7
figure 7

Contact stress distributions under load case 1 (LC1)

Full size image
Fig. 8
figure 8

Contact stress distribution under load case 2 (LC2)

Full size image

Similar to the optimized contact stress distribution after the shape optimization (Li et al. 2005), one can notice that after optimization, the lower stress level of the contact stress distribution under each load case is noticeably non-uniform even after the optimization, as can be seen in Figs. 7b and 8b. This is due to worst case design we adopted in this paper, in which the defined extreme reference stress is utilized in the optimization process.

The iteration histories of the objective function plotted in Fig. 9 shows a steady and continuous increase trend, requiring 76 iterations until convergence. Moreover, the evolutions of the variance of the contact stress and the maximum stress under each load cases, as depicted in Fig. 10(a) and 10(b), once again, illustrate the feasibility and stability of the proposed material stiffness optimization design under multiple load cases.

Fig. 9
figure 9

Iteration histories of the objective function

Full size image
Fig. 10
figure 10

Iteration histories of the variance and the maximum stress under two load cases

Full size image

Furthermore, the evolution histories of the Young’s modulus of the elastic structure are presented in Fig. 11. The Young’s modulus of the design domain are symmetrically distributed and range from 21.8 GPa to 182.3 GPa for the final optimized result. It is interesting to notice that, as the optimization proceeds, the areas near the locations of the load are inclined to possess a smaller Young’s modulus and vice versa. This result may relate with the energy distributions and needs further investigations.

Fig. 11
figure 11

Young’s modulus distribution at different iterations

Full size image

5.2 Elastic-to-elastic contact problem

The contact problem between two elastic bodies is studied in this example. As shown in Fig. 12, a concentrated load case and a distributed load case are applied on the top edge of the upper elastic body. Here, the design domain represented by the purple area is divided into an upper design domain and a lower design domain, which are of 1 mm height both, by the solid orange line representing contact region. The entire model is meshed with 160 × 80 quadrilateral elements, and 161 contact node pairs exist at the contact interface. STI is set as 0.95 and \(\rho\) is set as 0.05%.

Fig. 12
figure 12

The elastic-to-elastic contact model

Full size image

Different from the previous elastic-to-rigid contact problem, these two load cases are asymmetrical, which means the different allocations of the weight coefficients may lead to different results. Five allocation schemes of the weight coefficients are investigated and their influences on the iteration histories of the objective function are shown in Fig. 13.

Fig. 13
figure 13

Influences of five different allocation schemes on the iteration histories of the objective function

Full size image

One can notice that all five iteration curves follow a similar pattern and the change trend of the objective function is consistent. This indicates that the general convergence trend will not be affected by the different allocations of the weight coefficients in this example. Thus, an even allocation of \(w_{1} = w_{2} = 0.5\) is selected to illustrate the optimization effects.

Figures 14(a) and (b) illustrate the contact stress distributions under each load cases before and after optimization. Obviously, the peak contact stress is reduced remarkably and the contact stress field becomes much more uniform for both two load cases. The variance of the contact stress has decreased by 99.73% under load case 1 and 98.82% under load case 2. Moreover, the uniformity of the extreme reference stress is improved considerably too, as shown in Fig. 14(c).

Fig. 14
figure 14

Contact stress distributions before and after optimization

Full size image

Figure 15 depicts the contact stress distribution of the extreme reference stress, the stress under LC1 and the stress under LC2 before and after optimization. In the initial stress distribution, as shown in Fig. 15(a), the extreme reference stress is a partial combination of the stress under load case 1 and the stress under load case 2. After optimization, the distribution of the extreme reference stress is consistent with that of the contact stress under load case 2, as shown in Fig. 15(b). This could due to the state of the initial contact stress distribution under these two load cases, as the initial stress under load case 1 occupies only a small part of the left of the extreme reference stress and is more relatively evenly distributed than the stress under load case 2. Moreover, from the iteration histories of the variance and the maximum stress as presented in Fig. 16a, b respectively, one can notice that the stress under load case 1, which holds all along a larger variance and a larger maximum stress during the optimization process, exhibits a ‘worse’ distribution. In other words, load case 1 owes stronger relations with the most critical load case than that of load case 2 in this example. Thus the final extreme reference stress distribution is more inclined to the stress distribution under load case 1, even consistent with that as shown in Fig. 15(b). The results obtained here are optimal only in a sense of worst case design.

Fig. 15
figure 15

Comparison of the contact stress distribution among the extreme reference stress, the stress under LC1 and the stress under LC2

Full size image
Fig. 16
figure 16

Iteration histories of the variance and the maximum stress under two load cases

Full size image

The intermediate results of the Young’s modulus distribution are presented in Fig. 17. Obviously, no symmetries of the Young’s modulus distribution appear. As the iteration process proceeds, the areas with various Young’s modulus are enlarged gradually with a more and more gentle enlarging tendency. Still, areas far from the load locations tend to have a larger Young’s modulus. The final Young’s modulus of the design domain range from 0.24 to 295 GPa, which implies that the material stiffness is diversely distributed in a large range. This unique Young’s modulus distribution is favorable for a uniform contact stress distribution.

Fig. 17
figure 17

Young’s modulus distribution at different iterations

Full size image

5.3 A contact problem of three contact bodies

A contact problem of two elastic bodies and one rigid body is presented in Fig. 18. Different from the previous two examples, two contact regions are considered. Here, as described in Eq. 4, each contact region is optimized individually. Thus, two design domains named upper design domain and lower design domain are defined. Both design domains are of 2 mm height and are on the middle elastic body, as shown in Fig. 18. A concentrated load case and a distributed load case are applied on the top edge of the upper elastic body. These two elastic bodies are meshed with 120 × 80 quadrilateral elements, and there are 121 contact node pairs on the contact interface. STI is given as 0.85 and \(\rho\) is given as 1%. \(w_{1} = w_{2} = 0.5\) is adopted.

Fig. 18
figure 18

A contact problem of three contact bodies

Full size image

Figures 19 and 20 are the contact stress distributions before and after optimization for the upper contact region and the lower contact region respectively. Tables 1 and 2 summarize the optimization results. Before the optimization, as shown in Figs. 19a and 20a, two contact regions have a similar form of the distributions of the contact stress but with different magnitudes. After the optimization, the distributions of the contact stress are much more uniform for both two contact regions, as shown in Figs. 19b and 20b.

Fig. 19
figure 19

Contact stress distributions of the upper contact region

Full size image
Fig. 20
figure 20

Contact stress distributions of the lower contact region

Full size image
Table 1 Results before and after optimization for the upper contact region
Full size table
Table 2 Results before and after optimization for the lower contact region
Full size table

The convergence histories for both design domains are plotted in Fig. 21(a) and no oscillations appear. We find that the convergence rate for the lower contact region is faster than that of the upper contact region, which is 49 iterations vs 56 iterations. This may be accounted in that the initial contact stress distribution of the lower contact region is relatively flatter than that of the upper contact region under both load cases. As can be seen in Fig. 21(b), where the iteration histories of the variance are plotted, the variance for the lower contact region is actually smaller than that of the upper contact region under the same load cases. The dramatic reductions on the variances demonstrate the effectiveness and the capability of the proposed material stiffness design on dealing with the contact problems with multiple contact regions.

Fig. 21
figure 21

Iteration histories of the objective function and the variance under two load cases

Full size image

After 56 iterations, the final Young’s modulus of these two design domains are illustrated in Fig. 22. The final Young’s modulus of the upper design domain range from 3.84 to 9.91 GPa, and the distribution follows a similar rule with the previous examples, as shown in Fig. 22(a). However, with a similar extreme reference stress distribution, as shown in Figs. 19a and 20a, the Young’s modulus of the lower design domain, as presented in Fig. 22b, show a different distribution pattern, where the Young’s modulus decreases from the left to the right with a range from 0.39 to 0.55 GPa. This may due to the interaction between these two design domains and the interaction mechanism needs to be further studied.

Fig. 22
figure 22

Final Young’s modulus distributions for the upper and lower design domains

Full size image

6 Discussion and conclusions

Considering the significant effects of material stiffness on contact stress distribution and the universality of multiple loading conditions, the problem of material stiffness optimization in contact systems subjected to multiple load cases shall not be neglected. A heuristic-based material stiffness optimization design algorithm is developed for homogenizing the contact stress distribution in frictional elastic contact problems under multiple loading conditions. A weighted sum of the decrease levels of the contact stress under all load cases is constructed as the objective function and the Young’s modulus of the areas around the contact region is defined as the design variable. The individual criteria (Li et al. 2003) for contact problem with multiple contact regions is addressed and the worst case design (Ben-Tal et al. 2000; Li et al. 2005) is adopted. A power law function is utilized to control the Young’s modulus modification process.

Three numerical examples are investigated to evaluate the feasibility and effectiveness of the proposed material stiffness optimization under multiple load cases. The results indicate that after the material stiffness design, the variance of the contact stress under each loads can be reduced significantly (e.g. a reduction of 99.73% under load case 1 and 98.82% under load case 2 in the second example). Moreover, some new features of the material stiffness optimization with multiple loading conditions are obtained. It is found that the final distribution of the extreme reference stress owes a stronger relations with the most critical load case when the multiple loads are asymmetric, the convergence rate is affected by the initial contact stress distribution and that the final material stiffness (i.e., Young’s modulus) distribution may be affected by the interactions between multiple contact regions. We would like to underline the effectiveness of the proposed heuristic-based material stiffness optimization design algorithm on homogenizing the contact stress distribution, and the new features of the material stiffness optimization with multiple loading conditions.

For the manufacturing of the optimized continuous Young’s modulus distribution, additive manufacturing (Cramer et al. 2015) is a potential realizable technology. Through additive manufacturing, structures composed of various materials with properties varying continuously along the spatial dimension(s) could be achieved, which is the exact main feature of the Young’s modulus distribution obtained in this paper. Moreover, some post-processing treatments (e.g., region-averaging treatment of the Young’s modulus) can be conducted to convert the optimized continuous Young’s modulus distribution to a discrete and high-resolution Young’s modulus distribution, which is then much easier to be manufactured. Future development is also needed to promote the implementation of the variable Young’s modulus distribution in real life.