1 Introduction

The adhesives are one of the most important bonding methods of assembling shoes components. The application of adhesives to bond materials allows simplify the steps production on footwear when drastically reduced the number of production operations. Since 1970, the polyurethane (PU) adhesives solvent based was introduced to manufacture shoes because of its ability to bond a wide variety of materials (Yue and Yue 1997; Karmann and Gierenz 2001; Pizzi and Mittal 2003; Mayan et al. 1999).

Depending on the materials used for the sole and for the upper, various pretreatments could be needed to improve the bond (Falco 2007; Velez-Pages and Martin-Martinez 2005). Proper surface treatment is the key to obtaining good adhesive bonds, allowing removing dirt, grease, mod-release agents, processing additives, plasticizers, protective oils and other contaminants that could compromise the bonds (Velez-Pages and Martin-Martinez 2005).

There are available a lot of surface treatments, in this work will be considered the primer, mechanical and chemical treatments (Karmann and Gierenz 2001; Velez-Pages and Martin-Martinez 2005). Mechanical and chemical treatments are methods that aim to modification the surface to enhance the adhesive forces for high demands on bonded joints (Paiva et al. 2013; Paiva et al. 2014; Silva et al. 2011). The application of primer are also used in conjunction with a surface treatment either to improve adhesion performance (Velez-Pages and Martin-Martinez 2005; Silva et al. 2011). Primers consist in a solution of polymers in organic solvents that, in their composition, are related to the adhesive (Paiva et al. 2014; Silva et al. 2011; Houwink and Salomon 1967; Snogren 1974; Cepeda-Jiménez et al. 2003; Wake 1976).

PU is largely used for adhesives owing to their outstanding properties (Karmann and Gierenz 2001; Houwink and Salomon 1967). These types of adhesives are characterized because of their excellent adhesion, flexibility, low-temperature performance, high cohesive strength and cure speed (Skeist 1976; Siri 1984; Sultan Nasar et al. 1998). The formulation is based on thermoplastic PU resins (Sultan Nasar et al. 1998), fillers, resins, solvents and in some cases it is used catalysts as a crosslinking agent (Falco 2007; Silva et al. 2011; Sultan Nasar et al. 1998). Fillers are used to improve physical properties, like viscosity, temperature resistance, stability, under lower cost. In this work it will be considered the fumaric acid, silica, nitrocellulose and chlorinated rubber (Karmann and Gierenz 2001; Silva et al. 2011). Resins are usually used to increase tack and temperature resistance to the adhesive. In this work will be considered colophony, hydrocarbon, alkyl phenolic, terpene phenolic, cumarone-indene and vinyl chloride/acetate vinyl types of resins (Silva et al. 2011; Wake 1976; Skeist 1976; Siri 1984; Sultan Nasar et al. 1998). Solvents are mainly esters and ketones. The total solvent portion ranges is between 75 and 85 % (Sultan Nasar et al. 1998).

The PU adhesives available systems are classified as one-component and two-component systems (Silva et al. 2011; Skeist 1976; Siri 1984). The one-component system consists in an adhesive formulated with several components mixed and stored together (Silva et al. 2011). The two-component system consists in an adhesive and a catalyst stored separated, they are mixed just before the application because of their short pot life. In this system the cure develop rapidly between the poliol of the PU resin present on the adhesive and the NCO group of the catalyst (isocyanate type; Silva et al. 2011; Skeist 1976). The two components systems are used when heat resistance is required (Silva et al. 2011).

In PU adhesives solvent-based, after the evaporation of the solvent, heat and pressure are applied to melt the polymer and press the parts for adhesion, contributing to the crosslinking (Paiva et al. 2013; Paiva et al. 2014; Silva et al. 2011; Sultan Nasar et al. 1998). So, for bonding the sole, the adhesive film is activated by IR irradiation by 2–6 s, at 55–80 °C. Upon cooling the adhesive recrystallizes to give a strong and flexible bond (Paiva et al. 2013; Paiva et al. 2014; Silva et al. 2011).

In the footwear industry, the manufacture of the shoes, for assembling the sole to the upper, follow some steps as show on the Fig. 1. Each individual process step is important for the quality of the bonded product (Paiva et al. 2013; Paiva et al. 2014). Indeed, the selection of the weight composition of raw materials plays an important role aiming to manufacture the best adhesive joint, allowing accomplishing the demands of the customers.

Fig. 1
figure 1

Application of PU adhesive solvent based and the individual steps on the assembling process

Full size image

On other hand the creep rate and the peel strength are the most important mechanical properties for quality requirements of the adhesive joints to be considered in the footwear industry (Falco 2007; Silva et al. 2011). So, it is intended to develop a model capable to predict and optimize the creep rate and the peel strength depending on the composition of the raw materials used in the adhesive joint (Silva et al. 2011).

2 Problem definition and design approach

To manufacture the shoes, in this work it is considered the natural leather as material for the upper and the thermoplastic rubber (TR) as material for the sole. It is necessary to consider surface treatment on the materials to increase the mechanicals properties, so, physical and chemical surface treatments are applied such as mechanical carding and halogenations, respectively (Paiva et al. 2013; Paiva et al. 2014; Silva et al. 2011; Snogren 1974; Cepeda-Jiménez et al. 2003). The adhesive formulation is composed of a number of substances giving certain mechanical properties to final adhesive depending on the substrates that are part of the adhesive joint (Paiva et al. 2014; Wake 1976). The aim of this work is to develop a model where the design variables are the inputs on the solid raw materials that compose the formulation of the adhesives and the outputs are the mechanical properties of the manufactured adhesive joint. Therefore, it is considered the PU adhesives because their excellent adhesion. So, the design variables are the constituents such as polyurethanes (PUs), resins (REs) and additives (ADs) (Paiva et al. 2014).

The responses of the adhesive joint are measured by their mechanical properties, the creep rate and the peel strength. The peel strength is associated with the strength of bonded product and the creep rate is associated with the performance properties for temperature resistance of adhesives. So, both mechanical properties should be considered as measures of the quality of the adhesive joint in footwear industry.

In general, the peel strength must be maximized and the creep rate must be minimized satisfying the size or technological requirements. So, the optimal design depends on the constrained multi-objective optimization of both mechanical properties of the adhesive joint. Since, both objectives appear contradictory a Pareto front must be built aiming to find the trade-off between solutions minimizing creep rate and maximizing peel strength.

The proposed strategy for the multi-objective design optimization (MDO) of creep rate and peel strength is based on three columns as follows: (1) the construction of physical model representation; (2) the adopted multi-objective optimization algorithm; and (3) the architecture of the optimization model connecting the different modulus.

The first column of the proposed optimization strategy is the definition and construction of the physical model representing the adhesive joint of footwear product and the relationship between the design variables—the weight composition of raw materials, and the inherent structural response measured by creep rate and peel strength. The proposed approach for this first column is based on planned experimental measurements and using these testing results to develop the approximation model. First of all, the set of experiments are planned using the Taguchi method aiming to obtain a good coverage of the design space for the composition of the adhesive joint. Secondly, considering the experimental results obtained for Taguchi design points as input/output patterns, an Artificial Neural Network (ANN) is developed based on supervised evolutionary learning (Cheng et al. 2008; António and Hoffbauer 2010, 2013). This ANN learning procedure is equivalent to solve an optimization problem where the difference between the experimental results and the ones obtained from the ANN is minimized controlling the ANN parameters.

The second column of the optimization strategy is the MDO algorithm used in the constrained optimal design search based on creep rate minimization and peel strength maximization. A Genetic Algorithm based on dominance concepts is adopted supported by short and enlarged populations of solutions.

The third column of the optimization strategy is the architecture of optimization model connecting the different modulus collecting data necessary for multi-objective optimization algorithm which comes from the optimization problem formulation. A multi-objective approach based on the optimal design of adhesive composition to achieve the target of minimum creep rate and maximum peel strength under manufacturing constraints is proposed. During the optimization process the solutions are evaluated using the optimal ANN built in the first column of optimization strategy.

Inside the third column of the optimization strategy at the end of ANN optimal configuration search a ANN-based Monte Carlo simulation procedure is implemented aiming to study the sensitivity of the structural response of adhesive joint relatively to design variables of the MDO process. In particular the Sobol indices for global sensitivity analysis are used to establish the relative importance of the design variables (António and Hoffbauer 2010, 2013). Figure 2 shows the flow diagram referring the three columns of the proposed MDO approach.

Fig. 2
figure 2

Flow diagram of the proposed MDO approach for footwear adhesive joints

Full size image

3 Experimental tests

The proposed approach for the first column of the optimization strategy is based on planned experimental measurements necessary for the development of the approximation model. So, a set of experiments are implemented aiming to obtain data used in learning procedure of generation of the approximation model defining the behaviour of adhesive joint.

3.1 Materials

The TR material considered in this work is TTSC TR-2531-80C. The properties of this material were provided by the manufacturer of the sole (technical datasheet of the material) and are presented in Table 1. The Halinov 2190 (www.cipade.com) is used as halogenate for TR. The Plastik 6271 (www.cipade.com) is selected as a primer for the leather, an adhesive primer usually is a diluted solution of an PU adhesive in an organic solvent (Paiva et al. 2014; Silva et al. 2011) which depends on the nature of the substrate surface (Snogren 1974). The Cipadur 2230T (www.cipade.com) is applied as crosslinker to increase temperature resistance, in a dosage of 5 % of the adhesive trials planned by the Taguchi method.

Table 1 Physical properties of the TTSC TR-2531-80C
Full size table

The TR material considered in this work is TTSC TR-2531-80C. The properties of this material were provided by the manufacturer of the sole (technical datasheet of the material) and are presented in Table 1.

3.2 Experimental techniques

Taking into account the composition of adhesives this work focuses on creep rate and on peel strength measurements aiming to evaluate the mechanical behaviour of the PU adhesive solvent-based when bonding natural leather uppers to TR soles.

The creep rate (CR) is a property that determines the resistance to peeling by a constant load of the single lap joint stored at an elevated temperature (Silva et al. 2011; EN 1998). The principle of the creep test is suspending the test specimen in a heated cabinet with a constant peeling force applied between the two adherents. After a set time it’s measured the bond separation.

Peel strength (PS) is a property which determines the strength required to peel of two materials. This test enables to distinguish if an adhesive is fragile or ductile (Paiva et al. 2013; Paiva et al. 2014; Silva et al. 2011; EN 1998). The principle of the peel test is the peeling of the test specimen using a tensile machine while the force required to separate the two adherents is measured.

Both methods are applicable to joints where at least one of the adherents is flexible. To quantify these properties are tested with a standard test (EN 1998). The standard norm used for footwear industry adhesives is described on the EN 1392:1998 (EN 1998). This standard norm allows obtaining the creep rate in variation of displacement per unit of time. On other hand, the standard norm allows obtaining the peel strength per unit width, which is the average load per unit width, applied at an angle between 90° and 180°, depending on the flexibility of the substrate in relation to the joint needed to lead to failure (EN 1998).

3.2.1 Preparation of the single lap joint

The application of the surface treatment depends on the materials that are intended to be bonded. On the leather is necessary to apply a surface treatment, which is the mechanical treatment, and a primer to improve a surface interaction between adhesive and the adherent (Velez-Pages and Martin-Martinez 2005; Paiva et al. 2013; Paiva et al. 2014; Silva et al. 2011; Snogren 1974). A P24 aluminum oxide abrasive cloth is used for the mechanical treatment. The primer is applied and allowed to dry for at least 10 min at room temperature (Paiva et al. 2013; Paiva et al. 2014; Silva et al. 2011). It is necessary to consider a chemical treatment as a surface treatment on TR. In this work it is used a halogenated agent and allowed to dry at least 1 h at room temperature (Paiva et al. 2013; Paiva et al. 2014; Cepeda-Jiménez et al. 2003).

After the surface treatment of the adherents, the adhesives experiments planned by the Taguchi method are applied on both substrates and allowed to dry for 15 min at room temperature. To manufacture the single lap joints the adhesive films are activated by Infrared (IR) radiation at temperature of about 70 °C and during 6 s. The substrates are bonded in the desired position, as seen in Fig. 3, and the adhesive joint is subjected to a pressure of 4 bars during 5 s. The adhesive joints, after being pressed, are stored in standard conditions (23 °C, 50 % Hr) during 72 h, in order to ensure the complete cure of the adhesive (Paiva et al. 2013; Paiva et al. 2014; Silva et al. 2011).

Fig. 3
figure 3

Test piece geometry

Full size image

The adhesive joint studied is composed of two substrates (150 mm × 30 mm) bonded together in an area of 100 mm × 30 mm, as shown in Fig. 3. The experimental portion of this work consisted of the analysis of the creep rate and the peel strength in the single lap joint, subjected to tensile loading as shown in Fig. 4 according to the procedures defined in EN 1392:1998 (EN 1998).

Fig. 4
figure 4

a Creep rate test; b Peel strength test

Full size image

3.2.2 Creep rate test

The creep test is performed in a heated cabinet at temperature of 60 °C. Considering the unbonded ends of the test specimen of the single lap joint, carefully fold back the more flexible material of the both adherents taking care do not to peel any of the adhesive bonds. Then use a pen to make a mark on the stiffer of the two adherents at the point of separation. Firmly clamp the free end of the more flexible adherent of a single lap joint specimen into each of moveable clamps. On each moveable clamp support is applied a mass of 1.5 kg, as shown in Fig. 4a.

To obtain the results, it is necessary to open the heated cabinet over the time and mark the separations (in mm) of the bonds substrates while still loaded, to complete separation (EN 1998). With the creep experiment it is obtained a bond failure envelope that can be divided into three phases: primary, secondary, tertiary. Primary phase correspond to an instantaneous elastic strain, secondary phase represent the creep rate and the tertiary phase happen with the failure of the bond of the specimen (Silva et al. 2011). The primary and the tertiary phase are ignored on the calculation of the mean of the separation lengths of the bond (Silva et al. 2011; EN 1998).

The results are expressed as displacements (mm) versus time (minutes, min). Three adhesive joint specimens for each test were considered. The heated cabinet used is a Memmert (Germany), model UM 400.

3.2.3 Peel test

The peel test is performed in the testing machine at a speed of 50 mm/min. One of the free ends of the test specimen is firmly clamp into the jaw of the tensile testing machine. As the jaw separate it is possible to observe the bond failure. The results are expressed as load (N) versus displacement (mm). The peel strength per unit of width is determined by the ratio between the maximum force and the width of the overlap joint. For each test specimen when divide the average peeling force by the width of the specimen in millimeters, it’s possible to obtain the peel strength of each bond in N/mm. Three adhesive joint specimens for each test were considered. The tensile machine used is an Instron (Norwood, MA, USA), model 3367, with load cell of 30 kN, as shown in Fig. 4b.

3.3 Planning of experimental measurements

The Taguchi method (Taguchi and Konishi 1987) is adopted to plan the experimental tests (DOE) that further will be used in the ANN learning procedure. The objective of DOE is to reduce the variation in a process through robust design of experiments (DOE). The effect of many different parameters on the performance characteristic in a set of experiments can be analyzed by using orthogonal arrays. Once the parameters affecting the measuring process have been determined, the levels at which these parameters should be varied must be determined. In this work, the design of experiments are implemented using the Taguchi table L27(313) (Paiva et al. 2013; Paiva et al. 2014; Taguchi and Konishi 1987).

4 Multi-objective design optimization

4.1 Multi-objective based design formulation

The generic form of a MDO problem can be mathematically expressed as:

$$ {\text{Minimize}}\,{\mkern 1mu} {\mathbf{f}}({\mathbf{x}}) = \left\{ {f_{i} ({\mathbf{x}}):\Re^{n} \mapsto \Re ;\quad i = 1, \ldots ,\,m;\,{\mkern 1mu} m > 1} \right\},{\text{over}}\,{\mathbf{x}} $$

subject to

$$ g_{j} ({\mathbf{x}} )\ge 0 ;\,\,\,\,\left\{ {g_{j} ({\mathbf{x}} ) :\Re^{n} \mapsto \Re \, ;\quad j = 1 ,\ldots ,\,p} \right\} $$
(1)

and

$$ h_{k} ({\mathbf{x}} )= 0 ;\,\,\,\,\left\{ {h_{k} ({\mathbf{x}} ) :\Re^{n} \mapsto \Re \, ;\quad k = 1 ,\ldots ,\,r} \right\} $$

with contradictory objectives. In the above formulation \( f_{i} \, (i = 1, \ldots ,\,m ) \) are the objective functions, the constraints \( g_{j} ({\mathbf{x}} )\ge 0 \) and \( h_{k} ({\mathbf{x}} )= 0 \) (j = 1,…, p and k = 1,…, r) define the feasible space \( {\mathbf{Q}} \subseteq \Re^{n} \). Usually, the corresponding minimum with respect to all objective functions is located outside Q. There is no unique solution to a problem with more than one conflicting objectives and the existing solutions are denoted by Pareto-optimal solutions. The classification as “Pareto-optimal” depends on the concept of dominance according the following definitions (Deb 2001; Conceição António 2013):

Definition 1

(dominance) Let be \( {\mathbf{Q}} \subseteq \Re^{n} \) the subset in the minimization problem formulated in (1). A solution \( {\mathbf{x}}_{1} \in {\mathbf{Q}} \) dominates a solution \( {\mathbf{x}}_{2} \in {\mathbf{Q}} \), if the objective value for x 1 is smaller than the objective value for x 2 in at least one objective and is not bigger with respect to the other objectives:

$$ {\mathbf{x}}_{1} \,\, \prec \,\,{\mathbf{x}}_{2} \Leftrightarrow \,\,\,\left\{ {\begin{array}{c} {\forall i :1 \le i \le m\, \Rightarrow \,f_{i} ({\mathbf{x}}_{1} )\,\, \le \,\,f_{i} ({\mathbf{x}}_{2} )} \\ \wedge \\ {\exists j :1 \le j \le m\,\,,\,\,f_{j} ({\mathbf{x}}_{1} )\,\, < \,\,f_{j} ({\mathbf{x}}_{2} )} \\ \end{array} } \right. $$
(2)

where \( {\mathbf{x}}_{1} \,\, \prec \,\,{\mathbf{x}}_{2} \) denotes x 1 dominates x 2.

Definition 2

(Pareto optimal design): Let be \( {\mathbf{Q}} \subseteq \Re^{n} \) the subset in the minimization problem formulated in (1). A solution \( {\mathbf{x}}^{\ast} \in {\mathbf{Q}} \) is classified as Pareto optimal design if and only if it is not dominated by any other solution in Q. The set of all Pareto solutions is called the Pareto front, represented by X *,

$$ {\mathbf{x}}^{\ast} \in {\mathbf{X}}^{\ast}\,\,\, \Leftrightarrow \,\,\,\,\left\{ {\,{\mathbf{x}} \in {\mathbf{Q}} :\,\,\,{\mathbf{x}} \prec \,\,{\mathbf{x}}^{\ast}\,} \right\} = \left\{ \varnothing \right\} $$
(3)

The above definitions are essential for further Pareto evolutionary search developments for multi-objective optimization of composite structures.

4.2 Bi-objective optimization problem of adhesive joint

The proposed approach follows the problem definition established in previous section. The multi-objective optimization (MDO) problem formulated is based on minimization of objective functions in Eq. (1). However, in the proposed approach the performance of structural response of the footwear adhesive joints is measured by creep rate (CR) and the peel strength (PS). In general, the optimal design of adhesive joint is performed based on minimization of creep rate and maximization of peel strength. So, this design procedure must be formatted according the formulation in Eq. (1). The minimization of inverse of peel strength (1/PS) is adopted as second objective function to overcome this apparent difficulty.

Therefore, it is intended to develop a model capable to predict and simultaneously minimize the creep rate and the inverse of peel strength depending on the weight percentage of raw materials used in the composition of the adhesive joint. These design variables denoted by vector x with components x k , are the weight percentages of PUs, resins and additives in the adhesive composition. The mathematical formulation of the bi-objective optimization problem of adhesive joint is defined as creep rate and inverse of peel strength minimizations subject to technological constraints as follows,

$$ Minimize\,\,\,\left( {f_{ 1} ({\mathbf{x}} ) , { }f_{2} ({\mathbf{x}} ) { }} \right) , { }\,\,\,{\text{over}}\,\, \, {\mathbf{x}} $$
(4)
$$ {\text{with}}\,\,f_{1} ({\mathbf{x}} )= CR ({\mathbf{x}} )\,\,{\text{and}}\,\,f_{2} ({\mathbf{x}} )= \frac{1}{{PS ({\mathbf{x}} )}} $$

subject to:

$$ 10 \le \sum\limits_{k = 1}^{n} {\,x_{k} } \le 20 $$
(5)
$$ \sum\limits_{k = 1}^{r} {x_{n + k} } \le 1 $$
(6)
$$ \sum\limits_{k = 1}^{a} {x_{r + k} } \le 7 $$
(7)
$$ x_{k}^{l} \le x_{k} \le x_{k}^{u} ,\,\,\,\,\,\,k = 1, \ldots ,n + r + a $$
(8)

where n, r and a are the number of materials of each group of PUs, resins and additives considered for the adhesive joint, respectively. Those numbers will be defined in design process. The constants x l k and x u k are the lower and upper bounds of design variable x k , respectively.

4.3 Stages of MDO approach

The proposed MDO approach is based on mixed experimental–numerical procedures according Sect. 2. The strategy to build the MDO approach to solve the bi-objective optimization problem formulated from Eqs. (4) to (8) is based on three columns as previously referred: (1) the construction of physical model representation; (2) the adopted multi-objective optimization algorithm; and (3) the architecture of the optimization model connecting the different modulus.

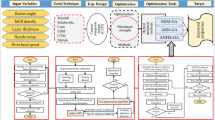
The experimental data obtained in Sect. 3 is essential to build the numerical model of physical phenomenon, which is the adhesive joint behavior. The numerical representation will be used in optimal design procedure. So, two stages are identified in numerical part of the proposed mixed experimental–numerical approach as shown in Fig. 5. These two stages are:

Fig. 5
figure 5

Integrated ANN learning and optimal design procedures

Full size image
  1. 1.

    ANN learning procedure where the experimental results are used to obtain the optimal ANN configuration, which supports the relationship between the weight composition of raw materials and the performance functions as creep rate and the peel strength;

  2. 2.

    Optimal design procedure where the MDO concepts are applied to search the constrained bi-objective optimization of the adhesive joint based on creep rate minimization and peel strength maximization using the weight composition of raw materials as design variables.

The procedure of the first stage begins defining the set of planned experiments based on Taguchi method is proposed in Sect. 3. Then, the experimental input/output patterns are used in learning procedure aiming to obtain the optimal ANN configuration (Cheng et al. 2008; Gupta et al. 2003). The ANN learning procedure is equivalent to solve an optimization problem based on minimization of the differences between the experimental results and the simulation values obtained from the ANN. So, detailing the process the optimal configuration of ANN is obtained minimizing the error between the simulated network outputs and the experimental data for creep rate (CR) and the peel strength (PS). In this stage the design variables are the weights of synapses, \( m_{\,ij}^{ (p )} \), and the biases, \( r_{\,k}^{ (p )} \), of the ANN.

The minimization of ANN learning procedure is performed using a single Genetic Algorithm denoted by \( {\mathbf{GA}}^{ (1 )} \) with appropriated genetic parameters. Since the GA is a population-based evolutionary method in this stage a population of solutions for ANN configuration denoted by \( {\mathbf{P}}^{ (t )} \) is considered at each t-generation. After the ANN learning procedure the optimal configuration denoted by \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \) is obtained and the construction of physical model representation is finished. This corresponds to optimal values for the weights of synapses, \( m_{\,ij}^{ (p )} \), and the biases, \( r_{\,k}^{ (p )} \), of the ANN.

During the optimal design procedure, the bi-objective optimization problem formulated from Eqs. (4) to (8) is solved using the MDO concepts. The evaluation of the objective functions are based on optimal configuration \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \) of the ANN obtained at the first stage. The optimal design procedure is a multi-objective constrained minimization performed using the genetic algorithm denoted by \( {\mathbf{GA}}^{ (2 )} \) with genetic parameters different from previous stage.

The trade-off between minimum creep rate and minimum inverse peel strength, depending on given size and technological constraints imposed on the weight composition of raw materials used in adhesive joint, is searched. A short population of solution, \( {\mathbf{X}}^{ (t )} \), is used to evolve through the \( {\mathbf{GA}}^{ (2 )} \) based on an elitist strategy. These solutions are associated with different compositions of PUs, resins and additives for the adhesive joint.

The best solutions of \( {\mathbf{X}}^{ (t )} \) are stored into an enlarged population, \( {\mathbf{EP}}^{ (t )} \) based on dominance concepts. The global Pareto-optimal front is built at this enlarged population using the concept of Pareto dominance (Conceição António 2013). The enlarged population is updated and ranked every generation and the worst ranking solutions are eliminated. The search method adopts an elitist strategy storing non-dominated solutions found during the evolutionary process into the enlarged dominance-based population. After the stopping criteria are reached, it is obtained the optimum adhesive composition. Figure 5 shows the integrated ANN learning and optimal design procedures.

Inside the integrated ANN learning and optimal design procedures at the end of ANN optimal configuration search a ANN-based Monte Carlo simulation procedure is implemented aiming to study the sensitivity of the structural response of adhesive joint relatively to design variables of the MDO process. This procedure is called sensitivity analysis (SA) as shown in Fig. 5.

4.4 First stage: ANN learning procedure

The ANN is a nonlinear dynamic modeling system inspired by our understanding and abstraction on the biological structure of the human brain. Its architecture and operating procedures are based on a large number of highly interconnected processing units denoted by neurons and the linkages are similar to the brain synapses as in biological sense. The operating procedures include attributes such as learning, thinking, memorizing, remembering, rationalizing and problem solving (Gupta et al. 2003).

In the ANN development a weight value is associated with each synaptic connection between processing units that is defined as the connection importance. The weight value acts as a multiplicative filter together with the activation procedure performed by an appropriated function. The ANN architecture is formed by several layers of neurons and different matrices with synaptic weights can be identified as linkage elements between layers. Learning of ANN occurs while modification of connection weight matrix is undertaken at the learning process. From examples of a phenomenon with particular behavior and following an appropriate learning rule the ANN acquires knowledge or relationship embedded in the input/output data. The ANNs are robust models having properties of universal approximation, parallel distributed processing, learning, adaptive behaviour and can be applied to multivariate systems (Cheng et al. 2008; Gupta et al. 2003).

In this work, the proposed ANN is organized into three layers of nodes (neurons): input, hidden and output layers. The synapses between input and hidden nodes and between hidden and output nodes are associated with weighted connections that establish the relationship between input data and output data. Deviations on neurons belonging to hidden and output layers are also considered in the proposed ANN model. In the developed ANN, the input data vector \( {\mathbf{D}}^{inp} \) is defined by a set of experimental values for design/input variables \( {\mathbf{x}} \), which are the weight composition of raw materials of the adhesive joint, such as PU’s, resins and additives as referred in previous sections. The corresponding output data vector \( {\mathbf{D}}^{out} \) contains the experimental values of the creep rate and of the peel strength.

The data vectors \( {\mathbf{D}}^{inp} \) and \( {\mathbf{D}}^{out} \) used to build the ANN needs to be normalized aiming to avoid numerical error propagation during the learning process. Then each component of normalized vectors are done as follows,

$$ \underline{D}_{k} = (D_{k} - D_{\hbox{min} } )- \frac{{D_{N}^{\hbox{max} } - D_{N}^{\hbox{min} } }}{{D_{\hbox{max} } - D_{\hbox{min} } }} + D_{N}^{\hbox{min} } $$
(9)

where D k is the k-th component of the vector of experimental values before normalization, D min and D max are the minimum and maximum values of D k , respectively, in the input/output data set to be normalized. According to Eq. (9), the data set is normalized to values D k , verifying the conditions

$$ D_{N}^{\hbox{min} } \le \,\,\,\underline{D}_{k} \le \,\,D_{N}^{\hbox{max} } $$
(10)

Depending on the input or output data, different maximum and minimum normalized values are used in Eq. (9).

The weights of the synapses, \( m_{\,ij}^{ (p )} \), and biases in the nodes or neurons at the hidden and output layers, \( r_{\,k}^{ (p )} \), are controlled during the learning procedure as shown in Fig. 5. The signal in each node is \( C_{k}^{ (p )} \) defined as the components of the vector \( {\mathbf{C}}^{ (p )} \) given by

$$ {\mathbf{C}}^{ (p )} = {\mathbf{M}}^{ (p )} \,{\mathbf{D}}^{ (p )} + {\mathbf{r}}^{ (p )} $$
(11)

where \( {\mathbf{M}}^{ (p )} \) is the matrix of the weights of synapses associated with the connections between input and hidden layer (p = 1) or between hidden and output layer (p = 2), \( {\mathbf{r}}^{ (p )} \) is the biases vector considered for the nodes of the hidden (p = 1) or output (p = 2) layers, \( {\mathbf{D}}^{ (p )} \) is the input data vector for the hidden (p = 1) or output (p = 2) layer.

The sums of the changed signals (total activation) in Eq. (11) are inserted in the Activation Functions. A sigmoid function is applied on each node on hidden layer while a linear function is considered for output layer. The activation of the k-th node of the hidden layer (p = 1) or output layer (p = 2) and is obtained through sigmoid functions as follows:

$$ A_{\,k}^{ (1 )} = \frac{1}{{1 + e^{{ - \eta \,C_{k}^{ (1 )} }} }} $$
(12)
$$ A_{\,k}^{ (2 )} = C_{k}^{ (2 )} $$
(13)

where \( A_{\,k}^{ (1 )} \) and \( A_{\,k}^{ (2 )} \) represent the activation functions of the signal of the nodes or neurons of the hidden and output layers, respectively. The scaling parameters η influence the sensitivity of the sigmoid activation function and must be controlled.

The supervised learning of ANN followed in this approach is an evolutionary optimization procedure performed by \( {\mathbf{GA}}^{ (1 )} \). This procedure is based on the minimization of the error between experimental output data and ANN simulated results. In the optimization process the weights of synapses and the biases in neurons are used as design variables. For each set of input data and any configuration of the weight matrices \( {\mathbf{M}}^{ (p )} \) and biases \( {\mathbf{r}}^{ (p )} \), with p = 1 and p = 2, a set of output results is obtained. These simulated output results are compared with the experimental output values obtained for the same input data to evaluate the difference (or error), which must be minimized during the learning procedure (Gupta et al. 2003).

The supervised learning of the proposed ANN is based on several measures of the error with the objective to accelerate and stabilize the learning process. The first measure is the root-mean-squared error defined as

$$ RMSE = \frac{1}{{N_{\exp } }}\,\sqrt {\sum\limits_{i = 1}^{{\,N_{\exp } }} {\left[ {\left( {CR_{i}^{sim} - CR_{i}^{\exp } } \right)^{\,2} + \left( {PS_{i}^{sim} - PS_{i}^{\exp } } \right)^{\,2} } \right]} } $$
(14)

where N exp is the number of experiments considered in the set of design points of Taguchi and the superscripts sim and exp denote the simulated and experimental data of creep rate, CR and peel strength, PS. To reinforce the error minimization a second measure is introduced based on the following mean relative error component:

$$ RE = \frac{1}{{N_{\exp } }}\sqrt {\sum\limits_{i = 1}^{{\,N_{\exp } }} {\left[ {\left( {\tfrac{{CR_{i}^{sim} - CR_{i}^{\exp } }}{{CR_{i}^{\exp } }}} \right)^{\,2} + \left( {\tfrac{{PS_{i}^{sim} - PS_{i}^{\exp } }}{{PS_{i}^{\exp } }}} \right)^{\,2} } \right]} } $$
(15)

The influence of the biases of the neurons of the hidden and output layers is also included to stabilize the learning process:

$$ {\varvec{\Gamma}}\,\, = \,\,\tfrac{1}{{N_{\exp } }}\,\,\sum\limits_{i = 1}^{{N_{\exp } }} {\left[ {\,\tfrac{1}{{N_{hid} }}\,\,\sum\limits_{k = 1}^{{N_{hid} }} {\left( {\,r_{k}^{ (1 )} } \right)^{\,2} } \,\, + \,\,\tfrac{1}{{N_{out} }}\,\,\sum\limits_{k = 1}^{{N_{out} }} {\left( {\,r_{k}^{ (2 )} } \right)^{\,2} } } \right]} $$
(16)

where N hid and N out are the number of neurons of the hidden layer and of the output layer, respectively.

The error measures presented from Eqs. (14) and (15) and biases component in Eq. (16) are aggregated using the following formula:

$$ F_{1} \left( {{\mathbf{M}}^{ (1 )} ,\,\,{\mathbf{r}}^{ (1 )} ,\,\,{\mathbf{M}}^{ (2 )} ,\,\,{\mathbf{r}}^{ (2 )} } \right) = c_{1} \,RMSE\,\,\, + \,\,c_{2} \,RE\,\, + \,\,c_{3} \,{\varvec{\Gamma}} $$
(17)

being the constants c k used to regularize the numerical differences of the three error terms stabilizing the numerical procedure. The weights of the synapses and biases can be changed until the value of F 1 falls within a prescribed value.

The adopted supervised learning process of the ANN is based on a Genetic Algorithm denoted by \( {\mathbf{GA}}^{ (1 )} \) (António 2001, 2002; António et al. 2004) using the weights of synapses \( {\mathbf{M}}^{ (p )} \), and biases of neural nodes at the hidden and output layers \( {\mathbf{r}}^{ (p )} \), as design variables as shown in Fig. 5. At this stage a population of solutions for ANN configuration denoted by \( {\mathbf{P}}^{ (t )} \) is considered at each t-generation.

A binary code format is used for these variables. The number of digits of each variable can be different depending on the connection between the input-hidden layers or hidden-output layers. The domain of the learning variables \( {\mathbf{M}}^{ (p )} \) and \( {\mathbf{r}}^{ (p )} \) (p = 1 and p = 2) and scaling parameter η can be tuning together the code format of design variables of the ANN learning procedure. The optimization problem formulation associated with the ANN learning process is based on the minimization of the function defined in Eq. (17) without constraints, as follows

$$ \begin{aligned} {\text{Maximize}}\,\,FIT^{ (1 )} = & K^{ (1 )} - F_{1} \left( {{\mathbf{M}}^{ (1 )} ,\,\,{\mathbf{r}}^{ (1 )} ,\,\,{\mathbf{M}}^{ (2 )} ,\,\,{\mathbf{r}}^{ (2 )} } \right)\,\,\,\,{\text{over}}\,\,\,\,{\mathbf{M}}^{ (p )} \,\,{\text{and}}\,\,{\mathbf{r}}^{ (p )} \\ & {\text{subject to}}\,\,{\mathbf{M}}^{ (p )} ,\,\,{\mathbf{r}}^{ (p )} \in \varOmega \,\, \left( {p = 1{\text{ and }}p = 2} \right) \\ \end{aligned} $$
(18)

where Ω is the domain of design variables in learning procedure, \( FIT^{ (1 )} \) is the fitness function in GA search to obtain the optimal ANN configuration, \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \) for the weight of synapses and biases in neurons. Since the selection operator of GA is fitness-based the function \( FIT^{ (1 )} \) must take positive values. So, the constant \( K^{ (1 )} \) must be large enough to obtain always positive fitness values.

The single Genetic Algorithm \( {\mathbf{GA}}^{ (1 )} \) used to solve the constrained optimization problem (with size constraints) defined in Eq. (18) performs in following sequence:

  • Step1: Initialization of population \( {\mathbf{P}}^{ (0 )} \). The initial population of design solutions for the learning variables \( {\mathbf{M}}^{ (p )} \) and \( {\mathbf{r}}^{ (p )} \) (p = 1 and p = 2) is randomly generated using a uniform probability distribution function (PDF).

  • Step 2: Mating selection mechanism. The population \( {\mathbf{P}}^{ (t )} \) is ranked according to individual fitness obtained using the formulae defined from Eqs. (15) to (18). The best-fitted elite group of \( {\mathbf{P}}^{ (t )} \) is determined. One couple of parents \( {\text{p}}_{ 1} \) and \( {\text{p}}_{ 2} \) per each offspring individual is generated. The procedure is elitist: one from the best-fitted group (elite) and another from the least fitted one.

  • Step 3: Offspring generation mechanism. The crossover operator generates a new chromosome (offspring) by recombination of the genetic material of each couple of parent chromosomes \( {\text{p}}_{ 1} \) and \( {\text{p}}_{ 2} \). The offspring genetic material is obtained using the multi-point combination technique known as parameterized uniform crossover (António 2002; António et al. 2004). This crossover operator is applied with a predefined probability to select the offspring genetic material from the best-fitted chromosome. The offspring generation mechanism is repeated until the offspring group \( {\mathbf{B}}^{ (t )} \) is completed.

  • Step 4: Intermediate selection. The current population \( {\mathbf{P}}^{ (t )} \) is transferred to an intermediate stage where is joined to the offspring group \( {\mathbf{B}}^{ (t )} \) generating the enlarged population \( {\mathbf{P}}^{ (t )} \cup {\mathbf{B}}^{ (t )} \).

  • Step 5: Elimination/Replacement by genetic similarity control. The enlarged population \( {\mathbf{P}}^{ (t )} \cup {\mathbf{B}}^{ (t )} \) is ranked according to the individual fitness. Then, the similarity control is performed gene by gene following an updating scheme during the evolutionary process. The objective is to control the population diversity keeping it in good level and reducing the endogamy properties of Crossover operator. This is followed by elimination of solutions with similar genetic properties and subsequent replacement by new randomly generated individuals. The new population \( {\mathbf{P}}^{ (t + 1,* )} \) is ranked and the individuals with worst fitness are replaced by a group of new solutions obtained from the Mutation operator. During this procedure the original size of the population is recovered.

  • Step 6: Mutation. In the presented approach the mutation genetic operator is used to overcome the problem induced by selection and crossover operators where can happen some generated solutions have a large percentage of equal genetic material. So, aiming to improve the diversity level a chromosome set group which genes are generated in a random way is introduced into the population. Since this new group of chromosomes will be recombined with the remaining individuals into the population during next generations this operation is called Implicit Mutation (António 2001).

  • Step 7: Final selection. After mutation, the new population \( {\mathbf{P}}^{ (t + 1 )} \) is obtained and the evolutionary process will continue until the stopping criteria are reached.

  • Step 8: Stopping criterion analysis. The stopping criterion used in the convergence analysis is based on the relative variation of the mean fitness of a reference group inside \( {\mathbf{P}}^{ (t + 1 )} \). The search is stopped if the mean fitness of the reference group does not evolve after a finite number of generations. Otherwise, the population evolves to the next generation returning to Step 2.

4.5 Second stage: optimal design procedure

The optimal design procedure is based on MDO concepts applied to solve the bi-objective constrained minimization problem formulated from Eqs. (4) to (8). The objectives to be minimized are the creep rate and the inverse of peel strength subject to technological constraints associated to the weight percentages of raw materials used in the composition of the adhesive joint. These design variables denoted by vector x with components x k , are the weight percentages of PUs, resins and additives in the adhesive composition.

The fitness assignment is based on an aggregation function of the two objectives \( f_{1} ({\mathbf{x}} )= CR ({\mathbf{x}} ) \) and \( f_{2} ({\mathbf{x}} )= \frac{1}{{PS ({\mathbf{x}} )}} \), and a graded penalization of constraint violation (António 2001, 2002). So, the original bi-objective optimization problem is transformed as follows:

$$ Maximize\,\,\,\,FIT^{ (2 )} = K^{ (2 )} - \alpha_{1} \,f_{1} ({\mathbf{x}} )\,\, - \,\,\alpha_{2} \,f_{2} ({\mathbf{x}} )- \alpha_{3} \,\sum\limits_{i = 1}^{{N_{g} }} {{\varvec{\Phi}}_{i} ({\mathbf{x}} )} ,{\text{over}}\,{\mathbf{x}} $$
(19)

with

$$ {\varvec{\Phi}}_{i} ({\mathbf{x}} )= \left\{ {\begin{array}{*{20}l} {0,} \hfill & {{\text{if }}\,\,\varphi_{\,i} ({\mathbf{x}} )\le 0} \hfill \\ {R_{i} \left| {\varphi_{i} ({\mathbf{x}} )} \right|^{{q_{i} }} ,} \hfill & {{\text{if}}\,\,\,\varphi_{\,i} ({\mathbf{x}} )> 0} \hfill \\ \end{array} } \right. $$
(20)

where \( \varphi_{\,i} ({\mathbf{x}} ) \) are the constraints defined from Eqs. (5) to (7) after normalization. Here, \( \varphi_{\,i} ({\mathbf{x}} )\le 0 \) are associated to the feasibility of the constraint \( \varphi_{\,i} ({\mathbf{x}} ) \). The N g constraints defined from Eqs. (5) to (7) must be normalized relatively to their bound limits aiming to avoid scaling effects. Unfeasible solutions of the problem are penalized depending on the total magnitude of the constraints violation. Furthermore, the penalization is applied on the graded degree of severity according to the difference between the current and the allowable constraint values. The constants q i and R i are evaluated considering two constraint violation degrees, i.e., strong penalization for large violation value and fair penalization for negligible violation of the constraints (António 2001, 2002; António et al. 2004). The constants α i are introduced for numerical regularization. Since the stochastic permutation of data in genetic search is performed using fitness-based selection procedures the fitness function \( FIT^{ (2 )} \) must be positive. So, the constant \( K^{ (2 )} \) is large enough to obtain always positive fitness values. The size constraints in Eq. (8) are not included in described procedure of penalization. They are imposed directly to the design space at the binary code format transformation used on genetic algorithm development.

The MDO process evolution is based on a short population of solutions \( {\mathbf{X}}^{ (t )} \) updated during the evolutionary search driven by the genetic algorithm, \( {\mathbf{GA}}^{ (2 )} \). An elitist strategy is adopted at evolution of \( {\mathbf{X}}^{ (t )} \). Each solution in \( {\mathbf{X}}^{ (t )} \) is ranked according its fitness value, which is related with the objective functions and the constraints of the problem. The trade-off between minimum creep rate and minimum inverse peel strength, depending on given size and technological constraints imposed on the weight composition of raw materials used in adhesive joint, is searched.

From Eqs. (19) and (20) it can be established that designs with good fitness and satisfying the constraints have priority in the rank process. Although this is necessary for bi-objective optimization problem it is not essential to build the optimal Pareto front. Indeed, the Pareto front depends on the dominance concept, which is applied at enlarged population. Here, the short population \( {\mathbf{X}}^{ (t )} \) is used as a nest where the good solutions are generated through the \( {\mathbf{GA}}^{ (2 )} \) based on an elitist strategy. At each generation the best solutions of \( {\mathbf{X}}^{ (t )} \) are stored into an enlarged population, \( {\mathbf{EP}}^{ (t )} \) based on dominance concepts. The global Pareto-optimal front is built at this enlarged population using the concept of Pareto dominance (Conceição António 2013).

Inside the enlarged population defined here as set \( {\mathbf{EP}}^{ (t )} \subseteq \Re^{n} \), individuals are sorted and ranked according to non-constrain-dominance. Following the definition by Deb (Deb 2001), an individual \( {\mathbf{x}}_{i} \in {\mathbf{EP}}^{ (t )} \) is said to constrain-dominate an individual \( {\mathbf{x}}_{j} \in {\mathbf{EP}}^{ (t )} \), if any of the following conditions are verified:

  1. 1.

    \( {\mathbf{x}}_{i} \) and \( {\mathbf{x}}_{j} \) are feasible, with

    1. (i)

      \( {\mathbf{x}}_{i} \) is no worse than \( {\mathbf{x}}_{j} \) for all objectives, and

    2. (ii)

      \( {\mathbf{x}}_{i} \) is strictly better than \( {\mathbf{x}}_{j} \) in at least one objective,

  2. 2.

    \( {\mathbf{x}}_{i} \) is feasible while individual \( {\mathbf{x}}_{j} \) is not,

  3. 3.

    \( {\mathbf{x}}_{i} \) and \( {\mathbf{x}}_{j} \) are both infeasible, but \( {\mathbf{x}}_{i} \) has smaller total constraint violation.

The constraint violation of an individual \( {\mathbf{x}} \) is defined to be equal to the sum of the violated constraint function values in the multi-objective optimization problem formulated from (4) to (8) (Conceição António 2013):

$$ \xi ({\mathbf{x}} )= \sum\limits_{i = 1}^{{N_{g} }} {\,{\varvec{\Gamma}}_{i} ({\mathbf{x}} )} $$
(21)

where \( {\varvec{\Gamma}}_{i} ({\mathbf{x}} )= {\varvec{\Gamma}}_{i} \left[ {\varphi_{i} ({\mathbf{x}} )} \right] \), with

$$ {\varvec{\Gamma}}_{i} \left[ {\varphi_{i} ({\mathbf{x}} )} \right] = \left\{ {\begin{array}{*{20}c} 0 & {\text{if}} & {\varphi_{i} ({\mathbf{x}} )\le 0} \\ {\varphi_{i} ({\mathbf{x}} )} & {\text{if}} & {\varphi_{i} ({\mathbf{x}} )> 0} \\ \end{array} } \right. $$
(22)

where \( \varphi_{\,i} ({\mathbf{x}} ) \) are the constraints defined from Eqs. (5) to (7) after normalization. The concept of constrain-domination enables to compare two individuals in problems having multiple objectives and constraints, since if \( {\mathbf{x}}_{i} \) constrain-dominates \( {\mathbf{x}}_{j} \), then \( {\mathbf{x}}_{i} \) is better than \( {\mathbf{x}}_{j} \). If none of the three conditions referred above are verified, then \( {\mathbf{x}}_{i} \) does not constrain-dominate \( {\mathbf{x}}_{j} \).

The Genetic Algorithm \( {\mathbf{GA}}^{ (2 )} \) is used to solve the bi-objective constrained optimization problem defined from Eqs. (4) and (8) and performs in following sequence (Conceição António 2013; António 2001, 2002; António et al. 2004):

  • Step1: Initialization of the short population \( {\mathbf{X}}^{ (0 )} \). The initial population of design solutions for x is randomly generated using a uniform probability distribution function (PDF).

  • Step 2: Mating selection mechanism. The short population \( {\mathbf{X}}^{ (t )} \) is ranked according to individual fitness defined in Eqs. (19) and (20). The elite group of \( {\mathbf{X}}^{ (t )} \) is determined. One couple of parents \( {\mathbf{z}}_{ 1} \) and \( {\mathbf{z}}_{ 2} \) per each offspring individual is generated. The mating selection is elitist: one parent comes from the elite group and another from the least fitted one.

  • Step 3: Offspring generation mechanism. The crossover operator generates a new offspring chromosome by recombination of the genes of each couple of parent chromosomes \( {\mathbf{z}}_{ 1} \) and \( {\mathbf{z}}_{ 2} \). The offspring genetic material is obtained using the multi-point combination technique known as parameterized uniform crossover (António 2001, 2002). This crossover operator is applied with a predefined probability to select the offspring genetic material from the best-fitted chromosome. The procedure is repeated until the offspring group \( {\mathbf{O}}^{ (t )} \) is completed.

  • Step 4: Intermediate selection. The current short population \( {\mathbf{X}}^{ (t )} \) is transferred to an intermediate stage where is joined to the offspring group \( {\mathbf{O}}^{ (t )} \) generating the intermediate short population \( {\mathbf{X}}^{ (t )} \cup {\mathbf{O}}^{ (t )} \).

  • Step 5: Elimination/Replacement by genetic similarity control. The population \( {\mathbf{X}}^{ (t )} \cup {\mathbf{O}}^{ (t )} \) is ranked according to the individual fitness. Then, the similarity control is performed gene by gene followed by elimination of solutions with similar genetic properties and subsequent replacement by new randomly generated individuals. The new short population \( {\mathbf{X}}^{ (t + 1,* )} \) is ranked and the individuals with worst fitness are replaced by a group of new solutions obtained from the Mutation operator. During this procedure the original size of the short population is recovered.

  • Step 6: Implicit Mutation. A chromosome set group which genes are generated in a random way is introduced into the population. This new group of chromosomes will be recombined with the remaining individuals into the population during next generations (António 2001, 2002). After mutation, the new short population \( {\mathbf{X}}^{ (t + 1 )} \) is obtained.

  • Step 7: Building of global Pareto front. At the beginning (t = 0), all individuals of short population, \( {\mathbf{X}}^{ (t + 1 )} \) are transferred to enlarged population, \( {\mathbf{EP}}^{ (t )} \). At each generation, for t > 0, the individuals generated by “new” inside \( {\mathbf{X}}^{ (t + 1 )} \) are transferred to \( {\mathbf{EP}}^{ (t )} \). A genetic similarity control is performed at \( {\mathbf{EP}}^{ (t )} \). The \( {\mathbf{EP}}^{ (t )} \) is organized based on the concept of dominance applied in each t-th generation of the evolutionary process (Conceição António 2013). To do this the concepts of dominance previously described are applied to individuals stored at \( {\mathbf{EP}}^{ (t )} \). Given the size and history of this population, the dominance is applied in the global sense, allowing the progressive construction of global Pareto front. As the process is continuously applied at every generation, it is possible that an individual with non-dominated status will be subsequently dominated. After some generations the individual solution \( {\mathbf{x}}_{i} \in {\mathbf{EP}}^{ (t )} \) is eliminated if \( rank ({\mathbf{x}}_{i} {\mathbf{)}} \ge \overline{r} \), where \( \overline{r} \) is the maximum ranking of \( {\mathbf{EP}}^{ (t )} \). This leads to an increased historical record of global rank 1 individuals/non-dominated solutions inside \( {\mathbf{EP}}^{ (t )} \) during the course of the evolutionary process obtaining finally the global Pareto front (Conceição António 2013). The enlarged population \( {\mathbf{EP}}^{ (t )} \) is continuously updated during the evolutionary process.

  • Step 8: Final selection. The new short population \( {\mathbf{X}}^{ (t + 1 )} \) is transferred to next generation and the evolutionary process will continue until the stopping criteria are reached.

  • Step 9: Stopping criterion analysis. The stopping criterion used in the convergence analysis is based on the relative variation of the mean fitness of a reference group inside short population \( {\mathbf{X}}^{ (t + 1 )} \) considering the constraints feasibility. The search is stopped if the mean fitness of the reference group does not evolve after a finite number of generations. Otherwise, the short population, \( {\mathbf{X}}^{ (t + 1 )} \) evolves to the next generation returning to Step 2. If the convergence is reached then the optimal Pareto front (rank 1) is found inside enlarged population \( {\mathbf{EP}}^{ (t )} \) (rank 1 solutions).

5 Global sensitivity analysis

The study of the influence of the weight composition of raw materials on the structural response of adhesive joint is performed based on the Global Sensitivity Analysis (GSA) supported by variance-based methods (António and Hoffbauer 2010, 2013; Borgonovo et al. 2003; Saltelli et al. 2006; António and Hoffbauer 2008). The creep rate, CR and the peel strength, PS are considered as measures of structural response of the adhesive joint. On other words, the objective is to measure and to rank the importance of the variability of design variables—the weight percentages of PUs, resins and additives in the adhesive composition, on the structural response of adhesive joint measured by creep rate, CR and the peel strength, PS.

Lets consider β j the response functional, denoting the creep rate or the peel strength. Assuming that the variables are independent, the variance of the conditional expectation \( {{var}} \left( {E\langle \beta_{j} |x_{i} \rangle } \right) \) is used as an indicator of the importance of the design variable x i on the variance of β j . This indicator is directly proportional to the importance of x i . In particular, the first-order global sensitivity index of Sobol (António and Hoffbauer 2010, 2013; Borgonovo et al. 2003; Saltelli et al. 2006; António and Hoffbauer 2008) is used as normalized indicator:

$$ S_{i} (\beta_{j} )= \frac{{{{var}} \left( {E\langle \beta_{j} |x_{i} \rangle } \right)}}{{{{var}} (\beta_{j} )}} $$
(23)

In this work, the above first-order global sensitivity index of Sobol is calculated using the Monte Carlo simulations method together ANN. So, the GSA is implemented using the optimal network configuration \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \) obtained at the end of first stage: ANN learning procedure of the proposed approach. Thus, is possible to avoid the exhaustive and costly experimental tests to obtain the variability of the input variables structural on response.

The methodology to obtain the first-order global sensitivity index of Sobol is based on the algorithm proposed by António and Hofbauer (António and Hoffbauer 2013, 2008), which is described as follows:

  • Step 1: Lets consider the non-correlated design variables vector x following a uniform probability distribution function \( Unif (0,\,\,1 ) \).

  • Step 2: Considers a set of random numbers \( {\varvec{\uplambda}}_{fix} \) following a uniform probability distribution function \( Unif (0,\,\,1 ) \). These N f random numbers are used to generate the fixed values for the design variable x i .

  • Step 3: For each design variable x i (not for itself) a sample matrix \( {\mathbf{J}}_{\alpha } \) is generated by independently collecting samples of (p − 1) random numbers following a uniform distribution \( Unif (0,\,\,1 ) \), where the size of the sample is N r .

  • Step 4: For each design variable x i a combination of values of \( {\varvec{\uplambda}}_{fix} \) and \( {\mathbf{J}}_{\alpha } \) is defined. The structural response of β j is evaluated for x using the optimal configuration of the ANN, \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \). The conditional expectation of structural response of adhesive joint is estimated and the mean values of this conditional expectation are calculated. Finally, the variance of the conditional expectation of structural response fixing each design variable x i is estimated. The procedure is repeated for all design variables.

  • Step 5: The variance of structural response \( {{var}} (\beta_{j} ) \), is estimated considering the previous simulations.

  • Step 6: Calculation of the global Sobol sensitivity index using Eq. (23) for all design variables.

6 Results, analysis and validation

6.1 Planned experimental testing and results

According to the first column of the proposed optimization strategy it id needed to built physical model representing the adhesive joint of footwear product and the relationship between the design variables—the weight composition of raw materials, and the inherent structural response measured by creep rate and peel strength. Then, these testing results are used the ANN learning procedure aiming to develop the approximation model.

Several compositions of raw materials are considered in the proposed planned tests, as shown in Table 2. The design points used to plan the experiments are considered as input values in the ANN learning procedure. A number of training data sets are selected inside the interval domain of each design (random) variable and levels defined in Table 2. The Taguchi values are selected according to the approach proposed by Taguchi and Konishi (Taguchi and Konishi 1987).

Table 2 Materials used in adhesive joint and Taguchi levels definition
Full size table

A number of 13 raw materials are considered in adhesive joint with variable weight percentage. The raw materials are grouped into PUs, resins (REs) and additives (ADs). Some constraints are imposed to the three groups as presented in Table 3. These constraints are associated with some technological acknowledge on adhesive joins used in footwear industry.

Table 3 Constraints considered in adhesive joint optimization definition
Full size table

Using the Taguchi Table L27(313) (Taguchi and Konishi 1987) the actual composition for each design point is obtained, as shown in Table 4. The values presented in Tables 4 and 5, are used as input/output patterns for learning procedure of ANN.

Table 4 Taguchi design points: % weight on formulation (design variables values)
Full size table
Table 5 Peel strength (N/mm) and Creep rate (mm/min) for Taguchi design points obtained by experiments
Full size table

From a first analysis of Tables 4 and 5 it is possible to see that maximizing the amount of colophony and hydrocarbon resin on the adhesive formulation, a very high creep rate is obtained. On other hand, maximizing the amount of resins and additives and minimizing the amount of PU on the adhesive formulation, we obtain very low peel strength. These features show the needs to implement a MDO procedure.

6.2 First stage: results and analysis of ANN learning procedure

As previously established a number of 13 raw materials are considered as input parameters against 2 output parameters, the creep rate CR and the peel strength, PS. A number of 8 neurons are considered for the hidden layer of the ANN topology. The ANN learning procedure described in Sect. 4.4 is applied in the ANN developments. The procedure is based on the solution of the maximization problem of fitness function \( FIT^{ (1 )} \) with size constraints that is defined in Eq. (18). The ANN learning procedure is performed by \( {\mathbf{GA}}^{ (1 )} \) using a population \( {\mathbf{P}}^{ (t )} \) with 30 individuals in evolutionary search. The population \( {\mathbf{P}}^{ (t )} \) is composed by 10 and 3 individuals/solutions in elite and mutation groups, respectively (António 2001, 2002; António et al. 2004). The binary code format with five digits is adopted for weights of synapses and biases of neural nodes. The domain of learning design variables Ω is associated with the intervals [−3, 3] and [−2, 2] for both input-hidden and hidden-output linkages, respectively. After 30.000 generations the ANN learning procedure is concluded. The constants in Eq. (18) are c 1 = 5000, c 2 = 1000, c 3 = 0 and \( K^{ (1 )} = 5. \times 10^{5} \).

Figures 6 and 7 show the evolution of the error parcels at ANN learning procedure based on \( {\mathbf{GA}}^{ (1 )} \) along first stage of the proposed optimization strategy. The root-mean-squared error (RMSE) mean relative error (RE) components are defined in Eqs. (14) and (15), respectively. The mean relative error of 3.45 % is reached for optimal configuration \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \) at the end of ANN learning procedure.

Fig. 6
figure 6

Evolution of root-mean squared error at ANN learning procedure based on \( {\mathbf{GA}}^{ (1 )} \)

Full size image
Fig. 7
figure 7

Evolution of mean relative error at ANN learning procedure based on \( {\mathbf{GA}}^{ (1 )} \)

Full size image

6.3 Second stage: results and analysis of the optimal design procedure

The objectives to be minimized are the creep rate, CR and the inverse of peel strength, 1/PS (equivalent to maximize PS) subject to technological constraints associated to the weight composition of raw materials used in the adhesive joint. The design variables are the weight percentages of PUs, resins and additives in the adhesive composition. The bi-objective optimization was formulated from Eqs. (4) to (8).

In the second stage the original constrained bi-objective optimization problem is transformed for evolutionary search format in Eqs. (19) and (20). The MDO process evolution is based on a short population of solutions \( {\mathbf{X}}^{ (t )} \) updated during the evolutionary search driven by the genetic algorithm, \( {\mathbf{GA}}^{ (2 )} \) and supported by an elitist strategy as explained in Sect. 4.5. Furthermore the global Pareto-optimal front is built along the evolutionary process at enlarged population, \( {\mathbf{EP}}^{ (t )} \) using the concepts of Pareto dominance detailed in Sects. 4.1 and 4.5. The fitness function \( FIT^{ (2 )} \), depends on design variables associated with the weight percentages of raw material constituents used in the adhesive formulation. The fitness evaluation is based on optimal configuration \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \) of the end of first stage of ANN learning procedure of the proposed MDO strategy approach as shown in Fig. 5.

The bi-objective optimization problem is solved with imposition of technological constraints defined from Eqs. (5) to (7). The constraints in those equations are normalized as previously referred in Sect. 4.5. The constants q i and R i in constraint terms on Eqs. (19) and (20) are calculated considering two constraint violation degrees, as follows:

  • a penalization equal to 100 for strong violation value equal to 0.1;

  • a penalization equal to 1 for fair violation value equal to 0.01.

The constants α 1 = α 2 = 0.5, α 3 = 1. and \( K^{ (2 )} = 1. \times 10^{4} \) are select for fitness function \( FIT^{ (2 )} \) defined in Eq. (19).

A short population \( {\mathbf{X}}^{ (t )} \) with 30 individuals is considered on the evolutionary search performed by \( {\mathbf{GA}}^{ (2 )} \). The elite and mutation groups used in \( {\mathbf{GA}}^{ (2 )} \) have 10 and 6 solutions, respectively (António 2001, 2002; António et al. 2004). The side constraints in Eq. (8) associated with upper and lower limits for design variables—the weight composition of raw materials are according to the third column of Table 2. The design variables are encoded using a binary code format with 5 digits. A number of 8000 generations is considered in MDO evolutionary search performed by \( {\mathbf{GA}}^{ (2 )} \) on to this second stage of the proposed optimization strategy approach.

Figure 8 shows the distribution of solutions at two moments of evolution of the enlarged population, \( {\mathbf{EP}}^{ (t )} \), namely for t = 2000 generations and t = 8000 generations. The concepts of Pareto dominance are applied to individuals stored in \( {\mathbf{EP}}^{ (t )} \). After some generations the individual solution \( {\mathbf{x}}_{i} \in {\mathbf{EP}}^{ (t )} \) is eliminated if \( rank ({\mathbf{x}}_{i} {\mathbf{)}} \ge \overline{r} \), where \( \overline{r} = 20 \) is the maximum ranking of \( {\mathbf{EP}}^{ (t )} \) as established in Sect. 4.5. An improvement is observed from generation t = 2000 to generation t = 8000 in ranked solutions. The minimization of both objectives drives the ranked solutions toward the left and lower corner of the graph.

Fig. 8
figure 8

Evolution of solutions (rank <21) for the constrained bi-objective optimization

Full size image

At the end of the optimization process, the Pareto front representing the frontier of the trade-off between the minimum creep rate and minimum inverse peel strength (maximum peel strength) for footwear adhesive joints is obtained, as shown in Fig. 9. The global dominance measured in enlarged population \( {\mathbf{EP}}^{ (t )} \) at end of optimal design procedure is used to trace the associated Pareto front. The performance of the proposed approach to search for Pareto front’s solutions considering the MDO problem can be observed.

Fig. 9
figure 9

Optimal Pareto front (8000 generations) for the constrained bi-objective optimization procedure with possible best trade-off solutions (dashed line circle)

Full size image

According to the considerations made in Sect. 4.3, the point on the optimal Pareto front associated with the minimum distance to origin (utopia point) can be defined as the best mathematical trade-off between the minimum creep rate and minimum inverse peel strength (maximum peel strength). Two points are identified by dashed line circle in Fig. 9. Their values of the objective functions of the bi-objective optimization problem and the corresponding optimal best trade-off solutions for the weight composition of raw material of the adhesive joint are presented in Fig. 10. The design variables are numbered according Table 2.

Fig. 10
figure 10

Compositions of the adhesive joint for two best trade-off solutions collected from the optimal Pareto front

Full size image

The optimal values shown in Fig. 10 are obtained under constraints on weight composition of raw materials of the adhesive joint as referred in Table 3. The feasibility of composition group values for the two trade-off solutions can be observed by comparison with constraint intervals presented in Table 6.

Table 6 Feasibility of composition group values for the two best trade-off solutions
Full size table

The optimal results corresponding to the two best trade-off solutions of the constrained bi-objective optimization problem solved using the proposed approach is consistent with the experimental testing data used to implement the model. Indeed, the creep rate and the inverse of peel strength are minimized when large quantities for PUs (design variables 1–3) and for some quantities of additives (design variables 10–13) are considered. In this case the resins` group is not important except the weight percentage of Vynil (design variable 9).

6.4 Experimental validation of results

Experimental tests are implemented using the optimal design values presented in previous section. In particular, the best trade-off Pareto front solution corresponding to numerical values CR = 0.011198 (mm/min), PS = 7.985 (N/mm) shown in Fig. 10, is used for experimental validation. The weight formulation (%) of raw materials of the solution is considered to build the test pieces for the experimental validation.

The validation results for peel strength are shown in Fig. 11. Since the perfect anchorage of the adhesive to TR in peel strength test the observed failure was cohesive. This failure occurs between the two vertical dashed lines as shown in Fig. 11. Over a load equal to 258 N corresponding to first vertical dashed line, the experiment is driven to trial the TR material instead the adhesive. This change of test conditions increases the load because the strength of TR is higher than the strength oh adhesive joint. The final failure occurred after the second vertical line in the TR material. From the previous considerations a mean failure load of adhesive joint is taken for peel strength calculation.

Fig. 11
figure 11

Peel experimental test curve obtained for the best trade-off Pareto solution with composition corresponding to CR = 0.011198 (mm/min), PS = 7.985 (N/mm) in Fig. 10

Full size image

The peel strength per unit of width was determined by the ratio between the force and the width of the overlap joint that is equal to 30 mm as referred in Sect. 3.2. So, the experimental peel strength value of 9.4 N/mm is considered, which is slightly upper the numerical result.

The same best trade-off solution with composition corresponding to CR = 0.011198 (mm/min), PS = 7.985 (N/mm) in Fig. 10 is considered for creep rate experimental test. The complete creep rate experimental test curve is shown in Fig. 12.

Fig. 12
figure 12

Creep rate experimental test curve (complete) obtained for the best trade-off Pareto solution with composition corresponding to CR = 0.011198 (mm/min), PS = 7.985 (N/mm) in Fig. 10

Full size image

Since the primary and the tertiary phase are ignored on the calculation of the mean of the separation lengths of the bond only the secondary phase in curve plotted in Fig. 12 is considered to evaluate the creep rate as referred in Sect. 3.2. The creep rate experimental test curve for the second phase is shown in Fig. 13. The slope of the line obtained by linear regression of the experimental results corresponds to the creep rate. This experimental value is equal to 0.0134 mm/min, which is close to the numerical one, CR = 0.011198 mm/min.

Fig. 13
figure 13

Creep rate experimental test curve (second phase) obtained for the best trade-off Pareto solution with composition corresponding to CR = 0.011198 (mm/min), PS = 7.985 (N/mm) in Fig. 10. Linear regression of experimental values is plotted

Full size image

6.5 Results and discussion of global sensitivity analysis (GSA)

The GSA indices are obtained through ANN-Monte Carlo approach based on the algorithm described in Sect. 5 (António and Hoffbauer 2013, 2008). Using the optimal configuration \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \) a Monte Carlo simulation procedure is implemented aiming to study the sensitivity of the structural response of adhesive joint relatively to design variables that are the weight composition of raw materials. The referred algorithm is designed to obtain the first-order global sensitivity index of Sobol as defined in Eq. (23). Two normalized Sobol indices are calculated as follows,

$$ S_{i} (CR )= \frac{{{{var}} \left( {E\langle CR|x_{i} \rangle } \right)}}{{{{var}} (CR )}} $$
(24)
$$ S_{i} (PS )= \frac{{{{var}} \left( {E\langle PS|x_{i} \rangle } \right)}}{{{{var}} (PS )}} $$
(25)

The above sensitivity indices are used to establish the relative importance of the design variables (António and Hoffbauer 2013, 2008). According the theory presented in Sect. 5, the samples size values N f  = 50 and \( N_{r} = 1 0 0 \) are used to obtain the conditional probability for Sobol index. Two sampling procedures are simulated using the optimal \( {\mathbf{P}}_{\text{ANN}}^{\text{opt}} \) and the following aspects are determined:

  • the contribution of the variance of the conditional expectation, \( {{var}} \left( {E\langle CR|x_{i} \rangle } \right) \) for total variance of creep rate, var(CR);

  • the contribution of the variance of the conditional expectation, \( {{var}} \left( {E\langle PS|x_{i} \rangle } \right) \) for total variance of peel strength, var(PS).

After, one first-order Sobol index per design variable x i is obtained using the Eq. (24). The histograms in Fig. 14 show the importance of the design variables measured by first-order Sobol index S i . Figure 14 shows the contribution (%) of the variance of the conditional expectation, \( {{var}} \left( {E\langle \beta {}_{j}|x_{i} \rangle } \right) \), for the total variance of β j , var(β j ), where β j can be creep rate or peel strength.

Fig. 14
figure 14

Importance measure of the input design variables by first-order Sobol index for Creep rate and Peel strength

Full size image

The performance of the adhesive joint is very sensitive to the influence of some weight compositions of raw-materials. The sensitivities depend on the considered performance measures. When the performance is measured by creep rate, the design variables such as weight percentages on PU (material 1 and 2), coumarone-indene resin (material 8) and the additive fumaric acid (material 10) are the most sensitive. If the performance is measured through the peel strength, the design variables such as weight percentages on PU (material 1, 2 and 3), colophony and coumarone-indene resins (material 4 and 8) and chlorinated rubber as additive (material 13) are the most sensitive.

However, in relation to weight percentage of colophony (material 4), the sensitivity is in the negative direction for the creep rate objective minimization. This means that it is a resin when considered on the adhesive composition of the formulation there is an increase of the creep rate. So, this explains why the results obtained in second stage of the optimal design procedure did not consider the colophony in the optimal solution as shown in Fig. 10.

Although the contribution of the additives is related with the improvement of mechanical behavior of PUs and resins, their influence on peel strength is shown through the sensitivities. However this is not observed for the weight percentage of Coumarone-Indene (material 8).

The GSA histograms in Fig. 14 can help the designer to decide on the most important design variables to be considered for the optimization in second stage of the procedure. However, this must be implemented with care due to the synergetic effects between different groups of raw materials used in the composition of the adhesive joints.

7 Conclusions and remarks

A mixed numerical-experimental approach capable to predict and optimize the performance of the footwear adhesive joints, based on the weight composition of used raw materials was presented. The proposed approach is supported by MDO concepts applied to the creep rate minimization and the peel strength maximization under technological constraints. The proposed approach is implemented considering two stages: (1) definition of the physical model based on planned experimental measurements and development of the ANN approximation model; (2) the development of the MDO algorithm that is the engine search of the bi-objective optimization based on the weight composition of adhesive joints.

First of all, the set of experiments are planned using the Taguchi method aiming to obtain a good relationship between performance measures and design variables—weight composition of raw materials used in adhesive joint. After, considering the experimental results obtained for Taguchi design points as input/output patterns, an ANN is developed based on supervised evolutionary learning using a genetic algorithm.

Secondly, a MDO algorithm based on dominance concepts and evolutionary search is proposed aiming to build the optimal Pareto front. The optimal design of adhesive composition to achieve the targets of minimum creep rate and minimum inverse peel strength (maximum peel strength) under manufacturing constraints is performed. The model uses the optimal ANN previously developed to evaluate the fitness functions and the constraints of the optimization problem.

Finally, a ANN-based Monte Carlo simulation procedure is implemented aiming to study the sensitivity of the creep rate and peel strength of the adhesive joint relatively to design variables—weight compositions of raw materials. In particular the Sobol indices for global sensitivity analysis are used to establish the relative importance of the design variables.

The results show the robustness of the proposed approach to build the optimal Pareto front enabling to establish the trade-off between minimum creep rate properties and minimum inverse peel strength (maximum peel strength) of the footwear adhesive joint using the weight composition of raw material constituents as design variables. The optimal results for both performance functions based on proposed approach are reached when large quantities for PUs and for some additives are considered. The performances of adhesive joints measured by creep rate and peel strength are very sensitive to the influence of some PUs and in some way are moderately sensitive to additives.

The proposed MDO approach supported by experimental tests shows improved explorative properties of raw materials and can be a powerfully tool for the designers of adhesive joints in footwear industry. In particular, since the optimal Pareto front is obtained it is possible to consider alternative designs for adhesive joints.