Fracture mechanics analysis of an anti-plane crack in gradient elastic sandwich composite structures

Abstract

The strain gradient elasticity theory is applied to the solution of a mode III crack in an elastic layer sandwiched by two elastic layers of infinite thickness. The model includes volumetric and surface strain gradient characteristic length parameters. Both the near-tip asymptotic stresses and the crack displacement are obtained. Due to stain gradient effects, the magnitudes of the stress ahead of the crack tip are significantly higher than those in the classical linear elastic fracture mechanics. When the gradient parameters reduce to sufficiently small, all results reduce to the conventional linear elastic fracture mechanics results. In addition to the single crack in the finite layer, the solution and the results for two collinear cracks are also established and given.

1 Introduction

Materials at small scales may have significant different behaviours from their bulks. Essential, they show strong size effect that has been observed in experimental studies. Fleck et al. (1994) observed that the normalized torsion hardening of thin copper wires increases significantly as the wire diameter decreases to below ~ 100 microns. Stolken (1997) observed a significant increase in the normalized bending hardening of a beam when its thickness decreases to below a few tens microns. Micro- and nano-indentations also suggest that the measured indentation hardness of metals and ceramics can be double to triple as the width of the indent decreases (Ma and Clarke 1995; Poole et al. 1996; McElhaney et al. 1998). Lam et al. (2003) found that the normalized rigidity of micron-sized beams exhibited an inverse squared dependence on the beam’s thickness. A micro-cantilever experiment also confirmed the size dependence of the stiffness of the material (McFarland and Colton 2005). In the recent years, several experimental and computational studies (Fang et al. 2011; Zeng et al. 2016; Thevamaran et al. 2016) reported that a novel class of materials with gradients nanostructures exhibited a pronounced the strain gradient. These studies represent the latest progress of strain gradient theory and phenomena.

Several theories have been proposed to account for the size effect of solids at small scales. The most classic well-known theories are non-local elasticity theory, couple stress theory and strain gradient theory. In particular, strain gradient effects of materials become important near a crack tip because of the dramatic change of strain gradient ahead of the crack front. A few studies related to a crack in infinite solids were conducted based on gradient elasticity theories. The pioneering works are gradient elasticity with anti-plane shearing of cracks that account for only two material characteristic length constants (these are the volumetric and surface strain gradients) (Vardoulakis et al. 1996). Exadaktylos et al. (1996) and subsequently Exadaktylos (1998) studied the mode I strain gradient fracture. Paulino et al. (2003) and Chan et al. (2008) applied gradient elasticity theory to mode III crack problems in functionally graded materials for cracks that are perpendicular and parallel to the material gradation. Fannjiang et al. (2002) employed a hyper-singular integral–differential equation technology to solve the mode III crack problem basic on strain gradient elasticity theory. Some interesting information related to dislocation based-gradient elastic fracture mechanics for the anti-plane crack problem is discussed by Mousavi and Aifantis (2005). An anti-plane analysis of an infinite plane with multiple cracks based on strain gradient theory was recently carried out by Karimipour and Fotuhi (2017). Very recently, Joseph et al. (2018) studied an infinite medium with a single crack. However, the nature of the stress at the crack tip of they obtained follows the traditional linear elastic fracture mechanics that against most available strain gradient fracture mechanics solutions. Analysis of strain gradient fracture poses significant challenging therefore numerical method such as finite element method has been developed by Wei (2006).

On the other hand, understanding the cracking behavior of multilayered composite materials is critical in understanding their strengths. Fracture mechanics studies of multilayered composite materials based on traditional elasticity theory have been carried out extremely. Strain gradient fracture of multilayered composite materials, however, is very rare. To the authors’ knowledge, most of the strain gradient related fracture studies have been limited to a homogeneous infinite medium. This paper establishes a general approach to investigate the anti-plane (mode III) fracture of an elastic layer sandwiched by two elastic layers with strain gradient effects. Both a single crack and a pair of collinear cracks are studied. The objective is to numerically estimate the crack displacement and the stresses near the crack tip to show the effects of material strain gradient and the finite layer thickness. A summary of the elastic strain gradient theory and the problem description are presented in Sect. 2. The solution of the crack problem through the hypersingular integral equation is given in Sect. 3. Important results for the crack displacement and the crack tip stresses are given in Sect. 4 and the conclusions are summarized in Sect. 5.

2 Theory background for the anti-plane deformation with strain gradient effects

The constitutive equations and theoretical formulations for the anti-plane deformation of strain gradient elastic materials approach considered here are similar to Vardoulakis et al. (1996) and Exadaktylos (1998) that consider two material gradient parameters that are responsible for material volumetric and surface strain gradient terms. Application and validation of this strain gradient theory have been confirmed by Giannakopoulos and Stamoulis (2007).

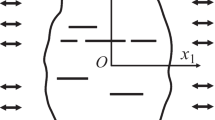
Figure 1 shows a crack of length 2a placed at the mid plane of a strain gradient layer with thickness (height) 2h and sandwiched by two strain gradient layers of infinite thickness. We consider the anti-plane problem such that the only non-vanishing displacement component is along the z axis and is denoted as w. According to the gradient elasticity theory, the stresses and couple stresses derived from the constitutive equations of gradient elasticity with surface energy are given as (Chan et al. 2008; Paulino et al. 2003; Vardoulakis et al. 1996):

$$ \sigma_{xz} = G\left[ {\frac{\partial w}{\partial x} - l^{2} \nabla^{2} \frac{\partial w}{\partial x}} \right],\quad \sigma_{yz} = G\left[ {\frac{\partial w}{\partial y} - l^{2} \nabla^{2} \frac{\partial w}{\partial y}} \right], $$

(1a)

$$ \mu_{xzx} = Gl^{2} \frac{{\partial^{2} w}}{{\partial x^{2} }},\quad \mu_{xzy} = Gl^{2} \frac{{\partial^{2} w}}{\partial x\partial y}, $$

(1b)

$$ \mu_{yzx} = G\left[ { - l'\frac{\partial w}{\partial x} + l^{2} \frac{{\partial^{2} w}}{\partial x\partial y}} \right],\quad \mu_{yzy} = G\left[ { - l'\frac{\partial w}{\partial y} + l^{2} \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right] $$

(1c)

Here $\nabla^{2} = \partial^{2} /\partial x^{2} + \partial^{2} /\partial y^{2}$, l and $l^{\prime}$ are the volumetric and surface material characteristic lengths, respectively, G is the shear modulus, $\sigma$ is the stress tensor, and $\mu$ is the couple stress tensor, l, $l'$ are material lengths related to volume and surface energy, respectively, restricted (in order for the strain energy density to be positive definite) such that $- 1 < l'/l < 1$ (Exadaktylos et al. 1996; Vardoulakis et al. 1996).

Fig. 1

A crack in a strain gradient layer sandwiched by two strain gradient layers (the strain gradients are in x and y directions)

The equilibrium equation remains the same as the classical one and is $\partial \sigma_{xz} /\partial x + \partial \sigma_{yz} /\partial y = 0$. This can be expressed in terms of the displacement component w with the help of Eqs. (1a)–(1c) as

$$ \left[ {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial y^{2} }}} \right] - l^{2} \left[ {\frac{{\partial^{4} w}}{{\partial x^{4} }} + 2\frac{{\partial^{4} w}}{{\partial x^{2} \partial y^{2} }} + \frac{{\partial^{4} w_{z} }}{{\partial y^{4} }}} \right] = 0 $$

(2)

The general solution of the fourth order differential Eq. (2) may be represented as; $w(x,y) = w^{c} (x,y) + w^{g} (x,y)$ (Mousavi and Aifantis 2005), where w^c is the general solution of the harmonic equation $\partial^{2} w/\partial x^{2} + \partial^{2} w/\partial y^{2} = 0$ and w^g is a particular solution of Eq. (2). Due to symmetry, only y ≥ 0 part of the layered material needs to be considered. The application of Fourier transform gives the solution of harmonic equation as

$$ w^{c} (x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {A(s)e^{ - \left| s \right|y} + C(s)e^{\left| s \right|y} } \right]e^{ - isx} {\text{d}}s} . $$

(3a)

A particular solution of Eq. (2) can be given as

$$ w^{g} (x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {B(s)e^{{ - \left| {s_{1} } \right|y}} + D(s)e^{{\left| {s_{1} } \right|y}} } \right]e^{ - isx} {\text{d}}s} . $$

(3b)

where $\left| {s_{1} } \right| = \sqrt {s^{2} + (1/l^{2} )}$. Combining Eqs. (3) and (4) gives the general solution of Eq. (2):

$$ w(x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {A(s)e^{ - \left| s \right|y} + B(s)e^{{ - \left| {s_{1} } \right|y}} + C(s)e^{\left| s \right|y} + D(s)e^{{\left| {s_{1} } \right|y}} } \right]} e^{ - isx} {\text{d}}s. $$

(4)

The constants A(s), B(s), C(s) and D(s) are to be determined from the boundary conditions of the problem. For the purpose of the following analysis, the shear stress $\sigma_{yz} (x,y)$ from Eqs. (1b) and (4) is written as

$$ \sigma_{yz} (x,y) = - \frac{G}{2\pi }\int_{ - \infty }^{\infty } {\left| s \right|\left[ {A(s)e^{ - \left| s \right|y} - C(s)e^{\left| s \right|y} } \right]} e^{ - isx} {\text{d}}s, $$

(5)

and the couple stress $\mu_{yzy} (x,y)$ from Eqs. (1f) and (4) is written as

$$ \begin{aligned} & \mu_{yzy} &= \frac{{Gl^{'} }}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ \begin{aligned} \left| s \right|A(s)e^{ - \left| s \right|y} + \left| {s_{1} } \right|B(s)e^{{ - \left| {s_{1} } \right|y}} \hfill \\ - \left| s \right|C(s)e^{\left| s \right|y} - \left| {s_{1} } \right|D(s)e^{{\left| {s_{1} } \right|y}} \hfill \\ \end{aligned} \right]} e^{ - isx} {\text{d}}s \\ & \quad + \frac{{Gl^{2} }}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ \begin{aligned} A(s)e^{ - \left| s \right|y} s^{2} + B(s)e^{{ - \left| {s_{1} } \right|y}} s_{1}^{2} + \hfill \\ C(s)e^{\left| s \right|y} s^{2} + D(s)e^{{\left| {s_{1} } \right|y}} s_{1}^{2} \hfill \\ \end{aligned} \right]} e^{ - isx} {\text{d}}s. \\ \end{aligned} $$

(6)

Applying the same to the sandwiching layers (the outer layers) to get

$$ w_{2} (x,y) = \frac{1}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {E(s)e^{ - \left| s \right|y} + F(s)e^{{ - \left| {s_{2} } \right|y}} } \right]} e^{ - isx} {\text{d}}s. $$

(7)

where $\left| {s_{2} } \right| = \sqrt {s^{2} + (1/l_{2}^{2} )}$. The constants E(s) and F(s) are to be determined from the boundary conditions of the problem. For the purpose of the following analysis, the shear stress $\sigma_{yz} (x,y)$ from Eqs. (1b) and (7) is written as

$$ \tau_{2yz} (x,y) = - \frac{{G_{2} }}{2\pi }\int_{ - \infty }^{\infty } {\left| s \right|E(s)e^{ - \left| s \right|y} } e^{ - isx} {\text{d}}s, $$

(8)

and the couple stress $\mu_{yzy} (x,y)$ from Eqs. (1f) and (4) is written as

$$ \begin{aligned} \mu_{2yzy} & = \frac{{G_{2} l_{2}^{'} }}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {\left| s \right|E(s)e^{ - \left| s \right|y} + \left| {s_{2} } \right|F(s)e^{{ - \left| {s_{2} } \right|y}} } \right]} e^{ - isx} {\text{d}}s \\ & \quad + \frac{{G_{2} l_{2}^{2} }}{2\pi }\int\limits_{ - \infty }^{\infty } {\left[ {E(s)e^{ - \left| s \right|y} s^{2} + F(s)e^{{ - \left| {s_{2} } \right|y}} s_{2}^{2} } \right]} e^{ - isx} {\text{d}}s. \\ \end{aligned} $$

(9)

The subscript 2 has been used to distinguish the outer layers from the middle layer.

3 Solution of the crack problem

The transmission conditions for ideal interface imply continuity of the stress, couple stress, displacements and rotations (Piccolroaz et al. 2012). From $\sigma_{yz} (x,h) = \tau_{2yz} (x,h)$ we get:

$$ A(s)e^{ - \left| s \right|h} - C(s)e^{\left| s \right|h} = \frac{{G_{2} }}{{G_{1} }}E(s)e^{ - \left| s \right|h} $$

(10)

From $\mu_{yzy} (x,h) = \mu_{2yzy} (x,h)$ we get:

$$ \begin{aligned} & l^{'} \left[ \begin{aligned} \left| s \right|A(s)e^{ - \left| s \right|h} + \left| {s_{1} } \right|B(s)e^{{ - h\left| {s_{1} } \right|}} \hfill \\ - \left| s \right|C(s)e^{\left| s \right|h} - \left| {s_{1} } \right|D(s)e^{{h\left| {s_{1} } \right|}} \hfill \\ \end{aligned} \right] + l^{2} \left[ \begin{aligned} A(s)e^{ - \left| s \right|h} s^{2} + B(s)e^{{ - h\left| {s_{1} } \right|}} s_{1}^{2} + \hfill \\ C(s)e^{\left| s \right|h} s^{2} + D(s)e^{{h\left| {s_{1} } \right|}} s_{1}^{2} \hfill \\ \end{aligned} \right] \\ & \quad = \frac{{G_{2} }}{G}l_{2}^{'} \left[ {\left| s \right|E(s)e^{ - \left| s \right|h} + \left| {s_{2} } \right|F(s)e^{{ - h\left| {s_{2} } \right|}} } \right] + \frac{{G_{2} }}{G}l_{2}^{2} \left[ {E(s)e^{ - \left| s \right|h} s^{2} + F(s)e^{{ - h\left| {s_{2} } \right|}} s_{2}^{2} } \right] \\ \end{aligned} $$

(11)

The displacement and its rotation are also continuous across the interface. Thus,

$$ A(s)e^{ - \left| s \right|h} + B(s)e^{{ - \left| {s_{1} } \right|h}} + C(s)e^{\left| s \right|h} + D(s)e^{{\left| {s_{1} } \right|h}} = E(s)e^{ - \left| s \right|h} + F(s)e^{{ - \left| {s_{2} } \right|h}} . $$

(12)

$$ - A(s)se^{ - \left| s \right|h} - B(s)s_{1} e^{{ - \left| {s_{1} } \right|h}} + C(s)se^{\left| s \right|h} + D(s)s_{1} e^{{\left| {s_{1} } \right|h}} = - E(s)se^{ - \left| s \right|h} - F(s)s_{2} e^{{ - \left| {s_{2} } \right|h}} . $$

(13)

Due to symmetry, the non-classical boundary condition on the cracked plane of the medium is $\mu_{yzy} (x,0) = 0$ for any value of x [derived from the variational principal (Chan et al. 2008; Paulino et al. 2003)]. Therefore

$$ l'\left[ \begin{aligned} \left| s \right|A(s) + \left| {s_{1} } \right|B(s) \hfill \\ - \left| s \right|C(s) - \left| {s_{1} } \right|D(s) \hfill \\ \end{aligned} \right] + l^{2} \left[ \begin{aligned} A(s)s^{2} + B(s)s_{1}^{2} + \hfill \\ C(s)s^{2} + D(s)s_{1}^{2} \hfill \\ \end{aligned} \right] = 0 $$

(14)

As usually in the fracture mechanics analysis, the crack surfaces are assumed to be subjected to an applied anti-plane shear stress $p(x)$ such that the following mixed boundary conditions on the y = 0 plane hold [these boundary conditions were also used by Paulino et al. (2003) and Chan et al. (2008)]:

$$ \tau_{y} (x,0) = - p,\quad \left| x \right| < a $$

(15a)

$$ w(x,0) = 0,\quad \left| x \right| \ge a $$

(15b)

3.1 The singular integral equation

The six boundary conditions, Eqs. (10)–(15) are sufficient for determining the full-field solution of the problem. For this, we introduce a discontinuity function g(x) along the cracked plane according to

$$ g(x) = 2\frac{\partial w(x,0)}{\partial x}. $$

(16)

By this define, the continuity condition for the displacement on the y = 0 plane requires that $g(x) = 0$ for $\left| x \right| \ge a$ and $\int_{ - a}^{a} {g\left( x \right)dx} = 0$, which is the single-value condition.

Substituting Eq. (4) into Eq. (16) and with Fourier inversion, a relationship between A(s), B(s), C(s) and D(s) can be obtained:

$$ A(s) + B(s) + C(s) + D(s) = \frac{i}{2s}\int_{ - a}^{a} {g(r)e^{isr} {\text{d}}r} , $$

(17)

The system of six equations, Eqs. (10)–(14) and (16), can be used to express A(s), B(s), C(s) D(s), E(s) and F(s), in terms of the single unknown function g(x). In particular, suppose the expressions for A(s) and C(s) are, respectively,

$$ A(s) = \overline{A} (s)\frac{i}{2s}\int_{ - a}^{a} {g(r)e^{isr} {\text{d}}r} $$

(18a)

and

$$ C(s) = \overline{C} (s)\frac{i}{2s}\int_{ - a}^{a} {g(r)e^{isr} {\text{d}}r} $$

(18b)

Then the shear stress on the cracked obtained with the submission of Eqs. (18a) and (18b) into Eq. (5) is

$$ \sigma_{yz} (x,0) = G\int_{ - a}^{a} {R(x,r)} g(r){\text{d}}r $$

(19)

where the integral kernel $R(x,r)$ is

$$ R(x,r) = \mathop {\lim }\limits_{y \to + 0} \frac{i}{2\pi }\int_{ - \infty }^{\infty } {\frac{1}{2}\frac{\left| s \right|}{s}\left( { - \overline{A} (s)e^{ - \left| s \right|y} + \overline{C} (s)e^{\left| s \right|y} } \right)e^{is(r - x)} {\text{d}}s} . $$

(20)

or

$$ R(x,r) = \mathop {\lim }\limits_{y \to + 0} \frac{1}{2\pi }\int_{0}^{\infty } {\left( {\overline{A} (s)e^{ - \left| s \right|y} - \overline{C} (s)e^{\left| s \right|y} } \right)\sin [s(r - x)]{\text{d}}s} . $$

(21)

In order to identify the asymptotic behaviour of $\overline{A} (s) - \overline{C} (s)$ for s at infinity, one can consider a crack of length 2a at the infinite medium of the same material of the layer. This is, one considers h to be equal to infinity. After examining, it is found that for large values of s, $\overline{C} (s)$ and $\overline{D} (s)$ become vanishing and $\overline{A} (s)$ approaches to $1 + l^{2} s^{2} + \frac{l'}{2}\left| s \right| - \left( {\frac{l'}{2l}} \right)^{2}$. This function is denoted as $\varLambda_{0} (s)$ in the following analysis. In fact, the expression of $\varLambda_{0} (s)$ has been obtained previously by Chan et al. (2008) and Paulino et al. (2003). The asymptotic analysis allowing splitting of the integral kernel $R(x,r)$ into two parts so that the stress of Eq. (18) can be re-written as:

$$ \sigma_{yz} (x,0) = G\int_{ - a}^{a} {\varOmega (x,r)} g(r){\text{d}}r + G\int_{ - a}^{a} {R_{\infty } (x,r)} g(r){\text{d}}r $$

(22)

where the regular kernel is

$$ \varOmega (x,r) = \frac{1}{2\pi }\int_{0}^{\infty } {\left( {\overline{A} (s) - \overline{C} (s) - \varLambda_{0} (s)} \right)\sin [s(r - x)]{\text{d}}s} , $$

(23)

and the singular kernel is

$$ R_{\infty } (x,r) = \frac{1}{2\pi }\int_{0}^{\infty } {\left[ {1 + l^{2} s^{2} + \frac{l'}{2}s - \left( {\frac{l'}{2l}} \right)^{2} } \right]\sin [s(r - x)]{\text{d}}s} . $$

(24)

The regular kernel, Eq. (23) can be evaluated by standard numerical integral technique. The singular kernel, Eq. (24) can be evaluated by hypersingular integral equation technique of Paulino et al. (2003) and Chan et al. (2003). As a result of such procedure, we get

$$ \begin{aligned} & \sigma_{yz} (x,0) = - \frac{{Gl^{2} }}{\pi }\int_{ - a}^{a} {\frac{g(r)}{{(r - x)^{3} }}{\text{d}}r} + \frac{{G\left( {1 - [l'/(2l)]^{2} } \right)}}{2\pi }\int_{ - a}^{a} {\frac{g(r)}{r - x}{\text{d}}r} \\ & \quad + \frac{Gl'}{4}g'(x) + G\int_{ - a}^{a} {\varOmega (x,r)} g(r){\text{d}}r \\ \end{aligned} $$

(25)

Equation (25) provides the expression for $\tau_{y} (x,0)$ outside as well as inside the crack. In the case of inside the crack, application of the crack face stress boundary condition, Eq. (15a) will yield the function g(x). Details will be given in following subsection

3.2 Numerical solution of the singular integral equation

In the case of inside the crack, applying the crack face stress boundary condition to Eq. (25) gives

$$ - \frac{{(l/a)^{2} }}{\pi }\int_{ - 1}^{1} {\frac{g(r)}{{(\overline{r} - \overline{x} )^{3} }}{\text{d}}\overline{r} } + \frac{{1 - [l'/(2l)]^{2} }}{2\pi }\int_{ - a}^{a} {\frac{g(r)}{{\overline{r} - \overline{x} }}{\text{d}}\overline{r} } + \frac{l'/a}{4}g'(\overline{x} ) + a\int_{ - 1}^{1} {\varOmega (x,r)} g(r){\text{d}}\overline{r} = - \frac{p}{G} $$

(26)

Here and in the following, the notations $\overline{x} = x/a$ and $\overline{r} = r/a$ are used. Equation (26) is a hypersingular integral equation. According to Chan et al. (2008) and Paulino et al. (2003), the solution of g(r) can be expressed in the following form:

$$ g(\overline{r} ) = \sum\limits_{{m{ = 1}}}^{\infty } {C_{m} U_{m} (\overline{r} )\sqrt {1 - \overline{r}^{2} } } $$

(27)

in which U_m is the Chebyshev polynomial of the second kind, $U_{m} (\overline{x} ) = \frac{{\sin [(m + 1){\text{ar}}\cos (\overline{x} )]}}{{\sqrt {1 - \overline{x}^{2} } }}$, and C_m are unknowns to be evaluated. It is observed that the single-value condition of g(x), Eq. (15b), is identically satisfied by Eq. (27). After substituting Eq. (27), truncated with the first M terms, into Eq. (26), following the same procedure of Chan et al. (2008) and Paulino et al. (2003), and through expansions and integrals of Chebyshev polynomials, which is listed in “Appendix” (Wei 2006), it can be seen that

$$ \begin{aligned} & - \frac{{(l/a)^{2} }}{{4(1 - \overline{x}^{2} )}}\sum\limits_{m = 1}^{M} {C_{m} \left[ {m(m + 1)U_{m + 1} (\overline{x} ) - (m^{2} + 3m + 2)U_{m - 1} (\overline{x} )} \right]} \\ & \quad - \frac{{1 - [l'/(2l)]^{2} }}{2}\sum\limits_{m = 1}^{M} {C_{m} T_{m + 1} (\overline{x} )} - \frac{l'/a}{4}\frac{1}{{\sqrt {1 - \overline{x}^{2} } }}\sum\limits_{m = 1}^{M} {(m + 1)T_{m + 1} (\overline{x} )C_{m} } \\ & \quad + a\sum\limits_{m = 1}^{M} {C_{m} } V_{m} (\overline{x} ) = - \frac{p}{G} \\ \end{aligned} $$

(28)

where T_m is the Chebyshev polynomial of the first kind $T_{m} (\overline{x} ) = \cos [m{\text{ar}}\cos (\overline{x} )]$, and V_m is

$$ V_{m} (\overline{x} ) = \int_{ - 1}^{1} {\varOmega (x,r)U_{m} (\overline{r} )\sqrt {1 - \overline{r}^{2} } {\text{d}}\overline{r} } , $$

(29)

For the case of infinite layer sandwiched layer thickness, the regular integral kernel $\varOmega (x,r)$ vanishes and Eq. (28) becomes:

$$ \begin{aligned} & - \frac{{(l/a)^{2} }}{{4(1 - \overline{x}^{2} )}}\sum\limits_{m = 1}^{\infty } {C_{m} \left[ {m(m + 1)U_{m + 1} (\overline{x} ) - (m^{2} + 3m + 2)U_{m - 1} (\overline{x} )} \right]} \\ & \quad - \frac{{1 - [l'/(2l)]^{2} }}{2}\sum\limits_{m = 1}^{\infty } {C_{m} T_{m + 1} (\overline{x} )} - \frac{l'/a}{4}\frac{1}{{\sqrt {1 - \overline{x}^{2} } }}\sum\limits_{m = 1}^{\infty } {(m + 1)T_{m + 1} (\overline{x} )C_{m} } = - \frac{p}{G} \\ \end{aligned} $$

(30)

The simplest method for solving the functional Eq. (28) is using an appropriate collocation in x. This is, we used M allocation points, x = x₁, x = x₂,…, x = x_M, so that Eq. (28) is satisfied for all allocation points. Therefore, Eq. (28) will yields M linear algebraic equations:

$$ \begin{aligned} & - \frac{{(l/a)^{2} }}{{4(1 - \overline{x}^{2} )}}\sum\limits_{m = 1}^{M} {C_{m} \left[ {m(m + 1)U_{m + 1} (\overline{x}_{m} ) - (m^{2} + 3m + 2)U_{m - 1} (\overline{x}_{m} )} \right]} \\ & \quad - \frac{{1 - [l'/(2l)]^{2} }}{2}\sum\limits_{m = 1}^{M} {C_{m} T_{m + 1} (\overline{x}_{m} )} - \frac{l'/a}{4}\frac{1}{{\sqrt {1 - \overline{x}^{2} } }}\sum\limits_{m = 1}^{M} {(m + 1)T_{m + 1} (\overline{x}_{m} )C_{m} } \\ & \quad + a\sum\limits_{m = 1}^{M} {C_{m} } V_{m} (\overline{x}_{m} ) = - \frac{p}{G},\quad m = 1,2, \ldots ,M \\ \end{aligned} $$

(31)

The solution of Eq. (28) will give C₁, C₂,…, C_M. In this paper, the allocation points are chosen according to:

$$ x_{m} = \cos \left[ {\frac{(m - 0.5)\pi }{M}} \right],\quad m = 1,2, \ldots ,M $$

(32)

After evaluating C_m from Eq. (31), the displacement field can be calculated from Eq. (4) since A(s), B(s), C(s) and D(s) have been expressed in terms of g(x). The associated stress can be obtained from the constitutive equations of Eqs. (1a)–(1c). Thus, the full field solution is obtained.

3.3 Fracture mechanics paramaters

Of particular interest are the crack opening displacement and the crack tip stress state. The displacement jump across the crack can be evaluated from $\Delta w(x,0) = \int_{ - a}^{x} {g(r){\text{d}}r}$. With the substituting of Eq. (27), we get

$$ \Delta w(x,0) = a\sum\limits_{m = 1}^{M} {C_{m} } \left( {\frac{{\sin [(m + 2){\text{arcos(}}x/a)]}}{2(m + 2)} - \frac{{\sin [m{\text{ arcos(}}x/a)]}}{2m}} \right),\quad \left| x \right| < a. $$

(33)

Due to symmetry, the displacement on the upper surface of the crack w(x,0) is half of $\Delta w(x,0)$. The maximum crack face displacement appears at x = 0 on the upper surface of the crack and is $w(0,0) = \frac{\Delta w(0,0)}{2} = - a\sum\limits_{m = 1}^{M} {C_{m} } \frac{\sin (m \, \pi / 2)}{4}\left( {\frac{1}{m + 2} + \frac{1}{m}} \right)$.

For gradient elasticity theory, $\tau_{y}$ have a strong singularity, which can not be described by conventional linear elasticity fracture mechanics. Note that the expression for $\tau_{y} (x,0)$ is valid for $\left| x \right| < a$ as well as $\left| x \right| > a$. Equation (25) provides the expression for $\tau_{y} (x,0)$ outside as well as inside the crack. With the substitution of the density function (27) and again through expansions of Chebyshev polynomials (Chan et al. 2008), the stress near the crack tip is found to be (neglect the secondary terms):

$$ \begin{aligned} \sigma_{yz} (x,0) & = - \frac{{G\left( {1 - [l_{1} /(2l)]^{2} } \right)}}{2}\sum\limits_{{m{ = 1}}}^{\infty } {C_{m} \left( {\overline{x} - \frac{\left| x \right|}{x}\sqrt {\overline{x}^{2} - 1} } \right)}^{m + 1} \\ & \quad + \frac{{G(l/a)^{2} }}{2}\sum\limits_{{m{ = 1}}}^{\infty } {C_{m} (m + 1)\left( {\overline{x} - \frac{\left| x \right|}{x}\sqrt {\overline{x}^{2} - 1} } \right)^{m - 1} \left[ {m\left( {1 - \frac{{\left| {\overline{x} } \right|}}{{\sqrt {\overline{x}^{2} - 1} }}} \right)^{2} + \frac{{\overline{x} - \frac{\left| x \right|}{x}\sqrt {\overline{x}^{2} - 1} }}{{\left( {\sqrt {\overline{x}^{2} - 1} } \right)^{3} }}} \right]} \\ \end{aligned} $$

(34)

The highest singularity is $(\overline{x} - 1)^{3/2}$. This is totally different from the conventional linear elasticity fracture mechanics result, which gives $(\overline{x} - 1)^{1/2}$ singularity.

Because the stresses are singular at the crack tips, it is necessary to study the intensity of the stress concentration near the crack front. For this, it is important to recognize that the stresses at the crack tip have (x² − a)^−3/2 singularity when x → a⁺ or x → − a⁻. Paulino et al. (2003) and Chan et al. (2008) defined the generalized stress intensity factor K_III according to

$$ K_{\text{III}} ( - a) = \mathop {\lim }\limits_{{x \to - a^{ - } }} \sqrt {2\pi (x + a)} (x + a)\sigma_{yz} (x,0) $$

(35a)

and

$$ K_{\text{III}} (a) = \mathop {\lim }\limits_{{x \to a^{ + } }} \sqrt {2\pi (x - a)} (x - a)\sigma_{yz} (x,0) $$

(35b)

and obtained the expressions as follows:

$$ K_{\text{III}} ( - a) = \frac{{\sqrt {\pi a} }}{2}G\sum\limits_{{m{ = 1}}}^{\infty } {( - 1)^{m} (m + 1)C_{1m} } $$

(36a)

and

$$ K_{\text{III}} (a) = \frac{{\sqrt {\pi a} }}{2}G\sum\limits_{{m{ = 1}}}^{\infty } {(m + 1)C_{1m} } $$

(36b)

4 The collinear crack problem

In formulating the problem, no conditions of symmetry with respect to x = 0 were assumed regarding the crack geometry and the external loads. Thus, the integral Eq. (21) derived in previous section is valid basically for any number of collinear cracks defined by y = 0, $b_{j} < x < c_{j}$, $\left( {j = 1 ,\ldots ,n} \right)$ along the x-axis with the additional single-value condition for each crack, namely $g_{j} (x) = 0$ for $\left| x \right| \notin (b_{j} ,c_{j} )$ and $\int_{{\,b_{j} }}^{{\,c_{j} }} {g_{j} (x){\text{d}}x} = 0$, where $\left( {j = 1 ,\; \ldots ,\;n} \right)$. The only change in the integral equation would be in replacing the integral $( - a ,\;a)$ by the sum of the integrals $L_{j} = (b_{j} ,\;c_{j} )$ corresponding to the collinear cracks, where $\left( {j = 1 ,\ldots ,n} \right)$ and $a_{j} = (c_{j} { - }b_{j} ) / 2$ is the half length of the jth crack.

Fig. 2

Two collinear cracks

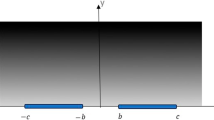
As an example, consider the case of two symmetrically located and symmetrically loaded collinear cracks (Fig. 2). That is, one assumes $b_{1} = b$, $c_{1} = b + 2a$, $b_{2} = - (b + 2a)$ and $c_{2} = - b$. The singular integral Eq. (26) becomes:

$$ \begin{aligned} & - \frac{{l^{2} }}{\pi }\int_{b}^{b + 2a} {\left( {\frac{1}{{(r - x)^{3} }} + \frac{1}{{(r + x)^{3} }}} \right)g(r){\text{d}}r} + \frac{{1 - [l'/(2l)]^{2} }}{2\pi }\int_{b}^{b + 2a} {\left( {\frac{1}{r - x} + \frac{1}{r + x}} \right)g(r){\text{d}}r} \\ & \quad + \frac{l'}{4}g'(x) + \int_{b}^{b + 2a} {\varOmega_{1} (x,r)} g(r){\text{d}}r = - \frac{p}{G} \\ \end{aligned} $$

(37)

where $\varOmega_{1} (x,r) = \varOmega (x,r) - \varOmega (x, - r)$. The integral Eq. (37) is solved under the single-value condition $\int_{\,b}^{\,c} {g(x){\text{d}}x} = 0$. By normalizing the length parameters according to $x = a\overline{x} + a + b$ and $r = a\overline{r} + a + b$, the integral Eq. (37) will be reduced to the following standard form

$$ \begin{aligned} & - \frac{{(l/a)^{2} }}{\pi }\int_{ - 1}^{1} {\left( {\frac{1}{{(\overline{r} - \overline{x} )^{3} }} + \frac{1}{{\left( {\overline{r} + \overline{x} + 2\frac{b + a}{a}} \right)^{3} }}} \right)g(r){\text{d}}r + \frac{{1 - [l'/(2l)]^{2} }}{2\pi }\int_{ - 1}^{1} {\left( {\frac{1}{{\overline{r} - \overline{x} }} + \frac{1}{{\overline{r} + \overline{x} + 2\frac{b + a}{a}}}} \right)g(r){\text{d}}r} } \\ & \quad + \frac{l'/a}{4}g'(x) + a\int_{ - 1}^{1} {\varOmega_{1} (x,r)} g(r){\text{d}}\overline{r} = - \frac{p}{G} \\ \end{aligned} $$

(38)

The solution of g has the same form as Eq. (27). With the substitution of Eq. (27) and applying the integral formulas of “Appendix”, Eq. (38) can be reduced to

$$ \begin{aligned} & - \frac{{(l/a)^{2} }}{{4(1 - \overline{x}^{2} )}}\sum\limits_{m = 1}^{\infty } {C_{m} \left[ {m(m + 1)U_{m + 1} (\overline{x} ) - (m^{2} + 3m + 2)U_{m - 1} (\overline{x} )} \right]} \\ & \quad + \frac{{(l/a)^{2} }}{{4(1 - \overline{x}^{2} )}}\sum\limits_{m = 1}^{\infty } {C_{m} \frac{1}{2} (m + 1 ) { }\left[ {x_{1} - \sqrt {x_{1}^{2} - 1} } \right]^{m - 1} \left[ {m\left( {1 - \frac{{x_{1} }}{{\sqrt {x_{1}^{2} - 1} }}} \right)^{2} + \frac{{\left[ {x_{1} - \sqrt {x_{1}^{2} - 1} } \right]}}{{(x_{1}^{2} - 1)^{3/2} }}} \right]} \\ & \quad - \frac{{1 - [l'/(2l)]^{2} }}{2}\sum\limits_{m = 1}^{\infty } {C_{m} T_{m + 1} (\overline{x} )} - \frac{{1 - [l'/(2l)]^{2} }}{2}\sum\limits_{m = 1}^{\infty } {C_{m} \left[ {x_{1} - \sqrt {x_{1}^{2} - 1} } \right]^{m + 1} } \\ & \quad - \frac{l'/a}{4}\frac{1}{{\sqrt {1 - \overline{x}^{2} } }}\sum\limits_{m = 1}^{\infty } {(m + 1)T_{m + 1} (\overline{x} )C_{m} } + a\sum\limits_{m = 1}^{\infty } {C_{m} } V_{m1} (\overline{x} ) = - \frac{p}{G} \\ \end{aligned} $$

(39)

where $x_{1} = \bar{x} + 2(b + a)/a$ and

$$ V_{m1} (\overline{x} ) = \int_{ - 1}^{1} {\left[ {\varOmega (x,r) - \varOmega (x, - r)} \right]U_{m} (\overline{r} )\sqrt {1 - \overline{r}^{2} } {\text{d}}\overline{r} } , $$

(40)

With the substitution of Eq. (23), it is found that

$$ V_{m1} (\overline{x} ) = \int_{ - 1}^{1} {\varOmega_{2} (x,r)U_{m} (\overline{r} )\sqrt {1 - \overline{r}^{2} } {\text{d}}\overline{r} } , $$

(41)

where

$$ \varOmega_{2} (x,r) = \frac{1}{2\pi }\int_{0}^{\infty } {2\left( {\overline{A} (s) - \overline{C} (s) - \varLambda_{0} (s)} \right)\sin (sr)\cos (sx){\text{d}}s} , $$

(42)

Again, the integral Eq. (39) can be solved by using an appropriate collocation in x.

5 Results and discussion

5.1 Convergence study

All results are given for a constant surface shear load $\sigma_{yz} (x,0) = - p_{0}$ on the crack faces. Firstly, the convergence study for the normalized crack face displacement is conducted for an infinite layer with volumetric strain gradient only ($l \ne 0$ and $l' = 0$). The value of M required for a convergent result depends on the relative value of strain gradient l to the crack length parameter a. For example, if l/a = 0.1, a value of M higher than 20 can give a result with negligible error. However, if l/a downs to 0.00005, the value of M for a convergent crack profile is higher than 300. If l/a downs to 0.00001, a value of M higher than 600 is required to give a convergent result. Despite the fact that the convergence depends on the strain gradient parameter, all calculations confirm that the results converge as the number of allocation points M increases.

5.2 A single layer

The crack face displacement profile for an infinite medium (i.e., h ≫ a) is plotted in Fig. 3 to show the effect of the gradient parameter l with choice of $l' = 0$. It can be seen that the displacement considerably decreases with the gradient parameter. The crack profile corresponding to l = 0.2a obtained here is very close to that given previously by Paulino et al. (2003). As the surface strain gradient ($l'$) increase, the displacement decreases monotonically. This means that in comparison to the classical elasticity fracture mechanics, strain gradient effect stiffens the crack. Also as the gradient parameter become sufficiently small (in current case, $l/a \le 0.001$), the result is almost identical to the conventional linear elastic fracture mechanics solution.

Fig. 3

Crack surface displacement profiles in an infinite medium under surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of $l' = 0$

In order to further demonstrate the strain gradient effect, it is necessary to evaluate the influence of different values of parameter $l'$. Therefore, in Fig. 4, the normalized crack face displacement is plotted as a function of the normalized position. Results for “layer height to crack length” ratio (h/a) equals to 1 and infinity are presented. With the stress-free boundary conditions on the layer surfaces, the crack face displacement is significantly increased due to finite layer thickness. This is especially obvious for higher (negative) gradient parameter ($l'$) magnitude. This fact suggests that contribution of surface energy on strain gradient fracture is very important and may not be omitted. Basically, under the region of the gradient parameter considered, crack displacement decreases with $l'$. In general, the effect of a negative $l'$ leads to a more compliant crack. On the contrary, the effect of a positive $l'$ leads to a stiffer crack. However, the influence of positive $l'$ is apparently less significant than the negative $l'$.

Fig. 4

Crack surface displacement profiles for crack face surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of l/a = 0.2 for different values of $l^{\prime}$

Since growth of a crack starts around its tips, it is essential to know the stress near the crack tips. For this consideration, the stresses at the right crack tip for different l/a and $l'/l$ values are obtained (the stresses at the left crack tip are same but with an opposite sign) to permit to assess the influence of the gradient parameters on the stress solutions. It is obvious from Fig. 5 that the magnitudes of the stresses increase as l/a increases and vice versa, suggesting that the stresses in strain gradient fracture are significantly larger than the classical field. This trend observation is the same as that made by Zhang et al. (1998) for an infinite medium. Generally, the effect of strain gradient on the crack in the finite layer is more significant than in the infinite layer when the crack length is large enough (e.g., a > h). Generally, finite layer border tends to enhance the stress level near the crack tip.

Fig. 5

Normalized stress $\tau_{y} (x,0)/p_{0}$ near the right crack tip for surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of $l' = 0$

Crack tip stresses with both volumetric and surface strain gradient (represented as l and $l'$, respectively) are presented in Fig. 6 for h/a = 1. It should be mentioned from the energy consideration that, depend on the materials, the constant l₁ may be positive or negative but its magnitude can not excesses l (Exadaktylos et al. 1996; Vardoulakis et al. 1996). Therefore, the results are presented for both positive and negative surface strain gradient material parameter $l'$ while maintaining the volumetric strain gradient material parameter l as a constant 0.2a. It may be seen that as the surface strain gradient $l'$ varies from − 0.9l to 0, the stress level is considerably reduced. Result for positive surface gradient is very close to that for zero surface strain gradient. Therefore, the effect of surface strain gradient is less prominent than volumetric strain gradient. The volumetric strain gradient dominates the crack tip behaviour in strain gradient fracture.

Fig. 6

Normalized stress $\tau_{y} (x,0)/p_{0}$ near the right crack tip for surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of l/a = 0.2 and h = a for different values of $l'$

Some sample results for the problem of two identical collinear cracks are also obtained when the surface gradient parameter is not included and the layer thickness is infinite. Figure 7 plots the crack displacement profiles for $l = 0.2a$ and $l = 0.5a$, respectively. The crack displacements for the collinear cracks are smaller than those for the single crack. The collinear crack solution approach the single crack solution when the crack space become large enough (e.g., for b higher than 10a). In Fig. 8, the stresses near the outer crack tip are plotted for selected values of crack spacing. It can be seen that the crack level is considerably enhanced if the two cracks become closer. Thus, interaction of collinear cracks considerably enhances the stress level at the crack tip. Once again, it is found that if the crack space is sufficiently large, effect of crack interaction becomes negligible and the stresses at both crack tips are identical and approach to the corresponding values of the single crack solution.

Fig. 7

Crack surface displacement profiles in an infinite medium with two collinear cracks under surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of $l' = 0$

Fig. 8

Normalized stress $\tau_{y} (x,0)/p_{0}$ near the outer crack tip for two collinear cracks in an infinite medium under surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of l = 0.2a and $l' = 0$

5.3 Layered structures

Figure 9 displays variation of the crack surface displacement with outer layer stiffness of a layered medium for h/a = 1.0; l/a = 0.2 and $l' = 0$. The values of the strain gradient l for the outer layers and the middle layers are same. As expected, the structure becomes stiffer and the crack surface displacement reduces when the shear modulus of the outer layer increases. The zero outer layer stiffness is related to a crack in a single layer. On the other hand, the infinite layer thickness corresponds to a single layer with its top and bottom surfaces fixed so that the displacements on its top and bottom surfaces are zero. Shown in Fig. 10 are the stresses at the right crack tip for the same conditions as for the Fig. 9. Apparently, the outer layers provide a constraint to the central layer so that the crack tip stresses are reduced. The higher the values of the shear modulus of the outer layer are, the lower the crack tip stresses.

Fig. 9

Crack surface displacement profiles in a layered medium under surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of h/a = 1.0; l/a = 0.2 and $l' = 0$

Fig. 10

Normalized stress $\tau_{y} (x,0)/p_{0}$ near the right crack tip in a layered medium under surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of h/a = 1.0; l/a = 0.2 and $l' = 0$

Finally, Fig. 11 depicts the effect of the layer thickness and strain gradient parameter on the stress intensity factor. Similar to the conventional linear elastic fracture mechanics, the magnitude of the stress intensity factor decreases as the layer thickness increases. Notice that when G₂/G = 1, the sandwiched layer and the outer layers will have same material properties and the problem becomes a crack in an infinite medium. As a result the stress intensity factor will show no dependence on the thickness of the sandwiched layer when G₂/G = 1. It is expected that when the layer thickness becomes sufficiently (e.g., h/a > 3), all results will converge to the solutions of a crack in an infinite medium. The results of Fig. 11 also confirm that the normalized stress intensity factor increase with the strain gradient parameter. This observation coincides with the result of Paulino et al. (2003).

Fig. 11

Normalized stress intensity factor (left crack tip) in a layered medium under surface shear load $\sigma_{yz} (x,0) = - p_{0}$ with choice of $l' = 0$ where $K_{ 0} = p_{0} \sqrt {\pi a}$

6 Conclusion

A crack in a finite elastic layer sandwiched by two elastic layers under anti-plane deformation has been studied using strain gradient elasticity theory, which involves volumetric and surface strain gradient material constants. The theoretical framework and corresponding computational implementation have been presented. The crack is considered to be parallel to the layer surface and is located at the center of the layer. The present hypersingular integral equation approach leads to a numerically tractable solution of the crack displacement profile and the stresses near the crack tip. In particular, when the gradient parameters are sufficiently small, the results from the current analysis model automatically reduce to the conventional linear fracture mechanics solution. Parametric studies including various strain gradient parameters and layer thickness have been conducted and discussed. Natural extensions of this research are the solution of an anti-plane shear crack where the crack is perpendicular to the layer border surface and the mode I and mode II fracture problems.

The studies mentioned above are mostly limited to the elastic fracture mechanics framework. Strain gradient fracture may also be significant for structures material with non-homogeneous interfaces at micro-scale. In a series of studies, Wu et al. (Wu et al. 2016a, b) have explored the thermally induced fracture of interface crack in bi-material structures; crack tip field and crack extension in functionally graded materials without piezoelectric effect (Shi et al. 2014) and with piezoelectric effect (Qiu et al. 2018), and film/substrate structures with ferroelectric effect (Wu et al. 2016a, b). Future research is clearly needed in studying the more challenging case of strain gradient plasticity fracture associated with the finite crack problem in non-homogeneous micro-structures.

Appendix

The following formulas (Chan et al. 2008; Fannjiang et al. 2002; Paulino et al. 2003) are used in deriving the hypersingular integral equations:

$$ \frac{1}{\pi }\int_{ - 1}^{1} {\frac{{U_{m} (r)\sqrt {1 - r^{2} } }}{ (r - x)}{\text{d}}r} = \left\{ {\begin{array}{*{20}l} { - T_{m + 1} (x),} \hfill & {m \ge 0 ,\left| x \right| < 1} \hfill \\ { - \, \left[ {x - \frac{\left| x \right|}{x}\sqrt {x^{2} - 1} } \right]^{m + 1} ,} \hfill & {m \ge 0 ,\left| x \right| > 1} \hfill \\ \end{array} } \right\}, $$

(43)

$$ \begin{aligned} & \frac{1}{\pi }\int_{ - 1}^{1} {\frac{{U_{m} (r)\sqrt {1 - r^{2} } }}{{ (r - x)^{3} }}{\text{d}}r} \\ & \quad = \left\{ {\begin{array}{*{20}l} {[(m^{2} + m)U_{m + 1} (x) - (m^{2} + 3m + 2)U_{m - 1} (x)]/[4(1 - x^{2} )],} \hfill & {m \ge 1 ,\left| x \right| < 1} \hfill \\ { - \frac{1}{2} (m + 1 ) { }\left[ {x - \frac{\left| x \right|}{x}\sqrt {x^{2} - 1} } \right]^{m - 1} \left[ {m\left( {1 - \frac{\left| x \right|}{{\sqrt {x^{2} - 1} }}} \right)^{2} + \frac{{\left[ {x - \frac{\left| x \right|}{x}\sqrt {x^{2} - 1} } \right]}}{{(x^{2} - 1)^{3/2} }}} \right],} \hfill & {m \ge 0 ,\left| x \right| > 1} \hfill \\ \end{array} } \right\}, \\ \end{aligned} , $$

(44)