Exploration of blood flow characteristics on mass-based hybrid ferromagnetic nanofluid with variable magnetized force-driven convective wedge

Abstract

The interaction of ferromagnetic properties and heat transfer offers a broad spectrum of biomedical applications. In fields such as electronics, energy storage, and biomedicine, the utilization of ferromagnetic nanoparticles has the potential to develop thermal management, energy conversion, and targeted therapeutic approaches. The main emphasis is on analysing a hybrid nanofluid flow with a mass-based composition, containing ferromagnetic nanoparticles (composed of Mn-ZnFe₂O₄/CoFe₂O₄ nanoparticles), over a convective wedge. The study becomes better with the addition of a hydromagnetic effect, which adds a layer of complexity and depth. The study also includes the structural behaviour of the effects of Joule dissipation. This study clarifies the complex interactions involving the nanoparticle shape, magnetization effects, viscous dissipation, radiative heat effects, and the influence of the mass of ferromagnetic nanoparticles. In particular, the implementation of Hamilton–Crosser conductivity model defines the role of various shapes of the nanoparticles. Standard similarity transformations rules are adopted to transform the governing partial differential equations and their boundary conditions into non-dimensional forms. The resulting transformed ordinary differential equations are then solved using the bvp5c solver with the shooting technique in MATLAB. Through careful observation and in-depth analysis of graphical illustrations, the impact of characterizing factors on the flow profiles is thoroughly studied. However, the significant outcomes of the study are presented as: the momentum boundary layer thickness retards with increasing magnetization, wedge angle parameter along with velocity ratio parameter. Further, the thickness of the thermal boundary layer shows the opposite impact with increasing thermal radiation and Biot and Eckert numbers, respectively.

Introduction

The utilization of ferromagnetic particles within heat transfer processes has attracted considerable attention owing to their distinctive thermal and magnetic characteristics. When incorporated into heat transfer fluids or materials, these particles have the capacity to amplify the effectiveness of heat transfer, provide a means for meticulous manipulation of thermal regulation, and offer practical value across an array of industrial and technological domains. Rashad [1] focused on investigating the effects of thermal radiation in conjunction with magnetohydrodynamics (MHD) on the slip flow behaviour of a ferrofluid as it flowed towards a non-isothermal wedge interface. The convective behaviour of a hybrid ferrofluid under the interaction of a magnetized dipole effect on an angled enlarged sheet was investigated using numerical simulations by Kamis et al. [2]. Shah et al. [3] focused on analysing the impression Cattaneo–Christov model on a microstructured ferrofluid over a sheet that is either being stretched or shrunk. The heat transportation that takes place over a rotating, stretchable disc in a magnetohydrodynamic (MHD) stagnation point flow of a ferrofluid was described in detail by Mustafa et al. [4]. Idris et al. [5] investigated the heat transportation features of a magnetized hybridized ferrofluid flowing over a moving permeable surface. The impact of viscous dissipation was also taken into consideration by the researchers.

A variety of industries, including power generation facilities, and refrigeration units, use wedge-configured heat exchangers. The distinctive wedge form allows for efficient heat transfer between fluids of different temperatures. Ghosh and Mukhopadhyay [6] looked at mixed convection flow in a Cu-water composition nanofluid that was made up of different-shaped nanoparticles. The behaviour of this specific nanofluid as it passed through a dynamically moving wedge was examined. To examine entropy formation in the context of fluid flow across a convectively heated, moving wedge, Berrehal et al. [7] conducted a research using a mass-based hybrid nanofluid model. The behaviour of an Al2O3-Cu nanofluid flowing over a moving permeable wedge under the influence of convective surface boundary restrictions was thoroughly investigated by Anuar et al. [8]. Through a numerical investigation, Habib et al. [9] delved into the transportation dynamics of MHD Prandtl nanofluid induced by a moving wedge, taking into account the presence of activation energy as well as suction or injection effects. Kebede et al. [10] examined thermal and mass transportation in an inconsistent flow of a tangent hyperbolic nanostructured fluid towards a wedge in motion. The analysis considered the impacts of both buoyancy and dissipation.

In engineering applications, magnetohydrodynamics can influence the behaviour of conducting fluids in systems such as electromagnetic pumps, generators, and certain cooling mechanisms. Sadighi et al. [11] explored the thermal and mass transport features of a nanostructured fluid flowing towards a porous enlarged interface while subjected to the influence of magnetohydrodynamics (MHD). In order to scrutinize this complex fluid behaviour, the study took into account the existence of specified boundary restrictions. In order to investigate the interaction of radiative heat flux of a hybridized nanostructured fluid towards a porous surface, Mahesh et al. [12] showed an enquiry with the interaction of both MHD coupling and couple stress effects. Moreover, the study took viscous dissipation into account when examining this complex fluid dynamic circumstances. Ahmed et al. [13] were primarily concerned in a computational study of the hydromagnetic flow of a nanostructured fluid with hyperbolic tangent features towards an extended sheet with nonlinear features. Rafique et al. [14] carried out a meticulous mathematical analysis of the hybridized nanofluid’s flow characteristic. This fluid had a variety of slip and viscosity properties, and the complex interaction of MHD had an impact on how it moved over a stretching surface. In order to examine the dynamics of a tri-hybrid nanofluid affected by MHD as it flowed through a nonlinear extending/contracting sheet, Mahmood et al. [15] deliberated a numerical investigation. Other factors, such as heat generation/absorption and slippery condition, were taken into consideration throughout the analysis.

Joule dissipation, also referred to as ohmic or electrical dissipation, is an occurrence that transpires when electrical currents traverse a conductive medium. This process transforms electrical energy into heat owing to the innate resistance of the material. Jamshed et al. [16] studied the characteristics associated with entropy optimization in the context of a viscous second-grade nanofluid that is subjected to thermal radiation. Pattnaik et al. [17] focused on examining a hybrid strategy to comprehend the computational interactions between radiative heat and chemical processes within the flow of a viscoelastic nanofluid. Pattnaik et al. [18] studied the characteristics of heat dissipation in a Casson fluid flow towards a permeable media, specifically towards an enlarging cylindrical surface. Pattnaik et al. [19] inspected the effects of dissipative energy and inertial drag, as well as particle shape, on the heat transportation features of a magnetized nanofluid. Baag et al. [20] focused on exploring the occurrence of free convection within a conducting nanofluid while it moved over an expanding surface. This analysis considered the interplay of a heat source and convective heating conditions at the boundary. Patnaik et al. [21] provided insight into the flow behaviour of a micropolar nanofluid subjected to mixed convective and radiative effects, dissipation, and magnetization. This study focused on a widening interface embedded in porous matrix, taking into account the impacts of double stratification as well as chemical reactions. Thumma et al. [22] explained the utilization of mathematical modelling to depict the simultaneous influence of thermal radiation along heat source on the movement of nanofluid towards a curved surface. Dogonchi et al. [23,24,25] explored the thermal energy storage system utilizing nano-enhanced phase change material (NEPCM), featuring an intricate charger. Their investigation delved into the impact of thermal radiation, Joule heating, and viscous dissipation on heat transfer mechanisms, alongside squeezing flow current, within a magnetohydrodynamic (MHD) nanofluid flow confined between parallel discs during suction/blowing. The governing equations were tackled using the Adomian decomposition method (ADM), with numerical analysis further conducted employing the finite element method (FEM). Results revealed the inefficacy of the proposed dilatant working fluid for heat transfer applications. Sayyedi et al. [26] studied the natural convection flow of a micropolar nanofluid (Al₂O₃/water) within a semi-annulus enclosure under the influence of an angled magnetic field. Their investigation scrutinized the effects of active factors on magneto-natural convection, employing computational methods including CVFEM and Ansys Fluent CFD code for conservative comparisons. The study contributes to understanding natural convection, crucial in various applications such as heat exchangers and geothermal systems. Furthermore, Afshar et al. [27] examined natural convection, a significant form of convective heat transfer, across various applications including heat exchangers, geothermal systems, and nanofluids. Finite element method (FEM) was employed to solve altered governing equations, showcasing numerical simulations of velocity distribution through streamlines and isotherms for diverse parameters. Trith et al. [28] investigated the impact of internal heat and concentration source block on magnetized Boussinesq-free double-diffusive convection within a nanofluid-filled C-shaped inclined restricted space. Their findings shed light on the performance of nanofluids within a C-shaped enclosure featuring heat and a solid-state source block, aiding engineers in devising effective thermal systems for various technological applications. Finally, Tayebi et al. [29] conducted a numerical analysis utilizing the finite element method (FEM) to model free convection generated by double-diffusion (DDNC) with Soret/Dufour effects of Nano-Encapsulated PCMs inside an I-shaped enclosure equipped with unique corrugated vertical walls under Neumann thermal and solutal conditions.

Novelty of the study

• The current article discusses employing the hydromagnetic effect on a mass-based ferromagnetic hybrid nanofluid applied towards a moving wedge.

• The thermal properties of the nanofluid flow are improved by investigating convective conditions.

• Analysing the impacts of Joule dissipation that offers valuable ipact on the dynamics of thermal transport.

• Exploring the effects of different particle shapes on the thermal transport mechanism.

• Investigating the relationship between the mass of ferromagnetic nanoparticles and their capacity to enhance the rate of heat transfer.

Modelling for mass-based ferromagnetic hybrid nanofluid transport

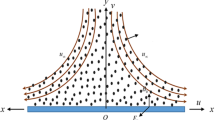
Let us analyse the blood flow of a consistent, two-dimensional, incompressible, laminar, hybridized nanofluid on a convectively heated, moving wedge. This scenario involves radiative flux, as illustrated in Fig. 1.

• Here, the Cartesian coordinates are denoted by $x$ and $y$, where the $x - {\text{axis}}$ taken along the wedge’s wall, and the $y - {\text{axis}}$ is perpendicular to it.

• The magnetized field $B(x) = B_{0} x^{{{{(\text{m} - 1)} \mathord{\left/ {\vphantom {{(\text{m} - 1)} 2}} \right. \kern-0pt} 2}}}$ is implemented normal to the wedge.

• The hybrid nanofluid’s ambient temperature denoted as $T_{\infty }$. The lower interface temperature is $T_{{\text{f}}}$.

• The convective heat transportation coefficient is $h_{{\text{f}}}$ and the temperature of wall is $T_{{\text{w}}}$, while the temperature has a steady worth $T_{\infty }$.

• The evolution of the Falkner–Skan framework while accounting for a moving wedge heated by convection is examined in this work.

• The velocities of wedge $\left( {U_{{\text{w}}} } \right)$ and free stream $\left( {U_{{\text{e}}} } \right)$are $U_{0} x^\text{m}$ and $U_{\infty } x^\text{m}$ , respectively, where $U_{\infty }$, $U_{0}$, and m are constants.

• Here, $m = \beta /2 - \beta$, where $\beta$ is the Hartree pressure gradient parameter which corresponds to $\omega = \beta \pi$ for a total angle of the wedge. $m = 1(\beta = 1)$ signifies the near the plane stagnation point on boundary layer flow of a vertical flat plate $\left( {\omega = \pi } \right)$. m $\left( {0 \le m \le 1} \right)$ is between 0 and 1 with $m = 0(\beta = 0)$ pertains to the boundary layer past a horizontal flat plate $\left( {\omega = 0} \right)$.

Fig. 1

Flow diagram of current problem

In this study, the thermal equilibrium exists between the fluid phase (particularly, blood) and the solid phase, which contains both the first nanoparticle (Mn-ZnFe₂O₄) and the second nanoparticle (CoFe₂O₄). We also discuss a no-slip requirement between these phases. With these assumptions established, the governing equations for the given problem as (Berrehal et al. [7]);

$$ u_{{\text{x}}} + v_{{\text{y}}} = 0 $$

(1)

$$ uu_{{\text{x}}} + vu_{{\text{y}}} = - \frac{{p_{{\text{x}}} }}{{\rho_{{{\text{hnf}}}} }} + \frac{{\mu_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}u_{{\text{yy}}} - \frac{{\sigma_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}B^{2} u $$

(2)

$$ uT_{{\text{x}}} + vT_{{\text{y}}} = \alpha_{{{\text{hnf}}}} T_{{{\text{yy}}}} + \frac{{\mu_{{{\text{hnf}}}} }}{{(\rho C_{{\text{p}}} )_{{{\text{hnf}}}} }}(u_{{\text{y}}} )^{2} - \frac{{(q_{{\text{r}}} )_{{\text{y}}} }}{{(\rho C_{{\text{p}}} )_{{{\text{hnf}}}} }} + \frac{{\sigma_{{{\text{hnf}}}} B^{2} u^{2} }}{{(\rho C_{{\text{p}}} )_{{{\text{hnf}}}} }} $$

(3)

Table 1 depicts the thermophysical appearance of the hybrid nanofluid based on the model proposed. Different shapes of nanoparticles are distinguished in Table 2. Table 3 represents mass-based model for hybrid nanofluid. The physical features of nanoparticles as well as base liquid are visualized in Table 4.

Table 1 Thermophysical models for hybrid nanofluid (Berrehal et al. [7])

Table 2 Different shapes of nanoparticles (Pattnaik et al. [19])

Table 3 Model for proposed mass-based hybrid nanofluid (Berrehal et al. [7])

Table 4 The physical aspects of Blood and Ferro fluids

Because the pressure remains constant within the inviscid flow, and the velocity of the primary stream A is equivalent to the velocity at the boundary layer’s edge. This relationship is derived from Eq. (2).

$$ U_{{\text{e}}} (x)\frac{{{\text{d}}U_{{\text{e}}} (x)}}{{{\text{d}}x}} = - \frac{{p_{{\text{x}}} }}{\rho } $$

(4)

Inserting Eq. (4) in Eq. (2) gives

$$ uu_{{\text{x}}} + vu_{{\text{y}}} = U_{{\text{e}}} (x)\frac{{{\text{d}}U_{{\text{e}}} (x)}}{{{\text{d}}x}} + \frac{{\mu_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}u_{{{\text{yy}}}} - \frac{{\sigma_{{{\text{hnf}}}} }}{{\rho_{{{\text{hnf}}}} }}B^{2} (u - u_{{\text{e}}} ) $$

(5)

From the approximation of Roseland, the radiative heat flux is given by

$$ q_{{\text{r}}} = - \frac{{4\sigma^{ * } }}{{3k^{ * } }}(T^{4} )_{{\text{y}}} \approx - \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}T_{{\text{y}}} $$

(6)

where $T^{4} \approx 4T_{\infty }^{3} T - 3T_{\infty }^{4}$ subsequently

$$ (q_{{\text{r}}} )_{{\text{y}}} \approx - \frac{{16\sigma^{ * } T_{\infty }^{3} }}{{3k^{ * } }}T_{{{\text{yy}}}} $$

(7)

By putting Eq. (6) into Eq. (3):

$$ uT_{{\text{x}}} + vT_{{\text{y}}} = \left[ {\alpha_{{{\text{hnf}}}} + \frac{{16\delta^{{^{ * } }} T_{\infty }^{3} }}{{3k^{ * } (\rho C_{{\text{p}}} )_{{{\text{hnf}}}} }}} \right]T_{{{\text{yy}}}} + \frac{{\mu_{{{\text{hnf}}}} }}{{(\rho C_{{\text{p}}} )_{{{\text{hnf}}}} }}(u_{{\text{y}}} )^{2} + \frac{{\sigma_{{{\text{hnf}}}} B^{2} u^{2} }}{{(\rho C_{p} )_{{{\text{hnf}}}} }} $$

(8)

The boundary conditions associated with Eqs. (1) to (5) and (8) can be formulated in the subsequent manner (Berrehal et al. [7]):

$$ {\text{At}}\,y = 0;\,v = 0,\,u = U_{{\text{w}}} (x) = U_{0} x^\text{m} , - k_{{{\text{hnf}}}} T_{{\text{y}}} = h_{{\text{f}}} (T_{{\text{f}}} - T), $$

$$ {\text{At}}\,y \to \infty ;\,u = U_{{\text{e}}} (x) = U_{\infty } x^\text{m} ,\,T = T_{\infty } . $$

(9)

The provided similarity transformations are regarded as being converted into ordinary differentials.

$$ \eta = y\left( {\frac{{(m + 1)U_{{\text{e}}} (x)}}{{2x\upsilon_{{\text{f}}} }}} \right)^{0.5} ,\,\theta = \frac{{T - T_{\infty } }}{{T_{{\text{f}}} - T_{\infty } }},\,u = U_{{\text{e}}} (x)f^{\prime}(\eta ),\,\psi = \left( {\frac{{2\upsilon xU_{{\text{e}}} (x)}}{m + 1}} \right)^{0.5} f, $$

(10)

By employing Eq. (10) in Eqs. (2) and (9), subsequent simplification leads to the following expression:

$$ f^{\prime\prime\prime} + \frac{{\mu_{{\text{f}}} }}{{\mu_{{{\text{hnf}}}} }}\frac{{\rho_{{{\text{hnf}}}} }}{{\rho_{{\text{f}}} }}\left\{ {ff^{\prime\prime} + \frac{2m}{{m + 1}}(1 - f^{{\prime}{2}} )} \right\} - \frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{{\text{f}}} }}M(f^{\prime} - 1) = 0 $$

(11)

$$ \left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }} + \frac{4}{3}Rd} \right)\theta^{\prime\prime} + \frac{{(\rho c_{{\text{p}}} )_{{{\text{hnf}}}} }}{{(\rho c_{{\text{p}}} )_{{\text{f}}} }}\Pr f\theta^{\prime} + \frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{{\text{f}}} }}\Pr Ecf^{{\prime\prime}{2}} + \frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{{\text{f}}} }}EcMf^{{\prime}{2}} = 0 $$

(12)

$$ \frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{{\text{f}}} }} = \left( {1 - \frac{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }}}}{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }} + \frac{{w_{{\text{f}}} }}{{\rho_{{\text{s}}} }}}}} \right)^{ - 2.5} ,\,\frac{{\rho_{{{\text{hnf}}}} }}{{\rho_{{\text{f}}} }} = \left( {1 - \frac{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }}}}{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }} + \frac{{w_{{\text{f}}} }}{{\rho_{{\text{s}}} }}}} + \frac{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }}}}{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }} + \frac{{w_{{\text{f}}} }}{{\rho_{{\text{s}}} }}}}\frac{{\rho_{{\text{s}}} }}{{\rho_{{\text{f}}} }}} \right) $$

$$ \frac{{(\rho c_{{\text{p}}} )_{{{\text{hnf}}}} }}{{(\rho c_{{\text{p}}} )_{{\text{f}}} }} = \left( {1 - \frac{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }}}}{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }} + \frac{{w_{{\text{f}}} }}{{\rho_{{\text{s}}} }}}} + \frac{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }}}}{{\frac{{w_{1} + w_{2} }}{{\rho_{{\text{s}}} }} + \frac{{w_{{\text{f}}} }}{{\rho_{{\text{s}}} }}}}\left[ {\frac{{(\rho c_{{\text{p}}} )_{{\text{s}}} }}{{(\rho c_{{\text{p}}} )_{{\text{f}}} }}} \right]} \right) $$

with boundary conditions

$$ f(0) = 0,\,f^{\prime}(0) = \lambda ,\,\theta^{\prime}(0) = - {\text{Bi}}\left[ {1 - \theta (0)} \right],\,f^{\prime}(\infty ) = 1,\,\theta (\infty ) = 0 $$

(13)

Here, $\lambda$ is indicating for the velocity ratio factor, where $\lambda = 0$ corresponds to a static wedge, $\lambda < 0$ correspond to wedge in motion against the stream, and $\lambda > 0$ is corresponding to the similar-direction wedge in motion with the stream.

The dimensionless parameters are

$$ \begin{gathered} m = \frac{\beta }{2 - \beta },\;\lambda = \frac{{U_{{\text{w}}} }}{{U_{{\text{e}}} }},\;,\;\Pr = \frac{{\upsilon_{{\text{f}}} }}{{\alpha_{{\text{f}}} }},\,Ec = \frac{{U_{{\text{e}}}^{{2}} }}{{c_{{\text{p}}} \Delta T}},M = \frac{{\sigma_{{\text{f}}} B_{0}^{2} }}{{\rho_{{\text{f}}} U_{{\text{e}}} }} \hfill \\ {\text{Bi}} = \left( {\frac{hx}{{k_{{\text{f}}} }}} \right){\text{Re}}_{{\text{x}}}^{ - 1/2} ,\;{\text{Re}}_{{\text{x}}} = \frac{{U_{{\text{e}}} x}}{{\upsilon_{{\text{f}}} }},\;Rd = \frac{{4\sigma^{ * } T_{\infty }^{3} }}{{k^{ * } k_{{\text{f}}} }} \hfill \\ \end{gathered} $$

(14)

The measurable parameters of practical significance are defined as

$$ \left| {\frac{{2{\text{Re}}_{{\text{x}}} }}{m + 1}} \right|^{1/2} Cf = \frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{{\text{f}}} }}f^{\prime\prime}(0),\;\left| {\frac{2}{{(m + 1){\text{Re}}_{{\text{x}}} }}} \right|^{1/2} Nu_{{\text{x}}} = - \left( {\frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }} + \frac{4}{3}Rd} \right)\theta^{\prime}(0) $$

(15)

Results and discussion

The current study investigates the movement of a mass-based hybrid nanofluid, comprising ferromagnetic nanoparticles, over a rotating wedge subjected to convective motion while considering variable magnetism. The study aims to acquire valuable insights into the behaviour of the nanofluid within convective conditions and various geometrical configurations. This is achieved by meticulous examination of factors such as the nanoparticles’ shape factor, wedge angle parameter, magnetic parameter, nanoparticle mass, radiative heat transfer, Biot number, and Eckert number. The computation dealt with the fixed values of the factors $M = 1$, $m = 0.5$, $\Pr = 21$, $Ec = 0.01$, $Rd = 0.5$, $w_{1} = 10\,{\text{gr}}$, $w_{2} = 10\,{\text{gr}}$, $n = 3$, $Bi = 0.5$, $w_{{\text{f}}} = 100\,{\text{gr}}$, and $\lambda = 0.1$ , whereas the variation of particular constraints presented in each figure. The present results are corroborated through a comparison with the earlier investigation conducted by Berrehal et al. [7], which demonstrated in Table 5. The physical significance of the effective factors is provided below. In Figs. 2 and 3, the impact of the wedge angle parameter $(m)$ on $f^{\prime}(\eta )$ and $\theta (\eta )$ is displayed under conditions of both the presence $(M \ne 0)$ and absence $(M = 0)$ of a magnetic field. In both figures, $m = 1(\beta = 1)$ indicates the stagnation point flow of the plane, $m = 0.2(\beta = {1 \mathord{\left/ {\vphantom {1 3}} \right. \kern-0pt} 3})$ is presents the wedge flow with $(\omega = {\pi \mathord{\left/ {\vphantom {\pi 3}} \right. \kern-0pt} 3})$, $m = 0(\beta = 0)$ implies the horizontal sheet, $m = - 0.0825(\beta = - 0.18)$ indicates the flow occurring over a downward slope to the point of separation. In Fig. 2, the pressure distribution along the surface is influenced by changes in the wedge angle. These adjustments in pressure gradients bring about modifications in the flow’s behaviour, ultimately leading to a reduction in the hydrodynamic boundary layer. Consequently, the $f^{\prime}(\eta )$ diminishes as the value of the wedge angle parameter increases. As depicted in Fig. 3, when the wedge angle parameter upsurges, the flow’s acceleration occurs due to the attenuation of the propelling force behind the fluid motion. This leads to an enhanced transfer of heat from the wedge’s surface to the fluid through the fluid particles and their associated temperatures. Consequently, the fluid’s temperature at the surface of the wedge experiences a reduction. The imposition of a magnetic field results in a reduction of the momentum boundary layer. This implies that the fluid layer in close proximity to the surface exhibits a decelerated flow. Conversely, the intensity of the magnetic field plays a more significant role in influencing the temperature distribution, amplifying its impact as the magnetic field strength grows. In Fig. 4, the influence of the velocity ratio factor on the fluid velocity profile is depicted. Upon close examination of the figure, a significant trend comes to light: as the parameter $\lambda < 1$ rises, there is a noticeable reduction in the thickness of the velocity bounding surface. The increasing value of parameter $\lambda$ signifies a scenario where the free stream velocity exceeds the stretching velocity within the fluid flow. This circumstance gives rise to a series of consequences. The augmented free stream velocity leads to elevated pressure levels, accompanied by intensified straining motion in the vicinity of the stagnation point. This phenomenon is attributed to the interplay between the forces associated with the fluid’s motion and the stretching of the fluid layer due to the differing velocities. Figures 5 and 6 display the variation of the mass of the first nanoparticle $(w_{1} )$ and the mass of the second nanoparticle $(w_{2} )$ on $f^{\prime}(\eta )$ and $\theta (\eta )$ , respectively. Here, $w_{1} = w_{2} = 0$ designates for pure blood. In Fig. 5, the hydrodynamic boundary layer increases noticeably when the mass of nanoparticles inside that fluid is increased. Nanoparticles may aggregate or agglomerate under particular conditions, such as high velocities. Larger groups are formed as a result of the clustering of the particles involved in this process. The velocity profile has increased mass as a result of the clustering effect. This effect results that an increase in nanoparticle mass injects more momentum into the fluid. The enhanced interactions between the nanoparticles and the nearby fluid particles are ultimately provide this extra momentum. From Fig. 6, it is revealed that the $\theta (\eta )$ rises by increasing the value of the mass of the nanoparticles. The thermal conductivity of materials can be influenced by nanoparticles. These nanoparticles accelerate the transfer of heat when their thermal conductivity is higher than that of the surrounding medium. The distribution of temperatures within the system is subsequently affected by this acceleration in heat transport. Additionally, a larger mass of nanoparticles has the ability to alter when heat is lost from a system or radiated from it. Figure 7 illustrates the thermal radiation characteristics of the blood-based ferromagnetic hybrid nanofluid concerning $\theta (\eta )$. This depiction is presented for both scenarios: one with the magnetic field effect incorporated and the other without. Thermal radiation involves the propagation of heat through electromagnetic waves, occurring devoid of the need for any intervening medium. Within the context of the blood-based ferromagnetic hybrid nanofluid, the phenomenon of thermal radiation assumes a pivotal role in facilitating the exchange of energy between the fluid and the solid surface. When $Rd = 0$, the significance of radiative effects diminishes, leaving conduction and convection as the predominant heat transfer mechanisms. This energy exchange can lead to a temperature rise near the stretching surface, influenced by factors such as surface emissivity and temperature gradient. However, these effects become notably more prominent and significant when a magnetic field is present. Figure 8 portrays the influence of the Eckert number on $\theta (\eta )$. The Eckert number, denoting the ratio of kinetic energy to thermal energy at the interface between the fluid and solid, assumes a pivotal role in characterizing the balance between these energies within the flow field. It serves as a fundamental descriptor of the equilibrium between thermal and kinetic phenomena within the system. Notably, the introduction of magnetic forces into the fluid flow and heat transfer dynamics is accountable for the observed elevation in the Eckert number when a magnetic field is present. This phenomenon underscores the significant impact magnetic forces wield on the interplay between kinetic and thermal energies within the context of the study. Figure 9 illustrates the impact of the thermal Biot number on the dispersion of fluid temperatures across different scenarios. The current investigation encompassed both low Biot number values $({\text{Bi}} < 1)$ and high Biot number values $({\text{Bi}} > 1)$. In a general sense, when ${\text{Bi}} < 1$, it denotes a thermally uniform with consistent temperature distributions within the material. In contrast, ${\text{Bi}} > 1$ indicates an uneven temperature spread within the material, signifying a more intricate circumstance. As the Biot number increases, the temperature profile rises. However, the impact is significantly more pronounced and substantial in the presence of magnetic field. Figure 10 illustrates the impact of several nanoparticle shapes, including spherical, cylindrical, brick, platelet, and blade structures, on the variation of the conductivity ratio with respect to volume percentage. The thermal conductivity ratio denotes the percentage of more thermally conductive the nanofluid is than the base fluid. The performance of nanofluids in transporting heat is greatly influenced by this characteristic. A nanofluid’s ability to conduct and transport heat is influenced by the distinct geometric properties of the various nanoparticle shapes. Due to their simplicity of usage and strong thermal conductivity enhancement, spherical nanoparticles are frequently used, especially at low volume fractions. With an increase in the volume proportion of spherical nanoparticles, the conductivity ratio typically rises linearly. In Figs. 11 and 12, the variation of magnetic parameter on the velocity gradient at the wall $(Cf)$ and the temperature gradient at the wall $(Nu_{{\text{x}}} )$ towards the mass of nanoparticles is shown. The analysis uncovers that $Cf$ exhibits an upward trend with increasing values of $M$, whereas the opposite pattern is observed for $Nu_{{\text{x}}}$. However, the magnetic field restricts the fluid’s capacity to conduct heat away from the surface, resulting in a reduction in heat transfer rate. In Figs. 13 and 14, the augmentation of wedge angle parameter on both $Cf$ and $Nu_{{\text{x}}}$ is depicted. Due to the increased fluid movement and improved thermal contact between the fluid and the surface, this lead to higher heat transfer rates. Figure 15 displays the enhancement of $Nu_{{\text{x}}}$ with rising value of radiation parameter with respect to the mass of nanoparticles. With a higher radiation parameter, radiative heat transfer takes on a more prominent role. This implies that thermal energy exchange occurs between surfaces via electromagnetic waves. In such scenarios, the potential for a substantial increase in the heat transfer rate becomes evident. Figure 16 displays the reduction in heat transfer rate with increasing value of Eckert number. Low Eckert numbers result in reduced heat transfer rates because there is insufficient fluid movement to efficiently remove thermal energy from the surface. Figure 17 visualized the upsurge in heat transfer rate with increasing value of Biot number. Due to enhanced thermal conduction within the solid material, a rise in the Biot number can accelerate the rate of heat transfer.

Table 5 The comparison value of $f^{\prime\prime}(0)$ at $w_{1} = w_{2} = 0,w_{{\text{f}}} = 100\,{\text{gr,}}\lambda { = 0,}M{ = 0}$

Fig. 2

Presentation of $m$ towards $f^{\prime}(\eta )$

Fig. 3

Presentation of $m$ towards $\theta (\eta )$

Fig. 4

Presentation of $\lambda$ towards $f^{\prime}(\eta )$

Fig. 5

Presentation of $w_{1}$ and $w_{2}$ towards $f^{\prime}(\eta )$

Fig. 6

Presentation of $w_{1}$ and $w_{2}$ towards $\theta (\eta )$

Fig. 7

Presentation of $Rd$ towards $\theta (\eta )$

Fig. 8

Presentation of $Ec$ towards $\theta (\eta )$

Fig. 9

Presentation of ${\text{Bi}}$ towards $\theta (\eta )$

Fig. 10

Presentation of $w_{1}$ and $w_{2}$ towards $\theta (\eta )$

Fig. 11

$M$ versus $Cf$

Fig. 12

$M$ versus $Nu_{{\text{x}}}$

Fig. 13

$m$ versus $Cf$

Fig. 14

$m$ versus $Nu_{{\text{x}}}$

Fig. 15

$Rd$ versus $Nu_{{\text{x}}}$

Fig. 16

$Ec$ versus $Nu_{{\text{x}}}$

Fig. 17

$M$ versus $Nu_{{\text{x}}}$

Final remarks

The flow of a mass-based hybrid nanofluid containing ferromagnetic nanoparticles across a rotating wedge with convective motion with variable magnetism is examined numerically. The modelling is accomplished through the utilization of the mass-based algorithm. In the framework of the Falkner–Skan problem, numerous nanoparticle shapes, including spheres, bricks, cylinders, platelets, and blades, have been investigated. Vertical plates, wedges, and horizontal plates are all included in this study. Several significant findings were derived from the investigation, encompassing the following:

• The analysis presented by comparing the current results in particular case shows the validation as well as the convergence property of the proposed methodology.

• Increasing the mass of ferromagnetic nanoparticles results in improved thermal characteristics of the fluid, including enhanced viscosity and conductivity.

• Emphasizing the significance, it is pointed out that the magnetic parameter, wedge angle parameter, and velocity ratio parameter collectively lead to a reduction in the thickness of the momentum boundary layer.

• It is important to highlight that the radiation parameter, Biot number, Eckert number, and magnetic parameter contribute to an enlargement in the thickness of the thermal boundary layer, but wedge angle parameter has reverse trend.

• Incorporating the radiation parameter, convective conditions, and wedge angle parameter amplifies the heat transfer rate, whereas the Eckert number and magnetic parameter have an opposite effect, diminishing the heat transfer rate.

• Observations reveal that when larger particle shapes are involved, a notable deceleration in the fluid temperature is marked.