Introduction

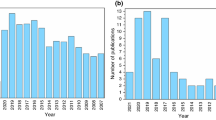
Over the decades, the energy demand has increased dramatically due to rapid population and economic growth. The emerging tremendous energy utilization leads to the enormous emission of CO2 (carbon dioxide) and yields harmful contents, leading to environmental pollution and global warming [1,2,3]. Phase change materials (PCMs) are endorsed as one of the potential thermal energy storage (TES) media that have been experiencing noteworthy interest over the globe [4,5,6]. Several techniques have flourished and enhanced thermal applications to preserve energy costs to treat these disasters. The TES system is a valuable tool for increasing energy efficiency to fill the disparity between energy demand and furnishing [7]. In general, TES systems are categorized as sensible heat thermal energy storage (SHTES) and other one is latent heat thermal energy storage (LHTES) systems. LHTES employs PCMs to accumulate energy and allows the systems to adopt and liberate a tremendous amount of heat energy with a thermal variation by the phase change process (PCP) of PCMs. It provides a large amount of heat storage density and can potentially preserve high heat as latent heat (LH) of fusion with a little number of PCMs and a moderate thermal variation [8,9,10]. However, the lower thermal conductivity of PCMs used in the LHTES system reduces thermal energy [11]. Heat transfer in PCMs has been considered an attractive research scope in thermal science. There are several approaches to enhance the thermal capability of PCM, i.e., the use of porous foams, miniature heat pipes, dispersion of nanoadditives with higher thermal conductivity in PCM, and micro- and macroencapsulation. The most feasible and economical strategy to enhance the thermal capacity of PCMs is the dispersion of high thermal conductivity nanoadditives in PCM (NePCM) [12, 13]. PCMs have become an alternative for thermal management owing to chemical steadiness, cheap rate, and large energy density. Energy and combustion systems usually embrace hydrodynamics, thermal transport, chemical reactions, and phase change (PC) over scales varying from macroscale to microscale via mesoscale. The studies related to PCMs are of substantial significance in several engineering and natural systems. It includes metal smelting and casting, Li-ion batteries, solar thermal energy storage, air-conditioning unit, refrigeration system, electronic cooling, drug delivery unit, crystal growth, TES in buildings, TES, welding, alloys, and metallurgical process [14,15,16,17,18,19,20,21,22]. The matter is exposed to a solid–liquid PCP. The number of research publications on heat transfer for PCMs by LBM has seen significant growth over the last ten years, as illustrated in Fig. 1.

Fig. 1
figure 1

Research articles published on PCM by LBM [23]

Full size image

Consequently, the moving interface separates two distinct phases and evolves the absorption or release of LH in the vicinity of the interface. Mathematical modeling of such a system is considered one of the challenging tasks due to complex boundary treatment and variations of the thermo-physical properties. Over the last three decades, LBM has been extensively acknowledged and used to numerically investigate challenging problems due to its advantage in the mesoscopic background and easy execution of boundary conditions in parallel computing. Theoretical, experimental, and numerical studies have yielded broad literature on different aspects of the PC study, encompassing fundamental studies of the PC phenomenon [2, 24], material features [25, 26], experimental techniques, thermal transport augmentation [3, 27,28,29], mathematical modeling, and numerical methods [30,31,32]. In contrast, the numerical simulation technique is a primary course of action due to its higher economy and efficiency, which significantly develops the understanding of melting and solidification processes in the TES system. Some of the familiar methods utilized to analyze the melting and solidification models so far as the finite element method (FEM) [33], finite difference method (FDM) [34], finite volume method (FVM) [35,36,37], and LBM [38, 39]. PCMs have extensive applications in various industries, including telecommunications, satellites, textiles, medicine, submarine equipment, and transportation, given their phase change temperatures [40], as some of the applications are depicted in Fig. 2.

Fig. 2
figure 2

Application span of PCMs [14,15,16,17,18,19,20,21,22]

Full size image

PCMs for thermal energy storage

PCMs are used to store thermal energy, as SHTES and LHTES are among the significant classes of modern materials that largely impart to the efficient use and preservation of solar energy and waste heat [41,42,43]. Nowadays, TES is recognized as a promising technology to encounter upcoming energy demand. TES is based on PCMs as an energy storage medium due to their cheap rate, easy availability, and high storage capacity [44]. Over the globe, researchers are investigating TES, especially PCM, for their significant benefits in assisting thermal comfort in houses or buildings, improving energy efficiency, and lending to the diminution of environmental pollution [45].

TES can be attained by heating, melting, solidifying, cooling, or vaporizing a material with the energy obtainable as heat when the process is reversed. PCM is the potential medium for TES owing to its extensive latent heat value (140–970 kJ/Kg) [46]. TES systems can potentially boost the effective exercise of thermal energy gadgets and assist in large-scale fuel substitution [47, 48]. For effective utilization of the TES system, PCM and HT mechanism selection plays a significant role [49]. HT augmentation in LHTES systems is attained by either geometric arrangement or thermal conductivity augmentation, and the usage of extended surfaces like fins (triangular, conical, square, and rectangular fins) or heat pipes is one of the standard techniques for thermal transport augmentation in LHTES systems [50, 51]. The suitable design of TES systems utilizing PCMs needs quantitative information about the PCM's HT and PCP. In Korea, radiant surface heating systems, conventionally worn in residential houses, have about 57% of the residential building energy utilization in heating [52]. The application of PCMs for solar TES capacities has obtained attention due to their vast storage capability and the isothermal nature of the storage technique [53]. PCM-TES has a potent energy-saving solution in air-conditioning applications [54].

Moreover, the applications of PCMs in diverse fields include thermal therapy of the human body, the thermal management of electronic devices, and flexible sensors [55]. Nanoencapsulated PCMs are considered one of the possible materials for TES [56, 57]. The application of organic PCMs can be used for TES systems such as biomass of maize straw and wood; synthesis of core–shell paraffin silica nanocomposite is used as PCM [58,59,60,61,62]. TES system is extensively utilized in waste heat recovery and consumption, building heating, air conditioning, solar thermal power plants, and compressed air energy storage [63,64,65,66]. The carbon-based nanostructures (CNs) with higher thermal conductivity can be considered for PCM to improve the thermal properties of the attained nanocomposites [67, 68]. The classification of PCMs for TES is exemplified in Fig. 3.

Fig. 3
figure 3

Classification of PCMs [47, 48]

Full size image

Governing equations

The governing equation of heat transfer for PCMs includes continuity, momentum, and energy equation, which are illustrated below in dimensional form [69,70,71]

$$\frac{\partial \rho }{{\partial t}} + \nabla \cdot\left( {\rho {\mathbf{u}}} \right) = 0$$
(1)
$$\frac{{\partial \left( {\rho {\mathbf{u}}} \right)}}{\partial t} + \nabla \cdot\left( {\rho {\mathbf{uu}}} \right) = - \nabla p + \nabla \cdot\left( {\mu \nabla {\mathbf{u}}} \right) + \rho F$$
(2)
$$\frac{\partial T}{{\partial t}} + \nabla \cdot\left( {{\mathbf{u}}T} \right) = \alpha \nabla^{2} T + q$$
(3)
$$F = g\beta_{\rm T} \left( {T - T_{\rm 0} } \right)$$
(4)

where g, ρ, p, u, μ, and T are the acceleration due to gravity, density, pressure, velocity, velocity, dynamic viscosity, and temperature, respectively. F symbolizes body force, and q stands for heat source term, which occurs through absorption or liberation of LH and is expressed as:

$$q = \left[ {\frac{{\partial \left( {\rho \Delta H} \right)}}{\partial t} + \nabla \cdot\left( {\rho {\mathbf{u}}\Delta H} \right)} \right]$$
(5)

In the above equation ΔH, the latent enthalpy of the computational cell experiences a PC, and if the material is pure, the second term can be ignored. So, q can become

$$q = - \frac{{\partial \left( {\rho \Delta H} \right)}}{\partial t} = - \frac{{\partial \left( {\rho Lf_{\rm l} } \right)}}{\partial t}$$
(6)

where L symbolizes the LH of melt and fl is a fraction of liquid, which can be determined as

$$f{}_{\rm l}\, = \frac{\Delta H}{L}$$
(7)

Non-dimensional form

$$\frac{\partial \rho }{{\partial t^{*} }} + \nabla \cdot\;\left( {\mathbf{U}} \right) = 0$$
(8)
$$\frac{{\partial {\mathbf{U}}}}{{\partial t^{*} }} + \nabla \cdot\left( {{\mathbf{UU}}} \right) = - \nabla P + \Pr \nabla^{2} {\mathbf{U}} + \Pr {\rm Ra}\theta$$
(9)
$$\frac{\partial \theta }{{\partial t^{*} }} + \nabla \cdot\left( {{\mathbf{U}}\theta } \right) = \nabla^{2} \theta - \frac{1}{\rm St}\frac{{\partial f_{\rm l} }}{\partial t}$$
(10)

The subsequent scaling parameters are utilized to acquire non-dimensional variables

$$\begin{gathered} X = \frac{x}{L},\,Y = \frac{y}{L},\,U = \frac{uL}{\alpha },\,t^{*} = \frac{t\alpha }{{L^{2} }}, \hfill \\ P = \frac{p}{{\rho \alpha^{2} }},\,\theta = \frac{{T - T_{\rm C} }}{{T_{\rm h} - T_{\rm c} }} \hfill \\ \end{gathered}$$
(11)

After exploring the general macroscopic governing equations of phase change materials for heat transfer, let us briefly look at the mesoscopic technique, i.e., LBM.

Lattice Boltzmann method

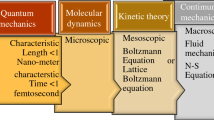
LBM has gained massive impetus in science and technology as the potential tool for solving various engineering applications. Namara and Zanetti (1988) introduced to beat the imperfections of lattice gas cellular automata (LGCA) [72]. It is a new technique in computational fluid dynamics (CFD). It is a mesoscopic scheme and is prominent among the recent simulation schemes established on the molecular hypothesis in CFD. It is established on the Boltzmann equation (BE), governed by the kinetic theory of gases [73]. These models incorporate essential physics [74, 75]. In LBM, the flow particles are replaced by distribution functions (DFs) of the fractious particles. LBM's evolution occurs through streaming and collision [73, 76,77,78,79,80]. With the Bhatnagar–Gross–Krook (BGK) collision model, LBM has developed astonishing advances in solving various problems associated with fluid flow. It is one of the most proficient pseudo-kinetic algorithms. The LBM approach solves several problems associated with fluid flow, thermal, species transport, multiphase, and heat transfer for phase change material (PCM). LBM has several advantages, such as coherent in the algorithm, proficiency in treating complicated geometrics, easy execution of boundary treatment, eminent accuracy, easiness in parallel computing, improved stability, modified pressure estimation, and robustness for non-trivial geometries and complex physical phenomena [81]. A thermal lattice Boltzmann method (TLBM) is utilized to solve the problems based on HT for PCMs [82,83,84,85].

A generalized form of the BE can be yielded as [86,87,88],

$$\frac{{\partial p_{\rm i} }}{\partial t} + {\mathbf{c}} \cdot \;\nabla p = \Omega$$
(12)

where p is the particle distribution function (PDF), t is time, c is lattice, and \(\Omega\) is the collision operator, and it is in integrodifferential form, which develops the solution of Eq. (12) complex. A simple approximation proposed by BGK is usually used to overwhelm this problem. It is represented as follows:

$$\Omega = \omega \left( {p^{\rm eq} - p} \right) = \frac{1}{\tau }\left( {p^{\rm eq} - p} \right)$$
(13)

where \(\omega ,p^{\rm eq} ,\;{\rm and}\;\tau\) are collision frequency, equilibrium distribution function (EDF), and relaxation factor, respectively.

The BE with BGK approximation can be given as,

$$\frac{{\partial p_{\rm i} }}{\partial t} + c_{\rm i} \nabla p_{\rm i} = \frac{1}{\tau }\left( {p^{\rm eq} - p} \right)$$
(14)

The discretization of Eq. (14) in space with time yields the lattice Boltzmann equation (LBE), which is introduced as follows [89, 90].

$$p_{\rm i} \left( {{\mathbf{x}} + {\mathbf{c}}_{\rm i} \Delta t,t + \Delta t} \right) - p_{\rm i} \left( {{\mathbf{x}},t} \right) = - \omega \left[ {p_{\rm i} \left( {{\mathbf{x}},t} \right) - p_{\rm i}^{\rm eq} \left( {{\mathbf{x}},t} \right)} \right]$$
(15)

The various symbols in the above equation \({\mathbf{x}},\,\Delta x,i,\,\Delta t,\,c_{\rm i} \,,\;p_{\rm i} {\text{and}}\;p_{\rm i}^{\rm eq}\) are coordinates, lattice step size, lattice link direction, time step, discrete velocity, PDF, and EDF.

  • Collision (RHS of Eq. 15)

    $$\overline{{p_{\rm i} }} \left( {{\mathbf{x}},t} \right) = p_{\rm i} \left( {{\mathbf{x}},t} \right) - \omega \left[ {p_{\rm i} \left( {{\mathbf{x}},t} \right) - p_{\rm i}^{\rm eq} \left( {{\mathbf{x}},t} \right)} \right]$$
    (16)

  • Streaming (LHS of Eq. 15)

    $$p_{\rm i} \left( {{\mathbf{x}} + {\mathbf{c}}_{\rm i} \Delta t,t + \Delta t} \right) = \overline{{p_{\rm i} }} \left( {{\mathbf{x}},t} \right)$$
    (17)

LBM for phase change materials

LBM for the PCMs in heat transfer is discussed herein. In general, for the study of the thermal field by LBM, there are three crucial approaches for attaining it, i.e., the multispeed approach [83] double distribution function (DDF) approach [84], and the passive scalar thermal lattice Boltzmann method (PS-TLBM) [91]. In the case of PCM for heat transfer, two distribution functions are utilized: flow field (p) and thermal field (q). LBM formulation for PCM is expressed as

$$p_{\rm i} \left( {{\mathbf{x}} + {\mathbf{c}}_{\rm i} \Delta t,t + \Delta t} \right) = p_{\rm i} \left( {{\mathbf{x}},t} \right) - \omega_{\rm p} \left[ {f_{\rm i} \left( {{\mathbf{x}},t} \right) - p_{\rm i}^{\rm eq} \left( {{\mathbf{x}},t} \right)} \right] + \Delta tF_{\rm i}$$
(18)
$$q_{\rm i} \left( {{\mathbf{x}} + {\mathbf{c}}_{\rm i} \Delta t,t + \Delta t} \right) = q_{\rm i} \left( {{\mathbf{x}},t} \right) - \omega_{\rm q} \left[ {q_{\rm i} \left( {{\mathbf{x}},t} \right) - q_{\rm i}^{\rm eq} \left( {{\mathbf{x}},t} \right)} \right]$$
(19)

where \(f_{\rm i}^{eq}\) and \(g_{\rm i}^{eq}\) are the EDF for flow and thermal fields, respectively, and they can be formulated as below.

$$p_{\rm i}^{\rm eq} = w_{\rm i} \rho \left( {{\mathbf{x}},t} \right)\left[ {1 + \frac{{6\left( {{\mathbf{u}}\cdot {\mathbf{c}}_{\rm i} } \right)}}{{2c_{\rm s}^{2} }} + \frac{{4.5\left( {{\mathbf{u}}\cdot {\mathbf{c}}_{\rm i} } \right)^{2} }}{{c_{\rm s}^{4} }} + \frac{{1.5\left( {{\mathbf{u}}\cdot {\mathbf{u}}} \right)}}{{c_{\rm s}^{2} }}} \right]$$
(20)
$$q_{\rm i}^{\rm eq} = w_{\rm i} T\left( {{\mathbf{x}},t} \right)\left[ {1 + \frac{{3\left( {{\mathbf{c}}_{\rm i} \cdot {\mathbf{u}}} \right)}}{{c_{\rm s}^{2} }}} \right]$$
(21)

where u, \(\rho\),\({\mathbf{c}}_{{\mathbf{i}}}\), and \(w_{\rm i}\) represents the macroscopic variables velocity, density, lattice link velocity, and mass function, respectively. The mass function (wi) for the D2Q9 model (which is mainly the preferred lattice arrangement) and lattice velocity (ci) can be written as,

$$w_{\rm i} = \;\left\{ \begin{gathered} {\raise0.7ex\hbox{$4$} \!\mathord{\left/ {\vphantom {4 9}}\right.\kern-0pt} \!\lower0.7ex\hbox{$9$}}\;;\quad i = 0 \hfill \\ {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 9}}\right.\kern-0pt} \!\lower0.7ex\hbox{$9$}}\;;\quad i = 1 - 4 \hfill \\ {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {36}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${36}$}}\;;\;i = 5 - 8\; \hfill \\ \end{gathered} \right.$$
(22)
$${\mathbf{c}}_{\rm i} = \left\{ \begin{gathered} \left( {0,0} \right)\quad \quad {\kern 1pt} {\kern 1pt} \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad \quad ;\quad i = 0 \hfill \\ c\left( {\left[ {\cos \left( {i - 1} \right){\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right],\left[ {\sin \left( {i - 1} \right){\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}} \right]} \right)\quad \quad \quad \quad \quad \quad \;;\;\;i = 1 - 4 \hfill \\ c\sqrt 2 \left( {\cos \left[ {\left( {i - 5} \right){\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}} + {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}} \right],\sin \left[ {\left( {i - 5} \right){\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}} + {\raise0.7ex\hbox{$\pi $} \!\mathord{\left/ {\vphantom {\pi 4}}\right.\kern-0pt} \!\lower0.7ex\hbox{$4$}}} \right]} \right)\;\;;\;i = 5 - 8 \hfill \\ \end{gathered} \right.\quad$$
(23)

The parameter collision frequency (ω) is a function of kinematic viscosity and thermal diffusivity; for example, collision frequency for flow and thermal are \(\omega_{\rm f} \;{\text{and}}\;\;\omega_{\rm g}\), respectively. These are expressed as,

$$\omega_{\rm p} = \frac{1}{3\nu + 0.5}$$
(24)
$$\omega_{\rm q} = \frac{1}{3\alpha + 0.5}$$
(25)

The fundamental hydrodynamic and macroscopic quantities such as density (ρ), velocity (u), and temperature (T) can be computed from the distribution by using the following equations

$$\rho \left( {{\mathbf{x}},t} \right) = \sum\limits_{\rm i} {p_{\rm i} } ({\mathbf{x}},t)$$
(26)
$${\mathbf{u}}\left( {{\mathbf{x}},t} \right) = \sum\limits_{\rm i} {\frac{{p_{\rm i} \left( {{\mathbf{x}},t} \right)c_{\rm i} }}{\rho }}$$
(27)
$$T = \sum\limits_{\rm i} {q_{\rm i} } \left( {{\mathbf{x}},t} \right)$$
(28)

The term 'Fi' is the term [92,93,94,95].

$$\begin{gathered} F_{\rm i} = w_{\rm i} F\frac{{c_{\rm i} }}{{e_{\rm s}^{2} }} \hfill \\ {\text{where }}e_{\rm s} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 {\sqrt 3 }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${\sqrt 3 }$}} \hfill \\ \end{gathered}$$
(29)

LBM for solid–liquid PC-based study on thermal LB model was suggested by shan [82]. By modifying the EDF of the thermal field, a recent approach can be evolved to address the LH source term. Later, Jiaung et al. [96] introduced a simplified energy model called the enthalpy-based model. The enthalpy-based method can be used for solid–liquid PC problems as it eliminates the requirements of meeting conditions at the interface position [71, 96, 97]. The total enthalpy (H) splits into sensible and LH enthalpy components in the vicinity of the solid–liquid interface (SLI) for PCM problems. The total enthalpy can be evaluated by Eq. (31).

$$H = {\text{CT}}({\mathbf{x}},t) + f_{\rm l} L({\mathbf{x}},t - \Delta t)$$
(30)
$$H = \sum\limits_{\rm i = 0}^{n - 1} {q_{\rm i} }$$
(31)

The temperature can be estimated by the total enthalpy as follows [98, 99]

$$T = \left\{ {\begin{array}{*{20}l} {\frac{H}{C};} & {T < T_{\rm s} } \\ {T_{\rm s} + \frac{{H - H_{\rm s} }}{{H_{\rm l} - H_{\rm s} }}\left( {T_{\rm l} - T_{\rm s} } \right);} & {T_{\rm s} \le T \le T_{\rm l} } \\ {T_{\rm l} + \left( {H - H_{\rm l} } \right)/C;\;} & {T > T_{\rm l} } \\ \end{array} } \right.$$
(32)

TS and Tl stand for solidus and liquidus temperatures, respectively (Tl ≥ TS and equal symbol denotes the PCP at a fixed temperature); and Hl and Hs are the total enthalpy representing the liquidus and solidus temperatures, respectively.

For the thermal field, the source term will be added to Eq. (19), and later, the thermal DF can be obtained as:

$$q_{\rm i} \left( {{\mathbf{x}} + {\mathbf{c}}_{\rm i} \Delta t,t + \Delta t} \right) = q_{\rm i} \left( {{\mathbf{x}},t} \right) - \omega_{\rm q} \left[ {g_{\rm i} \left( {{\mathbf{x}},t} \right) - q_{\rm i}^{\rm eq} \left( {{\mathbf{x}},t} \right)} \right] - w_{\rm i} \frac{L}{C}\left( {f_{\rm l} \left( {{\mathbf{x}},t} \right) - f_{\rm l} \left( {{\mathbf{x}},t - \Delta t} \right)} \right)$$
(33)

PCM with porous media

For the PCMs in porous media, the external force exercised by the porous medium on the fluid is considered. The expression is given by [100,101,102]

$$F = - \frac{\varepsilon \nu }{K}U - \frac{{\varepsilon c_{\rm F} }}{\sqrt K }\left| U \right|U + \varepsilon G$$
(34)

where ν, K, and cF are the kinematic viscosity, permeability, and dimensionless Forchheimer term, respectively (\(c_{\rm F} = {\raise0.7ex\hbox{${1.75}$} \!\mathord{\left/ {\vphantom {{1.75} {150\varepsilon^{3} }}}\right.\kern-0pt} \!\lower0.7ex\hbox{${150\varepsilon^{3} }$}}\)) stated by Fu et al. [103]\(\left| U \right| = \sqrt {u^{2} + v^{2} }\). The permeability (K) can be computed from Kozeny–Carman equation [104]\(K = {\raise0.7ex\hbox{${\varepsilon^{3} d_{\rm p}^{2} }$} \!\mathord{\left/ {\vphantom {{\varepsilon^{3} d_{\rm p}^{2} } {150(1 - \varepsilon^{2} )}}}\right.\kern-0pt} \!\lower0.7ex\hbox{${150(1 - \varepsilon^{2} )}$}}\), where dp is the mean diameter of pores of the porous medium. The first and second expressions on the RHS (right-hand side) in Eq. (34) stand for Darcy term and Forchheimer drag forces, respectively, amid a fluid and porous structure applied to describe the essence of the porous media to the fluid flow within the liquid regime. The third expression on the RHS in Eq. (34) symbolizes the buoyancy term in which the Boussinesq approximation is utilized; so, it is given by

$$G = g\beta_{\rm T} \left( {T - T_{\rm 0} } \right)$$
(35)

where g is acceleration owing to gravity, β represents the thermal expansion coefficient, which expresses variations in the volume of the molten PCMs owing to the thermal difference, and T0 is reference temperature.

LBM for nanoenhanced PCM

It is substantially acknowledged that when the nanoparticles are added to the water or some other working fluid, viscosity, thermal conductivity, and other physical properties will vary. The density of the nanofluid is expressed as [105,106,107],

$$\rho_{\rm nf} = \rho_{\rm f} \left( {1 - \phi } \right) + \rho_{\rm sp} \phi$$
(36)
$$\mu_{\rm nf} = \frac{{\mu_{\rm f} }}{{\left( {1 - \phi } \right)^{2.5} }}$$
(37)
$$\left( {\rho C_{\rm p} } \right)_{\rm nf} = \left( {\rho C_{\rm p} } \right)_{\rm f} \left( {1 - \phi } \right) + \left( {\rho C} \right)_{\rm sp} \phi$$
(38)
$$\left( {\rho \beta } \right)_{\rm nf} = \left( {\rho \beta } \right)_{\rm f} \left( {1 - \phi } \right) + \left( {\rho \beta } \right)_{\rm sp} \phi$$
(39)
$$\frac{{\sigma_{\rm nf} }}{{\sigma_{\rm f} }} = 1 + \frac{{3\left( {\frac{{\sigma_{\rm sp} }}{{\sigma_{\rm f} }} - 1} \right)\phi }}{{\left( {\frac{{\sigma_{\rm sp} }}{{\sigma_{\rm f} }} + 2} \right) - \left( {\frac{{\sigma_{\rm sp} }}{{\sigma_{\rm f} }} - 1} \right)\phi }}$$
(40)

In the above equations φ, ρnf, ρCnf, ρβnf, μnf, and σnf represent the volume fraction of nanoparticles, density of nanofluid, heat capacity, thermal expansion, dynamic viscosity, and electrical conductivity, and subscripts nf, f, and sp denotes nanofluid, base fluid, and solid particles.

LBM boundary condition for PCM

The perspective of the SLI can be traced by updating the liquid fraction Eq. (32), or the no-velocity condition and total enthalpy on the acting interface are dealt with immersed boundary condition. The no-slip condition is employed in the SLI, and the evolution of Eq. (18) is only executed at the melted regime. The no-slip/bounce-back boundary condition on the SLI dealt with immersed moving boundary condition initially suggested by Noble and Torczynski [108]. The benefit of this technique is that an integrated evolution equation of the density DF is implemented on the entire domain. Similarly, Cook et al. [109], Strack and Cook [110], and Wang et al. [111] have successfully implemented this technique to analyze particle–fluid systems. The immersed moving boundary condition is used to analyze the moving phase interface for PCMs. In this method, the evolution equation for the density DF, Eq. (15), can be updated as

$$p_{\rm i} \left( {{\mathbf{x}} + {\mathbf{c}}_{\rm i} \Delta t,t + \Delta t} \right) = p_{\rm i} \left( {{\mathbf{x}},t} \right) - \omega_{\rm p} \left( {1 - B} \right)\left[ {f_{\rm i} \left( {{\mathbf{x}},t} \right) - p_{\rm i}^{\rm eq} \left( {{\mathbf{x}},t} \right)} \right] + \Omega_{\rm i}^{s} + \Delta tF_{\rm i}$$
(41)

where B is the weighting factor associated with fluid fraction and Ω is the dimensionless relaxation parameter or extra collision term and can be written as,

$$B = \frac{{\left( {1 - f_{\rm l} } \right)\left( {\omega_{\rm f} - 0.5} \right)}}{{f_{\rm l} + \omega_{\rm f} - 0.5}}$$
(42)
$$\Omega_{\rm i}^{s} = p_{{\overline{i} }} \left( {{\mathbf{x}},t} \right) - p_{\rm i} \left( {{\mathbf{x}},t} \right) + p_{\rm i}^{\rm eq} \left( {\rho ,{\mathbf{u}}_{\rm s} } \right) - p_{\rm i}^{\rm eq} \left( {\rho ,{\mathbf{u}}} \right)$$
(43)

u and us are the macroscopic velocity and solid velocity, respectively. The boundary condition for flow and thermal field of LBM can be obtained from [78, 112,113,114].

Thermo-physical properties of PCM

The thermo-physical properties of some common PCM and solid nanoadditives in PCM as NePCM used in the present work are illustrated in Tables 1 and 2.

Table 1 Thermo-physical properties of PCM
Full size table
Table 2 Thermo-physical properties of nanoadditives
Full size table

Numerical modeling of PCM and NePCM

LBM Studies of PCM

In this section, the literature covering the heat transfer for phase change materials in cavities/enclosures by LBM is discussed herein in tabular form (Table 3).

Table 3 LBM studies for PCM for rectangular geometries
Full size table

Luo et al. [24] analyzed LB simulation for convection melting within the complex heat storage system occupied with PCMs for various Ra and Stefan numbers (St). The numerical consequences showed that the transient PCP depends on the geometrical and thermal parameters. Huang et al. [69] simulated the new LBM model for solid–liquid PCM for various Rayleigh numbers (Ra). Comparisons between the present results with the previous study demonstrate the feasibility and accuracy of the current approach concluded from the study. Later, Kebriti and Moqtaderi [70] examined convective solid–liquid phase change by employing LBM for various power-law indexes (n) and Ra. Results showed that as n augments flow at a specified Ra, the mean Nusselt number (\(\overline{Nu }\)) at the heated wall and the melting rate diminish. Sadehi et al. [115] investigated a numerical study on the solid–liquid phase change process of multilayer Rubitherm PCMs within a tubular heat exchanger. Employing PCMs with the lowest and highest melting temperature in the vicinity of cold and hot boundaries leads to higher amounts of liquid fraction during the process. The effects of PCMs with respect to thickness and melting temperature help to choose proper PCMs with high latent heat capacity which leads to fluctuating average temperature.

Huo and Rao [117] studied PCM-based battery thermal management at a low temperature within the vertical cavity. It was remarked that the temperature of the battery diminishes gradually, and thermal distribution can be assured with the help of the latent heat of PCMs. Moreover, lower thermal conductivity, higher LH, and more significant surrounding temperature can decelerate the solidification procedure of PCMs and maintain the battery temperature. However, at higher LH of PCMs, the temperature distribution of the battery gets non-uniform, diminishing the battery's life [138]. Fuentes et al. [118] delineated melting with convection and radiation within the participating PCM. It was observed that free convection acts an essential role in the transitional behavior of the overall HT process. The absorbed heat flux within the PCMs was more significant by 3%. On the other hand, the enhanced absorbed heat flux in PCMs has a negligible influence on the melted fraction. Liu and He [119] investigated solid–liquid phase change (SLPC) with free convection within porous media. The numerical outcomes show that the current model is efficient and accurate for studying transient SLPC within porous media.

Ren and Chan [120] elucidated PCM melting within the system utilizing interior fins. The study concluded that employing internal fins could heighten the HT in the PCM enclosure. The PCMs melt quicker if more fins are used. On the other hand, the quantity of melted PCMs at the final state gets less when the number of fins is added to the cavity. The melting rate of PCMs rises with the length of the fins. Zhu et al. [121] delineated 2D and 3D simulations for free convection melting within the square cavity. It was remarked that the melting rate of 2D is quicker than 3D in the primary stage, but the difference shrinks afterward during melting. At higher Ra, the Nu and melting rate increase. Enhancement in breadth has a minor effect on the interface, positions, and shapes in 3D, which signifies that 3D study is essential for related study.

Subsequently, Du et al. [122] proposed melting processes of large Prandtl number (Pr) PCMs by utilizing organic PCM. It was noticed that the numerical consequences agree with the existing data acquired numerically and experimentally. Compared with the existing LBM approaches, the current technique can capture the melting interface perfectly with a small grid density. Yehya et al. [123] explored the combined numerical and experimental characterization of an impure PCM employing TLBM. The numerical and experimental results demonstrate good agreement. The approach permits highlighting the behavior of PCMs and characterizes their thermo-physical properties. Huo and Rao [124] introduced LBM for solid–liquid PCP of PCM for constant heat flux. The consequences demonstrated that additional energy on the upper part of the left wall could emphasize the clockwise rotation. Additional input energy intent in the middle of the left wall is an efficient means to speed up the solid–liquid PCP and preserve the temperature of PCMs. Huang et al. [125] explored experimentally and numerically the melting process of PCMs embedded in open-cell metal foams by using LBM. The influence of foam porosity on the HT process in porous structures is investigated. The outcome indicates that at larger porosities of the metal foams, the PCMs prove to raise the melting speed. The importance of conduction in PCMs for the melting process in metal foam is noticed.

Consequently, Gao et al. [126] presented the melting of PCM within the porous media with conducting fins. The computational outcomes showed that the melting heat transfer could be improved by adding conducting fins in the porous material. The speed of melting rises with the enhancement in the length of the fin and diminishment in the heat capacity of the fin. On the other hand, the fin in the vertical position has no significant impact on the melting rate. Peng and sadaghiani [127] elucidated the improvement of the thermal function of PCM by employing alumina nanoparticles within the circular, rectangular enclosure. The results obtained by the variation of fin numbers conclude that the more the fins, the more the MAR parameter of PCM, and later the more the improved energy storage capability. Further, the effect of the addition of nanoparticles of Al2O3 into paraffin showed that 3% of nanoparticles can increase the MAR parameter rather than lower mass percentage. However, the nanoparticle concentration of more than 3% has no significant effect on the MAR parameter.

Ibrahem et al. [128] explored the effect of nanoparticles on the melting process with PCM for several pertinent parameters. It was found that the HT by conduction dominates in the initial melting phase, and then, the convection starts dominating. Also, the nanoparticles in the PCMs enhance the phase change. Besides, it was remarked that the thermal conductivity increases due to the addition of copper nanoparticles, but the melting rate and latent heat get reduced. Lin et al. [129] delineated the complex interaction of free convection and melting of PCM within a spherical capsule of various sizes. The influence of inhomogeneous PCM properties on the melting rate was nonlinear in various melting phases. Jourabian et al. [130] introduced thermal transport-free convection melting of PCMs in a partially heated square enclosure. When the heated plates are placed on top or middle of the enclosure, convection dominates in the top regime of the enclosure.

Gaedtke et al. [131] elucidated the total enthalpy-based simulation of melting in metal foam composite/paraffin PCM in 2D and 3D. The study describes the multidomain HT in 3D; the thermal conductivity of foam is 1000 times larger than paraffin. The expected sequence of the melting front and the effect of various foam-specific surface regions closely agree with the previous one. Yin et al. [132] conducted a study on SLPC at a pore scale with central moments in TES. It was noticed that higher stability was observed at higher Ra and low viscosity. Rui et al. [133] presented free convection melting within the square enclosure. It was remarked that the top heating wall increases the melting time of the solid phase, but has a minor influence on the PC in the bottom part. The higher liquid fraction in another model was about 16.8% augmentation, and the extra top heating hastens the mean melting time by 16.8%. Feng et al. [134] explored thermal performance evaluation for bionic porous ceramic PCM utilizing micro-computed tomography. The rate of melting increases significantly due to the heat transfer path. A higher thermal contact resistance leads to lower melting time which diminishes the augmentation effect of a porous frame. Liu et al. [135] delineated solid–liquid-based phase change HT within the confined annulus. It was observed that present outcomes found excellent agreement with the previous study. Liu et al. [136] introduced a numerical study of paraffin wax melting within circular tubes for various relevant parameters. It was remarked from the study that in the SLPC process for paraffin melting, heat conduction was the primary cause in the early phase of phase transformation. The enhancement in Rayleigh number (Ra) showed the augmentation in the strength of free convection, which reduces the lessen of the \(\overline{\mathrm{Nu} }\) due to the movement of the phase interface. Lu et al. [137] delineated HT augmentation analysis of electro-hydrodynamic (EHD) for SLPC inside a square cavity. Results showed that, during heating and injection from the lower portion, EHD rises thermal transport by modifying the onset of the flow motion within the liquid zone, whereas in the case of heating and injection from the left part, strong enough Coulomb force leads to the transition of the convection rolls which augments heat transfer at times of the melting.

Tao et al. [139] presented phase change heat transfer (HT hereafter) within metal foam or paraffin composite PCMs. The outcomes showed that the projected technique could enhance the HT process's uniformity and increase HT performance. Feng et al. [140] numerically examined the melting of nanoparticle-enhanced PCMs within the rectangular enclosure heated from the bottom portion. In the early conduction phase, melting was the dominating component in thermal transport behavior, and the melting interface was noticed.

Jourabian et al. [141] numerically studied the melting of nanoparticle-enhanced PCMs within the cylindrical tube. It was noticed that the melting point is uniform within the entire region of the cylinder at lower Ra. At the same time, it escalates at the top of the cylinder at intermediate Ra. In addition, unstable solid flow in the lower part of the cylinder at a Ra of 106 leads the melting time to acute after a specific point [142]. Talati and Taghilou [143] simulated the application of LBM on the PCM solidification inside a rectangular finned container. It was noticed that the maximal time needed for freezing the PCM occurs at the aspect ratio of 0.5. Heat loss diminishes by locating the PCM within the composite plane wall. Moreover, the maximum analytical overestimation takes place at AR = 0.5.

In another study, Jourabian et al. [144] numerically studied the melting process in the porous media along two heated cylinders. The influence of thermal conductivity ratio and porosity between PCMs and porous structure is explored. It was noticed that a reduction in porosity causes a diminishment in the system melting rate and TES capacity. Moreover, augmenting the thermal conductivity proportion of the porous matrix leads to the enhancement of the melting rate. Mabrouk et al. [145] introduced the effect of porosity on the PCMs' thermal performance within the porous rectangular channel for different porosity effects under the influence of Reynold number (Re). It can be remarked from the findings that the different features of metal foam, such as porosity and conductivity, decrease later, and the augmentation in Re enhances the melting due to unsteady, forced, and laminar convection.

Han et al. [146] proposed an LBM simulation of melting heat transfer within the composite PCM. Solid–liquid interface and dynamic temperature evolution are analyzed. The consequences illustrate that the thermal performance of PCMs enhances due to metal particles as nanoparticles. Li et al. [147] numerically investigated pore-scale gravity effects on the PC HT features. It was concluded from the study that free convection acts a substantial character in the melting process. In contrast, it steadily attenuates with the diminishment in gravity, which induces the inhibiting effect of the melting process and navigates the transition of the dominant HT mechanism from convection to conduction.

Shirbani et al. [148] studied the improved TES occupying metal foam as PCMs containing several pore arrangements. It was noticed from the study that large pores could render better free convection, increasing the HT rate and decreasing the melting period. Chiappini [149] numerically studied coupled lattice Boltzmann (LB) FVM for PCM analysis. It was concluded from the study numerical, and literature data have a good agreement for the upcoming model. Ren et al. [150] presented the LBM of PCM and HT characteristics within the multilayer deposition to attain rapid prototyping and assure bonding quality. The study noticed that prediction adopts the best possible temperature state for manufacturing and demonstrates the disparity in temperature trends at various positions.

Studies of NePCM by LBM and other traditional techniques

This present section studies the melting and solidification characteristics of NePCM in various applications with a brief description of boundary conditions and preferred models for formulation. A brief description of literature covering the heat transfer for NePCM in cavities/enclosures by LBM and other techniques is discussed herein in tabular form (Table 4).

Table 4 LBM, along with other techniques studies for NePCM for geometries
Full size table

The dispersion of hybrid nanoparticles in PCMs enclosed in a cavity with specific boundary conditions provides an enormous alteration of thermo-physical properties in the melting and solidification phase [163]. In this regard, Ghalambaz et al. [151] [164] analyzed the effect of 0–5% mass fraction Mg–MgO nanoparticles with paraffin wax in a square cavity. After melting, the thermo-physical properties were assumed to be constant; however, in the liquid phase, the hybrid nanofluids are assumed to be constant except for the density variation. A marginal variation in the liquid fraction has been observed due to the enhancement of dynamic viscosity greater than thermal conductivity enhancement. However, similar researchers analyzed the heat transfer of nanoencapsulated PCM in a porous cavity with the suspension of nanoparticles. The NePCM particles could be able to enhance the heat transfer up to 28% with a fusion temperature of 0.5 and inclination angle of 42°. However, Boukani et al. [165] analyzed the melting characteristics of NePCM in partially filled horizontal elliptical capsules with different aspect ratios and nanoparticle volume fractions. The increase in nanoparticle concentration enhances the melting rate, but decreases the NePCM volume change. It was also found that the shape of the solid–liquid interface is a function of both heat transfer rate and air void inside the capsule. To a similar extent, Selimefendigil et al. [155] analyzed the natural convection study of CuO–water nanofluid in a cavity with conductive partition and PCM under the effect of a uniform magnetic field. The results showed an average increase of heat transfer around 31.81% augmentation with a magnetic inclination of less than 5%. Chen et al. [1] elucidated a solid–liquid model for PCM melting, occupying porous media within the cylinder-shaped heat exchangers for different parameters. The adopted technique is accepted and applied for a broad range of PCM phase changes, which promotes the design and progress of PCM heat exchangers for TES systems was noticed from the study.

However, Ghalambaz et al. [156] and Zadeh et al. [166] analyzed the thermal performance and response time of the petal-shaped shell and tube TES unit. The optimum design could improve the amount of storage capacity by 23.3% with Cu and 22.5% with GO NePCM compared to average designs. The results of this study also indicated that the geometric parameters should be considered as a primary factor in TES. In comparison, Nayak et al. [158] analyzed a free convection heat transfer in NePCM inside a circular cold cylinder with a wavy hot baffle of varying amplitude subjected to a magnetic field. The amplification of Ra accounts for the fast movement of fluid, while Ha causes the slow movement of fluid depending upon the intensity of the natural convection of NePCM. Similar results with a CFD-developed model with a heat transfer acceleration by an increasing number of baffles to 3, 7, 11, and 15 baffles provide a water temperature enhancement up to 26.37%, 29.38%, 34.06%, and 37.36%, respectively [167]. Similarly, Zidan et al. [159] analyzed the natural convection and entropy of NePCM water over a reverse T-shaped porous cavity for low emaciation of energy consumption in buildings. The use of NePCM maintains the thermal management of buildings efficiently with a better heat transfer rate. With the amplification of Ra, the intensification of streamlines, velocity fields, and structural changes of the PCM zone attained a decrease of Da. There is an uplift in Nuavg with an increase in NP concentration from 1 to 5%, which ensures an increase in heat transfer due to the addition of NPs. However, Sadeghi et al. [160] investigate natural convection and entropy generation in a NePCM-based L-shaped cavity in which St, micro-rotation, and non-dimensional fusion develop a negative impact on heat transfer and reduce Nu up to 25%, 42%, and 15%, respectively. Similar results with PCM-based heat sinks were also observed in L-shaped paraffin–copper metal foam with heat enhancement in pulse tube with steady heat flux [168]. In a similar context, Ghalambaz et al.[162] modeled a nanoencapsulated PCM in a coaxial cylindrical cavity, which ensures an unsteady charging and discharging behavior of NePCM suspension with a higher value of temperature at the particle core and an increase in heat transfer rate.

Conclusions

This manuscript is proposed to assess the recent studies of PCMs for TES and heat transfer applications in fusion with LBM. In recent years, PCM has been recommended as a potential TES medium and receiving significant attention. LBM has evolved as a potential tool to solve problems based on fluid flow, thermal, multiphase, PCM, species transport, and many more studies. Most studies revealed that paraffin wax had been used as PCM for TES. A few studies have considered polyethylene glycol, lauric acid, and palmitic acid as PCM for TES. The literature associated with PCM for TES by LBM and other traditional techniques has been reviewed. TES is considered mainly from the theoretical point of view, considering various traditional techniques. The LHTES method via PCMs is an efficient means of TES and possesses the benefits of high-energy storage. The outcomes associated with various studies revealed pragmatic significance in an extensive range. PCM can be considered a future-generation energy source to encounter the increasing demand of energy sources such as solar thermal energy storage, air-conditioning unit, refrigeration system, electronic cooling, drug delivery unit, and crystal growth.

However, over the few years, the evolution of the particle-based discrete simulation method (LBM) has provided a robust and flexible approach to melting and solidification characteristics of PCM for various TES and heat transfer applications. This method develops a solid–liquid phase change model to simulate the transient phase change in porous media. It also combines an axisymmetric enthalpy change scheme to simulate the phase change efficiently by providing an elementary volume for modeling the PCM. Moreover, LBM coupled with single-relaxation and multirelaxation time schemes helps to simulate the fluid flow and temperature field. This new model is also applicable to predict the performance in various TES with brief ideas of heat transfer under various external forces. The approach is about enhancing the thermal transport area and augmenting the thermal conductivity of PCM simultaneously. Therefore, it is advised that future research focuses on the use of extended surfaces (fins, heat pipes), as well as the addition of high-conductivity materials, to improve heat transfer in LHTES systems. The authors proposed that more examination with visualization is needed to analyze the substantial augmentation in PCM for TES applications so that the changing of phase, such as the melting or solidification patterns within the PCM systems, can be characterized.