Magneto-hydrodynamic thermal convection of Cu–Al₂O₃/water hybrid nanofluid saturated with porous media subjected to half-sinusoidal nonuniform heating

Abstract

The present work aims to examine the thermal efficacy of half-sinusoidal nonuniform heating at different spatial frequencies for a porous natural convection system using Cu–Al₂O₃/water hybrid nanofluid and magnetic field. The system is presented utilizing a classical square enclosure heated nonuniformly at the bottom wall, and the sidewalls are allowed to exchange heat with the surroundings. The Brinkman–Forchheimer–Darcy model is adopted catering other additional terms for buoyant force and magnetic field. The governing equations are transformed into nondimensional forms and then solved numerically using a finite volume-based computing code. The importance and fundamental flow physics are explored in terms of the pertinent parameters such as the amplitude (I) and spatial frequency (f) of half-sinusoidal heating, Darcy–Rayleigh number (Ra_m), volume fraction of hybrid nanoparticles ($\phi$), and Hartmann number (Ha). The flow structure and heat transfer characteristics are analyzed and presented utilizing heatlines, streamlines and isotherms and average Nusselt number. The results show that the use of half-sinusoidal nonuniform heating along with hybrid nanofluid can be a viable method for enhancement and control of the overall thermal performance. The study indicates that half-sinusoidal heating could be a promising technique for better heat transfer even in the presence of flow dampening effects like porous media and magnetic fields.

Graphic abstract

Introduction

Buoyancy-driven fluid flow and convective heat transfer through the porous substrate is an important topic for research, and it finds numerous engineering applications such as heat exchangers, solar thermal systems, electronic equipment cooling, chemical reactors, management of nuclear waste, geothermal energy systems, energy storage and conservation system, oil and gas processing units, food grain processing units, bio-medical systems. In such applications, the presence of a porous substance (a solid matrix having continuous pores) causes more complex flow physics depending upon the thermal boundary conditions [1,2,3,4]. A thorough understanding of thermo-fluid flow behavior within the thermal system is crucial for modeling, designing, and operation of such devices and also a very tricky task for an optimum design by the manufacturer. Researchers are continuously paying their attention for achieving the efficient thermal design through numerical computations [5,6,7,8]. Some recent studies depicting the importance of porous media are deliberated toward the technology development [9,10,11,12,13]. These works address thermal analyses carried out experimentally on metallic foam or phase change material embedded with porous substances.

Industrial as well as domestic appliances subjected to temperature gradient face tremendous issues for dissipating the by-product heat (as a result of device operation) in an efficient manner so that the devices can operate within its safe operating temperatures. Thermal management of such a device is a serious challenge to the designer without compromising the efficacy of the device. In this context, the usage of nanofluids, which was first introduced by Choi [14], is a promising approach for improving the thermal conductivity of the working medium. Nanofluids utilize common working fluids/liquids along with dispersed solid particles of nanometer scale. The application of nanofluid has increased significantly even with the critical issues of suspensions and agglomeration of nanoparticles. In general, commonly available base fluids are water, ethylene glycol, bio-fluids, polymer solutions, oils, and lubricants, whereas commonly used nanoparticles are metallic particles of Cu, Al, Fe, Au and Ag, and nonmetallic particles made of CuO, Al₂O₃, Fe₃O₄, TiO₂, and SiC. Researchers have studied various geometrical configurations utilizing different types of nanofluids and reported about the heat transfer augmentation over the conventional base fluids, which is available in the literature [15,16,17,18,19,20,21]. Many researchers have also investigated different problems using nanofluids as working media in the presence of magnetic fields [22,23,24,25]. Detailed reviews are available in Refs. [26,27,28,29].

Although the addition of nanoparticles leads to the improvement in thermal conductivity of base fluids, it involves several issues like erosion due to suspended nanoparticles, pressure drop due to the higher viscosity, increased energy input to pump, flow instability, etc. [30]. The recent technological advancement in the area of heat transfer reveals that the thermal conductivity of conventional fluids (and also mono-nanofluids) can be augmented further by dispersing two or more different types of nanoparticles or their mixture as nanocomposites [30]. When the nanocomposite or individual nanoparticles are added in a suitable base fluid (liquid), it is known as a hybrid nanofluid and it shows better thermal conductivity over the pure base fluid or a mono-nanofluid. Usage of hybrid nanofluids can significantly boost up the thermal performance in numerous applications. Some of the beneficial aspects are documented in the literature in Refs. [19, 31,32,33]. However, the hybrid nanofluid shows a higher effective viscosity (particularly when concentration of nanoparticles increases) compared to the conventional fluid and also the mono-nanofluid. It incurs a higher input pumping energy due to reduced flow velocity (as the viscosity increases). The effective properties of hybrid nanofluids depend upon many factors like selection of nanoparticles and their combination, preparation and dispersion techniques, the shape and size of nanoparticles, agglomeration, measuring techniques, etc. In this context, detailed reviews on various aspects of hybrid nanofluids and future scope of further exploitation for potential applications are well documented in Refs. [30, 34, 35].

Suresh et al. [36] experimentally investigated the effects of Cu–Al₂O₃/water hybrid nanofluid and reported ~ 13.56% heat transfer augmentation over the pure water. Utilizing different types of hybrid nanofluids, several researchers have investigated the thermal performance of different complex problems such as MHD convection in a clear domain by Ghalambaz et al. [37], in a porous domain in the absence of magnetic field by Ghalambaz et al. [38], Chamkha et al. [39], and Al-Srayyih et al. [40]. MHD thermal convection of hybrid nanofluids through porous substances has been demonstrated in Refs. [41,42,43,44,45,46] and in many other works. However, in most of the aforementioned studies, the convective heat transfer characteristics have been investigated using the classical thermal boundary conditions, where heat source has been considered to be either of constant heat flux or constant temperature (isothermal) with some variation in length/position of the heat source. It has been found that, along with the spatially constant thermal boundary condition, as discussed above, the consideration of a nonuniform heating of hybrid nanofluid is also important from fundamentals as well as practical standpoints. For instance, Manna et al. [7] and Biswas et al. [47] have reported the beneficial aspects of a nonuniform heating over the uniform heating of porous media and found about 74–85% heat transfer enhancement. Several other researchers have also investigated the buoyancy-driven convective heat transfer in the porous substances considering a nonuniform sinusoidal heating at the bottom wall [48, 49], horizontal wall(s) [50], or sidewalls [51, 52]. However, the study addressing multi-frequency spatial heating following a half-sinusoidal profile is not attended so far, particularly with any hybrid nanofluid. It motivates to take up the present work using a hybrid nanofluid saturated porous system.

The sinusoidal heating condition has also been studied during natural convective heat transfer of nanofluid through the clear domain by Oztop et al. [53] and Mikhailenko et al. [54], through the porous domain by Alsabery et al. [55] and Arasteh et al. [56]. In other classes of work, the natural convective heat transfer of nanofluid flow through a porous media has been studied considering the effect of cavity shape like a sinusoidally wavy wall(s) [57,58,59]. The effect of an external magnetic field on buoyancy-driven thermal convection of nanofluid through porous media under the sinusoidal heating profile has been investigated by Sheremet and Pop [60], Malik and Nayak [61], Nazeer et al. [62], Javaherdeh and Najjarnezami [63], Pordanjani et al. [64], etc. The magneto-hydrodynamic thermal convection of nanomaterial migration in a sinusoidal-shaped porous cavity has been analyzed by Vo et al. [65], whereas Aly and Raizah [66] have investigated MHD convective heat transfer a ferrofluid filled porous cavity heated with a sinusoidal wavy rod.

Recently, enhanced convective heat transfer of hybrid nanofluid, heated sinusoidally, has been investigated by Tayebi and Chamkha [67]. In their study, they found that Cu–Al₂O₃/water hybrid nanofluid has superior heat transfer functionality compared to Al₂O₃/water mono-nanofluid and the base fluid (water). Takabi and Salehi [68] have analyzed the effect of sinusoidal corrugation at the sidewalls of a bottom heated enclosure filled with Cu–Al₂O₃/water hybrid nanofluid. They found that the heat transfer can be improved by adopting hybrid nanofluid compared to a mono-nanofluid. Ashorynejad and Shahriari [69] have studied the MHD convective heat transfer under the combined effect of wavy-walled enclosure, heated sinusoidally at the left side and open at the right side, filled with Cu–Al₂O₃/water hybrid nanofluid. They have reported the positive role of the hybrid nanofluid on the thermal performance of the cavity. Further to the above, the natural convective heat transfer in cavities has also been investigated by many researchers considering hybrid nanofluids as a working media along with [70, 71] or without [72] magnetic fields, or both magnetic fields and porous medium [73,74,75].

In summary, the selective literature survey clearly points to the importance and usage of sinusoidal heating in engineering applications. It also demonstrates that sinusoidal heating could be a rational approach for improving buoyancy-driven convective heat transfer and can be a powerful controlling means for thermal management. Most of the earlier works have considered a complete cycle of sinusoidal heating (Refs. [7, 47]). However, the present work differs to a great extent from the earlier works. With a complete cycle of the sinusoidal heating profile, one half of the cycle has a less effective role on the heating/convective process as the heat is rejected out though this half cycle. Only the other half cycle of the sinusoidal heating profile participates in the heating/convective process. This causes a loss of input energy or an increased cost of energy investment. Under the circumstances, the use of half-sinusoidal heating profile provides (with the help of proper electrical circuit design and suitable control arrangements) or offers efficient utilization of input energy (can reduce the need of input energy); thus, it enhances heat transfer process for the same work energy investment. In the literature, there exists no such fundamental analysis. Thus, the outcomes of this present study are very promising and could be helpful to the thermal community for future research and applications in a new direction. In regard to the application of half-sinusoidal heating profile, it could be used in many areas such as electronic components and devices, drying technology, etc. To explore this fact in a better way, the thermal performance of Cu–Al₂O₃/water hybrid nanofluid saturated with porous substrate packed in an enclosure subjected to multi-frequency spatial heating (following a half-sinusoidal function) along with magnetic fields is investigated. Therefore, the outcomes of the present study will contribute to modeling, designing, and development of devices subjected to the thermal applications magnetic fields.

Modeling aspects

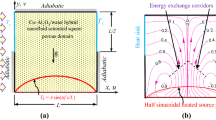
The problem of hybrid nanofluid saturated with porous media packed in a two-dimensional square enclosure having length L and height H is presented in Fig. 1a. The bottom wall of the enclosure is heated nonuniformly (by maintaining half-sinusoidal temperature profile, T_h, along x-direction as shown in the figure), whereas the sidewalls are diathermic and kept at a temperature T_c, which is lower than the minimum temperature of the half-sinusoidal temperature profile, T_h, of the bottom wall. Figure 1b illustrates the half-sinusoidal nonuniform temperature profiles for the bottom wall for two values of frequency parameter, f = 1 and f = 3. The top wall of the enclosure is thermally insulated. During the computation, the points of singularity at the junctions of hot bottom wall and cold side wall are handled by inserting insulation patches [2] suitably. The no-slip and no-penetration boundary conditions are imposed at all the walls of the enclosure. The gravity force is acting downward as indicated in Fig. 1a. The enclosure is filled with a porous substance saturated with Cu–Al₂O₃/water hybrid nanofluid. An external magnetic field of strength B is applied along the horizontal direction. It is assumed that the externally applied magnetic field is uniform over the enclosure which is filled with an electrically conducting fluid, and it results in the Lorentz force. The induced magnetic field is neglected; thus, the term representing the applied magnetic field appears in the y-momentum equation. In this study, the Joule heating and the Hall effect are also neglected.

Fig. 1

(Color figure online) a Schematic diagram of the physical domain packed with hybrid nanofluid saturated with porous media along with boundary conditions, b half-sinusoidal nonuniform temperature profiles for the heating along the bottom wall

Governing equations in dimensionless forms

The fluid flow and heat transfer inside the enclosure are assumed to be steady, Newtonian, laminar, and incompressible. The density variation in the working fluid is taken care of by the Boussinesq approximation. The porous medium is assumed to be hydrodynamically and thermally homogeneous and isotropic, uniform porosity and permeability throughout the porous domain. The viscous dissipation effect compared to conduction and convection terms in the energy balance equation is assumed to be negligible [1, 7, 8, 18, 76, 77]. Furthermore, the fluid and porous substrate are assumed in the local thermal equilibrium (LTE) condition [8, 47, 76, 77]. In this study, the hybrid nanofluid is modeled as a single-phase homogeneous fluid, whereas it is the mixture (at different proportions) of two different nanoparticles Cu and Al₂O₃ is dispersed in pure fluid (water). The nanoparticles are assumed to be uniform in size and are spherical in shape; the diameter of nanoparticles is in the order of ~ 1 nm. The nanoparticles are stable for all time and suspended homogeneously in the pure fluid without any sedimentation or agglomeration [68, 69]. In the present simulation, the thermophysical properties of the pure fluid (Pr = 6.93) as well as the nanoparticles (of Cu and Al₂O₃) are taken as constant assuming an average fluid temperature of 300 K [77,78,79], which are listed in Table 1. The modeling of hybrid nanofluid flow through the porous media is executed following the above assumptions and adopting the Brinkman–Forchheimer–Darcy model [3, 5]. This model addresses the resistive force fluid experiencing when passing through a porous medium. The resulting dimensional partial differential equations (PDEs) for mass, momentum, and energy equation can be written as [43, 61]

$$ \frac{\partial u}{\partial x} + \frac{\partial v}{\partial y} = 0 $$

(1)

$$ \frac{1}{{\varepsilon^{2}}}\left({u\frac{\partial u}{\partial x} + v\frac{\partial u}{\partial y}} \right) = - \frac{1}{{\rho_{\text{hnf}}}}\frac{\partial p}{\partial x} + \frac{{\nu_{\text{hnf}}}}{\varepsilon}\left({\frac{{\partial^{2} u}}{{\partial x^{2}}} + \frac{{\partial^{2} u}}{{\partial y^{2}}}} \right) - \left({\frac{{\nu_{\text{hnf}}}}{K}u + \frac{{F_{{\mathrm{c}}}}}{\sqrt K}u\sqrt {u^{2} + v^{2}}} \right) $$

(2)

$$ \begin{aligned} \frac{1}{{\varepsilon^{2}}}\left({u\frac{\partial v}{\partial x} + v\frac{\partial v}{\partial y}} \right) &= - \frac{1}{{\rho_{\text{hnf}}}}\frac{\partial p}{\partial y} + \frac{{\nu_{\text{hnf}}}}{\varepsilon}\left({\frac{{\partial^{2} v}}{{\partial x^{2}}} + \frac{{\partial^{2} v}}{{\partial y^{2}}}} \right) - \left({\frac{{\nu_{\text{hnf}}}}{K}v + \frac{{F_{{\mathrm{c}}}}}{\sqrt K}v\sqrt {u^{2} + v^{2}}} \right) - \frac{1}{{\rho_{\text{hnf}}}}\sigma_{\text{hnf}} B^{2} v \hfill \\ &\quad + \frac{{(\rho \beta)_{\text{hnf}}}}{{\rho_{\text{hnf}}}}g(T - T_{{\mathrm{c}}}) \hfill \\ \end{aligned} $$

(3)

$$ u\frac{\partial T}{\partial x} + v\frac{\partial T}{\partial y} = \alpha_{\text{hnf}} \left({\frac{{\partial^{2} T}}{{\partial x^{2}}} + \frac{{\partial^{2} T}}{{\partial y^{2}}}} \right) $$

(4)

Table 1 Thermophysical properties of water, Cu, and Al₂O₃ [36, 37, 39, 41]

Equations (2) and (3) indicate the Brinkman–Forchheimer–Darcy model for a buoyancy-driven flow in the presence of a magnetic field. The last two terms of Eq. (3) are due to magnetic force (involving $\sigma$) and buoyant force (involving g).

The above dimensional equations are modified into dimensionless forms for the purpose of this present investigation as

$$ \frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0 $$

(5)

$$ \frac{1}{{\varepsilon^{2}}}\left({U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y}} \right) = - \frac{{\rho_{\text{f}}}}{{\rho_{\text{hnf}}}}\frac{\partial P}{\partial X} + \frac{{\nu_{\text{hnf}} \Pr}}{{\nu_{\text{f}} \varepsilon}}\left({\frac{{\partial^{2} U}}{{\partial X^{2}}} + \frac{{\partial^{2} U}}{{\partial Y^{2}}}} \right) - \left({\frac{{\nu_{\text{hnf}} \Pr}}{{\nu_{\text{f}} {\text{Da}}}} + \frac{{F_{{\mathrm{c}}} \sqrt {U^{2} + V^{2}}}}{{\sqrt {\text{Da}} \varepsilon^{3/2}}}} \right)U $$

(6)

$$ \begin{aligned} \frac{1}{{\varepsilon^{2}}}\left({U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y}} \right) & = - \frac{{\rho_{\text{f}}}}{{\rho_{\text{hnf}}}}\frac{\partial P}{\partial Y} + \frac{{\nu_{\text{hnf}} \Pr}}{{\nu_{\text{f}} \varepsilon}}\left({\frac{{\partial^{2} V}}{{\partial X^{2}}} + \frac{{\partial^{2} V}}{{\partial Y^{2}}}} \right) - \left({\frac{{\nu_{\text{hnf}} \Pr}}{{\nu_{\text{f}} {\text{Da}}}} + \frac{{F_{{\mathrm{c}}} \sqrt {U^{2} + V^{2}}}}{{\sqrt {\text{Da}} \varepsilon^{3/2}}}} \right)V \\ & \quad - \frac{{\rho_{\text{f}}}}{{\rho_{\text{hnf}}}}\frac{{\sigma_{\text{hnf}}}}{{\sigma_{\text{f}}}}{\text{Ha}}^{2} V + \frac{{(\rho \beta)_{\text{hnf}}}}{{\rho_{\text{hnf}} \beta_{\text{f}}}}{\text{RaPr}}\theta \\ \end{aligned} $$

(7)

$$ \left({U\frac{\partial \theta}{\partial X} + V\frac{\partial \theta}{\partial Y}} \right) = \frac{{\alpha_{\text{hnf}}}}{{\alpha_{\text{f}}}}\left({\frac{{\partial^{2} \theta}}{{\partial X^{2}}} + \frac{{\partial^{2} \theta}}{{\partial Y^{2}}}} \right) $$

(8)

The symbols $\alpha_{\text{f}}$, $\beta_{\text{f}}$, $\nu_{\text{f}}$, $\rho_{\text{f}}$ and $\sigma_{\text{f}}$ indicate, respectively, the thermal diffusivity, volumetric thermal expansion coefficient, kinematic viscosity, density, and electrical conductivity of the base fluid. The above nondimensional governing Eqs. (5)–(8) are obtained using the following dimensionless variables

$$ \begin{aligned} & (X,Y) = (x,y)/H;(U,V) = (u,v)H/\alpha_{\text{f}}; \\ & \theta = (T - T_{{\mathrm{c}}})/(T_{{\mathrm{m}}} - T_{{\mathrm{c}}});P = (p - p_{{\mathrm{a}}})H^{2}/\rho_{\text{f}} \alpha_{\text{f}}^{2} \\ \end{aligned} $$

(9a)

$$ \begin{aligned} \Pr & = \frac{{\nu_{\text{f}}}}{{\alpha_{\text{f}}}};\quad {\text{Da}} = \frac{K}{{H^{ 2}}};\quad F_{{\mathrm{c}}} = \frac{1.75}{{\sqrt {150}}}; \\ {\text{Ra}} & = \frac{{g\beta_{\text{f}} (T_{{\mathrm{m}}} - T_{{\mathrm{c}}})H^{3}}}{{\nu_{\text{f}} \alpha_{\text{f}}}};\quad {\text{Ra}}_{\text{m}} = {\text{RaDa;}}\quad {\text{Ha}} = \frac{BH}{{\sqrt {\nu_{\text{f}} \rho_{\text{f}}/\sigma_{\text{f}}}}} \\ \end{aligned} $$

(9b)

where the dimensionless numbers are Rayleigh number (Ra), Darcy–Rayleigh number (Ra_m), Prandtl number (Pr), Darcy number (Da), Hartmann number (Ha), and Forchheimer coefficient ($F_{{\mathrm{c}}}$). The symbol $T_{{\mathrm{m}}}$ denotes the mean temperature of heating.

Thermophysical properties of hybrid nanofluid

In the dimensionless governing Eqs. (5)–(8), U and V are the velocity components in dimensionless coordinates in X and Y directions, $\theta$ is nondimensional temperature, P is nondimensional fluid pressure, $\varepsilon$ is the porosity of porous media, and g is the acceleration due to gravity. The thermophysical properties are presented by the subscript ``hnf'' for the hybrid nanofluid. All these properties are estimated on the basis of a mixture of Cu and Al₂O₃ hybrid nanoparticles volumetric concentration ($\phi$) in the pure fluid, so that

$$ \phi = \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} + \phi_{\text{Cu}} $$

(10)

The subscripts ``f'' and ``s'' are utilized for denoting the thermophysical properties for the pure fluid and the solid nanoparticles, respectively.

The effective density $\rho_{\text{hnf}}$, specific heat capacity $(c_{{\mathrm{p}}})_{\text{hnf}}$, thermal expansion coefficient $\beta_{\text{hnf}}$ of the hybrid nanofluid are expressed by [37, 39, 40, 43]

$$ \rho_{\text{hnf}} = (1 - \phi)\rho_{\text{f}} + \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} \rho_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} + \phi_{\text{Cu}} \rho_{\text{Cu}} $$

(11)

$$ (\rho c_{{\mathrm{p}}})_{\text{hnf}} = (1 - \phi)(\rho c_{{\mathrm{p}}})_{\text{f}} + \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} (\rho c_{{\mathrm{p}}} )_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} + \phi_{\text{Cu}} (\rho c_{{\mathrm{p}}} )_{\text{Cu}} $$

(12)

$$ (\rho \beta)_{\text{hnf}} = (1 - \phi)(\rho \beta)_{\text{f}} + \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} (\rho \beta )_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} + \phi_{\text{Cu}} (\rho \beta )_{\text{Cu}} $$

(13)

The hybrid nanofluid thermal diffusivity is expressed as

$$ \alpha_{\text{hnf}} = \frac{{k_{\text{hnf}}}}{{(\rho c_{{\mathrm{p}}})_{\text{hnf}}}} $$

(14)

The effective dynamic viscosity of the hybrid nanofluid is expressed following the classical Brinkman model [79] as:

$$ \mu_{\text{hnf}} = \frac{{\mu_{\text{f}}}}{{(1 - \phi)^{2.5}}} $$

(15)

Furthermore, the effective electrical conductivity of the hybrid nanofluid is calculated following the Maxwell model [80]

$$ \sigma_{\text{hnf}} = \sigma_{\text{f}} \left[{1 + \frac{{3(\sigma_{{\mathrm{s}}} /\sigma_{{\mathrm{f}}} - 1)\phi}}{{(\sigma_{{\mathrm{s}}} /\sigma_{{\mathrm{f}}} + 2) - (\sigma_{{\mathrm{s}}} /\sigma_{{\mathrm{f}}} - 1)\phi}}} \right] $$

(16a)

where

$$ \phi \sigma_{{\mathrm{s}}} = \phi_{\text{Cu}} \sigma_{\text{Cu}} + \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} \sigma_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} $$

(16b)

The effective thermal conductivity could be obtained by the Maxwell model [80] as

$$ k_{\text{hnf}} = k_{\text{f}} \left[{\frac{{(k_{\text{s}} + 2k_{\text{f}}) - 2\phi (k_{\text{f}} - k_{\text{s}})}}{{(k_{\text{s}} + 2k_{\text{f}}) + \phi (k_{\text{f}} - k_{\text{s}})}}} \right] $$

(17a)

where

$$ \phi k_{{\mathrm{s}}} = \phi_{\text{Cu}} k_{\text{Cu}} + \phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} k_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}} $$

(17b)

In the above equations, the thermal conductivities of Cu and Al₂O₃ and the pure fluid nanoparticles are expressed as $k_{\text{Cu}}$, $k_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}}$, and k_f, respectively. Such expressions have been used by many researchers as reported in the published literature. However, in reality, such classical models fail to accurately estimate the thermal conductivity (Maxwell model) as well as viscosity (Brinkman model) of the Cu–Al₂O₃/water hybrid nanofluid [36, 37, 39, 41, 81]. In order to get the correct effective thermal conductivity and viscosity for the hybrid nanofluid, the available experimental data [36] are utilized in the present study, which are tabulated in Table 2 for $\phi$ = 0.001–0.02. However, for extending the present numerical study, we have extrapolated the data little bit for a range of hybrid nanoparticles volume fraction $\phi$ = 0.03–0.05, which are indicated in the last three rows of Table 2.

Table 2 Effective thermal conductivity and dynamic viscosity [36] of Cu–Al₂O₃/water hybrid nanofluid

The overall heat transfer characteristics, the quantity of physical interest, are evaluated by calculating the average Nusselt number (Nu) at the bottom heated wall, which can be written as

$$ {\text{Nu}} = \frac{{k_{\text{hnf}}}}{{k_{\text{f}}}}\int\limits_{0}^{1} \left(- \left. {\frac{\partial \theta}{\partial Y}} \right|_{Y = 0} \right){\text{d}}X $$

(18)

Furthermore, the fluid flow structure within the computational domain is visualized by mapping the contours of streamlines. It is generated by using streamfunction $\psi$ and expressed through

$$ - \frac{\partial \psi}{\partial X} = V\quad {\text{and}}\quad \frac{\partial \psi}{\partial Y} = U $$

(19)

At all the walls of the enclosure, $\psi$ is zero. The presence of circular streamlines in a confined cavity/enclosure is very important to understand the associated flow physics. The circular streamlines indicate a rotating fluid flow usually mentioned as vortex or circulation. The presence of the circulation in a confined cavity like the present problem brings out many important flow physics under different parametric (as well as boundary) conditions. The location, strength, and size and shape of the circulation decide the local transport behavior of a undergoing process which may involve heat transfer and other transport phenomena. In general, "+ $\psi$'' indicates counterclockwise (CCW) fluid circulation and "− $\psi$'' indicates clockwise (CW) fluid circulation. The congested streamlines imply a stronger fluid velocity between the bounding streamlines. If the distance between the two successive streamlines is higher, the flow velocity becomes lower due to a wider flow area as per the mass balance/continuity equation.

Further to the above, the transport of thermal energy from the heated bottom wall to the cold sidewalls is visualized by mapping the contours of heatlines. The heatlines are basically obtained from the energy balance at the steady-state condition, and it is generated from the heatfunction ($\varPi$) [7, 47, 82], which can be expressed as

$$ - \frac{\partial \varPi}{\partial X} = V\theta - \frac{\partial \theta}{\partial Y}\quad {\text{and}}\quad \frac{\partial \varPi}{\partial Y} = U\theta - \frac{\partial \theta}{\partial X} $$

(20)

The above equations are solved in an integration approach considering the Dirichlet and Neumann boundary conditions for the temperature and zero surface velocity. At the beginning, the solution is started by setting a reference point for the $\varPi$ by setting as ``0'' at the central point of the bottom wall (X = 0.5, Y = 0); this also ensures a symmetrical pattern of the heatlines contours.

Boundary conditions for the computation

The dimensionless governing Eqs. (5)–(8) by applying the following boundary conditions:

• (a) U = V = 0, $\theta = \left| {I\sin (\pi fX)} \right|$ for the heated bottom wall (Y = 0),

• (b) U = V = $\frac{\partial \theta}{\partial Y} = 0$ for the top adiabatic wall (Y = 1),

• (c) U = V = 0, $\theta = 0$ for the cold sidewalls (X = 0,1),

where the symbol I denotes the dimensionless amplitude [I = A/(T_m − T_c)] of half-sinusoidal heating (temperature) profile and it can vary in between 0.1 and 1, whereas f stands for multi-frequency of half-sinusoidal heating (temperature) and it varies from 1 to 10 in this study.

Numerical procedure, grid independence test, and validation study

The dimensionless forms of the coupled nonlinear partial differential conservation Eqs. (5)–(8) along with the applied boundary conditions are transformed into a set of algebraic equations following the finite volume approach (FVM). The second-order central difference scheme for the diffusion terms and QUICK (a third-order upwind differencing scheme) for the advection terms are adopted during the discretization of the governing equations. Finally, the algebraic equations are solved following an iterative process through the Alternate Direction Implicit (ADI) sweep and the TDMA algorithm, invoking the SIMPLE algorithm [81]. The iterative solutions of the governing equations are achieved through the progressive minimization of the normalized residuals of the mass, momentum, and temperature equations. As the convergence criteria, the cutoff value is set for all residuals < 10⁻⁸. For a higher level of accuracy, the mass defect of the continuity equation of individual computing cells is also checked, which is set below 10⁻¹⁰. To achieve the required convergence, the values of underrelaxation factors are taken as 0.5, 1.0, and 0.7 for the velocity, pressure, and temperature, respectively. The whole numerical process is carried out using an indigenous FORTRAN computing CFD code.

Code validation

The indigenously developed computing code has already been validated in our earlier works on natural convection [7, 77, 82, 83], mixed convection [76, 84] problems. Furthermore, one new validation study of magneto-hydrodynamic natural convection is conducted here using a Al₂O₃-water nanofluid filled differentially heated cavity as reported by Ghasemi et al. [85]. The present set of governing equations is utilized as a special case by dropping the Darcy and Forchheimer terms (for porous medium) and setting porosity $\varepsilon$ = 1. The same set of governing equations and constitutive relations is utilized by setting $\phi_{\text{Cu}}$ = 0. It turns the governing equations shown for the hybrid nanofluid flow (consisting of two different nanoparticles) into the governing equations for the nanofluid flow of Al₂O₃/water.

The results of contour maps on streamlines and isotherms for Pr = 6.2, Ra = 10⁵, Ha = 60, and nanoparticles volume fractions $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}}$ = 0.03 are compared and illustrated in Fig. 2 (first row) and are found to be closer with the present simulated results (second row). The comparison of our results and those reported in the published literature [85] shows reasonable good agreement. Based on the reported earlier validations [7, 76, 77, 82,83,84] and this new validation, it is clear that the reliability and accuracy of the present computing code are satisfactory to carry out the numerical simulations.

Fig. 2

(Color figure online) Comparison of streamlines and isotherms contours maps of a differentially heated cavity with Pr = 6.2, Ra = 10⁵, Ha = 60, $\phi_{{{\text{Al}}_{ 2} {\text{O}}_{ 3}}}$ = 0.03 of present results with those of the benchmark problem of Ghasemi et al. [85]

Grid independence study

For ensuring the numerical results to be independent of the number of meshes, a grid independence test is conducted using the five different grid sizes (80 × 80, 120 × 120, 160 × 160, 200 × 200, and 250 × 250). The uniform structured grid is distributed over the computational domain. To compare different mesh results, the average Nusselt number (Nu) is computed at the bottom wall (Y = 0) for different Darcy–Rayleigh numbers (Ra_m = 10–10⁴) for the fixed values of Da = 10⁻⁴, $\varepsilon$ = 0.6, I = 1, f = 5, Ha = 30. The same is presented in Table 3. The successive errors in the estimation of the average Nu (as indicated in % in bracket) are compared with the immediate coarse grids, and it is found to be < 1.1% with 200 × 200 grid size. There is no significant change in the average Nu value beyond the grid size 200 × 200. Accordingly, 200 × 200 grid size is used throughout the numerical analysis of the studied problem.

Table 3 Grid sensitivity analysis for a range of Ra_m values (10–10⁴) at Da = 10⁻⁴, $\varepsilon$ = 0.6, I = 1, f = 5, $\phi$ = 0.02, Ha = 30

Results and discussion

The effect of multi-frequency half-sinusoidal heating of Cu–Al₂O₃/water hybrid nanofluid saturated with porous medium in a square cavity in presence of external magnetic field is analyzed numerically. The effect of different parametric variations on the thermo-flow physics is illustrated through the streamlines and isotherms. Heat energy transportation from the heat source to the heat sink is visualized using Bejan’s heatlines. Overall heat transfer characteristics under various selected effective parameters are presented in terms of the average Nusselt number (Nu). The analysis of the porous media is carried out for the variation in Darcy–Rayleigh number Ra_m = 10, 10², 10³, 10⁴, Darcy number Da = 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻², 10⁻¹ keeping the fixed values of porosity $\varepsilon$ = 0.6. Whereas the multi-frequency half-sinusoidal heating is analyzed by varying the amplitude as I = 0.05, 0.3, 0.5, 0.8, 1, the frequency of half-sinusoidal heating is varied as f = 1, 3, 5, 7, 10. The concentration of Cu–Al₂O₃/water hybrid nanofluid is varied as $\phi$ = 0.001–0.05. The strength of the externally applied magnetic field is varied as Ha = 0, 10, 30, and 50. All the results are presented in “Effect of operating convection regimes (Ra_m)”–“Influence of varying frequency (f) of half-sinusoidal heating” sections. Firstly, the effect of operating convection regimes varying Darcy–Rayleigh numbers on the thermo-fluid flow structure under the multi-frequency half-sinusoidal heating is presented in “Effect of operating convection regimes (Ra_m)” section. In the next “Effect of permeability of the porous media” section, the effect of varying permeability of the porous media on the thermo-fluid structure is illustrated. The effects of different amplitudes (I) of half-sinusoidal heating on heat and flow dynamics are presented in “Influence of variation in amplitude (I) of half-sinusoidal heating” section. In “Influence of varying frequency (f) of half-sinusoidal heating” section, dynamics of the heat and fluid flow under a range of multi-frequency heating are illustrated. The effects of varying external magnetic field strength are detailed in “Impact of Hartmann number (Ha)” section. Next, “Effect of nanoparticle volume concentration ($\phi$)” section demonstrates the effects of different nanoparticles volume fraction on the heat and fluid flow dynamics. The variation in local velocity, temperature, and the average Nu is illustrated in “Local velocity and temperature distributions” section. Finally, an overall heat transfer characteristics and thermal performance are reported in “Heat transfer characteristics” section for the selected effective parameters.

Effect of operating convection regimes (Ra_m)

In this section, the insights of the flow dynamics development within the enclosure along with thermal energy transportation from the heated bottom wall to the cold sidewalls are illustrated in terms of contour maps of streamlines (top row), isotherms (second row), and heatlines (third row) along with global heat transfer characteristics using average Nusselt number (below the heatline contours). The same is presented in Fig. 3 under different operating convection regimes by varying the values of Darcy–Rayleigh number (Ra_m = 10, 10², 10⁴) for the fixed values of Da = 10⁻⁴, Ha = 30, f = 1, I = 1, $\phi$ = 0.02. As the fluid flows through the porous layers, it creates resistance to flow. Thus, it is extremely pertinent to analyze the thermo-fluid behavior through the porous media using the dimensionless number of modified Rayleigh number or Darcy–Rayleigh number (Ra_m = Ra × Da), which is defined in Eq. (9b).

Fig. 3

(Color figure online) Effect of different Darcy–Rayleigh numbers (Ra_m) on the contour maps of streamlines (first row), isotherms (second row), and heatlines (third row) at Da = 10⁻⁴, Ha = 30, f = 1, I = 1, $\phi$ = 0.02. The intervals for the contours are taken as 0.2 for isotherms; 0.05 (first column), 0.5 (second column), 5 (third column) for streamlines; 0.2 (first column), 0.5 (second column), 2 (third column) for heatlines

From Fig. 3, it is observed that at a lower value of Ra_m = 10 (first column), the fluid layer near the heated bottom wall rises upward through the middle vertical region of the cavity due to the variation in fluid density. As the top wall is thermally insulated, upward fluid flow is obstructed by the top wall and then moved toward the sidewalls, where hot fluid rejects heat, and thereafter, the fluid is cooled and descends down along the sidewalls. Cold fluid further takes heat from the heated bottom wall. Thus, it is found the formation of two flow vortices, which effectively occupy the entire enclosure. These vortices distribute symmetrically about the mid-vertical plane of the enclosure; one vortex (at the left part) is rotating in anticlockwise (CCW) direction (marked with a positive sign) and another vortex (at the right part) is rotating in clockwise (CW) direction (marked with negative sign). Corresponding temperature distribution patterns can be visualized from the isotherm contour maps (second row). As the cavity fluid is heated at the bottom following half-sinusoidal nonuniform heating, the isotherm contours adjacent to the heated wall designate the peak temperature about the middle region of the enclosure and thereafter widen over the entire enclosure. For a better understanding of the heat flow dynamics within the enclosure, the Bejan’s heatline contour maps are illustrated in the third row of Fig. 3. The heatlines contours originate from the heated bottom wall and are connected in between the bottom heated wall and heat sinks located at the sidewalls, and it is marked with the arrowhead. It indicates a pathway for the fixed quantity of energy transportation. Due to the half-sinusoidal heating, the heat energy is transferred through a tapered corridor (from the bottom wall to the sidewalls) about the mid-vertical planes. Thereafter, the energy flow passage widens and expands to a maximum area near to the entire sidewalls of the enclosure.

As Ra_m increases from 10 to 10² (second column) and 10⁴ (third column), the fluid circulation strengths increase significantly and the centers of the flow vortices shift upward. It implies increment in the corresponding fluid Rayleigh numbers (Ra) from 10⁵ to 10⁸. In this context, it is pertinent that as the value of Ra_m increases the convection mode of heat transfer dominates over conduction and it becomes stronger at a higher value of Ra_m. As a result, weaker fluid circulation and lower heat transportation are observed at lower Ra_m. At the higher value of Ra_m, the strength of the fluid circulation increases substantially, which is reflected by the changes in the intensity of the maximum value of streamfunction ($|\psi|_{{\mathrm{max}}}$). The higher fluid velocity is attributed due to the increase in the temperature gradient as well as an increase in the inertial force over the viscous force; it results in enhanced thermal convection. Associated temperature distribution shows the crowded lines nearer to the heated bottom wall, which is further deformed and becomes parallel to the cold sidewalls. Such distribution of the isotherms shows a significant reduction in the thermal boundary layer thickness at the heated wall and cooled walls. This fact implies the increase in heat transfer at higher Ra_m. This is also evident from the heatline contour maps as the intensity of heatlines increases, and the maximum value of heatfunction $\varPi_{{\mathrm{max}}}$ also increases significantly. From the heatline contour maps, one interesting observation can be found as the convective heat transfer increases at higher Ra_m, the distribution of heatlines indicates higher magnitude of energy at the central point of the bottom wall. Thereafter, the heat energy flows through a narrow passage and then spreads over the entire sidewalls. As a result, areas beyond the energy flow pathway are filled with energy flow circulation cells similar to the streamline contour maps. The formation of such energy circulation cells is observed for Ra_m ≥ 10². As Ra_m increases from 10 to 10⁴, the width of the heat energy flow passage becomes narrower and the convective heat flux becomes stronger. Thus, the size of the inactive energy flow circulation cells increases. The magnitude of the enhanced convective heat transfer characteristics can be realized from the increasing values of average Nu at the heated bottom wall (as mentioned below the heatline contours).

Effect of permeability of the porous media

In order to understand the influence of the permeability parameter of the porous medium on the thermo-fluid phenomena, the variation in dimensionless Darcy number (Da) is analyzed and illustrated in Fig. 4 for three different Da values (10⁻⁵, 10⁻³, 10⁻¹) for the fixed values of Ra_m = 10³, f = 1, I = 1, Ha = 30, $\phi$ = 0.02. In this case, Ra_m (= Ra × Da) is kept at a fixed value; as a result, the fluid-based Ra decreases with the increasing Da. Figure 4 clearly demonstrates the symmetrical distribution of flow as well as temperature within the enclosure. Generally, the fluid flow faces relatively lower resistance, when Da is increasing (as likely from the reduced permeability of the porous matrix). This leads to an increase in the fluid velocity, which in turn leads to higher heat transfer rates from the heated wall to the cold walls. However, when the fluid–flow structures and the temperature pattern of different Da values (10⁻⁵, 10⁻³ and 10⁻¹) are compared, it shows an unusual pattern. As the fluid circulation strength ($|\psi|_{{\mathrm{max}}}$) becomes weaker, the maximum value of heatfunction ($\varPi_{{\mathrm{max}}}$) decreases significantly; the thicker thermal boundary layer thickness is noted along the heated wall. This happens so at the fixed value of Ra_m, the fluid-based Rayleigh number decreases with increasing Da. This results in weaker circulation even at higher Da value (= 10⁻¹). As the fluid velocity is less, it causes very lesser penetration of the flow through the porous media, resulting in a lower heat transfer rate, which is reflected by the average Nu value.

Fig. 4

(Color figure online) Effect of different Darcy numbers (Da) of the porous media on the contour maps of streamlines (first row), isotherms (second row), and heatlines (third row) at Ra_m = 10³, Ha = 30, f = 1, I = 1, $\phi$ = 0.02. The intervals for the contours are taken as 0.2 for isotherms; 5 (first and second columns), 0.05 (third column) for streamlines; 2 (first column), 1 (second column), 0.2 (third column) for heatlines

Influence of variation in amplitude (I) of half-sinusoidal heating

The flow physics, as well as the thermal behavior within the considered geometry, is critically governed by the thermal condition of the heat source. To illustrate this, the effect of varying dimensionless amplitude I = 0.3, 0.5, and 0.7 (of temperature) on the heat flow dynamics is investigated and consequent results are presented in Figs. 5 and 6, respectively, keeping fixed values at f = 1, Ra_m = 10³, Da = 10⁻⁴, Ha = 30, f = 1, $\phi$ = 0.02. Figure 5 depicts that when the amplitude I is lower (= 0.3), the temperature on the bottom wall is also lower (θ ≈ 0.3 at the middle point of the bottom wall). Corresponding flow fields indicate weaker fluid circulation and heat energy transportation. When the amplitude I increases to 0.5, the temperatures at the central point of the bottom wall become θ ≈ 0.5, and at the farthest ends it decreases (following half-sinusoidal temperature profile). As the temperature gradient increases, the heat transfer rate also increases significantly as reflected by the average Nu value. Further increasing the amplitude to I = 0.7, the above observations are amplified markedly. The maximum values of $|\psi|_{{\mathrm{max}}}$ and $\varPi_{{\mathrm{max}}}$ increase noticeably, and heat transfer magnitude increases monotonously.

Fig. 5

(Color figure online) Effect of different amplitudes of half-sinusoidal heating (I) on the contour maps of streamlines (first row), isotherms (second row), and heatlines (third row) at Ra_m = 10³, Da = 10⁻⁴, Ha = 30, f = 1, $\phi$ = 0.02. The intervals for the contours are taken as 0.1 for isotherms; 1 (first column), 5 (second and third columns) for streamlines; 0.2 (first column), 0.5 (second and third columns) for heatlines

Fig. 6

(Color figure online) Thermo-fluid flow phenomena near boundary of the bottom heated wall in terms of the velocity vectors and isotherms under multi-frequency half-sinusoidal heating for a Ra_m = 10³ and b) Ra_m = 10⁴ at Da = 10⁻⁴, Ha = 30, f = 1, $\phi$ = 0.02

For an in-depth understanding of the transport phenomena over the heated bottom wall under the varying amplitude I, Fig. 6 illustrates the blow-up view (for the lower portion of the enclosure) of the changes in the isotherms superimposed velocity vectors for I = 0.3, 0.5, and 1 at two different Ra_m = 10³ (Fig. 6a) and 10⁴ (Fig. 6b), respectively, for the fixed values of Da = 10⁻⁴, Ha = 30, f = 1, $\phi$ = 0.02. From Fig. 6a, it is observed that as I increases from 0.3 to 0.5 and 1, the temperature distribution along the bottom wall changes significantly. Furthermore, the peak in the temperature also modifies. The phenomena of velocity as well as thermal boundary layers can be visualized easily close to the bottom wall. From both sides, the cold fluids move downwards along the sidewalls and take a sharp turn (~ 90°) as it faces temperature near the bottom wall. Thereafter, it becomes an almost parallel pattern with the bottom wall and finally climbs upward and forms a central plume. The isotherm lines near to the bottom wall indicate the growth of the increasing boundary layer thickness at both halves of the enclosure. Of course, such a scenario of the boundary layer and fluid flow pattern modifies severely at higher amplitude I = 1 and higher value of Ra_m as shown in Fig. 6b. As the bottom wall is heated nonuniformly (following half-sinusoidal temperature condition), such unusual boundary layers grow monotonously (compared to uniform heating condition, not shown here) and it appears in a periodic manner. Corresponding velocity vectors clearly indicate the convective velocity (comparing the same reference vector), and its magnitude is markedly higher at Ra_m = 10⁴ compared to Ra_m = 10³. At the higher value of Ra_m, the fluid circulation is higher due to higher thermal energy transportation and it is stronger at I = 1, which is reflected by the densely distributed velocity vectors.

Influence of varying frequency (f) of half-sinusoidal heating

Further to the aforementioned analysis, the impact of variation in frequency f of nonuniform heating (following half-sinusoidal temperature profile) on the dynamics of thermo-fluid flow is investigated and illustrated in Fig. 7 for three different frequencies f = 3, 5, and 10 keeping other parameters fixed at Ra_m = 10³, Da = 10⁻⁴, I = 1, Ha = 30, $\phi$ = 0.02. Recalling earlier findings of overall flow structure (twin circulations), temperature distribution, Fig. 6 exhibits similar dynamics except for the bottom region (near to the heated wall) of the cavity and it persists for any spatial frequencies. Compared to the single frequency (f = 1), the strength of the fluid circulation (as denoted by $|\psi|_{{\mathrm{max}}}$) and a maximum value of heatfunction $\varPi_{{\mathrm{max}}}$ decrease with the increasing frequency. Of course, near-wall thermo-fluid flow behavior becomes more sensitive and complex at higher spatial frequencies. An increase in the frequency, overall flow structure doesn’t alter markedly, except the lower portion close to the heated bottom wall. It causes a modulation of both streamlines and isotherms with the change in the frequency. As the frequency increases, a number of tiny fluid circulation and energy circulation cell form, and this number is basically a function of the multi-frequency of heating. The temperature distribution (isotherms panel) of fluid nearer to the bottom wall indicates the presence of different numbers of peaks (3 peaks for f = 3, 5 peaks for f = 5, 10 peaks for f = 10 following the frequency of half-sinusoidal heating). Evidently, the temperature of the fluid layers close to the heated wall changes following the heating condition.

Fig. 7

(Color figure online) Effect of frequency of half-sinusoidal heating (f) on the contour maps of streamlines (first row), isotherms (second row), and heatlines (third row) at Ra_m = 10³, Da = 10⁻⁴, Ha = 30, I = 1, $\phi$ = 0.02. The intervals for the contours are taken as 0.1 for isotherms, 5 for streamlines, 2 for heatlines

Of course, in between any two temperature peaks a fall in the fluid temperature is noticeable, which is attributed due to the intermediate cooling (where $\theta$ approaches 0 value) of hot fluid by rejecting out heat through this wall. At the higher f values, more numbers of low-temperature points are noticeable. This results in a wavy pattern in streamlines as well as heatline contours maps (as in the first and third rows, respectively). It should be mentioned here that, due to intermediate cooling at the bottom wall, the magnitude of the overall heat transfer characteristic denoted by the average Nu (at the heated wall) decreases compared to the case of a single frequency (f = 1) of the half-sinusoidal heating. The maximum values of $|\psi|_{{\mathrm{max}}}$ and $\varPi_{{\mathrm{max}}}$ decrease marginally.

For a better understanding of the multi-frequency of half-sinusoidal heating effect on the heat flow dynamics, the blow-up view (for the lower portion of the enclosure) of the isotherms superimposed velocity vectors is analyzed for three different frequencies f = 3, 5, and 10 and is illustrated in Fig. 8a, b at two different Ra_m = 10³ and 10⁴, respectively, keeping other parameter fixed at I = 1, Ha = 30, $\phi$ = 0.02. As f increases from 1 (as shown in Fig. 6a, b—bottom row) to 3, 5, and 10, the temperature distribution along the bottom wall changes markedly. As the frequency f increases, the isotherm lines indicate the presence of multiple peaks over the entire heated wall and there exist velocity and thermal boundary layers stretched over the bottom wall. These numbers of peaks in isotherms (1 peak for f = 1, 3 peaks for f = 3, 5 peaks for f = 5 and 10 peaks for f = 10) are also a function of the half-sinusoidal frequency. Height in the peaks is also modulated by the frequency variation; the higher frequency causes a decrease in height of the peaks (although the number of peaks increases). From both sides, the downward-moving cold fluid takes a sharp turn (> 90°) as it faces temperature peaks near the bottom corners. Thereafter, it takes a wavy pattern and finally climbs upward and forms a central plume. The isotherm line near to the bottom wall indicates the growth of the wavy boundary layer at both halves of the enclosure. The formation of such undulation is more complex till f = 5, beyond which the undulation decreases as the isotherm peak height decreases. Such circumstances of the boundary layers and the fluid flow pattern modify severely at the higher Ra_m as shown in Fig. 8b. Interestingly, as the bottom wall is heated nonuniformly (following half-sinusoidal temperature condition), there exists a lower temperature at some points (as θ approaching 0 value). This results in an intermediate cooling effect of the hot fluid through the same bottom wall. This results in the formation of the wavy boundary layers, which is also supported by the velocity vector distribution. Such a usual boundary layer grows monotonously (compared to the case of the uniform heating condition, not shown here), and it appears in a periodic manner. Comparing the same reference vector length, the velocity vector distribution clearly indicates the convective velocity, which increases significantly at Ra_m = 10⁴ compared to that of Ra_m = 10³. At the higher value of Ra_m, densely distributed velocity vectors indicate a higher strength of fluid circulation due to higher thermal energy transportation.

Fig. 8

(Color figure online) Thermo-fluid flow phenomena near boundary of the bottom heated wall in terms of the velocity vectors and isotherms under multi-frequency half-sinusoidal heating for a Ra_m = 10³, and b Ra_m = 10⁴ at Da = 10⁻⁴, Ha = 30, I = 1, $\phi$ = 0.02

Impact of Hartmann number (Ha)

The impact of the externally applied magnetic field, denoted by the dimensionless Hartmann number (Ha), on the thermo-fluid flow is investigated and presented in Fig. 9 for Ha = 0 (no magnetic field), 10, and 50 considering other parameters fixed as Ra_m = 10³, Da = 10⁻⁴, f = 1, I = 1, $\phi$ = 0.02. For the understanding of in-depth flow physics under different magnetic fields, the no magnetic field case is simulated first and presented in the first column of Fig. 9. In general, there is no alteration in the fluid flow as well as energy transportation. However, without a magnetic field, the heat transfer is dominated by the thermal convection only. Of course, the presence of a magnetic field reduces the fluid velocity and such retardation is higher at higher Ha value. The reason behind such a reduction in the velocity can be easily understood. From the momentum Eq. (7), it is apparent that the presence of negative source terms (containing the Ha parameter) causes a decrease in the vertical velocity component as Ha increases. Hence, the magnetic force term counteracts the positive consequence of the buoyancy force. This results in a further reduction in the fluid velocity, which also puts some impacts on the energy Eq. (8). As a result, thermal energy transportation reduces with increasing Ha values. As the Ha value changes from 0 to 10 and then 50, the negative impact on the fluid flow, temperature distribution, and heatline contours is clearly noticeable from the magnitude of $|\psi|_{{\mathrm{max}}}$ and $\varPi_{{\mathrm{max}}}$. The associated heat transfer rate also decreases as reflected by the Nu values.

Fig. 9

(Color figure online) Effect of magnetic field strength in terms of Hartmann number (Ha) on the contour maps of streamlines (first row), isotherms (second row), and heatlines (third row) at Ra_m = 10³, Da = 10⁻⁴, f = 1, I = 1, $\phi$ = 0.02. The intervals for the contours are taken as 0.1 for isotherms, 5 for streamlines, 1 for heatlines

Effect of nanoparticle volume concentration ($\phi$)

Figure 10 depicts the effects of the addition of Cu–Al₂O₃ hybrid nanoparticles in the pure fluid (water) on the thermo-fluid flow structure under multi-frequency half-sinusoidal heating conditions at Ra_m = 10³, I = 1, f = 1, Ha = 30. For the comparison with no nanoparticles addition situation, the case of pure fluid ($\phi$ = 0) is simulated first under similar thermal boundary condition and presented in the first column of Fig. 10; thereafter, the case of two different volume concentrations of Cu–Al₂O₃ hybrid nanoparticles ($\phi$ = 0.001 and 0.03) is illustrated in the second and third columns, respectively. All the streamlines, isotherms, and heatline contours show the symmetrical distribution, and there is no such significant deviation in the contour maps for a different fraction of hybrid nanofluid volume concentrations. On the other hand, the addition of 0.001 Cu–Al₂O₃ hybrid nanoparticles in the pure water leads to a considerable increment in the fluid velocity compared to base fluid ($\phi$ = 0) as denoted by the magnitude of $|\psi|_{{\mathrm{max}}}$. This is attributed to the effects of the enhanced inertia force compared to the viscous force, as the effective thermal conductivity increases significantly with the addition of hybrid nanoparticles [36, 81]. As a result, the overall heat transfer rate increases compared to the case of pure water, which is reflected by the average Nu value. However, further augmentation of the hybrid nanoparticles concentration to 0.03 shows a decreasing trend of fluid velocity, heat energy transportation, and associated heat transfer, which is reflected by and $\psi_{{\mathrm{max}}}$, $\varPi_{{\mathrm{max}}}$ and the average Nu values, respectively. This is attributed due to the fact that by the addition of different combinations of nanoparticles into the base fluid, the effective dynamic viscosity increases. A higher concentration of hybrid nanoparticles causes more resistance to the fluid velocity through the increased shear stresses. Thus, the viscous force dominates over the inertia force. This leads to a reduction in fluid motion as well as heat energy transportation. As a result, the advection mechanism reduces and the associated overall heat transfer rate reduces (reflected by the average Nu values). Similar findings have already been documented in refs. [36, 67,68,69, 81].

Fig. 10

(Color figure online) Effect of Cu–Al₂O₃ hybrid nanoparticle concentration ($\phi$) on the contour maps of streamlines (first row), isotherms (second row), and heatlines (third row) at Ra_m = 10³, Da = 10⁻⁴, Ha = 30, f = 1, I = 1. The intervals for the contours are taken as 0.2 for isotherms, 5 for streamlines, 1 for heatlines

Local velocity and temperature distributions

For the completeness of the analysis and in-depth understanding of the thermo-flow physics, dimensionless local distribution of a vertical velocity component (V) and temperature ($\theta$) at the mid-vertical plane (Y = 0.5) is analyzed and presented in Fig. 11 under half-sinusoidal heating condition. The effect of Ra_m and Da (and also frequency and amplitude of half-sinusoidal heating) on the profile plots of vertical velocity and temperature is understandably not uniform across the width of the enclosure as shown in Fig. 11. It happens so as the governing momentum equations are nonlinear and coupled to temperature and pressure, and also involving the presence of different forces, namely buoyant force, magnetic force, pressure force, and Darcy and Forchheimer contributing force terms. The velocity and temperature become the function of the coordinate position (X, Y) and all the parameters (Ra_m, Da, Ha, f, I, $\phi$). All the governing equations are solved by applying the specific boundary conditions for different walls of the enclosure. The distribution of the variables (U, V, P and $\theta$) within the computing domain depends upon the governing equations, constitutive relations, and the applied boundary conditions. Thus, the profiles of V and $\theta$ become nonuniform for any values of Ra_m and Da. Particularly due to the fluid viscosity, the formation of boundary layers, bottom heating, and side cooling, the profiles become nonuniform across the width of the enclosure.

Fig. 11

(Color figure online) Mid-plane profiles of vertical velocity component (V) and temperature ($\theta$) for varying a frequency (f), b) amplitude (I) of half-sinusoidal heating (temperature), c Darcy–Rayleigh number (Ra_m), d Darcy number (Da), keeping other parameters fixed at $\phi$ = 0.02, Ha = 30

The variation in the V velocities and $\theta$ for different frequencies f = 1, 3, 5, and 10 is presented in Fig. 11a for the fixed values of Ra_m = 10³, Da = 10⁻⁴, I = 1, Ha = 30, $\phi$ = 0.02. Figure 11a depicts a high positive peak at the center (about X = 0.5) and two negative peaks toward both ends of the X-axis. This is attributed due to the formation of the thermal plume and two counterrotating flow vortices inside the enclosure. As the frequency increases, the peak velocity decreases marginally which is also evident from contour maps (as shown in Fig. 7). Corresponding nondimensional mid-plane temperature distribution supports the above findings, as $\theta$ is higher at the central point and $\theta$ approached to zero toward the sidewalls (X = 0 and 1) of the enclosure. With the increasing f, the peak value of $\theta$ decreases marginally and this is due to the reduction in thermal convection.

Figure 11b shows the effects of the variation in V velocity and $\theta$ for different values of dimensionless amplitude I = 0.05, 0.3, 0.5, 0.7, and 1 for the fixed values of Ra_m = 10³, Da = 10⁻⁴, f = 1, Ha = 30, $\phi$ = 0.02. The V velocity and $\theta$ plot indicates a wider range of variation in its dimensionless magnitudes. As the temperature of the fluid layers close to the bottom wall modifies drastically following the imposed heating condition—the local variation as well as mid-plane velocity and temperature along the X direction is affected severely and it modulates the dynamics of fluid flow and heat transfer. At a very low amplitude (I = 0.05), the temperature gradient is very low and it results in a very weaker thermal plume as well as weaker temperature. However, thermal convection increases substantially at every step increment of the amplitude. Associated heat transfer also increases markedly.

Figure 11c shows the effects of varying Ra_m = 10, 10², 10³, 10⁴ on the V velocity and $\theta$ for the fixed the values of Da = 10⁻⁴, f = 1, I = 1, Ha = 30, $\phi$ = 0.02. At a lower value of Ra_m, the thermal conduction (mode) drives the fluid flow as well as temperature distribution. Corresponding fluid motion is insignificantly weak. Of course, for Ra_m > 10, thermal convection mode dominates over the thermal conduction, resulting in the higher convective heat transfer and a significant rise in the V velocity. At every step of rise in Ra_m, the inclination of $\theta$ curve indicates marked changes. On the other hand, the permeability of the porous medium has a significant role in the thermal behavior of the system. Figure 11d depicts the effect of different Da = 10⁻⁵, 10⁻⁴, 10⁻³, 10⁻² and 10⁻¹ on the V velocity and $\theta$ distribution for the fixed values of Ra_m = 10³, Da = 10⁻⁴, f = 1, I = 1, Ha = 30, $\phi$ = 0.02. The V velocity and $\theta$ profile shows opposite trends (as expected from the usual notion) with increasing Da. With the increase in Da, the fluid velocity is supposed to be increasing—as the fluid flow faces less resistance. However, in the present study, Ra_m (= Ra × Da) is kept constant at 10³ for analyzing the effect of permeability of the porous medium by varying Da. As a result, the fluid-based Ra decreases with increasing Da. It causes a decrease in the fluid velocity and in turn temperature, which reduces the heat transfer from the heated wall. At a higher Da (= 10⁻¹), the local variation in mid-plane velocity and temperature along the X direction is affected severely. At this Da value, the associated fluid Ra becomes very low (= 10⁴), and the conduction mode of heat transfer controls the heat transfer, resulting in very low Nu value.

It is very pertinent to scrutinize the temperature profile along the heated wall under selected parameters for the half-sinusoidal nonuniform heating condition, and it is presented in Fig. 12a, b. Figure 12a depicts the variation in the local temperature $\theta$ along the X direction over the entire source length at Ra_m = 10³, Da = 10⁻⁴, I = 1, Ha = 30, $\phi$ = 0.02 under different frequency values (f = 1, 3, 5, and 10). At the single frequency (f = 1), the temperature at the center of the bottom wall is maximum and approaches zero at both ends (due to the presence of cold sidewalls) following the imposed half-sinusoidal temperature profile. Accordingly, the near-node fluid temperature changes (this is obvious in the steady-state situation). As the frequency increases from 1 to 3, there appear three numbers of temperature peaks at equidistance along the length X. In addition to both ends of low-temperature points (θ ≈ 0), a depression in the temperature (θ > 0) appears at the two more points as shown in the figure. This is attributed due to the imposed temperature condition. As a result, the slope of the temperature curve becomes sharper. Such kind of oscillation of the temperature profile is periodic in nature, and the oscillation is more as frequency f is increased to 5 or 10. As a result, more temperature depression points are noted. This results in loss of the heat of the cavity fluid through this bottom wall, leading to the lowering of thermal convection in the enclosure. Earlier findings (as shown in Figs. 7, 8) also support the above facts. On the other hand, Fig. 12b shows symmetrical temperature profiles at the bottom wall for the varying amplitude (I = 0.05, 0.3, 0.5, 0.7, and 1) of the half-sinusoidal heating at Ra_m = 10³, Da = 10⁻⁴, f = 1, Ha = 30, $\phi$ = 0.02. As I increases from 0.05, the temperature profile along the bottom wall X changes markedly. Thus, the near-wall fluid temperature modifies noticeably. As the frequency f = 1, the dimensionless temperature ($\theta$) peak remains at the central point of the bottom wall. The peak temperature increases markedly with the increasing I. This results in higher thermal convection, which is also supported in the earlier findings as shown in Figs. 5 and 6.

Fig. 12

(Color figure online) Variation in dimensionless local temperature ($\theta$) along the half-sinusoidally heated bottom wall under the effect of varying, a frequency (f), b) amplitude (I) at fixed values of Ra_m = 10³, ϕ = 0.02, Ha = 30

Heat transfer characteristics

Local heat transfer rate: local Nusselt number

Further to the aforementioned analysis, it is pertinent to investigate the distribution of the local Nusselt numbers at the heated bottom wall. Following the half-sinusoidal heating (temperature) condition, the variation in local Nusselt number (Nu) changes as the dimensionless local temperature ($\theta$) changes. The variation in the local Nu under the effect of varying frequencies (f) is depicted in Fig. 13a, b for two different Ra_m = 10⁴, and Ra_m = 10³ for the fixed values of Da = 10⁻⁴, I = 1, Ha = 30, ϕ = 0.02. As observed in Fig. 12, the dimensionless local temperature ($\theta$) oscillates along the length of the bottom wall as both the heating and cooling take place at the same wall in an alternate manner (following the frequency of half-sinusoidal heating). At both ends of the bottom wall, the temperature difference with the sidewalls becomes almost zero. Thus, the local Nu shows ``0'' value and thereafter starts increasing toward the central point. The local Nu profile reveals one interesting fact that local Nu can be positive and negative following the dimensionless temperature profile and it oscillates in a periodic manner. Increasing the frequency f from 1 to 3, 5, or 10, the local Nu severely affected due to the variation in the local temperature. Thus, the rate of local as well as average heat transfer rate decreases (as more number of depression points for temperature or intermediate cooling appears periodically). At the higher frequencies, the peak values of the local Nu (both positive and negative) are found to be consistently higher. However, the average Nu affected and it decreases. Patternwise, Fig. 13b exhibits similar nature with that of Fig. 13a except for the magnitude of local as well as average Nu, as at the lower Ra_m, the magnitude of Nu decreases.

Fig. 13

(Color figure online) Variation in local Nusselt number (Nu) under the effect of varying frequency (f) for a Ra_m = 10⁴, b Ra_m = 10³ at fixed values of Da = 10⁻⁴, I = 1, ϕ = 0.02, Ha = 30

Further to the above, the variation in local Nu under the effect of different Ra_m and Da is presented in Fig. 14a, b for the fixed values of I = 1, f = 1, Ha = 30, ϕ = 0.02. In continuation with the finding of Figs. 3 and 11c, as Ra_m increases from 10 to 10², convective heat transfer mode starts to dominate and becomes maximum at Ra_m = 10⁴. As a result, the temperature gradient with the sidewalls increases. This results in higher local temperature at the heated wall as well as near-wall fluid temperature, which in turn leads to higher local Nu distribution (and higher average Nu). The slope of the local Nu curve with the cold wall decreases markedly with the increasing Ra_m. Interestingly, as Ra_m increases, the peak depression in the local Nu profile is noted about the central point of the bottom wall. This is attributed due to the fact that as the convective heat transfer becomes stronger with the increasing Ra_m, it leads to a higher local temperature as well as higher fluid circulation. As a result, cold fluids from both ends (X = 0, 1) strikes the heated bottom wall and faces increasing temperature and it moves toward the center. It leads to a higher heat removal rate from the heated wall, as indicated by the increasing local Nu curve. However, after traversing a few distances, the cold fluid temperature reaches the heated wall temperature, leading to a decrease in the temperature difference with the heated wall and reduction in horizontal fluid velocity. Furthermore, as the fluid streams from both the ends rush toward the central plane of the enclosure (X = 0.5) and strikes over each other, it leads to the formation of a stagnation zone over certain horizontal portions near the heated wall. It causes no more heat transfer from the heated wall. As a result, the sharp fall in the local Nu around X = 0.5 is noted. This is an interesting finding of this case study. On the other hand, the variation in Da for the fixed values of Ra_m = 10³, I = 1, f = 1, Ha = 30, ϕ = 0.02 as shown in Fig. 14b depicts significant alteration in the local Nu profile as Da is increasing. Of course, as observed in Figs. 4 and 11d, lower Da corresponds to the higher fluid Ra; it results in a higher local Nu as well as higher average Nu values. The intensity of local Nu decreases significantly with increasing Da; although resistance to flow decreases, simultaneously fluid Ra decreases. Thus, the depression in the local Nu about the central point of the bottom wall decreases.

Fig. 14

(Color figure online) Variation in local Nusselt number (Nu) under the effect of varying a Darcy–Rayleigh number (Ra_m), b Darcy number (Da), c amplitude (I) of half-sinusoidal heating (temperature), d Hartmann number (Ha), e Cu–Al₂O₃ hybrid nanoparticles volumetric concentration ($\phi$) keeping a fixed value of f = 1

The variation in the local Nu with the varying I of half-sinusoidal heating (temperature) as shown in Fig. 14c (for Ra_m = 10³, Da = 10⁻⁴, f = 1, Ha = 30, ϕ = 0.02) also illustrates similar trends of local Nu distribution like Fig. 14b. However, as I increases from 0.05 to 1, the dimensionless local temperature ($\theta$) along the heated bottom wall increases markedly (as shown in Fig. 12b). Thus, the slope of the local Nu curve with the sidewalls decreases. It leads to an increase in the local Nu as well as average Nu. Similarly, depression in the local Nu about the central point of the bottom wall increases. The variation in local Nu under different strengths of the imposed magnetic fields (Ha = 0, 10, 30, and 50) is plotted in Fig. 14d for the fixed values of Ra_m = 10³, Da = 10⁻⁴, f = 1, I = 1, ϕ = 0.02. However, there is no marked change in the local Nu distribution with the increasing Ha values.

Finally, Fig. 14e depicts the variation in local Nu under different concentrations of Cu–Al₂O₃ hybrid nanoparticles ($\phi$) keeping fixed values of Ra_m = 10³, Da = 10⁻⁴, f = 1, I = 1, Ha = 30. The addition of Cu–Al₂O₃ hybrid nanoparticles in the base liquid increases the local Nu profile as well as average Nu up to $\phi$ < 0.33%, beyond which Nu value decreases. Such a decreasing effect of Nu is also observed in Fig. 10. Of course, the depression in the local Nu profile about the middle point of the bottom wall is persistent.

Overall heat transfer and average Nusselt number

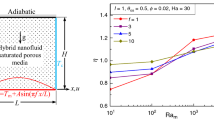
Now the overall thermal performances of the studied problem under multi-frequency half-sinusoidal heating (temperature) are analyzed and illustrated in Fig. 15 for different frequencies f (= 1, 3, 5, 10) for different values of Ra_m, Da, I, Ha, and ϕ. Figure 15a depicts the variation in the average Nu with the variation in Ra_m for the fixed values of Da = 10⁻⁴, I = 1, Ha = 30, ϕ = 0.02. At the lower value of Ra_m, the conduction mode drives the fluid flow, resulting in weaker fluid circulation in the enclosure and lower average Nu. However, for the Ra_m ≥ 10², thermal convection mode dominates the conduction mode; thus, consistently increasing Nu is observed irrespective of any frequency f. Interestingly, at lower Ra_m value up to < 120 (estimated point), higher frequency mode is found to be more advantageous compared to the case of single frequency, and beyond this point low frequency is always found to be superior.

Fig. 15

(Color figure online) Heat transfer characteristics with varying, a Darcy–Rayleigh number (Ra_m), b Darcy number (Da), c amplitude (I) of half-sinusoidal heating (temperature), d Hartmann number (Ha), e Cu–Al₂O₃ hybrid nanoparticles concentration (ϕ)

The increase in the permeability of the porous media on the overall thermal performance is illustrated in Fig. 15b for the different Ra_m = 10³, I = 1, Ha = 30, ϕ = 0.02. As Da (= Ra_m/Ra) value increases for the fixed Ra_m, the fluid-based Ra decreases. As a result, the decreasing trend of Nu with increasing Da is observed for any frequency f. As Ra is significantly low, the enhanced permeability of the porous media has no influence on the average Nu. This is an interesting finding over the existing notion of an increasing trend of Nu with increasing Da. Furthermore, the low frequency is always found to be superior up to Da > 10⁻³; beyond this, the higher frequency mode is found to be more advantageous as reflected by the Nu curve.

For the multi-frequency half-sinusoidal heating, the amplitude (I) is also an important factor for modulating the thermal performance. Figure 15c illustrates the effect of varying I for different frequencies f considering Ra_m = 10³, Da = 10⁻⁴, Ha = 30, ϕ = 0.02. The average Nu increases monotonically with increasing I for any frequency value. The low frequency is found to be superior after I = 0.3 compared to that of higher frequency mode as reflected by the Nu curve. At the lower amplitude, the thermal convection is very weak as a result of lower local temperature at the heated wall (as shown in Fig. 12b). The above findings are also supported by the earlier findings as shown in Figs. 5 and 14c.

The effect of externally applied magnetic field strength on the overall thermal performance is illustrated in Fig. 15d for different Ha values at Ra_m = 10³, Da = 10⁻⁴, I = 1, ϕ = 0.02. The average Nu decreases with increasing Ha. An increase in an imposed magnetic field causes a reduction in the fluid velocity and, in turn, inhibits the convective heat transfer (as shown in Fig. 9). Furthermore, low frequency f reflects a higher rate of heat transfer characteristics. Figure 15e illustrates the effect of different volume fractions of Cu–Al₂O₃/water hybrid nanofluid on overall thermal behavior at Ra_m = 10³, Da = 10⁻⁴, I = 1, Ha = 30. The addition of Cu–Al₂O₃ nanoparticles escalates the effective thermal conductivity of the fluid, resulting buoyancy force becomes stronger. Thus, the average Nu increases irrespective of any frequency f. As ϕ increases beyond 0.0033, it is seen that circulation strength reduces (as shown in Fig. 10). This is attributed due to the increase in the viscosity of the hybrid nanofluid. Thus, the resistance to the fluid flow increases besides the buoyancy force, as the dynamic viscosity of the hybrid nanofluid increases. Further increase in ϕ leads to a decrease in the average Nu monotonically. In this case also, the low frequency of half-sinusoidal heating is always found to be superior. Further to the above, during the analysis, it is also observed that at lower values of Ra_m (< 10²) the presence of Cu–Al₂O₃ nanoparticles causes a significant improvement in the average Nu compared to the pure fluid.

Conclusions

Significance and fundamental flow physics of hybrid nanofluid saturated with porous media under the effect of multi-frequency half-sinusoidal heating at the bottom of an enclosure in the presence of a magnetic field are analyzed numerically and presented in this study. The enclosure is isothermally cooled at the sides, and the top wall is insulated. The effects of pertinent parameters, such as Darcy–Rayleigh number, Darcy number, amplitude and frequency of half-sinusoidal heating, Hartmann number and hybrid nanoparticles concentrations, are investigated thoroughly. The salient outcomes of this study are summarized below:

• The amplitude and frequency of applied half-sinusoidal heating strongly modulate the natural convective heat transfer process. The half-sinusoidal heating with lower frequency can be a superior heating strategy at a higher value of Ra_m > 10². Higher frequency is only advantageous for the lower range of Ra_m (≤ 10²). In addition, both the circulation strength and average Nu are higher at the higher value of Ra_m.

• With the increase in the frequency of half-sinusoidal heating beyond f = 1 (up to 10), simultaneous heating and cooling take place at the heated wall, resulting in the periodic oscillation of the local temperature as well as local and average Nu. Heat transfer rate decreases with increasing frequency due to the presence of such an intermediate cooling effect.

• The multi-frequency spatial heating amplitude (I) also plays a crucial role in the overall thermo-fluid flow behavior. An increase in the amplitude leads to an increase in the heat transfer rate monotonically and becomes maximum at higher amplitude I = 1 and higher Ra_m.

• As Ra_m increases, more depression in the local Nu profile is noted about the central point of the bottom wall. This is attributed due to the formation of a stagnation zone over a certain horizontal portion near the heated wall, leading to a reduction in localized heat transfer from the heated wall. As a result, a sharp fall in the local Nu around X = 0.5 is noted. This is an interesting finding of this case study.

• The convective heat transfer of hybrid nanofluid is strongly affected by the permeability of the porous media. For the fixed values of R_am (= Ra × Da), an increase in Da results in a decrement of overall heat transfer rate, which contradicts the usual notion. The increase in Da corresponds to a decrement in the fluid-based Ra; it reduces the intensity of thermal convection as well as average Nu. This is also another interesting finding in this study.

• Addition of Cu–Al₂O₃ hybrid nanoparticles into the pure water does not always improve the heat transfer rate. The addition of Cu–Al₂O₃ nanoparticles enhances the effective thermal conductivity of the fluid; thus, the resistance to the fluid flow reduces, and the average Nu increases irrespective of any frequency f. As ϕ increases beyond 0.0033, the viscosity of the hybrid nanofluid increases, leading to a decrement in the average Nu monotonically. It is also observed that at lower values of Ra_m (< 10²) the presence of Cu–Al₂O₃ nanoparticles causes a significant improvement in the average Nu compared to the pure fluid.

• When the externally applied magnetic field strength (in terms of Ha) increases, the thermal buoyancy decreases, resulting in a decrease in the heat transfer rate monotonically irrespective of any f, I, Ra_m and ϕ.

• Thermal energy transports from the heat source to the heat sink under various thermal conditions are visualized using Bejan’s heatlines.

The results show that the multi-frequency half-sinusoidal nonuniform heating along with the hybrid nanofluid can be useful for controlling the overall thermal performance of a system even in the presence of flow dampening effects like porous media and magnetic fields. The findings of this study can easily be accommodated during the modeling, designing, and controlling thermo-fluid behavior of relevant thermal devices.