Optimal thermal performance of magneto-nanofluid flow in expanding/contracting channel

Abstract

In a thermodynamical system, loss of energy takes the center of attention. According to laws of thermodynamics, energy of the system remains conserve, but all energy is employed to add work, and some of it is converted to rise the temperature and eventually increases entropy. Entropy of the system only increases and can never decrease. For the optimal thermal performance of a system, we need entropy generated to be minimum. This paper explores the enhancement of entropy in magneto-hydrodynamics nanofluid flowing inside the parallel plate which has a capacity of expansion or contraction. The lower plate is heated from outside. The mathematical constitution for the mass, momentum and transport of heat is described by a set of PDEs, which in turn generates a series solution by adopting the homotopy analysis method under prescribed boundary values. Different nano-sized particles, i.e., copper, silver and alumina are uniformly mixed in water. The impact of various factors on temperature, Nusselt number and velocity are elaborated pictorially and tabularly.

Introduction

Systems are absolutely desired for the purpose of cooling of any machines which performs energy transport. Such machines are widely used in power plants, factories and transportation. Water and oils are most commonly used for heat transportation because of their fluidity, but low thermal transfer character is an area of concern for such fluids, whereas the heat conductivity of the metals is much higher as compared to conventional liquids. Hence, desire is to accumulate the properties of both the matters, to generate a medium which fluidly enables to transport of heat and conduct like metals or their oxides. The thermal efficiency of the system depends on the material used to transport heat energy. It is essential to realize the factor which reduces thermal efficiency. According to laws of thermodynamics, energy of the system remains conserve, but can be converted into other forms for the utility. More commonly, we say all the energies of the system are spent in doing work or to augment the temperature of the body. Many frictional forces arising from the magnetic field, porous spaces etc., elaborate in the enhancement of the temperature of the system. The thermal disorderliness in the system is always on the rise. Knowing the factors involved in entropy rise is always important to get optimal thermal efficiency of the system. Rise in use of nanofluids is one way to reduce the loss of energy.

The nanofluid, a novel type of fluid, possesses heat conductivity greater than that of ordinary fluids due to the proper suspension of metal’s nano-size particles in the fluid. In fact, the concept of nanofluids was the brainchild of Choi [1]. It was one of the promising aspects of thermal conductivity enhancement of fluids. Later, different mathematical models, namely continuum (homogenous) model for the flow of nanofluids [2], dispersion or suspension phase model [3] and the so-called Buongiorno’s model [4], were developed in brainstorm ways. Many researchers analyzed the transport of momentum and energy in the channel and through different geometries for nanofluids, like Seyednezhad et al. [5] most recently study solar heat exchanger with nanofluid for water purification. Nazoktabar et al. [6] work on thermostat placement and its effect on coolant. Arshad and Ali [7] do some experiments on a mini channel for pressure drop for nanofluid. Hayat et al. [8] reported flow of CNTs through non-Darcian porous medium over rotating disk. Sheikholeslami et al. [9] numerically show the effects of induced magnetic field on nanofluid. They also assumed KKL correlation Bhatti and Zeeshan forms analytic solutions for peristaltic transport of nanofluid with slip effects [10]. It is ensured that the magnetic field performs an important part in constructing a controlled cooling system. The technology of polymer, wire drawing, food production, hot rolling and paper production are the qualities of final products in manufacturing and industrial products. By introducing porous medium, the surface area of fluid and solids in contact with each other upsurges and as a consequence, they can be utilized as heat transfer or insulation devices in distinct systems. On account of such advantages, heat and fluid flow through porous media find marvelous applications including reservoirs of petroleum, crude oil, hydrology, gas production, geothermal energy system, design of heat exchanger, grain storage, movement of water in reservoirs, catalytic reactors, beds of fossil fuels, solar receivers etc. [11,12,13].

Nowadays, the technique involving porous medium and nanofluids jointly finds substantial consideration from many researchers and great demand from industry-based thermal systems. The rationality behind it is that in porous media, the contact area increases, while nanoparticles dispersed in nanofluid upsurge effective thermal conductivity leading to a dramatic enhancement of efficiency of traditional industrial heat transfer systems. The investigation regarding viscous fluids flow through a closed geometry with permeable space is of enduring significance in view of its applications to many scientific and industrial problems. Yuan [14] studied experimentally the significance of uniform injection and suction through the walls. A stable convective flow in a porous slab [15], pressure-driven flows in the permeable channel [16] and mixed convection flow with uniform wall heat flux [17] have been examined. Further, the impact of drag force and inertial terms in association with stability on mixed convection flow [18] through porous media was studied. The study of Sharma and Bera [19] discusses the stability of induced parallel flow in a saturated channel permeable space. The investigation explored detailing the effect of non-dimensional quantities such as Reynolds, Prandtl and modified Forchheimer number on flow concerned. They declared highly permeable porous medium basic flow of high velocity. It is deduced that instability is achieved, and both the walls of the channel are at almost the same temperature. Also, fluids can easily be unstabilized if the permeability of the porous medium is low. A mild augmentation in Re accelerates the advection in the direction of that wall, and the flow is destabilized due to the upward transportation of denser fluid. This is a “lift-up” mechanism in the presence of vertices in the flow domain. The regimes associated with such instabilities are functions of Darcy number and Re in the domain of Prandtl number. Recently, Xu and Cui [20] analyzed mix-convective slip flow through a porous channel saturated with nanofluid and driven by its moving wall. They ascertained that for lesser values of “Re,” the wall friction belittles rapidly and for large Re, its reduction is quite slow in response to continuously increase Re. Augmented slip parameter causes a decline in skin friction.

It is, in fact, the quantity and quality of heat are ultimately responsible for designing and developing engineering products or practical thermal systems. Fundamentally, the second law of thermodynamics develops a theory of irreversibility or entropy helps us in determining the standard and level of loss of energy in all thermo-fluidic processes. Second law of thermodynamics explained that in doing work, some useful energy is dissipated which consequently reduces the energy efficiency of the machine. This degrading of energy (destruction of energy or energy loss) that is irreversibility is proportional to entropy generation. Entropy analysis can be applied as a measure to determine the amount of such irreversibility. Generation of entropy in a certain system leads to reduction in available energy (exergy). So, optimal thermal performance can be obtained by minimizing entropy. Consequently, it is important to develop the relationship of entropy generation throughout several thermodynamic processes, where it is fitting to minimalize the entropy generation to take the advantages of better thermal performances. Bejan [21] was the pioneer revealing the grounds of the generation of entropy in the convection heat flow problem. He declared from his investigation that the temperature difference and velocity gradient are reasons for the production of entropy. Muhammad et al. [22] compared pure water, nanofluid with carbon nanotubes and hybrid nanofluid with carbon nanotubes and copper-oxide for melting heat transfer in squeezing flow. Abbasi et al. [23] examined entropy production inside the Poiseuille Benard flow. Weigand and Birkenfeld [24] obtained the similarity solutions of the entropy equation. Makinde and Beg [25] analyzed the irreversibility in magneto-hydrodynamics (MHD), reactive flow in a channel. An analytical investigation regarding the impact of couple stresses on entropy in a flow through parallel plates was considered by Aksoy [26]. In view of the minimization of entropy generation, many researchers [27,28,29,30,31] investigated the second law for the fluid and heat transport problem associated with different geometries, because of the aforementioned relevance of channel flow in porous medium and entropy generation to maximize the available energy in several thermal systems. Authors have been motivated to investigate an unsteady heat transfer analysis along with analysis of the second law of thermodynamics in a porous media in the channel. Goals of this research article reveal the concept of entropy generation in the unsteady flow of nanofluids in a porous media in which the bottom plate is fixed but heated from outside. Additionally, the coolant fluid added in the porous region moving with a particular velocity cools down the wall toward the upper plate that expands or contracts with time. Such aspect of the study has not been discussed yet.

Mathematical modeling

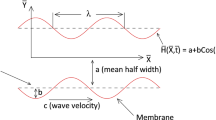
Unsteady flow is considered inside the two flat equidistant plates in Fig. 1, and the transverse magnetic field is considered on the flow. The lower wall, which is represented by the x-axis, is kept motionless and warmed from outside. Coolant fluid is introduced having a velocity $v_{\rm w}$ uniformly to cool down the upper wall, which expand/contract at the rate $b(t)$. Let y be direct vertically upward making an angle of 90° with the channel plates. Suppose that ${\bar{u}}$ defines x-component of velocity field and ${\bar{v}}$ is specified in y-component of velocity respectively. Flow is assumed to have no-slip velocity along the wall.

Fig. 1

Geometry of the flow problem

An incompressible, two-dimensional unsteady nanofluid in the presence of constant transverse magnetic field which generates ohmic dissipation is modeled using continuity, momentum and heat equations [32].

$${\bar{v}}_{\rm y} + {\bar{u}}_{\rm x} = 0,$$

(1)

$$\rho_{\rm nf} \left( {{\bar{u}}_{\rm t} + {\bar{u}} \cdot {\bar{u}}_{\rm x} + {\bar{v}} \cdot {\bar{u}}_{\rm y} } \right) = - \overline{p}_{\rm x} + \mu_{\rm nf} \left( {{\bar{u}}_{\rm xx} + {\bar{u}}_{\rm yy} } \right) - \sigma B_{\rm o}^{2} {\bar{u}},$$

(2)

$$\rho_{\rm nf} \left( {{\bar{v}}_{\rm t} + {\bar{u}} \cdot {\bar{v}}_{\rm x} + {\bar{v}} \cdot {\bar{v}}_{\rm y} } \right) = - \overline{p}_{\rm y} + \mu_{\rm nf} \left( {{\bar{v}}_{\rm xx} + {\bar{v}}_{\rm yy} } \right) - \sigma B_{\rm o}^{2} {\bar{v}},$$

(3)

$$\left( {\rho C_{\rm p} } \right)_{\rm nf} \left( {T_{\rm t} + {\bar{u}}T_{\rm x} + {\bar{v}}T_{\rm y} } \right) = k_{\rm nf} \left( {T_{\rm xx} + T_{\rm yy} } \right) + \sigma B_{\rm o}^{2} {\bar{u}}^{2} + \mu_{\rm nf} \left\{ {2\left( {{\bar{u}}_{\rm x} } \right)^{2} + 2\left( {{\bar{v}}_{\rm y} } \right)^{2} + \left( {{\bar{u}}_{\rm y} + {\bar{v}}_{\rm x} } \right)^{2} } \right\}.$$

(4)

Along with boundary conditions, [32]

$$\begin{aligned} & {\bar{u}} = 0,\quad {\bar{v}} = - {\bar{v}}_{\rm w} = - \Lambda \dot{a},\quad T\left( {\bar{x},\bar{y}} \right) = T_{\rm 2} \quad {\text{at}}\,\,\bar{y} = b(t), \\ & {\bar{u}} = {\bar{v}} = 0,\quad T\left( {\bar{x},\bar{y}} \right) = T_{1} \quad {\text{at}}\,\,\bar{y} = 0. \\ \end{aligned}$$

(5)

Here, $\Lambda = {\bar{v}}_{\rm w} / {\dot{b}}$ depicts the amount of wall porousness.

Now presenting the stream function

$$\bar{\psi } \, = \frac{{\upsilon \bar{x}}}{b}\bar{F}(\eta ,t), \, {\bar{u}} = \frac{{\upsilon \bar{x}}}{{b^{2} }}\bar{F}_{\eta } {\text{ and }}{\bar{v}} = - \frac{\upsilon }{b}\bar{F}.$$

(6)

where $\eta = \bar{y}/b$, by taking derivate of Eq. (2) with respect to y and Eq. (3) with respect to x and subtracting both equations to remove the pressure. Finally, replacing ${\bar{u}}$ and ${\bar{v}}$ from Eq. (6), the result is as follows.

$$\bar{F}_{\eta \eta \eta \eta } + \frac{{\Omega_{1} }}{{\Omega_{2} }} \cdot \left( {\left( {\alpha \cdot \eta + \bar{F}} \right)\bar{F}_{\eta \eta \eta } + \left( {3 \cdot \alpha - \bar{F}_{\eta } } \right)\bar{F}_{\eta \eta } } \right) - \frac{{\Omega_{1} }}{{\Omega_{2} }} \cdot b^{2} \cdot \upsilon_{\rm f}^{ - 1} \cdot \bar{F}_{\eta \eta {\rm t}} + \frac{{\Omega_{5} }}{{\Omega_{2} }} \cdot M \cdot \bar{F}_{\eta \eta } = 0,$$

(7)

where $\Omega_{1}$, $\Omega_{2}$ and $\Omega_{5}$ are fixed factors that are defined as

$$\Omega_{1} = \frac{{\rho_{\rm nf} }}{{\rho_{\rm f} }}, \, \Omega_{2} = \frac{{\mu_{\rm nf} }}{{\mu_{\rm f} }}, \, \Omega_{5} = \frac{{\sigma_{\rm nf} }}{{\sigma_{\rm f} }}.$$

(8)

The fundamental features of nanoparticles and Newtonian base fluid are shown in Table 1.

Table 1 Thermophysical properties of nanofluid

The BCs are:

$$\left. {\overline{F} \left( 0 \right) = 0,\,\,\overline{{F_{\eta } }} \left( 0 \right) = 0\,\,{\text{and}}\,\,\overline{{F_{\eta } }} \left( 1 \right) = 0,\,\,\overline{F} \left( 1 \right) = \frac{{\Omega_{1} }}{{\Omega_{2} }}\hbox{Re}.} \right\}$$

(9)

Reynolds number is demonstrated as ${\text{Re}} = {{bv_{\rm w} } \mathord{\left/ {\vphantom {{bv_{\rm w} } {\upsilon_{\rm f} }}} \right. \kern-0pt} {\upsilon_{\rm f} }}$. The same solution considering with respect to space plus time has established transformations defined by Majdalani et al. [33]. It could be achieved by taking $\alpha$ as static and $\bar{F} = \bar{F}(\eta )$, which results in $\bar{F}_{\eta \eta {\rm t}} = 0$. By understanding this consideration, $\alpha$ is essential to be defined by its primary value

$$\alpha = \frac{{b\dot{b}}}{{\upsilon_{\rm f} }} = \frac{{b_{\rm o} \dot{b}_{\rm o} }}{{\upsilon_{\rm f} }} = {\text{constant}}.$$

(10)

Here, $b_{\rm o}$ and $\dot{b}_{\rm o}$ show initial height and growth ratio of the channel, respectively. Integrate

Equation (10) with respect to time, we get.

$$\frac{b}{{b_{\rm o} }} = \sqrt {1 + 2\upsilon_{\rm f} \alpha tb_{\rm o}^{ - 2} } .$$

(11)

In order to identify the injection velocity variation, $v_{\rm w} = A\dot{b}$ by providing A as constant injection coefficient for the physical situation. Equations (10) and (11), it is obvious to express as

$$\frac{b}{{b_{\rm o} }} = \frac{{v_{\rm w} (0)}}{{v_{\rm w} (t)}} = \sqrt {1 + 2\upsilon_{\rm f} \alpha tb_{\rm o}^{ - 2} } .$$

(12)

Under the said assumptions, Eq. (7) becomes

$$\bar{F}_{\eta \eta \eta \eta } + \frac{{\Omega_{1} }}{{\Omega_{2} }} \cdot \left( {\left( {\alpha \cdot \eta + \bar{F}} \right) \cdot \bar{F}_{\eta \eta \eta } + \left( {3 \cdot \alpha - \bar{F}_{\eta } + \frac{{\Omega_{5} }}{{\Omega_{1} }} \cdot M} \right)\bar{F}_{\eta \eta } } \right) = 0.$$

(13)

Associated BCs are

$$\left. {\overline{F} \left( 0 \right) = 0,\,\,\overline{{F_{\eta } }} \left( 0 \right) = 0\,\,{\text{ and }}\,\,\overline{{F_{\eta } }} \left( 1 \right) = 0,\,\,\overline{F} \left( 1 \right) = 1.} \right\}$$

(14)

The thermal profile of the fluid may be stated as [34].

$$T\left( {\bar{x},\eta } \right) = T_{1} + \frac{{\mu_{\rm f} v_{\rm w} }}{{\rho bC_{\rm p} }}\left[ {f\left( \eta \right) + \frac{{\bar{x}^{2} }}{{a^{2} }}g\left( \eta \right)} \right].$$

(15)

The dimensionless form of temperature by using Eq. (15) can be marked down as [33]:

$$\theta = \frac{{T - T_{1} }}{{T_{2} - T_{1} }} = {\text{Ec}}(f + x^{2} g).$$

(16)

The Eckert number is interpreted as ${\text{Ec}} = \frac{{\mu_{\rm f} v_{\rm w} }}{{\left( {\rho bC_{\rm p} } \right)\left( {T_{2} - T_{1} } \right)}}$.

Introducing the normalized parameters [33]

$$\bar{\psi } = \psi \cdot bv_{\rm w} ,\,\,{\bar{u}} = u \cdot v_{\rm w} ,\,\,{\bar{v}} = v \cdot v_{\rm w} ,\,\,\bar{x} = x \cdot b(t),\,\,\bar{y} = y \cdot b(t),\,\,\overline{F} = F \cdot {\text{Re}} ,\,\,\bar{p} = p \cdot \rho v_{\rm w}^{2} .$$

(17)

Substituting Eqs. (16) and (17) into Eq. (4), we have

$$\left. \begin{aligned} & \Omega_{4} {\text{Ec}}\left( {f_{\eta \eta } + x^{2} g_{\eta \eta } } \right) + \Omega_{3} {\text{Br}}\left( {\alpha \eta + {\text{Re}} F} \right)\left( {f_{\eta } + x^{2} g_{\eta } } \right) + \Omega_{5} M{\text{BrRe}} F_{\eta }^{2} x^{2} \\ & \quad + \Omega_{2} {\text{BrRe}} \left( {2F_{\eta }^{2} + x^{2} F_{\eta \eta }^{2} } \right) = 0. \\ \end{aligned} \right\}$$

(18)

Comparing the coefficients of $x^{2}$ and the terms without $x^{2}$ of Eq. (18), then it becomes

$$\Omega_{4} {\text{Ec}}f_{\eta \eta } + \Omega_{3} {\text{Br}}\left( {\alpha \eta + {\text{Re}} F} \right)f_{\eta } + 2\Omega_{2} {\text{BrRe}} F_{\eta }^{2} = 0,$$

(19)

$$\Omega_{4} {\text{Ec}}g_{\eta \eta } + \Omega_{3} {\text{Br}}\left( {\alpha \eta + {\text{Re}} F} \right)g_{\eta } + \Omega_{5} M{\text{BrRe}} F_{\eta }^{2} + \Omega_{2} {\text{BrRe}} F_{\eta \eta }^{2} = 0,$$

(20)

where $\Pr = \frac{{\nu_{\rm f} \left( {\rho C_{\rm p} } \right)}}{{k_{\rm f} }}$ and $M = \frac{{\sigma_{\rm f} B_{0}^{2} a^{2} }}{{\mu_{\rm f} }}$ is the Prandtl number and magnetic field, respectively. Also, ${\text{Br}} = \Pr \cdot {\text{Ec}}$, where $\Omega_{3}$ and $\Omega_{4}$ are the fixed factors that are: $\Omega_{3} = \frac{{\left( {\rho C_{\rm p} } \right)_{\rm nf} }}{{\left( {\rho C_{\rm p} } \right)_{\rm f} }}$ and $\Omega_{4} = \frac{{k_{\rm nf} }}{{k_{\rm f} }}$.

The BCs from Eq. (5) in terms of $f$ and $g$ are as under

$$\begin{aligned} & f = 0,\,\,g = 0\quad {\text{at}}\,\,\eta = 0, \\ & f = \frac{1}{\text{Ec}},\,\,g = 0\quad {\text{at}}\,\,\eta = 1. \\ \end{aligned}$$

(21)

From Eq. (13), we achieve

$$\bar{F}_{\eta \eta \eta \eta } + \frac{{\Omega_{1} }}{{\Omega_{2} }} \cdot \left( {\left( {\alpha \cdot \eta + {\text{Re}} \cdot \bar{F}} \right) \cdot \bar{F}_{\eta \eta \eta } + \left( {3 \cdot \alpha - {\text{Re}} \cdot \bar{F}_{\eta } + \frac{{\Omega_{5} }}{{\Omega_{1} }} \cdot M} \right)\bar{F}_{\eta \eta } } \right) = 0.$$

(22)

And BCs from Eq. (14) takes the form

$$F_{\eta } (0) = F(0) = \, F_{\eta } (1) = 0, \, F(1) = 1.$$

(23)

In this circumstance, the non-dimensional (Nu) is found as under

$${\text{Nu}} = - \frac{{k_{\rm nf} }}{{k_{\rm f} }}\frac{\partial T}{\partial \eta }/(T_{2} - T_{1} ) = - \Omega_{4} \theta^{\prime } (0).$$

(24)

Solution of the problem

In this investigation, mathematical Eqs. (19), (20) and (22) along with the boundary conditions (16) and (23) are solved by the homotopy analysis method [35, 36] with MATHEMATICA package (BVPh 2.0). By selecting the appropriate guess that satisfied the boundary conditions, the associated auxiliary linear operators are

$$l_{1} (F) = F^{\prime \prime \prime \prime } ,$$

(25)

$$l_{2} (\theta ) = \theta^{\prime\prime}.$$

(26)

These auxiliary linear operators satisfy

$$l_{1} (Q_{1} \eta^{3} + Q_{2} \eta^{2} + Q_{3} \eta + Q_{4} ) = 0,$$

(27)

$$l_{2} (Q_{5} \eta + Q_{6} ) = 0,$$

(28)

where $Q_{\rm i}$ (i = 1, 2, 3, 4, 5, 6) are constants.

Zeroth-order deformation:

$$(1 - p)l_{1} (F(\eta ,p) - F_{0} (\eta )) = ph_{1} N_{1} (F(\eta ,p)),$$

(29)

$$F(0,p) = 0, \, F^{\prime}(0,p) = 0, \, F^{\prime}(1,p) = 0, \, F(1,p) = 1,$$

(30)

$$(1 - p)l_{2} (\theta (\eta ,p) - \theta_{0} (\eta )) = ph_{2} N_{2} (F(\eta ,p),\theta (\eta ,p)),$$

(31)

$$\theta (0,p) = 0, \, \theta (1,p) = 1.$$

(32)

mth-order deformation:

$$l_{1} (F_{\rm m} - x_{\rm m} F_{{\rm m} - 1} ) = h_{1} N_{1}^{\text{m}} ,$$

(33)

$$F_{\rm m} (0) = 0,\quad F^{\prime}_{\rm m} (0) = 0,\quad F^{\prime}_{\rm m} (1) = 0,\quad F_{\rm m} (1) = 1,$$

(34)

$$l_{2} (\theta_{\rm m} - x_{\rm m} \theta_{{\rm m} - 1} ) = h_{2} N_{2}^{\text{m}} ,$$

(35)

$$\theta_{\rm m} (0) = 0, \, \theta_{\rm m} (1) = 1.$$

(36)

where

$$N_{1}^{m} (\eta ) = \frac{{\partial^{4} F_{{\rm m} - 1} }}{{\partial \eta^{4} }} + \alpha \left( {\eta \frac{{\partial^{3} F_{{\rm m} - 1} }}{{\partial \eta^{3} }} + 3\frac{{\partial^{2} F_{{\rm m} - 1} }}{{\partial \eta^{2} }}} \right) + {\text{Re}} \sum\limits_{{\rm k} = 0}^{m - 1} {F_{{\rm m} -{\rm k} - 1} \frac{{\partial^{3} F_{\rm k} }}{{\partial \eta^{3} }} - {\text{Re}} \sum\limits_{{\rm k} = 0}^{m - 1} {\frac{{\partial F_{{\rm m} -{\rm k} - 1} }}{\partial \eta }\frac{{\partial^{2} F_{\rm k} }}{{\partial \eta^{2} }} ,} }$$

(37)

$$\left. \begin{aligned} & N_{2}^{m} (\eta ) = \Omega_{4} \frac{{\partial^{2} \theta_{{\rm m} - 1} }}{{\partial \eta^{2} }} + \Omega_{3} \Pr \alpha \eta \frac{{\partial \theta_{{\rm m} - 1} }}{\partial \eta } + \Omega_{3} \Pr {\text{Re}} \sum\limits_{{\rm k} = 0}^{m - 1} {\left( {\frac{{\partial \theta_{{\rm m} - 1 -{\rm k}} }}{\partial \eta }F_{\rm k} } \right)} \\ & \quad + \Omega_{2} {\text{BrRe}} \sum\limits_{{\rm k} = 0}^{m - 1} {\left( {2\left( {\frac{{\partial F_{{\rm m} - 1 -{\rm k}} }}{\partial \eta }} \right)\left( {\frac{{\partial F_{\rm k} }}{\partial \eta }} \right) + x^{2} \left( {\frac{{\partial^{2} F_{{\rm m} - 1 -{\rm k}} }}{{\partial \eta^{2} }}} \right)\left( {\frac{{\partial^{2} F_{\rm k} }}{{\partial \eta^{2} }}} \right)} \right)} + \Omega_{5} M{\text{BrRe}} \sum\limits_{{\rm k} = 0}^{m - 1} {\left( {\left( {\frac{{\partial F_{{\rm m} - 1 -{\rm k}} }}{\partial \eta }} \right)\left( {\frac{{\partial F_{\rm k} }}{\partial \eta }} \right)x^{2} } \right)} . \\ \end{aligned} \right\}$$

(38)

The general solutions are

$$F_{\eta } (\eta ) = F_{\eta }^{*} (\eta ) + Q_{1} + Q_{2} \eta + Q_{3} \eta^{2} + Q_{4} \eta^{3} ,$$

(39)

$$\theta_{\eta } (\eta ) = \theta_{\eta }^{*} (\eta ) + Q_{5} + Q_{6} \eta .$$

(40)

The convergence of two series is highly reliant on $h_{1} ,h_{2} .$; Eqs. (29) and (31) are convergent by selecting suitable h. The solution becomes

$$F = F_{0} (\eta ) + \sum\limits_{{\rm k} = 1}^{m} {F_{\rm k} (\eta ),}$$

(41)

$$\theta = \theta_{0} (\eta ) + \sum\limits_{{\rm k} = 1}^{m} {\theta_{\rm k} (\eta ).}$$

(42)

Following this method, the linear non-homogeneous differential equations are solved by Mathematica very comfortably. The first-order solutions are represented below.

The stream function and temperature distribution are also elaborated in Table 2 for the best of understanding.

Table 2 Stream function $\left( F \right)$ and temperature $\left( \theta \right)$ results for Cu–water nanofluid, at $\alpha = {\text{Re}} = 1,$ and $\varphi$ = 0.05

$$\begin{aligned} & F = \frac{1}{{1940400\Omega_{2}^{2} }}\eta^{2} \left( { - 1940400\left( { - 3 + 2\eta } \right)\Omega_{2}^{2} + \left( { - 1 + \eta } \right)^{2} } \right. \\ & \quad \left( {\left( { - 693\alpha^{2} \left( { - 39 - 52\eta - 30\eta^{2} + 160\eta^{3} } \right) } \right.} \right. \\ & \quad - 77{\text{Re}} \alpha \left( { - 465 - 284 \eta + 1337 \eta^{2} + 762 \eta^{3} - 485 \eta^{4} + 320 \eta^{5} } \right) \\ & \quad \left. { + 3{\text{Re}}^{2} \left( { - 761 - 7380\eta - 13999\eta^{2} + 8950\eta^{3} - 2905\eta^{4} - 504\eta^{5} - 1568\eta^{6} + 448\eta^{7} } \right)} \right)\Omega_{1}^{2} \\ & \quad - 462M^{2} \left( {\alpha \left( { - 13 - 29\eta - 80\eta^{2} + 100\eta^{3} } \right) + {\text{Re}} \left( { - 25 - 41\eta + 23\eta^{2} + 48\eta^{3} - 25\eta^{4} + 10\eta^{5} } \right)} \right)\Omega_{1} \Omega_{5} \\ & \quad \left. { - 231M^{4} \left( {3 + 4\eta - 30\eta^{2} + 20\eta^{3} } \right)\Omega_{5}^{2} } \right)h_{1}^{2} \\ & \quad \left. { - 13860\left( { - 1 + \eta } \right)^{2} \Omega_{2} \left( {\left( {7\left( {\alpha + 8\alpha \eta } \right) + 2{\text{Re}} \left( {16 + 5\eta - 6\eta^{2} + 4\eta^{3} } \right)} \right)\Omega_{1} + 7M^{2} \left( { - 1 + 2\eta } \right)\Omega_{5} } \right)h_{1} \left( {2 + h_{1} } \right)} \right) \\ \end{aligned}$$

(43)

$$\begin{aligned} \theta & = - 1/(25200\Omega_{2} )\eta ({\text{BrRe}} h_{2} ( - 3M^{2} \Omega_{5} (12{\text{Ec}}M(1 + 70\eta^{3} - 294\eta^{4} + 448\eta^{5} - 300\eta^{6} \\ & \quad + 75\eta^{7} )\Omega_{5} h_{2} - \Omega_{3} ((1 - 35\eta^{3} + 84\eta^{4} - 70\eta^{5} + 20\eta^{6} )h_{2} + Ec( - 1 + 35\eta^{3} \\ & \quad - 126\eta^{4} + 182\eta^{5} - 120\eta^{6} + 30\eta^{7} )h_{2} )) + \Omega_{1} ( - 12{\text{Ec}}M(6\alpha (7 - 35\eta^{3} \\ & \quad - 168\eta^{4} + 546\eta^{5} - 500\eta^{6} + 150\eta^{7} ) + {\text{Re}} (31 - 960\eta^{3} + 2034\eta^{4} - 972\eta^{5} \\ & \quad - 900\eta^{6} + 1215\eta^{7} - 560\eta^{8} + 112\eta^{9} ))\Omega_{5} h_{2} + \Omega_{3} ((3\alpha ( - 31 + 35\eta^{3} + 126\eta^{4} \\ & \quad - 210\eta^{5} + 80\eta^{6} ) + 2{\text{Re}} ( - 52 + 240\eta^{3} - 243\eta^{4} + 90\eta^{6} - 45\eta^{7} + 10\eta^{8} ))h_{2} \\ & \quad + {\text{Ec}}(3\alpha (1 - 35\eta^{3} - 84\eta^{4} + 378\eta^{5} - 380\eta^{6} + 120\eta^{7} ) + 2{\text{Re}} (7 - 240\eta^{3} \\ & \quad + 531\eta^{4} - 324\eta^{5} - 90\eta^{6} + 180\eta^{7} - 80\eta^{8} + 16\eta^{9} ))h_{2} ))) \\ & \quad + 72{\text{BrEcRe}} \Omega_{2}^{2} ( - 840( - 1 + 5\eta^{3} - 6\eta^{4} + 2\eta^{5} )h_{2} + ({\text{Br}}(10\alpha \eta^{2} (7 - 28\eta^{3} \\ & \quad + 30\eta^{4} - 9\eta^{5} ) + {\text{Re}} (10 + 105\eta^{3} - 42\eta^{4} - 600\eta^{6} + 975\eta^{7} - 560\eta^{8} \\ & \quad + 112\eta^{9} ))\Omega_{3} - 420{\text{Ec}}( - 1 + 5\eta^{3} - 6\eta^{4} + 2\eta^{5} )\Omega_{4} )h_{2}^{2} + 5( - 1 + \eta )h_{2} ({\text{Br}}( \\ & \quad - 14\alpha \eta^{2} (5 - 10\eta + 8\eta^{2} ) + 3{\text{Re}} ( - 1 - \eta - \eta^{2} - 36\eta^{3} + 104\eta^{4} \\ & \quad - 120\eta^{5} + 40\eta^{6} ))\Omega_{3} h_{2} - 420(1 - 2\eta + 2\eta^{2} )(2 + {\text{Ec}}\Omega_{4} h_{2} ))) \\ & \quad + \Omega_{2} ( - {\text{Br}}^{2} \Omega_{3}^{2} ((70\alpha^{2} (1 - 10\eta^{2} + 9\eta^{4} ) - 30{\text{Re}} \alpha ( - 2 + 21\eta^{2} + 35\eta^{3} - 14\eta^{4} \\ & \quad - 70\eta^{5} + 30\eta^{6} ) + {\text{Re}}^{2} ( - 8 - 945\eta^{3} + 378\eta^{4} + 1800\eta^{6} - 1575\eta^{7} \\ & \quad + 350\eta^{8} ))h_{2}^{2} + {\text{Ec}}(70\alpha^{2} (1 - 9\eta^{4} + 8\eta^{5} ) - 10{\text{Re}} \alpha ( - 13 + 7\eta^{2} + 210\eta^{5} \\ & \quad - 300\eta^{6} + 96\eta^{7} ) + {\text{Re}}^{2} (55 - 105\eta^{3} + 42\eta^{4} - 1800\eta^{6} + 3600\eta^{7} - 2240\eta^{8} + 448\eta^{9} ))) \\ & \quad + 12{\text{Br}}\Omega_{3} (70( - 10\alpha ( - 1 + \eta^{2} ) + 3{\text{Re}} (3 - 5\eta^{3} + 2\eta^{4} ))h_{2} + 35{\text{Ec}}( - 10\alpha ( - 1 + \eta^{2} ) \\ & \quad + 3{\text{Re}} (3 - 5\eta^{3} + 2\eta^{4} ))\Omega_{4} h_{2}^{2} + {\text{Ec}}h_{2} (70( - 10\alpha ( - 1 + \eta )\eta^{2} + {\text{Re}} (1 + 15\eta^{3} - 24\eta^{4} + 8\eta^{5} )) \\ & \quad + 70{\text{Ec}}( - 10\alpha ( - 1 + \eta )\eta^{2} + {\text{Re}} (1 + 15\eta^{3} - 24\eta^{4} + 8\eta^{5} ))\Omega_{4} h_{2} \\ & \quad + 3{\text{Br}}M{\text{Re}} (10\alpha \eta^{2} (7 - 28\eta^{3} + 30\eta^{4} - 9\eta^{5} ) \\ & \quad + {\text{Re}} (10 + 105\eta^{3} - 42\eta^{4} - 600\eta^{6} + 975\eta^{7} - 560\eta^{8} + 112\eta^{9} ))\Omega_{5} h_{2} )) \\ & \quad - 24({\text{BrEcRe}} ( - 1 + \eta )\Omega_{1} h_{2} ((6\alpha ( - 7 - 7\eta - 7\eta^{2} + 28\eta^{3} + 196\eta^{4} - 350\eta^{5} + 150\eta^{6} ) \\ & \quad + {\text{Re}} ( - 31 - 31\eta - 31\eta^{2} + 929\eta^{3} - 1105\eta^{4} - 133\eta^{5} + 767\eta^{6} - 448\eta^{7} + 112\eta^{8} ))h_{2} \\ & \quad + 30(7\alpha ( - 2 + \eta + 17\eta^{2} - 46\eta^{3} + 32\eta^{4} ) \\ & \quad + 2{\text{Re}} ( - 7 + 41\eta - 72\eta^{2} + 9\eta^{3} + 72\eta^{4} - 54\eta^{5} + 18\eta^{6} ))) \\ & \quad + 3(350(1 + \hbox{Ec}( - 1 + \eta ) + 2{\text{Ec}}^{2} ( - 1 + \eta )\Omega_{4} h_{2} + {\text{Ec}}^{3} ( - 1 + \eta )\Omega_{4}^{2} ) \\ & \quad + {\text{BrEc}}M{\text{Re}} \Omega_{5} (Mh_{2} ((1 + 70\eta^{3} - 294\eta^{4} + 448\eta^{5} - 300\eta^{6} + 75\eta^{7} )h_{2} \\ & \quad + 70( - 1 + \eta )^{2} \eta (3 - 8\eta + 8\eta^{2} h_{2} ) + 210( - 1 + 5\eta^{3} - 6\eta^{4} + 2\eta^{5} )h_{2} (2 + {\text{Ec}}\Omega_{4} h_{2} )))))). \\ \end{aligned}$$

(44)

Entropy generation

The equation for entropy generation (EG) of nanofluid flow can be expressed as [21]

$$S^{\prime\prime\prime}_{\rm gen} = \frac{{K_{\rm nf} }}{{T_{1}^{2} }}\left[ {\left( {T_{{\overline{x} }} } \right)^{2} + \left( {T_{{\overline{y} }} } \right)^{2} } \right] + \frac{{\mu_{\rm nf} }}{{T_{1} }} \cdot \left[ {2 \cdot \overline{v}_{{\overline{\rm y} }}^{2} + 2 \cdot \overline{u}_{{\overline{\rm x} }}^{2} + \overline{u}_{{\overline{\rm y} }}^{2} + \overline{v}_{{\overline{\rm x} }}^{2} + 2 \cdot \overline{u}_{{\overline{\rm y} }}^{2} \cdot \overline{v}_{{\overline{\rm x} }}^{2} } \right] + \frac{{\sigma_{\rm nf} }}{{T_{1} }}B_{\rm o}^{2} \overline{u}^{2} .$$

(45)

The above-mentioned equation implies the three effects which describes entropy generation: The first part of the equation is known for conduction effect, and it arises because of temperature difference in two walls; the second part of the equation is known as fluid friction irreversibility which is due to the presence of viscous effects, and finally, the last part of the equation is due to the magnetic effects in terms of joule dissipation irreversibility. In the presence of non-dimensional variables, the local entropy generation rate is specified as

$$N_{\rm e} = \frac{{S^{\prime\prime\prime}_{\rm gen} }}{{S_{\rm gen} }} = \Omega_{4} {\text{Ec}}^{2} \left( {f_{\eta }^{2} + 2x^{2} f_{\eta } g_{\eta } } \right) + \Omega_{2} \frac{\text{Br}}{\Omega }{\text{Re}} \left( {2\left( {F_{\eta }^{2} + F^{2} } \right) + x^{2} F_{\eta \eta }^{2} } \right) + \Omega_{5} M\frac{\text{Br}}{\Omega }x^{2} F_{\eta }^{2} .$$

(46)

The $N_{\rm e}$ number is obtained by taking ratio of entropy generation rate $S^{\prime\prime\prime}_{\rm gen}$ and its characteristic value $S_{\rm gen} = \frac{{K_{\rm f} (T_{2} - T_{1} )^{2} }}{{b^{2} T_{1}^{2} }}$. Equation (46) can also be expressed in the form as under:

$$N_{\rm e} = N_{\rm H} + N_{\rm F} ,\quad {\text{here,}}\,\,N_{\rm F} = N_{\rm f} + N_{\rm m} .$$

(47)

Here, entropy generation with respect to heat transfer is $N_{\rm H}$, entropy generation with respect to fluid friction is $N_{\rm f}$, and local entropy generation with respect to the magnetic field is $N_{\rm m}$. Another parameter is identified as Bejan number, and its range lies between 0 and 1 and defined as

$${\text{Be}} = \frac{{N_{\rm H} }}{{N_{\rm H} + N_{\rm F} }}.$$

(48)

Efficiency of code with convergence analysis

The velocity and temperature results in Eqs. (41) and (42) contain the auxiliary parameters $h_{1}$ and $h_{2}$, respectively. As pointed out by the originator of the homotopy analysis method, a faster convergence can be achieved by the optimum selection of the involved auxiliary parameters [28].

For the optimum values of $h_{1}$ and $h_{2}$, the residual errors were computed up to twenty fifth-order approximations over an embedding parameter $p \in \left[ {0, \, 1} \right]$ of velocity $E_{{{\rm F}^{\prime}}}$ and temperature distributions $E_{\theta }$, by the succeeding formulas:

$$E_{{{\rm F}^{\prime}}} = \sqrt {\frac{1}{26}\sum\limits_{{\rm i} = 0}^{25} {\left( {F^{\prime}\left( {i/25} \right)} \right)^{2} } } {\text{ and }}E_{\theta } = \sqrt {\frac{1}{26}\sum\limits_{{\rm j} = 0}^{25} {\left( {\theta \left( {j/25} \right)} \right)^{2} } } .$$

(49)

Result and discussion

For evaluating the results, the homotopy analysis method is used to discuss the behavior of stream function profile $\left( F \right),$ velocity profile $\left( {F'} \right)$ and temperature profile $\left( \theta \right)$ of nanofluid flow between two parallel plates under the effect of magnetohydrodynamics. The consequences are demonstrated graphically in Figs. 2–13 for different parameters like magnetic field ($M$), expansion ratio ($\alpha$), Reynolds number (Re), nanoparticle concentration ($\varphi$) and Eckert number (Ec) on $F$, $F'$ and $\theta$. Figure 2 shows the influence of Hartmann number on stream function. The results illustrate that augmenting the value of the Hartmann number (magnetic field parameter), the stream function boosts. It is due to the resistance generated by magnetic field lines which affects the trajectory of the particles. The same effects of expansion ratio are elaborated in Fig. 3 on stream function. Figure 4 shows the increasing behavior of stream function by increasing the value of Reynolds number. Inertial component of force dominants when compared to viscous components for the large values of “Re”. The performance of nanoparticle concentration on stream function is displayed in Fig. 5. It is observed that the stream function rises with the rise of nanoparticle concentration. It seems that there is slight difference in the trajectory of particles which is ignorable. Figure 6 shows the influence of three different kinds of nano-size particles like copper, silver and aluminum on stream function with 5% of concentration. It is observed that the stream function is greater for silver particles as compared to copper and aluminum. The velocity distribution of the nanofluid according to magnetic filed parameter is depicted in Fig. 7. The velocity distribution of nanofluid is going to be reduced with the higher values of magnetic field. It is because of the magnetic field applied on the system which produced a resistive force known as “Lorentz force,” which opposes flow of particles. Figures 8 and 9 represent the impact of “expansion ratio” and “Reynolds number” on velocity profile, respectively. Increasing the values of expansion ratio, the fluid velocity and the max value of the flow speed tilt a bit toward the lower plate. The consequence of variation in the Reynolds number on velocity profiles is similar to expansion ratio except for maximum values of velocity which has no change with an increase of Reynolds number. In Fig. 10, the influence of three different kinds of nano-size particles like copper, silver and alumina on velocity profile with the variation in $\eta$ is plotted. The graph illustrates that silver particle gives maximum velocity for $\eta < 0.5$ and a minimum velocity for $\eta > 0.5$ followed by copper and alumina. Impact of copper nanoparticles concentration $\varphi$ for velocity is exposed in Fig. 11. It can noticed from figure, velocity inside the walls is decreasing with comparison to the pure fluid ($\varphi$ = 0%). The density of the carrier fluid is enhanced when nanoparticles are substituted in the base fluid. Therefore, nanofluid turns into denser, so this change slows down the motion of base fluid. The temperature distribution is maximum for hydromagnetic flow with comparison to the hydrodynamic flow case. For large values of magnetic field, Lorentz force is more powerful. This powerful force gives rise to an enhancement in temperature distribution as exposed in Fig. 12. The impact of magnetic field and expansion ratio w.r.t Reynolds number on Nusselt number is presented in Figs. 13 and 14, respectively.

Fig. 2

Impact of magnetic field ($M$) on stream function $\left( F \right)$ when $\alpha = 1,{\text{Re}} = 5$ and ${\text{Br}} = 0.1$

Fig. 3

Effect of expansion ratio $\left( \alpha \right)$ on stream function $\left( F \right)$ for Cu–water nanofluid when ${\text{Re}} = 5$ and $\varphi = 0.05$

Fig. 4

Effect of Reynolds number on stream function for Cu–water nanofluid $\varphi = 0.05$

Fig. 5

Effect of ($\varphi$) on stream function $\left( F \right)$ for Cu–water when $\alpha = 1,{\text{Re}} = 5$ and $M = 1$

Fig. 6

Nanoparticles affect on stream function $\left( F \right)$ when $\varphi = 0.05$ and when $\alpha = 1,{\text{Re}} = 5$ and $M = 1$

Fig. 7

Impact of magnetic field ($M$) on velocity $\left( {F^{\prime}} \right)$ when ${\text{Ec}} = {\text{Re}} = \alpha = 1$

Fig. 8

Expansion ratio $\left( \alpha \right)$ effect on velocity $\left( {F^{\prime}} \right)$, for Cu–water nanofluid when ${\text{Re}} = 5$ and $\varphi = 0.05$

Fig. 9

Effect of Reynolds number $\left( {{\text{Re}} } \right)$ on velocity $\left( {F^{\prime}} \right)$, for Cu–water nanofluid when $\alpha = 5$ and $\varphi = 0.05$

Fig. 10

Nanoparticles affect on velocity profile when $\varphi = 0.05$

Fig. 11

Effect of $\varphi$ on velocity profile for Cu–water nanofluid, when ${\text{Re}} = 1$ and $\alpha = 1.$

Fig. 12

Impact of magnetic field ($M$) on temperature $\left( \theta \right)$ when ${\text{Ec}} = \alpha = {\text{Re}} = 1$ and ${\text{Br}} = 0.1$

Fig. 13

Impact of magnetic field ($M$) on the Nusselt number (Nu): a upper plate and b lower plate when $\alpha = {\text{Br}} = 1$ and ${\text{Ec}} = 0.1$

Fig. 14

Effect of expansion ratio ($\alpha$) on the Nusselt number (Nu): a upper plate and b lower plate when ${\text{Br}} = 1$ and ${\text{Ec}} = 1$

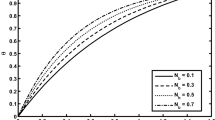
The influences of emerging parameters like magnetic field, expansion ratio, Reynolds number, nanoparticle concentration and Eckert number, on the loss of energy, i.e., generation of entropy (Ne) and an important indicator in terms of the Bejan number (Be), are elaborated through graphs in Figs. 15–19. In Fig. 15, the result of the variation in magnetic field (Hartmann number) on energy loss is shown. Loss of energy rises when the Lorentz or magnetic drag force interacted with the flowing nanofluid in the system. It is observed that the impact of the Hartmann Number $M$ on Ne is at its peak at left walls and gradually reduced through the interior of the channel. Minimum of entropy is observed in the interior region of the channel. It is also noticed that magnetic field makes the large origination of entropy in the system. In Fig. 16, consider the impact of group parameter ${\text{Br}}/\Omega$ on energy loss by virtue of entropy generation.

Fig. 15

Impact of magnetic field ($M$) on (Ne) when $\alpha = 0.5,{\text{Ec}} = 0.01,{{\text{Re}}} = 5$ and ${\text{Br}}/\Omega = 0.1$

Fig. 16

Impact of ${\text{Br}}/\Omega$ on Ne when $\alpha = 0.5,M = 1,{\text{Re}} = 5$ and ${\text{Ec}} = 0.01$

The ratio between the Brinkman number Br and dimensionless temperature difference $\Omega$ constitutes the group parameter ${\text{Br}}/\Omega$. The enhancement of group parameter reflects the enrichment of body force in the flow system, and in respond to this a significant rise in generation of entropy is observed, especially at the heated wall when compared to cooler wall. The Bejan number Be reaches max value but less than 0.5 near the middle of channel as a result of enhancement in heat transfer irreversibility with the smaller values of group parameter, although decline toward middle and left wall of channel. This entropy rise appears due to fluid heat transfer in a certain region of the flow geometry is shown in Fig. 17. Figure 18 shows that increasing the value of Expansion ratio, Bejan number decreased on the boundaries but increased inside the channel. The impression of magnetic field parameter on the Bejan number is illustrated in Fig. 19. The Bejan number is decreases with the increase in magnetic parameter, and this energy loss means the Lorentz or drag force is established among the fluid and magnetic field.

Fig. 17

Impact of (${\text{Br}}/\Omega$) on Bejan number (Be) when $\alpha = 0.5,M = 1,{\text{Re}} = 5$ and ${\text{Ec}} = 0.01$

Fig. 18

Impact of expansion ratio $\left( \alpha \right)$ on Bejan number (Be) when ${\text{Ec}} = 0.01,M = 1,{\text{Re}} = 5$ and ${\text{Br}}/\Omega = 0.1$

Fig. 19

Magnetic field ($M$) effect on Bejan number (Be) when $\alpha = 0.5,{\text{Ec}} = 0.01,{\text{Re}} = 5$ and ${\text{Br}}/\Omega = 0.1$

Figure 20 portrays the $h$-curves at thirtieth-order approximations for velocity and temperature, to estimate the suitable interval of convergence that visibly predicts admissible ranges for $h_{1}$ and $h_{2}$ to lie between − 1.3 to 0.3 and − 1.1 to 0.1. Eventually, Figs. 21 and 22 bear witness that the best optimum values of the $h$-curves for velocity and temperature, within admissible ranges, are $h_{1} = - 0.95$ and $h_{2} = - 0.85$, respectively. The residual errors for the convergence of analytical solutions are further elaborated in Table 3.

Fig. 20

$h$-curves

Fig. 21

Residual error for velocity profile

Fig. 22

Residual error for temperature profile

Table 3 Residual error estimation when $\alpha = 3$, ${\text{Re}} = 5$, $M = 4$ and ${\text{Br}} = 0.1$

Conclusions

In the current study, heat transfer and nanofluid flow between the two plates (which does not intersect each other, i.e., parallel plates) are investigated with respect to the ordinary movement of the upper plate. Using similarity transformation, partial differential equations are transformed into ordinary differential equations. The resulting system of ordinary differential equations is solved analytically by the homotopy analysis method, and effects of flow parameters like volume fractions of nanoparticles, magnetic field, Reynolds number and expansion ratio are discussed through graphically and in the form of tables. The results illustrate that the Nusselt number is a growing function of (Re) and volume fraction of nanoparticles. The major conclusion of the problem can be obtained as below:

• It is noticed that the nanofluid velocity decelerates by enhancing modified magnetic parameter and similar observations are for nanoparticles volume fraction, while enhancing the magnetic parameter temperature accelerates.

• The magnetic and Reynolds number are enhanced at upper plate ($\eta$ = 1) when Nusselt number rises, whereas reverse effect on Nusselt number at lower plate ($\eta$ = − 1).

• For higher values of particle volume fraction, fluid velocity drops and velocity achieve its maximum in retardation when magnetic field is vertically applied on flow direction.

• Energy loss with respect to entropy generation has heavy effect on the left side of the channel, and also the group parameter inside the channel minimum energy loss is observed.

• By neglecting the magnetic field, velocity gained higher value.