Darcy–Forchheimer flow of carbon nanotubes due to a convectively heated rotating disk with homogeneous–heterogeneous reactions

Abstract

Here, Darcy–Forchheimer flow of dissipating SWCNT and MWCNT nanofluids induced by rotation of disk with homogeneous–heterogeneous reactions and convective boundary condition is examined. Xue model of nanofluid is implemented in mathematical modeling. The resulting problems are computed for convergent optimal series solutions. Graphical results have been presented for physical quantities. Our findings indicate that skin friction coefficients and local Nusselt number are enhanced for larger values of nanoparticle volume fraction.

Introduction

The continuing interest of researchers in fluid flow by rotation of disk is because of its widespread geophysical and engineering applications such as centrifugal machinery, crystal growth process, pumping of metals at high melting point, thermal power generating systems, air cleaning machines, spin coating, and turbo machinery. The flow generated by the rotation of disk is interpreted by Von Karman [1]. Combined heat and mass transfer effects in flow induced by rotation of rough porous disk are analyzed by Turkyilmazoglu and Senel [2]. Rashidi et al. [3] scrutinized entropy generation due to slip flow of viscous liquid induced by a rotating porous disk with MHD. Nanofluid flow by rotation of disk is scrutinized by Turkyilmazoglu [4]. Hatami et al. [5] reported asymmetric laminar flow and heat transfer of viscous nanofluid between contraction and rotation of disks. They employed least square approach for solution development. Mustafa et al. [6] investigated nanofluid flow due to a stretching disk. It has been explored that uniform stretching of disk plays a substantial part in reduction in boundary layer thickness. Sheikholeslami et al. [7] discussed the numerical solution for the nanofluid deposition on an inclined rotating disk. Khan et al. [8] presented a numerical study for nanofluid flow caused by the rotation of disk employing Buongiorno’s model. Partial slip flow of water-based nanofluids near a convectively heated stretchable rotating disk with MHD is elaborated by Mustafa and Khan [9]. Recently, Hayat et al. [10] scrutinized partial slip effect in MHD flow of viscous nanofluid by rotation of disk.

Carbon nanotube is a nano-sized cylinder of carbon atom with nanometer in diameter and several millimeters in length. Applications of carbon nanotubes CNTs in electrical and electrical applications include sensors, conductors, energy conversion devices, displays, photovoltaics, field-effect transistors, field emission display, supercapacitors, semiconductor devices, smart textiles, and several others. Enhancement in effective thermal conductivity of oil-based nanotube suspension is studied by Choi et al. [11]. Highest thermal conductivity enhancement is observed for nanotubes in comparison with other nanostructured materials dispersed in fluids. Ramasubramaniam et al. [12] illustrated electrical applications of homogeneous carbon nanotube/polymer composite. A model which is valid for transport properties of carbon nanotubes-based composites is provided by Xue [13]. Heat transfer behavior by considering aqueous suspensions of multi-wall carbon nanotube flowing through a horizontal tube is explained by Ding et al. [14]. Numerical solution of heat transfer enhancement of multi-wall carbon nanotube is discussed by Kamali and Binesh [15]. Thermal transfer of carbon nanotubes in horizontal circular tube is investigated by Wang et al. [16]. The turbulent forced convection heat transfer of a functionalized multi-wall carbon nanotubes over a forward facing step is given by Safaei et al. [17]. Hayat et al. [18] analyzed stagnation point flow of water-based carbon nanotubes toward an impermeable stretching cylinder in the presence of homogeneous–heterogeneous reactions. Ellahi et al. [19] interpreted natural convective MHD flow of carbon nanotube along vertical cone. Karimipour et al. [20] utilized uniform heat flux for magnetic field and slip effects in laminar forced convection of water-based FMWNT carbon nanotubes in microchannels. Flow of nanofluids with different base fluids by an impermeable nonlinear stretchable surface with homogeneous–heterogeneous reactions and variable surface thickness is scrutinized by Hayat et al. [21]. Imtiaz et al. [22] explained thermal radiation effects in convective flow of water-based carbon nanotubes between stretchable rotating disks. Kandasamy et al. [23] elaborated combined effects of variable stream conditions and thermal radiation in magnetohydrodynamic unsteady flow of nanofluid over a porous wedge. Khan et al. [24] examined three-dimensional squeezing flow of nanofluid in a channel. Thermal performance of dissipating SWCNTs and MWCNTs between two concentric cylinders is described by Haq et al. [25]. Hayat et al. [26] investigated flow of dissipating SWCNTs and MWCNTs with porous space governed by Darcy–Forchheimer relation by rotating disk. Further recent investigations on nanofluids can be quoted through the studies [27,28,29,30,31,32,33,34,35,36,37,38,39,40].

Study and modeling of nonlinear flows through porous space is prominent area of research due to its enormous range of implications in geophysical, environmental, and industrial problems such as solar power, utilization of geothermal energy, chemical catalytic reactors, dryness of a porous solid, and the design of nuclear reactors. In 1856, Darcy presented a law which states that volumetric flux of fluid through medium is linearly proportional to pressure gradient. Inertia and boundary effects are neglected in classical Darcy’s law. As the velocity increases, the flow becomes nonlinear and thus we cannot neglect porous inertia effects. Thus, Forchheimer [41] accounted such affects by considering a quadratic term in momentum equation. Muskat [42] demonstrated this law is valid for high Reynolds number. Seddeek [43] investigated mixed convection flow about an isothermal vertical flat plate embedded in fluid-saturated porous space. Jha and Kaurangini [44] provided approximate analytical solutions for flow in parallel plates channel with porous space governed by Brinkman–Forchheimer-extended Darcy relation. Some recent researches on Darcy–Forchheimer flow can be seen in the investigations [45,46,47,48,49,50,51,52].

Several chemically reacting structures involve homogeneous–heterogeneous reactions such as catalysis, combustion, hydrometallurgical devices, biochemical systems, production of ceramics, and distillation processes. At different rates, homogeneous and heterogeneous reactions have a complex correlation. Chemical reactions are utilized in hydrometallurgical industry, hardware configuration, crops damaging through freezing, mist development and scattering, orchards of fruit trees, and several others. Merkin [53] interpret effects of homogeneous–heterogeneous reactions in boundary layer flow of viscous fluid over a flat surface. Further advancements about homogeneous–heterogeneous reactions are seen in studies [54,55,56,57,58,59,60,61].

Main intention of current investigation is to interpret homogeneous–heterogeneous reactions in flow of SWCNTs and MWCNTs with porous space governed by Darcy–Forchheimer relation. Flow is induced by a convectively heated rotating disk using Xue [13] model. Optimal homotopy analysis method (OHAM) [62,63,64,65,66,67,68,69,70] is utilized for convergent series solutions. Effects of several influential parameters on physical quantities of interest are analyzed.

Model development

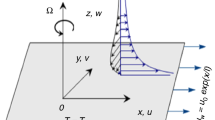
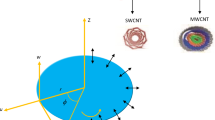
Convective flow of carbon nanotubes in porous space by rotation of disk is in the presence of homogeneous–heterogeneous reactions considered. It is assumed that flow is steady, incompressible, and axially symmetric and is placed at $z = 0.$ Here, velocity components in directions of increasing $(r,\,\varphi ,\,z)$ are $(u,\,v,\,w)$ (see Fig. 1). Surface is convectively heated featured by coefficient of heat transfer $h_{\text{f}}$ and hot fluid temperature $T_{\text{f}}$. For cubic catalysis, homogeneous reaction is [58]:

$$ A + 2B \to 3B,\,{\text{ rate}} = k_{\text{c}} ab^{2} . $$

(1)

Heterogeneous reaction at catalyst surface is

$$ A \to B,\,{\text{ rate}} = k_{\text{s}} a, $$

(2)

in which chemical species $A$ and $B$ have rate constants $k_{\text{c}}$ and $k_{\text{s}}$ with concentrations $a$ and $b$. Resulting expressions for 3D flow of carbon nanotubes in the absence of thermal radiation are [26, 58]:

$$ \frac{\partial u}{\partial r} + \frac{u}{r} + \frac{\partial w}{\partial z} = 0, $$

(3)

$$ u\frac{\partial u}{\partial r} - \frac{{v^{2} }}{r} + w\frac{\partial u}{\partial z} = \nu_{\text{nf}} \left( {\frac{{\partial^{2} u}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial u}{\partial r} - \frac{u}{{r^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) - \frac{{\nu_{\text{nf}} }}{{K^{ * } }}u - F^{ * } u^{2} , $$

(4)

$$ u\frac{\partial v}{\partial r} + \frac{uv}{r} + w\frac{\partial v}{\partial z} = \nu_{\text{nf}} \left( {\frac{{\partial^{2} v}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial v}{\partial r} - \frac{v}{{r^{2} }} + \frac{{\partial^{2} v}}{{\partial z^{2} }}} \right) - \frac{{\nu_{\text{nf}} }}{{K^{ * } }}v - F^{ * } v^{2} , $$

(5)

$$ u\frac{\partial w}{\partial r} + w\frac{\partial w}{\partial z} = \nu_{\text{nf}} \left( {\frac{{\partial^{2} w}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial w}{\partial r} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) - \frac{{\nu_{\text{nf}} }}{{K^{ * } }}w - F^{ * } w^{2} , $$

(6)

$$ u\frac{\partial T}{\partial r} + w\frac{\partial T}{\partial z} = \alpha_{\text{nf}} \left( {\frac{{\partial^{2} T}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial T}{\partial r} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right), $$

(7)

$$ u\frac{\partial a}{\partial r} + w\frac{\partial a}{\partial z} = D_{\text{A}} \left( {\frac{{\partial^{2} a}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial a}{\partial r} + \frac{{\partial^{2} a}}{{\partial z^{2} }}} \right) - k_{\text{c}} ab^{2} , $$

(8)

$$ u\frac{\partial b}{\partial r} + w\frac{\partial b}{\partial z} = D_{\text{B}} \left( {\frac{{\partial^{2} b}}{{\partial r^{2} }} + \frac{1}{r}\frac{\partial b}{\partial r} + \frac{{\partial^{2} b}}{{\partial z^{2} }}} \right) + k_{\text{c}} ab^{2} , $$

(9)

$$ u = 0,\quad v = r\varOmega ,\quad w = 0,\quad - k_{\text{nf}} \frac{\partial T}{\partial z} = h_{\text{f}} \left( {T_{\text{f}} - T} \right),\quad D_{\text{A}} \frac{\partial a}{\partial z} = k_{\text{s}} a,\quad D_{\text{B}} \frac{\partial b}{\partial z} = - k_{\text{s}} a\;{\text{at}}\;z = 0, $$

(10)

$$ u \to 0,\quad v \to 0,\quad T \to T_{\infty } ,\quad a \to a_{0} ,\quad b \to 0\;{\text{as}}\;z \to \infty . $$

(11)

Here, $K^{ * }$ stands for permeability of porous medium, $F^{ * } = \tfrac{{C_{\text{b}} }}{{rK^{{ *^{1/2} }} }}$ and $C_{\text{b}}$ for non-uniform inertia coefficient of porous space and drag coefficient, $T$ for the temperature, $\alpha_{\text{nf}}$ for the nanofluid thermal diffusivity and $T_{\infty }$ for the ambient fluid temperature. Analytical model recommended by Xue [13] satisfies:

$$ \begin{aligned} & \mu_{\text{nf}} = \tfrac{{\mu_{\text{f}} }}{{\left( {1 - \phi } \right)^{2.5} }},\quad \nu_{\text{nf}} = \tfrac{{\mu_{\text{nf}} }}{{\rho_{\text{nf}} }},\quad \alpha_{\text{nf}} = \tfrac{{k_{\text{nf}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{nf}} }},\quad \rho_{\text{nf}} = \rho_{\text{f}} \left( {1 - \phi } \right) + \rho_{\text{CNT}} \phi , \\ & \left( {\rho c_{\text{p}} } \right)_{\text{nf}} = \left( {\rho c_{\text{p}} } \right)_{\text{f}} \left( {1 - \phi } \right) + \left( {\rho c_{\text{p}} } \right)_{\text{CNT}} \phi ,\quad \tfrac{{k_{\text{nf}} }}{{k_{\text{f}} }} = \tfrac{{\left( {1 - \phi } \right) + 2\phi \tfrac{{k_{\text{CNT}} }}{{k_{\text{CNT}} - k_{\text{f}} }}\ln \tfrac{{k_{\text{CNT}} + k_{\text{f}} }}{{2k_{\text{f}} }}}}{{\left( {1 - \phi } \right) + 2\phi \tfrac{{k_{\text{f}} }}{{k_{\text{CNT}} - k_{\text{f}} }}\ln \tfrac{{k_{\text{CNT}} + k_{\text{f}} }}{{2k_{\text{f}} }}}}, \\ \end{aligned} $$

(12)

where $\mu_{\text{nf}}$ stands for nanofluid effective dynamic viscosity, $\phi$ for solid volume fraction of nanoparticles, $\mu_{\text{f}}$ for base fluids dynamic viscosity, $\rho_{\text{nf}}$ for density of nanofluid, $\rho_{\text{f}}$ for base fluid density, $\left( {\rho c_{\text{p}} } \right)_{\text{nf}}$ for nanofluid effective heat capacity, $\rho_{\text{CNT}}$ for density of carbon nanotubes, $k_{\text{CNT}}$ for thermal conductivity of CNTs and $k_{\text{f}}$ for base fluid thermal conductivity. The thermophysical characteristics of water and CNTs are demonstrated in Table 1.

Fig. 1

Flow configuration

Table 1 Thermophysical characteristics of water and CNTs

Considering

$$ \begin{aligned} & u = r\varOmega F^{\prime}(\zeta ),\quad v = r\varOmega G(\zeta ),\quad w = - \sqrt {2\varOmega \nu_{\text{f}} } F\left( \zeta \right), \\ & \varTheta (\zeta ) = \tfrac{{T - T_{\infty } }}{{T_{\text{f}} - T_{\infty } }},\quad a = a_{0} \varPhi (\zeta ),\quad b = a_{0} H(\zeta ),\quad \zeta = \sqrt {\tfrac{2\varOmega }{{\nu_{\text{f}} }}} z. \\ \end{aligned} $$

(13)

Expression (3) is trivially justified and Eqs. (4)–(12) yield

$$ \frac{1}{{\left( {1 - \phi } \right)^{2.5} \left( {1 - \phi + \tfrac{{\rho_{\text{CNT}} }}{{\rho_{\text{f}} }}\phi } \right)}}\left( {2F^{\prime\prime\prime} - \lambda F^{\prime}} \right) + 2FF^{\prime\prime} - F^{\prime 2} + G^{2} - F_{\text{r}} f^{\prime 2} = 0, $$

(14)

$$ \frac{1}{{\left( {1 - \phi } \right)^{2.5} \left( {1 - \phi + \tfrac{{\rho_{\text{CNT}} }}{{\rho_{\text{f}} }}\phi } \right)}}\left( {2G^{\prime\prime} - \lambda G} \right) + 2FG^{\prime} - 2F^{\prime}G - F_{\text{r}} G^{2} = 0,\, $$

(15)

$$ \frac{{k_{\text{nf}} }}{{k_{\text{f}} \left( {1 - \phi + \tfrac{{\left( {\rho c_{\text{p}} } \right)_{\text{CNT}} }}{{\left( {\rho c_{\text{p}} } \right)_{\text{f}} }}\phi } \right)}}\varTheta^{\prime\prime} + \mathop {Pr}\limits F\varTheta^{\prime} = 0, $$

(16)

$$ \frac{1}{Sc}\varPhi^{\prime\prime} + F\varPhi^{\prime} - K\varPhi H^{2} = 0, $$

(17)

$$ \frac{\delta }{Sc}H^{\prime\prime} + FH^{\prime} + K\varPhi H^{2} = 0, $$

(18)

$$ F = 0,\quad F^{\prime} = 0,\quad G = 1,\quad \varTheta^{\prime} = - \frac{{k_{\text{f}} }}{{k_{\text{nf}} }}\gamma \left( {1 - \varTheta } \right),\quad \varPhi^{{^{\prime } }} = K_{\text{s}} \varPhi ,\quad \delta H^{\prime} = - K_{\text{s}} \varPhi \;{\text{at}}\;\zeta = 0, $$

(19)

$$ F^{\prime} \to 0,\quad G \to 0,\quad \varTheta \to 0,\quad \varPhi \to 1,\quad H \to 0\;{\text{as}}\;\zeta \to \infty . $$

(20)

In above expressions, $F_{\text{r}}$ stands for Forchheimer number, $\lambda$ for porosity parameter, $\gamma$ for Biot number, $Sc$ for Schmidt number, $Pr$ for Prandtl number, $K_{\text{s}}$ for strength of heterogeneous reaction, $\delta$ for ratio of diffusion coefficients and $K$ for strength of homogeneous reaction which are defined as:

$$ \left. {\begin{array}{*{20}l} {\lambda = \tfrac{{\nu_{\text{f}} }}{{\varOmega K^{ * } }},\quad F_{\text{r}} = \tfrac{{C_{\text{b}} }}{{K^{{ *^{1/2} }} }},\quad \gamma = \tfrac{{h_{\text{f}} }}{{k_{\text{f}} }}\sqrt {\tfrac{{\nu_{\text{f}} }}{2\varOmega }} ,\quad Pr = \tfrac{{\nu_{\text{f}} }}{{\alpha_{\text{f}} }},} \hfill \\ {Sc = \tfrac{{\nu_{\text{f}} }}{{D_{\text{A}} }},\quad K_{\text{s}} = \tfrac{{k_{\text{s}} }}{{D_{\text{A}} }}\sqrt {\tfrac{{\nu_{\text{f}} }}{2\varOmega }} ,\quad K = \tfrac{{k_{\text{c}} a_{0}^{2} }}{2\varOmega },\quad \delta = \tfrac{{D_{\text{B}} }}{{D_{\text{A}} }}.} \hfill \\ \end{array} } \right\} $$

(21)

For $D_{\text{A}} = D_{\text{B}}$, we have $\delta = 1$ and thus

$$ \varPhi \left( \zeta \right) + H\left( \zeta \right) = 1. $$

(22)

Now Eqs. (17) and (18) yield

$$ \frac{1}{Sc}\varPhi^{\prime\prime} + F\varPhi^{\prime} - K\varPhi \left( {1 - \varPhi } \right)^{2} = 0. $$

(23)

Subjected boundary conditions are

$$ \varPhi^{\prime}\left( 0 \right) = K_{s} \varPhi \left( 0 \right) ,\quad \varPhi \left( \infty \right) \to 1. $$

(24)

Coefficients of skin friction and local Nusselt number are

$$ \left. {\begin{array}{*{20}c} {\left( {Re_{\text{r}} } \right)^{1/2} C_{\text{F}} = \tfrac{1}{{\left( {1 - \phi } \right)^{5/2} }}F^{\prime\prime}\left( 0 \right),} \\ {\left( {Re_{\text{r}} } \right)^{1/2} C_{\text{G}} = \tfrac{1}{{\left( {1 - \phi } \right)^{5/2} }}G^{\prime}\left( 0 \right),} \\ {\left( {Re_{\text{r}} } \right)^{ - 1/2} Nu = - \tfrac{{k_{\text{nf}} }}{{k_{\text{f}} }}\varTheta^{\prime}\left( 0 \right),} \\ \end{array} } \right\}\, $$

(25)

where $Re_{\text{r}} = \tfrac{{\left( {\varOmega r} \right)\,r}}{{2\nu_{\text{f}} }}$ stands for local rotational Reynolds number.

Solutions by OHAM

It has been observed that Eqs. (14)–(16) and (23) with boundary conditions (19), (20) and (24) are four nonlinear ordinary differential equations. In order to compute the solutions, we have employed optimal homotopy analysis method (OHAM). Auxiliary linear operators and initial guesses have been selected in the forms:

$$ F_{0} (\zeta ) = 0,\quad G_{0} (\zeta ) = e^{ - \upzeta } ,\quad \varTheta_{0} (\zeta ) = \frac{\gamma }{{\gamma + \tfrac{{k_{\text{nf}} }}{{k_{\text{f}} }}}}e^{ - \upzeta } ,\quad \varPhi_{0} (\zeta ) = 1 - \frac{1}{2}e^{{ - \rm{K}_{\text{s}} \upzeta }} , $$

(26)

$$ {\varvec{\tt{L}}}_{\text{F}} = \frac{{{\text{d}}^{3} F}}{{{\text{d}}\zeta^{3} }} - \frac{{{\text{d}}F}}{{{\text{d}}\zeta }},\quad {\varvec{\tt{L}}}_{\text{G}} = \frac{{{\text{d}}^{2} G}}{{{\text{d}}\zeta^{2} }} - G,\quad {\varvec{\tt{L}}}_{\varTheta } = \frac{{{\text{d}}^{2} \varTheta }}{{{\text{d}}\zeta^{2} }} - \varTheta ,\quad {\varvec{\tt{L}}}_{\varPhi } = \frac{{{\text{d}}^{2} \varPhi }}{{{\text{d}}\zeta^{2} }} - \varPhi . $$

(27)

The above linear operators obey

$$ \begin{array}{*{20}l} {{\varvec{\tt{L}}}_{\text{F}} \left[ {H_{1}^{ * } + H_{2}^{ * } e^{\zeta } + H_{3}^{ * } e^{ - \zeta } } \right] = 0,\quad {\varvec{\tt{L}}}_{\text{G}} \left[ {H_{4}^{ * } e^{\zeta } + H_{5}^{ * } e^{ - \zeta } } \right] = 0,} \hfill \\ {{\varvec{\tt{L}}}_{\varTheta } \left[ {H_{6}^{ * } e^{\zeta } + H_{7}^{ * } e^{ - \zeta } } \right] = 0,\quad {\varvec{\tt{L}}}_{\varPhi } \left[ {H_{8}^{ * } e^{\zeta } + H_{9}^{ * } e^{ - \zeta } } \right] = 0,} \hfill \\ \end{array} $$

(28)

in which $H_{\text{j}}^{ * }$ (j = 1–9) depicts the arbitrary constants. In view of above linear operators, we can easily develop zeroth- and mth-order deformation problem by BVPH2.0 of Mathematica.

Optimal convergence control parameters

We have solved momentum, energy and concentration equations through BVPh2.0. These expressions contain $\hbar_{\text{F}} ,$$\hbar_{\text{G}} ,$$\hbar_{\varTheta }$ and $\hbar_{\varPhi }$ which play significant role in homotopic solutions. To obtain optimal values of $\hbar_{\text{F}} ,$$\hbar_{\text{G}} ,$$\hbar_{\varTheta }$ and $\hbar_{\varPhi }$, the optimal analysis through minimization process is employed for average squared residual errors as follows:

$$ \varepsilon_{\text{m}}^{F} = \frac{1}{k + 1}\mathop \sum \limits_{{{\text{j}} = 0}}^{k} \left[ {{\varvec{\tt{N}}}_{\text{F}} \left( {\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{F}\left( \zeta \right),\,\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{G}\left( \zeta \right)} \right)_{{\upzeta = {\text{j}}\updelta \upzeta }} } \right]^{2} , $$

(29)

$$ \varepsilon_{\text{m}}^{G} = \frac{1}{k + 1}\mathop \sum \limits_{{{\text{j}} = 0}}^{k} \left[ {{\varvec{\tt{N}}}_{\text{G}} \left( {\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{F}\left( \zeta \right),\,\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{G}\left( \zeta \right)} \right)_{{\upzeta = {\text{j}}\updelta \upzeta }} } \right]^{2} , $$

(30)

$$ \varepsilon_{\text{m}}^{\varTheta } = \frac{1}{k + 1}\mathop \sum \limits_{j = 0}^{k} \left[ {{\varvec{\tt{N}}}_{\varTheta } \left( {\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{F}\left( \zeta \right),\,\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{G}\left( \zeta \right),\,\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{\varTheta }\left( \zeta \right)} \right)_{{\upzeta = {\text{j}}\updelta \upzeta }} } \right]^{2} , $$

(31)

$$ \varepsilon_{\text{m}}^{\varPhi } = \frac{1}{k + 1}\mathop \sum \limits_{{{\text{j}} = 0}}^{k} \left[ {{\varvec{\tt{N}}}_{\varPhi } \left( {\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{F}\left( \zeta \right),\,\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{G}\left( \zeta \right),\,\mathop \sum \limits_{{{\text{i}} = 0}}^{m} \hat{\varPhi }\left( \zeta \right)} \right)_{{\upzeta = {\text{j}}\updelta \upzeta }} } \right]^{2} . $$

(32)

Following Liao [62]:

$$ \varepsilon_{\text{m}}^{\rm{T}} = \varepsilon_{\text{m}}^{\rm{F}} + \varepsilon_{\text{m}}^{\rm{G}} + \varepsilon_{\text{m}}^{\Theta } + \varepsilon_{\text{m}}^{\Phi } , $$

(33)

where $\varepsilon_{\text{m}}^{\rm{T}}$ stands for total squared residual error, $\delta \zeta = 0.5$ and $k = 20$. The optimal values of convergence control variables for SWCNTs–water at second order of deformations are $\hbar_{\text{F}} = - 0.666682,$$\hbar_{\text{G}} = - 0.63389,$$\hbar_{\varTheta } = - 0.565967$ and $\hbar_{\varPhi } = - 1.88552$ and total averaged squared residual error is $\varepsilon_{\text{m}}^{\rm{T}} = 0.0247373$, while the optimal values of convergence control variables for MWCNTs–water are $\hbar_{\text{F}} = - 0.609874,$$\hbar_{\text{G}} = - 0.581243,$$\hbar_{\varTheta } = - 0.604961$ and $\hbar_{\varPhi } = - 1.8844$ and total averaged squared residual error is $\varepsilon_{\text{m}}^{\rm{T}} = 0.0296666.$ Total residual error graphs in SWCNTs and MWCNTs cases are plotted in Figs. 2 and 3, respectively. The individual average squared residual errors in SWCNTs and MWCNTs cases are interpreted in Tables 2 and 3. For higher order of approximations, the averaged squared residual errors decrease.

Fig. 2

Plots of total residual error in SWCNTs–water

Fig. 3

Plots of total residual error in MWCNTs–water

Table 2 Individual averaged squared residual errors in view of optimal data of auxiliary parameters in SWCNTs–water case

Table 3 Individual averaged squared residual errors in view of optimal data of auxiliary parameters in MWCNTs–water case

Discussion

This section consists of contribution of various flow variables such as porosity parameter $\lambda ,$ Forchheimer number $F_{\text{r}}$, nanoparticle volume fraction $\phi ,$ Biot number $\gamma ,$ strength of homogeneous reaction $K,$ Schmidt number $Sc$ and strength of heterogeneous reactions $K_{\text{s}}$ on $F^{\prime}\left( \zeta \right)$, $G\left( \zeta \right),$$\varTheta \left( \zeta \right)$ and $\varPhi \left( \zeta \right).$ Figure 4 is plotted to explore the impact of porosity parameter $\lambda$ on $F^{\prime}\left( \zeta \right).$ Higher estimation of porosity parameter causes lower velocity field $F^{\prime}\left( \zeta \right)$ for SWCNTs and MWCNTs cases. Figure 5 displays the variation in velocity $F^{\prime}\left( \zeta \right)$ for various values of Forchheimer number $F_{\text{r}} .$ An increment in Forchheimer number $F_{\text{r}}$ causes lower velocity field $F^{\prime}\left( \zeta \right)$ in SWCNTs and MWCNTs cases. Figure 6 shows that larger nanoparticle volume fraction $\phi$ produces stronger velocity field $F^{\prime}\left( \zeta \right)$ for SWCNTs and MWCNTs cases. Figure 7 scrutinizes that velocity field $G\left( \zeta \right)$ shows decreasing trend via larger porosity parameter $\lambda$ in SWCNTs and MWCNTs cases. Higher Forchheimer number $F_{\text{r}}$ constitutes a decrement in velocity field $G\left( \zeta \right)$ in SWCNTs and MWCNTs cases (see Fig. 8). An increment in $G\left( \zeta \right)$ is occurred for larger $\phi$ for both SWCNTs and MWCNTs cases (see Fig. 9). Figure 10 is sketched to elaborate the influence of porosity parameter $\lambda$ on $\varTheta \left( \zeta \right).$ By an increment in porosity parameter $\lambda ,$ the temperature $\varTheta \left( \zeta \right)$ enhances in SWCNTs and MWCNTs cases. Figure 11 reveals the features of Forchheimer number $F_{\text{r}}$ on $\varTheta \left( \zeta \right).$ Larger Forchheimer number $F_{\text{r}}$ produces higher-temperature field $\varTheta \left( \zeta \right)$ in SWCNTs and MWCNTs cases. Figure 12 shows that by increasing $\phi ,$ stronger $\varTheta \left( \zeta \right)$ is generated in SWCNTs and MWCNTs cases. Figure 13 is drawn to scrutinize that how $\varTheta \left( \zeta \right)$ is affected with variation in Biot number $\gamma .$ By increasing Biot number $\gamma ,$ strong convection produces which causes higher-temperature $\varTheta \left( \zeta \right)$ in SWCNTs and MWCNTs cases. Higher estimation of porosity parameter $\lambda$ leads to weaker concentration field $\varPhi \left( \zeta \right)$ in SWCNTs and MWCNTs cases (see Fig. 14). Figure 15 interprets that $\varPhi \left( \zeta \right)$ and related layer thickness show decreasing trend for increasing $F_{\text{r}}$. Behavior of $\phi$ on concentration field $\varPhi \left( \zeta \right)$ is presented in Fig. 16. Larger $\phi$ corresponds to increasing trend in the concentration field $\varPhi \left( \zeta \right)$ in SWCNTs and MWCNTs cases. Figure 17 presents the variation in $\varPhi \left( \zeta \right)$ for distinct values of $K.$ An increase in $K$ corresponds to lower $\varPhi \left( \zeta \right)$ in SWCNTs and MWCNTs cases. Figure 18 presents the curves of concentration $\varPhi \left( \zeta \right)$ for distinct values of $K_{\text{s}} .$ By enhancing strength of heterogeneous reaction $K_{\text{s}} ,$ diffusion reduces which enhances the concentration $\varPhi \left( \zeta \right)$ in SWCNTs and MWCNTs cases. More concentration $\varPhi \left( \zeta \right)$ is noted for higher Schmidt number $Sc$ (see Fig. 19). Figures 20–23 depict the skin friction coefficients $\left( {1/\left( {1 - \phi } \right)^{5/2} } \right)\,F^{\prime\prime}\left( 0 \right)$ and $\left( {1/\left( {1 - \phi } \right)^{5/2} } \right)\,G^{\prime}\left( 0 \right)$ for various values of $\phi ,$$\lambda$ and $F_{\text{r}} .$ It has been reported that for both SWCNTs and MWCNTs, skin friction coefficients are enhanced for larger values of $\phi .$ Figures 24 and 25 elucidate that local Nusselt number is enhanced for higher $\phi$ in SWCNTs and MWCNTs cases.

Fig. 4

Plots of $F'(\zeta )\;{\text{for}}\; \lambda$

Fig. 5

Plots of $F'(\zeta ) \;{\text{for}}\; F_{\text{r}}$

Fig. 6

Plots of $F'(\zeta ) \;{\text{for}}\;\phi$

Fig. 7

Plots of $G(\zeta ) \;{\text{for}}\;\lambda$

Fig. 8

Plots of $G(\zeta ) \;{\text{for}}\;F_{\text{r}}$

Fig. 9

Plots of $G(\zeta ) \;{\text{for}}\; \phi$

Fig. 10

Plots of $\varTheta (\zeta ) \;{\text{for}}\; \lambda$

Fig. 11

Plots of $\varTheta (\zeta )\;{\text{for}}\; F_{\text{r}}$

Fig. 12

Plots of $\varTheta (\zeta ) \;{\text{for}}\; \phi$

Fig. 13

Plots of $\varTheta (\zeta ) \;{\text{for}}\;\gamma$

Fig. 14

Plots of $\varPhi (\zeta )\;{\text{for}}\;\lambda$

Fig. 15

Plots of $\varPhi (\zeta )\;{\text{for}}\; F_{\text{r}}$

Fig. 16

Plots of $\varPhi (\zeta ) \;{\text{for}}\; \phi$

Fig. 17

Plots of $\varPhi (\zeta ) \;{\text{for}}\;K$

Fig. 18

Plots of $\varPhi (\zeta ) \;{\text{for}}\;K_{\text{s}}$

Fig. 19

Plots of $\varPhi (\zeta ) \;{\text{for}}\; Sc$

Fig. 20

Plots of $(1/\left( {1 - \phi } \right)^{5/2} )F''\left( 0 \right)\;{\text{for}}\;\phi \;{\text{and}}\; \lambda$

Fig. 21

Plots of $(1/\left( {1 - \phi } \right)^{5/2} )F''\left( 0 \right)\;{\text{for}}\; \phi \;{\text{and}}\;F_{\text{r}}$

Fig. 22

Plots of $(1/\left( {1 - \phi } \right)^{5/2} )G'\left( 0 \right) \;{\text{for}}\; \phi \;{\text{and}}\;\lambda$

Fig. 23

Plots of $(1/\left( {1 - \phi } \right)^{5/2} )G'\left( 0 \right)\;{\text{for}}\;\phi \;{\text{and}}\;F_{\text{r}}$

Fig. 24

Plots of $- (k_{\text{nf}} /k_{\text{f}} )\varTheta '\left( 0 \right) \;{\text{for}}\;\phi \;{\text{and}}\;\lambda$

Fig. 25

Plots of $- (k_{\text{nf}} /k_{\text{f}} )\varTheta '\left( 0 \right)\;{\text{for}}\;\phi \;{\text{and}}\;F_{\text{r}}$

Conclusions

Convective flow of water-based carbon nanotubes by rotating disk with Darcy–Forchheimer relation and homogeneous–heterogeneous reactions has been discussed. Main results are summarized as:

• An increase in nanoparticle volume fraction $\phi$ presents higher velocities $F^{\prime}\left( \zeta \right)$ and $G\left( \zeta \right).$

• Both $\varTheta \left( \zeta \right)$ and $\varPhi \left( \zeta \right)$ are increasing functions of nanoparticle volume fraction $\phi .$

• Higher porosity parameter $\lambda$ and Forchheimer number $F_{\text{r}}$ yield stronger temperature $\varTheta \left( \zeta \right)$ field while opposite behavior is observed for concentration $\varPhi \left( \zeta \right).$

• Larger $K_{\text{s}}$ and Schmidt number $Sc$ show stronger concentration field $\varPhi \left( \zeta \right).$

• Enhancement in temperature $\varTheta \left( \zeta \right)$ is anticipated for higher Biot number $\gamma .$

• Concentration $\varPhi \left( \zeta \right)$ is reduced for larger strength of homogeneous reaction $K.$

• Higher estimation of porosity parameter $\lambda$ and Forchheimer number $F_{\text{r}}$ yield higher skin friction coefficients.

• Heat transfer rate is enhanced for increasing values of porosity parameter $\lambda$ and Forchheimer number $F_{\text{r}}$.