Thermal and flow investigation of MHD natural convection in a nanofluid-saturated porous enclosure: an asymptotic analysis

Abstract

In the present investigation, asymptotic solutions are obtained regarding the laminar natural convection of a nanofluid in a porous enclosure subject to internal heating and magnetic field, which appears in a plethora of industrial and bioengineering applications. The complicated nature of the nanofluids along with the computational time needed for the magnetohydrodynamic numerical simulations makes this problem too difficult to face with. Hence, the innovation of this study relies on providing a first-principles approach that includes three kinds of widely utilized nanoparticles (Cu, Al₂O₃ and TiO₂) dispersed in aqueous suspension by incorporating a unified way for describing the nanofluid thermal conductivity and viscosity. In addition, the effect of the magnetic field, internal heating, porous medium permeability as well as nanoparticle size and volume fraction is examined via the derived analytical relationships. In brief, the current study suggests that the increase in the magnetic field intensity and the decrease in the medium permeability tend to suppress the nanofluid flow, thus resulting in deterioration of the heat transfer. This deterioration also occurs when the nanofluid becomes denser and the nanoparticles enlarge. Conversely, increasing the internal heating reinforces the convective currents in favor of cooling process. Finally, the present asymptotic solutions are expected to be very useful in various scientific fields given the rapidly growing interest in nanofluids.

Introduction

Investigating ways for heat transfer enhancement is considered to be crucial for the purpose of improving the existent energy devices and conceiving new innovative concepts. Apart from the adequacy of the engineering process, the appropriate working liquid coolant seems to be of major importance in optimizing the cooling efficiency. Some widely used working liquids are water, engine oil and ethylene glycol. The major drawback of these conventional fluids is their particularly low thermal conductivity in contrast to carbon nanotubes, metals or metal oxides for example.

The suspensions of the above-mentioned materials, in the form of nanoscaled particles within conventional base fluids for enhancing thermal conductivity of the mixture, were an inspiration that triggered a plethora of new research areas with encouraging results. Briefly, nanofluids, as these suspensions are named by Choi in 1995 [1], can be utilized in heat exchangers [2], energy storage systems [3], solar collectors [4] as well as separation of heavy metals from water [5]. Interestingly, the control of thermal conductivity by adding nanoparticles has also been applied in cancer therapy via hyperthermia, which aims to the tumor death via above-normal physiological temperatures [6]. The numerous applications of nanofluids are summarized in recent review studies such as [7, 8].

Out of the proposed engineering techniques for optimizing the heat transfer, the utilization of porous media seems to have attracted noticeable interest. The basic idea is the increase in the contact area between the solid surface and the working liquid. Studying of magnetohydrodynamic (MHD) natural convection in porous media is of great interest, since it can turn out to be the leading mode of heat transfer. Indicative applications include nuclear fusion reactors [9] as well as metallurgy industry, solar systems and geothermal energy extraction [10]. A plethora of industrial applications referring to nanofluid–porous media coupled technique, such as electronic cooling systems, production of oil and heat exchangers, can be found in review papers such as [11, 12]. Overall factors such as permeability of the solid matrix and the effective magnitudes of the nanofluids, namely thermal conductivity, viscosity, heat capacity, volumetric expansion coefficient, density and electrical conductivity of the nanofluid, determine the entire heat transfer and flow [13].

Kasaeian et al. [11] summarized the models for nanofluid flow and heat transfer in porous media regarding channels and enclosures of different geometries and boundary conditions. Focusing on MHD regime, there is a large number of numerical studies, such as [14,15,16]. On the other hand, there are few studies which try to analytically treat the problem of the nanofluid flow and heat transfer, such as [17, 18], mainly due to the complexity of the problem itself as well as the various factors that have to be considered. Numerical studies of the nanofluid MHD natural convection in porous media have demonstrated useful results. Nevertheless, they are restricted by the high computational cost appearing as the magnetic field increases. In particular, the boundary layers, which are formed at the walls, namely Hartmann layers (vertical to the magnetic field) and Roberts layers (parallel to the magnetic field), are narrow enough and should be numerically treated via dense grids [19]. However, when it comes to asymptotic solutions, neglecting the above boundary layers and focusing on the bulk of the enclosure seem to capture the basic trend of the process. As a consequence, practical dimensionless numbers, such as those of Prandtl (Pr), Grashof (Gr), Rayleigh (Ra = Pr·Gr) and Hartmann (Ha), are introduced which control the entire operation.

The current study deals with a shallow rectangular porous enclosure of large aspect ratio (length/height), which is rigid and fully saturated with nanofluid. Moreover, internal heating is implemented along with external constant magnetic field. The flow is kept laminar, mainly due to the relative low Rayleigh numbers being used. Closed-form solutions are derived using the asymptotic expansions method for the temperature and velocity fields regarding the core region. As a means to capture the performance of some commonly used nanoparticles, Cu, Al₂O₃ and TiO₂ nanoparticles are investigated which are assumed to be homogeneously suspended in water.

In particular, this investigation is an extension of the studies of Daniels and Jones [20] (hydrodynamic natural convection), as well as Benos et al. [21] (extension of [20] in MHD regime) and Benos and Sarris [22] (augmentation of [21] to consider also nanofluids), for the case of a porous shallow cavity filled with nanofluid. Finally, the results of the asymptotic analysis may be useful for preliminary design and optimization of the cooling process in porous enclosures in the presence of MHD phenomena. The technique of handling this type of MHD problems by utilizing the asymptotic expansions is detailed in the “Appendix” section.

Mathematical formulation

Flow configuration and boundary conditions

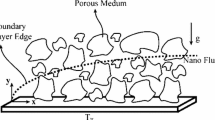
A rectangular porous cavity filled with a nanofluid is considered, as illustrated in Fig. 1. The walls are electrically insulated $\left( {\partial V_{\text{E}} /\partial \vec{n}_{ \bot } = 0} \right).$ V_E represents the electrostatic potential, while $\vec{n}_{ \bot }$ the perpendicular-to-the surface unit vector. The vertical walls are assumed isothermal, whereas the horizontal ones are regarded as adiabatic $\left( {\partial T /\partial \vec{n}_{ \bot } = 0} \right),$ where T stands for the nanofluid temperature. Finally, a volumetric internal heat source, Q, is implemented as well as an externally applied magnetic field, B₀, which, as it was ascertained in [21], can control the flow and, therefore, the heat transfer.

Fig. 1

Sketch of geometry and boundary conditions

The equations which characterize the present problem are continuity [Eq. (1)], momentum [Eqs. (2), (3)] and energy conservation [Eq. (4)]. In particular, in Eq. (2), the term $\sigma_{\text{nf}} B_{0}^{2} u$ represents the Lorentz force, while the porous enclosure is assumed to be isotropic and described similarly to [14, 15]. Besides, momentum is augmented with buoyancy forces by considering the usual Oberbeck–Boussinesq approximation, while in the energy conservation equation, Eq. (4), viscous dissipation and Joule heating have been ignored. Finally, the low magnetic Reynolds approximation is utilized with respect to the equation of magnetic induction [23].

$$\frac{\partial u}{\partial x} + \frac{\partial w}{\partial z} = 0$$

(1)

$$u\frac{\partial u}{\partial x} + w\frac{\partial u}{\partial z} = - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial P}{\partial x} + v_{\text{nf}} \left( {\frac{{\partial^{2} u}}{{\partial x^{2} }} + \frac{{\partial^{2} u}}{{\partial z^{2} }}} \right) + \frac{{\sigma_{\text{nf}} B_{0}^{2} u}}{{\rho_{\text{nf}} }} - \frac{{v_{\text{nf}} }}{K}u$$

(2)

$$u\frac{\partial w}{\partial x} + w\frac{\partial w}{\partial z} = - \frac{1}{{\rho_{\text{nf}} }}\frac{\partial P}{\partial z} + v_{\text{nf}} \left( {\frac{{\partial^{2} w}}{{\partial x^{2} }} + \frac{{\partial^{2} w}}{{\partial z^{2} }}} \right) + \beta_{\text{nf}} g\Delta T - \frac{{v_{\text{nf}} }}{K}w$$

(3)

$$u\frac{\partial T}{\partial x} + w\frac{\partial T}{\partial z} = a_{\text{nf}} \left( {\frac{{\partial^{2} T}}{{\partial x^{2} }} + \frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + \frac{Q}{{\left( {\rho C_{p} } \right)_{\text{nf}} }}$$

(4)

where u and w are the components of the horizontal and vertical velocity, respectively, P stands for the pressure while ΔΤ for the temperature difference. The so-called effective magnitudes of the properties of the nanofluid are the electrical conductivity, σ_nf, the volumetric expansion coefficient, β_nf, the kinematic viscosity, v_nf, the specific heat under constant pressure, C_p,nf, the nanofluid density, ρ_nf, and the thermal diffusivity, $a_{\text{nf}} = k_{\text{nf}} / (\rho C_{\text{p}} )_{\text{nf}} ,$ with k_nf being the nanofluid thermal conductivity. Finally, the boundary conditions pertaining to the temperature, the electrostatic potential and the no-slip condition at the walls are depicted in Fig. 1.

Physical and electrical properties of nanofluid

Similar to the majority of existing studies, the effective physical properties can be approximated as follows:

$$\rho_{\text{nf}} = \left( {1 - \varphi } \right)\rho_{\text{f}} + \varphi \rho_{\text{p}}$$

(5)

$$\left( {\rho C_{\text{p }} } \right)_{\text{nf}} = \left( {1 - \varphi } \right)\left( {\rho C_{\text{p }} } \right)_{\text{f}} + \varphi \left( {\rho C_{\text{p }} } \right)_{\text{p}}$$

(6)

$$\beta_{\text{nf}} = \left( {1 - \varphi } \right)\beta_{\text{f}} + \varphi \beta_{\text{p}}$$

(7)

$$\sigma_{\text{nf}} = \sigma_{\text{f}} \left[ {1 + \frac{{3\varphi \left( {\frac{{\sigma_{\text{p}} }}{{\sigma_{\text{f}} }} - 1} \right)}}{{\left( {\frac{{\sigma_{\text{p}} }}{{\sigma_{\text{f}} }} + 2} \right) - \varphi \left( {\frac{{\sigma_{\text{p}} }}{{\sigma_{\text{f}} }} - 1} \right)}}} \right]$$

(8)

In all the above equations, φ is the nanoparticle volume fraction, while the subscripts f, nf and p correspond to the base fluid, nanofluid and nanoparticle, respectively.

Effective viscosity and thermal conductivity

Nanofluids display various rheological behaviors owing to numerous factors such as nanoparticle size and concentration, temperature, dispersion state, sonication and shear rate [24]. The formation of aggregations is observed to influence nanofluid viscosity to a great extent, especially as the nanofluid becomes denser [25]. As it has been pointed out in [24], the viscosity data from a number of experimental works are scattered and not consistent even when the same kind of nanofluid is investigated. As for the theoretical models, the classical ones, such as the model of Brinkman [26], appear to be valid only for extremely low nanoparticle volume fractions, while it underestimates the value of viscosities for denser nanofluids. Nevertheless, a number of studies, such as [27], use these classical models to elaborate on thermal conductivity advantages, while others such as [22, 28] utilize viscosities which have taken into consideration the Brownian motion of nanoparticles. An elaborated review study concerning theoretical relationships for the dynamic viscosity of a plethora of nanofluids can be found in [24].

In addition to the complicated nature of the rheological properties of the suspensions of nanoparticles in conventional fluids, the mechanism that explains the abnormal enhanced thermal conductivity seems to be even more debatable. In brief, several models have been developed pertaining to the influence of the Brownian motion such as [29, 30]. The major disadvantage of Brownian models is that nanoconvection phenomena appear to be insignificant, as it has been observed in experiments such as [31]. Furthermore, the interfacial nanolayer, which is created around the particle as a result of the adhesion of liquid molecules, appears to be a very crucial factor [32,33,34]. Another important parameter is the shape as well as the size of the nanoparticles, as it has been pointed out by classical models such as the Hamilton–Crosser one [35] and its improvements [36]. Finally, a notable recent review on theoretical models of nanofluid thermal conductivity can be found on [37].

In the present study, with the aim of investigating the outcome of dissimilar nanoparticles, namely Cu, Al₂O₃ and TiO₂, on water-based nanofluid viscosity as realistically as possible, the empirical correlation of Corcione [38] is incorporated:

$$\frac{{\mu_{\text{nf}} }}{{\mu_{\text{f}} }} = \frac{1}{{1 - 34.87\left( {d_{\text{p}} /d_{\text{f}} } \right)^{ - 0.3} \varphi^{1.03} }}$$

(9)

where φ and d_p are the volume fraction and diameter of the nanoparticle, respectively, and d_f stands for the equivalent diameter of water molecule. It should be stressed that, at least for small nanoparticle concentrations and near room temperatures, Corcione found out that the relative viscosity is independent of the kind of the working nanoparticles. The experimental data that were examined in [38] consisted of copper, alumina, silica and titania particles, with a diameter of 25–200 nm, which were suspended in propylene glycol, ethanol, ethylene glycol and water. Furthermore, nanoparticle volume fractions were between 0.0001 and 0.071, while the temperatures were from 293 to 333 K.

On the other hand, an empirical relationship related to the effective thermal conductivity was also used for the present calculations, which was derived from [38]. More specifically, data from a wide range of experiments and nanofluids, consisting of copper, copper oxide, alumina and titania particles and ethylene glycol or water base fluids, were analyzed in [38]. The diameter was in the range of 10–150 nm, the volume fraction of nanoparticles, φ, was between 0.002 and 0.09 and the temperatures were from 294 to 324 K. The best-fit of the above-mentioned experimental data was found to be:

$$\frac{{k_{\text{nf}} }}{{k_{\text{f}} }} = 1 + 4\text{Re}_{\text{p}}^{0.4} {\rm Pr}_{\text{f}}^{0.66} \left( {T /T_{\text{fr}} } \right)^{10} \left( {k_{\text{p}} /k_{\text{f}} } \right)^{0.03} \varphi^{0.66}$$

(10)

where T is the nanofluid temperature, T_fr is the freezing point regarding the base fluid and k_p the thermal conductivity of the nanoparticle. Moreover, the dimensional parameters of Eq. (10) are described by:

$$\text{Re}_{\text{p}} = \frac{{2\rho_{\text{f}} k_{\text{B}} T}}{{\pi \mu_{\text{f}}^{2} d_{\text{p}} }}$$

(11)

$${\rm Pr}_{\text{f}} = \frac{{v_{\text{f}} }}{{a_{\text{f}} }}$$

(12)

In Eq. (11), the parameters that have not been mentioned are the Boltzmann constant, k_B, as well as v_f and α_f, which represent the base fluid kinematic viscosity and its thermal diffusivity, respectively.

The plots of the relative viscosity and thermal conductivity of Cu, Al₂O₃ and TiO₂ nanoparticles suspended in water, as described by Corcione [38], for nanoparticle volume fractions between 0 and 0.06 are presented in Fig. 2a, b, respectively. As it can be observed in both figures, for a reference d_p = 100 nm, the effective magnitudes increase by adding more nanoparticles in the base fluid, as in the majority of the theoretical models existing in the relative literature. On the one hand, the relative viscosity is independent of the nanoparticle selection, as can be observed by Eq. (9). On the other hand, as expected, the maximal values of nanoparticle thermal conductivity, namely that of copper in the present investigation, corresponds to the maximum of the resulting effective thermal conductivities, with Al₂O₃ having lower values but larger than TiO₂, as shown in Fig. 2b. In particular, as it can be observed in Table 1, the values of thermal conductivities regarding Cu, Al₂O₃ and TiO₂ are 401, 40 and 8.95 Wm⁻¹ K⁻¹, respectively. An interesting conclusion concerning the design of nanoparticles for heat exhaust applications is drawn via Fig. 3a, b. More specifically, for a reference volume fraction equal to 0.03, the nanoparticle size seems to influence the relative thermal conductivity, a fact that is going to potentially regulate the resulting flow and heat transfer, as it will be elaborated in the “Results” section. Again, the relative viscosity does not depend on the nanoparticle choice, while both μ_nf/μ_f and k_nf/k_f decrease with increasing nanoparticle size, as it has also been ascertained in studies such as [18, 22] which utilize different theoretical models. In Fig. 3b, the maximal values of thermal conductivity appear again for copper nanofluids with those of Al₂O₃ and TiO₂. Finally, the thermophysical properties of Cu, Al₂O₃ and TiO₂ and water are summarized in Table 1, as it can be provided by the literature [39, 40].

Fig. 2

Effect of the nanoparticle volume fraction, φ, on: a relative dynamic viscosity, μ_nf/μ_f and b relative thermal conductivity, k_nf/k_f, for d_p = 100 nm

Table 1 Thermophysical and electric properties of water, Cu, Al₂O₃ and TiO₂ [39, 40]

Fig. 3

Effect of the nanoparticle diameter, d_p, on: a relative dynamic viscosity, μ_nf/μ_f and b relative thermal conductivity, k_nf/k_f, for nanoparticle volume fraction, φ, equal to 0.03

Analytical solutions with the method of the matched asymptotic expansions

In this section, the analysis of Daniels and Jones [20] as well as Benos et al. [21] and Benos and Sarris [22] are followed. More specifically, the pressure terms from Eqs. (2) and (3) are eliminated, while the use of continuity equation leads to the dimensionless stream function and energy equations, as it is elaborated in the “Appendix” section:

$$\nabla^{4} \varPsi = {\rm Pr}_{\text{nf}}^{ - 1} \left( \varphi \right)\frac{{\partial (\nabla^{2} \varPsi ,\varPsi )}}{\partial (X,Z)} + \left( {{\text{Ha}}_{\text{nf}}^{2} \left( \varphi \right) + {\text{Da}}^{ - 1} } \right)\frac{{\partial^{2} \varPsi }}{{\partial Z^{2} }} + {\text{Ra}}_{\text{nf}} \left( \varphi \right)\frac{\partial \varTheta }{\partial X}$$

(13)

$$\nabla^{2} \varTheta + 1 = \frac{\partial (\varTheta ,\varPsi )}{\partial (X,Z)}$$

(14)

In the above system of equations, $\varPsi = \psi /\alpha_{\text{nf}}$ represents the dimensionless stream function, which can be defined by $u = \partial \psi /\partial Z$ and $w = - \partial \psi /\partial X$. The dimensionless coordinates in the horizontal and the vertical directions are $X = x /h$ and $Z = z /h,$ respectively, with h being the cavity height, while $\varTheta = T /(h^{2} Q /k_{\text{nf}} )$ corresponds to the dimensionless temperature of the nanofluid. Next, similar to [20,21,22] Ψ is converted into ψ, X to x, Z to z and Θ to T in order to simplify the representation of the mathematical problem.

The dimensionless group numbers pertaining to the nanofluid that appears in the governing equations are:

$${\rm Pr}_{nf} \left( \varphi \right) = \frac{{v_{\text{nf}} }}{{a_{\text{nf}} }}$$

(15)

$${\text{Ha}}_{\text{nf}} \left( \varphi \right) = B_{0} h\left( {\sigma_{\text{nf}} /\rho_{\text{nf}} v_{\text{nf}} } \right)^{1/2}$$

(16)

$${\text{Da}} = \frac{K}{{h^{2} }}$$

(17)

$${\text{Ra}}_{\text{nf}} \left( \varphi \right) = \frac{{g\beta_{\text{nf}} Qh^{5} }}{{\left( {\rho C_{\text{p}} } \right)_{\text{nf}} v_{\text{nf}} a_{\text{nf}}^{2} }}$$

(18)

where Pr_nf is the Prandtl number that correlates momentum to thermal diffusivity and Ha_nf is the Hartmann number, which measures the relative strength of electromagnetic to viscous forces. The Darcy number, Da, is a commonly used dimensionless parameter for studying heat transfer through porous media and indicates the relative effect of the permeability of the porous medium, K, over the characteristic length squared.

Finally, Ra_nf is the nanofluid Rayleigh number that is the ratio of buoyancy over viscosity forces multiplied by the ratio of momentum over thermal diffusivities. In general, Rayleigh number is the product between Grashof with Prandtl number and is related to buoyancy-driven flows. Generally, when Rayleigh number lies below a critical value, heat transfer is purely because of conduction. On the other hand, when Rayleigh exceeds that value, heat transfer is gradually enhanced owing to convection prevailing over conduction [41].

It should be mentioned that Pr_nf, Ha_nf and Ra_nf depend on the nanoparticle volume fraction, φ, and also on base fluid and nanoparticle selection, while Da is an intrinsic property of the porous cavity.

The boundary conditions regarding the vertical walls are:

$$\psi = \frac{\partial \psi }{\partial x} = T = 0$$

(19)

while for the horizontal ones:

$$\psi = \frac{\partial \psi }{\partial z} = \frac{\partial T}{\partial z} = 0$$

(20)

In addition to the aforementioned boundary conditions, the symmetries with regard to the stream function and temperature demonstrate that:

$$\psi (x,\,z) = - \psi (L - x,\,z)$$

(21)

$$T(x,\,z) = T(L - x,\,z)$$

(22)

If pure conduction prevails, according to [20], the temperature at z = 0 can be given via:

$$T = \frac{1}{2}x(L - x)$$

(23)

Furthermore, in [20] it was proved that when Rayleigh is of the order of L⁻¹, Eq. (23) is not adequate and should be altered with the intention of incorporating convection phenomena as well. In [20], the scaled Rayleigh number, Rs = Ra·L, was introduced that is of order one as L → ∞.

Similar to [20,21,22], the flow in the core region covers the largest part of the enclosure and the following length scales are introduced:

$$\xi = x /L,z = z$$

(24)

For brevity, the mathematical derivation of the solutions concerning the vertical velocity, stream function and temperature as well as emerging functions such as G, a_m, y_m, y_m,0 are shown in the “Appendix” section.

Finally, the stream function can be derived by:

$$\psi_{0} = - 2\,\,\frac{{a_{\text{m}}^{ - 1/2} \,G}}{{{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} }}\,\sinh \frac{1}{3}y_{\text{m}}$$

(25)

while the vertical velocity via:

$$w_{0} = - \frac{{\partial \psi_{0} }}{\partial \xi } = \frac{{{\text{Rs}}_{\text{nf}} \,G}}{{\left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)\left( {1 + 4\,\sinh^{2} \frac{1}{3}y_{\text{m}} } \right)}}$$

(26)

The temperature in core region can be expressed by:

$$\theta_{0} = a_{\text{m}}^{ - 1} \,{\text{Rs}}_{\text{nf}}^{ - 2} \left( {\cosh \frac{2}{3}y_{\text{m}} - \frac{1}{2}\cosh \frac{4}{3}y_{\text{m}} - \cosh \frac{2}{3}y_{{{\text{m}},0}} + \frac{1}{2}\cosh \frac{4}{3}y_{{{\text{m}},0}} } \right)$$

(27)

In this fashion, it should be mentioned that:

$$\begin{aligned} a_{\text{m}} & = f\left( {{\text{Ha}}_{\text{nf}} ,{\text{Da}}} \right),y_{\text{m}} = f\left( {{\text{Ha}}_{\text{nf}} ,{\text{Rs}}_{\text{nf}} ,{\text{Da}},\xi } \right), \, \\ y_{{{\text{m}},0}} & = f\left( {{\text{Ha}}_{\text{nf}} ,{\text{Rs}}_{\text{nf}} ,{\text{Da}}} \right),G = f\left( {{\text{Ha}}_{\text{nf}} ,{\text{Da}},z} \right) \\ \end{aligned}$$

(28)

Moreover, in the limiting case of ${\text{Da}}^{ - 1} \to 0,$ which stands for very large values of permeability, the asymptotic solutions, namely Eqs. (25)–(27), lead to the MHD results of Benos and Sarris [22]. For both ${\text{Da}}^{ - 1} \to 0$ and $\varphi = 0$, the above-mentioned solutions reduce to the pure fluid MHD results of Benos et al. [21]. Finally, if additionally ${\text{Ha}}_{\text{nf}} \to 0$, the hydrodynamic limit of Daniels and Jones [20] is exactly reestablished, namely:

$$\mathop {\lim }\limits_{{{\text{Ha}}_{\text{nf}} \to 0}} a_{\text{m}} = a_{\text{m,HD}} = \frac{1}{120 ,960}$$

(29)

$$\mathop {\lim }\limits_{{{\text{Ha}}_{\text{nf}} \to 0}} \psi_{0} = - \frac{2}{{\sqrt {a_{\text{m,HD}} } }}\frac{1}{24}\left( {\frac{1}{4} - z^{2} } \right)^{2} \sinh \left( {\frac{1}{3}y_{\text{m,HD}} } \right)$$

(30)

$$\mathop {\lim }\limits_{{{\text{Ha}}_{\text{nf}} \to 0}} w_{\text{an}} = \frac{\text{Rs}}{384}$$

(31)

with a_m,HD, y_m,HD being the limits of the corresponding a_m and y_m, respectively, in the hydrodynamic regime.

Similar to [20,21,22], the analytical solutions for the core region are valid for large aspect ratio enclosures at relatively small Rayleigh numbers along with high Hartmann numbers. To this end, the successful comparison of the asymptotic solutions against the numerical results was proved and analyzed in detail in [21]. Based on [21], the present asymptotic analysis cannot capture the nanofluid downward flow in the vicinity of the vertical cold boundaries and it is accurate only for laminar flows. All in all, small Rayleigh and/or large Hartmann numbers contribute in laminar flow establishment. In addition, small values of Darcy numbers are anticipated to decelerate the nanofluid flow and heat transfer, retain laminar flow and keep it near the conduction regime.

Finally, in order to quantify the heat transfer, the average Nusselt number, Nu_av, is utilized again as in [20,21,22] (convection to conduction heat transfer comparison). Thus, as Daniels and Jones [20] proved,

$${\text{Nu}}_{\text{av}} = \frac{1}{{T\left( {0.5L,0.5} \right)}}\int\limits_{ - 0.5}^{0.5} {\frac{\partial T}{\partial x}} \left( {0,z} \right){\text{d}}z = \frac{1}{{2T\left( {0.5L,0.5} \right)}} \sim \frac{1}{{2L\theta_{0} \left( {0.5} \right)}}.$$

(32)

Results and discussion

In the present problem concerning the flow and heat transfer of the nanofluid, the dimensionless numbers, namely Ha_nf, Rs_nf and Da, determine the entire cooling process. As it was pointed out in previous studies such as [21, 22, 27, 42] when the scaled Rayleigh number, Rs_nf, increases, the heat transfer is enhanced. This is evident via the increase in the vertical velocity, w₀, which, in turn, results in lower values of the temperature field, θ₀, in the core region as well as larger average Nusselt numbers, Nu_av. Contrary to the above trend, an increase in Ha_nf leads to deterioration of the heat transfer, since the magnetic field suppresses the nanofluid flow. Hence, on the one hand, the scaled Rayleigh number can be increased because of the increase in the volumetric internal heating, Q, while the Hartmann number due to the increase in the magnitude of the external magnetic field, B₀. On the other hand, the values of Ha_nf and Rs_nf can be regulated via the nanoparticle volume fraction, φ, Eqs. (16) and (18), respectively. The nanoparticle diameter is a parameter that implicitly affects the aforementioned dimensionless parameters via both nanofluid dynamic viscosity and thermal conductivity, as it can be inferred from Eqs. (9) and (10), respectively. The kind of nanoparticle seems to control only Rs_nf, since the latter is a function of nanoparticle thermal conductivity, k_p. In addition, Da is independent of nanoparticle selection and its concentration. In practice, a decrease in Da is expected to decelerate the nanofluid flow, which is equivalent to deterioration of the entire cooling process. Finally, Prandtl number does not affect the core region solutions pertaining to nanofluid velocity and temperature for these relatively small values of Rayleigh numbers assuring the establishment of laminar regime, as it was ascertained in [21]. For the rest of this section, the reference values for the nanoparticle volume fraction, φ, and its diameter, d_p, are set equal to 0.03 and 100 nm, respectively. Similar to this kind of parametric studies such as [22, 27, 42], the reference values of Ha and Rs, namely for pure water, give Q and B₀ that are used in the determination of new nanofluid dimensionless numbers, Ha_nf and Rs_nf, which, in turn, control the asymptotic solutions (Eqs. 25–27).

Effect of the nanoparticle selection

First of all, Eqs. (25)–(27) are used which express the asymptotic solutions in the core region concerning the stream function, vertical velocity and temperature at z = 0, respectively, for reference values of Ha = 0, Rs = 5000, Da = 10⁻², φ = 0.03 and d_p = 100 nm. Specifically, the above dimensionless magnitudes are plotted in Fig. 4a–c versus the horizontal direction, ξ, for three different nanoparticles, namely Cu, Al₂O₃ and TiO₂. As it can be observed in Fig. 4a, b, copper-based nanofluids seem to acquire the larger values of stream function and, as a consequence, the larger vertical velocities in the core region. Besides, TiO₂-based nanofluids appear to have slightly larger values of stream function and vertical velocity than alumina ones, but smaller compared to Cu nanofluids. As a result, smaller values of temperature are accomplished using Cu in comparison with using Al₂O₃ and TiO₂.

Fig. 4

a Stream function, ψ₀, b vertical velocity, w₀ and c temperature, θ₀, at the core region for Rs_nf = 5000, Ha_nf = 0, Da = 10⁻², φ = 0.03, d_p = 100 nm and different nanoparticles at the mid-cavity height (z = 0)

As it can be inferred from Fig. 4b, c the maximum core values at z = 0 of the vertical velocity, w₀, and temperature, θ₀, appear as expected at ξ = 0.5. Thus, for the sake of brevity, only the maximal values of w₀ and θ₀ are depicted in Fig. 5a–d for various values of Rs and Ha = 5 (Fig. 5a, c) and various values of Ha and Rs = 5000 (Fig. 5b, d). The general trend is that as the scaled Rayleigh number increases, the nanofluid flow is enhanced, as shown in Fig. 5a, which, in turn, results in better cooling that is evident via the gradual decreasing of the core temperature, as shown in Fig. 5c. In terms of heat transfer, in Fig. 5e, the average Nusselt number, Nu_av, is illustrated, which is a measure of convection as compared to conduction. Hence, as Rs increases convection dominates over conduction leading to larger values of Nu_av. On the contrary, larger values of Hartmann number result in larger Lorentz forces that tend to decelerate the nanofluid motion leading to a gradual conduction-dominated regime. As a consequence, as Ha increases, smaller values of w₀ and larger values of θ₀ are observed (Fig. 5b, d). The increasing of Hartmann, that is, equivalent to applying stronger magnetic fields, results in worse cooling, as shown in Fig. 5f. As it was pointed out above, the better cooling is accomplished by utilizing copper-based nanofluids, while nanofluids with TiO₂ slightly outweigh those of Al₂O₃ in the hydrodynamic regime. However, as Hartmann number increases, Al₂O₃-based nanofluids acquire slightly larger velocities (and thus smaller temperatures and larger Nu_av) due to the greater value of electrical conductivity of TiO₂ in comparison with Al₂O₃ (since ${\text{Ha}}_{\text{nf}} \sim \sigma_{\text{nf}}^{1/2}$). As it was elaborated in [21, 22], the Hartmann number plays the most important role in regulating the nanofluid flow and as a consequence the heat transfer. In fact, as Ha tends to 50, Nu_av acquires the pure conduction solution of 0.8 which is the same for all the nanofluids considered. In this limit, also the values of vertical velocity and temperature coincide, since conduction has completely prevailed over convection.

Fig. 5

a, b Vertical velocity, w₀, c, d temperature, θ₀ and e, f average Nusselt number, Nu_av, at the core region for Da = 10⁻², φ = 0.03, d_p = 100 nm and different kinds of nanoparticles at the center of the cavity (z = 0, ξ = 0.5) for various values of Rs and Ha = 5 (left) and various Ha and Rs = 5000 (right)

Effect of the nanoparticle diameter

The diameter of the nanoparticles, d_p, is also a crucial parameter that influences the nanofluid flow and heat transfer, since it appears in both dynamic viscosity, μ_nf, and thermal conductivity, k_nf, definitions of the empirical relationships of Corcione [38]. Hence, increasing the nanoparticle diameter results in both lowering of μ_nf and k_nf, as it was elaborated in Fig. 3a, b, respectively. Thus, for a constant nanoparticle volume fraction, namely φ = 0.03, the decreasing of nanofluid viscosity and thermal conductivity is expected to affect the main dimensionless numbers of the present problem that control the core region, namely Rs_nf and Ha_nf. In particular, focusing on Ha_nf, since it scales with μ ^−1/2_nf , it is anticipated to increase. On the other hand, Rs_nf is expected to decrease mainly due to the existence of $\alpha^{2}_{\text{nf}} \equiv [k_{\text{nf}} /(\rho C_{\text{p}} )_{\text{nf}} ]^{2}$ in the denominator. In this subsection, an Al₂O₃ nanofluid of 0.03 nanoparticle volume fraction and a Darcy number equal to 10⁻² is taken into account as the reference case study.

The gradual decrease in the vertical velocity at the center of the enclosure, as well as the corresponding increase in the core temperature due to Rs_nf decrease, is illustrated in Fig. 6a. Thus, as the size of the nanoparticles increases, the average Nusselt number also decreases up to the conduction value of 0.8. This subsection clarifies the general belief of using particles of tiny dimensions in the relative literature when it comes to optimal heat exhaust.

Fig. 6

a Temperature, θ₀, and vertical velocity, w₀, at the center of the cavity (z = 0, ξ = 0.5) and b average Nusselt number, Nu_av, as a function of nanoparticle diameter, d_p, and Rs = 5000, Ha = 5, Da = 10⁻² and φ = 0.03 considering an Al₂O₃ nanofluid

Effect of the nanoparticle volume fraction

Similar to the above analysis, an Al₂O₃ nanofluid is considered in this subsection in order to examine the influence of the nanoparticle volume fraction on nanofluid flow and heat transfer. As it was stressed in the previous studies of Benos and Sarris [22] and Benos et al. [27], the nanoparticle concentration is a very important factor that affects all the dimensionless numbers via the dependence of nanofluid physical and electric properties on it, as shown in Eqs. (5)–(10).

First of all, the influence of nanoparticle volume fraction on the vertical velocity, w₀, at the center of the cavity (ξ = 0.5, z = 0) is examined along with the analytical core temperature. As it is illustrated in Fig. 7a, the denser the nanofluid the larger the deterioration of the heat transfer. This is evident by the observed decrease in the nanofluid velocity as well as the increase in its temperature, since the low velocities tend to lessen the convection heat transfer in favor of conduction. As a consequence, the ratio of convection over conduction, which is equivalent to the average Nusselt number, Nu_av, decreases, as it is depicted in Fig. 7b. Finally, when conduction is the predominant heat transfer mode, the average Nusselt number reaches its minimal value of 0.8 regarding the present investigation. This worsening of the cooling process, as the concentration of nanoparticles increases concerning natural convection within enclosures, has also been observed in experimental studies such as [41] and numerical studies like [42, 43]. The current results, which are depicted in Fig. 7a, b, were derived for the following reference set of values: Rs = 5000, Ha = 5, Da = 10⁻² and d_p = 100 nm, while the range of nanoparticle volume fraction, φ, is between 0 and 0.06 in line with the study of Corcione [38].

Fig. 7

a Temperature, θ₀, and vertical velocity, w₀, at the center of the cavity (z = 0, ξ = 0.5) and b average Nusselt number, Nu_av, as a function of nanoparticle volume fraction, φ, for d_p = 100 nm, Rs = 5000, Ha = 5 and Da = 10⁻² considering an Al₂O₃ nanofluid

Effect of the Darcy number

Finally, since the main contribution of the present study is the extension of the asymptotic solutions for a porous medium, an analysis follows for the effect of Darcy number, Da. Specifically, the decrease in Da is a result of diminishing the permeability, Κ, of the medium. In turn, a decrease in Κ is equivalent to the enhancement of flow resistance, which leads to the deceleration of the nanofluid flow (i.e., lower velocities) and the remaining of the high temperatures in the core region of the enclosure in favor of conduction heat transfer mode. Conversely, for a very high Da number, the asymptotic solutions capture the solutions of the non-porous medium derived in [22].

Figure 8a–c corresponds to the following reference values, namely Rs = 5000, Ha = 5, d_p = 100 nm and φ = 0.03. For very small values of Da, the present asymptotic solutions regarding the core region yield the lowest vertical velocities (Fig. 8a). Besides, the pure conduction temperature profile of Eq. (23) (presented as “+” in Fig. 8b, c) and the limiting conduction value of Nu_av = 0.8 are reproduced for Da equal to 10⁻⁵ and 10⁻⁴. When the Darcy number equals to 10⁻³, the value of Nu_av is only 1.04% larger than the conduction value, while this deviation increases to 22.44% for Da = 10⁻², 59.12% for Da = 10⁻¹ and 68.19% for Da = 1 (10⁰ in Fig. 8c). Finally, for values larger than Da = 1, the value of Nu_av gradually reaches 1.35477, which is exactly the value of considering a non-porous cavity (presented as “x” in Fig. 8a–c).

Fig. 8

Effect of Darcy number, Da, on a vertical velocity, w₀, b temperature, θ₀, at the core region and c average Nusselt number, Nu_av, for d_p = 100 nm, Rs_nf = 5000, Ha_nf = 5, φ = 0.03 and d_p = 100 nm at the mid-cavity height (z = 0) considering an Al₂O₃ nanofluid

Conclusions

The natural convection within a shallow rectangular horizontal shallow cavity is investigated, subject to an external magnetic field and internal heating. The asymptotic expansion method is utilized in this study pertaining to the derivation of core stream function, vertical velocity and temperature and described in detail in the “Appendix” section. The range of the dimensionless numbers examined in the present investigation is similar to [21, 22], namely 0 ≤ Ha_nf ≤ 50 and 200 ≤ Rs_nf ≤ 5000, thus ensuring the laminar regime before any unstable or multicellular flow appears. The consideration of a porous cavity enhances the laminar nature of the flow, since it reduces the nanofluid velocities. In order to examine some widely utilized nanofluids, Cu, Al₂O₃ and TiO₂ nanoparticles were selected which are suspended in water. As for the variables of the nanoparticles, such as their diameter and volume fraction, their values are in accordance with the experiments that were taken into account by Corcione [38]. Furthermore, for the purpose of describing the dynamic viscosity and thermal conductivity, the relationships derived in [38] are incorporated, which are the optimal fitting result of experimental data for a range of nanoparticle concentrations, nanoparticle diameters, temperatures and different kinds of nanoparticles.

The present results indicate that the increase in magnetic field, which can be implicitly expressed by the increase in Hartmann number, leads to the deceleration of the nanofluid flow and thus in deterioration of the heat transfer. Conversely, convective currents are intensified by the internal heating increase, which is equivalent to Rayleigh number increase and results in enhancing convection over conduction leading to better cooling. Finally, a decrease in the nanoparticle content and size contributes in the enhancement of the entire heat transfer, which is evident through the increase in the core vertical velocities and the concomitant core temperature decreases with copper-based nanofluids proved to be the better coolants. The regulation of the heat transfer can also be accomplished via the use of a porous medium. This is an engineering technique for the purpose of optimizing the heat transfer mainly via the contact area increase between the coolant and the solid substrate. It was concluded that as the medium permeability increases, the flow resistance decreases leading to larger velocities that are equivalent to better cooling.

The main advantage of the present asymptotic analysis, which was proved to be accurate for handling the core region at the laminar regime [21], is the rough examination of how some significant design parameters influence the overall MHD natural convection. Hence, this rough sense of the effect of various factors on heat transfer, namely the nanofluid properties, the porous medium permeability as well as applied magnetic field and internal heating, is expected to be a very useful theoretical tool given the rapidly growing interest in the field of nanofluids. This field ranges from cooling devices, such as heat exchangers [2], to bioengineering applications such as magnetic hyperthermia cancer treatment [44].

Appendix

Derivation of the governing dimensionless equations

The governing system of two-dimensional steady-state, incompressible, MHD equations has been presented in Eqs. (1)–(4). Taking the derivative of Eqs. (2) and (3) with respect to z and x, respectively, and considering the continuity equation, Eq. (1):

$$u\frac{{\partial^{2} u}}{\partial z\partial x} + w\frac{{\partial^{2} u}}{{\partial z^{2} }} = - \frac{1}{{\rho_{\text{nf}} }}\frac{{\partial^{2} p}}{\partial z\partial x} + v_{\text{nf}} \frac{{\partial^{3} u}}{{\partial z\partial x^{2} }} + v_{\text{nf}} \frac{{\partial^{3} u}}{{\partial z^{3} }} - \frac{{\sigma_{\text{nf}} \,B_{\text{o}}^{2} }}{{\rho_{\text{nf}} }}\frac{\partial u}{\partial z} - \frac{{v_{\text{nf}} }}{K}\frac{\partial u}{\partial z}$$

(33)

$$u\frac{{\partial^{2} w}}{{\partial x^{2} }} + w\frac{{\partial^{2} w}}{\partial x\partial z} = - \frac{1}{{\rho_{\text{nf}} }}\frac{{\partial^{2} p}}{\partial x\partial z} + v_{\text{nf}} \frac{{\partial^{3} w}}{{\partial x^{3} }} + v_{\text{nf}} \frac{{\partial^{3} w}}{{\partial x\partial z^{2} }} + g\beta_{\text{nf}} \frac{\partial T}{\partial x} - \frac{{v_{\text{nf}} }}{K}\frac{\partial w}{\partial x}$$

(34)

Subtracting Eqs. (34) from (33):

$$u\frac{\partial }{\partial x}\left( {\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}} \right) + w\frac{\partial }{\partial z}\left( {\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}} \right) = v_{\text{nf}} \left( {\frac{{\partial^{3} u}}{{\partial x^{2} \partial z}} + \frac{{\partial^{3} u}}{{\partial z^{3} }} - \frac{{\partial^{3} w}}{{\partial x^{3} }} - \frac{{\partial^{3} w}}{{\partial z^{2} \partial x}}} \right) - \frac{{\sigma_{\text{nf}} \,B_{\text{o}}^{2} }}{{\rho_{\text{nf}} }}\frac{\partial u}{\partial z} - g\beta_{\text{nf}} \frac{\partial T}{\partial x} - \frac{{v_{\text{nf}} }}{K}\left( {\frac{\partial u}{\partial z} - \frac{\partial w}{\partial x}} \right)$$

(35)

The stream function ψ(x, z) is related to velocity components u and v via:

$$u = \frac{\partial \psi }{\partial z},\quad w = - \frac{\partial \psi }{\partial x}$$

(36)

Substituting Eqs. (36) in (35):

$$\frac{\partial \psi }{\partial z}\frac{\partial }{\partial x}\underbrace {{\left( {\frac{{\partial {}^{2}\psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }}} \right)}}_{{\nabla^{2} \psi }} - \frac{\partial \psi }{\partial x}\frac{\partial }{\partial z}\underbrace {{\left( {\frac{{\partial^{2} \psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }}} \right)}}_{{\nabla^{2} \psi }} = v_{\text{nf}} \underbrace {{\left( {\frac{{\partial^{4} \psi }}{{\partial x^{4} }} + 2\frac{{\partial^{4} \psi }}{{\partial x^{2} \partial z^{2} }} + \frac{{\partial^{4} \psi }}{{\partial z^{4} }}} \right)}}_{{\nabla^{4} \psi }} - \frac{{\sigma_{\text{nf}} \,B_{\text{o}}^{2} }}{{\rho_{\text{nf}} }}\frac{{\partial^{2} \psi }}{{\partial z^{2} }} - g\beta_{\text{nf}} \frac{\partial T}{\partial x} - \frac{{v_{\text{nf}} }}{\rm K}\underbrace {{\left( {\frac{{\partial {}^{2}\psi }}{{\partial x^{2} }} + \frac{{\partial^{2} \psi }}{{\partial z^{2} }}} \right)}}_{{\nabla^{2} \psi }}$$

(37)

Substituting also Eq. (36) in energy equation, namely Eq. (4), it turns out that:

$$\frac{\partial \psi }{\partial z}\frac{\partial T}{\partial x} - \frac{\partial \psi }{\partial x}\frac{\partial T}{\partial z} = a_{\text{nf}} \nabla^{2} T + \frac{Q}{{\left( {\rho \,c_{\text{p}} } \right)_{\text{nf}} }}$$

(38)

Next, the dimensional form of the stream function and energy equations are derived via considering the following magnitudes:

$$X = \frac{x}{h},\quad Z = \frac{z}{h},\quad \varPsi = \frac{\psi }{{a_{\text{nf}} }},\quad \varTheta = \frac{{T\left( {\rho c_{\text{p}} } \right)_{\text{nf}} a_{\text{nf}} }}{{h^{2} Q}}$$

(39)

Thus Eqs. (37) and (38) result in Eqs. (40) and (41), respectively:

$$\nabla^{4} \varPsi = {\rm Pr}_{\text{nf}}^{ - 1} \frac{{\partial (\nabla^{2} \varPsi ,\varPsi )}}{\partial (X,Z)} + {\text{Ha}}_{\text{nf}}^{2} \frac{{\partial^{2} \varPsi }}{{\partial Z^{2} }} + {\text{Ra}}_{\text{nf}} \frac{\partial \varTheta }{\partial X} + {\text{Da}}^{1} \nabla^{2} \varPsi$$

(40)

$$\nabla^{2} \varTheta + 1 = \frac{\partial (\varTheta ,\varPsi )}{\partial (X,Z)}$$

(41)

where the dimensionless numbers Da, Pr_nf, Ra_nf and Ha_nf have already been defined in Eqs. (15)–(18) of the main part of this study. Besides, X, Z, Θ and Ψ are converted to x, z, T and ψ, respectively, for the sake of simplicity.

Derivation of the ordinary differential equations using the asymptotic expansions method

The governing parameter of the present problem is ε, which can be defined as ε ≡ L⁻¹ ≪ 1, where L is the aspect ratio of the cavity that is very large, as it has already been stressed. The core flow covers most of the cavity and its solution relies on the length scales ξ and z (Eq. 24).

Similarly to [20,21,22], the stream function and the temperature fields are expanded with respect to ξ, z as follows:

$$\psi = \psi_{0} (\xi ,z) + L^{ - 1} \,\psi_{1} (\xi ,z) + L^{ - 2} \,\psi_{2} (\xi ,z) + \cdots$$

(42)

$$T = L^{2} \,T_{0} (\xi ,z) + L\,T_{1} (\xi ,z) + T_{2} (\xi ,z) + L^{ - 1} \,T_{3} (\xi ,z) + \cdots$$

(43)

These expansions are substituted into the flow and energy equations and their boundary conditions, which have been analyzed in the main part of the study, for the purpose of obtaining a system of coupled partial equations for the stream function and temperature for every order of magnitude of L.

Thus, substituting Eqs. (42), (43) into (40) in terms of ξ and z:

$$\begin{aligned} & L^{ - 4} \frac{{\partial^{4} \psi_{0} }}{{\partial \xi^{4} }} + 2L^{ - 2} \frac{{\partial^{4} \psi_{0} }}{{\partial \xi^{2} \partial z^{2} }} + \frac{{\partial^{4} \psi_{0} }}{{\partial z^{4} }} + L^{ - 5} \frac{{\partial^{4} \psi_{1} }}{{\partial \xi^{4} }} + 2L^{ - 3} \frac{{\partial^{4} \psi_{1} }}{{\partial \xi^{2} \partial z^{2} }} + L^{ - 1} \frac{{\partial^{4} \psi_{1} }}{{\partial z^{4} }} + \cdots \\ & \quad = {\rm Pr}_{\text{nf}}^{ - 1} \left[ {L^{ - 3} \frac{{\partial (\partial^{2} \psi_{0} /\partial \xi^{2} ,\psi_{0} )}}{\partial (\xi ,z)} + L^{ - 1} \frac{{\partial (\partial^{2} \psi_{0} /\partial z^{2} ,\psi_{0} )}}{\partial (\xi ,z)}} \right] \\ & \quad \quad + \,{\rm Pr}_{\text{nf}}^{ - 1} \left[ {L^{ - 4} \frac{{\partial (\partial^{2} \psi_{1} /\partial \xi^{2} ,\psi_{1} )}}{\partial (\xi ,z)} + L^{ - 2} \frac{{\partial (\partial^{2} \psi_{1} /\partial z^{2} ,\psi_{1} )}}{\partial (\xi ,z)}} \right] + \cdots \\ & \quad \quad + \,{\text{Ha}}_{\text{nf}}^{2} \frac{{\partial^{2} \psi_{0} }}{{\partial z^{2} }} + {\text{Ha}}_{\text{nf}}^{2} L^{ - 1} \frac{{\partial^{2} \psi_{1} }}{{\partial z^{2} }} + \cdots \\ & \quad \quad + \,\underbrace {{{\text{Ra}}_{\text{nf}} L}}_{{{\text{Rs}}_{\text{nf}} }}\frac{{\partial {\rm T}_{0} }}{\partial \xi } + \underbrace {{{\text{Ra}}_{\text{nf}} }}_{{{\text{Rs}}_{\text{nf}} L^{ - 1} }}\frac{{\partial {\rm T}_{1} }}{\partial \xi } + \cdots \\ & \quad \quad + \,{\text{Da}}^{ - 1} L^{ - 1} \frac{{\partial^{2} \psi_{0} }}{{\partial \xi^{2} }} + {\text{Da}}^{ - 1} \frac{{\partial^{2} \psi_{0} }}{{\partial z^{2} }} + {\text{Da}}^{ - 1} L^{ - 2} \frac{{\partial^{2} \psi_{1} }}{{\partial \xi^{2} }} + {\text{Da}}^{ - 1} L^{ - 1} \frac{{\partial^{2} \psi_{1} }}{{\partial z^{2} }} + \cdots \\ \end{aligned}$$

(44a)

Next, the terms of order one and L⁻¹ are equalized:

$$\frac{{\partial^{4} \psi_{0} }}{{\partial z^{4} }} - \left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)\frac{{\partial^{2} \psi_{0} }}{{\partial z^{2} }} = {\text{Rs}}_{\text{nf}} \frac{{\partial T_{0} }}{\partial \xi }$$

(44b)

$$\frac{{\partial^{4} \psi_{1} }}{{\partial z^{4} }} = {\rm Pr}_{\text{nf}}^{ - 1} \frac{{\partial (\partial^{2} \psi_{0} /\partial z^{2} ,\psi_{0} )}}{\partial (\xi ,z)} + \left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)\frac{{\partial^{2} \psi_{1} }}{{\partial z^{2} }} + {\text{Rs}}_{\text{nf}} \frac{{\partial T_{1} }}{\partial \xi } + {\text{Da}}^{ - 1} \frac{{\partial^{2} \psi_{0} }}{{\partial \xi^{2} }}$$

(44c)

Similarly, substituting Eqs. (42), (43) into (41) at order L², L and 1 it is obtained, respectively, as:

$$\frac{{\partial^{2} T_{0} }}{{\partial z^{2} }} = 0$$

(45a)

$$\frac{{\partial^{2} T_{1} }}{{\partial z^{2} }} = \frac{{\partial T_{0} }}{\partial \xi }\frac{{\partial \psi_{0} }}{\partial z}$$

(45b)

$$\frac{{\partial^{2} T_{2} }}{{\partial z^{2} }} = - 1 - \frac{{\partial^{2} T_{0} }}{{\partial \xi^{2} }} + \frac{{\partial T_{1} }}{\partial \xi }\frac{{\partial \psi_{0} }}{\partial z} + \frac{{\partial T_{0} }}{\partial \xi }\frac{{\partial \psi_{1} }}{\partial z} - \frac{{\partial T_{1} }}{\partial z}\frac{{\partial \psi_{0} }}{\partial \xi }$$

(45c)

The solution of Eq. (45a) with the adiabatic boundary conditions $\partial T_{0} /\partial z = 0$ at $z = \pm 0.5$ is:

$$T_{0} = \theta_{0} (\xi )$$

(46)

where θ₀ is a function of ξ, independent of z.

Derivation of the analytical solutions

Following the analysis of [20,21,22], only the stream functions of order one and temperatures of order L² are going to be analyzed which give a satisfactory picture of the nanofluid flow and heat transfer for the core region. Focusing on Eq. (44b), its complementary equation is:

$$\frac{{\partial^{4} \psi_{0} }}{{\partial z^{4} }} - \left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)\frac{{\partial^{2} \psi_{0} }}{{\partial z^{2} }} = 0$$

(47)

The general solution of the complementary equation is:

$$\psi_{0,c} = A(\xi )\cosh \left[ {\left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)z} \right] + B(\xi )\sinh \left[ {\left( {{\text{Ha}}_{\text{nf}}^{2} + {\text{Da}}^{ - 1} } \right)z} \right] + C(\xi )z + D(\xi )$$

(48a)

while its particular solution is in the same manner as [20,21,22]:

$$\psi_{{0,{\text{p}}}} = - \frac{{{\text{Rs}}_{\text{nf}} \theta_{0}^{{\prime }} }}{{{\text{Ha}}^{2} + {\text{Da}}^{ - 1} }}\frac{{z^{2} }}{2}$$

(48b)

Substituting the boundary conditions pertaining to ψ₀, namely Eqs. (19) and (20) of the main part of the present study, and adding the particular and general solutions:

$$\psi_{0} = \frac{{{\text{Rs}}_{\text{nf}} \theta_{0}^{{\prime }} }}{{{\text{Ha}}^{2} + {\text{Da}}^{ - 1} }} \cdot G(z)$$

(49)

where

$$G(z) = \frac{1}{2}\,\left( {\frac{{\cosh \left( {\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } z} \right)}}{{\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } \,\sinh \left( {\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } /2} \right)}} - \frac{{\coth \left( {\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } /2} \right)}}{{\sqrt {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } }} + \frac{1}{4} - z^{2} } \right)$$

(50)

Integrating in z Eq. (45c) and applying the boundary condition $\left. {\partial T_{2} /\partial z} \right|_{z = \pm 0.5} = 0$, the only consistent solution according to [21, 22] should obey the equation for θ₀:

$$\theta_{0}^{{\prime \prime }} + a_{\text{m}} \,R_{1}^{2} \,\left( {\theta_{0}^{{\prime }} } \right)^{2} \theta_{0}^{{\prime \prime }} + 1 = 0$$

(51)

where

$$\alpha_{m} = \frac{3}{{\left( {{\text{Ha}}^{2} + {\text{Da}}^{ - 1} } \right)^{2} }}\int\limits_{{{\raise0.5ex\hbox{$\scriptstyle { - 1}$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}}^{{{\raise0.5ex\hbox{$\scriptstyle 1$} \kern-0.1em/\kern-0.15em \lower0.25ex\hbox{$\scriptstyle 2$}}}} {G(z)^{2} {\text{d}}z} \Rightarrow$$

(52)

Following the analysis of [21], the first integration of Eq. (51) considering the symmetry condition of the solution yields:

$$\theta_{0}^{{\prime }} = a_{\text{m}}^{ - 1/2} \,R_{1}^{ - 1} \,\left[ {F_{\text{m}}^{ + } (\xi ) + F_{\text{m}}^{ - } (\xi )} \right]$$

(53)

where

$$F_{\text{m}}^{ \pm } (\xi ) = \left\{ {\frac{3}{2}a_{\text{m}}^{1/2} \,R_{1} \,\left( {\frac{1}{2} - \xi } \right) \pm \left[ {1 + \frac{9}{4}a_{\text{m}} \,R_{1}^{2} \left( {\xi - \frac{1}{2}} \right)^{2} } \right]^{1/2} } \right\}^{1/3}$$

(54)

Moreover, using $\sinh y_{\text{m}} = \sinh^{ - 1} \left[ {\frac{3}{2}a_{\text{m}}^{1/2} \,{\text{Rs}}_{\text{nf}} \left( {\xi - \frac{1}{2}} \right)} \right]$ with a further integration, a closed-form solution of the core stream function, vertical velocity and temperature is produced (Eqs. (25)–(27), respectively) where $y_{{{\text{m}},0}} = \sinh^{ - 1} \left( {\frac{3}{4}a_{\text{m}}^{1/2} {\text{Rs}}_{\text{nf}} } \right).$