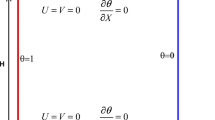Introduction

Numerical and experimental studies of convective heat transfer in enclosures filled with Newtonian fluids have been extensively reported in the literature [1, 2]. Some of these studies have considered enclosures with time-dependent thermal boundary conditions due to their importance in practical applications such as heating or cooling in buildings, storing food, and cooling of electronic components. Lage and Bejan [3] examined the effects of oscillating frequency of heat production on natural heat transfer in a square cavity. Roslan et al. [4] examined the natural convection heat transfer in an enclosure equipped with a cylindrical sinusoidal heat source. They demonstrated that the heat transfer rate increased as a result of increasing the oscillation of the heat source temperature. The maximum heat transfer augmentation was obtained for frequencies between 25π and 30π at a high amplitude and a moderate source radius. Wang et al. [5] studied unsteady oscillating heat transfer in a square cavity, where a cylinder with pulsed temporal temperature rotated at the center of the cavity. Their results indicated that the fluid flow and the heat transfer rate were strongly dependent on the pulsed temperature of the inner cylinder. They argued that the unsteady heat transfer was considerably higher than the steady heat transfer under the same conditions. Kalidasan et al. [6] investigated the enhancement of natural convection heat transfer in a square cavity filled with a nanofluid. The cavity was a forward-facing stepped rectangular enclosure with a partition and time-variant temperature on the stepped top wall. Their results revealed that the heat transfer rate increased with increasing oscillation range of temperature and decreased with increasing oscillation period of temperature.

In many industrial applications, natural convection has been considered as the main mechanism of heat transfer due to its simplicity and low cost. In majority of reported studies on natural convection, the working fluid is assumed to be Newtonian. However, this assumption is not valid in many scenarios as the fluid demonstrates non-Newtonian behavior. The precise prediction of non-Newtonian fluid behavior and transient heat transfer is essential to fully understand the heat transfer mechanism and improve the design of processes, which are combined with a solid–liquid phase change. Examples of these processes are metals and solidification of alloys [7, 8], injection and molding of polymers [9, 10], freezing of food [11,12,13], the processes in which fluid is in the liquid phase, such as the sterilization of materials liquid food [14, 15] and non-Newtonian fluid flow in horizontal and vertical ducts [16,17,18].

Natural convection of non-Newtonian fluids is a complex problem because adhesive forces should be calculated by the nonlinear relationship between shear stresses and deformation rates. The effective viscosity required to determine the adhesive forces is determined based on the slope of velocity profile at any particular time [19, 20]. Lamsaadi et al. [21] numerically examined the natural convection heat transfer in a horizontal rectangular chamber uniformly heated from the side and filled with non-Newtonian power-law fluids. They also presented an approximate analytical solution for the heat transfer. Turan et al. [22] studied the laminar natural convection heat transfer in a square enclosure filled with a Bingham fluid. Bingham plastics have a yield stress, and once the yield stress is exceeded, the materials will be flown. They found the Nusselt number of the Newtonian fluid to be greater than that of the Bingham fluid at a constant Grashof number.

Vinogradov et al. [23] examined the heat transfer performance of non-Newtonian dilatant fluids in square and rectangular chambers using the power-law model. They argued that despite the apparent difference in the heat transfer rate for the Newtonian and non-Newtonian fluids, the same behavior was observed in the form of transferring the multicellular flow structure to the single-cell regime. Matin et al. [24] considered a power-law fluid in a space between two square ducts at different temperatures and examined the heat transfer rate for different values of power-law index (n), Rayleigh number (Ra), Prandtl number (Pr), and aspect ratio. Their results showed that the heat transfer decreased as the power-law index increased from 0.6 to 1.4.

Jahanbakhshi et al. [25] investigated the effect of magnetic field on natural convection heat transfer in an L-shaped enclosure filled with a non-Newtonian fluid numerically. The governing equations were solved by finite-volume method using the SIMPLE algorithm. The power-law rheological model was used to characterize the non-Newtonian fluid behavior. It was revealed that heat transfer rate decreases for shear-thinning fluids (of power-law index, \(n < 1\)) and increases for shear-thickening fluids (\(n > 1\)) in comparison with the Newtonian ones. Thermal behavior of shear-thinning and shear-thickening fluids was similar to that of Newtonian fluids for the angle of enclosure \(\alpha < 60^{ \circ }\) and \(\alpha > 60^{ \circ }\), respectively.

Kim et al. [26] studied the unsteady natural convection heat transfer performance of non-Newtonian fluids in a square enclosure. They used a finite-volume method and demonstrated that the rheological properties of the fluid had a significant impact on the transient processes. Lemus-Mondaca [27] studied the two-dimensional unsteady heat transfer rate of Newtonian fluids and non-Newtonian fluids (pseudoplastic and dilatant) in a square enclosure. Guha and Pradhan [28] studied the heat transfer of non-Newtonian power-law fluids over a horizontal plane. They assumed the flow to be one-dimensional and found that dilatant non-Newtonian fluids had a larger heat transfer rate compared to the Newtonian and pseudoplastic non-Newtonian fluids at a constant Prandtl number.

Kefayati [29] developed a lattice Boltzmann model to examine the heat transfer of non-Newtonian molten polymer fluids in a square enclosure with sinusoidal boundary conditions. The argued that the heat transfer decreased with increasing power-law index. Zhang et al. [30] studied the heat transfer coefficient and surface frictional coefficient of non-Newtonian power-law fluids within a boundary layer. Their results demonstrated that the distribution of the thermal boundary layer depended on the velocity, the power-law index, and the Prandtl number. Moraga et al. [31] investigated three-dimensional natural convection heat transfer from a container enclosed by an enclosure. The container was saturated with a non-Newtonian power-law fluid and was surrounded by the air. The results were presented in terms of streamlines and isotherms for different Rayleigh numbers.

Crespí-Llorens et al. [32] experimentally investigated the heat transfer from pseudoplastic non-Newtonian fluids in a scraped surface heat exchanger (SSHE). They examined the pressure drop, heat transfer, and energy consumption for static and dynamic conditions of the scraped surface with pseudoplastic non-Newtonian fluids. Their results showed that the SSHE was suitable for industrial processes using non-Newtonian fluids due to their relatively large heat transfer compared to Newtonian fluids.

The application of non-Newtonian fluids to enhance the cooling performance of systems with unsteady oscillating heat flux has been considered by designers in the electronics industry. However, according to the authors’ best knowledge, limited research in this field has been reported in the literature. The aim of the present study is to simulate Newtonian and non-Newtonian fluids in a square enclosure with unsteady oscillating heat flux and evaluate the impact of effective parameters such as power-law index, Rayleigh number, oscillation, and heat source location on the natural convection heat transfer.

Problem definition

Figure 1 presents a schematic diagram of the square enclosure filled with non-Newtonian or Newtonian fluids. The right and left walls are at a uniform and relatively low temperature (\(T_{\text{c}}\)), and the top wall is thermally insulated. The bottom wall of the enclosure is partially heated by a heat source with fluctuating heat flux (\(q^{{\prime \prime }}\)). The rest of the bottom wall is thermally insulated. The heat flux is given by [33],

Fig. 1
figure 1

A schematic of the geometry

Full size image
$$q^{{\prime \prime }} = q_{0}^{{\prime \prime }} (1 + \cos (2\pi t/t_{\text{p}} ))$$

Laminar flow of both Newtonian and non-Newtonian fluids in the enclosure is considered. The Prandtl number is \(pr = 100\), and the fluids are assumed to be incompressible. The Boussinesq approximation is used to take into account the density variations in the buoyancy force.

Governing equations

In this study, the viscous non-Newtonian fluid is modeled by the power-law model. The relationship between the shear stress and the shear rate is given by [19],

$$\begin{aligned} & {\text{Shear}}\;{\text{stress}}\;{\text{for}}\;{\text{non - }}\;{\text{Newtonian}}\;{\text{fluid}}: \\ & \tau _{{ij}} = 2\mu _{{\text{a}}} D_{{ij}} = \mu _{{\text{a}}} \left( {\frac{{\partial u_{i} }}{{\partial x_{j} }} + \frac{{\partial u_{j} }}{{\partial x_{i} }}} \right) \\ \end{aligned}$$
(2)
$$\begin{aligned} & {\text{apparent}}\;{\text{viscosity}}\;{\text{for}}\;{\text{non - Newtonian}}\;{\text{fluid}}: \\ & \mu _{{\text{a}}} = \kappa \left\{ {2\left[ {\left( {\frac{{\partial u}}{{\partial x}}} \right)^{2} + \left( {\frac{{\partial v}}{{\partial y}}} \right)^{2} } \right] + \left( {\frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}}} \right)^{2} } \right\}^{{\frac{{n - 1}}{2}}} \\ \end{aligned}$$
(3)

where n and κ are empirical constants that are known as consistency and power-law indices, respectively.

Governing equations include the conservation of mass, x- and y-momentum, and energy [23].

$$\frac{\partial U}{\partial X} + \frac{\partial V}{\partial Y} = 0$$
(4)
$$\frac{\partial U}{\partial \tau } + U\frac{\partial U}{\partial X} + V\frac{\partial U}{\partial Y} = - \frac{\partial P}{\partial X} + Pr^{*} \left( {\frac{\partial }{\partial X}\left( {2\mu_{\text{a}}^{{\prime }} \frac{\partial U}{\partial X}} \right) + \frac{\partial }{\partial Y}\left( {\mu_{\text{a}}^{{\prime }} \left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)} \right)} \right)$$
(5)
$$\frac{\partial V}{\partial \tau } + U\frac{\partial V}{\partial X} + V\frac{\partial V}{\partial Y} = - \frac{\partial P}{\partial Y} + Pr^{*} \left( {\frac{\partial }{\partial X}\left( {\mu_{\text{a}}^{{\prime }} \left( {\frac{\partial U}{\partial Y} + \frac{\partial V}{\partial X}} \right)} \right) + \frac{\partial }{\partial Y}\left( {2\mu_{\text{a}}^{{\prime }} \frac{\partial V}{\partial Y}} \right)} \right) + Ra \cdot Pr \cdot \theta$$
(6)
$$\frac{\partial \theta }{\partial \tau } + U\frac{\partial \theta }{\partial X} + V\frac{\partial \theta }{\partial Y} = \left( {\frac{{\partial^{2} \theta }}{{\partial X^{2} }} + \frac{{\partial^{2} \theta }}{{\partial Y^{2} }}} \right)$$
(7)

The governing dimensionless parameters are defined as follows:

$$\begin{aligned} & X = \frac{x}{L},Y = \frac{y}{L},\tau = \frac{\alpha t}{{L^{2} }},U = \frac{uL}{\alpha },V = \frac{vL}{\alpha },P = \frac{{\bar{P}L^{2} }}{{\rho \alpha^{2} }},\theta = \frac{{T - T_{\text{c}} }}{\Delta T}, \\ & Pr^{ * } = \kappa /\rho \alpha^{2 - n} L^{2n - 2} ,Pr = \frac{\nu }{\alpha },\mu_{\text{a}}^{{\prime }} = \left\{ {2\left[ {\left( {\frac{\partial U}{\partial X}} \right)^{2} + \left( {\frac{\partial V}{\partial Y}} \right)^{2} } \right] + \left( {\frac{\partial V}{\partial X} + \frac{\partial U}{\partial Y}} \right)^{2} } \right\}^{{\frac{n - 1}{2}}} \\ & Ra = \frac{{g\beta L^{3} \Delta T}}{\nu \alpha },\Delta T = \frac{{q_{0}^{{\prime \prime }} L}}{k} \\ \end{aligned}$$
(8)

where n represents the power-law index.

The above-mentioned equations are used for simulating the Newtonian fluid by considering the power-law index to be n = 1.

The dimensionless initial conditions for the velocity and temperature are \(U = V = 0\) and \(\theta = 0\), respectively.

The non-dimensional boundary conditions are as follows: \(U = V = 0\) on the walls of the enclosure, \(\theta = 0\) on the left and right walls, \(\frac{\partial \theta }{\partial Y} = 0\) on the thermally insulated walls, \(\left( {\frac{\partial \theta }{\partial Y}} \right)_{Y = 0} = - \left( {1 + \cos \left( {\frac{2\pi \tau }{{\tau_{p} }}} \right)} \right)\) on the heat source,where \(\tau_{\text{p}} = \alpha t_{\text{p}} /L^{2}\) is the dimensionless form of the fluctuating period of the heat flux.

Numerical method

The computational domain is discretized to solve the partial derivative equations. Since these equations are written for different points of the computational domain, it is necessary to first divide the computational domain into a set of points and then assign a part of the domain to any point. The formulation of control volume, described by Patankar [34], and the SIMPLE algorithm are used to solve Eqs. 4–7 along with the initial and boundary conditions. The advection and diffusion terms are discretized by the power-law theory using a FORTRAN code. Also, for the convergence criterion, the maximum residual mass of the grid control volume is less than \(10^{ - 7}\).

After solving the governing equations for \(U,V,\theta\), other useful parameters such as Nusselt number are determined. The local Nusselt number on the heat source is defined by,

$$Nu_{\text{s}} = \frac{hL}{k}$$
(9)

where h is the convective heat transfer coefficient and is given by,

$$h = \frac{{q_{0}^{{\prime \prime }} }}{{T_{\text{s}} - T_{\text{c}} }}$$
(10)

The local Nusselt number is expressed using dimensionless parameters,

$$Nu_{\text{s}} (X) = \frac{1}{{\theta_{\text{s}} (X)}}$$
(11)

The average Nusselt number is determined by integrating \(Nu_{\text{s}}\) along the heat source,

$$Nu_{\text{m}} = \frac{1}{{W_{\text{s}} }}\int_{{X_{\text{s}} - 0.5W_{\text{s}} }}^{{X_{\text{s}} + 0.5W_{\text{s}} }} {Nu_{\text{s}} (X){\text{d}}X}$$
(12)

Time step and grid independency

To study the effect of time step on the computational results, the simulation is carried out for five different time steps and for a grid resolution of \(60 \times 60\). The enclosure is filled with a non-Newtonian fluid (\(n = 1.2,Ra = 105,\tau_{\text{p}} = 0.04,W_{\text{s}} = 0.5,X_{\text{s}} = 0.5\)). According to the results obtained for the periodic-state time history of \(Nu_{\text{m}}\) (Fig. 2a), the optimal time step \(\Delta \tau = \tau_{\text{p}} /4000\) is employed for further simulations. It should be noted that the time step study is carried out for two different oscillation periods (\(\tau_{\text{p}} = 0.4\;{\text{and}}\;4\)) and similar results were obtained.

Fig. 2
figure 2

a Average Nusselt number for different time steps and b average Nusselt number for different grid resolutions

Full size image

The grid resolution is also considered for five grid sizes and \(\Delta \tau = \tau_{\text{p}} /100\). Figure 2b shows the values of \(Nu_{\text{m}}\) for various grid resolutions. It is found that there is no difference between the results for the grid sizes larger than \(60 \times 60\). Hence, the grid resolution of \(60 \times 60\) is used for further simulations.

Validation

In order to verify the present simulations, the natural convection heat transfer of non-Newtonian power-law fluid in two centered square ducts at constant temperatures [24] is investigated where \(n = 0.6,1.0,1.2^{{_{{}} }}\), \({\text{AR}} = 0.25\),\(Pr = 100\), and e = 0. Figure 3 shows that the present results are in agreement with the results of Matin et al. [24]. In addition, the results are compared with the results of Turan et al. [35], who simulated the steady laminar natural convection in a two-dimensional square enclosure with side walls being under a constant temperature. The enclosure is filled with a non-Newtonian power-law fluid. The Nusselt number is compared with the results of Turan et al. [35] for different power-law indices (\(n = 0.6,1.0,1.2^{{_{{}} }}\)), \(Ra = 10^{4} ,10^{5}\), and \(Pr = 100\). The results are presented in Table 1. It is observed that the present results are in good agreement with the results of Turan et al. [35] with a maximum error of less than 4%.

Fig. 3
figure 3

Code validation for Newtonian (n = 1) and non-Newtonian (\(n = 0.6,1.4\)) fluids against the results of Matin et al. [24] for \(e = 0,Pr = 100,{\text{AR}} = 0.25\)

Full size image
Table 1 Comparison of the present results with the results of Turan et al. [35] for a square enclosure at Pr = 100
Full size table

Results

The effects of fluid type

In this section, an enclosure filled with non-Newtonian or Newtonian fluids is considered. An oscillating heat source with a length of \(W_{\text{s}} = 0.5\) and oscillating period of \(\tau_{\text{p}} = 0.04\) is located in the center of the bottom wall of the enclosure (\(X_{\text{s}} = 0.5\)). The Rayleigh number is \(Ra = 10^{5}\), the Prandtl number is \(Pr = 100\), and the modified Prandtl number is \(Pr^{ * } = 1.0\). In addition, the power-law effects are considered for shear-thinning or pseudoplastic fluids (n < 1), Newtonian fluids (n = 1), and shear-thickening or dilatant fluids (n > 1).

Figure 4 shows the periodic-state time history of \(Nu_{\text{m}}\) and the maximum temperature of the heat source (\(\theta_{\hbox{max} }\)) for three periods of oscillation, from the initial time to periodic-steady-state situation. In order to investigate the variation of \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\), the relative heat flux (\(q^{{\prime \prime }} /q_{0}^{{\prime \prime }}\)) is plotted above the figure. It is observed that the oscillations of \(Nu_{m}\) and \(\theta_{\hbox{max} }\) have the same response frequency with a low phase change.

Fig. 4
figure 4

Periodic-state time history for \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\) for Newtonian and non-Newtonian fluids at \(Ra = 10^{5}\) and \(\tau_{\text{p}} = 0.04\)

Full size image

It is also demonstrated that the heat transfer (the Nusselt number) decreases and the maximum temperature increases with the power-law index. Based on Eq. 13, it is concluded that the apparent viscosity and the shear stress increase with the power-law index, which leads to an increase in the heat transfer. On the other hand, it can be stated that increasing the apparent viscosity results in a decrease in the buoyancy force and the heat transfer. Increasing heat transfer from the heat source reduces its maximum temperature, which plays an important role in designing the electronic components.

Shear stress in terms of strain rate and apparent viscosity is given by [19]:

$$\tau_{\text{yx}} = m\left( {\dot{\gamma }_{\text{yx}} } \right)^{\text{n}} \to \mu = m\left( {\left| {\dot{\gamma }_{\text{yx}} } \right|} \right)^{{\text{n}} - 1}$$
(13)

Figures 5 and 6 show the streamlines and isothermal lines, respectively, for non-Newtonian (dashed lines) and Newtonian (solid lines) fluids. As \(q^{{\prime \prime }} /q_{0}^{{\prime \prime }}\) profile shows, these plots are drawn for a periodic-steady-state situation. The flow and heat transfer reach a periodic steady state after several periods. In the figures, five different times a–e of the cyclical state of the oscillatory mode of the heat source at \(Ra = 10^{5}\) are shown. These times, referred to Figs. 5 and 6, are as follows:

Fig. 5
figure 5

Streamlines for pseudoplastic and dilatant (solid lines) fluids in comparison with Newtonian one (dotted lines) at \(Ra = 10^{5}\)

Full size image
Fig. 6
figure 6

Isotherms for pseudoplastic and dilatant (solid lines) fluids in comparison with Newtonian one (dotted lines) at \(Ra = 10^{5}\)

Full size image
$$[({\text{a}})\;\tau = 0.34,({\text{b}}) = 0.34 + \tau_{\text{p}} /4,({\text{c}}) = 0.34 + \tau_{\text{p}} /2,({\text{d}}) = 0.34 + 3\tau_{\text{p}} /4,({\text{e}}) = 0.34 + \tau_{\text{p}} ]$$

As it can be seen, the power of the vortices decreases by increasing the power-law index which leads to a decrease in the heat transfer. It is also concluded from the isotherms that the density of isothermal lines on the heat source increases with the power-law index which results in a reduction in heat transfer and an increase in the temperature around the heat source. The values of \(\psi_{\hbox{max} }\) and \(\theta_{\hbox{max} }\) are presented in these figures for comparison. Streamlines of Newtonian and non-Newtonian fluids demonstrate that the vortices of pseudoplastic fluids with n = 0.6 and n = 0.8 are stronger than those of Newtonian fluids. Hence, a higher heat transfer is expected. Similarly, isothermal lines on the heat source are denser for the Newtonian fluid compared to non-Newtonian ones which leads to larger \(\theta_{\hbox{max} }\).

It is also observed that the vortices of dilatant fluids are weaker and smaller than those of Newtonian fluid. This is associated with a reduction in the heat transfer. Isotherms of dilatant fluids have a higher density around the heat source compared to those for the Newtonian fluid. This leads to larger \(\theta_{\hbox{max} }\) and a lower heat transfer. Physically, pseudoplastic fluids are more dilute than dilatant fluids. This makes it possible to change their density more when they are under thermal flux. The density change leads to change of buoyancy forces. This means larger buoyancy forces cause stronger rotation of the vortices in the enclosure, which results in a higher heat transfer rate. The shape of the vortices also illustrates this very well. For the pseudoplastic fluid, the vortices are larger and stronger than the dilatant fluids and cover a larger area of the enclosure. It is worth noting that the minimum value of \(\theta_{\hbox{max} }\) occurs at \(({\text{c}}) = 0.34 + \tau_{\text{p}} /2\), where the magnitude of the heat flux is zero due to the absence of a source of heat production inside the enclosure. This is true while the minimum value of \(\psi_{\hbox{max} }\) for stage (c) occurs just for the case n = 0.6. For the other cases, this is observed at the distance between (c) and (d) due to the phase delay of the oscillatory state.

The effects of Rayleigh number

In this section, the effects of Rayleigh number on the heat transfer and fluid flow are presented. A non-Newtonian dilatant fluid (n = 1.2) is considered, and the oscillation period is \(\tau_{\text{p}} = 0.04\).

Figure 7 shows the average Nusselt number on the heat source and the maximum temperature in the enclosure for three oscillating periods at different Rayleigh numbers. In addition, \(q^{{\prime \prime }} /q_{0}^{{\prime \prime }}\) is plotted for better understanding of the results. It is found that the heat transfer increases and the maximum temperature decreases as the Rayleigh number increases. \(Nu_{\text{m}}\) reaches its maximum when \(\theta_{\hbox{max} }\) is minimum. According to the definition of Rayleigh number, an increase of the Rayleigh number corresponds to an increase in the heat flux and therefore an increase in the heat transfer. In the initial oscillation period, the average Nusselt number is greater than that for the later oscillatory periods due to a higher gradient temperature between the fluid and the surface. Eventually, the average Nusselt number reaches a uniform periodic state. The figure shows a delayed phase generated by the increase of the Rayleigh number.

Fig. 7
figure 7

Periodic-state time history of \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\) for a non-Newtonian fluid with power-law index \(n = 1.2\) and \(\tau_{\text{p}} = 0.04\) at different Rayleigh numbers

Full size image

Figures 8 and 9 show the streamlines and isotherms, respectively, for a non-Newtonian dilatant fluid, n = 1.2, (solid lines), and Newtonian fluid (dotted lines) for different Rayleigh numbers. These figures are presented for a periodic steady state, when the flow and heat transfer reach a steady-state condition after several periods. Five different times a to e are presented from the cyclical oscillatory mode of the heat source, which are shown at the top of the figure. As shown in Fig. 8, two vortices are formed with respect to the symmetry of the enclosure. These vortices become stronger and denser and occupy a larger area of the enclosure as the Rayleigh number increases. Similarly, it can be seen from Fig. 9 that the density of isothermal lines on the heat source increases with increasing Rayleigh number, indicating a higher heat transfer. The buoyancy forces in the enclosure are strengthened as the Rayleigh number is increased. This results in strengthening of the vortices in the enclosure and causes higher heat transfer from the heat source to the cold walls.

Fig. 8
figure 8

Flow patterns at different Ra and time stages for non-Newtonian fluid with \(n = 1.2\) (solid lines) and Newtonian fluid (dashed lines)

Full size image
Fig. 9
figure 9

Isotherms at different Ra and time stages for non-Newtonian fluid with \(n = 1.2\)(solid lines) and Newtonian fluid (dashed lines)

Full size image

A comparison between the streamlines for the non-Newtonian dilatant fluid (solid lines) and the Newtonian fluid (dotted lines) reveals that the vortices corresponding to Newtonian fluid are larger and stronger for different Rayleigh numbers. This is due to the dilution of Newtonian fluid versus dilatant fluid, which makes the buoyancy forces have a higher power for the Newtonian fluid. This means generating larger and stronger vortices and higher heat transfer from the heat source to move the side of the cold walls. As Fig. 9 depicts, the isotherms of Newtonian fluid have a lower density compared to the dilatant fluid leading to higher heat transfer. It is worth noting that with increasing time from a to e, the heat transfer initially increases and then decreases to reach its initial value (see Figs. 7, 9). The lowest amount of \(\theta_{\hbox{max} }\) occurs at a time between (c) and (d), where the heat flux has the lowest value. This can be observed in Fig. 8. It should be noted that the minimum value of \(\theta_{\hbox{max} }\) does not occur at point (c) for lower Rayleigh numbers (\(Ra = 10^{4} ,10^{5}\)) due to the phase delay (see Table 2). However, it occurs at point (c) or close to the time for a larger Rayleigh number (\(Ra = 10^{6}\)).

Table 2 Time of \((Nu_{\text{m}} )_{\hbox{max} }\) for the time interval \(\tau = 0.34\) and \(\tau = 0.38 = 0.34 + \tau_{\text{p}}\) and the phase delay from the point \(({\text{c}}) = 0.34 + \tau_{\text{p}} /2\) for different Rayleigh numbers
Full size table

Table 2 presents the time of \((Nu_{\text{m}} )_{\hbox{max} }\) for the time interval \(\tau = 0.34\) and \(\tau = 0.38 = 0.34 + \tau_{\text{p}}\). The time delay is generated from the point \(({\text{c}}) = 0.34 + \tau_{\text{p}} /2\), where the heat flux has the minimum value. At a high Rayleigh number (\(Ra = 10^{6}\)), the phase delay is less than the point \(({\text{c}}) = 0.34 + \tau_{\text{p}} /2\) and the phase delay increases as the Rayleigh number decreases.

The variation in the heat source maximum temperature \((\theta_{\hbox{max} } )_{\hbox{max} }\) is shown in Fig. 10 when the periodic steady state is reached. In fact, the values of \((\theta_{\hbox{max} } )_{\hbox{max} }\) in each case are equal to the oscillation peaks indicated in Fig. 7. It should be noted that \((\theta_{\hbox{max} } )_{\hbox{max} }\) is a critical design parameter for electronic components. A decrease in the amount of \((\theta_{\hbox{max} } )_{\hbox{max} }\) results in an improvement in the performance of electronic components. As shown in Fig. 10, \((\theta_{\hbox{max} } )_{\hbox{max} }\) decreases with Rayleigh number due to an increase in the heat transfer and a decrease in the temperature. In addition, as the power-law index increases, the heat source maximum temperature increases. In fact, with increasing n, the concentration of fluid increases and the fluid moves more slowly. As a result, the shear stresses in the fluid become weaker and subsequently decrease the movement and the strength of vortices. This results in the accumulation of heat in the enclosure and therefore increases the maximum temperature.

Fig. 10
figure 10

Influence of Rayleigh number and power-law index on \((\theta_{\hbox{max} } )_{\hbox{max} }\)

Full size image

The effects of periodicity

The oscillating period of heat generation plays a critical role in the electronic cooling mechanism [36]. It is valuable to know how the maximum temperature of the heat source and the heat transfer change with the oscillation period. Figure 11 shows the periodic-state oscillation of \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\) for three complete periodic cycles at different oscillation periods. The enclosure is filled with a non-Newtonian dilatant fluid with n = 1.2 at Ra = 105. For a better comparison of the periodic results, dimensionless time on the horizontal axis is normalized by \(\tau_{\text{p}}\). It can be seen that as the oscillation period increases, the heat has more time to interact with the flow field, and as a result, the amplitude of oscillation for both \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\) increases. The fluid flow reaches the periodic steady state more quickly as the fluid oscillation period increases. There is not any noticeable change in the value of \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\) for the oscillation periods greater than 0.4.

Fig. 11
figure 11

Periodic-state time history for a\(Nu_{\text{m}}\) and b\(\theta_{\hbox{max} }\) for a non-Newtonian fluid (n = 1.2) at \(Ra = 10^{5}\) for different oscillation periods

Full size image

The effects of heat source location

Figure 12 shows the effect of the heat source location on the cooling performance of the enclosure. The study is carried out for both non-Newtonian and Newtonian fluids for \(Ra = 10^{5}\), \(\tau_{\text{p}} = 0.04\), and \(W_{\text{s}} = 0.5\). The value of \((\theta_{\hbox{max} } )_{\hbox{max} }\) is determined at different locations of the heat source on the bottom wall of the enclosure. It is demonstrated that \((\theta_{\hbox{max} } )_{\hbox{max} }\) increases as the power-law index (or apparent viscosity) increases. This is associated with a decrease in the heat transfer of the enclosure. This is due to the reduction in the strength of the vortices as the buoyancy forces are weakened. On the other hand, it can be observed that the location of the heat source on the lower wall does not have a significant effect on the heat transfer for both Newtonian and non-Newtonian fluids. Therefore, it is possible to place thermal elements in any place on the wall only based on the structural design requirements of the cooling device.

Fig. 12
figure 12

Effect of the location of heat source on \((\theta_{\hbox{max} } )_{\hbox{max} }\) at periodic steady state for Newtonian and non-Newtonian fluids at \(Ra = 10^{5}\) and \(\tau_{\text{p}} = 0.04\)

Full size image

Conclusions

Natural convection heat transfer in a square cavity filled with Newtonian and non-Newtonian power-law fluids is studied numerically. The influence of different effective parameters such as power-law index, Rayleigh number, oscillation, and heat source location on natural convection heat transfer is investigated. It is found that the heat generated by the heat source causes an oscillatory behavior of thermal and flow fields as well as thermal parameters such as \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\). The oscillation of these parameters follows the oscillation of the heat source with the same response frequency and a phase shift. The heat transfer decreases and the maximum temperature of the heat source increases with increasing power-law index. For non-Newtonian fluids, the apparent viscosity and the shear stress increase as the power-law index increases. On the other hand, an increase in the apparent viscosity results in a decrease in buoyancy forces and also in the heat transfer.

In general, the heat transfer of non-Newtonian pseudoplastic fluids is larger than Newtonian fluids and lower than dilatant fluids at similar conditions. It is also found that increasing the Rayleigh number is associated with increase in the strength of buoyant flow circulation cells, enhancing the heat removal from the heat source and therefore, decreasing the heat source maximum temperature. As the oscillation period increases, the heat has more time to interact with the flow field. As a result, the oscillation range increases for \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\). The fluid flow reaches a periodic steady state more quickly as the fluid oscillation period increases. There is not any noticeable change in the value of \(Nu_{\text{m}}\) and \(\theta_{\hbox{max} }\) for the oscillation periods greater than 0.4.

The location of the heat source on the lower wall does not have a significant effect on the heat transfer of Newtonian and non-Newtonian fluids. Therefore, it is possible to place thermal elements in any place on the wall that satisfies the design of cooling device. The authors believe that the findings of the present study will provide useful information for the electronics industry to keep the electronic components in safe and efficient operation conditions under oscillating heat production.