A Multi-Drug Pharmacokinectic Optimal Control Approach in Cancer Chemotherapy

Abstract

The mathematical study of the growth and treatment of cancer has been of great interest to researchers in the recent past as that can help clinical practitioners in adopting new treatment strategies to fight effectively against cancer. Although chemotherapy is the most common method of cancer treatment, the drug-resistant nature of tumor cells and the toxic effect of chemotherapeutic drugs on normal cells are major threats to the success of chemotherapy. In this paper, we propose a multi-drug chemotherapy model combined with an optimal control approach in which the amount of drugs is taken as control functions. The underlying mathematical model discusses the evolution of a heterogeneous tumor population and the dynamics of normal cells under chemotherapy. The model incorporates the pharmacokinetics of the anticancer agents as well. The proposed optimal control approach ensures maximum decay of the tumor cells while preserving a sufficient level of normal cells that would help faster recovery.

1 Introduction

Cancer, the abnormal growth of cells, is still one of the most deadly diseases, although different treatment processes are available. The scientists and medical practitioners working in these areas are looking for an effective treatment strategy to curtail the impact of this disease [11, 20]. Though many treatment techniques such as surgery, chemotherapy, radiation therapy, immunotherapy, targeted therapy, hormone therapy, stem cell transplant exist, chemotherapy is the most commonly used treatment method. A combination of chemotherapy with other techniques such as immunotherapy is also studied [2, 18, 21, 22]. The mathematical approach to studying this disease and the effectiveness of treatment became important among cancer researchers in the recent past as mathematical models can give more insight into the preclinical trials. The models can serve as a leading tool for research in chemotherapy to efficiently search and identify the most effective drug combinations for cancer patients [5, 12, 16, 24].

While studying the treatment mechanism of cancer, such as chemotherapy, it is essential to understand the growth of the tumor cells. There are different types of mathematical models of tumor growth available in the literature. At the earlier stages of the research, it was assumed that tumor cells are homogeneous, and the models addressed only a single type of tumor cells [27]. The growth of such cells is assumed to be either logistic or gomperztian. However, the biological study reveals that there are different types of tumor cells, and some cells are resistant to the treatment [9]. These drug-resistant tumor cells can be classified into two. Either the cells could be genetically resistant to a specific drug, or the resistance can be developed or induced from the interaction with the drug. In addition, there is a possibility of mutation of different groups of cells to one another [4, 8, 27]. Another significant hurdle to the success of chemotherapy is that the therapy can also affect the non-tumor normal cells. Therefore, the drugs should be administered in such a manner that the toxic effect of the treatment on normal cells is minimal. The success of the treatment depends on all the factors mentioned above. Hence, these crucial factors must be integrated into the mathematical model to have a more realistic approach.

Recently, Nanditha and Rajan [17] have proposed a better treatment protocol for single-drug chemotherapy. Similar works can be found in [3, 11, 12]. The theoretical and numerical study by [17] revealed that the sensitive tumor cells and mutated cells are reduced drastically at the end of the treatment. However, the resistant tumor cells are gradually increased at the end. Hence, it would be meaningful to administer another drug to destroy these drug-resistant tumor cells and thereby improve the efficiency of the treatment. The success of the treatment depends on how well we address the damage to the normal cells due to chemotherapy and the impact of the drug-resistant nature of tumor cells.

In this paper, we are trying to study the behavior of different types of cells during chemotherapy with the administration of multiple drugs. The proposed mathematical model analyzes the evolution of (i) a heterogeneous tumor population with three compartments and (ii) normal cells under the action of two different chemotherapeutic agents. In addition, the pharmacokinetics of the drugs injected into the patient is also incorporated. Further, we use control theory tools to design an optimal treatment strategy. The objective function of the optimal control problem ensures the minimization of the total number of tumor cells and the quantity of drugs administered. The goal of the optimal control problem is to minimize the tumor size and, at the same time, keep the number of normal cells at a healthy level by controlling the administration of the drugs with minimal toxic effects. Thus, our objective is to propose a model that results in a better treatment protocol.

The paper is organized as follows: In Sect. 2, we discuss the mathematical model that represents the evolution of different types of cells during chemotherapy. In Sect. 3, we study the tumor-free equilibrium points and their stability. We construct the optimal control problem and then analyze the existence of optimal control in Sect. 4. The characterization of optimal control is presented in Sect. 5. We conclude the paper by giving a numerical validation of the proposed theoretical results in Sect. 6 and with concluding remarks in Sect. 7.

2 Mathematical Model

In this section, we construct a mathematical model that incorporates the evolution of a heterogeneous tumor population and that of normal cells under the action of two different chemotherapeutic agents. Let N and V represent the normal cells and total volume of tumor cells, respectively. V is divided into three compartments, $S_{1}$, $S_{2}$, and $S_{3}$, according to its sensitivity toward different administered drugs. Let $S_{1}$ denote the tumor cell subpopulation that is sensitive to both drugs, $S_{2}$ be the tumor cell subpopulation that is resistant to the first drug but sensitive to the second drug, and $S_{3}$ be the third compartment of tumor cells which are resistant to the second drug but sensitive to the first drug. Thus, we have $V(t)=S_{1}(t)+S_{2}(t)+S_{3}(t)$ as the total number of tumor cells at any time t. Let $C_{1}$ and $C_{2}$ represent the concentration of the first and second drugs, respectively, at the tumor site at a specific time, and $\lambda _{1}$ and $\lambda _{2}$ be the clearance rates of the corresponding drugs. We use the logistic equation to model the growth of all types of cells with growth rates $r_{1},r_{2},r_{3}$, and $r_{4}$ for $S_{1}, S_{2}, S_{3}$, and N, respectively. Also, $K_{4},K_{1},K_{2}$, and $K_{3}$ represent the carrying capacity of normal cells and three types of tumor cells, respectively. We assume that the transition of tumor cells can occur within the compartments. Accordingly, a portion of the $S_{1}$ cells may convert into the other two compartments of cancer cells, $S_{2}$ and $S_{3}$, with a conversion rate of $\tau _{1}$ and $\tau _{2}$, respectively. Due to the drug’s action, drug-induced resistance can occur, resulting in a transition between $S_{2}$ and $S_{3}$ compartments. This is basically a genetic alteration accrued while developing resistance toward one agent accompanied by the development of hypersensitivity toward a second agent [19]. Hence, we assume that during the treatment, a portion of $S_{2}$ cells will become resistant to the second drug, but can be killed by the first drug, and a portion of $S_{3}$ cells will become resistant to the first drug but can be killed by the second drug. Therefore, the transition from $S_{2}$ to $S_{3}$ due to the action of the second drug is represented by $\tau _{23}(1-e^{-C_{2}})S_{2}$ with a conversion rate of $\tau _{23}.$ Similarly, the transition from $S_{3}$ to $S_{2}$ due to the action of the first drug is represented by $\tau _{32}(1-e^{-C_{1}})S_{3}$ with a conversion rate of $\tau _{32}.$ The toxic effect of administered drugs leads to the reduction of all types of cells. The killing effect of the first drug can be expressed as $a_{1}(1-e^{-C_{1}})S_{1}$, $a_{3}(1-e^{-C_{1}})S_{3}$, and $a_{N}(1-e^{-C_{1}})N$ for different types of cells. Similarly, the toxic effect of second chemotherapeutic agent on $S_{1}$, $S_{2}$, and N can be expressed as $b_{1}(1-e^{-C_{2}})S_{1}$, $a_{2}(1-e^{-C_{2}})S_{2}$, and $b_{N}(1-e^{-C_{2}})N$, respectively. It is also assumed that the sum of killing rates of the two drugs is much less than the natural growth rate of normal cells, i.e., $a_{N}+b_{N} < r_{4}$. The interaction between the tumor and normal cells is represented by $\gamma V(1-\frac{V}{T^{*}})$, where $T^{*}$ is the critical size of collection of tumor cells, and $\gamma$ has the unit of $time^{-1}$ [5]. Let the amount of first and second drugs injected at time t be denoted as u(t) and v(t), respectively. Hence, the proposed model is given by:

$$\begin{aligned} \frac{\hbox {d}S_{1}}{\hbox {d}t}= & {} r_{1}S_{1}\left( 1-\frac{V}{K_{1}}\right) -\tau _{1}S_{1}-\tau _{2}S_{1}-a_{1}(1-e^{-C_{1}})S_{1}-b_{1}(1-e^{-C_{2}})S_{1}, \nonumber \\ \frac{\hbox {d}S_{2}}{\hbox {d}t}= & {} r_{2}S_{2}\left( 1-\frac{V}{K_{2}}\right) +\tau _{1}S_{1}-a_{2}(1-e^{-C_{2}})S_{2}-\tau _{23}(1-e^{-C_{2}})S_{2}+\tau _{32}(1-e^{-C_{1}})S_{3}, \nonumber \\ \frac{\hbox {d}S_{3}}{\hbox {d}t}= & {} r_{3}S_{3}\left( 1-\frac{V}{K_{3}}\right) +\tau _{2}S_{1}-a_{3}(1-e^{-C_{1}})S_{3}-\tau _{32}(1-e^{-C_{1}})S_{3}+\tau _{23}(1-e^{-C_{2}})S_{2}, \nonumber \\ \frac{\hbox {d}N}{\hbox {d}t}= & {} r_{4}N\left( 1-\frac{N}{K_{4}}\right) +\gamma V\left( 1-\frac{V}{T^{*}}\right) -a_{N}(1-e^{-C_{1}})N-b_{N}(1-e^{-C_{2}})N,\nonumber \\ \frac{\hbox {d}C_{1}}{\hbox {d}t}= & {} u-\lambda _{1} C_{1},\nonumber \\ \frac{\hbox {d}C_{2}}{\hbox {d}t}= & {} v-\lambda _{2} C_{2}. \end{aligned}$$

(2.1)

The last two equations represent the pharmacokinetics of the two drugs used in therapy. All parameters in the proposed model are taken as positive. We use the following initial conditions:

$$\begin{aligned} S_{1}(0)=S_{0}^{1}, S_{2}(0)=S_{0}^{2}, S_{3}(0)=S_{0}^{3}, N(0)=N_{0}, C_{1}(0)=C_{0}^{1}, \text {and} C_{2}(0)=C_{0}^{2}.\nonumber \\ \end{aligned}$$

(2.2)

3 Steady States and Stability Analysis

In this section, we study the stability of tumor-free equilibrium points of the system. The equilibrium points of the system (2.1) are obtained by equating each equation in (2.1) to zero. Since we are considering tumor-free steady states, let us take $S_{1}=S_{2}=S_{3}=0$.

• 1. Drug-free, tumor-free equilibrium points: In the absence of chemotherapy drugs, we have $C_{1}=0$ and $C_{2}=0$. Then, we can see that $E_{1}=(0,0,0,0)$ and $E_{2}=(0,0,0,K_{4})$ are two equilibrium points. Here, the trivial equilibrium point $E_{1}$ is biologically insignificant. Some eigenvalues of the Jacobian matrix of the system at the point $E_{2}$ are positive. This means that point $E_{2}$ is unstable. It suggests that without any drug administration, the tumor size cannot be diminished to zero.

• 2. Tumor-free equilibrium points with the administration of a single drug: In this case, we examine the stability of the tumor-free equilibrium points in the presence of the first drug but in the absence of the second drug. Therefore, we have $C_{1}\ne 0$ and $C_{2}=0$ in this scenario. Then, we can see that $E_{3}=(0,0,0,N_{2}^{*},C_{1}^{*})$ is the only non-trivial steady state. Here, $N_{2}^{*}=K_{4}(1-(\frac{a_{N}}{r_{4}}(1-e^{-C_{1}^{*}}))$ and $C_{1}^{*}= \frac{u}{\lambda _{1}}$. It can be easily computed that $r_{3}$ is a positive eigenvalue of the Jacobian matrix of the system at the point $E_{3}$. This indicates that the point $E_{3}$ could be unstable. In other words, it implies that the administration of a single drug might not be enough to curtail the growth of the tumor.

• 3. Tumor-free equilibrium points with the administration of multiple drugs: In this case, we try to analyze the stability of the equilibrium points under the action of multiple drugs, i.e., both $C_{1}$ and $C_{2}$ are nonzero. Apart from the trivial point, $E_{4}=(0,0,0,N_{3}^{*},C_{1}^{*},C_{2}^{*})$ is the only steady state in this case. Here, $N_{3}^{*}=K_{4}(1-\frac{1}{r_{4}}(a_{N}(1-e^{-C_{1}^{*}})+b_{N}(1-e^{-C_{2}^{*}})))$, $C_{2}^{*}=\frac{v}{\lambda _{2}}$, and $C_{1}^{*}$ is same as above. It can be easily seen that the equilibrium point $E_{4}$ can be made stable if we impose some conditions on the drug administration rates u and v.

4 Optimal Control Problem

In this section, we pose the optimal control problem that minimizes the tumor growth and the toxic effect of anticancer agents while keeping the normal cells at a healthy level by controlling the administration of drugs. Let $[0,t_{f}]$ be the chemotherapy interval. Let us assume that the control functions u(t) and v(t) satisfy the following:

$$\begin{aligned} 0 \le u(t) \le u_\mathrm{max}< \infty ,\quad 0\le v(t)\le v_\mathrm{max}< \infty , \quad \forall t \in [0,t_{f}]. \end{aligned}$$

(4.1)

The function u(t) and v(t) are called admissible controls if they satisfy (4.1). The set of all admissible controls forms an admissible set U, i.e.,

$$\begin{aligned} U=\{(u,v)\in L^{\infty }([0,t_{f}], \mathbb {R}^{2}):u(t),v(t) \text {satisfy} (4.3) \}. \end{aligned}$$

(4.2)

We consider the following functional as the objective function of the control problem:

$$\begin{aligned} J(x,u,v)= \int ^{t_{f}}_{0} (qZ(t)+\beta _{1}u(t)+\beta _{2}v(t))\hbox {d}t, \end{aligned}$$

(4.3)

where $Z(t)=(S_{1}(t),S_{2}(t),S_{3}(t))^{T}$ and $q=(q_{1},q_{2},q_{3})$, $\beta _{1}$, and $\beta _{2}$ are positive weights. Hence, our objective function is of the form

$$\begin{aligned} J(x,u,v)= \int ^{t_{f}}_{0} (q_{1}S_{1}(t)+q_{2}S_{2}(t)+q_{3}S_{3}(t)+\beta _{1}u(t)+\beta _{2}v(t))\hbox {d}t. \end{aligned}$$

(4.4)

We now introduce a new constraint to the problem that ensures the patient’s wellness by limiting the toxicity of the injected drugs. The new constraint is that the total drug administered is limited by a constant c, i.e.,

$$\begin{aligned} \int _{0}^{t_{f}}(u+v)\hbox {d}t \le c. \end{aligned}$$

(4.5)

The above integral constraint can be incorporated into the model by introducing a new state variable M. Then, the constraint (4.5) can be expressed equivalently as

$$\begin{aligned} \frac{\hbox {d}M}{\hbox {d}t}=u+v \end{aligned}$$

(4.6)

with the boundary conditions $M(0)=0$ and $M(t_{f})\le c$. This modification produces a terminal inequality constraint.

In addition to (4.5), we impose another constraint that the chemotherapy does not kill too many healthy cells, i.e., we require that the number of normal cells stays above $75\%$ of the carrying capacity throughout the treatment. Thus, the state constraint is given by

$$\begin{aligned} N(t)-0.75K_{4}\ge 0. \end{aligned}$$

(4.7)

We reformulate (2.1) by incorporating the additional state Eq. (4.6) as,

$$\begin{aligned} \begin{aligned}&x^\prime (t)=f(t,x(t),u(t), v(t)),\quad t \in [0,t_{f}],\\&x(0)=x_{0},\\&M(t_{f}) \le c, \end{aligned} \end{aligned}$$

(4.8)

where $x=(S_{1},S_{2},S_{3},N,C_{1},C_{2},M) \in \mathbb {R}^{7}$ and $x_0 = ( S_{0}^{1}, S_{0}^{2}, S_{0}^{3}, N_{0}, C_{0}^{1}, C_{0}^{2},0).$

We can easily see that Theorems 4.1 and 4.2 are true for system (4.8).

Theorem 4.1

Solution of the system (4.8) is nonnegative for all $t \in [0,t_{f}]$ if the initial values are nonnegative.

Theorem 4.2

Every solution of model (4.8) is bounded for all t in $[0,t_{f}]$.

Now, our problem is to find a control $(u^{*},v^{*})$ in U such that it minimizes the objective functional J(x, u, v) in (4.3) subject to the constraints (4.8), (4.1), and (4.7). Then $(u^{*},v^{*})$ is referred to as optimal control. In the following section, we discuss the existence of an optimal control, $(u^{*},v^{*})$.

4.1 Existence of Optimal Control

Let us recall the optimal control problem for the sake of convenience:

$$\begin{aligned} \hbox {minimize}J(x,u,v)= \int ^{t_{f}}_{0} (qZ(t)+\beta _{1}u(t)+\beta _{2}v(t))\hbox {d}t \end{aligned}$$

(4.9)

subject to

$$\begin{aligned} \begin{aligned}&x^\prime (t)=f(t,x(t),u(t), v(t)),\quad t \in [0,t_{f}],\\&x(0)=x_{0},\\&M(t_{f}) \le c, \end{aligned} \end{aligned}$$

(4.10)

with control constraints

$$\begin{aligned} 0 \le u(t) \le u_\mathrm{max}< \infty ,\quad 0\le v(t)\le v_\mathrm{max}< \infty , \quad \forall t \in [0,t_{f}], \end{aligned}$$

(4.11)

and the state constraint

$$\begin{aligned} N(t)-0.75K_{4}\ge 0. \end{aligned}$$

(4.12)

The following theorem establishes the existence of optimal control for the problem (4.9) to (4.12). We use some results from [1, 6] for this purpose.

Theorem 4.3

Suppose that we have an optimal control problem of the form (4.9)–(4.12). Then, there exists an optimal solution $(x^{*},u^{*},v^{*})\in W^{1,\infty }([0,t_{f}], \mathbb {R}^{7})\times L^{\infty }([0,t_{f}],\mathbb {R}^{2})$ such that

$$\begin{aligned} J(u^{*},v^{*})=min\{J(u,v): (u,v) \in U\}. \end{aligned}$$

(4.13)

Proof

In order to prove Theorem 4.3, we make use of Theorem 1 [6] or Theorem 4.1 [1], and accordingly, we need to prove that the following conditions must be satisfied for the existence of $(x^{*},u^{*},v^{*})$:

• 1. There exists an admissible solution pair.

• 2. If $N(x,U,t)=\{(qZ(t)+\beta _{1}u(t)+\beta _{2}v(t)+\gamma ,f(t,x,u,v)):\gamma \le 0,(u,v) \in U\}$, then N(x, U, t) is convex in U for each (x, t).

• 3. U is closed and bounded.

• 4. There exists a number $\theta$ such that $\Vert x(t)\Vert \le \theta$ for all $t \in [0, t_{f}]$ and for all admissible solutions.

However, to prove the first condition, we need to prove the following result [23]:

• (a) f(., u, v) is continuous for all $(u,v) \in U.$

• (b) There exists positive constants $K_{1}$ and $K_{2}$ such that for all $(x,y,u,v) \in (\mathbb {R}^{7}_{+})^{2} \times U$,

  $$\begin{aligned} |f(x,u,v)| \le K_{1}(1+|x|+|u|+|v|) \end{aligned}$$

  (4.14)

  and

  $$\begin{aligned} |f(y,u,v)-f(x,u,v)| \le K_{2} |y-x|(1+|u|+|v|). \end{aligned}$$

  (4.15)

• (c) U is non-empty.

It can be easily seen from (2.1) that f(., u, v) is continuous. We further note that the continuity of the function f and the conditions (4.14) and (4.15) assure the existence of a solution of the system (2.1) [23].

Consider,

$$\begin{aligned} \begin{aligned} |f(x,u,v)|&\le (r_{1}+2\tau _{1}+2\tau _{2}+a_{1}+b_{1}+\gamma )|S_{1}|+(r_{2}+\gamma +a_{2}+2\tau _{23})\\&\quad |S_{2}|+(2\tau _{32}+r_{3}+a_{3}+\gamma )|S_{3}|+ (r_{4}+a_{N}+b_{N})|N| \\&\;\, +\lambda _{1} |C_{1}| +\lambda _{2} |C_{2}|+ \gamma \frac{|V_\mathrm{max}|^{2}}{T^{*}}+ 2(|u|+|v|), \end{aligned} \end{aligned}$$

where $|V| = |S_{1}+S_{2}+S_{3}|\le M_{1}+M_{2}+M_{3}=V_\mathrm{max}$, and $M_{1},M_{2}$, and $M_{3}$ are bounds of $S_{1},S_{2}$, and $S_{3}$, respectively.

Thus, we have

$$\begin{aligned} |f(x,u,v)| \le K_{1}(1+|x|+|u|+|v|), \end{aligned}$$

(4.16)

where

$$\begin{aligned} \begin{aligned} K_{1}&= \max \{r_{1}+2\tau _{1}+2\tau _{2}+a_{1}+b_{1}+\gamma ,r_{2}+a_{2}+\gamma +2\tau _{23}, 2\tau _{32}+ r_{3}\\&\quad +a_{3}+\gamma ,r_{4}+a_{N}+b_{N},\lambda _{1},\lambda _{2} , \gamma \frac{|V_\mathrm{max}|^{2}}{T^{*}},2\}. \end{aligned} \end{aligned}$$

Let $(x=[S_{1},S_{2},S_{3},N,C_{1},C_{2},M],y=[S'_{1},S'_{2}, S'_{3},N',C_{1}',C_{2}',M']) \in (\mathbb {R}^{7}_{+})^{2}$, and $(u,v) \in U$. Then from (2.1), we can write

$$\begin{aligned} \begin{aligned}&|f(y,u,v)-f(x,u,v)| \le \\&[r_{1}+2\tau _{1}+2\tau _{2}+2a_{1}+2b_{1}+\frac{r_{1}}{K_{1}}(2M_{1}+M_{2}+M_{3})\\&+\gamma + 2\gamma \frac{|V_\mathrm{max}|}{T^{*}}]|S'_{1}-S_{1}|+[r_{2}+ 2\tau _{23}+\gamma \\&+\frac{r_{2}}{K_{2}}(2M_{2}+M_{1}+M_{2})+2\gamma \frac{|V_\mathrm{max}|}{T^{*}})+2a_{2}]|S'_{2}-S_{2}|\\&+[r_{3}+2\tau _{32}+2a_{3}+ \gamma +\frac{r_{3}}{K_{3}}(2M_{3}+M_{2}+M_{1})\\&+2\gamma \frac{|V_\mathrm{max}|}{T^{*}}]|S'_{3}-S_{3}|+[r_{4}+2a_{N}+2b_{N}]|N'-N|\\&+[\lambda _{1}+a_{1}|M_{1}|+a_{3}|M_{3}|+2\tau _{32}|M_{3}|\\&+a_{N}|M_{4}|]|C_{1}'-C_{1}|+[b_{1}|M_{1}|+a_{2}|M_{2}|+2\tau _{23}|M_{2}|\\&+b_{N}|M_{4}|+\lambda _{2}]|C_{2}'-C_{2}|\\ \le&K_{2} (|y-x|)\\ \le&K_{2} |y-x| (1+|u|+|v|), \end{aligned} \end{aligned}$$

(4.17)

where $K_{2}$ is the maximum value of the coefficients and N is bounded by $M_{4}$.

Clearly, U is non-empty. Hence, there exists an admissible pair for the control problem.

Also, from the definition of the admissible control set U in (4.2), it can be easily shown that U is closed, bounded, and convex. The convexity of N(x, U, t) follows directly from the fact that U is convex. Moreover, from Theorem 4.2, we see that the fourth condition holds as well. This completes the proof of the theorem. $\square$

5 Characterization of Optimal Control

In the previous section, we discussed the existence of optimal control for the problem (4.9)–(4.12). Now, we derive the representations of the optimal control. In order to do this, we need to discuss certain necessary conditions for optimality. We make use of the Pontryagin’s minimum principle [1, 7, 13, 26], conditions from S.P. Sethi et al. [25] and Kamien et al. [10], and the generalized Legendre–Clebsch conditions [1, 14] for this purpose.

Theorem 5.1

Let $(u^{*},v^{*})$ be an optimal control of (4.9)– (4.12), and $x^{*}=[S_{1}^{*},S_{2}^{*},S_{3}^{*},N^{*},C_{1}^{*},C_{2}^{*},M^{*}]$ be the corresponding state vector. Then, there exist an adjoint state $p\in W^{1,\infty }([0,t_{f}],\mathbb {R}^{7})$ and a multiplier function $\eta \in L^{\infty }([0,t_{f}],\mathbb {R})$ satisfying the following:

$$\begin{aligned} \dot{p_{1}}= & {} -\left[ q_{1}+p_{1}\left[ r_{1}\left( 1-\frac{V}{K_{1}} -\frac{S_{1}}{K_{1}}\right) -\tau _{1}-\tau _{2} -a_{1}(1-e^{-C_{1}})-b_{1}(1-e^{-C_{2}})\right] \right. \nonumber \\&\left. +p_{2}\left( -\frac{r_{2}S_{2}}{K_{2}}+\tau _{1}\right) +p_{3} \left( -\frac{r_{3}S_{3}}{K_{3}} +\tau _{2}\right) +p_{4}\gamma \left( 1-\frac{2V}{T^{*}}\right) \right] , \nonumber \\ \dot{p_{2}}= & {} -\left[ q_{2}+ p_{1}\left( -\frac{r_{1}S_{1}}{K_{1}}\right) +p_{2} \left[ r_{2}\left( 1-\frac{V}{K_{2}}-\frac{S_{2}}{K_{2}}\right) -a_{2}(1-e^{-C_{2}})\right. \right. \nonumber \\&\left. \left. -\tau _{23}(1-e^{-C_{2}})\right] +p_{3}\left( -\frac{r_{3}S_{3}}{K_{3}}+ \tau _{23}(1-e^{-C_{2}})\right) + p_{4}\gamma \left( 1-\frac{2V}{T^{*}}\right) \right] , \nonumber \\ \dot{p_{3}}= & {} -\left[ q_{3}+p_{1} \left( -\frac{r_{1}S_{1}}{K_{1}}\right) +p_{2}\left( -\frac{r_{2}S_{2}}{K_{2}} +\tau _{32}(1-e^{-C_{1}})\right) \right. \nonumber \\&\left. +p_{3}[r_{3}\left( 1-\frac{V}{K_{3}}-\frac{S_{3}}{K_{3}}\right) -a_{3}(1-e^{-C_{1}})-\tau _{32}(1-e^{-C_{1}})]+p_{4}\gamma \left( 1-\frac{2V}{T^{*}}\right) \right] , \nonumber \\ \dot{p_{4}}= & {} -p_{4}(r_{4}\left( 1-\frac{2N}{K_{4}}\right) -a_{N}(1-e^{-C_{1}})-b_{N}(1-e^{-C_{2}}))+\eta , \nonumber \\ \dot{p_{5}}= & {} p_{1}a_{1}e^{-C_{1}}S_{1}-p_{2}\tau _{32}e^{-C_{1}}S_{3}+p_{3}(a_{3}e^{-C_{1}}S_{3}+\tau _{32}e^{-C_{1}}S_{3}) \nonumber \\&+p_{4}a_{N}e^{-C_{1}}N+p_{5}\lambda _{1}, \nonumber \\ \dot{p_{6}}= & {} p_{1}b_{1}e^{-C_{2}}S_{1}+p_{2}(a_{2}e^{-C_{2}}S_{2}+\tau _{23}e^{-C_{2}}S_{2})-p_{3}\tau _{23}e^{-C_{2}}S_{2} \nonumber \\&+p_{4}b_{N}e^{-C_{2}}N+p_{6}\lambda _{2},\nonumber \\ \dot{p_{7}}= & {} 0, \end{aligned}$$

(5.1)

where $p_{i}(t_{f})=0$ for $i=1,2,\ldots , 6$,

$$\begin{aligned} p_{7}(t_{f})=-\alpha ,\quad \alpha \le 0\quad \text {and}\quad \alpha (c-M(t_{f}))=0. \end{aligned}$$

(5.2)

Furthermore, $u^{*}$ and $v^{*}$ are given by

$$\begin{aligned}u^{*}= {\left\{ \begin{array}{ll} 0 &{} \psi _{1}>0 \\ u_\mathrm{max} &{} \psi _{1}<0 \\ singular/boundary &{} \psi _{1}=0, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned}v^{*}= {\left\{ \begin{array}{ll} 0 &{} \psi _{2}>0 \\ v_\mathrm{max} &{} \psi _{2}<0 \\ singular/boundary &{} \psi _{2}=0, \end{array}\right. } \end{aligned}$$

where $\psi _{1}=p_{5}+p_{7}+\beta _{1}$ and $\psi _{2}=p_{6}+p_{7}+\beta _{2}$ .

Proof

We have a pure state constraint, namely $S:= N(t)-0.75K_{4}\ge 0$, and the control functions satisfy the inequalities $0 \le u(t) \le u_\mathrm{max}$, and $0 \le v(t) \le v_\mathrm{max}$ for all $t \in [0,t_{f}]$. Let us take $u_\mathrm{max}=1=v_\mathrm{max}$ for simplicity. Then, the Lagrangian associated with this problem is:

$$\begin{aligned} L = H-w_{1}u-w_{2}(1-u)-w_{3}v-w_{4}(1-v)-\eta S, \end{aligned}$$

(5.3)

where H is the Hamiltonian defined by

$$\begin{aligned} \begin{aligned} H=&\, qZ+\beta _{1}u+\beta _{2}v+p_{1}(r_{1}S_{1}(1-\frac{V}{K_{1}})-\tau _{1}S_{1}-\tau _{2}S_{1}-a_{1}(1-e^{-C_{1}})S_{1}\\&-b_{1}(1-e^{-C_{2}})S_{1})+p_{2} (r_{2}S_{2}(1-\frac{V}{K_{2}})+\tau _{1}S_{1}+\tau _{32}(1-e^{-C_{1}})S_{3}\\&-a_{2}(1-e^{-C_{2}})S_{2}-\tau _{23}(1-e^{-C_{2}})S_{2})+p_{3} (r_{3}S_{3}(1-\frac{V}{K_{3}})+\tau _{2}S_{1}\\&-a_{3}(1-e^{-C_{1}})S_{3}-\tau _{32}(1-e^{-C_{1}})S_{3}+\tau _{23}(1-e^{-C_{2}})S_{2})+\\&p_{4} (r_{4}N(1-\frac{N}{K_{4}})+\gamma V(1-\frac{V}{T^{*}})-a_{N}(1-e^{-C_{1}})N-b_{N}(1-e^{-C_{2}})N)\\&+p_{5} (u-\lambda _{1} C_{1})+p_{6}(v-\lambda _{2} C_{2})+p_{7}(u+v). \end{aligned} \end{aligned}$$

(5.4)

The penalty multipliers $w_{1},w_{2},w_{3},w_{4}$, and $\eta$ satisfy the following complementary slackness conditions:

$$\begin{aligned} \begin{aligned}&w_{1} \ge 0, w_{1}u=0,\\&w_{2} \ge 0, w_{2}(1-u)=0,\\ \end{aligned} \end{aligned}$$

(5.5)

at the optimal $u^{*}$,

$$\begin{aligned} \begin{aligned}&w_{3} \ge 0, w_{3}v=0,\\&w_{4} \ge 0, w_{4}(1-v)=0, \end{aligned} \end{aligned}$$

(5.6)

at the optimal $v^{*}$, and

$$\begin{aligned} \eta \ge 0, \eta S= 0 {\text { at }} N^{*}. \end{aligned}$$

(5.7)

The adjoint Eq. (5.1) are formed from differentiating the Lagrangian, that is,

$$\begin{aligned} p^{\prime }(t)=-\frac{\partial L}{\partial x}(t). \end{aligned}$$

(5.8)

In addition, the final conditions are free for all state variables except M. Thus, we have $p_{i}(t_{f})=0$ for $i=1,2,\ldots ,6$. The terminal inequality constraint imposes an additional transversality condition given by (5.2) [1, 10].

Since the Lagrangian is linear in both u and v, the representations of the optimal controls can be determined from the sign of switching functions, $\frac{\partial L}{\partial u}$ and $\frac{\partial L}{\partial v}$.

$$\begin{aligned} \frac{\partial L}{\partial u}=\frac{\partial H}{\partial u}-w_{1}+w_{2}=p_{5}+p_{7}+\beta _{1}-w_{1}+w_{2}, \end{aligned}$$

(5.9)

and

$$\begin{aligned} \frac{\partial L}{\partial v}=\frac{\partial H}{\partial v}-w_{3}+w_{4}=p_{6}+p_{7}+\beta _{2}-w_{3}+w_{4}. \end{aligned}$$

(5.10)

Equivalently, we can consider the sign of $\psi _{1}=\frac{\partial H}{\partial u}$ and $\psi _{2}=\frac{\partial H}{\partial v}$ to determine the values of optimal controls $u^{*}$ and $v^{*}$ [10]. Hence, we characterize the optimal controls as:

$$\begin{aligned}u^{*}= {\left\{ \begin{array}{ll} 0 &{} \psi _{1}>0 \\ u_\mathrm{max} &{} \psi _{1}<0 \\ singular/boundary &{} \psi _{1}=0, \end{array}\right. } \end{aligned}$$

and

$$\begin{aligned}v^{*}= {\left\{ \begin{array}{ll} 0 &{} \psi _{2}>0 \\ v_\mathrm{max} &{} \psi _{2}<0 \\ singular/boundary &{} \psi _{2}=0 . \end{array}\right. } \end{aligned}$$

The proof is complete. $\square$

In the following section, we present a detailed analysis of both singular and boundary controls.

5.1 Singular Controls and Boundary Controls

In our problem, the Hamiltonian is linear in the control functions u and v. The coefficient of u and v in H could be equal to zero only for isolated instants. In such a case, the control is bang-bang. In other words, the control is a piecewise constant function, switching between its upper and lower bounds. Let

$$\begin{aligned} \psi _{1}:= p_{5}+p_{7}+\beta _{1} \text {and} \psi _{2}: =p_{6}+p_{7}+\beta _{2}. \end{aligned}$$

(5.11)

If the switching functions are zero on a subinterval of $[0,t_{f}]$, then the control is singular on that interval. Investigating the possibility of a singular subarc, $\psi _{i} = 0$ for $i=1,2$, with the state constraint S results in two possible solutions, an interior subarc and a boundary subarc (cf. [25]). We note that a solution is an interior subarc if $S >0$, and is a boundary subarc if $S = 0$. We will examine the representations of singular controls and the conditions necessary for the controls to be minimizing in the singular region, provided that the representations of the singular controls satisfy the control bounds. Note that each interval of singularity is a subinterval of $[0, t_{f}]$. In the following, we claim that the control in the interior is bang-bang control.

Theorem 5.2

Suppose that (u, v) be an optimal control of (4.9)–(4.12), then both u and v are bang-bang in the interior.

Proof

We prove the theorem by contradiction. We consider three different cases of control functions on a subinterval of $[0,t_{f}]$; namely, u is singular and v is bang-bang; u is bang-bang and v is singular, and both u and v are simultaneously singular.

Let u be a singular subarc on the interval $[t_{1u},t_{2u}] \subseteq [0,t_{f}]$ and v be bang-bang. For the interior subarc u, the switching function $\psi _{1}=0$ and the state constraint $S>0$. In this case, the characterization of the control in singular region is determined by taking the time derivatives of switching function (cf. [14, 25]). On the interval $[t_{1u},t_{2u}]$, the time derivatives of $\psi _{1}$ is zero. Thus,

$$\begin{aligned} \frac{\hbox {d}\psi _{1}}{\hbox {d}t}=p'_{5}=0. \end{aligned}$$

(5.12)

Taking the second derivative will give,

$$\begin{aligned} \frac{\hbox {d}^{2}\psi _{1}}{\hbox {d}t^{2}}=p^{\prime \prime }_{5}=A_{1}-(u-\lambda _{1}C_{1})B_{1}, \end{aligned}$$

(5.13)

where

$$\begin{aligned} A_{1}= & {} a_{1}p_{1}e^{-C_{1}}S'_{1}+a_{1}p'_{1}e^{-C_{1}}S_{1}-\tau _{32}p_{2}e^{-C_{1}}S'_{3}-\tau _{32}p'_{2}e^{-C_{1}}S_{3}\nonumber \\&+a_{3}p_{3}e^{-C_{1}}S'_{3}+a_{3}p'_{3}e^{-C_{1}}S_{3}+\tau _{32}p_{3}e^{-C_{1}}S'_{3}+\tau _{32}p'_{3}e^{-C_{1}}S_{3}\nonumber \\&+a_{N}p_{4}e^{-C_{1}}N'+a_{N}p'_{4}e^{-C_{1}}N+p'_{5}\lambda _{1}, \end{aligned}$$

(5.14)

$$\begin{aligned} B_{1}=&a_{1}p_{1}e^{-C_{1}}S_{1}-\tau _{32}p_{2}e^{-C_{1}}S_{3}+a_{3}p_{3}e^{-C_{1}}S_{3}+\tau _{32}p_{3}e^{-C_{1}}S_{3}\nonumber \\&+a_{N}p_{4}e^{-C_{1}}N. \end{aligned}$$

(5.15)

Hence, the control function u appears explicitly in the second derivative of the switching function. Therefore, the singularity is of order one. Since the control v is assumed to be bang-bang on the interval $[t_{1u},t_{2u}]$, the Legendre–Clebsch condition for the control to be minimizing is,

$$\begin{aligned} (-1)\frac{\partial }{\partial u}\frac{\hbox {d}^{2}\psi _{1}}{\hbox {d}t^{2}} \ge 0. \end{aligned}$$

(5.16)

Thus, $B_{1}\ge 0$. Now, from the expression of $p^\prime _{5}$ in (5.1) and that of $B_{1}$ in (5.15), it is clear that

$$\begin{aligned} p'_{5}=B_{1}+p_{5}\lambda _{1} \ge p_{5}\lambda _{1}. \end{aligned}$$

(5.17)

In other words,

$$\begin{aligned} p_{5} \ge e^{\lambda _{1}t}>0 \text {for all} t \in [t_{1u},t_{2u}]. \end{aligned}$$

(5.18)

This is a contradiction to the fact that $p_{5}+\beta _{1}+p_{7}=0$ throughout the interval since $\beta _{1}$ and $p_{7}$ are nonnegative. Hence, the singular control u is not optimal on any subinterval of $[0,t_{f}]$ if the control v is assumed to be bang-bang on that interval. Now, we consider the case of v being singular and u being bang-bang on some subinterval $[t_{1v},t_{2v}]$. We can see in the following equation that the control v is explicitly present in the second derivative of $\psi _{2}$:

$$\begin{aligned} \frac{\hbox {d}^{2}\psi _{2}}{\hbox {d}t^{2}}=p^{\prime \prime }_{6}=A_{3}-(v-\lambda _{2} C_{2})B_{3}, \end{aligned}$$

(5.19)

where

$$\begin{aligned} \begin{aligned} A_{3}&=b_{1}p_{1}e^{-C_{2}}S'_{1}+b_{1}p'_{1}e^{-C_{2}}S_{1}+a_{2}p_{2}e^{-C_{2}}S'_{2}+a_{2}p'_{2}e^{-C_{2}}S_{2}\\&\quad +\tau _{23}p_{2}e^{-C_{2}}S'_{2}+\tau _{23}p'_{2}e^{-C_{2}}S_{2}-\tau _{23}p_{3}e^{-C_{2}}S'_{2}-\tau _{23}p'_{3}e^{-C_{2}}S_{2}\\&\quad +b_{N}p_{4}e^{-C_{2}}N'+b_{N}p'_{4}e^{-C_{2}}N+p'_{6}\lambda _{2}, \end{aligned} \end{aligned}$$

(5.20)

and

$$\begin{aligned} \begin{aligned} B_{3}&=b_{1}p_{1}e^{-C_{2}}S_{1}+a_{2}p_{2}e^{-C_{2}}S_{2}+\tau _{23}p_{2}e^{-C_{2}}S_{2}-\tau _{23}p_{3}e^{-C_{2}}S_{2}\\&\quad +b_{N}p_{4}e^{-C_{2}}N. \end{aligned} \end{aligned}$$

(5.21)

On applying the Legendre–Clebsch condition, we get $B_{3} \ge 0$. From (5.1) and (5.21), one can see that

$$\begin{aligned} p'_{6}=B_{3}+p_{6}\lambda _{2} \ge p_{6}\lambda _{2}, \end{aligned}$$

(5.22)

that is,

$$\begin{aligned} p_{6} \ge e^{\lambda _{2}t}>0 \text {for all}t \in [t_{1v},t_{2v}]. \end{aligned}$$

(5.23)

This is a contradiction to the fact that $p_{6}+\beta _{2}+p_{7}=0$ throughout the interval. Hence, the singular control v cannot be optimal on any subinterval of $[0,t_{f}]$ if the control u is assumed to be bang-bang on that interval.

Now we derive the necessary conditions when both the controls are simultaneously singular on the same interval, $[t_{1},t_{2}] \subseteq [0,t_{f}]$. Then, by generalized Legendre–Clebsch condition, for the control u and v to be minimizing on the interval $[t_{1},t_{2}]$, the following matrix should be symmetric and nonnegative definite [1]:

$$\begin{aligned} A=\begin{pmatrix} (-1)\frac{\partial }{\partial u}\frac{\hbox {d}^{2}\psi _{1}}{\hbox {d}t^{2}} &{} (-1)\frac{\partial }{\partial v}\frac{\hbox {d}^{2}\psi _{1}}{\hbox {d}t^{2}} \\ (-1)\frac{\partial }{\partial u}\frac{\hbox {d}^{2}\psi _{2}}{\hbox {d}t^{2}} &{} (-1)\frac{\partial }{\partial v}\frac{\hbox {d}^{2}\psi _{2}}{\hbox {d}t^{2}} \end{pmatrix}. \end{aligned}$$

Here, the matrix A can be computed as

$$\begin{aligned} A=\begin{pmatrix} B_{1} &{} 0\\ 0 &{} B_{3} \end{pmatrix}. \end{aligned}$$

Clearly, the matrix is symmetric. Also, A is nonnegative definite if all the principle minors of A are nonnegative, that is, if $B_{1}\ge 0 \text {and} B_{3}\ge 0$. Now, these two conditions will lead to the conclusion that $p_{5}>0$ and $p_{6}>0$, as in (5.18) and (5.23), respectively. Hence, both the controls must be bang-bang for it to be optimal. $\square$

The following results provide the expression of the controls on the boundary.

Theorem 5.3

If u is a boundary subarc on the interval $[t_{1u},t_{2u}] \subseteq [0,t_{f}]$, then the representation of the control is given by

$$\begin{aligned} u_{b}=\frac{A_{2}}{a_{N}e^{-C_{1}}N}+\lambda _{1}C_{1}, \end{aligned}$$

(5.24)

where

$$\begin{aligned} \begin{aligned} A_{2}&=r_{4}N'(1-\frac{2N}{K_{4}})+\gamma V'(1-\frac{2V}{T^{*}})-a_{N}(1-e^{-C_{1}})N'\\&\quad -b_{N}(1-e^{-C_{2}})N'-b_{N}e^{-C_{2}}NC'_{2}. \end{aligned} \end{aligned}$$

(5.25)

Proof

For boundary subarc, the state constraint $S=0$. Taking a first time derivative of S yields

$$\begin{aligned} \begin{aligned} \frac{\hbox {d}S}{\hbox {d}t}=\frac{\hbox {d}N}{\hbox {d}t}&= r_{4}N(1-\frac{N}{K_{4}})+\gamma V(1-\frac{V}{T^{*}})-a_{N}(1-e^{-C_{1}})N\\&\quad -b_{N}(1-e^{-C_{2}})N. \end{aligned} \end{aligned}$$

Notice that the first derivative does not contain the control term explicitly. Hence, we will compute the second time derivative of S.

$$\begin{aligned} \frac{\hbox {d}^{2}S}{\hbox {d}t^{2}}=\frac{\hbox {d}^{2}N}{\hbox {d}t^{2}}=A_{2}-a_{N}e^{-C_{1}}N(u-\lambda _{1}C_{1}), \end{aligned}$$

(5.26)

where $A_{2}$ is defined in (5.25). The state constraint S is of order two since the control u is explicitly present in the second derivative of S [14, 25]. Now, equating (5.26) to zero gives

$$\begin{aligned} u=u_{b}=\frac{A_{2}}{a_{N}e^{-C_{1}}N}+\lambda _{1}C_{1}. \end{aligned}$$

(5.27)

Moreover, the regularity condition of state constraint is satisfied [14, 15] since

$$\begin{aligned} \frac{\partial }{\partial u}\frac{\hbox {d}^{2}S}{\hbox {d}t^{2}} =-a_{N}e^{-C_{1}}N \ne 0 \end{aligned}$$

(5.28)

on every boundary arc with $S= 0$. Also, the value of the multiplier $\eta$ can be computed by equating (5.19) to zero. $\square$

Fig. 1

Optimal state and control trajectories. The first row illustrates the variation of the drug dose rates. The second and third rows display the time dynamics of different cell populations during chemotherapy

Fig. 2

Behavior of switching functions $\psi _1$ and $\psi _2$. The top right corner of each subfigure is a zoomed-in plot of the same subfigure over the time interval [9.5, 30] for the first graph, $\psi _1$ and [8, 30] for the second graph, $\psi _2$

Fig. 3

Total tumor cells during therapy

Theorem 5.4

If v is a boundary subarc on the interval $[t_{1v},t_{2v}] \subseteq [0,t_{f}]$, then the representation of the control is given by,

$$\begin{aligned} v_{b}=\frac{A_{4}}{b_{N}e^{-C_{2}}N}+\lambda _{2}C_{2}, \end{aligned}$$

(5.29)

where

$$\begin{aligned} \begin{aligned} A_{4}=&r_{4}N'(1-\frac{2N}{K_{4}})+\gamma V'(1-\frac{2V}{T^{*}})-a_{N}(1-e^{-C_{1}})N'-b_{N}(1-e^{-C_{2}})N'\\&-a_{N}e^{-C_{1}}NC'_{1}. \end{aligned} \end{aligned}$$

(5.30)

Proof

The proof is similar to the proof of Theorem 5.3. $\square$

6 Numerical Solution

In this section, we numerically examine whether the model meets the objective of the problem. The optimal control problem (4.9)–(4.12) is solved using MATLAB coupled with APMonitor modeling language with the help of IPOPT solver. For the simulation of the model, we have used the parameters which have been taken from literature [3,4,5, 21]. The parameter values used for the computational purpose are given in the following table:

Parameter	Value
$r_{1}$	0.25 time$^{-1}$
$r_{2}$	0.15 time$^{-1}$
$r_{3}$	0.15 time$^{-1}$
$r_{4}$	1.2 time$^{-1}$
$K_{1}$	$10^6$ cells
$K_{2}$	$10^6$ cells
$K_{3}$	$10^6$ cells
$K_{4}$	$10^6$ cells
$\tau _{1}$	0.001 time$^{-1}$
$\tau _{2}$	0.001 time$^{-1}$
$a_{1}$	0.45 time$^{-1}$
$b_{1}$	0.15 time$^{-1}$
$a_{2}$	0.45 time$^{-1}$
$a_{3}$	0.45 time$^{-1}$
$\tau _{23}$	0.0001 time$^{-1}$
$\tau _{32}$	0.0001 time$^{-1}$
$a_{N}$	0.02 time$^{-1}$
$b_{N}$	0.02 time$^{-1}$
$\gamma$	0.028 time$^{-1}$
$T^{*}$	$3*10^5$ cells
$\lambda _{1}$	0.01 time$^{-1}$
$\lambda _{2}$	0.01 time$^{-1}$

Fig. 4

Behavior of cells during therapy

Figure 1 shows the corresponding solution trajectories and control trajectories for $\beta _{1}=1$ and $\beta _{2}=3$ with $t_f =30$ and $q:=(q_1,q_2,q_3)=(1,1,1)$. The constant c in the integral constraint in (4.5) is taken as 40.

It clearly demonstrates that the number of different subpopulations of tumor cells is decreasing to zero. Also, more than $95 \%$ of the normal cells are present throughout the treatment. Although there is a slight decline in normal cells at the beginning of the treatment, it maintains a healthy level throughout the therapy. This means that the toxicity of the drug is also minimized. Moreover, one can see that the pure state constraint $S=N(t)-0.75K_{4}$ is never zero throughout the therapy interval, and hence, there are no boundary controls. Also, we can observe that the control is bang-bang, switching between 0 and 1. The behavior of the switching functions is plotted in Fig. 2.

It is clear from these graphs that switching and control functions obey the control law that we established theoretically. Figure 3 illustrates the reduction of the total number of cancer cells throughout the chemotherapy interval. We can see that the total tumor size is reduced to zero at the end of the therapy.

6.1 Comparison Analysis

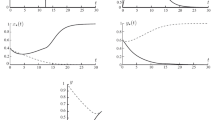
In [17], authors studied a single-drug optimal control chemotherapy model and illustrated that the model performs better than the model proposed by Mithra Shojania Feizabadi [4]. In single-drug chemotherapy, the drug injection rate is taken as a control function. Figure 4 illustrates the numerical result obtained from single-drug therapy.

Even though both drug-sensitive cells and mutated cells are reduced to zero at the end of the treatment, the increasing number of drug-resistant cells remains a threat. However, in the proposed multi-drug model ( see Figs. 1, 3), these limitations are addressed, and the proposed model ensures that cancer cells are destroyed during the treatment by maintaining the normal cells at a healthy level, which would lead to faster recovery of the patient.

7 Conclusions

In this paper, we proposed a model that examined the behavior of normal cells and different types of tumor cells during multi-drug chemotherapy. The pharmacokinetics of both drugs were incorporated into the model. The existence and the properties of solutions of the proposed models were analyzed. The resistant nature of tumor cells toward the injected drug is a known fact. We implemented a multi-drug chemotherapy approach to overcome this issue. It is also known that chemotherapeutic drugs can kill both the tumor and normal cells. Therefore, to assure the healthy recovery of patients, the toxic effect of drugs on normal cells, which is a significant obstacle to the success of therapy, should be addressed. We used tools of control theory to formulate a better treatment protocol. We designed a treatment strategy that minimizes the total tumor cells and the total drug toxicity. In the meantime, it maintained the normal cells at a healthy level throughout the treatment period. Moreover, we validated the theoretical results numerically. The numerical results confirmed that the proposed optimal treatment strategies reduced the total tumor size while preserving more than $95\%$ of healthy normal cells during and at the end of the therapy with minimal administration of chemotherapeutic drugs.