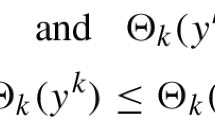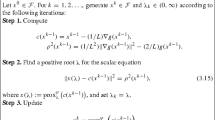1 Introduction

Many problems in statistics, machine learning or signal processing can be formulated as high-dimensional convex optimization problems [3, 12, 56, 59, 68, 69]. They typically involve a smooth term F and a nonsmooth regularization term G, and \(F+G\) is often minimized using (a variant of) Stochastic Gradient Descent (SGD) [47]. However, in many cases, G is not proximable; that is, its proximity operator does not admit a closed-form expression. In particular, structured regularization, like the total variation or its variants for images or graphs [10, 23, 24, 27, 31, 61, 63], or the overlapping group lasso [3], is known to have computationally expensive proximity operators. Also, when G is a sum of several regularizers, G is not proximable, even if the individual regularizers are, in general [60]. Thus, in many situations, G is not proximable, but it takes the form \(G = R + H \circ L\) where R, H are proximable and L is a linear operator. Therefore, in this paper, we study the problem

$$\begin{aligned} {\textbf {Problem (1)}}: \mathop {\mathrm {minimize}}\limits _{x\in {\mathcal {X}}}\, \Big (F(x)+R(x)+H(Lx)\Big ), \end{aligned}$$
(1)

where \(L: {\mathcal {X}}\rightarrow {\mathcal {Y}}\) is a linear operator, \({\mathcal {X}}\) and \({\mathcal {Y}}\) are real Hilbert spaces (all spaces are supposed of finite dimension), \(F:{\mathcal {X}}\rightarrow {\mathbb {R}}\) is a convex function, \(R:{\mathcal {X}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) and \(H:{\mathcal {Y}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) are proper, convex, lower semicontinuous functions; we refer to textbooks like [5, 9] for standard definitions of convex analysis. F is supposed to be \(\nu \)-smooth, for some \(\nu >0\); that is, it is differentiable on \({\mathcal {X}}\) and its gradient \(\nabla F\) is \(\nu \)-Lipschitz continuous: \(\Vert \nabla F(x)-\nabla F(x')\Vert \le \nu \Vert x-x'\Vert \), for every \((x,x') \in {\mathcal {X}}^2\).

Our contributions are the following. We recast Problem (1) as finding a zero of the sum of three operators, which are monotone in a primal–dual product space, under a particular metric (Sect. 2). Then, we apply Davis–Yin splitting (DYS) [28], a generic method for this type of monotone inclusions (Sect. 3). By doing so, we recover the existing PD3O [77] and two forms of the Condat–Vũ [22, 72] algorithms, but we also discover a new one, which we call the Primal–Dual Davis–Yin (PDDY) algorithm (Sect. 4). In other words, we discover PDDY as the fourth “missing link” in a group of primal–dual algorithms, which is self-consistent, in the sense that by exchanging the roles of the primal and dual terms \(R+H\circ L\) and \(R^* \circ (-L^*) + H^*\), or by exchanging the roles of two monotone operators in the construction, we recover this or that algorithm. Furthermore, the decomposition of the primal–dual monotone inclusion into three terms allows us to use an important inequality regarding DYS for the analysis of the algorithms. More precisely, we can apply Lemma 3.2, by instantiating the monotone operators and inner product with the ones at hand. Thanks to this property, we can easily replace the gradient \(\nabla F\) by a stochastic variance-reduced (VR) estimator, which can be much cheaper to evaluate (Sect. 5). Thus, we derive the first VR stochastic algorithms to tackle Problem (1), to the best of our knowledge. We also leverage the DYS representation of the algorithms to prove convergence rates; our analysis covers the deterministic and stochastic cases in a unified way (Sect. 5). Moreover, as a byproduct of our analysis, we discover the first linearly converging algorithm for the minimization of a smooth strongly convex function, using its gradient, under a linear constraint, without projections on it (Sect. 6). Its application to decentralized optimization is discussed in Appendix 1. Finally, numerical experiments illustrating the performance of the algorithms are presented in Sect. 7. A part of the proofs is deferred to Appendix 1, and additional linear convergence results are derived in Appendix 1.

1.1 Related Work

Splitting Algorithms: Algorithms allowing to solve nonsmooth optimization problem involving several proximable terms are called proximal splitting algorithms [6, 7, 19, 21, 25, 44, 57]. A classical one is the Douglas–Rachford algorithm [32, 51, 62, 70] (or, equivalently, the ADMM [8, 34, 35]) to minimize the sum of two nonsmooth functions \(R+H\). To minimize \(G = R+H \circ L\), the Douglas–Rachford algorithm can be generalized to the Primal–Dual Hybrid Gradient (PDHG) algorithm, a.k.a. Chambolle–Pock algorithm [11, 55]. Behind its success is the ability to handle the composite term \(H \circ L\) using separate activation of L, its adjoint operator \(L^T\), and the proximity operator of H. However, in many applications, the objective function involves a smooth function F, for instance, a least-squares term or a sum of logistic losses composed with inner products. To cover these applications, proximal splitting algorithms like the Combettes–Pesquet [20], Condat–Vũ [22, 72] and PD3O [77] algorithms have been proposed; they can solve the general Problem (1). These algorithms are primal–dual in nature; that is, they solve not only the primal problem (1), but also the dual problem, in a joint way. Many other algorithms exist to solve Problem (1), and we refer to [25] and [21] for an overview of primal–dual proximal splitting algorithms. We can also mention the class of projective splitting algorithms first proposed in [33] and further developed in several papers [2, 17, 41,42,43]. They proceed by building a separating hyperplane between the current iterate and the solution and then projecting the current iterate onto this hyperplane, to get closer to the solution. The projective splitting algorithms with forward steps [42, 43] are fully split and can solve Problem (1), as well.

Let us turn our attention to stochastic splitting algorithms. In machine learning applications, the gradient of F is often much too expensive to evaluate and replaced by a cheaper stochastic estimate. We can distinguish the two classes of standard stochastic gradients [36, 37, 47] and variance-reduced (VR) stochastic gradients [29, 36, 38, 40, 74, 79]. VR stochastic gradients are estimators that ensure convergence to an exact solution of the problem, like with deterministic algorithms; that is, the variance of the stochastic errors they induce tends to zero. For some problems, VR stochastic algorithms are significantly faster than their deterministic counterparts. By contrast, with standard stochastic gradients and constant stepsizes, the algorithms typically do not converge to a fixed point and continue to fluctuate in a neighborhood of the solution set; this can be sufficient if the desired accuracy is low and speed is critical. When \(L = I\), where I denotes the identity, solving Problem (1) with standard and with VR stochastic gradients was considered in [78] and in [58], respectively. In the general case \(L \ne I\) of interest in this paper, solving the problem with a standard stochastic gradient was considered in [80]. Thus, our proposed method is the first to allow solving the general Problem (1) in a flexible way, with calls to \(\nabla F\) or to standard or VR stochastic estimates.

1.2 Mathematical Background

We introduce some notions and notations of convex analysis and operator theory, see [5, 9] for more details. Let \({\mathcal {Z}}\) be a real Hilbert space. Let \(G:{\mathcal {Z}}\rightarrow {\mathbb {R}}\cup \{+\infty \}\) be a convex function. The domain of G is the convex set \({{\,\mathrm{dom}\,}}(G)=\{z\in {\mathcal {Z}}\;:\;G(z)\ne +\infty \}\), its subdifferential is the set-valued operator \(\partial G:z\in {\mathcal {Z}}\mapsto \{y\in {\mathcal {Z}}\ :\ (\forall z'\in {\mathcal {Z}})\ G(z)+\langle z'-z, y\rangle \le G(z')\}\), and its conjugate function is \(G^*:z\mapsto \sup _{z'\in {\mathcal {Z}}} \{\langle z,z'\rangle -G(z')\}\). If G is differentiable at \(z\in {\mathcal {Z}}\), \(\partial G(z)=\{\nabla G(z)\}\). We define the proximity operator of G as the operator \(\mathrm {prox}_G:z\in {\mathcal {Z}}\mapsto \mathop {\mathrm {arg\,min}}\limits _{z'\in {\mathcal {Z}}}\big \{G(z')+{\textstyle \frac{1}{2}}\Vert z-z'\Vert ^2\big \}\). Finally, given any \(b\in {\mathcal {Z}}\), we define the convex indicator function \(\iota _b:z\mapsto \{0\) if \(z=b\), \(+\infty \) otherwise\(\}\).

Let \(M : {\mathcal {Z}}\rightarrow 2^{\mathcal {Z}}\) be a set-valued operator. The inverse \(M^{-1}\) of M is defined by the relation \(z' \in M(z) \Leftrightarrow z \in M^{-1}(z')\). The set of zeros of M is \(\mathrm {zer}(M) :=\{z \in {\mathcal {Z}}, 0 \in M(z)\}\). M is monotone if \(\langle w-w',z-z' \rangle \ge 0\) and strongly monotone if there exists \(\mu >0\) such that \(\langle w-w',z-z' \rangle \ge \mu \Vert z-z'\Vert ^2\), for every \((x,x')\in {\mathcal {Z}}^2\), \(w \in M(z)\), \(w' \in M(z')\). M is maximally monotone if its graph is not contained in the graph of another monotone operator. The resolvent of M is \(J_{M} :=(I + M)^{-1}\). If G is proper, convex and lower semicontinuous, \(\partial G\) is maximally monotone, \(J_{\partial G} = {{\,\mathrm{prox}\,}}_{G}\), \(\mathrm {zer}(\partial G) = \mathop {\mathrm {arg\,min}}\limits G\) and \((\partial G)^{-1} = \partial G^*\).

A single-valued operator M on \({\mathcal {Z}}\) is \(\xi \)-cocoercive if \(\xi \Vert M(z) - M(z')\Vert ^2 \le \langle M(z) - M(z'),z-z' \rangle \), for every \((z,z')\in {\mathcal {Z}}^2\). The resolvent of a maximally monotone operator is 1-cocoercive and \(\nabla G\) is \(1/\nu \)-cocoercive, for any \(\nu \)-smooth function G.

The adjoint of a linear operator P is denoted by \(P^*\) and its operator norm by \(\Vert P\Vert \). P is self-adjoint if \(P=P^*\). Let \(P : {\mathcal {Z}}\rightarrow {\mathcal {Z}}\) be a self-adjoint linear operator. P is positive if \(\langle Pz,z \rangle \ge 0\), for every \(z \in {\mathcal {Z}}\), and strongly positive if, additionally, \(\langle Pz,z \rangle = 0\) implies \(z=0\). In this latter case, the inner product induced by P is defined by \(\langle z,z' \rangle _P :=\langle Pz,z' \rangle \) and the norm induced by P by \(\Vert z\Vert _P :=\langle z,z \rangle _P^{1/2}\). We denote by \({\mathcal {Z}}_P\) the real Hilbert space made from the vector space \({\mathcal {Z}}\) endowed with \(\langle \cdot ,\cdot \rangle _P\).

2 Primal–Dual Formulation and Optimality Conditions

For Problem (1) to be well posed, we suppose that there exists \(x^\star \in {\mathcal {X}}\), such that

$$\begin{aligned} 0\in \nabla F(x^\star ) +\partial R(x^\star ) +L^* \partial H(Lx^\star ). \end{aligned}$$
(2)

Then, \(x^\star \) is a solution to (1). For instance, a standard qualification constraint for this assumption to hold is that 0 belongs to the relative interior of \({{\,\mathrm{dom}\,}}(H) - L{{\,\mathrm{dom}\,}}(R)\) [20]. Then, for every \(x^\star \) satisfying (2), there exists \(y^\star \in \partial H (L x^\star )\) such that \(0\in \nabla F(x^\star ) +\partial R(x^\star ) +L^* y^\star \); equivalently, \((x^\star ,y^\star )\) is a zero of the set-valued operator M defined by

$$\begin{aligned} M : (x,y) \in {\mathcal {X}}\times {\mathcal {Y}} \mapsto \Big (\nabla F(x)+\partial R(x)+L^* y, -Lx +\partial H^*(y)\Big ). \end{aligned}$$
(3)

Conversely, for every \((x^\star ,y^\star ) \in \mathrm {zer}(M)\), \(x^\star \) is a solution to (1) and \(y^*\) is a solution to the dual problem

$$\begin{aligned} \mathop {\mathrm {minimize}}\limits _{y \in {\mathcal {Y}}} \,\Big ((F+R)^*(-L^* y) + H^*(y)\Big ), \end{aligned}$$
(4)

see Sect. 15.3 of [5]; moreover, there exist \(r^\star \in \partial R(x^\star )\) and \(h^\star \in \partial H^*(y^\star )\) such that, using 2-block vector notations in \({\mathcal {X}}\times {\mathcal {Y}}\),

$$\begin{aligned} \begin{bmatrix} 0 \\ 0\end{bmatrix} = \begin{bmatrix} \nabla F(x^\star )+ r^\star +L^* y^\star \\ -L x^\star +h^\star \end{bmatrix}. \end{aligned}$$
(5)

In the sequel, we let \((x^\star ,y^\star ) \in \mathrm {zer}(M)\) and \(r^\star ,h^\star \) be any elements such that Eq. (5) holds.

A zero of M is also a saddle point of the convex–concave Lagrangian function, defined as

$$\begin{aligned} {{\mathscr {L}}}(x,y) :=F(x)+R(x) - H^*(y) + \langle Lx,y \rangle . \end{aligned}$$
(6)

For every \(x \in {\mathcal {X}}\) and \(y \in {\mathcal {Y}}\), we define the Lagrangian gap at (x, y) as \({{\mathscr {L}}}(x,y^\star ) - {{\mathscr {L}}}(x^\star ,y)\). The following holds:

Lemma 2.1

(Lagrangian gap) For every \(x \in {\mathcal {X}}\) and \(y \in {\mathcal {Y}}\), we have

$$\begin{aligned} {{\mathscr {L}}}(x,y^\star ) - {{\mathscr {L}}}(x^\star ,y) = D_F(x,x^\star )+D_R(x,x^\star )+D_{H^*}(y,y^\star ), \end{aligned}$$
(7)

where the Bregman divergence of the smooth function F between any two points x and \(x'\) is \(D_F(x,x') :=F(x) - F(x') - \langle \nabla F(x'),x-x' \rangle \), and \(D_R(x,x^\star ) :=R(x) - R(x^\star ) - \langle r^\star ,x-x^\star \rangle \), \(D_{H^{*}}(y,y^\star ) :=H^*(y) - H^*(y^\star ) - \langle h^\star ,y-y^\star \rangle \).

Proof

Using the optimality conditions (5), we have

$$\begin{aligned} D_F(x,x^\star )+D_R(x,x^\star )&= (F+R)(x) - (F+R)(x^\star ) -\langle \nabla F(x^\star ) + r^\star ,x-x^\star \rangle \\&= (F+R)(x) - (F+R)(x^\star ) +\langle L^* y^\star ,x-x^\star \rangle \\&= (F+R)(x) - (F+R)(x^\star ) +\langle y^\star ,L x \rangle - \langle y^\star , L x^\star \rangle . \end{aligned}$$

We also have

$$\begin{aligned} D_{H^*}(y,y^\star )= & {} H^*(y) - H^*(y^\star ) -\langle L x^\star ,y-y^\star \rangle \\= & {} H^*(y) - H^*(y^\star ) -\langle L x^\star ,y \rangle +\langle y^\star ,L x^\star \rangle . \end{aligned}$$

Hence,

$$\begin{aligned}&D_F(x,x^\star )+D_R(x,x^\star )+D_{H^*}(y,y^\star )\\&\quad = (F+R)(x) - (F+R)(x^\star ) + H^*(y) - H^*(y^\star ) -\langle L x^\star ,y \rangle +\langle y^\star ,L x \rangle \\&\quad = {{\mathscr {L}}}(x,y^\star ) - {{\mathscr {L}}}(x^\star ,y).&\end{aligned}$$

\(\square \)

For every \(x \in {\mathcal {X}}\), \(y \in {\mathcal {Y}}\), Lemma 2.1 and the convexity of \(F,R,H^*\) imply that \( {{\mathscr {L}}}(x^\star ,y) \le {{\mathscr {L}}}(x^\star ,y^\star ) \le {{\mathscr {L}}}(x,y^\star ) \). So, the Lagrangian gap \({{\mathscr {L}}}(x,y^\star ) - {{\mathscr {L}}}(x^\star ,y)\) is nonnegative, and it is zero if x is a solution to Problem (1) and y is a solution to the dual problem (4). The converse is not always true, generally speaking. But in realistic situations, this is the case, and under mild assumptions, like strict convexity of the functions around \(x^\star \) and \(y^\star \), the Lagrangian gap converging to zero is a valid measure of convergence to a solution.

The operator M defined in (3) can be shown to be maximally monotone. Moreover, we have

$$\begin{aligned} M(x,y)&= \begin{bmatrix} \partial R(x) \\ 0 \end{bmatrix} + \begin{bmatrix} &{} L^* y \\ -L x\!\!&{} {}+\partial H^*(y)\end{bmatrix}+\begin{bmatrix} \nabla F(x)\\ 0\end{bmatrix} \end{aligned}$$
(8)
$$\begin{aligned}&= \begin{bmatrix} 0 \\ \partial H^*(y) \end{bmatrix} + \begin{bmatrix} \partial R(x)\!\!&{}{}+L^* y \\ -L x\end{bmatrix}+\begin{bmatrix} \nabla F(x)\\ 0\end{bmatrix}, \end{aligned}$$
(9)

and each term at the right-hand side of (8) or (9) is maximally monotone, see Corollary 25.5 in [5].

figure a

Note : the deterministic versions of the algorithms are obtained by setting \(g^{k+1}=\nabla F(x^k)\).

figure b

3 Davis–Yin Splitting

Solving Problem (1) boils down to finding a zero \((x^\star ,y^\star )\) of the monotone operator M defined in (3), which can be written as the sum of three monotone operators, like in (8) or (9). The method proposed by Davis and Yin [28], which we call Davis–Yin splitting (DYS), is dedicated to this problem; that is, find a zero of the sum of three monotone operators, one of which is cocoercive.

Let \({\mathcal {Z}}\) be a real Hilbert space. Let \({\tilde{A}}, {\tilde{B}}, {\tilde{C}}\) be maximally monotone operators on \({\mathcal {Z}}\). We assume that \({\tilde{C}}\) is \(\xi \)-cocoercive, for some \(\xi >0\). The DYS algorithm, denoted by \(\text {DYS}({\tilde{A}},{\tilde{B}},{\tilde{C}})\) and shown above, aims at finding an element in \(\mathrm {zer}({\tilde{A}}+{\tilde{B}}+{\tilde{C}})\), supposed nonempty. The fixed points of \(\text {DYS}({\tilde{A}},{\tilde{B}},{\tilde{C}})\) are the triplets \((v^\star , z^\star , u^\star )\in {\mathcal {Z}}^3\), such that

$$\begin{aligned} z^\star = J_{\gamma {\tilde{B}}}(v^\star ),\quad u^\star = J_{\gamma {\tilde{A}}}\big (2 z^\star - v^\star - \gamma {\tilde{C}}(z^\star )\big ),\quad u^\star = z^\star . \end{aligned}$$
(10)

These fixed points are related to the zeros of \({\tilde{A}}+{\tilde{B}}+{\tilde{C}}\) as follows, see Lemma 2.2 in [28]: for every \((v^\star , z^\star , u^\star )\in {\mathcal {Z}}^3\) satisfying (10), \(z^\star \in \mathrm {zer}({\tilde{A}}+{\tilde{B}}+{\tilde{C}})\). Conversely, for every \(z^\star \in \mathrm {zer}({\tilde{A}}+{\tilde{B}}+{\tilde{C}})\), there exists \((v^\star , u^\star ) \in {\mathcal {Z}}^2\), such that \((v^\star , z^\star , u^\star )\) satisfies (10). We have [28]:

Lemma 3.1

Suppose that \(\gamma \in (0,2\xi )\). Then, the sequences \((v^k)_{k\in {\mathbb {N}}}\), \((z^k)_{k\in {\mathbb {N}}}\), \((u^k)_{k\in {\mathbb {N}}}\) generated by \(\text {DYS}({\tilde{A}},{\tilde{B}},{\tilde{C}})\) converge to some elements \(v^\star \), \(z^\star \), \(u^\star \) in \({\mathcal {Z}}\), respectively. Moreover, \((v^\star , z^\star , u^\star )\) satisfies (10) and \(u^\star = z^\star \in \mathrm {zer}({\tilde{A}}+{\tilde{B}}+{\tilde{C}})\).

The following equality is at the heart of the convergence proofs:

Lemma 3.2

Let \((v^k,z^k,\) \(u^k) \in {\mathcal {Z}}^3\) be the iterates of the DYS algorithm, and \((v^\star , z^\star , u^\star )\in {\mathcal {Z}}^3\) be such that (10) holds. Then, for every \(k \ge 0\), there exist \(b^k \in {\tilde{B}}(z^k)\), \(b^\star \in {\tilde{B}}(z^\star )\), \(a^{k+1} \in {\tilde{A}}(u^{k+1})\) and \(a^\star \in {\tilde{A}}(u^\star )\), such that

$$\begin{aligned} \Vert v^{k+1} -v^\star \Vert ^2&= \Vert v^k - v^\star \Vert ^2 -2\gamma \langle b^k - b^\star ,z^{k} - z^\star \rangle -2\gamma \langle a^{k+1} - a^\star ,u^{k+1} - u^\star \rangle \nonumber \\&\quad -2\gamma \langle {\tilde{C}}(z^{k}) - {\tilde{C}}(z^\star ),z^{k} - z^\star \rangle +\gamma ^2\Vert {\tilde{C}}(z^{k}) - {\tilde{C}}(z^\star )\Vert ^2\\&\quad -\gamma ^2\Vert a^{k+1}+b^k - a^{\star }-b^\star \Vert ^2\nonumber . \end{aligned}$$
(11)

Proof

Since \(z^k = J_{\gamma {\tilde{B}}}(v^k)\), \(z^k \in v^k - \gamma {\tilde{B}}(z^k)\) by definition of the resolvent. Therefore, there exists \(b^k \in {\tilde{B}}(z^k)\), such that \(z^k = v^k - \gamma b^k\). Similarly, \(u^{k+1} \in 2z^k - v^k - \gamma {\tilde{C}}(z^{k}) - \gamma {\tilde{A}}(u^{k+1}) = v^k - 2\gamma b^k - \gamma {\tilde{C}}(z^{k}) - \gamma {\tilde{A}}(u^{k+1})\). Therefore, there exists \(a^{k+1} \in {\tilde{A}}(u^{k+1})\), such that

$$\begin{aligned} \left\{ \begin{array}{l} z^{k} = v^k - \gamma b^k \\ u^{k+1} = v^k - 2 \gamma b^k - \gamma {\tilde{C}}(z^{k}) - \gamma a^{k+1} \\ v^{k+1} = v^k + u^{k+1} - z^{k}. \end{array}\right. \end{aligned}$$
(12)

Moreover, \( v^{k+1} = v^{k} - \gamma b^k - \gamma {\tilde{C}}(z^{k}) - \gamma a^{k+1} \). Similarly, there exist \(a^\star \in {\tilde{A}}(u^\star )\) and \(b^\star \in {\tilde{B}}(z^\star )\), such that

$$\begin{aligned} \left\{ \begin{array}{l} z^\star = v^\star - \gamma b^\star \\ u^\star = v^\star - 2 \gamma b^\star - \gamma {\tilde{C}}(z^\star ) - \gamma a^\star \\ v^\star = v^\star + u^\star - z^\star , \end{array}\right. \end{aligned}$$
(13)

and

\( v^\star = v^\star - \gamma b^\star - \gamma {\tilde{C}}(z^\star ) - \gamma a^\star \). Therefore,

$$\begin{aligned} \Vert v^{k+1} - v^\star \Vert ^2 ={}&\Vert v^k - v^\star \Vert ^2 -2\gamma \Big \langle a^{k+1}+b^k + {\tilde{C}}(z^{k}) - \big (a^{\star }+b^\star + {\tilde{C}}(z^{\star })\big ),\\&v^{k} - v^\star \Big \rangle +\gamma ^2\big \Vert a^{k+1}+b^k + {\tilde{C}}(z^{k}) - \big (a^{\star }+b^\star + {\tilde{C}}(z^{\star })\big )\big \Vert ^2. \end{aligned}$$

By expanding the last squared norm and by using (12) and (13) in the inner product, we get

$$\begin{aligned} \Vert v^{k+1} - v^\star \Vert ^2&= \Vert v^k - v^\star \Vert ^2-2\gamma \langle b^k + {\tilde{C}}(z^{k})- \big (b^\star + {\tilde{C}}(z^\star )\big ),z^{k} - z^\star \rangle \\&\quad -2\gamma \langle a^{k+1}- a^\star ,u^{k+1} - u^\star \rangle \\&\quad -2\gamma \langle b^k + {\tilde{C}}(z^{k})- \big (b^\star + {\tilde{C}}(z^\star )\big ),\gamma b^k - \gamma b^\star \rangle \\&\quad -2\gamma \langle a^{k+1}- a^\star ,2 \gamma b^k + \gamma {\tilde{C}}(z^{k}) + \gamma a^{k+1} \\&\quad - \big (2 \gamma b^\star + \gamma {\tilde{C}}(z^{\star }) + \gamma a^\star \big ) \rangle \\&\quad +\gamma ^2\Vert a^{k+1}+b^k- \big (a^\star +b^\star \big )\Vert ^2+\gamma ^2\Vert {\tilde{C}}(z^{k})- {\tilde{C}}(z^\star )\Vert ^2\\&\quad +2\gamma ^2\langle a^{k+1}+b^k - \big (a^\star +b^\star \big ),{\tilde{C}}(z^{k})- {\tilde{C}}(z^\star ) \rangle \\&= \Vert v^k - v^\star \Vert ^2-2\gamma \langle b^k -b^\star ,z^{k} - z^\star \rangle -2\gamma \langle a^{k+1}- a^\star ,u^{k+1} - u^\star \rangle \\&\quad -2\gamma \langle {\tilde{C}}(z^{k})- {\tilde{C}}(z^\star ),z^{k} - z^\star \rangle +\gamma ^2\Vert {\tilde{C}}(z^{k})- {\tilde{C}}(z^\star )\Vert ^2\\&\quad -2\gamma ^2 \Vert b^k -b^\star \Vert ^2 -2\gamma ^2\langle a^{k+1}- a^\star ,2 b^k + a^{k+1} - 2 b^\star - a^\star \rangle \\&\quad +\gamma ^2\Vert a^{k+1}+b^k- \big (a^\star +b^\star \big )\Vert ^2. \end{aligned}$$

After combining the last three terms into \(-\gamma ^2\Vert a^{k+1}+b^k- \big (a^\star +b^\star \big )\Vert ^2\), we obtain the result. \(\square \)

4 A Class of Four Primal–Dual Optimization Algorithms

We now set \({\mathcal {Z}}:={\mathcal {X}}\times {\mathcal {Y}}\), where \({\mathcal {X}}\) and \({\mathcal {Y}}\) are the spaces defined in Sect. 2. To solve the primal–dual problem (8) or (9), which consists in finding a zero of the sum \(A+B+C\) of three operators in \({\mathcal {Z}}\), of which C is cocoercive, a natural idea is to apply the Davis–Yin algorithm DYS(A, B, C). But the resolvent of A or B is often intractable. In this section, we show that preconditioning is the solution; that is, we exhibit a strongly positive linear operator P, such that DYS\((P^{-1}A,P^{-1}B,P^{-1}C)\) is tractable. Since \(P^{-1}A,P^{-1}B,P^{-1}C\) are monotone operators in \({\mathcal {Z}}_P\), the algorithm will converge to a zero of \(P^{-1}A + P^{-1}B + P^{-1}C\), or, equivalently, of \(A+B+C\). Let us apply this idea in four different ways.

4.1 A New Primal–Dual Algorithm: The PDDY Algorithm

Let \(\gamma >0\) and \(\tau >0\) be real parameters. We introduce the four operators on \({\mathcal {Z}}\), using matrix-vector notations:

$$\begin{aligned} A(x,y)&=\begin{bmatrix} &{} L^* y \\ -L x\!\!&{}{}+\partial H^*(y)\end{bmatrix},&B(x,y)=\begin{bmatrix} \partial R(x) \\ 0 \end{bmatrix}\!,\ C(x,y)=\begin{bmatrix} \nabla F(x)\\ 0\end{bmatrix},\nonumber \\ P&=\begin{bmatrix} I&{} 0 \\ 0 &{} \ \ \frac{\gamma }{\tau }I - \gamma ^2 L L^* \end{bmatrix}. \end{aligned}$$
(14)

P is strongly positive if and only if \(\gamma \tau \Vert L\Vert ^2 < 1\). Since A, B, C are maximally monotone in \({\mathcal {Z}}\), \(P^{-1}A,P^{-1}B,P^{-1}C\) are maximally monotone in \({\mathcal {Z}}_P\). Moreover, \(P^{-1}C\) is \(1/\nu \)-cocoercive in \({\mathcal {Z}}_P\). Importantly, we have:

$$\begin{aligned}&P^{-1}C:(x,y) \mapsto \big (\nabla F(x),0\big ),&\ \ J_{\gamma P^{-1}B}:(x,y)\mapsto \big (\mathrm {prox}_{\gamma R}(x),y\big ),\nonumber \\&J_{\gamma P^{-1}A}:(x,y)\mapsto (x',y'),&\hbox { where } \left\lfloor \begin{array}{l} y' = \mathrm {prox}_{\tau H^*}\big (y+\tau L (x - \gamma L^* y)\big )\\ x'=x -\gamma L^* y'. \end{array}\right. \end{aligned}$$
(15)

The form of the last resolvent was shown in [55]; see also [25], where this resolvent appears as one iteration of the Proximal Method of Multipliers. We plug these explicit steps into the Davis–Yin algorithm DYS\((P^{-1}B,P^{-1}A,\) \(P^{-1}C)\) and we identify the variables as \(v^k = (p^k,q^k)\), \(z^k = (x^k,y^{k+1})\), \(u^k = (s^k,d^k)\), for some variables \((p^k, x^k, s^k) \in {\mathcal {X}}^3\) and \((q^k, y^k, d^k) \in {\mathcal {Y}}^3\). Thus, we do the following substitutions:

\(\bullet \ \ \)Using (15), the step \( z^k = J_{\gamma P^{-1}A}(v^k), \) is equivalent to

$$\begin{aligned} \left\lfloor \begin{array}{l} y^{k+1} = {{\,\mathrm{prox}\,}}_{\tau H^*}\big ((I-\tau \gamma LL^*)q^{k} +\tau L p^k \big )\\ x^k = p^k -\gamma L^* y^{k+1}. \end{array}\right. \end{aligned}$$

\(\bullet \ \ \)The step \( u^{k+1} = J_{\gamma P^{-1}B}\big (2z^k - v^k - \gamma P^{-1}C(z^k)\big ) \) is equivalent to

$$\begin{aligned}\left\lfloor \begin{array}{l} s^{k+1} ={{\,\mathrm{prox}\,}}_{\gamma R}\big (2x^k-p^k-\gamma \nabla F(x^k)\big )\\ d^{k+1} = 2y^{k+1} - q^k. \end{array}\right. \end{aligned}$$

\(\bullet \ \ \)Finally, the step \( v^{k+1} = v^k + u^{k+1} - z^k \) is equivalent to

$$\begin{aligned}\left\lfloor \begin{array}{l} p^{k+1} = p^k + s^{k+1} - x^k\\ q^{k+1} = q^k + d^{k+1} - y^{k+1}. \end{array}\right. \end{aligned}$$

We can replace \(q^k\) by \(y^k\) and discard \(d^k\), which is not needed. This yields the new Primal–Dual Davis–Yin (PDDY) algorithm, shown above (with \(g^{k+1}=\nabla F(x^k)\)). Note that it can be written with only one call to L and \(L^*\) per iteration. Also, the PDDY Algorithm could be overrelaxed [25], since this possibility exists for the Davis–Yin algorithm. We have:

Theorem 4.1

Suppose that \(\gamma \in (0,2/\nu )\) and that \(\tau \gamma \Vert L\Vert ^2<1\). Then, the sequences \((x^k)_{k\in {\mathbb {N}}}\) and \((s^k)_{k\in {\mathbb {N}}}\) generated by the PDDY Algorithm converge to the same solution \(x^\star \) to Problem (1), and the sequence \((y^k)_{k\in {\mathbb {N}}}\) converges to some dual solution \(y^\star \) of (4).

Proof

Under the assumptions of Theorem 4.1, P is strongly positive. Then, the result follows from Lemma 3.1 applied in \({\mathcal {Z}}_P\) and from the analysis in Sect. 2. \(\square \)

4.2 The PD3O Algorithm

We consider the same notations as in the previous section. We switch the roles of A and B and consider DYS\((P^{-1}A,P^{-1}B,P^{-1}C)\). Then, after some substitutions similar to the ones done to construct the PDDY algorithm, we recover exactly the PD3O algorithm proposed in [77]. Although it is not derived this way, its interpretation as a primal–dual Davis–Yin algorithm is mentioned by its author. Its convergence properties are the same as for the PDDY Algorithm, as stated in Theorem 4.1.

In a recent work [55], the PD3O algorithm has been shown to be an instance of the Davis–Yin algorithm, with a different reformulation, which does not involve duality. The authors of the present paper developed this technique further, applied it to the PDDY algorithm as well and obtained convergence rates and accelerations for both algorithms [26].

4.3 The Condat–Vũ Algorithm

Let \(\gamma >0\) and \(\tau >0\) be real parameters. We want to study the decomposition (9) instead of (8). For this, we define the operators

$$\begin{aligned} {\bar{A}}(x,y)=\begin{bmatrix}\partial R(x)&{}{} + L^* y \\ -L x&{}\end{bmatrix}\!,\ {\bar{B}}(x,y)=\begin{bmatrix} 0\\ \partial H^*(y)\end{bmatrix}\!,\ Q=\begin{bmatrix} K &{} \ 0 \\ 0\ &{} \ I \end{bmatrix}, \end{aligned}$$
(16)

where \(K :=\frac{\gamma }{\tau }I - \gamma ^2 L^* L\), and we define C like in (14). If \(\gamma \tau \Vert L\Vert ^2 < 1\), K and Q are strongly positive. In that case, since \({\bar{A}}\), \({\bar{B}}\), C are maximally monotone in \({\mathcal {Z}}={\mathcal {X}}\times {\mathcal {Y}}\), \(Q^{-1}{\bar{A}}\), \(Q^{-1}{\bar{B}}\), \(Q^{-1}C\) are maximally monotone in \({\mathcal {Z}}_Q\). Moreover, we have:

$$\begin{aligned} Q^{-1}C:(x,y)\mapsto \big (K^{-1}\nabla F(x)&,0\big ),\ \ \ J_{\gamma Q^{-1}{\bar{B}}}:(x,y)\mapsto \big (x,\mathrm {prox}_{\gamma H^*}(y)\big ),\\ J_{\gamma Q^{-1}{\bar{A}}}:(x,y)\mapsto (x',y'),&\hbox { where } \left\lfloor \begin{array}{l} x' = \mathrm {prox}_{\tau R}\big ((I-\tau \gamma L^* L) x-\tau L^* y \big )\nonumber \\ y'=y +\gamma L x'. \end{array}\right. \end{aligned}$$
(17)

If we plug these explicit steps into the Davis–Yin algorithm DYS\((Q^{-1}{\bar{A}},\) \(Q^{-1}{\bar{B}},Q^{-1}C)\) or DYS\((Q^{-1}{\bar{B}},Q^{-1}{\bar{A}},Q^{-1}C)\), and after straightforward simplifications, we recover the two forms of the Condat–Vũ algorithm [22, 72]; that is, Algorithms 3.1 and 3.2 of [22], respectively, see also in [25]. The Condat–Vũ algorithm has the form of a primal–dual forward–backward algorithm [16, 25, 44]. We have just shown that it can be viewed as a primal–dual Davis–Yin algorithm, with a different metric, as well. Furthermore, it is easy to show that \(Q^{-1}C\) is \(\xi \)-cocoercive, with \(\xi = (\frac{\gamma }{\tau } - \gamma ^2\Vert L\Vert ^2)/\nu \). Hence, convergence follows from Lemma 3.1, under the same condition on \(\tau \) and \(\gamma \) as in Theorem 3.1 of [22], namely \(\frac{\nu }{2} < \frac{1}{\tau } - \gamma \Vert L\Vert ^2\).

5 Stochastic Primal–Dual Algorithms

We now introduce stochastic versions of the PD3O and PDDY algorithms; we omit the analysis of stochastic versions of the Condat–Vũ algorithm, which is the same, with added technicalities due to cocoercivity with respect to the metric induced by Q in (16). Our approach has a ‘plug-and-play’ flavor: we show that we have all the ingredients to leverage the unified theory of stochastic gradient estimators recently presented in [36].

In the stochastic versions of the algorithms, the gradient \(\nabla F(x^k)\) is replaced by a stochastic gradient \(g^{k+1}\). That is, we consider a filtered probability space \((\Omega ,{\mathscr {F}},({\mathscr {F}}_k)_{k\in {\mathbb {N}}},{\mathbb {P}})\), an \(({\mathscr {F}}_k)\)-adapted stochastic process \((g^k)_{k\in {\mathbb {N}}}\), we denote by \({\mathbb {E}}\) the expectation and by \({\mathbb {E}}_k\) the conditional expectation w.r.t. \({\mathscr {F}}_k\). The following assumption is made on the process \((g^k)_{k\in {\mathbb {N}}}\).

Assumption 1

There exist \(\alpha ,\beta ,\delta \ge 0\), \(\rho \in (0,1]\) and a \(({\mathscr {F}}_k)_{k\in {\mathbb {N}}}\)-adapted stochastic process denoted by \((\sigma _k)_{k\in {\mathbb {N}}}\), such that, for every \(k \in {\mathbb {N}}\), \({\mathbb {E}}_k(g^{k+1}) = \nabla F(x^k)\), \(\ {\mathbb {E}}_k(\Vert g^{k+1} - \nabla F(x^\star )\Vert ^2) \le 2\alpha D_F(x^k,x^\star ) + \beta \sigma _k^2\ \), and \(\ {\mathbb {E}}_k(\sigma _{k+1}^2) \le (1-\rho )\sigma _k^2 + 2\delta D_F(x^k,x^\star )\).

Assumption 1 is satisfied by several stochastic gradient estimators used in machine learning, including some types of coordinate descent [73], variance reduction [38], and also compressed gradients used to reduce the communication cost in distributed optimization [4, 65, 75], see Table 1 in [36]. Also, the full gradient estimator defined by \(g^{k+1} = \nabla F(x^k)\) satisfies Assumption 1 with \(\alpha = \nu \), the smoothness constant of F, \(\sigma _k \equiv 0\), \(\rho = 1\), and \(\delta = \beta = 0\), see Theorem 2.1.5 in [54]. The loopless SVRG estimator [39, 45] also satisfies Assumption 1:

Proposition 5.1

(Loopless SVRG estimator) Assume that F is written as a sum \(F = \frac{1}{n}\sum _{i = 1}^n f_i,\) for some \(n\ge 1\), where for every \(i \in \{1,\ldots ,n\}\), \(f_i : {\mathcal {X}}\rightarrow {\mathbb {R}}\) is a \(\nu _i\)-smooth convex function. Let \(p \in (0,1)\), and \((\Omega ,{\mathscr {F}},{\mathbb {P}})\) be a probability space. On \((\Omega ,{\mathscr {F}},{\mathbb {P}})\), consider:

  • a sequence of i.i.d. random variables \((\theta ^k)_{k\in {\mathbb {N}}}\) with Bernoulli distribution of parameter p,

  • a sequence of i.i.d random variables \((\zeta ^k)_{k\in {\mathbb {N}}}\) with uniform distribution over \(\{1,\ldots ,n\}\),

  • the sigma-field \({\mathscr {F}}_k\) generated by \((\theta ^k,\zeta ^k)_{0 \le j \le k}\) and a \(({\mathscr {F}}_k)\)-adapted stochastic process \((x^k)_{k\in {\mathbb {N}}}\),

  • a stochastic process \(({\tilde{x}}^k)_{k\in {\mathbb {N}}}\) defined by \({\tilde{x}}^{k+1} = \theta ^{k+1} x^k + (1-\theta ^{k+1}){\tilde{x}}^{k}\),

  • a stochastic process \((g^{k})_{k\in {\mathbb {N}}}\) defined by \(g^{k+1} = \nabla f_{\zeta ^{k+1}}(x^k) - \nabla f_{\zeta ^{k+1}}({\tilde{x}}^{k}) + \nabla F({\tilde{x}}^{k})\).

Then, the process \((g^k)_{k\in {\mathbb {N}}}\) satisfies Assumption 1 with \(\alpha = 2\max _{i \in \{1,\ldots ,n\}} \nu _i\), \(\beta = 2\), \(\rho = p\), \(\delta = \alpha p /2\), and \(\sigma _k^2 = \frac{1}{n}\sum _{i=1}^n {\mathbb {E}}_k \Vert \nabla f_i({\tilde{x}}^{k}) - \nabla f_i(x^\star )\Vert ^2\).

Proof

The proof is the same as the proof of Lemma A.11 of [36], which is only stated for \((x^k)_{k\in {\mathbb {N}}}\) generated by a specific algorithm, but remains true for any \(({\mathscr {F}}_k)\)-adapted stochastic process \((x^k)_{k\in {\mathbb {N}}}\). \(\square \)

We can now exhibit our main results. In a nutshell, \(P^{-1}C(z^k)\) is replaced by the random realization \(P^{-1}(g^{k+1},0)\) and the last term of Eq. (11), which is nonnegative, is handled using Assumption 1.

5.1 The Stochastic PD3O Algorithm

The Stochastic PD3O Algorithm, shown above, has \({\mathcal O}(1/k)\) ergodic convergence in the general case. A linear convergence result in the strongly convex setting is derived in Appendix 1.

Theorem 5.1

Suppose that Assumption 1 holds. Let \(\kappa :=\beta /\rho \), \(\gamma , \tau >0\) be such that \(\gamma \le 1/{2(\alpha +\kappa \delta )}\) and \(\gamma \tau \Vert L\Vert ^2 < 1\). Set \(V^0 :=\Vert v^{0} - v^\star \Vert _P^2 + \gamma ^2 \kappa \sigma _{0}^2,\) where \(v^0 = (p^0,y^0)\). Then, for every \(k\in {\mathbb {N}}\),

$$\begin{aligned} {\mathbb {E}}\left( {{\mathscr {L}}}({\bar{x}}^{k},y^\star ) - {{\mathscr {L}}}(x^\star ,{\bar{y}}^{k+1})\right) \le \frac{V^0}{k \gamma }, \end{aligned}$$

where \({\bar{x}}^{k} = \frac{1}{k} \sum _{j = 0}^{k-1} x^j\) and \({\bar{y}}^{k+1} = \frac{1}{k} \sum _{j = 1}^{k} y^j\).

Proof

Using Lemma A.1, the convexity of F, R, \(H^*\), and Lemma 2.1,

$$\begin{aligned} {\mathbb {E}}_k \Vert v^{k+1} - v^\star \Vert _P^2&+ \kappa \gamma ^2{\mathbb {E}}_k\sigma _{k+1}^2 \le \Vert v^k - v^\star \Vert _P^2 + \kappa \gamma ^2\left( 1-\rho +\frac{\beta }{\kappa }\right) \sigma _k^2\nonumber \\&\quad -2\gamma (1-\gamma (\alpha +\kappa \delta )){\mathbb {E}}_k\left( {{\mathscr {L}}}(x^k,d^{\star }) - {{\mathscr {L}}}(x^\star ,d^{k+1})\right) . \end{aligned}$$

We have \(1 - \rho + \beta /\kappa = 1\), \(\gamma \le 1/2(\alpha +\kappa \delta )\). Set \( V^k :=\Vert v^{k} - v^\star \Vert _P^2 + \kappa \gamma ^2\sigma _{k}^2 \), for every \(k\in {\mathbb {N}}\). Then, \( {\mathbb {E}}_k V^{k+1} \le V^k -\gamma {\mathbb {E}}_k\left( {{\mathscr {L}}}(x^{k},d^\star ) - {{\mathscr {L}}}(x^\star ,d^{k+1})\right) \). Taking the expectation, \( \gamma {\mathbb {E}}\left( {{\mathscr {L}}}(x^{k},d^\star ) - {{\mathscr {L}}}(x^\star ,d^{k+1})\right) \le {\mathbb {E}}V^k - {\mathbb {E}}V^{k+1} \). Iterating and using the nonnegativity of \(V^k\), \( \gamma \sum _{j = 0}^{k-1} {\mathbb {E}}\left( {{\mathscr {L}}}(x^{j},d^\star ) - {{\mathscr {L}}}(x^\star ,d^{j+1})\right) \le {\mathbb {E}}V^0 \). Finally, note that \(d^{k+1} = y^{k+1}\) and \(d^{\star } = y^{\star }\). Indeed, \(y^k = q^k\) and \(q^{k+1} = q^k + d^{k+1} - y^k = d^{k+1}\). We can conclude using the convex-concavity of \({{\mathscr {L}}}\). \(\square \)

In the deterministic case \(g^{k+1} = \nabla F(x^k)\), we recover the same rate as in [77][Theorem 2].

Remark 5.1

(Primal–Dual gap) Deriving a similar bound on the stronger primal–dual gap \((F+R+H\circ L)({\bar{x}}^{k})+\big ((F+R)^*\circ (-L)+H^*\big )({\bar{y}}^{k})\) requires additional assumptions; for instance, even for the Chambolle–Pock algorithm, which is the particular case of the PD3O, PPDY and Condat–Vũ algorithms when \(F=0\), the best available result [13][Theorem 1] is not stronger than Theorem 5.1

Remark 5.2

(Particular case of SGD) In the case where \(H =0\) and \(L = 0\), the Stochastic PD3O Algorithm boils down to proximal stochastic gradient descent (SGD) and Theorem 5.1 implies that \({\mathbb {E}}\left( (F+R)({\bar{x}}^{k}) - (F+R)(x^\star )\right) \le V^0/(\gamma k) \).

This \({\mathcal O}(1/k)\) ergodic convergence rate unifies known results on SGD in the non-strongly-convex case, whenever the stochastic gradient satisfies Assumption 1.

5.2 The Stochastic PDDY Algorithm

We now analyze the proposed Stochastic PDDY Algorithm, shown above. For it too, we have \({\mathcal O}(1/k)\) ergodic convergence in the general case. A linear convergence result in the strongly convex setting is derived in Appendix 1.

Theorem 5.2

(Convergence of the Stochastic PDDY Algorithm) Suppose that Assumption 1 holds. Let \(\kappa :=\beta /\rho \), \(\gamma , \tau >0\) be such that \(\gamma \le 1/{2(\alpha +\kappa \delta )}\) and \(\gamma \tau \Vert L\Vert ^2 < 1\). Define \(V^0 :=\Vert v^{0} - v^\star \Vert _P^2 + \gamma ^2 \kappa \sigma _{0}^2,\) where \(v^0 = (p^0,y^0)\). Then, for every \(k\in {\mathbb {N}}\),

$$\begin{aligned} {\mathbb {E}}\left( D_F({\bar{x}}^{k},x^\star )+D_{H^*}({\bar{y}}^{k+1},y^\star )+ D_R({\bar{s}}^{k+1},s^\star )\right) \le \frac{V^0}{k \gamma }, \end{aligned}$$

where \({\bar{x}}^{k} = \frac{1}{k} \sum _{j = 0}^{k-1} x^j\), \({\bar{y}}^{k+1} = \frac{1}{k} \sum _{j = 1}^{k} y^j\) and \({\bar{s}}^{k+1} = \frac{1}{k} \sum _{j = 1}^{k} s^j\).

Proof

Using Lemma A.2 and the convexity of F, R, \(H^*\),

$$\begin{aligned} {\mathbb {E}}_k&\Vert v^{k+1} - v^\star \Vert _P^2 + \kappa \gamma ^2{\mathbb {E}}_k\sigma _{k+1}^2 \le \Vert v^k - v^\star \Vert _P^2 + \kappa \gamma ^2\left( 1-\rho +\frac{\beta }{\kappa }\right) \sigma _k^2\\&-2\gamma \big (1-\gamma (\alpha +\kappa \delta )\big ) \left( D_F(x^{k},x^\star ) + D_{H^*}(y^{k},y^\star )+{\mathbb {E}}_k D_R(s^{k+1},s^\star )\right) . \end{aligned}$$

Since \(1 - \rho + \beta /\kappa = 1\), \(\gamma \le 1/2(\alpha +\kappa \delta )\). Set \( V^k :=\Vert v^{k} - v^\star \Vert _P^2 + \kappa \gamma ^2\sigma _{k}^2 \). Then,

$$\begin{aligned} {\mathbb {E}}_k V^{k+1} \le V^k -\gamma {\mathbb {E}}_k\left( D_F(x^{k},x^\star ) + D_{H^*}(y^{k},y^\star )+D_R(s^{k+1},s^\star )\right) . \end{aligned}$$

Taking the expectation, \( \gamma {\mathbb {E}}\left( D_F(x^{k},x^\star ) + D_{H^*}(y^{k},y^\star )+D_R(s^{k+1},s^\star )\right) \le {\mathbb {E}}V^k - {\mathbb {E}}V^{k+1} \). Iterating and using the nonnegativity of \(V^k\), \( \gamma \sum _{j = 0}^{k-1} {\mathbb {E}}\big (D_F(x^{k},x^\star )+{}\) \( D_{H^*}(y^{k},y^\star )+D_R(s^{k+1},s^\star )\big ) \le {\mathbb {E}}V^0 \). We conclude using the convexity of the Bregman divergence in its first variable. \(\square \)

6 Linearly Constrained Smooth Optimization

In this section, we consider the problem

$$\begin{aligned} \mathop {\mathrm {minimize}}\limits _{x\in {\mathcal {X}}} \,F(x)\quad \hbox {s.t.}\quad Lx=b, \end{aligned}$$
(18)

where \(L:{\mathcal {X}}\rightarrow {\mathcal {Y}}\) is a linear operator, \({\mathcal {X}}\) and \({\mathcal {Y}}\) are real Hilbert spaces, F is a \(\nu \)-smooth convex function, for some \(\nu >0\), and \(b \in {{\,\mathrm{ran}\,}}(L)\), the range of L. This is a particular case of Problem (1) with \(R=0\) and

\(H =\iota _b\). We suppose that a solution \(x^\star \) exists, satisfying \(Lx^\star =b\) and \(0\in \nabla F(x^\star )+L^*y^\star \) for some \(y^\star \in {\mathcal {Y}}\). The stochastic PD3O and PDDY algorithms both revert to the same algorithm, shown above, which we call Linearly Constrained Stochastic Gradient Descent (LiCoSGD). It is fully split: it does not make use of projections onto the affine space \(\{x \in {\mathcal {X}}, L x = b\}\) and only makes calls to L and \(L^*\).

In the deterministic case \(g^{k+1} = \nabla F(x^k)\), LiCoSGD reverts to an instance of the algorithm first proposed by Loris and Verhoeven in [52] and rediscovered independently as the PDFP2O algorithm [15] and the Proximal Alternating Predictor–Corrector (PAPC) algorithm [30]. Convergence of this algorithm follows from Theorem 4.1, see other results in [25, 26]. Thus, LiCoSGD is a stochastic extension of this algorithm, for which Theorem 5.1 becomes:

Theorem 6.1

(Convergence of LiCoSGD) Suppose that Assumption 1 holds. Let \(\kappa :=\beta /\rho \), \(\gamma , \tau >0\) be such that \(\gamma \le 1/{2(\alpha +\kappa \delta )}\) and \(\gamma \tau \Vert L\Vert ^2 < 1\). Set \(V^0 :=\Vert v^{0} - v^\star \Vert _P^2 + \gamma ^2 \kappa \sigma _{0}^2,\) where \(v^0 = (w^0,y^0)\). Then, for every \(k\in {\mathbb {N}}\),

$$\begin{aligned} {\mathbb {E}}\left( F({\bar{x}}^{k})-F(x^\star )+\langle L{\bar{x}}^{k}-b,y^\star \rangle \right) \le \frac{V^0}{k \gamma }, \end{aligned}$$
(19)

where \({\bar{x}}^{k} = \frac{1}{k} \sum _{j = 0}^{k-1} x^j\), \(x^\star \) and \(y^\star \) are some primal and dual solutions.

The convex function \(x\mapsto F(x)-F(x^\star )+\langle Lx-b,y^\star \rangle \) is nonnegative and its minimum is zero, attained at \(x^\star \). Under additional assumptions, like strict convexity around \(x^\star \), this function takes value zero only if \(F(x)=F(x^\star )\) and \(Lx=b\), so that x is a solution.

We now state an important result: strong convexity of F is sufficient to get linear convergence. We denote by \(\omega (W)\) the smallest positive eigenvalue of a positive self-adjoint linear operator W. Then, it is easy to show that for every \(y \in {{\,\mathrm{ran}\,}}(L)\), \(\omega (LL^*)\Vert y\Vert ^2 \le \Vert L^* y\Vert ^2\). Also, \(\omega (LL^*)=\omega (L^*L)\).

Theorem 6.2

(Linear convergence of LiCoSGD with F strongly convex) Suppose that Assumption 1 holds, that F is \(\mu _F\)-strongly convex, for some \(\mu _F> 0\), and that \(y^0 \in {{\,\mathrm{ran}\,}}(L)\). Let \(x^\star \) be the unique solution of (18), \(y^\star \) be the unique element of \({{\,\mathrm{ran}\,}}(L)\) such that \(\nabla F(x^\star ) + L^* y^{\star } = 0\). Suppose that \(\gamma >0\) and \(\tau >0\) are such that \(\gamma \tau \Vert L\Vert ^2 < 1\) and \(\gamma \le 1/{\alpha + \kappa \delta }\), for some \(\kappa > \beta /\rho \). Define, for every \(k\in {\mathbb {N}}\),

$$\begin{aligned} V^k :=\Vert x^{k} - x^\star \Vert ^2+ \left( 1+\tau \gamma \omega (L^* L)\right) \Vert y^{k} - y^\star \Vert _{\gamma ,\tau }^2 + \kappa \gamma ^2{\mathbb {E}}\sigma _{k}^2, \end{aligned}$$
(20)

and

$$\begin{aligned} r :=\max \left( 1-\gamma \mu _F,1-\rho +\frac{\beta }{\kappa },\frac{1}{1+\tau \gamma \omega (L^* L)}\right) <1. \end{aligned}$$
(21)

Then, for every \(k\in {\mathbb {N}}\), \({\mathbb {E}}V^{k} \le r^k V^0\).

Proof

Noting that \(y^\star = d^\star = q^\star \) and applying Lemma A.1 with \(\gamma \le (\alpha +\kappa \delta )\),

$$\begin{aligned}&{\mathbb {E}}_k \Vert p^{k+1} - p^\star \Vert ^2 + {\mathbb {E}}_k\Vert q^{k+1} - q^\star \Vert _{\gamma ,\tau }^2 + \kappa \gamma ^2{\mathbb {E}}_k\sigma _{k+1}^2 \le \Vert p^{k} - p^\star \Vert ^2 + \Vert q^{k} - q^\star \Vert _{\gamma ,\tau }^2 \\&\quad -\gamma \mu _F\Vert x^{k}-x^\star \Vert ^2+ \kappa \gamma ^2\left( 1-\rho +\frac{\beta }{\kappa }\right) \sigma _k^2-\gamma ^2\Vert P^{-1}A(u^{k+1}) - P^{-1}A(u^{\star })\Vert _P^2.\nonumber \end{aligned}$$

Since the component of \(P^{-1}A(u^{k+1}) - P^{-1}A(u^{\star })\) in \({\mathcal {X}}\) is \(L^* d^{k+1} - L^* d^{\star }\), we have

$$\begin{aligned} {\mathbb {E}}_k \Vert p^{k+1}&- p^\star \Vert ^2 + {\mathbb {E}}_k \Vert q^{k+1} - q^\star \Vert _{\gamma ,\tau }^2 + \kappa \gamma ^2{\mathbb {E}}_k\sigma _{k+1}^2 \le \Vert x^{k} - x^\star \Vert ^2 + \Vert q^{k} - q^\star \Vert _{\gamma ,\tau }^2 \\&\quad -\gamma \mu _F\Vert p^{k}-p^\star \Vert ^2+ \kappa \gamma ^2\left( 1-\rho +\frac{\beta }{\kappa }\right) \sigma _k^2-\gamma ^2\Vert L^* d^{k+1} - L^* d^{\star }\Vert ^2. \end{aligned}$$

Inspecting the iterations of the algorithm, one can see that \(d^{0} \in {{\,\mathrm{ran}\,}}(L)\) implies \(d^{k+1} \in {{\,\mathrm{ran}\,}}(L)\). Since \(d^\star \in {{\,\mathrm{ran}\,}}(L)\), \(d^{k+1} - d^\star \in {{\,\mathrm{ran}\,}}(L)\). Therefore, \(\omega (LL^*)\Vert d^{k+1} - d^{\star }\Vert ^2 \le \Vert L^* d^{k+1} - L^* d^{\star }\Vert ^2\). Since \(q^{k+1} = d^{k+1} = y^{k+1}\) and \(x^k = p^k\),

$$\begin{aligned}&{\mathbb {E}}_k \Vert x^{k+1} - x^\star \Vert ^2 + (1+\gamma \tau \omega (LL^*)){\mathbb {E}}_k\Vert y^{k+1} - y^\star \Vert _{\gamma ,\tau }^2 + \kappa \gamma ^2{\mathbb {E}}_k\sigma _{k+1}^2\\&\quad \le (1-\gamma \mu _F)\Vert x^{k} - x^\star \Vert ^2 + \Vert y^{k} - y^\star \Vert _{\gamma ,\tau }^2+ \kappa \gamma ^2\left( 1-\rho +\frac{\beta }{\kappa }\right) \sigma _k^2. \end{aligned}$$

Thus, by setting \(V^k\) as in (20) and r as in (21), we have \( {\mathbb {E}}_k V^{k+1} \le r V^k\). \(\square \)

To the best of our knowledge, even in the deterministic case (with \(\alpha = \nu \), \(\rho = 1\), \(\delta = \beta = 0\), \(\kappa =1\)), this is a first time that a fully split algorithm using \(\nabla F\), L and \(L^*\) is shown to converge linearly to a solution of (18), whenever F is strongly convex. Also, the knowledge of \(\mu _F\) is not needed. We discuss the application of LiCoSGD to decentralized optimization in Appendix 1.

7 Experiments

We present numerical experiments for the PDDY, PD3O and Condat–Vũ (CV) [22][Algorithm 3.1] algorithms. We observed that the performance of these algorithms is nearly identical, when the same stepsizes are used, but the PDDY and PD3O algorithms have a larger range of stepsizes than the CV algorithm, so that they are often faster after tuning. We used \(\gamma \tau \Vert L\Vert ^2=0.999\), which was always the best choice for these two algorithms. So, we do not provide direct comparisons in the plots. Instead, we focus on how the choice of the stochastic gradient estimator affects the convergence speed; we compare the true gradient, the standard stochastic gradient estimator (SGD), the VR estimators SAGA [29] and SVRG [40, 74, 79]. We used closed-form expressions for \(\nu \) and tuned the stepsizes for all methods by running logarithmic grid search with factor 1.5 over multiples of \(\frac{1}{\nu }\). We used a batch size of 16 for better parallelism in the stochastic estimators. For SGD, we used a small value of \(\gamma \), such as \(\frac{0.01}{\nu }\).

Fig. 1
figure 1

Results for the PCA-Lasso experiment. Left: convergence w.r.t. the objective function; right: convergence in norm

Full size image

7.1 PCA-Lasso

In a recent work [71], the difficult PCA-based Lasso problem was considered: \(\min _x \frac{1}{2}\Vert Wx - a\Vert ^2 + \lambda \Vert x\Vert _1 + \lambda _1\sum _{i=1}^m \Vert L_i x\Vert \), where \(W\in {\mathbb {R}}^{n\times p}\), \(a\in {\mathbb {R}}^n\), \(\lambda , \lambda _1>0\) are given. We generated 10 matrices \(L_i\) randomly with standard normal i.i.d. entries, each with 20 rows. W and y were taken from the ‘mushrooms’ dataset in the libSVM base [14]. We chose \(\lambda =\frac{\nu }{10n}\) and \(\lambda _1=\frac{2\nu }{nm}\), where \(\nu \) is needed to compensate for the fact that we do not normalize the objective. The results are shown in Fig. 1. The advantage of using a VR stochastic gradient estimate is clear, with SAGA and SVRG being very similar.

Fig. 2
figure 2

Results for the MNIST experiment. Left: convergence w.r.t. the objective function; right: convergence in norm

Full size image

7.2 MNIST with Overlapping Group Lasso

We consider the problem where F is the \(\ell _2\)-regularized logistic loss and a group Lasso penalty. Given the data matrix \(W\in {\mathbb {R}}^{n\times p}\) and vector of labels \(a\in \{0,1\}^n\), \(F(x)=\frac{1}{n}\sum _{i=1}^n f_i(x) + \frac{\lambda }{2}\Vert x\Vert ^2\), where \(f_i(x)=-\big (a_i \log \big (h(w_i^\top x)\big ) + (1-a_i)\log \big (1-h(w_i^\top x)\big )\big )\), \(\lambda =\frac{2\nu }{n}\), \(w_i\in {\mathbb {R}}^p\) is the i-th row of W, and \(h:t\rightarrow 1/(1+e^{-t})\). The nonsmooth regularizer is given by \(\lambda _1\sum _{j=1}^m \Vert x\Vert _{G_j}\), where \(\lambda _1=\frac{\nu }{5n}\), \(G_j\subset \{1,\dotsc , p\}\) is a given subset of coordinates and \(\Vert x\Vert _{G_j}\) is the \(\ell _2\)-norm of the corresponding block of x. To apply splitting methods, we use \(L=(I_{G_1}^\top , \dotsc , I_{G_m}^\top )^\top \), where \(I_{G_j}\) is the operator that takes \(x\in {\mathbb {R}}^p\) and returns only the entries from block \(G_j\). Then, we can use \(H(y)=\lambda _1\sum _{j=1}^m\Vert y\Vert _{G_j}\), which is separable in y and, thus, proximable. We use the MNIST dataset [48] of 70000 black and white \(28\times 28\) images. For each pixel, we add a group of pixels \(G_j\) adjacent to it, including the pixel itself. Since there are some border pixels, groups consist of 3, 4 or 5 coordinates, and there are 784 penalty terms in total. The results are shown in Fig. 2. Here SAGA is a bit better than SVRG.

7.3 Fused Lasso Experiment

In the Fused Lasso problem, we are given a feature matrix \(W\in {\mathbb {R}}^{n\times p}\) and an output vector a, which define the least-squares function \(F(x)=\frac{1}{2}\Vert Wx-a\Vert ^2\). It is regularized with \(\frac{\lambda }{2}\Vert x\Vert ^2\) and \(\lambda _1\Vert Dx\Vert _1\), where \(\lambda =\frac{\nu }{n}\), \(\lambda _1=\frac{\nu }{10n}\) and \(D\in {\mathbb {R}}^{(p-1)\times p}\) has entries \(D_{i,i}=1\), \(D_{i, i+1}=-1\), for \(i=1,\dotsc , p-1\), and \(D_{ij}=0\) otherwise. We used again the ‘mushrooms’ dataset. The plots look very similar to the ones in Fig. 1, so we omit them.

8 Conclusion

We proposed a new primal–dual proximal splitting algorithm, the Primal–Dual Davis–Yin (PDDY) algorithm, to minimize a sum of three functions, one of which is composed with a linear operator. It is an alternative to the PD3O algorithm; they often perform similarly, but one or the other may be preferable for the problem at hand, depending on the implementation details. In particular, their memory requirements can be different. Furthermore, we proposed stochastic variants of both algorithms, studied their convergence rates, and showed by experiments that they can be much faster than their deterministic counterparts. We also showed that for linearly-constrained minimization of a strongly convex function, an instance of the stochastic PDDY algorithm, called LiCoSGD, converges linearly. We studied all algorithms within the unified framework of a stochastic generalization of Davis–Yin splitting for monotone inclusions. Our machinery opens the door to a promising class of new randomized proximal algorithms for large-scale optimization.