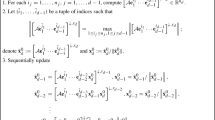On Approximation Algorithm for Orthogonal Low-Rank Tensor Approximation

Abstract

This work studies solution methods for approximating a given tensor by a sum of R rank-1 tensors with one or more of the latent factors being orthonormal. Such a problem arises from applications such as image processing, joint singular value decomposition, and independent component analysis. Most existing algorithms are of the iterative type, while algorithms of the approximation type are limited. By exploring the multilinearity and orthogonality of the problem, we introduce an approximation algorithm in this work. Depending on the computation of several key subproblems, the proposed approximation algorithm can be either deterministic or randomized. The approximation lower bound is established, both in the deterministic and the expected senses. The approximation ratio depends on the size of the tensor, the number of rank-1 terms, and is independent of the problem data. When reduced to the rank-1 approximation case, the approximation bound coincides with those in the literature. Moreover, the presented results fill a gap left in Yang (SIAM J Matrix Anal Appl 41:1797–1825, 2020), where the approximation bound of that approximation algorithm was established when there is only one orthonormal factor. Numerical studies show the usefulness of the proposed algorithm.

1 Introduction

Tensors (hypermatrices) play an important role in signal processing, data analysis, statistics, and machine learning nowadays, key to which are tensor decompositions/approximations [4, 6, 20, 37]. Canonical polyadic (CP) decomposition factorizes a data tensor into some rank-1 components. Such a decomposition can be unique under mild assumptions [21, 34, 36]. However, the degeneracy of the associated optimization problem requires one to impose additional constraints, such as nonnegativity, angularity, and orthogonality constraints [19, 26, 27]. Orthogonal CP approximation requires that one or more of the latent factors be orthonormal [11, 19], modeling applications arising from image processing, joint SVD, independent component analysis, DS-CDMA systems, and so on [5, 7, 32, 35, 38, 41, 42].

Most existing algorithms for orthogonal CP approximation are iterative ones [3, 11, 16, 23, 24, 28, 31, 41, 47, 48]; just to name a few. Specifically, alternating least squares (ALS) algorithms were developed in [3, 41, 47]: Chen and Saad [3] considered the model that all the factors are orthonormal and established the convergence of ALS under certain local assumptions; Sørensen et al. [41] considered the case that one of the factors is orthonormal, while the convergence was not provided. Such a gap was filled in [47] for generic tensors. Guan and Chu [11] considered the case that one or more of the factors are orthonormal, proposed a method that simultaneously updates two vectors corresponding to two factors, and proved the global convergence for generic tensors. Shifted type ALS algorithms were developed in [16, 31, 48]: Pan and Ng [31] considered symmetric tensors and established global convergence for generic tensors; Hu and Ye [16] studied the case where all factors are orthonormal and established the global and linear convergence of the algorithm; Yang [48] established the global convergence when the orthonormal factors are one or more than one. Local linear convergence of ALS was proved in [44] under certain positive definiteness assumptions. In the rank-1 approximation case, global linear convergence was shown to be valid for generic tensors [15]. Martin and Van Loan [28] and Li et al. [23] proposed Jacobi-type algorithms, where Li et al. [23] considered symmetric tensors and established the global convergence of the developed algorithms. Besides, Sørensen et al. [41] proposed a simultaneous matrix diagonalization approach for the problem with one orthonormal factor.

As a nonconvex problem, the solution quality of iterative algorithms depends on the initializer. To find a good initializer for iterative algorithms, Yang [48, Procedure 3.1] developed an approximation algorithm that first finds the orthonormal factors by using the celebrated higher-order SVD (HOSVD) [8] and then computes the non-orthonormal ones by solving rank-1 approximation problems. However, the approximation bound of Yang [48, Procedure 3.1] was only established when the number of orthonormal latent factors is one.

To fill this gap, by further exploring the multilinearity and orthogonality of the problem, we modify [48, Procedure 3.1] to devise a new approximation algorithm. A main feature of the proposed algorithm is that it can be either deterministic or randomized, depending on how to deal with a set of subproblems. Specifically, two deterministic and one randomized procedures are considered. The approximation lower bound is derived, both in the deterministic and in the expected senses, regardless of how many latent orthonormal factors there are. The approximation ratio depends on the size of the tensor, the number of rank-1 terms, and is independent of the problem data. Reducing to the rank-1 approximation case, the approximation ratio is of the same order as in [13, 51]. We provide numerical studies to show the efficiency of the introduced algorithm and its usefulness in tensor recovery and clustering.

In fact, approximation algorithms have already been widely studied for tensor approximations. For example, HOSVD, sequentially truncated HOSVD [45], and hierarchical HOSVD [10] are also approximation algorithms for the Tucker decomposition. On the other hand, several randomized approximation algorithms have been proposed in recent years for Tucker decomposition or t-SVD [1, 2, 29, 50]. The solution quality of the aforementioned algorithms was measured via error bounds. In the context of tensor best rank-1 approximation and related polynomial optimization problems, deterministic or randomized approximation algorithms were developed [9, 12, 13, 18, 39, 40], where the solution quality was measured by approximation bounds; our algorithm extends these to orthogonal rank-R approximations.

The rest of this work is organized as follows. Preliminaries are given in Sect. 2. The new approximation algorithm is introduced in Sect. 3, while the approximation bound is derived in Sect. 4. Section 5 provides numerical results, and Sect. 6 draws some conclusions.

2 Preliminaries

Throughout this work, vectors are written as boldface lowercase letters $({\mathbf {x}},{\mathbf {y}},\ldots )$, matrices correspond to italic capitals $(A,B,\ldots )$, and tensors are written as calligraphic capitals $(\mathcal {A}, \mathcal {B}, \cdots )$. $\mathbb R^{n_1\times \cdots \times n_d}$ denotes the space of $n_1\times \cdots \times n_d$ real tensors. For two tensors $\mathcal A,{\mathcal {B}}$ of the same size, their inner product $\langle {\mathcal {A}},{\mathcal {B}}\rangle$ is given by the sum of entry-wise products. The Frobenius (or Hilbert–Schmidt) norm of ${\mathcal {A}}$ is defined by $\Vert {\mathcal {A}}\Vert _F = \langle {\mathcal {A}},\mathcal A\rangle ^{1/2}$. $\otimes$ denotes the outer product. For ${\mathbf {u}}_j\in {\mathbb {R}}^{n_j}$, $j=1,\ldots ,d$, $\mathbf{u}_1\otimes \cdots \otimes {\mathbf {u}}_d$ denotes a rank-1 tensor in $\mathbb R^{n_1\times \cdots \times n_d}$, which is written as $\bigotimes ^d_{j=1}{\mathbf {u}}_j$ for short. For $j=1,\ldots ,d$ and for each j, if we are given R vectors of size $n_j$: ${\mathbf {u}}_{j,1},\ldots ,{\mathbf {u}}_{j,R}$, we usually collect them into a matrix $U_j=[{\mathbf {u}}_{j,1},\ldots ,\mathbf{u}_{j,R}] \in {\mathbb {R}}^{n_j\times R}$.

The mode-j unfolding of ${\mathcal {A}}\in \mathbb R^{n_1\times \cdots \times n_d}$, denoted as $A_{(j)}$, is a matrix in ${\mathbb {R}}^{n_j\times \prod ^d_{k\ne j}n_k}$. The product between a tensor ${\mathcal {A}}\in \mathbb R^{n_1\times \cdots \times n_d}$ and a vector $\mathbf{u}_j\in {\mathbb {R}}^{n_j}$ with respect to the j-th mode, written as ${\mathcal {A}}\times _j {\mathbf {u}}_j^\top$, is a tensor in $\mathbb R^{n_1\times \cdots \times n_{j-1}\times n_{j+1}\times \cdots \times n_d}$.

Given a d-th order tensor ${\mathcal {A}}\in \mathbb R^{n_1\times \cdots \times n_d}$, a positive integer R, decision matrices (factors) $U_j = [ \mathbf{u}_{j,1},\ldots ,{\mathbf {u}}_{j,R} ]\in {\mathbb {R}}^{n_j\times R}$, $j=1,\ldots ,d$, and coefficients $\sigma _i\in {\mathbb {R}}$, $i=1,\ldots ,R$, the orthogonal CP approximation under consideration can be written as [11]:

$$\begin{aligned} {\begin{aligned}&\min _{U_1,\ldots ,U_d,\sigma _1,\ldots ,\sigma _R} ~ \left\| {\mathcal {A}} - \sum \nolimits ^R_{i=1}\sigma _i \bigotimes \nolimits ^d_{j=1} \mathbf{u}_{j,i } \right\| _F ^2 \\&~ ~~~~~~~ \mathrm{s.t.}~ ~~~~~~~~ {\mathbf {u}}_{j,i}^\top \mathbf{u}_{j,i} =1, j=1,\ldots ,d-t, 1\le i \le R,\\&~~~~~~~~~~~~~~~~~~~~~ U_j^\top U_j = I, j=d-t+1,\ldots ,d, ~ { \sigma }_i\in {\mathbb {R}}, \end{aligned}} \end{aligned}$$

(2.1)

where $1\le t\le d$ denotes the number of latent orthonormal factors. The constraints mean that the last t latent factors are required to be orthonormal, while the first $d-t$ ones are not. However, due to the presence of the scalars $\sigma _i$, each column ${\mathbf {u}}_{j,i}$ of the first $d-t$ factors can be normalized. Using orthogonality, (2.1) can be equivalently formulated as a maximization problem [11]:

$$\begin{aligned} \begin{array}{ll} \max _{U_1,\ldots ,U_d} &{} G(U_1,\ldots ,U_d):= \sum \nolimits ^R_{i=1} \left\langle {\mathcal {A}} , \bigotimes \nolimits ^d_{j=1} \mathbf{u}_{j,i } \right\rangle ^2 \\ \mathrm{s.t.}&{}{\mathbf {u}}_{j,i}^\top {\mathbf {u}}_{j,i} =1, j=1,\ldots ,d-t, 1\le i \le R,\\ &{}U_j^\top U_j = I, j=d-t+1,\ldots ,d, \end{array} \end{aligned}$$

(2.2)

where the variables $\sigma _i$’s have been eliminated. The approximation algorithms and the corresponding analysis studied here are mainly focused on (2.2) .

Let $V\in {\mathbb {R}}^{m\times n}$, $m\ge n$. The polar decomposition of V is to decompose it into two matrices $U\in {\mathbb {R}}^{m\times n}$ and $H\in {\mathbb {R}}^{n\times n}$ such that $V=UH$, where U is columnwisely orthonormal, and H is a symmetric positive semidefinite matrix. Its relation with SVD is given below.

Theorem 2.1

(c.f. [14]) Let $V\in {\mathbb {R}}^{m\times n}$, $m\ge n$. Then, there exist $U\in {\mathbb {R}}^{m\times n}$ and a unique symmetric positive semidefinite matrix $H\in {\mathbb {R}}^{n\times n}$ such that

$$\begin{aligned} V = UH,~U^\top U = I\in {\mathbb {R}}^{n\times n}. \end{aligned}$$

(U, H) is the polar decomposition of V. If $\mathrm{rank}(V)=n$, then H is symmetric positive definite and U is uniquely determined.

Furthermore, let $H=Q\varLambda Q^\top$, $Q,\varLambda \in \mathbb R^{n\times n}$ be the eigenvalue decomposition of H, namely, $Q^\top Q = QQ^\top = I$, $\varLambda = \mathrm{diag}(\lambda _1,\ldots ,\lambda _n)$ be a diagonal matrix where $\lambda _1\ge \cdots \ge \lambda _n\ge 0$. Then, $U = PQ^\top$, and $V = P\varLambda Q^\top$ is a reduced SVD of V.

Let $V=[{\mathbf {v}}_1,\ldots ,{\mathbf {v}}_n]$ and $U=[\mathbf{u}_1,\ldots ,{\mathbf {u}}_n]$ where ${\mathbf {v}}_i,{\mathbf {u}}_i\in \mathbb R^m$, $i=1,\ldots ,n$. The following two lemmas are useful.

Lemma 2.1

Let $U\in {\mathbb {R}}^{m\times n}$ and $H\in {\mathbb {R}}^{n\times n}$ be two matrices generated by the polar decomposition of $V\in \mathbb R^{m\times n}$ such that $V=UH$, where U is columnwisely orthonormal and H is symmetric positive semidefinite. Let ${\mathbf {v}}_i$ and ${\mathbf {u}}_i$ be defined as above. Then, it holds that

$$\begin{aligned} \left\langle {\mathbf {u}}_i , {\mathbf {v}}_i\right\rangle \ge 0,~i=1,\ldots ,m. \end{aligned}$$

Proof

Since $V=UH$ and $U^\top U = I$, we have $U^\top V = H$, which means that $\left\langle {\mathbf {u}}_i , {\mathbf {v}}_i\right\rangle$ is exactly the i-th diagonal entry of H. As H is positive semidefinite, its diagonal entries are nonnegative. The desired result follows. $\square$

Denote $\left\| \cdot \right\| _*$ as the nuclear norm of a matrix, i.e., the sum of its singular values. From Theorem 2.1, we easily see that:

Lemma 2.2

Let U and V be defined as in Theorem 2.1. Then, $\left\langle U , V\right\rangle = \left\| V \right\| _*$.

Denote $G_{\max }$ as the maximal value of (2.2) and $\lambda _i(A_{(d)})$ the i-th largest singular value of $A_{(d)}$. We have the following result, whose proof is in Appendix A.

Lemma 2.3

It holds that $\sum ^R_{i=1}\lambda _i(A_{(d)})^2 \ge G_{\max }$ in (2.2).

3 Approximation Algorithm

The approximation algorithm proposed in this work inherits certain ideas from Yang [48, Procedure 3.1], and so we first briefly recall its strategy. [48, Procedure 3.1] obtained an approximation solution to (2.2) as follows: One first applies the truncated HOSVD [8] to get $U_d,\ldots ,U_{d-t+1}$. That is to say, for $j=d,\ldots ,d-t+1$, one unfolds ${\mathcal {A}}$ to $A_{(j)} \in \mathbb R^{n_j\times \prod ^d_{l\ne j}n_l}$ and performs the truncated SVD to get its left leading R singular vectors $\mathbf{u}_{j,1},\ldots ,{\mathbf {u}}_{j,R}$, forming the j-th factor $U_j=[{\mathbf {u}}_{j,1},\ldots ,{\mathbf {u}}_{j,R}]$. Once $U_d,\ldots ,U_{d-t+1}$ are obtained, one then approximately solves R tensor best rank-1 approximation problems:

$$\begin{aligned} { \begin{array}{ll} \max _{{\mathbf {u}}_{1,1},\ldots ,{\mathbf {u}}_{d-t,R} }&{} \left\langle {\mathcal {A}}\bigotimes \nolimits ^{d}_{j=d-t+1}{\mathbf {u}}_{j,i} , \bigotimes \nolimits ^{d-t}_{j=1}{\mathbf {u}}_{j,i} \right\rangle \\ &{}\mathrm{s.t.}~~ {\mathbf {u}}_{j,i}^\top {\mathbf {u}}_{j,i} =1, j=1,\ldots ,d-t, \end{array}} \end{aligned}$$

(3.3)

where the data tensors ${\mathcal {A}}\bigotimes ^{d}_{j=d-t+1}\mathbf{u}_{j,i}:={\mathcal {A}}\times _{d-t+1} {\mathbf {u}}_{d-t+1,i}^\top \times \cdots \times _d{\mathbf {u}}_{d,i}^\top \in {\mathbb {R}}^{n_1\times \cdots \times n_{d-t}}$, $i=1,\ldots ,R$.

The approximation bound of the above strategy was established when $t=1$ [48, Proposition 3.2]. However, when $t\ge 2$, it is difficult to build connections between orthonormal factors theoretically, making it hard to derive the approximation bound. Our new algorithm differs from [48] in the computation of the orthonormal factors $U_{d-1},\ldots ,U_{d-t+1}$. By taking (2.2) with $d= t=3$ as an example, we state our idea below and depict the workflow in Fig. 1.

Fig. 1

Workflow of Algorithm 1 for approximately solving (2.2) when $d=3$ and $t=3$. PD is short for polar decomposition

The computation of $U_3$ is the same as [48], namely, we let $U_3:=[{\mathbf {u}}_{3,1},\ldots ,{\mathbf {u}}_{3,R}]$ where ${\mathbf {u}}_{3,1},\ldots ,{\mathbf {u}}_{3,R}$ are the left R leading singular vectors of the unfolding matrix $A_{(d)} \in \mathbb R^{n_3\times n_1n_2}$. Then, finding $U_2$ can be divided into a splitting step and a gathering step. In the splitting step, with ${\mathbf {u}}_{3,1},\ldots ,{\mathbf {u}}_{3,R}$ at hand, we first compute R matrices $M_{2,1},\ldots ,M_{2,R}$, with

$$\begin{aligned} M_{2,i}:= {\mathcal {A}}\times _3{\mathbf {u}}_{3,i}^\top \in \mathbb {R}^{n_2\times n_1},~i=1,\ldots ,R. \end{aligned}$$

Then, using a procedure called $\texttt {get\_v\_from\_M}$ that will be specified later, we compute R vectors ${\mathbf {v}}_{2,i}$ of size $n_2$ from $M_{2,i}$ for each i. The principle of $\texttt {get\_v\_from\_M}$ is to retain as much of the information from $M_{2,i}$ as possible, and to satisfy some theoretical bounds. Three versions of such a procedure will be detailed later. In the gathering step, we first denote $V_2:=[\mathbf{v}_{2,1},\ldots ,{\mathbf {v}}_{2,R} ] \in {\mathbb {R}}^{n_2\times R}$, which may not be orthonormal and hence not feasible. To orthogonalize it, a straightforward idea is to find the nearest orthonormal matrix to $V_2$. This is equivalent to applying the polar decomposition to $V_2$, to obtain the orthonormal matrix $U_2 := [\mathbf{u}_{2,1},\ldots ,{\mathbf {u}}_{2,R}]$.

Computing $U_1$ is similar. In the splitting step, with $U_3$ and $U_2$ at hand, we first compute $M_{1,i}:= {\mathcal {A}}\times _2\mathbf{u}_{2,i}^\top \times {\mathbf {u}}_{3,i}^\top \in {\mathbb {R}}^{n_1}$, $i=1,\ldots ,R$. Since $M_{1,i}$’s are already vectors, we immediately let ${\mathbf {v}}_{1,i}=M_{1,i}$. In the gathering step, we let $V_1:=[{\mathbf {v}}_{1,1},\ldots ,{\mathbf {v}}_{1,R}]$ and then perform polar decomposition on $V_1$ to get $U_1$.

For general $d\ge 3$, we can similarly apply the above splitting step and gathering step to obtain $U_{d-1},U_{d-2},\ldots$, sequentially. In fact, the design of the splitting and gathering steps follows the principle that

$$\begin{aligned} {\cdots \ge \sum \nolimits ^R_{i=1} \left\langle \mathbf{u}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle ^2 \ge \alpha \sum \nolimits ^R_{i=1} \left\langle {\mathbf {u}}_{j+1,i} , \mathbf{v}_{j+1,i}\right\rangle ^2 \ge \cdots ,} \end{aligned}$$

(3.4)

where $\alpha \in (0,1)$ and this will be studied in detail later. If $t<d$, i.e., there exist non-orthonormal constraints, then with $U_{d-t+1},\ldots ,U_d$ at hand, we compute $U_1,\ldots ,U_{d-t}$ via approximately solving R tensor rank-1 approximation problems (3.3). The whole algorithm is summarized in Algorithm 1.

Some remarks on Algorithm 1 are given as follows.

Remark 3.1

• 1. When $t=1$, Algorithm 1 and [48, Procedure 3.1] are exactly the same if they take the same procedure $\texttt {rank1approx}$.

• 2. Since ${\mathcal {B}}_{j,i} = {\mathcal {A}} \times _{j+1}\mathbf{u}_{j+1,i}^\top \times _{j+2} \cdots \times _d{\mathbf {u}}_{d,i}^\top$ and ${\mathcal {B}}_{j-1,i} = {\mathcal {A}} \times _{j}\mathbf{u}_{j,i}^\top \times _{j+1} \cdots \times _d{\mathbf {u}}_{d,i}^\top$, we have the relation that

  $$\begin{aligned} {\mathcal {B}}_{j-1,i} = {\mathcal {B}}_{j,i} \times _j{\mathbf {u}}_{j,i}^\top . \end{aligned}$$

  This recursive definition on ${\mathcal {B}}_{j,i}$ reduces its computational complexity.

• 3. Computing ${\mathbf {v}}_{j,1},\ldots ,{\mathbf {v}}_{j,R}$ can be done in parallel.

• 4. The algorithm does not guarantee that the generated objective value is larger than certain values, such as $\sum ^R_{i=1}{\mathcal {A}} ({i,\ldots , i})^2$ (here $A ({i_1,\ldots , i_d})$ denotes the $(i_1,\ldots ,i_d)$-th entry of ${\mathcal {A}}$, and we assume that ${\mathcal {A}}(1,\ldots , 1)^2\ge {\mathcal {A}}(2,\ldots , 2)^2\ge \cdots$). This objective function corresponds to the feasible point $U_j$’s with ${\mathbf {u}}_{j,i}= {\mathbf {e}}_i$, where ${\mathbf {e}}_i$ is a vector of the proper size such that its i-th entry is 1 and other entries are 0.

On the procedure $\texttt {get\_v\_from\_M}$: How to obtain ${\mathbf {v}}_{j,i}$ from $M_{j,i}$ is important both in theory and practice. To retain more information in ${\mathbf {v}}_{j,i}$ from $M_{j,i}$, we expect that

$$\begin{aligned} \left\| {\mathbf {v}}_{j,i} \right\| ^2 \ge \beta \left\| M_{j,i} \right\| _F^2, \end{aligned}$$

(3.5)

where $\beta \in (0,1)$. We provide three procedures to achieve this, two deterministic and one randomized. To simplify the notations in the procedures, we omit the footscripts j and i. In the procedures, $M\in {\mathbb {R}}^{n\times m}$, ${\mathbf {v}}\in \mathbb R^n$, and ${\mathbf {y}}\in {\mathbb {R}}^m$.

The first idea is straightforward: we let ${\mathbf {v}}$ be M times its leading right unit singular vector:

The second one is to first pick the row of M with the largest magnitude, normalize it to yield a column vector ${\mathbf {y}}$, and then let ${\mathbf {v}}=M{\mathbf {y}}$:

The third one is to first randomly and uniformly pick a row of M, normalize it to yield ${\mathbf {y}}$, and then let ${\mathbf {v}} = M{\mathbf {y}}$:

The analysis of the procedures will be given in the next section.

On the procedure $\texttt {rank1approx}$: To be more general, $\texttt {rank1approx}$ in Algorithm 1 can be any efficient approximation algorithm for solving tensor best rank-1 approximation problems, such as [13, Algorithm 1 with DR 2], [51, Sect. 5], [48, Procedure 3.3], or even Algorithm 1 itself (the case that $R=1$ and $t=d$). For the purpose of approximation bound analysis, we require $\texttt {rank1approx}$ to have an approximation bound characterization, i.e., for any m-th order data tensor $\mathcal C\in {\mathbb {R}}^{n_1\times \cdots \times n_m}$ (assuming that $n_1\le \cdots \le n_m$), the normalized solution $(\mathbf{x}_1,\ldots ,{\mathbf {x}}_m)$ returned by $\texttt {rank1approx}$ admits an approximation bound of the form:

$$\begin{aligned} { \begin{aligned}&\left\langle {\mathcal {C}} , \bigotimes \nolimits ^m_{j=1}{\mathbf {x}}_j\right\rangle \ge \frac{ \left\| {\mathcal {C}} \right\| _F}{ \zeta (m) },~\forall {\mathcal {C}}\in {\mathbb {R}}^{n_1\times \cdots \times n_m},~m\ge 1, \end{aligned}} \end{aligned}$$

(3.6)

where $1/\zeta (m) \le 1$ represents the approximation factor. For He et al. [13, Approximation 1 with DR 2], it can be checked from He et al. [13, Sect. 3.1] that when $m\ge 3$,

$$\begin{aligned}{\zeta (m) = \sqrt{ \prod \nolimits ^{m-2}_{j=1} n_j }\cdot \sqrt{n_1}.} \end{aligned}$$

For Yang [48, Procedure 3.3], it follows from Yang [48, Proposition 3.1] that

$$\begin{aligned} \zeta (m) = \left\{ \begin{array}{ll} \sqrt{ {\prod }^{m-1}_{j=1}n_j\cdot {\prod }^{m/2-2}_{j=1}n_{2j+1} \cdot n_2^{-1} }\sqrt{n_{m-1}n_m}, &{} m~\mathrm{even~and}~m\ge 4,\\ \sqrt{{\prod }^{m-1}_{j=2}n_j\cdot {\prod }^{(m+1)/2-2}_{j=1}n_{2j}}\sqrt{n_{m-1}n_m},&{} m~\mathrm{odd~and}~m\ge 3. \end{array}\right. \end{aligned}$$

When $m=1,2$, namely ${\mathcal {C}}$ is a vector or a matrix, we have that $\zeta (1)=1$ and $\zeta (2)=\sqrt{n_1}$ for both algorithms.

Computational complexity of Algorithm 1: to simplify the presentation, we consider $n_1=\cdots =n_d=n$. Computing $U_d$ is a truncated SVD, whose complexity is $O(n^2\cdot n^{d-1})$. In the computation of $U_{d-1}$, computing ${\mathcal {B}}_{d-1,i}$ and $M_{d-1,i}$ requires $O(n^d)$ flops. As $M_{d-1,i}\in {\mathbb {R}}^{n\times n^{d-2}}$, computing ${\mathbf {v}}_{d-1,i}$ requires $O(n^2\cdot n^{d-2})$ flops if Procedure A is used, while it takes $O(n\cdot n^{d-2})$ flops for Procedures B and C. In any case, this is dominated by $O(n^d)$. Thus, the complexity of the splitting step is $O(Rn^d )$. The main effort of the gathering step is the polar decomposition of $V_{d-1,i}\in {\mathbb {R}}^{n\times R}$, with complexity $O(R^2n)$. Hence, computing $U_{d-1}$ requires $O(Rn^d) + O(R^2n)$ flops.

The complexity of computing $U_{d-2}$ is similar: from Remark 3.1, computing ${\mathcal {B}}_{d-2,i}$ and $M_{d-2,i}$ needs $O(n^{d-1})$ flops. The total complexity of $U_{d-2}$ is $O(Rn^{d-1}) + O(R^2n) .$

For $U_{d-3},\ldots ,U_{d-t+1}$, the analysis is analogous. Denote $O(\texttt {rank1approx}(\cdot ))$ as the complexity of the rank-1 approximation procedure, depending on which procedure is used. Then, the updating of $U_1,\ldots ,U_{d-t}$ has complexity

$$\begin{aligned} O(Rn^{d-t+1}) + O(R\cdot \texttt {rank1approx}({\mathcal {B}}_{d-t+1,i}\times _{d-t+1}{\mathbf {u}}_{d-t+1,i}^\top )), \end{aligned}$$

where the first term comes from computing ${\mathcal {B}}_{d-t+1,i}$. Summarizing the above discussions, we have:

Proposition 3.1

(Computational complexity of Algorithm 1) Assume that $n_1=n_2=\cdots =n_d=n$. The computational complexity of Algorithm 1 is

$$\begin{aligned}&O(n^{d+1}) + \sum ^{t+1}_{j=2} O(Rn^{d-j+2}) + O(tR^2n)\\&\quad + O(R\cdot \texttt {rank1approx}(\mathcal {B}_{d-t+1,i}\times _{d-t+1}{\mathbf {u}}_{d-t+1,i}^\top )). \end{aligned}$$

In particular, if $t=d$, then it is

$$\begin{aligned} {O(n^{d+1}) + \sum \nolimits ^{d+1}_{j=2} O(Rn^{d-j+2}) + O(dR^2 n) ,} \end{aligned}$$

which is dominated by $O(n^{d+1})$.

Note that Yang [48, Procedure 3.1] requires t SVDs of size $n\times n^{d-1}$, while Algorithm 1 performs only one SVD of this size plus additional operations of smaller sizes. This makes Algorithm 1 more efficient, which will be confirmed by numerical observations.

4 Approximation Bound

Approximation bound results for general tensors with $1\le t\le d$ are presented in Sect. 4.1, and then, we give the results for nearly orthogonal tensors in Sect. 4.2.

To begin with, we need some preparations. Recall that there is an intermediate variable ${\mathbf {y}}$ in Procedures A–C. This variable is important in the analysis. To distinguish ${\mathbf {y}}$ with respect to each i and j, when obtaining ${\mathbf {v}}_{j,i}$, we denote the associated ${\mathbf {y}}$ as ${\mathbf {y}}_{j,i}$, which is of size $\prod ^{j-1}_{k=1}n_k$. The procedures show that $\mathbf{v}_{j,i} = M_{j,i}{\mathbf {y}}_{j,i}$. Since $M_{j,i} = \texttt {reshape}\left( {\mathcal {B}}_{j,i}, n_j, \prod \nolimits ^{j-1}_{k=1} n_k \right)$ and ${\mathcal {B}}_{j,i }={\mathcal {A}} \times _{j+1}{\mathbf {u}}_{j+1,i}^\top \times _{j+2} \cdots \times _d{\mathbf {u}}_{d,i}^\top$, we have the following expression of $\left\langle {\mathbf {u}}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle$:

$$\begin{aligned} \left\langle {\mathbf {u}}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle= & {} \left\langle {\mathbf {u}}_{j,i} , M_{j,i}{\mathbf {y}}_{j,i}\right\rangle \nonumber \\= & {} \left\langle M^\top _{j,i}{\mathbf {u}}_{j,i} , {\mathbf {y}}_{j,i}\right\rangle \nonumber \\= & {} \left\langle {\mathcal {A}}\times _j\mathbf {u}_{j,i}^\top \times _{j+1}\cdots \times _d{\mathbf {u}}^\top _{d,i} , {\mathcal {Y}}_{j,i}\right\rangle , \end{aligned}$$

(4.7)

where we denote

$$\begin{aligned} {\mathcal {Y}}_{j,i} := \texttt {reshape}(\mathbf{y}_{j,i},n_1,\ldots ,n_{j-1}) \in {\mathbb {R}}^{n_1\times \cdots \times n_{j-1}}. \end{aligned}$$

(4.8)

Note that $\left\| {\mathcal {Y}}_{j,i} \right\| _F =1$ according to Procedures A–C.

The above expression is only well defined when $j\ge 2$ (see Algorithm 1). To make it consistent when $j=1$ (which happens when $t=d$), we set ${\mathcal {Y}}_{1,i}=\mathbf{y}_{1,i}=1$. We also denote $M_{1,i}:={\mathcal {B}}_{1,i} = \mathbf{v}_{1,i}$ accordingly. It is clear that (4.7) still makes sense when $j=1$.

On the other hand, $V_j$ in the algorithm is only defined when $j=d-t+1,\ldots ,d-1$. For convenience, we denote

$$\begin{aligned} V_d=[{\mathbf {v}}_{d,1},\ldots ,{\mathbf {v}}_{d,R}] \in {\mathbb {R}}^{n_d\times R} \, \mathrm{with}\, {\mathbf {v}}_{d,i}:= \lambda _i(A_{(d)} ){\mathbf {u}}_{d,i}, ~i=1,\ldots , R. \end{aligned}$$

(4.9)

We then define ${\mathcal {B}}_{d-t,i}$. Note that in the algorithm, ${\mathcal {B}}_{j,i}$ is only defined when $j\ge d-t+1$. We thus similarly define ${\mathcal {B}}_{d-t,i}:= \mathcal A\times _{d-t+1}\mathbf{u}_{d-t+1,i}^\top \times _{d-t+2}\cdots \times _d{\mathbf {u}}_{d,i}^\top \in {\mathbb {R}}^{n_1\times \cdots \times n_{d-t}}$, $i=1,\ldots ,R$. When $t=d$, ${\mathcal {B}}_{0,i}$’s are scalars.

4.1 Approximation Bound for General Tensors

When $t=1$, Algorithm 1 coincides with Yang [48, Procedure 3.1] if they take the same best rank-1 approximation procedure. Thus, similar to Yang [48, Proposition 3.2], we have:

$$\begin{aligned} G(U_1,\ldots ,U_d)= & {} \sum ^R_{i=1} \left\langle \mathcal A\times _d{\mathbf {u}}_{d,i}^\top , \bigotimes ^{d-1}_{j=1} \mathbf{u}_{j,i}\right\rangle ^2 \ge \sum ^R_{i=1}\frac{ \left\| \mathcal A\times _d{\mathbf {u}}^\top _{d,i} \right\| _F ^2}{\zeta (d-1)^2}\nonumber \\= & {} \sum ^R_{i=1}\frac{\lambda _i(A_{(d)} )^2}{\zeta (d-1)^2} , \end{aligned}$$

(4.10)

where the inequality comes from (3.6), and the last equality is due to that the unfolding of ${\mathcal {A}}\times _d{\mathbf {u}}_{d,i}^\top$ to a vector is exactly ${\mathbf {v}}_{d,i}$ defined in (4.9).

The remaining part is focused on the $t\ge 2$ cases. We first present an overview and informal analysis of the approximation bound, under the setting that (3.4) holds with a factor $\alpha _j$, and then we detail $\alpha _j$. The formal approximation bound results are stated in the last of this subsection.

Lemma 4.4

(Informal approximation bound of Algorithm 1) Let $2\le t\le d$ and let $U_1,\ldots ,U_d$ be generated by Algorithm 1. If for each $d-t+1\le j\le d-1$, there holds

$$\begin{aligned} { \sum \nolimits ^R_{i=1} \left\langle {\mathbf {u}}_{j,i} , \mathbf {v}_{j,i}\right\rangle ^2 \ge \alpha _j \sum \nolimits ^R_{i=1} \left\langle \mathbf {u}_{j+1,i} , {\mathbf {v}}_{j+1,i}\right\rangle ^2,} \end{aligned}$$

(4.11)

where $\alpha _j\in (0,1]$, then we have the following approximation bound:

$$\begin{aligned} G(U_1,\ldots ,U_d)\ge & {} \frac{1}{\zeta (d-t)^2}\prod \nolimits ^{d-1}_{j=d-t+1}\alpha _j \cdot \sum \nolimits ^R_{i=1} \lambda _i(A_{(d)})^2\\\ge & {} \frac{1}{ \zeta (d-t)^2} \prod \nolimits ^{d-1}_{j=d-t+1}\alpha _j \cdot G_{\max }, \end{aligned}$$

where $1/\zeta (d-t)$ is the rank-1 approximation ratio of $n_1\times \cdots \times n_{d-t}$ tensors, as noted in (3.6).

Proof

To make the analysis below consistent with the case $t=d$ that does not require perform rank-1 approximation, we denote $\zeta (0)=1$ and $\bigotimes ^0_{j=1}{\mathbf {u}}_{j,i} = 1$. It holds that

$$\begin{aligned} G(U_1,\ldots ,U_d)= & {} \sum ^R_{i=1} \left\langle {\mathcal {A}} , \bigotimes \nolimits ^d_{j=1} \mathbf{u}_{j,i } \right\rangle ^2 \\= & {} \sum ^R_{i=1} \left\langle {\mathcal {B}}_{d-t,i} , \bigotimes \nolimits ^{d-t}_{j=1} {\mathbf {u}}_{j,i} \right\rangle ^2\\\ge & {} \frac{1}{\zeta (d-t)^2} \sum ^R_{i=1} \left\| \mathcal {B}_{d-t,i} \right\| _F ^2 { =\frac{1}{\zeta (d-t)^2} \max _{ \left\| \mathcal {Y} \right\| _F =1} \left\langle {\mathcal {B}}_{d-t,i} , {\mathcal {Y}}\right\rangle } \\\ge & {} \frac{1}{\zeta (d-t)^2} \sum ^R_{i=1} \left\langle {\mathcal {B}}_{d-t,i} , {\mathcal {Y}}_{d-t+1,i}\right\rangle ^2; \end{aligned}$$

here, the first inequality follows from the setting (3.6), and the second one is due to that ${\mathcal {Y}}_{d-t+1,i}\in {\mathbb {R}}^{n_1\times \cdots \times n_{d-t}}$ defined in (4.8) satisfies $\left\| {\mathcal {Y}}_{d-t+1,i} \right\| _F =1$. From the definition of ${\mathcal {B}}_{d-t,i}$ and (4.7), we have

$$\begin{aligned} \left\langle {\mathcal {B}}_{d-t,i} , {\mathcal {Y}}_{d-t+1,i}\right\rangle= & {} \left\langle {\mathcal {A}}\times _{d-t+1}\mathbf{u}_{d-t+1,i}^\top \times _{d-t+2}\cdots \times _d\mathbf{u}_{d,i}^\top , {\mathcal {Y}}_{d-t+1,i}\right\rangle \\= & {} \left\langle {\mathbf {u}}_{d-t+1,i} , {\mathbf {v}}_{d-t+1,i}\right\rangle . \end{aligned}$$

It thus follows from (4.11) that

$$\begin{aligned} G(U_1,\ldots ,U_d)\ge & {} \frac{1}{\zeta (d-t)^2}\sum ^R_{i=1} \left\langle {\mathbf {u}}_{d-t+1,i} , {\mathbf {v}}_{d-t+1,i}\right\rangle ^2 \\\ge & {} \cdots \\\ge & {} \frac{1}{\zeta (d-1)^2}\prod \nolimits ^{d-t}_{j=d-t+1}\alpha _j \cdot \sum \nolimits ^R_{i=1} \left\langle {\mathbf {u}}_{d,i} , \mathbf {v}_{d,i}\right\rangle ^2. \end{aligned}$$

From (4.9) and that $\left\| {\mathbf {u}}_{j,i} \right\| =1$, we see that $\sum ^R_{i=1} \left\langle {\mathbf {u}}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle ^2 = \sum \nolimits ^R_{i=1}\lambda _i(A_{(d)})^2 \ge G_{\max },$ where Lemma 2.3 gives the inequality. The result follows. $\square$

4.1.1 On Chain Inequality (4.11)

To establish the connection between $\left\langle \mathbf{u}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle$ and $\left\langle \mathbf{u}_{j+1,i} , {\mathbf {v}}_{j+1,i}\right\rangle$, we need to detail (3.5). We first simply assume that (3.5) holds with a factor $\beta _j$, and later we present $\beta _j$ in Lemma 4.6. The proofs of Lemmas 4.5 and 4.6 are left to Appendix A.

Lemma 4.5

Let $2\le t\le d$ and let $U_1,\ldots ,U_d$ be generated by Algorithm 1. If for each $d-t+1\le j\le d-1$, there holds

$$\begin{aligned} \left\| {\mathbf {v}}_{j,i} \right\| ^2 \ge \beta _j \left\| M_{j,i} \right\| _F ^2, ~i=1,\ldots ,R, \end{aligned}$$

(4.12)

where $\beta _j\in (0,1]$ (if $j=1$ then (4.12) holds with $\beta _j=1$), then we have for $j=d-t+1,\ldots ,d-1$, and $i=1,\ldots ,R,$

$$\begin{aligned} \sum ^R_{i=1} \left\langle {\mathbf {u}}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle ^2 \ge \frac{\beta _j}{R}\sum ^R_{i=1} \left\langle {\mathbf {u}}_{j+1,i} , \mathbf{v}_{j+1,i}\right\rangle ^2. \end{aligned}$$

Remark 4.2

When $j=1$ (this happens when $t=d$), according to Algorithm 1, ${\mathbf {v}}_{1,i}={\mathcal {B}}_{1,i}=M_{1,i}$ for each i, and so (4.12) holds with $\beta _1=1$.

We then specify (4.12). Denote $\mathop {{}{\mathsf {E}}}$ as the expectation operator.

Lemma 4.6

For $2\le j\le d-1$, if ${\mathbf {v}}_{j,i}$ is generated from $M_{j,i}$ by Procedures  or , then it holds that

$$\begin{aligned} \left\| {\mathbf {v}}_{j,i} \right\| ^2 \ge \frac{1}{n_j} \left\| M_{j,i} \right\| _F ^2. \end{aligned}$$

If ${\mathbf {v}}_{j,i}$ is generated by Procedure , then it holds that

$$\begin{aligned} {{\,\mathrm{\mathop {\mathsf {E}}}\,}} \left\| {\mathbf {v}}_{j,i} \right\| ^2 \ge \frac{1}{n_j} \left\| M_{j,i} \right\| _F ^2. \end{aligned}$$

The above two lemmas show that (4.12) is crucial in deriving the approximation bound. (4.12) also implies that it is possible to devise get_v_from_M without using the form $M_{j,i}{\mathbf {y}}_{j,i}$, which can be studied in the future.

4.1.2 Putting the Pieces Together

Let $\beta _j$ be such that

$$\begin{aligned} \beta _j = {n_j^{-1}} ~\mathrm{if ~} 2\le j\le d-1,\quad \mathrm{and}\quad \beta _j = 1 \mathrm{~if}~j=1. \end{aligned}$$

Based on (4.10) and Lemmas 4.4–4.6, the main results are stated as follows.

Theorem 4.2

(Formal approximation bound) Let $1\le t\le d$ and let $U_1,\ldots ,U_d$ be generated by Algorithm 1. For $j=d-t+1,\ldots ,d-1,~i=1,\ldots ,R$, if ${\mathbf {v}}_{j,i}$’s are generated deterministically by Procedures or , then

$$\begin{aligned}G(U_1,\ldots ,U_d)\ge & {} \frac{1}{\zeta (d-t)^2} \prod \nolimits ^{d-1}_{j=d-t+1}\frac{\beta _j}{R} \cdot \sum \nolimits ^R_{i=1} \lambda _i(A_{(d)})^2\\\ge & {} \frac{1}{\zeta (d-t)^2 } \prod \nolimits ^{d-1}_{j=d-t+1}\frac{\beta _j}{R} \cdot G_{\max }; \end{aligned}$$

if ${\mathbf {v}}_{j,i}$’s are generated randomly by Procedure , then

$$\begin{aligned}{{\,\mathrm{\mathop {{}\mathsf {E}}}\,}}G(U_1,\ldots ,U_d)\ge & {} \frac{1}{ \zeta (d-t)^2 }\prod \nolimits ^{d-1}_{j=d-t+1}\frac{\beta _j}{R} \cdot \sum \nolimits ^R_{i=1} \lambda _i(A_{(d)})^2\\\ge & {} \frac{1}{ \zeta (d-t)^2 } \prod \nolimits ^{d-1}_{j=d-t+1}\frac{\beta _j}{R} \cdot G_{\max }. \end{aligned}$$

The ratio ${\frac{1}{\zeta (d-t)^2} \prod \nolimits ^{d-1}_{j=d-t+1}\frac{\beta _j}{R}}$ is

$$\begin{aligned} \left\{ \begin{array}{ll} \frac{1}{R^{d-1}\prod ^{d-1}_{j=2}n_j} , &{} t=d, \\ \frac{1}{R^{t-1}\zeta (d-t)^2\prod ^{d-1}_{j=d-t+1}n_j}, &{}1\le t< d. \end{array}\right. \end{aligned}$$

Discussions on the approximation bound are left to Appendix B. In particular, the empirical study indicates that the approximation bound might be independent of R. However, how to improve it still needs further study.

Reducing to the best rank-1 approximation problem $\max _{\Vert {\mathbf {u}}_j\Vert =1,1\le j\le d} \left\langle {\mathcal {A}} , \bigotimes ^d_{j=1}{\mathbf {u}}_j\right\rangle$ i.e., $R=1,t=d$, from Theorem 4.2 we have the following corollary.

Corollary 4.1

Let ${\mathbf {u}}_j$, $1\le j\le d$ be generated by Algorithm 1 with $R=1$ and $t=d$. Then, the approximation ratio is $\frac{1}{\sqrt{\prod ^{d-1}_{j=2}n_j }}$ (either in the deterministic or the expected sense).

The above ratio is of the same order as [13, 51], which is not the best to date [12, 40] (it lacks a factor $\sqrt{ \prod ^{d-1}_{j=2}\log n_j }$). However, our aim is not to compare them in the context of rank-1 approximation. Moreover, even in this case, Algorithm 1 with Procedures B and C is new (in fact, after this work is almost finished, we find that in the rank-1 setting, Algorithm 1 with Procedure A is essentially the same as [13, Algorithm 1 with DR 2].).

4.2 Approximation Results for Nearly Orthogonal Tensors

We consider the following type of tensors in this subsection:

Assumption 4.1

$$\begin{aligned} {\mathcal {A}} = \sum \nolimits ^R_{i=1}\sigma _i { \bigotimes \nolimits ^d_{j=1} \mathbf{u}^*_{j,i } } + {\mathcal {E}}, \end{aligned}$$

(4.13)

where the last t $U^*_j$’s are orthonormal, and the first $(d-t)$ $U^*_j$’s are columnwisely normalized. We assume that $\sigma _1> \cdots>\sigma _R>0$. ${\mathcal {E}}$ denotes the noisy tensor.

The cases that $\sigma _{i_1}=\sigma _{i_2}$ for some $1\le i_1<i_2\le R$ need more assumptions and analysis, which is out of the current scope.

Running Algorithm 1 on ${\mathcal {A}}$ with $t\ge 2$, it is easy to obtain the following results.

Proposition 4.2

Let ${\mathcal {A}}$ satisfy Assumption 4.1 with $t\ge 2$ and ${\mathcal {E}}=0$. Let $U_1,\ldots ,U_d$ be generated by Algorithm 1, where t in the algorithm takes the same value as that in the assumption. Then,

$$\begin{aligned} G({U_1,\ldots ,U_d}) = \sum \nolimits ^R_{i=1}\sigma _i^2 = G_{\max },\quad \mathrm{and}\quad {U_j = U_j^*},~j=1,\ldots ,d, \end{aligned}$$

where for $U_j = U^*_j$, we ignore the sign, i.e., it in fact holds ${\mathbf {u}}_{j,i} = \pm {\mathbf {u}}^*_{j,i}$ for each j and i.

Remark 4.3

This proposition also shows that Algorithm 1 is well designed for orthogonal tensors.

The proof is left to Appendix A. From its proof and by matrix perturbation theory, it is not hard to obtain the perturbed version of Proposition 4.2:

Proposition 4.3

Under the setting of Proposition 4.2, if ${\mathcal {E}}\ne 0$ is small enough, then we have $G({U_1,\ldots ,U_d}) = G_{\max } - O( \left\| {\mathcal {E}} \right\| )$, where the constant behind the big O is nonnegative, and

$$\begin{aligned} \min \{{ \left\| {\mathbf {u}}_{j,i}+ {\mathbf {u}}^*_{j,i} \right\| , \left\| \mathbf{u}_{j,i}-{\mathbf {u}}^*_{j,i} \right\| }\} = O( \left\| \mathcal E \right\| ),\quad j=1,\ldots ,d,\quad i=1,\ldots ,R. \end{aligned}$$

It remains to consider the case that $t=1$ in Assumption 4.1, i.e., only $U^*_d$ is orthonormal. In general, if there are no additional assumptions on $U^*_j$, $j=1,\ldots ,d-1$, then it is hard to obtain the approximation results. For instance, if $A = PQ^\top$ where P is orthonormal but Q is not, then it is hard to recover P and Q. We thus make the following incoherence assumption:

Assumption 4.2

There exists at least one $U^*_j$, $1\le j\le d-1$ that is incoherent with modules $0\le \delta <1$, i.e.,

$$\begin{aligned} \exists 1\le j \le d-1, ~\mathrm{with}~ \left| \left\langle {\mathbf {u}}^*_{j,i_1} , {\mathbf {u}}^*_{j,i_2} \right\rangle \right| \le \delta ,~\forall i_1\ne i_2. \end{aligned}$$

It is clear that $U^*_j$ is a nearly orthonormal matrix if $\delta$ is small enough. In what follows, we assume without loss of generality that $U^*_{d-1}$ satisfies Assumption 4.2. We immediately have:

Proposition 4.4

If $U^*_{d-1}$ is incoherent with modules $\delta$, then $U^*_{-d}$ is also incoherent with modules $\delta$.

We consider the expression of $A_{(d)} A^\top _{(d)}$. Let $\varSigma := \mathrm{diag}(\sigma _1,\ldots ,\sigma _R)$ and $U^*_{-d}\in \mathbb R^{\prod ^{d-1}_{j=1}n_j\times R }$ be the matrix whose i-th column is the vectorization of $\bigotimes ^{d-1}_{j=1}\mathbf{u}^*_{j,i}$. We have

$$\begin{aligned} A_{(d)}A^\top _{(d)}&= {U^*_d} \varSigma {(U^*_{-d})^\top {U^*_{-d}}} \varSigma {(U^*_d)^\top } + O({\mathcal {E}})\\&= {U^*_d} \varSigma ^2 {(U^*_d)^\top } + {U^*_d} \varSigma \\&\quad \times \left[ {\begin{matrix} 0&{} ({{\mathbf {u}}^*_{-d,1})^\top {\mathbf {u}}^*_{-d,2}} &{}\cdots &{} {({\mathbf {u}}^*_{-d,1})^\top {\mathbf {u}}^*_{-d,R}}\\ \vdots &{}0&{}\ddots &{} \vdots \\ \vdots &{}\ddots &{}0 &{} \vdots \\ {(\mathbf{u}^*_{-d,R})^\top {\mathbf {u}}^*_{-d,1}} &{} \cdots &{} {(\mathbf{u}^*_{-d,R})^\top {\mathbf {u}}^*_{-d,R-1}} &{} 0 \end{matrix}} \right] \varSigma {(U^*_d)^\top } \\&\quad +\, O({\mathcal {E}}) \\&= {U^*_d} \varSigma ^2 {(U^*_d)^\top } + O(\delta ) + O({\mathcal {E}}), \end{aligned}$$

namely, $A_{(d)}A_{(d)}^\top$ is a perturbation of the eigen-decomposition ${U^*_d} \varSigma ^2 {(U^*_d)^\top }$, given that $\delta$ and ${\mathcal {E}}$ are small enough. If Assumption 4.1 holds, by matrix perturbation theory, the above discussion implies that

$$\begin{aligned} \min \{{ \left\| {\mathbf {u}}_{d,i}+ {\mathbf {u}}^*_{d,i} \right\| , \left\| {\mathbf {u}}_{d,i}-{\mathbf {u}}^*_{d,i} \right\| } \} = O(\delta ) + O( \left\| {\mathcal {E}} \right\| ),~i=1,\ldots ,R, \end{aligned}$$

where $U_d$ is generated by the algorithm. It then follows that ${\mathcal {A}}\times _d {{\mathbf {u}}_{d,i}^{\top }}$ is a nearly rank-1 tensor with perturbation $O(\delta ) + O({\mathcal {E}})$, and so

$$\begin{aligned} \min \{ \left\| {\mathbf {u}}_{j,i}+ {\mathbf {u}}^*_{j,i} \right\| , \left\| \mathbf{u}_{j,i}-{\mathbf {u}}^*_{j,i} \right\| \} = O(\delta ) + O( \left\| \mathcal E \right\| ),~j=1,\ldots ,d-1. \end{aligned}$$

We thus have a similar result as Proposition 4.3:

Proposition 4.5

Denote $U_1,\ldots ,U_d$ as the factors generated by Algorithm 1, where Assumption 1 holds with $t=1$; furthermore, Assumption 4.2 holds. If $\mathcal E$ and $\delta$ are small enough, and we also set $t=1$ in the algorithm, then $G({U_1,\ldots ,U_d}) = G_{\max } - O(\delta ) - O( \left\| {\mathcal {E}} \right\| )$, where the constants behind the big O are nonnegative, and

$$\begin{aligned}&\min \left\{ { \left\| {\mathbf {u}}_{j,i}+ {\mathbf {u}}^*_{j,i} \right\| , \left\| \mathbf{u}_{j,i}-{\mathbf {u}}^*_{j,i} \right\| } \right\} \\&\quad = O(\delta ) + O( \left\| \mathcal E \right\| ),\quad j=1,\ldots ,d,\quad i=1,\ldots ,R. \end{aligned}$$

5 Numerical Study

We evaluate the performance of Algorithm 1 with Procedures A–C, and compare them with Yang [48, Procedure 3.1]. All the computations are conducted on an Intel i7-7770 CPU desktop computer with 32 GB of RAM. The supporting software is MATLAB R2019b. The MATLAB package Tensorlab [46] is employed for tensor operations. The MATLAB code is available in the folder “alg” of https://github.com/yuningyang19/epsilon-ALS with the name “approx_alg_new”.

Performance of approximation algorithms: we compare Algorithm 1 with Procedures A–C with [48, Procedure 3.1] in this part. They are, respectively, marked as Algorithm 1 (A), Algorithm 1 (B), Algorithm 1 (C), and Yang2020. All the algorithms employ the same $\texttt {rank1approx}$ procedure [48, Procedure 3.2] for solving the rank-1 approximation subproblems. The tensors ${\mathcal {A}} \in \mathbb R^{n\times n\times n\times n}$ are randomly generated where every entry obeys the standard normal distribution. The presented results are averaged over 50 instances for each case.

We first fix $R=10$, and let n vary from 10 to 100. The results are depicted in Fig. 2. Algorithm 1 (A) is in red with star markers, Algorithm 1 (B) is in magenta with circle markers, Algorithm 1 (C) is in blue with square markers, and Yang2020 is in black with right arrow markers. The left panels show the curves of the objective values $G(U_1,\ldots ,U_d)$ versus n, from which we observe that Algorithm 1 (A) performs the best, followed by Algorithm 1 (B). This is because by using SVDs, Procedure A retains more information in ${\mathbf {v}}$ than other procedures. Yang2020 performs not as well as Algorithm 1, and its performance gets worse when t increases. This also has been reported in [48, Table 3.1], while the performance of Algorithm 1 is more stable. Therefore, we may conclude that Algorithm 1 exploits the structure of the problem better than Yang2020. The right panels show the CPU time versus n, from which we see that Yang2020 needs more time than Algorithm 1. This is because Yang2020 requires to perform t SVDs of size $n\times n^{d-1}$, while the most expensive step of Algorithm 1 is only one SVD of this size. Considering Procedures A–C themselves, Algorithm 1 (A) is the most expensive one, followed by Algorithm 1 (B). The randomized version, i.e., Algorithm 1 (C), is the cheapest one.

Fig. 2

Performance of Algorithm 1 (A) (red and star markers), Algorithm 1 (B) (magenta and circle markers), Algorithm 1 (C) (blue and square markers), and [48, Procedure 3.1] (black and right arrow markers) for approximately solving (2.2) where ${\mathcal {A}} \in {\mathbb {R}}^{n\times n\times n\times n}$ are randomly generated. n varies from 10 to 100

Fig. 3

Performances of Algorithm 1 (A) (red and star markers), Algorithm 1 (B) (magenta and circle markers), Algorithm 1 (C) (blue and square markers), and [48, Procedure 3.1] (black and right arrow markers) for approximately solving (2.2) where ${\mathcal {A}} \in {\mathbb {R}}^{80\times 80\times 80\times 80}$ are randomly generated. R varies from 5 to 80

We then fix $n=80$, $t=3$, and vary R from 5 to 80. The results are plotted in Fig. 3, from which we still observe that Algorithm 1 (A) performs the best in terms of the objective value. Considering the CPU time, Algorithm 1 (B) and 1 (C) seem to be far better. This shows the superiority of SVD-free procedures for computing the vector ${\mathbf {v}}$ concerning the CPU time.

Performance of approximation algorithms plus ALS for factor recovery: the tensors are generated similarly as [41, 48]: ${\mathcal {A}} = \mathcal B/ \left\| {\mathcal {B}} \right\| + \beta \cdot {\mathcal {N}}/\Vert {\mathcal {N}}\Vert$, where ${\mathcal {B}} = \sum ^R_{i=1} \sigma _i { \bigotimes \nolimits ^d_{j=1} \mathbf{u}^*_{j,i } }$, ${\mathcal {N}}$ is an unstructured tensor, and $\beta$ denotes the noise level. Here we set $\beta =0.1$, $R=10$, $d=4$, and n varies from 60 to 90. $\sigma _i$, ${U^*_j}$, and ${\mathcal {N}}$ are randomly drawn from a uniform distribution in $[-1,1]$. The last t ${U^*_j}$ are then orthonormalized by using the orth function, while the first $(d-t)$ ones are columnwisely normalized. We only test $t=3$ and $t=4$ cases. We compare $\epsilon$-ALS [48] with $\epsilon =10^{-8}$ initialized by different initializers generated respectively by Yang2020, Algorithm 1 (A), Algorithm 1 (B), and Algorithm 1 (C). $\epsilon$-ALS initialized by random initializers is used as a baseline. The stopping criterion for $\epsilon$-ALS is $\sum ^d_{j=1}{ \left\| U^{(k+1)}_j -U^{(k)}_j \right\| _F / \left\| U^{(k)}_j \right\| _F } \le 10^{-5}$ or $k\ge 2000$. The relative error is defined as follows [41, 48]:

$$\begin{aligned} \mathrm{rel.err} = \sum \nolimits ^d_{j=1} \left\| {U^*_{j}} - U^\mathrm{out}_{j}\cdot \varPi _{j} \right\| _F/ \left\| U_{j} \right\| _F, \end{aligned}$$

where $\varPi _{j}=\arg \min _{\varPi \in \varvec{\varPi }} \left\| {U^*_{j}} - U^{\mathrm{out}}_{j}\cdot \varPi \right\| _F$, $\varvec{\varPi }$ denotes the set of permutation matrices, and $U^{\mathrm{out}}_j$’s are the factors output by the iterative algorithm. Finding the permutation can be efficiently done by the Hungarian algorithm [22]. The presented results are averaged over 50 instances for each case.

The results when $t=3$ and $t=4$ are reported in Tables 1 and 2, in which ‘$\hbox {rel.err}^0$’ and ‘$\hbox {time}^0$, respectively, represent the relative error and CPU time evaluated at the initializers. From the tables, we first observe that $\epsilon$-ALS initialized by Yang2020 and Algorithm 1 outperforms those with random initializations, considering both relative error and computational time. Comparing Algorithm 1 with Yang2020, we can see that in most cases, $\epsilon$-ALS initialized by Algorithm 1 performs comparable or slightly better. Comparing among $\epsilon$-ALS initialized by the three versions of Algorithm 1, Algorithm 1 (C) is slightly worse in terms of time; this is because although Algorithm 1 (C) is the most efficient, $\epsilon$-ALS initialized by it needs more iterations than the others. Therefore, it would be necessary to further improve the efficiency of the iterative algorithms.

Table 1 $\epsilon$-ALS initialized by different strategies

Table 2 $\epsilon$-ALS initialized by different strategies

Next, we fix $d=t=4$, $n=100$, $\beta =0.1$, and vary R from 10 to 100. We also fix $n=50$, $R=10$, and vary $\beta$ from 0.05 to 1. Plots of relative error of different methods are depicted in Fig. 4. From the table, we still observe that $\epsilon$-ALS initialized by approximation algorithms performs better than that with random initializers, and the iterative algorithm initialized by Algorithm 1 is comparable with that initialized by Yang2020.

CP approximation for clustering: tensor CP approximation for clustering works as follows: Suppose that we have N samples ${\mathcal {A}}_1,\ldots ,{\mathcal {A}}_n \in \mathbb R^{n_1\times \cdots \times n_d}$, $d\ge 2$. For a given parameter R, and for unknown variables $A\in \mathbb R^{N\times R}, U_j\in {\mathbb {R}}^{n_j\times R}$, $j=1,\ldots ,d$, one solves the following problem first:

$$\begin{aligned} \begin{aligned}&\min _{{A,U_1,\ldots ,U_d}} ~ \sum ^N_{k=1} \left\| {\mathcal {A}}_k - \sum \nolimits ^R_{i=1} a^k_{i}\bigotimes \nolimits ^d_{j=1}\mathbf{u}_{j,i} \right\| _F ^2 \\&~ \mathrm{s.t.}~~ A=(a^k_i) \in {\mathbb {R}}^{N\times R}, U_j^\top U_j = I, 1\le j\le d, \end{aligned} \end{aligned}$$

(5.14)

where in $a^k_i\in {\mathbb {R}}$, k represents the row index while i is the column index. Write $\mathbf{a}^k:=[a^k_1,\ldots ,a^k_R]^\top \in {\mathbb {R}}^R$, i.e., it is the transpose of the k-th row of A. Equation (5.14) means that one finds a common subspace in $\mathbb R^{n_1\times \cdots \times n_d}$, which is spanned by the basis $\bigotimes ^d_{j=1}{\mathbf {u}}_{j,i}$, $i=1,\ldots ,R$, and projects the samples onto this subspace. ${\mathbf {a}}^k$ can be seen as a representation of ${\mathcal {A}}_k$. This can be regarded as a dimension reduction procedure [32, 35]. By stacking $\mathcal A_k$’s into a $(d+1)$-th order tensor ${\mathcal {A}}$ with $\mathcal A(k,:,\ldots ,:)={\mathcal {A}}_k$, and denoting ${\mathbf {a}}_i$ as the i-th column of A, the objective function of (5.14) can be written as $\left\| {\mathcal {A}} - \sum ^R_{i=1}{\mathbf {a}}_i \otimes \mathbf{u}_{1,i}\otimes \cdots \otimes {\mathbf {u}}_{d,i} \right\| _F ^2$, and so (5.14) reduces to (2.2). Once $A=[{\mathbf {a}}_1,\ldots ,{\mathbf {a}}_R]$ is obtained, we use K-means for clustering, with the transpose of the rows of A, namely, ${\mathbf {a}}^k$’s being the new samples. The cluster error is defined as follows: Let $K\ge 2$ be the given clusters, $\phi _0: \mathbb R^{n_1\times \cdots \times n_d} \rightarrow \{1,\ldots ,K\}$ be the true clustering mapping, and $\phi$ be the estimated one. Denote $\mathrm{card}(\cdot )$ the cardinality of a set and $I(\cdot )$ the indicator function. The following metric is used to measure clustering performance [43]:

$$\begin{aligned} \mathrm{cluster~ err.}:= & {} \genfrac(){0.0pt}1{N}{2}^{-1}\mathrm{card} \left( \{i,j\}: I \left( \psi (\mathcal A_i)=\psi ({\mathcal {A}}_j) \right) \ne I \left( \psi _0(\mathcal A_i)=\psi _0 ({\mathcal {A}}_j) \right) ,i<j \right) . \end{aligned}$$

We solve (5.14) by $\epsilon$-ALS initialized by Algorithm 1 (A), (B), and by random initialization, with $R=30$ for the problem. For the first two initializations, the max iterations of $\epsilon$-ALS are set to 10, while it is 1000 for the random initialization. We also compare them with vanilla K-means, namely the original samples ${\mathcal {A}}_k$’s are first vectorized and then clustered by K-means. The dataset COIL-100 http://www.cs.columbia.edu/CAVE/software/softlib/coil-100.php is used, which consists of 100 objects, each containing 72 images of size $128\times 128$ viewing from different angles. In our experiment, we each time randomly select $K=\{5,7,9,11,15,20 \}$ objects, each object randomly selecting $M=50$ images, resulting into a third-order tensor ${\mathcal {A}} \in {\mathbb {R}}^{50K\times 128\times 128}$ that consists of 50K samples. For each case we run 50 instances and present the averaged results in Table 3.

Fig. 4

Comparisons of relative error of $\epsilon$-ALS initialized by Algorithm 1 (A) (red and star markers), Algorithm 1 (B) (magenta and circle markers), [48, Procedure 3.1] (black and right arrow markers), and random initializers (black and diamond markers). Left panel: n is fixed to 100, $\beta =0.1$, $t=4$, while R varies from 10 to 100. Right panel: n is fixed to 50, $t=4$, $R=10$, while the noise level $\beta$ varies from 0.05 to 1

Table 3 CP approximation for clustering via first solving (5.14) by Algorithm 1 (A) + $\epsilon$-ALS, Algorithm 1 (B) + $\epsilon$-ALS, and random + $\epsilon$-ALS

Considering the clustering error, we observe from the table that armed with the approximation algorithm, CP approximation-based method achieves better performance than the vanilla K-means, while Algorithm 1 (A) is slightly better than Algorithm 1 (B). However, if starting from a random initializer, CP approximation based method is worse than vanilla K-means. This shows the usefulness of the introduced approximation algorithm. Considering the computational time, we see that the first two methods are also better than vanilla K-means. This is because $\epsilon$-ALS is stopped within 10 iterations and because the sample size after reduction is $R=30$. On the other side, the sample size for the vanilla K-means is $128^2$. We also observe that Random + $\epsilon$-ALS usually cannot stop within 1000 iterations, making it the slowest one.

Fig. 5

Cluster error and CPU time of CP approximation for clustering of one instance with varying R from 10 to 100, and $K=5$. Left: cluster error versus R; right: CPU time versus R

We next show the influence of R on the performance. We fix an instance with $K=5$, and vary R from 10 to 100. We plot the cluster error and CPU time of Algorithm  1 (A) + $\epsilon$-ALS in Fig. 5. We see that the cluster error does not change a lot when R varies, while around $R=30$, the cluster error seems to be slightly better than the other cases. This together with the CPU time shown in the right panel explains why we choose $R=30$ in the experiment.

6 Conclusions

In [48], an approximation procedure was proposed for orthogonal low-rank tensor approximation, while the approximation bound was only established when the number of latent orthonormal factors is one. To fill this gap, a modified approximation algorithm was developed in this work. It allows either deterministic or randomized procedures to solve some key subproblems in the algorithm, therefore giving more flexibility. The approximation bound, both in the deterministic and the expected senses, has been established regardless of how many orthonormal factors there are. Moreover, compared with Yang [48, Procedure 3.1] which requires t SVDs of size $n\times n^{d-1}$, the modified algorithm involves only one SVD of this size (plus other operations of smaller size), making it more efficient. Numerical tests were provided to verify the usefulness of the algorithm, and its performance is favorably compared with Yang [48, Procedure 3.1]. One of the future work is that in Algorithm 1, instead of obtaining ${\mathcal {B}}_{j,i}$ from ${\mathcal {A}}\times _{j+1} \mathbf{u}^{\top }_{j+1,i}\cdots \times _d{\mathbf {u}}^{\top }_{d,i}$, other choices of mixing ${\mathcal {A}}$ and ${\mathbf {u}}_{j,i}$ are possible. On the other hand, approaches for finding global solutions can be studied, where a possible way is to use convex relaxation as those for rank-1 approximation [17, 30, 49]. Another possible research thread is to extend the notion of best rank-1 approximation ratio of a tensor space [25, 33] to the best rank-R approximation ratio setting and study its properties.

Appendices

A Proofs

Proof of Lemma 2.3

One notices that

$$\begin{aligned} \sum \nolimits ^R_{i=1}\lambda _i(A_{(d)})^2= & {} \max _{X_i} \sum \nolimits ^R_{i=1} \left\langle A_{(d)} , X_i\right\rangle ^2 ~\mathrm{s.t.}~ \Vert X_i\Vert _F=1, \mathrm{rank}(X_i)=1,\\&\left\langle X_i , X_j\right\rangle =0, i\ne j, \end{aligned}$$

where $X_i\in {\mathbb {R}}^{n_d\times \prod ^{d-1}_{k=1}n_k}$. The above problem is equivalent to

$$\begin{aligned} \max _{U,V}~\sum \nolimits ^R_{i=1} \left( \mathbf{u}_i^{\top }A_{(d)}{\mathbf {v}}_i\right) ^2~\mathrm{s.t.}~ U^{\top }U=I, \Vert {\mathbf {v}}_i\Vert =1, \end{aligned}$$

where $U=[{\mathbf {u}}_1,\ldots ,{\mathbf {u}}_R]\in {\mathbb {R}}^{n_d\times R}$ and $V=[{\mathbf {v}}_1,\ldots ,{\mathbf {v}}_R]\in \mathbb R^{\prod ^{d-1}_{k=1}n_k \times R }$. Note that the above maximization problem is a relaxation of (2.2); thus $\sum \nolimits ^R_{i=1}\lambda _i(A_{(d)})^2 \ge G_{\max }$. $\square$

Proof of Lemma 4.5

Since the orthonormal $U_j$’s, $j=d-t+1,\ldots ,d-1$, are given by the polar decomposition of $V_j$, from Lemma 2.1, we have $\left\langle {\mathbf {u}}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle \ge 0$. Using the relation that $a_1^2 + \cdots + a_R^2 \ge \frac{1}{R} \left( a_1+\cdots + a_R \right) ^2$ for nonnegative $a_i$’s, we have

$$\begin{aligned} \sum \nolimits ^R_{i=1} \left\langle {\mathbf {u}}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle ^2 \ge \frac{1}{R} \left( \sum \nolimits ^R_{i=1} \left\langle \mathbf{u}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle \right) ^2 = \frac{1}{R} \left\langle U_j , V_j\right\rangle ^2 \end{aligned}$$

for each j. Lemma 2.2 shows that $\left\langle U_j , V_j\right\rangle = \left\| V_j \right\| _*$; the norm relationship gives that $\left\| V_j \right\| _* \ge \left\| V_j \right\| _F$. Thus,

$$\begin{aligned} \sum \nolimits ^R_{i=1} \left\langle {\mathbf {u}}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle ^2 \ge \frac{1}{R} \left\| V_j \right\| _F ^2. \end{aligned}$$

We distinguish the cases that $j\le d-2$ and $j=d-1$. For the former case,

$$\begin{aligned} \sum \nolimits ^R_{i=1} \left\langle {\mathbf {u}}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle ^2\ge & {} \frac{1}{R} \left\| V_j \right\| _F ^2 =\frac{1}{R}\sum \nolimits ^R_{i=1} \left\| \mathbf{v}_{j,i} \right\| ^2\nonumber \\ \mathrm{(by}~\mathrm{(}4.12\mathrm{))}~~~~\ge & {} \frac{\beta _j}{R} \sum \nolimits ^R_{i=1} \left\| M_{j,i} \right\| _F ^2 \nonumber \\= & {} \frac{\beta _j}{R}\sum \nolimits ^R_{i=1} \left\| \mathcal A\times _{j+1}{\mathbf {u}}^\top _{j+1,i}\times _{j+2}\cdots \times _d\mathbf{u}^\top _{d,i} \right\| _F ^2 \nonumber \\\ge & {} \frac{\beta _j}{R}\sum \nolimits ^R_{i=1} \left\langle \mathcal A\times _{j+1}{\mathbf {u}}^\top _{j+1,i}\times _{j+2}\cdots \times _d\mathbf{u}^\top _{d,i} , {\mathcal {Y}}_{j+1,i}\right\rangle ^2\nonumber \\ {\mathrm{(by}}~\mathrm{(}4.7\mathrm{))} ~~~~= & {} \frac{\beta _j}{R} \sum \nolimits ^R_{i=1} \left\langle \mathbf{u}_{j+1,i} , {\mathbf {v}}_{j+1,i}\right\rangle ^2, \end{aligned}$$

(A.15)

where the equality in the third line follows from that $M_{j,i}$ is the unfolding of ${\mathcal {B}}_{j,i} = {\mathcal {A}} \times _{j+1}\mathbf{u}^\top _{j+1,i}\times _{j+2}\cdots \times _d{\mathbf {u}}^\top _d$, and the third inequality uses the fact that $\left\| {\mathcal {Y}}_{j+1,i} \right\| _F =1$ where ${\mathcal {Y}}_{j,i}$ was defined in (4.8).

When $j=d-1$, since ${\mathcal {Y}}_{d,i}$ is not defined, there is a slight difference after the third line of (A.15). In this case, we have

$$\begin{aligned} \sum \nolimits ^R_{i=1} \left\langle {\mathbf {u}}_{d-1,i} , \mathbf{v}_{d-1,i}\right\rangle ^2\ge & {} \frac{\beta _{d-1}}{R}\sum \nolimits ^R_{i=1} \left\| \mathcal A\times _d{\mathbf {u}}^\top _{d,i} \right\| _F ^2\\= & {} \frac{\beta _{d-1}}{R}\sum \nolimits ^R_{i=1}\lambda _i(A_{(d)})^2 = \frac{\beta _{d-1} }{R}\sum \nolimits ^R_{i=1} \left\langle \mathbf{u}_{d,i} , {\mathbf {v}}_{d,i}\right\rangle ^2, \end{aligned}$$

where the first inequality comes from a similar analysis as (A.15), the first equality follows from the definition of $U_d$, and the last one is due to the definition of $V_d$ in (4.9). The desired inequality thus follows. $\square$

Proof of Lemma 4.6

If ${\mathbf {v}}_{j,i}$ is generated by Procedure A, we have

$$\begin{aligned} \left\| {\mathbf {v}}_{j,i} \right\| ^2 =\lambda _{\max }^2(M_{j,i} ) \ge \frac{1}{n_j} \left\| M_{j,i} \right\| _F ^2, \end{aligned}$$

where $\lambda _{\max }(\cdot )$ denotes the largest singular value of a matrix.

If ${\mathbf {v}}_{j,i}$ is generated by Procedure B, we have

$$\begin{aligned} \left\| {\mathbf {v}}_{j,i} \right\| ^2 = \left\| M_{j,i}{\mathbf {y}}_{j,i} \right\| ^2 = \sum ^{n_j}_{k=1} { \left\langle {\mathbf {m}}_{j,i}^k , \frac{\mathbf{m}_{j,i}^{{{\bar{k}}}} }{ \left\| {\mathbf {m}}_{j,i}^{{{\bar{k}}}} \right\| } \right\rangle ^2} \ge { \left\| {\mathbf {m}}_{j,i}^{{{\bar{k}}}} \right\| ^2} \ge \frac{1}{n_j} \left\| M_{j,i} \right\| _F ^2, \end{aligned}$$

where we recall that ${\mathbf {m}}_{j,i}^k$ denotes the k-th row of $M_{j,i}$, and ${\mathbf {m}}_{j,i}^{{{\bar{k}}}}$ is the row with the largest magnitude.

If ${\mathbf {v}}_{j,i}$ is generated by Procedure C, since ${{\bar{k}}}$ is uniformly and randomly chosen from $\{1,\ldots ,n_j\}$, this means that with equal probability, the random variable $\left\| {\mathbf {v}}_{j,i} \right\| ^2$ takes the value $\sum ^{n_j}_{k=1}{ \left\langle {\mathbf {m}}_{j,i}^k , {\mathbf {m}}_{j,i}^s/ \left\| {\mathbf {m}}_{j,i}^s \right\| \right\rangle ^2}$, $s=1,\ldots ,n_j$, i.e.,

$$\begin{aligned} \mathop {\mathsf {Prob}} \left\{ \left\| {\mathbf {v}}_{j,i} \right\| ^2 = \sum ^{n_j}_{k=1} { \left\langle {\mathbf {m}}_{j,i}^k , \frac{\mathbf{m}_{j,i}^s }{ \left\| {\mathbf {m}}_{j,i}^s \right\| } \right\rangle ^2} \right\} = \frac{1}{n_j},~s=1,\ldots ,n_j. \end{aligned}$$

Therefore,

$$\begin{aligned} {{\,\mathrm{\mathop {\mathsf {E}}}\,}} \left\| {\mathbf {v}}_{j,i} \right\| ^2 = \frac{1}{n_j}\sum ^{n_j}_{s=1} \sum ^{n_j}_{k=1} { \left\langle {\mathbf {m}}_{j,i}^k , \frac{\mathbf{m}_{j,i}^s }{ \left\| {\mathbf {m}}_{j,i}^s \right\| } \right\rangle ^2} \ge \frac{1}{n_j} \sum ^{n_j}_{s=1} { \left\| \mathbf{m}_{j,i}^s \right\| ^2} =\frac{1}{n_j} \left\| M_{j,i} \right\| _F ^2. \end{aligned}$$

The proof has been completed. $\square$

Proof of Proposition 4.2

To achieve this, we first show that $V_j$ generated by Algorithm 1 satisfies

$$\begin{aligned} V_j = U^*_j \cdot \varSigma , ~j=d-t+1,\ldots ,d, \end{aligned}$$

(A.16)

where $\varSigma = \mathrm{diag}(\sigma _1,\ldots ,\sigma _R)$. If (A.16) holds, then since $U_j$ generated by the algorithm is given by the polar decomposition of $V_j$, by Assumption 4.1, it follows

$$\begin{aligned} U_j=U^*_j, ~j=d-t+1,\ldots ,d. \end{aligned}$$

(A.17)

(A.16) can be proved by the induction method starting from $j=d$. When $j=d$, this is in fact given by (4.9). To see this, we only need to show that $\lambda _i(A_{(d)}) = \sigma _i$ where we recall that $\lambda _i(\cdot )$ denotes the i-th largest singular value of a matrix. Let $U^*_{-d}\in {\mathbb {R}}^{\prod ^{d-1}_{j=1}n_j\times R }$ be the matrix whose i-th column is the vectorization of $\bigotimes ^{d-1}_{j=1}{\mathbf {u}}^*_{j,i}$. Under Assumption 4.1 when $t\ge 2$, $U^*_{-d}$ is orthonormal, giving that ${U^*_d} \varSigma {(U^*_{-d})^\top }$ is a reduced SVD of $A_{(d)}$, and the results follow. Assume that (A.16) holds when $j=d,d-1,\ldots ,m$; then ${U_j=U^*_j},j=d,d-1,\ldots ,m$. Therefore, it follows from the algorithm that

$$\begin{aligned} {\mathcal {B}}_{m-1,i}={\mathcal {A}}\times _m {\mathbf{u}^{\top }_{m,i}}\times _{m+1}\times \cdots \times _d{\mathbf{u}_{d,i}^{\top }} = \sigma _i \bigotimes \nolimits ^{m-1}_{j=1} {\mathbf{u}^*_{j,i}}, \end{aligned}$$

which is a rank-1 tensor. Since $M_{j-1,i}$ is the unfolding of ${\mathcal {B}}_{m-1,i}$, it can be seen that ${\mathbf {y}}_{m-1,i}$ generated by Procedures A–C is just the vectorization of $\bigotimes ^{m-2}_{j=1}{{\mathbf {u}}^*_{j,i}}$, and so $\mathbf{v}_{m-1,i} = \sigma _i{{\mathbf {u}}^*_{m-1,i}}$, which demonstrates that (A.16) holds when $j=m-1$. Thus, (A.16) and (A.17) are valid for $j=d-t+1,\ldots ,d$.

Since ${\mathcal {A}}\times _{d-t+1} {\mathbf{u}^{\top }_{d-t+1,i}}\times _{m+1}\times \cdots \times _d{\mathbf{u}_{d,i}^{\top }}$ is of rank-1, the rank-1 approximation procedure generates that ${\mathbf {u}}_{j,i}={\mathbf {u}}^*_{j,i}$, $j=1,\ldots ,d-t$. Hence, $G({U_1,\ldots ,U_d}) = G({U^*_1,\ldots ,U^*_d}) = \sum ^R_{i=1}\sigma _i^2$. This completes the proof. $\square$

B Empirical Discussions on the Approximation Bound

Lemma 4.5 shows that the approximation ratio arises from two folds of each factor: the lower bound of $\left\| {\mathbf {v}}_{j,i} \right\| ^2/ \left\| M_{j,i} \right\| _F ^2$ and the lower bound of $\sum ^R_{i=1} \left\langle \mathbf{u}_{j,i} , {\mathbf {v}}_{j,i}\right\rangle ^2/ \left\| V_j \right\| _F ^2$. The former reaches the worst bound $1/n_j$ when $M_{j,i}$ is row-wisely orthogonal and each row has equal magnitude; the latter attains the worst bound 1/R when $V_j$ is of rank-1 and each column admits equal magnitude. In reality, these two worst cases rarely occur simultaneously, meaning that it is possible to further improve the theoretical lower bound. Here, we show the real ratio and the theoretical ratio via examples as follows.

Fig. 6

Real ratio versus theoretical ratio

We generate tensors ${\mathcal {A}}\in {\mathbb {R}}^{n\times n\times n\times n}$, where every entry obeys the standard normal distribution. We set $t=4$ for the problem. n varies from 10 to 100, where for each n, 50 instances are generated. We use Procedure A in the algorithm. In Fig. 6(a), we plot the curve of the real ratio $\left( \sum ^R_{i=1} \left\| \mathbf{v}_{j,i} \right\| ^2/ \left\| M_{j,i} \right\| _F ^2 \right) /R$ and the curve of the theoretical ratio 1/n when $j=1,2$. The figure shows that although the real ratio is better, it still approaches the theoretical one as n increases. In Fig. 6b, we fix $n=100$ and vary R from 10 to 100. We plot the real ratio $\sum ^R_{i=1} \left\langle {\mathbf {u}}_{j,i} , \mathbf{v}_{j,i}\right\rangle ^2/ \left\| V_j \right\| _F ^2$ and the theoretical one 1/R. The figure shows that the real ratio is far better, while it also decreases as R increases.

To further investigate the influence of n and R on the bound, we also plot the total real ratio $\frac{G(U_1,\ldots ,U_d)}{\sum ^R_{i=1}\lambda _{\max }(A_{(d)})^2}$ and the theoretical one ${1}/{R^3n^2}$ in Fig. 6c. The tensors are the same as above, where in the left panel, we vary n from 10 to 100 with $R=10$ fixed; in the right one, R varies from 10 to 100 with $n=100$ fixed. The real ratio is in red, and the theoretical ratio is in black with diamond markers. We see that the real ratio decreases as n increases, confirming the observation of Fig. 6a. Moreover, the real ratio is almost parallel to the theoretical ratio, showing that the theoretical ratio is reasonable up to a constant (if we view R as a constant). The right panel shows that when R increases, the real ratio does not decrease as much as the theoretical one, showing that the term $1/R^3$ might be too loose in the theoretical ratio. Thus we also plot the curve of $\frac{1}{n^2}$, which is in black with right arrow markers. We see that $1/n^2$ is still under the curve of the real ratio, meaning that it is possible to improve the theoretical ratio in the absence of R.

C Another $\texttt {get\_v\_from\_M}$ Procedure

Proposition C.6

Let ${\mathbf {v}}\in {\mathbb {R}}^n$ be generated from $M\in \mathbb R^{n\times m}$ by Procedure D. Then it holds that ${{\,\mathrm{\mathop {\mathsf {E}}}\,}} \left\| {\mathbf {v}} \right\| ^2 = \frac{1}{m} \left\| M \right\| _F ^2$.

Proof

The proof is based on Lemmas C.7 and C.8. $\square$

Lemma C.7

Let ${\mathbf {y}}$ be randomly and uniformly drawn from the unit sphere ${\mathbb {S}}^{m-1}$ in ${\mathbb {R}}^m$. Then, it holds that

$$\begin{aligned} {{\,\mathrm{\mathop {\mathsf {E}}}\,}}({\mathbf {y}}(k))^2 = {1}/{m},~{{\,\mathrm{\mathop {\mathsf {E}}}\,}}{\mathbf {y}}({k_1}) {\mathbf {y}}({k_2}) = 0, \end{aligned}$$

where $k,k_1,k_2=1,\ldots ,m$, $k_1\ne k_2$, and ${\mathbf {y}}(k)$ denotes the k-th entry of ${\mathbf {y}}$.

Proof

The first property comes from He et al. [12, p. 896]. The second one uses symmetry. Let ${\mathbf {z}}\in {\mathbb {R}}^n$ be defined such that ${{\mathbf {z}}(k)= {\mathbf {y}}(k)}$ for all $k\ne k_1$, and ${{\mathbf {z}}({k_1})=- {\mathbf {y}}({k_1})}$. Then, $\mathbf{z}$ is also uniformly distributed on the unit sphere, which means that ${{\,\mathrm{\mathop {{}\mathsf {E}}}\,}}{{\mathbf {z}}({k_1}) {\mathbf {z}}({k_2})} = {{\,\mathrm{\mathop {{}\mathsf {E}}}\,}}{{\mathbf {y}}({k_1}) {\mathbf {y}}({k_2}})$. By the definition of ${\mathbf {z}}$, this means that ${{\,\mathrm{\mathop {{}\mathsf {E}}}\,}}{{\mathbf {y}}({k_1})\mathbf{y}({k_2})}=0$. Since $k_1$ and $k_2$ can be arbitrary, the results follow. $\square$

Lemma C.8

Let ${\mathbf {y}}$ be randomly and uniformly drawn from $\mathbb S^{m-1}$. For any constant vector ${\mathbf {a}}\in {\mathbb {R}}^m$, it holds that ${{\,\mathrm{\mathop {\mathsf {E}}}\,}} \left\langle {\mathbf {a}} , {\mathbf {y}}\right\rangle ^2 = m^{-1}{ \left\| {\mathbf {a}} \right\| ^2}.$

Proof

We have from Lemma C.7 that

$$\begin{aligned} {{\,\mathrm{\mathop {\mathsf {E}}}\,}} \left\langle {\mathbf {a}} , {\mathbf {y}}\right\rangle ^2= & {} {{\,\mathrm{\mathop {\mathsf {E}}}\,}}\sum \nolimits ^m_{k_1=1}\sum \nolimits ^m_{k_2=1} {{\mathbf {a}}({k_1}) {\mathbf {y}}({k_1}) {\mathbf {a}}({k_2}) {\mathbf {y}}({k_2})} \\= & {} \sum \nolimits ^m_{k=1} {({\mathbf {a}}(k))^2 ({\mathbf {y}}(k))^2} + \sum \nolimits _{k_1\ne k_2} {{\mathbf {a}}({k_1}) {\mathbf {a}}({k_2}) {\mathbf {y}}({k_1}) {\mathbf {y}}({k_2})} = m^{-1}{ \left\| {\mathbf {a}} \right\| ^2} . \end{aligned}$$

$\square$

Remark C.4

Proposition C.6 shows that if Procedure D is used in Algorithm 1, then the approximation bound will be worse than that based on the other three procedures, as m is usually far larger than n in our context. Thus, we only leave this procedure in the appendix for potential interest.