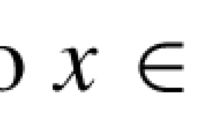On Set Containment Characterizations for Sets Described by Set-Valued Maps with Applications

Abstract

In this paper, dual characterizations of the containment of two sets involving convex set-valued maps are investigated. These results are expressed in terms of the epigraph of a conjugate function of infima associated with corresponding set-valued maps. As an application, we establish characterizations of weak and proper efficient solutions of set-valued optimization problems in the sense of vector criteria.

1 Introduction

The containment problem, deciding whether a given set A is contained in (or into) a second one B (which are usually called contained and container, respectively), was first posed by Mangasarian [1] in 2000 in the framework of machine learning in order to include, as a hard constraint, in certain separation models, the condition that a given polyhedron A is contained into one halfspace B of the two halfspaces determined by the optimal separating hyperplane. Obviously, the hard constraint was directly derived from the classical non-homogeneous Farkas lemma. The containment problem was then extended by the same Mangasarian [2] and many other authors (see, e.g., [3,4,5,6,7,8], and the recent works [9, 10]) to different pairs of sets A/B, e.g., polyhedron/polyhedron, convex set/convex set, convex set/reverse convex set, etc., described by means of convex (or quasiconvex) real (or extended real-valued) functions. As a matter of fact, any dual characterization of the containment of the solution set of a given system into the solution set of a second one can be seen as an extended Farkas lemma. This family of dual characterization has been underpinned to characterize solutions and the strong duality of different classes of optimization, including the classical convex programming problems, DC optimization problems, robust optimization problems, quasiconvex optimization problems, vector optimization problems and so on, see, e.g., [11,12,13,14,15,16,17] and the references therein. More precisely, observe that one can check the minimality of a feasible solution x of a given scalar optimization problem P appealing to some characterization of the containment of the feasible set A of P into the upper level set $B = \{x\in {\mathbb R}^n : f(x)\geqq f(\bar{x})\}$ of the objective function f; so that the characterization of the containment convex set/reverse convex set is crucial in convex optimization. But, these generalizations mentioned above and applications have so far been limited particularly to systems without input data uncertainty of given functions although the input data, in nearly all practical applications of mathematical optimization problems, are not known exactly due to forecasting errors or lack of complete information. For this reason, the values of given functions can be made to vary in a specified uncertainty sets, and therefore, set-valued maps have been considered to address these situations.

The purpose of this paper is to establish dual conditions characterizing set containments for sets described by convex set-valued maps and to show that, like their vector counterparts in vector optimization problems, these results have concerned applications in deriving characterizations for weak and proper efficient solutions of set-valued optimization problems via vector criteria (see, e.g., [18, 19]). These are achieved by employing the classical convex separation theorem and the description of the epigraph of a support function which is expressed in terms of infima associated with corresponding set-valued maps.

It is worth mentioning that the vector solutions, given by a vector criterion, for set-valued optimization problems have been underpinned to find the solutions of a set type (see, e.g., [20]), given by a set criterion which seems to be appropriate when the decision maker’s preference is based on comparing among values of the set-valued objective map (see, e.g., [21, 22]). In addition, they have been used to study characterizations of the robust efficient solutions to vector optimization problem under data uncertainty (see, e.g., [23]).

The layout of the paper is as follows. In the next section, we collect some definitions, notations and preliminary results that will be used later in the paper. In Sect. 3, we investigate the epigraphical calculus with conjugate set-valued maps. Section 4 establishes various (asymptotic) dual characterizations of set containments. Then, in Sect. 5, the results established in Sect. 4 are applied in order to provide characterizations for weakly efficient solutions as well as properly efficient solutions for convex set-valued optimization problems in the sense of vector criteria. Section 6 summaries the obtained results.

2 Notations and Preliminaries

Let us reproduce some notations, basic definitions and preliminary results which will be used throughout this paper. We denote by ${\mathbb R}^n$ the n-dimensional Euclidean space with the inner product $\langle \cdot ,\cdot \rangle$ and the associated Euclidean norm $\Vert \cdot \Vert$. The nonnegative orthant of ${\mathbb R}^n$ is denoted by ${\mathbb R}^n_+$ and is defined by ${\mathbb R}^n_+:=\{(x_1,\ldots ,x_n)\in {\mathbb R}^n : x_i\geqq 0, \ i=1,\ldots ,n\}$.

2.1 Sets and Extended Real-Valued Functions

A nonempty subset S of ${\mathbb R}^n$ is said to be a cone if $t S\subseteq S$ for all $t\geqq 0$. A cone S is said to be pointed if $S\cap (-S)=\{0\}$. The dual (positive polar) cone and the strict positive dual cone of cone S are, respectively, defined by

$$\begin{aligned} S^+:&=\{v\in {\mathbb R}^n : \langle v,x\rangle \geqq 0 \text { for all } x\in S\} \text { and }\\ S^{+i}:&=\{v\in {\mathbb R}^n : \langle v,x\rangle > 0 \text { for all } x\in S\backslash \{0\}\}. \end{aligned}$$

For a set E in ${\mathbb R}^n$, we say E is convex whenever $t x_1 +(1-t)x_2\in E$ for all $t\in [0,1]$, $x_1, x_2\in E$. By $\mathrm{int}(E)$ (resp. $\mathrm{cl}(E)$, $\mathrm{conv}(E)$) we will denote the interior (resp. closure, convex hull) of the set E. We shall denote the cone generated by the setE by $\mathrm{cone}E=\cup _{\alpha \geqq 0}\alpha E$.

For the set E in ${\mathbb R}^n$, the support function$\sigma _E$ is defined by $\sigma _E(u):=\sup _{x\in E}\langle u,x \rangle$ and the indicator function$\delta _E$ respect to a set E is defined as

$$\begin{aligned} \delta _E(x):= \left\{ \begin{array}{ll} 0 , &{}\quad \text{ if } \ x\in E;\\ +\infty , &{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

Let f be a function from ${\mathbb R}^n$ to ${\mathbb R}\cup \{\pm \infty \}$, the effective domain and the epigraph are, respectively, defined by

$$\begin{aligned} \mathrm{dom}f&:=\{x\in {\mathbb R}^n : f(x)<+\infty \} \text { and }\\ \mathrm{epi}f&:=\{(x,\alpha )\in {\mathbb R}^n \times {\mathbb R}: f(x)\leqq \alpha \}. \end{aligned}$$

We say that f is proper if $f(x)>-\infty$ for all $x\in {\mathbb R}^n$ and $\mathrm{dom}f\ne \emptyset$. If $\mathrm{epi}f$ is closed, we say that f is a lower semicontinuous function. A function f is said to be convex if $f(t x_1+(1-t)x_2)\leqq t f(x_1)+(1-t)f(x_2)$, for all $t\in [0,1]$, for all $x_1, x_2\in {\mathbb R}^n$ with the conventions:

$$\begin{aligned} (+\infty )+(-\infty )=(-\infty )+(+\infty )=0\cdot (+\infty )=+\infty , \ 0\cdot (-\infty )=0. \end{aligned}$$

For a proper lower semicontinuous convex function $f:{\mathbb R}^n \rightarrow {\mathbb R}\cup \{\pm \infty \}$, the conjugate function of f, $f^*:{\mathbb R}^n\rightarrow {\mathbb R}\cup \{\pm \infty \}$, is defined by

$$\begin{aligned} f^*(v)=\sup \{ \langle v,x\rangle -f(x): x\in {\mathbb R}^n\} \text { for any } v\in {\mathbb R}^n. \end{aligned}$$

It is worth noting that for each $v\in {\mathbb R}^n$, u can be regarded as a function on ${\mathbb R}^n$ in such away that $v(x):=\langle v,x \rangle$, for any $x\in {\mathbb R}^n$. Thus, for any $\alpha \in {\mathbb R}$ and any function $f:{\mathbb R}^n\rightarrow {\mathbb R}\cup \{\pm \infty \}$, we have

$$\begin{aligned} \mathrm{epi}(f+v+\alpha )^*=\mathrm{epi}f^*+(v,-\alpha ). \end{aligned}$$

(1)

It is also worth noting that

$$\begin{aligned} (0,0)\in \mathrm{epi}f^*+(\{0\}\times {\mathbb R}_+ )\Leftrightarrow (0,0)\in \mathrm{epi}f^*. \end{aligned}$$

(2)

The following lemmas are recalled.

Lemma 1

[24, 25] Let $f_1,f_2:{\mathbb R}^n\rightarrow {\mathbb R}\cup \{\pm \infty \}$ be proper convex functions such that $\mathrm{dom}f_1\cap \mathrm{dom}f_2\ne \emptyset$.

• (i) If $f_1$ and $f_2$ are lower semicontinuous, then,

  $$\begin{aligned} \mathrm{epi}(f_1+f_2)^*=\mathrm{cl}(\mathrm{epi}f^*_1+\mathrm{epi}f^*_2). \end{aligned}$$

• (ii) If $f_1$ or $f_2$ is continuous at some $\bar{x}\in \mathrm{dom}f_1\cap \mathrm{dom}f_2$, then,

  $$\begin{aligned} \mathrm{epi}(f_1+f_2)^*=\mathrm{epi}f^*_1+\mathrm{epi}f^*_2. \end{aligned}$$

Lemma 2

[26] Let I be an arbitrary index set, and let $f_i$, $i\in I$, be proper lower semicontinuous convex functions on ${\mathbb R}^n$. Suppose that there exists $x_0\in {\mathbb R}^n$ such that $\sup _{i\in I}f_i(x_0)<+\infty$. Then,

$$\begin{aligned} \mathrm{epi}\left( \sup _{i\in I}f_i\right) ^*=\mathrm{cl}\left( \mathrm{conv}\bigcup _{i\in I}\mathrm{epi}f^*_i\right) , \end{aligned}$$

where $\sup _{i\in I}f_i : {\mathbb R}^n\rightarrow {\mathbb R}\cup \{\pm \infty \}$ is defined by $(\sup _{i\in I}f_i)(x)=\sup _{i\in I}f_i(x)$ for all $x\in {\mathbb R}^n$.

2.2 Set-Valued Maps

Let $K\subseteq {\mathbb R}^p$ be a nonempty convex cone. For a set-valued map $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$, the domain and graph of F are, respectively, defined by

$$\begin{aligned} \mathrm{dom}(F):&=\{x\in {\mathbb R}^n : F(x)\ne \emptyset \} \text { and }\\ \mathrm{gph}(F):&=\{(x,y)\in {\mathbb R}^n \times {\mathbb R}^p : x\in \mathrm{dom}(F), \ y\in F(x)\}. \end{aligned}$$

F is called proper if $\mathrm{dom}(F)\ne \emptyset$. For a nonempty set E in ${\mathbb R}^n$, we write $F(E):=\cup _{x\in E}F(x)$. The indicator function $\widetilde{\delta }_E$ of E in the set-valued version is defined as

$$\begin{aligned} \widetilde{\delta }_E(x):= \left\{ \begin{array}{ll} \{0\} , &{}\quad \text{ if } \ x\in E;\\ \emptyset , &{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

Convexity is among the assumptions we need to prove our results. Let $C\subseteq {\mathbb R}^n$ be a nonempty convex set. The set-valued map F is said to be K-convex onC if for any $x_1, x_2\in C$ and any $t\in [0,1]$,

$$\begin{aligned} t F(x_1)+(1-t)F(x_2)\subseteq F(t x_1+(1-t)x_2)+K \end{aligned}$$

with the conventions:

$$\begin{aligned} B+\emptyset =\emptyset , \text { and } t\cdot \emptyset =\emptyset , \end{aligned}$$

for any subset B of ${\mathbb R}^p$ and for any real number t. We also say that F is K-convex (see, e.g., [27]) if $\mathrm{dom}(F)$ is a convex set and F is K-convex on $\mathrm{dom}(F)$. In addition, if F is K-convex, then $F(x)+K$ is convex for any $x\in {\mathbb R}^n$ (see, e.g., [28, Remark 4]). Moreover, K-convexity of F is connected to convexity of its associated map of infima for the scalar set-valued map. In what follows, given a proper scalar set-valued map $H:{\mathbb R}^n\rightrightarrows {\mathbb R}$, by $\varphi _H:{\mathbb R}^n\rightarrow {\mathbb R}\cup \{\pm \infty \}$ we denote its associated map of infima, i.e.,

$$\begin{aligned} \varphi _H(x):= \left\{ \begin{array}{ll} \inf \{t\in {\mathbb R}: t\in H(x)\} , &{}\quad \text{ if } \ x\in \mathrm{dom}(H);\\ +\infty , &{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

It could be convenient to observe that $\varphi _H$ is an extended real-valued function and $\mathrm{dom}\varphi _H=\mathrm{dom}(H)$. Concerning the set-valued map F, F is K-convex if and only if $\varphi _{\lambda \circ F}$ is convex for all $\lambda \in K^+$, where

$$\begin{aligned} (\lambda \circ F)(x):= \left\{ \begin{array}{ll} \{\langle \lambda ,y \rangle : y\in F(x)\} , &{}\quad \text{ if } \ x\in \mathrm{dom}(F);\\ \emptyset , &{}\quad \text{ otherwise }. \end{array} \right. \end{aligned}$$

Clearly, $\mathrm{dom}(F)=\mathrm{dom}(\lambda \circ F)$ for every $\lambda \in K^+$.

In addition, K-convexity of F is related to the upper semicontinuity of $\varphi _{\lambda \circ F}$ for any $\lambda \in K^+$. In this way, let us reproduce the notions of lower K-continuity and upper K-continuity for set-valued maps.

Definition 1

[18, Definition 7.1] and [29, Definition 2.5.16] Let $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$ be a proper set-valued map and $x\in \mathrm{dom}(F)$ be given.

• (i) F is said to be lower K-continuous at x if for any open set V such that $F(x)\cap V\ne \emptyset$, there exists a neighborhood U of x, such that

  $$\begin{aligned} F(u)\cap (V-K)\ne \emptyset , \ \forall u\in U. \end{aligned}$$

• (ii) F is said to be upper K-continuous at x if for any open set $V\supseteq F(x)$, there exits a neighborhood U of x, such that

  $$\begin{aligned}F(u)\subseteq V+K, \ \forall u\in U. \end{aligned}$$

• (iii) F is said to be lower (upper) K-continuous on $\mathrm{dom}(F)$ if it is lower (upper) K-continuous at all $x\in \mathrm{dom}(F)$.

• (iv) F is said to be K-continuous on $\mathrm{dom}(F)$ if it is lower K-continuous and upper K-continuous on $\mathrm{dom}(F)$.

Remark

The lower and upper K-continuity (resp. lower and upper $(-K)$-continuity) for single-valued maps collapse to the usual lower semicontinuity (resp. upper semicontinuity) for real-valued functions where $p:=1$ and $K:={\mathbb R}_+$.

With the aid of the following results, we can see that K-convexity of F guarantees the upper semicontinuity of $\varphi _{\lambda \circ F}$ for any $\lambda \in K^+$ provided that F has nonempty values on ${\mathbb R}^n$.

Lemma 3

[30, Theorem 4.1] If a proper set-valued map F is lower $(-K)$-continuous on $\mathrm{dom}(F)$, then $\varphi _{\lambda \circ F}$ is upper semicontinuous for each $\lambda \in K^+$.

Lemma 4

[30, Corollary 4.15(i)] Let $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$ be a set-valued map with nonempty values, i.e., $\mathrm{dom}(F)={\mathbb R}^n$. If F is K-convex, then it is lower $(-K)$-continuous on ${\mathbb R}^n$.

However, when dealing with an extended real-valued convex function, the properness and the lower semicontinuity are usually needed. The following result provides a sufficient condition to guarantee the lower semicontinuity of $\varphi _{\lambda \circ F}$ for any $\lambda \in K^+$.

Lemma 5

[30, Theorem 4.1] If a proper set-valued map F is upper K-continuous on $\mathrm{dom}(F)$, then $\varphi _{\lambda \circ F}$ is lower semicontinuous for each $\lambda \in K^+$.

In the next example, we show that we cannot confirm the lower semicontinuity of $\varphi _{\lambda \circ F}$ for any $\lambda \in K^+$ if F is not upper K-continuous on $\mathrm{dom}(F)$.

Example 1

Let $F(x):=\{(y_1,y_2)\in {\mathbb R}^2 : \text {exp}(y_1)-x\leqq y_2\}$ for $x\in {\mathbb R}$ and $K:={\mathbb R}\times {\mathbb R}_+$. We can see that $\mathrm{dom}(F)={\mathbb R}$ and F is K-convex. However, F is not upper K-continuous on $\mathrm{dom}(F)$. In fact, considering $x_0:=0$ and $V:=\{(y_1,y_2)\in {\mathbb R}^2 : y_2>0\}$. So, $F(x_0)\subseteq V$ and for any $\epsilon >0$, $\frac{2\epsilon }{3}\in ]-\epsilon ,\epsilon [$ and $(\ln (\frac{\epsilon }{3}),-\frac{\epsilon }{3})\in F(\frac{2\epsilon }{3})$ but $(\ln (\frac{\epsilon }{3}),-\frac{\epsilon }{3})\notin V+K=V$. On the one hand, we can see that for each $\lambda :=(\lambda _1,\lambda _2)\in K^+=\{0\}\times {\mathbb R}_+$,

$$\begin{aligned} \varphi _{\lambda \circ F}(x)= \left\{ \begin{array}{ll} -\lambda _2x , &{}\quad \text{ if } \ \lambda _1=0, \lambda _2>0;\\ 0 , &{}\quad \text{ if } \ \lambda _1=0, \lambda _2= 0, \end{array} \right. \end{aligned}$$

for all $x\in {\mathbb R}$. So, $\varphi _{\lambda \circ F}$ is proper lower semicontinuous for all $\lambda \in K^+$.

For the properness of $\varphi _{\lambda \circ F}$ for each $\lambda \in K^+$, it easily follows that if the proper set-valued map F has compact values on $\mathrm{dom}(F)$, it is evident that $\varphi _{\lambda \circ F}(x)\in {\mathbb R}$ for each $x\in \mathrm{dom}(F)$ and $\lambda \in K^+$. Consequently, $\varphi _{\lambda \circ F}$ is proper for all $\lambda \in K^+$.

Remark

Another way to confirm the properness of $\varphi _{\lambda \circ F}$ for each $\lambda \in K^+$ is dealing with the notion of K-bounded from below. Let us recall that the proper set-valued map $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$ is said to be K-bounded from below on $\mathrm{dom}(F)$ if there exists $a\in {\mathbb R}^p$ such that $F(x)\subseteq a+K$ for all $x\in \mathrm{dom}(F)$.

In the case where F is K-bounded from below on $\mathrm{dom}(F)$, $\varphi _{\lambda \circ F}$ is proper for each $\lambda \in K^+$. In fact, the conclusion will follow from [31, Lemma 2.1(i)] if we show that $\varphi _{\lambda \circ F}$ is ${\mathbb R}_+$-bounded from below on $\mathrm{dom}(\lambda \circ F)=\mathrm{dom}(F)$. To see this, let $\lambda \in K^+$ be given. By the K-boundedness from below of F on $\mathrm{dom}(F)$, there exists $a\in {\mathbb R}^p$ such that $F(x)\subseteq a+K$ for all $x\in \mathrm{dom}(F)$. It then follows that for any $x\in \mathrm{dom}(F)$ and any $y\in (\lambda \circ F)(x)$, there exists $y'\in F(x)$ such that $y=\langle \lambda , y'\rangle$, and so, $y=\langle \lambda ,a+k \rangle =\langle \lambda , a\rangle +\langle \lambda , k\rangle \in \langle \lambda , a\rangle +{\mathbb R}_+$ for some $k\in K$, showing that $\varphi _{\lambda \circ F}$ is ${\mathbb R}_+$-bounded from below on $\mathrm{dom}(\lambda \circ F)$.

Remark

We also point out that the compactness as well as the K-boundedness may fail to be true, while $\varphi _{\lambda \circ F}$ is lower semicontinuous for all $\lambda \in K^+$ (see, Example 1).

Now, we close this section by recalling the definition of a conjugate function of a proper scalar set-valued map given by Lee and Tuan [32] and the result needed in the sequel. Let $H:{\mathbb R}^n\rightrightarrows {\mathbb R}$ be a given proper set-valued map. The conjugate function of a given proper scalar set-value map H is the single-valued function $H^*$, $H^*:{\mathbb R}^n\rightarrow {\mathbb R}\cup \{\pm \infty \}$, such that, for any $v\in {\mathbb R}^n$,

$$\begin{aligned} H^*(v):=\sup \{\langle v,x\rangle -y: x\in \mathrm{dom}(H), \ y\in H(x)\}. \end{aligned}$$

Lemma 6

[32, Remark 4.1.]

For any proper set-valued map $H:{\mathbb R}^n\rightrightarrows {\mathbb R}$ such that $\varphi _H(x)>-\infty$ for all $x\in \mathrm{dom}(H)$, the identity $H^*=(\varphi _{H})^*$ holds.

3 Epigraphical Calculus with Conjugate Set-Valued Maps

Let S be a nonempty closed convex cone of ${\mathbb R}^m$ whose interior is possibly empty, and $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ be a proper set-valued map. We begin by considering the following set:

$$\begin{aligned} A:=\{x\in {\mathbb R}^n : G(x)\cap -S\ne \emptyset \}. \end{aligned}$$

The set A can be regarded as a feasible set in set-valued optimization problems in the literature. It can also be seen as an extension of the feasible set in vector optimization problems as well as scalar optimization problems. Indeed, by making $G(x):=\{g(x)\}$ where $g:{\mathbb R}^n\rightarrow {\mathbb R}^m$ is a vector-valued function, the set A collapses to $\{x\in {\mathbb R}^n : g(x)\in -S\}$ which can be express by scalarization in terms of a system of infinitely many inequalities $\{x\in {\mathbb R}^n : \langle \mu ,g(x) \rangle \leqq 0, \ \forall \mu \in S^+\}$. In particular, the set A can be seen as the feasible set for reliably robust optimization problems (see, e.g., [33] and the references therein). Indeed, by taking $G(x):=\{g_j(x,v) : v\in \mathcal {V}\}$ and $S:={\mathbb R}^m_+$, where $g_j: {\mathbb R}^n\times \mathcal {V}\rightarrow {\mathbb R}$, $j=1,2,\ldots ,m$, are real-valued functions and $\mathcal {V}$ is an uncertainty set. This means that the constraints $g_j(x,v)\leqq 0$, $j=1,2,\ldots ,m$, may not be fulfilled for every realization of the uncertain parameter $v\in \mathcal {V}$.

Concerning the set A described by the set-valued map, unlike various related works in the literature on vector optimization problems when dealing with scalarization, a gap may occur between the set A and the set

$$\begin{aligned} \{x\in {\mathbb R}^n : \varphi _{\mu \circ G}(x)\leqq 0, \ \forall \mu \in S^+\}, \end{aligned}$$

as the following example shows.

Example 2

Let $G(x):=\{(z_1,z_2)\in {\mathbb R}^2 : \text {exp}(z_1)-x\leqq z_2\}$ for $x\in {\mathbb R}$ and $S:={\mathbb R}\times {\mathbb R}_+$. We see that $\mathrm{dom}(G)={\mathbb R}$ and $\{x\in {\mathbb R}: G(x)\cap -S\ne \emptyset \}=\ ]0,+\infty [$. On the other hand, for each $\mu :=(\mu _1,\mu _2)\in S^+=\{0\}\times {\mathbb R}_+$,

$$\begin{aligned} \varphi _{\mu \circ G}(x)= \left\{ \begin{array}{ll} -\mu _2x , &{}\quad \text{ if } \ \mu _1=0, \mu _2> 0;\\ 0 , &{}\quad \text{ if } \ \mu _1=0, \mu _2= 0, \end{array} \right. \end{aligned}$$

for all $x\in {\mathbb R}$. So, $\{x\in {\mathbb R}: \varphi _{\mu \circ G}(x)\leqq 0,\ \forall \mu \in S^+\}=[0,+\infty [ \ \ne A$.

In the following, we need some sufficient conditions to confirm that $A=\{x\in {\mathbb R}^n : \varphi _{\mu \circ G}(x)\leqq 0, \ \forall \mu \in S^+\}$. Afterward, we can make the properties on the set A by making assumptions on the function $\varphi _{\mu \circ G}$ for all $\mu \in S^+$. For this propose, in the rest of this paper, we always say that Assumption (A) holds if one of the following conditions holds:

• (A1) For each $x\in \mathrm{dom}(G)$, there exists $z\in G(x)$ such that $\varphi _{\mu \circ G}(x)=\langle \mu ,z \rangle$ for every $\mu \in S^+$.

• (A2) For each $x\in \mathrm{dom}(G)$, G(x) is a compact subset of ${\mathbb R}^m$.

In addition, we say that G is S-proper if $\varphi _{\mu \circ G}$ is proper for all $\mu \in S^+$. We also say that F is nonnegatively S-lsc if $\varphi _{\mu \circ G}$ is lower semicontinuous for all $\mu \in S^+$.

Remark

We point out that (A1) and (A2) are independent of each other.

Example 3

Let $S:={\mathbb R}^2_+$, $G(x):=\{(z_1,z_2)\in {\mathbb R}^2 : (z_1-x)^2+(z_2-1)^2\leqq 1\}$ for every $x\in {\mathbb R}$. It is evident that G(x) is compact for all $x\in \mathrm{dom}(G)={\mathbb R}$. On the one hand, we get that for each $\mu :=(\mu _1,\mu _2)\in S^+={\mathbb R}^2_+$, $\varphi _{\mu \circ G}(x)=\mu _1 x+\mu _2-\sqrt{\mu ^2_1+\mu ^2_2}$ for all $x\in {\mathbb R}$. So, for any $z:=(z_1,z_2)\in G(1)$,

• If $z_1=0$, we must have $z_2\ne 0$, and hence, $\varphi _{(0,1)\circ G}(1)=0\ne z_2=\langle (0,1),z \rangle$;

• If $z_1\ne 0$, $\varphi _{(1,0)\circ G}(1)=0\ne z_1=\langle (1,0),z \rangle$.

This shows that (A1) does not hold.

Example 4

Let $S:={\mathbb R}\times {\mathbb R}_+$ and $G(x):=\{(x,r)\in {\mathbb R}^2 : r\geqq \max \{x,0\}\}$ for every $x\in {\mathbb R}$. It is clear that G(x) is not compact for every $x\in \mathrm{dom}(G)={\mathbb R}$, so that (A2) fails. However, (A1) is fulfilled. In fact, for each $\mu :=(\mu _1,\mu _2)\in S^+=\{0\}\times {\mathbb R}_+$,

$$\begin{aligned} \varphi _{\mu \circ G}(x)= \left\{ \begin{array}{ll} \mu _2x , &{}\quad \text{ if } \ x>0 \ \text{ with } \text{ a } \text{ minimizer } \ (x,x)\in G(x);\\ 0 , &{}\quad \text{ if } \ x\leqq 0 \ \text{ with } \text{ a } \text{ minimizer } \ (x,0)\in G(x). \end{array} \right. \end{aligned}$$

In order to derive the dual characterizations of set containments, the expression of the epigraph of the support function is needed. Before doing so, we prove the following proposition.

Proposition 1

Let $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ be proper, S-proper, S-convex and nonnegatively S-lsc. Then, $\cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*$ is a convex cone.

Proof

By taking $\mu :=0$, one observes that $(0,0)\in \cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*$. Now, let $t>0$ and $(u,\alpha )\in \cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*$. It follows that there exists $\mu _0\in S^+$ such that $(u,\alpha )\in \mathrm{epi}(\varphi _{\mu _0 \circ G})^*$. This together with Lemma 6 in turn gives us the following inequality

$$\begin{aligned} t\alpha&\geqq t(\mu _0\circ G)^*(u)\\&=t\sup \{\langle u,x \rangle -r: x\in \mathrm{dom}(\mu _0\circ G), \ r\in (\mu _0\circ G)(x)\}\\&=t\sup \{\langle u,x \rangle -\langle \mu _0,z\rangle : x\in \mathrm{dom}(G), \ z\in G(x)\}\\&=\sup \{\langle tu,x \rangle -\langle t\mu _0,z \rangle : x\in \mathrm{dom}((t\mu _0)\circ G), \ \ z\in G(x)\}\\&=((t\mu _0)\circ G)^*(tu), \end{aligned}$$

which is nothing else than

$$\begin{aligned} t(u,\alpha )\in \mathrm{epi}((t\mu _0)\circ G)^*=\mathrm{epi}(\varphi _{(t\mu _0) \circ G})^*\subseteq \cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*. \end{aligned}$$

Hence, $\cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*$ is a cone.

Now, let $(u_1,\alpha _1),(u_2,\alpha _2)\in \cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*$ and $t\in [0,1]$ be arbitrary. This implies that there exist $\mu _1,\mu _2\in S^+$ such that $(\varphi _{\mu _1 \circ G})^*(u_1)\leqq \alpha _1$ and $(\varphi _{\mu _2 \circ G})^*(u_2)\leqq \alpha _2$. It follows from the definition of conjugate function that

$$\begin{aligned} \langle u_1,x\rangle -(\varphi _{\mu _1 \circ G})(x)\leqq \alpha _1 \text { and } \langle u_2,x\rangle -(\varphi _{\mu _2 \circ G})(x)\leqq \alpha _2, \end{aligned}$$

(3)

for all $x\in {\mathbb R}^n$. Let us note in addition that, for each $x\in {\mathbb R}^n$,

$$\begin{aligned}&t\varphi _{\mu _1 \circ G}(x)+(1-t)\varphi _{\mu _2 \circ G}(x)\nonumber \\= & {} \inf \{\langle t \mu _1, y\rangle : y\in G(x)\}+\inf \{ \langle (1-t)\mu _2,y\rangle : y\in G(x)\}\nonumber \\\leqq & {} \inf \{\langle t \mu _1+(1-t)\mu _2,y \rangle : y\in G(x)\}\nonumber \\= & {} \varphi _{(t \mu _1+(1-t)\mu _2) \circ G}(x). \end{aligned}$$

(4)

Combining now (3) and (4), we get

$$\begin{aligned} t \alpha _1+(1-t)\alpha _2\geqq \langle t u_1+(1-t)u_2,x \rangle -\varphi _{(t \mu _1+(1-t)\mu _2) \circ G}(x). \end{aligned}$$

This entails that $(\varphi _{(t \mu _1+(1-t)\mu _2) \circ G})^*(t u_1+(1-t)u_2)\leqq t \alpha _1+(1-t)\alpha _2$, and therefore,

$$\begin{aligned} t(u_1,\alpha _1)+(1-t)(u_2,\alpha _2)&=(t u_1+(1-t)u_2,t \alpha _1+(1-t)\alpha _2)\\&\in \mathrm{epi}(\varphi _{(t \mu _1+(1-t)\mu _2) \circ G})^*\\&\subseteq \cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*, \end{aligned}$$

showing that $\cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*$ is a convex set. The proof is complete. $\square$

Proposition 2

Let $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ be a proper set-valued mapping satisfying (A), and let $A:=\{x\in {\mathbb R}^n : G(x)\cap -S\ne \emptyset \}$. Then,

• (i) $A=\{x\in {\mathbb R}^n : \sup _{\mu \in S^+}\varphi _{\mu \circ G}(x)\leqq 0\}$.

• (ii) In addition, if G is S-convex and nonnegatively S-lsc, then the following statements hold:

  • (a) $A\ne \emptyset \Leftrightarrow (0,-1)\notin \mathrm{cl}(\cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*)$.

  • (b) $A\ne \emptyset \Rightarrow \mathrm{epi}\sigma _A=\mathrm{cl}(\cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*)$.

Proof

• (i) Let $x\in A$ be arbitrary. So, there exists $z\in G(x)$ such that $-z\in S$. It then follows that, for each $\mu \in S^+$, $\varphi _{\mu \circ G}(x)\leqq \langle \mu ,z \rangle \leqq 0,$ and hence, $\sup _{\mu \in S^+}\varphi _{\mu \circ G}(x)\leqq 0$. Conversely, let $x\in {\mathbb R}^n$ be such that $\sup _{\mu \in S^+}\varphi _{\mu \circ G}(x)\leqq 0$. Consequently, x must be an element in $\mathrm{dom}(G)$.

  • Suppose that $x\notin A$. We have that $z\notin -S$ for every $z\in G(x)$. By Assumption (A1), there exists $z_0\in G(x)$ such that

    $$\begin{aligned} \varphi _{\mu \circ G}(x)=\langle \mu ,z_0 \rangle , \ \forall \mu \in S^+. \end{aligned}$$

    (5)

    As $z_0\notin -S$, there exists $\mu _0\in S^+\backslash \{0\}$ such that $\langle \mu _0,z_0 \rangle >0$. It follows from (5) that $\varphi _{\mu _0\circ G}(x)>0$, a contradiction. Consequently, $x\in A$.

  • As G(x) is compact for all $x\in \mathrm{dom}(G)$ by (A2), the Sion minimax theorem (see, e.g., [34, Theorem 4.2$'$]) yields

    $$\begin{aligned} \inf _{z\in G(x)}\sup _{\mu \in S^+}\langle \mu ,z \rangle =\sup _{\mu \in S^+}\varphi _{\mu \circ G}(x)\leqq 0, \end{aligned}$$

    and so, there exists $z_0\in G(x)$ such that $\sup _{\mu \in S^+}\langle \mu ,z_0 \rangle \leqq 0$. This implies that $z_0\in -S$, and therefore, $x\in A$.

• (ii) Suppose that G is S-convex and nonnegatively S-lsc. Then, $\varphi _{\mu \circ G}$ is a proper lower semicontinuous convex function for each $\mu \in S^+$.

  • (a) By (i), [3, Lemma 3.1(a)], Lemma 2 and Proposition 1, we have

    $$\begin{aligned} A\ne \emptyset \Leftrightarrow (0,-1)&\notin&\mathrm{cl}\left( \mathrm{cone}\ \mathrm{epi}\left( \sup _{\mu \in S^+}\varphi _{\mu \circ G}\right) ^*\right) \nonumber \\= & {} \mathrm{cl}(\cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*). \end{aligned}$$

    (6)

  • (b) By [3, Lemma 3.1(b)] and Lemma 2, the conclusion easily follows from the equations in (6). $\square$

4 Dual Characterizations of Set Containments

The aim of this section is to show how the dual characterizations of set containments are related to the closure of a characteristic convex cone.

For a proper set-valued map $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ and a nonempty closed convex cone S of ${\mathbb R}^m$, we define the characteristic coneC(G, S) by

$$\begin{aligned} C(G,S):=\cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*, \end{aligned}$$

which expresses the epigraph of the support function of the feasible set by the epigraphs of the conjugate functions involving the infima associated with the constraints.

We now derive a dual characterization of set containment, which will allow us to characterize a weak minimality in set-valued optimization problems in the next section, in terms of C(G, S).

Theorem 1

Let $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ be a proper, S-convex and nonnegatively S-lsc set-valued mapping satisfying (A), $K\subseteq {\mathbb R}^p$ be a nonempty closed convex cone with nonempty interior, and $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$ be K-proper, K-convex and nonnegatively K-lsc such that $\mathrm{dom}(F)={\mathbb R}^n$. Given $e\in \mathrm{int}K$, then the following statements are equivalent:

• (i) $\{x\in {\mathbb R}^n : G(x)\cap -S\ne \emptyset \}\subseteq \{x\in {\mathbb R}^n : F(x)\cap -\mathrm{int}K=\emptyset \}$;

• (ii) There exists a vector $\lambda \in K^+\backslash \{0\}$ with $\langle \lambda ,e\rangle =1$ such that

  $$\begin{aligned} (0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(C(G,S)). \end{aligned}$$

Proof

[(i)$\Rightarrow$(ii)] Suppose that (i) holds, that is, $F(A)\cap -\mathrm{int}K=\emptyset$. It then follows that

$$\begin{aligned} (F(A)+K)\cap -\mathrm{int}K=\emptyset . \end{aligned}$$

Otherwise, there exist $k\in K$, $x\in A$ and $y\in F(x)$ such that $-y-k\in \mathrm{int}K$. So, $-y=-y-k+k\in \mathrm{int}K+K=\mathrm{int}K$, and therefore, $y\in F(A)\cap -\mathrm{int}K\ne \emptyset$, a contradiction.

By the definition, K-convexity of F ensures the convexity of $F(A)+K$. Applying now the proper convex separation theorem [35, Theorem 11.3], we can get a vector $\bar{\lambda }\in {\mathbb R}^p \backslash \{0\}$ such that

$$\begin{aligned} 0\leqq \langle \bar{\lambda },y+k+\widehat{k}\rangle , \text { for all } y\in F(A), \ k\in K, \text { and } \widehat{k}\in \mathrm{int}K. \end{aligned}$$

(7)

Since K is nonempty and convex, $K=\mathrm{cl}(\mathrm{int}K)$ [35, Theorem 6.3]. Thus, for every $k\in K$, there exists $\{k_l\}\subset \mathrm{int}K$ such that $k_l\rightarrow k$ as $l\rightarrow +\infty$. So, for every $y\in F(A)$, relation (7) in turn gives us that $\langle \bar{\lambda },y+k_l \rangle \geqq 0$. Passing to the limit, we see that $\langle \bar{\lambda },y+k \rangle \geqq 0$, thereby showing that

$$\begin{aligned} 0\leqq \langle \bar{\lambda }, y+k \rangle , \text { for all } y\in F(A) \text { and } k\in K. \end{aligned}$$

(8)

As $A\ne \emptyset$ and $\mathrm{dom}(F)={\mathbb R}^n$, taking $\bar{x}\in A$ and $\bar{y}\in F(\bar{x})$. We now show that $\bar{\lambda }\in K^+$. Assume by contradiction that there exists $k_0\in K$ such that $\langle \bar{\lambda },k_0 \rangle <0$. Then, we can find $n_0\in \mathbb {N}$ such that $-\langle \bar{\lambda },n_0k_0 \rangle >\langle \bar{\lambda },\bar{y} \rangle$. This contradicts (8) due to $n_0k_0\in K$. Consequently, $\bar{\lambda }\in K^+$. As $\bar{\lambda }\ne 0$ and $e\in \mathrm{int}K$, one has $\langle \bar{\lambda },e \rangle >0$. Put $\lambda :=\frac{1}{\langle \bar{\lambda },e \rangle }\bar{\lambda }$. It is clear that $\langle \lambda ,e\rangle =1$ and $\lambda \in K^+$. In particular, taking $k:=0$ in (8), it leads to $\langle \lambda , y \rangle \geqq 0$ for every $y\in F(x)$ and $x\in A,$ which in turn allows to the assertion $\varphi _{\lambda \circ F}(x)\geqq 0$ for all $x\in A$, or equivalently, $\varphi _{\lambda \circ F}(x)+\delta _A(x)\geqq 0$ for all $x\in {\mathbb R}^n$. This together with the definition of $\mathrm{epi}(\varphi _{\lambda \circ F}+\delta _A)^*$ yields $(0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F}+\delta _A)^*$. Since F is K-proper, $\varphi _{\lambda \circ F}(x)\in {\mathbb R}$ for all $x\in {\mathbb R}^n$. Also, by the K-convexity of F, we have that $\varphi _{\lambda \circ F}$ is a convex function, and consequently, it is a continuous function. As $\delta _A$ is a proper lower semicontinuous convex function, and $\mathrm{epi}\delta ^*_A=\mathrm{epi}\sigma _A$, the conclusion will easily follow from Lemma 1 together with Proposition 2(ii).

[(ii)$\Rightarrow$(i)] The proof is done by contradiction. Assume the assertion (ii) holds true and there exist $x\in A$ and $y\in F(x)$ such that $-y\in \mathrm{int}K$. Since $A\ne \emptyset$, it follows from Proposition 2(ii) that

$$\begin{aligned} (0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(\cup _{\mu \in S^+}\mathrm{epi}(\varphi _{\mu \circ G})^*)=\mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{epi}\sigma _A. \end{aligned}$$

Then, there exists $(u,\alpha )\in \mathrm{epi}\sigma _A$ such that $-(u,\alpha )\in \mathrm{epi}(\varphi _{\lambda \circ F})^*$. This implies that $\langle u,x \rangle \leqq \sigma _A(u)\leqq \alpha$ and

$$\begin{aligned} \langle -u,x \rangle -\langle \lambda ,y \rangle&\leqq \sup \{\langle -u,x \rangle -\langle \lambda ,y \rangle : x\in {\mathbb R}^n, \ y\in F(x)\}\\&=(\lambda \circ F)^*(-u)\leqq -\alpha . \end{aligned}$$

So, $\langle \lambda ,y \rangle \geqq 0$, which contradicts to the fact that $\langle \lambda ,y \rangle <0$ due to $-y\in \mathrm{int}K$. Consequently, (i) must be true. $\square$

Let us denote by $\Gamma$ the set of all triplets (K, e, F) such that $K\subseteq {\mathbb R}^p$ is a nonempty closed convex cone with nonempty interior, $e\in \mathrm{int}K$, and F is K-proper, K-convex and nonnegatively K-lsc such that $\mathrm{dom}(F)={\mathbb R}^n$.

Corollary 1

Let $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ be a proper, S-convex and nonnegatively S-lsc set-valued mapping satisfying (A). Then, the following statements are equivalent:

• (i) For each $(K,e,F)\in \Gamma$,

  $$\begin{aligned}&\ [\forall x\in {\mathbb R}^n, \ G(x)\cap -S\ne \emptyset \Rightarrow F(x)\cap -\mathrm{int}K=\emptyset ]\\ \Leftrightarrow&\ [\exists \lambda \in K^+\backslash \{0\}, \ \langle \lambda ,e\rangle =1, \ (0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+C(G,S)]; \end{aligned}$$

• (ii) The convex cone C(G, S) is closed.

Proof

[(ii) $\Rightarrow$ (i)] The desired results can be obtained immediately by Theorem 1 and the closedness of C(G, S).

[(i) $\Rightarrow$ (ii)] Let $(u,\alpha )\in \mathrm{cl}(C(G,S))$. Applying Theorem 1 with $p:=1$, $K:={\mathbb R}_+$, $e:=1$, and $F(x):=\{\langle -u,x \rangle +\alpha \}$ for all $x\in {\mathbb R}$, we get that

$$\begin{aligned} \forall x\in {\mathbb R}^n, \ G(x)\cap -S\ne \emptyset \Rightarrow F(x)\cap -\mathrm{int}K=\emptyset , \end{aligned}$$

due to $\lambda :=1$ and $\mathrm{epi}(\varphi _{\lambda \circ F})^*=\mathrm{epi}(\langle -u,\cdot \rangle +\alpha )^*=(-u,-\alpha )+(\{0\}\times {\mathbb R}_+)$. We can see that $(K,e,F)\in \Gamma$. So, by (i), we have

$$\begin{aligned} (0,0)\in (-u,-\alpha )+(\{0\}\times {\mathbb R}_+)+C(G,S)\subseteq (-u,-\alpha )+C(G,S), \end{aligned}$$

and the proof is complete. $\square$

Corollary 2

[Characterization of the Slater condition] Let $K\subseteq {\mathbb R}^p$ be a nonempty closed convex cone with nonempty interior, and $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$ be K-proper, K-convex and nonnegatively K-lsc such that $\mathrm{dom}(F)={\mathbb R}^n$. Given $e\in \mathrm{int}K$, then the following statements are equivalent:

• (i) $\exists x\in {\mathbb R}^n, \ F(x)\cap -\mathrm{int}K\ne \emptyset$;

• (ii) $\forall \lambda \in K^+\backslash \{0\} \text { s.t. } \langle \lambda ,e\rangle =1, \ (0,0)\notin \mathrm{epi}(\varphi _{\lambda \circ F})^*$.

Proof

By taking $G(x):=\{0\}$ for all $x\in {\mathbb R}^n$ in Theorem 1, we have for each $\mu \in S^+$, $\varphi _{\mu \circ G}(x)=0$ for all $x\in {\mathbb R}^n$. Thus,

$$\begin{aligned} (\varphi _{\mu \circ G})^*(v):= \left\{ \begin{array}{ll} 0 , &{} \ \text{ if } \ v=0;\\ +\infty , &{} \ \text{ otherwise }, \end{array} \right. \end{aligned}$$

and so, $C(G,S)=\{0\}\times {\mathbb R}_+$ which is closed. The desired result is a straightforward consequence of Theorem 1 together with relation (2). $\square$

Example 5

Let $K:={\mathbb R}^2_+$, $F(x):=\{(y_1,y_2)\in {\mathbb R}^2 : (y_1-x)^2+(y_2-1)^2\leqq 1\}$ for every $x\in {\mathbb R}$. We get that for each $\lambda :=(\lambda _1,\lambda _2)\in K^+={\mathbb R}^2_+$, $\varphi _{\lambda \circ F}(x)=\lambda _1 x+\lambda _2-\sqrt{\lambda ^2_1+\lambda ^2_2}$ for all $x\in {\mathbb R}$. So,

$$\begin{aligned} (\varphi _{\lambda \circ F})^*(v):= \left\{ \begin{array}{ll} \sqrt{\lambda ^2_1+\lambda ^2_2}-\lambda _2 , &{} \ \text{ if } \ v=\lambda _1;\\ +\infty , &{} \ \text{ otherwise }. \end{array} \right. \end{aligned}$$

Hence, $\mathrm{epi}(\varphi _{\lambda \circ F})^*=\{\lambda _1\}\times [\sqrt{\lambda ^2_1+\lambda ^2_2}-\lambda _2,+\infty [$ for every $\lambda \in K^+$. By taking $e:=(1,1)$, $\bar{\lambda }:=(0,1)$, we have $(0,0)\in \mathrm{epi}(\varphi _{\bar{\lambda }\circ F})^*$. Thus, by Corollary 2, we conclude that there is no $x\in {\mathbb R}$ such that $F(x)\cap -\mathrm{int}K\ne \emptyset$.

The next set containment characterization is motivated by the notion of proper minimality in set-valued optimization problems via vector approach.

Theorem 2

Let $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ be a proper, S-convex and nonnegatively S-lsc set-valued mapping satisfying (A), $K\subseteq {\mathbb R}^p$ be a nonempty closed convex cone, and $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$ be K-proper, K-convex and nonnegatively K-lsc such that $\mathrm{dom}(F)={\mathbb R}^n$. Given $e\in K\backslash \{0\}$, then the following statements are equivalent:

• (i) There exists a convex cone $\widehat{K}\subseteq {\mathbb R}^p$ with $K\backslash \{0\}\subseteq \mathrm{int}\widehat{K}$ such that $\{x\in {\mathbb R}^n : G(x)\cap -S\ne \emptyset \}\subseteq \{x\in {\mathbb R}^n : F(x)\cap -\widehat{K}=\{0\}\}$;

• (ii) There exists a vector $\lambda \in K^{+i}$ with $\langle \lambda ,e\rangle =1$ such that

  $$\begin{aligned} (0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(C(G,S)). \end{aligned}$$

Proof

[(i)$\Rightarrow$(ii)] Suppose that there exists a convex cone $\widehat{K}\subseteq {\mathbb R}^p$ with $K\backslash \{0\}\subseteq \mathrm{int}\widehat{K}$ such that $A\subseteq \{x\in {\mathbb R}^n : F(x)\cap -\widehat{K}=\{0\}\}$, and consequently, $F(A)\cap -\widehat{K}=\{0\}$. Since $\mathrm{int}\widehat{K}=\{x\in {\mathbb R}^n : \langle u,x\rangle >0, \ \forall u\in \widehat{K}^+\backslash \{0\}\}$ (see, e.g., [19, Lemma 1.26, p. 19]), we have $0\notin \mathrm{int}\widehat{K}$. We claim that

$$\begin{aligned} (F(A)+K)\cap -\widehat{K}=\{0\}. \end{aligned}$$

(9)

It is clear that $0\in (F(A)+K)\cap -\widehat{K}$ due to $F(A)\cap -\widehat{K}=\{0\}$. Let $z\in (F(A)+K)\cap -\widehat{K}$ be arbitrary. Then, there exist $y_A\in F(A)$ and $k_A\in K$ such that $z=y_A+k_A$. If $k_A\ne 0$, this together with the relation $K\backslash \{0\}\subseteq \mathrm{int}\widehat{K}$ gives us that $y_A=z-k_A\in -\widehat{K}-\mathrm{int}\widehat{K}=-\mathrm{int}\widehat{K}\subseteq -\widehat{K}$. Thus, $y_A\in F(A)\cap -\widehat{K}$, and consequently, $y_A=0$, a contradiction. Thus, we actually have $k_A=0$, which implies that $z\in F(A)\cap -\widehat{K}=\{0\}$. This shows that $(F(A)+K)\cap -\widehat{K}\subseteq \{0\}$, and therefore, (9) holds.

Moreover, as $(F(A)+K)\cap -\widehat{K}=\{0\}$, we also have $(F(A)+K)\cap -\mathrm{int}\widehat{K}=\emptyset$. By the separation theorem, there is $\bar{\lambda }\in {\mathbb R}^p \backslash \{0\}$ such that

$$\begin{aligned} 0\leqq \langle \bar{\lambda },y+k+\widehat{k}\rangle , \text { for all } y\in F(A), \ k\in K, \text { and } \widehat{k}\in \mathrm{int}\widehat{K}. \end{aligned}$$

(10)

Since $A\ne \emptyset$ and $\mathrm{dom}(F)={\mathbb R}^n$, we can take $\bar{x}\in A$ and $\bar{y}\in F(\bar{x})$. Let us prove that $\bar{\lambda }\in \widehat{K}^+$. On the contrary, suppose that there exists $\widehat{k}_0\in \widehat{K}$ such that $\langle \bar{\lambda },\widehat{k}_0 \rangle <0$. So, we can find $n_0\in \mathbb {N}$ such that $-\langle \bar{\lambda },n_0\widehat{k}_0 \rangle >\langle \bar{\lambda },\bar{y} \rangle$. On the one hand, due to $n_0\widehat{k}_0\in \widehat{K}=\mathrm{cl}(\mathrm{int}\widehat{K})$, there exists $\{\widehat{k}_l\}\subset \mathrm{int}\widehat{K}$ such that $\widehat{k}_l\rightarrow n_0\widehat{k}_0$. From (10), for each $l\in \mathbb {N}$, we conclude that $0\leqq \langle \bar{\lambda },\bar{y}+\widehat{k}_l\rangle$. Passing to the limit, we have $0\leqq \langle \bar{\lambda },\bar{y}+n_0\widehat{k}_0\rangle$, a contradiction. Consequently, $\bar{\lambda }\in \widehat{K}^+$ and it then follows from the fact that $K^+\backslash \{0\}\subseteq \mathrm{int}\widehat{K}$, $\bar{\lambda }\in K^{+i}$. In addition, we get that $\langle \lambda ,e \rangle =1$ when $\lambda :=\frac{1}{\langle \bar{\lambda },e \rangle }\bar{\lambda }\in K^{+i}$, and hence, we deduce from (10) that $\langle \lambda ,y\rangle \geqq 0$ for every $y\in F(A)$. As we have seen in the proof of Theorem 1 (the implication (i)$\Rightarrow$(ii)), the previous inequality allows us to prove that $(0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(C(G,S))$, and the assertion follows.

[(ii)$\Rightarrow$(i)] Assume by contradiction that statement (iii) holds true and for every convex cone $\widehat{K}\subseteq {\mathbb R}^p$ fulfilling $K\backslash \{0\}\subseteq \mathrm{int}\widehat{K}$, its holds

$$\begin{aligned} \exists x\in A, \ F(x)\cap -\widehat{K}\ne \{0\}. \end{aligned}$$

(11)

Since $(0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(C(G,S))=\mathrm{epi}(\varphi _{\lambda \circ F})^*+ \mathrm{epi}\sigma _A$, we have that $\varphi _{\lambda \circ F}(x)+\delta _A(x)\geqq 0$ for every $x\in {\mathbb R}^n$, or equivalently, $\langle \lambda ,y\rangle \geqq 0$ for every $y\in F(A)$. We see that $K\backslash \{0\}\subseteq \{y\in {\mathbb R}^p : \langle \lambda ,y \rangle > 0\}$. Let

$$\begin{aligned} \widehat{K}_0:=\{y\in {\mathbb R}^p : \langle \lambda ,y \rangle > 0\}\cup \{0\}. \end{aligned}$$

So, $\widehat{K}_0$ is a convex cone fulfilling $K\backslash \{0\}\subseteq \mathrm{int}\widehat{K}_0$. In view of (11), there exists $x_0\in A$ such that $F(x_0)\cap - \widehat{K}_0\ne \{0\}$, which gives us $0\ne -y_0\in \widehat{K}_0$ for some $y_0\in F(x_0)$. So, $0>\langle \lambda , y_0 \rangle \geqq 0$, a contradiction. Therefore, (i) holds. $\square$

Before closing this section, we point out that in the study of dual characterizations of set containments, Jeyakumar gave ([3, Theorem 4.1]) a characterization of the set containment of a nonempty closed convex set, defined by infinitely many convex constraints, in a reverse convex set, i.e., $\{x\in {\mathbb R}^n : f_j(x)\geqq 0, \ j=1,2,\ldots ,p\}=\{x\in {\mathbb R}^n : f(x)\in {\mathbb R}^p_+\}$ where $f_j$ are real-valued convex function on ${\mathbb R}^n$ and $f(x):=(f_1(x),f_2(x),\ldots ,f_p(x))$. Further study has been done for cone-convex inequalities (see, e.g., [15, Theorem 2.1] and [5, Theorem 3.1]). The set-valued counterpart of the mentioned reverse convex set is the set of the form $\{x\in {\mathbb R}^n : F(x)\subseteq K\}$, which is the container in the following the dual characterization of the containment between sets defined through set-valued functions.

Theorem 3

Let $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ be a proper, S-convex and nonnegatively S-lsc set-valued mapping satisfying (A), $K\subseteq {\mathbb R}^p$ be a nonempty closed convex cone, and $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$ be K-proper, K-convex and nonnegatively K-lsc such that $\mathrm{dom}(F)={\mathbb R}^n$. Then, the following statements are equivalent:

• (i) $\{x\in {\mathbb R}^n : G(x)\cap -S\ne \emptyset \}\subseteq \{x\in {\mathbb R}^n : F(x)\subseteq K\}$;

• (ii) $\forall \lambda \in K^+$, $(0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(C(G,S)).$

Proof

[(i)$\Rightarrow$(ii)] Assume that (i) holds. Let $\lambda \in K^+$ be arbitrary. By (i), we actually have $\langle \lambda ,y \rangle \geqq 0$ for every $y\in F(x)$ and every $x\in A$. As seen before, (i) entails $(0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(C(G,S))$. So, (ii) has been proved.

[(ii)$\Rightarrow$(i)] Suppose that (ii) holds. Assume by contradiction that there exist $x\in A$ and $y\in F(x)$ such that $y\notin K$. So, there is $\lambda \in K^+$ such that $\langle \lambda ,y \rangle <0$. By (ii), $(0,0)\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(C(G,S))=\mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{epi}\sigma _A$. In a similar manner to the first argument in the proof of Theorem 1, we would have $\langle \lambda ,y \rangle \geqq 0$, a contradiction. Consequently, (i) must be true. $\square$

5 Application to Set-Valued Optimization via Vector Criteria

In this section, with the aid of Theorem 1 and Theorem 2, we will establish characterizations of a weak minimal solution and a proper minimal solution for a set-valued optimization problem in the sense of vector criteria. In what follows, K and B represent a nonempty closed convex pointed cone and a nonempty subset of ${\mathbb R}^p$, respectively. Then, the point $y\in B$ is said to be a:

• (i) (Pareto) minimal point $(y\in \text {Min}(B,K))$ if $(B-y)\cap -K=\{0\}$;

• (ii) Weak minimal point $(y\in \text {WMin}(B,K))$ if $\mathrm{int}K\ne \emptyset$ and $(B-y)\cap -\mathrm{int}K=\emptyset$;

• (iii) Properly minimal point $(y\in \text {PMin}(B,K))$ if there exists a convex cone $\widehat{K}$ such that $K\backslash \{0\}\subseteq \mathrm{int}\widehat{K}$ and $y\in \text {Min}(B,\widehat{K})$.

Let $F:{\mathbb R}^n\rightrightarrows {\mathbb R}^p$ and $G:{\mathbb R}^n\rightrightarrows {\mathbb R}^m$ be proper set-valued maps. Let us consider the following set-valued optimization problem:

$$\begin{aligned} \mathrm{Min}_K F(x) \text { s.t. } x\in A:=\{x\in {\mathbb R}^n : G(x)\cap -S\ne \emptyset \}, \end{aligned}$$

(12)

where S is a nonempty closed convex cone of ${\mathbb R}^m$.

Definition 2

[18, 19] An element $\bar{x}\in A$ is called a weak efficient solution (resp. proper efficient solution) of (12) if

$$\begin{aligned} F(\bar{x})\cap \text {WMin}(F(A),K)\ne \emptyset \end{aligned}$$

(resp. $F(\bar{x})\cap \text {PMin}(F(A),K)\ne \emptyset$), or equivalently, there exists $\bar{y}\in F(\bar{x})$ such that $\bar{y}\in \text {WMin}(F(A),K)$ (resp. $\bar{y}\in \text {PMin}(F(A),K)$).

In the following result, we will give the characterization of a weak efficient solution of (12).

Theorem 4

[Characterization of weak efficient solution] Assume all conditions of Theorem 1 hold. Let $\bar{x}\in A$ and $e\in \mathrm{int}K$ be given. Then, the following statements are equivalent:

• (i) $\bar{x}$ is a weakly efficient solution of (12);

• (ii) There exist $\bar{y}\in F(\bar{x})$ and $\lambda \in K^+\backslash \{0\}$ with $\langle \lambda ,e \rangle =1$ such that

  $$\begin{aligned} (0,-\langle \lambda , \bar{y} \rangle )\in \mathrm{epi}(\varphi _{\lambda \circ F})^*+\mathrm{cl}(C(G,S)). \end{aligned}$$

  (13)

Proof

[(i)$\Rightarrow$(ii)] Suppose that (i) holds, that is, there exists $\bar{y}\in F(\bar{x})$ such that $(F(A)-\bar{y})\cap -\mathrm{int}K=\emptyset$. Applying now Theorem 1 with $x\mapsto F(x)-\bar{y}$, which is K-convex, there exists $\lambda \in K^+\backslash \{0\}$ with $\langle \lambda ,e \rangle =1$ such that $(0,0)\in \mathrm{epi}(\varphi _{\lambda \circ (F(\cdot )-\bar{y})})^*+\mathrm{cl}(C(G,S)).$ Note that

$$\begin{aligned} \varphi _{\lambda \circ (F(\cdot )-\bar{y})}(x)&=\inf \{\langle \lambda , y-\bar{y}\rangle : y\in F(x)\}\\&=\inf \{\langle \lambda ,y\rangle : y\in F(x)\}-\langle \lambda ,\bar{y}\rangle \\&=\varphi _{\lambda \circ F}(x)-\langle \lambda ,\bar{y}\rangle . \end{aligned}$$

This together with (1) in turn implies that (13) holds.

The statement (ii)$\Rightarrow$(i) follows from the reversible character of the proof that (i)$\Rightarrow$(ii). $\square$

Similarly, with the aid of Theorem 2, we can get the necessary and sufficient conditions for a feasible point to be a proper efficient solution of (12), and the proof is omitted for brevity.

Theorem 5

[Characterization of proper efficient solution] Assume all conditions of Theorem 2 hold. Let $\bar{x}\in A$ and $e\in K\backslash \{0\}$ be given. Then, the following statements are equivalent:

• (i) $\bar{x}$ is a properly efficient solution of (12);

• (ii) There exist $\bar{y}\in F(\bar{x})$ and $\lambda \in K^{+i}$ with $\langle \lambda ,e \rangle =1$ such that (13) holds.

6 Conclusions

In this paper, we have employed the classical convex separation theorem and the description of the epigraph of a support function to provide necessary and sufficient conditions for set containments involving convex set-valued maps. These conditions are expressed in terms of the epigraphs of the conjugate functions involving the infima associated with corresponding set-valued maps. Moreover, as an application, the obtained results are then applied to provide characterizations for weakly efficient solutions as well as properly efficient solutions for convex set-valued optimization problems in the sense of vector criteria.