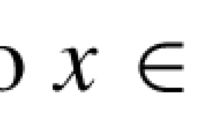Optimality conditions and minimax properties in set optimization

Abstract

In this paper, we consider a generalization of the Gerstewitz’s function to present several optimality conditions and existence theorems for a set optimization problem without convexity assumptions. A characterization of set solutions for a set-valued optimization problem is given via minimax inequalities.

1 Introduction

It is well-known that the minimax theory is very important in several areas and has many applications as, for instance, in methods, techniques and algorithm implementations. On the other hand, there is an increasing interest in the research about the set-valued optimization problems whose solutions are given by sets.

This paper is motivated by [6, 13]. We present some optimality conditions and minimax properties for a set-valued optimization problem which general form is the following one:

$$\begin{aligned} \text {(P)} \left\{ \begin{array}{l} \text{ Minimize } F(x) \\ \text{ subject } \text{ to } x\in C \end{array}\right. \end{aligned}$$

where E is a normed vector space ordered by a convex cone K, X is a nonempty set, $C\subset X$ and $F:X\rightrightarrows E$ is a set-valued map.

There are several solutions associated to (P) (see [9] for more details). If we consider the vector criterion of solution the above problem is called vector set-valued optimization problem while if we study set solutions then the problem (P) is called set optimization problem. We are interested in set solutions but we also study optimality conditions for vector optimization.

The aim of this paper is to apply the generalization of the Gerstewitz’s function introduced in [5, 6] to give optimality conditions for a set optimization problem. In addition, by following the vector results given in [13], we show minimax properties for a nonconvex vector set-valued optimization problem. In Sect. 2 we give the notations and the generalizations of the Gerstewitz’s function which are considered through the paper. Section 3 is devoted to optimality conditions. We give two existence theorems of weakly l-minimal and l-minimal sets for families of K-compact sets respectively. Motivated by [13], in Sect. 4, we present several minimax properties via the family of functionals that define the order cone. We consider general classes of set-valued maps without convexity assumptions and characterize solutions of set type. Finally, we present some conclusions and possible future research.

2 Notations and preliminaries results

Throughout this work, we will assume that E is a normed vector space partially ordered by a convex cone and closed $K\subset E$ such that $K\cap (-K)=\{0\}$. We denote by $E^*$ the dual space of E and by $K^*$ the negative polar cone of K, that is, $K^*=\{f\in E^*:f(k)\le 0\, \forall k\in K\}$. We also assume that K is solid, that is, its topological interior is nonempty.

If $y,z\in E$ we denote by $y\le z$ (resp. $y<z$) iff $z-y\in K$ (resp. $z-y\in \mathrm {int}\,K$). Given $x,\, y\in E$, we denote $[x,y]=\{ z\in E:x\le z\le y\}$.

Let $A\subset E$ a nonempty set. We denote the topological interior by ${\text {int}}(A)$, the frontier by $\partial (A)$ and the convex hull of A by ${\text {co}}A$. ${\text {Min}}A=\{x\in A:(x-K)\cap A=\{x\}\}$ denotes the minimal elements of A and ${\text {WMin}}A=\{y\in A:(y-{\text {int}}K)\cap A=\emptyset \}$ the weakly minimal elements of A. Replacing K by $-K$ we obtain the maximal elements $\mathop {\hbox {Max}}\limits A$ and the weakly maximal elements ${\text {WMax}}A$ respectively. Given $x\in E$ we denote by $A_x=A\cap (x-K)$ the section of A at x.

It is said that A is K-proper if $A+K\ne E$; K-convex if $A+K$ is a convex set; K-closed if $A+K$ is a closed set; K-bounded if for some $t>0$ one has $A\subset t\mathbb {B}+K$ (where $\mathbb {B}$ is the open unit ball in E); K-compact if any cover of A of the form $\{U_k+K:U_k \text{-open }\}$ admits a finite subcover. Every K-compact set is K-closed and K-bounded (see [14]).

We denote by $\wp _0(E)$ (resp. $\wp _{0K}(E)$) the family of nonempty subsets (resp. K-proper subsets) of E.

To present the set criterion of solution for a set optimization problem, it is necessary to consider set relations. We focus on the following one, called lower set relation. Given $A,\, B\in \wp _{0}(E)$, $A\le ^l B$ iff $B\subset A+K$. This set relation was presented by the first time in the framework of vector spaces in [11]. It is clear that

$$\begin{aligned} A\le ^l B \Longleftrightarrow A+K\le ^l B+K. \end{aligned}$$

(1)

We also define $A\ll ^{l}B$ iff $B\subset A+{\text {int}}K$. Denote $A\sim ^l B$ iff $A\le ^l B$ and $B\le ^l A$.

A sequence $\{A_n\}\subset \wp _0(E)$ is l-decreasing if $A_{n+1}\le ^l A_n$ for all n. For a family of sets $\mathcal {S}\subset \wp _0(E)$ and $A\in \wp _0(E)$ we denote by $\mathcal {S}^{l}_{A}=\{X\in \mathcal {S}|\, X\le ^{l}A\}$ the l-section of $\mathcal {S}$ at A.

Definition 1

Given $\mathcal {S}\subset \wp _0(E)$. It is said that $A\in \mathcal {S}$ is

• an l-minimal set of $\mathcal {S}$, $A\in l-{\text {Min}}\mathcal {S}$, if $B\in S$ and $B\le ^l A$ imply that $A\le ^l B$.

• a weakly l-minimal set of $\mathcal {S}$, $A\in l-{\text {WMin}}\mathcal {S}$, if $B\in \mathcal {S}$ and $B\ll ^l A$ imply $A\ll ^l B$.

It is easy to check that $l-{\text {Min}}\mathcal {S}\subset l-{\text {WMin}}\mathcal {S}$.

We denote by $F :X\rightrightarrows E$ a set-valued map where X is a nonempty set. We say that its domain is $C\subset X$, $\mathrm {dom}\,F=C$, if $F(x)\ne \emptyset$ for every $x\in C$ and $F(x)=\emptyset$ elsewhere. We denote by $F(A)=\bigcup _{x\in A}F(x)$ the image of the set $A\subset C$ under F and by $\mathcal {F}=\{F(x):x\in C\}$ the family of the image sets of F on C.

Whenever “N” denotes some property of sets in E, it is said that F is “N”-valued if F(x) has the property “N” for every $x\in C$.

Definition 2

It is said that ${\bar{x}}\in C$ is:

• an l-minimal (resp. weakly l-minimal) solution of (P), $\bar{x}\in l-{\text {Min}}F$ (resp. $\bar{x}\in l-{\text {WMin}}F$), if $F(\bar{x})\in l-{\text {Min}}\mathcal {F}$ (resp. $F(\bar{x})\in l-{\text {WMin}}\mathcal {F}$).

• a minimal (resp. weakly minimal) solution of (P), $\bar{x}\in {\text {Min}}F$ (resp. $\bar{x}\in {\text {WMin}}F$) if $F({\bar{x}})\cap {\text {Min}}F(C)\ne \emptyset$ (resp. $F({\bar{x}})\cap {\text {WMin}}F(C)\ne \emptyset$).

Note that if F is a vector valued map the notion of l-minimal (resp. weakly l-minimal) solution of (P) is equivalent to minimal (weakly minimal) solution of (P).

Example 1

Consider $E=\mathbb {R}^{2}$,  $K=\mathbb {R}^{2}_+$ and $C=[0,1]$. Let F be defined as follows: $F(0)=[(-1,-1),(1,1)]$ and $F(\lambda )=\{(x,y):x^2+y^2\le \lambda ^2\}$ for $\lambda \in (0,1]$. It is easy to check that F is a convex-valued, K-closed-valued, K-bounded-valued map, $l-{\text {Min}}F=\{0\}$ and $l-{\text {WMin}}F=\{0,\, 1\}$.

In the sequel we consider that F is K-proper valued since if there exists ${\bar{x}}\in C$ such that $F({\bar{x}})+K=E$, we have that ${\bar{x}}$ is a strong solution since $F({\bar{x}})\le ^{l}F(x)$ for all $x\in C$ and the problem (P) would be trivial.

Fixed $A\in \wp _0(E)$ and $e\in {\text {int}}(K)$ the generalized Gerstewitz’s function is denoted by $\xi _{e,A}:E\longrightarrow \mathbb {R}\cup \{-\infty \}$ and defined by

$$\begin{aligned} \xi _{e,A}(x)={\text {inf}}\{t\in \mathbb {R}:x \in te-K+A\} \text{ for } \text{ each } x\in E. \end{aligned}$$

Analogously, if $e\in -{\text {int}}K$ we define $\phi _{e,A}:E\longrightarrow \mathbb {R}\cup \{-\infty \}$ by

$$\begin{aligned} \phi _{e,A}(x)={\text {inf}}\{t\in \mathbb {R}:x \in te+K+A\} \text{ for } \text{ each } x\in E. \end{aligned}$$

In [1,2,3,4, 13] the authors consider the above functions for A a singleton, $A=\{a\}$. Taking $e'=-e$ we obtain

$$\begin{aligned} \xi _{e',a}(y)=\phi _{e,y}(a). \end{aligned}$$

(2)

It is well-known that such functions have many useful properties of separation and monotonicity which play a central role in the proofs of the main results of the above papers.

Note that $\phi _{e,A}(\cdot )$ is finite if and only if A is K-proper and $\displaystyle {\phi _{e,A}(y)={\text {inf}}_{a \in A} \phi _{e,a}(y)}$. In addition, if A is K-closed, then

$$\begin{aligned} \phi _{e,A}(y)=\displaystyle {\min _{a \in A} \phi _{e,a}(y)}. \end{aligned}$$

(3)

(see [5, 6]). From now on, we consider $A\in \wp _{0K}(E)$, that is, $\phi _{e,A}(\cdot ):E\rightarrow \mathbb {R}$ is a real function.

We remark that $\phi _{e,A}(\cdot )$ is a continuous, decreasing (i.e., $y\le z\Rightarrow \phi _{e,A}(z)\le \phi _{e,A}(y)$) and strict decreasing (i.e., $y<z\Rightarrow \phi _{e,A}(z)< \phi _{e,A}(y)$) function. In general, $\phi _{e,A}(\cdot )$ is not convex, as the following example shows:

Example 2

Consider $E=\mathbb {R}^{2}$ ordered by the Pareto cone, $K=\mathbb {R}_{+}^2$. If $e=(-1,-1)$,   $A=\{(x,y):y=-x^2-4x-3,\, x\in [-1,0]\}$, $y=(-1,0)$, $y'=(0,-3)$ it easy to check that $\phi _{e,A}(y)=\phi _{e,A}(y')=0$ and $\phi _{e,A}(\frac{1}{2}y+\frac{1}{2} y')>0.$

The function $\phi _{e,A}(\cdot )$ is convex if A is K-convex (see [5]).

Definition 3

Fixed $e\in -{\text {int}}K$ and $A\in \wp _{0K}(E)$. The function

$$\begin{aligned}G_{e}(A,\cdot ):\wp _{0K}(E) \longrightarrow \mathbb {R}\cup \{\infty \}\end{aligned}$$

is defined by setting

$$\begin{aligned} G_{e}(A,B)=\mathop {\hbox {sup}}\limits _{b\in B} \{\phi _{e,A}(b)\} \quad \text{ for } \quad B\in \wp _{0K}(E). \end{aligned}$$

(4)

Now we illustrate that the above generalization of $\phi _{e,A}(\cdot )$ could be calculated easily.

Example 3

Consider $E=\mathbb {R}^{2}$ ordered by the Pareto cone, $K=\mathbb {R}^2_+$. If $e=(-1,-1)$,  $A=[(0,-1),(2,-1)]$ and $\mathcal {S}=\{[(\lambda , 0),(\lambda ,1)] :\lambda \in [0,\infty )\}$ we have

$$\begin{aligned} G_e(A,[(\lambda , 0),(\lambda ,1)])=\left\{ \begin{array}{cc} -1 &{} \text{ if } \lambda \in [1,\infty )\\ -\lambda &{} \text{ if } \lambda \in [0,1) \end{array}\right. . \end{aligned}$$

3 Optimality conditions

In the sequel, we denote $e\in -{\text {int}}K$. We study several types of efficient solutions by using the functions defined in the previous section.

The following characterization of the weakly minimal elements extends [4, Corollary 3.1(a)] and [14, Theorem 2.15] (for quasiconvex functions).

Proposition 1

Let $A\in \wp _0(E)$ and ${\bar{a}}\in A$. Then ${\bar{a}}\in {\text {WMin}}A$ if and only if

$$\begin{aligned} \mathop {\hbox {max}}\limits _{a\in A}\phi _{e,A}(a)=\phi _{e,A}({\bar{a}})=0. \end{aligned}$$

Proof

From [6, Proposition 2.20] and [6, Lemma 2.17] we conclude. $\square$

Fixed $y\in E$ it is possible to obtain a sufficient condition for weakly minimality via a certain level set of $\phi _{e,A}(y)$.

Proposition 2

[6] Let $y\in Y$, $A\in \wp _{0K}(E)$ and $\phi _{e,A}(y)=t_0\in \mathbb {R}$. Consider $A_{t_{0}}(y)=\{a \in A :\phi _{e,a}(y)\le t_{0} \}$. Then

$$\begin{aligned} A_{t_{0}}(y) \subset {\text {WMin}}A. \end{aligned}$$

In general, $A_{t_{0}}(y)=\{a\in A:y\in t_0e+a+K\} \ne {\text {WMin}}A$ even when A is compact, as we deduce the following example.

Example 4

Consider $E=\mathbb {R}^{2}$ and $K=\mathbb {R}^2_+$. For $y=(-1,2)$, $e=(-1,-1)$ and $A={\text {co}}(\{(0,1),(0,3),(1,0),(2,1)\})$ is easy to check that

$$\begin{aligned} \phi _{e,A}(y)&= 1\\ A_{1}(y)&= [(0,1), (0,3)]\\ {\text {WMin}}A&= [(0,1), (0,3)]\cup [(0,1), (1,0)]. \end{aligned}$$

Therefore, ${\text {WMin}}A \ne A_{1}(y).$

Proposition 3

Let $B\in \wp _{0K}(E)$, $\lambda ,\, \mu \in \mathbb {R}$ verify $\mu =\mathop {\hbox {max}}\limits \{\phi _{e,A}(b):b\in B\}$ and $\lambda =\min \{\phi _{e,A}(b):b\in B\}$. Then

• (i) $\phi _{e,A}^{-1}(\mu )\cap B\subset {\text {WMin}}B$.

• (ii) $\phi _{e,A}^{-1}(\lambda )\cap B \subset {\text {WMax}}B$.

Proof

Let see (i), (ii) follows analogously.

Let $b\in B$ be such that $\mu =\phi _{e,A}(b)$. Suppose that there exists $b'\in B$ such that $b'\in b-{\text {int}}K$. Since $\phi _{e,A}(\cdot )$ is strict decreasing, we have $\mu =\phi _{e,A}(b)< \phi _{e,A}(b')$ which is a contradiction with $\mu$. $\square$

In the following example we show that the previous result could be false if we replace ${\text {Min}}B$ by ${\text {WMin}}B$. In addition, in general, ${\text {WMin}}B\supsetneq \phi _{e,A}^{-1}(\mu )\cap B$ and ${\text {WMax}}B \supsetneq \phi _{e,A}^{-1}(\lambda ) \cap B$.

Example 5

Consider $E=\mathbb {R}^{2}$ and $K=\mathbb {R}^2_+$ the Pareto cone. Let $e=(-1,-1)$, $A={\text {co}}(\{(0,0),(0,1),(1,0),(1,1)\})$, $B={\text {co}}(\{(-1,0),(-2,0),(-2,1),(-1,1)\})$. We can easily prove that

$$\begin{aligned} {\text {Min}}B&= \{(-2,0)\}\\ {\text {WMin}}B&= [(-2,0),(-2,1)]\cup [(-2,0),(-1,0)]\\ \mathop {\hbox {Max}}\limits B&= \{(-1,1)\}\\ {\text {WMax}}B&= [(-2,1),(-1,1)]\cup [(-1,0),(-1,1)] \end{aligned}$$

However, $\mathop {\hbox {max}}\limits \phi _{e,A}(B)=2$, $\min \phi _{e,A}(B)=1$ but $\phi _{e,A}^{-1} (2)\cap B=\{(-2,\eta ):\eta \in [0,1]\} \nsubseteq {\text {Min}}B$, $\phi _{e,A}^{-1} (1)\cap B= \{(-1,\eta ):\eta \in [0,1]\} \nsubseteq \mathop {\hbox {Max}}\limits B$. In addition, $(-1,0)\in {\text {WMin}}B$, $(-2,1)\in {\text {WMax}}B$ but $\phi _{e,A}((-1,0))=1<2$ and $\phi _{e,A}((-2,1))=2>1.$

There exist families of sets which allow to locate all minimal elements of a set.

Corollary 1

Let $B\subset E$ and $\mathcal {S}\in \wp _0(E)$. The following conditions hold:

• (i) If $A\le ^l B$ for all $A\in \mathcal {S}$, then $\bigcup _{A \in \mathcal {S}}(\phi _{e,A}^{-1}(0)\cap B)\subset {\text {WMin}}B$.

• (ii) If $B\cap \partial (B+K)\subset {\bigcup _{A \in \mathcal {S}}}\partial (A+K)$, then ${{\text {WMin}}B\subset \bigcup _{A \in \mathcal {S}} (\phi _{e,A}^{-1}(0)\cap B)}.$

Proof

(i) Let $b'\in {\bigcup _{A \in \mathcal {S}}} (\phi _{e,A}^{-1}(0)\cap B)$, then $b'\in B$ and there exists $A'\in \mathcal {S}$ with $\phi _{e,A'}(b')=0$. Since $B\subset A'+K$, by [6, Lemma 2.17(ii)], we deduce $\phi _{e,A'}(b)\le 0$ for all $b\in B$. Thus,

$$\begin{aligned} \mathop {\hbox {max}}\limits \{\phi _{e,A'}(B)\}=\phi _{e,A'}(b')=0 \end{aligned}$$

and, by Proposition 3(i), we have $b\in {\text {WMin}}B.$

(ii) Let $b\in {\text {WMin}}B$, then $b\in B\cap \partial (B+K)$. By condition (ii), there exists $A'\in \mathcal {S}$ such that $b\in \partial (A'+K)$ and according to [6, Lemma 2.17(iv)], we obtain $\phi _{e,A'}(b)=0$. $\square$

In terms of optimality conditions for a family of sets we obtain the following results.

Proposition 4

Let $A\in \mathcal {S}$ be a K-closed set. If $\mathop {\hbox {max}}\limits _{B\in \mathcal {S}} G_e(A,B)=0$ then $l-{\text {Min}}\mathcal {S}=\{B\in \mathcal {S}:A\sim ^l B\}$.

Proof

Suppose that $G_e(A,B)\le 0$ for all $B\in \mathcal {S}$. Then $A\le B$ for all $B\in \mathcal {S}$ by [6, Theorem 3.10(iii)] and we conclude. $\square$

Proposition 5

Suppose that $\mathcal {S}$ is a family of K-closed and K-bounded sets. Let $A\in \mathcal {S}$. The following statements are equivalent,

• (i) $A\in l-{\text {Min}}\mathcal {S}$

• (ii) if $B\in \mathcal {S}$ verifies that $G_{e}(B,A)\le 0$ then $G_{e}(A,B)\le 0$

• (iii) $G_{e}(B,A)>0$ for all $B\in \mathcal {S}$ such that $B\not \sim ^l A$.

Proof

It follows from the definition of l-minimal set and [6, Theorem3.10]. $\square$

Now, we show that fixed $A\in \wp _{0K}(E)$, it is possible to assert the existence of weak l-minimal of $\mathcal {S}$ since $l-{\text {WMin}}\mathcal {S}^l_{A}\subset l-{\text {WMin}}\mathcal {S}$ by [7, Proposition3.2].

Proposition 6

Let $\mathcal {S}$ be a family of K-compact sets and $A\in \wp _{0K}(E)$. Suppose that $\mathcal {S}^{l}_{A}\ne \emptyset$ and every chain verifying

$$\begin{aligned} 0\le G_{e}(A,B_{1})<\dots<G_{e}(A,B_{n})< G_{e}(A,B_{n+1})<\cdots \end{aligned}$$

with $B_i\in \mathcal {S}^l_A$ has a maximal element in $\{G_{e}(A,B):B\in \mathcal {S}^l_{A}\}$. Then $l-{\text {WMin}}\mathcal {S}^{l}_{A}\ne \emptyset$.

Proof

Suppose that $l-{\text {WMin}}\mathcal {S}^l_A=\emptyset$, then there exists a sequence $\{B_{n}\}\subset \mathcal {S}^l_A$ such that

$$\begin{aligned}\dots \ll ^l B_{n}\ll ^l\dots \ll ^l B_{2}\ll ^l B_1\le ^{l} A.\end{aligned}$$

Since the operator $G_e(A,\cdot )$ is monotonic ([6, Theorem 3.9(i)]) we obtain an strict increasing chain

$$\begin{aligned}G_e(A,A)=0\le G_{e}(A,B_{1})<G_{e}(A,B_{2})<\dots<G_{e}(A,B_{n})<\cdots \end{aligned}$$

with $B_{i}\in \mathcal {S}^l_{A}$. By hypothesis, there exists $B\in \mathcal {S}_{A}^l$ such that

$$\begin{aligned}G_{e}(A,B_i)\le G_{e}(A,B) \text{ for } \text{ all } i.\end{aligned}$$

To end the proof, it is sufficient to prove that $B\in l-{\text {WMin}}\mathcal {S}_A^{l}$. On the contrary, there exist $B'\in \mathcal {S}$ such that $B'\ll ^l B$. Therefore, $B'\in \mathcal {S}^l_{A}$ and, again, by [6, Theorem 3.9(i)], $G_{e}(A,B)<G_{e}(A,B')$, which contradicts the maximality of $G_{e}(A,B)$. $\square$

Theorem 1

Let $\mathcal {S},\, A\subset \wp _{0K}(E)$ be such that ${G_e(A,\bigcup _{B\in \mathcal {S}}B)=m}<\infty$. Suppose that $X=\{B\in \mathcal {S}:G_{e}(A,B)=m\}$ is nonempty and each l-decreasing sequence in X has a unique lower bounded in $\mathcal {S}$, then $l-{\text {Min}}\mathcal {S}\ne \emptyset .$

Proof

Let $B\in X$. Suppose that $l-{\text {Min}}\mathcal {S}^l_B=\emptyset$. Then we can obtain an l-decreasing $\{B_n\}\subset \mathcal {S}^{l}_B$ such that $B_n\not \sim ^l B_{n+1}$ for each n. On the other hand, since $B_{n}\le ^l B$, ${\bigcup _{B\in \mathcal {S}}B\le ^{l}B_n}$ and $G_{e}(A,\cdot )$ is decreasing with respect to $\le ^l$ we have

$$\begin{aligned}G_{e}(A,B_n)=m \text{ for } \text{ all } n.\end{aligned}$$

Thus, by hypothesis, there exists $B_0\in \mathcal {S}$ such that $B_{0}\le ^l B_n$ for all n and, in addition, $B_0\in l-{\text {Min}}\mathcal {S}$ since $B_0$ is unique one. $\square$

The following example illustrates that the condition on X is necessary in the above result.

Example 6

Consider $E=\mathbb {R}^{2}$,  $K=\mathbb {R}^{2}_+$ and $\mathcal {S}=\{B_\lambda :\lambda \in \mathbb {R}^{+}\}$ where $B_\lambda = \{(x,y)\in \mathbb {R}^2:0<x\le \lambda ,\, y\ge \frac{1}{x}\}$. Then it is easy to check that for $e=(-1,-1)$ and $A=\{(0,0)\}$, we deduce that $\{B_n:n\in \mathbb {N}\}$ is an l-decreasing sequence such that ${G_{e}(A, B_n)=G_{e}(A,\bigcup _{\lambda } B_\lambda )}=0$ for all n but $l-{\text {Min}}\mathcal {S}= \emptyset$.

Theorem 2

Let $A\in \wp _{0,K}(E)$ be a K-closed set. Suppose that there exists $x_{0}\in C$ such that $F(x_0)$ is K-compact and $G_{e}(A,F(C))=G_{e}(A,F(x_{0}))=m< \infty$. Then $x_{0}\in {\text {WMin}}F\subset l-{\text {WMin}}F$.

Proof

Let us see $x_0\in {\text {WMin}}F$. Since $F(x_{0})$ is K-compact, by [6, Proposition 3.4], there exists $y_0\in F(x_{0})$ such that

$$\begin{aligned} G_{e}(A,F(x_{0}))=\mathop {\hbox {max}}\limits _{y\in F(x_0)}\phi _{e,A}(y)=\phi _{e,A}(y_0)=m \end{aligned}$$

and, by Proposition 3, we have $y_{0}\in {\text {WMin}}F(x_{0})$. Since $\phi _{e,A}(\cdot )$ is strict decreasing we deduce $y_{0}\in {\text {WMin}}F(C)$. Hence, $x_{0}$ is a weakly minimal solution.

We conclude, applying [6, Theorem 2.10]. $\square$

Theorem 3

Suppose that F is K-closed valued. Let $x_{0}\in C$ be such that:

• (i) ${\bigcup _{F(x)\in \mathcal {F}^l_{F(x_0)}}F(x)}$ is K-compact

• (ii) for each l-decreasing sequence $\{F(x_n)\}\subset \mathcal {F}$ with $G(F(x_0),F(x_n))=m\in \mathbb {R}$ for all n there exists ${\bar{x}}\in C$ such that $G_{e}(F({\bar{x}}), F(x_{0}))+m\le 0$.

Then $l-{\text {Min}}F\ne \emptyset$.

Proof

By (i) and taking into account properties given in [6], there exist $m\in \mathbb {R}$ and $x'\in C$ such that $F(x') \le ^l F(x_0)$ and for all $x\in C$ with $F(x)\le ^l F(x_0)$

$$\begin{aligned}m=G(F(x_0),F(x'))\ge G(F(x_0),F(x)).\end{aligned}$$

In particular, $m\ge 0$ since $G(F(x_0),F(x_0))=0.$ Suppose that $x'\not \in l-{\text {Min}}F$. Thus, there exists $x_1\in C$ with $F(x_1)\le ^l F(x')$ and $F(x')\not \le ^l F(x_1)$. Again, if $x_1$ is not an l-minimal of (P) we can obtain an l-decreasing sequence $\{F(x_n)\}\subset \mathcal {F}^l_{F(x_0)}$ such that

$$\begin{aligned} \cdots \ge G(F(x_0),F(x_n))\ge \cdots \ge G(F(x_0),F(x_1))\ge G(F(x_0),F(x'))=m. \end{aligned}$$

Thus, we obtain an l-decreasing sequence $\{F(x_n)\}\subset \mathcal {F}^l_{F(x_0)}$ such that $m=G(F(x_0),F(x_n))$ for all n. By (ii), there exists ${\bar{x}}\in C$ such that

$$\begin{aligned}G_{e}(F({\bar{x}}), F(x_{0}))+m\le 0\end{aligned}$$

or $G_{e}(F({\bar{x}}), F(x_{0})+me)\le 0$, since $G_{e}(F({\bar{x}}), F(x_{0}))+m=G_{e}(F({\bar{x}}), F(x_{0})+me)$ by [6]. Hence,

$$\begin{aligned} F(x_{0})+me \subset F({\bar{x}})+K \end{aligned}$$

(5)

If there exists $x''\in C$ such that $F({\bar{x}})\subset F(x'')+K$, then $F(x'')\subset F(x_0)+me+K$ (by $G(F(x_0),F(x''))\le m$). From (5), we obtain $F(x'')\subset F({\bar{x}})+K$ and we conclude ${\bar{x}} \in l-{\text {Min}}F$. $\square$

4 Minimax conditions for problem (P)

In this section, we are interested in the situation where K is defined by functionals of the negative polar cone $K^*$.

Li et al. [13] present necessary and sufficient optimality conditions of minimax type for vector solutions of problem (P). We show that our generalization of the Gerstewitz’s function allows us to obtain analogous results of minimax type for set solutions.

We study set solutions of a general nonconvex set-valued optimization problem and give a characterization of the l-minimal solutions of (P) via minimax inequalities and a necessary condition for the existence for a constrained problem.

In the sequel, we denote $\Gamma \subset E^*\backslash \{0\}$ such that $K=\{y\in E:f (y)\le 0\, \forall \, f\in \Gamma \}$. Assume that ${\text {int}}K\ne \emptyset$ and $e\in {\text {int}}K$. From (2) and [1, Proposition 2.3] we obtain

$$\begin{aligned} \phi _{e,a}(y) =\mathop {\hbox {sup}}\limits _{f\in \Gamma } \frac{f(y)-f(a)}{f(e)}. \end{aligned}$$

(6)

Consequently, $\phi _{e,A}(\cdot )$ and $G_{e}(\cdot , \cdot )$ can be rewritten as follows:

Proposition 7

Let $A\in \wp _{0}(E)$ and $e\in -{\text {int}}K$. Then for $y\in E$,

$$\begin{aligned} \phi _{e,A}(y)=\mathop {{\text {inf}}}\limits _{a\in A}\mathop {\hbox {sup}}\limits _{f\in \Gamma } \frac{f(y)-f(a)}{f(e)} \end{aligned}$$

and for $B\in \wp _{0}(E)$,

$$\begin{aligned} G_{e}(A,B)=\mathop {\hbox {sup}}\limits _{b\in B}\mathop {{\text {inf}}}\limits _{a\in A}\mathop {\hbox {sup}}\limits _{f\in \Gamma } \frac{f(b)-f(a)}{f(e)}. \end{aligned}$$

Note that, according to [6], if A and B are K-compact we can replace the first “supremum” by “maximum” and the “infimum” by “minimum” in the above expressions.

From now on, we assume $K=\{y\in E:f (y)\le 0,\, f(e)=1\, \text{ for } \text{ all } f\in \Gamma \}$. It is always possible since if $\Gamma '=\{\frac{f}{f(e)}:f\in \Gamma \}$ then $K=\{y\in E:f' (y)\le 0\, \text{ for } \text{ all } f'\in \Gamma '\}$.

We are now going to establish a characterization of minimax type for the l-minimal solutions of problem (P).

Theorem 4

Let F be K-closed valued. Then $x_{0}$ is an l-minimal solution of (P) if and only if

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{y_{0}\in F(x_{0})}\min _{y\in F(x)} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y_0)-f(y)\}\} >0 \text{ for } x\in C \text{ with } F(x)\not \sim ^l F(x_{0}) \end{aligned}$$

(7)

and

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{y_{0}\in F(x_{0})}\min _{y\in F(x)} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y_0)-f(y)\}\} =0 \text{ for } x\in C \text{ with } F(x) \sim ^l F(x_{0}). \end{aligned}$$

(8)

Proof

Suppose that $x_0$ is an l-minimal solution of (P) and $F(x)\not \sim ^l F(x_{0})$. Thus, $F(x)\not \le ^l F(x_{0})$ and, by [6, Theorem 3.10(iii)], $G_{e}(F(x),F(x_{0}))> 0$ or equivalently, by Proposition 7 and (3),

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{y_{0}\in F(x_{0})} \min _{y\in F(x)} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y_0)-f(y)\}> 0. \end{aligned}$$

On the other hand, suppose that $x\in C$ and $F(x) \sim ^l F(x_{0})$. Applying [6, Theorem 3.10(iii)] now yields $G_{e}(F(x),F(x_{0}))=0$ or equivalently,

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{y_{0}\in F(x_{0})} \min _{y\in F(x)} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y_0)-f(y)\}= 0. \end{aligned}$$

Reciprocally. Suppose that (7) and (8) hold.

Let us prove that $x_0$ is an l-minimal solution of (P). On the contrary, there exists $x\in C$ such that $F(x)\le ^{l} F(x_{0})$ and $F(x_0)\nleq ^l F(x)$. Again by [6, Theorem 3.10(iii)] and Proposition 7,

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{y_{0}\in F(x_{0})}\min _{y\in F(x)} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y_0)-f(y)\} \le 0 \end{aligned}$$

which is a contradiction since $F(x)\not \sim ^l F(x_{0})$. $\square$

As a consequence, we obtain the following characterization of vector solutions.

Corollary 2

Suppose that F is a single-valued map. Then $x_0\in C$ is a minimal solution of (P) if and only if $F(x_0)$ is the unique solution of problem

$$\begin{aligned} \min _{F(x)\in F(C)} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(F(x_0))-f(F(x))\}. \end{aligned}$$

In the following example we show that the above results allow us to simplify the problem (P) to a Pareto problem (that is, via the Pareto cone).

Example 7

Consider $E=\mathbb {R}^{2}$, K such that $K^*$ is generated by $\{f_1=(-2,1),\, f_2=(1,-3)\}$, $e=(-1,-1)$ and $F=(F_1,F_2):\mathbb {R}\rightarrow \mathbb {R}^{2}$. According to Theorem 4 and (7) we obtain

$$\begin{aligned} \begin{array}{l} \mathop {\hbox {max}}\limits \{ \frac{1}{f_1(e)}f_1(F(x_0)-F(x)),\frac{1}{f_2(e)}f_2(F(x_0)-F(x))\}=\\ \mathop {\hbox {max}}\limits \{-2F_1(x_0)+F_2(x_0)+2F_1(x)-F_2(x),\\ \qquad \qquad \qquad \qquad \qquad \frac{1}{2}(F_1(x_0)-3F_2(x_0)-F_1(x)+3F_2(x))\}>0 \\ \end{array} \end{aligned}$$

for $F(x_0)\ne F(x)$ and $x\in C$. Thus, $(x_0,F(x_0))$ is a solution of problem (P) if and only if $x_0$ is a Pareto solution of problem

$$\begin{aligned} \min (H_1(x),H_2(x)) \end{aligned}$$

where $H_1(x)=2F_1(x)-F_2(x)$ and $H_2(x)=-\frac{1}{2}F_1(x)+\frac{3}{2}F_2(x)$.

In the sequel, we study a constrained problem. Consider (P) such that

$$\begin{aligned} C=\{x\in X :G(x)\cap (-D)\ne \emptyset \} \end{aligned}$$

being G a set-valued map from X to a topological vector space Z ordered by a solid convex cone $D\subset Z$.

Theorem 5

Let F be K-closed valued, $\Lambda \subset Z^*{\setminus } \{0\}$ and $D=\{y\in Z:g(y)\le 0 \text{ for } \text{ all } g\in \Lambda \}$. If $x_{0}$ is an l-minimal solution of problem (P), then the following minimax inequality holds for any $x\in C$ such that $F(x)\not \sim ^l F(x_{0})$

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{ f\in \Gamma , \, g\in \Lambda ,\, y_{0}\in F(x_{0}),\, z\in G(x) } \{f(y_0)-f(y)+ g(z)\}>0 \text{ for } \text{ any } y\in F(x). \end{aligned}$$

Proof

Suppose that $x\in C$ and $F(x)\not \sim ^l F(x_{0})$. Then, by definition of l-minimal solution, we have $F(x)\nleq ^l F(x_{0})$, that is, $G_{e}(F(x),F(x_{0}))> 0$ or equivalently,

$$\begin{aligned} G_{e}(F(x),F(x_{0}))=\mathop {\hbox {sup}}\limits _{y_{0}\in F(x_{0})}\phi _{e,F(x)}(y_{0})> 0. \end{aligned}$$

Thus, there exists $y'\in F(x_{0})$ such that $\phi _{e,F(x)}(y')>0$ and, by Proposition 7,

$$\begin{aligned} \phi _{e,F(x)}(y')=\mathop {{\text {inf}}}\limits _{y\in F(x) }\mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y')-f(y)\}>0. \end{aligned}$$

Whence

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y')-f(y)\}>0 \text{ for } \text{ all } y\in F(x). \end{aligned}$$

Since the above condition is for some $y'\in F(x_{0})$ we obtain

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{y_{0}\in F(x_{0})} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y_0)-f(y)\}>0 \text{ for } \text{ all } y\in F(x). \end{aligned}$$

(9)

On the other hand, if $x\in C$ there exists $z'\in G(x)\cap (-D)$. Thus, $g(z')\ge 0$ for all $g\in \Lambda$ and from (9),

$$\begin{aligned} \mathop {\hbox {sup}}\limits _{y_{0}\in F(x_{0})} \mathop {\hbox {sup}}\limits _{f\in \Gamma } \{f(y_0)-f(y)\}+\mathop {\hbox {sup}}\limits _{z\in G(x)}\mathop {\hbox {sup}}\limits _{g\in \Lambda } \{g(z)\}> 0 \text{ for } \text{ all } y\in F(x) \end{aligned}$$

and we conclude. $\square$

Corollary 3

Suppose that F is single-valued. If $x_0\in C$ is a minimal solution of the constrained problem (P) then for any $x\in C$ the following inequality holds

$$\begin{aligned} \mathop {{\text {inf}}}\limits _{x\in C}\,\mathop {\hbox {sup}}\limits _{f\in \Gamma ,\,g\in \Lambda ,\, z\in G(x) } \{f(F(x_0))-f(F(x))+g(z)\}\ge 0. \end{aligned}$$

Note that Theorem 3.2 and Corollary 3.1 in [13] are a sufficient condition and a characterization for a vector set-valued optimization problem respectively. On the other hand, in terms of vector problems with feasible set given by a set-valued map (G) we obtain in the above Corollary a necessary condition not like Corollaries 3.2, 3.3 and 3.4 in [13].

See [16] for others minimax theorems in the sense of set optimization.

4.1 Particular case: Polyhedral cone

The expression (6) for the functional $\phi _{e,a}(\cdot )$ can be more simplified if we consider E ordered by a polyhedral cone.

In the sequel we consider $E=\mathbb {R}^{n }$ and K a closed polyhedral cone such that $K^*$ is generated by $\{h_{1},\dots ,h_{m}\}$. It is easy to check that if $e\in -{\text {int}}K$ and $a,\,x\in E$ then:

$$\begin{aligned} \phi _{e,a}(x)=\mathop {\hbox {max}}\limits _{i} \left\{ \frac{\langle h_{i},x \rangle -\langle h_{i},a \rangle }{\langle h_{i},e \rangle } \right\} . \end{aligned}$$

being $\langle \cdot ,\cdot \rangle$ the euclidean scalar product. In particular, if $K=\mathbb {R}^{n}_+$, that is, for $i\in \{1,\dots ,n\}$, $h_{i}=(0,\dots ,\overbrace{-1}^{i},\dots ,0)$. If $e=(-1,\dots ,-1)$, $a=(a_{1},\dots ,a_{n})$, $x=(x_{1},\dots ,x_{n})$,

$$\begin{aligned} \phi _{e,a}(x)=\mathop {\hbox {max}}\limits _{i} \left\{ x_{i}-a_{i} \right\} \text{ for } \text{ each } y\in E. \end{aligned}$$

Let A be a K-bounded set. Given an element $h\in K^*$ we define

$$\begin{aligned} h\star A= \mathop {\hbox {sup}}\limits \{\langle h,a\rangle :a \in A\}. \end{aligned}$$

Such a operation is well-defined since A is a K-bounded set, $h\star A<\infty$. Indeed, by [14, Proposition 3.4], h(A) is h(K)-bounded. Since $h\in K^*$, h(K) is $\{0\}$ or $\mathbb {R}^-$ and therefore $h (A)\subseteq \mathbb {R}$ is a bounded set ($h(K)=\{0\}$) or upper bounded set ($h(K)=\mathbb {R}^-$).

Proposition 8

If $A\subseteq \mathbb {R}^n$ is K-bounded and K-closed, then A has support points for each $h \in K^*$.

Proof

Since $h \star A=\mathop {\hbox {sup}}\limits \{\langle h,a\rangle :a \in A\}<\infty$ and $h \in K^*$, we have $h \star A=h \star (A+K)$. From the continuity of h, if $A+K$ is closed, the set $h(A+K)=\{h(a+k):a+k\in A+K\}$ is a closed set in $\mathbb {R}$. Thus, there exist $a\in A$ such that $\langle h,a\rangle =h \star A$. $\square$

Proposition 9

Let $A,\, B\subset \mathbb {R}^n$ be K-compact sets and $e\in -{\text {int}}K$ and $\langle h_{i},e\rangle =1$ for all $i\in \{1,\dots ,m\}$. Then

$$\begin{aligned} G_{e}(A,B)\ge \mathop {\hbox {max}}\limits _{i}\{h_{i}\star B-h_{i}\star A \}. \end{aligned}$$

(10)

Proof

Suppose that $G_{e}(A,B)=r\in \mathbb {R}$, according to [6, Proposition 3.2],

$$\begin{aligned}B\subset A+re+K.\end{aligned}$$

Therefore, for each $b\in B$ there exist $a\in A$ and $k\in K$ such that $b=a+re+k$. For $i\in \{1,\dots ,m\}$ we obtain $\langle h_{i},b\rangle = \langle h_{i},a \rangle + \langle h_{i},re \rangle + \langle h_{i},k\rangle \le \langle h_{i},a\rangle +r.$ Thus, $\langle h_{i},b\rangle \le h_{i}\star A+r$ and $h_{i}\star B\le h_{i}\star A+r$ for each $i\in \{1,\dots ,m\}.$ Consequently,

$$\begin{aligned} \mathop {\hbox {max}}\limits _{i}\{h_{i}\star B- h_{i}\star A\}\le r. \end{aligned}$$

$\square$

In the following example, we illustrate that the inequality (10) could be strict.

Example 8

Let $\mathbb {R}^{2}$ be ordered by the Pareto cone, $K=\mathbb {R}^2_+$. Consider $h_{1}=(-1,0)$, $h_{2}=(0,-1)$ and $e=(-1,-1)$. If $A=[(4,5),(5,4)]$ and $B=\{[(\frac{1}{2},0),(0,5)]\}$ then,

$h_{1}\star A=-4$ and $h_{2}\star A=-4$

$h_{1}\star B=0$ and $h_{2}\star B=0$

${\mathop {\hbox {max}}\limits \limits _{i}\{h_{i}\star B-h_{i}\star A\}=4}.$

However $G_{e}(A,B)\ne 4$ since $(1,0)\in B$ but $(1,0)\not \in A+4e+K$.

Remark 1

We emphasize that whenever A is a singleton it is clear that the equality (10) holds but it could be false if B is a singleton. Indeed, if $B=\{(0,0)\}$ in Example 8 we have $G_{e}(A,(0,0))\ne \mathop {\hbox {max}}\limits \limits _{i}\{h_{i}\star (0,0)-h_{i}\star A \}.$

5 Conclusions

By using a generalization of the Gerstewitz’s function, $G_{e}(\cdot ,\cdot )$, we have obtained several optimality conditions and minimax results in the framework of set optimization. We show that such a function can be rewritten in a simpler form when the order cone K is defined by a functionals set. Thus, the expression $G_e(A,B)$ could be easier to compute.

As future research we propose to study a generalized parametric system with set-valued map and establish equilibrium problems on nets by following [15] or [12] and [1] respectively.

Likewise, it would be interesting to give algorithms to find set solutions by applying different variants of the Gerstewitz’s function as Jahn cited in [8]. A preliminary paper in this direction cold be K$\ddot{\text{ o }}$bis et al. [10].