1 Introduction

In this work, our focus is placed on developing an efficient approximate method for solving the fractional constrained optimization problems. A fractional constrained optimization problem can be considered as an isoperimetric fractional variational problem (IFVP) or fractional optimal control problem (FOCP). Thus, it is worthwhile to find an efficient approximate method for solving such problems.

Fractional variational problems (FVPs), isoperimetric fractional variational problems, and FOCPs are three different types of fractional optimization problems. General optimality conditions have been developed for FVPs, IFVPs, and FOCPs. For instance in [1], the author has achieved the necessary optimality conditions for FVPs and IFVPs with Riemann-Liouville derivatives. Hamiltonian formulas for fractional optimal control problems with Riemann-Liouville fractional derivatives have been derived in  [2, 3]. In [4] the authors present necessary and sufficient optimality conditions for a class of FVPs with respect to Caputo fractional derivative. Agrawal [5] provides Hamiltonian formulas for FOCPs with Caputo fractional derivatives. Optimality conditions for fractional variational problems with functionals containing both fractional derivatives and integrals are presented in [6]. Such formulas are also developed for FVPs with other definitions of fractional derivatives in  [7, 8]. Agrawal  [9] includes discussion about a General form of FVPs; the author claims that the derived equations are general form of Euler-Lagrange equations for problems with fractional Riemann-Liouville, Caputo, Riesz-Caputo, and Riesz-Riemann-Liouvile derivatives. Other generalizations of Euler-Lagrange equations for problems with free boundary conditions can be found in [10–13] as well. It is known that optimal solution of fractional variational and optimal control problems should satisfy Euler-Lagrange and Hamiltonian systems, respectively [1–3, 5]. Hence, solving Euler-Lagrange equations and Hamiltonian systems leads to optimal solution of FVPs or FOCPs. Except for some special cases in FVPs  [14], it is hard to find exact solution for Euler-Lagrange and Hamiltonian equations, specially when the problem has boundary conditions. Examples of numerical simulations for fractional optimal control problems with Riemann-Liouville fractional derivatives can be found in [2, 3, 15–17]. There also exist some numerical methods for solving fractional variational problems. For instance finite element method in [18, 19] and fractional variational integrator in [20] are developed and applied for some classes of FVPs. In  [5], the classical discrete direct method for solving variational problems is generalized for FVPs. Numerical simulations for FOCPs with Caputo fractional derivatives are developed in  [5] and  [22], where the author has solved the Hamiltonian equations approximately. A general class of FVPs in  [23] and a class of FOCPs in  [24] are solved directly without using Euler-Lagrange and hamiltonian formulas. Through the use of operational matrix of fractional integration and gauss quadrature formula,  [25] presents approximate direct method for solving a class of FOCPs. An approximate method for solving FVPs with Lagrangian containing fractional integral operators is provided in  [26]; the authors approximately transform fractional problem into regular problem by decomposing fractional integral operator with the finite series in terms of derivative operators. We refer readers interested in fractional calculus of variations to  [27].

The epsilon method has been first introduced by Balakrishnan in  [28]. Later, Frick  [29, 30] developed the method for solving optimal control problems. In this paper, we apply combination of Ritz and epsilon methods for solving fractional constrained optimization problems. These problems can also have a group of boundary conditions. Our development in Epsilon-Ritz method has the property that the approximate solutions satisfy all initial and boundary conditions of the problem. The implemented method reduces the given constrained optimization problem to the problem of finding optimal solution of a real value function. First, unknown functions are expanded with polynomial basis and unknown coefficients, then an algebraic function, which should be optimized with respect to its variables, in terms of unknown coefficients is achieved. We study the convergence of the approximate method and present numerical examples to illustrate the applicability of the new approach.

This paper is organized as follows. Section 2 presents problem formulation. In Sect. 3, epsilon method is applied to reduce constrained optimization problem of Sect. 2 to an unconstrained problem. In Sect. 4 we solve the unconstrained problem, constructed in Sect. 3, using Ritz method, to achieve an approximate solution of the main problem. Section 5 discusses on the convergence of the method presented in Sect. 4 and finally Sect. 6 reports numerical findings and demonstrates the accuracy of the numerical scheme by considering some test examples. Section 7 consists of a brief summary.

2 Statement of the Problem

Consider the following fractional constrained optimization problem:

$$\begin{aligned} {\hbox {min}} \quad J[y_1,\dots ,y_m]= \int \limits _{t_0}^{t_1}F(t,y_1,\dots ,y_m,\dots ,{^C _{t_0}D^{\alpha _r}_{t}y_r},\dots )\mathrm{d}t, \end{aligned}$$

subject to

$$\begin{aligned} G_l(t,y_1,\dots ,y_m,\dots ,{^C _{t_0}D^{\alpha _r}_{t}y_r},\dots )=0, \quad l=1,\dots ,L, \end{aligned}$$

where \(n-1<\alpha _r\le n\), \(n\in \mathbb {N}\), \(L\) is the number of constraints, functions \(F\) and \(G\) are continuously differentiable with respect to all their arguments, and functional \(J\) is bounded from below, i.e., there exist \(\lambda \in \mathbb {R}\) such that \(J[y_1,\dots ,y_m]\ge \lambda \). The fractional derivatives are defined in the Caputo sense

$$\begin{aligned} ^C _{t_0}D^{\alpha }_{t}y(t)= \frac{1}{\Gamma (n-\alpha )} \int \limits _{t_0}^{t}(t-\tau )^{n-\alpha -1} y^{(n)}(\tau )\mathrm{d}\tau , \quad n-1<\alpha <n, \end{aligned}$$

In cases when \(\alpha =n\), the Caputo derivative is defined \( ^C _{t_0}D^{\alpha }_{t}y(t)=y^{(n)}(t)\). In the above problem functionals \(F\) and \(G\) can contain fractional derivatives for some of the variables \(y_j\), \(1 \le j \le m\), (not necessarily for all \(y_j\)s) and each variable can have initial or boundary conditions.

3 Epsilon Method

Without loss of generality, we let \(t_0=0\), \(t_1=1\), and \(t\in [0,1]\) in the problem of Sect. 2.

$$\begin{aligned}&\displaystyle {\hbox {min}} \quad J[y_1,\dots ,y_m]= \int \limits _{0}^{1}F(t,y_1,\dots ,y_m,\dots ,{^C _{0}D^{\alpha _r}_{t}y_{r}},\dots )\mathrm{d}t \end{aligned}$$
(1)
$$\begin{aligned}&\displaystyle G_l(t,y_1,\dots ,y_m,\dots ,{^C _{0}D^{\alpha _r}_{t}y_{r}},\dots )=0, \quad l=1,\dots ,L, \end{aligned}$$
(2)

where \(n-1<\alpha _r\le n\), \(1\le r \le m\) and \(L\) is the number of constraints. In the problem (1) – (2) each variable \(y_j\), \(1\le j \le m\), can be considered in the following three cases:

  1. (i)

    \(y_j\) has no derivative, neither initial nor boundary conditions.

  2. (ii)

    \(y_j\) has fractional derivative of order at most \(\alpha _j\) and initial conditions

    $$\begin{aligned} y_j^{(i)}(0)=y_{j0}^{i}, \quad 0 \le i \le \lceil \alpha _j \rceil -1. \end{aligned}$$
  3. (iii)

    \(y_j\) has fractional derivative of order at most \(\alpha _j\) and initial and boundary conditions

    $$\begin{aligned} y_j^{(i)}(0)=y_{j0}^{i},\quad y_j^{(i)}(1)=y_{j1}^{i}, \quad 0 \le i \le \lceil \alpha _j \rceil -1. \end{aligned}$$

In this paper, it is considered that the constrained problem (1) – (2) has minimum \(\mu =J[y_{\mu }^1,\dots ,y_{\mu }^m]\) on

$$\begin{aligned} X&= \{ (y_1,\dots ,y_m)\\&\in \prod _{j=1}^m E_j[0,1]: G_l(t,y_1,\dots ,y_m,\dots ,{^C _{0}D^{\alpha _r}_{t}y_{r}},\dots )=0, 1 \le l \le L\}, \end{aligned}$$

where

$$\begin{aligned} E_j[0,1]=C[0,1], \end{aligned}$$

when \(y_j\) belongs to the case (i),

$$\begin{aligned} E_j[0,1]=\{y(t)\in C^{\lceil \alpha _j \rceil }[0,1]: y_j^{(i)}(0)=y_{j0}^{i}, 0 \le i \le \lceil \alpha _j \rceil -1\}, \end{aligned}$$

when \(y_j\) belongs to the case (ii), and

$$\begin{aligned} E_j[0,1]=\{y(t)\in C^{\lceil \alpha _j \rceil }[0,1]: y_j^{(i)}(0)=y_{j0}^{i}, y_j^{(i)}(1)=y_{j1}^{i}, 0 \le i \le \lceil \alpha _j \rceil -1\}, \end{aligned}$$

when \(y_j\) belongs to the case (iii).

Note that here \((C^n[0,1],\parallel . \parallel _n)\) is the Banach space

$$\begin{aligned} C^n[0,1]=\{f(t) : f^{(n)}(t)\in C[0,1]\}, \end{aligned}$$

where

$$\begin{aligned} \parallel f \parallel _n=\parallel f \parallel _{\infty }+\parallel f' \parallel _{\infty }+\dots +\parallel f^{(n)} \parallel _{\infty }. \end{aligned}$$

Consider the following optimization problem:

$$\begin{aligned} {\hbox {min}} \quad J_{\epsilon }[y_1,\dots ,y_m]&= \int \limits _{0}^{1}F(t,y_1,\dots ,y_m,\dots ,{^C _{0}D^{\alpha _r}_{t}y_{r}},\dots )\mathrm{d}t\nonumber \\&+\frac{1}{\epsilon }\sum _{l=1}^L\int \limits _0^1 G_l^2(t,y_1,\dots ,y_m,\dots ,{^C _{0}D^{\alpha _r}_{t}y_{r}},\dots )\mathrm{d}t, \quad \quad \end{aligned}$$
(3)

where \(\epsilon >0\) is given.

We solve the unconstrained problem (3) instead of the constrained optimization problem (1)–(2) for sufficiently small value of \(\epsilon \). Theorem 5.3 ensures that solving problem (3) with Ritz method leads to an approximate solution for the problem (1)–(2).

4 Ritz Approximation Method

Since Legendre Polynomials have been applied to approximate functions in the subsequent development, we state some basic properties of these polynomials. Of course it is possible to use other types of polynomials, such as Taylor, Bernstein, etc, for approximations.

4.1 Legendre Polynomials

The Legendre polynomials are orthogonal polynomials on the interval \([-1,1]\) and can be determined with the following recurrence formula:

$$\begin{aligned} L_{i+1}(y)=\frac{2i+1}{i+1}yL_i(y)-\frac{i}{i+1}L_{i-1}(y),\quad i=1,2,3,\dots \end{aligned}$$

where \(L_0(y)=1\) and \(L_1(y)=y\). By the change of variable \(y=2t-1\) we will have the well-known shifted Legendre polynomials. Let \(p_m(t)\) be the shifted Legendre polynomials of order \(m\) which are defined on the interval \([0,1]\) and can be determined with the following recurrence formula

$$\begin{aligned} p_{m+1}(t)&= \frac{2m+1}{m+1}(2t-1)p_m(t)-\frac{m}{m+1}p_{m-1}(t), \quad m=1,2,3,\dots \\&p_0(t)=1, \quad p_1(t)=2t-1. \end{aligned}$$

We also have analytical form of the shifted Legendre polynomial of degree \(i,\) \(p_i(t)\) as follows

$$\begin{aligned} p_i(t)=\sum _{k=0}^{i}(-1)^{i+k}\frac{(i+k)!t^k}{(i-k)!(k!)^2}, \quad i=0,1,2,... \quad . \end{aligned}$$

In Sect. 4.2, we minimize functional (3) on the set of all polynomials that satisfy initial and boundary conditions of the problem (1) – (2). Lemma 4.1 shows that all such polynomials have the same form.

Lemma 4.1

Let \(p(t)\) be a polynomial that satisfies the following conditions

$$\begin{aligned} p^{(l)}(0)=y_0^l, \quad p^{(l)}(1)=y_1^l, \quad 0\le l \le n, \end{aligned}$$

then \(p(t)\) has the following form

$$\begin{aligned} p(t)=\sum _{j=0}^k c_j t^{n+1}(t-1)^{n+1}p_j(t)+w(t), \end{aligned}$$

where, \(k\in Z^+\), \(c_j \in \mathbb {R}\), and \(w(t)\) is the Hermit interpolating polynomial of degree at most \(2n+1\) that satisfies above conditions.

Proof

Obviously we have

$$\begin{aligned} p(t)=p(t)-w(t)+w(t), \end{aligned}$$

where

$$\begin{aligned} p^{(l)}(0)-w^{(l)}(0)=0, \quad p^{(l)}(1)-w^{(l)}(1)=0, \quad 0\le l \le n. \end{aligned}$$

So we have

$$\begin{aligned} p(t)-w(t)=t^{n+1}(t-1)^{n+1}s(t), \end{aligned}$$

where \( s(t)=\sum _{j=0}^k c_j p_j(t)\). \(\square \)

Remark 4.1

Considering above lemma, it is easy to see that polynomial \(p(t)\), that satisfies conditions

$$\begin{aligned} p^{(l)}(0)=y_0^l, \quad 0\le l \le n, \end{aligned}$$

has the form

$$\begin{aligned} p(t)=\sum _{j=0}^k c_j t^{n+1}p_j(t)+w(t), \end{aligned}$$

where, \(k\in Z^+\), \(c_j \in \mathbb {R}\), and \(w(t)\) is the Hermit interpolating polynomial that satisfies given conditions.

4.2 Approximation

Consider expansions \(y_{j,\epsilon }^k(t)\), \(1\le j \le m\), in the following forms:

$$\begin{aligned} y_{j,\epsilon }^k(t) = {C_{j,\epsilon }^k}^T.\Psi _k(t), \quad \Psi _k(t)=\left( \begin{array}{c} p_0(t) \\ p_1(t) \\ \vdots \\ p_k(t) \\ \end{array} \right) , \quad C_{j,\epsilon }^k=\left( \begin{array}{c} c_{j,\epsilon }^0 \\ c_{j,\epsilon }^1 \\ \vdots \\ c_{j,\epsilon }^k \\ \end{array} \right) , \end{aligned}$$
(4)

for when \(y_j\) belongs to the case (i).

$$\begin{aligned} y_{j,\epsilon }^k(t) = {C_{j,\epsilon }^k}^T.\Psi _k(t)+w_j(t), \quad \Psi _k(t)=\left( \begin{array}{c} p_0(t)t^{\lceil \alpha _j \rceil } \\ p_1(t)t^{\lceil \alpha _j \rceil } \\ \vdots \\ p_{k}(t)t^{\lceil \alpha _j \rceil } \\ \end{array} \right) \!, \quad C_{j,\epsilon }^k=\left( \begin{array}{c} c_{j,\epsilon }^0\\ c_{j,\epsilon }^1 \\ \vdots \\ c_{j,\epsilon }^k \\ \end{array} \right) \!,\quad \quad \end{aligned}$$
(5)

for when \(y_j\) belongs to the case (ii). Here, \(w_j\) is the Hermit interpolating polynomial that satisfies all initial conditions of \(y_j\).

$$\begin{aligned} \begin{aligned} y_{j,\epsilon }^k(t)&= {C_{j,\epsilon }^k}^T.\Psi _k(t)+w_j(t),\\ \Psi _k(t)&=\left( \begin{array}{c} p_0(t)t^{\lceil \alpha _j \rceil }(t-1)^{\lceil \alpha _j \rceil } \\ p_1(t)t^{\lceil \alpha _j \rceil }(t-1)^{\lceil \alpha _j \rceil } \\ \vdots \\ p_{k}(t)t^{\lceil \alpha _j \rceil }(t-1)^{\lceil \alpha _j \rceil } \\ \end{array} \right) , \quad C_{j,\epsilon }^k=\left( \begin{array}{c} c_{j,\epsilon }^0 \\ c_{j,\epsilon }^1 \\ \vdots \\ c_{j,\epsilon }^k \\ \end{array} \right) , \end{aligned} \end{aligned}$$
(6)

for when \(y_j\) belongs to the case (iii). In this case, \(w_j\) is the Hermit interpolating polynomial that satisfies all initial and boundary conditions of \(y_j\).

Substituting \(y_{j,\epsilon }^k\), \(1\le j \le m\), in (3), we achieve

$$\begin{aligned} J_{\epsilon }[C_{1,\epsilon }^k,\dots ,C_{m,\epsilon }^k]&= \int \limits _0^1 [F(t, y_{1,\epsilon }^k,\dots , y_{m,\epsilon }^k,\dots ,{^C _{0}D^{\alpha _r}_{t} y_{r,\epsilon }^k},\dots )\nonumber \\&+\frac{1}{\epsilon }\sum _{l=1}^L G_l^2(t, y_{1,\epsilon }^k,\dots , y_{m,\epsilon }^k,\dots ,{^C _{0}D^{\alpha _r}_{t} y_{r,\epsilon }^k},\dots )]\mathrm{d}t, \quad \quad \end{aligned}$$
(7)

which is an algebraic function of unknowns \(c_{j,\epsilon }^i, i=0,1,\dots ,k, j=1,\dots ,m\). If \(c_{j,\epsilon }^i\)s be determined by minimizing function \(J_{\epsilon }\), then by (4) – (6) we achieve functions that approximate minimum value of \(J_{\epsilon }\) in (7) and also satisfy all initial and boundary conditions of the problem. According to differential calculus, the following system of equations is the necessary condition of optimization for the function

(7).

$$\begin{aligned} \frac{\partial J_{\epsilon }}{\partial c_{j,\epsilon }^i}=0, \quad 1\le j \le m, \quad 0\le i \le k. \end{aligned}$$
(8)

By solving the system (8), we can determine the minimizing values of \(c_{j,\epsilon }^i\)s, \(i=0,1,\dots ,k\), \(j=1,\dots ,m\) for function (7). Hence, we achieve functions \(y_{j,\epsilon }^k\), \(1\le j \le m\), by (4) – (6), which approximate minimum value of \(J\) by

$$\begin{aligned} J[C_{1,\epsilon }^k,\dots ,C_{m,\epsilon }^k]=\int _0^1 F(t, y_{1,\epsilon }^k,\dots , y_{m,\epsilon }^k,\dots ,{^C _{0}D^{\alpha _r}_{t} y_{r,\epsilon }^k},\dots )\mathrm{d}t, \end{aligned}$$
(9)

while

$$\begin{aligned} \parallel G_l(t,y_{1,\epsilon }^k,\dots ,y_{m,\epsilon }^k,\dots ,{^C _{0}D^{\alpha _r}_{t} y_{r,\epsilon }^k},\dots )\parallel _{L^2[0,1]} \simeq 0, \quad l=1,\dots , L, \end{aligned}$$

and also satisfy all initial and boundary conditions of the problem.

5 Convergence

Let

$$\begin{aligned} E[0, 1]=\{f(t)\in C^n [0,1] : f^{(j)}(0)=f_{0}^j, f^{(j)}(1)=f_{1}^j,j=0,1,\dots ,n-1\}, \end{aligned}$$

where \(f_{0}^j\) and \(f_{1}^j\) are given constant values. The following lemma plays an important role in our discussion. The lemma shows that polynomial functions of the metric space \(E[0,1]\) are dens.

Lemma 5.1

Let \(f(t)\in E[0,1]\). There exist a sequence of polynomial functions \(\{s_k(t)\}_{k\in N} \subset E[0,1]\) such that \(s_k \rightarrow f\) with respect to \(\parallel . \parallel _n\).

Proof

[23]. \(\square \)

Consider the normed space \((F_m [0,1],\parallel . \parallel )\) as follows

$$\begin{aligned} F_m[0,1]=\prod _{j=1}^m E_j[0,1],\quad \parallel (y_1,\dots ,y_m) \parallel = \sum _{j=1}^{m} \parallel y_j \parallel _{E_j}, \end{aligned}$$

where \(\parallel y_j \parallel _{E_j}=\parallel y_j \parallel _{\infty }\) when \(y_j\) belongs to the case (i), \(\parallel y_j \parallel _{E_j}=\parallel y_j \parallel _{\lceil \alpha _j \rceil } \) when \(y_j\) belongs to the case (ii) or (iii).

Consider \(H_m^k[0,1]\) as follows:

$$\begin{aligned} H_m^k[0,1]=\prod _{j=1}^m (E_j[0,1]\bigcap < \{p_i\}_{i=0}^k>), \end{aligned}$$

where \(< \{p_i\}_{i=0}^k >\) is the Banach space generated by the Legendre polynomials of degree at most \(k\). Of course \(H_m^k[0,1]\) is a subspace of \(F_m[0,1]\).

Let \(y\in C^{n}[0,1]\). For Caputo fractional derivative of order \(\alpha \), \(n-1<\alpha \le n\), we have \( ^C _{0}D^{\alpha }_{t}y(t) \in C[0,1] \) [31–33]. We also have

$$\begin{aligned} ^C _{0}D^{\alpha }_{t}y(t)&= \frac{1}{\Gamma {(n-\alpha )}}\int \limits _0^t (t-s)^{n-\alpha -1}y^{(n)}(s)\mathrm{d}s,\\ \mid {^C _{0}D^{\alpha }_{t}y(t)}\mid&\le \frac{1}{\Gamma {(n-\alpha )}}\int \limits _0^t (t-s)^{n-\alpha -1}\mid y^{(n)}(s) \mid \mathrm{d}s\\&\le \frac{\parallel y^{(n)} \parallel _{\infty }}{\Gamma {(n-\alpha )}} \int _0^t (t-s)^{n-\alpha -1}\mathrm{d}s=\frac{\parallel y^{(n)} \parallel _{\infty } t^{n-\alpha }}{\Gamma {(n-\alpha )}(n-\alpha )}\le \frac{\parallel y^{(n)} \parallel _{\infty } }{\Gamma {(n-\alpha +1)}}. \end{aligned}$$

So

$$\begin{aligned} \parallel {^C _{0}D^{\alpha }_{t}y}\parallel _{\infty } \le \frac{\parallel y^{(n)} \parallel _{\infty } }{\Gamma {(n-\alpha +1)}}, \quad n-1<\alpha \le n. \end{aligned}$$
(10)

Now consider (3) as functional \(J_{\epsilon }:F_m[0,1] \rightarrow \mathbb {R}.\) Lemma 5.2 shows that \(J_{\epsilon }\) is continuous on it’s domain. We use this important property later in Theorem 5.2. The following theorem from real analysis plays key role in the proof of Lemma 5.2.

Theorem 5.1

Let \(f\) be continuous mapping of a compact metric space \(X\) into a metric space \(Y\), then \(f\) is uniformly continuous.

Proof

[34]. \(\square \)

Lemma 5.2

The functional \(J_{\epsilon }\) is continuous on \((F_m[0,1],\parallel . \parallel )\).

Proof

Let \((y_1^*,\dots ,y_m^*)\in F_m[0,1]\). \(\eta >0\) is given. Consider \(d>0\) and

$$\begin{aligned} I=[0,1]\times [-L-d,L+d]\times \dots \times [-L-d,L+d], \end{aligned}$$

where \( L=max \{ \parallel y_1^* \parallel _{\infty },\dots ,\parallel y_m^* \parallel _{\infty },\dots , \parallel {^C _{0}D^{\alpha _r}_{t}y_r^*}\parallel _{\infty },\dots \}.\)

Obviously \(Y^*(t)=(t,y_1^*(t),\dots ,y_m^*(t),\dots ,{^C _{0}D^{\alpha _r}_{t}y_r^*(t)},\dots ) \in I,\) \(t\in [0,1]. \) \(\gamma >0\) is given. Let \(\delta >0\) and \(\parallel (y_1,\dots ,y_m)-(y_1^*,\dots ,y_m^*)\parallel <\delta \), hence we have \(\parallel y_{j}-y_{j}^*\parallel _{E_j}<\delta \), \(1\le j\le m,\) and according to (10) it is easy to see that for small enough value of \(\delta \) we have

$$\begin{aligned}&Y(t)=(t,y_1(t),\dots ,y_m(t),\dots ,{^C _{0}D^{\alpha _r}_{t}y_r(t)},\dots ) \in I, \\&\mid Y(t)-Y^*(t)\mid <\gamma , \quad t\in [0,1]. \end{aligned}$$

Since functions \(F\) and \(G_l\), \( l=1,\dots , L,\) are continuous on \(I\) and \(I\) is a compact set, according to Theorem 5.1, \(R=F+\frac{1}{\epsilon }\sum _{l=1}^L G_l^2\) is uniformly continuous on \(I\). So if \(\gamma >0\) be sufficiently small, then \(\mid Y(t)-Y^*(t)\mid <\gamma \) implies that \(\mid R(Y(t))-R(Y^*(t)) \mid < \eta \), \(t\in [0,1]\), and \( \mid J_{\epsilon }[y_1,\dots ,y_m]-J_{\epsilon }[y_1^*,\dots ,y_m^*]\mid <\eta .\) \(\square \)

Theorem 5.2

Let \(\mu _{\epsilon }\) be the minimum of the functional \(J_{\epsilon }\) on \(F_m[0,1]\) and also let \(\hat{\mu }_{\epsilon ,k}\) be the minimum of the functional \(J_{\epsilon }\) on \(H_m^k[0,1]\), then \(\lim _{k \rightarrow \infty }\hat{\mu }_{\epsilon ,k}=\mu _{\epsilon }.\)

Proof

For any given \(\eta >0\), let \((y_{1,\epsilon }^*,\dots ,y_{m,\epsilon }^*)\in F_m[0,1]\) such that

$$\begin{aligned} J_{\epsilon }[y_{1,\epsilon }^*,\dots ,y_{m,\epsilon }^*]<\mu _{\epsilon }+\eta . \end{aligned}$$

Such \((y_{1,\epsilon }^*,\dots ,y_{m,\epsilon }^*)\) exists by the properties of minimum. According to Lemma 5.2, \(J_{\epsilon }\) is continuous on \(( F_m[0,1],\parallel . \parallel )\) so we have

$$\begin{aligned} \mid J_{\epsilon }[y_1,\dots ,y_m]-J_{\epsilon }[y_{1,\epsilon }^*,\dots ,y_{m,\epsilon }^*]\mid < \eta , \end{aligned}$$
(11)

provided that \(\parallel (y_1,\dots ,y_m)-(y_{1,\epsilon }^*,\dots ,y_{m,\epsilon }^*)\parallel <\delta \). According to Weierstrass theorem  [34] and Lemma 5.1, for large enough value of \(k\) there exist \((\gamma _1^k,\dots ,\gamma _m^k)\in H_m^k[0,1]\) such that \(\parallel (\gamma _1^k,\dots ,\gamma _m^k)-(y_{1,\epsilon }^*,\dots ,y_{m,\epsilon }^*) \parallel <\delta \). Moreover let \((y_{1,\epsilon }^k,\dots ,y_{m,\epsilon }^k)\) be the element of \(H_m^k[0,1]\) such that \(J_{\epsilon }[y_{1,\epsilon }^k,\dots ,y_{m,\epsilon }^k]=\hat{\mu }_{\epsilon ,k}\), then using (11) we have

$$\begin{aligned} \mu _{\epsilon } \le J_{\epsilon }[y_{1,\epsilon }^k,\dots ,y_{m,\epsilon }^k] \le J_{\epsilon }[\gamma _1^k,\dots ,\gamma _m^k]<\mu _{\epsilon }+2\eta . \end{aligned}$$

Since \(\eta >0\) is arbitrary, it follows that: \( \lim _{k \rightarrow \infty }\hat{\mu }_{\epsilon ,k}=\mu _{\epsilon }.\) \(\square \)

Theorem 5.3

Let \(\{\epsilon _j\}_{j \in N}\downarrow 0\) be a sequence of monotonically decreasing positive real numbers. Suppose \(\hat{\mu }_{\epsilon _j,k}=J_{\epsilon _j}[y_{1,\epsilon _j}^k,\dots ,y_{m,\epsilon _j}^k]\) be the minimum of the functional \(J_{\epsilon _j}\) on \(H_m^k[0,1]\), then for given \(\eta >0\) there exist a sequence of natural numbers \(\{k_j\}_{j\in N}\) such that

$$\begin{aligned} {\mu }_{\epsilon _j,k_j}:=J[y_{1,\epsilon _j}^{k_j},\dots ,y_{m,\epsilon _j}^{k_j}]< \mu +\eta , \quad j \in N, \end{aligned}$$

and

$$\begin{aligned} \lim _{j \rightarrow \infty } \parallel G_l(t,y_{1,\epsilon _j}^{k_j},\dots ,y_{m,\epsilon _j}^{k_j}, \dots ,{^C _{0}D^{\alpha _r}_{t}y_{r,\epsilon _j}^{k_j}},\dots ) \parallel _{L^2[0,1]} =0, \quad l=1,\dots ,L. \end{aligned}$$

Proof

\(\eta >0\) is given. Suppose \(\mu _{\epsilon _j}=J_{\epsilon _j}[y_{1,\epsilon _j},\dots ,y_{m,\epsilon _j}]\) be the minimum of the functional \(J_{\epsilon _j}\) on \(F_m[0,1]\). It is obvious that

$$\begin{aligned} \mu _{\epsilon _j} \le J_{\epsilon _{j}}[y_{\mu }^{1},\dots ,y_{\mu }^{m}]=\mu , \quad j \in N. \end{aligned}$$
(12)

On the other hand according to Theorem 5.2 we have

$$\begin{aligned} \lim _{k\rightarrow \infty }\hat{\mu }_{\epsilon _j,k}={\mu }_{\epsilon _j}, \quad j \in N. \end{aligned}$$
(13)

So considering (12) and (13), \(\forall j \in N\) there exist \(k_j\in N\) such that

$$\begin{aligned} J_{\epsilon _j}[y_{1,\epsilon _j}^{k_j},\dots ,y_{m,\epsilon _j}^{k_j}]< \mu +\eta , \end{aligned}$$
(14)

and we have

$$\begin{aligned} \mu _{\epsilon _{j},k_j}=J[y_{1,\epsilon _j}^{k_j},\dots ,y_{m,\epsilon _j}^{k_j}]\le J_{\epsilon _j}[y_{1,\epsilon _j}^{k_j},\dots ,y_{m,\epsilon _j}^{k_j}]< \mu +\eta . \end{aligned}$$

Now according to (14) and the assumption \(J[y_1,\dots ,y_m]\ge \lambda \), it is easy to see that

$$\begin{aligned} 0\le \frac{1}{\epsilon _j} \sum _{l=1}^L \int \limits _0^1 G_l^2(t, y_{1,\epsilon _j}^{k_j},\dots , y_{m,\epsilon _j}^{k_j},\dots ,{^C _{0}D^{\alpha _r}_{t} y_{r,\epsilon _j}^{k_j}},\dots )\mathrm{d}t< \mu +\eta -\lambda , \quad \! j \!\in \! N.\nonumber \\ \end{aligned}$$
(15)

Thus, (15) leads to: \( \lim _{j \rightarrow \infty } \sum _{l=1}^L \int \limits _0^1 G_l^2(t, y_{1,\epsilon _j}^{k_j},\dots , y_{m,\epsilon _j}^{k_j},\dots ,{^C _{0}D^{\alpha _r}_{t} y_{r,\epsilon _j}^{k_j}},\dots )\mathrm{d}t=0.\) \(\square \)

6 Illustrative Test Problems

In this section we apply the method presented in Sect. 4.2 for solving the following test examples. The well-known symbolic software “Mathematica” has been employed for calculations and creating figures.

Example 6.1

Consider the one dimensional integer order FOCP

$$\begin{aligned} {\hbox {min}} \quad J&= \frac{1}{2}\int \limits _0^1 [x^2(t)+u^2(t)]\mathrm{d}t,\\ \dot{x}(t)&= -x(t)+u(t),\quad x(0)=1. \end{aligned}$$

For above problem there exist optimal solution

$$\begin{aligned} x(t)&= \cosh (\sqrt{2}t)+\beta \sinh (\sqrt{2}t),\\ u(t)&= (1+\beta \sqrt{2})\cosh (\sqrt{2}t)+(\sqrt{2}+\beta )\sinh (\sqrt{2}t),\\ \beta&= -\frac{\cosh (\sqrt{2})+\sqrt{2} \sinh (\sqrt{2})}{\sqrt{2}\cosh (\sqrt{2})+ \sinh (\sqrt{2})}\simeq -0.98, \end{aligned}$$

and minimum value \(J[x(t),u(t)]=0.192909\)  [35]. Let

$$\begin{aligned} G(t,x(t),u(t),\dot{x}(t))=\dot{x}(t)+x(t)-u(t), \end{aligned}$$

and \(\epsilon =0.00001\) in (3). Consider approximations (4) and (5), respectively, as \( u^8_\epsilon (t)=\sum _{j=0}^8 u_\epsilon ^jp_j(t)\) and \(x^8_\epsilon (t)=\sum _{j=0}^8 x_\epsilon ^jp_j(t)t+1. \) Substituting approximations \(u^8_\epsilon (t)\) and \(x^8_\epsilon (t)\) in functional \(J_{0.00001}[x,u]\) to achieve function (7) and solving the system (8) we will have

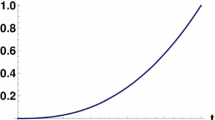
$$\begin{aligned}&x_\epsilon ^0=-1.00579,x_\epsilon ^1=0.328916,x_\epsilon ^2=-0.0457689,x_\epsilon ^3=0.00495371,\\&x_\epsilon ^4=-0.000365183, x_\epsilon ^5=0.0000250667,x_\epsilon ^6=-1.26624\times 10^{-6},\\&x_\epsilon ^7=5.96762\times 10^{-8}, x_\epsilon ^8=-1.47141\times 10^{-11},\\&u_\epsilon ^0=-0.166106,u_\epsilon ^1=0.186771,u_\epsilon ^2=-0.0264288,u_\epsilon ^3=0.00609059,\\&u_\epsilon ^4=-0.000372721, u_\epsilon ^5=0.0000479288,u_\epsilon ^6=-1.87093\times 10^{-6},\\&u_\epsilon ^7=1.66111\times 10^{-7}, u_\epsilon ^8=1.57738\times 10^{-8},\\&J[x_\epsilon ^8,u_\epsilon ^8]=0.192909,\quad \parallel G(t,x_\epsilon ^8,u_\epsilon ^8,\dot{x}_\epsilon ^8) \parallel _{L^2[0,1]}=1.42204\times 10^{-12}. \end{aligned}$$

Figure 1 shows the approximate and exact solutions of the problem.

Fig. 1
figure 1

Exact and approximate values of state and control variables for example 6.1

Full size image

Example 6.2

Consider the following IFVP

$$\begin{aligned} {\hbox {min}} \quad J[y_1,y_2]=\int \limits _0^1 \left( {^C _{0}D^{\frac{1}{2}}_{t}y_1}+2^C _{0}D^{\frac{1}{2}}_{t}y_2-\frac{8t^{\frac{3}{2}}}{3\sqrt{\pi }}-\frac{{15\sqrt{\pi }}t^{2}}{8}\right) ^2 \mathrm{d}t, \end{aligned}$$

subject to

$$\begin{aligned}&\displaystyle \int \limits _0^1 [5(y_1(t)-1)^2+6y_2^2(t)]\mathrm{d}t=2,&\\&\displaystyle y_1(0)=1,\quad y_1(1)=2,\quad y_2(0)=0, \quad y_2(1)=1.&\end{aligned}$$

For the given problem, we have minimizing functions \(y_1(t)=t^2+1\) and \(y_2(t)=t^{\frac{5}{2}}\) with \(J[y_1,y_2]=0\). The problem is solved, substituting approximations (6) with \(w_1(t)=1+t\), \(w_2(t)=t\) and \(k=4\) in (7) and solving the system (8). Table 1 shows \(\mu _{\epsilon ,k} \) and \(E_{\epsilon ,k}=\mid \int _0^1 [5(y_{1,\epsilon }^k(t)-1)^2+6{y_{2,\epsilon }^k}^2(t)]\mathrm{d}t-2 \mid ,\) for \(k=4\) and \(\epsilon =0.1,0.01,0.001\).

Table 1 Absolute errors in example 6.2
Full size table

Example 6.3

Consider the IFVP

$$\begin{aligned} {\hbox {min}} \quad J[y]=\int \limits _0^1 \left( ^C _{0}D^{\frac{1}{2}}_{t}y(t)+{^C _{0}D^{\frac{3}{2}}_{t}y(t)}-\frac{15\sqrt{\pi }t}{8} - \frac{15 \sqrt{\pi }t^2}{16}\right) ^2 \mathrm{d}t, \end{aligned}$$

subject to

$$\begin{aligned}&\displaystyle \int \limits _0^1 y^2(t)\mathrm{d}t=\frac{1}{6},&\\&\displaystyle y(0)=0,\quad y'(0)=0, \quad y(1)=1,\quad y'(1)=\frac{5}{2}.&\end{aligned}$$

For the given problem we have \(y(t)=t^{\frac{5}{2}}\) as minimizing function with \(J[y]=0\). Applying approximation (6) with \(w(t)=t^2+\frac{1}{2}t^2(t-1)\) and solving the system (8), approximate solution for the problem is achieved. Table 2 shows values of \(\mu _{\epsilon ,k}\) and \(E_{\epsilon ,k}=\mid \int _0^1 {y_{\epsilon }^k}^2(t)\mathrm{d}t-\frac{1}{6} \mid \) for different values of \(\epsilon \) and basis functions \(k\).

Table 2 Absolute errors in example 6.3
Full size table

Example 6.4

Consider the two dimensional integer order FOCP

$$\begin{aligned} {\hbox {min}} \quad J&= \frac{1}{2}\int \limits _0^1 [x_1^2(t)+x_2^2(t)+u^2(t)]\mathrm{d}t,\\ \dot{x_1}(t)&= -x_1(t)+x_2(t)+u(t),\\ \dot{x_2}(t)&= -2x_2(t),\\ x_1(0)&= 1, \quad x_2(0)=1. \end{aligned}$$

For above problem we have optimal solution

$$\begin{aligned} x_1(t)&= -\frac{3}{2}e ^{-2t}+2.48164 e ^{-\sqrt{2}t}+0.018352 e ^{\sqrt{2}t},\\ x_2(t)&= e ^{-2t},\\ u(t)&= \frac{\hbox {e}^{-2t}}{2}-1.02793e ^{-\sqrt{2}t}+0.0443056e ^{\sqrt{2}t}, \end{aligned}$$

and minimum value \(J[x_1,x_2,u]=0.431984\)  [17]. Let

$$\begin{aligned} G_1(t,x_1(t),x_2(t),u(t),\dot{x_1}(t),\dot{x_2}(t))&= \dot{x_1}(t)+x_1(t)-x_2(t)-u(t),\\ G_2(t,x_1(t),x_2(t),u(t),\dot{x_1}(t),\dot{x_2}(t))&= \dot{x_2}(t)+2x_2(t), \end{aligned}$$

and \(\epsilon =0.00001\) in (3). Approximations (4) for \(u(t)\) and (5) for \(x_1(t)\) and \(x_2(t)\) with \(w_1(t)=w_2(t)=1\) are considered. Substituting the approximations in functional \(J_{0.00001}[x_1,x_2,u]\) as (7) and solving the system (8), we achieve the following approximate values for the problem:

$$\begin{aligned} J[x_{1,\epsilon }^5,x_{2,\epsilon }^5,u_{\epsilon }^5]&= 0.431987\\ \parallel G_1(t,x_{1,\epsilon }^5,x_{2,\epsilon }^5,u_{\epsilon }^5,\dot{x}_{1,\epsilon }^5,\dot{x}_{2,\epsilon }^5)\parallel _{L^2[0,1]}&= 2.5596\times 10^{-12},\\ \parallel G_2(t,x_{1,\epsilon }^5,x_{2,\epsilon }^5,u_{\epsilon }^5,\dot{x}_{1,\epsilon }^5,\dot{x}_{2,\epsilon }^5)\parallel _{L^2[0,1]}&= 0. \end{aligned}$$

Figure 2 demonstrates exact and approximate solutions of the problem.

Fig. 2
figure 2

Exact and approximate values of state and control variables in example 6.4

Full size image

Example 6.5

Consider the two dimensional FOCP

$$\begin{aligned} {\hbox {min}} \quad J=\int \limits _0^1 \left[ \left( x_1(t)-1-t^{\frac{3}{2}}\right) ^2+\left( x_2(t)-t^{\frac{5}{2}}\right) ^2+\left( u(t)-\frac{3\sqrt{\pi }}{4}t+t^{\frac{5}{2}}\right) ^2\right] \mathrm{d}t, \end{aligned}$$

subject to

$$\begin{aligned}&\displaystyle ^C _{0}D^{\frac{1}{2}}_{t}x_1(t)=x_2(t)+u(t),&\\&\displaystyle ^C _{0}D^{\frac{1}{2}}_{t}x_2(t)=x_1(t)+\frac{15\sqrt{\pi }}{16}t^2-t^{\frac{3}{2}}-1,&\\&\displaystyle x_1(0)=1,\quad x_2(0)=0.&\end{aligned}$$

For above problem optimal solution \(x_1(t)=1+t^{\frac{3}{2}}\), \(x_2(t)=t^{\frac{5}{2}}\), \(u(t)=\frac{3\sqrt{\pi }}{4}t-t^{\frac{5}{2}}\) and minimum value \(J[x_1,x_2,u]=0\) are available. Let

$$\begin{aligned}&G_1(t,x_1(t),x_2(t),u(t),{^C _{0}D^{\frac{1}{2}}_{t}x_1(t)},{^C _{0}D^{\frac{1}{2}}_{t}x_2(t)})={^C _{0}D^{\frac{1}{2}}_{t}x_1(t)}-x_2(t)-u(t),\\&G_2(t,x_1(t),x_2(t),u(t),{^C _{0}D^{\frac{1}{2}}_{t}x_1(t)},{^C _{0}D^{\frac{1}{2}}_{t}x_2(t)})\\&\quad ={^C _{0}D^{\frac{1}{2}}_{t}x_2(t)}-x_1(t)-\frac{15\sqrt{\pi }}{16}t^2+t^{\frac{3}{2}}+1. \end{aligned}$$

We solve the problem with considering approximation (4) for \(u(t)\) and (5) for \(x_1(t)\) and \(x_2(t)\) with \(w_1(t)=1\) and \(w_2(t)=0\), respectively. Table 3 shows values of approximate minimum \(\mu _{\epsilon ,k}\) and

$$\begin{aligned} E_{1,\epsilon }^k&= \parallel G_1(t,x_{1,\epsilon }^k,x_{2,\epsilon }^k,u_{\epsilon }^k,{^C _{0}D^{\frac{1}{2}}_{t}x_{1,\epsilon }^k},{^C _{0}D^{\frac{1}{2}}_{t}x_{2,\epsilon }^k})\parallel _{L^2[0,1]},\\ E_{2,\epsilon }^k&= \parallel G_2(t,x_{1,\epsilon }^k,x_{2,\epsilon }^k,u_{\epsilon }^k,{^C _{0}D^{\frac{1}{2}}_{t}x_{1,\epsilon }^k},{^C _{0}D^{\frac{1}{2}}_{t}x_{2,\epsilon }^k})\parallel _{L^2[0,1]}, \end{aligned}$$

for different values of \(\epsilon \) and \(k\).

Table 3 Absolute errors in example 6.5
Full size table

7 Conclusions

An approximate method based upon epsilon and Ritz methods is developed for solving a general class of fractional constrained optimization problems. First, by applying the epsilon method, the constrained optimization problem is reduced to an unconstrained problem, then using Ritz method with special type of polynomial basis functions, the unconstrained optimization problem is reduced to the problem of finding optimal solution of a real value function. The proposed polynomial basis functions have great flexibility in satisfying initial and boundary conditions. The convergence of the method is extensively discussed and illustrative test examples including IFVPs and FOCPs are presented to demonstrate efficiency of the new technique.