Uniqueness and Ergodicity of Stationary Directed Polymers on $\mathbb {Z}^2$

Abstract

We study the ergodic theory of stationary directed nearest-neighbor polymer models on $\mathbb {Z}^2$, with i.i.d. weights. Such models are equivalent to specifying a stationary distribution on the space of weights and correctors that satisfy certain consistency conditions. We show that for a prescribed weight distribution and corrector mean, there is at most one stationary polymer distribution which is ergodic under the $e_1$ or $e_2$ shift. Further, if the weights have more than two moments and the corrector mean vector is an extreme point of the superdifferential of the limiting free energy, then the corrector distribution is ergodic under each of the $e_1$ and $e_2$ shifts.

1 Introduction

Directed polymers with bulk disorder were introduced in the statistical physics literature by Huse and Henley [17] in 1985 to model the domain wall separating the positive and negative spins in the ferromagnetic Ising model with random impurities. These models have been the subject of intense study over the past three decades; see the recent surveys [7, 8, 13, 16]. Much of the reason for the interest in these models is due to the conjecture that under mild hypotheses, such models are members of the Kardar–Parisi–Zhang (KPZ) universality class, which is an extremely wide-ranging class of models believed to have the same statistical and structural properties. See [9, 10, 15, 26, 27] for recent surveys.

Much like characterization of the Gaussian universality in terms of variants of the central limit theorem (CLT), the KPZ class is characterized by its scaling exponents and limit distributions. In the context of the directed polymer models we study in this paper, the conjecture is that the appropriately centered and normalized finite volume free energy converges to a limit distribution which is independent of the random environment that the polymer lives in. The KPZ scaling theory [22, 24] predicts that the fluctuations around the limiting free energy are of the order of the cube root of the size of the volume, in contrast to the square root in the classical CLT. Moreover, the limiting distribution is not Gaussian. The effect of the environment is felt only through the centering and normalizing constants, which play a role similar to that of the mean and standard deviation in the CLT.

The scaling theory also predicts the values of these two non-universal constants if one has a complete description of the spatially-ergodic and temporally-stationary measures for the polymer model. See [30] for an example of this computation in the setting of the semi-discrete polymer model introduced by O’Connell and Yor in [25]. In the mathematics literature, stationary polymer models have been studied primarily in the context of solvable models, which have product-form stationary distributions. The first such solvable stationary polymer model was the aforementioned model due to O’Connell and Yor. The first discrete model was introduced by Seppäläinen in [29]. See also the models introduced in [3, 11, 31, 32] and studied further in [2, 5, 6]. Such models remain to date the only polymer models for which the KPZ universality conjectures have been verified.

In the present paper, we investigate the ergodic theory of stationary directed polymers on the lattice ${{\,\mathrm{\mathbb {Z}}\,}}^2$ with general i.i.d. weights and nearest-neighbor steps. The solvable model in [29] is an example of the type of model we study. Specializing our results to the case where the limiting free energy is everywhere differentiable, we show that the ergodic distributions form a one-parameter family, indexed by the derivative of the free energy. This differentiability is satisfied in the model in [29] and is conjectured to hold generally. As a consequence, our results imply that the ergodic measures constructed in [29] are the only such measures in that model, which verifies that the hypotheses of the scaling theory are satisfied. More generally, we give conditions under which one can conclude that a stationary distribution is ergodic as well as conditions under which an ergodic measure is unique.

Apart from being fundamental objects for the study of the scaling theory, classifying stationary ergodic polymer measures is important for addressing several other questions. We mention two.

Our results on the classification of stationary and ergodic polymer measures can be reformulated in terms of a characterization of the stationary and ergodic global physical solutions to a discrete version of the viscous stochastic Burgers equation

$$\begin{aligned} \partial _t U=\frac{1}{2}\partial _{xx}U+\frac{1}{2}\partial _x U^2+\partial _x\dot{W}, \end{aligned}$$

where $\dot{W}$ is space-time white noise. This connection is the focus of our companion paper [20]. See also the discussion in [21].

In the language of statistical mechanics, stationary directed polymer measures are in correspondence with shift-covariant semi-infinite Gibbs measures which are consistent with the quenched point-to-point polymer measures. For a discussion of this point of view, we refer the reader to [18, 19].

We close this introduction by giving an outline of the rest of the paper. We introduce polymer measures and stationary polymer measures in Sect. 2 then state our main results in Sect. 3. In Sect. 4, we define and study our main tool, which we call the update map. The proofs of the main theorems are then given in Sect. 5.

2 Setting

2.1 Random Polymer Measures

Let $\varOmega _0=\mathbb {R}^{\mathbb {Z}^2}$ and equip it with the product topology and product Borel $\sigma$-algebra $\mathcal {F}_0$. A generic point in $\varOmega _0$ will be denoted by $\omega$. Let $\{\omega _x(\omega ):x\in \mathbb {Z}^2\}$ be the natural coordinate projections. The number $\omega _x$ models the energy stored at site x and is called the weight or potential or environment at x. Define the natural shift maps$T_z:\varOmega _0\rightarrow \varOmega _0$, $z\in \mathbb {Z}^2$, by $\omega _x(T_z \omega ) = \omega _{x+z}(\omega )$. We are given a probability measure $\mathbb {P}_0$ on $(\varOmega _0,\mathcal {F}_0)$ such that $\{\omega _x:x\in \mathbb {Z}^2\}$ are i.i.d. under $\mathbb {P}_0$ and $\mathbb {E}_0[\vert \omega _0\vert ]<\infty$.

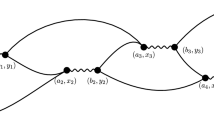
Let $\varPi _{u,v}$ be the set of up-right paths, i.e. paths in $\mathbb {Z}^2$ with steps in $\{e_1,e_2\}$, from u to v. For $m\le n$ in $\mathbb {Z}\cup \{\pm \infty \}$ we write $x_{m,n}$ to denote a path $(x_m,x_{m-1},\dotsc ,x_n)$ and we will use the convention that $x_k\cdot (e_1+e_2)=k$.

Given the weights, the quenched point-to-point polymer measures are probability measures on up-right paths between two fixed sites in which the probability of a path is proportional to the exponential of its energy:

$$\begin{aligned} Q_{u,v}^\omega (x_{m,n})=\frac{e^{\sum _{k=m+1}^{n}\omega _{x_k}}}{Z_{u,v}^\omega }\,,\quad x_{m,n}\in \varPi _{u,v},v\ge u. \end{aligned}$$

(2.1)

Here, $Z_{u,v}^\omega$ is the quenched point-to-point partition function given by

$$\begin{aligned} Z_{u,v}^\omega =\sum _{x_{m,n}\in \varPi _{u,v}}e^{\sum _{k=m+1}^{n}\omega _{x_k}},\quad {v\ge u}, \end{aligned}$$

(2.2)

with the convention that an empty sum equals 0. (Thus, $Z_{u,u}^\omega =1$ and $Z_{u,v}^\omega =0$ when $v\not \ge u$.)

A computation shows that the point-to-point measure is a backward Markov chain starting at v, taking steps $\{-e_1,-e_2\}$, and with absorption at u. If we define

$$\begin{aligned} B_u(x,y,\omega )=\log Z^\omega _{u,y}-\log Z^\omega _{u,x},\quad x,y\ge u,\ \end{aligned}$$

then the transition probabilities of this Markov chain are given by

(2.3)

Note that if $x=u+ke_i$, $k\in \mathbb {N}$, then the chain takes $-e_i$ steps until it reaches u. The processes $B_u$ satisfy the (rooted) cocycle property

$$\begin{aligned}&B_u(x,y,\omega )+B_u(y,z,\omega )=B_u(x,z,\omega ),\quad x,y,z\ge u. \end{aligned}$$

(2.4)

Since $Z^\omega _{u,v}$ satisfies the recurrence

$$\begin{aligned} Z_{u,x}=e^{\omega _x}(Z_{u,x-e_1}+Z_{u,x-e_2}),\quad x-u\in \mathbb {N}^2, \end{aligned}$$

(2.5)

we see that $B_u$ also satisfies the recovery property

$$\begin{aligned}&e^{-B_u(x-e_1,x,\omega )}+e^{-B_u(x-e_2,x,\omega )}=e^{-\omega _x},\quad x-u\in \mathbb {N}^2. \end{aligned}$$

(2.6)

Note also that

$$\begin{aligned} B_u(x,y,T_z\omega )=B_{u+z}(x+z,y+z,\omega ) \end{aligned}$$

(2.7)

and that if $x,y\le v$, then $B_u(x,y,\omega )$ is a function of $\{\omega _z:z\le v\}$ and is hence independent of $\{\omega _z:z\not \le v\}$.

A stationary polymer measure is one that retains the properties (2.4), (2.6), (2.7), and the above independence structure, but without a reference to the roots u and $u+z$. This leads us to the notion of corrector distributions.

2.2 Corrector Distributions

Extend the measurable space $(\varOmega _0,\mathcal {F}_0)$ to $(\varOmega ,\mathcal {F})$ where $\varOmega =\mathbb {R}^{\mathbb {Z}^2}\times \mathbb {R}^{\mathbb {Z}^2\times \mathbb {Z}^2}$, equipped with the product topology, and $\mathcal {F}$ is the product Borel $\sigma$-algebra. Now, $\omega$ will denote a generic point in $\varOmega$ and $\{\omega _x(\omega ):x\in \mathbb {Z}^2\}$ and $\{B(x,y,\omega ):x,y\in \mathbb {Z}^2\}$ denote the natural coordinate projections. The natural shift maps are now given by $T_z:\varOmega \rightarrow \varOmega$, $z\in \mathbb {Z}^2$, with $\omega _x(T_z \omega ) = \omega _{x+z}(\omega )$ and $B(x,y,T_z\omega )=B(x+z,y+z,\omega )$. We will abuse notation and keep using $\omega _x$ and $T_z$ to denote, respectively, the natural projections and shifts on the original space $\varOmega _0$.

We say that a probability measure $\mathbb {P}$ on $(\varOmega ,\mathcal {F})$ is a stationary future-independent$L^1$corrector distribution with$\varOmega _0$-marginal$\mathbb {P}_0$ if it satisfies the following:

I. Distributional Properties: for all $x,y,z\in \mathbb {Z}^2$

• (a) Prescribed marginal: the $\varOmega _0$-marginal is $\mathbb {P}_0$,

• (b) Stationarity: $\mathbb {P}$ is invariant under $T_z$,

• (c) Integrability: $\mathbb {E}[\vert B(x,y)\vert ]<\infty$,

• (d) Future-independence: for any down-right path ${{\,\mathrm{\mathbf {y}}\,}}=(y_k)_{k\in \mathbb {Z}}$, i.e. $y_{k+1}-y_k\in \{e_1,-e_2\}$, $\{B(x,y,\omega ):\exists v\in {{\,\mathrm{\mathbf {y}}\,}}:x,y\le v\}$ and $\{\omega _z:z\not \le v,\forall v\in {{\,\mathrm{\mathbf {y}}\,}}\}$ are independent.

II. Almost Sure Properties: for $\mathbb {P}$-almost every $\omega$ and all $x,y,z\in \mathbb {Z}^2$

• (e) Cocycle: $B(x,y)+B(y,z)=B(x,z)$,

• (f) Recovery: $e^{-B(x-e_1,x)}+e^{-B(x-e_2,x)}=e^{-\omega _x}$.

We say $\mathbb {P}$ is ergodic under $T_z$ (or $T_z$-ergodic) if $\mathbb {P}(A)\in \{0,1\}$ for all sets $A\in \mathcal {F}$ such that $T_zA =A$. As it is customary with probability notation (and was already done above), we will often omit the $\omega$ from the arguments of B(x, y) and $\omega _x$. A function B satisfying property (e) is called a cocyle. If it also satisfies (f) then it is called a corrector. Our use of the word “corrector” comes from an analogy with stochastic homogenization. See e.g. [1, p. 467]. The recovery equation (f) is the analogue of (3.4) in that paper.

2.3 Stationary Polymer Measures from Corrector Distributions

A stationary polymer measure is given by first specifying a stationary future-independent corrector distribution $\mathbb {P}$ with an i.i.d. $\varOmega _0$-marginal $\mathbb {P}_0$. Given a realization of the environment $\omega$, the quenched polymer measure$Q_v^\omega$ rooted at $v\in \mathbb {Z}^2$ is a Markov chain starting at v and having transition probabilities

(2.8)

Observe that . Hence, stationary polymer measures are in fact examples of the familiar model of a random walk in a stationary random environment (RWRE).

The quenched point-to-point measure (2.1) can also be viewed as a forward Markov chain starting at u, taking steps $\{e_1,e_2\}$, with absorption at v and transitions

$$\begin{aligned} \overrightarrow{{\pi }}_v(x,x+e_i,\omega ){=}\frac{e^{\omega _{x{+}e_i}}Z_{x{+}e_i{,}v}^\omega }{Z_{x{,}v}^\omega } {=}e^{\omega _x{-}\overline{B}_v(x,x{+}e_i)}\,, \ u\le x\le v, x\ne v, i\in \{1,2\}, \end{aligned}$$

(2.9)

where now $\overline{B}_v(x,y,\omega )=\log Z^\omega _{x,v}-\log Z^\omega _{y,v}+\omega _x-\omega _y$. This structure also leads to stationary polymer measures that are stationary (forward) RWREs with steps $\{e_1,e_2\}$ and whose transitions are of the form $\overrightarrow{{\pi }}(x,x+e_i,\omega )= e^{\omega _x-\overline{B}(x,x+e_i,\omega )}$, $i\in \{1,2\}$, where $\overline{B}$ is an $L^1$ stationary corrector but with the recovery equation replaced by $e^{-\omega _x}=e^{-\overline{B}(x,x+e_1)}+e^{-\overline{B}(x,x+e_2)}$ and future-independence replaced by past-independence (defined in the obvious way). The two points of view are in fact equivalent due to the symmetry of $\mathbb {P}_0$ with respect to reflections of the axes.

It should be noted that although the weights $\{\omega _x:x\in \mathbb {Z}^2\}$ are i.i.d. under $\mathbb {P}_0$, the transitions (and $\{\overrightarrow{{\pi }}(x,x+e_1):x\in \mathbb {Z}^2\}$) are highly correlated, causing the paths of the RWREs to be superdiffusive with a 2/3 scaling exponent. See for example Theorem 7.2 of [12].

2.4 Stationary Polymer Measures with Boundary

Another, perhaps more familiar, way of introducing stationary polymer measures comes by considering solutions to the recursion (2.5), but with appropriate boundary conditions. This is how these measures were introduced in the study of solvable models mentioned in the introduction. We explain in this section how this viewpoint is the same as the one via the framework of corrector distributions.

Given a stationary future-independent corrector distribution $\mathbb {P}$ with an i.i.d. $\varOmega _0$-marginal $\mathbb {P}_0$, a down-right path ${{\,\mathrm{\mathbf {y}}\,}}=y_{-\infty ,\infty }$ with $y_m\cdot (e_1-e_2)=m$ for $m\in \mathbb {Z}$, and a point $u\in {{\,\mathrm{\mathbf {y}}\,}}$, define the quenched path-to-point partition functions

$$\begin{aligned} Z_{u,v}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }=\sum _{x_{m,n}\in \varPi _{{{\,\mathrm{\mathbf {y}}\,}},v}}e^{B(u,x_m)+\sum _{k=m+1}^{n}\omega _{x_k}}. \end{aligned}$$

(2.10)

Here, $\varPi _{{{\,\mathrm{\mathbf {y}}\,}},v}$ is the set of up-right paths $x_{m,n}$ that start at a point $x_m\in {{\,\mathrm{\mathbf {y}}\,}}$, exit ${{\,\mathrm{\mathbf {y}}\,}}$ right away, i.e. $x_{m+1}\not \in {{\,\mathrm{\mathbf {y}}\,}}$, and end at $x_n=v$. Recall that an empty sum is 0. If $v\in {{\,\mathrm{\mathbf {y}}\,}}$, then $\varPi _{{{\,\mathrm{\mathbf {y}}\,}},v}$ consists of a single path and $Z_{u,v}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }=e^{B(u,v)}$.

The cocycle and recovery properties (e) and (f) imply that $e^{B(u,x)}$ satisfies the same recurrence relation (2.5) as $Z^{{{\,\mathrm{\mathbf {y}}\,}},\omega }_{u,x}$. Since the two also match for $x\in {{\,\mathrm{\mathbf {y}}\,}}$ we deduce that $Z^{{{\,\mathrm{\mathbf {y}}\,}},\omega }_{u,x}=e^{B(u,x)}$ for all x for which $\varPi _{{{\,\mathrm{\mathbf {y}}\,}},x}\not =\varnothing$. In particular, this definition is independent of the boundary ${{\,\mathrm{\mathbf {y}}\,}}$ and gives a stationary field $\{e^{B(u,v)}:u,v\in \mathbb {Z}^2\}$ of point-to-point partition functions. Also, this explains why B is called a corrector: it corrects the potential $\{\omega _x:x\in \mathbb {Z}^2\}$, turning the superadditive $\log Z_{u,v}^\omega$ into an additive cocycle $\log Z_{u,v}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }$. This is a key idea in stochastic homogenization theory. For more, see for example Sect. 2 of [23].

The corresponding quenched path-to-point polymer measure is given by

$$\begin{aligned} Q_{u,v}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }(x_{m,n})=\frac{e^{B(u,x_m) + \sum _{k=m+1}^{n}\omega _{x_k}}}{Z_{u,v}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }}\,,\quad x_{m,n}\in \varPi _{{{\,\mathrm{\mathbf {y}}\,}},v}. \end{aligned}$$

$Q_{u,v}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }$ is the distribution of a Markov chain starting at v and having transition probabilities

until reaching ${{\,\mathrm{\mathbf {y}}\,}}$. In other words, this is exactly the quenched distribution $Q^\omega _v$, until absorption at ${{\,\mathrm{\mathbf {y}}\,}}$ and the path-to-point polymer measure is exactly the stationary polymer measure introduced above.

One can also go in the other direction: starting from a stationary model with boundary we can define a corrector distribution. More precisely, suppose we are given a boundary down-right path ${{\,\mathrm{\mathbf {y}}\,}}=y_{-\infty ,\infty }$ with $y_m\cdot (e_1-e_2)=m$ for $m\in \mathbb {Z}$ and a point $u\in {{\,\mathrm{\mathbf {y}}\,}}$. Abbreviate ${{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+=\{z\in \mathbb {Z}^2:z\not \le v,\forall v\in {{\,\mathrm{\mathbf {y}}\,}}\}$. Equip $\varOmega _{{{\,\mathrm{\mathbf {y}}\,}}}=\mathbb {R}^{{{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+}\times \mathbb {R}^{{{\,\mathrm{\mathbf {y}}\,}}}$ with the product topology and Borel $\sigma$-algebra and denote the natural projections of an element $\omega \in \varOmega _{{{\,\mathrm{\mathbf {y}}\,}}}$ by $\omega _z$, $z\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+$, and $\bar{\omega }_v$, $v\in {{\,\mathrm{\mathbf {y}}\,}}$. Suppose we are given a probability measure $\mathbb {P}_1$ on $\varOmega _{{{\,\mathrm{\mathbf {y}}\,}}}$ under which $\{\omega _z:z\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+\}$ and $\{\bar{\omega }_v:v\in {{\,\mathrm{\mathbf {y}}\,}}\}$ are independent and such that the distribution of $\{\omega _z:z\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+\}$ is the same under $\mathbb {P}_1$ as under $\mathbb {P}_0$.

Let $m_0=u\cdot (e_1-e_2)$, so that $u=y_{m_0}$. For $m\in \mathbb {Z}$ let $B(u,x_m)=\sum _{i=m_0}^{m-1}\bar{\omega }_i$ for $m\ge m_0$ and $B(u,x_m)=-\sum _{i=m}^{m_0-1}\bar{\omega }_i$ for $m\le m_0$. Define the path-to-point partition function $Z_{u,v}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }$, $v\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+\cup {{\,\mathrm{\mathbf {y}}\,}}$, by (2.10). The probability measure $\mathbb {P}_1$ is said to be a stationary polymer model with boundary${{\,\mathrm{\mathbf {y}}\,}}$ if the distribution of

$$\begin{aligned} \{\omega _{v+z},Z_{u,y+z}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }/Z_{u,u+z}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }:v\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+,\,y\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+\cup {{\,\mathrm{\mathbf {y}}\,}}\}, \end{aligned}$$

induced by $\mathbb {P}_1$, does not depend on $z\in \mathbb {Z}_+^2$.

For $x,y\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+\cup {{\,\mathrm{\mathbf {y}}\,}}$ let

$$\begin{aligned} B_{{{\,\mathrm{\mathbf {y}}\,}}}(x,y)=\log Z_{u,y}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }-\log Z_{u,x}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }. \end{aligned}$$

Then the above definition is equivalent to saying that the distribution of

$$\begin{aligned} \{\omega _{v+z},B_{{{\,\mathrm{\mathbf {y}}\,}}}(x+z,y+z):v\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+,\,x,y\in {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+\cup {{\,\mathrm{\mathbf {y}}\,}}\}, \end{aligned}$$

induced by $\mathbb {P}_1$, is the same for all $z\in \mathbb {Z}_+^2$. Kolmogorov’s consistency theorem allows then to extend $\mathbb {P}_1$ to a probability measure $\mathbb {P}$ on $(\varOmega ,\mathcal {F})$ and a few direct computations check that $\mathbb {P}$ is a stationary future-independent corrector distribution with $\varOmega _0$-marginal $\mathbb {P}_0$.

2.5 The Stationary Log-Gamma Polymer

As mentioned earlier, stationary polymer measures with boundaries were a crucial tool in the study of solvable models. In this section we recall the example of Seppäläinen’s log-gamma polymer [29], which fits our setting. Related models include the stationary semi-discrete model in [25], where the boundary $(-\infty ,\infty ) \times \{0\}$ was used, which is analogous to $y_{-\infty ,\infty }=\mathbb {Z}e_1$, and the models studied in [3, 11, 32], where $y_{-\infty ,0} = \mathbb {Z}_+ e_2$ and $y_{0,\infty }=\mathbb {Z}_+ e_1$ were used. In all of these models, the reference point is taken to be $u=0$.

For $\theta >0$ let ${{\,\mathrm{\mathbb {W}}\,}}_\theta$ denote the distribution of a random variable X such that $e^{-X}$ is gamma-distributed with scale parameter 1 and shape parameter $\theta$. Let $\overline{{{\,\mathrm{\mathbb {W}}\,}}}_\theta$ denote the distribution of $-X$. The log-gamma polymer is the directed polymer measure on $\mathbb {Z}^2$ with $\mathbb {P}_0$ being the product measure ${{\,\mathrm{\mathbb {W}}\,}}_\rho ^{\otimes \mathbb {Z}^2}$ for some $\rho >0$.

Consider the boundary path $y_{-\infty ,0}=\mathbb {Z}_+ e_2$ and $y_{0,\infty }=\mathbb {Z}_+ e_1$ and the origin point $u=0$. Then ${{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+=\mathbb {N}^2$. Fix $\theta \in (0,\rho )$ and let $\mathbb {P}_1$ be the product probability measure ${{\,\mathrm{\mathbb {W}}\,}}_\rho ^{\otimes \mathbb {N}^2}\otimes {{\,\mathrm{\mathbb {W}}\,}}_\theta ^{\otimes {\mathbb {N}e_1}}\otimes \overline{{{\,\mathrm{\mathbb {W}}\,}}}_{\rho -\theta }^{\otimes {\mathbb {N}e_2}}$. The path-to-point partition functions $Z_{0,x}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }$, $x\in \mathbb {Z}_+^2$, can be computed inductively by the equations

$$\begin{aligned} Z_{0,x}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }=e^{\omega _x}(Z_{0,x-e_1}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }+Z_{0,x-e_2}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }),\quad x\in \mathbb {N}^2, \end{aligned}$$

and the initial conditions

$$\begin{aligned} Z_{0,0}^{{{\,\mathrm{\mathbf {y}}\,}},\omega } = 1, \quad Z_{0,me_1}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }=e^{\sum _{i=0}^{m-1}\bar{\omega }_{ie_1}}\quad \text {and}\quad Z_{0,me_2}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }=e^{-\sum _{i=1}^{m}\bar{\omega }_{ie_2}},\quad m\in \mathbb {Z}_+. \end{aligned}$$

Equivalently, $B_{{{\,\mathrm{\mathbf {y}}\,}}}(x,x+e_i)$, $i\in \{1,2\}$, $x\in \mathbb {Z}_+^2$, are computed inductively using

$$\begin{aligned} \begin{aligned}&e^{B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_1,x)}=e^{\omega _x}\bigl (1+e^{B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_1-e_2,x-e_2)}e^{-B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_1-e_2,x-e_1)}\bigr ),\\&e^{B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_2,x)}=e^{\omega _x}\bigl (1+e^{B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_1-e_2,x-e_1)}e^{-B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_1-e_2,x-e_2)}\bigr ), \end{aligned} \end{aligned}$$

(2.11)

for $x\in \mathbb {N}^2$, and the initial conditions $B_{{{\,\mathrm{\mathbf {y}}\,}}}(me_1,(m+1)e_1)=\bar{\omega }_{me_1}$ and $B_{{{\,\mathrm{\mathbf {y}}\,}}}(me_2,(m+1)e_2)=-\bar{\omega }_{(m+1)e_2}$, $m\in \mathbb {Z}_+$. Compare to (3.2) in [29]. Then $B_{{{\,\mathrm{\mathbf {y}}\,}}}(x,y)$, $x,y\in \mathbb {Z}_+^2$, are computed via the cocycle property that $B_{{{\,\mathrm{\mathbf {y}}\,}}}$ satisfies. The Burke property [29, Theorem 3.3] implies that $\mathbb {P}_1$ is stationary in the sense of the previous section.

Alternatively, one can use the boundary path $y_{-\infty ,0}=\mathbb {Z}_+e_2$ and $y_{0,\infty }=\mathbb {Z}_+ e_1$ and then ${{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+=\mathbb {Z}\times \mathbb {N}$ and $\mathbb {P}_1$ would be the product measure ${{\,\mathrm{\mathbb {W}}\,}}_\rho ^{\otimes {{\,\mathrm{\mathbb {I}}\,}}_{{{\,\mathrm{\mathbf {y}}\,}}}^+}\otimes {{\,\mathrm{\mathbb {W}}\,}}_\theta ^{\otimes {{\,\mathrm{\mathbf {y}}\,}}}$. The partition functions $Z_{0,x}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }$, $x\in \mathbb {Z}\times \mathbb {Z}_+$, are now computed inductively by the equations

$$\begin{aligned} Z_{0,x}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }=\sum _{m=0}^\infty e^{\sum _{i=0}^m\omega _{x-ie_1}}Z_{0,x-e_2-me_1}^{{{\,\mathrm{\mathbf {y}}\,}},\omega },\quad x\in \mathbb {Z}\times \mathbb {N}, \end{aligned}$$

and the initial conditions

$$\begin{aligned} Z_{0,0}^{{{\,\mathrm{\mathbf {y}}\,}},\omega } = 1, \quad Z_{0,me_1}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }=e^{\sum _{i=0}^{m-1}\bar{\omega }_{ie_1}}\quad \text {and}\quad Z_{0,-me_1}^{{{\,\mathrm{\mathbf {y}}\,}},\omega }=e^{-\sum _{i=1}^{m}\bar{\omega }_{-ie_1}},\quad m\in \mathbb {Z}_+. \end{aligned}$$

Equivalently, $B_{{{\,\mathrm{\mathbf {y}}\,}}}(x,x+e_i)$, $i\in \{1,2\}$, $x\in \mathbb {Z}\times \mathbb {Z}_+$ are computed inductively using

$$\begin{aligned}&e^{B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_2,x)}=e^{\omega _x}\Bigl (1+\sum _{m=1}^\infty \prod _{i=1}^m e^{\omega _{x-ie_1}-B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_2-ie_1,x-e_2-(i-1)e_1)}\Bigr ), \nonumber \\&e^{B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_1,x)}=e^{\omega _x}\bigl (1+e^{B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_1-e_2,x-e_2)}e^{-B_{{{\,\mathrm{\mathbf {y}}\,}}}(x-e_1-e_2,x-e_1)}\bigr ), \end{aligned}$$

(2.12)

for $x\in \mathbb {Z}\times \mathbb {N}$, and the initial conditions $B_{{{\,\mathrm{\mathbf {y}}\,}}}(me_1,(m+1)e_1)=\bar{\omega }_{me_1}$, $m\in \mathbb {Z}$. Analysis of the general polymer model with boundary conditions of this type plays a key role in our analysis. See in particular the discussion in Sect. 4.2.

By the uniqueness in Lemma 4.3, the distribution of $\{B_{{{\,\mathrm{\mathbf {y}}\,}}}(x,x+e_i):x\in \mathbb {Z}_+^2\}$ in this construction is the same as the one in the above construction. Consequently, $\mathbb {P}_1$ is again stationary in the sense of the previous section. See Lemma 4.9 for the details of this argument.

3 Main Results

Consider a stationary future-independent $L^1$ corrector distribution $\mathbb {P}$ with $\varOmega _0$-marginal $\mathbb {P}_0$. By shift-invariance and the cocycle property,

$$\begin{aligned} \mathbb {E}[B(0,x+y)]=\mathbb {E}[B(0,x)]+\mathbb {E}[B(x,x+y)]=\mathbb {E}[B(0,x)]+\mathbb {E}[B(0,y)], \end{aligned}$$

for all $x,y\in \mathbb {Z}^2$. Hence, there exists a unique vector ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\in \mathbb {R}^2$, called the mean vector, such that $\mathbb {E}[B(0,x)]=x\cdot {{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}$ for all $x\in \mathbb {Z}^2$. In particular, ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\cdot e_i=\mathbb {E}[B(0,e_i)]$.

Our first main result is on the uniqueness of ergodic corrector distributions with prescribed i.i.d. $\varOmega _0$-marginal and mean ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\cdot e_i$.

Theorem 3.1

Fix an i.i.d. probability measure $\mathbb {P}_0$ on $(\varOmega _0,\mathcal {F}_0)$ with $L^1$ weights. Fix a number $\alpha \in \mathbb {R}$. Fix $i\in \{1,2\}$. There is at most one stationary $T_{e_i}$-ergodic future-independent $L^1$ corrector distribution $\mathbb {P}$ with $\varOmega _0$-marginal $\mathbb {P}_0$ and such that ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\cdot e_i=\alpha$.

In terms of stationary polymers with boundary ${{\,\mathrm{\mathbf {y}}\,}}={{\,\mathrm{\mathbb {Z}}\,}}e_1$, this theorem says that, in general, the $T_{e_1}$-ergodic stationary distributions form a one parameter family, indexed by the mean of the boundary weights. The formulation in terms of corrector distributions allows us to extend this result to more general boundary geometries.

We next turn to the question of determining which values of the parameter ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}$ admit ergodic stationary polymers. To state our second result we need a few more definitions and some more hypotheses. Recall the point-to-point partition functions (2.2). Assume that $\mathbb {E}[\vert \omega _0\vert ^p]<\infty$ for some $p>2$. Then Theorem 2.2(a), Remark 2.3, and Theorems 2.4, 2.6(b), and 3.2(a) of [28] imply that there exists a deterministic continuous 1-homogenous concave function $\varLambda _{\mathbb {P}_0}:\mathbb {R}_+^2\rightarrow \mathbb {R}$ such that $\mathbb {P}_0$-almost surely

$$\begin{aligned} n^{-1}\log Z_{0,\lfloor {n\xi }\rfloor }^\omega \mathop {\longrightarrow }_{n\rightarrow \infty }\varLambda _{\mathbb {P}_0}(\xi )\quad \text {for all }\xi \in \mathbb {R}_+^2. \end{aligned}$$

(3.1)

Given $\xi \in (0,\infty )^2$, let

$$\begin{aligned} \partial \varLambda _{\mathbb {P}_0}(\xi )=\bigl \{{{\,\mathrm{\mathbf {b}}\,}}\in \mathbb {R}^2: {{\,\mathrm{\mathbf {b}}\,}}\cdot (\xi -\zeta )\le \varLambda _{\mathbb {P}_0}(\xi )-\varLambda _{\mathbb {P}_0}(\zeta ),\ \forall \zeta \in \mathbb {R}_+^2\bigr \} \end{aligned}$$

(3.2)

denote the superdifferential of $\varLambda _{\mathbb {P}_0}$ at $\xi$. This is a convex set. Let ${{\,\mathrm{ext}\,}}\partial \varLambda _{\mathbb {P}_0}(\xi )$ denote its extreme points. If $\xi \in (0,\infty )^2$ then $\varLambda _{\mathbb {P}_0}$ is differentiable at $\xi$ if and only if

$$\begin{aligned} \partial \varLambda _{\mathbb {P}_0}(\xi )={{\,\mathrm{ext}\,}}\partial \varLambda _{\mathbb {P}_0}(\xi )=\{\nabla \varLambda _{\mathbb {P}_0}(\xi )\}. \end{aligned}$$

(3.3)

Otherwise, ${{\,\mathrm{ext}\,}}\partial \varLambda _{\mathbb {P}_0}(\xi )$ consists of exactly two points (see Lemma 4.6(c) in [19]). It is conjectured that $\varLambda _{\mathbb {P}_0}$ is differentiable on $(0,\infty )^2$ and then (3.3) holds for all $\xi \in (0,\infty )^2$. Note that due to the homogeneity of $\varLambda _{\mathbb {P}_0}$, $\partial \varLambda _{\mathbb {P}_0}(\xi )=\partial \varLambda _{\mathbb {P}_0}(c\xi )$ for all $\xi \in (0,\infty )^2$ and $c>0$.

Before presenting our second main result in the present paper, we record some useful inputs from our companion paper [19]. The first is Lemma 4.5(a) in that paper and it characterizes the possible mean vectors of corrector distributions.

Lemma 3.2

If $\mathbb {P}$ is a stationary future-independent corrector distribution with an $\varOmega _0$-marginal given by i.i.d. $L^p$ weights, $p>2$, then ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\in \partial \varLambda _{\mathbb {P}_0}(\xi )$ for some $\xi \in \{t e_1 + (1-t) e_2 : 0< t < 1\}=]e_1,e_2[$.

The second is Theorem 4.7 in that paper and gives existence of corrector distributions for each such mean.

Lemma 3.3

For each ${{\,\mathrm{\mathbf {b}}\,}}$ with the property that ${{\,\mathrm{\mathbf {b}}\,}}\in \partial \varLambda _{\mathbb {P}_0}(\xi )$ for some $\xi \in ]e_1,e_2[$ and for each probability measure $\mathbb {P}_0$ on $\varOmega _0$ under which the weights are i.i.d. and in $L^p$ for some $p>2$, there exists a stationary future-independent $L^1$ corrector distribution $\mathbb {P}$ with $\varOmega _0$-marginal $\mathbb {P}_0$ such that ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}={{\,\mathrm{\mathbf {b}}\,}}$.

Let ${{\,\mathrm{\mathcal {C}}\,}}_{\mathbb {P}_0}$ denote the collection of all stationary future-independent $L^1$ corrector distributions with $\varOmega _0$-marginal $\mathbb {P}_0$. In words, the last lemma says that as $\mathbb {P}$ varies over ${{\,\mathrm{\mathcal {C}}\,}}_{\mathbb {P}_0}$, its mean vector ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}$ spans all of $\bigcup _{\xi \in ]e_1,e_2[}\partial \varLambda _{\mathbb {P}_0}(\xi )$. The next result is an immediate consequence of Lemmas 4.7(b) and 4.7(d) in [19] and Lemma C.1 in [18]. It says that in fact as $\mathbb {P}$ spans ${{\,\mathrm{\mathcal {C}}\,}}_{\mathbb {P}_0}$ each coordinate of ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}$ spans $(\mathbb {E}_0[\omega _0],\infty )$.

Lemma 3.4

Fix an i.i.d. probability measure $\mathbb {P}_0$ on $(\varOmega _0,\mathcal {F}_0)$ with $L^p$ weights, for some $p>2$. Then $\{{{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}: \mathbb {P}\in {{\,\mathrm{\mathcal {C}}\,}}_{\mathbb {P}_0}\}$ is a closed curve in $\mathbb {R}^2$ and for each $i \in \{1,2\}$, $\{{{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\cdot e_i : \mathbb {P}\in {{\,\mathrm{\mathcal {C}}\,}}_{\mathbb {P}_0}\} = (\mathbb {E}_0[\omega _0],\infty )$.

Our second main result in this paper gives a convenient tool which allows us to identify ergodic stationary corrector distributions.

Theorem 3.5

Fix an i.i.d. probability measure $\mathbb {P}_0$ on $(\varOmega _0,\mathcal {F}_0)$ with $L^p$ weights, for some $p>2$. Suppose $\mathbb {P}$ is a stationary future-independent corrector distribution with $\varOmega _0$-marginal $\mathbb {P}_0$. If ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\in {{\,\mathrm{ext}\,}}\partial \varLambda _{\mathbb {P}_0}(\xi )$ for some $\xi \in ]e_1,e_2[$, then $\mathbb {P}$ is ergodic under $T_{e_1}$ and $T_{e_2}$.

In principle, this result leaves open the possibility that there could be ergodic stationary distributions with mean vectors which are not extreme points of the superdifferential of the free energy. Nevertheless, in our setting, it is expected that $\varLambda _{\mathbb {P}_0}$ is differentiable, in which case every element of the superdifferential would be extreme. In particular, under this hypothesis, for each $\xi \in ]e_1,e_2[$, Lemma 3.3 furnishes a future-independent $L^1$ corrector distribution $\mathbb {P}_\xi$ with $\varOmega _0$-marginal $\mathbb {P}_0$ such that ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}=\nabla \varLambda _{\mathbb {P}_0}(\xi )$. Then, under the hypothesis of differentiability, using Theorems 3.1 and 3.5 we have the following complete characterization of all ergodic stationary polymer measures.

Corollary 3.6

Fix an i.i.d. probability measure $\mathbb {P}_0$ on $(\varOmega _0,\mathcal {F}_0)$ with $L^p$ weights, for some $p>2$. Assume $\varLambda _{\mathbb {P}_0}$ is differentiable on $(0,\infty )^2$. Then for $i \in \{1,2\}$, the collection of $T_{e_i}$-ergodic stationary corrector distributions is exactly given by $\{\mathbb {P}_\xi : \xi \in ]e_1,e_2[\}$. In particular, for each $\xi \in ]e_1,e_2[$ and each $i\in \{1,2\}$, $\mathbb {P}_\xi$ is the unique $T_{e_i}$-ergodic future-independent corrector distribution with $\varOmega _0$-marginal $\mathbb {P}_0$ and such that ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}=\nabla \varLambda _{\mathbb {P}_0}(\xi )$.

As a consequence, the above and Lemma 3.4 imply that the one-parameter family of ergodic measures constructed in [29] is unique and assumption (2-6) of the scaling theory in [30] is satisfied.

4 The Update Map

4.1 Motivation

In order to study the ergodic theory of stationary distributions or, equivalently, of corrector distributions, it will be convenient to reformulate the recovery and cocycle properties in exponentiated form. Given $B:\mathbb {Z}^2\times \mathbb {Z}^2\rightarrow \mathbb {R}$ define the random variables $V_{n,k}=e^{\omega _{(n,k)}}$, $X_{n,k}=e^{B((n,k-1),(n+1,k-1))}$, and $Y_{n,k}=e^{B((n,k-1),(n,k))-\omega _{(n,k)}}$ for $n,k\in \mathbb {Z}$. The next lemma rewrites the corrector property in terms of this notation. Compare (4.1) with (2.11).

Lemma 4.1

B is a corrector if and only if the following hold for all $n,k\in \mathbb {Z}$:

$$\begin{aligned} Y_{n+1,k} = 1 + \frac{V_{n,k}}{X_{n,k}}Y_{n,k}\quad \text {and}\quad X_{n,k+1} = V_{n+1,k}\Bigl (1 + \frac{X_{n,k}}{V_{n,k}Y_{n,k}}\Bigr ). \end{aligned}$$

(4.1)

Proof

The cocycle property (e) is equivalent to

$$\begin{aligned} B(x-e_2,x) - B(x-e_1,x)= B(x-e_1-e_2,x-e_1)-B(x-e_1-e_2,x-e_2) \end{aligned}$$

for all $x\in \mathbb {Z}^2$. Together, the cocycle and the recovery properties (e) and (f) are equivalent to

$$\begin{aligned}&e^{B(x-e_2,x)-\omega _x} =1+e^{B(x-e_1-e_2,x-e_1)-\omega _{x-e_1}}e^{\omega _{x-e_1}}e^{-B(x-e_1-e_2,x-e_2)}\quad \text {and}\\&e^{B(x-e_1,x)} =e^{\omega _x}\Bigl (1+ e^{B(x-e_1-e_2,x-e_2)-\omega _{x-e_2}}e^{\omega _{x-e_2}}e^{-B(x-e_1-e_2,x-e_1)}\Bigr ) \end{aligned}$$

holding for all $x\in \mathbb {Z}^2$. Plug in $x=(n+1,k)$ in the first equation and $x=(n,k)$ in the second one, then apply the definitions of V, X, and Y. $\square$

We will see in Lemma 4.3 below that iterating the first equation in (4.1) gives

$$\begin{aligned} Y_{n+1,k} = 1 + \sum _{j=-\infty }^{n} \prod _{i=j}^{n} \frac{V_{i,k}}{X_{i,k}}\quad \text {for all }n,k\in \mathbb {Z}. \end{aligned}$$

(4.2)

Compare with (2.12) to see that this sum can be viewed as defining a polymer with boundary conditions.

We now motivate the main tool in the proofs of Theorems 3.1 and 3.5, which we will call the update map$\varPhi$.

First, observe that if the variables $\{V_{n,k},X_{n,0}:n\in \mathbb {Z},k\in \mathbb {Z}_+\}$ are given, then the variables $\{X_{n,k}:n\in \mathbb {Z},k\in \mathbb {N}\}$ can be computed by induction on k, via (4.2) and the second equation in (4.1), provided one shows that (4.2) defines the unique solution to the recursion in the first equation in (4.1).

This observation and the equivalence of stationary corrector distributions and stationary polymer measures with boundary, discussed in Sect. 2.4 (with here ${{\,\mathrm{\mathbf {y}}\,}}=\mathbb {Z}e_1$), reduce the problem of finding a stationary corrector distribution $\mathbb {P}$ with $\varOmega _0$-marginal $\mathbb {P}_0$ to the question of finding a process $\{V_{n,k},X_{n,0}:n\in \mathbb {Z},k\in \mathbb {Z}_+\}$ such that $\{\log V_{n,k}:n\in \mathbb {Z},k\in \mathbb {Z}_+\}$ are i.i.d. with marginal $\mathbb {P}_0$ and, after computing $\{X_{n,k}:n\in \mathbb {Z},k\in \mathbb {N}\}$ as described in the previous paragraph, the process $\{V_{n,k},X_{n,k}:n\in \mathbb {Z},k\in \mathbb {Z}_+\}$ is stationary under shifts in both the n and the k indices.

Stationarity of this process under shifts in the n index can be guaranteed by starting with any process $\{V_{n,k},X_{n,0}:n\in \mathbb {Z},k\in \mathbb {Z}_+\}$ that is already stationary under these shifts. Hence, the task is to ensure that the process $\{V_{n,k},X_{n,k}:n\in \mathbb {Z},k\in \mathbb {Z}_+\}$ is also stationary under shifts in the k index.

This question can be formulated as a fixed point problem. Begin by taking $\{\log V_{n,0} : n\in \mathbb {Z}\}$ i.i.d. with marginal $\mathbb {P}_0$ and consider a stationary sequence $X=\{X_{n,0}:n\in \mathbb {Z}\}$, independent of the V-variables. Compute the next row of variables, $\overline{X}=\{X_{n,1}:n\in \mathbb {Z}\}$ via (4.1) and (4.2). This defines an update map: if we denote the distribution of $A=\{\log X_{n,0}:n\in \mathbb {Z}\}$ by $\mu$, the updated distribution $\varPhi (\mu )$ is the distribution of $\overline{A}=\{\log X_{n,1}:n\in \mathbb {Z}\}$. A more precise definition is given in Definition 4.5 below. In order to construct a corrector distribution with a desired mean, we then need only find a distribution $\mu$ that is a fixed point for the map $\varPhi$ and such that the expected value of $\log X_{0,0}$ takes a prescribed value.

One way to find this fixed point is to follow a procedure familiar from the theory of Markov chains. Namely, one starts with an arbitrary stationary process $A=\{\log X_{n,0}:n\in \mathbb {Z}\}$ that has the prescribed mean, then computes the distribution of the stationary process $\overline{A}=\{\log X_{n,1}:n\in \mathbb {Z}\}$. It will turn out that this process has the same mean. One might then expect the distributions we obtain by iterating this procedure to converge to a distribution which is stationary under the update rule, so long as there is a unique such distribution. A natural way to ensure that this holds is to show that this update map $\varPhi$ is a contraction in an appropriate space.

4.2 Preliminaries

We now begin working toward a precise definition of the map $\varPhi$ mentioned above. As one can see from the discussion in the previous section, the first step in even defining the update map is to ensure that (4.2) is the unique solution to the recurrence in first equation in (4.1) within the class of processes that we study. Additionally, we need to prove that the map can be iterated. These technical points are the focus of the present section.

The definition and properties of the update map $\varPhi$ that we study in this section and in Sect. 4.3 require fewer assumptions than our main results. Hence, the next two sections have their own setting and notation and can be read independently.

Suppose that we are given a stationary process $X=\{X_n : n \in \mathbb {Z}\}$ and an i.i.d. sequence $V=\{V_n : n \in \mathbb {Z}\}$ with $X_0 > 0$ and $V_0 > 0$ almost surely. Assume the two families are independent of each other and denote their joint distribution by P, with expectation E. Suppose $E[|\log X_0 |] < \infty$ and $E[|\log V_0|] < \infty$. Let ${{\,\mathrm{\mathcal {I}}\,}}$ denote the shift-invariant $\sigma$-algebra of the process $\{(X_n, V_n) : n \in \mathbb {Z}\}$ and assume that

$$\begin{aligned} E[\log X_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}] > E[\log V_0]\quad P\text {-almost surely.} \end{aligned}$$

(4.3)

Lemma 4.2

Suppose that $Y=\{Y_n:n\in \mathbb {Z}\}$ satisfies the recursion

$$\begin{aligned} Y_{n+1}&= 1 + V_nX_n^{-1}Y_n,\quad P\text {-almost surely and for all }n\in \mathbb {Z}. \end{aligned}$$

(4.4)

Then $n^{-1} \text{1 }\{0<Y_0<\infty \}\log Y_n\rightarrow 0$ almost surely.

Proof

Let $a\in \mathbb {R}$ and $\varepsilon > 0$ be given and abbreviate $U_k = \log V_k - \log X_k$. Define

$$\begin{aligned} F_0^\varepsilon (a) = a\ \text {and}\ F^\varepsilon _{n+1}(a) = \log \left( 1 + \exp \left\{ F_{n}^\varepsilon (a) + U_n - E[U_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}] + \varepsilon \right\} \right) \quad \text {for }n\in \mathbb {Z}_+. \end{aligned}$$

An induction argument shows that for any $n \in \mathbb {N}$, we have

$$\begin{aligned} F_n^\varepsilon (a)&= \log \Bigl (1 + \sum _{m=1}^{n-1} \exp \Bigl \{ \sum _{k=m}^{n-1}( U_k - E[U_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}] + \varepsilon ) \Bigr \}\\&\qquad \qquad \qquad \qquad + \exp \Bigl \{a+\sum _{k=0}^{n-1} (U_k - E[U_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}] + \varepsilon ) \Bigr \} \Bigr ). \end{aligned}$$

As usual, we take an empty sum to be zero. Rearranging we get

$$\begin{aligned} n^{-1}\log \Bigl (e^{F_n^\varepsilon (a)}-1\Bigr )= & {} \varepsilon +n^{-1}\log \Bigl (\sum _{m=1}^{n-1} \exp \Bigl \{ \sum _{k=m}^{n-1}( U_k - E[U_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}] ) \Bigr \}\\&+ \exp \Bigl \{a+\sum _{k=0}^{n-1} (U_k - E[U_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}]) \Bigr \} \Bigr ) \end{aligned}$$

and therefore

$$\begin{aligned} \Bigl |n^{-1}\log \Bigl (e^{F_n^\varepsilon (a)}-1\Bigr )-\varepsilon \Bigr |\le n^{-1}(\vert a\vert +\log n) +n^{-1}\max _{0\le m\le n-1}\Bigl | \sum _{k=m}^{n-1}( U_k - E[U_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}] ) \Bigr |. \end{aligned}$$

(4.5)

Birkhoff’s ergodic theorem implies that

$$\begin{aligned} \lim _{n\rightarrow \infty }n^{-1}\sum _{k=0}^{n-1} (U_k - E[U_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}])=0. \end{aligned}$$

A calculus exercise implies then that the right-hand side in (4.5) vanishes as $n\rightarrow \infty$. Thus, $F_n^\varepsilon (a)=\log (1+e^{n\varepsilon +o(n)})$ and therefore $n^{-1}F_n^\varepsilon (a)\rightarrow \varepsilon$P-almost surely, for any $a\in \mathbb {R}$.

Another induction (using the fact that $E[U_0\,|\,\bar{{\,\mathrm{\mathcal {I}}\,}}]\le 0$) shows that on the event $0<Y_0<\infty$, we have $0\le \log Y_n\le F_n^\varepsilon (\log Y_0)$ for all $n\in \mathbb {N}$. The claim of the lemma follows. $\square$

The next lemma proves that (4.2) is the unique stationary and almost surely finite solution to the recurrence in first equation in (4.1).

Lemma 4.3

The process $Y= \{Y_n : n \in \mathbb {Z}\}$ given by

$$\begin{aligned} Y_n&= 1 + \sum _{m=-\infty }^{n-1} \prod _{k=m}^{n-1} \frac{V_k}{X_k} \end{aligned}$$

(4.6)

is the unique stationary and almost surely finite solution to (4.4). For any other process Y for which (4.4) holds P-almost surely for all $n\in \mathbb {Z}$, Y must satisfy $P\bigl \{\lim _{j\rightarrow -\infty }\vert Y_j\vert \rightarrow \infty \bigr \}> 0$ and then either Y is stationary and $P(\vert Y_{0}\vert = \infty ) >0$ or Y is not stationary.

Proof

Suppose Y is given by (4.6). By the ergodic theorem and (4.3)

$$\begin{aligned} \lim _{m\rightarrow -\infty } \frac{1}{\vert m\vert } \sum _{k=m}^{n-1}\left( \log V_k - \log X_k\right) = E\left[ \log V_0 - \log X_0 \,|\, {{\,\mathrm{\mathcal {I}}\,}}\right] < 0\quad \text {almost surely.} \end{aligned}$$

(4.7)

Hence $1< Y_n < \infty$ almost surely. It is also clear that Y is stationary and that (4.6) implies (4.4).

Conversely, let Y satisfy (4.4) P-almost surely and for all $n\in \mathbb {Z}$. Iterating (4.4) implies that whenever $j < n-1$, we must have

$$\begin{aligned} Y_{n}&= 1 + \sum _{m=j+1}^{n-1} \prod _{k=m}^{n-1} \frac{V_k}{X_k} + Y_{j} \prod _{k=j}^{n-1} \frac{V_{k}}{X_{k}}. \end{aligned}$$

(4.8)

Suppose now that

$$\begin{aligned} P\Bigl \{\varliminf _{j\rightarrow - \infty } \vert j\vert ^{-1} \log \vert Y_j\vert > 0\Bigl \} =0, \end{aligned}$$

(4.9)

where we take the convention that $\log \infty = \infty$. Then this and (4.7) imply that almost surely

$$\begin{aligned} \varliminf _{j\rightarrow -\infty } \vert Y_j\vert \prod _{k=j}^{n-1} \frac{V_{k}}{X_{k}} = 0. \end{aligned}$$

In this case, taking $j\rightarrow -\infty$ in (4.8) along a subsequence that realizes this liminf implies Y is given by (4.6) almost surely and for all $n\in \mathbb {Z}$.

If, alternatively, the probability in (4.9) is positive, then with positive probability $\vert Y_j\vert \rightarrow \infty$ as $j \rightarrow -\infty$. If we furthermore assume that Y is stationary, then the ergodic theorem implies that $\vert Y_0\vert =\infty$ on the event $\{\vert Y_j\vert \rightarrow \infty \}$. To see this last claim note that for any $c>0$, $|k|^{-1}\sum _{i=k}^0\text{1 }\{|Y_k|\ge c\}\rightarrow P( |Y_0|\ge c \,|\, {{\,\mathrm{\mathcal {I}}\,}})$ almost surely. Consequently,

$$\begin{aligned} P\bigl \{ |Y_0|\not =\infty , |Y_k|\rightarrow \infty \bigr \}&= E\bigl [ \text{1 }\{|Y_0|\not =\infty \} \text{1 }\{|Y_k|\rightarrow \infty \} \bigr ]\\&= E\bigl [ P(|Y_0|\not =\infty \,|\, {{\,\mathrm{\mathcal {I}}\,}}) \text{1 }\{|Y_k|\rightarrow \infty \} \bigr ] = 0. \end{aligned}$$

The lemma is proved. $\square$

Given the setting at the beginning of the section, define $Y=\{Y_n:n\in \mathbb {Z}\}$ by (4.6). By Lemma 4.3, Y satisfies (4.4) and $1<Y_0<\infty$ almost surely. Define the stationary process

$$\begin{aligned} \overline{X}_n&= V_{n+1}(1+ V_n^{-1}X_nY_n^{-1}) = V_{n+1} Y_{n+1} \,\frac{X_n}{V_nY_n}\in (0,\infty )\,,\quad n\in \mathbb {Z}. \end{aligned}$$

(4.10)

An induction argument shows that for $n\in \mathbb {N}$, we have

$$\begin{aligned} Y_1V_1\prod _{k=1}^n \overline{X}_k&= Y_{n+1}V_{n+1}\prod _{k=1}^n X_k. \end{aligned}$$

(4.11)

Lemma 4.2 implies that $\log Y_n/n\rightarrow 0$ almost surely. Also, $\log \overline{X}_0>\log V_1$ almost surely. Hence, Birkhoff’s ergodic theorem implies $\log \overline{X}_0$ is integrable and

$$\begin{aligned} E[\log \overline{X}_0\, |\, {{\,\mathrm{\mathcal {I}}\,}}] = E[\log X_0\, |\, {{\,\mathrm{\mathcal {I}}\,}}]. \end{aligned}$$

(4.12)

Lemma 4.4

Suppose $\{(X_n^1, V_n, Y_n^1,\overline{X}^1_n) : n \in \mathbb {Z}\}$ and $\{(X_n^2, V_n, Y_n^2,\overline{X}^2_n) : n \in \mathbb {Z}\}$ both satisfy equations (4.6) and (4.10). Note that both families share the same V variables. Suppose also that $X_n^1 \le X_n^2$ for all $n\in \mathbb {Z}$. Then $Y_n^1 \ge Y_n^2$ and $\overline{X}_n^1\le \overline{X}_n^2$ for all $n\in \mathbb {Z}$.

Proof

It follows immediately that if $X_n^1\le X_n^2$ for all $n\in \mathbb {Z}$, then

$$\begin{aligned} Y_n^1&= 1 + \sum _{m=-\infty }^{n-1} \prod _{k=m}^{n-1} \frac{V_k}{X_k^1} \ge 1 + \sum _{m=-\infty }^{n-1} \prod _{k=m}^{n-1} \frac{V_k}{X_k^2} = Y_n^2. \end{aligned}$$

Then one has $X_n^1/Y_n^1 \le X_n^2/Y_n^2$ for all $n\in \mathbb {Z}$. It follows that

$$\begin{aligned} \overline{X}_n^1&= V_{n+1}\Bigl (1+ \frac{X_{n}^1}{V_{n} Y_{n}^1 }\Bigr ) \le V_{n+1}\Bigl (1+ \frac{X_{n}^2}{V_{n} Y_{n}^2 }\Bigr ) = \overline{X}_{n}^2. \end{aligned}$$

The claim now follows by inductively repeating the above argument. $\square$

4.3 Definition and Properties

We are now ready to give the precise definition of the update map $\varPhi$. Given a Polish space $\mathbb {X}$, let $\mathcal {M}_1(\mathbb {X})$ denote the set of Borel probability measures on $\mathbb {X}$. Expectation with respect to a measure $\mu \in \mathcal {M}_1(\mathbb {X})$ is denoted by $E^{\mu }$. Let $\varOmega _A=\varOmega _W=\mathbb {R}^\mathbb {Z}$. We denote the coordinate projection random variables on $\varOmega _A$ by $(A_n : n \in {{\,\mathrm{\mathbb {Z}}\,}})$ and on $\varOmega _W$ by $(W_n : n \in {{\,\mathrm{\mathbb {Z}}\,}})$. Similarly, on the space $\varOmega _A \times \varOmega _W$, we denote the natural coordinate projections by $((A_n,W_n) : n \in {{\,\mathrm{\mathbb {Z}}\,}})$. The spaces $\varOmega _A$ and $\varOmega _A \times \varOmega _W$ come equipped with a natural group of shift operators. Call ${{\,\mathrm{\mathcal {I}}\,}}$ the shift-invariant $\sigma$-algebra on $\varOmega _A$ and ${{\,\mathrm{\mathcal {I}}\,}}^0$ the shift-invariant $\sigma$-algebra on $\varOmega _A \times \varOmega _W$. Abusing notation and identifying ${{\,\mathrm{\mathcal {I}}\,}}$ with ${{\,\mathrm{\mathcal {I}}\,}}\times \varOmega _W$ in $\varOmega _A \times \varOmega _W$, we have ${{\,\mathrm{\mathcal {I}}\,}}\subset {{\,\mathrm{\mathcal {I}}\,}}^0$.

Recalling how X, V, and Y were introduced in Section 4.1, it is most natural to formulate the definition of $\varPhi$ in terms of the variables $A_n=\log X_n$, $W_n=\log V_n$, and $\overline{A}_n=\log \overline{X}_n$.

Definition 4.5

Let $\varGamma$ be a probability measure $\varGamma \in \mathcal {M}_1(\mathbb {R})$ with $\int \vert s\vert \,\varGamma (ds)<\infty$. Let $M_0=\int s\,\varGamma (ds)$.

The update map$\varPhi =\varPhi _\varGamma :\mathcal {M}_1(\mathbb {R}^\mathbb {Z})\rightarrow \mathcal {M}_1(\mathbb {R}^\mathbb {Z})$ maps a probability measure $\mu \in \mathcal {M}_1(\varOmega _A)$ which satisfies $E^\mu [A_0 | {{\,\mathrm{\mathcal {I}}\,}}] > M_0$, $\mu$-almost surely, to the probability measure $\varPhi (\mu )\in \mathcal {M}_1([-\infty ,\infty ]^\mathbb {Z})$ as follows. Let $A=(A_n)_{n\in \mathbb {Z}}$ have distribution $\mu$ and let $(W_n)_{n\in \mathbb {Z}}$ be i.i.d. $\varGamma$-distributed random variables, independent of A. Then, $\varPhi (\mu )$ is the probability distribution of $(\overline{A}_n)_{n\in \mathbb {Z}}$ defined through

$$\begin{aligned} \overline{X}_n&= V_{n+1}(1+ V_n^{-1}X_nY_n^{-1}), \end{aligned}$$

where $\overline{X}_n = e^{\overline{A}_n}$, $V_n = e^{W_n}$, $X_n = e^{A_n}$, and $Y_n$ is given by

$$\begin{aligned} Y_n&= 1 + \sum _{m=-\infty }^{n-1} \prod _{k=m}^{n-1} \frac{V_k}{X_k}. \end{aligned}$$

Two consequences of (4.12) are that $E^{\varPhi (\mu )}[A_0]=E^\mu [A_0]$ and $E^{\varPhi (\mu )}[A_0 | {{\,\mathrm{\mathcal {I}}\,}}]>M_0$, $\varPhi (\mu )$-almost surely. This means that the map $\varPhi$ is mean-preserving and that it can be iterated.

Next, we turn to proving that $\varPhi$ is a contraction. To achieve this we will rely on couplings in the natural product spaces. Let $(A^1,A^2)=\{(A^1_n,A^2_n):n\in \mathbb {Z}\}$ and $(A^1,A^2,W)=\{(A^1_n,A^2_n,W_n):n\in \mathbb {Z}\}$ be the natural coordinate projections on $\varOmega _A\times \varOmega _A$ and $\varOmega _A\times \varOmega _A\times \varOmega _W$, respectively. Equip all these spaces with the product topologies, Borel $\sigma$-algebras, and natural shifts.

Given two stationary probability measures $\mu ^1,\mu ^2$ on $\varOmega _A$, let ${{\,\mathrm{\mathcal {M}}\,}}(\mu ^1,\mu ^2)$ denote all stationary probability measures on $\varOmega _A\times \varOmega _A$, with marginals $\mu ^1$ and $\mu ^2$. Define the $\bar{\rho }$ distance:

$$\begin{aligned} \bar{\rho }(\mu ^1,\mu ^2)&= \inf _{\lambda \in {{\,\mathrm{\mathcal {M}}\,}}(\mu ^1,\mu ^2)} E^\lambda \bigl [|A_0^1 - A_0^2|\bigr ]. \end{aligned}$$

(4.13)

By the ergodic decomposition theorem, when $\mu ^1$ and $\mu ^2$ are ergodic the infimum may be taken over ergodic measures $\lambda$. It is shown in [14, Theorem 8.3.1] that the $\bar{\rho }$ distance is a metric and the infimum is achieved. Our main technical result is a positive-temperature analogue of an argument originally due to Chang [4]. Note that the technical assumption $P(V_0>c) >0$ for all c, required in [4], is not needed in positive temperature.

Proposition 4.6

Let $\mu ^1$ and $\mu ^2$ be two ergodic probability measures on $\varOmega _A$. Assume $E^{\mu ^i}[\vert A_0\vert ]<\infty$ and $E^{\mu ^{i}}[A_0]> M_0$, $i\in \{1,2\}$. Then $\bar{\rho }(\varPhi (\mu ^1),\varPhi (\mu ^2)) \le \bar{\rho }(\mu ^1,\mu ^2)$. If in addition $\mu ^1 \ne \mu ^2$ but $E^{\mu _1}[A_0]= E^{\mu _2}[A_0]$, then $\bar{\rho }(\varPhi (\mu ^1),\varPhi (\mu ^2)) < \bar{\rho }(\mu ^1,\mu ^1)$.

Proof

Fix an ergodic $\lambda \in {{\,\mathrm{\mathcal {M}}\,}}(\mu ^1,\mu ^2)$ and let $P=\lambda \otimes \varGamma ^{\otimes \mathbb {Z}}\in \mathcal {M}_1(\varOmega _A\times \varOmega _A\times \varOmega _W)$. We denote the corresponding expectation by E. Being a product of an ergodic measure and a product measure, P is also ergodic. Let $A_n^3 = A_n^1 \vee A_n^2$. Then

$$\begin{aligned} E[ A_0^3 ] \ge E[A_0^1]=E^{\mu ^1}[A_0]> M_0. \end{aligned}$$

Thus, the setting at the beginning of the section applies to $X^3=\{X_{n}^3 : n \in {{\,\mathrm{\mathbb {Z}}\,}}\}= \{e^{A_{n}^3}:n\in \mathbb {Z}\}$ and $V = \{V_n : n \in {{\,\mathrm{\mathbb {Z}}\,}}\}= \{e^{W_n} : n \in {{\,\mathrm{\mathbb {Z}}\,}}\}$. For $i \in \{1,2,3\}$, construct $\overline{A}^i=\{\overline{A}_n^i:n\in \mathbb {Z}\}$ using (4.6) and (4.10), with the convention that $\overline{X}^i = (\overline{X}^i_n : n \in {{\,\mathrm{\mathbb {Z}}\,}})= \{e^{\overline{A}^i_n} : n \in {{\,\mathrm{\mathbb {Z}}\,}}\}$. Lemma 4.4 implies that P-almost surely $\overline{A}_0^3 \ge \overline{A}_0^1 \vee \overline{A}_0^2$. Hence P-almost surely and for all $n\in \mathbb {Z}$

$$\begin{aligned} \begin{aligned}&| A_0^1 - A_0^2| = 2 A_0^1 \vee A_0^2 - A_0^1 - A_0^2 = 2 A_0^3 - A_0^1 - A_0^2\quad \text {and}\\&| \overline{A}_0^1 - \overline{A}_0^2| = 2 \overline{A}_0^1 \vee \overline{A}_0^2 - \overline{A}_0^1 - \overline{A}_0^2 \le 2 \overline{A}_0^3 - \overline{A}_0^1 - \overline{A}_0^2. \end{aligned} \end{aligned}$$

(4.14)

By (4.12) we have $E[\overline{A}_0^i]=E[\log \overline{X}_0^i] = E[\log X_0^i]=E[A_0^i]=E[A_0^i]$ for $i\in \{1,2,3\}$. This and (4.14) give

$$\begin{aligned} E[| \overline{A}_0^1 {-} \overline{A}_0^2|] \le E[2 \overline{A}_0^3 {-} \overline{A}_0^1 {-} \overline{A}_0^2] {=}E[2 A_0^3 {-} A_0^1 {-} A_0^2] {=} E[|A_0^1 {-}A_0^2|] = E^\lambda [|A_0^1 {-} A_0^2|]. \end{aligned}$$

The left hand side is greater than $\bar{\rho }(\varPhi (\mu ^1), \varPhi (\mu ^2))$. The first claim now follows by taking the infimum over $\lambda$ on the right hand side.

Turning to the second claim, suppose that $E^{\mu _1}[A_{0}] = E^{\mu _2}[A_{0}]$ and that $\mu ^1 \ne \mu ^2$. Let $\lambda \in \mathcal {M}(\mu ^1,\mu ^2)$ be an ergodic minimizer of (4.13). Then there exists an integer $n > 1$ with

$$\begin{aligned} P\bigl \{A_{1}^1< A_{1}^2{,} A_{m}^1 \le A_{m}^2{,} 1 \le m< n{,} A_{n}^1> A_{n}^2\bigr \} {=} \lambda \bigl \{A_{1}^1< A_{1}^2{,} A_{m}^1 \le A_{m}^2{,} 1 \le m < n{,} A_{n}^1> A_{n}^2\bigr \} > 0. \end{aligned}$$

Under the event above, we have

$$\begin{aligned} \Bigl (\sum _{k=m}^n A_{k}^1\Bigr ) \vee \Bigl (\sum _{k=m}^n A_{k}^2\Bigr ) < \sum _{k=m}^n A_{k}^3 \end{aligned}$$

whenever $1 \le m < n$. This is equivalent to

$$\begin{aligned} \Bigl (\prod _{k=m}^n X_{k}^1 \Bigr )\vee \Bigl (\prod _{k=m}^n X_{k}^2\Bigr ) < \prod _{k=m}^n X_{k}^3. \end{aligned}$$

(4.15)

We also have $X_k^1 \vee X_k^2 \le X_k^3$ for all $k\in \mathbb {Z}$. Then the representation (4.6) of $Y^i$, $i\in \{1,2,3\}$, gives $Y_{n+1}^3 < Y_{n+1}^1 \wedge Y_{n+1}^2$ and from (4.10), it follows that for $i \in \{1,2\}$

$$\begin{aligned} \overline{X}_{n+1}^i = V_{n+2}\Bigl (1 + \frac{X_{n+1}^i}{V_{n+1}Y_{n+1}^i}\Bigr ) < V_{n+2}\Bigl (1 + \frac{X_{n+1}^3}{V_{n+1}Y_{n+1}^3}\Bigr ) = \overline{X}_{n+1}^3. \end{aligned}$$

Thus, $P\bigl (\overline{A}_{n+1}^1 \vee \overline{A}_{n+1}^2 < \overline{A}_{n+1}^3 \bigr ) > 0.$ In particular,

$$\begin{aligned} \bar{\rho }(\varPhi (\mu ^1),\varPhi (\mu ^2))&\le E[|\overline{A}_0^1 - \overline{A}_0^2|] = E[| \overline{A}_{n+1}^1 - \overline{A}_{n+1}^2|] \\&= E[ 2\overline{A}_{n+1}^1 \vee \overline{A}_{n+1}^2 - \overline{A}_{n+1}^1 - \overline{A}_{n+1}^2] \\&< E[2 \overline{A}_{n{+}1}^3 {-} \overline{A}_{n{+}1}^1 {-} \overline{A}_{n{+}1}^2] {=} E[|A_0^1 {-} A_0^2|] {=} E^\lambda [|A_0^1 {-} A_0^2|] {=} \bar{\rho }(\mu ^1,\mu ^2). \end{aligned}$$

The result follows. $\square$

Let ${{\,\mathrm{\mathcal {M}}\,}}_e^{\alpha }(\varOmega _A)$ be the set of ergodic probability measures $\mu \in \mathcal {M}_1(\varOmega _A)$ with marginal mean $E^\mu [A_0]=\alpha$. The following is an immediate consequence of the previous proposition.

Corollary 4.7

For each $\alpha > M_0$ there exists at most one $\mu \in {{\,\mathrm{\mathcal {M}}\,}}_e^\alpha (\varOmega _A)$ with $\varPhi (\mu ) = \mu$.

Lemma 4.8

Suppose $\mu \in {{\,\mathrm{\mathcal {M}}\,}}_1(\varOmega _A)$ is stationary, $\varPhi (\mu ) = \mu$, and for some constant $\alpha > M_0$ we have

(4.16)

Then $\mu \in {{\,\mathrm{\mathcal {M}}\,}}_e^{\alpha }(\varOmega _A)$.

Proof

By the ergodic decomposition theorem, there exists $Q_\mu \in \mathcal {M}_1\bigl ({{\,\mathrm{\mathcal {M}}\,}}_e^{\alpha }(\varOmega _A)\bigr )$ with

$$\begin{aligned} \mu = \int _{{{\,\mathrm{\mathcal {M}}\,}}_e^{\alpha }(\varOmega _A)}\nu \, Q_\mu (d\nu ). \end{aligned}$$

Let $\phi$ be a bounded measurable function on $\varOmega _A$. Then

$$\begin{aligned} E^{\varPhi (\mu )}[\phi (A)] = E^{\mu }E^{\varGamma ^{\otimes \mathbb {Z}}}[\phi (\overline{A})]&= \int _{{{\,\mathrm{\mathcal {M}}\,}}_e^\alpha (\varOmega _A)} E^{\nu }E^{\varGamma ^{\otimes \mathbb {Z}}}[\phi (\overline{A})]\, Q_\mu (d\nu )\\&= \int _{{{\,\mathrm{\mathcal {M}}\,}}_e^\alpha (\varOmega _A)} E^{\varPhi (\nu )}[\phi (A)] \,Q_\mu (d\nu ). \end{aligned}$$

This is equivalent to $\varPhi (\mu ) = \int \varPhi (\nu )\, Q_\mu (d\nu )$. Since $\varPhi (\mu ) = \mu$, uniqueness in the ergodic decomposition theorem implies that $Q_\mu \circ \varPhi ^{-1} = Q_\mu$. In particular, $\varPhi (\nu )\in {{\,\mathrm{\mathcal {M}}\,}}_e^\alpha (\varOmega _A)$ for $Q_\mu$-almost every $\nu$. Also, for any $k \in \mathbb {N}$

$$\begin{aligned} \int _{{{\,\mathrm{\mathcal {M}}\,}}_e^{\alpha }(\varOmega _A)} \bar{\rho }(\nu ,\varPhi (\nu ))\,Q_\mu (d\nu ) = \int _{{{\,\mathrm{\mathcal {M}}\,}}_e^{\alpha }(\varOmega _A)} \bar{\rho }(\varPhi ^k( \nu ),\varPhi ^{k+1}(\nu ))\,Q_\mu (d\nu ). \end{aligned}$$

The inequality in Proposition 4.6 then implies that

$$\begin{aligned} Q_\mu \left( \left\{ \nu \in {{\,\mathrm{\mathcal {M}}\,}}_e^{\alpha }(\varOmega _A) : \bar{\rho }(\nu ,\varPhi (\nu )) = \bar{\rho }(\varPhi ^k(\nu ), \varPhi ^{k+1}(\nu )) \text { } \forall k \in \mathbb {N}\right\} \right) = 1. \end{aligned}$$

By the second part of Proposition 4.6 it must be the case that $\nu = \varPhi (\nu )$ for $Q_\mu$-almost every $\nu$. Corollary 4.7 then implies that $Q_\mu$ is a Dirac mass and so $\mu \in {{\,\mathrm{\mathcal {M}}\,}}_e^{\alpha }(\varOmega _A)$. $\square$

We close this section with a proof of the stationarity mentioned at the end of Sect. 2.5.

Lemma 4.9

Fix $\rho>\theta >0$. Assume $\{V_n:n\in \mathbb {Z}\}$ are i.i.d. such that $1/V_0$ is gamma-distributed with scale parameter 1 and shape parameter $\rho$. Assume $X_n$ are i.i.d. such that $1/X_0$ is gamma-distributed with scale parameter 1 and shape parameter $\theta$. Assume the two families of random variables are independent. Then $\{\overline{X}_n:n\in \mathbb {Z}\}$, defined by (4.10), has the same distribution as $\{X_n:n\in \mathbb {Z}\}$.

Proof

Let $Y'_0$ be independent of $\{X_n,V_n:n\in \mathbb {Z}_+\}$ with $1/Y_0'$ being gamma-distributed with scale parameter 1 and shape parameter $\rho -\theta$. Define $\{Y_n':n\in \mathbb {N}\}$ and $\{\overline{X}'_n:n\in \mathbb {Z}_+\}$ inductively using

$$\begin{aligned} Y'_{n+1}=1+V_nX_n^{-1}Y_n\quad \text {and}\quad \overline{X}_n'=V_{n+1}(1+V_n^{-1}X_n/Y_n'). \end{aligned}$$

The Burke property [29, Theorem 3.3] tells us that $\{(Y'_{m+n},\overline{X}'_{m+n},X_{m+n},V_{m+n}):n\in \mathbb {Z}_+\}$ has the same distribution for all $m\in \mathbb {Z}_+$ and that $\{\overline{X}'_n:n\in \mathbb {Z}_+\}$ has the same distribution as $\{X_n:n\in \mathbb {Z}_+\}$.

Using Kolmogorov’s extension theorem we can extend the above random variables to a family $\{(Y'_n,\overline{X}'_n,X_n,V_n):n\in \mathbb {Z}\}$. In particular, the distribution of $\overline{X}'$ is the same as that of the process X and $Y'$ and $\overline{X}'$ satisfy the above induction for all $n\in \mathbb {Z}$.

By the uniqueness in Lemma 4.3, $Y'$ must equal the process Y defined by (4.6), which then implies that $\overline{X}'$ is the same as $\overline{X}$ defined by (4.10). The claim now follows because we already established that $\overline{X}'$ has the same distribution as X. $\square$

5 Proof of Theorems 3.1 and 3.5

Fix an i.i.d. probability measure $\mathbb {P}_0$ on $(\varOmega _0,\mathcal {F}_0)$ with $L^1$ weights. Let $\mathbb {P}$ be a stationary future-independent $L^1$ corrector distribution with $\varOmega _0$-marginal $\mathbb {P}_0$. Let $X_n=e^{B(ne_1,(n+1)e_1)}$, $Y_n=e^{B(ne_1,ne_1+e_2)-\omega _{ne_1+e_2}}$, and $V_n=e^{\omega _{ne_1+e_2}}$, $n\in \mathbb {Z}$. Future independence implies the two processes X and V are independent of each other. Let ${{\,\mathrm{\mathcal {I}}\,}}$ be the invariant $\sigma$-algebra for the process (X, V). Let $\mu$ be the distribution of $A=\{\log X_n:n\in \mathbb {Z}\}$. Let $M_0=\mathbb {E}[\omega _0]=\mathbb {E}[\log V_0]$. Recovery (f) implies that $B(0,e_1)>\omega _{e_1}$ and hence $\mathbb {E}[\log A_0\,|\,{{\,\mathrm{\mathcal {I}}\,}}]=\mathbb {E}[B(0,e_1)\,|\,{{\,\mathrm{\mathcal {I}}\,}}]>\mathbb {E}[\omega _0]$. In particular, $\alpha ={{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\cdot e_1=\mathbb {E}[B(0,e_1)]>M_0$.

Lemma 5.1

There exists a Borel-measurable map $F:\mathbb {R}^\mathbb {Z}\times \mathbb {R}^{\mathbb {Z}\times \mathbb {N}}\rightarrow \mathbb {R}^{\mathbb {Z}^2\times \mathbb {Z}^2}$ such that $\mathbb {P}$-almost surely,

$$\begin{aligned}&\{B(x,y,\omega ):x,y\in \mathbb {Z}\times \mathbb {Z}_+\}\\&\qquad =F\bigl (\{B(ne_1,(n+1)e_1):n\in \mathbb {Z}\},\{\omega _{ne_1+ke_2}:n\in \mathbb {Z},k\in \mathbb {N}\}\bigr ). \end{aligned}$$

Proof

Lemma 4.1 implies that Y satisfies (4.4). Since it is a stationary almost surely finite process, Lemma 4.3 implies that Y has the representation (4.6). Then the second equation in (4.1) says that $e^{B(ne_1+e_2,(n+1)e_1+e_2)}$ is equal to $\overline{X}_n$, defined by (4.10). This argument shows that the process $\{B(ne_1,ne_1$$+ e_2),B(ne_1+e_2,(n+1)e_1+e_2):n\in \mathbb {Z}\}$ is a measurable function of $\{B(ne_1,(n+1)e_1):n\in \mathbb {Z}\}$ and $\{\omega _{ne_1+e_2}:n\in \mathbb {Z}\}$.

Since $\mathbb {P}$ is stationary, we have that $\overline{A}=\{\log \overline{X}_n:n\in \mathbb {Z}\}$ has the same distribution $\mu$ as A. In other words, $\varPhi (\mu )=\mu$. This lets us repeat the above procedure inductively to get that $\{B(x,x+e_i):x\in \mathbb {Z}\times \mathbb {Z}_+,i=1,2\}$ is a measurable function of $\{B(ne_1,(n+1)e_1):n\in \mathbb {Z}\}$ and $\{\omega _{ne_1+ke_2}:n\in \mathbb {Z},k\in \mathbb {N}\}$. We also have $B(x+e_i,x)=-B(x,x+e_i)$, $\mathbb {P}$-almost surely. Then the cocycle property (e) implies that for $x,y\in \mathbb {Z}\times \mathbb {Z}_+$, B(x, y) is the sum of $B(x_k,x_{k+1})$ along any path with steps $\{\pm e_1,\pm e_2\}$ from x to y. The claim of the lemma follows. $\square$

Corollary 5.2

If $\mathbb {P}'$ is a stationary future-independent $L^1$ corrector distribution with $\varOmega _0$-marginal $\mathbb {P}_0$ and the distributions of $\{B(ne_1,(n+1)e_1):n\in \mathbb {Z}\}$ under $\mathbb {P}'$ and $\mathbb {P}$ match, then $\mathbb {P}'=\mathbb {P}$.

Proof

Lemma 5.1 implies that the distributions of $\{B(x,y):x,y\in \mathbb {Z}\times \mathbb {Z}_+\}$ under $\mathbb {P}$ and $\mathbb {P}'$ match. Then stationarity of the two probability measures implies $\mathbb {P}=\mathbb {P}'$. $\square$

Proof of Theorem 3.1

As was mentioned in the proof of Lemma 5.1, $\mu$ is a fixed point of $\varPhi$. Corollary 4.7 says that there exists at most one ergodic such $\mu$. Corollary 5.2 thus implies that there exists at most one $T_{e_1}$-ergodic $\mathbb {P}$. Switching $e_1$ and $e_2$ around in the definitions of X and Y we get the same result for the $T_{e_2}$ shift. $\square$

Proof of Theorem 3.5

Theorem 4.4 and Lemma 4.5(c) in [19] imply that $n^{-1}B(0,ne_1)$ converges almost surely to ${{\,\mathrm{\mathbf {m}}\,}}_\mathbb {P}\cdot e_1$. Since $B(0,ne_1)=\sum _{m=0}^{n-1}A_m$ we have that (4.16) holds and Lemma 4.8 says that $\mu$ is ergodic. Corollary 5.2 says $\mathbb {P}$ is determined by $\mu \otimes \varGamma ^{\otimes (\mathbb {Z}\times \mathbb {Z}_+)}$. Since this is a product of an ergodic measure and a product measure, it is ergodic. Ergodicity of $\mathbb {P}$ under the $T_{e_1}$ shift follows. A symmetric argument gives the ergodicity under the $T_{e_2}$ shift. $\square$