The High Temperature Crossover for General 2D Coulomb Gases

Abstract

We consider N particles in the plane, influenced by a general external potential, that are subject to the Coulomb interaction in two dimensions at inverse temperature $\beta$. At large temperature, when scaling $\beta =2c/N$ with some fixed constant $c>0$, in the large-N limit we observe a crossover from Ginibre’s circular law or its generalisation to the density of non-interacting particles at $\beta =0$. Using Ward identities and saddle point methods we derive a partial differential equation of generalised Liouville type for the crossover density. For radially symmetric potentials we present some asymptotic results and give examples for the numerical solution of the crossover density. These findings generalise previous results when the interacting particles are confined to the real line. In that situation we derive an integral equation for the resolvent valid for a general potential as well, and present the analytic solution for the density in the case of a Gaussian plus logarithmic potential.

1 Introduction and Main Results

Particle systems that interact logarithmically—the Coulomb repulsion in two dimensions (2D)—and that are subject to a confining potential, at temperature T parametrised by $\beta ^{-1}=k_BT$, enjoy an intimate relationship with Random Matrix Theory, see e.g., [31, 32]. Here, one has to distinguish two cases.

When the N particles are constrained to the one-dimensional real line (1D) or a subset of it, such systems can be realised as eigenvalues of random $N\times N$ matrices whose entries follow a Gaussian or more general distribution. In that case, the inverse temperature $\beta$ takes the specific values 1, 2 and 4 for self-adjoint matrices with real, complex or quaternionic entries, and we refer to [46] for a discussion of these classical Gaussian ensembles. For general $\beta >0$—the so-called $\beta$-ensembles—other realisations exist, such as tri-diagonal matrices [27] or in terms of Dyson’s Brownian motion [3], generalising Dyson’s original proposal [29] for $\beta =1,2$, see also [5] for an invariant realisation. While for large N on a global scale, the limiting spectral density is given by Wigner’s semi-circle for all $\beta >0$ for ensembles with Gaussian potential, on a local scale the statistics strongly depends on $\beta$. For the classical ensembles the local statistics of particles (or eigenvalues) is very well understood and known to be universal, (see e.g., [1, Chap. 6]), whereas progress for $\beta$-ensembles has been rather recent, cf. [15, 16, 56]. For general $\beta$ the statistics can be described in terms of different stochastic differential operators in the bulk and at the edges, and we refer to [49, 54, 55].

Turning to the case when the particles move into the plane, thus representing a true 2D Coulomb gas, much less is known for general $\beta >0$. First, for matrices with complex Gaussian entries without further symmetry—the complex Ginibre ensemble—the corresponding complex eigenvalues yield a standard Coulomb gas at $\beta =2$. For real or quaternionic matrix entries one obtains point processes of Pfaffian type [30, 35, 44] that differ from the standard 2D Coulomb gas at $\beta =1$ or 4¹. Only normal random matrices with complex or quaternionic entries provide realisations at $\beta =2$ and 4, see e.g., [22] and [37], respectively. The eigenvalue statistics of complex normal and complex Ginibre matrices happen to agree, but not their eigenvector statistics [21]. Again, on a global scale the limiting spectral density is given by Girko’s circular law for all $\beta >0$ for a Gaussian potential. Relatively little is known about the local statistics beyond $\beta =2$. Only at the particular value $\beta =2$ the point process is determinantal, and local universality has been shown for invariant (see e.g.,[2, 9, 12, 36, 39]) and Wigner ensembles [53]. For general $\beta$ the low temperature limit corresponding to $\beta \gg 1$ is subject of ongoing research (see e.g.,[7]), due to the conjectured condensation on the so-called Abrikosov lattice, and we refer to [52] for a recent review and references. For other mechanisms of spontaneous symmetry breaking see [24].

Recently, the opposite high temperature limit $\beta \rightarrow 0$ has been studied for $\beta$-ensembles with real [3, 5, 28] or real positive eigenvalues [4]. Here, $\beta$ is not kept fixed in the large-N limit, and a different scaling $\beta =\frac{2c}{N}$ with a constant $c\in (-1,\infty )$, was identified in [3]. There, for a Gaussian potential the solution for the limiting global density $\rho _c(x)$ was given in terms of parabolic cylinder functions and was shown to interpolate between Wigner’s semi-circle distribution at large $c\gg 1$ and a Gaussian one at $c=0$. Furthermore, allowing for a weakly attracting interaction $c<0$ that can lead to a condensation of eigenvalues, it is believed [3] to converge towards a Dirac delta when $c\downarrow -1$.

In this article we will study the corresponding limit for genuine 2D Coulomb gases in the plane, with a general confining potential. The possibility of taking such a limit, leading to a crossover between the circular law and a Gaussian density for a Gaussian potential, was already mentioned in [13, 20]. We will find an extended parameter range $c\in (-2,\infty )$ compared to 1D, with convergence to a Dirac delta when $c\downarrow -2$. The latter was already observed and in fact proven for a Gaussian plus linear potential in [18, 19]. There, the limiting behaviour of so-called vortex systems in the plane was analysed and the existence of a solution for the limiting global density was shown. The fact that both for $d=1,2$ dimensions a lower bound for $c>-d$ exists, follows from the requirement of the finiteness of the partition function.

Before giving more details let us summarise our main results and the methods used. We first derive an integral equation valid for a finite number of N particles in 2D, that relates the 1- and 2-point correlation functions among these, see Theorem 1. It is shown to follow from Ward identities also called loop-equations, and the same statement can be formulated in 1D. When scaling $\beta =\frac{2c}{N}$ we use heuristic saddle point methods in the large-N limit to derive a non-linear differential equation for the limiting global density of particles $\rho _c$, formulated in (11) in Theorem 2. This technique illuminates the order of the contributions from energy, entropy and self-energy as functions of N, $\beta$ and dimension. The same result follows from Theorem 1 when assuming factorisation of correlation functions. Asymptotic features of the solution of (11) for radially symmetric potentials as well as examples for numerical solutions thereof are presented. In 1D we slightly generalise the results of [3] to general potentials and present an analytic solution for the corresponding density for a Gaussian plus logarithmic potential.

Let us set the stage for the 2D Coulomb gas. We study an ensemble of N charged particles in the plane, that interact logarithmically under the influence of an external confining potential Q. Labelling the particle’s positions in the plane by $\varvec{\zeta }=(\zeta _1, \ldots ,\zeta _{N}) \in \mathbb {C}^N$, the associated Gibbs measure at inverse temperature $\beta$ is given by

$$\begin{aligned} \displaystyle d\mathbf {P}_N(\varvec{\zeta })= p_N (\varvec{\zeta })\prod _{j=1}^{N}dA(\zeta _j)\ ,\ \ \ p_N (\varvec{\zeta })= \frac{1}{ Z_N} \prod _{j>k=1}^N |\zeta _j-\zeta _k|^{\beta } e^{-m\sum _{j=1}^N Q(\zeta _j)} . \end{aligned}$$

(1)

Here, dA is the area measure (i.e., 2-dimensional Lebesgue measure divided by $\pi$), $p_N (\varvec{\zeta })$ is the joint density of particles, and $Z_N$ stands for the normalising partition function. The choice of the scaling parameter m, that may depend on N and $\beta$, determines the limiting behaviour of our ensemble. In order to distinguish it from N counting the number of particles, and to emphasise the analogy to the semi-classical expansion, several authors call m an “inverse Planck constant” $1/\hbar$, see e.g. [57]². Throughout this article, we assume that Q is smooth and sufficiently large near infinity (e.g., $Q(z) -\log |z|^2\rightarrow \infty$ as $|z|\rightarrow \infty$), so that $Z_N < \infty$.

The quantities determining the system $\varvec{\zeta }=\{ \zeta _j\}^{n}_{j=1}$ are the following k-point correlation functions defined as the expectation values $\mathbf {E}_N$ with respect to the Gibbs measure (1):

$$\begin{aligned} R_{N,k}(z_1,\ldots ,z_{k}):= N^k\ \mathbf {E}_N\left( \prod _{j=1}^k\rho _N(z_j)\right) \ , \quad \text {for}\quad k=1,\ldots , N\ , \end{aligned}$$

(2)

when all arguments are mutually distinct, $z_i\ne z_j$, $\forall i,j=1,\ldots ,k$, and zero for any pair of arguments coinciding. Here,

$$\begin{aligned} \rho _N(z)=\frac{1}{N} \sum _{j=1}^N \delta (z-\zeta _j) \end{aligned}$$

(3)

is the normalised counting function. We remark that once properly normalised, the $R_{N,k}(z_1,\ldots ,z_{k})$ can be interpreted as the probability to find k particles at given positions $z_1,\ldots ,z_{k}$.

We are now ready to state our first result valid at finite-N.

Theorem 1

Given Gibbs measure (1) with a $C^2$-smooth potential Q, the following relation between 1- and 2-point correlation functions holds for every finite N:

$$\begin{aligned} \frac{\beta }{2} \int _{\mathbb {C}} \frac{R_{N,2}(\zeta ,\eta ) }{\zeta -\eta } dA(\eta )= m(\partial _\zeta Q(\zeta )) R_{N,1}(\zeta ) + \partial _\zeta R_{N,1}(\zeta ). \end{aligned}$$

(4)

Equation (4) can be used as a starting point for a systematic expansion in the large-N limit, cf. [57] for earlier work. While we will use Ward identities to prove it, alternatively Itô’s stochastic calculus could be used, under slightly stronger assumptions. Let us introduce the connected 2-point correlation function

$$\begin{aligned} R_{N,2}^\mathrm{conn}(\zeta ,\eta ) := R_{N,2}(\zeta ,\eta ) -R_{N,1}(\zeta ) R_{N,1}(\eta )\ . \end{aligned}$$

(5)

For a non-vanishing $R_{N,1}(\zeta ) \ne 0$ we can then rewrite Eq. (4) as follows

$$\begin{aligned} \frac{\beta }{2} \int _{\mathbb {C}} \frac{R_{N,1}(\eta ) -B_N(\zeta ,\eta )}{\zeta -\eta } dA(\eta ) = m\partial _\zeta Q(\zeta )+ \partial _\zeta \log [R_{N,1}(\zeta )]\ . \end{aligned}$$

(6)

Here, $B_{N}(\zeta ,\eta ) :=-{R_{N,2}^\mathrm{conn}(\zeta ,\eta ) }/{R_{N,1}(\zeta )}$ is defined such that it corresponds to the Berezin–kernel at $\beta =2$. While this is a well-studied object at $\beta =2$, little is known for general $\beta >0$, see however some remarks in [9]. In order to arrive at the mean field Eq. (11) below, that determines the limiting density in the particular large-N limit that we consider, we would have to show that the connected 2-point function (5) is sub-leading. This is equivalent to show the factorisation of the 2-point function on the global level—a property sometimes called mean field or propagation of chaos [18]—and we expect it to hold up to order $O(N^{-2})$, from the experience with 1D at $\beta =1,2,4$ [6, 40].

Let us turn to the large-N behaviour of (1) in the high temperature regime $\beta \rightarrow 0$. It is clear that this regime implies weaker correlations among particles. In the extreme case $\beta \equiv 0$, the particles become independent from each other, their k-point correlation functions trivially factorise and become proportional to $\prod _{j=1}^k e^{-Q(\zeta _j)}$, normalised with respect to the area measure. Our main purpose in this paper is to investigate the crossover phenomenon between fixed and vanishing $\beta$. For instance, in the case of a Gaussian potential $Q(\zeta )=|\zeta |^2$, we study the smooth interpolation between Ginibre’s circular law and the Gaussian distribution. The possibility of such a crossover regime was already mentioned in [13]. The precise scaling we have to impose in (1) is to set

$$\begin{aligned} m=1\quad \text {and} \quad \beta =\frac{2c}{N} \quad \text {for fixed} \quad c\in (-2,\infty ). \end{aligned}$$

(7)

Here, c is kept fixed when $N\rightarrow \infty$, and we can allow for a weakly attracting interaction with negative c as well. The same scaling (7) was found on the real line in one dimension [5], with fixed $c\in (-1,\infty )$.

On the other hand, for the more standard scaling

$$\begin{aligned} m=\frac{\beta }{2} \, N, \end{aligned}$$

(8)

Chafaï, Hardy and Maïda showed on a non optimal scale, using concentration of measure in Wasserstein distance, that if $\beta$ is bigger than $\beta _0 \log N/N$ for some constant $\beta _0$, there is no such crossover phenomenon, and the limiting global density follows from (15) below, see [20]. We expect from the saddle point method that as long as $1/m=o(1)$ this remains true. In the following we will keep $\beta$ fixed when taking the scaling limit (8).

In Sect. 3, we will heuristically calculate the free energy functional$F[\rho ]$ in terms of the probability density function $\rho$, that is associated to the Gibbs measure (1). Here, we will utilise the saddle point method in the large-N limit. In the high temperature regime (7) we obtain the following formula

$$\begin{aligned} \begin{aligned} F\equiv F_c[\rho ]&= \int _{\mathbb {C}} Q(\zeta ) \rho (\zeta ) dA(\zeta )-c \int _{\mathbb {C}^2} \log |\zeta -\eta | \rho (\zeta ) \rho (\eta ) dA(\zeta ) dA(\eta )\\&\quad +\,\int _{\mathbb {C}} \rho (\zeta ) \log \rho (\zeta ) dA(\zeta ). \end{aligned} \end{aligned}$$

(9)

While the first line can be easily seen to follow from the energy in (1), the second line is the so-called entropy contribution. The saddle point condition

$$\begin{aligned} 0=\frac{\delta F_c[\rho ] }{\delta \rho (\zeta )}=Q(\zeta ) -2c \int _{\mathbb {C}} \log |\zeta -\eta | \rho (\eta )dA(\eta )+\log \rho (\zeta )+1\ , \end{aligned}$$

(10)

is imposed in order to extremise the free energy. Whether it is a minimum or a maximum is determined by a second functional derivative of $F_c[\rho ]$. Equation (10) has the limiting density $\rho _c(\zeta )=\lim _{N\rightarrow \infty }\frac{1}{N} R_{N,1}(\zeta )$ as its solution. Applying the Laplace operator $\varDelta =\partial {\bar{\partial }}$ to (10) and using that its Green’s function is the logarithm, we obtain that the crossover density $\rho _c$ satisfies (11) below. This leads us to propose the following extension of [18, Theorem 6.1] for a general potential.

Theorem 2

The limiting density function $\rho _c$ minimises (resp., maximises) the free energy functional $F_c[\rho ]$ given in (9) for $c>0$ (resp., $<0$), and solves the following mean field equation:

$$\begin{aligned} 0 = \varDelta Q(\zeta )-c \, \rho _c(\zeta ) + \varDelta \log \rho _c(\zeta ). \end{aligned}$$

(11)

We wish to emphasise that we currently do not have a complete proof for this statement. However, if the factorisation or mean field property of the 2-point correlation function (5) holds, in the sense that for any continuous, bounded function $f(\zeta ,\zeta ')$ on $\mathbb {C}^2$,

$$\begin{aligned} \begin{aligned} \lim _{N \rightarrow \infty } \frac{1}{N^2}\int _{\mathbb {C}^2} f(\zeta ,\zeta ') R_{N,2}(\zeta ,\zeta ') dA(\zeta ) dA(\zeta ')= \int _{\mathbb {C}^2} f(\zeta ,\zeta ')\rho _c(\zeta ) \rho _c(\zeta ') dA(\zeta ) dA(\zeta '), \end{aligned} \end{aligned}$$

(12)

the mean field equation (11) follows from (4) in Theorem 1. Namely, imposing the scaling (7) on (4) and normalising the 1-point function $R_{N,1}(\zeta )$ by $\frac{1}{N}$, the anti-holomorphic derivative ${\bar{\partial }}_{\zeta }$ of the limit of (4) directly leads to (9), when neglecting the contribution from the limit of $B_N$ in the sense of (12). For the minimising (maximising) property we only have heuristic arguments.

Remark 1

For the choice of potential

$$\begin{aligned} Q(z) \equiv Q_N(z):=\lambda |z|^2+\frac{1}{2N} \left( \eta \bar{z} + \bar{\eta } z \right) , \quad \text {with fixed} \quad \lambda >0,\ \eta \in \mathbb {C}, \end{aligned}$$

(13)

the joint distribution (1) can be identified with the system of stationary states of N vortices in the plane, cf [18]. In [18, Theorem 6.1] in the limit (7) (using different conventions for our constant c) the free energy functional of vortices (9) was rigorously derived for potential (13). The mean field equation (11) for this potential was proven, including the existence and the minimising (maximising) property for $c>0(<0)$ of its solution. The authors also showed convergence towards the Dirac measure in the limit $c\downarrow -2$, see [19].

We now compare the above free energy (9) and resulting mean field equation (11) to the standard large-N scaling limit (8), which is well understood, see [52] for a recent review. Here, only the first line in (9) will contribute in this limit, leading to the weighted-logarithmic energy functional

$$\begin{aligned} F[\rho ]= \int _{\mathbb {C}} Q(\zeta ) \rho (\zeta ) dA(\zeta )-\int _{\mathbb {C}^2} \log |\zeta -\eta | \rho (\zeta ) \rho (\eta ) dA(\zeta ) dA(\eta )\ , \end{aligned}$$

(14)

and under some regularity and growth assumptions on Q, the one particle distribution $\rho$ weakly converges toward the equilibrium measure minimising $F[\rho ]$, see e.g. [48, 51]. Moreover, by standard logarithmic potential theory

$$\begin{aligned} 0= \varDelta Q(\zeta ) -\rho (\zeta ) \end{aligned}$$

(15)

is valid on the limiting support of the measure S which has to be compact and is called the droplet. For Gaussian potential $Q(z)=|z|^2$ for example, this gives the circular law, with a constant density on the unit disc. Note that (15) also can be obtained from (14) by requiring a saddle point condition as in (10). We emphasize that the standard choice of scaling (8) makes the droplet and density $\rho$ independent of the inverse temperature $\beta$. Notice that in our derivation under the scaling (7) we do not make any assumption about the compactness of the support, see also [18]. For the saddle point method in 1D using the resolvent see however the discussion in Sect. 3.3.

We turn to the discussion of features of the solution of the mean field equation (11). Defining $\psi _c := \log \rho _c$, it is rewritten as follows

$$\begin{aligned} c \, e^{\psi _c(\zeta )} = \varDelta Q(\zeta )+\varDelta \psi _c(\zeta ) , \end{aligned}$$

(16)

which is a differential equation of generalised Liouville type. In case that $\varDelta Q \equiv 0$ would hold, the Eq. (16) reduces to the standard Liouville equation whose explicit solutions are well-known, see e.g., [23]. However, also in view of the result (15) in the standard scaling limit, we cannot assume that $\varDelta Q$ is small or even negligible in any sense. For that reason we have been unable to provide an explicit solution for (11), or equivalently (16), even in the Gaussian case. We are unaware of a deeper relation between Liouville’s equation and Dyson’s Brownian motion in general in 2D. However, let us mention [25] where methods from Gaussian multiplicative chaos were utilised in the renormalisation of Liouville quantum gravity.

Let us discuss now several special cases. For the choice of a radially symmetric potential we can provide the asymptotic behaviour of the limiting density for large $r=|z|$. In this case we can explicitly check the interpolating property of the solution to (11) in the limits $c\rightarrow 0$ and $c\gg 1$, as we will further exemplify for monic so-called Freud potentials, that are a special case of Mittag–Leffler potentials named in [10]. In addition, we will present two examples for a numerical solution of (11), for a Gaussian and quartic monic potential.

1.1 Radially Symmetric Potentials

Suppose that the external potential is radially symmetric, i.e., there exists a function $f: \mathbb {R}_+ \rightarrow \mathbb {R}$ satisfying

$$\begin{aligned} f(r) = f\Big (\sqrt{x^2+y^2}\Big ) := Q(z), \quad \text {with}\quad z=x+iy. \end{aligned}$$

(17)

Let us denote the radial part of crossover density $\rho _c$ by

$$\begin{aligned} g_c(r)= g_c\Big (\sqrt{x^2+y^2}\Big ):= \frac{1}{\pi }\,\rho _c(z)\ . \end{aligned}$$

(18)

Here, the factor $1/\pi$ comes from the fact that $\rho _c(z)$ is a density function with respect to the area measure. By definition, we have

$$\begin{aligned} \int _{0}^{\infty } r \, g_c(r) dr=\frac{1}{2\pi } \end{aligned}$$

(19)

for the normalisation. Notice that the 2D Laplace operator $\varDelta$ acts on the radial density as

$$\begin{aligned} \varDelta =\frac{1}{4}\left( \partial _x^2+\partial _y^2\right) = \frac{1}{4} \left( \partial _r^2+\frac{1}{r} \partial _r \right) . \end{aligned}$$

(20)

Combining (11) and (20), we obtain following ordinary differential equation for the radial crossover density:

$$\begin{aligned} 4\pi c \, g_c(r)=f''(r)+\frac{1}{r} \, f'(r) + \frac{g''_c(r)g_c(r)-\left( g'_c(r) \right) ^2}{g_c(r)^2}+\frac{1}{r}\,\frac{ g'_c(r)}{g_c(r)}\ , \end{aligned}$$

(21)

where we have put the density on the left-hand side. The asymptotic behaviour of $g_c$ for large radii,

$$\begin{aligned} g_c(r)=r^{2c}e^{-f(r)+o(\log r)}, \quad \text {as} \quad r\rightarrow \infty \ , \end{aligned}$$

(22)

can be easily seen. Multiplying (21) by r and integrating it using the normalisation (19), we obtain

$$\begin{aligned} 2c=\left[ rf'(r)+r\left( \log g_c(r)\right) '\right] _0^\infty \ , \end{aligned}$$

(23)

from which (22) follows. In fact the function $r^{2c}e^{-f(r)}$ solves the “homogeneous” equation (21), where the left-hand side is set to zero. However, due to the non-linearity of the equation, the solution is not given by this “homogeneous” solution plus a special solution.

Example

A particular realisation of a rotationally invariant potential is given by the monomials, so-called Freud or Mittag–Leffler potentials (cf. [10])

$$\begin{aligned} Q(z)= \frac{1}{2} |z|^{2\alpha }, \quad \alpha \ge 1. \end{aligned}$$

(24)

In this case we obtain for r times (21)

$$\begin{aligned} 4\pi c \, r \, g_c=2\alpha ^2 r^{2\alpha -1} +\left( r \, (\log g_c)'\right) '. \end{aligned}$$

(25)

Note that for these homogeneous potentials, the different scalings of the ensemble (1), $m=\beta N/2$ and $m=1$, can be related by simple rescaling of the point particles. Therefore, by (15), it is easy to calculate the radial density in the limit when $c \rightarrow \infty$. As a result, the extremal cases of the solutions of (11) including their normalisations are given by

$$\begin{aligned} g_c(r)\sim {\left\{ \begin{array}{ll} \displaystyle \frac{1}{\pi \, 2^{1/\alpha }\, \varGamma (1+1/\alpha )} \, \exp \left( -\frac{1}{2}\, r^{2\alpha }\right) &{}\text {as} \quad c \rightarrow 0; \\ \displaystyle \frac{\alpha ^2}{2\pi c} \, r^{2\alpha -2}\, \mathbb {1}_{[0,(2c/\alpha )^{1/2\alpha }]}&{}\text {as} \quad c \rightarrow \infty . \end{array}\right. } \end{aligned}$$

(26)

These are of course just special cases for $g_c(r)\sim e^{-f(r)}$ for $c\rightarrow 0$ and $g_c(r)\sim \varDelta f(r) \mathbb {1}_S$ for $c\rightarrow \infty$ on the corresponding droplet S.

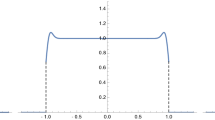
We present now two examples for numerical solutions of (25) at specific values of c. In Fig. 1 below the case $\alpha =1$ of a Gaussian and in Fig. 2 of a quartic potential with $\alpha =2$ are shown. We obtain the numerical solutions not only for positive c but also for negative c. The conjecture is that as c goes to its critical (negative) value $-2$, the ensemble collapses at the origin, i.e., the one particle density converges towards a Dirac delta. While for $\alpha =1$ this is known [19] we observe that a similar behaviour occurs for $\alpha =2$.

Fig. 1

The numerical solution for our interpolating radial density $g_c(r)$ in 2D (full blue line) of our mean field equation (25) is shown for the Gaussian potential $Q(z)=|z|^2/2$, with parameter c decreasing from $c=200$ to $c=-1.9$. What is also shown is the limiting circular law from (26) for large c (two top plots, dotted lines) as well as the limiting Gaussian density (dashed orange lines) for $c=0$. Note that the normalisation is with respect to the radial measure $2\pi \,r$ in 2D, see (19). For that reason the area under the curves does not agree

Fig. 2

The same plots as in Figure 1 are shown for a quartic potential $Q(z)=|z|^4/2$. Here, for large c the limiting circular law is replaced by a parabola, and for $c=0$ the Gaussian by $e^{-r^4/2}$, see (26). The approach to the conjectured Dirac delta looks similar to the previous figure at $c=-1.9$

The remainder of this article is organised as follows. Section 2 is devoted to the proof of Theorem 1 using Ward identities. In Sect. 3, we will introduce the saddle point method in a heuristic way. In Sect. 3.1 the two different scalings (7) and (8) leading to the respective free energies (9) and (14) will become evident. This leads to the different mean field equations in 2D given above as shown in Sect. 3.2. In Sect. 3.3 in the 1D case we derive a mean field equation for the resolvent for a general potential, slightly generalising [3].

For completeness we also illustrate the example in 1D for a Gaussian plus logarithmic potential from Sect. 3.3

$$\begin{aligned} V_a(x)= \frac{1}{2} x^2-a\log |x|\ , \quad a>-1\ , \end{aligned}$$

(27)

in Figs. 3, 4 and 5. The associated resolvent equation can be solved, following [4] closely. The resulting interpolating density $\rho _c(\lambda )$ is then given by Kummer’s (confluent) hypergeometric function, see (70), with special cases shown below.

Fig. 3

The plot displays the interpolating density $\rho _c(\lambda )$ in 1D against $\lambda \in \mathbb {R}$. It is illustrating the analytic result (70) for $a=\frac{1}{2}$ with parameter c decreasing from $c=10$ to $c=-0.9$. The figure indicates the logarithmic repulsion at the origin. For large c the density converges to the semi-circle and this repulsion only becomes visible on a local scale. Here and below in Fig. 5 the normalisation constant of the density is determined numerically. The convergence to the conjectured Dirac delta at $c=-1$ is also visible

Fig. 4

The same plot as in Fig. 3 for $a=0$, reproducing the findings of [3]. It shows the progressive transition from Wigner’s semi-circle ($c=\infty$) through the Gaussian distribution ($c=0$) to the conjectured Dirac delta ($c=-1$)

Fig. 5

The same plot as in Fig. 3 for $a=-\frac{1}{2}$, representing a logarithmic attraction towards the origin

2 Ward Identities and Proof of Theorem 1

In this section, we discuss Ward identities for 2D Coulomb gases. They have been utilised already to derive the equation for the density function (15) for 2D Coulomb gases, with standard scaling (8), see [57] and [1, Chap. 39]. We adapt the proof presented in [8, 9] to derive the appropriate Ward identity for the 2D Coulomb gas distributed according to (1). For an alternative proof using so-called integration by parts see also [10, 11], and for the general form of Ward identities we refer the reader to [42, Appendix 6]. The proof for the Ward identities in 1D follows along the very same lines, leading the Eq. (4) without factor 1 / 2 on the left hand side, and we will not give further details here.

For a test function $\psi \in C_0^\infty (\mathbb {C})$ and $\varvec{\zeta }=(\zeta _1, \ldots , \zeta _N)$, let us denote

$$\begin{aligned} \begin{aligned} \mathrm{I}_N[\psi ](\varvec{\zeta })&=\frac{1}{4} \sum _{j,k:j\ne k}^N \frac{\psi (\zeta _{j})-\psi (\zeta _{k})}{\zeta _{j}-\zeta _{k}},\\ \mathrm{II}_N[\psi ](\varvec{\zeta })&= m\sum _{j=1}^{N} \partial Q(\zeta _j) \psi (\zeta _{j}),\\ \mathrm{III}_N[\psi ](\varvec{\zeta })&= \sum _{j=1}^N \partial \psi (\zeta _{j}), \end{aligned} \end{aligned}$$

(28)

and define Ward’s (stress energy) functional $W_N^+$ as

$$\begin{aligned} W_N^+[\psi ]= \beta \, \mathrm{I}_N[\psi ]- \mathrm{II}_N[\psi ]+\mathrm{III}_N[\psi ]. \end{aligned}$$

(29)

From now on, we write $\mathbf {E}_N$ for the expectation with respect to (1). We first prove the following form of Ward’s identity:

Lemma 1

For the definitions (28) and (29) the following expectation value holds:

$$\begin{aligned} \mathbf {E}_N W_N^+[\psi ]=0. \end{aligned}$$

(30)

Proof

By definition, the partition function $Z_N$ is given as

$$\begin{aligned} Z_N= \int _{\mathbb {C}^N} \exp \left[ \beta \sum _{j > k=1}^N \log |\eta _{j}-\eta _{k}| - m\sum _{j=1}^{N} Q(\eta _{j}) \right] \prod _{j=1}^{N}dA(\eta _j). \end{aligned}$$

For a fixed sequence $\varvec{\zeta }=(\zeta _1,\ldots ,\zeta _N)$ and a positive constant $\varepsilon$, let us denote

$$\begin{aligned} \varvec{\eta } := (\eta _1, \ldots , \eta _N), \quad \eta _{j}:=\zeta _j+\frac{\varepsilon }{2}\psi (\zeta _{j}). \end{aligned}$$

(31)

Then as $\varepsilon \rightarrow 0$, we have

$$\begin{aligned} \log |\eta _{j}-\eta _{k}|= \log |\zeta _{j}-\zeta _{k}|+\frac{\varepsilon }{2} \mathrm {Re}\, \frac{\psi (\zeta _{j})-\psi (\zeta _{k})}{\zeta _{j}-\zeta _{k}}+ O(\varepsilon ^2), \end{aligned}$$

thus leading to

$$\begin{aligned} \beta \sum _{j> k=1}^N \log |\eta _{j}-\eta _{k}|= \beta \sum _{j >k=1}^N \log |\zeta _{j}-\zeta _{k}|+\varepsilon \beta \, \mathrm {Re}\, \Big [ \mathrm{I}_N[\psi ](\varvec{\zeta }) \Big ]+O(\varepsilon ^2). \end{aligned}$$

Since we assume that Q is $C^2$-smooth, we have

$$\begin{aligned} m\sum _{j=1}^{N} Q(\eta _{j})=m\sum _{j=1}^{N} Q(\zeta _{j})+\varepsilon \mathrm {Re}\, \Big [ \mathrm{II}_N[\psi ](\varvec{\zeta }) \Big ]+O(\varepsilon ^2). \end{aligned}$$

Note that due to the fact that the Jacobian of (31) is given as

$$\begin{aligned} dA(\eta _{j})&=\left( \left| 1+\frac{\varepsilon }{2}\partial \psi (\zeta _{j}) \right| ^2- \left| \frac{\varepsilon }{2}{\bar{\partial }}\psi (\zeta _{j}) \right| ^2 \right) dA(\zeta _{j})\\&= \Big ( 1+\varepsilon \mathrm {Re}\, \partial \psi (\zeta _{j})+O(\varepsilon ^2) \Big ) dA(\zeta _{j}), \end{aligned}$$

we have

$$\begin{aligned} \prod _{j=1}^{N}dA(\eta _j)= \left( 1+\varepsilon \mathrm {Re}\, \Big [ \mathrm{III}_N[\psi ](\varvec{\zeta }) \Big ]+O(\varepsilon ^2) \right) \prod _{j=1}^{N} dA(\zeta _j). \end{aligned}$$

Combining all the above equations, we obtain

$$\begin{aligned} Z_N =\int _{\mathbb {C}^n} \prod _{j>k=1}^N |\zeta _j-\zeta _k|^{\beta } e^{-m\sum _{j=1}^N Q(\zeta _j)} \left( 1+\varepsilon \mathrm {Re}\left[ W_N^+[\psi ](\varvec{\zeta }) \right] +O(\varepsilon ^2) \right) \prod _{j=1}^{N} dA(\zeta _{j}). \end{aligned}$$

Observe that since the partition function $Z_N$ does not depend on $\varepsilon$, the coefficient of $\varepsilon$ in the right-hand side of above identity is zero, i.e., $\mathrm {Re}\, \mathbf {E}_N W_N^+[\psi ]=0.$ Now (30) follows by the same argument with $i \psi$. $\square$

Next we prove Theorem 1 equation (4) using the previous Lemma 1 equation (30).

Proof

Suppose that the point $\zeta \in \mathbb {C}$. Recall that $R_{N,k}$ is the k-point correlation function (2) for the 2D Coulomb gas given by (1). Let $\psi \in C_0^\infty (\mathbb {C})$ be an arbitrary test function. By definition, we have

$$\begin{aligned} \mathbf {E}_N \mathrm{I}_N[\psi ]&=\frac{1}{4}\int _{\mathbb {C}^2}\frac{\psi (\zeta )-\psi (\eta )}{\zeta -\eta } R_{N,2}(\zeta ,\eta ) dA(\zeta )dA(\eta )\\&=\frac{1}{2} \int _{\mathbb {C}}\psi (\zeta )\int _{\mathbb {C}} \frac{R_{N,2}(\zeta ,\eta ) }{\zeta -\eta } dA(\eta ) dA(\zeta ) ,\\ \mathbf {E}_N \mathrm{II}_N[\psi ]&= m \int _{\mathbb {C}} \psi (\zeta ) \partial Q(\zeta ) R_{N,1}(\zeta ) dA(\zeta ),\\ \mathbf {E}_N \mathrm{III}_N[\psi ]&= \int _{\mathbb {C}} \partial \psi (\zeta ) R_{N,1}(\zeta )dA(\zeta )= -\int _{\mathbb {C}} \psi (\zeta ) \partial R_{N,1}(\zeta ) dA(\zeta ). \end{aligned}$$

Therefore (30) is rewritten as

$$\begin{aligned} \frac{\beta }{2} \int _{\mathbb {C}}\psi (\zeta ) \left( \int _{\mathbb {C}} \frac{R_{N,2}(\zeta ,\eta ) }{\zeta -\eta } dA(\eta ) \right) dA(\zeta )= \int _{\mathbb {C}} \psi (\zeta ) \Big ( m\partial Q(\zeta ) R_{N,1}(\zeta )+\partial R_{N,1}(\zeta ) \Big ) dA(\zeta ). \end{aligned}$$

Since $\psi$ is an arbitrary test function, (4) follows. $\square$

3 The Saddle Point Method in 2D and 1D

In this section our approach will be more heuristic. First, we will calculate the free energy functional $F_N[\rho _N]$ for large but finite N, both for the 1D and 2D case together. In this way it will become clear, how the respective dimension $d=1,2$ enters. Furthermore, we will see how imposing the different scaling limits (7) and (8) leads to different limiting free energies (9) and (14), respectively, that arise from a different order in N. Only after imposing the saddle point condition upon the limiting free energy functionals, we have to specify the dimension d. In 2D ($d=2$) we can use the Laplace operator to directly obtain an equation for the limiting density. In contrast, in 1D ($d=1$) we have to first pass over to the resolvent G(z) or Stieltjes transform of the limiting density, to find a closed form equation that determines it, and then finally obtain the limiting density by taking the discontinuity along its support. We refer the reader to [45, Chaps. 4, 5] for the general concepts of the saddle point method in 1D and to [57] in 2D.

3.1 The Free Energy in 2D and 1D

We begin by writing down the partition function for the Gibbs measures (1) for 2D and for 1D in a unified way,

$$\begin{aligned} Z_N=\int \prod _{j>k=1}^N |\zeta _j-\zeta _k|^{\beta } e^{-m\sum _{j=1}^N Q(\zeta _j)} \prod _{j=1}^{N}d\mu _d(\zeta _j). \end{aligned}$$

(32)

Here, for $d=2$ we integrate over $\mathbb {C}^N$ and $d\mu _2=dA$ is the area measure, that is the 2D Lebesgue measure over $\pi$, whereas for $d=1$ we integrate over $\mathbb {R}^N$ and $d\mu _1(\zeta )=d\zeta$ is the flat Lebesgue measure in 1D. Clearly, the integrand can be written as the exponential of the following energy function $E_N[ \varvec{\zeta } ]$

$$\begin{aligned} E_N[ \varvec{\zeta } ]:= m \sum _{j=1}^{N} Q(\zeta _{j}) - \beta \sum _{j>k=1}^N \log |\zeta _{j}-\zeta _{k}| \ . \end{aligned}$$

(33)

Our first goal is to change variables from the particle positions $\zeta _{j=1,\ldots ,N}$ to the normalised one-point counting function $\rho _N(z)$ from (3)

$$\begin{aligned} \rho _N(z)=\frac{1}{N}\sum _{j=1}^N \delta ^{(d)}(z-\zeta _{j})\ , \end{aligned}$$

(34)

such that we can write

$$\begin{aligned} \begin{aligned} Z_N&= \int \exp [-E_N[ \rho _N]] J_N[\rho _N] \mathcal {D}[\rho _N] = \int \exp [-F_N[ \rho _N]] \mathcal {D}[\rho _N]. \end{aligned} \end{aligned}$$

(35)

Here, $F_N[\rho _N]$ is the free energy functional for large but finite N we seek for, $\mathcal {D}[\rho _N]$ is the integration over the counting measure, and $J_N[\rho _N]$ is the Jacobian that formally reads

$$\begin{aligned} J_N[\rho _N]=\int \delta \left( \rho _N(z)-\frac{1}{N}\sum _{j=1}^N \delta ^{(d)}(z-\zeta _{j})\right) \prod _{k=1}^N d\mu _d(\zeta _k)\ . \end{aligned}$$

(36)

Its contribution to the free energy is called entropy. By standard thermodynamic arguments the ensemble will converge towards to the limiting density (equilibrium measure) that minimises or maximises the free energy, depending on the sign of $\beta$.

We begin by expressing the energy (33) in terms of the counting function (34). For the first term we simply have

$$\begin{aligned} m\sum _{j=1}^{N} Q(\zeta _{j})= N \int \rho _N(z)Q(z)d\mu _d(z)\ . \end{aligned}$$

For the second term in (33) we can write, after symmetrising,

$$\begin{aligned} -\frac{\beta }{2}\sum _{j,k: j\ne k}^N \log |\zeta _{j}-\zeta _{k}| =&-N^2\frac{\beta }{2} \int \rho _N(z)\rho _N(z')\log |z-z'|d\mu _d(z)d\mu _d(z')\\&+N\frac{\beta }{2} \int \rho _N(z) \log \ell (z) d\mu _d(z). \end{aligned}$$

Because the sum does not contain points at equal argument we have to subtract the diagonal contribution which is divergent. As we are only interested in the density on a global, macroscopic scale which is much larger than the mean particle distance, we have introduced a short-distance cut-off$\ell (z)$ which may be position-dependent. This term is also called self-energy, and because the mean particle distance depends on the dimension d, in the bulk of the spectrum we have for large N

$$\begin{aligned} \ell (z) \simeq \left( \frac{1}{N\rho _N(z)}\right) ^{1/d}\ ,\quad \text {with}\ d=1,2\ , \end{aligned}$$

(37)

see e.g., [45] for $d=1$ and [57, Sect. 2] for $d=2$. Clearly this argument is not rigorous. The last ingredient we miss is the Jacobian (36) which for large-N follows from Sanov’s Theorem, cf. [17, 26]:

$$\begin{aligned} J_N[\rho _N]= \exp \left[ -N \int \rho _N(z) \log \rho _N(z) d\mu _d(z)-N \log N+\gamma _d N+o(N) \right] . \end{aligned}$$

(38)

Here, $\gamma _d$ is some constant, see [57, Eq. (2.15)] for $d=2$, which is apparently unknown for $d=1$ [45]. Collecting all contributions we obtain the following result for the free energy functional at large-N:

$$\begin{aligned} \begin{aligned} F_N[\rho _N]\approx&\ m N \int Q(z) \rho _N(z) d\mu _d(z) -\frac{\beta }{2}N^2 \int \rho _N(z)\rho _N(z')\log |z-z'|d\mu _d(z)d\mu _d(z')\\&+\frac{N}{2d}(2d-\beta ) \int \rho _N(z) \log \rho _N(z) d\mu _d(z)+C_d \left( \int \rho _N(z) d\mu _d(z) -1\right) . \end{aligned} \end{aligned}$$

(39)

We have added a term that ensures the correct normalisation of the density, and the constant $C_d$ is called Lagrange multiplier. For simplicity we have suppressed all other constants and o(N) terms here, as they will not play any rôle later.

Notice that for $\beta =2$ in $d=1$ and for $\beta =4$ in $d=2$ the term in the second line of (39) is absent, see e.g. [6, 40, 57], respectively. For these particular values of $\beta$ the free energy (and the resolvent to be defined later) can be recursively expanded in powers of $1/N^2$ also called genus expansion, whereas the expansion is in powers of 1 / N in all other cases. For recent mathematical work in 1D and 2D see [14] and [34, 43], respectively.

Let us now discuss the two different scaling large-N limits (7) and (8) of the free energy (39), starting with the more standard limit (8).

• (i) First, let $m=\beta N/2$ and $\beta =O(1)$ be fixed according to (8) which is the standard scaling limit for $\beta$-ensembles. Then the leading contribution of the free energy (39) is of order $N^2$ (from the first line) and results from the contribution of the energy terms only. Assuming that the Lagrange multiplier $C_d$ is of order unity we obtain

  $$\begin{aligned} F[\rho ]&= \lim _{N\rightarrow \infty }\frac{2F_N[\rho _N]}{\beta N^2}\\&=\int Q(\zeta ) \rho (\zeta ) d\mu _d(\zeta )-\int \log {|\zeta -\eta |} \rho (\zeta ) \rho (\eta ) d\mu _d(\zeta ) d\mu _d(\eta )\ . \end{aligned}$$

  It agrees with the functional (14). The equation determining the density $\rho _*$, that minimises the free energy, is given by the saddle point equation, a necessary condition to have an extremum. We therefore require the functional derivative of F to vanish at the equilibrium density $\rho _*$:

  $$\begin{aligned} 0=\frac{\delta F(\rho )}{\delta \rho (\zeta )}\Big |_{\rho =\rho _*}=Q(\zeta )-2 \int \log |\zeta -\eta | \, \rho _*(\eta ) \, d\mu _d(\eta )\ , \end{aligned}$$

  (40)

  the compactly supported Frostman equilibrium measure. From a heuristic point of view we can easily see that this minimises the free energy. Taking a second functional derivative that we regularise by choosing $\xi$ slightly away from $\zeta$, we have

  $$\begin{aligned} \frac{\delta ^2 F(\rho )}{\delta \rho (\zeta )\delta \rho (\xi )}\Big |_{\rho =\rho _*}=-2 \log |\zeta -\xi | >0 \ , \end{aligned}$$

  (41)

  which is clearly positive and thus is a minimum, as for $\xi \approx \zeta$ the logarithm becomes negative. We refer to standard literature [51] for a rigorous derivation of the solution of (40). For the relation to a Coulomb gas in $d=1,2$ we also refer to [41] and [38, 48], respectively.

• (ii) Second, let $m=1$ and $\beta = 2c /N$ for some $c \in (-d,\infty )$ which agrees with our proposed scaling (7) for $d=2$, and with [3] for $d=1$. In this case we have that both energy and entropy contribute, and the leading order in (39) is now rather N. Therefore we obtain instead

  $$\begin{aligned} F_c[\rho ]&=\lim _{N\rightarrow \infty } \frac{F_N[\rho _N]}{N}\\&= \int Q(\zeta ) \rho (\zeta ) d\mu _d(\zeta )-c \int \log {|\zeta -\eta |} \rho (\zeta ) \rho (\eta ) d\mu _d(\zeta ) d\mu _d(\eta )\\&\quad +\int \rho (\zeta ) \log \rho (\zeta ) d\mu _d(\zeta )\ , \end{aligned}$$

  which agrees with the free energy claimed in (9). Here, the corresponding saddle point equation reads

  $$\begin{aligned} \begin{aligned} 0&=\frac{\delta F_c(\rho )}{\delta \rho }\Big |_{\rho =\rho _c} =Q(\zeta )-2c \int \log |\zeta -\eta | \, \rho _c(\eta ) \, d\mu _d(\eta ) + \log \rho _c(\zeta )+1. \end{aligned} \end{aligned}$$

  (42)

  The second functional derivative that decides whether we have a minimum or a maximum leads to

  $$\begin{aligned} \frac{\delta ^2 F_c(\rho )}{\delta \rho (\zeta )\delta \rho (\xi )}\Big |_{\rho =\rho _c}=-2c \log |\zeta -\xi | +\frac{\delta ^{(d)}(\zeta -\xi )}{\rho _c(\zeta )} \ . \end{aligned}$$

  (43)

  Due to our regularisation $\xi \approx \zeta$ the logarithm becomes negative and, ignoring the second term at this scale, we obtain a minimum for $c>0$ and a maximum for $c<0$. This statement has been made rigorous for the Gaussian plus linear potential for $d=2$ in [18]. For $c=0$ we do not have an extremum, and the solution of (42) for $c=0$ leads to $\rho _{c=0}(\zeta )\sim \exp [-Q(\zeta )]$, as is expected for non-interacting particles.

Let us also comment on the phenomenon of negative values of c and on the existence of a lower bound, both for 2D and 1D. Because a negative value of c corresponds to a (weakly) attractive Coulomb interaction, it is not surprising that at some critical value the eigenvalues all collapse to the origin, the minimum of the potential Q, as illustrated in Sect. 1, cf. [3] for a discussion of 1D. A more quantitative analysis of the partition function $Z_N$ in 2D shows that it diverges at $c=-2$. Namely, integrating (1) over N complex variables $\zeta _j=x_j+iy_j$ can be written as a single integral over the 2N-dimensional vector $R=(x_1,y_1,\ldots ,x_N,y_N)$ of length $|R|^2= \sum _{j=1}^N|\zeta _j|^2$. Choosing polar coordinates for R and extracting powers of radius |R| from the Vandermonde determinant, it is easy to see that the radial integral ceases to exist at the origin for sufficiently large N when the exponent in $|R|^{N(c+2)-(c+1)}$ becomes too negative, that is at $c=-2$. A similar calculation in 1D yields a critical value $c=-1$ there.

3.2 Saddle Point Equation for the Density in 2D

If we want to transform the saddle point equation into a closed differential equation for $\rho _c$ we have to distinguish now the cases $d=1$ and $d=2$. While $d=1$ is considerably more complicated, passing through the resolvent as explained in the next subsection, $d=2$ is in principle very simple. This is due to the fact that the Laplacian acting on the logarithm gives a Dirac delta, which in our convention (20) reads $\varDelta \log |z|=\frac{\pi }{2}\delta ^{(2)}(z)$. In the limit (i) above we thus obtain from (40) that

$$\begin{aligned} \varDelta Q(\zeta )-\rho _*(\zeta )=0\ , \end{aligned}$$

(44)

which holds on the limiting support that has to be compact, the droplet, as claimed in (15). For the limit (ii) from (42) we get

$$\begin{aligned} \varDelta Q(\zeta ) -c \, \rho _c(\zeta ) + \varDelta \log \rho _c(\zeta ) =0\ , \end{aligned}$$

(45)

which is supported a priori on the entire complex plane. This is the mean field equation (11). As already explained in the introduction we have been unable to solve this equation analytically. We refer again to the numerical solution for two examples presented there for radially symmetric potentials, to which we turn now.

For simplicity, we focus on the potentials $Q(z)=|z|^{2\alpha }/2$, where $\alpha \ge 1$. Recall that the radial part $g_c(|z|):=\rho _c(z)/\pi$ of the crossover density satisfies

$$\begin{aligned} 4\pi c \, r \, g_c(r)=2\alpha ^2 r^{2\alpha -1} +\left( r \, (\log g_c(r))'\right) '. \end{aligned}$$

(46)

Based on this it is not difficult to see the asymptotic behaviour in c for $c\rightarrow \infty$ and $c\rightarrow 0$ as quoted in (26). Namely, for $c\rightarrow \infty$ in order to get a finite answer on left- and right-hand side we need that $g_c(r)\sim 1/c$. Neglecting the last term in (46), which self-consistently leads from (45) to (44), we are lead to

$$\begin{aligned} g_c(r)\sim \frac{\alpha ^2}{2\pi c} r^{2\alpha -2} \ . \end{aligned}$$

The limiting support on a disc of radius b simply follows by imposing the normalisation condition

$$\begin{aligned} \frac{1}{2\pi }=\int _0^b dr r g_c(r)= \frac{\alpha }{4\pi c} b^{2\alpha } \ , \end{aligned}$$

which leads to $b=(2c/\alpha )^{1/(2\alpha )}$ as claimed in (26).

For $c\rightarrow 0$ we then obtain $g_c(r)\sim k\exp [-r^{2\alpha }/2]$ and we simply have to compute the normalisation constant k from

$$\begin{aligned} \frac{1}{2\pi }=\int _0^\infty dr \, r \, k \, \exp (-r^{2\alpha }/2)=k 2^{\frac{1}{\alpha }-1}\varGamma (1+1/\alpha )\ , \end{aligned}$$

this time supported on the entire plane. This implies $k=1/(\pi 2^{1/\alpha }\varGamma (1+1/\alpha ))$ as claimed in (26). Of course, the statement $g_c(r)\sim k\exp [-Q(r)]$ holds for more general radially symmetric potentials in the limit $c\rightarrow 0$, with the difficulty to determine the normalisation constant k for a given Q.

When stating our main results we have derived already the asymptotic behaviour (22) for radially symmetric potentials for large radii $r\rightarrow \infty$. Let us add a few remarks here about a possible expansion for small r. Assuming that $g_c(0)\ne 0$, which will be true for c not too large, let us denote

$$\begin{aligned} \begin{aligned} g_c(r):&=g_c(0)\,\exp \left( \sum _{j=1}^{\infty } a_j\,r^{2j} \right) , \end{aligned} \end{aligned}$$

(47)

in order to obtain an expansion for small r. By inserting the above expression in (46) and comparing the coefficients, one can iteratively express the $a_j$ through $g_c(0)$, thus leading to

$$\begin{aligned} \begin{aligned} a_1&= {\left\{ \begin{array}{ll} \pi cg_c(0)-\frac{1}{2} &{}\text {if }\alpha =1\\ \pi c g_c(0) &{}\text {if }\alpha =2 \end{array}\right. }, \\ a_2&= {\left\{ \begin{array}{ll} \frac{1}{4}(\pi c g_c(0))^2-\frac{1}{8}\pi c g_c(0) &{}\text {if }\alpha =1\\ \frac{1}{4}(\pi c g_c(0))^2-\frac{1}{2} &{}\text {if }\alpha =2 \end{array}\right. }. \end{aligned} \end{aligned}$$

(48)

We can immediately compare this to what we have obtained in the previous paragraph for $c\rightarrow 0$, where we found $g_{c=0}(0)=1/(\pi 2^{1/\alpha }\varGamma (1+1/\alpha ))$. Therefore $cg_{c=0}(0)$ is vanishing in the limit $c\rightarrow 0$ and we have

$$\begin{aligned} \begin{aligned} g_c(r)={\left\{ \begin{array}{ll} g_c(0) \left( 1-\frac{1}{2} r^2+O(r^6) \right) &{}\text {if }\alpha =1\\ g_c(0) \left( 1-\frac{1}{2} r^4+O(r^6) \right) &{}\text {if }\alpha =2 \end{array}\right. }\ , \end{aligned} \end{aligned}$$

(49)

which agrees with $g_{c=0}(r)=g_{c=0}(0)\exp (-r^{2\alpha }/2)$. In fact it is not difficult to see that for $c\rightarrow 0$ all other coefficients vanish and $a_j=-\frac{1}{2} \delta _{j,\alpha }$. For $c\rightarrow \infty$ the assumption $g_c(0)\ne 0$ breaks down unless $\alpha =1$, where we obtain $g_c(0)\sim \frac{1}{2\pi c}$.

This ends our short survey on the asymptotic behaviour of the solution of (46) in c and radius r for $\alpha =1,2$.

3.3 Saddle Point Equation for the Density in 1D

We will now discuss the saddle point equation in 1D where we will focus on the second limit (ii) above, using (42). It turns out that in order to determine the solution for the density it is more convenient to pass through the resolvent to be defined in (51) below, and we will illustrate this through an example.

Denoting the particle positions by $\lambda \in \mathbb {R}$ (instead of $\zeta$), the real potential Q by V, and writing $\rho _c$ for the limiting density function on $\mathbb {R}$, we may differentiate (42) with respect to $\lambda$:

$$\begin{aligned} 0=V'(\lambda )-2c\, \text {Pr} \int _{\mathbb {R}} \frac{\rho _c(\lambda ')}{\lambda -\lambda '}d\lambda ' +\Big ( \log \rho _c (\lambda ) \Big )'. \end{aligned}$$

(50)

Here, we have to take the principal value (Pr) of the real integral. Let us denote by $G_c(z)$ the Stieltjes transformation (or resolvent) of the limiting density $\rho _c$. It is given as

$$\begin{aligned} G_c(z):=\int _{\mathbb {R}} \frac{\rho _c(\lambda )}{\lambda -z}d\lambda , \quad z \in \mathbb {C}\setminus \mathbb {R}. \end{aligned}$$

(51)

From the normalisation of the density we can see that at large argument it behaves as $G_c(z)\sim -\frac{1}{z}$. Our next goal is to derive a closed form equation for the resolvent. To that aim we multiply equation (50) by $\rho _c(\lambda )/(\lambda -z)$ and integrate over the real line, to obtain

$$\begin{aligned} 0=\int _{\mathbb {R}} \frac{V'(\lambda )\rho _c(\lambda )}{\lambda -z}d\lambda -2c\, \text {Pr} \int _{\mathbb {R}^2} \frac{\rho _c(\lambda )}{\lambda -z} \frac{ \rho _c(\lambda ')}{\lambda -\lambda '}d\lambda ' d\lambda +\int _{\mathbb {R}} \frac{\rho '_c(\lambda )}{\lambda -z}d\lambda . \end{aligned}$$

(52)

The last term can be most easily rewritten, after using integration by parts:

$$\begin{aligned} \int _{\mathbb {R}}\frac{\rho '_c(\lambda )}{\lambda -z} d\lambda ={G_c}'(z). \end{aligned}$$

(53)

For the second term with the double integral we use the identity

$$\begin{aligned} \frac{1}{\lambda -z} \frac{1}{\lambda -\lambda '}=-\left( \frac{1}{\lambda -z}-\frac{1}{\lambda -\lambda '}\right) \frac{1}{\lambda '-z}, \end{aligned}$$

to observe that

$$\begin{aligned} \text {Pr} \int _{\mathbb {R}^2} \frac{\rho _c(\lambda )}{\lambda -z} \frac{ \rho _c(\lambda ')}{\lambda -\lambda '}d\lambda ' d\lambda = -\left( \int _{\mathbb {R}} \frac{\rho _c(\lambda )}{\lambda -z} d\lambda \right) ^2 +\text {Pr} \int _{\mathbb {R}^2} \frac{\rho _c(\lambda )}{\lambda -\lambda '} \frac{ \rho _c(\lambda ')}{\lambda '-z}d\lambda ' d\lambda , \end{aligned}$$

after dropping the principal value in the first term on the right-hand side. Observing that both integrals agree after a change of variables, we thus obtain

$$\begin{aligned} \text {Pr} \int _{\mathbb {R}^2} \frac{\rho _c(\lambda )}{\lambda -z} \frac{ \rho _c(\lambda ')}{\lambda -\lambda '}d\lambda ' d\lambda = -\frac{1}{2} G_c^2(z). \end{aligned}$$

(54)

For the remaining first term in (52) we have to make a further approximation. In the standard scaling limit (8) for particles on $\mathbb {R}$ the limiting density has compact support, for sufficiently confining potentials. Then, one can easily define a contour in the complex plane that encircles the support, but not the point $z\in \mathbb {C}\setminus \mathbb {R}$. In our case only for large c we know that the limiting support localises on the semi-circle or its generalisation. But also for small c the density typically decreases exponentially for large arguments, e.g. for the class of Freud potentials. We therefore assume that we may truncate the integral on a large interval J, making an exponentially small error. At the end of the calculation we can then take the limit $J\rightarrow \mathbb {R}$. Note that we can allow $V'$ to have poles on the real line, as in one of our examples below, but not to have a cut that extends to infinity.

Let us therefore define a contour $\mathcal {C}_J$ that encircles J in counter-clockwise fashion and does not contain the point $z\in \mathbb {C}\setminus \mathbb {R}$. We can then use the residue theorem to arrive at

$$\begin{aligned} \begin{aligned} \int _{\mathbb {R}} \frac{V'(\lambda )\rho _c(\lambda )}{\lambda -z}d\lambda&\approx \int _{J}\rho _c(\lambda ) \oint _{\mathcal {C}_J}\frac{1}{w-\lambda } \frac{V'(w)}{w-z} \frac{dw}{2\pi i} d\lambda \\&=\oint _{\mathcal {C}_J} G_c(w) \frac{V'(w)}{w-z}\frac{dw}{2\pi i}\\&=\oint _{\infty } \frac{G_c(w) V'(w)}{w-z}\frac{dw}{2\pi i} + G_c(z) V'(z)\ . \end{aligned} \end{aligned}$$

(55)

In the second step we have interchanged integrations, to obtain an expression depending only on the resolvent. In the last step we have pulled the contour to infinity, picking up the contribution from the pole at z. Here nothing depends any more on the regularising integral J. Combining all the above Eqs. (53), (54) and (55) we obtain the following closed form equation, assuming that our prescribed cut-off procedure can be made rigorous:

$$\begin{aligned} 0=\oint _{\infty } \frac{G_c(w) V'(w)}{w-z}\frac{dw}{2\pi i} + G_c(z) V'(z) + c \, G_c^2(z)+{G_c}'(z). \end{aligned}$$

(56)

The remaining contribution at infinity is not easily evaluated for a general potential V. In the standard limit (8) at fixed $\beta$ an ansatz can be made for the compact support to consist of a finite union of intervals.

Example 1

Here, we consider the Gaussian potential $V_G(w)=w^2/2$, cf. [3]. In that case we may exploit the behaviour of the resolvent (51) at infinity, $G_c(w)\sim -1/w$, to evaluate the contour integral in (56) at infinity to give unity. We thus have

$$\begin{aligned} 0=1 + G_c(z) z + c \, G_c^2(z)+{G_c}'(z)\ . \end{aligned}$$

(57)

which agrees with the equation found in [3]. There, the derivation of (57) could be made rigorous using [50]. In [3] this equation was solved for the density $\rho _c$ by taking the discontinuity of $G_c$ along the real line, see (69) below. We will illustrate this procedure with a more general example below. Consequently, the authors of [3] found the following explicit formula for the crossover density $\rho _c$, expressed in terms of the parabolic cylinder function D:

$$\begin{aligned} \rho _c(\lambda )=\frac{1}{\sqrt{2\pi } \, \varGamma (1+c) } |D_{-c} (i\lambda ) |^{-2} . \end{aligned}$$

(58)

Example 2

We now slightly extend the previous example by considering a Gaussian potential with an additional logarithmic singularity. A similar case was considered on $\mathbb {R}_+$ in [4]. For any real parameter $a>-1$, let us consider the potential

$$\begin{aligned} V_a(x)= \frac{1}{2} x^2-a\log |x|\ . \end{aligned}$$

(59)

The contour integral in (56) at infinity can be solved as in the previous example, as the pole of $V_a'$ does not contribute there. Therefore, the resolvent $G_{c,a}$ satisfies the following Riccati type equation

$$\begin{aligned} 0=1 + G_{c,a}(z) \left( z-\frac{a}{z}\right) + c \, G_{c,a}^2(z)+{G_{c,a}}'(z)\ . \end{aligned}$$

(60)

Let us denote

$$\begin{aligned} G_{c,a}(z)=:\frac{1}{c}\Big ( \log u(z) \Big )'. \end{aligned}$$

(61)

Then, the ODE (60) can be rewritten in terms of the new function u(z) as

$$\begin{aligned} 0=cu(z)+(z-a/z)u'(z)+u''(z)\ . \end{aligned}$$

(62)

A further change of variables to $w=-z^2/2$, with $u(z)=:f(-z^2/2=w)$, casts this into the form of Kummer’s differential equation

$$\begin{aligned} w \, f''(w)+\left( \frac{1-a}{2}-w \right) f'(w)-\frac{c}{2}f(w)=0. \end{aligned}$$

(63)

Moreover, since $G_{c,a}(z)\sim -1/z$ near infinity, we have $u(z)\sim |z|^{c}$ and thus

$$\begin{aligned} f(w) \sim |w|^{-c/2}, \quad |w|\rightarrow \infty \ . \end{aligned}$$

(64)

It is well-known that the solution of (63) satisfying (64) is uniquely determined (up to a multiplicative constant) and reads

$$\begin{aligned} f(w)= U\left( \frac{c}{2}, \frac{1-a}{2}, w \right) , \end{aligned}$$

(65)

see e.g., [47, p. 322]. Here, U is Kummer’s (confluent) hypergeometric function given as the analytic continuation of the integral representation

$$\begin{aligned} U(\alpha ,\gamma ,z)=\frac{1}{\varGamma (\alpha )} \int _{0}^{\infty } e^{-z t} t^{\alpha -1} (1+t)^{\gamma -\alpha -1} dt, \quad ( \mathrm {Re}\,\alpha >0). \end{aligned}$$

(66)

Now let us introduce

$$\begin{aligned} \begin{aligned} y(z):=e^{z^2/4} z^{-a/2} u(z), \end{aligned} \end{aligned}$$

(67)

which, upon using (62), leads to

$$\begin{aligned} y''(z)+\Big [ c-\frac{1}{2}+\frac{a}{2}-\frac{1}{4}z^2-\left( \frac{a^2}{4}+\frac{a}{2}\right) \frac{1}{z^2} \Big ]y(z)=0. \end{aligned}$$

(68)

By the inversion formula, the crossover density $\rho _{c,a}(\lambda )$ is given as

$$\begin{aligned} \begin{aligned} \rho _{c,a}(\lambda )&=\frac{1}{\pi } \lim \limits _{\varepsilon \rightarrow 0} \mathrm {Im}\Big [ G(\lambda -i\varepsilon )\Big ]\\&=\frac{1}{c \pi } \frac{1}{|y(\lambda )|^2} \Big ( \mathrm {Im}[ y'(\lambda )] \mathrm {Re}[y(\lambda )]- \mathrm {Im}[y(\lambda )] \mathrm {Re}[y'(\lambda )] \Big ) , \end{aligned} \end{aligned}$$

(69)

for $\lambda \in \mathbb {R}$. Observe here that by (68), the term $( \mathrm {Im}y' \, \mathrm {Re}y- \mathrm {Im}y \, \mathrm {Re}y')$ is constant along the real line, having a vanishing derivative. Therefore, by (65), we finally conclude that

$$\begin{aligned} \rho _{c,a}(\lambda )= \frac{1}{Z(c,a)}\, e^{-\frac{1}{2}\lambda ^2+a\log |\lambda | } \, \left| U\left( \frac{c}{2},\frac{1-a}{2},-\frac{\lambda ^2}{2}\right) \right| ^{-2}, \end{aligned}$$

(70)

where Z(c, a) is a normalisation constant. This is the solution for the crossover density for the potential (59). Unfortunately we have been unable to determine the normalisation analytically for general parameter values a and c, except for $c=0$ or $a=0$ as shown below. For that reason, in the plots presented at the end of Sect. 1 the normalisation has been computed numerically.

In the particular case $c=0$ we observe that

$$\begin{aligned} U(0,\gamma ,z)\equiv 1, \end{aligned}$$

(71)

see [47, p. 327]. Therefore, we obtain the expected extremal case that

$$\begin{aligned} \rho _{0,a}(\lambda )=\frac{1}{2^{(1+a)/2}\, \varGamma ( \frac{1+a}{2})} \, e^{-\frac{1}{2}\lambda ^2+a\log |\lambda | }, \end{aligned}$$

(72)

with the density being proportional to $e^{-V}$. On the other hand, if $a=0$, we can recover the density in [3], due to the identity (see e.g., [47, p. 328])

$$\begin{aligned} D_{-c}(iz) =2^{-c/2} \, e^{z^2/4}\, U\left( \frac{c}{2}, \frac{1}{2}, -\frac{z^2}{2} \right) . \end{aligned}$$

(73)

In Sect. 1 in Fig. 3 (resp., Fig. 5) we show an example for the crossover density (70) with $a=1/2$ (resp., $a=-1/2$). For comparison in Fig. 4 the known case $a=0$ from [3], interpolating between Gauss’ and Wigner’s semi-circular distribution, is also given.