Edge Behavior of Two-Dimensional Coulomb Gases Near a Hard Wall

Abstract

We consider a two-dimensional determinantal Coulomb gas confined by a class of radial external potentials. In the limit of large number of particles, the Coulomb particles tend to accumulate on a compact set S, the support of the equilibrium measure associated with a given external potential. If the particles are forced to be completely confined in a disk ${\mathcal {D}}$ due to a hard-wall constraint on ${\partial }{\mathcal {D}}\subset {\text {Int}}S$, then the equilibrium configuration changes and the equilibrium measure acquires a singular component at the hard wall. We study the local statistics of Coulomb particles in the vicinity of the hard wall and prove that their local correlations are expressed in terms of “Laplace-type” integrals, which appear in the context of truncated unitary matrices in the regime of weak non-unitarity.

1 Introduction

In this paper, we are interested in the local statistics of the two-dimensional Coulomb gas model which consists of N particles interacting via a repulsive Coulomb potential on the complex plane ${\mathbb {C}}$. The system of Coulomb particles with an external potential Q is defined by the Gibbs density

$$\begin{aligned} {{\mathbf {P}}}_{N,\beta }(\zeta _1,\ldots , \zeta _N) = \frac{1}{Z_{N,\beta }} e^{-\beta H_N(\zeta _1,\ldots ,\zeta _N)},\quad \zeta _1,\ldots ,\zeta _N \in {\mathbb {C}}, \end{aligned}$$

(1.1)

where $\beta >0$ denotes the inverse temperature and $H_N(\zeta _1,\ldots ,\zeta _N)$ is the Hamiltonian of the system at position $(\zeta _1,\ldots ,\zeta _N)\in {\mathbb {C}}^N$, given by

$$\begin{aligned} H_{N}(\zeta _1,\ldots , \zeta _N) = -\sum _{j\ne k}\log |\zeta _k-\zeta _j| + N\sum _{j=1}^{N}Q(\zeta _j). \end{aligned}$$

Here, $Z_{N,\beta }$ is the partition function defined by $Z_{N,\beta } = \int _{{\mathbb {C}}^N}e^{-\beta H_N} dA_n,$ where $dA_n = dA^{\otimes n}$ is a normalized Lebesgue measure on ${\mathbb {C}}^n$ with $dA(x+iy)= dxdy/\pi$. For the special choice $\beta =1$, the system has a determinantal structure and has a close relationship with some non-Hermitian random matrix ensembles. When $\beta =1$, the Gibbs distribution in (1.1) coincides with the joint distribution of eigenvalues in random normal matrix models (see e.g., [15, 19]) and in the case of $Q(\zeta )=|\zeta |^2$, the particle system corresponds to the eigenvalues of complex Ginibre matrices, which are $N \times N$ non-Hermitian matrices whose entries are i.i.d. complex Gaussians with mean zero and variance 1/N [27].

If the external potential grows sufficiently fast near infinity, the particles tend to accumulate on a compact set, which is called the droplet. More precisely, as $N\rightarrow \infty$, the empirical measure $\mu _N = N^{-1}\sum _{j=1}^{N}{\delta _{\zeta _j}}$ of the system $\{\zeta _j\}$ weakly converges to an equilibrium measure with compact support, which minimizes the weighted logarithmic energy

$$\begin{aligned} I_Q[\mu ]:= \int \!\!\!\int _{{\mathbb {C}}^2}\log \frac{1}{|\zeta -\eta |}d\mu (\zeta )d\mu (\eta )+\int _{{\mathbb {C}}}Q(\zeta )d\mu (\zeta ) \end{aligned}$$

(1.2)

among all probability measures on ${\mathbb {C}}$. See [29, 32]. Central limit theorems for the fluctuations of the linear statistics have been proved in [41] for the Ginibre ensemble and [3] for random normal matrix ensembles.

Microscopic behaviors of Coulomb gases are relatively less known. Exact results are known for $\beta = 1$, the determinantal case, due to the correlation structure expressed by orthogonal polynomials. In the bulk of the droplet, the support of the equilibrium measure, universality of the Ginibre kernel

$$\begin{aligned} G(z,w) = e^{z{\bar{w}}-|z|^2/2-|w|^2/2} \end{aligned}$$

(1.3)

has been obtained from an asymptotic expansion of the reproducing kernel for polynomial Bergman spaces. See [3, 11]. At a regular boundary point of the droplet, universality for the kernel

$$\begin{aligned} G(z,w) F(z+{\bar{w}}), \end{aligned}$$

(1.4)

where G is the Ginibre kernel (1.3) and F is the free boundary plasma function defined by

$$\begin{aligned} F(z) = \frac{1}{2} {\text {erfc}}\left( \frac{z}{\sqrt{2}}\right) =\frac{1}{\sqrt{2\pi }} \int _{-\infty }^{0} e^{-(z-t)^2/2}dt, \end{aligned}$$

has been proved in [30] by obtaining an asymptotic expansion for orthogonal polynomials near the boundary.

If a boundary confinement is imposed to the Coulomb gas system, edge behaviors of the particles may change. One may consider Coulomb gases forced to be in a certain region of the plane. This kind of confinement can be achieved by redefining the external potential to be $+\infty$ outside the region. A Coulomb gas system with a hard edge, the case when the region of confinement is exactly the droplet, was studied in several researches [20, 29, 44]. In this case, the equilibrium measure does not change, but the local statistics at the hard edge are described by a different kernel. The Coulomb gas system properly centered and rescaled at the hard edge converges to a determinantal point process with the kernel

$$\begin{aligned} G(z,w) H(z+{\bar{w}}),\quad {\text {Re}}z ,\,{\text {Re}}w \le 0, \end{aligned}$$

(1.5)

where G is the Ginibre kernel and H is the hard edge plasma function

$$\begin{aligned} H(z)= \frac{1}{\sqrt{2\pi }}\int _{-\infty }^{0} \frac{e^{-(z-t)^2/2}}{F(t)}dt,\quad {\text {Re}}z \le 0 \end{aligned}$$

for a class of external potentials containing radially symmetric potentials [1, 5]. A family of boundary confinements which interpolates between a free boundary (1.4) and a hard edge (1.5) has been studied in [7].

Fig. 1

Eigenvalue density profiles of the Ginibre ensemble with a free boundary (left) and confined in a unit disk (middle) and in a disk of radius $r=0.8$ (right) when $n=100$

In this paper, we will study the Coulomb gases confined in a proper subset of the droplet. Figure 1 shows the eigenvalue density profiles of the Ginibre ensemble $(Q(\zeta )=|\zeta |^2)$ with different boundary confinements. It is well known that the empirical measure for Ginibre ensemble converges to the uniform measure on the unit disk. In Fig. 1, the graph on the left shows the density profile of the particles without any constraints on the boundary, where the local behavior of the system near the edge $|\zeta |=1$ is expressed in terms of the free boundary function F in (1.4). The graph in the middle is for the hard edge case where the particles are confined in the droplet (the unit disk) and the local behavior is expressed in terms of the hard edge plasma function H in (1.5). If the Coulomb particles are confined in a smaller disk with radius $r<1$, then a “hard wall” appears along the boundary of the disk and the equilibrium measure changes. In this case, the local behavior is no longer described by the “error function” type kernels such as (1.4) or (1.5). We shall show that the Coulomb particle system, properly rescaled at the hard wall in the inward normal direction, converges to the determinantal point process with kernel in the form of a Laplace-type integral

$$\begin{aligned} K^{(0)}(z,w)= \int _{0}^{1} t \,e^{-t(z+{\bar{w}})} dt ,\quad {\text {Re}}z, {\text {Re}}w > 0 \end{aligned}$$

and this kernel is universal for a class of radially symmetric potentials. Furthermore, under a small perturbation in the external potential obtained by adding a logarithmic singularity at the boundary $- \frac{\alpha }{N}\log (r-|\zeta |)$ for $\alpha >-1$, the limiting correlation kernel is of the form

$$\begin{aligned} K^{(\alpha )}(z,w) = (2{\text {Re}}z)^{\alpha /2}(2{\text {Re}}w)^{\alpha /2}\int _{0}^{1} \frac{t^{\alpha +1}}{\Gamma (\alpha +1)}e^{-t(z+{\bar{w}})} \,dt,\quad {\text {Re}}z,{\text {Re}}w > 0. \end{aligned}$$

(1.6)

The limiting kernel (1.6) coincides with the kernel found for truncated unitary matrices in [48]. More precisely, a non-Hermitian matrix J which is the upper left block of a unitary matrix U taken randomly from the unitary group U(M) was studied in [48]. The eigenvalues of the matrix J are located in the unit disk, and in the case when the size of the truncation is $N\times N$ with $N=M-1-\alpha$ for a non-negative integer $\alpha$, the system of eigenvalues properly rescaled at the circle in the inward normal direction converges to the determinantal point process with correlation kernel (1.6) as $N\rightarrow \infty$. This agreement is due to the fact that the joint distribution of the eigenvalues for truncated unitary matrices agrees with that of two-dimensional Coulomb gases confined in a unit disk with a hard wall at the unit circle, especially when the external potential is $Q(z) = -\frac{\alpha }{N}\log (1-|z|^2)$ for $|z|\le 1$. An application of this model in physics can be found in the theory of quantum chaotic scattering. See [21, 23, 24] for the random matrix approach to the chaotic scattering and results on random contractions and deformations of Hermitian matrices.

Remark

In this paper, we use the terminology “hard edge” for the case when the boundary confinement is imposed exactly on the boundary of the droplet and “hard wall” for the case when the confinement is raised in the interior of the droplet in order to distinguish these two cases with different edge behaviors. The “hard wall” case studied in this paper is related to the hard edge ensembles in the Hermitian random matrix theory, which is usually associated with the Bessel kernel [20, 45]. The “hard edge” case in this paper, studied for example in [1, 5, 43], is more related to the “soft/hard edge” in the Hermitian theory [16], the case when the soft edge meets a hard edge cut.

The outline of the paper is the following. In Sect. 2, we introduce two-dimensional Coulomb gas ensembles with a hard wall and state the main results. In Sect. 3, we compute edge scaling limits at the hard wall by approximating weighted orthonormal polynomials. Section 4 deals with a rescaled version of Ward’s equation, which gives an abstract approach to universality for the kernel (1.6).

Notation

${\mathbb {H}}_{+}= \{z\in {\mathbb {C}}: {\text {Re}}z > 0\}$ is the right half plane and ${\mathbb {R}}_{+} = \{x\in {\mathbb {R}}: x>0\}$ is the positive real line. D(p, r) is the open disk with center p and radius r. ${\partial }$ and ${\bar{{\partial }}}$ denote the usual complex derivatives and $\Delta = {\partial }{\bar{{\partial }}}$ denotes the usual Laplacian on ${\mathbb {C}}$ divided by 4. ${{\mathbf {1}}}_{U}$ denotes the characteristic function of a set U. $dA = dxdy/\pi$ denotes the Lebesgue measure on ${\mathbb {C}}$ divided by $\pi$ and $ds(\zeta )=\frac{1}{2\pi }|d\zeta |$ denotes the arclength measure divided by $2\pi$. We use the symbol $\delta _N$ for the number $\delta _N = N^{-\frac{1}{2}}\log N$.

2 Main Results

2.1 Equilibrium Measures and Droplets

Consider a potential $Q:{\mathbb {C}}\rightarrow {\mathbb {R}}\cup \{+\infty \}$ which is lower semi-continuous and $Q < +\infty$ on a set of positive area. Suppose that Q satisfies the growth condition

$$\begin{aligned} \liminf _{|\zeta |\rightarrow \infty } Q(\zeta )/\log |\zeta |^2 > 1. \end{aligned}$$

(2.1)

This assumption guarantees the existence of the equilibrium measure $\sigma$, the unique probability measure minimizing the weighted logarithmic energy (1.2) among all positive unit Borel measures on ${\mathbb {C}}$. The measure $\sigma$ has a compact support S called the droplet. More details can be found in [42, Section 1].

For a parameter $\tau >0$, we consider the potential $\tau ^{-1}Q$ and the corresponding weighted logarithmic energy problem. Under the assumptions on Q above, for $\tau$ with $0<\tau \le 1$ there exists the unique equilibrium measure $\sigma _\tau$ associated with the external potential $\tau ^{-1}Q$. We write $S_\tau$ for the support of the measure $\sigma _\tau$, called the $\tau$-droplet. One can consider $\tau$-droplets for $\tau >1$. For this, the growth assumption $\liminf _{|\zeta |\rightarrow +\infty } Q(\zeta )/\log |\zeta |^2 > \tau$ instead of (2.1) yields the existence and compactness of $S_\tau$. It is well known that $S_\tau$ increases with $\tau$ and evolves according to Laplacian growth. We refer to [29, 30, 47] for more results and discussions on this topic.

Throughout the paper, we suppose that Q is radially symmetric, write $Q(\zeta )=q(r)$ for $r=|\zeta |$. Under the assumption that Q is subharmonic on ${\mathbb {C}}$ and q is smooth on ${\mathbb {R}}^{+}$, the droplet $S=S_1$ is the ring

$$\begin{aligned} \{\zeta \in {\mathbb {C}}: \rho _0 \le |\zeta | \le \rho _1 \} \end{aligned}$$

where $\rho _0$ is the smallest number such that $q'(r) > 0$ for all $r>\rho _0$ and $\rho _1$ is the smallest number such that $\rho _1q'(\rho _1)=2$. Moreover, the equilibrium measure $\sigma$ is of the form

$$\begin{aligned} d\sigma (\zeta ) = \Delta Q(\zeta ) \,{{\mathbf {1}}}_{S}(\zeta ) \,dA(\zeta ) = \frac{1}{4\pi }(rq'(r))' {{\mathbf {1}}}_{S}\,dr\,d\theta , \quad \zeta = re^{i\theta }. \end{aligned}$$

(2.2)

Here, dA denotes the two-dimensional Lebesgue measure divided by $\pi$ and ${{\mathbf {1}}}_{U}$ denotes the indicator function for a subset $U \subset {\mathbb {C}}$. See [42, Section 4.6] for the proof.

For $\rho _0 \le r \le \rho _1$, the equilibrium measure of the set $S \cap D(0,r)$ is

$$\begin{aligned} \sigma (S\cap D(0,r)) = \frac{1}{2}rq'(r), \end{aligned}$$

which increases with r and takes values in [0, 1]. Also note that for given $\tau$ with $0<\tau \le 1$, the droplet $S_\tau$ is the set given by

$$\begin{aligned} S_\tau = \{\zeta \in {\mathbb {C}}: \rho _0 \le |\zeta | \le \rho _\tau \}, \end{aligned}$$

where $\rho _\tau$ is the smallest number such that $\rho _\tau q'(\rho _\tau )=2\tau$.

2.2 Localization

For a given potential Q and a disk ${\mathcal {D}}=D(0,{\rho _{*}})$ of center 0 and radius $\rho _{*}$, we define the localized potential $Q^{\mathcal {D}}$ by

$$\begin{aligned} Q^{{\mathcal {D}}} = Q\cdot {{\mathbf {1}}}_{{\mathcal {D}}} + \infty \cdot {{\mathbf {1}}}_{{\mathbb {C}}{\setminus } {\mathcal {D}}}. \end{aligned}$$

The particles picked randomly with respect to the Gibbs measure (1.1) under the external potential $Q^{{\mathcal {D}}}$ are completely confined to the set ${\mathcal {D}}$, i.e., this localization of the external potential defines the Coulomb gas system constrained to ${\mathcal {D}}$.

In general, this type of localization can be considered for any set of positive area. The droplets associated with the localized potentials (called the local droplets) have been studied in [29, 37]. In [1, 6], the local statistics of Coulomb gas constrained to its droplet S have been studied. Redefining the potential to be $+\infty$ outside of a neighborhood of the droplet has a negligible effect on the statistics of the system. However, if the boundary of ${\mathcal {D}}$ meets the droplet, then the local statistic of the particles at ${\partial }{\mathcal {D}}$ changes considerably. See the kernels in (1.4) and (1.5).

Back to the radially symmetric case, fix a radially symmetric potential Q for which the droplet is $S = \{\zeta \in {\mathbb {C}}: \rho _0 \le |\zeta | \le \rho _1\}.$ We assume that Q is strictly subharmonic in a neighborhood of ${\partial }{\mathcal {D}}= \{|\zeta | = \rho _{*}\}$, which implies that the function $rq'(r)$ is strictly increasing near $r=\rho _{*}$.

Assume that $\rho _0 < \rho _{*} \le \rho _1$. In this case, the equilibrium measure $\sigma ^{{\mathcal {D}}}$ associated with $Q^{{\mathcal {D}}}$ should be supported in the ring

$$\begin{aligned} S^{{\mathcal {D}}} = \{\zeta \in {\mathbb {C}}: \rho _0 \le |\zeta | \le \rho _{*}\}. \end{aligned}$$

In the case of $\rho _0<\rho _{*} < \rho _1$, the equilibrium measure still satisfies the Gauss’s law so that its density should be $\Delta Q$ in $S^{{\mathcal {D}}}$. The rest of charges are concentrated on the boundary. Considering the balayage problem finding a measure sweeping out the measure $\sigma$ in (2.2) from $S {\setminus } {\mathcal {D}}$ to ${\partial }{\mathcal {D}}$, we obtain

$$\begin{aligned} d\sigma ^{{\mathcal {D}}} = \Delta Q\, {{\mathbf {1}}}_{S^{{\mathcal {D}}}} \,dA + \frac{1-\tau _{*}}{\rho _{*}}\, ds,\quad \tau _{*} = \frac{1}{2}\rho _{*}q'(\rho _{*}), \end{aligned}$$

(2.3)

where ds is the arclength measure on ${\partial }{\mathcal {D}}$ divided by $2\pi$. For the details of the balayage measure, see [42, Section 2.4]. We also refer to [17, Section 4.1] for the detailed argument for finding the equilibrium measure. The macroscopic statistic of the system depends on the specific external potential Q (or $Q^{{\mathcal {D}}}$), but the expression of the equilibrium measure has a fairly universal form.

We refer that this kind of localization can be considered as a condition on the “exterior hole event” for the Coulomb particle system. Conditioning on the hole event that there is no particle in a disk in the interior of the droplet also leads that the equilibrium measure has a singular component on the boundary of the disk. In [26], a system of the zero set of the Gaussian entire function conditioned on the hole event has been studied, where a forbidden region emerges in contrast to the Coulomb gas system.

2.3 Scaling Limits of Coulomb Gas Systems

Let ${\mathcal {D}}= D(0,\rho _{*})$ with $\rho _0<\rho _{*} <\rho _1$ and fix a number $\alpha > -1$ and a real-valued function h which is radially symmetric and smooth. We define an N-dependent potential $Q_N^{{\mathcal {D}}}$ by adding a logarithmic singularity along the hard wall and a perturbation h to the original potential Q,

$$\begin{aligned} Q_N^{{\mathcal {D}}}(\zeta ) = Q(\zeta ) - \frac{\alpha }{N}\log (\rho _{*} - |\zeta |) - \frac{1}{N}h(\zeta ),\quad \zeta \in {\mathcal {D}}, \end{aligned}$$

(2.4)

while $Q_N^{{\mathcal {D}}}=+\infty$ on ${\mathbb {C}}{\setminus } {\mathcal {D}}$. This choice of the potential gives a generalization of the potential $-\frac{\alpha }{N}\log (1-|\zeta |^2)$ localized to the unit disk $|\zeta |\le 1$, which appears in the study of truncated unitary matrices.

Remark

Adding an N-dependent constant to the potential does not change the problem, so we can assume that $h(\rho _*)=0$. In the following, we shall use this normalization.

Consider the Coulomb gas system $\Phi ^{{\mathcal {D}}}=\{\zeta _j\}_1^N$ associated with the potential $Q_N^{{\mathcal {D}}}$. As a point process, the distribution of the system is described by correlation functions. For an integer k with $1\le k \le N$, the k-point correlation function ${\mathbf {R}}_{N,k}$ is defined by

$$\begin{aligned} {\mathbf {R}}_{N,k}(\zeta _1,\ldots ,\zeta _k) = \frac{N!}{(N-k)!} \int _{{\mathbb {C}}^{N-k}} {{\mathbf {P}}}_{N,\beta }(\zeta _1,\ldots ,\zeta _N)\, dA(\zeta _{k+1})\cdots dA(\zeta _{N}), \end{aligned}$$

where ${{\mathbf {P}}}_{N,\beta }$ is the Boltzmann–Gibbs distribution defined in (1.1) associated with the external potential $Q_{N}^{{\mathcal {D}}}$. It is well known that when $\beta =1$, the Coulomb gas system is determinantal, i.e., the k-point correlation function is expressed by the determinant

$$\begin{aligned} {\mathbf {R}}_{N,k}(\zeta _1,\ldots , \zeta _k) = \det \left( {\mathbf {K}}_{N}(\zeta _i,\zeta _j)\right) _{i,j=1}^k \end{aligned}$$

(2.5)

where ${\mathbf {K}}_{N}$ is a function on ${\mathcal {D}}^2$ called a correlation kernel of the process. Here ${\mathbf {K}}_{N}$ can be taken as the reproducing kernel of a space of weighted polynomials. More precisely, it is expressed as the sum of weighted orthonormal polynomials

$$\begin{aligned} {\mathbf {K}}_{N}(\zeta ,\eta ) = \sum _{j=0}^{N-1}p_{N,j}(\zeta )\,{\bar{p}}_{N,j}(\eta )\, e^{-N(Q_{N}^{{\mathcal {D}}}(\zeta )+Q_N^{{\mathcal {D}}}(\eta ))/2}. \end{aligned}$$

Here $p_{N,j}$ is an orthonormal polynomial of degree j with respect to the measure $e^{-NQ_N^{{\mathcal {D}}}}dA$. In this paper, we study the case $\beta =1$, the determinantal case.

For the system $\Phi ^{{\mathcal {D}}}=\{\zeta _j\}_1^N$, we define a rescaled system $\{z_j\}_1^N$ at a point on the hard wall ${\partial }{\mathcal {D}}$ when $\rho _0<\rho _{*}<\rho _1$. Fix a point $p\in {\partial }{\mathcal {D}}$ and rescale the system by setting

$$\begin{aligned} \zeta _j = p + \mathrm {n}\frac{\rho _{*}\, z_j}{N(1-\tau _{*})},\quad j=1,\ldots , N, \end{aligned}$$

(2.6)

where $\tau _*$ is the number in (2.3) and $\mathrm {n}$ is the unit inward normal to ${\partial }{\mathcal {D}}$ at p. Write

$$\begin{aligned} \gamma _N = \frac{\rho _{*}}{N(1-\tau _{*})}. \end{aligned}$$

Note that the scaling factor $\gamma _N$ is a radius of the disk at p such that

$$\begin{aligned} N\cdot \sigma _{{\mathcal {D}}} \left( D(p,\gamma _N)\right) = C(1+ o(1)), \quad N\rightarrow \infty \end{aligned}$$

(2.7)

where C is a positive constant. With this scale, a nontrivial scaling limit of the system can be obtained. We may assume that $p = \rho _{*} \in {\partial }{\mathcal {D}}\cap {\mathbb {R}}_{+}$ and the normal is in the negative real direction. The rescaled process $\{z_j\}_1^N$ is also determinantal with correlation kernel

$$\begin{aligned} K_{N}(z,w) = \gamma _N^2 {\mathbf {K}}_{N}(\rho _{*}-\gamma _N z, \rho _{*}-\gamma _N w). \end{aligned}$$

We write $R_{N,k}$, $K_N$ for the k-point correlation function and the correlation kernel of the process $\{z_j\}_1^N$, respectively. We are now ready to state one of our main results. Let ${\mathbb {H}}_{+}$ denote the right half plane $\{z\in {\mathbb {C}}: {\text {Re}}z >0\}$.

Theorem 2.1

Let $R_{N,k}$ be the k-point correlation function of the rescaled system $\{z_j\}_1^N$. For $z_1,\ldots , z_k \in {\mathbb {C}}$,

$$\begin{aligned} \lim _{N\rightarrow \infty } R_{N,k}(z_1,\ldots ,z_k) = \det \Big ( K^{(\alpha )}(z_i,z_j)\Big )_{i,j=1}^{k}, \end{aligned}$$

where

$$\begin{aligned} K^{(\alpha )}(z,w) = (2{\text {Re}}z)^{\frac{\alpha }{2}}(2{\text {Re}}w)^{\frac{\alpha }{2}}\int _{0}^{1} \frac{t^{\alpha +1}}{\Gamma (\alpha +1)}\, e^{-t(z+{\bar{w}})} \,dt \cdot {{\mathbf {1}}}_{{\mathbb {H}}_{+}}(z)\,{{\mathbf {1}}}_{{\mathbb {H}}_{+}}(w).\nonumber \\ \end{aligned}$$

(2.8)

The convergence is uniform for $z_1,\ldots ,z_k$ in any compact subset of ${\mathbb {H}}_{+}$.

This theorem establishes the universality of the edge behavior near the hard wall for a class of radially symmetric potentials. We expect that this kernel $K^{(\alpha )}$ would be universal beyond the radial case.

Remark

The usual scaling factor in dimension 2 is $(N\Delta Q)^{-\frac{1}{2}}$ while the appropriate scaling factor $\gamma _N$ at a hard wall is more similar to dimension 1. The difference comes from the fact that in the hard wall case, the particles are densely distributed on the boundary as the equilibrium measure (2.3) shows. If $\rho _{*} = \rho _1$, then the hard wall is on the exterior boundary of the original droplet S and the localization doesn’t change the droplet and the equilibrium measure. In this case, an appropriate microscopic scale at a boundary point (where ${\partial }S$ is smooth and $\Delta Q$ does not vanish) to obtain a nontrivial scaling limit is $(N\Delta Q)^{-\frac{1}{2}}$. See [1, 5,6,7].

Fig. 2

Graphs of the limiting 1-point density $R(x)=K^{(\alpha )}(x,x)$ for $x\in {\mathbb {R}}_{+}$ with $\alpha =0$ (left), $\alpha =-0.5$ (middle), and $\alpha =1$ (right)

Let $\{\zeta _j\}_1^N$ be a random system of Coulomb particles associated with $Q_{N}^{{\mathcal {D}}}$ defined in (2.4). Write $|\zeta |_N$ for the maximal modulus of $\{\zeta _j\}_1^N$, i.e.,

$$\begin{aligned} |\zeta |_N = \max _{1\le j\le N}|\zeta _j|. \end{aligned}$$

Rescaling $|\zeta |_N$ about the radius $\rho _{*}$, we define a random variable $\omega _N$ by

$$\begin{aligned} \omega _N = 2\gamma _N^{-\frac{\alpha +2}{\alpha +1}}\left( \frac{\rho _{*}}{\Gamma ( \alpha +3)}\right) ^{\frac{1}{\alpha +1}} \left( \rho _{*} - |\zeta |_N \right) . \end{aligned}$$

Theorem 2.2

The random variable $\omega _N$ converges in distribution to the Weibull distribution. For $x \ge 0$,

$$\begin{aligned} \lim _{N\rightarrow \infty }{\mathbb {P}}_N(\omega _N \le x) = 1- e^{-x^{\alpha +1}}. \end{aligned}$$

When $\alpha =0$, $\omega _N$ follows the exponential distribution in the large N limit. This convergence to the exponential distribution in the presence of the hard-wall constraint on the unit circle also can be found in [25].

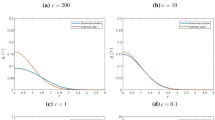
The maximal modulus has fluctuation of order $O(N^{-\frac{\alpha +2}{\alpha +1}})$ near the hard wall. One can see the microscopic effect of the logarithmic singularity $-\frac{\alpha }{N}\log (\rho _{*} - |z|)$ in the external potential at the hard wall $|\zeta | = \rho _{*}$. (See Fig. 2.) Recall that R stands for the 1-point density. If $\alpha$ is positive, then there is a repulsion between the particles and the hard wall so that $R = 0$ at the wall. If $\alpha$ is negative, then there is an attraction between them so that $R=\infty$. Microscopic effects of a logarithmic singularity (insertion of a point charge) in the bulk have been studied in [8].

We shall give a proof of Theorems 2.1 and 2.2 using the asymptotics of orthonormal polynomials in Sect. 3.

Remark

In the free boundary case, it was proved that a properly scaled maximal modulus of Coulomb gases follows Gumbel distribution for $Q(\zeta )=|\zeta |^2$ (complex Ginibre ensemble) [40] and for a class of radially symmetric potentials [13]. In the hard edge case, the case when the Coulomb particles are confined to the droplet S, i.e., $\rho _{*} = \rho _1$ in our setting, the distribution of a properly scaled maximal modulus converges to the exponential distribution when $\alpha =0$. See [43]. In this case, the scaling factor is of order $N^{-1}$ while in the case when $\rho _{*}<\rho _1$ the appropriate scale to obtain a nontrivial scaling limit is of order $N^{-2}$.

Remark

For the potential $Q(\zeta ) = -\frac{\alpha }{N}\log (1-|\zeta |^2)$, the convergence of the distribution of the maximal modulus to the Weibull distribution same as in Theorem 2.2 has been studied in [28, 35]. We also remark that the distribution of the radial deviation of the extremal eigenvalue has been derived in the context of chaotic scattering in [22]. The distribution of the maximal modulus of Coulomb gases associated with a Coulomb potential generated by a charged background has been investigated in [12, 14]. Intermediate large deviations between the large deviation and the typical fluctuation of the maximal modulus of Coulomb gases have been studied in [35].

2.4 Hard Wall Ward’s Equation

We shall discuss an abstract approach to universality based on Ward’s equation, a differential equation of $R(z)=K(z,z)$. The rescaled version of Ward’s equation considered in this paper does not depend on specific potentials Q, and we shall describe solutions R of the equation under some appropriate assumptions on R.

Theorem 2.1 shows the universality of limiting correlation functions for radially symmetric potentials. One can observe that the limiting correlation kernel $K=K^{(\alpha )}$ is invariant under the vertical translation,

$$\begin{aligned} K(z,w) = K(z+is, w+is),\quad s\in {\mathbb {R}}, \end{aligned}$$

i.e., the limiting 1-point function $R(z)=K(z,z)$ is a function only in ${\text {Re}}z$.

We consider a class of functions of the form “Laplace-type integral”

$$\begin{aligned} K_f(z,w) = (2{\text {Re}}z)^{\frac{\alpha }{2}}(2{\text {Re}}w)^{\frac{\alpha }{2}}\int _{0}^{\infty } f(t)\, e^{-t(z+{\bar{w}})}\, dt,\quad z,w\in {\mathbb {H}}_{+}\end{aligned}$$

(2.9)

for some Borel measurable function f on ${\mathbb {R}}_{+}$. This means that $K_f$ is of the form

$$\begin{aligned} (2{\text {Re}}z)^{\frac{\alpha }{2}}(2{\text {Re}}w)^{\frac{\alpha }{2}}\Phi (z,w), \end{aligned}$$

where $\Phi$ is an Hermitian-analytic function, i.e., $\Phi (z,w) = \overline{\Phi (w,z)}$ and $\Phi (z,w)$ is analytic in z and ${\bar{w}}$. If a Hermitian-analytic function $\Phi$ is invariant under the vertical translation, $\Phi (z,w)$ can be written as an analytic function in $z+{\bar{w}}$.

Theorem 2.3

The limiting correlation kernel K in (2.8) satisfies the mass-one equation

$$\begin{aligned} \int _{{\mathbb {H}}_{+}} |K(z,w)|^2 \, dA(w) = K(z,z), \end{aligned}$$

(2.10)

and the hard wall Ward’s equation

$$\begin{aligned} {\bar{\partial }}C(z) = R(z) - \Delta \log R(z),\quad z\in {\mathbb {H}}_{+}, \end{aligned}$$

(2.11)

where $R(z)=K(z,z)$ and C is the Cauchy transform

$$\begin{aligned} C(z)=\int _{{\mathbb {H}}_{+}} \frac{|K(z,w)|^2}{K(z,z)}\frac{dA(w)}{z-w}. \end{aligned}$$

Conversely, if a function $K_f$ of the form (2.9) satisfies the mass-one Eq. (2.10), then there exists a Borel measurable set E in ${\mathbb {R}}_{+}$ such that $f(t)=\Gamma (\alpha +1)^{-1}t^{\alpha +1}\cdot {{\mathbf {1}}}_{E}$ almost everywhere in ${\mathbb {R}}_{+}$. If $K_f$ satisfies the hard wall Ward’s equation (2.11), then there exists a connected set I in ${\mathbb {R}}_{+}$ such that $f(t)=\Gamma (\alpha +1)^{-1}t^{\alpha +1}\cdot {{\mathbf {1}}}_{I}$ almost everywhere in ${\mathbb {R}}_{+}$.

In the converse statement, if we take $I=(0,1)$, then $f(t)=\Gamma (\alpha +1)^{-1}t^{\alpha +1}\cdot {{\mathbf {1}}}_{(0,1)}$ so that $K_f$ agrees with the limiting correlation kernel K in (2.8).

Equation (2.11) is derived by rescaling Ward identities from field theories, which give exact relations for the correlation functions. We shall discuss the derivation of (2.11) in Sect. 4. The Ward’s equation approach to universality of scaling limits has been studied in the papers [5,6,7,8] and so on. This approach does not use the asymptotics of orthogonal polynomials directly. It focuses on the structure of the limiting kernel and its properties which do not depend on specific potentials.

2.5 Ward’s Equation Approach Beyond the Radial Case

One may consider the elliptic Ginibre ensemble with external potential $Q(\zeta ) = |\zeta |^2 - t{\text {Re}}\zeta ^2$ ($|t|<1$), where the droplet is an elliptic disk expressed by the equation $\frac{1-t}{1+t}\,x^2 + \frac{1+t}{1-t}\,y^2 \le 1$. We impose the hard-wall constraint on the boundary of “$\tau$-droplet” $S_\tau = \{x+iy : \frac{1-t}{1+t}\,x^2 + \frac{1+t}{1-t}\,y^2 \le \tau \}$ for some $\tau$ with $0<\tau <1$ so that the particles are completely confined to the $\tau$-droplet. We rescaled the system confined by the localized potential $Q^{S_\tau }$ at a point p on the boundary of the $\tau$-droplet with respect to an appropriate microscopic scale $\gamma _N(p)$ satisfying (2.7). For simplicity, we take $p \in {\mathbb {R}}_{+}\cap {\partial }S_\tau$ and rescale the system via $\zeta = p -\gamma _n(p) z$ as in (2.6). Here $\gamma _N$ should be of order $N^{-1}$ due to the balayage measure supported on the hard wall.

Define a function ${\mathcal {Q}}(\zeta ,\eta ) = \zeta {\bar{\eta }} - t(\zeta ^2 + {{\bar{\eta }}}^2)/2$ which is analytic in $\zeta$, ${{\bar{\eta }}}$ and satisfies ${\mathcal {Q}}(\zeta ,\zeta )=Q(\zeta )$. We write for $\zeta = p -\gamma _N z$ and $\eta = p-\gamma _N w$

$$\begin{aligned} \Phi _N(z,w) = \gamma _N^2 \sum _{j=0}^{N-1}p_{N,j}(\zeta ){\bar{p}}_{N,j}(\eta ) \,e^{-N{\mathcal {Q}}(\zeta ,\eta )} \end{aligned}$$

so that $K_N(z,w) = \Phi _N(z,w) \cdot e^{N({\mathcal {Q}}(\zeta ,\eta ) - Q(\zeta )/2-Q(\eta )/2)}{{\mathbf {1}}}_{S_\tau }(\zeta ){{\mathbf {1}}}_{S_\tau }(\eta )$. Here, $\Phi _N$ is Hermitian-analytic and ${\mathcal {Q}}(\zeta ,\eta ) - Q(\zeta )/2 - Q(\eta )/2 = -i\gamma _N\cdot p(1-t){\text {Im}}(z-w)+O(\gamma _N^2)$ as $N\rightarrow \infty$, which is negligible in the determinant (2.5).

If $\Phi _N$ converges to a limit $\Phi$ uniformly in compact subsets in ${\mathbb {H}}_{+}$ as $N\rightarrow \infty$, then $\Phi$ is Hermitian-analytic and for some additional term $c_N$ which does not change the determinant, a limit K of $c_N\cdot K_N$ has the form $K(z,w)=\Phi (z,w)$ for $z,w\in {\mathbb {H}}_{+}$. This means that the 1-point function $R(z)=K(z,z)$ determines the correlation kernel by analytic continuation.

If we assume that K is invariant under a vertical translation, which is very natural and holds true at least in the free boundary case [See the ${\text {erfc}}$-kernel in (1.4)], then the 1-point function R is a function in ${\text {Re}}z$ and K is a holomorphic function in $z+{\bar{w}}$. Considering the Laplace transform, K can be written in the form $K_f$ (2.9) with $\alpha =0$ for some Borel function f. Solving the hard wall Ward’s equation (2.11), we obtain that $f = t\cdot {{\mathbf {1}}}_{I}$ almost everywhere for some interval I. Scaling factor $\gamma _N$ and the decay rate of R as $x\rightarrow \infty$ determine the interval I. If we choose $\gamma _N$ so that $R(0)=\frac{1}{2}$ and if R(x) has a heavy tail in the sense that $R(x) \sim C/x^2$ as $x\rightarrow \infty$, then $I=(0,1)$.

This “abstract” approach can be applied to not only the elliptic case but also more general cases. The structure of the kernel and the Ward’s equation does not depend on a specific potential. We will leave the hard wall scaling limit for the elliptic Ginibre ensemble and establishing universality of the limit for general potentials for the next project.

2.6 Comments and Related Works

2.6.1 Ward’s Equation Approach for Microscopic Scaling Limits

Differently from at the hard wall, at a point p in the bulk or on a smooth (free) boundary with $\Delta Q(p) > 0$, a limiting correlation kernel K for a properly rescaled system (with rescaling factor $(N\Delta Q(p))^{-1/2}$) has the structure $K(z,w) = G(z,w)\Phi (z,w)$ for a class of smooth potentials. Here, G is the Ginibre kernel (1.3) and $\Phi$ is an analytic function in z and ${\bar{w}}$ with $\Phi (z,w) = \overline{\Phi (w,z)}$. In this case, a limiting correlation kernel $K= G\cdot \Phi$ satisfies the Ward’s equation ${\bar{\partial }}C = R - 1 -\Delta \log R$ on ${\mathbb {C}}$, and with the assumption that R is invariant under the vertical translation, solving the Ward’s equation gives $\Phi (z,w)=(\gamma * {{\mathbf {1}}}_{I})(z+{\bar{w}})$ for some connected set $I\subset {\mathbb {R}}$. Here $\gamma *f$ denotes the analytic continuation of the convolution of a bounded function f and $\gamma (z) = (2\pi )^{-\frac{1}{2}}e^{-\frac{1}{2}z^2}$. In the bulk scaling, $I={\mathbb {R}}$ so that $\Phi = 1$ and $K=G$, the usual Ginibre kernel. In the edge scaling, $I = (-\infty ,0)$ so that $\Phi (z,w) = F(z+w)$ and $K(z,w) = G(z,w)\cdot F(z+w)$ in (1.4), the usual error function kernel. See [5]. Finally, we refer to [6] for the Ward equation approach for the scaling limits near a singular boundary point both in the free boundary and hard edge cases and [2] for the Ward’s equation approach to universality in the regime of weakly non-Hermitian.

2.6.2 Coulomb Gases with a Hard Wall

A family of two-dimensional Coulomb gases confined to an ellipse has been investigated in [39]. This model gives an elliptic generalization of truncated unitary matrix ensembles and also new universality classes in the limit of weak and strong non-Hermiticity. The asymptotic expansion of orthogonal polynomials for a class of hard edge potentials has been investigated in [31]. In [25], the fluctuation of the extremal Coulomb particles has been studied for the case when the hard wall constraint on the unit circle is imposed. For Coulomb gases in any dimension, the third-order transition between the ‘pushed’ and the ‘pulled’ phases, which correspond to the cases of $\rho _{*} < \rho _1$ and $\rho _{*} > \rho _1$, respectively, in our setting, has been studied in [17].

2.6.3 Open Problems

In this paper, the main results are obtained for the two-dimensional determinantal case with radially symmetric potentials. A natural question is to ask about the universality of scaling limits in Theorem 2.1 and fluctuations of the maximal radius in Theorem 2.2 for general potentials beyond the radially symmetric case. Microscopic scaling limits of general two-dimensional $\beta$-ensembles remain unknown for the hard wall case as well as the free boundary case. See [9, 36] for the study of microscopic properties of $\beta$-ensembles. One may ask about the scaling limits of planar Pfaffian point processes such as real and symplectic Ginibre ensembles with a hard wall.

3 Hard Wall Scaling Limits

For a number $\alpha > -1$ and a smooth real-valued function h which is radially symmetric, we consider the potential

$$\begin{aligned} Q_N(\zeta )=Q(\zeta ) - \frac{\alpha }{N}\log (\rho _{*}-|\zeta |)-\frac{1}{N}h(\zeta ),\quad |\zeta |<\rho _{*}. \end{aligned}$$

Here, we assume that $h(\rho _*)=0$ as we remarked in Sect. 2.3. Since Q is radially symmetric, the orthonormal polynomials $p_{N,j}$ can be taken as monomials. For the Coulomb gas system $\Phi ^{{\mathcal {D}}}$ associated with the localized potential

$$\begin{aligned} Q^{{\mathcal {D}}}_N(\zeta ) = Q_N(\zeta )\cdot {{\mathbf {1}}}_{{\mathcal {D}}}(\zeta ) + \infty \cdot {{\mathbf {1}}}_{{\mathbb {C}}{\setminus }{\mathcal {D}}}(\zeta ),\quad {\mathcal {D}}= D(0,\rho _{*}) \end{aligned}$$

defined in Sect. 2.2, the corresponding correlation kernel is given by

$$\begin{aligned} {\mathbf {K}}_N(\zeta ,\eta ) = \sum _{j=0}^{N-1}\frac{(\zeta {\bar{\eta }})^j}{\Vert \zeta ^j\Vert ^2_{L^2(\mu _N)}}e^{-N(Q_{N}(\zeta )+Q_{N}(\eta ))/2}{{\mathbf {1}}}_{{\mathcal {D}}}(\zeta ) {{\mathbf {1}}}_{{\mathcal {D}}}(\eta ), \end{aligned}$$

(3.1)

where $d\mu _N = e^{-N Q_{N}}{{\mathbf {1}}}_{{\mathcal {D}}}dA$. Here, we write $p_{N,j}$ for the orthonormal polynomial of degree j with respect to the measure $\mu _N$, i.e.,

$$\begin{aligned} p_{N,j}(\zeta ) = \zeta ^j /\Vert \zeta ^j\Vert _{L^2(\mu _N)}. \end{aligned}$$

(3.2)

We define the rescaled correlation kernel

$$\begin{aligned} K_N(z,w) = \gamma _N^2 {\mathbf {K}}_N(\rho _*-\gamma _N z,\rho _* - \gamma _N w) \end{aligned}$$

at the hard wall with respect to the microscopic scale

$$\begin{aligned} \gamma _N = \frac{\rho _*}{N(1-\tau _*)},\quad \text {where}\quad \tau _* = \frac{1}{2}\rho _* q'(\rho _*). \end{aligned}$$

(3.3)

3.1 Asymptotics of Rescaled Correlation Kernels

We define a number

$$\begin{aligned} m_N = N\tau _{*} + M\sqrt{N} \end{aligned}$$

(3.4)

for sufficiently large M. We consider the orthonormal polynomial $p_{N,j}$ in (3.2) of degree j with $m_N \le j \le N-1$ for sufficiently large M. These terms of degree higher than $m_N$ are dominant in the sum (3.1) near the boundary ${\partial }{\mathcal {D}}$. Write

$$\begin{aligned} K_N^{\#}(z,w)= \gamma _N^2 \sum _{j = m_N}^{N-1} p_{N,j}(\zeta ){\bar{p}}_{N,j}({\eta })\, e^{-N(Q_{N}(\zeta )+Q_{N}(\eta ))/2}{{\mathbf {1}}}_{{\mathcal {D}}}(\zeta ){{\mathbf {1}}}_{{\mathcal {D}}}(\eta ) \end{aligned}$$

(3.5)

where $\zeta = \rho _{*} - \gamma _N z$, $\eta =\rho _{*} - \gamma _N w$.

To compute the limit of $K_N^{\#}$ as $N\rightarrow \infty$, we first consider the function

$$\begin{aligned} V_{\tau }(r)=q(r) - 2\tau \log r,\quad r>0. \end{aligned}$$

By the definition of $\tau _*$ in (3.3), we have

$$\begin{aligned} V_{\tau }'(\rho _{*}) = q'(\rho _{*})-\frac{2\tau }{\rho _{*}} = \frac{1}{\rho _{*}}\left( \rho _{*}\,q'(\rho _{*}) - {2\tau } \right) =\frac{2}{\rho _{*}}\left( \tau _{*} - \tau \right) \end{aligned}$$

so that the Taylor expansion

$$\begin{aligned} V_{\tau }(r) = V_{\tau }(\rho _{*}) + \frac{2}{\rho _{*}}\left( \tau _{*}-\tau \right) (r-\rho _{*}) + O(r-\rho _{*})^2,\quad r\rightarrow \rho _{*}, \end{aligned}$$

(3.6)

holds. Since $V_\tau '' (r) = q''(r) + 2\tau /r^2$, the error term in (3.6) is bounded by $C|r-\rho _*|^2$ for some positive constant C, which is uniform for all $\tau$ with $0\le \tau \le 1$ and all r in a neighborhood of $\rho _*$. We write $\tau _j = j/N$.

Lemma 3.1

Assume that j is in the range $m_N \le j \le N-1$. We have

$$\begin{aligned} e^{NV_{\tau _j}(\rho _{*})}\, \Vert \zeta ^j\Vert _{L^2(\mu _N)}^2 = 2\rho _{*} \,\Gamma (\alpha +1) \left( \frac{\rho _{*}}{2N\left( \tau _j-\tau _{*}\right) }\right) ^{\alpha +1}(1+o(1)) \end{aligned}$$

as $N\rightarrow \infty .$ Here, $\tau _* = \frac{1}{2}\rho _* q'(\rho _*)$ in (3.3) and the error term o(1) is uniform in j.

Proof

Recall that $\delta _N = N^{-1/2}\log N$. For fixed j, we see that

$$\begin{aligned} \Vert \zeta ^j\Vert ^{2}_{L^2(\mu _N)} = \int _{\rho _{*} -\delta _N}^{\rho _{*}} 2r^{2j+1}\,e^{-NQ_N(r)}\,dr + \int _{0}^{\rho _{*}-\delta _N}2r^{2j+1}\,e^{-NQ_N(r)} \,dr. \end{aligned}$$

(3.7)

By (3.6), the first integral in the right-hand side is calculated as

$$\begin{aligned}&\int _{\rho _{*}-\delta _N}^{\rho _{*}} \!\!2r(\rho _{*}-r)^{\alpha } e^{h(r)} e^{-NV_{\tau _j}(r)}\,dr\\&\quad =2\rho _{*} \int _{\rho _*-\delta _N}^{\rho _*} \!(\rho _*-r)^{\alpha } e^{-NV_{\tau _j}(r)} dr \, (1+o(1)) \\&\quad =2\rho _{*} \, e^{-NV_{\tau _j}(\rho _{*})}\int _{0}^{\delta _N}t^{\alpha }e^{-\frac{2N}{\rho _{*}}\left( \tau _j-\tau _{*}\right) t}dt \, (1+o(1)), \end{aligned}$$

where $o(1)\rightarrow 0$ uniformly in j as $N\rightarrow \infty$. Observing that the integral converges to the Gamma function

$$\begin{aligned} \int _{0}^{\delta _N} t^{\alpha } e^{-\frac{2N}{\rho _*}(\tau _j - \tau _*)t}dt = \left( \frac{\rho _{*}}{2N\left( \tau _j-\tau _{*}\right) }\right) ^{\alpha +1} \int _{0}^{\infty } s^{\alpha } e^{-s} ds\, (1+o(1)), \end{aligned}$$

we have the asymptotic estimate for the first integral

$$\begin{aligned}&\int _{\rho _{*}-\delta _N}^{\rho _{*}} 2r(\rho _{*}-r)^{\alpha } e^{h(r)} e^{-NV_{\tau _j}(r)}\,dr \\&\quad = 2\rho _{*} \, \Gamma (\alpha +1) \, e^{-NV_{\tau }(\rho _{*})} \left( \frac{\rho _{*}}{2N\left( \tau _j-\tau _{*}\right) }\right) ^{\alpha +1} (1+o(1)). \end{aligned}$$

Now it suffices to show that the second integral in the right-hand side of (3.7) is negligible. We observe that for $\tau _j = j/N$ with $m_N \le j \le N-1$

$$\begin{aligned} V_{\tau _j}'(r) = \frac{1}{r}\left( rq'(r) - 2\tau _j\right) \le \frac{1}{r}\left( rq'(r) - \frac{2m_N}{N}\right) . \end{aligned}$$

Since Q is subharmonic in ${\mathbb {C}}$ and $\rho _* q'(\rho _*) = 2\tau _*$, the function $rq'(r)$ is increasing in r and

$$\begin{aligned} V_{\tau _j}'(r) \le \frac{1}{r}\left( \rho _{*}\, q'(\rho _{*}) - 2\left( \tau _{*} + \frac{M}{\sqrt{N}}\right) \right) = -\frac{2M}{r\sqrt{N}},\quad r\le \rho _{*}. \end{aligned}$$

(3.8)

Thus, we see that $V_{\tau _j}$ is decreasing and for all r with $r\le \rho _{*}-\delta _N$

$$\begin{aligned} V_{\tau _j}(r)\ge V_{\tau _j}(\rho _{*}-\delta _N). \end{aligned}$$

By the mean-value theorem, we obtain the expansion

$$\begin{aligned} V_{\tau _j}(\rho _{*} -\delta _N) = V_{\tau _j}(\rho _{*}) - V_{\tau _j}'(r_{*})\,\delta _N \end{aligned}$$

(3.9)

for some $r_{*} \in [\rho _{*}-\delta _N,\rho _{*}]$. Hence, there exists a constant $c>0$ such that for all j

$$\begin{aligned}&e^{NV_{\tau _j}(\rho _{*})}\int _{0}^{\rho _{*}-\delta _N}\! 2r\,(\rho _{*}-r)^{\alpha }e^{h(r)} e^{-NV_{\tau _j}(r)} dr \\&\quad \le 2\rho _* \sup _{[0,\rho _*]} |e^h| \cdot e^{-N(V_{\tau _j}(\rho _{*}-\delta _N)-V_{\tau _j}(\rho _{*}))} \int _{0}^{\rho _*-\delta _N} (\rho _* - r)^{\alpha } dr\\&\quad \le \frac{2\rho _{*}^{\alpha +2}}{\alpha +1} \sup _{[0,\rho _*]} |e^h| \cdot e^{-\frac{2M\sqrt{N}}{r_*}\delta _N} = O(N^{-c M}). \end{aligned}$$

In the second inequality, we have used (3.8) and (3.9). The proof is complete.

$\square$

A function $c(\zeta ,\eta )$ is called a cocycle if $c(\zeta ,\eta ) = g(\zeta ){\bar{g}}(\eta )$ for a continuous unimodular function g. Note that multiplying the correlation kernel by a cocycle does not change the correlation function, which is expressed by a determinant in (2.5).

Lemma 3.2

There exists a cocycle $c(z,w) = \exp (-\frac{\tau _{*}}{1-\tau _{*}} i {\text {Im}}(z-w))$ such that

$$\begin{aligned} K_N^{\#}(z,w)&= c(z,w)(2{\text {Re}}z)^{\frac{\alpha }{2}}(2{\text {Re}}w)^{\frac{\alpha }{2}} \int _{0}^{1} \frac{t^{\alpha +1}}{\Gamma (\alpha +1)} e^{-t(z+{\bar{w}})} dt \\&\quad \cdot {{\mathbf {1}}}_{{\mathbb {H}}_{+}}(z){{\mathbf {1}}}_{{\mathbb {H}}_{+}}(w) \,(1+o(1)), \end{aligned}$$

where $o(1)\rightarrow 0$ uniformly for z, w in any compact subset of ${\mathbb {H}}_{+}$ as $N\rightarrow \infty$.

Proof

Let ${\mathcal {K}}$ be a compact subset of ${\mathbb {H}}_{+}$. For all $\tau _j=j/N$ with $m_N \le j \le N-1$ and for $\zeta = \rho _{*} - \gamma _N z$ with $\gamma _N = \frac{\rho _*}{N(1-\tau _*)}$ in (3.3), we have

$$\begin{aligned} Q(\zeta )-2\tau _j\log \zeta&= V_{\tau _j}(|\rho _*-\gamma _N z|) - 2\tau _j \cdot i{\text {Im}}\log (\rho _* -\gamma _N z) \\&= V_{\tau _j}(\rho _{*})-\frac{2\left( \tau _{*}-\tau _j \right) }{N(1-\tau _{*})}{\text {Re}}z + \frac{2\tau _j}{N(1-\tau _{*})} i{\text {Im}}z + O(N^{-2}) \end{aligned}$$

by the expansion of $V_{\tau }$ in (3.6). Note that the O-constant is uniform for all j and $z \in {\mathcal {K}}$. Also we observe that

$$\begin{aligned} (\rho _{*} - |\rho _{*} - \gamma _N z|)^{\alpha } e^{h(\rho _* -\gamma _N z)} = (\gamma _N {\text {Re}}z)^{\alpha }(1+o(1)). \end{aligned}$$

For each $\tau$ and z, we write

$$\begin{aligned} f_{\tau }(z) = (\tau -\tau _{*})^{\frac{\alpha +1}{2}} \exp \left( - \frac{\tau -\tau _{*}}{1-\tau _{*}} \,z \right) . \end{aligned}$$

Combining with Lemma 3.1, we obtain

$$\begin{aligned} \frac{\zeta ^j \, e^{-\frac{N}{2}Q_{N}(\zeta )}}{\Vert \zeta ^j\Vert _{L^2(\mu _N)}}&= (\gamma _N {\text {Re}}z)^{\frac{\alpha }{2}} \left( \frac{2^{\alpha } N^{\alpha +1}(\tau _j-\tau _*)^{\alpha +1}}{\rho _*^{\alpha +2}\,\Gamma (\alpha +1)} \right) ^{\frac{1}{2}}\\&\quad e^{-\frac{N}{2}(Q(\zeta ) - 2\tau _j\log \zeta -V_{\tau _j}(\rho _*))} (1+o(1)) \\&= \frac{1}{\rho _{*}} \left( \frac{N}{\Gamma (\alpha +1)}\right) ^{\frac{1}{2}} \frac{(2{\text {Re}}z)^{\frac{\alpha }{2}}}{(1-\tau _{*})^{\frac{\alpha }{2}}} e^{-\frac{\tau _{*}}{1-\tau _{*}}i {\text {Im}}z} f_{\tau _j}(z) \,(1+o(1)), \end{aligned}$$

where $o(1)\rightarrow 0$ uniformly for $z\in {\mathcal {K}}$ and j with $m_N \le j \le N-1$ as $N\rightarrow \infty$. We write

$$\begin{aligned} c(z,w) = \exp \left( -\frac{\tau _{*}}{1-\tau _{*}} i {\text {Im}}(z-w)\right) , \end{aligned}$$

which is a cocycle. Since $p_{N,j}(\zeta ) = \zeta ^j/\Vert \zeta ^j\Vert _{L^2(\mu _N)}$, we can write the sum $K_N^{\#}$ in (3.5) as

$$\begin{aligned} K_N^{\#}(z,w) =\gamma _N^2 \sum _{j = m_N}^{N-1} \frac{(\zeta {\bar{\eta }})^j \, e^{-\frac{N}{2}(Q_N(\zeta )+Q_N(\eta ))}}{\Vert \zeta ^j\Vert _{L^2(\mu _N)}^2} \cdot {{\mathbf {1}}}_{{\mathcal {H}}_N}(z){{\mathbf {1}}}_{{\mathcal {H}}_N}(w), \end{aligned}$$

where ${\mathcal {H}}_N=\{z\in {\mathbb {C}}: \rho _{*} -\gamma _N z \in {\mathcal {D}}\}$. Note that ${{\mathbf {1}}}_{{\mathcal {H}}_N}$ converges to ${{\mathbf {1}}}_{{\mathbb {H}}_{+}}$ in the sense of $L^1_{\text {loc}}$ as $N\rightarrow \infty$. Using the Riemann sum approximation with step length $N^{-1}$, we have

$$\begin{aligned} K_N^{\#}(z,w)&= \frac{(2{\text {Re}}z)^{\frac{\alpha }{2}}(2{\text {Re}}w)^{\frac{\alpha }{2}}}{\Gamma (\alpha +1)(1-\tau _{*})^{\alpha +2}} \,c(z,w)\, {{\mathbf {1}}}_{{\mathbb {H}}_{+}}(z){{\mathbf {1}}}_{{\mathbb {H}}_{+}}(w)\\&\quad \frac{1}{N}\!\!\sum _{j= m_N}^{N-1} f_{\tau _j}(z) f_{\tau _j}({\bar{w}})\,(1+o(1))\\&=\frac{(2{\text {Re}}z)^{\frac{\alpha }{2}}(2{\text {Re}}w)^{\frac{\alpha }{2}}}{\Gamma (\alpha +1)(1-\tau _{*})^{\alpha +2}} \,c(z,w)\, {{\mathbf {1}}}_{{\mathbb {H}}_{+}}(z){{\mathbf {1}}}_{{\mathbb {H}}_{+}}(w)\\&\quad \int _{0}^{1-\tau _{*}} \!\!\!s^{\alpha +1} e^{-\frac{s}{1-\tau _{*}}(z+{\bar{w}})} ds\,(1+o(1)), \end{aligned}$$

where $o(1)\rightarrow 0$ locally uniformly in ${\mathbb {H}}_{+}$ as $N\rightarrow \infty$. By the change of variable $s=(1-\tau _{*})t$, we obtain the convergence

$$\begin{aligned} K_N^{\#}(z,w)&= \frac{(2{\text {Re}}z)^{\frac{\alpha }{2}}(2{\text {Re}}w)^{\frac{\alpha }{2}}}{\Gamma (\alpha +1)} \,c(z,w)\, {{\mathbf {1}}}_{{\mathbb {H}}_{+}}(z){{\mathbf {1}}}_{{\mathbb {H}}_{+}}(w)\\&\quad \int _{0}^{1} t^{\alpha +1}\, e^{-t(z+{\bar{w}})}dt\, (1+o(1)) \end{aligned}$$

as $N\rightarrow \infty$, which proves the lemma. $\square$

3.2 Discarding the Lower Degree Polynomials

This subsection provides some estimates for the weighted orthonormal polynomials of degree j with $0\le j< m_N$, where $m_N$ is the number in (3.4), and we shall prove that the weighted polynomials of lower degree can be neglected in the sum (3.1).

First we consider the case when $N(\tau _{*}-\delta _N)\le j\le m_N$ where $\tau _*$ is the number in (3.3) and $\delta _N= N^{-\frac{1}{2}}\log N$. This means that for $\tau _j = j/N$,

$$\begin{aligned} \tau _{*}-\delta _N \le \tau _j \le \tau _{*} + M/\sqrt{N}. \end{aligned}$$

(3.10)

Recall that $\rho _{*}q'(\rho _{*})=2\tau _{*}$ and $rq'(r)$ is increasing. Since Q is strictly subharmonic near $|\zeta |=\rho _{*}$, for each $\tau$ in this region (3.10) there exists $\rho _\tau$ in a neighborhood of $\rho _{*}$ such that $\rho _{\tau }q'(\rho _\tau )=2\tau$ and $\Delta Q(\rho _\tau )>\epsilon$ for some positive number $\epsilon$ which is independent of $\tau$. We observe that $V_{\tau _j}'(\rho _{\tau _j})=0$ and $V_{\tau _j}''(\rho _{\tau _j})=4\Delta Q(\rho _{\tau _j})$ and obtain that

$$\begin{aligned} V_{\tau _j}(r) = V_{\tau _j}(\rho _{\tau _j}) + {2\Delta Q(\rho _{\tau _j})}(r-\rho _{\tau _j})^2 +O(|r-\rho _{\tau _j}|)^3, \quad r\rightarrow \rho _{\tau _j},\qquad \end{aligned}$$

(3.11)

where the O-constant is uniform for all j and r in a neighborhood of $\rho _*$. We also observe that the following asymptotic expansion holds:

$$\begin{aligned} 2(\tau _{*}-\tau )= & {} \rho _{*} q'(\rho _{*})- \rho _\tau q'(\rho _\tau )=4\rho _{*} \Delta Q(\rho _{*})(\rho _{*}-\rho _\tau )+O(|\rho _{*}-\rho _\tau |)^2,\\&\quad \rho _\tau \rightarrow \rho _{*}, \end{aligned}$$

which implies the asymptotic relation

$$\begin{aligned} \rho _{*}-\rho _{\tau } = \frac{\tau _{*}-\tau }{2\rho _{*} \Delta Q(\rho _{*})}+O(|\tau _{*}-\tau |)^2,\quad \tau \rightarrow \tau _{*}. \end{aligned}$$

(3.12)

Here, the O-constant is uniform for all $\tau$ in a neighborhood of $\tau _*$.

The following lemma gives an estimate of $\Vert \zeta ^j\Vert _{L^2(\mu _N)}$. For the statement, we write

$$\begin{aligned} \varphi _{\alpha }(\xi ) = \int _{0}^{\infty } s^{\alpha }e^{-\frac{1}{2}(s-\xi )^2}\,ds\quad \text{ and }\quad \xi _{\tau } = \sqrt{4N\Delta Q(\rho _*)}(\rho _*-\rho _\tau ). \end{aligned}$$

(3.13)

Lemma 3.3

We obtain for each j with $N(\tau _{*}-\delta _N)\le j\le m_N$

$$\begin{aligned} \Vert \zeta ^j\Vert ^2_{L^2(\mu _N)} = C N^{-\frac{\alpha +1}{2}} e^{-NV_{\tau _j}(\rho _{\tau _j})}\varphi _{\alpha }(\xi _{\tau _j})(1+o(1)),\quad N\rightarrow \infty , \end{aligned}$$

where the constant C is given by $C= 2\rho _{*} (4\Delta Q(\rho _{*}))^{-\frac{\alpha +1}{2}}$.

Proof

By (3.12), there exist positive constants $c_1$ and $c_2$ such that for all j

$$\begin{aligned} -c_1 M\cdot N^{-1/2} \le \rho _{*} - \rho _{\tau _j} \le c_2 \,\delta _N. \end{aligned}$$

Similar to the proof of Lemma 3.1, we derive the estimate

$$\begin{aligned} \Vert \zeta ^j\Vert ^2_{L^2(\mu _N)} = 2\rho _{*} \,e^{-NV_{\tau _j}(\rho _{\tau _j})} \int _{\rho _{\tau _j}-\delta _N}^{\rho _{*}} (\rho _{*} - r)^{\alpha } e^{-2N\Delta Q(\rho _{*})(r-\rho _{\tau _j})^2}dr\,(1+o(1)) \end{aligned}$$

(3.14)

as $N\rightarrow \infty$ by using the expansion (3.11). Changing the variable $s=\sqrt{4N\Delta Q(\rho _{*})}(r-\rho _{\tau _j})$ in (3.14), we obtain

$$\begin{aligned} \Vert \zeta ^j\Vert ^2_{L^2(\mu _N)} = 2\rho _{*} \, e^{-NV_{\tau _j}(\rho _{\tau _j})}(4N\Delta Q(\rho _{*}))^{-\frac{\alpha +1}{2}}\varphi _{\alpha }(\xi _{\tau _j}) \,(1+o(1)),\quad N\rightarrow \infty , \end{aligned}$$

which completes the proof. $\square$

Lemma 3.4

Let ${\mathcal {K}}$ be a compact subset of ${\mathbb {H}}_{+}$. We obtain for $\zeta =\rho _{*} - \gamma _N z$

$$\begin{aligned} \gamma _N^2\sum _{j=N(\tau _{*}-\delta _N)}^{m_N} |p_{N,j}(\zeta )|^2 e^{-NQ_N^{{\mathcal {D}}}(\zeta )}=O(N^{-(1+\frac{\alpha }{2})}\log N), \quad N\rightarrow \infty , \end{aligned}$$

where the O-constant is uniform for $z\in {\mathcal {K}}$.

Proof

Observe that for each j

$$\begin{aligned} |p_{N,j}(\zeta )|^2 e^{-NQ_N^{{\mathcal {D}}}(\zeta )} =\frac{N^{\frac{\alpha +1}{2}}}{C\varphi _{\alpha }(\xi _{\tau _j})}|\zeta |^{2j} e^{-N (Q_N(\zeta ) -V_{\tau _j}(\rho _{\tau _j}))}\cdot {{\mathbf {1}}}_{{\mathcal {D}}}(\zeta )\,(1+o(1)) \end{aligned}$$

by Lemma 3.3. Here, $\varphi _{\alpha }$ and $\xi _\tau$ are defined in (3.13) before Lemma 3.3 and C is the constant in Lemma 3.3. Using the expansions (3.11) and (3.12), we obtain

$$\begin{aligned}&|p_{N,j}(\zeta )|^2 e^{-NQ_N^{{\mathcal {D}}}(\zeta )}\\&\quad = \frac{N^{\frac{\alpha +1}{2}}}{C\varphi _{\alpha }(\xi _{\tau _j})}(\rho _*-|\zeta |)^{\alpha } e^{-N (V_{\tau _j}(|\zeta |) -V_{\tau _j}(\rho _{\tau _j}))} \cdot {{\mathbf {1}}}_{{\mathcal {D}}}(\zeta )\,(1+o(1)) \\&\quad =\frac{N^{\frac{\alpha +1}{2}}(\gamma _N {\text {Re}}z)^{\alpha }}{C\varphi _{\alpha }(\xi _{\tau _j})} e^{-2N\Delta Q(\rho _{\tau _j})(\rho _{*}-\rho _{\tau _j} - \gamma _N {\text {Re}}z)^2}\cdot {{\mathbf {1}}}_{{\mathbb {H}}_{+}}(z)\,(1+o(1))\\&\quad =C_1N^{\frac{1-\alpha }{2}} ({\text {Re}}z)^{\alpha } \frac{e^{-\frac{1}{2}\xi _{\tau _j}^2}}{\varphi _{\alpha }(\xi _{\tau _j})}\cdot {{\mathbf {1}}}_{{\mathbb {H}}_{+}}(z)\,(1+o(1)) \end{aligned}$$

for some constant $C_1$ which is independent of j. Here $o(1)\rightarrow 0$ uniformly for $z\in {\mathcal {K}}$ as $N\rightarrow \infty$. By the definition of $\xi _{\tau _j}$ in (3.13), $\xi _{\tau _j}$ is in the range

$$\begin{aligned} -c_1 M \le \xi _{\tau _j} \le c_2 \log N \end{aligned}$$

for some positive constant $c_1$ and $c_2$. Noting that for all $\xi$ with $\xi \ge -c_1M$ and $\alpha >-1$

$$\begin{aligned} e^{\frac{1}{2}\xi ^2} \varphi _{\alpha }(\xi ) = \int _{0}^{\infty } s^\alpha e^{-\frac{1}{2}s^2} e^{s\xi } \,ds \ge \int _{0}^{\infty } s^{\alpha } e^{-\frac{1}{2}s^2} e^{-c_1sM} ds \ge C_2M^{-(\alpha +1)} \end{aligned}$$

for some constant $C_2$, we obtain a bound $|p_{N,j}|^2 e^{-NQ_N^{{\mathcal {D}}}} \lesssim M^{\alpha +1}N^{\frac{1-\alpha }{2}}$ for $z\in {\mathcal {K}}$. Since the sum contains $O(N\delta _N)$ terms and $\gamma _N = O(N^{-1})$, there exists a positive constant $C_3$ such that for $z\in {\mathcal {K}}$ and sufficiently large N

$$\begin{aligned} \gamma _N^2 \sum _{N(\tau _{*}-\delta _N)}^{m_N} |p_{N,j}(\zeta )|^2 e^{-NQ_N^{{\mathcal {D}}}(\zeta )}\le C_3 M^{\alpha +1} N^{-\frac{\alpha +1}{2}}\delta _N, \end{aligned}$$

which completes the proof. $\square$

For the lower degree polynomials with $j \le N(\tau _{*}-\delta _N)$, the localization of the potential Q to ${\mathcal {D}}= D(0,\rho _{*})$ does not have considerable effect on the asymptotics of weighted polynomials because the weighted orthogonal polynomial $|p_{N,j}|^2 e^{-NQ_N}$ tends to decay exponentially outside the set $D(0,\rho _{\tau _j})$ which is at least $O(\delta _N)$-distance away from the hard wall ${\partial }{\mathcal {D}}$. The sum of lower degree terms with $j \le N(\tau _{*}-\delta _N)$ can be estimated as follows:

Lemma 3.5

Let ${\mathcal {K}}$ be a compact subset of ${\mathbb {H}}_{+}$. We obtain for $\zeta = \rho _{*} - \gamma _N z$

$$\begin{aligned} \gamma _N^2 \sum _{j=0}^{N(\tau _{*}-\delta _N)} |p_{N,j}(\zeta )|^2 e^{-NQ_{N}^{{\mathcal {D}}}(\zeta )} = O(e^{-c(\log N)^2}),\quad N\rightarrow \infty , \end{aligned}$$

where c is a positive constant and the O-constant is uniform for $z\in {\mathcal {K}}$.

Proof

Write $\tau _{*}^{(0)}=\tau _{*}-\delta _N$ and $\tau _{*}^{(1)}=\tau _{*}-\frac{1}{2}\delta _N$. Recall that $\rho _\tau$ denotes the unique number in a neighborhood of $\rho _*$ satisfying $\rho _\tau q'(\rho _\tau )=2\tau$. We write $\rho _{*}^{(0)}=\rho _{\tau _{*}^{(0)}}$ and $\rho _{*}^{(1)}=\rho _{\tau _{*}^{(1)}}$ for simplicity. We first observe that by (3.12) there exists a constant $c_1>0$ such that $\rho _{*} - \rho _{*}^{(1)} > c_1\delta _N$ and $\rho _{*}^{(1)}-\rho _{*}^{(0)}> c_1\delta _N$ simultaneously. Since for each $\tau \le \tau _{*}^{(0)}$ it holds that $V_{\tau }(r) \le V_{\tau }(\rho _{*}^{(1)})$ for all r with $\rho _{*}^{(0)}\le r \le \rho _{*}^{(1)}$, we obtain that for j with $j\le N\tau _{*}^{(0)}$

$$\begin{aligned} \Vert \zeta ^j\Vert ^2_{L^2(\mu _N)}\ge \int _{\rho _{*}^{(0)}}^{\rho _{*}^{(1)}} 2r(\rho _{*} - r)^{\alpha } e^{h(r)} e^{-NV_{\tau _j}(r)} dr \ge C_1 \delta _N^{\alpha +1} e^{-NV_{\tau _j}(\rho _{*}^{(1)})} \end{aligned}$$

(3.15)

for some constant $C_1>0$, where $\tau _j = j/N$. Observing that for $\tau \le \tau _*^{(0)}$ and $r=|\rho _{*}-\gamma _N z|$ with $z\in {\mathcal {K}}$

$$\begin{aligned} V_{\tau }(r)- V_{\tau }(\rho _{*}^{(1)})&= V_{\tau _{*}^{(1)}}(r)-V_{\tau _{*}^{(1)}}(\rho _{*}^{(1)})+2(\tau -\tau _{*}^{(1)})\log \frac{\rho _{*}^{(1)}}{r}\\&\ge 2\Delta Q(\rho _{*}^{(1)}) (r-\rho _{*}^{(1)})^2 + O(r-\rho _*^{(1)})^3 \ge c_2 \,\delta _N^2 \end{aligned}$$

for some constant $c_2>0$, we have for all j with $j\le N\tau _{*}^{(0)}$

$$\begin{aligned} e^{-N(V_{\tau _j}(r)- V_{\tau _j}(\rho _{*}^{(1)}))} = O(e^{-c_2(\log N)^2}) \end{aligned}$$

as $N\rightarrow \infty$. Combining this with (3.15) gives

$$\begin{aligned} |p_{N,j}(\zeta )|^2 e^{-NQ_N(\zeta )} = e^{h(\zeta )}(\rho _{*} - |\zeta |)^{\alpha }\frac{e^{-NV_{\tau _j}(|\zeta |)}}{\Vert \zeta ^j\Vert ^2_{L^2(\mu _N)}} \le C_2 \gamma _N^{\alpha } \delta _N^{-(\alpha +1)} e^{-c_2(\log N)^2}. \end{aligned}$$

(3.16)

Since the sum has O(N) terms and each term has a bound as (3.16), we conclude that there exists a constant $c>0$ such that as $N\rightarrow \infty$,

$$\begin{aligned} \gamma _N^2 \sum _{j= 0}^{N(\tau _{*}-\delta _N)}|p_{N,j}(\zeta )|^2e^{-NQ_N(\zeta )} = O(e^{-c(\log N)^2}), \end{aligned}$$

which completes the proof. $\square$

Combining Lemmas 3.4 and 3.5, we obtain that for $\zeta = \rho _{*} - \gamma _N z$

$$\begin{aligned} \gamma _N^2 \sum _{j=0}^{m_N}|p_{N,j}(\zeta )|^2 e^{-NQ_{N}(\zeta )} = O(N^{-(1+\frac{\alpha }{2})}\log N),\quad N\rightarrow \infty . \end{aligned}$$

Here, O-constant is uniform in compact subsets of ${\mathbb {H}}_{+}$. By the Cauchy–Schwarz inequality, we have

$$\begin{aligned}&\gamma _N^2 \sum _{j=0}^{m_N}p_{N,j}(\zeta ){\bar{p}}_{N,j}(\eta ) e^{-\frac{N}{2}(Q_{N}(\zeta )+Q_{N}(\eta ))} \\&\quad \le \left( \gamma _N^2 \sum _{j=0}^{m_N} |p_{N,j}(\zeta )|^2 e^{-NQ_{N}(\zeta )}\right) ^{\frac{1}{2}} \left( \gamma _N^2 \sum _{j=0}^{m_N} |p_{N,j}(\eta )|^2 e^{-NQ_{N}(\eta )}\right) ^{\frac{1}{2}} \\&\quad = O(N^{-(1+\frac{\alpha }{2})}\log N), \end{aligned}$$

Hence, the rescaled correlation kernel can be written as

$$\begin{aligned} K_N(z,w) = K_N^{\#}(z,w) + o(1), \end{aligned}$$

where $o(1)\rightarrow 0$ as $N\rightarrow \infty$ locally uniformly in ${\mathbb {H}}_{+}$. Now Lemma 3.2 completes the proof of Theorem 2.1.

3.3 Maximal Modulus

In this subsection, we prove Theorem 2.2. We first observe that the distribution function of $|\zeta |_N = \max _{1\le j\le N}|\zeta _j|$ is expressed as the gap probability that there is no particle outside a disk, i.e.,

$$\begin{aligned} {\mathbb {P}}_N(|\zeta |_N \le r) = \int _{D(0,r)^N}{{\mathbf {P}}}_{N,1}(\zeta _1,\ldots ,\zeta _N)\,dA(\zeta _1)\cdots dA(\zeta _N). \end{aligned}$$

Since $Q_N$ is radially symmetric, the determinantal structure of the system gives that

$$\begin{aligned} {\mathbb {P}}_N(|\zeta |_N \le r) = \prod _{j=0}^{N-1} \left( 1 - \int _{{\mathcal {D}}{\setminus } D(0,r)} |p_{N,j}|^2 e^{-NQ_N} dA \right) \end{aligned}$$

(3.17)

for $r\le \rho _{*}$. See [38, Section 15.1] and [18] for the computation of gap probabilities. Also note that it was observed in [34] that in the case when $Q(\zeta ) = |\zeta |^2$, the maximal modulus of the particles has the same distribution as that of independent random variables.

Write

$$\begin{aligned} a_N = \frac{1}{2}\,\gamma _N^{\frac{\alpha +2}{\alpha +1}}\left( \frac{\rho _{*}}{\Gamma (\alpha +3)}\right) ^{-\frac{1}{\alpha +1}},\quad \gamma _N = \frac{\rho _{*}}{N(1-\tau _{*})} \end{aligned}$$

(3.18)

where $2\tau _* = \rho _*q'(\rho _*)$. The rescaled maximal modulus

$$\begin{aligned} \omega _N = a_N^{-1}\cdot (\rho _{*} -|\zeta |_N ) \end{aligned}$$

has a distribution

$$\begin{aligned} {\mathbb {P}}_N\left( \omega _N \ge x\right) = {\mathbb {P}}_N\left( |\zeta |_N \le \rho _{*} - a_N \,x\right) . \end{aligned}$$

We consider the sum

$$\begin{aligned} I_N(x):=\sum _{j=0}^{N-1}\int _{{\mathcal {D}}{\setminus } D(0,\rho _N(x))}|p_{N,j}|^2 e^{-NQ_N} dA, \quad \rho _N(x) = \rho _{*} - a_N\, x,\qquad \end{aligned}$$

(3.19)

and obtain the following lemma.

Lemma 3.6

We have that for $x\ge 0$,

$$\begin{aligned} \lim _{N\rightarrow \infty } I_N(x) = x^{\alpha +1}. \end{aligned}$$

Here the convergence is uniform in ${\mathbb {R}}_{+}$.

Proof

As in Sect. 3.1, we write the integral in (3.19) in terms of the function $V_{\tau }$,

$$\begin{aligned} I_N(x) = \sum _{j=0}^{N-1} \Vert \zeta ^j\Vert _{L^2(\mu _N)}^{-2}\int _{\rho _N(x)}^{\rho _{*}} 2r(\rho _{*}-r)^{\alpha }e^{h(r)}e^{-NV_{\tau _j}(r)} \, dr, \end{aligned}$$

where $V_{\tau }(r) = q(r) - 2\tau \log r$ and $\tau _j = j/N$. First fix j with $m_N \le j \le N-1$ where $m_N =N\tau _{*}+M\sqrt{N}$ for sufficiently large M. Let ${\mathcal {K}}$ be a compact subset of ${\mathbb {R}}_{+}$. From the proofs of Lemmas 3.1 and 3.2, we obtain that for all $x\in {\mathcal {K}}$

$$\begin{aligned}&\Vert \zeta ^j\Vert _{L^2(\mu _N)}^{-2}\int _{\rho _N(x)}^{\rho _*} 2r(\rho _*-r)^{\alpha }e^{h(r)}e^{-NV_{\tau _j}(r)} \, dr \nonumber \\&\quad = \frac{1}{\Gamma (\alpha +1)}\left( \frac{2N(\tau _j-\tau _{*})}{\rho _*}\right) ^{\alpha +1}\nonumber \\&\qquad \int _{\rho _N(x)}^{\rho _*} (\rho _*-r)^{\alpha } e^{-N(V_{\tau _j}(r)-V_{\tau _j}(\rho _*))} dr \,(1+o(1))\nonumber \\&\quad = \frac{1}{\Gamma (\alpha +1)}\left( \frac{2N(\tau _j-\tau _{*})}{\rho _*}\right) ^{\alpha +1} \int _{0}^{a_N x} s^{\alpha } e^{-\frac{2N}{\rho _{*}}(\tau _j-\tau _{*})\cdot s} ds \,(1+ o(1))\nonumber \\&\quad = \frac{1}{\Gamma (\alpha +1)} \int _{0}^{b_{\tau _j} x} t^{\alpha } e^{-t} dt\, (1+o(1)) = \frac{\gamma (\alpha +1, b_{\tau _j} \,x)}{\Gamma (\alpha +1)} \, (1+o(1)), \end{aligned}$$

(3.20)

where $\gamma (a,x)$ is the lower incomplete gamma function and $b_{\tau } = \frac{2N(\tau -\tau _{*})}{\rho _{*}} \cdot a_N$. Here, $o(1)\rightarrow 0$ uniformly in ${\mathcal {K}}$ as $N\rightarrow \infty$ and the error bound also can be taken uniformly in j with $m_N\le j \le N-1$. The definition of $a_N$ in (3.18) implies that

$$\begin{aligned} b_{\tau _j} = O\left( N^{-\frac{1}{\alpha +1}}(\tau _j-\tau _{*})\right) . \end{aligned}$$

Using the asymptotic expansion of the lower incomplete gamma function near 0, we have

$$\begin{aligned} \gamma (\alpha +1, b_{\tau _j} x) = \frac{1}{\alpha +1}(b_{\tau _j} x)^{\alpha +1} + O(b_{\tau _j}^{\alpha +2}),\quad N\rightarrow \infty . \end{aligned}$$

Thus, the integral (3.20) can be estimated as

$$\begin{aligned} \Vert \zeta ^j\Vert _{L^2(\mu _N)}^{-2}\int _{\rho _N(x)}^{\rho _{*}} 2r(\rho _{*}-r)^{\alpha }e^{h(r)}e^{-NV_{\tau _j}(r)} \, dr = \frac{(b_{\tau _j} x)^{\alpha +1}}{\Gamma (\alpha +2)}\,(1+o(1)). \end{aligned}$$

Taking the sum over all j with $m_N \le j \le N-1$ as in the proof of Lemma 3.2, we obtain

$$\begin{aligned} I_N^{\#}(x):= \sum _{j= m_N}^{N-1} \frac{(b_{\tau _j} x)^{\alpha +1}}{\Gamma (\alpha +2)} = \frac{(\alpha +2)\,x^{ \alpha +1}}{N(1-\tau _{*})^{\alpha +2}} \sum _{j= m_N}^{N-1} (\tau _j-\tau _{*})^{\alpha +1}, \end{aligned}$$

and by the Riemann sum approximation with step length 1/N, we have

$$\begin{aligned} I_N^{\#}(x)= \frac{(\alpha +2)\,x^{ \alpha +1}}{(1-\tau _{*})^{\alpha +2}} \int _{0}^{1-\tau _{*}} s^{\alpha +1} ds \,(1+o(1)) = x^{\alpha +1}\,(1+o(1)),\quad N\rightarrow \infty . \end{aligned}$$

It is a direct result from Sect. 3.2 that all the other terms are negligible in the sum $I_N(x)$. Indeed, by Lemmas 3.4 and 3.5, for all $x\in {\mathcal {K}}$

$$\begin{aligned} \sum _{j=0}^{m_N}\int _{{\mathcal {D}}{\setminus } D(0,\rho _N(x))}|p_{N,j}|^2 e^{-NQ_N} dA = o(1) \end{aligned}$$

as $N\rightarrow \infty$. Hence, the proof is complete. $\square$

Proof of Theorem 2.2

It follows from Lemma 3.6 and (3.17) that

$$\begin{aligned} \log {\mathbb {P}}_N(\omega \ge x) = -I_N(x)+o(1) = -x^{\alpha +1} +o(1) \end{aligned}$$

locally uniformly in x as $N\rightarrow \infty$. Hence, we completed the proof. $\square$

4 Rescaled Ward’s Equation at the Hard Wall

In this section, we analyze a rescaled version of limiting Ward’s equation

$$\begin{aligned} {\bar{\partial }}C(z) = R(z) -\Delta \log R(z),\quad z\in {\mathbb {H}}_{+}\end{aligned}$$

(4.1)

called the hard wall Ward’s equation and prove Theorem 2.3.

We shall explain Ward identities briefly which has been proved in [4, Proposition 3.1], [5, Theorem 4.1]. Ward identities we consider here are identities of correlation functions obtained from the invariance of the partition function of the particle system under the reparameterization. See e.g., [46, 47] for the method of Ward identities in physics. We also refer to [33, Appendix 6] for Ward identities in the context of conformal field theory. While Ward identities to be described below shows a global relation between correlation functions, the rescaled version of Ward’s equation (4.1) gives a local information of them.

4.1 Ward Identities

We borrow some notations from the literature [4, 5]. For a test function $\psi \in C^{\infty }_0({\mathcal {D}})$, we define random variables

$$\begin{aligned} \mathrm {I}_N[\psi ]&= \frac{1}{2}\sum _{j\ne k}\frac{\psi (\zeta _j)-\psi (\zeta _k)}{\zeta _j-\zeta _k}, \quad \mathrm {II}_N[\psi ] = N\sum _{j=1}^{N} {\partial }Q_N(\zeta _j)\cdot \psi (\zeta _j),\\ \mathrm {III}_N[\psi ]&=\sum _{j=1}^{N} {\partial }\psi (\zeta _j) \end{aligned}$$

where $\{\zeta _j\}_{j=1}^N$ is the Coulomb gas system associated with an external potential $Q_{N}^{{\mathcal {D}}}$. Consider the Hamiltonian of the system

$$\begin{aligned} H_N(\zeta _1, \ldots , \zeta _N) = -\sum _{j\ne k}\log |\zeta _k - \zeta _j| + N\sum _{j=1}^{N}Q_N^{{\mathcal {D}}}(\zeta _j). \end{aligned}$$

We write ${{\mathbf {E}}}_N$ for the expectation with respect to the Boltzmann–Gibbs density defined in (1.1) associated with the potential $Q_N^{{\mathcal {D}}}$ at inverse temperature $\beta =1$. The distributional form of Ward identity from [4, 5] is the relation that

$$\begin{aligned} {{\mathbf {E}}}_{N}[\mathrm {I}_N[\psi ]-\mathrm {II}_N[\psi ]+\mathrm {III}_N[\psi ]]=0. \end{aligned}$$

(4.2)

A short proof for this identity using the integration by parts from [10, Section 4.2] is as follows. Consider the expectation ${{\mathbf {E}}}_{N}[{\partial }\psi (\zeta _j)]$ for a test function $\psi \in C_0^{\infty }({\mathcal {D}})$. The integration by parts gives that for all j

$$\begin{aligned} {{\mathbf {E}}}_{N}[{\partial }\psi (\zeta _j)] = {{\mathbf {E}}}_{N}[{\partial }_{\zeta _j} H_N(\zeta _1,\ldots ,\zeta _N) \cdot \psi (\zeta _j)] , \end{aligned}$$

which proves (4.2).

Now we rescale the system $\Phi ^{{\mathcal {D}}}$ at the hard wall and derive an equation. With rescaling via

$$\begin{aligned} \zeta = \rho _{*} - \gamma _N z, \quad \eta = \rho _{*} - \gamma _N w, \end{aligned}$$

we write the rescaled correlation kernel and correlation functions as

$$\begin{aligned} K_N(z,w) = \gamma _N^2 {\mathbf {K}}_N(\zeta , \eta )\quad \text{ and }\quad R_{N,k}(z,w) = \gamma _N^{2k}\, {\mathbf {R}}_{N,k}(\zeta ,\eta ). \end{aligned}$$

Write $R_{N} = R_{N,1}$ and ${\mathbf {R}}_{N}={\mathbf {R}}_{N,1}$ for simplicity. Now we define the Berezin kernel

$$\begin{aligned} B_N(z,w) = \frac{|K_N(z,w)|^2}{K_N(z,z)}=\frac{R_N(z)R_N(w) - R_{N,2}(z,w)}{R_N(z)}, \end{aligned}$$

and the Cauchy transform

$$\begin{aligned} C_N(z) = \int _{{\mathbb {C}}} \frac{B_N(z,w)}{z-w} dA(w). \end{aligned}$$

Lemma 4.1

We obtain that

$$\begin{aligned} {\bar{\partial }}C_N(z) = R_N(z) - \Delta \log R_N(z) + o(1), \end{aligned}$$

where $o(1)\rightarrow 0$ locally uniformly in ${\mathbb {H}}_{+}$ as $N\rightarrow \infty$.

Proof

We apply the argument in [5] to the hard wall case in a straightforward way. As in [5, Theorem 7.1], we consider a test function $\psi$ whose support is contained in ${\mathbb {H}}_{+}$. Then for sufficiently large N, the test function $\psi _N$ defined by

$$\begin{aligned} \psi _N(\zeta )=\psi (\gamma _N^{-1}(\rho _{*}-\zeta )) \end{aligned}$$

has its support in ${\mathcal {D}}$. Now we write the expectation of random variables in the Ward identity (4.2) in terms of the rescaled correlation functions as follows:

$$\begin{aligned} {{\mathbf {E}}}_N\,\mathrm {I}_N[\psi _N]&= \frac{1}{2}\int \!\!\!\int _{{\mathbb {C}}^2}\frac{\psi _N(\zeta )-\psi _N(\eta )}{\zeta -\eta }\, {\mathbf {R}}_{N,2}(\zeta ,\eta ) \,dA(\zeta )dA(\eta ) \\&=-\frac{1}{2\gamma _N}\int \!\!\!\int _{{\mathbb {C}}^2}\frac{\psi (z)-\psi (w)}{z-w} \, R_{N,2}(z,w)\, dA(z) dA(w) \\&=-\gamma _N^{-1}\int _{{\mathbb {C}}} \psi (z) \, dA(z)\int _{{\mathbb {C}}} \frac{R_{N,2}(z,w)}{z-w}dA(w), \\ {{\mathbf {E}}}_N\,\mathrm {II}_N[\psi _N]&=N \int _{{\mathbb {C}}} {\partial }Q_N(\zeta )\, \psi _N(\zeta )\, {\mathbf {R}}_{N}(\zeta )\,dA(\zeta )\\&=N\int _{{\mathbb {C}}} {\partial }Q_N(\rho _{*} -\gamma _N z) \, \psi (z) \,R_{N}(z)\,dA(z),\\ {{\mathbf {E}}}_N\mathrm {III}_N[\psi _N]&= \int _{{\mathbb {C}}} {\partial }\psi _N(\zeta )\, {\mathbf {R}}_{N}(\zeta )\,dA(\zeta )=-\gamma _N^{-1} \int _{{\mathbb {C}}}{\partial }\psi (z)\,R_{N}(z)\,dA(z) \\&= \gamma _N^{-1}\int _{{\mathbb {C}}} {\partial }R_{N}(z)\, \psi (z) \,dA(z). \end{aligned}$$

Since $\psi$ is arbitrary, we obtain from Ward identity (4.2) that

$$\begin{aligned} \int _{{\mathbb {C}}} \frac{R_{N,2}(z,w)}{z-w} dA(w) = -N\gamma _N {\partial }Q_N(\rho _{*} - \gamma _N z)\cdot R_{N}(z) + {\partial }R_N(z) \end{aligned}$$

in the sense of distributions in ${\mathbb {H}}_{+}$. Dividing each side by $R_N$ and taking a ${\partial }$-derivative, we have

$$\begin{aligned} R_N(w)-{\bar{\partial }}C_N(z) = \Delta \log R_N(z)+o(1) \end{aligned}$$

since $N\gamma _N^2 \Delta Q_N(\rho _{*}-\gamma _N z) = o(1)$ locally uniformly in ${\mathbb {H}}_{+}$ as $N\rightarrow \infty$. $\square$

4.2 Mass-one Equation and Hard Wall Ward’s Equation

Let $K_{f}$ be a kernel of the form

$$\begin{aligned} K_{f}(z,w) = (2{\text {Re}}z)^{\frac{\alpha }{2}}(2{\text {Re}}w)^{\frac{\alpha }{2}}\int _{0}^{\infty } f(t)\,e^{-t(z+{\bar{w}})}\, dt,\quad z,\,w\in {\mathbb {H}}_{+}\end{aligned}$$

for some Borel measurable function f on ${\mathbb {R}}_{+}$.

Lemma 4.2

The mass-one equation

$$\begin{aligned} \int _{{\mathbb {H}}_{+}} |K_f(z,w)|^2 dA(w) = K_f(z,z),\quad z\in {\mathbb {H}}_{+}\end{aligned}$$

holds if and only if $f(s)=\Gamma (\alpha +1)^{-1} s^{\alpha +1}\cdot {{\mathbf {1}}}_{E}(s)$ almost everywhere for some Borel set E in ${\mathbb {R}}_{+}$.

Proof

Write $z=x+iy$ and $w=u+iv$ for $x,y,u,v \in {\mathbb {R}}$ and compute the integral in the mass-one equation as follows:

$$\begin{aligned}&\int _{{\mathbb {H}}_{+}}|K_f(z,w)|^2 \,dA(w)\\&\quad =(2{\text {Re}}z)^{{\alpha }}\!\!\int _{{\mathbb {H}}_{+}}\int _{0}^{\infty }\!\!\!\!\int _{0}^{\infty }(2{\text {Re}}w)^{{\alpha }} e^{-s(z+{\bar{w}})}e^{-t({\bar{z}}+w)}f(s)f(t)\,ds \,dt \,dA(w)\\&\quad =\frac{(2x)^{{\alpha }}}{\pi }\!\!\int _{0}^{\infty }\!\!\!\!\int _{0}^{\infty }\!\!\!\!\int _{0}^{\infty }\!\!\!\!\int _{{\mathbb {R}}} (2u)^{{\alpha }}e^{-x(s+t)}e^{iy(t-s)}e^{-u(s+t)}e^{iv(s-t)}f(s)f(t)\,dv\,du\,ds\,dt\\&\quad =(2x)^{{\alpha }}\!\!\int _{0}^{\infty }\!\!\!\!\int _{0}^{\infty } 2 (2u)^{{\alpha }}e^{-2x \cdot s} e^{-2s \cdot u}\, f(s)^2 du\,ds\\&\quad = (2x)^{\alpha }\int _{0}^{\infty } e^{-2x\cdot s}\, f(s)^2 \frac{\Gamma (\alpha +1)}{s^{\alpha +1}}\,ds. \end{aligned}$$

Thus, the mass-one equation holds if and only if for all $x>0$

$$\begin{aligned} \int _{0}^{\infty } e^{-2x\cdot s} f(s) ^2 \frac{\Gamma (\alpha +1)}{s^{\alpha +1}}\, ds = \int _{0}^{\infty } e^{-2x\cdot s} f(s) \,ds, \end{aligned}$$

which implies that $f(s) =\Gamma (\alpha +1)^{-1} s^{\alpha +1}{{\mathbf {1}}}_{E}(s)$ almost everywhere for some Borel measurable set E in ${\mathbb {R}}_{+}$. $\square$

Lemma 4.3

The hard wall Ward’s equation

$$\begin{aligned} {\bar{\partial }}C(z) = R(z) -\Delta \log R(z),\quad z\in {\mathbb {H}}_{+}\end{aligned}$$

holds for $K_f$ if and only if there exists a connected set E in ${\mathbb {R}}_{+}$ such that $f(s) = \Gamma (\alpha +1)^{-1} s^{\alpha +1} \cdot {{\mathbf {1}}}_{E}(s)$ almost everywhere in ${\mathbb {R}}_{+}$.

Proof

First we compute the Cauchy transform as follows: for $z=x+iy$

$$\begin{aligned} R(z)\, C(z)&=\int _{{\mathbb {H}}_{+}} |K_f(z,w)|^2 \frac{1}{z-w}\, dA(w) \\&=\frac{(2x)^{\alpha }}{\pi }\!\int _{0}^{\infty }\!\!\!\!\int _{0}^{\infty }\!f(s)\,f(t)\!\int _{-\infty }^{\infty }\int _{-x}^{\infty } (2(u+x))^{\alpha } e^{-(s+t)(u+2x)}\,\\&\quad \frac{e^{i(s-t)v}}{-(u+iv)}\,du\,dv \, ds\,dt. \end{aligned}$$

Using the fact that

$$\begin{aligned} \int _{-\infty }^{\infty }\frac{e^{i(s-t)v}}{u+iv}\frac{dv}{\pi }= {\left\{ \begin{array}{ll} -2 e^{u(t-s)}\,{{\mathbf {1}}}_{t>s},&{}\quad \mathrm {if}\quad u<0,\\ 2e^{u(t-s)}\,{{\mathbf {1}}}_{t<s}, &{}\quad \mathrm {if} \quad u>0, \end{array}\right. } \end{aligned}$$

we obtain that $R(z)C(z)=-L_1(z) + L_2(z),$ where

$$\begin{aligned} L_1(z) = (2x)^{\alpha }\int _{0}^{\infty }\!\!\!\int _{0}^{\infty } f(s)f(t) \!\int _{0}^{\infty } 2(2(u+x))^{\alpha }e^{-2x(s+t)}e^{-2s\cdot u}du \, ds\,dt, \end{aligned}$$

and

$$\begin{aligned} L_2(z) = (2x)^{\alpha }\int _{0}^{\infty }\!\!\!\int _{0}^{t}f(s)f(t)\!\int _{-x}^{\infty }2(2(u+x))^{\alpha }e^{-2x(s+t)} e^{-2s\cdot u} \,du\, ds\,dt. \end{aligned}$$

A simple calculation gives

$$\begin{aligned} L_1(z)&= (2x)^{\alpha } \int _{0}^{\infty }\!\!\!\int _{0}^{\infty } f(s)f(t)\,e^{-2x\cdot t} s^{-(\alpha +1)} \Gamma (\alpha +1, 2xs) \,ds\,dt \\&= R(z)\int _{0}^{\infty } f(s)\,s^{-(\alpha +1)} \Gamma (\alpha +1, 2xs)\,ds, \end{aligned}$$

and

$$\begin{aligned} L_2(z) = (2x)^{\alpha }\int _{0}^{\infty }\!\!\!\int _{0}^{t} f(s)f(t)\, e^{-2x\cdot t} s^{-(\alpha +1)} \Gamma (\alpha +1) \,ds\,dt. \end{aligned}$$

Here, $\Gamma (\alpha +1,x)=\int _{x}^{\infty } t^{\alpha } e^{-t} dt$ is the upper incomplete gamma function. Since $L_1$, $L_2$, and R are functions of $x={\text {Re}}z$ only, we see that

$$\begin{aligned} -{\bar{\partial }}\left( \frac{L_1}{R}\right) =\int _{0}^{\infty } f(s) (2x)^{\alpha }\,e^{-2x\cdot s} ds =R(z). \end{aligned}$$

Thus, the hard wall Ward’s equation is equivalent to the relation

$$\begin{aligned} {\bar{\partial }}\left( \frac{L_2}{R}\right) = {\bar{\partial }}\left( \frac{L_1}{R} + C\right) = -R + {\bar{\partial }}{C} = - {\bar{\partial }}\left( \frac{{\partial }R}{R}\right) , \end{aligned}$$

which implies that

$$\begin{aligned} L_2 + {\partial }R = c R \end{aligned}$$

for some constant c. This relation can be written as

$$\begin{aligned} \int _{0}^{\infty }\!\!\!\int _{0}^{t}&f(s) f(t) \, e^{-2x\cdot t}s^{-(\alpha +1)}\Gamma (\alpha +1)\,ds\,dt = \int _{0}^{\infty } (t+c)\,f(t)\, e^{-2x\cdot t} dt \end{aligned}$$

so that we obtain

$$\begin{aligned} \int _{0}^{t}f(s) s^{-(\alpha +1)}\Gamma (\alpha +1)\,ds = t+c \end{aligned}$$

when $f(t)\ne 0$. This gives $f(t)= \Gamma (\alpha +1)^{-1} t^{\alpha +1}\cdot {{\mathbf {1}}}_{E}(t)$ a.e. for some subset E of ${\mathbb {R}}_{+}$. Hence, E is connected since for each $t\in E$, $|E \cap (0,t) | = t+c$ where |E| denotes Lebesgue measure of a set $E\subset {\mathbb {R}}$. $\square$