The complexity of CO-agent scheduling to minimize the total completion time and total number of tardy jobs

Abstract

In this paper, we revisit a two-agent scheduling problem on a single machine. In this problem, we have two competing agents A and B, which means that the job set of agent A and the job set of agent B are disjoint. The objective is to minimize the total completion time of agent A, under the constraint that the total number of tardy jobs of agent B is no larger than a given bound. The complexity of this problem was posed as open in Agnetis et al. (Oper Res 52:229–242, 2004). Leung et al. (Oper Res 58:458–469, 2010a, b. https://doi.org/10.1287/opre.1090.0744ec) showed that the problem is binary NP-hard. However, their NP-hardness proof has a flaw. Here, we present a new NP-hardness proof for this problem. Our research shows that the problem is still NP-hard even if the jobs of agent A have a common processing time.

1 Introduction

Suppose that there are two competing agents A and B, which compete to perform their respective jobs on a common machine. For each $X\in \{A, B\}$, we use ${{\mathcal {J}}}^{(X)}$ to denote the set of jobs of agent X, and the jobs in ${{\mathcal {J}}}^{(X)}$ are called X-jobs. The assumption of “competing agents” means that ${{\mathcal {J}}}^{(A)}\cap {{\mathcal {J}}}^{(B)}=\emptyset$.

Suppose that ${{\mathcal {J}}}^{(A)} =\{J_1^{(A)}, J_2^{(A)}, \ldots , J_{n_A}^{(A)}\}$ and ${{\mathcal {J}}}^{(B)} =\{J_1^{(B)}, J_2^{(B)}, \ldots , J_{n_B}^{(B)}\}$. For $X\in \{A, B\}$, each X-job $J_j^{(X)}\in {{\mathcal {J}}}^{(X)}$ has a processing time $p_j^{(X)}>0$. Each B-job $J_j^{(B)}$ also has a due date $d_j^{(B)}$. Given a feasible schedule $\sigma$, $C_j^{(X)}(\sigma )$ is the completion time of $J_j^{(X)}$, $X\in \{A, B\}$. $U_j^{(B)}(\sigma )=1$ if $C_j^{(B)}(\sigma )> d_j^{(B)}$ and $U_j^{(B)}(\sigma )=0$ if $C_j^{(B)}(\sigma )\le d^{(B)}_j$. For $X\in \{A, B\}$, let $f^{(X)}$ be the scheduling criterion of agent X which depends only on the completion times of the X-jobs. Following the three-parameter notation introduced by Graham et al. (1979), the constrained scheduling problem on a single machine to minimize $f^{(A)}$ under the constraint that $f^{(B)}$ cannot exceed an upper bound Q can be denoted by $1||f^{(A)}: f^{(B)}\le Q$.

The classical two-agent scheduling model was first introduced by Baker and Smith (2003) and Agnetis et al. (2004). Agnetis et al. (2004) considered various constrained scheduling problems for competing agents. They provided an $O(n\log n)$-time algorithm for problem $1||\sum C_{j}^{(A)}: f_{\max }^{(B)}\le Q$, an $O(n\log n)$-time algorithm for problem $1||\sum U_{j}^{(A)}: f_{\max }^{(B)}\le Q$, and an $O(n^{3})$-time algorithm for problem $1||\sum U_{j}^{(A)}: \sum U_j^{(B)}\le Q$. But the computational complexity of problem $1||\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$ was posed as open in Agnetis et al. (2004).

Ng et al. (2006) showed that problem $1||\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$ is NP-hard under high-multiplicity (HM) encoding and can be solved in pseudo-polynomial time under binary encoding. HM encoding is an encoding system which was proposed in Hochbaum and Shamir (1991) and Clifford and Posner (2001). Under this system, the input length of k identical jobs of processing time p of the same type is just $O(\log (k+2)+\log (p+2))$. This means that the work in Ng et al. (2006), in fact, does not solve the open problem posed in Agnetis et al. (2004), since we usually study computational complexity under binary encoding.

Table 1 Job data in instance ${{\mathcal {J}}}$

Binary NP-hardness of problem $1||\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$ was first presented in Leung et al. (2010), and a formal proof was published in Leung et al. (2010b). By using the NP-complete even–odd partition for the reduction, Leung et al. (2010b) showed that problem $1||\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$ is binary NP-hard. Unfortunately, their proof has a logical flaw. Thus we revisit problem $1||\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$.

Although the NP-hardness proof in Leung et al. (2010b) is invalid, we happily find that the authors have in fact provided a reasonable and wonderful procedure for the NP-hardness proof, which is very useful in our research. In this paper, we first show that a special version of the even–odd partition is NP-complete. Then, by using an arbitrary instance of the special version of the even–odd partition for the reduction, we construct a new job instance for problem $1||\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$. Finally, by borrowing the proof procedure provided in Leung et al. (2010b), we show that problem $1||\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$ is NP-hard even if the jobs of agent A have a common processing time.

In Sect. 2, by constructing a counterexample, we point out the logical flaw in the NP-hardness proof in Leung et al. (2010b). In Sect. 3, we present the NP-hardness proof of problem $1|p_j^{(A)}=p^{(A)}|\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$.

2 The logical flaw and a counterexample

The following is the well-known even–odd partition problem. By Garey and Johnson (1979), the even–odd partition is binary NP-complete.

Even–Odd Partition Given a set of $2n+1$ positive integers $a_1, a_2,\ldots , a_{2n}$ and H such that $H=\frac{1}{2}\sum ^{2n}_{j=1}a_j$, does there exist a partition $(I_1, I_2)$ of the index set $\{1,2,\ldots , 2n\}$ such that $|I_1\cap \{2j-1, 2j\}|= 1$ and $|I_2\cap \{2j-1, 2j\}|= 1$ for each $j=1, 2, \ldots , n$, and $\sum _{j\in I_1}a_j=\sum _{j\in I_2}a_j=H$?

By using the even–odd partition for the reduction, Leung et al. (2010b) showed that problem $1||\sum C_{j}^{(A)}: \sum U_j^{(B)}\le Q$ is binary NP-hard. Let us recall some related discussions in Leung et al. (2010b).

Let $\sigma _{i}=a_{2i}-a_{2i-1}$, $i=1,2,\ldots ,n$. Since each pair of integers $\{a_{2i-1}, a_{2i}\}$ must be put into two different sets, Leung et al. (2010b) assumed that the given instance of the even–odd partition satisfies the following three properties:

Property 1

$a_{1}>(2n+2)\max (\sigma _{1},\ldots ,\sigma _{n})$.

Property 2

$a_{2i-1}>\sum _{j=1}^{2i-2}a_{j}$.

Property 3

$a_{i}/j$ is an integer for each $1\le i\le 2n$ and $1\le j\le n$.

For a given instance of the even–odd partition, Leung et al. (2010b) constructed an instance ${{\mathcal {J}}}$ of the scheduling problem $1||\sum C^{(A)}_j:\sum U^{(B)}_j\le Q$ with $3n+1$ jobs: 2nP-jobs and a large R-job for agent B, and nQ-jobs for agent A. The processing times and due dates for these jobs are shown in Table 1.

• L is an integer larger than 2H.

• $x_1 = 1$, $x_i= \frac{n-i+1}{n-i+2}a_{2i-3}$ for $i = 2,\ldots , n-1$, and $x_n = \frac{1}{2}a_{2n-3}+a_{2n-5}$. Note that $x_1< x_2<\cdots < x_n$, and they are all integers.

• $l_{i}\sigma _{i} =\frac{1}{n-i+1}a_{2i-1}$, $i=1,2,\ldots ,n$.

Let the threshold for the total completion time of agent A be TC, where

$$\begin{aligned} TC= & {} \sum ^{n}_{i=1}(n-i)[a_{2i}+(l_i-1)\sigma _i] +\sum ^{n}_{i=1}(n-i+1)x_i\\&+\, \frac{1}{2}\sum ^{n}_{i=1}l_i\sigma _i =H+\frac{1}{2}\sum ^{n}_{i=1}(l_i-1)\sigma _i, \end{aligned}$$

and let the threshold for the number of tardy jobs of agent B be n. The decision problem asks whether there is a feasible schedule for instance ${{\mathcal {J}}}$ such that $\sum C^{(A)}_j\le TC$ and $\sum U^{(B)}_j\le n$.

Observation 2.1

A partition $(I_1, I_2)$ of $\{1,2, \ldots , 2n\}$ with $|I_1\cap \{2i-1, 2i\}|= 1$ and $|I_2\cap \{2i-1, 2i\}|= 1$ for each $i=1, 2, \ldots , n$ is a solution for the instance of the even–odd partition if and only if the following condition (C1) holds.

Proof

Let $(I_1, I_2)$ be a partition of $\{1,2, \ldots , 2n\}$ such that $|I_1\cap \{2i-1, 2i\}|= 1$ and $|I_2\cap \{2i-1, 2i\}|= 1$ for each $i=1, 2, \ldots , n$. Then, $(I_1, I_2)$ is a solution for the instance of the even–odd partition if and only if $\sum _{j\in I_1} a_j= \sum _{j\in I_2} a_j= H$, which is equivalent to the weakened version $\sum _{j\in I_1} a_j= \sum _{j\in I_2} a_j$, since $H=\frac{1}{2}\sum ^{2n}_{j=1}a_j$. Now, we have

$$\begin{aligned}&\mathop \sum \limits _{j\in I_1} a_j= \mathop \sum \limits _{j\in I_2} a_j\\&\Leftrightarrow \mathop \sum \limits _{i:2i-1\in I_1} a_{2i-1}+\mathop \sum \limits _{i:2i\in I_1} a_{2i} = \mathop \sum \limits _{i:2i-1\in I_2} a_{2i-1}+\mathop \sum \limits _{i:2i\in I_2} a_{2i}\\&\Leftrightarrow \mathop \sum \limits _{i:2i-1\in I_1} a_{2i-1}+\mathop \sum \limits _{i:2i-1\in I_2} a_{2i} = \mathop \sum \limits _{i:2i-1\in I_2} a_{2i-1}+\mathop \sum \limits _{i:2i-1\in I_1} a_{2i}\\&\Leftrightarrow \mathop \sum \limits _{i:2i-1\in I_1} a_{2i-1}-\mathop \sum \limits _{i:2i-1\in I_1} a_{2i} = \mathop \sum \limits _{i:2i-1\in I_2} a_{2i-1}-\mathop \sum \limits _{i:2i-1\in I_2} a_{2i}\\&\Leftrightarrow \mathop \sum \limits _{i:2i-1\in I_1}\sigma _i = \mathop \sum \limits _{i:2i-1\in I_2}\sigma _i\\&\Leftrightarrow \mathop \sum \limits _{i:2i-1\in I_1}\sigma _i = \mathop \sum \limits _{i:2i-1\in I_2}\sigma _i= \frac{1}{2}\mathop \sum \limits _{i=1}^{n}\sigma _i, \end{aligned}$$

as required in the observation. $\square$

Observation 2.2

Leung et al. (2010b) presented the binary NP-hardness proof of problem $1||\sum C^{(A)}_j:\sum U^{(B)}_j\le Q$ by proving that the instance of the even–odd partition has a solution if and only if instance ${{\mathcal {J}}}$ has a feasible schedule $\pi$ such that $\sum C^{(A)}_j(\pi )\le TC$ and $\sum U^{(B)}_j(\pi )\le n$. If their Lemma 1 (pp. 3–4) and Lemma 10 (p. 15) are correct, then the following statement holds.

Statement 1For every partition$(I_1, I_2)$of the index set$\{1,2, \ldots , 2n\}$with$|I_1\cap \{2i-1, 2i\}|= 1$and$|I_2\cap \{2i-1, 2i\}|= 1$for each$i=1, 2, \ldots , n$, the above condition (C1) and the following condition (C2) are equivalent.

Proof

See “Appendix”. $\square$

However, Statement 1 is invalid. We illustrate this by the following instance ${{\mathcal {I}}}$ of the even–odd partition with $n=4$.

The instance ${{\mathcal {I}}}= (a_1, a_2, \ldots , a_8, H)$ is obtained by setting $a_{1}=264$, $a_{2}=288$, $a_{3}=576$, $a_{4}=600$, $a_{5}=1848$, $a_{6}=1872$, $a_{7}=5544$, $a_{8}=5568$, and $H= 8280$.

We can easily observe that instance ${{\mathcal {I}}}$ satisfies the above three properties and has a solution $(I_1, I_2)$ with $I_{1}=\{1,3,6,8\}$ and $I_{2}=\{2,4,5,7\}$ such that $\sum _{j\in I_{1}}a_{j}=\sum _{j\in I_{2}}a_{j}=8280=H$. Recall that $\sigma _{i}=a_{2i}-a_{2i-1}$ and $l_{i}\sigma _{i}=\frac{1}{n-i+1}a_{2i-1}$ for each $i=1,2,\ldots ,n$. We then have $\sigma _{1}=\sigma _{2} =\sigma _{3}=\sigma _{4}=24$, $l_{1}\sigma _{1}=\frac{1}{4}a_{1}=66$, $l_{2}\sigma _{2}=\frac{1}{3}a_{3}=192$, $l_{3}\sigma _{3}=\frac{1}{2}a_{5}=924$, and $l_{4}\sigma _{4}=a_{7}=5544$. Thus

$$\begin{aligned} \sum _{2i-1\in I_1}\sigma _i= & {} \sum _{2i-1\in I_2}\sigma _i= \frac{1}{2}\sum _{i=1}^{n}\sigma _i=48, \\ \sum _{2i-1\in I_{1}}l_{i}\sigma _{i}= & {} l_{1}\sigma _{1} +l_{2}\sigma _{2}=66+192=258 \end{aligned}$$

and

$$\begin{aligned} \sum _{2i-1\in I_{2}}l_{i}\sigma _{i} =l_{3}\sigma _{3}+l_{4}\sigma _{4} =924+5544=6468. \end{aligned}$$

It follows that $\sum _{2i-1\in I_{1}}l_{i}\sigma _{i}\ne \sum _{2i-1\in I_{2}}l_{i}\sigma _{i}$. This means that Statement 1 is invalid.

The above discussion shows that the NP-hardness proof in Leung et al. (2010b) has a logical flaw (in their Lemmas 1 and 10). Moreover, on p. 5, lines 6–8, the authors wrote: “Thus, a feasible schedule with $\sum C_j^a \le TC$ is obtained when the total processing time of the on-time P-jobs is exactly $A+\frac{1}{2}\sum _{i=1}^{n}(l_i-1)\sigma _i$. But this occurs only when there is a solution for the instance of the even–odd partition problem.” By checking the context in Leung et al. (2010b), we find that the second sentence is confusing.

From Observations 2.1 and 2.2, we guess (or conclude) that the authors in Leung et al. (2010b) have mistakenly assumed that condition (C1) is equivalent to (C2). This may be the reason for the logical flaw in Leung et al. (2010b).

We cannot find a method to amend this flaw directly. The computational complexity of problem $1||\sum C^{(A)}_j: \sum U^{(B)}_j\le Q$ should then be restudied.

3 NP-hardness proof

The following is the well-known partition problem. By Garey and Johnson (1979), the partition is binary NP-complete.

Partition Given a set of n positive integers $x_1, x_2,\ldots , x_{n}$ and a positive integer E such that $E=\frac{1}{2}\sum ^{n}_{j=1}x_j$, does there exist a partition $(I_1, I_2)$ of the index set $\{1,2,\ldots , n\}$, such that $\sum _{j\in I_1}x_j=\sum _{j\in I_2}x_j=E$?

From the NP-completeness proof of the partition in Garey and Johnson (1979), the following result is observed.

Lemma 3.1

The partition is also binary NP-complete for the instances $(x_1, x_2,\ldots , x_{n}, E)$ in which the n positive integers $x_1, x_2,\ldots , x_{n}$ are mutually distinct.

By using the partition for the reduction, we now show that a special version of the even–odd partition is also binary NP-complete.

Lemma 3.2

The even–odd partition is also binary NP-complete for the instances $(a_1, a_2,\ldots , a_{2n}, H)$ in which the n integers $|a_2-a_1|, |a_4-a_3|, \ldots , |a_{2n}- a_{2n-1}|$ are mutually distinct.

Proof

Suppose that ${{\mathcal {I}}}=(x_1, x_2, \ldots , x_n, E)$ is an instance of the partition. From Lemma 3.1, we may assume that $x_1, x_2,\ldots , x_{n}$ are mutually distinct. We construct an instance ${{\mathcal {I}}}'= (a_1, a_2, \ldots , a_{2n}, H)$ of the even–odd partition in the following way:

$$\begin{aligned}&a_{2i-1}=1, a_{2i}= x_i+1 \text{ for } i=1,2, \ldots , n,\\&\quad \text{ and } H= E+n. \end{aligned}$$

Since $a_{2i}- a_{2i-1}= x_i$ for $i=1,2, \ldots , n$, instance ${{\mathcal {I}}}'$ guarantees that $|a_2-a_1|, |a_4-a_3|, \ldots , |a_{2n}- a_{2n-1}|$ are mutually distinct.

For each partition $(I_1, I_2)$ of the index set $\{1,2, \ldots , n\}$, we define

$$\begin{aligned} I_1'= \{2i-1: i\in I_2, ~1\le i\le n\}\cup \{2i: i\in I_1, ~1\le i\le n\} \end{aligned}$$

and

$$\begin{aligned} I_2' =\{2i-1: i\in I_1, ~1 \le i\le n\}\cup \{2i: i\in I_2, ~1\le i\le n\}. \end{aligned}$$

Then, $(I_1', I_2')$ is a partition of the index set $\{1,2, \ldots , 2n\}$ such that $|I_1'\cap \{2j-1, 2j\}|= |I_2'\cap \{2j-1, 2j\}|= 1$ for each $j=1, 2, \ldots , n$. Moreover, we have that $\sum _{j\in I_1'} a_j= \sum _{2i-1\in I_1'} a_{2i-1}+ \sum _{2i\in I_1'} a_{2i} =\sum _{i\in I_2} 1+ \sum _{i\in I_1} (x_{i}+1)=\sum _{i\in I_1}x_{i}+ |I_1|+ |I_2|= \sum _{i\in I_1}x_{i}+n$. For $I_2'$, we have a similar result. We then have

$$\begin{aligned} \sum _{j\in I_1'} a_j= \sum _{i\in I_1}x_{i}+ n \text{ and } \sum _{j\in I_2'} a_j= \sum _{i\in I_2}x_{i}+ n. \end{aligned}$$

First, suppose that $(I_1, I_2)$ is a solution for instance ${{\mathcal {I}}}$ of the partition. We then have that $\sum _{j\in I_1}x_j=\sum _{j\in I_2}x_j=E$. From the definition of $(I_1', I_2')$, $(I_1', I_2')$ is a partition of the index set $\{1,2, \ldots , 2n\}$ such that $|I_1'\cap \{2j-1, 2j\}|= |I_2'\cap \{2j-1, 2j\}|= 1$ for each $j=1, 2, \ldots , n$. Furthermore, we have that $\sum _{j\in I_1'} a_j= \sum _{i\in I_1}x_{i}+ n= E+ n= H$ and $\sum _{j\in I_2'} a_j= \sum _{i\in I_2}x_{i}+ n= E+ n= H$. That is, $\sum _{j\in I_1'} a_j=\sum _{j\in I_2'} a_j= H$. Hence, $(I_1', I_2')$ is a solution for instance ${{\mathcal {I}}}'$ of the even–odd partition.

Conversely, suppose that $(I_1', I_2')$ is a solution for instance ${{\mathcal {I}}}'$ of the even–odd partition. We then have that $(I_1', I_2')$ is a partition of the index set $\{1,2, \ldots , 2n\}$ such that $\sum _{j\in I_1'} a_j= \sum _{j\in I_2'} a_j= H$ and $|I_1'\cap \{2j-1, 2j\}|= |I_2'\cap \{2j-1, 2j\}|= 1$ for each $j=1, 2, \ldots , n$. From the definition of $(I_1', I_2')$, $(I_1, I_2)$ is a partition of the index set $\{1,2, \ldots , n\}$. And we have that $\sum _{i\in I_1}x_{i}=\sum _{j\in I_1'} a_j-n= H-n= E$ and $\sum _{i\in I_2}x_{i}=\sum _{j\in I_2'} a_j-n= H-n= E$. That is, $\sum _{i\in I_1}x_{i}= \sum _{i\in I_2}x_{i}= E$. Hence, $(I_1, I_2)$ is a solution for instance ${{\mathcal {I}}}$ of partition.

From the above discussion, $(I_1, I_2)$ is a solution for instance ${{\mathcal {I}}}$ of the partition if and only if $(I_1', I_2')$ is a solution for instance ${{\mathcal {I}}}'$ of the even–odd partition. Consequently, this special version of the even–odd partition is binary NP-complete. The lemma follows. $\square$

For the above special version of the even–odd partition in Lemma 3.2, we have the following observations:

• Deleting a pair $\{a_{2j-1}, a_{2j}\}$ with $a_{2j-1}= a_{2j}$ (if any) will result in an equivalent instance. Then we may assume that $a_{2j-1}\ne a_{2j}$.

• Exchanging (if necessary) the indices of $a_{2j-1}$ and $a_{2j}$ will not affect the problem. Then we may assume that $a_{2j-1}< a_{2j}$.

• Renumbering (if necessary) the n pairs $\{a_{2j-1}, a_{2j}\}$, $j=1,2, \ldots , n$, will not affect the problem. From Lemma 3.2, we may assume that $a_{2}-a_{1}< a_4- a_3< \cdots < a_{2n}-a_{2n-1}$.

• Replacing (if necessary) each pair $\{a_{2j-1}, a_{2j}\}$ with a new pair $\{a_{2j-1}+K_j, a_{2j}+K_j\}$, $j=1,2,\ldots , n$, and replacing H with $H+\sum _{j=1}^n K_j$ will result in a new equivalent instance, where $K_1, K_2,\ldots , K_n$ are n nonnegative integers with polynomial size in that of $(a_1, a_2, \ldots , a_{2n}, H)$. By choosing suitable $K_1, K_2,\ldots , K_n$, we can guarantee that $a_1+K_1< a_2+K_1< a_3+K_2< a_4+K_2< \cdots< a_{2n-1}+K_n < a_{2n}+K_n$. Then we may assume that $a_1< a_2< \cdots < a_{2n}$. Note that, if necessary, we may also assume that $a_1$ is suitably large.

• Instance $(a_1,a_2, \ldots , a_{2n}, H)$ is equivalent to instance $(2a_1,2a_2, \ldots , 2a_{2n}, 2H)$. Thus, we may assume that all the integers in instance $(a_1,a_2, \ldots , a_{2n}, H)$ are even.

Based on the above discussion, in the remainder of this paper we consider only the instance $(a_1, a_2, \ldots , a_{2n}, H)$ of the even–odd partition such that all the $2n+1$ integers are even, and moreover,

$$\begin{aligned} n(a_{2n}-a_{2n-1})< a_1< a_2< \cdots < a_{2n}, \end{aligned}$$

(1)

and

$$\begin{aligned} 2\le a_{2}-a_{1}< a_4- a_3< \cdots < a_{2n}-a_{2n-1}. \end{aligned}$$

(2)

We are ready to show the NP-hardness of problem $1|p_{j}^{(A)}= p^{(A)}|\sum C^{(A)}_j: \sum U^{(B)}_j\le Q$.

Theorem 3.1

Problem $1|p_{j}^{(A)}= p^{(A)}|\sum C^{(A)}_j: \sum U^{(B)}_j\le Q$ is binary NP-hard.

Proof

For a given instance ${{\mathcal {I}}}=(a_1, a_2, \cdots , a_{2n}, H)$ of the even–odd partition with all the $2n+1$ integers in the instance being even and with the two properties in (1) and (2), we construct a job instance ${{\mathcal {J}}}$ as follows: there are $3n+1$ jobs of two types, nA-jobs $J^{(A)}_1, J^{(A)}_2,\ldots , J^{(A)}_n$ and $2n+1$B-jobs $J^{(B)}_1, J^{(B)}_2,\ldots , J^{(B)}_{2n}$, $J^{(B)}_R$, where each $J^{(B)}_j$ with $1\le j\le 2n$ is called a normal B-job, and $J^{(B)}_R$ is called the restricted B-job. The processing times and due dates are displayed in Table 2.

Table 2 The scheduling instance ${{\mathcal {J}}}$

Fig. 1

The due dates for B-jobs in instance ${{\mathcal {J}}}$

• $M_j= 3H(a_{2j}-a_{2j-1})+(n-j)(a_{2j}-a_{2j-1})- a_{2j-1}$ for $i=1, 2, \ldots , n$.

• $L=n^{2} p^{(A)}+ n\sum _{j=1}^{2n} p_j^{(B)}$ is a sufficiently large number.

Note that the definitions of processing times and due dates for normal B-jobs can be rewritten together as

$$\begin{aligned} \left\{ \begin{array}{lll} p^{(B)}_{j'}&{}=&{} M_j+a_{j'}, \\ d^{(B)}_{j'}&{}=&{} \sum \nolimits _{k=1}^{j-1} p_{2k}^{(B)}+ \lfloor {j'/2}\rfloor p^{(A)}+ p^{(B)}_{j'} \end{array}\right. \end{aligned}$$

(3)

for every $j'\in \{2j-1, ~2j\}$, $j=1,2, \ldots , n$.

Let the upper bound of $\sum U_j^{(B)}$ be defined by $Q= n$, and the threshold value of $\sum C_j^{(A)}$ be given by

$$\begin{aligned} Y= \frac{n(n+1)}{2}p^{(A)}+ \sum _{j=1}^{n}(n-j)p_{2j}^{(B)}+ 3H\delta , \end{aligned}$$

(4)

where $\delta = \frac{1}{2}\sum _{j=1}^{n}(a_{2j}-a_{2j-1})$. It is not hard to verify that $L>Y$.

The decision asks whether there is a feasible schedule $\sigma$ on the above job instance such that

$$\begin{aligned} \sum C^{(A)}_{j}(\sigma )\le Y \text{ and } \sum U^{(B)}_j(\sigma )\le n. \end{aligned}$$

(5)

Clearly, the above construction can be done in polynomial time.

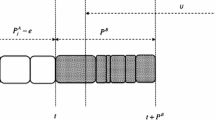
Note that $p^{(A)}< a_1$ and $p^{(B)}_{2j-1}< p^{(B)}_{2j}$ for $j=1,2, \ldots , n$. We then have $d^{(B)}_{2j}-d^{(B)}_{2j-1}= p^{(A)} +(a_{2j}-a_{2j-1})$ for $j=1,2, \ldots , n$. Figure 1 shows the structure of the due dates for all B-jobs in instance ${{\mathcal {J}}}$.

For convenience, we call ${{\mathcal {I}}}=(a_1, a_2, \cdots , a_{2n}, H)$ the partition instance in the sequel. We set ${{\mathcal {J}}}^{(A)}= \{J_1^{(A)}, J_2^{(A)}, \ldots , J_n^{(A)}\}$ and ${{\mathcal {J}}}^{(B)}= \{J_1^{(B)}, J_2^{(B)}, \ldots , J_{2n}^{(B)}, J_R^{(B)}\}$. Since the n jobs in ${{\mathcal {J}}}^{(A)}$ are indistinguishable, in the sequel we consider only the schedules $\sigma$ for instance ${{\mathcal {J}}}$, in which the A-jobs are scheduled in the order of their indices in $\sigma$, i.e.,

$$\begin{aligned} J_{1}^{(A)} \prec _{\sigma } J_{2}^{(A)} \prec _{\sigma } \cdots \prec _{\sigma } J_{n}^{(A)}. \end{aligned}$$

(6)

For each schedule $\sigma$ of ${{\mathcal {J}}}$ (or of ${{\mathcal {J}}}^{(B)}$), we use ${{\mathcal {O}}}(\sigma )$ to denote the set of on-time B-jobs in $\sigma$.

Outline of our proof According to the principle of NP-hardness, we need to show that the partition instance ${{\mathcal {I}}}=(a_1, a_2, \cdots , a_{2n}, H)$ has a solution if and only if there is a feasible schedule $\sigma$ of the scheduling instance ${{\mathcal {J}}}$ such that the two inequalities in Eq. (5) are satisfied. To this end, the following work will be done in the sequel:

• Some useful inequalities are established in Eqs. (7)–(11).

• Two important inequalities related to the due dates for B-jobs are established in Lemma 3.3.

• Nice sequences are introduced, followed by the establishment of some useful inequalities related to nice sequences in Lemma 3.4.

• Some useful properties of the optimal schedules of problem $1||\sum U_j^{(B)}$ are established in Lemma 3.5. From Lemma 3.5, we see that $\sum U^{(B)}_j(\sigma )\le n$ in (5) is equivalent to $\sum U^{(B)}_j(\sigma )= n$.

• From the previous equations and from Lemmas 3.3–3.5, some useful properties of the efficient schedules (which are feasible schedules of problem $1||\sum C_j^{(A)}: \sum U_j^{(B)}=n$ with $\sum C_j^{(A)}\le Y$) are established in Lemma 3.6.

• The schedules corresponding to the nice sequences are introduced, followed by the establishment of an exact expression for the value $\sum C_j^{(A)}(\sigma )$ in Eq. (19) for every such schedule $\sigma$.

• Finally, by using Lemma 3.6 and Eq. (19), we can show that the partition instance ${{\mathcal {I}}}= (a_1, a_2, \ldots , a_{2n}, H)$ has a solution if and only if the job instance ${{\mathcal {J}}}$ has an efficient schedule. The result then follows.

Now let us begin our proof. From the definition of $M_j$, for $j=1,2,\ldots , n-1$, we have

$$\begin{aligned}&M_{j+1}- M_{j}\\&\quad = 3H(a_{2j+2}- a_{2j+1})+ (n-j-1)\\&\qquad (a_{2j+2}- a_{2j+1})- a_{2j+1}\\&\qquad - 3H(a_{2j}- a_{2j-1})- (n-j)(a_{2j}- a_{2j-1})+ a_{2j-1}\\&\quad> 3H(a_{2j+2}- a_{2j+1})- a_{2j+1}\\&\qquad - \,3H(a_{2j}- a_{2j-1})- n(a_{2j}- a_{2j-1})\\&\quad \ge 6H- n(a_{2j}- a_{2j-1})- a_{2j+1}~~~~\text{(From } (2))\\&\quad> 6H- a_1 - a_{2n}~~~~\text{(From } (1) \text{ and } (2))\\&\quad> 4H>0,\quad \text{(Since } 2H= a_1+\cdots +a_{2n}) \end{aligned}$$

that is,

$$\begin{aligned} M_{j+1}- M_{j}> 4H> 0. \end{aligned}$$

(7)

Consequently, we have

$$\begin{aligned} M_1< M_2< \cdots < M_n. \end{aligned}$$

(8)

From the definitions of the due dates and processing times for B-jobs, we further have

$$\begin{aligned} 3H< p_{1}^{(B)}< p_{2}^{(B)}< \cdots< p_{2n}^{(B)}< p_{R}^{(B)}, \end{aligned}$$

(9)

and

$$\begin{aligned} d_{1}^{(B)}< d_{2}^{(B)}< \cdots< d_{2n}^{(B)}< d_{R}^{(B)}. \end{aligned}$$

(10)

From (1) and (2), we have that $np^{(A)}< n^{2}(a_{2n}-a_{2n-1})< n a_1< \sum _{k=1}^{n} a_{2k-1}< H$, that is,

$$\begin{aligned} H> np^{(A)}. \end{aligned}$$

(11)

The following lemma establishes two important inequalities related to the due dates for B-jobs.

Lemma 3.3

• (i) $d_{2j}^{(B)} < 3H+p_1^{(B)} + p_3^{(B)} + \cdots +p_{2j-1}^{(B)}, \text{ for } j=1,2,\ldots , n$, and

• (ii) $d_{R}^{(B)} < 3H+p_1^{(B)} + p_3^{(B)} + \cdots +p_{2n-1}^{(B)} +p_{R}^{(B)}$.

Proof

For $j=1,2,\ldots , n$, we have

$$\begin{aligned}&3H+p_1^{(B)} + p_3^{(B)} + \cdots +p_{2j-1}^{(B)}\\&\quad = 2H+H+\mathop \sum \limits _{k=1}^{j}(M_k+ a_{2k-1})\\&\quad> \mathop \sum \limits _{k=1}^{j}(M_k+ a_{2k-1})+2H+np^{(A)}~~~~\text{(From } (11))\\&\quad> \mathop \sum \limits _{k=1}^{j}(M_k+ a_{2k})+np^{(A)}\\&\quad > d_{2j}^{(B)}. \end{aligned}$$

This proves (i).

Note that we also have

$$\begin{aligned}&3H+p_1^{(B)} + p_3^{(B)} + \cdots +p_{2n-1}^{(B)} +p_{R}^{(B)}\\&\quad = H+2H+\mathop \sum \limits _{k=1}^{n}(M_k+ a_{2k-1})+L\\&\quad> np^{(A)}+\mathop \sum \limits _{k=1}^{n}M_k+2H+L~~~~\text{(From } (11))\\&\quad > np^{(A)}+\mathop \sum \limits _{k=1}^{n}M_k+H+L\\&\quad = d_{R}^{(B)}. \end{aligned}$$

This proves (ii). The lemma follows. $\square$

For an index $j\in \{1,2, \ldots , n\}$, a sequence $(1', 2', \ldots , j')$ of indices in $\{1,2, \ldots , 2j\}$ is called a j-nice sequence if $k'\in \{2k-1, 2k\}$ for $k=1,2,\ldots , j$. An n-nice sequence is also called a nice sequence. It is easy to see that if $(1', 2', \ldots , n')$ is a nice sequence, then $(1', 2', \ldots , j')$ is a j-nice sequence for $j=1,2, \ldots , n$. The following lemma establishes some useful inequalities related to nice sequences.

Lemma 3.4

Let $(1', 2', \ldots , j')$ be a j-nice sequence, where $j\in \{1,2, \ldots , n\}$. Then we have the following inequalities:

• (i) $\lfloor {j'/2}\rfloor p^{(A)} + \sum _{k=1}^{j} p_{k'}^{(B)} \le d_{j'}^{(B)}$;

• (ii) $n p^{(A)} + \sum _{k=1}^{n} p_{k'}^{(B)} +p_R^{(B)} \le d_{R}^{(B)}$ if and only if $\sum _{k=1}^{n} a_{k'} \le H$;

• (iii) $(j+1) p^{(A)} + \sum _{k=1}^{j} p_{k'}^{(B)} > d_{j'}^{(B)}$ if $j\le n-1$.

Proof

The proof will follow from Eqs. (3), (9), and (10) and the definition of $d_{R}^{(B)}$.

The result in (i) holds, since $\lfloor {j'/2}\rfloor p^{(A)} + \sum _{k=1}^{j} p_{k'}^{(B)} \le \lfloor {j'/2}\rfloor p^{(A)} + \sum _{k=1}^{j-1} p_{2k}^{(B)} +p_{j'}^{(B)}= d_{j'}^{(B)}$.

The result in (ii) follows by noting that $n p^{(A)} + \sum _{k=1}^{n} p_{k'}^{(B)} +p_R^{(B)} = n p^{(A)} + \sum _{k=1}^{n} M_k +L + \sum _{k=1}^n a_{k'}$ and $d_{R}^{(B)}= n p^{(A)} + \sum _{k=1}^{n} M_k +L + H$.

The result in (iii) holds, since $(j+1) p^{(A)}+\sum _{k=1}^{j} p_{k'}^{(B)} \ge j p^{(A)} +1+ \sum _{k=1}^{n-1}(a_{2k}-a_{2k-1})+ \sum _{k=1}^{j}(M_k+a_{2k-1}) \ge j p^{(A)}+ \sum _{k=1}^{j}(M_k+a_{2k})+1 = d_{2j}^{(B)}+1> d_{2j}^{(B)}$. The lemma follows. $\square$

To proceed with our proof, we next establish two lemmas which will be used in our discussion.

Lemma 3.5

For problem $1||\sum U^{(B)}_j$ on B-jobs ${{\mathcal {J}}}^{(B)}$ (without considering A-jobs), every optimal schedule $\pi$ has the following properties:

• (i) the (optimal) value of $\pi$ is given by $\sum U^{(B)}_j(\pi )= n$;

• (ii) exactly one job of each pair $\{J^{(B)}_{2j-1}, J^{(B)}_{2j}\}$, $1\le j\le n$, is on time in $\pi$;

• (iii) $J^{(B)}_{R}$ is on time in $\pi$ and is scheduled after all the other on-time B-jobs in $\pi$;

• (iv) all on-time B-jobs are scheduled in the EDD order in $\pi$;

• (v) all tardy B-jobs are scheduled after the restricted B-job $J^{(B)}_{R}$ in $\pi$.

Proof

Property (i) can be proved by applying the algorithm presented by Moore (1968) for the problem $1||\sum U_j$. In what follows, we will prove it in a different way to save space.

We first prove the following weakened version of property (i):

$$\begin{aligned}&(i')~{ the}~{ optimal}~{ value}~{ of}~{ problem}~1||\sum U^{(B)}_j\\&\quad { on}~{ the}~{ instance}~{ of}~B{\text{- }}{} { jobs}~{ is}~{ at}~{ most}~n. \end{aligned}$$

To prove ($\hbox {i}'$), we consider the schedule $\sigma = (J_{1}^{(B)}, J_{3}^{(B)}, \ldots , J_{2n-1}^{(B)}, J_{R}^{(B)}, J_{2}^{(B)},J_{4}^{(B)},\ldots , J_{2n}^{(B)})$. Since $J_{R}^{(B)}$ has a very large processing time L, the nB-jobs $J_{2}^{(B)},J_{4}^{(B)},\ldots , J_{2n}^{(B)}$ are tardy in $\sigma$. We will show that the other $n+1$B-jobs $J_{1}^{(B)}, J_{3}^{(B)}, \ldots , J_{2n-1}^{(B)}, J_{R}^{(B)}$ are on time in $\sigma$.

From Lemma 3.4(i), by setting $j'= 2j-1$ for each j with $1\le j\le n$, we have $C_{2j-1}^{(B)}(\sigma ) = \sum _{k=1}^j p^{(B)}_{2k -1}\le d^{(B)}_{2j-1}$. This implies that $J_{1}^{(B)}, J_{3}^{(B)}, \ldots , J_{2n-1}^{(B)}$ are on time in $\sigma$.

Note that $C_{R}^{(B)}(\sigma )= \sum _{k=1}^{n}p^{(B)}_{2k -1} +p^{(B)}_{R} < n p^{(A)}+ \sum _{k=1}^{n}p^{(B)}_{2k -1} +p^{(B)}_{R}$. Since $\sum _{k=1}^{n} a_{2k-1}< H$, from Lemma 3.4(ii), we have $C_{R}^{(B)}(\sigma )< d_{R}^{(B)}$. Thus, $J^{(B)}_R$ is on time in $\sigma$. This proves property ($\hbox {i}'$).

Now we consider an optimal schedule $\pi$ for problem $1||\sum U^{(B)}_j$ on B-jobs ${{\mathcal {J}}}^{(B)}$. Let ${{\mathcal {O}}}(\pi )$ be the set of on-time B-jobs in $\pi$.

By contradiction, suppose that property (ii) does not hold for $\pi$. Let j be the smallest index in $\{1,2, \ldots , n\}$ so that $\{J_{2j-1}^{(B)}, J_{2j}^{(B)}\}$ violates property (ii). Then, for each k with $1\le k\le j-1$, exactly one job of each pair $\{J^{(B)}_{2k-1}, J^{(B)}_{2k}\}$ is on time in $\pi$, and moreover, $J_{2j-1}^{(B)}$ and $J_{2j}^{(B)}$ are either both tardy or both on time in $\pi$.

From property ($\hbox {i}'$), there are at least n on-time jobs among $\{J_1^{(B)}, J_2^{(B)}, \ldots , J_{2n}^{(B)}\}$ in $\pi$, or equivalently, $|{{\mathcal {O}}}(\pi )\cap \{J_1^{(B)}, J_2^{(B)}, \ldots , J_{2n}^{(B)}\}|\ge n$. Let v be the smallest index in $\{j, j+1,\ldots , n\}$ such that $|{{\mathcal {O}}}(\pi )\cap \{J_1^{(B)}, J_2^{(B)}, \ldots , J_{2v}^{(B)}\}|\ge v$.

If $v=j$, by the choices of j and v, $|{{\mathcal {O}}}(\pi )\cap \{J_{2k-1}^{(B)}, J_{2k}^{(B)}\}|=1$ for $k=1, 2,\ldots , j-1$ and $\{J_{2j-1}^{(B)}, J_{2j}^{(B)}\}\subseteq {{\mathcal {O}}}(\pi )$. Thus, from (9), (10), and Lemma 3.3(i), we have

$$\begin{aligned} d_{2j}^{(B)}= & {} \max \{d_{i}^{(B)}: i=1,2, \ldots , 2j\}\\\ge & {} \max \{C_{i}^{(B)}(\pi ): J_{i}^{(B)}\in {{\mathcal {O}}}(\pi )\cap \{J_1^{(B)}, J_2^{(B)}, \ldots , J_{2j}^{(B)}\}\}\\\ge & {} \mathop \sum \limits _{k=1}^{j-1} \min \{p_{2k-1}^{(B)}, p_{2k}^{(B)}\} + p_{2j-1}^{(B)}+ p_{2j}^{(B)}\\= & {} \mathop \sum \limits _{k=1}^{j-1} p_{2k-1}^{(B)} + p_{2j-1}^{(B)}+ p_{2j}^{(B)}\\> & {} 3H +\mathop \sum \limits _{k=1}^{j} p_{2k-1}^{(B)}\\> & {} d_{2j}^{(B)}, \end{aligned}$$

a contradiction. Consequently, we have

$$\begin{aligned} v>j \text{ and } {{\mathcal {O}}}(\pi )\cap \{J_{2j-1}^{(B)}, J_{2j}^{(B)}\} =\emptyset . \end{aligned}$$

(12)

From the definition of v, we further have

$$\begin{aligned} |{{\mathcal {O}}}(\pi )\cap \{J_1^{(B)}, J_2^{(B)}, \ldots , J_{2v}^{(B)}\}|= v. \end{aligned}$$

(13)

Now we suppose that ${{\mathcal {O}}}(\pi )\cap \{J_1^{(B)}, J_2^{(B)}, \ldots , J_{2v}^{(B)}\} =\{J_{1'}^{(B)}, J_{2'}^{(B)}, \ldots , J_{v'}^{(B)}\}$ so that $1'< 2'< \cdots < v'$. From the choices of j and v, together with (12) and (13), we have

$$\begin{aligned} \left\{ \begin{array}{ll} J_{k'}^{(B)} \in \{J_{2k-1}^{(B)}, J_{2k}^{(B)}\}, &{}\text{ for } k=1, 2, \ldots , j-1, \\ J_{k'}^{(B)} \in \{J_{2k+1}^{(B)}, J_{2k+2}^{(B)}, \ldots , J_{2v-2}^{(B)}\}, &{}\text{ for } k=j, j+1, \ldots , v-2,\\ J_{(v-1)'}^{(B)} = J_{2v-1}^{(B)}, &{}\\ J_{v'}^{(B)} = J_{2v}^{(B)}. &{} \end{array}\right. \end{aligned}$$

Consequently, from the definitions of $J_{2j-1}^{(B)}$ and $J_{2j}^{(B)}$ and (9), we have

$$\begin{aligned} \left\{ \begin{array}{ll} p_{k'}^{(B)} \ge p_{2k-1}^{(B)}= M_k +a_{2k-1}, &{}\text{ for } k=1, 2, \ldots , j-1, \\ p_{k'}^{(B)} \ge p_{2k+1}^{(B)} = M_{k+1} +a_{2k+1}, &{}\text{ for } k=j, j+1, \ldots , v-2,\\ p_{(v-1)'}^{(B)} = p_{2v-1}^{(B)}= M_{v} +a_{2v-1}, &{}\\ p_{v'}^{(B)} = p_{2v}^{(B)}= M_{v} +a_{2v}. &{} \end{array}\right. \end{aligned}$$

(14)

Note that $v\ge j+1$. From (7), we have $p_{2v}^{(B)} = M_{v}+ a_{2v}> M_j+ a_{2j-1}+4H= p_{2j-1}^{(B)}+4H> p_{2j-1}^{(B)}+3H$. From (9), (10), (14), and Lemma 3.3(i), we have

$$\begin{aligned} d_{2v}^{(B)}= & {} \max \{d_{k'}^{(B)}: k=1,2, \ldots , v\}\\\ge & {} \max \{C_{k'}^{(B)}(\pi ): k=1,2, \ldots , v\}\\\ge & {} \mathop \sum \limits _{k=1}^{v} p_{k'}^{(B)} \\= & {} \mathop \sum \limits _{k=1}^{j-1} p_{k'}^{(B)} +\mathop \sum \limits _{k=j}^{v-2} p_{k'}^{(B)}+p_{(v-1)'}^{(B)}+ p_{v'}^{(B)}\\\ge & {} \mathop \sum \limits _{k=1}^{j-1} p_{2k-1}^{(B)} + \mathop \sum \limits _{k=j+1}^{v-1} p_{2k-1}^{(B)} + p_{2v-1}^{(B)}+p_{2v}^{(B)}\\> & {} 3H+ \mathop \sum \limits _{k=1}^{v} p_{2k-1}^{(B)}\\> & {} d_{2v}^{(B)}, \end{aligned}$$

a contradiction. Property (ii) follows.

From properties ($\hbox {i}'$) and (ii), the restricted B-job $J_R^{(B)}$ must be on time in $\pi$. Since $p^{(B)}_{R}=L$ is a sufficiently large integer, all the other on-time B-jobs must be scheduled before $J^{(B)}_{R}$. This proves property (iii).

From properties ($\hbox {i}'$), (ii), and (iii), we certainly have $\sum U_j^{(B)}(\pi )=n$, and so property (i) follows.

The above three properties enable us to define $J_{j'}^{(B)}$, $1\le j\le n$, to be the unique job in ${{\mathcal {O}}}(\pi )\cap \{J_{2j-1}^{(B)}, J_{2j}^{(B)}\}$. Note that, from property (iii), $J_{R}^{(B)}$ is the last on-time job in $\pi$.

To prove property (iv), by contradiction, we suppose that there are two indices i and j with $d_{i'}^{(B)}< d_{j'}^{(B)}$ such that $J_{i'}^{(B)}$ is scheduled after $J_{j'}^{(B)}$ in $\pi$. For our purpose, we may choose such a pair (i, j) so that i is as small as possible. From (10), we have $1\le i<j\le n$. By the choice of (i, j), all the jobs $J_{k'}^{(B)}$, $1\le k\le i$, and $J_{j'}^{(B)}$ are completed by time $C_{i'}^{(B)}(\pi )$ in $\pi$. We then have

$$\begin{aligned} C_{i'}^{(B)}(\pi )\ge & {} \mathop \sum \limits _{k=1}^{i} p_{k'}^{(B)} + p_{j'}^{(B)}\\\ge & {} 3H + \mathop \sum \limits _{k=1}^{i} p_{2k-1}^{(B)} ~~~~~\text{(From } (9))\\> & {} d_{2i}^{(B)} ~~~~~\text{(From } \text{ Lemma }~3.3(\mathrm{i}))\\\ge & {} d_{i'}^{(B)}. ~~~~~\text{(From } (10)) \end{aligned}$$

This contradicts our assumption that $J_{i'}^{(B)}$ is on time in $\pi$. Property (iv) follows.

Finally, if property (v) is violated, there must be a tardy B-job $J_x^{(B)}$ which is scheduled before the restricted B-job $J_R^{(B)}$ in $\pi$. Then all the jobs $J_{k'}^{(B)}$, $1\le k\le n$, $J_{x}^{(B)}$ and $J_{R}^{(B)}$ are completed by time $C_{R}^{(B)}(\pi )$ in $\pi$. As a result, we have

$$\begin{aligned} C_{R}^{(B)}(\pi )\ge & {} \mathop \sum \limits _{k=1}^{n} p_{k'}^{(B)}+ p_{R}^{(B)}+ p_{x}^{(B)}\\\ge & {} 3H + \mathop \sum \limits _{k=1}^{n} p_{2k-1}^{(B)}+ p_{R}^{(B)} ~~~~~\text{(From } (9))\\> & {} d_{R}^{(B)}. ~~~~~\text{(From } \text{ Lemma }~3.3(\mathrm{ii}))\\ \end{aligned}$$

This contradicts property (iii). The lemma follows. $\square$

From Lemma 3.5, $\sum U^{(B)}_j(\sigma )\le n$ in (5) is equivalent to $\sum U^{(B)}_j(\sigma )= n$. Thus, we define an efficient schedule to be a feasible schedule $\sigma$ for instance ${{\mathcal {J}}}$ such that

$$\begin{aligned} \sum C^{(A)}_{j}(\sigma )\le Y \text{ and } \sum U^{(B)}_j(\sigma )= n. \end{aligned}$$

(15)

Lemma 3.6

Suppose that instance ${{\mathcal {J}}}$ has efficient schedules, and let $\sigma$ be an efficient schedule for instance ${{\mathcal {J}}}$ such that $\sum C_j^{(A)}(\sigma )$ is as small as possible. Then $\sigma$ has the following properties:

• (i) the properties (ii)–(v) in Lemma 3.5 are still valid for $\sigma$;

• (ii) all the A-jobs are scheduled before $J^{(B)}_{R}$ in $\sigma$;

• (iii) let $J_{j'}^{(B)}$, $1\le j\le n$, be the on-time B-job in $\{J_{2j-1}^{(B)}, J_{2j}^{(B)}\}$. Then $J_{j'}^{(B)}\prec _{\sigma } J_{j+1}^{(A)}$ and $J_{j}^{(A)}\prec _{\sigma } J_{(j+1)'}^{(B)}$ for $j=1,2,\ldots , n-1$;

• (iv) for each $j=1,2,\ldots , n$, there are only two possible configurations for the triple $\{J_{2j-1}^{(B)}, J_{j}^{(A)}, J_{2j}^{(B)}\}$ in $\sigma$:

  • either $J_{2j-1}^{(B)}$ is on time, $J_{2j}^{(B)}$ is tardy, and $J_{2j-1}^{(B)}$ and $J_{j}^{(A)}$ are scheduled consecutively in this order,

  • or $J_{2j-1}^{(B)}$ is tardy, $J_{2j}^{(B)}$ is on time, and $J_{j}^{(A)}$ and $J_{2j}^{(B)}$ are scheduled consecutively in this order.

Proof

Suppose that $\sigma$ is an efficient schedule for instance ${{\mathcal {J}}}$ such that $\sum C_j^{(A)}(\sigma )$ is as small as possible. Then $\sum U_j^{(B)}(\sigma )=n$. This means that the schedule obtained from $\sigma$ by deleting the A-jobs is also an optimal schedule for problem $1||\sum U^{(B)}_j$ on B-jobs ${{\mathcal {J}}}^{(B)}$. Consequently, the properties (ii)–(v) in Lemma 3.5 are still valid for $\sigma$.

Since $p^{(B)}_{R}=L>Y$ is a sufficiently large integer, all A-jobs must be scheduled before $J^{(B)}_{R}$ in $\sigma$. Property (ii) follows.

Recall that ${{\mathcal {O}}}(\sigma )$ is the set of on-time B-jobs in $\sigma$. The above discussion enables us to define $J_{j'}^{(B)}$, $1\le j\le n$, to be the unique job in ${{\mathcal {O}}}(\sigma )\cap \{J_{2j-1}^{(B)}, J_{2j}^{(B)}\}$. Then $(1', 2', \cdots , n')$ is a nice sequence. From property (i) and Lemma 3.5, in schedule $\sigma$, the on-time B-jobs are scheduled in the order

$$\begin{aligned} J_{1'}^{(B)} \prec _{\sigma } J_{2'}^{(B)} \prec _{\sigma } \cdots \prec _{\sigma } J_{n'}^{(B)}. \end{aligned}$$

(16)

Recall that A-jobs are scheduled in the order as (6), i.e.,

$$\begin{aligned} J_{1}^{(A)} \prec _{\sigma } J_{2}^{(A)} \prec _{\sigma } \cdots \prec _{\sigma } J_{n}^{(A)}. \end{aligned}$$

To prove property (iii), by contradiction, we suppose that there is some $j\in \{1,2, \ldots , n-1\}$ so that either $J_{j+1}^{(A)}\prec _{\sigma } J_{j'}^{(B)}$ or $J_{(j+1)'}^{(B)}\prec _{\sigma } J_{j}^{(A)}$.

If $J_{j+1}^{(A)}\prec _{\sigma } J_{j'}^{(B)}$, from (6) and (16), we have $\{J_{1}^{(A)}, \cdots , J_{j+1}^{(A)}\}\prec _{\sigma } J_{j'}^{(B)}$, and $\{J_{1'}^{(B)}, \cdots , J_{(j-1)'}^{(B)}\}\prec _{\sigma } J_{j'}^{(B)}$. Thus, from Lemma 3.4(iii), we have $C_{j'}^{(B)}(\sigma ) \ge (j+1) p^{(A)}+\sum _{k=1}^{j} p_{k'}^{(B)}> d_{j'}^{(B)}$. This contradicts our assumption that $J_{j'}^{(B)}$ is on time in $\sigma$.

Now, by the choice of j, we must have $J_{(j+1)'}^{(B)}\prec _{\sigma } J_{j}^{(A)}$. From (6) and (16), again, there must be a pair of indices x and y with $1\le x< y\le n$ such that $J_{y'}^{(B)}\prec _{\sigma } J_{x}^{(A)}$ and $J_{y'}^{(B)}$ and $J_{x}^{(A)}$ are consecutively scheduled in $\sigma$, i.e., $C_{y'}^{(B)}(\sigma ) =S_{x}^{(A)}(\sigma )$, where $S_{x}^{(A)}(\sigma )$ is the starting time of $J_{x}^{(A)}$ in $\sigma$. Let $\sigma '$ be the new schedule obtained from $\sigma$ by exchanging the positions of $J_{y'}^{(B)}$ and $J_{x}^{(A)}$. From Lemma 3.4(i), we have $C_{y'}^{(B)}(\sigma ') = C_{x}^{(A)}(\sigma ) = \sum _{k=1}^y p_{k'}^{(B)} + x p^{(A)} \le \sum _{k=1}^y p_{k'}^{(B)} + (y-1) p^{(A)}\le d_{y'}^{(B)}$. This implies that $J_{y'}^{(B)}$ is also on time in $\sigma '$, and so $\sum U_j^{(B)}(\sigma ')= \sum U_j^{(B)}(\sigma )= n$. But $\sum C_j^{(A)}(\sigma ')< \sum C_j^{(A)}(\sigma )$. This contradicts the definition of $\sigma$. Property (iii) follows.

To prove property (iv), we note from property (iii) that

$$\begin{aligned} J_{(j-1)'}^{(B)} \prec _{\sigma } J_{j}^{(A)} \prec _{\sigma } J_{(j+1)'}^{(B)} \text{ and } J_{j-1}^{(A)} \prec _{\sigma } J_{j'}^{(B)} \prec _{\sigma } J_{j+1}^{(A)}. \end{aligned}$$

(17)

By contradiction, suppose that there is some index $j\in \{1,2, \ldots , n\}$ such that the triple $\{J_{2j-1}^{(B)}, J^{(A)}_{j}, J_{2j}^{(B)}\}$ violates property (iv).

Let $S^{(j)}(\sigma )=\min \{S_{2j-1}^{(B)}, S_{j}^{(A)}, S_{2j}^{(B)}\}$ be the earliest starting time for the three jobs $J_{2j-1}^{(B)}, J_{j}^{(A)}, J_{2j}^{(B)}$ in $\sigma$. From (17), $J_{k'}^{(B)}$ and $J_{k}^{(A)}$, $1\le k\le j-1$, are just all the jobs completed by time $S^{(j)}(\sigma )$, implying that $S^{(j)}(\sigma )=\sum _{k=1}^{j-1} p_{k'}^{(B)}+(j-1) p^{(A)}$. Thus, we have

$$\begin{aligned} \sum _{k=1}^{j-1}p_{2k-1}^{(B)}+ (j-1)p^{(A)}\le S^{(j)}(\sigma )\le \sum _{k=1}^{j-1}p_{2k}^{(B)}+ (j-1)p^{(A)}. \end{aligned}$$

(18)

Suppose that $j'= 2j-1$ and $J_{j}^{(A)}$ is scheduled before $J_{2j-1}^{(B)}$. Then we have

$$\begin{aligned} C_{2j-1}^{(B)}(\sigma )= & {} S^{(j)}(\sigma )+p^{(A)} +p_{2j-1}^{(B)}\\\ge & {} \mathop \sum \limits _{k=1}^{j-1}p_{2k-1}^{(B)}+ (j-1)p^{(A)}+p^{(A)}\\&+\,M_j+ a_{2j-1}~~~~~\text{(From } (18))\\= & {} \mathop \sum \limits _{k=1}^{j-1}(M_k+a_{2k-1})+p^{(A)}+ (j-1)p^{(A)}\\&+\,M_j+ a_{2j-1}\\\ge & {} \mathop \sum \limits _{k=1}^{j-1}(M_k+a_{2k})+1+ (j-1)p^{(A)}\\&+\,M_j+ a_{2j-1}\\= & {} d_{2j-1}^{(B)}+ 1 \\> & {} d_{2j-1}^{(B)}. \end{aligned}$$

This contradicts our assumption that $J^{(B)}_{2j-1}=J^{(B)}_{j'}$ is on time in $\sigma$.

From (17) and the choice of j, the above discussion implies that $j'= 2j$ and $J_{j}^{(A)}$ is scheduled after $J_{2j}^{(B)}$. Let $\sigma '$ be the new schedule obtained from $\sigma$ by exchanging the positions of $J_{j}^{(A)}$ and $J_{2j}^{(B)}$. From property (iii), the completion times for other jobs except $J_{j}^{(A)}$ and $J_{2j}^{(B)}$ in $\sigma '$ are the same as they are in $\sigma$. From (18), we have $C_{2j}^{(B)}(\sigma ') = S^{(j)}(\sigma )+p^{(A)} +p_{2j}^{(B)} \le \sum _{k=1}^{j}p_{2k}^{(B)}+ jp^{(A)}= d_{2j}^{(B)}$. Then $J_{2j}^{(B)}$ is still on time in $\sigma '$, and so $\sum U_j^{(B)}(\sigma ') = \sum U_j^{(B)}(\sigma )$. But then $\sum C^{(A)}_j(\sigma ')< \sum C^{(A)}_j(\sigma )$. This contradicts the choice of $\sigma$. Property (iv) follows. $\square$

Given a nice sequence $(1',2',\ldots , n')$, let $(1'',2'',\ldots , n'')$ be the sequence such that $\{j',j''\}= \{2j-1, 2j\}$ for $j=1, 2, \ldots , n$. We then define a schedule $\sigma$ of ${{\mathcal {J}}}$ corresponding to the nice sequence $(1',2',\ldots , n')$ in the following way:

$$\begin{aligned}&\{J_1^{(A)}, J_{1'}^{(B)}\}\prec _{\sigma } \{J_2^{(A)}, J_{2'}^{(B)}\}\prec _{\sigma }\cdots \prec _{\sigma } \{J_n^{(A)}, J_{n'}^{(B)}\}\\&\quad \prec _{\sigma } J_{R}^{(B)}\prec _{\sigma } \{J_{j''}^{(B)}: j=1,2, \ldots , n\}, \end{aligned}$$

where, for $j=1,2, \ldots , n$, we have

$$\begin{aligned} \left\{ \begin{array}{ll} J_j^{(A)} \prec _{\sigma } J_{j'}^{(B)}, &{}\text{ if } j'= 2j,\\ J_{j'}^{(B)} \prec _{\sigma } J_{j}^{(A)}, &{}\text{ if } j'= 2j-1. \end{array}\right. \end{aligned}$$

For $j=1,2, \ldots , n$, we have

$$\begin{aligned}C_j^{(A)}(\sigma ) =\left\{ \begin{array}{ll} j p^{(A)} +\sum _{k=1}^j p_{k'}^{(B)}, &{}\text{ if } j'=2j-1,\\ j p^{(A)} +\sum _{k=1}^{j-1} p_{k'}^{(B)}, &{}\text{ if } j'=2j. \end{array}\right. \end{aligned}$$

Hence, we have

$$\begin{aligned}&\mathop \sum \limits _{j=1}^{n} C_{j}^{(A)}(\sigma )\\&\quad = \mathop \sum \limits _{j=1}^{n}j p^{(A)} +\mathop \sum \limits _{j: j'=2j-1} \mathop \sum \limits _{k=1}^j p_{k'}^{(B)} \\&\qquad + \,\mathop \sum \limits _{j: j'=2j} \mathop \sum \limits _{k=1}^{j-1} p_{k'}^{(B)} \\&\quad = \frac{n(n+1)}{2}p^{(A)}+\mathop \sum \limits _{j:j'=2j-1} (n+1-j)p_{2j-1}^{(B)}\\&\qquad +\,\mathop \sum \limits _{j:j'=2j} (n-j)p_{2j}^{(B)}\\&\quad = \frac{n(n+1)}{2} p^{(A)}+\mathop \sum \limits _{j=1}^{n}(n-j)p^{(B)}_{2j} \\&\qquad +\, \mathop \sum \limits _{j:j'=2j-1} p_{2j-1}^{(B)}\\&\qquad -\, \mathop \sum \limits _{j:j'=2j-1}(n-j)\left( p^{(B)}_{2j}-p^{(B)}_{2j-1}\right) \\&\quad = \frac{n(n+1)}{2} p^{(A)}+\mathop \sum \limits _{j=1}^{n}(n-j)p^{(B)}_{2j} \\&\qquad +\, \mathop \sum \limits _{j:j'=2j-1} (M_j+a_{2j-1})\\&\qquad -\, \mathop \sum \limits _{j:j'=2j-1}(n-j)(a_{2j}-a_{2j-1})\\&\quad = \frac{n(n+1)}{2} p^{(A)}+\mathop \sum \limits _{j=1}^{n}(n-j)p^{(B)}_{2j}\\&\qquad +\, \mathop \sum \limits _{j:j'=2j-1}3H(a_{2j}-a_{2j-1}). \end{aligned}$$

From the definition of Y in (4), we have

$$\begin{aligned} \sum _{j=1}^{n} C_{j}^{(A)}(\sigma )=Y-3H\delta +\sum _{j:j'=2j-1}3H(a_{2j}-a_{2j-1}).\nonumber \\ \end{aligned}$$

(19)

Now let us return to the NP-hardness proof. We need to show in the following that the partition instance ${{\mathcal {I}}}= (a_1, a_2, \ldots , a_{2n}, H)$ has a solution if and only if the job instance ${{\mathcal {J}}}$ has an efficient schedule. Note that $M_j= 3H(a_{2j}-a_{2j-1})+(n-j)(a_{2j}-a_{2j-1})- a_{2j-1}$. Then we have

$$\begin{aligned}&M_j+ a_{2j-1}- (n-j)(a_{2j}-a_{2j-1})= 3H(a_{2j}-a_{2j-1}) \nonumber \\&\quad \text{ for } j=1, 2, \ldots , n. \end{aligned}$$

(20)

Suppose first that the partition instance ${{\mathcal {I}}}$ has a solution. Then there is a partition $(I_1, I_2)$ of the index set $\{1,2,\ldots , 2n\}$ such that $|I_1\cap \{2j-1, 2j\}|= |I_2\cap \{2j-1, 2j\}|= 1$ for $j=1, 2, \ldots , n$, and $\sum _{j\in I_1}a_j=\sum _{j\in I_2}a_j=H$. For our purpose, we write $I_1= \{1', 2', \ldots , n'\}$ and $I_2= \{1'', 2'', \ldots , n''\}$ such that $\{j', j''\}= \{2j-1, 2j\}$ for $j=1, 2, \ldots , n$. Then $\sum _{k=1}^n a_{k'}=\sum _{k=1}^n a_{k''}=H$. Recall that $\delta =\frac{1}{2} \sum _{j=1}^n (a_{2j}-a_{2j-1})$. Then $2\delta = \sum _{j:j'=2j-1}(a_{2j}-a_{2j-1})+\sum _{j:j'=2j}(a_{2j}-a_{2j-1})$ and $\sum _{j:j'=2j-1}(a_{2j}-a_{2j-1}) - \sum _{j:j'=2j}(a_{2j}-a_{2j-1}) = \sum _{j=1}^n a_{j''} - \sum _{j=1}^n a_{j'}=H-H=0$. Therefore, we have

$$\begin{aligned} \delta =\sum _{j:j'=2j-1}(a_{2j}-a_{2j-1}). \end{aligned}$$

(21)

Let $\sigma$ be the schedule of ${{\mathcal {J}}}$ corresponding to the nice sequence $(1',2',\ldots , n')$.

From (19) and (21), we have $\sum C_{j}^{(A)}(\sigma )=Y$.

For each $j\in \{1,2, \ldots , n\}$, from Lemma 3.4(i), we have $C_{j'}^{(B)}(\sigma ) = \sum _{k=1}^j p_{k'}^{(B)} + \lfloor {j'/2}\rfloor p^{(A)}\le d^{(B)}_{j'}$. Hence, the nB-jobs $J_{j'}^{(B)}$, $1\le j\le n$, are on time in $\sigma$. For the restricted B-job $J_{R}^{(B)}$, from Lemma 3.4(ii) and from the fact that $\sum _{k=1}^n a_{k'}=H$, we have $C_{R}^{(B)}(\sigma ) = \sum _{k=1}^n p_{k'}^{(B)} + n p^{(A)}+ p_{R}^{(B)}\le d^{(B)}_{R}$. Thus, $J_{R}^{(B)}$ is also on time in $\sigma$. Since $J_{R}^{(B)}$ has a sufficiently large processing time, it is easy to verify that all the B-jobs in $\{J_{j''}^{(B)}: j=1,2, \ldots , n\}$ are tardy in $\sigma$. It follows that $\sum U_j^{(B)}(\sigma )=n$. Thus, $\sigma$ is an efficient schedule for instance ${{\mathcal {J}}}$.

Conversely, suppose that $\sigma$ is an efficient schedule for instance ${{\mathcal {J}}}$. Then, $\sum C^{(A)}_{j}(\sigma )\le Y$ and $\sum U^{(B)}_j(\sigma )= n$. For our purpose, we may assume that $\sigma$ is chosen such that $\sum C^{(A)}_{j}(\sigma )$ is as small as possible. Recall that ${{\mathcal {O}}}(\sigma )$ is the set of on-time B-jobs in $\sigma$. According to Lemma 3.6, $J_{R}^{(B)}$ is on time in $\sigma$. Then $|{{\mathcal {O}}}(\sigma )\cap \{J_{1}^{(B)}, J_{2}^{(B)}, \ldots , J_{2n}^{(B)} \}|=n$. Assume that ${{\mathcal {O}}}(\sigma )\cap \{J_{1}^{(B)}, J_{2}^{(B)}, \ldots , J_{2n}^{(B)} \}= \{J_{j'}^{(B)}: 1\le j\le n\}$ such that $1'< 2'<\cdots < n'$. From Lemma 3.6, we have $j'\in \{2j-1, 2j\}$ for $j=1,2, \ldots , n$, and moreover, $(1', 2', \ldots , n')$ is a nice sequence and $\sigma$ is the schedule of ${{\mathcal {J}}}$ corresponding to $(1',2', \ldots , n')$.

Set $I_1= \{j': 1\le j\le n\}$ and $I_2= \{1,2, \ldots , 2n\}\setminus I_1$. We will show that $(I_1, I_2)$ is a solution for the partition instance ${{\mathcal {I}}}$.

Since $J_{R}^{(B)}$ is on time in $\sigma$, we have $d_R^{(B)} \ge C_R^{(B)} = n p^{(A)} + \sum _{j=1}^n p_{j'}^{(B)} + p_R^{(B)}$. From Lemma 3.4(ii), we have

$$\begin{aligned} \sum _{j\in I_1} a_{j}= \sum _{j=1}^n a_{j'} \le H. \end{aligned}$$

(22)

Since $\sum C_{j}^{(A)}(\sigma )\le Y$, from (19), we have $Y\ge \sum C_{j}^{(A)}(\sigma )= Y-3H\delta + \sum _{j:j'=2j-1}3H(a_{2j}-a_{2j-1})$, implying that $\sum _{j:j'=2j-1}(a_{2j}-a_{2j-1})\le \delta$. Note that $\delta =\frac{1}{2}\sum _{j=1}^{n} (a_{2j}-a_{2j-1})$. Then we have $\sum _{j:j'=2j-1}(a_{2j}-a_{2j-1})\le \sum _{j:j'= 2j}(a_{2j}-a_{2j-1})$, or equivalently,

$$\begin{aligned} \sum _{j\in I_2} a_{j}\le \sum _{j\in I_1} a_{j}. \end{aligned}$$

(23)

Since $\sum _{j\in I_1} a_{j}+ \sum _{j\in I_2} a_{j}=2H$, from (22) and (23), we conclude that $\sum _{j\in I_1} a_{j}= \sum _{j\in I_2} a_{j}=H$. Consequently, $(I_1, I_2)$ is a solution for the partition instance ${{\mathcal {I}}}$. The result follows. $\square$

We use $1||\text{ Lex } (\gamma _1, \gamma _2)$ to denote the single machine hierarchical optimization problem, where $\gamma _1$ is the primary criterion and $\gamma _2$ is the secondary criterion. The objective is to minimize the secondary criterion $\gamma _2$ under the constraint that the primary criterion $\gamma _1$ is optimized.

From the above discussion, we have the following corollary.

Corollary 3.1

Problem $1|p_j^{(A)}= p^{(A)}|\text{ Lex } (\sum U_j^{(B)}, \sum C_j^{(A)})$ is binary NP-hard.

Appendix: Proof of Observation 2.2

Proof

The proof of Lemma 1 in Leung et al. (2010b) is based on the assumption that there exists a solution for the given instance of the even–odd partition, that is, there is a partition $(I_1, I_2)$ of the index set $\{1, 2, \ldots , 2n\}$ with $|I_1\cap \{2i-1, 2i\}|= 1$ and $|I_2\cap \{2i-1, 2i\}|= 1$ for each $i=1, 2, \ldots , n$ such that $\sum _{j\in I_1} a_j= \sum _{j\in I_2} a_j= H$. From Observation 2.1, the condition $\sum _{j\in I_1} a_j= \sum _{j\in I_2} a_j= H$ is equivalent to condition (C1). The aim of their Lemma 1 is to show that there is a schedule such that $\sum C_j^a\le TC$ and $\sum U_j^b\le n$. This is achieved by constructing a schedule $\pi$.

To guarantee that their constructed schedule $\pi$ satisfies $\sum U_j^b(\pi )\le n$, the R-job must be on time in the schedule. Then we have

$$\begin{aligned}&\mathop \sum \limits _{i:2i-1\in I_1} p_{2i-1}+\mathop \sum \limits _{i:2i\in I_1} p_{2i}+ \mathop \sum \limits _{i=1}^{n} x_{i}+ L\\&\quad = \mathop \sum \limits _{i:2i-1\in I_1}a_{2i-1}+\mathop \sum \limits _{i:2i\in I_1}(a_{2i}+(l_{i}-1)\sigma _i)\\&\qquad + \,\mathop \sum \limits _{i=1}^{n} x_{i}+ L \\&\quad = \mathop \sum \limits _{i=1}^{n}x_{i}+ H+ L+\mathop \sum \limits _{i:2i\in I_1} (l_{i}-1)\sigma _i \\&\quad = \mathop \sum \limits _{i=1}^{n}x_{i}+ H+ L+\mathop \sum \limits _{i:2i\in I_1} l_{i}\sigma _i\\&\qquad -\,\mathop \sum \limits _{i:2i\in I_1}\sigma _i+\mathop \sum \limits _{i:2i-1\in I_1} l_{i}\sigma _i - \mathop \sum \limits _{i:2i-1\in I_1} l_{i}\sigma _i \\&\quad = \mathop \sum \limits _{i=1}^{n} x_{i}+ H+ L+\mathop \sum \limits _{i=1}^{n}l_{i}\sigma _i\\&\qquad -\,\mathop \sum \limits _{i:2i-1\in I_1}l_{i}\sigma _i -\mathop \sum \limits _{i:2i\in I_1}\sigma _i \\&\quad = \mathop \sum \limits _{i=1}^{n} x_{i}+ H+ L+\mathop \sum \limits _{i=1}^{n}l_{i}\sigma _i\\&\qquad -\,\mathop \sum \limits _{i:2i-1\in I_1}l_{i}\sigma _i -\frac{1}{2}\mathop \sum \limits _{i=1}^{n} \sigma _i\\&\quad \le d_{R}= \mathop \sum \limits _{i=1}^{n} x_{i}+ \left[ H+ \frac{1}{2}\mathop \sum \limits _{i=1}^{n} (l_{i}-1)\sigma _i\right] + L. \end{aligned}$$

Thus, we have $\sum _{i:2i-1\in I_1}l_{i}\sigma _i\ge \frac{1}{2}\sum _{i=1}^{n}l_{i}\sigma _i$.

On the other hand, to guarantee that the total completion time of agent A is no more than TC, we should have

$$\begin{aligned}&\mathop \sum \limits _{i:2i-1\in I_1}(n-i+1)p_{2i-1}+\mathop \sum \limits _{i:2i\in I_1} (n-i)p_{2i}\\&\qquad +\,\mathop \sum \limits _{i=1}^{n}(n-i+1)x_{i}\\&\quad = \mathop \sum \limits _{i:2i-1\in I_1}(n-i+1)a_{2i-1}+\mathop \sum \limits _{i:2i\in I_1}(n-i)(a_{2i}\\&\qquad +\,(l_{i}-1)\sigma _i)+\mathop \sum \limits _{i=1}^{n}(n-i+1)x_{i}\\&\qquad +\,\mathop \sum \limits _{i:2i-1\in I_1}(n-i)(a_{2i}+(l_{i}-1)\sigma _i)\\&\qquad -\,\mathop \sum \limits _{i:2i-1\in I_1} (n-i)(a_{2i}+(l_{i}-1)\sigma _i)\\&\quad = \mathop \sum \limits _{i=1}^{n}(n-i)(a_{2i}+(l_{i}-1)\sigma _i)\\&\qquad +\,\mathop \sum \limits _{i=1}^{n}(n-i+1)x_{i}+\mathop \sum \limits _{i:2i-1\in I_1} a_{2i-1}\\&\qquad -\,\mathop \sum \limits _{i:2i-1\in I_1} (n-i)(a_{2i}- a_{2i-1}+(l_{i}-1)\sigma _i)\\&\quad = \mathop \sum \limits _{i=1}^{n}(n-i)(a_{2i}+(l_{i}-1)\sigma _i)+ \mathop \sum \limits _{i=1}^{n}(n-i+1)x_{i} \\&\qquad +\,\mathop \sum \limits _{i:2i-1\in I_1} (a_{2i-1}-(n-i)l_{i}\sigma _i)\\&\quad = \mathop \sum \limits _{i=1}^{n}(n-i)(a_{2i}+(l_{i}-1)\sigma _i)\\&\qquad + \,\mathop \sum \limits _{i=1}^{n}(n-i+1)x_{i}+\mathop \sum \limits _{i:2i-1\in I_1} l_{i}\sigma _{i}\\&\quad \le TC=\mathop \sum \limits ^{n}_{i=1}(n-i)(a_{2i}+(l_i-1)\sigma _i)\\&\qquad +\mathop \sum \limits ^{n}_{i=1}(n-i+1)x_i+\frac{1}{2}\mathop \sum \limits ^{n}_{i=1}l_i\sigma _i. \end{aligned}$$

Thus, we have $\sum _{i:2i-1\in I_1}l_{i}\sigma _i\le \frac{1}{2}\sum _{i=1}^{n}l_{i}\sigma _i$.

From the above discussion, we can see that the correctness of their Lemma 1 needs the correctness of condition (C2), i.e., $\sum _{i:2i-1\in I_1}l_{i}\sigma _i = \sum _{i:2i-1\in I_2}l_{i}\sigma _i= \frac{1}{2}\sum _{i=1}^{n}l_{i}\sigma _i$. Consequently, the correctness of their Lemma 1 requires that

The proof of Lemma 10 in Leung et al. (2010b) is based on the assumption that there exists a solution for problem $1||\sum C_j^a\le TC:\sum U_j^b\le n$ on the constructed scheduling instance. The aim is to show that there exists a solution for the instance of the even–odd partition.

Their proof also uses the results in their Lemmas 2–9. We do not need to state all of the steps, but the R-job must be on time, and the total completion time for agent A is no more than TC. Then, from Lemmas 2–9, we have

$$\begin{aligned}&\mathop \sum \limits _{i=1}^{n}p_{2i}+\mathop \sum \limits _{i=1}^{n}x_i+L-\mathop \sum \limits _{i:P_{2i-1} \text{ is } \text{ early }}l_i\sigma _i\\&\quad = \mathop \sum \limits _{i=1}^{n}(a_{2i}+(l_{i}-1)\sigma _i)+ \mathop \sum \limits _{i=1}^{n} x_{i}+ L\\&\qquad -\,\mathop \sum \limits _{i:P_{2i-1} \text{ is } \text{ early }}l_i\sigma _i\\&\quad = H+\frac{1}{2}\mathop \sum \limits _{i=1}^{n}\sigma _i+\mathop \sum \limits _{i=1}^{n}(l_{i}-1)\sigma _i+\mathop \sum \limits _{i=1}^{n}x_{i}+ L\\&\qquad -\,\mathop \sum \limits _{i:P_{2i-1} \text{ is } \text{ early }}l_i\sigma _i\\&\quad = \mathop \sum \limits _{i=1}^{n}x_{i}+ H+ L+\mathop \sum \limits _{i=1}^{n}l_{i}\sigma _i-\frac{1}{2}\mathop \sum \limits _{i=1}^{n}\sigma _i\\&\qquad -\,\mathop \sum \limits _{i:P_{2i-1} \text{ is } \text{ early }}l_i\sigma _i \\&\quad \le d_{R}= \mathop \sum \limits _{i=1}^{n} x_{i}+\left[ H+ \frac{1}{2}\mathop \sum \limits _{i=1}^{n} (l_{i}-1)\sigma _i\right] + L, \end{aligned}$$

and

$$\begin{aligned}&\mathop \sum \limits _{i=1}^{n}(n-i)p_{2i}+\mathop \sum \limits _{i=1}^{n}(n-i+1)x_{i}\\&\qquad +\,\mathop \sum \limits _{i:P_{2i-1} \text{ is } \text{ early }}l_i\sigma _i\\&\quad = \mathop \sum \limits _{i=1}^{n}(n-i)(a_{2i}+(l_{i}-1)\sigma _i)\\&\qquad +\,\mathop \sum \limits _{i=1}^{n}(n-i+1)x_{i} +\mathop \sum \limits _{i:P_{2i-1} \text{ is } \text{ early }}l_i\sigma _i\\&\quad \le TC=\mathop \sum \limits ^{n}_{i=1}(n-i)(a_{2i}+(l_i-1)\sigma _i)\\&\qquad +\,\mathop \sum \limits ^{n}_{i=1}(n-i+1)x_i+\frac{1}{2}\mathop \sum \limits ^{n}_{i=1}l_i\sigma _i. \end{aligned}$$

Hence, we have that

$$\begin{aligned} \sum _{i:P_{2i-1} \text{ is } \text{ early }}l_i\sigma _i\ge \frac{1}{2}\sum _{i=1}^{n}l_{i}\sigma _i \text{ and } \sum _{i:P_{2i-1} \text{ is } \text{ early }}l_i\sigma _i\le \frac{1}{2}\sum _{i=1}^{n}l_{i}\sigma _i. \end{aligned}$$

That is,

Note that condition ($\hbox {C2}'$) is potentially implied in the proof of their Lemma 10. After this, the authors of Leung et al. (2010b) directly conclude that the instance of the even–odd partition has a solution. In the normal deduction, we should add the following procedure.

Let $I_1= \{2i-1: P_{2i-1} \text{ is } \text{ early }\}\cup \{2i: P_{2i} \text{ is } \text{ early }\}$ and $I_2= \{1, 2, \ldots , 2n\}\setminus I_1$. The results in their Lemmas 2-9 imply that $|I_1\cap \{2i-1, 2i\}|= 1$ and $|I_2\cap \{2i-1, 2i\}|= 1$ for each $i=1, 2, \ldots , n$. Now condition ($\hbox {C2}'$) can be rewritten as condition (C2), i.e., $\sum _{i:2i-1\in I_1}l_i\sigma _i= \sum _{i:2i-1\in I_2}l_i\sigma _i= \frac{1}{2}\sum _{i=1}^{n}l_{i}\sigma _i$. Thus, from Observation 2.1, the correctness of their Lemma 10 requires that

From equations (A) and (B), we conclude that if their Lemmas 1 and 10 are correct, then for every partition $(I_1, I_2)$ of the index set $\{1,2, \ldots , 2n\}$ with $|I_1\cap \{2i-1, 2i\}|= 1$ and $|I_2\cap \{2i-1, 2i\}|= 1$ for each $i=1, 2, \ldots , n$, the two conditions (C1) and (C2) are equivalent. $\square$