Single-machine scheduling with job-dependent machine deterioration

Abstract

We consider the single-machine scheduling problem with job-dependent machine deterioration. In the problem, we are given a single machine with an initial nonnegative maintenance level, and a set of jobs each with a non-preemptive processing time and a machine deterioration. Such a machine deterioration quantifies the decrement in the machine maintenance level after processing the job. To avoid a machine breakdown, one should guarantee a nonnegative maintenance level at any time point, and whenever necessary, a maintenance activity must be allocated for restoring the machine maintenance level. The goal of the problem is to schedule the jobs and the maintenance activities such that the total completion time of jobs is minimized. There are two variants of maintenance activities: In the partial maintenance case, each activity can be allocated to increase the machine maintenance level to any level not exceeding the maximum; in the full maintenance case, every activity must be allocated to increase the machine maintenance level to the maximum. In a recent work, the problem in the full maintenance case was proven NP-hard; several special cases of the problem in the partial maintenance case were shown to be solvable in polynomial time, but the complexity of the general problem was left open. In this paper we first prove that the problem in the partial maintenance case is binary NP-hard, thus settling the open problem; we then design a 2-approximation algorithm and a branch-and-bound exact search algorithm. Computational experiments are conducted for the two algorithms to examine their practical performance.

1 Introduction

In many scheduling problems, processing a job on a machine causes the machine to deteriorate to some extent, and maintenance activities need to be executed in order to restore the machine capacity. Scheduling problems with maintenance activities have been investigated extensively since the work of Lee and Liman (1992).

A maintenance activity is normally described by two parameters, the starting time and the duration. If these two parameters are given beforehand, a maintenance activity is referred to as fixed; otherwise it is called flexible. Various scheduling models with fixed maintenance activities, in different machine environments and with job characteristics, have been comprehensively surveyed by Schmidt (2000), Lee (2004) and Ma et al. (2010).

A number of researchers have conducted studies with flexible maintenance activities. Qi et al. (1999) considered a single-machine scheduling problem to simultaneously schedule jobs and maintenance activities, with the objective of minimizing the total completion time of jobs. They showed that the problem is NP-hard in the strong sense and proposed heuristics and a branch-and-bound exact algorithm. (Qi (2007) later analyzed the worst-case performance ratio for one of the heuristics, the shortest processing time first or SPT.) Lee and Chen (2000) studied a multiple-parallel-machine scheduling problem where each machine must be maintained exactly once, with the goal of minimizing the total weighted completion time of jobs. They proved the NP-hardness for some special cases and proposed a branch-and-bound exact algorithm based on column generation; the NP-hardness for the general problem is implied. Kubzin and Strusevich (2006) considered a two-machine open-shop and a two-machine flow-shop scheduling problem in which each machine must be maintained exactly once, and the duration of each maintenance activity depends on its starting time. The objective is to minimize the maximum completion time of all jobs and all maintenance activities. The authors, among others, showed that the open-shop problem is polynomial time solvable for quite general functions defining the duration of maintenance in its starting time; they also proved that the flow-shop problem is binary (i.e., weakly) NP-hard and presented a fully polynomial time approximation scheme (FPTAS) (Kubzin and Strusevich 2006).

Returning to single-machine scheduling problems, Chen (2008) studied the periodic maintenance activities of a constant duration not exceeding the available period, with the goal of minimizing the maximum completion time of jobs (that is, the makespan). The author presented two mixed-integer programs and heuristics; computational experiments were also conducted to examine their performance. Mosheiov and Sarig (2009) considered the problem where a machine needs to be maintained prior to a given deadline, with the aim of minimizing the total weighted completion time of jobs. They showed the binary NP-hardness, and they presented a pseudo-polynomial time dynamic programming algorithm and an efficient heuristic. Luo et al. (2010) investigated a similar variant in which the jobs are weighted and the duration of the maintenance is a nondecreasing function of the starting time (which must be prior to a given deadline). Their objective was to minimize the total weighted completion time of jobs; the authors showed the binary NP-hardness, and for the special case of concave duration function, they proposed a $(1 + \sqrt{2}/2 + \epsilon )$-approximation algorithm for any $\epsilon > 0$. Yang and Yang (2010) considered a position-dependent aging effect described by a power function under maintenance activities and variable maintenance duration considerations simultaneously; they examined two models with the objective of minimizing the makespan, and for each of these, they presented a polynomial time algorithm.

Scheduling on two identical parallel machines with periodic maintenance activities was examined by Sun and Li (2010), where the authors presented approximation algorithms with constant performance ratios for minimizing the makespan or minimizing the total completion time of jobs. Xu et al. (2010) considered a case where the length of time between two consecutive maintenance activities is bounded; they presented an approximation algorithm for the multiple-parallel-machine scheduling problem to minimize the completion time of the last maintenance, and for the single-machine scheduling problem to minimize the makespan.

1.1 Problem definition

Considering machine deterioration in the real world, in a recent work by Bock et al. (2012), a new scheduling model subject to job-dependent machine deterioration was introduced. In this model, the single machine must have a nonnegative maintenance level ($\mathrm{ML}$) at any time point, specifying its current maintenance state. (A negative maintenance level indicates the machine breakdown, which is prohibited.) We are given a set of jobs $\mathcal{J} = \{J_i \mid i = 1, 2, \ldots , n\}$, where each job $J_i = (p_i, \delta _i)$ is specified by its non-preemptive processing time$p_i$ and machine deterioration$\delta _i$. The machine deterioration $\delta _i$ quantifies the decrement in the machine maintenance level after processing job $J_i$. (That is, if before the processing of job $J_i$, the maintenance level is $\mathrm{ML}$, then afterward the maintenance level reduces to $\mathrm{ML}- \delta _i$, which suggests that $\mathrm{ML}$ has to be at least $\delta _i$ in order for the machine to process job $J_i$.)

Clearly, to process all the jobs, maintenance activities ($\mathrm{MA}$s) need to be allocated inside a schedule to restore the maintenance level, preventing a machine breakdown. Given that the machine can have a maximum maintenance level of $\mathrm{ML}^{\max }$, and assuming a unit maintenance speed, an $\mathrm{MA}$ of a duration D would increase the maintenance level by $\min \{D, \mathrm{ML}^{\max } - \mathrm{ML}\}$, where $\mathrm{ML}$ is the maintenance level before the $\mathrm{MA}$.

With an initial machine maintenance level $\mathrm{ML}_0$, $0 \le \mathrm{ML}_0 \le \mathrm{ML}^{\max }$, the goal of the problem is to schedule the jobs and necessary $\mathrm{MA}$s such that all jobs can be processed without a machine breakdown, and the total completion time of the jobs is minimized.

There are two variants of the problem, depending on whether one has the freedom to choose the duration of an $\mathrm{MA}$: In the partial maintenance case, the duration of each $\mathrm{MA}$ can be anywhere between 0 and $\mathrm{ML}^{\max } - \mathrm{ML}$, where $\mathrm{ML}$ is the maintenance level before the $\mathrm{MA}$. In the full maintenance case, however, the duration of every $\mathrm{MA}$ must be exactly $\mathrm{ML}^{\max } - \mathrm{ML}$, consequently increasing the maintenance level to the maximum value $\mathrm{ML}^{\max }$. Let $C_i$ denote the completion time of job $J_i$, for $i = 1, 2, \ldots , n$. In three-field notation, the two problems discussed in this paper are denoted as $1 \mid p\mathrm{MA}\mid \sum _j C_j$ and $1 \mid f\mathrm{MA}\mid \sum _j C_j$, where $p\mathrm{MA}$ and $f\mathrm{MA}$ refer to the partial and the full maintenance, respectively.

1.2 Prior work and our contribution

Bock et al. (2012) proved that $1 \mid f\mathrm{MA}\mid \sum _j C_j$ is NP-hard, even when $p_i = p$ for all i or when $p_i = \delta _i$ for all i, both by a reduction from the Partition problem (Garey and Johnson 1979); while all the jobs have the same deterioration, i.e., $\delta _i = \delta$ for all i, the problem can be solved in $O(n \log n)$ time. For the partial maintenance case, Bock et al. (2012) showed that the SPT rule gives an optimal schedule for $1 \mid p\mathrm{MA}\mid \sum _j C_j$ when $p_i < p_j$ implies $p_i + \delta _i \le p_j + \delta _j$ for each pair of i and j (which includes the special cases where $p_i = p$ for all i, $\delta _i = \delta$ for all i, or $p_i = \delta _i$ for all i). The complexity of the general problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$ was left as an open problem. Also, to the best of our knowledge, no approximation algorithms have been designed for either problem.

Our main contribution in this paper is settling the binary NP-hardness of the general problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$. Such NP-hardness might appear a bit surprising at first glance, since one has so much freedom in choosing the starting time and the duration of each $\mathrm{MA}$. Our reduction is from the Partition problem as well, using a kind of job swap argument. This reduction is presented in Sect. 3, following some preliminary properties we observe for the problem in Sect. 2. In Sects. 4 and 5, we propose a 2-approximation algorithm and a branch-and-bound exact search algorithm for $1 \mid p\mathrm{MA}\mid \sum _j C_j$, respectively. Computational experiments are conducted for the two algorithms to examine their practical performance, with the statistics reported in Sect. 5. We conclude the paper in Sect. 6 with a discussion on the (in-)approximability.

Lastly, we would like to point out that when the objective is to minimize the makespan $C_{\max }$, i.e., the maximum completion time of jobs, $1 \mid p\mathrm{MA}\mid C_{\max }$, can be trivially solved in O(n) time, and $1 \mid f\mathrm{MA}\mid C_{\max }$ is NP-hard but admits an $O\left( n^2 (\mathrm{ML}^{\max })^2 \log \left( \sum _{i=1}^n (p_i + \delta _i)\right) \right)$ time algorithm based on dynamic programming (and thus admits an FPTAS) (Bock et al. 2012).

2 Preliminaries

Given a feasible schedule $\pi$ to the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$, which specifies the start processing time for each job and the starting time and the duration of each $\mathrm{MA}$, we slightly abuse $\pi$ to also denote the permutation of the job indices $(1, 2, \ldots , n)$ in which the jobs are processed in order: $\pi = (\pi _1, \pi _2, \ldots , \pi _n)$. The following lemma is proved in Bock et al. (2012).

Lemma 1

Bock et al. (2012) There is an optimal schedule $\pi$ to the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$ such that the total maintenance duration before the processing of job $J_{\pi _i}$ equals $\max \left\{ 0, \sum _{j = 1}^i \delta _{\pi _j} - \mathrm{ML}_0\right\}$, for each $i = 1, 2, \ldots , n$.

Lemma 1 essentially states that each $\mathrm{MA}$ should be pushed back later in the schedule as much as possible until it is absolutely necessary, and its duration should be minimized just for processing the succeeding job. In the sequel, we limit our discussion to feasible schedules satisfying these two properties. We define the separation job in such a schedule $\pi$ as the first job that requires an $\mathrm{MA}$ (of a positive duration).

Lemma 2

Suppose that $J_{\pi _k}$ is the separation job in an optimal schedule $\pi$ for the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$. Then,

• the jobs before the separation job $J_{\pi _k}$ are scheduled in the SPT order;

• the jobs after the separation job $J_{\pi _k}$ are scheduled in the shortest sum-of-processing-time-and-deterioration first (SSF) order;

• the jobs adjacent to the separation job $J_{\pi _k}$ satisfy

  $$\begin{aligned}&p_{\pi _{k-1}} + \min \{\delta _{\pi _{k-1}}, \delta _{\pi _k} - \delta \} \le p_{\pi _k} + (\delta _{\pi _k} - \delta ) \\&\quad \le p_{\pi _{k+1}} + \max \{0, \delta _{\pi _{k+1}} - \delta \}, \end{aligned}$$

  where $\delta = \mathrm{ML}_0 - \sum _{i=1}^{k-1} \delta _{\pi _i}$ is the remaining maintenance level before the first $\mathrm{MA}$.

Proof

Starting with an optimal schedule satisfying the properties stated in Lemma 1, one may apply a simple job swap procedure if the job order is violated either in the prefix or in the suffix of job order separated by the separation job $J_{\pi _k}$. This procedure would decrease the value of the objective, contradicting the optimality. That is, we have (see Fig. 1 for an illustration)

$$\begin{aligned}&p_{\pi _1} \le p_{\pi _2} \le \cdots \le p_{\pi _{k-1}}, \ \text{ and }\end{aligned}$$

(1)

$$\begin{aligned}&p_{\pi _{k+1}} + \delta _{\pi _{k+1}} \le p_{\pi _{k+2}} + \delta _{\pi _{k+2}} \le \cdots \le p_{\pi _n} + \delta _{\pi _n}. \end{aligned}$$

(2)

Fig. 1

An illustration of the optimal schedule $\pi$ stated in Lemma 2, where the separation job is $J_{\pi _k}$; the width of a framebox does not necessarily equal the processing time of a job or the duration of an $\mathrm{MA}$

Let $\delta = \mathrm{ML}_0 - \sum _{i=1}^{k-1} \delta _{\pi _i}$ denote the remaining maintenance level before the first $\mathrm{MA}$. Because $\delta < \delta _{\pi _k}$, an (the first) $\mathrm{MA}$ of duration $\delta _{\pi _k} - \delta$ needs to be performed for processing the separation job $J_{\pi _k}$. Since $\pi$ is optimal, a swap of the two jobs $J_{\pi _k}$ and $J_{\pi _{k+1}}$ does not decrease the objective, that is,

$$\begin{aligned} \left\{ \begin{array}{ll} p_{\pi _k} + (\delta _{\pi _k} - \delta ) \le p_{\pi _{k+1}} + (\delta _{\pi _{k+1}} - \delta ), &{}\quad \text{ if }\quad \delta _{\pi _{k+1}} > \delta ;\\ p_{\pi _k} + (\delta _{\pi _k} - \delta ) \le p_{\pi _{k+1}},&{}\quad \text{ otherwise }. \end{array}\right. \end{aligned}$$

Similarly, a swap of the two jobs $J_{\pi _{k-1}}$ and $J_{\pi _k}$ does not decrease the objective, that is,

$$\begin{aligned} \left\{ \begin{array}{ll} p_{\pi _{k-1}} \le p_{\pi _k}, &{}\quad \text{ if }\quad \delta _{\pi _{k-1}} \ge \delta _{\pi _k} - \delta ;\\ p_{\pi _{k-1}} + \delta _{\pi _{k-1}} \le p_{\pi _k} + (\delta _{\pi _k} -\delta ), &{}\quad \text{ otherwise }. \end{array}\right. \end{aligned}$$

These together give

$$\begin{aligned} p_{\pi _{k-1}} + \min \{\delta _{\pi _{k-1}}, \delta _{\pi _k} - \delta \}\le & {} p_{\pi _k} + (\delta _{\pi _k} - \delta ) \le p_{\pi _{k+1}}\nonumber \\&+\max \{0, \delta _{\pi _{k+1}} - \delta \}. \end{aligned}$$

(3)

This proves the lemma. $\square$

From Lemma 2, one can see that the separation job in an optimal schedule is unique, in the sense that it cannot always be “appended” to either the prefix SPT order or the suffix SSF order. This is reflected in our NP-completeness reduction in Sect. 3, where we force a certain scenario to happen.

3 Proving the binary NP-hardness of the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$

Our reduction is from the classic NP-complete problem Partition (Garey and Johnson 1979), formally defined as follows:

Partition:

Instance: A set X of n positive integers $X = \{x_1, x_2, \ldots , x_n\}$, with $\sum _{i=1}^n x_i = 2B$.

Query: Is there a subset $X_1 \subset X$ such that $\sum _{x \in X_1} x = \sum _{x \in X - X_1} x = B$?

We abuse X to denote the instance of Partition with the set $X = \{x_1, x_2, \ldots , x_n\}$ and $\sum _{i=1}^n x_i = 2B$. The corresponding instance I of the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$ is constructed in polynomial time, as follows:

$$\begin{aligned} \begin{array}{rl} \hbox {Number of jobs:}&{}\quad 2n + 3;\\ \hbox {Job processing time:}&{}\quad p_{n+1+i} = p_i = \sum \limits _{j=1}^i x_j,\\ &{}\qquad \hbox { for } i = 0, 1, 2, \ldots , n,\\ &{}\quad p_{2n+2} = M - 2B;\\ \hbox {Machine deterioration:} &{}\quad \delta _{n+1+i} = \delta _i = M - 2p_i,\\ &{}\quad \text{ for } i = 0, 1, 2, \ldots , n,\\ &{}\quad \delta _{2n+2} = 0;\\ \hbox {Initial maintenance level:} &{}\qquad \mathrm{ML}_0 = \sum \limits _{i=0}^n \delta _i - 2B;\\ \hbox {Maximum maintenance level:} &{}\quad \mathrm{ML}^{\max } = \sum \limits _{i=0}^n \delta _i;\\ \hbox {Objective threshold:} &{}\quad Q = Q_0 + B, \end{array} \end{aligned}$$

where M is a large integer:

$$\begin{aligned} M > (4n + 8) B, \end{aligned}$$

(4)

and $Q_0$ is the total completion time of jobs for an initial infeasible schedule$\pi ^0$ (see Fig. 2).

We note that in the instance $p_{n+1} = p_0 = \sum _{j=1}^0 x_j = 0$ due to the empty range for j. Recall that $\delta$ denotes the remaining maintenance level before the first $\mathrm{MA}$. In the initial schedule $\pi ^0$, we have

$$\begin{aligned} \delta = \mathrm{ML}_0 - \sum _{i=0}^n \delta _i = - 2B. \end{aligned}$$

(5)

Thus, $\pi ^0$ is infeasible. The duration of the first $\mathrm{MA}$ is 2B, which boosts the machine maintenance level from $-2B$ to 0, sufficient for processing the separation job $J_{2n+2}$ (recall that $\delta _{2n+2} = 0$). The value of $Q_0$ is calculated as follows:

$$\begin{aligned} Q_0= & {} \sum _{j=0}^n C_j + \sum _{j=0}^{n+1} C_{2n+2 -j}\nonumber \\= & {} \sum _{j=0}^n \sum _{i=0}^j p_i + (n+2)\left( \sum _{j=0}^n p_j + 2B + p_{2n+2}\right) \nonumber \\&+\sum _{j=0}^n \sum _{i=0}^j \left( p_{2n+1 -i} + \delta _{2n+1 -i}\right) \nonumber \\= & {} \sum _{j=0}^n (n-j+1) p_j + (n+2)\left( \sum _{j=0}^n p_j + 2B+p_{2n+2}\right) \nonumber \\&+ \sum _{j=0}^n (j+1)(p_{n+1+j} + \delta _{n+1+j}), \end{aligned}$$

(6)

where $C_j$ is the completion time of job $J_j$ in the initial schedule $\pi ^0$ and, in particular, $C_{2n+2} = \sum _{j=0}^n p_j + 2B + p_{2n+2}$.

Fig. 2

The initial infeasible schedule $\pi ^0$ for the instance I with the separation job $J_{2n+2}$; $\pi ^0$ satisfies all properties stated in Lemma 2. All $\mathrm{MA}$s are indicated by their respective durations [for the first $\mathrm{MA}$, its duration is $\delta _{2n+2} - \delta = 2B$, by Eq. (5)]

The job order in this initial schedule $\pi ^0$ is $(J_0, J_1, \ldots , J_n, J_{2n+2}, J_{2n+1}, J_{2n}, \ldots , J_{n+1})$, and the first $\mathrm{MA}$ precedes job $J_{2n+2}$, which is regarded as the separation job (see Fig. 2). Before the separation job $J_{2n+2}$, the machine maintenance level is allowed to go into negative, but has to be restored to zero just for processing $J_{2n+2}$ (recall that $\delta _{2n+2} = 0$); afterward, a machine breakdown is no longer tolerated. From $\mathrm{ML}_0 = \sum _{i=0}^n \delta _i - 2B$, we know that $\pi ^0$ is infeasible due to a machine breakdown before the first $\mathrm{MA}$; we will convert it to a feasible schedule later. The query of the decision version of the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$ is whether there exists a feasible schedule $\pi$ such that the total completion time of jobs is no more than $Q = Q_0 + B$.

Despite the infeasibility, the initial schedule $\pi ^0$ has all the properties stated in Lemma 2, with the separation job $J_{2n+2}$ at the center position. The first $n+1$ jobs are in the SPT order and the last $n+1$ jobs are in the SSF order; since $\delta = -2B$, $p_n = p_{2n+1} = 2B$, $\delta _n = \delta _{2n+1} = M - 4B$, $p_{2n+2} = M - 2B$, $\delta _{2n+2} = 0$, Eq. (3) is also satisfied due to the value M in Eq. (4):

$$\begin{aligned}&p_n + \min \{\delta _n, \delta _{2n+2} - \delta \} < p_{2n+2} + (\delta _{2n+2} - \delta ) \\&\quad = p_{2n+1} + \max \{0, \delta _{2n+1} - \delta \}. \end{aligned}$$

In the remainder of this section, we will show that there is a subset $X_1 \subset X$ of sum exactly B if and only if the initial schedule $\pi ^0$ can be converted into a feasible schedule $\pi$ with a total completion time of jobs of no more than $Q = Q_0 + B$, through a repeated job swap procedure.

In summary, the basic idea in the reduction is as follows. We set up the processing times and machine deterioration in such a way that each processing time unit t of a job increases its machine deterioration by 2t. Therefore, the initial schedule $\pi ^0$ provides a lower bound of the total completion time of jobs. Since too small a total processing time for the jobs scheduled before the job $J_{2n+2}$ causes machine deterioration that is too significant, resulting in machine breakdown, $\pi ^0$ is unfortunately infeasible. We thus seek to reduce the maintenance deterioration by increasing the total processing time of the jobs scheduled before job $J_{2n+2}$, through a sequence of job swaps. The equivalence between the two problems results from the fact that we can identify the existence of a Partition solution by finding a schedule that reduces the total machine deterioration before job $J_{2n+2}$ in $\pi ^0$ by exactly 2B, which is the absolute minimum necessary machine deterioration reduction.

Note that the two jobs $J_i$ and $J_{n+1+i}$ are identical, for $i = 0, 1, \ldots , n$. In any schedule with job $J_{2n+2}$ at the center position, if exactly one of $J_i$ or $J_{n+1+i}$ is scheduled before $J_{2n+2}$, then we always say that $J_i$ is scheduled before $J_{2n+2}$, while $J_{n+1+i}$ is scheduled after $J_{2n+2}$. Also, when the two jobs $J_i$ and $J_{n+1 + i}$ are both scheduled before $J_{2n+2}$, then $J_{n+1 + i}$ precedes $J_i$; when the two jobs $J_i$ and $J_{n+1 + i}$ are both scheduled after $J_{2n+2}$, then $J_i$ precedes $J_{n+1 + i}$.

3.1 Proof of “if”

In this subsection, we show that if there is a subset $X_1 \subset X$ of sum exactly B, then the initial infeasible schedule $\pi ^0$ can be converted into a feasible schedule $\pi$ with total completion time of no more than $Q = Q_0 + B$. We also demonstrate the repeated job swap procedure leading to this successful schedule $\pi$.

Suppose that the indices of the elements in the subset $X_1$ are $\{i_1, i_2, \ldots , i_m\}$, satisfying $1 \le i_1< i_2< \cdots < i_m \le n$. Starting with the initial schedule $\pi ^0$, we sequentially swap job $J_{i_\ell - 1}$ with job $J_{n+1 + i_\ell }$, for $\ell = 1, 2, \ldots , m$. Such a job swap between $J_{i_\ell - 1}$ and $J_{n+1 + i_\ell }$ is referred to as a “regular” job swap. Let $\pi ^{\ell }$ denote the schedule after the $\ell$th job swap.

Lemma 3

For each $1 \le \ell \le m$,

• the schedule $\pi ^{\ell }$ with the separation job $J_{2n+2}$ satisfies the properties in Lemma 2;

• the $\ell$th job swap decreases the total machine deterioration before the separation job $J_{2n+2}$ by $2 x_{i_\ell }$;

• the $\ell$th job swap increases the total completion time by $x_{i_\ell }$.

Proof

Recall that the two jobs $J_{i_\ell }$ and $J_{n+1 + i_\ell }$ are identical. Before the $\ell$th job swap between $J_{i_\ell - 1}$ and $J_{n+1 + i_\ell }$ (in schedule $\pi ^{\ell -1}$), the jobs between $J_{i_\ell - 1}$ and $J_{n+1 + i_\ell }$ are

$$\begin{aligned}&\pi ^{\ell -1}: (J_{i_\ell - 1}, J_{i_\ell }, J_{i_\ell + 1}, \ldots , J_n, J_{2n+2}, J_{2n+1}, J_{2n}, \ldots ,\\&\quad J_{n+1 + i_\ell + 1},J_{n+1 + i_\ell }). \end{aligned}$$

After the swap (in schedule $\pi ^\ell$), this sub-schedule becomes

$$\begin{aligned}&\pi ^\ell : (J_{n+1 + i_\ell }, J_{i_\ell }, J_{i_\ell + 1}, \ldots , J_n, J_{2n+2}, J_{2n+1}, J_{2n}, \ldots ,\\&\quad J_{n+1 + i_\ell + 1},J_{i_\ell - 1}). \end{aligned}$$

By simple induction, all jobs before $J_{n+1 + i_\ell }$ have processing times less than $p_{i_\ell }$, and thus the jobs before the separation job $J_{2n+2}$ are in SPT order; for a similar reason, the jobs after the separation job $J_{2n+2}$ are in SSF order.

By the $\ell$th job swap, the change in the total machine deterioration before the separation job $J_{2n+2}$ is $\delta _{i_\ell } - \delta _{i_\ell - 1} = - 2(p_{i_\ell } - p_{i_\ell - 1}) = - 2x_{i_\ell }$, that is, it decreases by $2x_{i_\ell }$. Therefore, the duration of the first $\mathrm{MA}$ also decreases by $2 x_{i_\ell }$. Since $J_n$ always immediately precedes $J_{2n+2}$ and $p_n < p_{2n+2}$, the first half of Eq. (3) holds; since $p_{2n+2} + \delta _{2n+2}$ is the smallest among all jobs, the second half of Eq. (3) holds. That is, the schedule $\pi ^\ell$ satisfies all properties in Lemma 2.

For ease of presentation, let $C_i$ denote the completion time of job $J_i$ in schedule $\pi ^\ell$, and let $C'_i$ denote the completion time of job $J_i$ in schedule $\pi ^{\ell - 1}$. Compared with the schedule $\pi ^{\ell - 1}$ ($\ell \ge 1$), after the $\ell$th job swap between $J_{i_\ell - 1}$ and $J_{n+1 + i_\ell }$,

• the completion times of jobs preceding $J_{n+1 + i_\ell }$ are unchanged; in particular, the starting processing time $S_{n+1 + i_\ell }$ of $J_{n+1 + i_\ell }$ in $\pi ^\ell$ and the starting processing time $S'_{i_\ell - 1}$ of $J_{i_\ell - 1}$ in $\pi ^{\ell - 1}$ satisfy $S_{n+1 + i_\ell } = S'_{i_\ell - 1}$;

• $C_{n+1 + i_\ell } - C'_{i_\ell - 1} = (S_{n+1 + i_\ell } + p_{i_\ell }) - (S'_{i_\ell - 1} + p_{i_\ell - 1}) = p_{i_\ell } - p_{i_\ell - 1} = x_{i_\ell }$;

• the completion time of each job between $J_{i_\ell }$ and $J_n$ (inclusive, $n - i_\ell +1$ of them) increases by $x_{i_\ell }$;

• the duration of the first $\mathrm{MA}$ decreases by $2 x_{i_\ell }$;

• the completion time of each job between $J_{2n+2}$ and $J_{n+1+i_\ell + 1}$ (inclusive, $n - i_\ell +1$ of them) decreases by $x_{i_\ell }$; in particular, the starting processing time $S_{i_\ell - 1}$ of $J_{i_\ell - 1}$ in $\pi ^\ell$ and the starting processing time $S'_{n+1 + i_\ell }$ of $J_{n+1 + i_\ell }$ in $\pi ^{\ell - 1}$ satisfy $S_{i_\ell - 1} = S'_{n+1 + i_\ell } - x_{i_\ell }$;

• $C_{i_\ell - 1} - C'_{n+1+i_\ell } = (S_{i_\ell - 1} + (\delta _{i_\ell - 1} + p_{i_\ell - 1})) - (S'_{n+1 + i_\ell } + (\delta _{i_\ell } + p_{i_\ell })) = - x_{i_\ell } + (\delta _{i_\ell - 1} + p_{i_\ell - 1}) - (\delta _{i_\ell } + p_{i_\ell }) = - x_{i_\ell } - (p_{i_\ell - 1} - p_{i_\ell }) = 0$;

• from the last item, the completion times of jobs succeeding $J_{i_\ell - 1}$ are unchanged.

In summary, there are $n - i_\ell + 2$ jobs, each with completion time that increases by $x_{i_\ell }$, and there are $n - i_\ell + 1$ jobs, each with completion time that decreases by $x_{i_\ell }$. Therefore, the $\ell$th job swap between $J_{i_\ell - 1}$ and $J_{n+1 + i_\ell }$ increases the total completion time by $x_{i_\ell }$. This completes the proof. $\square$

Theorem 1

If there is a subset $X_1 \subset X$ of sum exactly B, then there is a feasible schedule $\pi$ for instance I with total completion time of no more than $Q = Q_0 + B$.

Proof

Let the indices of the elements in the subset $X_1$ be $\{i_1, i_2, \ldots , i_m\}$, such that $1 \le i_1< i_2< \cdots < i_m \le n$. Starting with the initial schedule $\pi ^0$, we sequentially swap the job $J_{i_\ell - 1}$ with job $J_{n+1 + i_\ell }$, for $\ell = 1, 2, \ldots , m$. Let $\pi ^{\ell }$ denote the schedule after the $\ell$th job swap, and let $Q_\ell$ denote the total completion time of jobs in $\pi ^\ell$.

From Lemma 3 we know that the ending schedule $\pi ^m$ satisfies all the properties in Lemma 2. Also, the total machine deterioration before the separation job $J_{2n+2}$ in $\pi ^m$ is

$$\begin{aligned} \sum _{i=0}^n \delta _i - 2 \sum _{\ell =1}^m x_{i_\ell } = \sum _{i=0}^n \delta _i - 2B = \mathrm{ML}_0, \end{aligned}$$

suggesting that $\pi ^m$ is a feasible schedule. (The first $\mathrm{MA}$ has zero duration and thus becomes unnecessary.)

Moreover, the total completion time of jobs in $\pi ^m$ is $Q_m = Q_0 + \sum _{\ell =1}^m x_{i_\ell } = Q_0 + B$. Therefore, the schedule $\pi ^m$ obtained from the initial schedule $\pi ^0$ through the repeated job swap procedure is a desired one. $\square$

3.2 Proof of “only if”

In this subsection, we show that if there is a feasible schedule $\pi$ for the constructed instance I with total completion time of no more than $Q = Q_0 + B$, then there is a subset $X_1 \subset X$ of sum exactly B. Assume without loss of generality that schedule $\pi$ satisfies the properties in Lemma 2. We start with some structural properties which schedule $\pi$ must have.

Lemma 4

Excluding job $J_{2n+2}$, there are at least n and at most $n+1$ jobs scheduled before the first $\mathrm{MA}$ in the schedule $\pi$.

Proof

Recall that in Eq. (4) we set M to be a large value such that $M > (4n + 8)B$. Using $M > (4n + 6)B$, it follows from $M - 4B = \delta _n< \delta _{n-1}< \cdots< \delta _1 < \delta _0 = M$ that the initial machine maintenance level

$$\begin{aligned} \mathrm{ML}_0= & {} \sum _{i=0}^n \delta _i - 2B> (n+1) (M - 4B) - 2B\\= & {} n M + M -(4n + 6)B > n M. \end{aligned}$$

We thus conclude that at least n jobs, excluding $J_{2n+2}$ which has 0 deterioration, can be processed before the first $\mathrm{MA}$.

Nevertheless, if there were more than $n+1$ jobs scheduled before the first $\mathrm{MA}$, excluding $J_{2n+2}$, then their total machine deterioration would be greater than $(n + 2)(M - 4B)$. Using $M > (4n + 8)B$, we have

$$\begin{aligned} (n + 2)(M - 4B)= & {} (n + 1)M + M - (4n + 8)B \\> & {} (n + 1)M> \sum _{i=0}^n\delta _i > \mathrm{ML}_0, \end{aligned}$$

contradicting the feasibility of the schedule $\pi$. $\square$

Lemma 5

There are at most $n+1$ jobs scheduled after job $J_{2n+2}$ in schedule $\pi$.

Proof

We prove the lemma by contradiction. First, noting that the job $J_{2n+2}$ has a much larger processing time than any other job ($M - 2B$ vs. 2B), we conclude that the earliest possible position for $J_{2n+2}$ in schedule $\pi$ is immediately before the first $\mathrm{MA}$. We disallow a zero duration $\mathrm{MA}$, and thus job $J_{2n+2}$ can never be the separation job in $\pi$ due to $\delta _{2n+2} = 0$.

If $J_{2n+2}$ is scheduled after the separation job, by Eq. (2) or the SSF rule, for every job $J_i$ scheduled after $J_{2n+2}$ we have $p_{2n+2} \le p_i + \delta _i$. If $J_{2n+2}$ is scheduled immediately before the first $\mathrm{MA}$, by Eq. (3), for the separation job $J_i$ we have $p_{2n+2} \le p_i + (\delta _i - \delta )$; by Eqs. (2) and (3), for every other job $J_i$ scheduled after $J_{2n+2}$ we have $p_{2n+2} \le p_i + \delta _i$. Therefore, the completion time of a job scheduled $\ell$ positions after job $J_{2n+2}$ is at least $(\ell + 1) \times p_{2n+2}$. If there were $n+2$ jobs scheduled after $J_{2n+2}$, then the total completion time of the last $n+3$ jobs would be at least

$$\begin{aligned} \sum _{\ell =0}^{n+2} (\ell +1) p_{2n+2}= & {} \frac{(n+3)(n+4)}{2} p_{2n+2}\\= & {} \frac{(n+3)(n+4)}{2} (M - 2B). \end{aligned}$$

However, using $p_j \le 2B$ for $j \ne 2n+2$, one can see that Eq. (6) is simplified as

$$\begin{aligned} Q_0= & {} \sum _{j=0}^n (n-j+1) p_j + (n+2)\\&\left( \sum _{j=0}^n p_j + 2B + (M - 2B)\right) + \sum _{j=0}^n (j+1)(M - p_j)\\= & {} \frac{(n+2)(n+3)}{2} M + 2\sum _{j=0}^n (n-j+1) p_j\\\le & {} \frac{(n+2)(n+3)}{2} M + 4B\sum _{j=0}^n (n-j+1)\\= & {} \frac{(n+2)(n+3)}{2} M + 2(n+1)(n+2)B. \end{aligned}$$

Using $M > (3n+6)B$,

$$\begin{aligned}&\frac{(n+3)(n+4)}{2} (M - 2B) \ge Q_0 + (n+3)M \\&\quad - (3n^2 + 13n + 16) B> Q_0 + (2n+2)B, \end{aligned}$$

that is, we would have total completion time of the last $n+3$ jobs in $\pi$ strictly greater than $Q = Q_0 + B$, contradicting our assumption. $\square$

Combining Lemmas 4 and 5, we have the following lemma regarding the position of $J_{2n+2}$ in schedule $\pi$. This conclusion is to be used in the remainder of the section.

Lemma 6

In schedule $\pi$, the position of job $J_{2n+2}$ has only three possibilities:

Case 1::

There are $n+2$ jobs before the first $\mathrm{MA}$, $\pi _{n+2} = 2n+2$, and $J_{\pi _{n+3}}$ is the separation job.

Case 2::

There are $n+1$ jobs before the first $\mathrm{MA}$, $J_{\pi _{n+2}}$ is the separation job, and $\pi _{n+3} = 2n+2$.

Case 3::

There are n jobs before the first $\mathrm{MA}$, $J_{\pi _{n+1}}$ is the separation job, and $\pi _{n+2} = 2n+2$.

Proof

Note that the processing time of job $J_{2n+2}$ is strictly greater than that of any other job, while the sum of its processing time and its machine deterioration ($p_{2n+2} + \delta _{2n+2}$) achieves the minimum among all the jobs. Because $J_{2n+2}$ cannot act as the separation job due to $\delta _{2n+2} = 0$, by Lemma 2, it can only be either the last job scheduled before the first $\mathrm{MA}$ or the first job scheduled after the separation job (through possible job swaps, if necessary).

Using Lemma 4, if there are $n+2$ jobs scheduled before the first $\mathrm{MA}$ in $\pi$, then the last job scheduled before the first $\mathrm{MA}$, $J_{\pi _{n+2}}$, is $J_{2n+2}$. The job $J_{\pi _{n+3}}$ is the separation job. Such a schedule is illustrated in Fig. 3a.

Fig. 3

An illustration of the three possible positions of job $J_{2n+2}$ in a feasible schedule $\pi$

If there are $n+1$ jobs scheduled before the first $\mathrm{MA}$ in $\pi$, then from Lemma 5, job $J_{2n+2}$ is scheduled after the first $\mathrm{MA}$, and thus it is scheduled after the separation job, which is $J_{\pi _{n+2}}$. That is, $\pi _{n+3} = n+2$. Such a schedule is illustrated in the upper part of Fig. 3b.

If there are n jobs scheduled before the first $\mathrm{MA}$ in $\pi$, then from Lemma 5, job $J_{2n+2}$ is scheduled after the first $\mathrm{MA}$, and thus it is scheduled after the separation job, which is $J_{\pi _{n+1}}$. That is, $\pi _{n+2} = n+2$. Such a schedule is illustrated in Fig. 3c.

This completes the proof of the lemma. $\square$

Recall that the job order in the initial infeasible schedule $\pi ^0$ is $(J_0, J_1, \ldots , J_n, J_{2n+2}, J_{2n+1},$$J_{2n}, \ldots , J_{n+2}, J_{n+1})$, and the first $\mathrm{MA}$ is executed before the processing of job $J_{2n+2}$, which is regarded as the separation job (see Fig. 2). In the sequel, we will again convert $\pi ^0$ into our target schedule $\pi$ through a repeated job swap procedure. During such a procedure, the job $J_{2n+2}$ is kept at the center position, and a job swap always involves a job before $J_{2n+2}$ and a job after $J_{2n+2}$.

In cases 1 and 3 of schedule $\pi$ (shown in Fig. 3a and c, respectively), job $J_{2n+2}$ is at the center position (recall that there are in total $2n + 3$ jobs), and therefore the target schedule is well set. In Case 2, as shown in the upper part of Fig. 3b, $J_{2n+2}$ is at position $n+3$, not the center position; we thus exchange $J_{2n+2}$ and $J_{\pi _{n+2}}$ to obtain a schedule $\pi '$ shown in the lower part of Fig. 3b, which is the target schedule with job $J_{2n+2}$ at the center position. (Note that in Case 2, after we have converted $\pi ^0$ into $\pi '$ through a repeated job swap procedure, we exchange $J_{2n+2}$ back to position $n+3$ to obtain the final schedule $\pi$.) Our primary goal is to convert schedule $\pi ^0$ through a repeated job swap procedure, keeping job $J_{2n+2}$ at the center position and keeping the first $\mathrm{MA}$ immediately before job $J_{2n+2}$ (to be detailed next). At the end of this procedure, we achieve a schedule as shown in Fig. 4a. From this schedule, we obtain the target schedule $\pi$ as follows: In Case 1, we swap job $J_{2n+2}$ and the first $\mathrm{MA}$ (i.e., moving the first $\mathrm{MA}$ one position backward and merging it with the immediately succeeding $\mathrm{MA}$). In Case 2, we swap $J_{2n+2}$ and its immediate successor $\mathrm{MA}$ (i.e., moving the immediate successor $\mathrm{MA}$ one position forward and merging it with the first $\mathrm{MA}$). In Case 3, we swap the first $\mathrm{MA}$ and its immediately preceding job (i.e., moving the first $\mathrm{MA}$ one position forward).

In the target schedule $\pi$ ($\pi$ in Cases 1 and 3, or $\pi '$ in Case 2), in the sequel we focus on the jobs, with the understanding that $\mathrm{MA}$’s of proper duration are inserted when needed. Let $R = \{r_1, r_2, \ldots , r_m\}$ denote the subset of indices such that both $J_{r_j}$ and $J_{n+1 + r_j}$ are among the first $n+1$ jobs, where $0 \le r_1< r_2< \cdots < r_m \le n$, and $L = \{\ell _1, \ell _2, \ldots , \ell _m\}$ denote the subset of indices such that both $J_{\ell _j}$ and $J_{n+1 + \ell _j}$ are among the last $n+1$ jobs, where $0 \le \ell _1< \ell _2< \cdots < \ell _m \le n$. Note that $J_{2n+2}$ is at the center position, and thus it must be $|R| = |L|$, and we let $m = |R|$. Clearly, all these $\ell _j$’s and $r_j$’s are distinct from one another. See Fig. 4b for an illustration.

Fig. 4

An illustration of the expected schedule at the end of the repeated job swap procedure, and its relationship to the target schedule $\pi$

In the repeated job swap procedure leading from the initial infeasible schedule $\pi ^0$ to the target feasible schedule, the jth job swap is the swapping of the two jobs $J_{\ell _j}$ and $J_{n+1 + r_j}$. The resulting schedule after the jth job swap is denoted as $\pi ^j$, for $j = 1, 2, \ldots , m$. In Sect. 3.1, the job swap between $J_{\ell _j - 1}$ and $J_{n+1 + \ell _j}$ is “regular” in the sense that $\ell _j = r_j - 1$, but here, $\ell _j$ and $r_j$ do not necessarily relate to each other. We note that immediately after the swap, a job sorting is needed to restore the SPT order for the prefix and the SSF order for the suffix (see the last paragraph before Sect. 3.1 for possible re-indexing of the jobs).

The following Lemma 7 on the jth job swap, when $\ell _j < r_j$, is an extension of Lemma 3.

Lemma 7

For each $1 \le j \le m$, if the schedule $\pi ^{j-1}$ satisfies the first two properties in Lemma 2 and $\ell _j < r_j$, then

• the schedule $\pi ^j$ satisfies the first two properties in Lemma 2;

• the jth job swap decreases the total machine deterioration before the center job $J_{2n+2}$ by $\delta _{\ell _j} - \delta _{r_j} = 2 \sum _{k=\ell _j+1}^{r_j} x_k$;

• the jth job swap increases the total completion time by at least $\sum _{k=\ell _j+1}^{r_j} x_k$; and the increment equals $\sum _{k=\ell _j+1}^{r_j} x_k$ if and only if $\ell _j > r_{j-1}$.

Proof

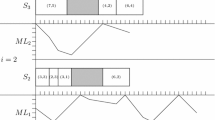
Note that $0 \le r_1< r_2< \cdots < r_m \le n$, $0 \le \ell _1< \ell _2< \cdots < \ell _m \le n$, and all these $\ell _j$’s and $r_j$’s are distinct from each other. Since $\ell _j < r_j$, we assume without loss of generality that $r_{j'-1}< \ell _j < r_{j'}$ for some $j' \le j$, that is, the $j-j'$ jobs $J_{n+1 + r_{j'}}, J_{n+1 + r_{j'+1}}, \ldots , J_{n+1 + r_{j-1}}$ have been moved to be between $J_{\ell _j}$ and the center job $J_{2n+2}$ in the schedule $\pi ^{j-1}$. See Fig. 5 for an illustration of part of the schedule $\pi ^{j-1}$, from job $J_{\ell _j}$ to job $J_{n+1 + \ell _j}$.

The jth job swap between the two jobs $J_{\ell _j}$ and $J_{n+1 + r_j}$ decreases the total machine deterioration before the center job $J_{2n+2}$ by $\delta _{\ell _j} - \delta _{r_j} = 2 \sum _{k=\ell _j+1}^{r_j} x_k$.

To estimate the total completion time, we decompose the jth job swap between the two jobs $J_{\ell _j}$ and $J_{n+1 + r_j}$ as a sequence of $r_j - \ell _j$ “regular” job swaps:

• a regular job swap between $J_{r_j - 1}$ and $J_{n+1 + r_j}$ (marked by * in Fig. 5),

• a regular job swap between $J_{r_j - 2}$ and $J_{n+1 + r_j-1}$ (marked by $ in Fig. 5),

• $\ldots$,

• a regular job swap between $J_{\ell _j + 1}$ and $J_{n+1 + \ell _j+2}$,

• a regular job swap between $J_{\ell _j}$ and $J_{n+1 + \ell _j+1}$ (marked by # in Fig. 5);

that is, between the two jobs $J_k$ and $J_{n+1 + k+1}$, for $k = r_j - 1, r_j - 2, \ldots , \ell _j + 1, \ell _j$. One clearly sees that, since $J_j$ is the same as $J_{n+1 + j}$, the net effect of this sequence of $r_j - \ell _j$ regular job swaps is the job swap between $J_{\ell _j}$ and $J_{n+1 + r_j}$. We note that the order of these regular job swaps is important, and guarantees that at the time of such a swap, job $J_k$ is positioned before the center job $J_{2n+2}$, and job $J_{k+1}$ (which is the same as, and thus can be taken as, job $J_{n+1 + k+1}$) is positioned after the center job $J_{2n+2}$ (see the last paragraph before Sect. 3.1 for possible re-indexing of the jobs). For each such regular job swap between the two jobs $J_k$ and $J_{n+1 + k+1}$, we can apply (almost, see below) Lemma 3 to conclude that it increases the total completion time by at least$x_{k+1}$.

From the proof of Lemma 3, the increment in the total completion time equals $x_{k+1}$ if and only if there are exactly $n-k+1$ jobs between $J_{n+1 + k+1}$ and $J_n$ (inclusive), that is, none of the $j-j'$ jobs $J_{n+1 + r_{j'}}, J_{n+1 + r_{j'+1}}, \ldots , J_{n+1 + r_{j-1}}$ should have been moved between $J_k$ and the center job $J_{2n+2}$ in the schedule $\pi ^{j-1}$. Therefore, the jth job swap increases the total completion time by at least$\sum _{k=\ell _j+1}^{r_j} x_k$, and the increment equals $\sum _{k=\ell _j+1}^{r_j} x_k$ if and only if $\ell _j > r_{j-1}$ (i.e., $j' = j$). This proves the lemma.

Fig. 5

The repeated job swap procedure leading from the initial infeasible schedule $\pi ^0$ to the target schedule. The figure illustrates the moment before the jth job swap between $J_{\ell _j}$ and $J_{n+1 + r_j}$, where $\ell _j < r_j$. The jth job swap is decomposed into a sequence of regular job swaps between $J_k$ and $J_{n+1 + k+1}$, for $k = r_j-1$ (marked by *), $r_j-2$ (marked by $), $\ldots$, $\ell _j+1$, $\ell _j$ (marked by #). If $r_{j'-1}< \ell _j < r_{j'}$ for some $j' \le j$, then the $j-j'$ jobs $J_{n+1 + r_{j'}}, J_{n+1 + r_{j'+1}}, \ldots , J_{n+1 + r_{j-1}}$ have been moved to be between the jobs $J_{\ell _j}$ and $J_{r_j}$

Lemma 8

For each $1 \le j \le m$, if the schedule $\pi ^{j-1}$ satisfies the first two properties in Lemma 2 and $\ell _j > r_j$, then

• the schedule $\pi ^j$ satisfies the first two properties in Lemma 2;

• the jth job swap increases the total machine deterioration before the center job $J_{2n+2}$ by $\delta _{r_j} - \delta _{\ell _j} = 2 \sum _{k=r_j+1}^{\ell _j} x_k$;

• the jth job swap increases the total completion time by at least $\sum _{k=r_j+1}^{\ell _j} x_k$.

Proof

We first prove an analog to Lemma 3 on the job swap between the two jobs $J_{i_\ell + 1}$ and $J_{n+1 + i_\ell }$, which is called an “inverse regular” job swap. It can be viewed as the inverse operation of the regular job swap between the two jobs $J_{i_\ell }$ (which is the same as $J_{n+1 + i_\ell }$) and $J_{n+1 + i_\ell + 1}$ (which is the same as $J_{i_\ell + 1}$).

Let $\sigma '$ denote the schedule before the job swap between $J_{i_\ell + 1}$ and $J_{n+1 + i_\ell }$, in which the jobs between $J_{i_\ell + 1}$ and $J_{n+1 + i_\ell }$ are

$$\begin{aligned}&\sigma ': \ (J_{i_\ell + 1}, J_{i_\ell + 2}, \ldots , J_n, J_{2n+2}, J_{2n+1}, J_{2n}, \ldots , \\&\quad J_{n+1 + i_\ell + 1}, J_{n+1 + i_\ell }). \end{aligned}$$

Let $\sigma$ denote the schedule after the job swap. After re-indexing the two jobs $J_{n+1 + i_\ell }$ and $J_{i_\ell }$ and re-indexing the two jobs $J_{n+1 + i_\ell + 1}$ and $J_{i_\ell + 1}$, this sub-schedule becomes

$$\begin{aligned}&\sigma : \ (J_{i_\ell }, J_{i_\ell + 2}, \ldots , J_n, J_{2n+2}, J_{2n+1}, J_{2n}, \ldots , \\&\quad J_{i_\ell + 1}, J_{n+1 + i_\ell + 1}). \end{aligned}$$

For ease of presentation, let $C_i$ denote the completion time of job $J_i$ in schedule $\sigma$, and let $C'_i$ denote the completion time of job $J_i$ in schedule $\sigma '$. Compared with $\sigma '$,

• the completion times of jobs preceding $J_{n+1 + i_\ell }$ are unchanged; in particular, the starting processing time $S_{n+1 + i_\ell }$ of $J_{n+1 + i_\ell }$ in $\sigma$ and the starting processing time $S'_{i_\ell + 1}$ of $J_{i_\ell + 1}$ in $\sigma '$ satisfy $S_{n+1 + i_\ell } = S'_{i_\ell + 1}$;

• $C_{n+1 + i_\ell } - C'_{i_\ell + 1} = (S_{n+1 + i_\ell } + p_{i_\ell }) - (S'_{i_\ell + 1} + p_{i_\ell + 1}) = p_{i_\ell } - p_{i_\ell + 1} = - x_{i_\ell + 1}$;

• the completion time of each job between $J_{i_\ell + 2}$ and $J_n$ (inclusive, $n - i_\ell - 1$ of them) decreases by $x_{i_\ell + 1}$;

• the duration of the first $\mathrm{MA}$ increases by $2 x_{i_\ell + 1}$;

• the completion time of each job between $J_{2n+2}$ and $J_{n+1+i_\ell + 1}$ (inclusive, $n - i_\ell + 1$ of them) increases by $x_{i_\ell + 1}$; in particular, the starting processing time $S_{i_\ell + 1}$ of $J_{i_\ell + 1}$ in $\sigma$ and the starting processing time $S'_{n+1 + i_\ell }$ of $J_{n+1 + i_\ell }$ in $\sigma '$ satisfy $S_{i_\ell + 1} = S'_{n+1 + i_\ell } + x_{i_\ell + 1}$;

• $C_{i_\ell + 1} - C'_{n+1+i_\ell } = (S_{i_\ell + 1} + (\delta _{i_\ell + 1} + p_{i_\ell + 1})) - (S'_{n+1 + i_\ell } + (\delta _{i_\ell } + p_{i_\ell })) = x_{i_\ell + 1} + (\delta _{i_\ell + 1} + p_{i_\ell + 1}) - (\delta _{i_\ell } + p_{i_\ell }) = x_{i_\ell + 1} - (p_{i_\ell + 1} - p_{i_\ell }) = 0$;

• consequently, the completion times of jobs succeeding $J_{i_\ell + 1}$ are unchanged.

The total completion time of jobs in the schedule after this inverse regular job swap increases by at least $x_{i_\ell + 1}$. Note that the increment equals $x_{i_\ell + 1}$ if and only if there are exactly $n - i_\ell + 1$ jobs between $J_{2n+2}$ and $J_{n+1+i_\ell + 1}$ (inclusive), that is, none of the $j-1$ jobs $J_{\ell _1}, J_{\ell _2}, \ldots , J_{\ell _{j-1}}$ should have been moved between the center job $J_{2n+2}$ and $J_{n+1 + i_\ell }$ in schedule $\pi ^{j-1}$.

Using the above analog of Lemma 3, the rest of the proof of the lemma is similar to the proof of Lemma 7 by decomposing the jth job swap between the two jobs $J_{\ell _j}$ and $J_{n+1 + r_j}$ as a sequence of $\ell _j - r_j$ “inverse regular” job swaps, between the two jobs $J_{k+1}$ and $J_{n+1 + k}$ for $k = \ell _j - 1, \ell _j - 2, \ldots , r_j + 1, r_j$. $\square$

Theorem 2

If there is a feasible schedule $\pi$ for the instance I with total completion time of no more than $Q = Q_0 + B$, then there is a subset $X_1 \subset X$ of sum exactly B.

Proof

We start with a feasible schedule $\pi$ (which is $\pi$ for Case 1 and Case 3, or $\pi '$ for Case 2, as illustrated in Lemma 6), which has the first two properties stated in Lemma 2 and for which the total completion time is no more than $Q = Q_0 + B$.

Excluding job $J_{2n+2}$ at the center position, using the first $n+1$ jobs and the last $n+1$ job in $\pi$, we determine the two subsets of indices $R = \{r_1, r_2, \ldots , r_m\}$ and $L = \{\ell _1, \ell _2, \ldots , \ell _m\}$, and define the corresponding m job swaps. We then repeatedly apply the job swap to convert the initial infeasible schedule $\pi ^0$ into $\pi$. We calculate the following quantities at the end of this procedure, by distinguishing the three different cases as stated in Lemma 6.

In Case 1 (of Lemma 6), the total machine deterioration of the first $n+1$ jobs in $\pi$ is

$$\begin{aligned} \sum _{i=0}^n \delta _i - 2 \sum _{\ell _j < r_j} \sum _{k=\ell _j+1}^{r_j} x_k + 2 \sum _{\ell _j > r_j} \sum _{k=r_j+1}^{\ell _j} x_k = \mathrm{ML}_0 - \delta , \end{aligned}$$

implying that

$$\begin{aligned} \sum _{\ell _j < r_j} \sum _{k=\ell _j+1}^{r_j} x_k - \sum _{\ell _j > r_j} \sum _{k=r_j+1}^{\ell _j} x_k = B + \frac{1}{2} \delta , \end{aligned}$$

(7)

where $\delta \ge 0$ is the remaining machine maintenance level before the first $\mathrm{MA}$.

On the other hand, the total completion time of jobs in schedule $\pi$ is at least

$$\begin{aligned}&Q_0 + \sum _{\ell _j < r_j} \sum _{k=\ell _j+1}^{r_j} x_k + \sum _{\ell _j> r_j} \sum _{k=r_j+1}^{\ell _j} x_k = Q_0 + B + \frac{1}{2} \delta \\&\quad + 2 \sum _{\ell _j > r_j} \sum _{k=r_j+1}^{\ell _j} x_k. \end{aligned}$$

It follows that (1) $\delta = 0$; (2) there is no pair of swapping jobs $J_{\ell _j}$ and $J_{n+1 + r_j}$ such that $\ell _j > r_j$; and (3) $\ell _1< r_1< \ell _2< r_2< \cdots< \ell _m < r_m$ (from the third item of Lemma 7). Therefore, from Eq. (7), for the subset $X_1 = \cup _{j=1}^m \{x_{\ell _j+1}, x_{\ell _j+2}, \ldots , x_{r_j}\}$, we have $\sum _{x \in X_1} x = B$. That is, the instance X of the Partition problem is a yes-instance.

In Case 2 (of Lemma 6), after all m job swaps, the first $\mathrm{MA}$ immediately precedes $J_{2n+2}$ and has duration $- \delta$, since $\delta _{2n+2} = 0$, where $\delta \ge 0$ is the remaining machine maintenance level before the first $\mathrm{MA}$. $J_{2n+2}$ and its immediately succeeding $\mathrm{MA}$ and the following job need to be swapped to obtain schedule $\pi$. Thus, the first two $\mathrm{MA}$’s are merged (to become the first $\mathrm{MA}$), resulting in a positive duration. The total machine deterioration of the first $n+1$ jobs in $\pi$ (before the first $\mathrm{MA}$) is

$$\begin{aligned} \sum _{i=0}^n \delta _i - 2 \sum _{\ell _j < r_j} \sum _{k=\ell _j+1}^{r_j} x_k + 2 \sum _{\ell _j > r_j} \sum _{k=r_j+1}^{\ell _j} x_k = \mathrm{ML}_0 - \delta , \end{aligned}$$

implying that Eq. (7) still holds in this case.

On the other hand, the total completion time of jobs in schedule $\pi$ is at least

$$\begin{aligned}&Q_0 + \sum _{\ell _j < r_j} \sum _{k=\ell _j+1}^{r_j} x_k + \sum _{\ell _j> r_j} \sum _{k=r_j+1}^{\ell _j} x_k \\&\quad +\, (\delta _{\pi _{n+2}} + p_{\pi _{n+2}} - p_{2n+2}) \ge Q_0 + B + \frac{1}{2} \delta \\&\quad +\, 2 \sum _{\ell _j > r_j} \sum _{k=r_j+1}^{\ell _j} x_k. \end{aligned}$$

Then, similarly to Case 1, it follows that (1) $\delta = 0$; (2) there is no pair of swapping jobs $J_{\ell _j}$ and $J_{n+1 + r_j}$ such that $\ell _j > r_j$; and (3) $\ell _1< r_1< \ell _2< r_2< \cdots< \ell _m < r_m$. Therefore, from Eq. (7), for the subset $X_1 = \cup _{j=1}^m \{x_{\ell _j+1}, x_{\ell _j+2}, \ldots , x_{r_j}\}$, we have $\sum _{x \in X_1} x = B$. That is, the instance X of the Partition problem is a yes-instance.

In Case 3 (of Lemma 6), after all m job swaps, the first $\mathrm{MA}$ immediately precedes $J_{2n+2}$ and has duration $- \delta$, since $\delta _{2n+2} = 0$, where $\delta \le 0$ is the remaining machine maintenance level before the first $\mathrm{MA}$. Therefore, $J_{\pi _{n+1}}$ and the first $\mathrm{MA}$ need to be swapped to obtain the schedule $\pi$. The total machine deterioration of the first $n+1$ jobs in $\pi$ (before the first $\mathrm{MA}$) is

$$\begin{aligned} \sum _{i=0}^n \delta _i - 2 \sum _{\ell _j < r_j} \sum _{k=\ell _j+1}^{r_j} x_k + 2 \sum _{\ell _j > r_j} \sum _{k=r_j+1}^{\ell _j} x_k = \mathrm{ML}_0 - \delta , \end{aligned}$$

implying that Eq. (7) still holds in this case, except that here $\delta \le 0$.

On the other hand, the total completion time of jobs in schedule $\pi$ is at least

$$\begin{aligned}&Q_0 + \sum _{\ell _j < r_j} \sum _{k=\ell _j+1}^{r_j} x_k + \sum _{\ell _j> r_j} \sum _{k=r_j+1}^{\ell _j} x_k + (- \delta )\\&\quad \ge Q_0 + B - \frac{1}{2} \delta + 2 \sum _{\ell _j > r_j} \sum _{k=r_j+1}^{\ell _j} x_k. \end{aligned}$$

Then, similarly to Case 1, except that here $\delta \le 0$, it follows that 1) $\delta = 0$; 2) there is no pair of swapping jobs $J_{\ell _j}$ and $J_{n+1 + r_j}$ such that $\ell _j > r_j$; and 3) $\ell _1< r_1< \ell _2< r_2< \cdots< \ell _m < r_m$. Therefore, from Eq. (7), for the subset $X_1 = \cup _{j=1}^m \{x_{\ell _j+1}, x_{\ell _j+2}, \ldots , x_{r_j}\}$, we have $\sum _{x \in X_1} x = B$. That is, the instance X of the Partition problem is a yes-instance. $\square$

The following theorem follows immediately from Theorems 1 and 2.

Theorem 3

The problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$ is binary NP-hard.

4 A 2-approximation algorithm for $1 \mid p\mathrm{MA}\mid \sum _j C_j$

Recall that in the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$, we are given a set of jobs $\mathcal{J} = \{J_i, i = 1, 2, \ldots , n\}$, where each job $J_i = (p_i, \delta _i)$ is specified by its non-preemptive processing time$p_i$ and its machine deterioration$\delta _i$. The machine deterioration $\delta _i$ quantifies the decrement in the machine maintenance level after processing the job $J_i$. The machine has an initial machine maintenance level $\mathrm{ML}_0$, $0 \le \mathrm{ML}_0 \le \mathrm{ML}^{\max }$, where $\mathrm{ML}^{\max }$ is the maximum maintenance level. The goal is to schedule the jobs and necessary $\mathrm{MA}$s of any duration such that all jobs can be processed without a machine breakdown, and that the total completion time of jobs is minimized.

In this section, we present a 2-approximation algorithm, denoted as $\mathcal{A}_1$, for the problem. The algorithm $\mathcal{A}_1$ produces a feasible schedule $\pi$ satisfying the first two properties stated in Lemma 2, suggesting that if the third property is violated, then a local job swap can further reduce the total completion time.

In the algorithm $\mathcal{A}_1$, the first step is to sort the jobs in SSF order (and thus we assume without loss of generality that) $p_1 + \delta _1 \le p_2 + \delta _2 \le \cdots \le p_n + \delta _n$. In the second step, the separation job is determined to be $J_k$, where k is the maximum index such that $\sum _{i=1}^{k-1} \delta _i \le \mathrm{ML}_0$. In the last step, the jobs preceding the separation job $J_k$ are re-sorted in SPT order, denoted by $(J_{i_1}, J_{i_2}, \ldots , J_{i_{k-1}})$, and the jobs succeeding the separation job are $(J_{k+1}, J_{k+2}, \ldots , J_n)$. That is, the solution schedule is

$$\begin{aligned} \pi= & {} (J_{i_1}, J_{i_2}, \ldots , J_{i_{k-1}}; \mathrm{MA}_1, J_k; \mathrm{MA}_2, J_{k+1}, \mathrm{MA}_3, \\&\quad J_{k+2}, \ldots , \mathrm{MA}_{n-k+1}, J_n), \end{aligned}$$

where $\mathrm{MA}_1 = \sum _{j=1}^k \delta _j - \mathrm{ML}_0$ and $\mathrm{MA}_i = \delta _{k-1+i}$ for $i = 2, 3, \ldots , n-k+1$.

Let $\pi ^*$ denote an optimal schedule satisfying all properties stated in Lemma 2, and its separation job is $J_{\pi ^*_{k^*}}$:

$$\begin{aligned} \pi ^*= & {} \left( J_{\pi ^*_1}, J_{\pi ^*_2}, \ldots , J_{\pi ^*_{k^*-1}}; \mathrm{MA}^*_1, J_{\pi ^*_{k^*}}; \mathrm{MA}^*_2, J_{\pi ^*_{k^*+1}}, \right. \\&\left. \mathrm{MA}^*_3,J_{\pi ^*_{k^*+2}}, \ldots , \mathrm{MA}^*_{n-k^*+1}, J_{\pi ^*_n}\right) . \end{aligned}$$

Let $C_i$ ($C^*_i$, respectively) denote the completion time of job $J_{\pi _i}$ ($J_{\pi ^*_i}$, respectively) in schedule $\pi$ ($\pi ^*$, respectively); the makespans of $\pi$ and $\pi ^*$ are $C_{\max }$ and $C^*_{\max }$, respectively, and (recall that $\mathrm{ML}_0 < \sum _{i=1}^n \delta _i$)

$$\begin{aligned} C_{\max } = C^*_{\max } = \sum _{i=1}^n (p_i + \delta _i) - \mathrm{ML}_0. \end{aligned}$$

(8)

Lemma 9

For every $i \ge k$ we have

$$\begin{aligned} \sum _{j=i}^n (p_j + \delta _j) \ge \sum _{j=i}^n (p_{\pi ^*_j} + \delta _{\pi ^*_j}). \end{aligned}$$

Proof

Since $p_1 + \delta _1 \le p_2 + \delta _2 \le \cdots \le p_n + \delta _n$, $\sum _{j=i}^n (p_j + \delta _j)$ is the maximum sum of processing times and machine deterioration, over all possible subsets of $n-i+1$ jobs. $\square$

Theorem 4

The algorithm $\mathcal{A}_1$ is an $O(n\log n)$-time 2-approximation algorithm for the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$.

Proof

We compare the two schedules $\pi$ obtained by the algorithm $\mathcal{A}_1$ and $\pi ^*$, an optimal schedule satisfying the properties stated in Lemma 2. Using Eq. (8) and Lemma 9, it is clear that $C_i \le C^*_i$ for each $i = n, n-1, \ldots , \max \{k, k^*\}$.

Suppose that $k < k^*$; then for each i such that $k \le i < k^*$, we have

$$\begin{aligned} C_i= & {} C_n - \sum _{j=i+1}^n (p_j + \delta _j)\\\le & {} C^*_n - \sum _{j=i+1}^n (p_{\pi ^*_j} + \delta _{\pi ^*_j})\\= & {} \sum _{j=1}^i (p_{\pi ^*_j} + \delta _{\pi ^*_j}) - \mathrm{ML}_0\\= & {} \sum _{j=1}^i p_{\pi ^*_j} - \left( \mathrm{ML}_0 - \sum _{j=1}^i \delta _{\pi ^*_j}\right) \\\le & {} \sum _{j=1}^i p_{\pi ^*_j} = C^*_i. \end{aligned}$$

Therefore, we have $C_i \le C^*_i$ for each $i = n, n-1, \ldots , k$. It follows that

$$\begin{aligned} \sum _{i=k}^n C_i \le \sum _{i=k}^n C^*_i \le \sum _{i=1}^n C^*_i = \text{ OPT }. \end{aligned}$$

(9)

On the other hand, by SPT order, the algorithm $\mathcal{A}_1$ achieves a minimum total completion time of jobs of $\{J_1, J_2, \ldots , J_{k-1}\}$. One clearly sees that in the optimal schedule $\pi ^*$, the sub-total completion time of $\{J_1, J_2, \ldots , J_{k-1}\}$ is upper-bounded by $\text{ OPT }$. Since the total completion time of the first k jobs of schedule $\pi$ is minimal, it can be concluded that

$$\begin{aligned} \sum _{i=1}^{k-1} C_i \le \sum _{i=1}^n C^*_i = \text{ OPT }. \end{aligned}$$

(10)

Merging Eqs. (9) and (10), we conclude that the total completion time for schedule $\pi$ is

$$\begin{aligned} \sum _{i=1}^{k-1} C_i + \sum _{i=k}^n C_i \le 2 \cdot \text{ OPT }. \end{aligned}$$

This proves the performance ratio of 2. The running time of the algorithm $\mathcal{A}_1$ is dominated by two times of sorting, each taking $O(n\log n)$ time. Therefore, $\mathcal{A}_1$ is an $O(n\log n)$-time 2-approximation algorithm for the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$.

In a two-job instance $I = \{J_1 = (1, \lambda ), J_2 = (\lambda - 1, 1), \mathrm{ML}_0 = \mathrm{ML}^{\max } = \lambda \}$, where $\lambda$ is sufficiently large, we have $p_2 + \delta _2 < p_1 + \delta _1$. Therefore, the solution schedule by the algorithm $\mathcal{A}_1$ is $\pi = (J_2, \mathrm{MA}_1, J_1)$, for which the total completion time is $C_2 + C_1 = (\lambda - 1) + ((\lambda - 1) + 1 + 1) = 2 \lambda$. One can have another schedule $(J_1, \mathrm{MA}_1, J_2)$, for which the total completion time is $C_1 + C_2 = 1 + (1 + (\lambda - 1) + 1) = \lambda + 2$. This shows that the performance ratio 2 is tight. $\square$

5 A branch-and-bound exact algorithm for $1 \mid p\mathrm{MA}\mid \sum _j C_j$

In this section, we briefly introduce a branch-and-bound exact search algorithm for the problem $1 \mid p\mathrm{MA}\mid \sum _j C_j$. The key properties of an optimal schedule to be used in the search are summarized in Lemma 2, which are heavily used to prune the search tree in the branch-and-bound algorithm. At the high level, we will first select a job of positive deterioration as the separation job, then search for a subset of jobs of total deterioration no more than the initial maintenance level $\mathrm{ML}_0$, to be processed in SPT order before the first $\mathrm{MA}$, and lastly process the remainder of the jobs in SSF order after the separation job, each preceded by a partial maintenance. If the properties in Lemma 2 are all satisfied, then we achieve a feasible schedule, which updates the current best schedule.

5.1 The description of the algorithm

We use the 2-approximation algorithm $\mathcal{A}_1$ to obtain a near-optimal schedule and set the total completion time of jobs in this schedule as the initial global upper bound, denoted as U, on the optimum. The bound U is updated whenever a feasible schedule is found to have a lower total completion time.

In more algorithmic detail, we create the root node for the search tree and n child nodes (they are level-2 nodes) each corresponding to selecting a job as the separation job. For the purpose of searching for a subset $\mathcal{S}$ of jobs with total deterioration of no more than $\mathrm{ML}_0$, we re-index the jobs in SPT order with an overhead of $O(n \log n)$ time: $p_1 \le p_2 \le \cdots \le p_n$. Consider a node in the branch-and-bound search tree, which is a descendant of the level-2 node corresponding to selecting $J_k$ as the separation job, in which it has already been decided whether each of the jobs $J_1, J_2, \ldots , J_{j-1}$ will be in the subset $\mathcal{S}$. We branch the node to two child nodes corresponding to selecting and not selecting job $J_j$ into $\mathcal{S}$, respectively, where $j \ne k$.

If $J_j$ is selected into $\mathcal{S}$ but $\sum _{J_i \in \mathcal{S}} \delta _i > \mathrm{ML}_0$, then the new node is infeasible. We thus assume in the following discussion that if $J_j$ is selected into $\mathcal{S}$, then $\sum _{J_i \in \mathcal{S}} \delta _i \le \mathrm{ML}_0$, noting that an intermediate search node has to be feasible for further branching, that is, we have $\sum _{J_i \in \mathcal{S}} \delta _i \le \mathrm{ML}_0$ before making decision on $J_j$.

Leaf node In either case of $\mathcal{S}$, if none of the jobs $J_{j+1}, \ldots , J_n$ (excluding $J_k$) can be squeezed before the first $\mathrm{MA}$, then the new node is a leaf node representing a schedule with the jobs of $\mathcal{S}$ processed before the first $\mathrm{MA}$, job $J_k$ being the separation job, and all the other jobs processed in SSF order after the separation job. If the third property stated in Lemma 2 is satisfied, then the schedule is feasible, for which the total completion time of jobs can be calculated. If this total completion time of jobs is less than U, then U is updated and the corresponding schedule is saved; otherwise, the schedule is discarded.

Intermediate node If there are jobs among $J_{j+1}, \ldots , J_n$ (excluding $J_k$) that can be squeezed before the first $\mathrm{MA}$, then we know that the total completion time of jobs in any feasible schedule branched from this new node is greater than or equal to the total completion time of jobs attained by the sub-schedule $\sigma$ that is defined as follows: In $\sigma$, the jobs of $\mathcal{S}$ are processed in SPT order, followed by the first $\mathrm{MA}$ of duration $\max \{0, \delta _k - \delta \}$ (where $\delta = \mathrm{ML}_0 - \sum _{J_i\in \mathcal{S}} \delta _i$), then by the separation job $J_k$, and lastly by the jobs of $\{J_1, J_2, \ldots , J_j\} \setminus (\mathcal{S} \cup \{J_k\})$ in SSF order. The total completion time of jobs in the sub-schedule $\sigma$ is a lower bound on the total completion time of jobs in any feasible schedule branched from the new node. Therefore, if this lower bound is already larger than U, then the new node is cut off from further search; otherwise the new node is ready for further branching on job $J_{j+1}$ (if $j+1 \ne k$, or otherwise further branching on job $J_{j+2}$).

Termination At the end, when there is no more intermediate node for further branching, we return the upper bound U and the saved feasible schedule associated with U. The saved schedule is optimal, and U is the minimum total completion time of jobs.

5.2 Implementation details

We sort the jobs in SPT order of their processing time: $p_1 \le p_2 \le \cdots \le p_n$.

Let D denote a node in the branch-and-bound search tree, which is a descendant of the level-2 node corresponding to selecting $J_k$ as the separation job, and in which the subset of jobs $\mathcal{S}_D = \{J_{[1]}, J_{[2]}, \ldots , J_{[n_D]}\} \subseteq \{J_1, J_2, \ldots , J_{j-1}\}$ are selected to be processed before the separation job $J_k$ (the jobs of $\{J_1, J_2, \ldots , J_{j-1}\} \setminus \mathcal{S}_D$, excluding $J_k$, are processed after $J_k$).

Let $\varDelta$ denote the total machine deterioration before the first $\mathrm{MA}$ associated with D, that is, $\varDelta = \sum _{i=1}^{n_D} \delta _{[i]}$, and $\delta = \mathrm{ML}_0 - \varDelta$.

Let $\sigma _D$ denote the sub-schedule associated with the node D, in which the jobs of $\mathcal{S}_D$ are processed in SPT order, followed by the first $\mathrm{MA}$ of duration $\max \{0, \delta _k - \delta \}$, then by the separation job $J_k$, and lastly by the jobs of $\{J_1, J_2, \ldots , J_{j-1}\} \setminus (\mathcal{S}_D \cup \{J_k\})$ in SSF order. That is, this sub-schedule only processes the jobs of $\{J_1, J_2, \ldots , J_{j-1}\} \cup \{J_k\}$. We note that for D, $\varDelta \le \mathrm{ML}_0$, and the total completion time of jobs in this sub-schedule $\sigma _D$ is less than U, since otherwise D must have been cut off from the search tree.

Table 1 When $\mathrm{ML}^{\max } = 50$, the average ratio between the total completion time of jobs in the schedule by the 2-approximation algorithm $\mathcal{A}_1$ and the minimum total completion time of jobs by the algorithm BnB, and the average run times of BnB in seconds

From D, we branch as follows into at most two child nodes $D_{+j}$ and $D_{-j}$, corresponding to whether or not to process the job $J_j$ (if $j \ne k$) before the separation job $J_k$, respectively.

For $D_{-j}$, the sub-schedule $\sigma _{D_{-j}}$ is generated by inserting $J_j$ into the SSF order in the sub-schedule $\sigma _D$, and its total completion time of jobs is checked against U. $D_{-j}$ is cut off from the search tree if the total completion time of jobs in this sub-schedule $\sigma _{D_{-j}}$ is greater than or equal to U. If $D_{-j}$ stays, then it inherits from D the $\varDelta$.

For $D_{+j}$, if $\varDelta + \delta _j > \mathrm{ML}_0$, suggesting that job $J_j$ cannot possibly be squeezed in before the first $\mathrm{MA}$, then $D_{+j}$ is cut off from the search tree. Otherwise, the sub-schedule $\sigma _{D_{+j}}$ is generated by inserting $J_j$ after the SPT order in the sub-schedule $\sigma _D$, and its total completion time of jobs is checked against U. $D_{+j}$ is cut off from the search tree if the total completion time of jobs in this sub-schedule $\sigma _{D_{+j}}$ is greater than or equal to U. If $D_{+j}$ stays, then its total machine deterioration before the first $\mathrm{MA}$ is updated to $\varDelta + \delta _j$.

We have three remarks. First, if $j = k$, that is, $J_j$ is the separation job, then from D we branch into at most two child nodes by considering the job $J_{j+1}$. Second, when j reaches n, each of $\sigma _{D_{-j}}$ and $\sigma _{D_{+j}}$, if feasible, becomes a full schedule; it is discarded if the third property stated in Lemma 2 is violated or its total completion time of jobs is greater than or equal to U; otherwise U is updated and the full schedule is saved. Lastly, we explore the nodes in the branch-and-bound search tree in a depth-first search (DFS) order, mainly in order to avoid storing too many nodes in the computer memory.

Table 2 When $\mathrm{ML}^{\max } = 100$, the average ratio between the total completion time of jobs in the schedule by the 2-approximation algorithm $\mathcal{A}_1$ and the minimum total completion time of jobs by the algorithm BnB, and the average run times of BnB in seconds

Table 3 When $\mathrm{ML}^{\max } = 200$, the average ratio between the total completion time of jobs in the schedule by the 2-approximation algorithm $\mathcal{A}_1$ and the minimum total completion time of jobs by the algorithm BnB, and the average run times of BnB in seconds

Table 4 When $\mathrm{ML}^{\max } = 50$, the average number of jobs processed before the first $\mathrm{MA}$ in the optimal schedule

Table 5 When $\mathrm{ML}^{\max } = 100$, the average number of jobs processed before the first $\mathrm{MA}$ in the optimal schedule

Table 6 When $\mathrm{ML}^{\max } = 200$, the average number of jobs processed before the first $\mathrm{MA}$ in the optimal schedule

5.3 Computational experiments

We denote our branch-and-bound exact search algorithm as BnB. Clearly, the worst-case time complexity of BnB is exponential in n. In this part, we report the computational experiments conducted to evaluate its real performance. We note that we performed the search in depth-first order; this way, we save only a linear number of intermediate nodes in the memory.

The algorithm BnB is implemented in MATLAB. All the experiments were run on a desktop computer with a 2.5 GHz dual core processor and 4 GB RAM. The collected times are the actual run times for the program, in seconds.

The instances used in the experiments were generated randomly in the following way. We chose to set the number of jobs n to be 10, 20, 30, 40 and 50. The job processing time for every job in the instances is drawn from the uniform distribution over the real interval [1, 100], and rounded to its closest integer; its machine deterioration is drawn from the uniform distribution over the real interval $[1, \mathrm{ML}^{\max }]$, where $\mathrm{ML}^{\max }$ is the maximum maintenance level and was set to 50, 100 or 200. The initial maintenance level $\mathrm{ML}_0$ is set to $\left\lfloor \mu \mathrm{ML}^{\max }\right\rfloor$, for $\mu = 0.1, 0.2, \ldots , 1.0$. For each triple of $(n, \mathrm{ML}^{\max }, \mathrm{ML}_0)$, 50 random instances were generated, and the average run time of the algorithm BnB over these 50 instances was collected.

Recall that we use the 2-approximation algorithm $\mathcal{A}_1$ to obtain a near-optimal schedule and set the total completion time for jobs in this schedule as the initial global upper bound U. For every instance, we calculate the ratio between this initial value of U and the final value of U, which is the minimum total completion time of jobs. For each triple of $(n, \mathrm{ML}^{\max }, \mathrm{ML}_0)$, the average ratio over the 50 instances was collected. The average run times and the average ratios are presented in Tables 1, 2 and 3, corresponding to $\mathrm{ML}^{\max } = 50, 100, 200$, respectively, where for each table entry, the first value is the average ratio when it is at least 1.0001, and the second value is the average run time. Note that in the table entries, when the average ratio is less than 1.0001, it is deemed too insignificant to be reported and is not included in the corresponding table entry.

From Tables 1, 2 and 3, we observe that in general, the algorithm BnB took less time to complete when the initial maintenance level $\mathrm{ML}_0$ was low. We speculate that for a low $\mathrm{ML}_0$, there are fewer jobs to be scheduled before the first $\mathrm{MA}$, and thus the search tree is shorter. Consequently, the overall size of the search tree is smaller. On the other hand, we also observe that the algorithm BnB spent less time on instances with large n and large $\mathrm{ML}^{\max }$. One possible explanation is that for large $\mathrm{ML}^{\max }$, the maintenance activities make a larger contribution to the total completion time, and thus help in using the lower bound estimation to determine the infeasibility of an early search node when there are a large number of jobs (particularly, $n = 40, 50$). See the branching step at the intermediate node in the description of the algorithm.

The total completion time of jobs in the schedule generated by the 2-approximation algorithm $\mathcal{A}_1$ is generally very close to the optimum, and in fact in more than 50% of instances, it is already optimal. We thus recommend using the 2-approximation algorithm $\mathcal{A}_1$ in practice, as its time complexity is very low.

For every instance, we collected the number of jobs processed before the first $\mathrm{MA}$. For each triple of $(n, \mathrm{ML}^{\max }, \mathrm{ML}_0)$, the average number over the 50 instances was collected. These average numbers are shown in Tables 4, 5, and 6, corresponding to $\mathrm{ML}^{\max } = 50, 100, 200$, respectively.

From Tables 4, 5, and 6, we observe that in most cases, the average number of jobs before the first $\mathrm{MA}$ in the optimal schedules correlates with the initial maintenance level $\mathrm{ML}_0$ and the total number of jobs. In our simulated small instances, these numbers are all small, and thus our BnB algorithm benefits greatly from them, evidenced by its low average run times shown in Tables 1, 2, and 3.

6 Concluding remarks

We investigated single-machine scheduling with job-dependent machine deterioration, recently introduced by Bock et al. (2012), with the objective of minimizing the total completion time of jobs. In the partial maintenance case, we proved the binary NP-hardness for the general problem, thus addressing the open problem left in the previous work. From an approximation perspective, we designed a 2-approximation, for which the ratio 2 is tight on a trivial two-job instance. This 2-approximation algorithm was then used in the design of a branch-and-bound exact search algorithm, for which we conducted computational experiments to examine its practical performance.

The 2-approximation algorithm is simple, and the computational experiments show its effectiveness. It is the first approximation algorithm presented for the problem. Our major contribution is the non-trivial binary NP-hardness proof, which might seem surprising at first glance, since one has so much freedom in choosing the starting time and the duration of the maintenance activities.

In the branch-and-bound exact search algorithm, the key is to determine the best subset of jobs to be processed before the first maintenance. This might look similar to the well-known knapsack problem, by regarding the negated job processing time as “value”, the machine deterioration as “size”, and the initial machine maintenance level as the knapsack capacity. However, they are quite different due to the jobs outside the knapsack being processed in specific SSF order. As a result, the recursive modification of the objective function is complex, and we leave the development of a generalized dynamic programming as an open question.

It would be interesting to further explore the (in-)approximability for the problem. It would also be interesting to study the problem in the full maintenance case, which has been shown to be NP-hard, from the approximation algorithm perspective. Approximating the problem in the full maintenance case seems more challenging, where we need to deal with multiple bin-packing sub-problems, and the interrelationship among them is very complex.