1 Introduction

In the past decades, scheduling with machine availability had been a hot topic in scheduling research. For our purpose, we only consider the single-machine scheduling problem in which a maintenance activity (MA) of length \(p_0\) on the machine is required at a given time period. This means that the MA must be performed at some time interval of length \(p_0\) without interruption.

1.1 Problem Formulation

According to the requirements for the MA and the features of the machine for processing jobs, the following three assumptions are studied in the literature, separately.

Assumption (A)

The MA is required in a fixed time interval \([T-p_0, T]\) with \(T\geqslant p_0\), and the job processing is of preemptive and resumable. Moreover, we use (\(A^*\)) to denote the assumption that the MA is required in a fixed time interval \([T-p_0, T]\), and the job processing is of nonpreemptive.

Assumption (B)

The MA is required in a relaxed time interval [0, T] with \(T\geqslant p_0\), and the job processing is of nonpreemptive. In this case, [0, T] is called the execution window of the MA.

Assumption (C)

The MA is required in a relaxed time interval \([T_0, T]\) with \(T_0+p_0\leqslant T\), and the job processing is of nonpreemptive. In this case, \([T_0, T]\) is called the execution window of the MA.

Given an assumption (X) with \(X\in \{A, B, C\}\), we consider a set of n jobs \(\{J_1, J_2, \cdots , J_n\}\) to be processed on the machine. Each job \(J_j\) has a processing time \(p_j\), a due date \(d_j\), and a weight \(w_j\). We also regard MA as a dummy job \(J_0\) with processing time \(p_0\). The \(J_1, J_2, \cdots , J_n\) are called normal jobs in the sequel. In a feasible schedule \(\sigma \), we use \(S_j(\sigma )\) and \(C_j(\sigma )\) to denote the starting time and completion time of job \(J_j\), respectively, \(j=0,1, \cdots , n\). Note that \(C_0(\sigma )=S_0(\sigma )+p_0\), and, for different choices of X, \(S_0(\sigma )\) has the following properties:

$$\begin{aligned} \left\{ \begin{array}{ll} S_0(\sigma )=T-p_0, &{}\text{ under } \text{ Assumption } \text{(A) },\\ 0\leqslant S_0(\sigma ) \leqslant T-p_0, &{}\text{ under } \text{ Assumption } \text{(B) },\\ T_0\leqslant S_0(\sigma ) \leqslant T-p_0, &{}\text{ under } \text{ Assumption } \text{(C) }. \end{array}\right. \end{aligned}$$

For each \(j\in \{1, 2, \cdots , n\}\), we call \(J_j\) early if \(C_j(\sigma )\leqslant d_j\), and call \(J_j\) tardy if \(C_j(\sigma )> d_j\), and moreover, \(U_j(\sigma )\) is used to denote the tardy indicator number of job \(J_j\). The scheduling cost function of the schedule \(\sigma \) is of the form

$$\begin{aligned} f(\sigma )= f(C_1(\sigma ), C_2(\sigma ), \cdots , C_n(\sigma )), \end{aligned}$$

which is a function of the completion times of the n jobs \(J_1, J_2, \cdots , J_n\). We assume in this paper that f is a regular cost function, which means that \(f(t_1, t_2, \cdots , t_n)\) is nondecreasing in each ordinate of \((t_1, t_2, \cdots , t_n)\geqslant 0\). In particular, \(\sum w_jU_j = \sum _{j=1}^{n} w_jU_j(\sigma )\) is a regular cost function. In the following, the single-machine scheduling problem with a machine availability under Assumption (X) for minimizing the regular cost function f will be denoted by

$$\begin{aligned} 1, h_1|\text{ MA },\,(X)|f. \end{aligned}$$

1.2 Previous Work

Problems \(1, h_1|\text{ MA },\,(A)|f\) and \(1, h_1|\text{ MA },\,(A^*)|f\) were first studied in Lee [1]. Under assumption (A), the author showed that problems \(1,h_1|\text{ MA },\,(A)|C_{\max }\), \(1,h_1|\text{ MA },\,(A)|\sum C_i\) and \(1,h_1|\text{ MA },\,(A)|L_{\max }\) can be solved optimally by an arbitrary sequence, the Shortest Processing Time (SPT) rule, and the Earliest Due Date (EDD) rule, respectively, and problem \(1,h_1|\text{ MA },\,(A)|\sum U_i\) can be solved optimally by applying modified Moore-Hodgsons algorithm. Under assumption (\(A^*\)), they showed that problems \(1,h_1|\text{ MA },\,(A^*)|C_{\max }\), \(1,h_1|\text{ MA },\,(A^*)|L_{\max }\) and \(1,h_1|\text{ MA },\,(A^*)|\sum U_i\) are binary NP-hard, and provided a heuristic for problem \(1,h_1|\text{ MA },\,(A^*)|C_{\max }\).

When every job has a positive tail, for problem \(1, h_1|\text{ MA },\,(A^*), q_i|D_{\max }\), Kacem [2] proposed a tight 3/2-approximation heuristic method. The author also presented a dynamic programming algorithm and showed that the problem has a fully polynomial-time approximation scheme (FPTAS) by exploiting the well-known approach of Ibarra and Kim [3]. Yuan et al. [4] studied a more general version of the above problem in which there are several forbidden intervals. They provided a pseudo-polynomial-time algorithm for the version with a fixed number of forbidden intervals, while no polynomial-time approximation algorithm with a fixed performance ratio exists for the version with just two forbidden intervals. They also developed a polynomial-time approximation scheme (PTAS) for the version with a single forbidden interval.

Mosheiov [5] studied problem \(1, h_1|\text{ MA },\,(B)|\sum w_jC_j\). They showed that the problem is NP-hard and presented a heuristic method for solving this problem. Yang et al. [6] considered problem \(1, h_1|\text{ MA },\,(C)|C_{\max }\), and presented NP-hardness proof and provided a heuristic algorithm with time complexity \(O(n\log n)\). Yang et al. [7] considered problem \(1, h_1|\text{ MA },\,(C)|\sum C_j\). For the resumable version, they proposed an SPT optimal algorithm, while for the nonresumable version, they analyzed the relative error bound of SPT algorithm. Furthermore, they proposed a dynamic programming algorithm and a branch-and-bound algorithm to solve this problem optimally.

There are also extensive achievements for other types of MA in scheduling research, and some of them can be found in Chen [8, 9], Cui and Lu [10], Lee and Kim [11], Liu et al. [12], Sbihi and Varnier [13], and Yu et al. [14].

1.3 Our Contribution

We say that two scheduling problems \(\mathcal{P}'\) and \(\mathcal{P}''\) are linearly equivalent if an optimal schedule of each of \(\mathcal{P}'\) and \(\mathcal{P}''\) can be transferred into an optimal schedule of the other one in O(n) time. The main contributions of this paper are as follows.

We first study the equivalence of problems \(1, h_1|\text{ MA },\,(X)|f\) for \(X\in \{A, B, C\}\), and obtain the following results:

  • For every regular cost function f, problem \(1, h_1|\text{ MA },\,(A)|f\) is equivalent to problem \(1, h_1|\text{ MA },\,(B)|f\). Moreover, if \(T-(T_0+p_0)\geqslant p_{\max }\), where \(p_{\max }\) is the maximum processing time of the jobs, then problem \(1, h_1|\text{ MA },\,(C)|f\) is also equivalent to problems \(1, h_1|\text{ MA },\,(A)|f\) and \(1, h_1|\text{ MA },\,(B)|f\).

As applications, we further study problem \(1, h_1|\text{ MA },\,(X)|\sum w_jU_j\) for \(X\in \{A, B, C\}\). By applying the equivalence results and using the discussion in Yuan and Lin [15], the problem apart from the case that “\(X=C\) and \(T-(T_0+p_0)< p_{\max }\)” is linearly equivalent to problem \(1||\sum w_jU_j\) by only modifying the due dates.

Finally, for the version with \(X=C\) and without the restriction \(T-(T_0+p_0)\geqslant p_{\max }\), we show that problem \(1, h_1|\text{ MA },\,(C)|\sum w_jU_j\) is also solvable in pseudo-polynomial time, and the subproblem \(1, h_1|\text{ MA },\,(C),\, p_j=p|\sum w_jU_j\) is solvable in polynomial time.

In the literature, problem \(1||\sum w_jU_j\), together with its subproblems \(1||\sum U_j\) and \(1|p_j=p|\sum w_jU_j\), has been well studied. Then we summarize the time-complexity results of problem \(1, h_1|\text{ MA },\,(X)|\sum w_jU_j\) for \(X\in \{A, B, C\}\) in Table 1, where \(X=C'\) means that \(X=C\) and \(T-(T_0+p_0)\geqslant p_{\max }\), and moreover, \(P=\sum _{j=1}^n p_j\), \(W=\sum _{j=1}^n w_j\), and \(T^*=T-(T_0+p_0)+1\).

Table 1 The time complexity of problem \(1, h_1|\text{ MA },\,(X)|\sum w_jU_j\)
Full size table

1.4 Organization of This Paper

In Sect. 2, we discuss the equivalence of problem \(1, h_1|\text{ MA },\,(X)|f\) for \(X\in \{A, B, C\}\). In Sect. 3, we study problem \(1, h_1|\text{ MA },\,(X)|\sum w_jU_j\) for \(X\in \{A, B, C\}\) and its subversions.

2 The Equivalence Proof

Consider an instance I of problem \(1, h_1|\text{ MA },\,(X)|f\) with \(X\in \{A, B, C\}\). The n normal jobs in I are given by \(J_1, J_2, \cdots , J_n\) with each job \(J_j\) has a processing time \(p_j\). The MA (regarded as dummy job \(J_0\) in the sequel) in I has length \(p_0\) and an execution window \([T_0, T]\). If \(X=A\), then \(T_0=T-p_0\); if \(X=B\), then \(T_0=0\) and \(T\geqslant p_0\); and if \(X=C\), then \(T_0\geqslant 0\) and \(T_0+p_0 \leqslant T\). Moreover, we assume that the cost function f to be minimized is regular. For a schedule \(\sigma \) of \(J_0, J_1, \cdots , J_n\) and for each index \(i\in \{1, 2, \cdots , n\}\), we use \(J_{\sigma [i]}\) to denote the i-th completed job (excluding the dummy job \(J_0\)) in \(\sigma \). Then we have

$$\begin{aligned} C_{\sigma [1]}(\sigma )< C_{\sigma [2]}(\sigma )< \cdots < C_{\sigma [n]}(\sigma ). \end{aligned}$$
(2.1)

If \(P=p_1+p_2+\cdots +p_n \leqslant T_0\), then, in an optimal schedule for problem \(1, h_1|\text{ MA },\,(X)|f\) with \(X\in \{A, B, C\}\), we can always schedule the n jobs in the time interval [0, P] before the execution window \([T_0, T]\) of MA. Thus, in this case, the problem \(1, h_1|\text{ MA },\,(X)|f\) with \(X\in \{A, B, C\}\) is equivalent to the standard single-machine scheduling problem 1||f. Hence, we assume that

$$\begin{aligned} P=p_1+p_2+\cdots +p_n > T_0. \end{aligned}$$
(2.2)

This implies that, in any feasible schedule, the makespan is at least \(p_0+P\).

For problem \(1, h_1|\text{ MA },\,(A)|f\), preemption is allowed in processing of the normal jobs. In a feasible schedule, a job is called interrupted if it is scheduled in at least two separated intervals. Since the regularity of f, the following result was observed and widely used in the literature.

Lemma 2.1

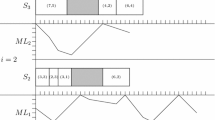
There exists an optimal schedule for problem \(1, h_1|\text{ MA },\,(A)|f\) such that there is no idle time between the processing of the \(n+1\) jobs \(J_0, J_1, \cdots , J_n\), there is at most one interrupted job, and moreover, if \(J_j\) is the interrupted job in the schedule, then \(J_j\) is split into just two parts \(J_j'\) and \(J_j''\) such that \(J_j'\) is scheduled directly before \(J_0\) and \(J_j''\) is scheduled directly after \(J_0\).

In the following, a schedule with the properties described in Lemma 2.1 is called a proper schedule. Given a feasible schedule \(\sigma \) of problem \(1, h_1|\text{ MA },\,(A)|f\), we can obtain a proper schedule \(\sigma '\) in the following way: Fix the dummy job \(J_0\) (MA) in the interval \([T-p_0, T]\), and then schedule the jobs \(J_1, J_2, \cdots , J_n\) preemptively in the remaining idle space according to the order \(J_{\sigma [1]}\prec J_{\sigma [2]} \prec \cdots \prec J_{\sigma [n]}\). It is not hard to verify that \(\sigma '[i]= \sigma [i]\) and \(C_{\sigma '[i]}(\sigma ') \leqslant C_{\sigma [i]}(\sigma )\) for all \(i\in \{1, 2, \cdots , n\}\). Thus, we have \(f(\sigma ') \leqslant f(\sigma )\). In the case that \(\sigma \) is optimal for problem \(1, h_1|\text{ MA },\,(A)|f\), \(\sigma '\) is also optimal. Note that \(\sigma '\) can be obtained from \(\sigma \) in O(n) time. Then we will only consider proper schedules when problem \(1, h_1|\text{ MA },\,(A)|f\) is in consideration.

Given a proper schedule \(\sigma \) of problem \(1, h_1|\text{ MA },\,(A)|f\), we define a schedule \(\sigma ^*\) of problem \(1, h_1|\text{ MA },\,(B)|f\) or problem \(1, h_1|\text{ MA },\,(C)|f\), call the nonpreemptive counterpart of \(\sigma \), in the following way:

  • If there is no interrupted job in \(\sigma \), then set \(\sigma ^*:=\sigma \).

  • If \(J_j\) is the interrupted job in \(\sigma \), then let \(\sigma ^*\) be the nonpreemptive schedule obtained from \(\sigma \) by swapping the schedules of \(J_j'\) and \(J_0\).

Conversely, given a schedule \(\pi \) of problem \(1, h_1|\text{ MA },\,(B)|f\) or problem \(1, h_1|\text{ MA },(C)|f\), we define a schedule \(\pi ^{[*]}\) of problem \(1, h_1|\text{ MA },\,(A)|f\), call the preemptive counterpart of \(\pi \), in the following way:

  • Fix the dummy job \(J_0\) (MA) in the interval \([T-p_0, T]\), and then schedule the normal jobs \(J_1, J_2, \cdots , J_n\) preemptively in the remaining idle space according to the order \(J_{\pi [1]}\prec J_{\pi [2]} \prec \cdots \prec J_{\pi [n]}\).

It is not hard to see that \(\sigma ^*\) can be obtained from \(\sigma \) in O(n) time, and \(\pi ^{[*]}\) can be obtained from \(\pi \) in O(n) time. We will use \(\text{ opt }^{(X)}\) to denote the optimal value of problem \(1, h_1|\text{ MA },\,(X)|f\) with \(X\in \{A, B, C\}\) on instance I.

Lemma 2.2

We have the following statements:

  1. (i)

    \(\mathrm{opt}^{(A)}=\mathrm{opt}^{(B)}\), and moreover, if \(\sigma \) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(A)|f\) and \(\pi \) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(B)|f\), then \(\sigma ^*\) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(B)|f\) and \(\pi ^{[*]}\) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(A)|f\).

  2. (ii)

    In the case that \(T-(T_0+p_0)\geqslant p_{\max }\), we further have \(\mathrm{opt}^{(A)}=\mathrm{opt}^{(B)}=\mathrm{opt}^{(C)}\), and moreover, if \(\sigma \) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(A)|f\) and \(\pi \) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(C)|f\), then \(\sigma ^*\) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(C)|f\) and \(\pi ^{[*]}\) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(A)|f\).

Proof

To prove statement (i), we assume that \(\sigma \) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(A)|f\) and \(\pi \) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(B)|f\). Then

$$\begin{aligned} \text{ opt }^{(A)}= f(\sigma ) \text{ and } \text{ opt }^{(B)}=f(\pi ). \end{aligned}$$
(2.3)

Since \(\sigma ^*\) is a feasible schedule of problem \(1, h_1|\text{ MA },\,(B)|f\) and \(\pi ^{[*]}\) is a feasible schedule of problem \(1, h_1|\text{ MA },\,(A)|f\), we have

$$\begin{aligned} \text{ opt }^{(B)} \leqslant f(\sigma ^*) \text{ and } \text{ opt }^{(A)} \leqslant f(\pi ^{[*]}). \end{aligned}$$
(2.4)

From the definitions of \(\sigma ^*\) and \(\pi ^{[*]}\), we have \(C_j(\sigma ^*)= C_j(\sigma )\) and \(C_j(\pi ^{[*]}) \leqslant C_j(\pi )\) for all \(j\in \{1, 2, \cdots , n\}\). Thus, we have

$$\begin{aligned} f(\sigma ^*)=f(\sigma ) \text{ and } f(\pi ^{[*]})\leqslant f(\pi ). \end{aligned}$$
(2.5)

From equations (2.3), (2.4) and (2.5), we conclude that

$$\begin{aligned} f(\sigma ^*)=\text{ opt }^{(B)} = \text{ opt }^{(A)} = f(\pi ^{[*]}). \end{aligned}$$
(2.6)

It follows from (2.6) that \(\text{ opt }^{(A)}=\text{ opt }^{(B)}\) and \(\sigma ^*\) and \(\pi ^{[*]}\) are optimal for problems \(1, h_1|\text{ MA },\,(B)|f\) and \(1, h_1|\text{ MA },\,(A)|f\), respectively, as required.

To prove statement (ii), we assume that \(\sigma \) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(A)|f\) and \(\pi \) is an optimal schedule of problem \(1, h_1|\text{ MA },\,(C)|f\). Note that problem \(1, h_1|\text{ MA },\,(B)|f\) is a relaxation of problem \(1, h_1|\text{ MA },\,(C)|f\). Thus, from statement (i), we have

$$\begin{aligned} f(\sigma )= \text{ opt }^{(A)} = \text{ opt }^{(B)} \leqslant \text{ opt }^{(C)} = f(\pi ). \end{aligned}$$
(2.7)

We claim that \(\sigma ^*\) is a feasible schedule of problem \(1, h_1|\text{ MA },\,(C)|f\).

Indeed, if there is no interrupted job in \(\sigma \), then \(\sigma ^*=\sigma \) is clearly a feasible schedule of problem \(1, h_1|\text{ MA },\,(C)|f\). If \(J_j\) is the interrupted job in \(\sigma \), then \(\sigma ^*\) is obtained from \(\sigma \) by swapping the schedule of \(J_j'\) and \(J_0\). Let \(p_j'\) be the processing time of \(J_j'\). From the assumption that \(T-(T_0+p_0)\geqslant p_{\max }\), the starting time of the dummy job \(J_0\) in \(\sigma ^*\) is given by \(S_0(\sigma ^*) = S_0(\sigma )- p_j' = T-p_0 -p_j' > T-p_0-p_j \geqslant T-p_0-p_{\max }\geqslant T_0\). Thus, \(\sigma ^*\) is a feasible schedule of problem \(1, h_1|\text{ MA },\,(C)|f\). The claim follows.

As stated in the proof of statement (i), from the definitions of \(\sigma ^*\) and \(\pi ^{[*]}\), we have \(C_j(\sigma ^*)= C_j(\sigma )\) and \(C_j(\pi ^{[*]}) \leqslant C_j(\pi )\) for all \(j\in \{1, 2, \cdots , n\}\). Together with the feasibility of \(\sigma ^*\) and \(\pi ^{[*]}\), we have

$$\begin{aligned} \text{ opt }^{(C)}\leqslant f(\sigma ^*)=f(\sigma ) \text{ and } \text{ opt }^{(A)}\leqslant f(\pi ^{[*]})\leqslant f(\pi ). \end{aligned}$$
(2.8)

From (2.7) and (2.8), we conclude that

$$\begin{aligned} f(\sigma ^*)=\text{ opt }^{(C)} =\text{ opt }^{(B)}=\text{ opt }^{(A)} = f(\pi ^{[*]}). \end{aligned}$$
(2.9)

It follows from (2.9) that \(\text{ opt }^{(A)}=\text{ opt }^{(B)}=\text{ opt }^{(C)}\) and \(\sigma ^*\) and \(\pi ^{[*]}\) are optimal for problems \(1, h_1|\text{ MA },\,(C)|f\) and \(1, h_1|\text{ MA },\,(A)|f\), respectively. The result follows.

From Lemma 2.2, we obtain the following main result of this section.

Theorem 2.1

For every regular cost function f, problem \(1, h_1|\text{ MA },\,(A)|f\) is equivalent to problem \(1, h_1|\text{ MA },\,(B)|f\). Moreover, if \(T-(T_0+p_0)\geqslant p_{\max }\), where \(p_{\max }\) is the maximum processing time of the jobs, then problem \(1, h_1|\text{ MA },\,(C)|f\) is also equivalent to problems \(1, h_1|\text{ MA },\,(A)|f\) and \(1, h_1|\text{ MA },\,(B)|f\).

3 The Total Weighted Number of Tardy Jobs

Consider problem \(1, h_1|\text{ MA },\,(X)|\sum w_jU_j\) with \(X\in \{A, B, C\}\). For each \(j\in \{1, 2, \cdots ,n\}\), job \(J_j\) is indicated by a triple \((p_j, d_j, w_j)\). For convenience, we write \(J_j=(p_j, d_j, w_j)\) for all jobs \(J_j\). Then we call \(\{(p_j, d_j, w_j): 1\leqslant j\leqslant \,\,n\}\) a job instance.

Now we use \(X=C'\) to indicate that \(X=C\) and \(T-(T_0+p_0)\geqslant p_{\max }\). From Theorem 2.1, together with the result in Lemma 2.2, the three problems \(1, h_1|\text{ MA },\,(X)|\sum w_jU_j\) on job instance \(\{(p_j, d_j, w_j): 1\leqslant j\leqslant \,\,n\}\), \(X\in \{A, B, C'\}\), are linearly equivalent.

For problem \(1, h_1|\text{ MA },\,(A)|\sum w_jU_j\) on job instance \(\{(p_j, d_j, w_j): 1\leqslant j\leqslant n\}\), the dummy job \(J_0\) (MA) occupies a fixed interval \([T-p_0, T]\) and the jobs are processed preemptively. Thus, from the discussion in Yuan and Lin [15], problem \(1, h_1|\text{ MA },\,(A)|\sum w_jU_j\) on job instance \(\{(p_j, d_j, w_j): 1\leqslant j\leqslant \,\, n\}\) is linearly equivalent to problem \(1||\sum w_jU_j\) on job instance \(\left\{ \left( p_j, d'_j, w_j\right) : 1\leqslant j\leqslant n\right\} \), where

$$\begin{aligned} d'_j=\left\{ \begin{array}{ll} d_j, &{}\text{ if } d_j \leqslant T-p_0,\\ T-p_0, &{}\text{ if } T-p_0<d_j \leqslant T,\\ d_j-p_0, &{}\text{ if } d_j >T.\end{array}\right. \end{aligned}$$

Thus we have the following result.

Theorem 3.1

For each \(X\in \{A, B, C'\}\), problem \(1, h_1|\text{ MA },\,(X)|\sum w_jU_j\) on job instance \(\{(p_j, d_j, w_j): 1\leqslant j\leqslant \,\, n\}\) is equivalent to problem \(1||\sum w_jU_j\) on job instance \(\left\{ \left( p_j, d'_j, w_j\right) : 1\leqslant j\leqslant \,\, n \right\} \).

Note that the classical scheduling problem \(1||\sum w_jU_j\) was well studied in the literature. Karp [20] showed that the problem is NP-hard even when the jobs have a common due date. Lawler and Moore [16] presented an O(nP)-time algorithm, and Sahni [17] presented an O(nW)-time algorithm. For the subproblem \(1||\sum U_j\), Moore [18] presented an \(O(n\log n)\)-time algorithm. As for the subproblem \(1|p_j=p|\sum w_jU_j\), an \(O(n\log n)\)-time algorithm was presented in Morton and Pentico [19]. From Theorem 3.1, the time complexity of problem \(1, h_1|\text{ MA },\,(X)|\sum w_jU_j\) with \(X\in \{A, B, C'\}\) and its subversions with \(w_j=1\) or \(p_j=p\) can be completely determined, as described in Table 1.

In the following we consider problem \(1, h_1|\text{ MA },\,(C)|\sum w_jU_j\). Lee [1] showed that problem \(1, h_1|\text{ MA },\,(C)|C_{\max }\) is NP-hard even when \(T_0=T-p_0\). Then we have the following observation.

Observation 3.1

Problem \(1, h_1|\text{ MA },\,(C)|\sum U_j\) is NP-hard even when \(T_0=T-p_0\) and \(d_j=d\).

For problem \(1, h_1|\text{ MA },\,(C),\, p_j=p|\sum w_jU_j\) in which the MA has length \(p_0\) and execution window \([T_0, T]\), we have the following lemma.

Lemma 3.1

Let k be the maximum integer with \(kp+p_0 \leqslant T\), i.e., \(k= \lfloor \frac{T-p_0}{p_0}\rfloor \). Let \(T'=\max \{kp, T_0\}+p_0\). Then there is an optimal schedule \(\sigma \) of problem \(1, h_1|\text{ MA },\,(C),\, p_j=p|\sum w_jU_j\) such that the MA is scheduled in the interval \([T'-p_0, T']\) and the normal jobs are scheduled in the time space \([0, kp]\cup [T',+\infty )\).

Proof

From the definition of k and \(T'\), it is not hard to verify that \([T'-p_0, T']\subseteq [T_0, T]\). Thus it is feasible to schedule the dummy job \(J_0\) (MA) in the fixed interval \([T'-p_0, T']\). Note that \(kp\leqslant T'-p_0\) and \((k+1)p +p_0> T\).

If \(k\geqslant n\), then the condition \(p_j=p\) for all \(j\in \{1, 2, \cdots , n\}\) enables us to schedule all the normal jobs before the fixed interval \([T'-p_0, T']\) for processing \(J_0\). Thus, the required optimal schedule exists.

Suppose in the following that \(k< n\). Then the definition of k implies that at most k normal jobs are scheduled before \(J_0\) in every feasible schedule. Let \(\sigma \) be an optimal schedule of problem \(1, h_1|\text{ MA },\,(C),\, p_j=p|\sum w_jU_j\) in which the normal jobs scheduled before \(J_0\) are as many as possible and are processed consecutively, and subject to this, \(J_0\) is scheduled as early as possible. Since \(kp\leqslant T'-p_0\) and \((k+1)p +p_0> T\), by the shifting argument, we can verify that exact k normal jobs are scheduled before \(J_0\) and the interval \([T'-p_0, T']\) is occupied by \(J_0\) in \(\sigma \). This further implies that the normal jobs are scheduled in the time space \([0, kp]\cup [T',+\infty )\). The result follows.

Theorem 3.2

Problem \(1, h_1|\text{ MA },\,(C),\, p_j=p|\sum w_jU_j\) is solvable in \(O(n\log n)\) time.

Proof

Let k and \(T'\) be the same as that in Lemma 3.1. We consider a job instance \(I=\{(p, d_j, w_j): 1\leqslant j\leqslant \,\, n\}\) of problem \(1, h_1|\text{ MA },\,(C),\, p_j=p|\sum w_jU_j\). From Lemma 3.1, the problem on instance I is equivalent to schedule the n normal jobs in the time space \([0, kp]\cup [T',+\infty )\) for minimizing \(\sum w_jU_j\) with \([kp, T']\) being a forbidden interval. Since kp, the left point of the forbidden interval \([kp, T']\), is an integer multiple of the common processing time p, allowing preemption will not change the scheduling problem with the forbidden interval \([kp, T']\). By the discussion in Yuan and Lin [15], the problem in consideration on instance I is linearly equivalent to the problem \(1|p_j=p|\sum w_jU_j\) on instance \(I'=\left\{ \left( p, d'_j, w_j\right) : 1\leqslant j\leqslant \,\, n \right\} \), where

$$\begin{aligned} d'_j=\left\{ \begin{array}{ll} d_j, &{}\text{ if } d_j \leqslant kp,\\ kp, &{}\text{ if } kp<d_j \leqslant T',\\ d_j-(T'-kp), &{}\text{ if } d_j >T'.\end{array}\right. \end{aligned}$$

Since problem \(1|p_j=p|\sum w_jU_j\) is solvable in \(O(n\log n)\) time as presented in Morton and Pentico [19], we conclude that problem \(1, h_1|\text{ MA },\,(C),\, p_j=p|\sum w_jU_j\) is solvable in \(O(n\log n)\) time. The result follows.

Now we consider the general problem \(1, h_1|\text{ MA },\,(C)|\sum w_jU_j\) in which the MA has length \(p_0\) and execution window \([T_0, T]\). Since the tardy jobs can be scheduled after the dummy job \(J_0\) and all early normal jobs in a feasible schedule, we only consider the schedule of the dummy job and the early normal jobs in feasible schedules. For a feasible schedule \(\sigma \), we can rewrite it as \(\sigma =(\sigma ', J_0, \sigma '')\), where \(\sigma '\) is the subschedule of the early normal jobs scheduled before \(J_0\) in \(\sigma \) and \(\sigma ''\) is the subschedule of the early normal jobs scheduled after \(J_0\) in \(\sigma \). Moreover, we use \(P(\sigma ')\) and \(P(\sigma '')\) to denote the total processing times of the jobs in \(\sigma '\) and in \(\sigma ''\), respectively. In the case that the jobs in each of \(\sigma '\) and \(\sigma ''\) are scheduled in the EDD order, we call \(\sigma \) an (EDD, EDD)-schedule. By the swapping argument and the shifting argument, we can show the following lemma for optimal schedules.

Lemma 3.2

For problem \(1, h_1|\text{ MA },\,(C)|\sum w_jU_j\), there is an optimal schedule \(\sigma =(\sigma ', J_0, \sigma '')\) such that

  1. (i)

    \(\sigma \) is an (EDD, EDD)-schedule,

  2. (ii)

    The jobs in \(\sigma '\) are scheduled in the time interval \([0, P(\sigma ')]\) without idle time,

  3. (iii)

    The dummy job \(J_0\) is processed in the interval \([T'-p_0, T']\), where \(T' = \max \{P(\sigma '), T_0\} +p_0\leqslant T\), and

  4. (iv)

    The jobs in \(\sigma ''\) are scheduled in the time interval \([T', T'+P(\sigma '')]\) without idle time.

In general, we can guess the completion time t of the dummy job \(J_0\). Since \([T_0, T]\) is the execution window of MA which is of length \(p_0\), we have \(t\in [T_0+p_0, T]\). For each choice of t, we will solve the problem optimally under the restriction that the dummy job \(J_0\) is scheduled in the interval \([t-p_0, t]\). This can be realized from a dynamic programming algorithm by using a variation of Lemma 3.2.

Assume that the normal jobs are indexed according to EDD order such that \(d_1\leqslant d_2\leqslant \cdots \leqslant d_n\). Given \(t\in [T_0+p_0, T]\), we first introduce the following notation and terminology.

  • \(\Omega (t)\) is the set consisting of the triples (k, u, v) with \(0\leqslant k\leqslant \,\, n\), \(0\leqslant u\leqslant \,\, t-p_0 \leqslant T-p_0\), and \(0\leqslant v\leqslant \,\, P\). Then \(|\Omega (t)|= O(n(T-p_0)P)\).

  • For each triple \((k, u, v)\in \Omega (t)\), we use \(\mathcal{P}_t(k, u, v)\) to denote the problem for scheduling jobs \(J_0, J_1, \cdots , J_k\) to minimize \(\sum _{j=1}^k w_jU_j(\sigma )\) of the legal schedules \(\sigma \), where a schedule \(\sigma =(\sigma ', J_0, \sigma '')\) of \(J_0, J_1, \cdots , J_k\) is legal for problem \(\mathcal{P}_t(k, u, v)\) if it is an (EDD, EDD)-schedule such that \(J_0\) is scheduled in the time interval \([t-p_0, t]\), the jobs in \(\sigma '\) are scheduled in the time interval [0, u] without idle time, and the jobs in \(\sigma ''\) are scheduled in the time interval \([t,t+v]\) without idle time.

  • For each triple \((k, u, v)\in \Omega (t)\), we use \(F_t(k, u,v)\) to denote the optimal value of problem \(\mathcal{P}_t(k, u, v)\). Clearly, \(F_t(k, u,v)\) can be assumed by a legal schedule of \(\mathcal{P}_t(k, u, v)\). In the case that problem \(\mathcal{P}_t(k, u, v)\) has no feasible schedule, we just define \(F_t(k, u,v)= +\infty \). Then \(F_t(0,0,0)=0\) and \(F_t(0, u, v)= +\infty \) if \((u,v)\ne (0,0)\).

In general, suppose that (k, u, v) is a triple in \(\Omega (t)\) with \(1\leqslant k\leqslant \,\, n\). Let \(\sigma =(\sigma ', J_0, \sigma '')\) be a legal schedule of problem \(\mathcal{P}_t(k, u, v)\) assuming \(F_t(k, u,v)\). We distinguish the following three cases.

  • \(J_k\) is tardy in \(\sigma \). Then \(\sigma \) is also a legal schedule of problem \(\mathcal{P}_t(k-1, u, v)\) assuming \(F_t(k-1, u,v)\). In this case, we have \(F_t(k, u,v)=F_t(k-1, u,v)+w_k\).

  • \(J_k\) is early in \(\sigma \) and is assigned to \(\sigma '\). Then \(J_k\) is the last job in \(\sigma '\). Let \(\sigma '-J_k\) be the schedule obtained from \(\sigma '\) by deleting the last job \(J_k\). Then \((\sigma '-J_k, J_0, \sigma '')\) is a legal schedule of problem \(\mathcal{P}_t(k-1, u-p_k, v)\) assuming \(F_t(k-1, u-p_k,v)\). In this case, we have \( d_k\geqslant u\) and \(F_t(k, u,v)=F_t(k-1, u-p_k,v)\).

  • \(J_k\) is early in \(\sigma \) and is assigned to \(\sigma ''\). Then \(J_k\) is the last job in \(\sigma ''\). Let \(\sigma ''-J_k\) be the schedule obtained from \(\sigma ''\) by deleting the last job \(J_k\). Then \((\sigma ', J_0, \sigma ''-J_k)\) is a legal schedule of problem \(\mathcal{P}_t(k-1, u, v-p_k)\) assuming \(F_t(k-1, u,v-p_k)\). In this case, we have \(d_k\geqslant t+v\) and \(F_t(k, u,v)=F_t(k-1, u,v-p_k)\).

Combining the above discussions, we design the following dynamic programming (DP) algorithm.

3.1 DP Algorithm

For determining the values \(F_t(k, u,v)\) for all \((k, u,v)\in \Omega (t)\).

Step 1 (Initialization)

$$\begin{aligned} F_t(k,u,v)=\left\{ \begin{array}{ll} 0, &{}\text{ if } (k,u,v)=(0,0,0),\\ +\infty , &{}\text{ if } k=0 \text{ and } (u,v)\ne (0,0),\\ +\infty , &{}\text{ if } (k, u, v)\notin \Omega (t).\end{array}\right. \end{aligned}$$

Step 2 (Recursion)

$$\begin{aligned} F_t(k,u,v)= \min \left\{ \begin{array}{ll} F_t(k-1,u,v) + w_k, &{}\\ F_t(k-1,u-p_k,v),&{} \text{ if } d_k\geqslant u, \\ F_t(k-1,u,v-p_k),&{} \text{ if } d_k\geqslant t+v.\end{array}\right. \end{aligned}$$

Equivalently,

$$\begin{aligned}&\qquad F_t(k,u,v)\\&= \left\{ \begin{array}{ll} F_t(k-1,u,v) + w_k, &{}\text{ if } d_k< u,\\ \min \left\{ F_t(k-1,u-p_k,v),F_t(k-1,u,v) + w_k\right\} ,&{} \text{ if } u \leqslant d_k <t+v, \\ \min \left\{ F_t(k-1,u,v-p_k),F_t(k-1,u-p_k,v),F_t(k-1,u,v) + w_k\right\} ,&{} \text{ if } d_k\geqslant t+v.\end{array}\right. \end{aligned}$$

In the above DP algorithm, we have totally \(|\Omega (t)|\) states, and each iteration runs in a constant time. Note that \(|\Omega (t)|= O(n(T-p_0)P)\). Then the DP algorithm runs in \(O(n(T-p_0)P)\) time for given \(t\in [T_0+p_0, T]\). In the case that \(t=T\), the above DP algorithm solves problem \(1, h_1|\text{ MA },\,(A^*)|\sum w_jU_j\).

From Lemma 3.2, the optimal value of problem \(1, h_1|\text{ MA },\,(C)|\sum w_jU_j\) is given by

$$\begin{aligned} \min \{F_t(n, u,v): t\in [T_0+p_0, T],\, (n,u,v)\in \Omega (t)\}. \end{aligned}$$

By setting \(T^*= T-(T_0+p_0)+1\), which is the number of choices of t, we conclude the following result.

Theorem 3.3

Problem \(1, h_1|\text{ MA },\,(A^*)|\sum w_jU_j\) is solvable in \(O(n(T-p_0)P)\) time, and Problem \(1, h_1|\text{ MA },\,(C)|\sum w_jU_j\) is solvable in \(O(nT^*(T-p_0)P)\) time.