Integrated production and outbound distribution scheduling problems with job release dates and deadlines

Abstract

In this paper, we study an integrated production and outbound distribution scheduling model with one manufacturer and one customer. The manufacturer has to process a set of jobs on a single machine and deliver them in batches to the customer. Each job has a release date and a delivery deadline. The objective of the problem is to issue a feasible integrated production and distribution schedule minimizing the transportation cost subject to the production release dates and delivery deadline constraints. We consider three problems with different ways how a job can be produced and delivered: non-splittable production and delivery (NSP–NSD) problem, splittable production and non-splittable delivery problem and splittable production and delivery problem. We provide polynomial-time algorithms that solve special cases of the problem. One of these algorithms allows us to compute a lower bound for the NP-hard problem NSP–NSD, which we use in a branch-and-bound (B&B) algorithm to solve problem NSP–NSD. The computational results show that the B&B algorithm outperforms a MILP formulation of the problem implemented on a commercial solver.

1 Introduction

Supply chain management is an active domain consisting of the optimization and management of flows between different actors that generally have conflicting objectives, which makes the coordination of their decisions a crucial issue.

In this paper, we study an integrated production and outbound distribution scheduling (IPODS) model with one manufacturer and one customer. The manufacturer has to process a set of jobs on a single machine and deliver them in batches to the customer. Each job has a release date and a delivery deadline. The release dates may correspond to the raw material availability dates or to the delivery dates of semi-finished products coming from suppliers or classically from another unmodeled part of the factory that have to be processed further and then sent to the customer. As observed commonly in practice, delivery is outsourced to a third-party logistics provider that owns a sufficiently large number of vehicles. According to the European Commission (2011), in 2010, the share of own-account transport is around 15% of the tonne-km generated in road freight transport. This means that transport is mostly outsourced to independent partners like third-party logistics providers. In some cases, the manufacturer outsources all logistic activities, including the delivery schedule planning and the transportation, to the third-party logistics provider. In other cases, planning of delivery is still handled by the manufacturer and the third-party logistics provider is just a pure transporter. Hsiao et al. (2010) conducted an empirical study among actual Dutch and Vietnamese food processing companies that indicates that among 114 enquired companies, 79 companies outsourced their outbound transportation activity, while only 42 outsourced the transportation management activity. In this paper, we consider the latter case, where the delivery schedule remains under the control of the manufacturer. The objective of the problem is to build a feasible integrated production and distribution schedule minimizing the transportation cost subject to production release dates and delivery deadline constraints. A recent survey by Moons et al. (2017) as well as the state-of-the-art review given below, reveal that only a few study in integrated production and distribution scheduling problems consider jointly production release dates and delivery due dates. However, as stated by Jamili et al. (2016), the presence of job release dates is a consequence of the existence several suppliers for production raw material, which is highly relevant in many applications. Moreover, the model we consider is appropriate for perishable products. Among them, fresh products like fruits or vegetables provide a particularly clear insight into the effects of transportation costs on food prices (Volpe et al. 2013). In the survey of Moons et al. (2017), 13 papers involving integrated production and distribution scheduling of perishable products are discussed. Among them Chen et al. (2009), justify the consideration of delivery deadlines for perishable products, mainly due to the fact that they deteriorate rapidly. The presence of production release times can also be an intrinsic characteristic of perishable products. In particular Russel et al. (2008) and Chiang et al. (2009) consider an integrated production and distribution problem in the newspaper industry where production release date are necessary to represent early and late editions.

We consider three problems with different ways how a job can be produced and delivered: non-splittable production and delivery (NSP–NSD) problem, splittable production and non-splittable delivery (SP–NSD) problem and splittable production and delivery (SP–SD) problem. As noticed by Chen and Pundoor (2009), there are practical situations that justify all these cases. While non-splitting delivery hypothesis is commonly considered, splitting delivery may allow, as remarked by Dror and Trudeau (1989), to save transportation costs.

We refer to recent surveys of Chen (2010), Wang et al. (2014) and Moons et al. (2017). Before presenting the related literature, recall the notation introduced by Chen (2010) to represent the IPODS models. It is a five-field notation, $\alpha |\beta |\pi |\delta |\gamma$, where $\alpha$, $\beta$ and $\gamma$ specify, respectively, the machine environment, the job characteristics and the optimality criterion as the classical three-field classification for scheduling problems (Graham et al. 1979). Some new objective functions linked to transportation are introduced, such as maximum delivery time denoted by $D_{\max }$, total delivery time denoted by $\sum D_i$ or total trip-based transportation cost denoted by TC. Fields $\pi$ and $\delta$ specify, respectively, the characteristics of delivery process and the number of customers. The number of customers is specified by one value of $\{1,k,n\}$, where $\delta =1$ for single customer, $\delta =k\ge 2$ means there are multiple customers, and $\delta =n$ means that each order belongs to a different customer. The characteristics of delivery process include vehicle characteristics (number and capacity of vehicles) and delivery methods. The vehicle characteristics are specified by V(x, y), where $x\in \{1, v, \infty \}$ represents the number of vehicles, and $y\in \{1,c,\infty ,Q\}$ represents the capacity of vehicles. Field values $\{1,c,\infty \}$ and Q distinguish, respectively, the possible capacities of vehicles when jobs have equal size, and the limited capacity of vehicles when jobs have general size. The delivery methods include: individual and immediate delivery (iid), direct batch delivery (direct), batch routing delivery (routing), shipping with fixed delivery departure dates (fdep), and splittable delivery (split), i.e., an order can be split and delivered by several vehicles.

When considering production only, our model concerns single machine scheduling problems with release dates minimizing the maximum lateness $L_{\max }$. The problem without release dates $1||L_{\max }$ can be solved by Jackson’s earliest due date (EDD) rule introduced by Jackson (1955). This problem is a special case of the problem $1|prec|L_{\max }$ solved by a polynomial-time algorithm provided by Lawler (1973). The problem with release dates and preemption $1|r_j, pmtn|L_{\max }$ can be solved by Jackson’s preemptive earliest due date (EDD-preemptive) rule introduced by Jackson (1955). This problem is a special case of the problem $1|prec, r_j, pmtn|L_{\max }$ solved by a polynomial-time algorithm provided by Baker et al. (1983). Lenstra et al. (1977) proved the NP-hardness of the problem $1|r_j|L_{\max }$. Carlier (1982) provided the first efficient branch-and-bound algorithm to solve this problem.

The research on the IPODS problems with release dates concentrates on the (iid) and (direct) models. As proved by Chen (2010), the problems with individual and immediate delivery, (i) $1|r_j|V(\infty , 1), iid|n|D_{\max }$, (ii) $1|r_j, prec|V(\infty , 1), iid|n|$ $D_{\max }$, (iii) $Pm|r_j|V(\infty , 1), iid|n|D_{\max }$, (iv) $Fm|r_j|V(\infty , 1), iid|n|D_{\max }$ are strongly NP-hard. Liu and Cheng (2002) proved the NP-hardness of the problem (v) $1|r_j, s_j, pmtn|V(\infty ,$ $1), iid|n|D_{\max }$. In these problems, the jobs are delivered individually and immediately to the customers upon their completion while minimizing the maximum delivery time. For problems (i), (ii), (iii) and (v), approximation algorithms and/or polynomial-time approximation schemes were provided by Potts (1980), Hall and Shmoys (1989, 1992), Mastrolilli (2003), Zdrzaka (1994) and Liu and Cheng (2002). Gharbi and Haouari (2002) developed a branch-and-bound algorithm for problem (iii). Kaminsky (2003) proposed an asymptotic optimality analysis of the longest delivery time algorithm for problem (iv). Few articles consider (direct) or (routing) delivery. Lu et al. (2008) provided a polynomial-time algorithm for the problem $1|r_j, pmtn|V(1, c), direct|1|D_{\max }$. For the problem $1|r_j|V(1, c), direct|1|D_{\max }$ they proved its NP-hardness and proposed an approximation algorithm with worst-case ratio of 5 / 3, which was later improved to 3 / 2 by Liu and Lu (2011). Recently, Zhong and Jiang (2016) considered problems $1|r_j|V(1, c), direct|1|D_{\max }+TC$ and $1|r_j|V(1, c), direct|1|\sum D_i+TC$ and provided a polynomial algorithm for the first one while they prove NP-hardness of the second one and give a heuristic with a worst-case ratio of 2. Mazdeh et al. (2008) provided a branch-and-bound algorithm for a special case of the NP-hard problem $1|r_j|V(\infty ,\infty ), direct|n|\sum F_j + TC$, where $\sum F_j$ represents the total flow time. Mazdeh et al. (2012) provided a branch-and-bound algorithm for a special case of the similar problem involving the sum of weighted flow time, $1|r_j|V(\infty ,\infty ), direct|n|\sum w_jF_j + TC$. Selvarajah et al. (2013) provided an evolutionary meta-heuristic for the same problem in the general case and a polynomial-time algorithm for the special case with a common weight and preemptive production, i.e., $1|r_j, pmtn|V(\infty ,\infty ), direct|n|\sum wF_j + TC$ and $1|r_j, pmtn|V(\infty ,\infty ), direct|n|\sum wC_j + TC$. As mentioned above, Jamili et al. (2016) solved the problem involving the average delivery time and the total cost via a tabu search heuristic. There are some articles considering the on-line problem, i.e., the information related to a job becomes known when this job is released. Ng and Lu (2012) investigated the problems of Lu et al. (2008) in an on-line environment. Averbakh and Xue (2007) provided a 2-competitive algorithm for the on-line problem $1|r_j, pmtn|V(\infty , \infty ), direct|k|\sum D_j+TC$. Recent work on other on-line or semi-on-line integrated production-distribution scheduling problems can be found in Averbakh (2010), Averbakh and Baysan (2012, 2013a, b), and Feng et al. (2016).

Some IPODS problems with maximum lateness $L_{\max }$ or delivery deadline $\overline{d}_j$, and transportation cost TC have been investigated in the literature. Polynomial-time algorithms were provided for problems with a fixed number of customers k. These are $1||V(\infty , \infty ), direct|k|L_{\max }+TC$ by Hall and Potts (2003), $1||V(\infty , c), direct|k|L_{\max }+TC$ by Pundoor and Chen (2005) and $1||V(1,\infty ),routing|k|L_{\max }+TC$ by Chen (2010). In the latter paper, a polynomial-time algorithm was also provided for problem $1||V(v,\infty ), direct|1|L_{\max }+TC$ with a fixed number of vehicles v. Polynomial-time algorithms were also proposed by Hall and Potts (2005) for problem $1||V(1,\infty ),$ $direct|1|L_{\max }+TC$ and by Chen and Pundoor (2009) for problem $1|pmtn, \overline{d}_j|V(\infty , Q), direct, split|1|TC$.

Wang and Lee (2005) proved the NP-hardness of the problem $1|\overline{d}_j|V(\infty , 1),iid|n|TC$ with two types of vehicles and provided a pseudo-polynomial-time dynamic programming algorithm for a special case and a branch-and-bound exact algorithm for the same problem to minimize the sum of the total weighted tardiness and the total shipping cost. Chen and Pundoor (2009) proved the NP-hardness of the problems without production preemption, $1|\overline{d}_j|V(\infty , Q), direct|1|TC$ and $1|\overline{d}_j|V(\infty , Q), direct,split|1|TC$, and provided approximation algorithms with worst-case ratio of 2 (see more details below). Zhong et al. (2010) proposed a polynomial-time heuristic algorithm for a strongly NP-hard problem with delivery deadline, a fixed vehicle departure time and different shipping modes, and showed that its worst-case performance ratio was bounded by 2. Stecke and Zhao (2007) studied the same problem with a more general shipping cost structure and two different delivery cases, and proposed a polynomial-time algorithm for the partial delivery case and a heuristic for the no partial delivery case. More recently, Leung and Chen (2013) considered the problems involving maximum lateness and TC in a setting where there are a fixed possible vehicle departure time dates. Mensendiek et al. (2015) considered the maximum lateness criterion in a parallel machine environment when the set of possible delivery dates are also fixed. Li et al. (2015) extended this model to a parallel batching machine environment.

There are only a few papers studying the IPODS problem with the consideration of jobs release dates and due dates or deadlines at the same time. Fu et al. (2012) considered a coordinated production and distribution schedule in which each job has a production time window and a promised delivery time. Contrarily to our model where actual delivery times must be determined, there are fixed delivery times on which delivery batches made of completed jobs can be assigned, with limited delivery capacities. The objective is to select a subset of jobs to process and deliver, so as to maximize a global profit. NP-hardness results and approximation algorithms have been given. As also mentioned above, Russel et al. (2008) and Chiang et al. (2009) considered an integrated production and vehicle routing problem in the newspaper industry with production release dates corresponding to different editions and delivery deadlines. In both cases, the problem is solved via two-phase methods. In Chapter 4 of the recent book of Ullrich (2013a), the cost-cutting potential of integrated supply chain scheduling has been demonstrated via computational experiments on supply chain scenarios including integrated machine and delivery scheduling with job release dates, batch capacities, holding costs and earliness and tardiness penalties. An integrated parallel machine scheduling and vehicle routing problem with time windows has been considered by Ullrich (2013b) but the time windows concern the delivery part while production jobs are subject to machine ready times. Recently Condotta et al. (2013) proposed an efficient tabu search algorithm for problem $1|r_j|V(v,c),$ $direct|1|L_{\max }.$ Note that this problem does not include transportation costs. Our paper consider an IPODS problem with jobs release dates, delivery deadlines and transportation cost, which can be appropriate for practical cases as stated above, such as production and distribution of perishable products. To the best of our knowledge, the problem has never been considered in the literature.

The closest related research has been provided by Chen and Pundoor (2009) without considering release dates (see also the description above). They investigated an IPODS model in a supply chain where a manufacturer needs to process a set of jobs at a single production line, pack the completed jobs to form delivery batches, and deliver them to a customer. They investigated problems in scenarios (with or without splitting in production and distribution) that inspired us for the present paper. Different from their model, we consider that the jobs have equal size and possibly different release dates. Our objective is to propose solution algorithms for the three considered problems, i.e., SP–NSD, SP–SD and NSP–NSD, for each of which we consider two scenarios: (1) decentralized system scenario where the production schedule and the delivery schedule are decided in a sequential order (i.e., first the production schedule, then the delivery schedule); (2) integrated system scenario where an integrated production distribution schedule is built. In the decentralized system scenario, we review known exact algorithms in the literature to solve the production scheduling problems (i.e., problems NSP and SP) and develop exact algorithms to solve the distribution scheduling problems (i.e., problems NSD and SD). In the integrated system scenario, we proposed algorithms to solve three new IPODS problems with job release dates and deadlines. Note that incorporating release dates deeply changes the problem structure, as the production scheduling problem becomes NP-hard in the non-preemptive case. (see also Example 3 in Sect. 2) A question arises as to whether polynomial cases can however be exhibited. Another non-trivial issue is to design computationally efficient methods for large instances of the problem. This paper aims to tackle these two questions, that appear to be interrelated as we propose a polynomial-time algorithm for a special case that we use to compute lower bounds into an efficient branch-and-bound method.

This paper is organized as follows. In Sect. 2, we formally describe the problems, introduce notations and terminology and provide examples to illustrate the problem properties. Section 3 is devoted to the decentralized system scenario. Section 4 deals with the integrated system scenario. In particular, we propose polynomial-time algorithms for two special cases of problems SP–NSD and SP–SD and a branch-and-bound algorithm for problem NSP–NSD. In Sect. 5, we evaluate the performance of this branch-and-bound algorithm by comparing it to a mixed-integer linear programming (MILP) formulation ion randomly generated instances. Section 6 contains some conclusions and perspectives.

2 Problems and notations

A set of jobs $N=\{1,\ldots ,n\}$ has to be processed on a single machine. Each job $j\in N$ has a release date $r_j$, a processing time $p_j$ and a delivery deadline $\overline{d}_j$. After processing on the machine, the jobs can be grouped into batches of maximum size $c>0$, corresponding to a full truck load, and then sent to a single customer location. The jobs are unit sized, i.e., a truck can carry at most c jobs at a time. As mentioned by Chen (2010), even if this hypothesis is restrictive, most of the literature considers this case. Delivery is handled by a third-party logistic providers that has an infinite number of vehicles. A batch is available to be delivered when all jobs of this batch are completed. The transportation time of a batch and the corresponding subcontracting cost are supposed to be independent on the batch constitution. Hence, we can assume without loss of generality that the transportation time is 0 and the transportation cost of a batch is 1. It follows that the delivery deadline is also the production deadline.

Let $(\sigma , \theta )$ denote an integrated production and distribution schedule, where $\sigma$ and $\theta$ are, respectively, the production schedule and the delivery schedule. In this integrated schedule, $C_j(\sigma )$ is the completion time of job j on the machine and $D_j(\theta )$ is the delivery time of job j to the customer location. When there is no ambiguity, we use $C_j$ and $D_j$ instead of $C_j(\sigma )$ and $D_j(\theta )$ to simplify the notations.

We consider two scenarios: (1) decentralized system scenario, where the production schedule and the delivery schedule are decided in a sequential order (i.e., first the production schedule, then the delivery schedule); (2) integrated system scenario, where an integrated production distribution schedule is issued. Next, the induced scheduling problems are formally defined and 3 examples are given to illustrate the problem properties.

2.1 Decentralized system scenario

Production scheduling problem

The objective is to determine a feasible production schedule in which the jobs are completed before or at their deadline. We investigate the problem in two cases:

• Non-splittable production (NSP) problem A job is non-preemptable (or non-splittable) in production. Using the three-field notation $\alpha |\beta |\gamma$ for machine scheduling problems (Graham et al. 1979), this problem can be denoted by $1|r_j, \overline{d}_j|-$.

• Splittable production (SP) problem A job can be split in production. This problem can be denoted by $1|r_j, pmtn, \overline{d}_j|-$.

Fig. 1

Optimal schedules for the three integrated problems. a An optimal schedule for NSP–NSD problem. b An optimal schedule for SP–NSD problem. c An optimal schedule for SP–SD problem

Distribution scheduling problem The objective is to obtain a delivery schedule minimizing the transportation cost TC subject to the delivery release dates fixed by the production schedule and the delivery deadlines. A delivery schedule is an assignment of jobs to batches, along with the departure time for each batch. We investigate the problem in two cases:

• Non-splittable delivery (NSD) problem A finished job must be delivered in one batch. A delivery schedule defines a partition of the jobs.

• Splittable delivery (SD) problem A finished job can be split and delivered in several batches. We assume that the capacity occupied by a job in a batch is equal to the delivered fraction of the job.

2.2 Integrated system scenario

The objective is to determine an integrated production and distribution schedule minimizing the transportation cost TC subject to the delivery deadlines. We consider the integrated problem in three cases with different ways how a job can be produced and delivered.

• Non-splittable production and delivery (NSP–NSD) problem a job is non-preemptable (or non-splittable) in production and a finished job must be delivered in one batch. Using the five-field notation proposed by Chen (2010), this problem can be denoted by $1|r_j, \overline{d}_j|V(\infty , c), direct|1|TC$, where $V(\infty , c)$ and direct mean that we consider the direct batch delivery by an unlimited number of trucks with the capacity of c.

• Splittable production and non-splittable delivery (SP–NSD) problem a job can be preempted in production, and a finished job must be delivered in one batch. This problem can be denoted by $1|r_j, pmtn, \overline{d}_j|$ $V(\infty , c), direct|1|TC$.

• Splittable production and delivery (SP–SD) problem a job can be preempted in both production and delivery. This problem can be denoted by $1|r_j, pmtn, \overline{d}_j|V(\infty , c), direct, split|1|TC$.

Table 1 Example for the integrated problems

We do not consider the non-splittable production and splittable delivery (NSP-SD) problem, because according to Lemma 2 in Sect. 3.2, for any feasible NSP production schedule, there exists an optimal NSD delivery schedule.

2.3 Illustrative examples

Example 1

To illustrate the three integrated problems, we consider the following example with seven jobs where the vehicle capacity c is equal to 2. Table 1 gives the jobs’ parameters.

Figure 1 shows the optimal schedules for the integrated problems. In what follows, in a production schedule, [j] means that job j is produced without preemption. In a delivery schedule, [j] means that job j is delivered without splitting. When [j] is preceded by a constant $\alpha$, $0<\alpha <1$, this means that a part $\alpha$ of job j is produced or delivered.

Problem NSP–NSD: In an optimal schedule as shown in Fig. 1a, the production sequence is $([2], [1], [3], [4], [5], [6], [7])$. There exists an idle time before job 2, because if another job was processed before 2, then job 2 would be late. A similar reason holds for the second idle time. There are six delivery batches: $\{[2]\},\{[1], [3]\}, \{[4]\}, \{[5]\}, \{[6]\}$ and $\{[7]\}$, which depart at times 4, 10, 12, 15, 18 and 19, respectively.

Problem SP–NSD: In an optimal schedule as shown in Fig. 1b, the production sequence is $(\frac{1}{2}[1], [2], [3], \frac{1}{2}[1], [4], \frac{1}{3}[6], [5],$ $\frac{2}{3}[6], [7])$, where jobs 1 and 6 are split into two parts. The optimal schedule has five delivery batches: $\{[2]\}, \{[1], [3]\}, \{[4]\}, \{[5]\}$ and $\{[6], [7]\}$, which depart at times 4, 8, 10, 15 and 18, respectively. Since job 2 cannot be delivered with any other job, the transportation cost cannot be improved for the first 4 jobs with the non-splittable delivery. However, we can split job 6 in production in order to deliver jobs 6 and 7 in one batch.

Problem SP–SD: In an optimal schedule as shown in Fig. 1c, the production sequence is the same as for problem SP–NSD. The optimal schedule has four delivery batches: $\{\frac{1}{2}[1], [2], \frac{1}{2}[3]\}$, $\{\frac{1}{2}[3]$, $\frac{1}{2}[1], [4]\}$, $\{[5]\}$ and $\{[6], [7]\}$, which depart at times 5, 10, 15 and 18, respectively. The first delivery batch consists of half of job 1, whole job 2 and half of job 3. With the splittable delivery, the first four jobs can be delivered in two full batches. Recall that the capacity occupied by a job in a batch is equal to the delivered fraction of the job.

Note that in the above problems, the jobs delivered together are not necessarily sequenced consecutively, which makes the considered problems different from classical batching models.

Example 2

To illustrate the benefit of integration of production and distribution decisions in the case of problem NSP–NSD, we consider the following example with five jobs where the vehicle capacity c is equal to 3. Table 2 gives the jobs’ parameters.

Table 2 Example for evaluation of the benefit of integration

Fig. 2

Schedules for the individual problems and the integrated problem. a A schedule for decentralized scheduling problems (NSP and NSD). b An optimal schedule for NSP–NSD problem

Figure 2a shows a feasible schedule for the decentralized system scenario. Figure 2b shows an optimal schedule in the integrated system scenario. We compare the two schedules to evaluate the benefit of integration.

Decentralized system scenario (solve NSP then NSD): Applying Carlier’s algorithm (see Sect. 3.1), we stop when we find the first feasible production schedule. As shown in Fig. 2a, the production sequence is ([4], [1], [2], [5], [3]). All jobs are completed before their deadline. With this production schedule, the best delivery schedule consists of four delivery batches: $\{[1]\},\{[2]\}, \{[5]\}$ and $\{[3], [4]\}$, which depart at times 14, 16, 18 and 26, respectively.

Centralized system scenario (solve NSP–NSD): In an optimal integrated schedule as shown in Fig. 2b, the production sequence is ([1], [2], [5], [3], [4]). The optimal schedule has two delivery batches: $\{[1],[2],[5]\}$ and $\{[3],[4]\}$, which depart at times 14 and 28, respectively. Comparing with the schedule for individual problems, we observe that with the integration, the transportation cost is reduced by 50%.

Example 3

To illustrate the effect of job release dates, we consider the following example with or without job release dates in the case of problem NSP–NSD where the vehicle capacity c is equal to 3. Table 3 gives the jobs’ parameters with job release dates.

Table 3 Example for evaluation of the effect of job release dates

Fig. 3

Schedules for the individual problems and the integrated problem. a An optimal schedule for case with job release dates. b An optimal schedule for case without job release dates

Figure 3a, b shows an optimal schedule for problem NSP–NSD in the case with job release dates and without job release dates, respectively.

Problem NSP–NSD in the case with job release dates: As shown in Fig. 3a, the production sequence is ([1], [2], [5], [3], [6], [4], [7]). The optimal schedule has five delivery batches:: $\{[1]\},\{[2]\}, \{[5], [3]\},\{[6]\},\{[4]\}$ and $\{[7]\}$, which depart at times 13, 22, 26, 30 and 32, respectively.

Problem NSP–NSD in the case without job release dates: As shown in Fig. 3b, the production sequence is ([1], [2], [6], [5], [3], [7], [4]). The optimal schedule has three delivery batches: $\{[1],[2],[6]\}$, $\{[5],[3],[7]\}$ and $\{[4]\}$, which depart at times 14, 25 and 29, respectively. Comparing with the case with job release dates, we observe that job release dates strongly impact on the optimal schedule of our problem.

3 Decentralized system scenario

In the decentralized scenario, the production schedule and the delivery schedule are established sequentially. We review known exact algorithms to solve the production scheduling problems (i.e., problems NSP and SP) and we propose exact algorithms to solve the distribution scheduling problems (i.e., problems NSD and SD).

3.1 Production scheduling problem

The objective is to determine a feasible production schedule in which the jobs are completed before or at their deadline. We introduce first the concepts of production triplet (see Definition 1) and production block (see Definition 2). Then we investigate problems NSP and SP.

Definition 1

In a production schedule $\sigma$, a production triplet is a job or a part of job, which is processed without preemption. Let $V_j(\sigma )=(J_j,a_j,b_j)$ denote production triplet j, where the job $J_j\in N$ is scheduled in the time interval $[a_j, b_j]$, $a_j$ and $b_j$ represent, respectively, the starting time and ending time of the triplet. Hence the production schedule $\sigma$ can be represented by a sequence of production triplets denoted by $V(\sigma )$.

Definition 2

In a production schedule $\sigma$, a production block is defined as a subset of jobs that are processed consecutively without idle time. We define the starting time of the block as the minimum starting time of jobs of the block and the ending time of the block as the maximum completion time of jobs of the block. The sequence of jobs is not taken into account in the definition of a block. Let $K_i(\sigma )$ denote the $i^{th}$ production block in $\sigma$.

Problem NSP

In this problem, a job is non-preemptable (or non-splittable) in production. This decision problem, denoted by $1|r_j, \overline{d}_j|-$, is NP-complete (Garey and Johnson 1979). Carlier (1982) proposed an efficient binary branch-and-bound algorithm to solve a head–tail problem where a job j is available for processing on the machine at release date $r_j$ (called also head), and has to spend an amount of time $p_j$ on the machine and an amount of time $q_j$ (called tail) in the system after its processing. The objective is to minimize $\max _{j\in N}(C_j+q_j)$. It is well-known that this problem is equivalent to the problem $1|r_j|L_{\max }$, where $L_{\max } = \max _{j\in N} L_j= \max _{j\in N} (C_j-d_j)$, $L_j$ is the lateness and $d_j$ is the due date (i.e., it can be violated). Indeed, if we define $q_j=\max _{i\in N}d_i-d_j$, then minimizing $\max _{j\in N}(C_j+q_j)$ is equivalent to minimizing $L_{\max }$. Furthermore, the problem $1|r_j, \overline{d}_j|-$ is nothing but the decision version of the optimization problem $1|r_j|L_{\max }$, i.e., does there exist a production schedule $\sigma$ such that $L_{\max }(\sigma )\le 0$ ? It immediately follows that problem NSP can be solved by applying Carlier’s branch-and-bound algorithm and stopping when a feasible solution with $L_{\max }\le 0$ is found.

For further usage, we review the Carlier’s branch-and-bound algorithm for the problem $1|r_j|L_{\max }$. The algorithm computes a lower bound and an upper bound for each node based on preemptive and non-preemptive EDD rules (Jackson 1955), respectively.

• Preemptive EDD rule at each decision point t in time, consisting of each release date and each job completion time, schedule one of the available jobs j (i.e., $r_j\le t$) with the earliest due date, interrupting the job in process at t, if it exists. If no jobs are available at a decision point, schedule an idle time until the next release date.

• Non-preemptive EDD rule at each decision point t in time, consisting of each starting time of production block and each job completion time, schedule an available job j (i.e., $r_j\le t$) with the earliest due date without preemption. If no jobs are available at a decision point, schedule an idle time until the next release date.

At every node u, the algorithm runs the preemptive EDD rule to obtain a lower bound and the node is pruned if the upper bound does not exceed the lower bound. Otherwise, the algorithm constructs the non-preemptive EDD schedule, possibly updating the upper bound, and the branching scheme depends on the analysis of this schedule. We suppose that jobs are renumbered according to the sequence in the obtained schedule. Let l be the job with the smallest index such that $L_l=L_{\max }$. Let $h\le l$ be the job with the largest index such that $h = 1$ or $C_{h-1} < s_h$ where $s_h$ is the starting time of job h. Let [h, l] denote the set of jobs from h to l, defining a critical block. If $d_l =\max _{k\in [h,l]}d_k$, then the obtained schedule is optimal. Otherwise, the algorithm defines a critical job $e\in [h,l]$ with the largest index such that $d_e > d_l$ and a critical set $J= [e+1,l]$. The algorithm considers two subsets of schedules corresponding to two nodes $u_1$ and $u_2$. Let $r_j(u)$ and $d_j(u)$ be the release date and the due date of job j at node u, respectively.

• At node $u_1$, the algorithm requires the critical job to be processed before the jobs of the critical set by setting

  $$\begin{aligned} d_e(u_1)= & {} \max _{j\in J}d_j(u)-\sum _{j\in J}p_j\end{aligned}$$

  (1)
  $$\begin{aligned} d_k(u_1)= & {} d_k(u), k\in N\backslash \{e\}\end{aligned}$$

  (2)
  $$\begin{aligned} r_k(u_1)= & {} r_k(u), k\in N \end{aligned}$$

  (3)

• At node $u_2$, the algorithm requires the critical job to be processed after the jobs of the critical set by setting

  $$\begin{aligned} r_e(u_2)= & {} \min _{j\in J}r_j(u)+\sum _{j\in J}p_j\end{aligned}$$

  (4)
  $$\begin{aligned} r_k(u_2)= & {} r_k(u), k\in N\backslash \{e\}\end{aligned}$$

  (5)
  $$\begin{aligned} d_k(u_2)= & {} d_k(u), k\in N \end{aligned}$$

  (6)

Problem SP In this problem, the preemption is allowed in production. This problem, denoted by $1|r_j, pmtn, \overline{d}_j|-$, is a decision problem corresponding to the optimization problem $1|r_j, pmtn|L_{\max }$, which is solved with the preemptive EDD rule in $O(n\log n)$ time (Horn 1974). Hence problem SP can be solved with the preemptive EDD rule in $O(n\log n)$ time. Since the preemption occurs only at release dates in the schedule generated with the preemptive EDD rule, there are at most $n-1$ preemptions. Hence there are O(n) production triplets in this production schedule.

3.2 Distribution scheduling problem

The objective is to obtain a delivery schedule minimizing the transportation cost TC subject to the delivery release dates fixed by the production schedule $\sigma$ and the delivery deadlines. We assume that the jobs are indexed in the increasing completion time, i.e., $C_1(\sigma )<\cdots <C_n(\sigma )$. This sorting operation requires $O(n\log n)$ time. Here, $\sigma$ can be a NSP schedule or a SP schedule. We recall that there are O(n) production triplets in $\sigma$ (see Sect. 3.1). We first provide a general property for problems NSD and SD. Then we investigate problems NSD and SD separately.

Lemma 1

There exists an optimal solution for problems NSD and SD, such that each batch is delivered at its completion time, i.e., when all jobs (or parts of jobs) of the batch are completed.

Proof

Consider an optimal delivery solution for problem NSD and SD that does not satisfy the property. We can anticipate the delivery time of each batch to its completion time without changing the number of delivery batches.$\square$

Problem NSD In this case, a finished job must be delivered in a single batch. We propose a polynomial-time greedy algorithm (see algorithm GA1) to solve problem NSD.

Algorithm GA1

Step 1 :

Let $N'\subseteq N$ denote the set of undelivered jobs. Set the current delivery time $T=\max _{j\in N'}C_j(\sigma )$.

Step 2 :

Find the set of undelivered jobs with deadlines greater than or equal to T. Let $S\subseteq N'$ denote this set.

Step 3 :

If $|S|< c$, deliver all jobs of S in one batch departing at time T. Otherwise, deliver the last c completed jobs of S in one delivery batch departing at time T. Then, update $N'$. If all jobs are delivered, then STOP. Otherwise, go to step 1.

Theorem 1

Algorithm GA1 finds an optimal delivery schedule for problem NSD in $O(n^2)$ time.

Proof

We first prove the complexity. Steps 1 and 2 require O(n) time both at each iteration. Since the jobs of N are sorted in the increasing completion time, the jobs of S obtained at the step 2 are also sorted in the increasing completion time. Hence, step 3 requires O(1) time at each iteration. Since there are at most n iterations, the complexity is $O(n^2)$.

Then we prove that algorithm GA1 provides an optimal solution. Suppose that there is an optimal delivery schedule $\theta ^*$ respecting Lemma 1 for problem NSD. Let $\theta$ be the delivery schedule generated by algorithm GA1. Suppose that the k last delivery batches are the same in the two schedules and the $(k+1)$th last delivery batch $B_{k+1}$ is different in the two schedules. According to Lemma 1 and the step 1 of algorithm GA1, $B_{k+1}(\theta ^*)$ and $B_{k+1}(\theta )$ are delivered at the same time $T=\max _{j\in N'}C_j(\sigma )$ where $N'$ is the set of delivered jobs before the k last delivery batches. Let S be the set of delivered jobs before the k last delivery batches with the deadline greater than or equal to T. We distinguish two cases:

• if $|S|< c$, it is clear that the jobs of $B_{k+1}(\theta ^*)$ are in $B_{k+1}(\theta )$. We can put all jobs j, such that $j\in B_{k+1}(\theta )$ and $j\notin B_{k+1}(\theta ^*)$, in $B_{k+1}(\theta ^*)$ without increasing the number of delivery batches. Now $B_{k+1}(\theta ^*)$ becomes the same as $B_{k+1}(\theta )$.

• if $|S|\ge c$, we have $|B_{k+1}(\theta )|=c$ and $B_{k+1}(\theta ^*)\subset S$. If $|B_{k+1}(\theta ^*)|<c$, we fill $B_{k+1}(\theta ^*)$ with some jobs of S that are not in $B_{k+1}(\theta ^*)$ and update the delivery time of modified batches. Now we do not increase the number of batches and have $|B_{k+1}(\theta ^*)|=c$. If there exists a job j such that $j\notin B_{k+1}(\theta )$ and $j\in B_{k+1}(\theta ^*)$, then there exists another job i such that $i\in B_{k+1}(\theta )$, $i\notin B_{k+1}(\theta ^*)$ and $C_j<C_i$ because job i is one of the last c completed jobs. We can interchange jobs i and j in $\theta ^*$ without changing the number of batches and update the delivery time of modified batches. We repeat this operation until $B_{k+1}(\theta ^*)$ becomes the same as $B_{k+1}(\theta )$.

Hence, we can transform any optimal schedule $\theta ^*$ to $\theta$ without increasing the transportation cost.$\square$

Problem SD: In this case, a finished job can be split and delivered in several batches. We propose a polynomial-time greedy algorithm (see algorithm GA2) for problem SD.

Algorithm GA2

Step 1 :

Let $V'\subseteq V(\sigma )$ denote the set of production triplets (see Definition 1) corresponding to the undelivered parts of jobs. Set current delivery time $T=\max _{V_j\in V'}b_j$.

Step 2 :

Find the set of production triplets corresponding to the jobs with a deadline greater than or equal to T from $V'$. Let $S\subseteq V'$ denote this set.

Step 3 :

If $\sum _{V_j\in S} (b_j-a_j)/p_{J_j} < c$, deliver the parts of jobs corresponding to S in one batch, which departs at time T. Otherwise, create one batch departing at time T as follows: iteratively, if the remaining capacity of the batch, denoted by $c'$, is large enough, add the part of job corresponding to the last completed production triplet $V_j\in S$ in the delivery batch, otherwise split $V_j=(J_j,a_j,b_j)$ into two production triplets $(J_j, a_j, b_j-c' p_{J_j})$ and $(J_j, b_j-c' p_{J_j}, b_j)$. Put the part of job $J_j$ corresponding to $(J_j, b_j-c' p_{J_j}, b_j)$ in the batch to form a full batch. Then update $V'$. If all jobs are delivered, then STOP. Otherwise, go to step 1.

Theorem 2

Algorithm GA2 finds an optimal delivery schedule for problem SD in $O(n^2)$ time.

Proof

The proof is similar to Theorem 1 proof.$\square$

As discussed in Sect. 2, we do not consider the non-splittable production and splittable delivery (NSP-SD) problem, because according to Lemma 2, for any feasible NSP schedule, there exists an optimal NSD delivery schedule.

Lemma 2

For any given feasible NSP schedule, there exists an optimal delivery schedule in which the jobs are not split.

Proof

For a given NSP schedule, algorithm GA2 finds an optimal delivery schedule, which is a NSD schedule. In fact, in the case NSP, each production triplet $V_j$ corresponds to a non-split job $J_j$, i.e., $b_j-a_j=p_{J_j}$. At step 3 of algorithm GA2, when we create a full batch in the case $\sum _{V_j\in S} (b_j-a_j)/p_{J_j} > c$, we do not split any production triplet, i.e., the jobs are put in the delivery batch without splitting.$\square$

4 Integrated system scenario

The integrated scheduling problem amounts to compute an integrated schedule minimizing the transportation cost TC subject to the delivery deadlines. In what follows, we first consider problems SP–NSD and SP–SD, then problem NSP–NSD.

4.1 Problems SP–NSD and SP–SD

In this section, we first give some properties of optimal solutions for problems SP–NSD and SP–SD. Then we provide a polynomial-time algorithm that solves these problems in two special cases. This algorithm will be used to compute lower bounds inside the branch-and-bound algorithm that solves problem NSP–NSD.

Lemma 3

An optimal integrated schedule for problems SP–NSD and SP–SD, if it exists, satisfies the following properties:

• (1) Each job is processed in one production block only.

• (2) Each production block starts at the minimum release date of jobs within this block.

• (3) Each batch is delivered at its completion time when all jobs (or parts of jobs) of the batch are completed.

Fig. 4

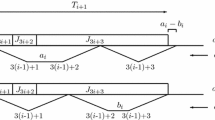
Illustration of property 1 of Lemma 3

Fig. 5

Illustration of property 2 of Lemma 3

Proof

• (1) Suppose there exists an optimal integrated schedule $(\sigma ^*, \theta ^*)$, which does not satisfy property 1, such that job j is the first job preempted and scheduled in several production blocks. Let $K_i$ be the first block containing job j (see Fig. 4a). We reschedule as early as possible the rest of job j in the idle times after $K_i$ (see Fig. 4b). Consequently, job j is processed only in $K_i$. Delivery schedule $\theta ^*$ is also feasible for the new production schedule. So, this new integrated schedule is also optimal. We can repeat this argument a finite number of times until property 1 is satisfied.

• (2) Suppose there exists an optimal integrated schedule $(\sigma ^*, \theta ^*)$, which satisfies property 1 but does not satisfy property 2, such that production block $K_i$ is the first block that does not satisfy property 2. Suppose job j has the earliest release date among the jobs of block $K_i$. We reschedule job j as early as possible without changing other jobs. We distinguish two cases: in the first case, the completion time of the production block $K_{i-1}$ is less than $r_j$ (see Fig. 5a) and in the new production schedule all blocks before $K'_i$ satisfy property 2 (see Fig. 5b); in the second case, the completion time of the production block $K_{i-1}$ is greater than or equal to $r_j$ (see Fig. 5c) and in the new production schedule all blocks before $K_i$ satisfy property 2 (see Fig. 5d). In the new production schedules (b) and (d), we reduce the total size of blocks that do not satisfy property 2. The delivery schedule $\theta ^*$ is also feasible for these new production schedules. So this new integrated schedule is also optimal. We can repeat this argument in polynomial time until property 2 is satisfied.

• (3) The proof is the same as Lemma 1. $\square$

Lemma 4

An optimal integrated schedule for problems SP–NSD and SP–SD, if it exists, is such that the structure of production blocks, consisting of the jobs composition, the starting time and the ending time of each block, is the same as that constructed by the preemptive EDD rule.

Proof

Suppose there exists an optimal integrated schedule $(\sigma ^*, \theta ^*)$, which satisfies the properties of Lemma 3 but does not satisfy the property of Lemma 4. Let $(K_1^*, \ldots , K_l^*)$ be the set of production blocks of $\sigma ^*$. Let $\sigma$ denote the production schedule constructed by the preemptive EDD rule. Let $(K_1, \ldots , K_u)$ be the set of production blocks of $\sigma$. Suppose $K_i^*$ and $K_i$ are the first blocks that are different in the two schedules.

According to the preemptive EDD rule, in $\sigma$ there is a idle time only if there is no available job. Hence there is no idle time among the split parts of each job. In addition, at each idle time end, the rule schedules always one of remaining jobs with the earliest release date. Consequently, $\sigma$ satisfies the properties of Lemma 3.

According to property 2 of Lemma 3, $K_i^*$ and $K_i$ must start at the same time. Noting that in $\sigma$ there is a idle time only if there is no available job, we know that all jobs of $K_i^*$ must be in $K_i$, i.e., $K_i^*\subseteq K_i$.

Suppose job j is the first job such that $j\notin K_i^*$ and $j\in K_i$. Since the jobs before j of $K_i$ are also in $K_i^*$, we know that $K_i^*$ can finish only at or after $r_j$. According to property 2 of Lemma 3, the block including job j must start before or at $r_j$. Consequently, job j must be in $K_i^*$, which is in conflict with the assumption of job j. That means that all jobs of $K_i$ must be in $K_i^*$, i.e., $K_i\subseteq K_i^*$.

Hence, we have $K_i = K_i^*$ and the ending times of $K_i$ and $K_i^*$ are the same. So $K_i^*$ and $K_i$ are not the first blocks that are different in the two schedules. Hence the property of Lemma 4 is satisfied. $\square$

Now, we introduce the Shortest Remaining Processing Time (SRPT) rule to construct a production schedule for problems SP–NSD and SP–SD.

SRPT rule at each decision point t in time, consisting of each release date and each job completion time, schedule an available job j (i.e., $r_j\le t$) with the shortest remaining processing time. If no jobs are available at a decision point, schedule an idle time until the next release date.

Next, we provide a polynomial-time algorithm (see algorithm GA3) for problems SP–NSD and SP–SD in the following two special cases:

Case 1 :

The vehicle capacity is unlimited, i.e., $c=\infty$.

Case 2 :

The set of jobs N can be divided into two subsets of jobs $N_1$ and $N_2$. $\forall j\in N_1$, $\not \exists j'\in N_1$ such that $r_j\le r_{j'} < r_j+p_j$. $\forall j\in N_1$ and $i\in N_2$, $r_j+p_j \le r_i$. In any production block of the schedule constructed by preemptive EDD rule, the jobs of $N_2$ have the same release date.

Algorithm GA3

Step 1 :

Generate a production schedule $\sigma$ with the preemptive EDD rule. If $C_j(\sigma )\le \overline{d}_j, \forall j\in N$, go to Step 2, otherwise there is no solution and STOP.

Step 2 :

Let $N'\subseteq N$ denote the set of undelivered jobs. Set the current delivery time $T=\max _{j\in N'}C_j(\sigma )$.

Step 3 :

Find the set of undelivered jobs with deadlines greater than or equal to T. Let S denote this set.

Step 4 :

If $|S|< c$, deliver the jobs of S in one batch, which departs at time T. Otherwise, reschedule the jobs of S in $\sigma$ with the SRPT rule and do not change the schedule of other jobs. Then, deliver the last c completed jobs of S in one batch, which departs at time T. Then update $N'$. If all jobs are delivered, then STOP. Otherwise, go to step 2.

Theorem 3

Algorithm GA3 finds an optimal integrated schedule for problems SP–NSD and SP–SD in the special case 1 in $O(n^2)$ time, and the special case 2 in $O(n^2\log n)$ time.

Proof

We first prove the complexity of algorithm GA3. At step 1, the generation of $\sigma$ takes $O(n\log n)$ time. We take O(n) time to check feasibility of the solution. At each iteration, step 2 and step 3 take O(n) time, respectively. The step 4 takes O(1) time for the case $|S|\le c$ and takes $O(n\log n)$ time to reschedule the jobs of S with the SRPT rule for the case $|S|> c$. There are O(n) iterations. We note that for the problem in the special case 1, at step 4 we have always $|S|\le c$. It follows that algorithm GA3 finds an integrated schedule for problems SP–NSD and SP–SD in the special case 1 in $O(n^2)$ time, and the special case 2 in $O(n^2\log n)$ time.

Next, we prove that the algorithm provides an optimal solution. Let us add a fictive job 0, such that $r_0=p_0=\overline{d}_0=0$. Let $(\sigma , \theta )$ denote the integrated schedule provided by algorithm GA3 with k batches. Let $B_i$ denote the $i^{th}$ last batch of $\theta$. Let $|B_i|$ denote the size of $B_i$. Let $T(B_i)$ denote the departure date of $B_i$. Since $\overline{d}_0=0$, it is clear that $T(B_k) =0$. We use a recursion argument to prove that algorithm GA3 constructs a solution with minimum $T(B_i)$, among all feasible solutions.

Using the preemptive EDD rule at step 1 guarantees that $T(B_1)$ is minimum. Suppose that $T(B_i)$ is minimum, for a given $1\le i \le k-1$, and prove that $T(B_{i+1})$ is minimum. We consider the two special cases 1 and 2 separately.

Case 1 Since $c=\infty$, the algorithm generates a non-full batch $|B_i|<c$. Since $B_i$ delivers all undelivered available jobs at time $T(B_i)$, $T(B_{i+1})$ is a production completion time of one job with a deadline lower than $T(B_i)$. According to the preemptive EDD rule, we cannot anticipate the maximum production completion time of all jobs with a deadline lower than $T(B_i)$. Hence $T(B_{i+1})$ is minimum,

Case 2 In this case, if the algorithm generates a non-full batch $|B_i|<c$, with the same argument as for the 1, we can prove that $T(B_{i+1})$ is minimum. If the algorithm generates a full batch $|B_i|=c$, we can also prove the minimization of $T(B_{i+1})$ as follows:

• if $T(B_{i+1})$ is a production completion time of one job with a deadline lower than $T(B_i)$, according to the preemptive EDD rule, we cannot anticipate the maximum production completion time of all jobs with a deadline lower than $T(B_i)$.

• if $T(B_{i+1})$ is a production completion time of one job of $N_1$ with a deadline greater than or equal to $T(B_i)$, according to the preemptive EDD rule, the completion times of jobs of $N_1$ cannot be anticipated and the SRPT rule does not change the completion times of jobs in $N_1$, hence we cannot anticipate $T(B_{i+1})$. If $T(B_{i+1})$ is a production completion time of one job j of $N_2$ with a deadline greater than or equal to $T(B_i)$, algorithm GA3 guarantees that this job is executed before all jobs of $B_i$ in $\sigma$. Since the release dates of the jobs of $N_2$ are equal in each production block, using SRPT rule minimizes $T(B_{i+1}) =C_j$.

In the two special cases, we prove that $T(B_{i+1})$ is minimum. Consequently, for any other solution with $k'$ batches, we have $k \le k'$ and algorithm GA3 generates a solution with the minimum number of batches to deliver all jobs. $\square$

Remark that the computational complexities of problems SP–NSD and SP–SD are still open in the general case.

4.2 Problem NSP–NSD

It can be observed easily that problem $1|r_j, \overline{d}_j|-$ reduces to problem NSP–NSD, i.e., it is a special case of problem NSP–NSD with $c=1$. Consequently, problem NSP–NSD is NP-hard in the strong sense. In this section, we first present two heuristics to determine upper bounds of TC. Then, we describe a branch-and-bound algorithm to solve problem NSP–NSD. Finally, we provide a mixed-integer linear programming (MILP) model, which is used to evaluate the performance of the branch-and-bound algorithm.

4.2.1 Heuristics

In our branch-and-bound algorithm, we will use two heuristics that try to construct a feasible integrated schedule for problem NSP–NSD.

The first heuristic, denoted by H1, uses the non-preemptive EDD rule, which forces to create a production schedule without preemption. If the obtained production schedule is feasible, then we apply Algorithm GA1.

Heuristic H1

Step 1 :

Create a production schedule $\sigma$ with the non-preemptive EDD rule. If $C_j(\sigma )\le \overline{d}_j, \forall j\in N$, go to step 2. Otherwise, the algorithm cannot provide a feasible solution and STOP.

Step 2 :

Apply Algorithm GA1 to compute a delivery schedule.

The second heuristic, denoted by H2, uses a SP–NSD integrated schedule computed by Algorithm GA3 to construct, if possible, a feasible integrated schedule for problem NSP–NSD.

Heuristic H2

Step 1 :

Create a priority list of jobs, such that in the given schedule $(\sigma ,\theta )$, if $D_i(\theta ) < D_j(\theta )$, job i must be before job j in the list, and if $D_i(\theta ) = D_j(\theta )$ and $C_i(\sigma ) < C_j(\sigma )$, job i must be before job j in the list.

Step 2 :

Schedule each job as early as possible without preemption. When there are several jobs that can be scheduled, we choose the job with the highest priority. Let $\sigma '$ be the constructed production schedule. If $C_j(\sigma ')\le \overline{d}_j, \forall j\in N$, go to step 3. Otherwise, the algorithm cannot provide a feasible solution and STOP.

Step 3 :

Apply Algorithm GA1 to compute a delivery schedule.

4.2.2 Branch-and-bound algorithm

We propose a branch-and-bound algorithm (see Algorithm B1) for problem NSP–NSD based on the branch-and-bound algorithm of Carlier recalled in Sect. 3.1.

In the search tree, a node u is characterized by: release dates $r_j(u)$, deadlines $\overline{d}_j(u)$ of jobs $j\in N$, a lower bound of $L_{\max }$ denoted by $LB(L_{\max }, u)$, an upper bound of $L_{\max }$ denoted by $UB(L_{\max }, u)$, a lower bound of TC denoted by LB(TC, u), an upper bound of TC denoted by UB(TC, u), the current best upper bound of TC denoted by $UB^*(TC)$, and precedence constraints between the jobs. If node u is the root of search tree, $r_j(root)$ and $\overline{d}_j(root)$ represent the original release dates and deadlines, respectively.

Algorithm B1 first applies Carlier’s algorithm. When a feasible solution, i.e., $UB(TC,u)<n+1$ (line 7 of Algorithm B1) or $UB(L_{\max }, u)\le 0$ (line 12 of Algorithm B1), is found at node u, we apply another branch-and-bound algorithm denoted by Algorithm B2 from node u to try to find a locally optimal solution minimizing TC. When algorithm B2 stops, algorithm B1 continues the branching of Carlier’s algorithm for the remaining active nodes (line 10 of Algorithm B1).

In Algorithm B2, the lower bound LB(TC, u) is computed by solving two relaxed problems, each satisfying one of the two conditions defining the two special cases of problem SP–NSD. The upper bound UB(TC, u) is obtained by applying the two heuristics H1 and H2. Branching in Algorithm B2 is achieved by assigning to each position of the production schedule a job satisfying a set of dominance conditions. Moreover, when Algorithm B2 applies Algorithm GA3, heuristics H1 and H2, the modified deadlines $\overline{d}_j(u)$ are used to determine a feasible production schedule according to Carlier’s algorithm, while the original deadlines $\overline{d}_j(root)$ are used to determine the delivery schedule.

Algorithm B2

Lower bound At node u, we solve two relaxed problems, which satisfy the conditions of the two special cases of SP–NSD:

Case 1 :

Set $c=n$.

Case 2 :

Divide the set of jobs N in two subsets of jobs $N_1$ and $N_2$ as follows. $\forall j\in N_1$, $\not \exists j'\in N_1$ such that $r_j(u)\le r_{j'}(u) < r_j(u)+p_j$. $\forall j\in N_1,$ $\forall i\in N_2$, $r_j(u)+p_j \le r_i(u)$. Schedule the jobs with the preemptive EDD rule, then find, for each production block, the smallest release date of jobs of $N_2$ in this block. Replace the release date of each job in $N_2$ by the corresponding smallest release date of its production block.

We solve these relaxed problems by applying Algorithm GA3: execute step 1 of Algorithm GA3 with $\overline{d}_j(u)$ for $j\in N$, and execute the remaining steps of the algorithm with the original deadlines, i.e., $\overline{d}_j(root)$ for $j\in N$. Let $(\sigma _1, \theta _1)$ and $(\sigma _2, \theta _2)$ denote the obtained SP–NSD integrated schedules for the above problems, respectively. Set $LB(TC, u)=\max \{TC(\sigma _1, \theta _1), TC(\sigma _2, \theta _2)\}$.

Upper bound Firstly, generate a NSP–NSD integrated schedule by applying heuristic H2 with the above obtained schedule $(\sigma _2, \theta _2)$ and the original deadlines, i.e., $\overline{d}_j(root)$ for $j\in N$. Secondly, generate a second NSP–NSD integrated schedule by applying heuristic H1: execute step 1 of heuristic H1 with $\overline{d}_j(u)$ for $j\in N$, and execute step 2 of the heuristic with the original deadlines, i.e., $\overline{d}_j(root)$ for $j\in N$. Finally, if one or both constructed integrated schedules are feasible, set UB(TC, u) as the smallest TC among the two schedules. Otherwise, set $UB(TC, u)=n+1$. Update $UB^*(TC)$ if necessary.

Branching if $LB(TC,u)< UB^*(TC,u)$ for a node u, firstly choose one job to be scheduled in the current production position. Job j is a valid candidate if it satisfies the following conditions. Let $N'$ denote the set of unscheduled jobs without job j.

active scheduling rule :

$r_j(u) < \min _{k\in N'}(r_k(u)+p_k)$

deadline rule :

$r_j(u) + p_j \le \min _{k\in N'}(\overline{d}_k(u)-p_k)$

precedence relations rule :

j has no predecessors in $N'$.

Then, require the valid candidate j to be scheduled at the current production position and let $u'$ be the corresponding new node. Set $r_k(u') = \max (r_k(u), r_j(u)+p_j), \forall k\in N'$.

Example

To illustrate Algorithm B1, we consider the following example with seven jobs where the vehicle capacity c is equal to 2. Table 4 gives the jobs’ parameters.

Table 4 Example to illustrate the branch-and-bound Algorithm B1

Figure 6 illustrates the search tree of the branch-and-bound Algorithm B1. At the root, i.e., node 1, since $UB(L_{\max }, u)>0$ and $LB(L_{\max }, u)\le 0$, we check UB(TC, u) and LB(TC, u). Since $UB(TC, 1)=8$, i.e., the algorithm does not find a feasible NSP schedule, the algorithm branches as Carlier’s algorithm. Here, we have the critical job $e=3$ and the critical set $J=\{1,2,4\}$.

Fig. 6

Illustration of the branch-and-bound algorithm B1

At node 2, Carlier’s algorithm requires the critical job to be processed before the jobs of the critical set by setting the deadline of the critical job 3 to $\overline{d}_3(2)=29$. Since $LB(L_{\max }, 2)=6$ and $UB(L_{\max }, 2)=6$, the algorithm ensures that there is no feasible NSP–NSD schedule for node 2.

At node 3, Carlier’s algorithm requires the critical job to be processed after the jobs of the critical set by setting the release date of the critical job 3 to $r_3(3)=72$. Since $LB(L_{\max }, 3)=0$ and $UB(L_{\max }, 3)=0$, the algorithm ensures that there is at least one feasible NSP–NSD schedule. Then it applies Algorithm B2. The precedence relations enforce that the job 3 has to be processed after the jobs 1, 2 and 4. Since initially $LB(TC, 3)=4$ and $UB(TC, 3)=5$, the branching is performed as prescribed by Algorithm B2. $UB^*(TC)$ is updated to 5.

For the first position of the production schedule, Algorithm B2 finds that job 5 is the only job that meets the dominance conditions among the candidates. By scheduling job 5 at the first position, node 4 is generated. Since $r_k(3)< r_5(3)+p_5(3), \forall k\in N\backslash \{5\}$, the algorithm does not change the release dates. Since $LB(TC, 4)=4$ and $UB(TC, 4)=5$, the algorithms goes on branching. We still have $UB^*(TC)=5$.

The algorithm finds the only candidate 7 for the second position of the production schedule. By scheduling job 7 at the second position, node 5 is generated. Since $r_k(4)< r_7(4)+p_7, \forall k\in N\backslash \{5,7\}$, the algorithm does not change the release dates. Since $LB(TC, 5)=4$ and $UB(TC, 5)=5$, the algorithms continues to branch. We still have $UB^*(TC)=5$.

For the third position of the production schedule, Algorithm B2 finds a set of candidates $\{1,2,4\}$.

By scheduling job 1 at the third position, node 6 is generated. The algorithm sets $r_2(6)=\max \{r_2(5), r_1(5)+p_1\}=48$ and $r_4(6)=\max \{r_4(5), r_1(5)+p_1\}=48$. With this modified setting, there is no feasible solution for problem SP–NSD in the two special cases. Hence there is no feasible solution for problem NSP–NSD.

By scheduling job 2 in the third position, node 7 is generated. The algorithm sets $r_1(7)=\max \{r_1(5), r_2(5)+p_2\}=56$ and $r_4(7)=\max \{r_4(6), r_2(6)+p_2\}=56$. With this modified setting, there is no feasible solution for problem SP–NSD in the two special cases. Hence there is no feasible solution for problem NSP–NSD.

By scheduling job 4 at the third position, node 8 is generated. The algorithm sets $r_1(8)=\max \{r_1(5), r_4(5)+p_4\}=41$ and $r_2(8)=\max \{r_2(5), r_4(5)+p_4\}=41$. With this modified setting, Algorithm B1 computes $LB(TC, 8)=5$ and $UB(TC, 8)=5$, a local optimal solution is found. Since there is no active node, the algorithm stops and an global optimal solution for problem NSP–NSD is found (see Fig. 7).

Fig. 7

An optimal solution for problem NSP–NSD

Figure 7 shows an optimal solution problem for NSP–NSD. The production sequence is (5, 7, 4, 1, 2, 6, 3). There are five delivery batches: $\{7\},\{5, 1\}, \{2\}, \{4, 6\},$ and $\{3\}$, which depart at times 16, 54, 72, 80, and 99, respectively.

4.2.3 Mixed-integer linear programming model

The proposed mixed-integer linear program is valid thanks to the following lemma.

Lemma 5

There exists an optimal integrated schedule for problem NSP–NSD, such that each batch is delivered at one delivery deadline of job.

Proof

Suppose that there is an optimal integrated schedule for problem NSP–NSD that does not satisfy the property. We can change the delivery time of each batch to satisfy the property without changing the number of delivery batches.$\square$

We propose a MILP model, which extends the time-indexed scheduling model as defined by Queyranne and Schulz (1994). We note that $\{\min _{j\in N}r_j, \min _{j\in N}r_j+1, \ldots , \min (\max _{i\in N}r_i + \sum _{i\in N}p_i, \max _{i\in N}\overline{d}_i)\}$ is the set of possible production starting times. Let T denote this set. In this model, according to Lemma 5, we can suppose that each delivery batch departs at one job deadline. Note that one batch departs at a delivery deadline of job (which can be out of this batch) between the last production completion time of jobs in this batch and the earliest deadline of jobs in this batch. Let $s_1, \ldots , s_u$ denote the possible delivery batch departure dates.

Decision variables

• $x_{it}= \left\{ \begin{array}{ll} 1, &{} \quad \text{ if } \text{ production } \text{ job } i{ startsattime}t, \\ &{} i\in \{1,\ldots ,n\}, t\in T\\ 0, &{} \quad \text{ otherwise } \end{array} \right.$

• $y_{iq}= \left\{ \begin{array}{ll} 1, &{} \quad \text{ if } \text{ job } i{ isdeliveredattime}s_q, \\ &{} i\in \{1,\ldots ,n\}, q\in \{1,\ldots ,u\}\\ 0, &{} \quad \text{ otherwise } \end{array} \right.$

• $w_q=$ number of batches departing at time $s_q$, $q\in \{1,\ldots ,u\}$

MILP

$$\begin{aligned} \min \sum _{q=1}^{u}{w_q} \end{aligned}$$

(7)

$$\begin{aligned} \text{ s.t. } \qquad \quad \sum _{t\in T} x_{it}=1,&i\in \{1,\ldots ,n\} \end{aligned}$$

(8)

$$\begin{aligned} \sum _{i=1}^n\sum _{k=\max \{r_i, t+1-p_i\}}^t x_{ik}\le 1,&t\in T \end{aligned}$$

(9)

$$\begin{aligned} x_{it}=0,&i\in \{1,\ldots ,n\}, \nonumber \\&t<r_i \text{ or } t>\overline{d}_i-p_i \end{aligned}$$

(10)

$$\begin{aligned} \sum _{t\in T}tx_{jt}+p_j\le \sum _{q=1}^u(y_{jq}s_q),&j\in \{1,\ldots ,n\} \end{aligned}$$

(11)

$$\begin{aligned} \sum _{i=1}^n{y_{iq}} \le cw_q,&q\in \{1,\ldots ,u\} \end{aligned}$$

(12)

$$\begin{aligned} \sum _{q=1}^u{y_{iq}}=1,&i\in \{1,\ldots ,n\} \end{aligned}$$

(13)

$$\begin{aligned} y_{iq}=0,&i\in \{1,\ldots ,n\},\nonumber \\&q\in \{1,\ldots ,u\}, \overline{d}_i<s_q\end{aligned}$$

(14)

$$\begin{aligned} y_{iq} \in \{0,1\},&i\in \{1,\ldots ,n\}, \nonumber \\&q\in \{1,\ldots ,u\} \end{aligned}$$

(15)

$$\begin{aligned} w_q\in \mathbb {N},&q\in \{1,\ldots ,u\} \end{aligned}$$

(16)

$$\begin{aligned} x_{it} \in \{0,1\},&i\in \{1,\ldots ,n\}, t\in T \end{aligned}$$

(17)

In MILP, the objective function is to minimize the transportation cost. Constraints (8) ensure that any job i starts its processing once. Constraints (9) guarantee that the interval $[t, t+1],$ for each t,  is occupied by at most one job. The interval $[t, t+1]$ is occupied by job i only if job i starts its processing in the interval $[\max \{r_i, t+1-p_i\},t]$. Constraints (10) ensure that job i starts its processing in the interval $[r_i, \overline{d}_i-p_i]$. Constraints (11) ensure that each job is delivered after or at its production completion time. Constraints (12) are the batch capacity constraints. Constraints (13) ensure that each job is delivered in one batch only. Constraints (14) are the delivery deadlines constraints. Constraints (15)–(17) give the domain of definition of each variable.

5 Computational results

In this section, we evaluate the performance of the branch-and-bound Algorithm B1 by comparing it with MILP. The branch-and-bound algorithm is implemented in C++ and the MILP model is implemented in Cplex V12.1. The experiments are carried out on a DELL 2.50 GHz personal computer with 8 GB RAM.

We reuse the method of Briand et al. (2010) to generate instances. We consider $n\in \{10, 20, 30, 50, 70, 100, 150, 200, 300, 500\}$. The integers $p_j$, $r_j$ and $\overline{d}_j$ are generated, respectively, from the uniform distributions [1, 50], [0, $\alpha \sum _{j=1}^np_j$] and $[(1-\beta )a\sum _{j=1}^np_j, a\sum _{j=1}^np_j]$, where $\alpha , \beta \in \{0.2, 0.4, 0.6, 0.8, 1\}$ and $a\in \{100, 110\%\}$. If $\overline{d}_j< r_j+p_j$, $\overline{d}_j$ is updated to $r_j+p_j$. The transportation cost of one batch is equal to 1. We choose a set of hard instances as follows: we apply the branch-and-bound algorithm of Carlier to find the minimum $L_{\max }$ for each instance, if the problem for this instance cannot be solved at the root of the search tree, we consider this instance as a hard instance. If the found $L_{\max }$ of this hard instance is positive, we add this value to each $\overline{d}_j$ of this instance to ensure that we have at least one feasible solution. For $n\le 70$, we consider the batch capacity $c\in \{2, 3, \lceil {\frac{n}{8}}\rceil , \lceil {\frac{n}{4}}\rceil \}$, and $c\in \{\lceil {\frac{n}{50}}\rceil , \lceil {\frac{n}{30}}\rceil , \lceil {\frac{n}{20}}\rceil , \lceil {\frac{n}{10}}\rceil \}$ for $n\ge 100$. 80 hard instances for each value of n are generated. A total number of 800 hard instances are generated.

Table 5 Performance of the branch-and-bound Algorithm B1

Table 6 Performance of MILP

Table 7 Gaps of solutions of the branch-and-bound Algorithm B1

Table 8 Gaps of solutions of MILP

Tables 5, 6, 7 and 8 illustrate the performance of branch-and-bound Algorithm B1. Imposing 5 min as the limit of execution time, we use the following measures to compare the branch-and-bound algorithm with the MILP model.

Fea :

the percentage of instances for which a feasible solution is determined within the given time.

Opt :

the percentage of instances that are solved to optimality within the given time.

Node :

the average number of explored nodes.

Time :

the average CPU time in seconds.

Gap1 :

the relative gap measured by $(UB^*(TC)- LB^*(TC))/LB^*(TC)$, where $UB^*(TC)$ and $LB^*(TC)$ are the best upper bound and lower bound. We consider the instances for which we obtained at least one feasible solution (optimal solution included).

Gap2 :

the relative gap for the instances for which we obtained at least one feasible solution (optimal solution excluded).

The results show that the branch-and-bound Algorithm B1 outperforms the MILP model. From Tables 5 and 6, we observe that the average execution time and the number of nodes obtained by the MILP model are always larger than the branch-and-bound algorithm. MILP cannot find a feasible solution with $n\ge 100$. The branch-and-bound algorithm solves all instances with $n\le 20$ optimally within a very short execution time (less than one second), and more than 90% of instances with $n\le 70$ are solved within an average execution time of less than 40 s. The branch-and-bound algorithm solves 32.5% of instances optimally with n up to 500 and 5 min as time limit.

Consulting the gaps in Tables 7 and 8, we observe that the branch-and-bound algorithm has a much better performance. On average, Gap1 and Gap2 of the branch-and-bound algorithm are lower than 0.8 and 14% when $n\le 70$. However, the maximum Gap2 shows some hard cases for the branch-and-bound algorithm when $n\ge 100$. For the MILP model, on average, Gap1 and Gap2 exceed 20 and 30%, respectively, when $n= 50$.

Table 9 Results of the first feasible solution obtained by the branch-and-bound algorithm

When the number of jobs is very large, it is difficult to construct a simple heuristic that guarantees that a feasible solution is found (especially when deadlines are tight). For this reason, for large instances, the B&B algorithm could be stopped after a fixed amount of time and/or when a first feasible solution is found. We report in Table 9 the results when a first feasible solution is found. We use the following measures.

Gap3 :

average gap between the cost of the final solution of the B&B (computational times limited to 5 min) and the first obtained feasible solution.

%Imp :

average percentage of instances where the two solutions are different.

Gap4 :

average gap between the cost of the final solution of the B&B and the first obtained feasible solution, for instances where they are different.

The results show that the algorithm find a feasible solution for each instance and that good solutions can be found for large instances within a reasonable amount of computational time (43 s on average for $n=500$). The relative gap (Gap4) decreases when n increases, justifying the use of the B&B algorithm as a good heuristic.

6 Conclusions

In this paper, we studied an integrated production and outbound distribution scheduling problem in a supply chain with one manufacturer and one customer in the presence of production release dates and delivery due dates. We considered a single machine production and a direct batch delivery. Moreover, we considered an important feature in production and distribution: splittable or non-splittable production/distribution. We first investigated the scheduling problems induced by the decentralized system scenario. We reviewed the production scheduling problems (i.e., problems SP and NSP) and provided two polynomial-time algorithms to solve the distribution scheduling problems (i.e., problems SD and NSD). Then we investigated the scheduling problems in the integrated system scenario (i.e., problems SP–NSD, SP–SD and NSP–NSD). We provided a polynomial algorithm to solve two special cases of problems SP–NSD and SP–SD. We also provided a branch-and-bound algorithm for problem NSP–NSD and evaluated its performance with numerical experiments. As illustrated by Example 3 in Sect. 2, the presence of release dates deeply changes the problem structure compared to the problem without release dates that was efficiently solved by Chen and Pundoor (2009). The result show that our method obtains reasonable gap, even for large instances and can be used a good heuristic. Furthermore, the proposed algorithm has a better performance than the MILP model and can solve more than 90% of instances with $n\le 70$ optimally within an average execution time less than 40 s. Several important research issues remain open for future investigations. A first research direction is to clarify the complexity of problems SP–NSD and SP–SD. Solving one of these problems efficiently would provide a better lower bound for the branch-and-bound algorithm that solves problem NSP–NSD. A second issue is to consider the same model with a limited number of vehicles and/or with fixed pickup times. Finally, one might consider extending the model to production systems with parallel machines.