Size Effect’s Influence on the Magnetic Phase Transitions in the Nanosized Magnets

Abstract

We present a simple approach (the mean spin method) to investigate the influence of the size of nanoparticles (thickness of ultrathin films) and the concentration of $\ll$magnetic atoms$\gg$ on the critical temperature and magnetic susceptibility in the magnetic phase transition region. The critical spin-spin correlation indices for nanosized magnets are calculated using the scaling relation. It is shown that the critical concentration $p_C$ of the transition from an ordered to an unordered state increases as the characteristic size of nanoparticles (thickness of ultrathin films) decreases. The results obtained by the mean spin method are in qualitative agreement with the Monte Carlo simulation and experimental data.

1 Introduction

Numerous experimental studies suggest the significant influence of a nanoparticle (thickness of ultrathin films) size on the critical temperature of the magnetic phase transition. For example, the size effect was studied in ultrathin magnetic films [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18], among them there are epitaxial films of Ni, Ni/Re, Ni/W [4, 9, 11] and polycrystalline films of $Ni/SiO_{2}$ [1], antiferromagnetic films of CoO, NiO [3, 5, 7, 16], nanocomposite films $Fe_{2}O_{3}, Pr_{0.5}Sr_{0.5}MnO_{3}, MnP$ [17, 18] and $Ni_{50}Fe_{50}, NiO/CoO$ [5, 10] alloys. There were materials with different magnetic order in those experiments [19,20,21,22,23,24,25,26,27,28,29].

There are different approaches for theoretical study of the size effects’ influence on the critical characteristics of the magnetic phase transition: calculations done with high-temperature expansion in the approximation of the Ising model [30, 31], the renormalization group approach [32], the VCE-method [33, 34], the Monte Carlo method [35,36,37,38] and Green functions techniques in the d-f model approximation [39, 40]. And there are also studies of the finite-size effects’ influence on the critical temperature of the magnetic phase transition based on the thermodynamic approach [41] and mean field approximation [42, 43].

Another theoretical method of studying of magnetic phase transitions is the random interaction field method which is a variant of the effective field methods. This approach has a rather long history [44]; much later, it was successfully used to study the magnetic properties of the interacting nanoparticles’ systems [45, 46]. The significant development and applications of the random interaction field approximation are presented in the works of V.I. Belokon with co-authors [47, 48], where they studied the magnetic phase transitions in the bulk systems. We should also note the studies of Saber et al. of the magnetic phase transitions in different nanomagnets using random fields’ model [49,50,51,52,53,54,55].

In this work, in the approximation of the random interaction field method, we have studied the dependence of the critical temperature of the phase transition of nanosized magnetic on their characteristic size and concentration of the $\ll$magnetic atoms$\gg$¹.

2 The Nanoparticle’s Model

To investigate the influence of dimensional and concentration effects on the critical temperature of the magnetic phase transition, we use the following model:

M1. A dilute nanosized magnet is a parallelepiped with magnetic atoms distributed with probability p over the N nodes of the cubic crystalline lattice.

M2. The direct exchange interaction fields H between atoms are distributed randomly and only apply between the nearest neighbours.

M3. The atomic magnetic moments and external magnetic field $H_{ex}$ are oriented along some axis Oz (the Ising model approximation).

Let us number (arbitrarily) all magnetic atoms. The distribution function of the random interaction fields H on an atom with number n is defined [47] as follows:

$$\begin{aligned} \begin{aligned}&W_n(H)=\int \delta \Biggl ( H-\biggl [\sum _{k} h_{nk}(\mathbf {r}_k,\mathbf {m}_k)+H_{ex}\biggr ]\Biggl )\cdot \\ {}&\cdot \prod _{k}F_n(\mathbf {m}_k)\delta (\mathbf {r}_k-\mathbf {r}_{0k})d\mathbf {r}_k d\mathbf {m}_k, \end{aligned} \end{aligned}$$

(1)

where $\delta (x-x_0)$ — is the Dirac function, $h_{nk}=h_{nk}(\mathbf {r}_k,\mathbf {m}_k)$ — the field on the n-th atom created by atoms with magnetic moments $\mathbf {m}_k$ which are located at the nodes with coordinates $\mathbf {r}_k$, $\mathbf {r}_{0k}$ — the coordinates of the lattice’s nodes, and $F_n(\mathbf {m}_k)$ the distribution function of the magnetic moments on the n-th atom which in the Ising model approximation can be represented as:

$$\begin{aligned} \begin{aligned}&F_n(\mathbf {m}_k)=[\alpha _k\delta (\theta _k)+\beta _k\delta (\theta _k-\pi )]\cdot \\&\cdot [(1-p_k)\delta (m_k)+p_k\delta (m_k-m_{0k})], \end{aligned} \end{aligned}$$

(2)

where $\theta _k$ is an angle between $\mathbf {m}_k$ and the Oz axis, $m_{0k}$ — a magnetic moment of the k-th atom, $p_k$ — a probability that there is a magnetic atom at the node $\mathbf {r}_k$, and $\alpha _k$ and $\beta _k=1-\alpha _k$ are probabilities of orientation of an atom’s magnetic moment along the Oz axis (when $\theta _k=0$) and against it (when $\theta _k=\pi$) respectively. These probabilities can be defined as the average thermodynamic values of the vector $\mathbf {m}_k/m_{0k}$:

$$\begin{aligned} \begin{aligned}&\alpha _k=\frac{\exp (\frac{m_{0k}H}{k_BT})}{\exp (\frac{m_{0k}H}{k_BT})+\exp (-\frac{m_{0k}H}{k_BT})},\\ {}&\beta _k=\frac{\exp (-\frac{m_{0k}H}{k_BT})}{\exp (\frac{m_{0k}H}{k_BT})+\exp (-\frac{m_{0k}H}{k_BT})}, \end{aligned} \end{aligned}$$

(3)

where $k_B$ — the Boltzmann constant, T — temperature.

According to the (M 2), we define the exchange interaction fields between magnetic atoms as follows: between the nearest neighbours it is $h_{nk}=J_{nk} m_k \cos \theta _k$, and $h_{nk}=0$ between all other atoms. Here $J_{nk}=A_{nk}/m_{n}m_{k}$ is the reduced exchange interaction constant, and, in turn, $A_{nk}$ is the constant of exchange interaction between the n-th and the k-th atoms. In this approximation, it is possible to construct characteristic distribution functions of interaction fields

$$\begin{aligned} \begin{aligned} A_n(\rho )&=\int W_n(H)\exp (i\rho H)=\\&=\prod _{\{nk\}}\bigg \{1-p_k+p_k\big [\alpha _k\exp (i\rho [h_{nk}(\mathbf {r}_{0k},m_{0k})+\\&+H_{ex}]) +\beta _k\exp (i\rho [-h_{nk}(\mathbf {r}_{0k},m_{0k})+H_{ex}])\big ]\bigg \} \end{aligned} \end{aligned}$$

(4)

Here the summation is over the nearest neighbours of the n-th atom. Then, the distribution function of interaction fields with n-th atom can be represented as:

$$\begin{aligned} \begin{aligned}&W_n(H)=\int \prod _{\{nk\}}\bigg \{1-p_k+p_k\big [\alpha _k\exp (i\rho [h_{nk}(\mathbf {r}_{0k},m_{0k})+\\&+H_{ex}]) +\beta _k\exp (i\rho [-h_{nk}(\mathbf {r}_{0k},m_{0k})+\\&+H_{ex}])\big ]\bigg \}\exp (-i\rho H)dH \end{aligned} \end{aligned}$$

(5)

In the approximation of the $\ll$average spin$\gg$ method [47], in (5), the average thermodynamic values $\alpha _k$ and $\beta _k$ are replaced with averaged values $\langle \alpha _n\rangle$ and $\langle \beta _n\rangle$ with the distribution function of interaction fields $W_n (H)$. The average relative magnetic moment $\mu _n$ can be defined as the difference between $\langle \alpha _n\rangle$ and $\langle \beta _n\rangle : \mu _n=\langle \alpha _n\rangle -\langle \beta _n\rangle$; and $\langle \alpha _n\rangle$ and $\langle \beta _n\rangle$ can be defined via $\mu _n$ as

$$\begin{aligned} \langle \alpha _n\rangle =\frac{1+\mu _n}{2}, ~\langle \beta _n\rangle =\frac{1-\mu _n}{2} \end{aligned}$$

(6)

so it is not difficult to obtain a system of N self-consistent equations with N variables which defines the relation between the average magnetic moment of the n-th atom and average magnetic moments of the neighbours’ atoms:

$$\begin{aligned} \begin{aligned}&\mu _n=\int \tanh \left( \frac{m_{0n}H}{k_BT}\right) W_n\left( H,\alpha _k\rightarrow \frac{1+\mu _n}{2},\right. \\&\left. \beta _k\rightarrow \frac{1-\mu _n}{2}\right) dH \end{aligned} \end{aligned}$$

(7)

The system of Eq. (7) allows to find (see Appendix 1) the critical temperature of a phase transition:

$$\begin{aligned} \begin{aligned}&x_n=\sum _{\{l\}}\int x_l \frac{\partial }{\partial \mu _l} W_n\left( H,\alpha _{nk}\rightarrow \frac{1+\mu _n}{2},\right. \\ {}&\left. \beta _{nk}\rightarrow \frac{1-\mu _n}{2}\right) \cdot \tanh \left( \frac{m_{0n}H}{k_bT_c}\right) dH, \end{aligned} \end{aligned}$$

(8)

where $x_n=\frac{\partial \mu _n}{\partial \mu _1}\Bigm |_{(\mu _1\rightarrow 0,...\mu _N\rightarrow 0)}$ there is summation over the nearest neighbours.

The systems of Eqs. (7) and (8) allow us to study the temperature behaviour of the average magnetic moment, the temperature dependence of the magnetic phase transition on the size of magnets, their crystal structure and concentration of magnetic atoms.

3 Magnetic Phase Transitions in Nanoparticles

Consider a cubic-shaped nanoparticle with $N_{a}$ atoms on the edge, N cites of the lattice are packed with $N_{f}$ ferromagnetic atoms with magnetic moments $m_{0}$, i.e. average probability by nodes is $\langle p \rangle =N_{f}/N$. We assume that all constants of exchange interaction between atoms are the equal ($J_{nk}=J$) and there are no external fields ($H_{ex}=0$). Let us determine the relative average magnetic moment of the nanoparticle per atom:

$$\begin{aligned} \langle m \rangle =\frac{1}{N}\sum _{l=1}^N \mu _{l}, \end{aligned}$$

(9)

where $\mu _{l}$ are the atoms’ magnetic moments calculated via Eq. (7).

3.1 Size Effect in Undiluted Ferromagnets ($p=1$)

The calculation results of the dependence of the average magnetic moment $\langle m \rangle$ on the temperature for nanoparticles of different size are on Fig. 1. The calculations were carried out using the relations (7). It is obvious that the Curie temperature $T_{C}$ increases with increasing of nanoparticles’ size. This behaviour of $T_{C}$ is associated with an increase in the number of the nearest neighbours, as the size of the nanoparticle increases.

Fig. 1

The dependence of the average magnetic moment $\langle m \rangle$ on the critical temperature $t=k_{B}T/Jm_{0}^{2}$ and the number of atoms on the edge of the nanoparticle $N_{a}$ for the BCC crystal lattice

Figure 2 shows the dependence of the relative critical temperature of the phase transition $t_{C}=k_{B}T_C/Jm_{0}^{2}$ on the nanoparticles’ size $D=aN_{a}$ (a is the lattice parameter) for different crystalline structures calculated with Eq. (8). It is easy to see from the illustration that the temperature $t_{C}$ significantly depends not only on the size of the nanoparticles but also on the type of the crystal lattice. This result is consistent with the experimental data [26, 28] (see Fig. 3).

Fig. 2

The dependence of the reduced critical phase transition temperature $t_C=k_BT_C/Jm_0^{2}$ on the number of atoms on the edge of the nanoparticle $N_a$ for different crystal lattices. $t_{C_\infty }$ is the reduced Curie temperature for bulk material

Fig. 3

Dependence of the relative critical temperature $\tau _C=T_C(d)/T_{C_\infty }$ on the size of nanoparticles (BSS). The blue dots are the experimental results on EuS [26], the orange squares are $Fe_3O_4$ [28]

3.2 The Curie Temperature of Diluted Ferromagnets

There are temperature dependencies of the average magnetic moment $\langle m \rangle$ for nanoparticles with the BCC lattice type and three atoms on the edge ($N_{a}=3$, $N=35$) for different concentrations of magnetic atoms $\langle p \rangle$ on Fig. 4.

The concentration $\langle p \rangle$ can only take a discrete set of values due to the finite number of atoms.

Fig. 4

The dependence of the average magnetic moment of a nanoparticle $\langle m \rangle$ of size $N_{a}=3$ on the relative temperature t for the different concentration values of magnetic atoms $\langle p \rangle$

The $\langle p \rangle$ decrease leads to the decrease of the average magnetic moment and the Curie temperature $T_{C}$. The obtained result is quite understandable: the decrease in the number of magnetic atoms reduces the average magnetic moment of a nanoparticle and the number of the nearest neighbours that determine the critical temperature of the phase transition. The dependence of the critical temperature of the phase transition $T_{C}$ on the concentration of magnetic atoms $\langle p \rangle$ is shown on Fig. 5.

With $\langle p \rangle$ decreasing, the Curie temperature drops to zero at some critical concentration $p_{C}$ which is defined by (8) with $T_C=0$:

$$\begin{aligned} x_n=\sum _{\{l\}}\int dH\ x_l \left. \frac{\partial W_n(H, p)}{\partial \mu _l}\right| _{p=p_C}. \end{aligned}$$

There, the system transits from a ferromagnetic state to either a paramagnetic state. The linear decrease of the Curie temperature is associated with the decrease of the number of the nearest neighbours that determine the critical temperature of the phase transition far from the critical concentration $p_{C}$. The same is applicable to the decrease of the critical concentration $p_{C}$.

Fig. 5

The dependence of the relative Curie temperature $t_{C}=k_{B}T_{C}/Jm_{0}^{2}$ of nanoparticles on the average concentration of magnetic atoms $\langle p \rangle$ and the number of atoms on the edge $N_{a}$ for (a) SC and (b) BCC lattices

The critical concentration $p_{C}$ decreases with increasing of nanoparticles’ size up to the value $p_{C\infty }$ corresponding to the bulk material. The calculations of $p_{C\infty }$ were done using the relations (7) (the average spin method). They show that the values of the critical concentration for cubic lattices are lower than the values calculated by us using the Monte Carlo method and the site percolation thresholds presented in [56]. For comparison, Table 1 gives an estimate of the critical concentration using the ratio $p_{C}=2/z$, obtained by the average spin method in the approximation of normal distribution of random interaction fields [56].

Note that the Curie temperature goes to zero at $\langle p \rangle =0$ which corresponds to $p_{C}=0$.

Table 1 Critical concentrations of the phase transition $p_ {c \infty }$ calculated by us, compared to the site and the bond percolation thresholds obtained by other authors. z is the number of nearest neighbours

4 Magnetic Phase Transitions in Ultrathin Films

4.1 Ultrathin Film Model

To assess the size effect and concentration effects on the critical temperature of the magnetic phase transition, we use the same nanoparticle model (see Sec. 2). But for an ultrathin film, we change the first point (M1): an ultrathin film consists of N monolayers with magnetic atoms randomly distributed in each layer at the nodes of the cubic crystal lattice with a concentration $p_{n}$, and leave the second and third ones unchanged.

In the same manner as before, it is easy to calculate the distribution functions over the interaction fields $W_{n}(H)$ (see (19)–(21) in Appendix 2) using the abovementioned formalism. Then, one can derive the equations that determine the average magnetic moments $\mu _{n}$ in each monolayer of the film (see (22)–(24)).

The systems of Eqs. (19)–(24) allow us to study the influence of the size and concentration effects on the critical temperature of the magnetic phase transition $T_C$ of ultrathin films with different crystalline structure as well as to study the features of magnetization near the critical point.

4.2 Curie Temperature of Undiluted Ferromagnetic Film

The Curie temperature $T_C$ dependence on the undiluted ferromagnetic films’ thickness is shown on Fig. 6. It was calculated with the Eqs. (25)–(27) in Appendix 2. The simulation was carried out in the approximation of the equality of the exchange interaction constants in all monolayers of the film and between them: $(i_{1,2}=\cdots =i_{n,n}=\cdots =i_{N,N}=1)$ and $H_{ex}=0$.

Fig. 6

The dependence of the relative critical temperature of the phase transition $t_C=k_BT_C/Jm_0^{2}$ on the thickness of the ultrathin film N (in monolayers) calculated within (a) $\ll$average spin$\gg$ method and (b) Monte-Carlo method for different crystalline cubic lattices: simple cubic (SC), body-centered cubic (BCC) and face-centered cubic (FCC)

It follows from Fig. 6 that the rate of change $t_C$ and its limit value $t_{C_\infty }$ essentially depend on the type of the crystalline lattice. An increase in $t_C$ with an increase in the number of monolayers is naturally associated with an increase in the average number of nearest neighbours. Moreover, we obtained the values of $t_{C_\infty }$ that turned out to be higher than the values calculated by us by the Monte Carlo method and lower than those obtained by the $\ll$average spin$\gg$ method $t_{C_\infty }=z$[36].

The orientation of the crystallographic axes relative to the film surface affects the critical temperature of the phase transition only within the thickness range of 10 monolayers or less. The above noted feature is related to the difference in the number of nearest neighbours located in the same monolayer and in the neighbouring layers. For example, let us consider a film with a body-centered lattice (BCC), with crystallographic axes parallel to the surface (e.g. $\langle 100\rangle$). In this case, any atom in the n-th monolayer does not have nearest neighbours in the same layer ($(z_{n,n}=0$), while it has 4 neighbour atoms in the monolayer $z_{n-1,n}=z_{n,n+1}=4)$ next to it. In the case when a film of the same material grows in the $\langle 111\rangle$ plane, the number of nearest neighbours changes to $z_{n,n}=6$ and $z_{n-1,n}=z_{n,n+1}=3$ respectively.

A comparison of the dependence of $t_C$ on the thickness of an ultrathin film, calculated by us using the Monte Carlo and $\ll$average spin$\gg$ methods, is shown on Fig. 7 together with experimental results[9]. For thin films ($N<10$), the $\tau _c$ values obtained by the Monte Carlo method are slightly higher than the values obtained by the $\ll$average spin$\gg$ method. At the same time, for $N>10$, the calculations basically coincide.

Fig. 7

The dependence of the relative critical temperature of the phase transition $\tau _c$ on the thickness of ultrathin film N (in monolayers) calculated via the $\ll$average spin$\gg$ (blue line) method and using Monte Carlo simulations (red dashed line). The dots show the experimental data [9] for $Ni\ (111)$ films grown on different substrates

Modeling of the dependence of the relative change in temperature of the phase transition $\varepsilon (N)=1-T_C(N)/T_{C_\infty }$ on the thickness of films of different crystal structures can be approximated by the scaling relation:

$$\begin{aligned} \varepsilon (D)=1-\frac{T_C(D)}{T_C(D\rightarrow \infty )}=\Big (\frac{\xi _0}{D}\Big )^\lambda , \end{aligned}$$

(10)

where D — film thickness, $\xi _0$ and $\lambda$ — experimentally determined constants. The constant $\lambda =1/\nu$ is expressed in terms of the critical value of spin-spin correlations $\nu$[58,59,60].

The approximation results are summarized in Table 2 for comparison with experimental data. Obviously, the calculated values of the argument $\lambda$ and the critical spin-spin correlation index $\nu$ are close to the experimental values obtained on the films of Ni/Cu(111), Ni(111)/W(110) and $Ni\ Cu(100)$.

Table 2 Calculated in this work and experimental values of the argument $\lambda$ and the critical exponent $\nu$

Note that the values of the critical correlation exponent $\nu$ are greater than the value $\nu =0.63$ obtained within renormalization-group calculations in the framework of the three-dimensional Ising model, but less than the value $\nu =0.705$ obtained in the framework of the three-dimensional Heisenberg model [66, 67].

4.3 Features of the Magnetic Phase Transition in a Diluted Ferromagnetic Ultrathin Film

Figure 8 shows the results of modeling of the concentration dependence on the critical temperature of the magnetic phase transition for films of various thicknesses. It was done with the relations (22)–(24), in which we assumed $p_1=\cdots =p_n=\cdots =p_N=p$ and $i_{1,2}=\cdots =i_{n,n}=\cdots =i_{N,N}=1$. The figure shows a quite natural result: the Curie temperature decreases as a result of the fact that the decrease in the concentration of magnetic atoms p leads to the decrease in the interaction between them.

Fig. 8

Relative Curie temperature $t_C=k_BT_C/Jm_0^{2}$ dependence on the magnetic atoms concentration p and film thickness N (in monolayers) for different crystalline lattices (the bottom line is for $N=2$, the medium is for $N=3$, the top is for $N=5$ and $N=8$ and these lines coincide)

Fig. 9

The dependence of the critical concentration $p_C$ on the film thickness N (in monolayers) for different crystal lattices

We also note that the critical concentration $p_C$ depends on the film thickness and its crystal lattice (see Fig. 9) which is related to the change in the number of the nearest neighbours. Therefore, the curve $p_C=p_C(N)$ asymptotically tends to the concentration corresponding to the “massive” sample with an increase in the number of monolayers as in the case of nanoparticles (see Section 3.2): $p_{C_\infty }=0.31$ is for simple lattice, $p_{C_\infty }=0.25$ is for body-centered lattice and $p_{C_\infty }=0.16$ is for face-centered lattice.

4.4 Features of the Magnetic Phase Transition in an Antiferromagnetic Ultrathin Film

We use the model described in Section 4.1 to study the effect of the film thickness on the critical temperature of the phase transition in a two-sublattice antiferromagnet. We discuss the simplest case of undiluted antiferromagnet $(p_1=\cdots =p_n=\cdots =p_N=1)$ when there are both

• 1. A ferromagnetic interaction between the atoms inside the monolayers and

• 2. An antiferromagnetic interaction between the atoms in the neighbouring monolayers

with equal in absolute value exchange constants.

We studied the dependence of the relative change in the critical temperature of the phase transition $\varepsilon _{Neel}(N)=\Big (t_{Neel}^{N\rightarrow \infty }-t_{Neel}(N)\Big )/t_{Neel}^{N\rightarrow \infty }$ on the film thickness within Eqs. (25)-(27) with the purpose of comparison with experimental results for $CoO/SiO_{2}$ [2, 3] films. The following values of the relative constants of the exchange interaction were suggested: $i_{n,n}=1, i_{n-1,n}=i_{n,n+1}=-1$.

Modeling of the $\varepsilon _{Neel}(N)$ dependence on the film thickness showed that it was well described by the scaling relation 10 with the arguments values $\lambda$ and the correlation length $\xi _{0}$ presented in Table 3.

Table 3 Experimental and calculated values of the argument $\lambda$ and critical exponent of spin-spin correlations $\nu$

The calculated values of the $\lambda$ and $\nu$ are quite close to the experimental ones obtained on $CoO/SiO_{2}$ [2, 3] films, as it follows from Table 3. We note that our values of $\lambda$ are slightly higher than in the calculations performed by the Monte Carlo method in the framework of the 3D Ising model [68] — ($\lambda =1.5587$) or in the Heisenberg model [69] — ($\lambda$=1.4212).

4.5 Dependence of Magnetic Susceptibility on the Ultrathin Film Thickness

We discuss an ultrathin film of undiluted ferromagnet located in an external field $H_{ex}$. The system of Eqs. (22)–(24) for determining the magnetic moments of atoms in each layer can be represented in this case as follows:

$$\begin{aligned} \begin{aligned} \mu _1&=\int \tanh \left( \frac{h+(z_{1,1}+z{1,2})h_{ex}}{t}\right) W_1(h,\mu _1,\mu _2)dh,\\ \mu _n&=\int \tanh \left( \frac{h+(z_{n,n}+z_{n-1,n}+z_{n,n+1})h_{ex}}{t}\right) \cdot \\&\cdot W_n(h,\mu _n,\mu _{n-1},\mu _{n+1})dh,\\ \mu _N&=\int \tanh \left( \frac{h+(z_{N,N}+z_{N-1,N})h_{ex}}{t}\right) \cdot \\&\cdot W_N(h,\mu _{N-1},\mu _{N})dh, \end{aligned} \end{aligned}$$

(11)

where $h=H/(m_1 J_{11}) h_{ex}=H_{ex}/(m_1 J_{11})$ is relative external field, and $W_n (H)$ is interaction field distribution function (see Appendix 2). It is not difficult to get the system of equations for magnetic susceptibility calculation in each layer (see Appendix 4) within the initial magnetic susceptibility definition and the Eq. (11):

$$\begin{aligned} \chi _n=\lim _{H_{ex}\rightarrow 0}\left( \frac{d\mu _n}{dH_{ex}}\right) =\frac{1}{m_1J_{11}}\lim _{h_{ex}\rightarrow 0}\left( \frac{d\mu _n}{dh_{ex}}\right) \end{aligned}$$

(12)

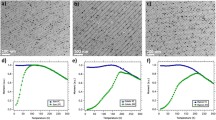
For comparison with the experimental data of [10], using the relations (32)–(34), we calculated the temperature dependence of the magnetic susceptibility for the films of the thickness of $N= 2,3$ and 5 ML, for comparison with the experimental data [10], within the relations (32)–(34). The calculation results are presented on Fig. 10.

Fig. 10

The dependence of relative magnetic susceptibility $\chi /\chi _{max}$ on the relative temperature $T/T_c$ for ultrathin films of various thickness. The dots show experimental results [10]

It is seen from the figures that, as the film thickness decreases, the temperature dependence of magnetic susceptibility $\chi =\chi (T)$ is described with the function centered on the value of the temperature $T_c (N)$ This is consistent with the experimental data [10].

5 Conclusion

This work develops the $\ll$average spin$\gg$ method based on the assumption that the interaction field between the magnetic moments of atoms is random. It allows to study the influence of the size effect and the concentration of magnetic atoms on the critical temperature of the phase transition of nanoparticles and ultrathin films.

It is shown that the decrease in the characteristic dimensions of a nanomagnet leads to a drop in the Curie temperature (or the Neel temperature in AF). This behaviour of the critical temperature of the phase transition $T_{C}$ is determined by a decrease in the number of nearest neighbours.

The dependence of $T_{C}$ on the characteristic dimensions calculated in the framework of the $\ll$average spin$\gg$ agrees well with the experimental data [1,2,3,4,5,6,7,8,9,10,11,12,13,14,15, 19,20,21,22,23,24,25,26, 28, 29, 70,71,72,73].

The Monte Carlo modeling of the size dependence of the critical phase transition temperature showed that the values of $T_C$ calculated for ultrathin films with the thickness less than 10 monolayers slightly exceed the values obtained by the $\ll$average spin$\gg$ method. And for thickness of more than 10 monolayers, the results both methods coincide.

We calculated the critical exponent of spin-spin correlations $\nu$ for nanoparticles and for ultrathin films within scaling relation 10. The values of the critical exponent $\nu$ for ultrathin films coincide with the experimental data [61,62,63,64,65]. The deviations of values of $\nu$ from the experimental ones are due to the limitations of the nanoparticles and ultrathin films models. Thus, the model assumes that the crystal lattice of a nanoparticle is cubic (simple, base-, or face-centered), while the nanosized magnets studied in experiments have spinel or perovskite structure or they are polycrystals.

The study of the dependence of the critical temperature of the phase transition $T_{C}$ on the concentration of magnetic atoms $p_{C}$ has shown that, at the critical concentration $p_{C}$, the Curie temperature drops to zero. The critical $p_{C}$ values, as well as the percolation threshold, are determined by the type of crystal lattice (in our model it corresponds to the number of the nearest neighbours). In addition, a decrease in the size of nanosized magnets leads to an increase in $p_{C}$, which, on average, is also associated with a decrease in the number of nearest neighbours. We also note the advantage of the $\ll$average spin$\gg$ method, compared to the mean field approximation: within the framework of the latter, $p_{C}=0$, as well as the values of the Curie temperature, are higher than the values of $T_{C}$, obtained with the $\ll$average spin$\gg$ method.

Appendices

Appendix 1. The Solution of the Main Eq. (7)

Let us rewrite the Eq. (7) here and see how we can solve it:

$$\begin{aligned} \begin{aligned}&\mu _n=\int \tanh \left( \frac{m_{0n}H}{k_BT}\right) W_n\left( H,\alpha _k\rightarrow \frac{1+\mu _n}{2},\right. \\&\left. \beta _k\rightarrow \frac{1-\mu _n}{2}\right) dH \end{aligned} \end{aligned}$$

(13)

Let us represent the (13) in the form $\mu _n = f_n(\mu _1,\dots ,\mu _n,\dots ,\mu _N)$, where $f_n$ is a monotonically increasing function with the following properties:

• 1. $\mu _n = f_n(\mu _1\rightarrow 0,\dots ,\mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0)\rightarrow 0$ since $\alpha _n \rightarrow 1/2$ and $\beta _n \rightarrow 1/2$ when $\mu _n \rightarrow 0$, and then the distribution function W(H) becomes symmetric (even) with respect to $H=0$;

• 2. $0 <= |f_n(\mu _1,\dots ,\mu _n,\dots ,\mu _N)| \le 1$, since the function is limited.

The next statement is a bit complicated, read it carefully: the equation $\mu _n = f_n(\mu _1,\dots ,\mu _n,\dots ,\mu _N)$ has a non-zero solution $\mu _n$ in the case, when, while varying one of the variables $\mu _k$ in the region $(\mu _1\rightarrow 0,\dots ,\mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0)$, the speed of changing of $f_n$ is higher than the speed of changing of $\mu _n$ (see the schematic illustration 11):

$$\begin{aligned} \left. \frac{\partial f_n}{\partial \mu _k}\right| _{(\mu _1\rightarrow 0,\dots ,\mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0)} > \left. \frac{\partial \mu _n}{\partial \mu _k}\right| _{(\mu _1\rightarrow 0,\dots ,\mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0)} \end{aligned}$$

(14)

The critical condition is then:

$$\begin{aligned} \left. \frac{\partial f_n}{\partial \mu _k}\right| _{(\mu _1\rightarrow 0,\dots ,\mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0)} = \left. \frac{\partial \mu _n}{\partial \mu _k}\right| _{(\mu _1\rightarrow 0,\dots ,\mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0)} . \end{aligned}$$

(15)

Let us take $k=1$ and define $x_n = \partial \mu _n/\partial \mu _k|_{(\mu _1\rightarrow 0,\dots ,\mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0)}$. Then,

$$\begin{aligned} x_n = \sum \limits _{l=1}^N \left. \frac{\partial f_n}{\partial \mu _l}\right| _{(\mu _1\rightarrow 0,\dots ,\mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0)} x_l \end{aligned}$$

(16)

If the Eq. (16) are in the form $\mu _n=f_n(\mu _1, ...\mu _n, ...\mu _N)$ then the conditions for the existence of non-zero solutions of the system (7) can be set as follows:

$$\begin{aligned} \begin{aligned} x_n=\frac{\partial \mu _n}{\partial \mu _k} \Bigm |_{(\mu _1\rightarrow 0,...\mu _N\rightarrow 0)} \le \ \frac{\partial {f_n}}{\partial \mu _k} \Bigm |_{(\mu _1\rightarrow 0,...\mu _N\rightarrow 0)} \end{aligned} \end{aligned}$$

(17)

The derivatives are taken at the critical point (the average magnetic moments are $\mu _1\rightarrow 0,\dots \mu _n\rightarrow 0,\dots ,\mu _N\rightarrow 0$ at $T\rightarrow T_c$). We obtain the system of N equations for N unknown variables $\{T_c,x_2,x_3,\dots ,x_N \}$ where $\mu _k=\mu _1$ and derivative (7) are with respect to $\mu _1$:

$$\begin{aligned} x_n&=\sum _{\{l\}}\int \tanh \left( \frac{m_{0n}H}{k_bT_c}\right) \frac{\partial W_n}{\partial \mu _l}\\&\cdot \left\{ H,\alpha _{nk}\rightarrow \frac{1+\mu _n}{2},\beta _{nk}\rightarrow \frac{1-\mu _n}{2}\right\} x_ldH, \end{aligned}$$

(18)

where the summation $\{l\}$ is over the nearest neighbours.

Fig. 11

The solution of the equation $\tanh (\alpha x) = x$ exists when $\alpha > 1$

Appendix 2. The Equations for the Magnetic Moments of Atoms and for the Critical Temperature of an Ultrathin Film

We use the Eq. (5) to calculate the distribution function of random interaction field $W_n (h)$ in each monolayer of an ultrathin film. The following equations are the result of integration of (5):

$$\begin{aligned} \begin{aligned} W_1(h)= \sum \limits _{k_1=0}^{z_{11}}\sum \limits _{l_1=0}^{k_{1}} \sum \limits _{k_2=0}^{z_{12}}\sum \limits _{l_2=0}^{k_{2}} C_{z_{11}}^{k_1}C_{k_{1}}^{l_1}C_{z_{12}}^{k_2}C_{k_{2}}^{l_2}p_1^{k_1}(1-p_1)^{z_{12}-k_2}\times \\ \\ \frac{(1+\mu _1)^{l_1}(1-\mu _1)^{k_1-l_1}(1+\mu _2)^{l_2} (1-\mu _2)^{k_2-l_2}}{2^{k_1+k_2}}\times \\ \\ \delta \left( h-[(2l_1-k_1)m_{01}J_{1,1}+(2l_2-k_2)m_{02}J_{1,2}+(z_{11}+z_{12})H_{ex}]\right) , \end{aligned} \end{aligned}$$

(19)

$$\begin{aligned} W_n(h)&=\sum \limits _{k_1=0}^{z_{n-1,n}}\sum \limits _{l_1=0}^{k_{1}}\sum \limits _{k_2=0}^{z_{n,n}} \sum \limits _{l_2=0}^{k_2}\sum \limits _{k_3=0}^{z_{n,n+1}}\sum \limits _{l_3=0}^{k_3} C_{z_{n-1,n}}^{k_1}C_{k_{1}}^{l_1} C_{z_{n,n}}^{k_2}C_{k_{2}}^{l_2}C_{z_{n,n+1}}^{k_3}C_{k_3}^{l_3} p_{n-1}^{k_1}(1-p_{n-1})^{z_{n-1,n}-k_1} \times \\& p_n^{k_2}(1-p_n)^{z_{n,n}-k_2}p_{n+1}^{k_3}(1-p_{n+1})^{z_{n,n+1}-k_3}(1+\mu _n)^{l_1} \frac{(1-\mu _n)^{k_1-l_1}(1+\mu _{n-1})^{l_2}(1-\mu _{n-1})^{k_2-l_2} (1+\mu _{n+1})^{l_3}}{2^{k_1+k_2+k_3}} \times \\& \delta (h-[(2l_1-k_1)m_{0n-1}J_{n-1,n}+(2l_2-k_2)m_{0n}J_{n,n}+(2l_3-k_3)m_{0n+1}J_{n,n+1}+(z_{n-1,n}+z_{n,n}+z_{n,n+1})H_{ex}]), \end{aligned}$$

(20)

$$\begin{aligned} W_N(h)&=\sum \limits _{k_1=0}^{z_{N-1,N}}\sum \limits _{l_1=0}^{k_{1}} \sum \limits _{k_2=0}^{z_{N,N}}\sum \limits _{l_2=0}^{k_2} C_{z_{N-1,N}}^{k_1}C_{k_{1}}^{l_1} C_{z_{N,N}}^{k_2}C_{k_{2}}^{l_2} p_{N-1}^{k_1}(1-p_{N-1})^{z_{N-1,N}-k_1}p_N^{k_2}(1-p_N)^{z_{N,N}-k_2} \times\\& \frac{(1+\mu _{N-})^{l_1}(1-\mu _{N-1})^{k_1-l_1}(1+\mu _{N})^{l_2} (1-\mu _{N})^{k_2-l_2}}{2^{k_1+k_2}} \times \\& \delta (h-[(2l_1-k_1)m_{0N-1}J_{N-1,N}+(2l_2-k_2)m_{0N}J_{N,N}(z_{N-1,N}+z_{N,N})H_{ex}]). \end{aligned}$$

(21)

where $\delta (h-h_0)$ is the Dirac delta function. There is the set of equations for calculation of the average magnetic moments of a layered film:

$$\begin{aligned} \mu _1=&\sum \limits _{k_1=0}^{z_{11}}\sum \limits _{l_1=0}^{k_{1}} \sum \limits _{k_2=0}^{z_{12}}\sum \limits _{l_2=0}^{k_{2}} C_{z_{11}}^{k_1}C_{k_{1}}^{l_1}C_{z_{12}}^{k_2}C_{k_{2}}^{l_2} p_1^{k_1}(1-p_1)^{z_{11}-k_1}p_2^{k_2}(1-p_1)^{z_{12}-k_2} \times \frac{(1+\mu _1)^l_1(1-\mu _1)^{k_1-l_1}(1+\mu _2)^l_2 (1-\mu _2)^{k_2-l_2}}{2^{k_1+k_2}} \times \\& \tanh \left( \frac{(2l_1-k_1)+(2l_2-k_2)i_{1,2}+(z_{11}+z_{12})h_{ex}}{t}\right) , \end{aligned}$$

(22)

$$\begin{aligned} \mu _n&=\sum \limits _{k_1=0}^{z_{n-1,n}}\sum \limits _{l_1=0}^{k_{1}} \sum \limits _{k_2=0}^{z_{n,n}}\sum \limits _{l_2=0}^{k_2} \sum \limits _{k_3=0}^{z_{n,n+1}}\sum \limits _{l_3=0}^{k_3} C_{z_{n-1,n}}^{k_1}C_{k_{1}}^{l_1} C_{z_{n,n}}^{k_2}C_{k_{2}}^{l_2}C_{z_{n,n+1}}^{k_3}C_{k_3}^{l_3} \times \\& p_{n-1}^{k_1}(1-p_{n-1})^{z_{n-1,n}-k_1}p_n^{k_2} (1-p_n)^{z_{n,n}-k_2}p_{n+1}^{k_3}(1-p_{n+1})^{z_{n,n+1}-k_3} \times \\& (1+\mu _n)^{l_1}(1-\mu _n)^{k_1-l_1} (1+\mu _{n-1})^{l_2}(1-\mu _{n-1})^{k_2-l_2} \times \\& \tanh \left( \frac{(2l_1-k_1)i_{n-1,n}+(2l_2-k_2)i_{n,n}+(2l_3-k_3)i_{n,n+1}+(z_{n-1,n}+z_{n,n}+z_{n,n+1})h_{ex}}{t}\right) , \end{aligned}$$

(23)

$$\begin{aligned} \mu _N=& \sum \limits _{k_1=0}^{z_{N-1,N}}\sum \limits _{l_1=0}^{k_{1}} \sum \limits _{k_2=0}^{z_{N,N}}\sum \limits _{l_2=0}^{k_{2}} C_{z_{N-1,N}}^{k_1}C_{k_{1}}^{l_1}C_{z_{N,N}}^{k_2}C_{k_{2}}^{l_2} \times p_{N-1}^{k_1}(1-p_{N-1})^{z_{N-1,N}-k_1}p_N^{k_2}(1-p_N)^{z_{N,N}-k_2} \times \\& \frac{(1+\mu _{N-1})^l_1(1-\mu _{N-1})^{k_1-l_1}(1+\mu _N)^l_2 (1-\mu _N)^{k_2-l_2}}{2^{k_1+k_2}} \times \tanh \left( \frac{(2l_1-k_1)i_{N-1,N}+(2l_2-k_2)i_{N,N}+(z_{1N-1,N}+z_{N,N})h_{ex}}{t}\right) , \end{aligned}$$

(24)

In the system (22)–(24), $p_n$ - is a concentration of magnetic atoms in the n-th layer, $i_{n,n}=J_{n,n} m_{0n})/J_{11} m_{01}$, $i_{n-1,n} =J_{n-1,n} m_{0n-1}/J_{11} m_{01}$, $i_{n,n+1} =J_{n,n+1} m_{0n+1}/J_{11}m_{01}$, $z_{n,n}$, $J_{n,n}$ - numbers of the nearest neighbours and constants of exchange interaction between atoms with a layer number n; $z_{n\pm 1,n}$ - numbers of the nearest neighbours of the n-th atom located in the $(n\pm 1)$-th layers; $J_{n\pm 1,n}$ are constants of exchange interaction between atoms located in neighbouring layers; $m_{0n}$ - a magnetic moment of the n-th atom; $t=k T/J_{11} m_{01}$, $h_{ex}=H_{ex}/J_{11} m_{01}$. It should be noted that the set of the Eqs. (22)–(24) determines the magnetic moments in each monolayer of an ultrathin film. Such set of equations was proposed by Saber et al. [49, 50, 74] within the framework of an effective field theory using an improved configurational averaging procedure.

There is the set of equations for the temperature of the phase transition.

$$\begin{aligned} 1 &= \sum \limits _{k_1=0}^{z_{11}}\sum \limits _{l_1=0}^{k_{1}} \sum \limits _{k_2=0}^{z_{12}}\sum \limits _{l_2=0}^{k_{2}} C_{z_{11}}^{k_1}C_{k_{1}}^{l_1}C_{z_{12}}^{k_2}C_{k_{2}}^{l_2} p_1^{k_1}(1-p_1)^{z_{11}-k_1}p_2^{k_2}(1-p_1)^{z_{12}-k_2}\cdot \\& \cdot \frac{(2l_1-k_1)+(2l_2-k_2)x_2}{2^{k_1+k_2}} \tanh \left( \frac{(2l_1-k_1)+(2l_2-k_2)i_{1,2}+(z_{11}+z_{12})h_{ex}}{t_c}\right) , \end{aligned}$$

(25)

$$\begin{aligned} x_n =& \sum \limits _{k_1=0}^{z_{n-1,n}}\sum \limits _{l_1=0}^{k_{1}}\sum \limits _{k_2=0}^{z_{n,n}} \sum \limits _{l_2=0}^{k_2}\sum \limits _{k_3=0}^{z_{n,n+1}}\sum \limits _{l_3=0}^{k_3} C_{z_{n-1,n}}^{k_1}C_{k_{1}}^{l_1} C_{z_{n,n}}^{k_2}C_{k_{2}}^{l_2}C_{z_{n,n+1}}^{k_3}C_{k_3}^{l_3}\cdot \cdot p_{n-1}^{k_1}(1-p_{n-1})^{z_{n-1,n}-k_1}p_n^{k_2}(1-p_n)^{z_{n,n}-k_2} p_{n+1}^{k_3}(1-p_{n+1})^{z_{n,n+1}-k_3}\\&\cdot \frac{(2l_1-k_1)x_{n-1}+(2l_2-k_2)x_n+(2l_3-k_3)x_{n+1}}{2^{k_1+k_2+3}}\cdot \cdot \tanh \left( \frac{(2l_1-k_1)i_{n-1,n}+(2l_2-k_2)i_{n,n}+(2l_3-k_3)i_{n,n+1}+(z_{n-1,n}+z_{n,n}+z_{n,n+1})h_{ex}}{t_c}\right) , \end{aligned}$$

(26)

$$\begin{aligned} x_N &= \sum \limits _{k_1=0}^{z_{N-1,N}}\sum \limits _{l_1=0}^{k_{1}} \sum \limits _{k_2=0}^{z_{N,N}}\sum \limits _{l_2=0}^{k_{2}} C_{z_{N-1,N}}^{k_1}C_{k_{1}}^{l_1}C_{z_{N,N}}^{k_2}C_{k_{2}}^{l_2} p_{N-1}^{k_1}(1-p_{N-1})^{z_{N-1,N}-k_1}p_N^{k_2}(1-p_N)^{z_{N,N}-k_2}\cdot \\& \cdot \frac{(2l_1-k_1)+(2l_2-k_2)x_{N-1}}{2^{k_1+k_2}} \tanh \left( \frac{(2l_1-k_1)i_{N,N}+(2l_2-k_2)i_{N,N-1}+(z_{N-1,N}+z_{N,N})h_{ex}}{t_c}\right) , \end{aligned}$$

(27)

Appendix 3. Monte Carlo Simulation Technique for Utrathin Films

The Monte Carlo simulations of the phase transition in a dilute magnet ultrathin film were carried out within the framework of the Ising model. It was assumed that the distribution of magnetic atoms with an average concentration p over the lattice sites is random. The size of the sample was $100\times 100 \times N$ where the film thickness $N\in [1,20]$. The calculation was carried out using the Hamiltonian:

$$\begin{aligned} \mathcal {H} = -J\left( \frac{1}{2}\sum \limits _{\{i,j\}}c_ic_js_is_j + h\sum \limits _{i} c_is_i\right) , \end{aligned}$$

(28)

where $s_i = \pm 1$ is spin variable of the magnetic moment of an atom located at the i-th site of the lattice; J is the energy of exchange interaction between two neighbouring magnetic atoms; h is the ratio of the energy of the external magnetic field to the energy of exchange interaction,

$$\begin{aligned} c_i = \left\{ \begin{array}{ll} 1, &{} \text {if}\ i \text {-th node is occupied by a magnetic atom,}\\ 0, &{} \text {if it is a non-magnetic atom } \end{array} \right. \end{aligned}$$

(29)

The critical temperature of the phase transition was determined from the magnetic susceptibility:

$$\begin{aligned} \chi =\frac{N}{t}\left[ \langle M^2 \rangle - \langle M \rangle ^2\right] , \end{aligned}$$

(30)

where M is the order parameter:

$$\begin{aligned} M = \frac{1}{N} \left[ \langle \sum \limits _{i}^{N_m}s_i\rangle \right] . \end{aligned}$$

(31)

Here N and $N_m = pN$ are the total number of nodes and magnetic nodes in the lattice respectively; $t = k_BT/J$ is the relative temperature; the brackets $\langle \rangle$ and [] denote averaging over $10^6$ Monte Carlo steps and $2\cdot 10^3$ of different lattice configurations respectively. In the simulation, the Wolff cluster algorithm was used [75], which has proven to be highly precise and fast compared to the classical Metropolis-Hastings algorithm, as well as highly efficient compared to other cluster algorithms.

Appendix 4. Calculation of Magnetic Susceptibility

$$\begin{aligned} \begin{aligned} \chi _1=&\int \frac{1}{t~ ch^2\left( \frac{h+(z_{11}+z_{12})h_{ex}}{t}\right) }W_1(h,\mu _1,\mu _2)dh\ +\\ + \chi _1&\int \tanh \left( \frac{h+(z_{11}+z_{12})h_{ex}}{t}\right) \frac{\partial W_1(h,\mu _1,\mu _2)}{\partial \mu _1}dh+\\ + \chi _2&\int \tanh \left( \frac{h+(z_{11}+z_{12})h_{ex}}{t}\right) \frac{\partial W_1(h,\mu _1,\mu _2)}{\partial \mu _2}dh, \end{aligned} \end{aligned}$$

(32)

$$\begin{aligned} \begin{aligned} \chi _n=&\int \frac{1}{t~ ch^2\left( \frac{h+(z_{n,n}+z_{n-1,n}+z_{n,n+1})h_{ex}}{t}\right) } W_n(h,\mu _n,\mu _{n-1},\mu _{n+1})dh\ +\\ + \chi _n&\int \tanh \left( \frac{h+(z_{n,n}+z_{n-1,n}+z_{n,n+1})h_{ex}}{t}\right) \frac{\partial W_n(h,\mu _n,\mu _{n-1},\mu _{n+1})}{\partial \mu _2}dh\ +\\ +\chi _{n-1}&\int \tanh \left( \frac{h+(z_{n,n}+z_{n-1,n}+z_{n,n+1})h_{ex}}{t}\right) \frac{\partial W_{n-1}(h,\mu _n,\mu _{n-1},\mu _{n+1})}{\partial \mu _{n-1}}dh\ +\\ +\chi _{n+1}&\int \tanh \left( \frac{h+(z_{n,n}+z_{n-1,n}+z_{n,n+1})h_{ex}}{t}\right) \frac{\partial W_{n+1}(h,\mu _n,\mu _{n-1},\mu _{n+1})}{\partial \mu _{n+1}}dh, \end{aligned} \end{aligned}$$

(33)

$$\begin{aligned} \begin{aligned} \chi _N=&\int \frac{1}{t~ ch^2\left( \frac{h+(z_{N,N}+z_{N-1,N})h_{ex}}{t}\right) } W_N(h,\mu _N,\mu _{N-1})dh\ +\\ \\ +\chi _N&\int \tanh \left( \frac{h+(z_{N,N}+z_{N-1,N})h_{ex}}{t}\right) \frac{\partial W_N(h,\mu _N,\mu _{N-1})}{\partial \mu _N}dh\ +\\ \\ +\chi _{N-1}&\int \tanh \left( \frac{h+(z_{N,N}+z_{N-1,N})h_{ex}}{t}\right) \frac{\partial W_{N-1}(h,\mu _N,\mu _{N-1})}{\partial \mu _{N-1}}dh \end{aligned} \end{aligned}$$

(34)