Thermodynamic Properties of the Core/Shell Antiferromagnetic Ising Nanocube

Abstract

Using the effective field theory with correlations, the effects of the exchange interaction on the thermal behaviors of the total magnetization, internal energy, specific heat, entropy, and free energy of a transverse antiferromagnetic Ising nanocube are investigated. The phase diagram is also calculated and discussed in detail.

1 Introduction

Magnetic nanoparticle (NP) systems have received much attention over the last decade [1–4], because of their great interest in various disciplines such as ultra-high-density recording media [5] and biomedicine [4–6]. Moreover, when the size of a magnetic NP decreases to a nanometer scale, the magnetic and thermodynamic properties of these NPs become quite different from those observed in the bulk materials [7].

From the experimental point of view, there are many methods that have been used to prepare various types of magnetic NP systems which have many applications in different types of nanotechnology areas [8–12]. On the other hand, the magnetic and thermodynamic properties of these NP systems have been studied by a variety of techniques, such as the mean-field theory (MFT) [13], effective-field theory (EFT) with correlations [14–17], Green functions (GF) formalism [18], variational-cumulant expansion (VCE) [19], and Monte Carlo (MC) simulations [20–22]. Based on the EFT with correlations, Canko et al. [23] have investigated the magnetic and the thermodynamic properties of a cylindrical spin-1 Ising nanotube, and they have also investigated the magnetic susceptibility, specific heat, internal energy, and free energy of a cylindrical mixed spin-$\frac {1}{2}$ and spin-1 Ising nanotube [24]. In their both works, they have observed first- and second-order phase transitions. By using the same method, the temperature and the applied field dependencies of the magnetic properties (magnetization, susceptibility, specific heat, and internal energy) of the ferro- and antiferromagnetic cylindrical mixed spin-$\frac {1}{2}$ core and spin-1 shell Ising nanotube system have been investigated by Şarlı [25]. He has observed that the interaction parameter between the shell and the core affects the magnetic properties of the nanotube system. Kantar et al. [26] have investigated the thermal and magnetic properties of a ternary Ising spins ($\frac {1}{2},1,\frac {3}{2}$) magnetic NPs with core-shell structure, within the framework of the EFT with correlations. They have found that the system undergoes first- and second-order phase transitions and exhibits a tricritical point, reentrant, and five different types of compensation behaviors. Similarly, Taşkın et al. [27] have investigated the effects of the crystal field at the surface shell and bilinear interactions among the core and surface shell on the magnetic and the thermodynamic properties of a cylindrical Ising nanotube composed of a spin-$\frac {1}{2}$ core surrounded by a spin-$\frac {3}{2}$ shell system. They have observed that the system exhibits first- and second-order phase transitions and also critical end points. Recently, Bouhou et al. [28] have investigated the effect of the core/shell interfacial coupling, the surface shell exchange coupling, and the surface shell transverse field on the magnetic and thermodynamic properties of an antiferromagnetic core/shell magnetic NP on a HCP lattice. They have found a number of interesting phenomena such as the existence of the compensation temperature.

The purpose of the present work is to contribute with the same thematic to investigate the effect of the exchange coupling between the core and shell on the magnetic and thermodynamic properties of the core/shell antiferromagnetic Ising nanocube. For this aim, we have organized the paper as follows: In Section 2, we outline the formalism of the system. The results and discussion are presented in Section 3 and finally Section 4 contains a brief conclusion.

Fig. 1

Schematic representation of magnetic spins in a cubic nanoparticle. Solid, dotted, and dashed lines represent the exchange interactions of the surface shell, core, and interface, respectively

2 Model and Formalism

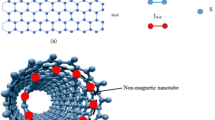
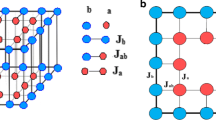
We consider an antiferromagnetic nanocube consisting of surface shell and core, where each site is occupied by an Ising spin-$\frac {1}{2}$ as depicted in Fig. 1. The inner spins are called the core (c) region which is surrounded by the outer spins that are known as the surface shell (s) of the particle. The number of core spins is N _c =27 and the number of surface shell spins is N _s =98. The Hamiltonian of the system is expressed as follows

$$\begin{array}{@{}rcl@{}} H &=&-J_{s}\sum\limits_{<ij>}{\sigma_{i}^{z}}{\sigma_{j}^{z}}-J_{c}\sum\limits_{<nm>}\sigma _{n}^{z}{\sigma_{m}^{z}}-J_{cs}\sum\limits_{<im>}{\sigma_{i}^{z}}{\sigma_{m}^{z}} \\ &&-{\Omega}_{s}\sum\limits_{i}{\sigma_{i}^{x}}-{\Omega}_{c}\sum\limits_{m}{\sigma_{m}^{x}}, \end{array} $$

(1)

where ${\sigma _{i}^{z}}$ and ${\sigma _{i}^{x}}$ denote, respectively, the z and x components of a quantum spin operator $\overrightarrow {\sigma }$ of magnitude $\sigma =\pm \frac {1}{2}$ at the site i. J _s , J _c and J _{c s} are the exchange interactions between the nearest-neighbor magnetic spins in the surface shell, the core and between the core and surface shell interface (J _{c s} <0), respectively. Ω _s represents the transverse field at the surface shell, and Ω _c is the transverse field in the core.

The theory to be used is the EFT in which the attention is focused on the cluster comprising just a single selected spin and the neighboring spins with which it directly interacts. To this end, the Hamiltonian is split into two parts

$$ H=H^{\prime}+H_{i}. $$

(2)

The first term denoted by $H^{^{\prime }}$ does not depend on the site i, while the second term H _i includes all contributions associated with the site i :

$$ H_{i}=-A{\sigma_{i}^{z}}-{\Omega}_{\alpha }{\sigma_{i}^{x}}, $$

(3)

where

$$ A=\sum\limits_{j}J_{ij}{\sigma_{j}^{z}}, $$

(4)

and Ω _α =Ω _s or Ω _c (Ω _s if the site α belongs to the surface shell of the nanocube and Ω _c if not).

Using the approximation introduced by Sá Barreto et al. [29], we obtain the identity

$$ \left\langle {\sigma_{i}^{z}}\right\rangle =\left\langle \frac{Tr\left[ {\sigma_{i}^{z}}e^{-\beta H_{i}}\right] }{Tr\left[ e^{-\beta H_{i}}\right] } \right\rangle , $$

(5)

where the angular bracket 〈⋯〉 denotes the canonical thermal average, β=1/k _B T with k _B stands for the Boltzmann constant, and T is the temperature. If the exchange interactions are restricted only to the nearest-neighbors and using the EFT with a probability distribution technique [30], the longitudinal magnetization of the system would be given by

$$ {m_{i}^{z}}=\left\langle {\sigma_{i}^{z}}\right\rangle =\left\langle f_{z}\left( A,{\Omega}_{\alpha }\right) \right\rangle , $$

(6)

with

$$ f_{z}(A,{\Omega}_{\alpha })=\frac{A}{2\sqrt{A^{2}+{\Omega}_{\alpha }^{2}}} \tanh \left( \frac{\beta }{2}\sqrt{A^{2}+{\Omega}_{\alpha }^{2}}\right) . $$

(7)

To perform the thermal averaging on the right-hand side of (6 ), we follow the general approach described in Ref. [30]. First of all, in the spirit of the EFT, multispin-correlation functions are approximated by products of single spin averages. We then take advantage of the integral representation of the Dirac’s delta distribution in order to write (6) in the following form

$$ {m_{i}^{z}}=\int {dyf_{z}(y,{\Omega} }_{\alpha }{)\frac{1}{2\pi }\int }\left[ { d\lambda \exp (iy\lambda ){\prod}_{j}}\left\langle {\exp (i\lambda J_{ij}{\sigma_{j}^{z}})}\right\rangle \right]. $$

(8)

In the calculation of (8), the commonly used approximation has been made according to which the multi-spin correlation functions are decoupled into products of the spin average. To make progress, we introduce the probability distribution of the spin variable ${\sigma _{j}^{z}}$ [31]:

$$ \ P({\sigma_{j}^{z}})=\frac{1}{2}\left[ \left( 1-2{m_{i}^{z}}\right) \delta ({\sigma_{j}^{z}}+\frac{1}{2})+\left( 1+2{m_{i}^{z}}\right) \delta (\sigma_{j}^{z}-\frac{1}{2})\right] . $$

(9)

The explicit formulation of magnetizations have a long expressions, so they will not be given here. But they are given in AAppendix . The total longitudinal magnetization per site is given by

$$ M_{T}=\frac{1}{125}\left( 98M_{s}+27M_{c}\right) , $$

(10)

where M _s and M _c represent, respectively, the surface shell and core longitudinal magnetizations of the nanocube, which are given by

$$ M_{c}=\frac{1}{27}\left( 8m_{c_{1}}^{z}+12m_{c_{2}}^{z}+6m_{c_{3}}^{z}+m_{c_{4}}^{z}\right) , $$

(11)

and

$$ M_{s}=\frac{1}{98}\left( 8m_{s_{1}}^{z}+24m_{s_{2}}^{z}+12m_{s_{3}}^{z}+24m_{s_{4}}^{z}+24m_{s_{5}}^{z}+6m_{s_{6}}^{z}\right) . $$

(12)

By using the approximated spin correlation identities introduced by Sá Barreto et al. [32]

$$ \left\langle f_{i}\sigma_{i}\right\rangle =\left\langle f_{i}\frac{ Tr_{i}(\sigma_{i}\exp (-\beta H_{i}))}{Tr_{i}(\exp (-\beta H_{i}))} \right\rangle , $$

(13)

we can easily obtain the internal energy U of the system from the thermodynamic average of the Hamiltonian, as it has done by Kaneyoshi et al. [33] in the mixed-spin system

$$\begin{array}{@{}rcl@{}} U &=&\left\langle H\right\rangle =-\frac{1}{2}(\frac{1}{125}(8\left\langle u_{s_{1}}\right\rangle +24\left\langle u_{s_{2}}\right\rangle +12\left\langle u_{s_{3}}\right\rangle +24\left\langle u_{s_{4}}\right\rangle +24\left\langle u_{s_{5}}\right\rangle \\ &&+6\left\langle u_{s_{6}}\right\rangle +8\left\langle u_{c_{1}}\right\rangle +12\left\langle u_{c_{2}}\right\rangle +6\left\langle u_{c_{3}}\right\rangle +\left\langle u_{c_{4}}\right\rangle ))-{\Omega}_{s}(\frac{1}{98}(8m_{s_{1}}^{x} \\ &&+24m_{s_{2}}^{x}+12m_{s_{3}}^{x}+24m_{s_{4}}^{x}+24m_{s_{5}}^{x}+6m_{s_{6}}^{x}))-{\Omega}_{c}(\frac{1}{27}(8m_{c_{1}}^{x}+12m_{c_{2}}^{x} \\ &&+6m_{c_{3}}^{x}+m_{c_{4}}^{x})) \end{array} $$

(14)

where

$$ \left\langle u_{i}\right\rangle =\left\langle \sum\limits_{j}J_{ij}\sigma_{j}^{z}f_{z}\left( \sum\limits_{j}J_{ij}{\sigma_{j}^{z}},{\Omega}_{i}\right) \right\rangle . $$

(15)

The specific heat of the system is obtained from the relation:

$$ C_{h}=\frac{\partial U}{\partial T}. $$

(16)

The entropy of the system is obtained numerically by the following relation:

$$ S={\int\limits_{0}^{T}}\frac{C_{h}}{T^{^{\prime }}}dT^{^{\prime }}. $$

(17)

The free energy of the system is defined as:

$$ F=U-TS. $$

(18)

By solving all these equations numerically, we can easily obtain the magnetic and the thermodynamic properties of the nanocube system.

3 Numerical Results and Discussions

In this section, we investigate the magnetic and thermodynamic properties of our system within the formulations given in Section 2. Toward this end, we take J _c as a unit of the energy and we define the reduced exchange interactions and transverse fields as (r _{c s} =J _{c s} /J _c , r _s =J _s /J _c , ω _s =Ω _s /J _c , and ω _c =Ω _c /J _c ).

The effect of the core/shell antiferromagnetic interfacial coupling on the magnetic and thermal properties of the particle is examined in Figs. 2, 3, 4, 5, and 6 for some selected values of r _{c s} (r _{c s} =−0.1, −0.3, and −0.5) and with a fixed value of r _s =0.05, ω _s =0.2, and ω _c =0.8. Also, the phase diagram (k _B T _{c o m p} /J _c , k _B T _c /J _c −r _{c s} ) of the particle is plotted in Fig. 7 for the same physical parameters as those in the latter figures.

Fig. 2

Effect of the core/shell antiferromagnetic interfacial coupling r _{c s} on the temperature dependence of the total magnetization of the system for r _s =0.05, ω _s =0.2, and ω _c =0.8

Fig. 3

Effect of the core/shell antiferromagnetic interfacial coupling r _{c s} on the temperature dependence of the internal energy of the system for r _s =0.05, ω _s =0.2, and ω _c =0.8

Fig. 4

Effect of the core/shell antiferromagnetic interfacial coupling r _{c s} on the temperature dependence of the specific heat of the system for r _s =0.05, ω _s =0.2, and ω _c =0.8

Fig. 5

Effect of the core/shell antiferromagnetic interfacial coupling r _{c s} on the temperature dependence of the entropy of the system for r _s =0.05, ω _s =0.2, and ω _c =0.8

Fig. 6

Effect of the core/shell antiferromagnetic interfacial coupling r _{c s} on the temperature dependence of the free energy of the system for r _s =0.05, ω _s =0.2, and ω _c =0.8

Fig. 7

Phase diagram of the system in (k _B T _{c o m p} /J _c , k _B T _c /J _c −r _{c s} ) plane for r _s =0.05, ω _s =0.2 and ω _c =0.8

In Fig. 2, we depict the temperature dependence of the total magnetization M _T . As seen from this figure, there are two zeros in magnetization curves for different r _{c s} values. The first one corresponds to the compensation temperature, whereas the second occurs at the critical temperature of the system. The existence of the compensation temperature is a typical characteristic of the antiferromagnetic materials behavior, namely the N-type [34]. The compensation point has also been obtained theoretically in Refs. [15, 28, 35, 36] and experimentally by Estrader et al. [3] for the magnetization of the core/shell particles based on F e-oxides and M n-oxides. We can clearly see, at zero temperature, that the M _T curves have three saturation magnetizations M _{s a t} =−0.218, −0.342, and −0.369 when the core/shell antiferromagnetic interfacial coupling are selected as r _{c s} =−0.1, −0.3, and −0.5, respectively, which indicate that the saturation value of the total longitudinal magnetization decreases with the decrease of r _{c s} .

Figure 3 shows the internal energy versus reduced temperature (k _B T/J _c ). One can see that the internal energy curves have a fluctuation at the compensation temperatures and present a discontinuity of the curvature at the critical temperatures. In addition, for any fixed value of k _B T/J _c , the weaker exchange interaction between the core and shell makes the internal energy U decreasing.

On the other hand, we present the specific heat of the particle in Fig. 4. It is clearly seen from this figure that the curves of the specific heat curves exhibit two peaks. The first one which has a rounded shape corresponds to the compensation temperature, while the second one occurs at the critical temperature. It is also seen that these peaks move to high temperatures as the absolute value of r _{c s} increases, confirming that the compensation and the critical temperatures increase with the increase of the absolute value of the interfacial exchange interaction. We can also notice from this figure that the specific heat is higher in the ordered state than in the disordered one.

Figure 5 shows the effect of r _{c s} on the entropy of the system. It is clearly seen from this figure that at k _B T/J _c =0.0, the entropy of the system is equal to zero and it increases with increasing the temperature in order to minimize the free energy of the system as clearly shown in Fig. 6 which presents the free energy of the particle as a function of reduced temperature. We can also see from the last figure that the free energy curves do not exhibit a discontinuous behavior at the critical temperature. Therefore, we can notice that the system presents only a second order transition. We can also notice from the Fig. 6 that the free energy is equal to the internal energy at the ground state (k _B T/J _c =0.0), which is obvious, because the entropy gives a minor contribution to the free energy at low temperatures as it is mentioned above.

In order to investigate the influence of r _{c s} on both critical and compensation temperatures of the nanocube, we have plotted the phase diagram (k _B T _{c o m p} /J _c , k _B T _c /J _c −r _{c s} ) of the particle in Fig. 7, which represents the variation of the critical and the compensation temperatures of the system with r _{c s} . We can clearly see from this figure that the curve of k _B T _c /J _c divides the phase diagram into two regions, the ordered one is named an antiferromagnetic phase, whereas the other which is disordered is named a paramagnetic phase. We can also see from this figure that both the compensation and critical temperatures of the system increase as the absolute value of r _{c s} increases. The behavior of these curves is similar with that obtained by Yüksel et al. [35] for a ferrimagnetic NP with spin-$\frac {3}{2}$ core and spin-1 shell structure.

4 Conclusion

In this work, we have investigated the effect of core/shell antiferromagnetic interfacial coupling on the magnetic and the thermodynamic properties of an antiferromagnetic Ising nanocube by using the EFT based on the probability distribution technique with correlations. We have found that r _{c s} has strong effects on these properties for a given parameters. It is observed that the magnetization curves show the existence of the N-type behavior in which one compensation temperature appears below the transition temperature. We can conclude from the above section that the compensation and critical temperatures increase with increasing the absolute value of r _{c s} and the system exhibits just a second-order phase transition as it is confirmed by the free energy.

Appendix: Equations of the Core and Surface Shell Magnetizations

Within the framework of the effective field theory with correlations, four longitudinal magnetizations on the core, namely $m_{c_{1}}^{z}$, $m_{c_{2}}^{z}$, $m_{c_{3}}^{z}$, and $m_{c_{4}}^{z}$, and six longitudinal magnetizations on the surface shell, namely $m_{s_{1}}^{z}$, $m_{s_{2}}^{z}$ , $m_{s_{3}}^{z}$, $m_{s_{4}}^{z}$, $m_{s_{5}}^{z}$ and $m_{s_{6}}^{z}$, can be obtained as:

Magnetization of the central spin c ₁:

$$\begin{array}{@{}rcl@{}} m_{c_{1}}^{z} &=&\frac{1}{2^{(2N_{3})}}\sum\limits_{\mu_{1}=0}^{N_{3}}\sum\limits_{\mu_{2}=0}^{N_{3}}C_{\mu _{1}}^{N_{3}}C_{\mu_{2}}^{N_{3}}\left( 1-m_{c_{2}}^{z}\right)^{\mu_{1}}\left( 1+m_{c_{2}}^{z}\right)^{N_{3}-\mu_{1}} \\ &&\times \left( 1-m_{s_{4}}^{z}\right)^{\mu_{2}}\left( 1+m_{s_{4}}^{z}\right)^{N_{3}-\mu_{2}}\times f_{z}(J_{c}(N_{3}-2\mu_{1}) \\ &&+J_{cs}(N_{3}-2\mu_{2})+h,{\Omega}_{c}) \end{array} $$

(19)

Magnetization of the central spin c ₂:

$$\begin{array}{@{}rcl@{}} m_{c_{2}}^{z} &=&\frac{1}{2^{(3N_{2})}}\sum\limits_{\mu_{1}=0}^{N_{2}}\sum\limits_{\mu_{2}=0}^{N_{2}}\sum\limits_{\mu _{3}=0}^{N_{2}}C_{\mu_{1}}^{N_{2}}C_{\mu_{2}}^{N_{2}}C_{\mu_{3}}^{N_{2}}\left( 1-m_{c_{1}}^{z}\right)^{\mu_{1}}\left( 1+m_{c_{1}}^{z}\right)^{N_{2}-\mu_{1}} \\ &&\times \left( 1-m_{c_{3}}^{z}\right)^{\mu_{2}}\left( 1+m_{c_{3}}^{z}\right)^{N_{2}-\mu_{2}}\left( 1-m_{s_{5}}^{z}\right)^{\mu_{3}}\left( 1+m_{s_{5}}^{z}\right)^{N_{2}-\mu_{3}} \\ &&\times f_{z}(J_{c}(2N_{2}-2(\mu_{1}+\mu_{2}))+J_{cs}(N_{2}-2\mu_{3})+h,{\Omega}_{c}) \end{array} $$

(20)

Magnetization of the central spin c ₃:

$$\begin{array}{@{}rcl@{}} m_{c_{3}}^{z} &=&\frac{1}{2^{(2N_{1}+N_{4})}}\sum\limits_{\mu_{1}=0}^{N_{4}}\sum\limits_{\mu _{2}=0}^{N_{1}}\sum\limits_{\mu_{3}=0}^{N_{1}}C_{\mu_{1}}^{N_{4}}C_{\mu_{2}}^{N_{1}}C_{\mu_{3}}^{N_{1}}\left( 1-m_{c_{2}}^{z}\right)^{\mu_{1}}\left( 1+m_{c_{2}}^{z}\right)^{N_{4}-\mu_{1}} \\ &&\times \left( 1-m_{c_{4}}^{z}\right)^{\mu_{2}}\left( 1+m_{c_{4}}^{z}\right)^{N_{1}-\mu_{2}}\left( 1-m_{s_{6}}^{z}\right)^{\mu_{3}}\left( 1+m_{s_{6}}^{z}\right)^{N_{1}-\mu_{3}} \\ &&\times f_{z}(J_{c}(N_{4}+N_{1}-2(\mu_{1}+\mu_{2}))+J_{cs}(N_{1}-2\mu_{3})+h,{\Omega}_{c}) \end{array} $$

(21)

Magnetization of the central spin c ₄:

$$\begin{array}{@{}rcl@{}} m_{c_{4}}^{z} &=&\frac{1}{2^{(N_{6})}}\sum\limits_{\mu_{1}=0}^{N_{6}}C_{\mu_{1}}^{N_{6}}\left( 1-m_{c_{3}}^{z}\right) ^{\mu_{1}}\left( 1+m_{c_{3}}^{z}\right)^{N_{6}-\mu_{1}} \\ &&\times f_{z}(J_{c}(N_{6}-2\mu_{1})+h,{\Omega}_{c}) \end{array} $$

(22)

Magnetization of the surface spin s ₁:

$$\begin{array}{@{}rcl@{}} m_{s_{1}}^{z}&=&\frac{1}{2^{N_{3}}}\sum\nolimits_{\mu_{1}=0}^{N_{3}}C_{\mu_{1}}^{N_{3}}\left( 1-m_{s_{2}}^{z}\right) ^{\mu_{1}}\!\left( 1+m_{s_{2}}^{z}\right)^{N_{3}-\mu_{1}} \\&&\times f_{z}(J_{s}(N_{3}-2\mu_{1})+h,{\Omega}_{s}) \end{array} $$

(23)

Magnetization of the surface spin s ₂:

$$\begin{array}{@{}rcl@{}} m_{s_{2}}^{z} &=&\frac{1}{2^{(2N_{1}+N_{2})}}\sum\limits_{\mu_{1}=0}^{N_{1}}\sum\limits_{\mu _{2}=0}^{N_{1}}\sum\limits_{\mu_{3}=0}^{N_{2}}C_{\mu_{1}}^{N_{1}}C_{\mu_{2}}^{N_{1}}C_{\mu_{3}}^{N_{2}}\left( 1-m_{s_{1}}^{z}\right)^{\mu_{1}}\left( 1+m_{s_{1}}^{z}\right)^{N_{1}-\mu_{1}} \\ &&\times \left( 1-m_{s_{3}}^{z}\right)^{\mu_{2}}\left( 1+m_{s_{3}}^{z}\right)^{N_{1}-\mu_{2}}\left( 1-m_{s_{4}}^{z}\right)^{\mu_{3}}\left( 1+m_{s_{4}}^{z}\right)^{N_{2}-\mu_{3}} \\ &&\times f_{z}(J_{s}(2N_{1}+N_{2}-2(\mu_{1}+\mu_{2}+\mu_{3}))+h,{\Omega}_{s}) \end{array} $$

(24)

Magnetization of the surface spin s ₃:

$$\begin{array}{@{}rcl@{}} m_{s_{3}}^{z} &=&\frac{1}{2^{2N_{2}}}\sum\nolimits_{\mu_{1}=0}^{N_{2}}\sum\nolimits_{\mu_{2}=0}^{N_{2}}C_{\mu _{1}}^{N_{2}}C_{\mu_{2}}^{N_{2}}\left( 1-m_{s_{2}}^{z}\right)^{\mu_{1}} \\ &&\times \left( 1+m_{s_{2}}^{z}\right)^{N_{2}-\mu_{1}}\!\left( 1-m_{s_{5}}^{z}\right)^{\mu_{2}}\!\left( 1+m_{s_{5}}^{z}\right)^{N_{2}-\mu _{2}}\\&&\times f_{z}(J_{s}(2N_{2}-2(\mu_{1}+\mu_{2}))+h,{\Omega}_{s}) \end{array} $$

(25)

Magnetization of the surface spin s ₄:

$$\begin{array}{@{}rcl@{}} m_{s_{4}}^{z} &=&\frac{1}{2^{(N_{1}+2N_{2})}}\sum\limits_{\mu_{1}=0}^{N_{1}}\sum\limits_{\mu _{2}=0}^{N_{2}}\sum\limits_{\mu_{3}=0}^{N_{2}}C_{\mu_{1}}^{N_{1}}C_{\mu_{2}}^{N_{2}}C_{\mu_{3}}^{N_{2}}\left( 1-m_{c_{1}}^{z}\right)^{\mu_{1}}\left( 1+m_{c_{1}}^{z}\right)^{N_{1}-\mu_{1}} \\ &&\times \left( 1-m_{s_{2}}^{z}\right)^{\mu_{2}}\left( 1+m_{s_{2}}^{z}\right)^{N_{2}-\mu_{2}}\left( 1-m_{s_{5}}^{z}\right)^{\mu_{3}}\left( 1+m_{s_{5}}^{z}\right)^{N_{2}-\mu_{3}} \\ &&\times f_{z}(J_{s}(2N_{2}-2(\mu_{2}+\mu_{3}))+J_{cs}(N_{1}-2\mu_{1})+h,{\Omega}_{s}) \end{array} $$

(26)

Magnetization of the surface spin s ₅:

$$\begin{array}{@{}rcl@{}} m_{s_{5}}^{z} &=&\frac{1}{2^{(3N_{1}+N_{2})}}\sum\limits_{\mu_{1}=0}^{N_{1}}\sum\limits_{\mu _{2}=0}^{N_{1}}\sum\limits_{\mu_{3}=0}^{N_{2}}\sum\limits_{\mu_{4}=0}^{N_{1}}C_{\mu_{1}}^{N_{1}}C_{\mu _{2}}^{N_{1}}C_{\mu_{3}}^{N_{2}}C_{\mu_{4}}^{N_{1}} \\ &&\times\left( 1-m_{c_{2}}^{z}\right)^{\mu_{1}}\left( 1+m_{c_{2}}^{z}\right)^{N_{1}-\mu_{1}} \left( 1-m_{s_{3}}^{z}\right)^{\mu_{2}} \\ &&\times\left( 1+m_{s_{3}}^{z}\right)^{N_{1}-\mu_{2}}\left( 1-m_{s_{4}}^{z}\right)^{\mu_{3}}\left( 1+m_{s_{4}}^{z}\right)^{N_{2}-\mu_{3}} \\ &&\times \left( 1-m_{s_{6}}^{z}\right)^{\mu_{4}}\left( 1+m_{s_{6}}^{z}\right)^{N_{1}-\mu_{4}}f_{z}(J_{s}(2N_{1}+N_{2}\\&&\qquad-2(\mu_{2}+\mu_{3}+\mu_{4})) \\ &&+J_{cs}(N_{1}-2\mu_{1})+h,{\Omega}_{s}) \end{array} $$

(27)

Magnetization of the surface spin s ₆:

$$\begin{array}{@{}rcl@{}} m_{s_{6}}^{z} &=&\frac{1}{2^{(N_{1}+N_{4})}}\sum\limits_{\mu_{1}=0}^{N_{1}}\sum\limits_{\mu_{2}=0}^{N_{4}}C_{\mu _{1}}^{N_{1}}C_{\mu_{2}}^{N_{4}}\left( 1-m_{c_{3}}^{z}\right)^{\mu_{1}}\\&&\times\left( 1+m_{c_{3}}^{z}\right)^{N_{1}-\mu _{1}} \left( 1-m_{s_{5}}^{z}\right)^{\mu_{2}} \\ &&\times \left( 1+m_{s_{5}}^{z}\right)^{N_{4}-\mu_{2}}f_{z}(J_{s}(N_{4}-2\mu_{2})\\&&+J_{cs}(N_{1}-2\mu_{1})+h,{\Omega}_{s}) \end{array} $$

(28)

With N ₁=1, N ₂=2, N ₃=3, N ₄=4 and N ₆=6 denote respectively the coordination number, and ${C_{k}^{l}}$ are the binomial coefficients ${C_{k}^{l}}=\frac {l!}{k!(l-k)!}$.