1 Introduction

Magnetic nanoparticles have attracted much attention in recent decades because of their excellent magnetic properties, and with their small size, the study of the magnetic and thermal characteristics of nanoparticles such as nanos- phere, nanotube, and nanocube using several types of methods [1,2,3,4,5] was theoretically and experimentally investigated. Vasilakaki et al. [6] studied in detail the thermal and magnetic transition properties of core/shell antiferromagnetic/ferrimagnetic nanoparticles using the Monte Carlo simulation technique with the Metropolis algorithm. Magnetic phase transitions and hysterical characteristics of a core/shell nanometry based on the MC simulation method have been studied [7,8,9,10,11,12]. An interesting property in these magnetic systems is the presence of a compensating temperature in which all magnetization is zero at a temperature below the critical temperature [13,14,15,16]. This point of compensation at the finite temperature is only found when the near-neighbor interaction between the spin σ = ±3 /2 and ±1 /2 and the spin S = ±7 /2, + 5 /2, ±3 /2, and ±1 /2 is taken into consideration. It is pointed out that for appropriate values of the system parameters, the multiple compensation and transition temperatures vary with the change in the particle size value. Wang et al. [17] determined the phase diagram of Ising nanoparticles with cubic structures. Our system consists of two different species of magnetic spin components, the spin σ and the spin S with antiferromagnetic interface coupling (Fig. 1). We perform the MC simulation using the Metropolis algorithm and determine the radius effects of the spherical nanoparticle, probability (p) of impurity, and other system parameters on the phase

transition characteristics of the system under consideration. The outline of this article is as follows: in Section 2, we present our model. The results and discussions are given in Section 3, and, finally, Section 4 contains our conclusions.

Fig. 1
figure 1

Schematic representation of the system

Full size image

2 Model and Monte Carlo Simulation

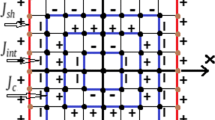
The system is a core/shell nanoparticle of two concentric spheres of radius R C and R S, respectively; we apply free boundary conditions in all directions. The Hamiltonian of the system is given as:

$$\begin{array}{@{}rcl@{}} H&=&-J_{\mathrm{C}} \sum\limits_{ij} {\sigma_{i} \sigma_{j} } -J_{\mathrm{S}}\sum\limits_{ij} {\varepsilon_{i}\varepsilon_{j} S_{i} S_{j} } -J_{\text{int}} \sum\limits_{ij} {\sigma_{i} \varepsilon_{j} S_{j} }\\ &&-H\sum\limits_{j}{(\sigma_{j} +\varepsilon_{j} S_{j}})-{\Delta} \sum\limits_{j} {\varepsilon_{j} {S_{j}^{2}}}\end{array} $$
(1)

The interaction between two neighboring atoms belonging to the same zone of radius r ≤ R C or radius R C ≤ r ≤ R S is ferromagnetic whereas the interaction between an atom belonging to the radius zone r ≤ R C and an atom belonging to the radius zone R C < r ≤ R S is antiferromagnetic. The radius area R C < r ≤ R S is randomly diluted with a p to model the presence of a nonmagnetic impurity among S-type atoms. ε j takes 1 if site j is occupied and take 0 if the site is unoccupied. The J C, J S, and J int are the exchange interaction parameters between σ and σ, S and S, and σ and S, respectively. We used the parameter k B T/J C where k B is the Boltzmann constant which is equal to unity. The moment values of the spins are σ= ±3/2 and ±1/2 and S = ± 7/2, ±5/2, ±3/2, and ±1 /2. The quantities defined below were calculated using Monte Carlo simulations and used to estimate the critical and compensation temperatures for the model.

Our data were generated with 10 4 Monte Carlo steps per spin. We take a nanoparticle of a core radius R C = 6 and a shell thickness R S = 2; the number of spins in the core is N C = 925, and the number of spins in the shell is N S = p.1184 (N = N C + N S = 2109).

The magnetizations:

$$ m_{\mathrm{C}} =\frac{1}{N_{\mathrm{C}}}\sum\limits_i{\sigma_{i}} $$
(2)
$$ m_{\mathrm{S}} =\frac{1}{N_{\mathrm{S}} }\sum\limits_{j} {\varepsilon_{j}S_{j}} $$
(3)

The total magnetization:

$$\begin{array}{@{}rcl@{}} m_{\text{tot}} =\frac{1}{2}({m_{\mathrm{C}}}+{pm_{\mathrm{S}}} ) \end{array} $$
(4)

The internal energy per site:

$$\begin{array}{@{}rcl@{}} E=\frac{\left\langle H \right\rangle }{N_{\mathrm{C}} +N_{\mathrm{S}}} \end{array} $$
(5)

3 Results and Discussion

Figure 2 (a1, a2) shows the phase diagram of the ground state (Δ, H) which shows the existence of 20 configurations ((− 1/2, − 1/2), (− 3/2, − 1/2), (− 1/2, 1/2), (− 3/2, 1/2), (1/2, − 1/2), (3/2, − 1/2), (1/2, 1/2), (3/2, 1/2), (− 3/2, − 3/2), (− 3/2, − 5/2), (− 3/2, − 7/2), (− 3/2, 3/2), (− 3/2, 5/2), (3/2, − 7/2)), (3/2, 3/2), (3/2, 5/2), (3/2, 7/2), (3/2, − 3/2), (3/2, − 5/2), (− 3/2, 7/2)), which are stable.

Fig. 2
figure 2

The ground-state phase diagram: a in the plane (Δ, H), b in the plane (J int, H), and c in the plane (J S, H) (J C = 1.0, J S = 0.1, and J int = −1.0)

Full size image

The phase diagram of the ground state (J int, H) shows the existence of four configurations ((− 3/2, 7/2), (3/2, 7/2), (3/2, − 7/2), (− 3/2, − 7/2)), which are stable for J int < 0 and H > 0; J int > −2 and H > 0; J int < 0 and H < 0; and J int > −2 and H < 0, respectively (Fig. 2 (b)).

Figure 2 (c) illustrates the phase diagram of the ground state (J S, H) which shows the existence of 16 configurations ((− 3/2, − 1/2), (− 3/2, 1 /2), (3 /2, − 1/2), (3 /2, 1 /2), (− 3/2, − 3/2), (− 3/2, − 5/2), (− 3/2, − 7/2), (− 3/2, 3 /2), (− 3/2, 5 /2), (3 /2, − 7/2), (3 /2, 3 /2), (3 /2, 5 /2), (3 /2, 7 /2), (3 /2, − 3/2), (3 /2, − 5/2), (− 3/2, 7 /2)), which are stable.

Figure 3a presents the total magnetization with respect to the reduced temperature k B T/ J C; it can be seen that the magnetization curves have two zeros. The first corresponds to the temperature value at which the total magnetization (m T) reduces to zero, while the subnetworks m C and m S are different from zero; it corresponds to the compensation temperature (T comp). The second zero indicates the temperature at which the m T, m C, and m S magnetizations decrease to zero; it corresponds to the critical temperature of the system Cuirie temperature (T C). For p = 0.7, J S/J C = 0.1 and J int/J C = −0.1 show a T comp such that m T = 0 and 0 < T comp < T C. Figure 3b shows that for p = 0.7, J S/J C = 0.3 and J int/J C = −0.1 show no compensation effect. Figure 3c shows that for p = 0.42, J S/J C = 0.1 and J int/J C = −0.1 shows no compensation effect. Figure 3d presents that the total magnetization is a function of temperatures for different probabilities (J S/J C = 0.1, J int/J C = −0.1, and Δ = 0).

Fig. 3
figure 3

Core magnetizations (m C ), sell magnetizations (m S ), and total magnetization (m T ) for various temperatures (k B T/ J C) for p = 0.7: a J S/ J C = 0.1, J int/ J C = −0.1, and Δ = 0; b for p = 0.7: J S/ J C = 0.3, J int / J C = −0.1, and Δ = 0; and c for p = 0.42: J S/ J C = 0.1, J int/ J C = −0.1, and Δ = 0. d Total magnetizations is a function of temperatures: J S/ J C = 0.1, J int/ J C = −0.1, and Δ = 0

Full size image

In order to study the influence of J S/J C on both critical and system compensation temperatures, the phase diagram is plotted in Fig. 4a, in the plane (T, J S/J C). It may be noted that as the value of J S/J C increases, the T C remains constant; for compensation, it exists only when J S/J C is less than 0.3 and increases linearly with J S/J C.

Fig. 4
figure 4

Critical temperatures (T C ) and compensation temperatures (T c o m p ) is a function probability (p) for a J S/J C = 0.7 and J int/ J C = −0.1, b J int/ J C = 0.3 and J S/J C = 0.4, and c J int/J C = −0.1 and J S/J C = 0.2

Full size image

In the plane (T, J int/J C), the absolut value |J int/J C| increases and the T C increases; for compensation, it exists only when |J int/J C| is less than 2.6 and increases linearly with |J int/J C| (Fig. 4b).

The T C remains constant, and the temperature compensation increases slightly with the p (Fig. 4c).

Figure 5a, b shows that the region of the magnetic hysteresis cycle decreases with increasing temperature and disappears completely for T = 6.0

Fig. 5
figure 5

Magnetic hysteresis cycle for different values of temperatures for a p = 0.7, J S/ J C = 0.1, J int/J C = −0.1, and Δ = 0 and b p = 0.7, J S/J C = 0.1, J int/J C = −0.1, and Δ = −1.0

Full size image

4 Conclusions

In this work, we used the Monte Carlo simulation using the Metropolis algorithm to study the phase diagrams and the thermal and magnetic properties of a diluted system. We studied the influences of interactions between crystal fields, interfacial interaction, and exchange interaction on critical behaviors and system compensation for a spherical nanoparticle. It can be seen that, depending on the set of Hamiltonian parameters, we can have different types of topologies of phase diagrams with many interesting phenomena. As regards the compensation temperature, we have shown that it exists only within a certain range of system parameters; this range depends closely on the Hamiltonian parameters.