1 Introduction

The Blume-Emery-Grifftihs (BEG) model is a spin-1 Ising model with nearest-neighbor interactions and up-down symmetry and has originally been studied in the context of superfluidity and phase separation in helium mixtures [1]. Since then, many variations of this model were carried out by using different techniques to investigate its various aspects.

It’s phase diagrams were studied by using Monte Carlo (MC) simulations [2], reentrant behavior by using real space renormalization group [3], multicritical phase diagrams by the mean-field theory [4], new phases and multiple re-entrance behavior in terms of MC renormalization-group theory [5], random-anisotropy effects by using mean-field theory, transfer-matrix calculations, and position-space renormalization-group calculations [6], the model on the square lattice using a real-space renormalization group procedure [7], global Bethe lattice consideration in terms of exact recursion relations [8], phase diagrams on the simple cubic lattice by the linear chain approximation [9], MC study at the ferromagnetic-antiquadrupolar-disordered phase interface [10], the ferrimagnetic phase on the cellular automaton [11], magnetic behavior in one dimension by means of the Green’s functions and equations of motion formalism [12], the phase diagrams on simple-cubic lattice investigated using mean field theory and MC simulation [13], and so on.

Fig. 1
figure 1

The phase diagrams on the (K,T) planes for given values of p when α=−1.0 corresponding to the ±J model a q=3.0, b q=4.0, and c q=6.0

Full size image

In recent years, there has been considerable interest in understanding the effects of randomness on phase transitions. A new decoration method was presented which allows the quenched spin-1 Ising model on a regular lattice along a line in the plane of exchange interaction parameters versus temperature to be mapped onto a certain class of mixed-spin decorated-lattice problem [14]. The equilibrium properties of the BEG model with bilinear quenched disorder were studied for both attractive and repulsive biquadratic interactions [15]. The three-dimensional ±J Ising spin model with uniform biquadratic exchange interaction, K, was studied by MC simulations [16]. The spin-1 ±J Ising model with uniform biquadratic couplings on simp]e cubic lattice was studied by the non-equilibrium relaxation and the equilibrium MC methods [17]. The spin-1 ±J Ising model with uniform biquadratic couplings on a simple cubic lattice was studied by the MC simulation using the non-equilibrium relaxation method [18]. The critical behavior of the spin-1 bond and crystal field dilution of the BEG model have been investigated on simple cubic lattice within the framework of the effective field theory (EFT) [19]. The spin-1 BEG spin-glass model was studied by using the extended mean-field renormalization group approximation and the pair approximation based on Bogoliubov inequality for the free energy [20]. ±J model was exploited on the Bethe lattice for the spin-1 Blume-Capel model [21].

The spin-1 BEG model gives a staggered quadrupole (SQ) phase, which owes its existence to the biquadratic exchange interaction K, in addition to the other regular phases. There are some works indicating the existence of this phase as follows: A SQ phase for a spin-1 Ising system with K and anisotropic energy was studied by using the MC simulation and it was found that for SQ phase to be seen the addition of J is not necessary [22]. The spin-1 Ising model on the simple cubic lattice with bilinear and biquadratic interactions and anisotropic energy was investigated and it was found that SQ phase occurs as long as K is negative large enough [23]. The re-entrant phase transition of the BEG model with no bilinear interaction was studied by mapping into the spin-1/2 Ising model [24]. EFT based on a finite cluster theory that correctly incorporates the single-site kinematic relations was applied to the BEG model with positive K interactions in order to test its ability to deal with magnetic systems having competing interactions [25]. The spin-1 BEG model was studied using the mean field theory for a thin film [26]. The SQ ordering of the biquadratic exchange model on layered square lattices was examined, and it was found that the ground state are multiply degenerated in this model, the SQ phase appears at sufficiently low finite temperatures on the three-dimensional lattice but does not appear on the two-dimensional lattice [27]. Within the EFT, the SQ phase and bicritical point of spin-1 bond and anisotropy dilution of the BEG model was studied on simple cubic lattice in the restricted range of K and J interaction ratio α≤-1 [28].

In this work, the spin-1 model with J and K exchange interactions is analyzed on the Bethe lattice (BL) in terms of exact recursion relations. By using a bimodal random distribution with an adjustable parameter α, we study both ±J-model and bond-dilution. The possible phase diagrams of the model are obtained by studying the thermal variations of order-parameters. It was found that the model gives second-order phase transitions line which separate the ferromagnetic (F) or antiferromagnetic (AF) phases from the paramagnetic (P) phase. The staggered quadrupolar phase is also found at high enough negative K values and the lines of which are also separated from the P phase.

The rest of the work is set up as follows: Section 2 is devoted to the formulation on the BL. Section 3 contains the results, i.e., the phase diagrams, and their discussions and, a brief summary.

2 The Thermodynamic Functions in Terms of Exact Recursion Relations

In order to simulate the random J model, we assume a bimodal distribution of J interactions given in the form as

$$ P({J_{ij}})=p\delta({J_{ij}}-J)+(1-p)\delta({J_{ij}-\alpha{J}}) $$
(1)

where the first term turns on the J interactions ferromagnetically with probability p and the second term with an adjustable parameter α either turns on J interactions ferromagnetically (α>0) or antiferromagnetically (α<0) or turns off J interactions (α=0) with probability 1−p.

This distribution is to be applied to the thermodynamic functions obtained from the Hamiltonian containing only J and K interactions acting only nearest-neighbor sites on the BL and given as

$$ \mathcal{H} = -{\sum}_{<ij>} J_{ij} S_{i} S_{j}-K {\sum}_{<ij>}{S_{i}^{2}} {S_{j}^{2}}. $$
(2)

with S i taking the values ±1 and 0 for the spin-1.

In order to obtain the phase diagrams for the given system parameters, first the order-parameters must be obtained in terms of the recursion relations on the BL. In doing so, one should start with the partition function as in many statistical physics problems which is given as

$$\begin{array}{@{}rcl@{}} Z &=& \sum\limits_{All\hspace{0.15 cm}Config.}\ e^{-\beta \mathcal{H}} = {\sum}_{Spc}\ P(Spc), \end{array} $$
(3)

where P(S p c) can be thought of as an unnormalized probability distribution and β=1/(k T), k is the Boltzmann constant which is set equal to 1 for convenience.

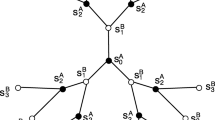
After some straightforward calculations on the BL [21], the recursion relations are found from the ratios of partial partition functions, g n ’s, and are given as

$$\begin{array}{@{}rcl@{}} X^{(ij)}_{n} &=& \frac{g_{n}(+1)}{g_{n}(0)}\\ &=&\frac{e^{\beta(J_{ij}+K)}[X_{n-1}^{(ij)}]^{q-1} +e^{\beta(-J_{ij}+K)}[Y_{n-1}^{(ij)}]^{q-1}+1} {[X_{n-1}^{(ij)}]^{q-1}+[Y_{n-1}^{(ij)}]^{q-1}+1}, \\ Y^{(ij)}_{n} &=& \frac{g_{n}(-1)}{g_{n}(0)}\\ &=&\frac{e^{\beta(-J_{ij}+K)}[X_{n-1}^{(ij)}]^{q-1} +e^{\beta(J_{ij}+K)}[Y_{n-1}^{(ij)}]^{q-1}+1} {[X_{n-1}^{(ij)}]^{q-1}+[Y_{n-1}^{(ij)}]^{q-1}+1}\\ \end{array} $$
(4)

where q is the number of the nearest-neighbors, i.e., coordination number.

It should be mentioned that an averaging procedure must be carried out over the bilinear interaction distribution P(J i j ) to get the correct recursion relations for the random J model, i.e.,

$$\begin{array}{@{}rcl@{}} X_{n} &=& \int X_{n}^{(ij)} P(J_{ij}) dJ_{ij}=\int X_{n}^{(ij)} [p \delta(J_{ij}-J)\\ &&+(1-p) \delta(J_{ij}-\alpha J)] dJ_{ij}, \\ Y_{n} &=& \int Y_{n}^{(ij)} P(J_{ij}) dJ_{ij}=\int Y_{n}^{(ij)} [p \delta(J_{ij}-J)\\ &&+(1-p) \delta(J_{ij}-\alpha J)] dJ_{ij}. \end{array} $$
(5)

Note also that in order to study the AF interactions, one needs to partition the BL into two sub-lattices A and B, therefore, the recursion relations take the form

$$\begin{array}{@{}rcl@{}} &&{X_{n}^{A}}=f(X_{n-1}^{B}, Y_{n-1}^{B}), \\ && {Y_{n}^{B}}=f(X_{n-2}^{A}, Y_{n-2}^{A}). \end{array} $$
(6)

Since all the sites are equivalent deep inside the BL, one can pick a central spin, S 0, and calculate its order parameters accordingly. Thus, the first-order parameter, i.e., magnetization, is given in terms of the recursion relations for the sub-lattices respectively as

$$\begin{array}{@{}rcl@{}} M_{A}=\frac{[{X_{n}^{A}}]^{q}-[{Y_{n}^{A}}]^{q}}{[{X_{n}^{A}}]^{q}+[{Y_{n}^{A}}]^{q}+1} \end{array} $$
(7)

and

$$\begin{array}{@{}rcl@{}} M_{B}=\frac{[X_{n-1}^{B}]^{q}-[Y_{n-1}^{B}]^{q}}{[X_{n-1}^{B}]^{q}+[Y_{n-1}^{B}]^{q}+1} \end{array} $$
(8)

and the quadrupolar moments for the sub-lattices are given as

$$\begin{array}{@{}rcl@{}} Q_{A}=\frac{[{X_{n}^{A}}]^{q}+[{Y_{n}^{A}}]^{q}}{[{X_{n}^{A}}]^{q}+[{Y_{n}^{A}}]^{q}+1} \end{array} $$
(9)

and

$$\begin{array}{@{}rcl@{}} Q_{B}=\frac{[X_{n-1}^{B}]^{q}+[Y_{n-1}^{B}]^{q}}{[X_{n-1}^{B}]^{q}+[Y_{n-1}^{B}]^{q}+1}. \end{array} $$
(10)

To obtain the phase diagrams, the thermal variation of the order parameters is to be studied. The procedure is as follows: first the recursion relations are calculated by using an iteration scheme, then the found values of the recursion relations are inserted into the definitions of the order-parameters to obtain their thermal variations for given K, q and p. Thus, the next section is devoted to the phase diagrams of the model in addition to our results, discussions and comparisons whenever possible.

3 The Phase Diagrams, Results, and Comparisons

The phase diagrams of the model are calculated for q=3,4, and 6 which correspond to the honeycomb, square, and simple cubic lattices, respectively. The solid lines, T c -lines, separate the ordered phases F and AF from the P phase while the dotted-dashed lines, T S Q -lines, separate the SQ phase from the P phase. Note also that the SQ lines are the combinations of points at which magnetization is zero and the sublattice quadrupolar moments, Q A and Q B , coincide.

Figure 1 is obtained for α=−1.0 corresponding to the ±J model on the (K,T) planes for given values of p. The T c -lines emerge from about K=−1.0 at T=0.0, the temperatures of which increase as K, p, and q increase. Further increase of K stabilizes the lines at constant T’s which are higher for higher p and q. The T S Q -lines are only seen for q=4 and 6 which also emerge from K=−1.0 at T=0.0, but extends towards higher negative K’s. They have the same values for all p and increase in temperature for higher q. The reentrant behavior is only seen for q=6 when p=1, see Fig. 1c. These figures are similar with Fig. 4 of [17] and Fig. 3 of [18]. The T c -lines can also be compared with Fig. 2 of [3].

Figure 2 are also obtained for α=−1.0, i.e., ±J model, on the (p,T) planes for given values of K. The T c and T S Q -lines are symmetric with respect to p=0.5, since AF phase is dominant for \(p=0.5\rightarrow 0.0\) and F phase for \(p=0.5\rightarrow 1.0\) as seen from Eq.(1). When q=3.0, only T c -lines are seen separating AF and F phases from the P phase for left and right of K=0.5, respectively. All the lines converge to same p at zero temperature in the AF and F regions. We still see the same behavior for the T c -lines when q=4.0 and 6.0, but for the latter the K=−1.0 line is separated from the rest. In addition, the T c -lines extend further towards p=0.5 with increasing q. It should also be mentioned that the T S Q -lines are also seen as straight lines for both q=4.0 and 6.0, which increase in temperature as K increases negatively, but for these values of K no T c -lines are seen.

Fig. 2
figure 2

The phase diagrams on the (p,T) planes for given values of K when α=−1.0 corresponding to the ±J model a q=3.0, b q=4.0, and c q=6.0

Full size image

The next figures, Fig. 3, are obtained for α=0.0 corresponding to the bond diluted model on the (K,T) planes for given values of p. All the T c -lines emerge from K=−1.0 at zero temperature. Then, they increase in temperature with increasing K, p, and q. They eventually become constant at some temperatures for further increase of K. It also clear that T c -lines separate the F phase from the P phase only. The reentrant behavior is also seen for q=6 when p=0.9 and 1.0.

Fig. 3
figure 3

The phase diagrams on the (K,T) planes for given values of p when α=0.0 corresponding to bond diluted model with only T c -lines a q=3.0, b q=4.0, and c q=6.0

Full size image

The next figures are obtained on the (p,T) planes for given values of K for the bond diluted model again and given in Fig. 4. Only T c -lines are seen which separate F and P phase regions. Again, as K,p, and q increase, their temperatures increase. The lines for higher positive K’s are straight, except very close to p=0. The straightness is somewhat spoiled as K becomes more negative.

Fig. 4
figure 4

The phase diagrams on the (p,T) planes for given values of K when α=0.0 corresponding to bond diluted model with only T c -lines a q=3.0, b q=4.0, and c q=6.0

Full size image

Figures 5 and 6 only show the existence and behavior of the T S Q -lines for q=4 and 6, which was not observed for q=3, for α=0.0. In the first ones, i.e., Fig. 5 on the (K,T) planes for given p, all the lines emerge from K=−1.0 and are almost straight for higher K’s but as K gets smaller the reentrant behavior appears for K=0.1,0.05,0.01 and K=0.6−0.01 for q=4 and 6, respectively. They become much clear for lower p values. Figure 6 are plotted on the (p,T) planes for given K when q=4 and 6, again the T S Q was not observed for q=3. For higher negative K’s, the lines are almost straight but as K grows, the lines turn back to p=0, which were emerged from higher temperatures at zero p=0, presenting reentrant behavior again.

Fig. 5
figure 5

The phase diagrams on the (K,T) planes for given values of p when α=0.0 corresponding to bond diluted model with only T S Q -lines a q=4.0 and b q=6.0

Full size image
Fig. 6
figure 6

The phase diagrams on the (p,T) planes for given values of K when α=0.0 corresponding to bond diluted model with only T S Q -lines a q=4.0 and b q=6.0

Full size image

To end this, we again note the the spin-1 model is studied on the BL with random bilinear J and biquadratic K exchange interactions. The randomization effects of J is studied by using a bimodal random distribution with an adjustable parameter α which let us study the cases of ±J-model (α=−1.0) and bond-dilution α=0.0. The phase diagrams are obtained on the (K,T) and (p,T) planes for given values of p and K, respectively. It is found that the model gives only second-order phase transitions lines separating the F and AF phases from the P phase. The staggered quadrupolar phase is only seen for higher negative K values at lower temperatures for the coordination numbers q=4 and 6, only and present reentrant behavior for lower K values, i.e in the range 0.0 to −1.0. It should also be mentioned that our results are in total agreement with itself and the literature.