1 Introduction

The BEG model Hamiltonian consists of bilinear and biquadratic exchange interaction parameters in addition to the crystal field term. Since the spin-1 model is the lowest model consisting of all these parameters, it was thoroughly investigated by using numerous techniques. A closed-form expression for the critical surface of second-order transitions was formulated as a three-state vertex model [1]. Dimensionality effects with repulsive K < 0 were examined by using the mean field (MF) and renormalization-group (RG) studies [2] and it was shown that the results obtained by MF theory were applicable to three-dimensional systems [3]. The random-anisotropy model was considered by using the MF theory, transfer-matrix calculations and position-space (RG) calculations [4]. It was analyzed by using Monte Carlo (MC) RG study on the cubic lattice with K < 0 [5]. It is proven that BEG model can be transformed into either a spin-l/2 Ising model or a 3-state Potts model [6]. It was studied within the framework of a finite cluster theory on a diamond lattice [7]. The model with transverse D and, the longitudinal and transverse magnetic fields was studied via the MFA [8]. The dynamic behavior was studied by using the path probability method of Kikuchi [9]. The linear chain approximation was used to examine it’s phase diagrams [10]. A two-fold Cayley tree graph with q coordinated sites was solved exactly using the ERR’s [11]. The two-particle cluster approximation was used to examine the reentrant behavior [12]. The transverse field effects on bulk melting and layering sublimation transition was studied in the MFT [13]. The random quantum transverse field effects were considered in the effective field theory (EFT) [14]. A classical spin model with NN and NNN interactions was proposed for a large class of lattices [15]. The antiferromagnetic (AFM) model with K < 0 was studied using the lowest approximation of the cluster variation (CV) method [16]. The AFM model was examined by using the ERR’s on the BL [17]. The exact solution was obtained by the Green’s function and equations of motion formalism [18]. The critical exponents and phase diagrams were calculated with K and D interactions under constant J [19]. The model on finite-size Cayley tree were investigated using the ERR’s [20]. The random transverse D effects were examined by the EFT [21]. The phase transitions under the random K were investigated on the BL and its phase diagrams were calculated [22, 23]. The thermodynamics of the AFM model were investigated with a longitudinal magnetic field [24]. The exact Helmholtz free energy of one-dimensional model was derived [25]. The model was considered on the BL with J and K exchange interactions [26]. Lastly, the spin-crossover and Prussian blue analogs materials were investigated in 2D with a three-state within the BEG model [27].

The spin-1 BEG model with special attention given to the SQ phase has also attracted a lot of attention. The MC simulation was used to calculate the phase diagrams of a 2-d case [28]. An upper bound was obtained for the critical temperature associated with second-order phase transitions of the 2-d model [29]. A plaquette of four-spin interaction was investigated by means of the CV method in the square approximation [30]. The 3-d semi-infinite model with K < 0 were investigated within the framework of the MF approximation in comparison to the real-space RG technique [31]. The thermodynamic response functions were studied in thin films [32]. A finite cluster theory based on the EFT was applied to the model [33]. The range of parameters in a close neighborhood of the AFM three-state Potts model was considered [34]. It was studied in the two-particle cluster approximation on hypercubic lattices [35]. The CV method in pair approximation (PA) was used in the site-diluted model [36]. The MC results were presented at the ferromagnetic-antiquadrupolar-disordered phase interface [37]. The PA in the CV method was examined to study the thermal variations of the order parameters with K < 0 [38]. The model was studied by using the MFT and some new phases were obtained [39]. The model was simulated on a cellular automaton (CA) for a simple cubic lattice [40, 41]. The SQ phase and bicritical point of the bond and anisotropy diluted model was studied in the EFT [42]. It was simulated using the cooling algorithm which was improved from the Creutz cellular automaton (CCA) under periodic boundary conditions [43, 44]. The 4-d model was simulated using the CA cooling algorithm improved from the 3-d BEG model algorithm on the hypercubic lattices [45]. It was investigated by using the MFT and MC simulation [46]. The ferromagnetic version of model in the region of K < 0 was considered on a Cayley tree of coordination z [47]. And the MC simulation technique was used to study the critical behavior of a three-state spin model on [48].

The bond dilution of the BEG model, i.e. J is either turned on or off with some probability, was only considered in a few works: The bond and crystal field diluted model in the presence of magnetic field were considered on a simple cubic lattice by using the EFT [49]. The effect of bond-dilution on a quantum transverse model was investigated within an expansion technique for cluster identities of a spin-1 localized spin system [50]. The model with uniform K was studied by the MC simulation using the non-equilibrium relaxation method [51]. The spin-1 bond and crystal field diluted model was investigated within the framework of the EFT [52]. Note also that the Blume-Capel model was also studied on the BL for the ± J distribution with a competing adjustable parameter α which alters the strength of bilinear exchange interaction parameter for the FM phase (J > 0) with respect to AFM phase (J < 0) with probabilities p and 1 − p [53].

This work considers the random bond-dilution effects of Jij, which is either turned on with probability p or turned off with 1 − p, between the NN spins for the spin-1 BEG model on the BL consisting of two interpenetrating equivalent sublattices A and B for given coordination number z. After obtaining the necessary equations in terms of the ERR’s, we first present the thermal variations of the order-parameters showing all types of phase transitions and phase regions of the model. Then we exhibit the phase diagrams on the (D/J, T/J) and (K/J, T/J) planes for given values of K/J and D/J, respectively, for z = 3, 4, 5 and 6. We especially focus on the behavior of the staggered quadrupolar (SQ) phase and the bicritical points.

The rest of this work is arranged as follows: The formulation on the BL in terms of the ERR’s is given in Section 1, the thermal variations of the order-parameters are discussed in Section 2, Section 3 is devoted to the phase diagrams and the final section contains our findings and conclusions.

2 Spin-1 Model in Terms of ERR’s on the BL

The well-known spin-1 BEG model Hamiltonian in terms of the random bilinear exchange interaction parameter Jij and constant biquadratic exchange interaction parameter K between the NN spins and the constant crystal field parameter which is active at each spin site is given in the form:

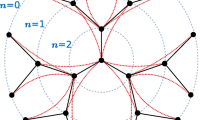
$$ \begin{array}{@{}rcl@{}} \mathcal{H} & = & -\sum\limits_{\langle ij \rangle}J_{ij}{S_{i}^{A}}{S_{j}^{B}}- K\sum\limits_{\langle ij \rangle}({S_{i}^{A}})^{2}({S_{j}^{B}})^{2} -D\sum\limits_{i}({S_{i}^{A}})^{2}- D\sum\limits_{j} ({S_{j}^{B}})^{2} \end{array} $$
(1)

where \({S_{i}^{A}}=\pm 1,0\) and \({S_{j}^{B}}=\pm 1,0\) are the values of spins located at i th and j th lattice points, respectively. The construction of the BL with sublattice A and B is depicted in Fig. 1 with z = 3.

Fig. 1
figure 1

The BL of coordination number z = 3. The superscripts over spins S, denote the sublattice A or B, while the subscripts denote the shell number of the BL

Full size image

Jij is the random bilinear exchange interaction parameter which is assumed to be distributed according to the binary probability distribution function P(Jij)

$$ P(J_{ij})=p\delta(J_{ij}-J)+(1-p)\delta(J_{ij}), $$
(2)

where p indicates the probability or the bond concentration with 0 ≤ p ≤ 1, i.e it was turned on ferromagnetically with p or turned off with 1 − p.

The partition function of the model is given as

$$ Z=\sum e^{-\beta \mathcal{H}}=\sum\limits_{Spc}P(Spc) $$
(3)

where Spc refers to the spin configurations. The probability functions P for each sublattice are given as

$$ \begin{array}{@{}rcl@{}} P({S_{0}^{A}})&=&\exp\left[ \beta D({S_{0}^{A}})^{2} \right]\left[g_{n}({S_{0}^{A}}) \right]^{z} \end{array} $$
(4)
$$ \begin{array}{@{}rcl@{}} P({S_{1}^{B}})&=&\exp\left[ \beta D({S_{1}^{B}})^{2} \right]\left[g_{n-1}({S_{1}^{B}}) \right]^{z} \end{array} $$
(5)

where the subscripts 0 and 1 refer to the zeroth and first shells and n counts the number of the shells of the BL. The gn functions are the partial partition functions of a branch of the BL which are written in terms of summation over the spin set \(\{ {S_{1}^{B}}\}\) for \(g_{n}({S_{0}^{A}})\) as

$$ g_{n}({S_{0}^{A}})=\sum\limits_{\{{S_{1}^{B}}\}}\exp \left[\beta(J_{ij}{S_{0}^{A}}{S_{1}^{B}} +K({S_{0}^{A}})^{2}({S_{1}^{B}})^{2}) +D({S_{1}^{B}})^{2} \right][g_{n-1}({S_{1}^{B}})]^{z-1} $$
(6)

and similarly over the spin set \(\{ {S_{1}^{A}}\}\) for \(g_{n-1}({S_{1}^{B}})\) as

$$ g_{n-1}({S_{1}^{B}})=\sum\limits_{\{{S_{2}^{A}}\}}\exp \left[\beta(J_{ij}{S_{2}^{A}}{S_{1}^{B}} +K({S_{2}^{A}})^{2}({S_{1}^{B}})^{2}) +D({S_{2}^{A}})^{2} \right][g_{n-2}({S_{2}^{A}})]^{z-1} $$
(7)

The ratios of these gn functions for each sublattice are assumed to be similar with the equations of state in the ERR approach [17, 23, 53]. Thus, the ERR’s belonging to each sublattice A and B are given respectively as

$$ X_{n}=\frac{g_{n}(+1)}{g_{n}(0)},\quad Y_{n}=\frac{g_{n}(-1)}{g_{n}(0)} $$
(8)

and

$$ A_{n-1}=\frac{g_{n-1}(+1)}{g_{n-1}(0)},\quad B_{n-1}=\frac{g_{n-1}(-1)}{g_{n-1}(0)} $$
(9)

The explicit expressions of these ERR’s have the following forms:

$$ \begin{array}{@{}rcl@{}} X_{n}^{(ij)}&=&\frac{e^{\beta(J_{ij}+K+D)}[A_{n-1}^{(ij)}]^{z-1} +e^{\beta(-J_{ij}+K+D)}[B_{n-1}^{(ij)}]^{z-1}+1} {e^{\beta D}[A_{n-1}^{(ij)}]^{z-1}+e^{\beta D}[B_{n-1}^{(ij)}]^{z-1}+1}, \end{array} $$
(10)
$$ \begin{array}{@{}rcl@{}} Y_{n}^{(ij)}&=&\frac{e^{\beta(-J_{ij}+K+D)}[A_{n-1}^{(ij)}]^{z-1} +e^{\beta(J_{ij}+K+D)}[B_{n-1}^{(ij)}]^{z-1}+1} {e^{\beta D}[A_{n-1}^{(ij)}]^{z-1}+e^{\beta D}[B_{n-1}^{(ij)}]^{z-1}+1}, \end{array} $$
(11)

and

$$ \begin{array}{@{}rcl@{}} A_{n-1}^{(ij)}&=&\frac{e^{\beta(J_{ij}+K+D)}[X_{n-2}^{(ij)}]^{z-1} +e^{\beta(-J_{ij}+K+D)}[Y_{n-2}^{(ij)}]^{z-1}+1} {e^{\beta D}[X_{n-2}^{(ij)}]^{z-1}+e^{\beta D}[Y_{n-2}^{(ij)}]^{z-1}+1}, \end{array} $$
(12)
$$ \begin{array}{@{}rcl@{}} B_{n-1}^{(ij)}&=&\frac{e^{\beta(-J_{ij}+K+D)}[X_{n-2}^{(ij)}]^{z-1} +e^{\beta(J_{ij}+K+D)}[Y_{n-2}^{(ij)}]^{z-1}+1} {e^{\beta D}[X_{n-2}^{(ij)}]^{z-1}+e^{\beta D}[Y_{n-2}^{(ij)}]^{z-1}+1}. \end{array} $$
(13)

The final expressions, i.e. after the implementation of bond dilution function P(Jij), are obtained simply by integrations as

$$ \begin{array}{@{}rcl@{}} X_{n}&=&\int X_{n}^{(ij)}P(J_{ij})dJ_{ij} =\int X_{n}^{(ij)}[p\delta(J_{ij}-J)+(1-p)\delta(J_{ij})]dJ_{ij}, \\ Y_{n}&=&\int Y_{n}^{(ij)}P(J_{ij})dJ_{ij} =\int Y_{n}^{(ij)}[p\delta(J_{ij}-J)+(1-p)\delta(J_{ij})]dJ_{ij} \\ A_{n-1}&=&\int A_{n-1}^{(ij)}P(J_{ij})dJ_{ij} =\int A_{n-1}^{(ij)}[p\delta(J_{ij}-J)+(1-p)\delta(J_{ij})]dJ_{ij} \\ B_{n-1}&=&\int B_{n-1}^{(ij)}P(J_{ij})dJ_{ij} =\int B_{n-1}^{(ij)}[p\delta(J_{ij}-J)+(1-p)\delta(J_{ij})]dJ_{ij} \end{array} $$
(14)

After obtaining the bond-diluted ERR’s, the order-parameters, i.e. magnetization and quadrupolar moments, are given for the sublattice A as

$$ \begin{array}{@{}rcl@{}} m_{A}&=&\langle {S_{0}^{A}} \rangle= \frac{e^{\beta D}[{X_{n}^{z}}-{Y_{n}^{z}}]}{e^{\beta D}[{X_{n}^{z}}+{Y_{n}^{z}}]+1}, \end{array} $$
(15)
$$ \begin{array}{@{}rcl@{}} q_{A}&=&\langle ({S_{0}^{A}})^{2} \rangle= \frac{e^{\beta D}[{X_{n}^{z}}+{Y_{n}^{z}}]}{e^{\beta D}[{X_{n}^{z}}+{Y_{n}^{z}}]+1}, \end{array} $$
(16)

and similarly for the sublattice B as

$$ \begin{array}{@{}rcl@{}} m_{B}&=& \langle {S_{1}^{B}} \rangle=\frac{e^{\beta D}[A_{n-1}^{z}-B_{n-1}^{z}]}{e^{\beta D}[A_{n-1}^{z}+B_{n-1}^{z}]+1}, \end{array} $$
(17)
$$ \begin{array}{@{}rcl@{}} q_{B}&=& \langle ({S_{1}^{B}})^{2} \rangle= \frac{e^{\beta D}[A_{n-1}^{z}+B_{n-1}^{z}]}{e^{\beta D}[A_{n-1}^{z}+B_{n-1}^{z}]+1}. \end{array} $$
(18)

The phase diagrams of the model are calculated thorough the thermal variations of the order-parameters. The phase transitions lines, i.e. second- or first-order, separate the different phase regions of the model which are identified accordingly

  • The ferromagnetic phase F: mA = mB≠ 0, qA = qB = q ≠ 0

  • The paramagnetic phase P: mA = mB = 0, qA = qB = q ≠ 0

  • The ferrimagnetic phase FI: mA≠mB≠ 0, qA≠qB

  • The staggered quadrupolar phase SQ: mA = mB = 0, qA≠qB

It should be noted that instead of these order-parameters, the total magnetization m, the staggered magnetization ms and the “staggered quadrupolar moment”qs are commonly used in obtaining the phase diagrams which are given respectively as

$$ \begin{array}{@{}rcl@{}} m=\frac{1}{2}(m_{A}+m_{B}), \qquad m_{s}=\frac{1}{2}(m_{A}-m_{B}) \quad \text{and} \quad q_{s}=\frac{1}{2}(q_{A}-q_{B}). \end{array} $$
(19)

In order to classify the type of the phase transitions, one may need to consult to the free energy which is obtained simply by \(F=-kT\ln Z\) and given as

$$ \begin{array}{@{}rcl@{}} -\beta F&=&\frac{1}{2-z}\ln \left[e^{\beta D}(A_{n-1}^{z-1}+B_{n-1}^{z-1})+1 \right] +\frac{z-1}{2-z}\ln \left[e^{\beta D}(X_{n}^{z-1}+Y_{n}^{z-1})+1 \right] \\ & &+\ln \left[e^{\beta D}({X_{n}^{z}}+{Y_{n}^{z}})+1 \right] \end{array} $$
(20)

Numerical analysis of these formulations are required to calculate the phase diagrams of the model from thermal analysis which is carried out in the next section.

3 The Thermal Variations of the Order-Parameters

The obtaining of the phase diagrams requires the study of order-parameters thermally. Thus, we present the thermal variations of magnetizations mA and mB and, quadrupolar moments, qA and qB, belonging to the sublattices A and B together with m, ms and qs in this section. This will inform readers how to determine the type of phase transitions, i.e. second- or first-order, and different phase regions. In studying this section, the phase identification rules given on page 6 should be reminded.

The Fig. 2a-c, obtained for z = 3, K/J = − 1.2: (a) D/J = 1.5 and p = 0.1 (see Fig. 2a), (b) D/J = 1.5 and p = 1.0 (see Fig. 2b), and D/J = 0.5 and p = 1.0 (see Fig. 2c), show that the model gives only the second-order phase transitions following the F-SQ-P, F-P and SQ-P phases, respectively. Figure 2a shows that mA = mB = m = 1.0 and qA = qB = 1.0 with qs = 0.0 indicating the F phase which terminate at the first Tc, where mA = mB go to zero and qA = qB make a little peak. Afterwards, magnetizations always remain at zero. The quadrupolar moments are separated at the kink where qB first decreases (qA increases) then increases (qA decreases) combining at the second Tc. qs present a closed half loop between these two Tc’s indicating the SQ phase. Finally, qA = qB leading to qs = 0, magnetizations are already zero, indicating the P phase. Figure 2b is the well-known behavior of m’s and q’s. They all start from their GS values, i.e. 1.0, then as temperature increases the magnetizations go to zero and quadrupolar moments present peak at the Tc separating the F and P phases. Afterwards mA = mB = 0.0 and qs = 0.0. Figure 2c shows that mA = mB = 0.0 and, qA = 1.0 and qB = 0.0, i.e. qs≠ 0.0. As the temperature increases, qB increases but qA decreases to eventually combine at the Tc and they always stay to be equal afterwards giving qs = 0.0 indicating SQ-P phase transition.

Fig. 2
figure 2

The temperature dependence of the order parameters illustrated for z = 3, K/J = − 1.2, D/J = 1.5: a p = 0.1, b p = 1.0 and, c z = 3, K/J = − 1.2, D/J = 0.5 and p = 1.0. They approve the correctness of the phase diagram of Fig. 5a

Full size image

The Fig. 3a–b, obtained for z = 4, K/J = − 1.0 and p = 0.3, show that the model gives F-SQ-P and F-P phase transitions with increasing temperature, respectively. Figure 3a is obtained for D/J = 1.0 and is similar to the Fig. 2a with the exception of observing a Tt instead of the first Tc of Fig. 2a. As seen, the magnetizations jump to zero discontinuously where qA and qB jump to different nonzero values and then again combine at the Tc. Again the F-SQ-P phases are observed in order. The next one is obtained when D/J = 2.0 presenting the second-order F-P phase transition as in Fig. 2b. The Fig. 3c calculated for z = 6, K/J = − 1.0, D/J = − 0.1 and p = 1.0, show that the model gives P-F-P phase transitions with increasing temperature. All the order-parameters start from zero, mA = mB remains zero and qA = qB increases with increasing temperature. At the first Tc, mA = mB gains some value and qA = qB present a kink. With the increase of temperature, they all increase to give peaks at some maxima. Then, mA = mB go to zero and qA = qB presents second kink at the second Tc.

Fig. 3
figure 3

The thermal variations of the order parameters illustrated for z = 4, K/J = − 1.0 and p = 0.3: a D/J = 1.0 and b D/J = 2.0 and, c z = 6, K/J = − 1.0, D/J = − 0.1 and p = 1.0. They are obtained with relation to the phase diagrams Fig. 6b, d

Full size image

Figure 4 shows the details of obtaining Fig. 5d, i.e. z = 6 and K/J = − 1.2. Figure 4a is calculated for D/J = 1.2 and p = 1.0. Here, one clearly see the existence of FI phase. As seen, ms≠ 0.0 at low temperatures, i.e. mA≠mB≠ 0.0 and qA≠qB, indicating the FI phase. The sublattice order-parameters combine at the temperature where ms becomes zero. Then mA = mB and qA = qB follows different paths in the F region. Again the magnetizations go to zero continuously at the Tc and quadrupolar moments present little kinks with the start of the P phase. Figure 4b is obtained for D/J = 4.0 and p = 0.1. It is clear that mA = mB = qA = qB starting from zero temperature in the F phase, then they are separated indicating the existence of ms which correspond to the FI phase region. The magnetizations become zero with qA≠qB indicating the SQ phase. It is clear that mA and mB jump to zero indicating the first order phase transition temperature Tt. Figure 4c obtained for D/J = 5.5 and p = 0.1, show that mA and mB go to zero continuously in contrary to the previous figure. Otherwise, they are similar.

Fig. 4
figure 4

The temperature dependence of the order parameters illustrated for z = 6 and K/J = − 1.2: a D/J = 1.2 and p = 1.0, b D/J = 4.0 and p = 0.1 and c D/J = 5.5 and p = 0.1. All are in agreement with Fig. 5d

Full size image
Fig. 5
figure 5

The phase diagrams on the (D/J, T/J) plane when K/J = − 1.2: a z = 3, b z = 4, c z = 5, and d z = 6. The solid- and dashed-lines correspond to the Tc- and Tt-lines, respectively. Intersection points at which SQ-P phase lines and F-P ones meet on the Tt-line are the BCP’s

Full size image

4 The Phase Diagrams

Our system parameters include K, D and J, see (1), in addition to temperature, T, coordination number z and probability p. J is usually taken to be a scaling parameter. Thus, we are left with K/J, D/J, T/J, z and p. Therefore, one can obtain the phase diagrams on the (D/J, T/J) and (K/J, T/J) planes for given K/J and D/J, respectively. The probability p values are taken with increment 0.1 in the range 0.1 ≤ p ≤ 1.0 and z = 3, 4, 5 and 6. The p = 1.0 case is the well-known BEG model as given in the references, while p = 0 case just turns off J.

Our first phase diagrams are presented on the (D/J, T/J) planes, see Fig. 5, for K/J = − 1.2 with the given p and z values above. In Fig. 5a plotted for z = 3, the second-order phase transition lines, i.e. Tc-lines, separate the phases P, SQ and F as the border-line between them. As the temperature is increased the system goes into the P phase which surrounds SQ and F phases appearing at lower temperatures. As seen the Tc-lines separating F and P and, SQ and P phases emerge from the same D/J at zero temperature. The first lines move towards right as D/J increases which are seen at higher T/J as p is increased. The latter ones make a closed loop all terminating at zero D/J. It is clear that these lines present reentrant behavior for some p values. This reentrance behavior appears to be more pronounced for the small p. The SQ phase region becomes smaller when p increases while those of F phase is becoming larger. With other words, two fixed values of the D/J appear at T/J = 0. Indeed, the SQ-P and the SQ-F phase transition lines meet at multicritical points which lead to multicritcal lines that take place at D/J = z(− 1.0 − K/J) for T/J = 0 and all p. The second fixed values are related to the SQ-P phase transition lines which go to D/J = 0 at T/J = 0. It is important to note that by increasing the value of D/J from D/J = 0, the SQ-P transition temperature increases and passes by a smooth maximum and then reduces rapidly to zero at D/J = 0.6, according to D/J = z(− 1.0 − K/J).

For z = 4, the topology of the phase diagram change qualitatively. Indeed, in Fig. 4b the SQ phase is separated from the P phase by the Tc-lines and from the F phase by the first-order lines, i.e. Tt-lines. These two lines meet with other Tc-lines separating the P and F phases for all p at the so-called BCP. Corresponding to the coordinates of the BCP, the values of D/J decrease while that of T/J, first increase and then decrease further with the increase of p. Here again, D/J takes two fixed values at absolute zero temperature, the first one concerning the Tc-lines between SQ and P phases at D/J = 0 and the second one related to the Tt-lines between the SQ and F phases at D/J = z(− 1.0 − K/J).

The phase diagrams for z = 5 and 6, Fig. 5c and d respectively, are very similar with the z = 4 case, i.e. Fig. 5b. The main difference arises from the existence of the ferrimagnetic (FI) phase found for all p. For these values, we see the sequences of the phases as P-SQ-FI-F and/or P-SQ-F. In addition, the four Tc-lines connect at tetracritical points. It should be noted that the detailed analysis for the existence FI phase and tetracritical point was not carried out in this work which we hope to carry out in our next work.

It is worth noticing that by changing z from 4 to 6, the phase diagrams change only quantitatively. As seen from the Fig. 5a-d, the dependence of T/J on the value of D/J is very similar in these curves. Indeed, we found that not only when D/J is fixed, the F-P critical temperature takes larger value with the increase of p but also the SQ-P critical temperature decreases when increasing p. We also remark that the SQ phase region increases when z increases. The reentrant behavior is seen for p = 0.1 when z = 4. It also exists for z = 5 and 6 where it is seen at lower D/J’s in contrary to the z = 3 and 4 for which it appears at higher D/J’s. It should also be noted that:

  1. i

    - the critical SQ-F Tc-lines for z = 3 as the SQ-F first order transition line for z > 3 emerges at T/J = 0 with the values of D/J = z(− 1.0 − K/J).

  2. ii

    - F phase represents the ground state (GS) for D/J > z(− 1.0 − K/J) while the disordered SQ phase becomes the GS for 0 < D/J < z(− 1.0 − K/J). The P phase is the GS for D/J < 0.

  3. iii

    - the SQ-P critical line approaches the zero-temperature phase boundary with a negative slope for z < 4, with a positive slope for z > 4 and with an infinite gradient for z = 4. This situation is then typical for the reentrant phenomenon which appears at sufficiently high coordination number z > 4 and becomes more pronounced as z is higher.

Again, Fig. 6 are displayed on the (D/J, T/J) planes with K/J = − 1.0 for given p and z which are similar with the Fig. 5. In this case, F phase represents the GS for D/J > 0 while the disordered P phase becomes the GS for D/J < 0. For z = 3, the SQ phase exists for only p = 0.1 and 0.2 at small finite non-zero temperature. As the value of D/J is increased from D/J = 0, the SQ-P transition temperature increases and passes by a smooth maximum and then reduces rapidly to zero at D/J = 0. However, the F-P critical temperature exhibits a smooth monotonous decline with decreasing D/J. For z = 4,5 and 6, the range of p in which the system has BCP expands with the increase of z. All transition lines emerge from T/J = 0 at D/J = 0.

Fig. 6
figure 6

The phase diagrams on the (D/J, T/J) plane when K/J = − 1.0: a z = 3, b z = 4, c z = 5, and d z = 6

Full size image

The final exhibit of this kind of phase diagram is obtained for K/J = − 0.9 as shown in Fig. 7. It is very interesting since the system may present double BCP for given parameters when z ≥ 4. Again, the phase transitions lines are only of Tc-lines for z = 3 with all p. The value of the critical temperature increases when D/J and p also increase. The SQ phase appears for p = 0.1 only in a closed region which is surrounded by the P phase. The Fig. 7b-d present the fact that the system presents double BCP’s. Indeed, for z ≥ 4, the system has always double BCP’s. The range of p in which the system has BCP’s expands with the increase of z. With the increase of p, the range of D/J in which the system has BCP’s decreases. Starting from the lowest and ending up at the highest temperature, the system undergoes the following sequence of second-order phase transitions F-P-SQ-P and F-P-F-P. The first one is obtained for p = 0.1 (Fig. 7a), p = 0.1 − 0.3 (Fig. 7b, c) and p = 0.1 − 0.4 (Fig. 7d). However, the occurrence of the second one is related to a high enough coordination number z and p. The system then presents a double reentrant behavior.

Fig. 7
figure 7

The phase diagrams on the (D/J, T/J) plane when K/J = − 0.9: a z = 3, b z = 4, c z = 5, and d z = 6

Full size image

The next phase diagrams are calculated on the (K/J, T/J) planes for given values of D/zJ when p changes from 0.1 to 1.0 by the increase of 0.1 and for z = 3, 4, 5 and 6. In here we have used D/zJ instead of D/J, this scaling causes all the lines emerge from the same K/J value, i.e. independent from z.

The obtained phase diagrams for D/zJ = 0 are shown in Fig. 8. Figure 8a plotted for z = 3, shows the critical temperature as a function of K/J in an absence of the single-ion anisotropy (D/J = 0). In this particular case, the ordered ferromagnetic phase (F) represents the GS for K/J > − 1.0, while the disordered paramagnetic phase (P) becomes the GS for D/J < − 1.0. The SQ phase does not appear. The system always undergoes second order F-P phase transition for any value of p. Note that all the Tc-lines vanish at K/J = − 1.0 which is independent from the value of p. On Fig. 8b-d, the phase diagrams obtained for z = 4,5 and 6, respectively, show two Tc-lines for each p. The first Tc-lines originate from K/J = − 1.0 and behave similarly as in the z = 3 case separating the F and P phases in the K/J > − 1.0 region. It is clear that as z increases these lines appear at higher temperatures. They are also seen at higher temperatures for higher p values for all z. The second Tc-lines also originate from K/J = − 1.0 and are seen in the region with K/J < − 1.0. They appear at higher temperatures for lower p separating the SQ and P phases. The reentrant phenomena is also obvious in this case.

Fig. 8
figure 8

The phase diagrams on the (K/J, T/J) plane when D/zJ = 0.0. The number accompanying each curve denotes the p between 0.1 and 1.0 with the increment of 0.1: az = 3, b z = 4, c z = 5, and d z = 6

Full size image

The phase diagrams for D/zJ = 0.5 are shown in Fig. 9. As seen from the phase diagram on Fig. 9a plotted for z = 3, the F-P critical temperature exhibits a smooth monotonous decline with decreasing K/J while by the increase of K/J from negative values, the SQ-P critical line approaches the zero-temperature with a negative slope which appears more pronounced when p is smaller. These lines combine for each p, when they approach the zero-temperature phase boundary between SQ and F phases, at multi-critical point which lead to multicritcal lines that take place at K/J = − 1.5 for all p. For z > 3, Fig. 9b-d, the phase transitions are of the form of Tc-lines in the high temperature region and of the form of Tt-lines in the region of low temperatures, for all p. It is noteworthy that not only when K/J is fixed, the F-P critical temperature takes larger value with the increase of p but also the SQ-P critical temperature decreases when increasing p. As seen the wing-shaped Tc-lines present little kinks at their minima from where the Tt-lines appear which terminate at K/J = − 1.5 for all p and z. It is obvious that BCP’s also appear at the minima of these Tc-lines. The left wing separates the SQ and P phases, while the right wing separates the F and P phases. It is also clear that by decreasing p values, the BCP’s are shifted towards more positive values of K/J and it gradually appears as lower T/J for lower p while all the Tt-lines separating SQ and F phases go to zero temperature at K/J = − 1.5 independently to p and z according to K/J = − 1 − D/zJ.

Fig. 9
figure 9

The phase diagrams on the (K/J, T/J) plane when D/zJ = 0.5. The number accompanying each curve denotes p between 0.1 and 1.0 with the increment of 0.1: az = 3, b z = 4, c z = 5, and d z = 6. The solid- and dashed-lines correspond to the Tc- and Tt-lines, respectively. Intersection points at which SQ-P phase lines and F-P ones meet on the Tt-line are the BCP’s

Full size image

The next phase diagrams are obtained on the (K/J, T/J) planes when p = 1.0 with D/zJ between 0.1 and 0.5 with the increment of 0.05 for all z. The system presents only Tc-lines when z = 3 again, Fig. 10a. For each p, the SQ-P and F-P Tc-lines meet only at zero temperature. On the other hand, when K/J is fixed, the critical temperature takes larger value with the increase of D/zJ. We also remark that the SQ phase region increases when z increases. For z = 4,5 and 6, as shown in Fig. 10b-d, the system exhibits BCP’s again. The Tt-lines separating SQ and F phases go to zero temperature at K/J = − 1 − D/zJ. Here again, for fixed K/J, the critical temperature takes larger value with the increase of D/zJ and z.

Fig. 10
figure 10

The phase diagrams on the (K/J, T/J) plane when p = 1.0. The number accompanying each curve denotes the value of D/zJ between 0.1 and 0.5 with the increment of 0.05: az = 3, b z = 4, c z = 5, and d z = 6

Full size image

Our previous Figs. 5, 6 and 7 have shown that there exists critical values of the parameter p, say pc, for which different trends of the model emerged. We find instructive to illustrate this problem by generating phase boundaries in the (p, T/J) plane for a selected value of the reduced single-ion anisotropy D/J for z = 3 − 6. This is depicted in Fig. 11 for D/J = 0.6 and selected values of K/J and in Fig. 12 for K/J = − 1.2 for selected values of D/J. Surprisingly, critical values of p derived are often connected to bicritical points (panels b,c,d). In Fig. 11a, for K/J = − 1.15, pc = 0.528. For p > pc, the system undergoes a second-order transition F-P and shows the same trends as the pure BEG model corresponding to p = 1. Below pc, the behavior is completely different. Indeed, one gets second-order transitions F-SQ-P. This behavior changes in other panels where first-order transitions appear at low temperature at any value of p leading to bicritical points. In Fig. 11c, for K/J = − 1.1, it can be seen that there is one critical value pc = 0.801 above which only F-P transition exists whereas below, a F-SQ-P transition emerges. Due to the re-entrant behavior of the first-order transition line, this critical value pc is not connected to the associated bicritical point (p = 0.754) whereas for K/J = − 1.0, this occurs and pc = 0.596. The same observations can be done in panel (d). Beyond the re-entrant behavior observed for some values of K/J, the system behaves for few values of p close to p = 1 as the pure BEG model due to the SQ-F-P transition which prevails. Figure 12 shares almost the same features with Fig. 11 and critical values of p could be determined for selected values of D/J.

Fig. 11
figure 11

The phase diagrams on the (p, T/J) plane when D/J = 0.6. The number accompanying each curve denotes the value of K/J between − 0.8 and − 1.2 with the increment of 0.05: a z = 3, b z = 4, c z = 5 and d z = 6

Full size image
Fig. 12
figure 12

The phase diagrams on the (p, T/J) plane when K/J = − 1.2. The number accompanying each curve denotes the value of D/J between 0.8 and 2.0 with the increment of 0.2: az = 3, b z = 4, c z = 5 and d z = 6

Full size image

Without going into details, we should note that the phase diagrams on the (D/J, T/J) planes of [29, 31, 39, 43], on the (K/J, T/J) planes of [32, 34, 40, 41, 45] and on both planes of [33, 38, 42, 48] are similar with the ones that are obtained in this work. Note also that for the case of the bond dilution we also see similar phase diagrams in [51]. The existence of tetracritical point are also obtained as the case in [29, 31, 46].

5 Conclusion

The bond-dilution effects of Jij between the NN spins are studied randomly for the spin-1 BEG model on the BL consisting of two interpenetrating equivalent sublattices A and B for given coordination number z in terms of ERR’s. Jij is either randomly turned on with probability p or turned off with 1 − p. K between the NN spins and the D of the sublattices A and B are taken as constants. Thermal variations of the order-parameters are studied numerically to obtain the phase diagrams on the (D/J, T/J) and (K/J, T/J) planes. We found that the model presents both first- and second-order phase transitions. In addition to the well-known ferromagnetic (F), paramagnetic (P) and ferrimagnetic (FI) phases, the staggered quadrupolar (SQ) phases is also observed. The BCP, double BCP’s and tetracritical points are also observed. As a last word, we say that our calculations show an overall agreement with the literature.