Introduction

The assessment of prolongation of the QT interval from an ECG is a standard component of drug development because of the toxicities associated with QT interval prolongation [1–4]. Because of the regulatory implications, such assessments were typically made using results from a ‘thorough QT’ (TQT) study. The outline of the design, conduct, and analysis of TQT studies has been described in the International Conference on Harmonisation E14 Guidance [5]. Briefly, male and female subjects are administered placebo, active control, active drug, or a supratherapeutic dose of active drug in either a parallel (most common) or crossover manner. Time-matched serial ECGs and pharmacokinetic samples are collected, and cardiac parameters, like QT interval, PR interval, and RR interval, are extracted from the ECG by a cardiologist blinded to treatment. The QT intervals are then corrected for heart rate, typically using Fridericia’s correction (QTcF intervals), and analyzed using the intersection–union test (IUT). Clinically meaningful prolongation is declared if the upper 1-sided 95% confidence interval of the largest placebo-corrected, time matched change from baseline, i.e., double-delta QTcF interval (ddQTcF) exceeds 10 ms.

The IUT, however, has been criticized for its high false positive rate [6]. As an alternative to the IUT, exposure–response modeling has been proposed [4, 6–8] as this approach maintains the Type I error [6, 9]. Under this approach, all individual responses are pooled and then linear and nonlinear mixed effect models are utilized to assess the relationship between ddQTcF intervals and drug and metabolite concentrations. If the upper 95% confidence interval of the predicted ddQTcF at the geometric mean maximal concentration (Cmax) at the therapeutic dose exceeds 10 ms, the drug is declared to significantly prolong QT intervals.

The most common model seen in the literature is a linear mixed effects model using drug concentrations as the dependent variable, both subject (as reflected by the intercept) and concentration as correlated random effects, and the residual error is treated as a simple normal random effect [4, 10–12]. Sometimes covariates, such as sex [13], weight [11], or nominal time [14, 15], are used or tested in the model. Sometimes more complex residual error structures, such as using a spatial covariance, are reported [16]. Sometimes, nonlinear models, like an Emax or sigmoid Emax model, are reported [17]. Further, there have also been suggestions that for some drugs, like moxifloxacin, hysteresis between ddQTcF intervals and drug concentrations may be present which may require correction [18, 19]. The point is, the analysis of ddQTcF interval data is not as straightforward as first reported. As such, an FDA-industry-academia white paper on this topic is expected to be released in 2017 in an attempt to harmonize these analyses.

Recently, the requirements for TQT studies, which are costly and difficult to perform, have been relaxed as sponsors may now be allowed to show that such studies are unnecessary when data are collected from properly designed single-ascending dose (SAD) and multiple-ascending dose (MAD) studies are analyzed [2, 15]. The utilization of SAD and MAD study data raises some issues not seen with a TQT study, namely sample size. TQT studies are usually powered with regards to the IUT and not with regards to concentration-QT (C-QT) modeling. Consequently, these studies are over-powered when it comes to C-QT modeling. Further, because SAD and MAD studies are often parallel group designs, variability is increased because each subject no longer acts as their own control and also the dependent variable changes from time-matched differences in QTcF intervals (double-delta correction) to change from predose baseline values (so-called single-delta or dQTcF intervals).

The assessment for prolongation is based on the geometric mean Cmax at the therapeutic dose and whether the upper 1-sided 95% confidence interval exceeds 10 ms. This prediction is made using the “best” model approach. In C-QT modeling, a single model is never used. Model development is an iterative process where candidate models are developed, compared to other reference models, and discarded or kept [20]. In the end, a final or “best” model is selected based on some best fit criteria, like the likelihood ratio test. This is the forward–backward selection process. Alternatively, all candidate models can be fit to the data and then ranked based on some selection metric, like the Akaike Information Criteria (AIC), finite-sample size AIC (AICc), or Bayesian information criteria where the model with the smallest metric is the “best” model. Prediction of QTc interval prolongation at Cmax is then based on the “best” model. This approach may not be generalizable to all settings, but it is the recommended approach by regulatory authorities.

When a “best” model is selected based on the observed data, and subsequent predictions are made from that model, the predictions are known to be overly precise because they do not account for model selection uncertainty [21]. Leo Breiman, one of the most influential statisticians of the last century, said the model selection problem and model dimensionality was the “quiet scandal of statistics” [22]. Bornkamp [23] shows how model selection uncertainty may result in different conclusions from a Phase 2 dose–response study in diabetes patients. Model uncertainty may be of concern in SAD and MAD studies because of the relative small numbers of subjects per cohort. One way to correct the impact of model uncertainty is by pre-specification of the model to be used prior to data analysis, but such a model may not best fit the data. Another way to account for model uncertainty is to make predictions based on model-averaging (MA) [21]. MA weights the predictions from a set of candidate models with the weights dependent on the goodness of fit of the individual models. Models with better goodness of fit are given higher weight in the prediction.

Between the time this paper was submitted for publication and the time of its publication, a publication of very similar nature was published in Pharmaceutical Statistics by Sebastien et al. [24]. In that paper the authors examined the utility of model-averaging in concentration-QT modeling using three mixed effect models for model averaging: linear model with intercept, Emax model with intercept, and exponential model with intercept. Their simulation was of a TQT crossover study with 3 treatments (placebo and two doses), 30 subjects in total, having ECGS and pharmacokinetic samples collected at nine time points. Drug concentrations were simulated using a 1-compartment model with first order absorption. Importantly, they examined four different data generating mechanisms for ddQTcF: no relationship between drug concentration and effect, linear relationship with intercept, Emax model with intercept, and exponential model with intercept. There was little difference in coverage and model predictions between the best model and model averaged approach leading them to recommend that either a formal selection criteria or model averaging approach be used for concentration-QT analyses. Their results are biased, however, to the extent that the data generating mechanism was the same as least one of them models used to analyze the data and the results may be overly optimistic. If the same data generating mechanism is used as the model used to analyze the data, it would be expected that the true parameter estimates can be recovered and any model predictions will be close to the true value. This study illustrates a problem with many TQT simulation studies—the data generating mechanism is basically the same as the model used to analyze the data. This is not necessarily a flaw but represents the “best case scenario.” A more realistic measure would be to use a more realistic data generating mechanism and then determine how the model-averaged approach works. Such an approach could be done by first resampling actual ECG data from placebo-treated subjects, add on a drug effect, and then analyze the resulting data. Another approach would be to use a more physiologic baseline model, add on drug effect, and then analyze the data. This is the approach used in this paper; using data generating mechanisms distinct from the models used to analyze the data, the results of Sebastian et al. are extended to more realistic conditions. The hypothesis of this simulation study was that in the modeling of C-QT data using data generating mechanisms separate and distinct from the data analysis models, model-averaging will result in more reliable estimates of the degree of prolongation at Cmax and will protect against model misspecification.

Method of model-averaging

The method is as follows:

  1. 1.

    Let R be the total number of possible candidate models that minimized successfully and were fit using maximum likelihood.

  2. 2.

    Rank all R models based on smallest AIC (for very small sample sizes AICc should be used).

  3. 3.

    The arithmetic difference in AIC, called Δi, is calculated for each model as the difference in the AIC and the model with the smallest AIC serving as the reference model.

  4. 4.

    Akaike weights w are calculated for each of the R models as

    $$w_{i} = \frac{{\exp \left( { - \frac{1}{2}\Delta_{i} } \right)}}{{\sum\limits_{r = 1}^{R} {\exp \left( { - \frac{1}{2}\Delta_{r} } \right)} }}.$$
    (1)
  5. 5.

    Let \(\hat{E}_{i}\) be the prediction estimate for the ith model. The model-averaged (MA) estimate of the prediction, \(\hat{E}_{ma}\), is calculated across models as

    $$\hat{E}_{ma} = \sum\limits_{i = 1}^{R} {w_{i} \hat{E}_{i} } .$$
    (2)

A modification of the method is to use the small sample size corrected AIC (AICc) or Bayesian information criterion (BIC) to compute the weights. Model-averaging can be done for both the mean estimate and confidence intervals, although it can be problematic for averaging model confidence intervals.

A demonstration of the model-averaging calculations is seen in Table 1. In this example, 4 candidate models were tested using AIC as the weighting metric. The “best model” was a traditional linear mixed effect model and the predicted effect at Cmax was 8.92 ms. Based on the MA approach, the predicted effect was slightly larger, 8.96 ms, because although the average prediction was largely dominated by the “best” model, Models 2 and 3 still contributed almost 19% to the weighting. It should be clear that if the weight of the best model is >0.9, MA is probably not needed and inference can be made on the best conditional model.

Table 1 Table showing the calculation of predicted effect using model-averaging
Full size table

Model-averaging has received little attention in the literature. A keyword search of PubMed with “model averaging” in the title only has 112 references starting from 1999 with few applications being reported in drug development. Jin et al. [25] reported on the application of model averaging two dose selection for a combination drug product, while Schorning et al. [26] and Verrier et al. [27] reported on the using of model-averaging to select doses in Phase 2. Outside of drug development, model-averaging has been used to improve prediction in ecology [28, 29], epidemiology [30–32], pharmacoeconomics [33, 34], and genetics [35–38]. What these reports have generally found is that model averaging performs the same, if not better, than traditional modeling methods across various measures of performance.

Example in practice

Drug X is being developed for the treatment of cancer. This study was a phase 1, open label first-in-human study in adult patients with relapsed or refractory cancer in which a single dose of drug X was administered on Day -2. Once-daily dosing began on Day 1 of Cycle 1. In one cohort of patients, ECGs were collected at Day -2 and Day 15 of Cycle 1 at predose (within 0.5 h of dosing), 2, 4, 6, and 24 h postdose, while in the other cohort predose ECG assessments were done on Cycle 1 Day 1, Cycle 1 Day 8, Cycle 1 Day 22, and Day 1 of each subsequent 28 day cycle. ECG monitoring was done in triplicate, within 30 min of nominal times, and transmitted electronically for central reading. QTcF intervals were extracted by a cardiologist and averaged. Blood samples were collected at ECG times and analyzed for plasma drug X concentrations.

Predose ECG measurements on Day -2 were treated as the baseline. Single-delta QTcF intervals (dQTcF) were calculated at every time point using time-matching. Drug X concentrations less than the limit of quantification of the assay were set to zero. Time matched concentration-dQTcF intervals were analyzed using the following prespecified models:

  1. 1.

    Linear mixed effect model with random intercept only (null model).

  2. 2.

    Linear mixed effect model with random intercept and drug concentration as a random effect. Uncorrelated random effects (standard model).

  3. 3.

    Model 2 with correlated random effects.

  4. 4.

    Model 1 with quadratic drug concentration term treated as a fixed effect.

  5. 5.

    Model 2 with quadratic drug concentration term treated as a fixed effect.

  6. 6.

    Emax model with intercept. Emax, EC50, and intercept are treated as uncorrelated random effects.

  7. 7.

    Model 6 with no random effect on Emax term.

  8. 8.

    Model 6 with no random effect on EC50 term.

  9. 9.

    Model 6 with no random effect on both Emax and EC50.

  10. 10.

    Emax model without intercept. All model parameters treated as uncorrelated random effects.

  11. 11.

    Model 10 without random effect on Emax term.

  12. 12.

    Model 10 without random effect on EC50 term.

  13. 13.

    Model 10 without random effect on Emax and EC50 term.

  14. 14.

    Exponential model of the form

    $$effect = {\text{Emax}}\left( {1 - \exp \left( { - \beta *conc} \right)} \right)$$
    (3)

    where Emax is the maximal effect that is treated as a random effect and β is the exponential slope treated as a fixed effect.

All random effects in the models above were assumed to be normally distributed. All models were fit using Gaussian adaptive quadrature using the NLMIXED procedure in SAS, Version 9.3 (SAS Institute, Cary NC). Models were ranked smallest to largest based on the Akaike Information Criteria (AIC) [39, 40]. The best fit model was one that had converged successfully without errors, had the smallest AIC, and all parameter estimates were statistically significant (p < 0.05) based on the t test (parameter/standard error of the parameter). At the therapeutic dose (120 mg once daily) the predicted median steady-state maximal concentration (Cmax,ss) was 282 ng/mL. The predicted dQTcF interval at the therapeutic dose and the corresponding two-sided 90% confidence interval (equivalent to the one-sided 95% CI) was calculated. Akaike weights were calculated for all models. The MA dQTcF interval and dQTcF interval using the best model were calculated and compared.

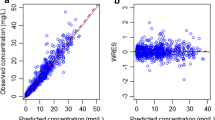
Table 2 presents the results from each model and the model averaged estimate. The best model was Model 8, although many models had AIC values close to the best model. Figure 1 presents a scatter plot of Drug X concentrations against dQTcF intervals overlaid with a nonparametric smoother and predictions from the linear mixed effect model and best model. The estimate of dQTcF intervals at 282 ng/mL under the best model was 6.19 ms with a 1-sided 95% CI of 8.12 ms, whereas the model averaged estimate was slightly higher at 6.22 ms and 1-sided 95% CI of 8.17 ms.

Table 2 Model-averaging results for Drug X at therapeutic Cmax of 282 ng/mL
Full size table
Fig. 1
figure 1

Scatter plot of Drug X concentrations against dQTcF intervals. Different doses are denoted by different symbols. The solid red line is the model prediction using Model 1. The solid black line is the nonparametric smooth to the data using a LOESS smoother. The solid line is the model prediction using the best model (Model 12). The Cmax at the therapeutic dose is the noted with the dashed line at 282 ng/mL (Color figure online)

Full size image

Methods

Monte Carlo simulation of the performance of model-averaged prediction

SAD/MAD and TQT simulation

To understand the performance of the MA approach compared to the traditional best model approach a Monte Carlo simulation was performed. Two types of study designs were utilized:

  1. (1)

    Data were simulated from a parallel-group single ascending dose (SAD) study having 6 subjects per group with doses of 10, 50, 100, 200, 400, 600 and 800 mg. Pharmacokinetic and ECG samples were collected at 0, 1, 2, 3, 4, 5, 6, 8 and 12 h after dosing. Predose ECGs were collected at −30, −15 and −5 min prior to dosing. Single-delta QTcF (dQTcF) intervals, which were the dependent variable used in the analysis, were calculated by subtracting the mean predose baseline QTcF interval from the QTcF interval at each time point.

  2. (2)

    Data were simulated from a hypothetical TQT study having 40 patients (20 males and 20 females). Subjects were randomized to receive in a crossover fashion a single-dose dose of placebo, 50, or 500 mg of drug. Three different sampling designs were tested:

    1. (i)

      Pharmacokinetic and ECG samples were collected at 0, 1, 2, 3 and 4 h after dosing.

    2. (ii)

      Pharmacokinetic and ECG samples were collected at 0, 1, 2, 3, 4, 5, 6, 8 and 12 h after dosing.

    3. (iii)

      Pharmacokinetic and ECG samples were collected at 0, 0.5, 1, 1.5, 2, 2.5, 3, 3.5, 4, 5, 6, 8 and 12 h after dosing.

Double-delta QTcF intervals (ddQTcF) were calculated in each drug treatment period by first subtracting the predose value from each post-dose time point (generating the dQTcF interval) and then subtracting the time-matched dQTcF interval in the placebo period. ddQTcF intervals were the dependent variable in the analysis.

Pharmacokinetic data were simulated from a 1-compartment model with absorption. Population mean parameters were: CL = 40 L/h; V = 125 L; and Ka = 0.5 per h. Between-subject variability was 30% for each pharmacokinetic parameter. Proportional residual variability was 10% for observed concentrations. Under this model, average maximal drug concentrations (Cmax) were ~200 ng/mL at 50 mg and ~2000 ng/mL at 500 mg (~25% CV for both). Supplemental Figs. 1 and 2 present representative concentration–time profiles for each study design.

Two types of baselines were studied. The first baseline was assumed to be a constant within an individual. This is the baseline studied by Sebastian et al. [24]. QTcF intervals in the absence of drug (QTcF drug_free ) were simulated as:

$$QTcF\left( t \right)_{drug\_free} = QTcF0$$
(4)

where QTcF0 was the baseline QTcF interval at time 0 which had a mean of 395 ms for females and 378 ms for males and a BSV of 4.2%. The second baseline studied was a more realistic, physiologically based one, reported by Grosjean and Urien [41], where QTcF intervals had a circadian rhythm. Under this model, QTcF drug_free was simulated with 2-cosinor functions:

$$QTcF\left( t \right)_{drug\_free} = QTcF0\left( {1 + A_{1} \cos \left( {\frac{\pi }{12}\left( {t - \varPhi_{1} } \right)} \right) +\, A_{2} \cos \left( {\frac{\pi }{6}\left( {t - \varPhi_{2} } \right)} \right)} \right)$$
(5)

where t is time post-dose, A 1 and A 2 are amplitudes, and Φ −1 and Φ 2 are phases. All parameters were log-normal in distribution. Model parameters were reported in Table 6 of Grosjean and Urien [41]. The population mean A 1 and A 2 were 0.0052 and 0.01 with BSV of 69 and 38%, respectively. The population mean Φ −1 and Φ 2 were 20.5 h and 14.2 h with BSV of 33 and 44%, respectively. Drug effect was simulated based on simulated drug concentrations using a standard linear model:

$$effect = \beta_{1} \times \left[ {conc} \right]$$
(6)

where β 1 , the slope, was log-normal in distribution with a BSV of 30%. The slope was systematically varied in the simulation from 0 to 0.01 ms/ng/mL. QTcF intervals in the presence of drug were equal to:

$$QTcF\left( t \right) = QTcF\left( t \right)_{drug\_free} + \,effect.$$
(7)

Observed QTcF intervals had mean QTcF(t) with normally distributed random variability of 4 ms. Supplemental Figs. 3 and 4 present representative concentration-dQTc and ddQTcF plots time profiles for each study design, respectively, under a circadian baseline.

The dependent variable (denoted DV, which was dQTcF for SAD/MAD studies and ddQTcF for TQT study) was analyzed using linear and nonlinear mixed effects models [20, 42–44]:

  1. 1.

    Linear mixed effect model with random intercept only (null model). Residual variance is simple variance matrix.

  2. 2.

    Linear mixed effect model with random intercept and drug concentration as an uncorrelated random effect. This is the standard or typical model used to analyze ddQTcF intervals. Residual variance is simple variance matrix.

  3. 3.

    Model 2 with correlated random effects.

  4. 4.

    Model 2 with quadratic concentration as a fixed effect.

  5. 5.

    Model 4 with correlated random effects.

  6. 6.

    Nonlinear Emax model with intercept. All model parameters (E0, Emax, and EC50) are treated as random effects.

  7. 7.

    Model 7 with Emax treated as a fixed effect.

  8. 8.

    Model 7 with EC50 treated as a fixed effect.

  9. 9.

    Model 7 with Emax and EC50 treated as fixed effects.

  10. 10.

    Nonlinear Emax model without intercept. Emax and EC50 are treated as random effects.

  11. 11.

    Model 10 with EC50 treated as a fixed effect.

  12. 12.

    Sigmoid Emax model with intercept. E0, Emax, and EC50 are treated as random effects. Hill coefficient γ treated as a fixed effect.

  13. 13.

    Model 12 with E0 treated as a fixed effect.

  14. 14.

    Model 12 with Emax treated as a fixed effect.

  15. 15.

    Model 12 with EC50 treated as a fixed effect.

  16. 16.

    Model 12 with Emax and E0 treated as a fixed effect.

  17. 17.

    Sigmoid Emax model without intercept. Emax and EC50 are treated as random effects. Hill coefficient γ treated as a fixed effect.

  18. 18.

    Exponential model

    $$DV = \theta_{0} \times \exp \left( {1 - \theta_{1} conc} \right)$$
    (8)

    where Emax is treated as a random effect.

  19. 19.

    Power model with intercept

    $$DV = \theta_{0} + conc^{{\theta_{1} }}$$
    (9)

    where the intercept was treated as a random effect.

  20. 20.

    Modified power model without intercept.

All random effects in the models above were assumed to be normally distributed. All models were fit using the NLMIXED procedure in SAS using maximum likelihood estimation. The best model was chosen based on prespecifying the criteria for a “best model” [45, 46]. These criteria were successful model convergence, smallest information criterion, and all parameter estimates were statistically significant (p < 0.05). Three different information criterion were tested: AIC, AICc, and BIC. For each of these information criterion, the best model was selected using that information criterion and the model-averaging predictions were done based on weights using that information criterion. The degree of prolongation was estimated at Cmax values of 200, 500, 1000 and 2000 ng/mL using the best model and by model-averaging. For both the best model and model-averaging approach, 90% confidence intervals were also calculated. For the model-averaged confidence intervals, the approach of Burnham and Anderson [21] was used. Specifically, the 2-sided 90% confidence intervals were calculated for each model. The upper interval was chosen as the 1-sided 95% confidence interval and then the model averaged average confidence interval was calculated using the same weights used to define the model-averaged mean estimate.

The following endpoints were calculated for each combination of the slope (as defined by Eq. (6)) and true Cmax value:

  1. 1.

    The percent ratio of the best model point estimate to the MA point estimate (calculated as the (best model point estimate)/(model averaged estimate) × 100%);

  2. 2.

    The percent ratio of the best model 2-sided 90% CI range to the MA 2-sided 90% CI;

  3. 3.

    The percent ratio of the best model upper 2-sided 90% CI to the MA upper 2-sided 90% CI; and

  4. 4.

    Whether the 90% 2-sided CI for the best model and MA approach contained the true drug effect (coverage).

A total of 200 replicates were generated for every combination of sampling scheme and slope and the marginal median values reported.

TQT simulation with non-inclusive data generating model (effect of gross model misspecification)

One concern about the validity of the SAD/MAD and TQT results was that the data generating model (Eq. (6)–(7)) was similar to one of the candidate models for the best model and MA approach, i.e., a linear model was used to simulate the data and to analyze the data in both the best model and MA approach. This may result in an inherent bias in how well these methods are performing. To examine the impact of this bias, the TQT simulation was repeated using a circadian baseline with three data generating models:

$$effect = \exp \left( {\frac{Slope}{7}Conc} \right) + Slope\sqrt {Conc} .$$
(10)
$$effect = 12\left( {1 - \exp \left( { - \frac{Conc}{Slope \times 50,000}} \right)^{Slope \times 100} } \right).$$
(11)
$$effect = \left\{ {\begin{array}{ll} 0 & {Conc{ < 1000}} \\ {\frac{{10 \times Conc^{2} }}{{\left( {Slope \times 100000} \right)^{2} + Conc^{2} }}} & {Conc \, \ge { 1000}} \\ \end{array} } \right..$$
(12)

These general shape of the effect profiles are shown in Supplemental Fig. 6. Note the difference between Eqs. (10)–(12) and Eq. (6). The data generating model was not one of the candidate models used in the analysis. The new drug effect model was not meant to simulate reality but to ensure that the data generating model was different than the candidate models used to fit the data.

Results

SAD/MAD studies

Figure 2 presents the median ratio percent of the best model to the model-averaged results for the SAD study under a constant and circadian QTcF baseline. A value greater than 100% indicates the best model had a higher value than the MA value. All the results were within ~90 to ~105% with most of the simulations being near 100%, indicating that the best model and MA had similar predictions and confidence intervals. There were small differences between the information criteria selection metrics with BIC generally producing greater agreement between the two approaches. For the best model approach, Supplemental Fig. 5 presents a stacked bar chart of the most frequently chosen best model for each study design, baseline, and information criterion used for model selection. Two things became apparent in the data. First, there were small differences in which model was chosen most frequently using the different information criterion with the BIC being more conservative at declaring a drug effect than AIC or AICc when no drug effect was present. Second, there was a difference in which model was chosen most frequently depending on whether the baseline was constant or circadian in a SAD study design, but not so much under a TQT design. When a drug effect was present, Models 2, 9, and 15 were the most frequently chosen model across all study designs and baselines.

Fig. 2
figure 2

Panel plot from Monte Carlo simulation of the ratio of the best model estimate to the MA estimate for the SAD study design. The median ratio in percent of the best model estimate to the model averaged estimate plotted as a function of the slope of the true slope parameter stratified by selection criteria and different levels of Cmax (200, 500, 1000 and 2000 ng/mL). Plotted are the mean, upper 2-sided 90% CI, and CI range. A value of 100% implies no difference between estimates. Legend: open blue circle, point estimate; dark red plus, CI range; green cross, upper confidence interval (Color figure online)

Full size image

Figure 3 presents the coverage for the approaches. For a 90% confidence interval the coverage should be approximately 90%. Coverage was mostly similar between the approaches but sometimes coverage was worse with the best model approach (see Cmax 2000 ng/mL with slope = 0.001). Coverage tended to decrease with increasing Cmax but approached their asymptote as the signal-to-noise increased, i.e., as the slope was increased. Coverage was uniformly lower with a circadian rhythm baseline than coverage seen with a constant baseline. Little difference was observed between confidence intervals derived from the best model compared to the MA approach, but coverage did not approach nominal values and was smaller coverage than expected. At the highest two Cmax values, a difference using BIC as the model selection metric was noted—coverage tended to be even smaller than the other metrics with the MA approach having slightly better coverage than the best model. The results from the SAD simulations, using either a constant QTcF baseline or circadian rhythm baseline, or using AIC, AICc, or BIC as the metric for model selection, no appreciable difference between the best model and MA approach was generally observed.

Fig. 3
figure 3

Panel plot from Monte Carlo simulation coverage for the best model approach and the MA approach for the SAD study design. The percent of simulations where the 2-sided 90% CI contained the true drug effect (coverage) for the best model approach and the MA approach. Compared were models chosen or weighted based on AIC, AICc, and BIC. A 90% CI should have an approximate coverage of 90% (gray line). Legend: open blue circle best model using AIC, open brown triangle model averaged using BIC, brick red dashed line with plus sign best model using AICc, purple dashed line with open square model averaged using AICc, turquoise dashed and dotted line with X symbol best model using BIC, green dashed and dotted line with asterisk model averaged using BIC (Color figure online)

Full size image

TQT studies

Figure 4 presents the median ratio percent of the best model to the model-averaged results for the TQT study. All the results were within 95–105% and practically all results were near 100% indicating that the best model and MA had similar values. Figure 5 presents the coverage results for the TQT study. Coverage under the TQT design was near the 90% nominal value except when there was only 5 sampling points per subject. Under these conditions, coverage dipped to near 40% in some circumstances. But for 9 and 13 sampling points per subject, coverage was near nominal levels. Regardless of the conditions, no difference was observed in the coverage between the best model and MA approach.

Fig. 4
figure 4

Panel plot from Monte Carlo simulation of the ratio of the best model estimate to the MA estimate for the TQT study design. The median ratio in percent of the best model estimate to the model averaged estimate plotted as a function of the slope of the true slope parameter stratified by selection criteria, different levels of Cmax (200, 500, 1000 and 2000 ng/mL), and different sampling schemes (5, 9, and 13 data points). Plotted are the mean, upper 2-sided 90% CI, and CI range. A value of 100% implies no difference between estimates. Legend: open blue circle, point estimate; dark red plus, CI range; green cross, upper confidence interval (Color figure online)

Full size image
Fig. 5
figure 5

Panel plot from Monte Carlo simulation coverage for the best model approach and the MA approach for the TQT study design. The percent of simulations where the 2-sided 90% CI contained the true drug effect (coverage) for the best model approach and the MA approach. Compared were models chosen or weighted based on AIC, AICc, and BIC. A 90% CI should have an approximate coverage of 90% (gray line). Legend: open blue circle best model using AIC; open Brown triangle, model averaged using BIC; brick red dashed line with plus sign, best model using AICc; purple dashed line with open square, model averaged using AICc; turquoise dashed and dotted line with X symbol, best model using BIC; green dashed and dotted line with asterisk, model averaged using BIC (Color figure online)

Full size image

Results of TQT simulation with non-inclusive data generating model (effect of gross model misspecification)

With a data generating model that is very distinct from the models used to analyze the data, some differences between the best model and MA approach emerge. Figure 6 presents the median ratio percent of the best model to the model-averaged results for a non-inclusive data generating model using AIC as the selection metric. Supplemental Figs. 7 and 8 show the results for AICc and BIC, respectively. With Eq. (10), which was an exponentially increasing function with no asymptote, differences were observed with 5 sampling points but decreased with increasing sampling points such that at 13 sampling points there was no difference between the best model and MA results. With Eq. (11), which was a hyperbolic model similar in shape to an Emax model, there was no difference between best model and the MA approach. With Eq. (12), which was a step function at low slope values but changing to an Emax type model at higher slope values, differences were not seen with 5 sampling points, but were observed with 9 and 13 sampling points. At the midpoint of the concentration range, 500 and 1000 ng/mL, with both 9 and 13 sampling points, the best model estimates and confidence intervals were considerably larger than the MA approach, but this flipped at the highest Cmax examined, 2000 ng/mL, wherein the MA estimates and confidence intervals were larger. Under all conditions, the results were within −10 to +30%.

Fig. 6
figure 6

Panel plot from Monte Carlo simulation of the ratio of the best model estimate to the MA approach for the TQT study design where the data generating model was noninclusive, the baseline was circadian, and using AIC as the selection metric. The median ratio in percent of the best model estimate to the model averaged estimate plotted as a function of the slope of the true slope parameter stratified by the data generating mechanism, different levels of Cmax (200, 500, 1000 and 2000 ng/mL) and different sampling schemes (5, 9, and 13 data points). Plotted are the mean, upper 1-sided 95% CI, and CI range. A value of 100% implies no difference between estimates. Legend: open blue circle, point estimate; dark red plus, CI range; green cross, upper confidence interval (Color figure online)

Full size image

For the best model approach, Supplemental Fig. 9 presents a stacked bar chart of which model was chosen most frequently stratified by the data generating equation and information criterion used for model selection. Like the previous simulations, there was little difference in which model was chosen most frequently in terms of information criterion used for model selection. Because of the very different data generating mechanisms, it would be inappropriate to draw conclusions across equations. What was surprising, however, was how often a linear model was chosen despite the curvilinear nature of the data generating mechanism.

Figure 7 presents the coverage results for the noninclusive data generating models. Although there was no difference between the MA and best model approach, coverage depended on the true Cmax concentration and slope and could be quite different from nominal values. Under many conditions the coverage was horrible. For instance, the coverage using Eq. (12) with 5 sampling points when the Cmax was 2000 ng/mL showed that the coverage was less than 20%, which means that in fewer than 20% of the confidence intervals generated was the true drug effect contained within (the nominal effect should be 90% for a 90% CI). Nevertheless, these additional simulations, which were quite artificial and were purposefully designed to test model misspecification, could not detect any real differences between the MA and best model approach.

Fig. 7
figure 7

Panel plot from Monte Carlo simulation coverage of the best model estimate to the MA approach for the TQT study design where the data generating model was noninclusive and the baseline was circadian. The percent of simulations where the 2-sided 90% CI contained the true drug effect (coverage) for the best model approach and the MA approach. Compared were models chosen or weighted based on AIC, AICc, and BIC. A 90% CI should have an approximate coverage of 90% (gray line). Legend: open blue circle, best model using AIC; open brown triangle, model averaged using BIC; brick red dashed line with plus sign, best model using AICc; purple dashed line with open square, model averaged using AICc; turquoise dashed and dotted line with X symbol, best model using BIC; green dashed and dotted line with asterisk, model averaged using BIC (Color figure online)

Full size image

Discussion

Cleaskens and Hjort [47] showed that inference based on a model post-selection results in standard errors that are too small (resulting in too small of CIs) and the associated point estimates may be biased in the case of a normal linear model. They show analytically and through simulation that model-averaging can correct for post-model selection bias. Sebastian et al. [24] applied model averaging to the concentration-QT modeling setting and showed few differences between the traditional best model and MA approach. They concluded that either approaches could be used but that whichever method is selected should be systematically used. Their results may be biased, however, because the data generating mechanism for their simulations was the same as one of the models used to analyze the data. Of course the results would appear favorable under these conditions.

This paper extends those results by using data generating mechanisms that were more realistic (circadian rhythm baseline) and, despite their artificial nature, used data generating models that were very distinct from the models used to analyze the data. The results from the simulation in this paper show that Cleaskens and Hjort’s concern is unnecessary in the case of concentration—QT modeling. All the simulation results suggest that the current approach of making predictions of QT interval prolongation conditional on a best model results in point estimates and confidence intervals of nearly equal predictability as MA estimates. When differences are noted, it was the best model approach that resulted in estimates higher than the MA approach, but these differences were often small, usually less than 20%.

The results also suggest that model averaging is practically insensitive to the choice of the information criteria used for model weighting and best model selection. The ratios of best model to MA were nearly identical for AIC, AICc, and BIC. There were some differences with regards to coverage, with MA showing a slight edge, but the absolute differences were small enough to be ignored. Further, the choice of best model was largely the same regardless of the information criterion used, although AIC and AICc seemed more sensitive at declaring a drug effect when a drug effect was not present, i.e., when the slope was 0. This result is consistent with the known conservativeness of BIC because of its enhanced penalty for adding parameters to a model.

An early reviewer of this paper was concerned about the poor coverage results for some of the simulations. For the SAD study, when the data generating mechanism was a linear relationship between drug and QT interval prolongation and using a circadian baseline, coverage was often less than the nominal 90% and, in some cases, as low as 40–60%. The reason for the poor coverage was likely due to poor correction of the underlying circadian rhythm using a single-delta correction in the SAD study. With this correction, the predose baseline value is subtracted from all postdose values; it will not completely control for the circadian nature of the interval throughout the day, particularly when the rhythm is at its peak or nadir. Two points support this hypothesis. One is when the TQT and SAD simulations were conducted without having a circadian component as part of the data generating mechanism. In this case, coverage levels approached near nominal levels and were similar to reported values in Sebastian et al. [24]. This explanation is also supported by the results of the TQT simulation. In those simulations, double-delta correction is expected to better control for underlying circadian rhythms and the results showed this as coverage improved to near nominal levels when there were more than 9 or more sampling points. One solution to control for this misspecification of baseline correction is to include nominal time in the model as a fixed factor effect; this may be useful to control for circadian effects in the data and future models should consider this [48].

Coverage was indeed quite poor when the data generating mechanism was not of the same functional form as one of the analysis models. In some cases, coverage was U-shaped, monotonically decreasing, or reverse U-shaped—and this was with a TQT design. Coverage could not be improved using a MA approach. This is because the models that were chosen as the candidate set of models were not even close to the functional form of the data generating mechanism. It’s expected that a best model approach will not give any kind of reasonable coverage when the model is markedly misspecified, but it also highlights that neither will the MA approach when all the candidate models are misspecified. When the data generating model was of a different functional form from any of the candidate analysis models model-averaging will not save an analysis from a poor choice of models. One or more models in the set of analysis models must have a suitable functional form; you can’t just use any set of models and then use model-averaging to get a reasonable prediction estimate. These results suggest that care should be taken to ensure that a reasonable selection of models are chosen for the set of candidate models used in model averaging.

While these results suggest that it is unnecessary to model average predictions, MA may offer some advantages. Bloomfield [49] cautioned that choosing an incorrect model may lead to an inaccurate estimate of the slope and, as by corollary when applied to a C-QT analysis, an inaccurate point estimate of the predicted QTcF interval. Model-averaging could protect against such model misspecification. In fact, the MA approach fits in nicely with George Box’s [50] quote about all models being wrong. The MA approach assumes that no model is right and that the true prediction lies somewhere between all the predictions from a set of reasonable candidate models. This may be more palatable to a non-technical consumer of the data compared results from a best model approach because there is always the question of whether you have “the right model”. As modelers, we know there is no right model, but to a nontechnical reviewer that subtlety is lost on them. Using an estimate from a large set of candidate models could offer protection and have greater face validity than results obtained based on a single model.

What is appealing about the MA approach is that the two methods appear to converge to the same results in cases of reasonable signal to noise with a large number of samples used in the analysis. Why the results were so similar may be that 1 or 2 models in the MA approach dominate the weights of the other models, in such a case, it is likely the best model and MA result will converge to the same value. In the limiting case, where the best model is far and away better than any other competitor models, the model-averaging estimate will be the best-model estimate since its weight will be 100%. In most other cases, however, the model-averaging estimate will be a blend of a few different models. For five competing models, a difference of 7 points in the AIC will result in the best model accounting for at least 90% of the weighted estimate. In the simulation above, where there were 20 different models, a difference in AIC of at least 10 points was needed for the best-model to account for 90% or mores of the weighted estimate.

In summary, while the current practice using the best model produces reasonable estimates, the MA approach can further strengthen the conclusions drawn from a concentration-QTc interval analysis. These results show under most circumstances, the best model approach and MA approach give similar results and when they do differ they do so within a reasonable degree of error. Further, the MA approach is relatively easy to perform, requires no additional models than already performed for the best model approach, and offers an additional layer of confidence in cases where there might be model misspecification or model uncertainty.