Abstract
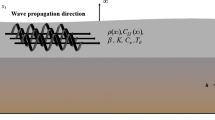
This paper developed a simplified 2D semi-analytical model to investigate the dispersion characteristics of propagating guided wave (GW) modes in functionally graded material (FGM) plates. The model was developed using the global matrix method. FGM plate is a composite plate made up of different materials in a graded pattern. Ultrasonic Guided waves propagated through FGM plates retain distinct dispersion characteristics. Therefore, it is significant to excerpt the correlation between the dispersion curves of GWs and the material properties of FGM plates. The volume fraction, which describes the material characterization of FGM plates, is calculated using the power law. Group velocity, phase velocity, and frequency–wavenumber dispersion curves are used to determine the dispersion characteristics of FGM plates. The 2D semi-analytical model is used to investigate the dispersion characteristics of GWs in various types of FGM plates. The normalized vertical displacements generated by transient surface excitations using the developed model were compared to those obtained using Abaqus numerical simulation and found to be in good agreement. The developed model shows that it can accurately predict dispersion properties and time-history responses of FGM plates. It is envisaged that these results are expected to provide theoretical guidance for nondestructive evaluation (NDE) and material characterization of FGM plates.
Graphical Abstract

Similar content being viewed by others
Avoid common mistakes on your manuscript.
Introduction
Functionally graded materials (FGM) are the newest materials in the composites group [1, 2] consisting of a graded pattern of material composition. The FGM plates have a lot of applications in nuclear projects, space systems, energy storage, communication, and civil engineering. Ultrasonic-guided wave-based techniques provide an accurate procedure for structural health monitoring of composite structures [3]. Tuning of appropriate Guided ultrasonic waves (GUWs) modes plays an important role in the nondestructive evaluation and characterization [4] of material elastic properties. When compared to ultrasonic bulk waves, GUWs provide a longer inspection range, higher versatility, and optimum coverage of the waveguide cross-section.
The dispersion curves are a set of curves that show how wave modes propagate in a given geometry. The dispersion associated with each wave mode can be seen using these curves. Group velocity dispersion curves are highly useful for determining guided wave modes in guided wave tests. Group velocity represents the velocity of energy transportation.
The general behavior of wave propagation in isotropic and anisotropic media is documented in standard textbooks [5,6,7]. It is usually very difficult to obtain analytical solutions for wave propagation in an inhomogeneous plate with an arbitrary material variation [8]. As a result, the study will be aided by the use of an appropriate laminate model. This is very feasible because the accuracy of results can be controlled by choosing a proper number of layers [9]. The formulation of a theoretical model for the investigation of dispersion properties and the elastodynamic response of isotropic and composite structures is addressed in several studies. Reddy [10] employed a shear-flexible finite element to investigate the transient response of layered anisotropic composite plates. Yang and Yuan [11] examined the transient wave propagation in isotropic plates and showed that the higher-order theory can predict wave behavior closely with exact linear wave solutions at higher frequencies. Santosa and Pao [12] used the method of generalized rays to calculate the transient wave propagation in isotropic plates. Liu et al. [13] introduced a hybrid numerical method for transient wave analysis in anisotropic laminated plates. Lih and Mal [14] developed an approximate plate theory for wavefield calculations in composite laminates. Nastos et al. [15] proposed the finite wavelet domain method based on the layer-wise laminate plate theory for wave propagation analysis. Mahmoud et al. [16] suggested a model, where a 3-D problem was converted into a series of 2-D problems, each representing a plane wave along a given direction of propagation. Liu et al. [17] used a double Fourier transform to analyze transient behavior in an anisotropic laminated plate due to a point load. Chen et al. [18] constructed a reverberation matrix and presented the characteristic equation governing waves' dispersion. Chakraborty et al. [19] applied the Spectral Finite Element Method (SFEM) based on the first-order shear deformation plate theory for the formulation of the spectral element in the frequency domain and approximated the solutions with trigonometric polynomials.
Yu et al. [20] applied the Legendre orthogonal polynomial series expansion approach for guided wave analysis in FG spherical curved plates. Bennai et al. [21] derived wave equations by the principle of minimization of energies. Azizi et al. [22] developed a new set of differential equations that predicts the propagation and dispersion of first symmetric and antisymmetric Lamb wave modes in FGM plates. Moradi-Dastjerdi et al. [23] explained the stress wave propagation of orthotropic plates made of FGM and dynamic responses are evaluated using a mesh-free method. Bednarik et al. [24] used the transfer matrix method for studying the elastic waves propagating in the FGM plates. Yang et al.[25] proposed a boundary element method (BEM) for wave propagation models in FGM in the frequency domain. Lin et al. [26] analyzed wave propagation in FGM plates using the transform method. Amor et al. [27] used Peano-series expansion method for finding the lamb wave modes in FGM plates. Karami et al. [28] developed a nonlocal shear deformable FGM plate model for wave analysis. Othmani et al. [29] studied the dispersion characteristics of Lamb waves in FGM plates using the Legendre polynomial series expansion method. Zhu et al. [30] developed dispersion curves that are generally used for anisotropic viscoelastic/elastic FGM plates. Jie et al. [31] analyzed guided wave propagation behavior in FGM structure by using the three-dimensional elasticity theory. Hebaz et al. [32] proposed the discontinuous Galerkin finite element method (DG-FEM) for the evaluation of Lamb wave characteristics in FG plates.
While the above methods either involved finite element (FE) discretization or approximation along with the thickness, a 'global matrix method' was presented by Mal [33], where the stresses and displacements in various layers were exactly represented in the frequency–wavenumber domain. It was mentioned that this method can eliminate the problems of numerical instabilities at higher frequencies that appear in the “transfer matrix method” [34] and the surface impedance matrix method [35]. In the “'Global matrix method” [35], a large single matrix is assembled, using systems of equations from individual layers within the multilayer system. The speed of computation is relatively slow due to the large matrix size. This method was later adopted by Lih and Mal [14] for the formulation of guided wave propagation problems in laterally unbounded multilayered composite laminates subject to time-harmonic disturbances. In these papers, triple integral transforms were used to formulate the response problem, two in space and one in the time domain. Using this approach, the most computational effort is involved in evaluating the double wavenumber integral. To evaluate the double integral for dissipative media an ''adaptive surface-fitting scheme'' using material dissipation was used [14].To reduce the computation effort, Banerjee et al. [36] proposed a new wavenumber integral method, wherein the double integral was transformed, using contour integration, into a single integral, which can then be evaluated numerically using conventional integration schemes. Later, Pol and Banerjee [37] developed a simplified 2D semi-analytical model based on a global matrix method for investigating the dispersion characteristics of propagating guided wave (GW) modes in multilayered composite laminates due to transient surface excitations. On the other hand, commercially available finite element packages may handle wave propagation problems with structures of complex geometries and can capture reflections from the lateral boundaries of the structure. The FE approach is more computationally intensive than the previous theoretical methods.
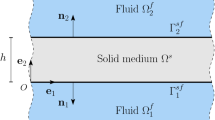
It is evident from the literature review that simplified theoretical models for determining the effect of a particular GW mode on the time-domain response of an FGM plate under high-frequency transient surface loading are not available. In this study, the FGM plate is considered as a multilayer composite plate (Fig. 1), and the properties of individual layers are regarded as constant. The properties at the middle surface of individual layers are determined by using the volume fraction power law. The vertical response and dispersion behavior of FGM plates are analyzed using the 2D semi-analytical method. The phase velocity, group velocity, and frequency–wavenumber dispersions curves, of FGM plates of different volume fraction indexes, are evaluated. The surface motion is computed for transient narrowband vertical excitations and the normalized displacements were correlated with those obtained from the numerical simulation using Abaqus FEA. For validation of the semi-analytical model with available results in the literature an aluminum–zirconia FGM square plate is used. The studies are further extended for the aluminium–alumina FGM plate and carbon–silicon carbide FGM Plate with different volume fraction indices. It is shown here that the semi-analytical model is precise and gives correct results.
Characteristics of the FGM plate
The FG plate's material composition is varying continuously in the thickness direction, with metal and ceramic materials on the bottom and top surfaces, respectively. The power–law distribution of the volume fraction is given in Eq. (1)
where h denotes the thickness of the plate and k denotes the volume fraction index. The material constants such as Modulus of elasticity and Poisson ratio, density of the FGM plate, denoted by P(z), at a depth of ‘z’ from the middle surface can be written as Eq. (2)
where t and b denote the plate’s top surface and bottom surface, respectively.
The FGM plate properties are graded through volume fraction power law distribution and the corresponding numerical values are illustrated in Fig. 2. For instance, k = 1, represents the linear variation in the composition of the material in the FGM Plate. The value k = 0 for the ceramic plate and k = ∞ for the metal plate.
Theoretical and Numerical modeling
Mal [33] developed a global matrix method for the solution of 3D wave propagation problems in laterally unbounded multilayered anisotropic media subjected to time-harmonic disturbances. The solution for total 6N unknown constants for an FGM plate comprising N layers was derived from a global matrix of (6N × 6N) which was developed by applying interface continuity and stress conditions at the free surfaces [33]. The displacements and stresses are correlated in the frequency and wavenumber domain using six unknown constants. From the global matrix of size 6N × 6N, interface continuity conditions and stress conditions on the free surface were used to obtain the values of the 6N unknown constants. The present method does not suffer numerical instabilities at higher frequencies, as it suffers in the Thomson–Haskell method [38, 39]. Later, Pol and Banerjee developed a formulation for the 2D model for the transversely isotropic model [37] using the global matrix method.
Matrix Representation of the Solution Within a Layer of FGM Plate
The global matrix method is applied to a simplified 2D plane strain model of a laterally unbounded FGM plate in the X1–X3 plane (Fig. 1). For a 2D problem, the governing equations of motion [37] in a layer of thickness H are given by Eqs. (3) and (4).
where the displacement and stress components are denoted by \({u}_{i}\) and \(\sigma_{ij}\)\(\left( {i = 1,3;j = 1,3} \right)\), respectively, and ρ is the density of the material. The stress–strain relationships (Hooke’s law) for the plate are given in Eq. (5)
where \({u}_{ij}\) is the first derivative of the displacement components, and \({c}_{11}\) through \({c}_{55}\) are the elastic material constants. We further assume that the potential functions (\({\phi}_{1},{\phi}_{3}\)) are related to the displacement components through Eq. (6)
This is under the assumptions of the displacement field for corresponding three-dimensional problems in a transversely isotropic media without loss of any generality [40]. Substituting this displacement field in the stress–strain relationships in Eq. (5), the governing equations of motion in terms of potential functions [37] can be expressed in matrix form as in Eq. (7)
By performing the following Fourier transformation on the field variables [37] from the spatial and time domain to the frequency (ω) and wavenumber (k1, k3) domain \(\hat{{\phi}}(k_{1} ,k_{3} ,{\omega}),\) we get Eqs. (8) and (9).
By applying the Fourier transform to Eq. (7), the equations of motion in the frequency and wavenumber domain can be expressed in matrix form as in Eq. (10).
The solution to Eq. (10) is referred to as eigenvalue problem. For a non-trivial solution of the potential functions [37], the determinant of the 2 × 2 matrix has to be zero, which will give \(k_{3}^{2}\) as roots (eigenvalues) as a function of \(k_{1}\). The characteristic equation is given by Eq. (11)
where \({a}_{1} = \frac{c_{33}}{\rho},\; {{a}_{2}} = \frac{c_{11}}{\rho},\;{a}_{5} = \frac{c_{55}}{\rho}\) and \(a_{3} = \frac{{\left( {c_{13} + c_{55} } \right)}}{\rho }.\)
Equation (10) can be solved to obtain the two roots of \(k_{3}^{2}\) as
Thus, the roots of \({\text{k}}_{3}\) can be defined by the vertical wavenumbers \(\eta_{1}\) and \(\eta_{2}.\) The “vertical” wavenumbers.
\({{{\eta}}}_{{{i}}}\), \((i = 1,2)\) are subject to the restriction, Im(\(\eta_{i}\)) ≥ 0, to ensure the outgoing wave condition at infinity and exponential decay of the evanescent waves in the layers at high frequencies. The next step is to reduce by one dimension the integrals in Eq. (7) using a contour in the complex \(k_{3}\)-plane consisting of the real axis together with a large semicircle in the upper half-plane, the contributions from this semicircle being vanishingly small [40]. With this device, the integration with respect \({\text{k}}_{3}\) can be replaced by appropriate contributions from the roots of the integrands.
Therefore, the matrix form of the general solution of the potential function [37] can be represented as Eq. (12)
where \({{q}}_{ij}\) are the eigenvectors and are given by
The quantities \({{A}}_{{{i}}}^{ + }\) and \({{A}}_{{{i}}}^{{{ - }}}\)\(\left( {i = 1,2} \right)\) are four unknown constants, which control the terms associated with upward and downward going waves as determined by the vertical wavenumbers ηi [37]. It is therefore customary to express stresses (\({\hat{{\sigma }}}_{{1{{3}}}},\;{\hat{{\sigma }}}_{{{{33}}}}\)) and displacements (\({\hat{{u}}}_{1},{\hat{{u}}}_{3}\)) in the frequency and wavenumber in condensed matrix form as in Eq. (13).
where
The quantity \({{E}}_{ + } (x_{3} )\) and \({{E}}_{ - } ({{x}}_{3} )\) stands for the downward and upward going wave respectively. For a given problem, the unknown constants will be calculated [37] using the imposed displacement and stress boundary conditions at the top and bottom layers.
Global Matrix Formulation for the FGM Plate
To facilitate the application of the appropriate boundary conditions at the top and bottom surfaces [37] and the interfaces for an FGM plate comprising of N layers (see Fig. 1), it is convenient to introduce the four-dimensional “stress–displacement vector: \(\left\{ {\hat{S}^{m} } \right\}\)”, in the transformed domain through Eq. (14).
where m denotes the layer number.
The arguments, \(k_{1}\) and \(\omega\) in \(\left\{ {\hat{S}^{m} } \right\}\) will be omitted for brevity. It should be noted that in absence of interfacial forces, \(\left\{ {\hat{S}^{m} (x_{3} )} \right\}\) is continuous in the domain, \(x_{3}^{m - 1} < x_{3} < x_{3}^{m}\) and that in the mth layer, \(\left\{ {\hat{S}^{m} (x_{3} )} \right\}\) can be expressed in a partitioned matrix product form as Eq. (15)
where \(A_{ \pm }^{m}\) are complex constants related to down-going and upgoing waves within the mth layer, and \(E_{ \pm }^{m}\) are the ‘vertical’ propagation vectors given by Eq. (16)
The 4N constants \(A^{m}\) (m = 1, 2,…, N) must be obtained from the interface conditions and the appropriate boundary conditions on the top and bottom surfaces of the plate.
To demonstrate the solution procedure, we first consider the case where a time-dependent normal point excitation (line load along x3) is applied to the top surface of the plate denoted by \(f(t)\delta\), where \(\delta\) is the usual ‘Dirac delta function [37], and its double Fourier transform by \(\hat{f}(\omega )\). Thus, the stress boundary conditions at the topmost surface and the lowermost (Nth) free surface are given as Eqs. (17a) and (17b)
where \(\left[ {{\hat{{Q}}}^{1} } \right] = \left[ {{{Q}}_{21}^{1} {{Q}}_{22}^{1} {{E}}_{ - }^{1} } \right],\;\left[ {{\hat{{Q}}}^{{{N}}} } \right] = \left[ {{{Q}}_{21}^{\rm N} {{ E}}_{ + }^{{{N}}} {{Q}}_{21}^{\rm N} } \right],\;\left[ {{\hat{{F}}}} \right] = \left[ {\begin{array}{*{20}c} {{\hat{{\sigma }}}_{{{{13}}}} } \\ {{\hat{{\sigma }}}_{{{{33}}}} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {{0}} \\ {{\hat{{f}}}} \\ \end{array} } \right].\)
If there is no delamination at the mth interface, the traction and displacement components must be continuous across the interface parallel to the X1X2—plane, which gives us:
where \(X_{3}^{m}\) is the location of the interface between the layers m and m − 1. Thus, at the mth interface
Finally, the above Eqs. (17a), (17b) and (18) can be represented [37] in a condensed global matrix (4N × 4N) form as Eq. (19).
The determinant of the 4N \(\times\) 4 N matrix will produce the dispersion relation of the form as in Eq. (20).
We can evaluate the roots of \({k}_{1} \mathrm{for range of values of }\omega ,\) and subsequently find out the phase velocity C by the relation \(C = \, {\omega \mathord{\left/ {\vphantom {\omega k}} \right. \kern-0pt} k}_{1}\). The phase velocity dispersion curve is obtained by plotting the phase velocity ‘C’ against the frequency, \(\omega.\) The group velocity dispersion curve is obtained by plotting group velocity ‘Cg’, versus the frequency \(\omega\) using the relation \(C_{g} = d\omega/dk_{1}\). Group velocity is usually considered to be the propagation speed of a wave packet (envelope) with a central frequency carrying maximum energy, whereas, each frequency component in the packet is propagated at its phase velocity. It should be noted that for a fixed frequency, Eq. (18) has a finite number of real roots and an infinite number of complex roots [37]. The real roots represent the propagating guided waves in the plate, while the complex roots represent non-propagating modes that decay exponentially with propagation distance from the source.
The unknown constants [A] are determined using LU decomposition of Eq. (19). The vertical surface displacement (x3 = 0) can therefore be written in the following form Eq. (21).
It is now desired to invert the solution back to the spatial domain through Eq. (22).
The amplitudes of the non-propagating modes become negligible in comparison with the propagating modes at distances from the source larger than only a few multiples of the plate thickness [41]. Since this condition is satisfied in most guided wave applications, the residue contributions from the complex roots can be neglected without impacting the accuracy of the results [37]. Thus, the integration in Eq. (22) can be solved exactly by applying Cauchy’s residue theorem [42] on the real roots of \(k_{1} (k_{r}\), where r = 1 to NR, NR = no. of real roots) as Eq. (23).
Finally, an inverse Fourier transform is performed to obtain the results in the time domain.
Considering the case of time-dependent point excitation on the top surface and applying the stress boundary conditions at the free surfaces of the plate, the responses at the desired location can be obtained.
Dynamic Analysis Using Numerical Simulation
A 4-noded 3-D linear shell element (S4R) was employed in the numerical modeling with commercially available finite element software Abaqus FEA. The S4R element is a three-dimensional, doubly-curved, four-node shell element with six degrees of freedom per node that uses bilinear interpolation. For guided waves, narrowband tone burst excitation has been used. A 5-cycle Hanning sine pulse is used as the source of excitation. Excitations of various central frequencies are used to determine the vertical response. The group velocity of a propagating guided wave mode is obtained from the time-displacement response data of the received signal as explained in Sect. 4. Material characterization is attained by plotting group velocity dispersion curves. An explicit scheme is used for dynamic analysis. S4R elements are used because the structure’s loading and geometry are axisymmetric. Mindlin–Reissner type of flexural theory that includes transverse shear is used for the small-strain shell elements analysis. In addition to requiring less time to run the analysis, the reduced integration has an outstanding impact on the accuracy of the element for a given problem. The time increment size should be small enough to cover the smallest natural period. The element size should have been small enough just to capture wavelength but not so small that the wave passes through it in a single increment. Using Abaqus FEA, all input data must be entered in consistent units.
Results and Discussions
The FGM plate is divided into 20 layers for analysis purposes both in semi-analytical models and numerical simulations. Each layer is considered isotropic. The density, Modulus of elasticity, and Poisson’s ratio of individual layers are determined by using power law.
In the 2D-semi analytical model, the FGM plate is considered with semi-infinite boundary conditions to avoid edge reflections. FGM square plates of 0.5 m sides are considered for the numerical simulation. The thickness, density, and stiffness coefficients of individual layers are given as input parameters in the semi-analytical model and the dispersion curves are obtained for different k values. The model is validated using Literature results. The results are also verified with the FEA-based Abaqus simulation.
For the numerical simulation, the representation of the FGM plate along with a source of vertical transient excitation and receivers is shown in Fig. 3. A 5-cycle Hanning sine pulse is used as the source of excitation. The receiver is located at 0.1 m (node1) and 0.2 m (node2) distance from the source of excitation as shown in Fig. 3. The group velocity of a propagating guided wave mode in the semi-analytical model and simulation is obtained from the time-displacement response data of the received signal by Eq. (24).
where ∆t is the interval of time between the peaks of time-displacement response envelopes of the propagating mode in the received signal, at the receivers of distance ∆s between them.
Numerical examples for the calculation of dispersion curves in FGM plates are presented to verify and validate the semi-analytical model. We have used the MATLAB program to solve 2D semi-analytical models. From the time-displacement data of the developed models, wavelet transformation of the signal is carried out by using the AGU-Vallen tool, and the group velocity of the guided wave is further computed to validate the semi-analytical model. The wave propagation study is carried out on aluminium zirconium FGM plates, aluminium alumina FGM plates, and Carbon Silicon carbide FGM plates of different volume fraction indices (k values), and dispersion characteristics are evaluated for material characterization.
Aluminum Zirconium FGM Plate
The semi-analytical model is developed for the Aluminum Zirconium FGM plate. For validation of the model, the problem solved in the paper by Dan Sun et al. [43] was used. Material properties of the FG plate are tabulated in Table 1. The material properties are assumed to vary continuously with thickness and follow a volume fraction power law. Dan Sun et al. [41] utilized Hamilton's principle for developing wave propagation equations in the FGM plate by considering the effects of transverse shear deformation and rotary inertia. The width and thickness of the FGMplate are 0.2 m and 0.01 m. The material properties presented in the Table1 are taken from Praveen and Reddy [44]. Dan Sun et al. [43] plotted frequency–wavenumber curves for different k (k = 0,0.5,1.5) values.
The thickness, density, and stiffness coefficients of individual layers are given as input parameters in the semi-analytical model and the dispersion curves are obtained for different k values. The proposed method utilizes two fundamental Lamb wave modes, A0 and S0, to characterise FGM plates. The dispersion curves such as the phase velocity curves, group velocity curves, and frequency–wavenumber curves of FGM plates are illustrated in Fig. 4a to f. The obtained results are compared to those found in the literature, as shown in Fig. 5, showing excellent agreement. The FGM plate with k = 0 (zirconia) has the highest phase velocity and group velocity of guided waves, followed by the FGM plate with k = 0.5, and phase velocity and group velocity reduce with an increase in k value. The frequency of wave propagation in the FGM plate decreases as the volume fraction index k is increased. The asymmetric A0 mode has a large dispersion characteristic, especially in lower frequency bandwidth, as seen in Fig. 4, whereas the symmetric S0 mode is almost non-dispersive in the frequency ranges under consideration.
Dispersion curves for aluminium–zirconia FGM Plate of different volume fraction (k) indexes (semi-analytical method): a phase velocity dispersion curves (A0 mode), b phase velocity dispersion curves (S0 mode), c group velocity dispersion curves (A0 mode), d group velocity dispersion curves (S0 mode), e frequency–wavenumber dispersion curves (A0 mode), f frequency–wavenumber dispersion curves (S0 mode)
Aluminium-Alumina FGM Plates
The material that constitutes the FGM plate is a mixture of aluminium and alumina. Semi-infinite FGM plate of 1 mm thickness is used as a semi-analytical model. The material properties are tabulated in Table 2. The plate is divided into 20 individual layers.
Dispersion Characteristics
The thickness, density, and stiffness coefficients of individual layers are given as input parameters in the semi-analytical model and the dispersion curves are obtained for different k values and plotted in Fig. 6a to f. In the frequency ranges under consideration, the asymmetric A0 mode has a lot of dispersion, especially in the lower frequency ranges, but the symmetric S0 mode is almost non-dispersive. The volume fraction index “k” effect on wave propagation is determined. The results show that the waves’ phase and group velocity decrease with the k value. The guided waves are dispersive at low frequencies and asymptotically attain a particular value at higher frequencies.
Dispersion curves for aluminium–alumina FGM plate of different volume fraction (k) indexes (semi-analytical method): a Phase velocity dispersion curves (A0 mode), b phase velocity dispersion curves (S0 mode), c group velocity dispersion curves (A0 mode), d group velocity dispersion curves (S0 mode), e frequency–wavenumber dispersion curves (A0 mode), f frequency–wavenumber dispersion curves (S0 mode)
Surface Loading Response
The vertical surface displacements due to narrowband point excitations on the plate's surface are calculated to identify the influence of the fundamental A0 mode on GW propagation in the FGM plate. Due to vertical surface excitation, it is expected that the A0 mode will dominate out-of-plane motion. The response due to narrowband excitation is found by the 2-D semi-analytical model and Abaqus numerical simulation.
Numerical Simulation
The numerical model of the FGM plate is developed using the FEM-based software Abaqus/CAE (Complete Abaqus Environment). Simulation is carried out by using the S4R shell element. The explicit method is used to analyze the wave propagation in FGM plates. The only fixed–fixed boundary condition is considered in the finite element model to eliminate errors accumulating due to imperfect boundary conditions. The finite element has six degrees of freedom per node, thereby allowing both translation and rotation in all directions. To achieve good accuracy time step resolution [45] is to use a minimum of 20 points per cycle at the highest frequency as shown in Eq. (25). For a good spatial resolution, [46] recommends 20 nodes per wavelength as given in Eq. (26), where the wavelength of the A0 mode at the highest frequency of interest is considered for \(\lambda_{\min }\).
The time period is taken as 300 µs, mesh size 1 mm, and time increment as 0.1 µs, in the present study according to the above equations.
The FGM plate as shown in Fig. 3 is divided into 20 layers along the direction of thickness. As the material property does not change very sharply in the thickness direction for practical FGM plates, the material property variation within an element could be assumed as different order polynomials as per Han et al. [47]. The Power law is used for determining the volume fraction. For guided waves, narrowband tone burst excitation has been actively used. A 5-cycle Hanning sine pulse with central frequency ‘\(\omega\)’ can be written as in Eq. (27).
Excitations of various central frequencies are used to determine the vertical response. For a central frequency of 150 kHz, the time-domain excitation (source) signal and the corresponding frequency spectrum are presented in Fig. 7. From the time of maximum response under the two nodes at 0.1 m (Node1) and 0.2 m (Node2) from the source point, the group velocity (Eq. (24)), is obtained for different frequencies, and dispersion curves are plotted. The results are compared with those for an isotropic homogeneous (0.5 × 0.5 m), 1 mm thick Aluminium plate for validation of the numerical model. The normalized vertical surface displacement at 0.1 m and 0.2 m from 150 kHz transient narrowband surface excitation for Aluminium and Aluminium Alumina FGM plate (k = 15) are illustrated in Fig. 8a and b respectively.
Wavelet Transformation for Mode Identification
Wavelet transformations (WTs) are calculated using AGU-Vallen Wavelet with a particular central frequency and have been used extensively in the research of wavelet analysis in the field of guided wave acoustic emission [48]. The wavelet transformation (WT) tool is a useful tool for time–frequency analysis for sudden signal changes. Using time-displacement data obtained from the FEA-based Abaqus model, the group velocity of the guided wave in the aluminium plate is computed using the AGU-Vallen tool to validate the numerical model. From the 2D color contour plot of the wavelet transform, the time of 150 kHz energy peak at node1 and node 2 at a distance of 0.1 m and 0.2 m from 150 kHz transient narrowband surface excitation are 60 µs and 110 µs respectively (Fig. 9a and b). By using this data in Eq. (24) the group velocity of the guided wave at 150 kHz for the aluminium plate of 1 mm thickness is 2000 m/sec.
The group velocity of the guided wave in the aluminium plate at 150 kHz obtained from the Vallen WT diagram is 2170 m/s.
Comparison of Semi-analytical Model Response and Numerical Response
The vertical surface excitation of 150 kHz, 5 cycle Hanning sine pulse is applied on the surface of the aluminium alumina FGM plate of thickness of 1 mm. The size of the plate used for numerical simulation is 05 m × 0.5 m. An infinite plate of 1 mm thickness is used for the semi-analytical model. The generated waveforms are normalized to their peak amplitudes both theoretically and numerically. The group velocity of the guided wave in the aluminium plate is compared in Table 3. In the theory, we expressed the thickness and frequency in mm and MHz respectively, whereas Abaqus FEA utilizes consistent units. The different unit systems do not affect the phase of the waveform, but the amplitude will be different. The mentioned unit system has been adopted during theoretical implementation to achieve rapid convergence of the roots and numerical stability [36]. The normalized vertical responses are measured at node 1 and node 2 as shown in Fig. 10a and b by using a semi-analytical method for aluminium and aluminium alumina FGM plates. Comparison of normalized vertical surface displacements obtained from the semi-analytical model and the numerical simulation at a 0.1 m (Node1), b 0.2 m (Node2) from 150 kHz transient broadband surface excitation on the aluminium plate are shown in Fig. 11a and b respectively. The influence of edge reflection is eliminated by using the infinite plate in the semi-analytical model. The fluctuations in the numerical model are due to reflection from the edges of the plate.
Comparison of group velocity dispersion curves from the Semi-analytical method and numerical simulation of the aluminium–alumina FGM Plate for different k values (A0 mode) are presented in Fig. 12. As eminent from Fig. 12, the group velocity of the guided wave in the Aluminium Plate is 2189 m/s and alumina plate is 3220 m/s for a frequency of 150 kHz. The volume fraction distributions influence the dispersion curves of the FGM plate. The maximum Amplitude of displacement was found to be increasing with the k Value. The vertical displacement response is maximum for aluminium plates and minimum for Alumina plates. The response under the second node away from the source is less than the first node. Dispersion curves obtained by the semi-analytical method match with simulation curves in all the cases.
Carbon–Silicon Carbide FGM Plate
The study is further extended to a carbon–silicon carbide FGM plate. The material properties of the plate are presented in Table 4. Normalized vertical surface displacement obtained from the numerical simulation at Node1and Node2 from 150 kHz transient narrowband surface excitation for carbon plate and carbon-silicon carbide FGM plate = 1 are plotted in Fig. 13a and b respectively. A comparison of normalized vertical surface displacements obtained from the semi-analytical model and the numerical simulation at Node1and Node2 from 150 kHz transient broadband surface excitation on the carbon–silicon carbide FGM plate (k = 1) is shown in Fig. 14a and b respectively. For carbon–silicon carbide FGM plate, the group velocity of the wave is minimum in carbon plate and maximum when the plate is fully silicon carbide. The dispersion curve of the FGM plate with other k values is between C plate and SiC plate. Maximum displacement response occurs for carbon plate and minimum response occurs under SiC plate. The group velocity of the guided wave in the carbon plate is 1861 m/s and SiC plate is 3180 m/s for a frequency of 150 kHz. All the results show that there is a reduction in group velocity with material index (k) value. Dispersion curves obtained by the semi-analytical method match with simulation curves in all the cases. The asymmetric A0 mode has a lot of dispersion, especially at lower frequencies, whereas the symmetric S0 mode is almost non-dispersive in the frequency ranges under concern, as seen in Fig. 15. Dispersion curves of FGM plate (A0 mode) for different k values are obtained by the semi-analytical method as already explained procedure and compared with the simulation model in Fig. 16.
Dispersion curves for C–SiC FGM Plate of different volume fraction(k) indexes using Semi-analytical method: a Phase velocity dispersion curves (A0 mode), b phase velocity dispersion curves (S0 mode), c group velocity dispersion curves (A0mode), d group velocity dispersion curves (S0 mode), e frequency–wavenumber dispersion curves (A0 mode), f frequency–wavenumber dispersion curves (S0 mode)
Conclusions
The dispersion behavior of individual propagating guided wave modes in FGM plates due to vertical surface excitations was presented and evaluated using a simple 2D semi-analytical model based on the global matrix approach. The semi-analytical approach is distinctive in that it may be used to evaluate the effect of individual Guided wave modes on the total time response even without extensive computations. The response signals estimated using the theory and the numerical simulation by Abaqus CAE demonstrate good agreement for all of the examples investigated. It is also worth noting that the Abaqus model takes more than two hours to run, but the semi-analytical model merely takes a few seconds. In individual mode, a frequency–dependent velocity was observed. The waveform gets distorted as it moves away from the source. The gradient coefficient affects the shape of guided wave dispersion curves. According to the findings, the guided wave’s phase velocity and group velocity decrease as the volume fraction index increases. For a large frequency value, dispersion curves for an FGM plate converge to a particular phase velocity and group velocity value. The displacement response is lowest for ceramic plates and highest for metal plates, and it increases as the materials index value increases. The asymmetric A0 mode exhibits a lot of dispersion, particularly at lower frequencies, whereas the symmetric S0 mode is almost non-dispersive in the frequency ranges considered. For all of the cases analyzed, the A0 mode is observed to be predominant.
Finally, the obtained findings demonstrate the semi-analytical model's ability to rapidly evaluate the amplitude and form distortion of a single propagating guided wave mode in the time-domain response signal. This method is both quick and precise.
Data Availability
All data generated or analysed during this study are included in this published article.
References
Koizumi M (1993) The concept of FGM. Ceram Trans Funct Gradient Mater 34:3–10
Yamanouchi M, Koizumi M, Hirai T, Shiota I (1990) Proceedings of the 1st international symposium on functionally gradient materials, Sendai, Japan
Su Z, Ye L, Lu Y (2006) Guided Lamb waves for identification of damage in composite structures: a review. J Sound Vib 295:753–780. https://doi.org/10.1016/j.jsv.2006.01.020
Maslov KI, Kundu T (1997) Selection of lamb modes for detecting internal defects in laminated composites. Ultrasonics 35:141–150. https://doi.org/10.1016/S0041-624X(96)00098-4
Rose JL (2014) Ultrasonic guided waves in solid media. Cambridge University Press, London. https://doi.org/10.1017/CBO9781107273610
Graff KF (1975) Wave motion in elastic solids. Dover, New York
Achenbach JD (1973) Wave propagation in elastic solids. North-Holland, Amsterdam
Liu GR, Han X, Lam KY (1999) Stress waves in functionally gradient materials and its use for material characterization. Composites B 30:383–394. https://doi.org/10.1016/S1359-8368(99)00010-4
Bian ZG, Lim CW, Chen WQ (2006) On functionally graded beams with integrated surface piezoelectric layers. Compos Struct 72:339–351. https://doi.org/10.1016/j.compstruct.2005.01.005
Reddy JN (1983) Dynamic (transient) analysis of layered anisotropic composite material plates. Int J Numer Methods Eng 19:237–255. https://doi.org/10.1002/nme.1620190206
Yang S, Yuan FG (2005) Transient wave propagation of isotropic plates using a higher-order plate theory. Int J Solids Struct 42:4115–4153. https://doi.org/10.1016/j.ijsolstr.2004.12.014
Santosa F, Pao YH (1989) Transient axially asymmetric response of an elastic plate. Wave Motion 11:271–295. https://doi.org/10.1016/0165-2125(89)90006-1
Liu GR, Tani J, Ohyoshi T, Watanabe K (1991) Transient wave in anisotropic laminated plates. Part 1: theory; Part 2: application. J Vib Acoust 113:230–234. https://doi.org/10.1115/1.2930174
Lih SS, Mal AK (1995) On the accuracy of approximate plate theories for wavefield calculations in thick laminates. Wave Motion 21:17–34. https://doi.org/10.1016/0165-2125(94)00038-7
Nastos CV, Saravanos DA (2020) A finite wavelet domain method for wave propagation analysis in thick laminated composite and sandwich plates. Wave Motion. https://doi.org/10.1016/j.wavemotion.102543
Mahmoud A, Shah AH, Dong SB (2006) Transient response of transversely isotropic composite plates to a point source impact. ASME J Appl Mech 73:338341. https://doi.org/10.1016/j.ultras.2006.05.180
Liu GR, Lam KY, Ohyoshi T (1997) A technique for analyzing elastodynamic responses of anisotropic laminated plates to line loads. Composites B 28:667–677. https://doi.org/10.1016/S1359-8368(96)00080-7
Chen WQ, Wang HM, Bao RH (2007) On calculating dispersion curves of waves in a functionally graded elastic plate. Compos Struct 81:233–242. https://doi.org/10.1016/j.compstruct.2006.08.009
Chakraborty A, Gopalakrishnan S (2004) A spectrally formulated finite element for wave propagation analysis in layered composite media. Int J Solids Struct 41:51–55. https://doi.org/10.1016/j.ijsolstr.2004.03.011
Yu JG, Wu B, He CF (2007) Characteristics of guided waves in graded spherical curved plates. Int J Solids Struct 44:3627–3637. https://doi.org/10.1016/j.wavemoti.2006.11.002
Bennai R, Fourn H, Atmane HA, Tounsi A, Bessaim A (2019) Dynamic and wave propagation investigation of FGM plates with porosities using a four-variable plate theory. Wind Struct 28(1):49–62. https://doi.org/10.12989/WAS.2019.28.1.049
Aziz N, Saadatpour MM, Mahzoon M (2019) Analyzing first symmetric and antisymmetric Lamb wave modes in functionally graded thick plates by using spectral plate elements. Int J Mech Sci. https://doi.org/10.1016/J.IJMECSCI.2018.10.030
Dastjerdi RM, Khabisi HM, Baghbani R (2017) Mesh-free dynamic analyses of FGM sandwich plates resting on a Pasternak elastic foundation. Mech Adv Compos Struct 4:153–168. https://doi.org/10.22075/MACS.2017.11043.1107
Bednarika M, Cervenkaa M, Groby JP, Lottonb P (2018) One-dimensional propagation of longitudinal elastic waves through functionally graded materials. Int J Solids Struct 146:43–54. https://doi.org/10.1016/J.IJSOLSTR.2018.03.017
Yang Y, Liu Y (2020) A new boundary element method for modeling wave propagation in functionally graded materials. Eur J Mech A Solids. https://doi.org/10.1016/j.euromechsol.2019.103897
Lin YH, Ing YS, Ma CC (2015) Two-dimensional transient analysis of wave propagation in functionally graded piezoelectric slabs using the transform method. Int J Solids Struct 52:72–82. https://doi.org/10.1016/J.IJSOLSTR.2014.09.021
Amor MB, Salah IB, Ghazlen MHB (2015) Propagation behavior of Lamb waves in functionally graded piezoelectric plates. Acta Acust United Acust 101(3):435–442. https://doi.org/10.3813/AAA.918839
Karami B, Jangorban M, Li L (2018) On guided wave propagation in fully clamped porous functionally graded nanoplates. Acta Astronaut 143:380–390. https://doi.org/10.1016/j.actaastro.2017.12.011
Othmani C, Takali F, Njeh A (2017) Theoretical study on the dispersion curves of Lamb waves in piezoelectric semiconductor sandwich plates GaAs-FGMPM-AlAs: Legrendre polynomial series expansion. Superlattices Microstruct 106:86–101. https://doi.org/10.1016/j.spmi.2017.03.036
Zhu F, Wang B, Qian ZH, Pan E, Kuznetsova IE (2018) Accurate characterization of 3D dispersion curves and mode shapes of waves propagating in generally anisotropic viscoelastic/elastic plates. Int J Solids Struct 150:52–65. https://doi.org/10.1016/j.ijsolstr.2018.06.001
Gao J, Yan L, Mingfang Z, Mingkun L, Hongye L, Bin W, Cunfu H (2021) Analysis of longitudinal guided wave propagation in the functionally graded hollow cylinder using state-vector formalism and Legendre polynomial hybrid approach. J Nondestr Eval 40:33. https://doi.org/10.1007/s10921-021-00764-y
Hebaz SE, Benmeddoura F, Moulin E, Assaad J (2018) Semi-analytical discontinuous Galerkin finite element method for the calculation of dispersion properties of guided waves in plates. J Acoust Soc Am 143(1):460–469. https://doi.org/10.1121/1.5021588
Mal AK (1988) Wave propagation in layered composite laminates under periodic surface loads. Wave Motion 10:257–266. https://doi.org/10.1016/0165-2125(88)90022-4
Knopoff LA (1964) matrix method for elastic wave problems. Bull Seismol Soc Am 54:431–438. https://doi.org/10.1785/BSSA0540010431
Li R, Yen KH (1972) Elastic waves guided by a solid layer between adjacent substrates. IEEE Trans Microwave Theory Tech 20(7):477–486. https://doi.org/10.1109/TMTT.1972.1127788
Banerjee S, Prosser W, Mal AK (2005) Calculation of the response of a composite plate to localized dynamic surface loads using a new wavenumber integral method. ASME J Appl Mech 72:18–24. https://doi.org/10.1115/1.1828064
Pol B, Banerjee S (2013) Modeling and analysis of propagating guided wave modes in a laminated composite plate subject to transient surface excitations. Wave Motion 50:964–978. https://doi.org/10.1016/J.WAVEMOTI.2013.04.003
Thomson WT (1950) Transmission of elastic waves through a stratified solid medium. J Appl Phys 21:89–93. https://doi.org/10.1063/1.1699629
Haskell NA (1953) Dispersion of surface waves on multilayered media. Bull Seismol Soc Am 43:17–34. https://doi.org/10.1785/BSSA0430010017
Buchwald VT (1961) Rayleigh waves in transversely isotropic media. Q J Mech Appl Math 14(3):293–317. https://doi.org/10.1093/qjmam/14.3.293
Vasudevan N, Mal AK (1985) Response of an elastic plate to localized transient sources. ASME J Appl Mech 52(2):356–362. https://doi.org/10.1115/1.3169053
Ahlfors LV (1979) Complex analysis. McGraw Hill, New York
Sun D, Luo SN (2011) Wave propagation and dynamic response of rectangular functionally graded material plates with completed clamped supports under impulse load. Eur J Mech A Solids 30:396–408. https://doi.org/10.1016/J.EUROMECHSOL.2011.01.001
Praveen GN, Reddy JN (1998) Nonlinear dynamic thermoelastic analysis of functionally graded ceramic–metal plates. Int J Solids Struct 35:4457–4476. https://doi.org/10.1016/S0020-7683(97)00253-9
Bartoli I, Lanza di Scalea F, Fateh M, Viola E (2005) Modeling guided wave propagation with application to the long-range defect detection in railroad tracks. NDT&E Int 38:325–334. https://doi.org/10.1016/j.ndteint.2004.10.008
Moser F, Jacobs LJ, Qu J (1999) Modeling elastic wave propagation in waveguides with the finite element method. NDT&E Int 32:225–234. https://doi.org/10.1016/S0963-8695(98)00045-0
Han X, Liu GR, Lam KY (2001) Transient waves in plates of functionally graded materials. Int J Numer Methods Eng 52:853–865. https://doi.org/10.1002/nme.237
Hamstad MA, Gallaghar AO, Gary JA (2002) Wavelet transformation applied to acoustic emission signals: part1: source identification. J Acoust Emission 20:39–61
Acknowledgements
We would like to express thanks to the QIP Centre, Central Library and Computer Centre, Indian Institute of Technology, Bombay. We also acknowledge QIP Centre, for supporting the research under Quality Improvement Scheme, Directorate of Technical Education, Kerala.
Author information
Authors and Affiliations
Contributions
Conceptualization: NIN, SB; methodology: NIN; formal analysis and investigation: NNI; writing—original draft preparation: NIN; writing—review and editing: SB; supervision: SB.
Corresponding author
Ethics declarations
Competing interests
The authors declare that we have no conflicts of interest that might be interpreted as influencing the research “Conflicts of interest none”.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Narayanan, N.I., Banerjee, S. A Simplified 2D Semi-Analytical Model for the Analysis of Dispersion Behavior in Functionally Graded Material Plates. J. dynamic behavior mater. 9, 179–197 (2023). https://doi.org/10.1007/s40870-023-00371-0
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s40870-023-00371-0