1 Introduction

Microcracks are often the earliest symptoms of damage in concrete (and other quasi-brittle materials) preceding the mm-size macro-defects. Volumetrically distributed microcracks initiate in response to excessive mechanical loads and durability stressors (e.g., drying, freezing, excessive temperature, deleterious chemical reactions). Microcracks significantly affect the performance of material; its load-bearing capacity and mass transport properties which determine its durability [1] and service life performance. Estimating the amount of volumetric cracking within concrete is the key to early damage diagnostics and durability prognostics that would enable stakeholders to take timely preventive maintenance actions.

Linear acoustic techniques use the principles of elastic wave propagation in a linear elastic medium and are among the most effective NDE methods to identify cracking. This is mainly due to the high acoustic impedance (defined as the product of density and wave propagation velocity) contrast between cracks and the surrounding concrete. Resonance-based methods [2], (linear) ultrasonic wave velocity and attenuation measurements and ultrasonic pulse-echo [3] have long been adapted and used for concrete inspection. However, these conventional methods can only detect mm-size cracks, while showing no or little sensitivity to the accumulation of microcracks. Consequently, these methods remain largely inapplicable to early damage detection.

Nonlinear acoustics-based testing methods constitute an emerging class of NDE techniques with demonstrated higher sensitivity to micro-damage in diverse materials (including concrete) compared to conventional linear acoustic techniques [4, 5]. These methods use acoustics to detect a select signature of material elastic nonlinearity, which is in turn attributed to the presence of compliant links within the mesoscopic structure of the material [6]. Whereas linear methods consist in simply measuring velocity, frequency or amplitude to infer elastic moduli and attenuation for instance, nonlinear methods consist in measuring the amplitude or strain (\(\varepsilon )\) dependence of these parameters. In nonlinear acoustics-based testing, material is typically strained over a range 10\(^{-6}< \varepsilon < 10 ^{-5}\) and its nonlinearity is deduced from the subtle strain-induced changes in material response measured in terms of e.g., generation of higher harmonics, shift in resonance frequency, relative changes in wave speed, and attenuation. Presence of microcracks introduces soft bonds within the damaged material structure and thus, induces (or adds to) elastic nonlinearity. In principle, under ideal circumstances, even a single micro-crack is detectable by nonlinear techniques [7]. In contrast, in linear ultrasonic testing, pulses of very small amplitude (\(\varepsilon < 10^{-7})\) are emitted into the test medium by an emitting transducer and recorded by a receiving transducer (the same transducer could be both emitting and receiving). From the arrival time and amplitude of the received energy and propagation distance, the average wave speed and attenuation of the medium over the propagation path is obtained. These quantities are functions of the average linear elastic material parameters that only start to change at later stages of the damage progress i.e., when the amount of microcracking is large enough to alter the average material parameters [8]. The common evolution of nonlinear and linear elastic properties with the damage progress/scale is shown schematically in Fig. 1 [5, 9, 10]. This trend suggests that monitoring nonlinear and linear material parameters provides complementary information on the state of material and if combined, can lead to improved assessment of damage progression.

Fig. 1
figure 1

Schematic evolution of nonlinear and linear elastic parameters with the damage progress or scale. Nonlinear parameters are more sensitive to early and/or microscopic damage whereas linear parameters change significantly at later stages of damage progress and are particularly useful for identifying macroscopic defects

Full size image

Nonlinear resonance acoustic spectroscopy (NRAS), a.k.a. nonlinear resonance ultrasound spectroscopy (NRUS), and its variations are resonance-based testing techniques, which use the strain-dependent shift in the resonance frequency to discern the hysteretic nonlinearity (explained in detail in Sect. 2) of the test medium. To conduct NRAS, continuous waves or chirps (i.e., signals of linearly increasing frequency) with different amplitudes are used to excite one or multiple vibrational modes of the material [11, 12]. NRAS has been used for assessing thermal damage [11] and carbonation [13] in concrete. Leśnicki et al. [14] introduced an impact-based version of NRAS called nonlinear impact resonance acoustic spectroscopy (NIRAS), where increasing levels of strain are induced by hammer strikes or drop ball impacts of growing intensity. NIRAS has been used for monitoring the damage in large concrete prisms subjected to accelerated alkali–silica reaction (ASR) [14]. Although applicable to the testing of large concrete samples, this method still requires multiple mechanical impacts. Nonlinear reverberation spectroscopy (NRS) is a variation of NRAS that exploits the gradual shift in the frequency of the free vibrational response following a period of steady-state harmonic excitation generating strain \(\varepsilon \) in the range of 10\(^{-6 }\)–10\(^{-5}\). The main advantage of NRS over NRAS and NIRAS is the reduced data collection time since only a single excitation level is required. NRS was first used for thermal damage assessment of carbon fiber reinforced plastic (CFRP) composites [15]. This method was extended to test a fatigued steel industrial sample with complex geometry by Van Damme et al. [16]. Eiras et al. [17] introduced an impact version of NRS to monitor concrete deterioration due to freeze-thaw (FT) cycles; the frequency shift in the vibrational response of the samples to a single hammer impact is obtained using short time Fourier transform (STFT). Recently, Dahlen et al. [18] used a parametric signal model to approximate the reverberation signal as a combination of vibrational modes taking into account the contributions of the higher harmonics. Each mode is modeled as an exponentially decaying signal with both phase and attenuation expressed as independent polynomial functions of time. This analysis approach has been implemented to obtain the hysteretic nonlinearity of concrete with three damage levels induced by hammer impacts. While producing more accurate results, this approach is purely mathematical and does not take into account the interrelation between nonlinear attenuation and frequency shift [19,20,21].

In this study, impact nonlinear resonant acoustic spectroscopy termed here INRAS (instead of INRS) is used to monitor standard concrete prisms undergoing progressive FT damage. Both single-impact and multi-impact variations are carried out and several data analysis approaches are proposed to extract nonlinear parameters from the test results at different damage levels. In addition, standard (linear) dynamic modulus measurements are also conducted and the results from different testing and analysis approaches are compared.

Next, we introduce an impact-based version of dynamic acousto-elastic testing (DAET), referred to as IDAET. DAET is a relatively recent development in the field of nonlinear acoustics. Acousto-elasticity is the phenomenon describing the stress-induced changes in the velocity of acoustic waves propagating through a medium under quasi-static stress. DAET is the dynamic equivalent of acousto-elastic testing that uses the coupling of a low frequency (LF) and high frequency (HF) acoustic waves [22]. The LF wave source (pump) actuates the test sample by sinusoidal excitations that set a steady-state cyclic strain field within the sample. A pair of HF ultrasound transducers (probe) simultaneously probes the changes in the ultrasound pulse velocity and attenuation at varying strain levels throughout the test: before “turning on” the strain pump, during the cycling straining (fast dynamics), and after “turning off” the pump as the sample slowly recovers (slow dynamics). From the strain-induced changes in wave velocities (or attenuations) over the fast- and slow-dynamics [23, 24] phases of the test, a host of classical and hysteretic (explained in the following section) nonlinear parameters is extracted. DAET is different from NRUS in that: (1) it gives a more comprehensive picture of material nonlinearity by providing parameters describing both classical and hysteretic (non-classical) nonlinearities, and (2) it can be used to localize nonlinearity [7, 25]. DAET has been previously used for characterizing the nonlinear elastic behavior of disparate rocks [22, 26, 27] and detecting the extent of fatigue and stress corrosion cracks in aluminum [28]. The impact-based DAET was first introduced in [29], where concrete with alkali-silica reaction damage were evaluated; but only classical nonlinear parameter was reported in this study. Eiras et al. [30] recently proposed an impact-based DAET that uses a continuous wave probe mounted on the surface. The nonlinearity of a single concrete sample is calculated from the instantaneous phase shift between the pre-impact and perturbed post-impact parts of the continuous response. In our version of IDAET, we use a series of discrete pulses to probe the impact-induced changes in compressional wave velocities. Concrete prisms with different FT damage levels are studied and the IDAET results are compared against those from INRAS.

This paper begins with a brief theoretical background on classical versus non-classical (hysteretic) nonlinearity and nonlinear acoustic testing followed by a description of the test samples and the testing program. We introduce two impact-based nonlinear acoustic testing techniques: INRAS and IDAET. Three new approaches for analyzing single-impact INRAS data are presented. The single-impact INRAS results are compared against those from the multi-impact INRAS. Finally, the results of INRAS and IDAET on two sets of concrete samples with different levels of FT damage are discussed.

2 Theoretical Background

2.1 Classical and Non-Classical Nonlinearity

Materials such as rocks and concrete exhibit both classical and non-classical elastic nonlinearities. Nonlinearity implies that stress is not proportional to strain; the elastic modulus E is not constant but strain-dependent. Classical nonlinearity is modeled by expressing E as a polynomial function of strain \(\varepsilon \) (see the first three terms on the right hand side of Eq. (1)). It has been observed that materials with a “rigid brick within a compliant matrix” mesoscopic structure such as rocks and concrete show in addition hysteresis and end-point memory [6]. One of the most widely used models to include this non-classical nonlinear behavior in the stress-strain constitutive relation is a phenomenological description based on the Preisach–Mayergoyz space (P-M space) [31] resulting in the following 1-D equation for the elastic modulus [32]:

$$\begin{aligned} E=E_0 [1+\beta \varepsilon +\delta \varepsilon ^{2}+\cdots +\alpha (\Delta \varepsilon +sign\left( {\dot{\varepsilon }} \right) \varepsilon )] \end{aligned}$$
(1)

where \(E_0 \) is the linear elastic modulus, \(\beta \) and \(\delta \) are the classical quadratic and cubic nonlinear parameters, respectively, \(\Delta \varepsilon \) is the maximum strain amplitude, \({\dot{\varepsilon }}\) is the strain rate, and \(sign\left( {\dot{\varepsilon }} \right) =1\), if \({\dot{\varepsilon }}> 0\), \(sign\left( {\dot{\varepsilon }} \right) =-1\), if \({\dot{\varepsilon }}< 0\). Nonlinear parameter \(\alpha \) gives a measure of material hysteresis. As such, ‘non-classical nonlinearity’ is often interchanged with ‘hysteretic nonlinearity’.

The simple model of Eq. (1) can explain some of the fundamental observations made during the nonlinear acoustic testing of cementitious materials. For example, this model predicts a nearly linear strain-dependence for resonant frequency and modal damping ratio during a nonlinear resonance test [6], formally expressed as [33, 34]:

$$\begin{aligned} \frac{f-f_0 }{f_0 }=\alpha _f \Delta \varepsilon =\alpha _f (\varepsilon -\varepsilon _0 ) \end{aligned}$$
(2)
$$\begin{aligned} \frac{1}{Q}-\frac{1}{Q_0 }=\alpha _Q \Delta \varepsilon =\alpha _Q (\varepsilon -\varepsilon _0 ) \end{aligned}$$
(3)

where \(f_0 \) is the linear resonance frequency measured at\(\varepsilon _0 \) and f is the resonance frequency at each incremental strain level \(\varepsilon \). The parameters \(\alpha _f \) and \(\alpha _Q \) are proportional to the nonlinear hysteretic parameter \(\alpha \) in the constitutive relation (Eq. (1)). These two parameters are not independent; the ratio \(\alpha _Q /\alpha _f \) is a constant that is independent of strain amplitude and proportional to the so-called Read number r [19, 21, 34]. In DAET, on the other hand, we quantify nonlinearity based on the measured (pump) strain-induced velocity changes. The relative change in the velocity of HF (probe) waves is approximately one half of the corresponding variations in elastic modulus [35]:

$$\begin{aligned} \frac{\Delta c}{c_0 }\approx \frac{1}{2}\frac{\Delta E}{E_0 } \end{aligned}$$
(4)

where \(c_0 \) is the reference wave velocity, the HF wave velocity in the absence of LF perturbation, and \(\Delta c\) is the velocity shift as a result of LF perturbations. Substituting Eq. (1) in Eq. (4) gives a relation between the relative velocity measurement and nonlinear material:

$$\begin{aligned} \frac{\Delta c}{c_0 }=\frac{1}{2}\frac{\Delta E}{E_0 }=\frac{1}{2}(\beta \varepsilon +\delta \varepsilon ^{2}+\cdots )+O({\Delta }\varepsilon ,{\dot{\varepsilon }, \alpha )} \end{aligned}$$
(5)

where \(O({\Delta }\varepsilon , {\dot{\varepsilon }}, \alpha )\) measures the initial instantaneous drop in wave velocity (immediately after turning on the pump) or the so-called ‘offset’ caused by conditioning. Eq. (5) involves classical and non-classical nonlinear parameters suggesting that both sets of parameters can be extracted from DAET results.

2.2 Post-Perturbation Slow Recovery

Although the classical and non-classical models described above accurately describe most of the observations, it does not capture the post-perturbation relaxation (slow dynamics) and the interplay between conditioning and relaxation phenomena. To describe the relaxation phenomenon, one can employ the soft ratchet model proposed by Vakhnenko et al. [36]. The soft ratchet model is physics-based, but includes phenomenological components consistent with observations of hysteretic nonlinearity in sedimentary rocks. At the core of this model is an assumption of asymmetry in breakage (opening) and healing (recovery) of microcracks and intergrain cohesive bonds. At a given stress level \(\sigma \), the constituent concentration of defects g approaches a stress-dependent equilibrium state \(g_\sigma \) according to the following equation:

$$\begin{aligned} \frac{\partial g}{\partial t}=-[\nu H\left( {g-g_\sigma } \right) +\mu H\left( {g_\sigma -g} \right) ]\left( {g-g_\sigma } \right) \end{aligned}$$
(6)

where H(x) is the Heaviside step function. When \(g<g_\sigma \), the restored bonds are ruptured (\(\frac{\partial g}{\partial t}<0)\)at the breakage rate of \(\mu \); when \(g>g_\sigma \), the ruptured bonds are restored (\(\frac{\partial g}{\partial t}>0)\)at the recovery rate of \(\nu \). Vakhnenko et al. [36] assert that since there are many more ways for the bonds to break than for them to restore, \(\nu \ll \mu \). The breakage rate and recovery rate are expressed as \(\mu =\mu _0 \hbox {exp}(-U/kT)\) and \(\nu =\nu _0 \hbox {exp}(-W/kT)\), respectively. In these expressions, U and W are the activation barriers for the processes of bond restoration and breakage, k is the Boltzmann constant, and T is the temperature.

Table 1 Proportions and properties of the two concrete mixtures
Full size table

We use the soft-ratchet model to describe the transient changes in micro-defect concentration after a short-lived hammer strike: the disturbance caused by the hammer strike initially drives up the concentration of microcracks (by opening them) towards the equilibrium quantity \(g_\sigma \) at the rate of \(\mu .\) However, the impact is short-lived, thus \(g_\sigma \) drops quickly after the impact force is removed, leading to \(g\gg g_\sigma \). As such, the system is driven towards the restoration of the bonds or recovery at the rate of \(\nu \). The duration of the impact compared to the resolution of data is too short to allow us to study the phenomenon associated with the bond breakage, but we can study the post-impact recovery. Following the assumptions made in Vakhnenko et al. [36] (independent and uniform activations barriers U and W), the model can be further simplified as:

$$\begin{aligned} \frac{\partial c}{\partial t}=-\nu c \end{aligned}$$
(7)

where c is an actual defect concentration of defects. This leads to:

$$\begin{aligned} c=Ae^{-\nu t} \end{aligned}$$
(8)

To relate the defect concentration c to the elastic properties of the material, we consider the first-order approximation of the elastic modulus [36, 37]:

$$\begin{aligned} E=\left( {1-c/c_{cr} } \right) E_0 \end{aligned}$$
(9)

where \(E_0 \) is the elastic modulus of the material at the defect-free state while \(c_{cr} \) is the critical concentration of defects. Substituting Eq. (14) in Eq. (15), gives:

$$\begin{aligned} E=E_0 \left( {1+Ae^{-\nu t}/c_{cr} } \right) \end{aligned}$$
(10)

According to this model, the relative change of elastic modulus (or resonance frequency) is an exponential function of time:

$$\begin{aligned} \frac{f-f_0 }{f_0 }\propto \frac{E-E_0 }{E_0 }=Ae^{-\nu t}/c_{cr} \end{aligned}$$
(11)

3 Materials and Test Methods

We use concrete undergoing FT damage as our experimental example. Concrete exposed to repeated FT cycles in regions with cold and wet climates deteriorates both externally (surface scaling) and internally (volumetric cracking). There are standardized guidelines to evaluate the susceptibility of concrete mixtures to FT damage in the laboratory, for example: ASTM C666/C666M-03 [38], JIS A 1148-2001 [39], and Rilem TC 176-IDC [40]. The common procedure consists of subjecting standard specimens to accelerated FT cycles and monitoring properties linked to the accumulating damage. The external damage (scaling) is often evaluated by mass loss [40], whereas internal damage (cracking) is evaluated by measuring the decrease in ultrasonic pulse velocity [40] or fundamental transverse resonance frequency [38,39,40]. Length change measurement is also prescribed by a few standards [38, 40].

Fig. 2
figure 2

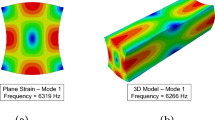
INRAS setup: an instrumented hammer is used to excite the first flexural mode of the sample with free–free boundary conditions. A miniature accelerometer records the vibrational response. The level of strain is controlled by the intensity of the hammer strike. The modal shape of the first flexural mode is determined using a finite element method (FEM) model and represented below the setup

Full size image

3.1 Description of Test Samples

A total of four \(7.62 \times 7.62 \times 40.64\) cm\(^{3}\) prismatic concrete samples of two different mixtures are used for this series of experiments. As shown in Table 1, the two mixtures are designed to have similar properties (w/c, slump and strength) except that an air-entraining agent (AE) is added to one to purposefully improve its FT performance. No air-entraining admixture is used for the other mixture (NonAE). After being cured for 14 days in an environment of 23 \(^{\circ }\)C and 100% relative humidity, the specimens are immersed in water and placed in the freeze-thaw (FT) chamber. In order to promote FT damage, the procedure prescribed by standard ASTM C666/C666M-03 [38] is closely followed. The temperature of the specimens inside FT chamber fluctuates from 40\(^{\circ }\)F to 0\(^{\circ }\)F and back to 40\(^{\circ }\)F every 5 h. To conduct the acoustic tests, the specimens are removed from the chamber when they are the warmest (at 40\(^{\circ }\)F) after 15–18 full FT cycles. Before conducting the tests, the specimens are dried with a towel and all the tests are completed within 30 min of the removal of the specimens from the chamber.

The two air-entrained samples (AE6 and AE7) went through 300 freeze-thaw cycles over a period of 63 days. The two non-air entrained samples (NonAE1 and NonAE2) are extensively damaged after only 55 freeze-thaw cycles and thus removed from the chamber.

3.2 Resonance Frequency Measurements

The common standard method to assess the internal damage due to FT consists in measuring the (linear) resonance frequency according to the guidelines provided by ASTM C215 standard [43]. The specimen is supported on two edges placed at 0.224 of the length from each end to simulate free–free boundary conditions. A mechanical impact at the center of the specimen excites the flexural mode of vibration. The response is recorded by a supersensitive piezoelectric probe and analyzed by GrindoSonic MK5 Industrial Instrument to directly obtain the resonance frequency. The test is repeated three times and the average reading is reported as the linear resonance frequency.

3.3 Impact Nonlinear Resonant Acoustic Spectroscopy (INRAS)

To conduct INRAS, the prismatic concrete sample is placed on a soft supporting foam to simulate free–free boundary conditions. As shown schematically in Fig. 2, we follow a procedure similar to that prescribed in ASTM C215 [43]. An instrumented hammer (PCB 086C03) is used to excite the transverse flexural mode by gently hitting the center of the sample (red circle in Fig. 2). A miniature accelerometer (Bruel & Kjaer 4374) glued at one end of the sample captures the vibrational response. After being amplified by NEXUS\(^\mathrm{TM}\) conditioning amplifier (1 mV/(ms\(^{-2}))\), the acceleration is recorded at a sampling rate of 1 MHz by a National Instruments PXIe-5170R acquisition card. The level of strain is controlled by the intensity of the hammer strike. Multi-impact INRAS requires the recording of the response for hammer strikes of increasing intensity ranging from very gentle to stronger (\(\varepsilon > 10^{-6}\)) impacts. To conduct a single-impact INRAS, on the other hand, a single but sufficiently strong hammer strike (\(\varepsilon > 10^{-6}\)) is adequate.

3.4 Impact Dynamic Acousto-Elastic Testing (IDAET)

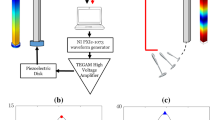
The schematic of our IDAET setup is shown in Fig. 3. Similar to INRAS, an instrumented hammer is used as the LF (typically a few kHz depending on the material and geometry of the specimen) vibrational source or ‘pump’. A miniature accelerometer (Bruel & Kjaer 4374) is used to record the LF strain field. A pair of HF compressional wave ultrasound transducers (Olympus A101S-RB) is used to ‘probe’ the impact-induced changes in ultrasonic wave velocities. As shown in Fig. 3, the probing transducers are centered along the length of the specimen, but positioned near the bottom of its height, where the maximum flexural strain is expected. The data acquisition sequence is as follows. The HF emitter sends pulses every 150 \(\mu \)s throughout the experiment, with each pulse consists of 3 cycles at 500 kHz. The pulsing interval is chosen to be larger than the time it takes for the recorded ultrasonic coda (i.e., arrivals due to the scattering of ultrasonic energy) to be fully attenuated so that it does not affect the subsequent recording. At the same time, it should be as short as possible to allow the collections of sufficient data points during the transient LF perturbation.

Fig. 3
figure 3

a IDAET setup: an instrumented hammer is used to excite the flexural mode of the sample with free–free boundary conditions (LF vibration). A miniature accelerometer records the LF vibrational response while a pair of HF ultrasonic transducers is used to ‘probe’ the impact-induced wave ultrasonic velocity changes. b Schematics detailing how the LF strain is estimated based on the positions of the probing transducers (black circle)

Full size image

In this study, IDAET is repeated three times for each sample following a specific protocol. Both LF and HF signals are sampled at 50 MHz. With reference to Fig. 3, the travel distance for HF waves is 7.62 cm. Considering an average compressional wave velocity of 4500 m/s, it takes about 17 \(\mu \)s for the HF compressional wave to travel across the specimen. A sufficiently strong hammer strike is used to excite the first flexural mode of the specimen after about 200 ms. The resonance frequency of this mode is about 1800 Hz, equivalent to a period of 0.56 ms. Considering the ratio 17 \(\mu \)s/0.56 ms = 0.03, we can safely assume that the strain level remains unchanged during the HF probe travel time.

4 Data Analysis Approaches

4.1 Maximum Strain Calculation

In both INRAS and IDAET, we choose to excite the transverse flexural modes of the specimen. Consequently, the resulting absolute maximum strain in the specimen occurs at the top or bottom surface in the middle of the specimen. Assuming the dominance of the first flexural mode, the maximum strain amplitude \(\varepsilon _{max} \) can be estimated from the maximum out-of-plane acceleration at one end of the specimen \(\ddot{u}\) measured on the same surface as the one struck by the hammer. For a beam with free–free boundary conditions [15]:

$$\begin{aligned} \varepsilon _{max} =\frac{0.219\pi (3.0112)^{2}D}{8f^{2}\sqrt{12}L^{2}}\ddot{u} \end{aligned}$$
(12)

where D is the width of the specimen, f denotes the resonance frequency of the first flexural mode and L is the length of the specimen. Before using Eq. (12), the acceleration data is filtered using a second order band-pass Butterworth filter with cutoff frequencies at 600 Hz and 3000 Hz to remove the DC offset, low, and high frequency noise.

4.2 Analysis of INRAS Data

The goal of data analysis here is to quantify the downward shift in resonant frequencies with increasing strain levels. In this section, we describe the different approaches that we have employed to analyze multi-impact and single-impact INRAS data.

4.2.1 Fast Fourier Transform (FFT)

In case of multi-impact INRAS, the frequency spectra of the vibrational responses to individual impacts can be simply obtained using FFT. This is similar to the procedure adopted by Leśnicki et al. [14]. Zero-padding is used to increase the frequency resolution. And the frequency peak is further refined with a parabolic function. To find the frequency shift, we apply a total of 30 manual impacts per measurement. The impacts are divided into 3x10-impact groups with respect to their intensities: low, medium, and high. To avoid the influence of ‘conditioning’, the transient distortion of response caused by the preceding stronger impacts, only impacts with monotonically increasing strain amplitudes are retained for the subsequent analysis. In other words, data corresponding to impacts of amplitudes lower than that of the preceding impacts is removed from the analysis. The (linear) resonance frequency \(f_0 \) estimated from the first impact with the lowest amplitude serves as the reference. Frequency shift (\({\Delta }f=f-f_0 )\) is obtained by measuring the changes in resonance frequencies relative to \(f_0 \) at gradually increasing strain amplitudes. The hysteresis nonlinearity parameter \(\alpha _f \) is then extracted following Eq. (2). Although data collection with multiple impacts for a large number of samples is tedious, the data analysis is rather straightforward. However, this analysis suffers from limitations inherent to FFT; for instance, the amplitude spectrum gives an averaged frequency content of the impact over its entire duration.

4.2.2 Windowed Reverberation Fitting (WRF)

Windowed reverberation fitting (WRF) is used to calculate the frequency shift in the vibrational response to one single impact. The impact has to be strong enough to generate sufficient strain within the material (10\(^{-6}\)–10\(^{-5})\) in order to mobilize nonlinearity. WRF and STFT have similar principles and as will be demonstrated in Sect. 5.2 yield similar instantaneous frequencies. However, WRF parameters can be readily used to estimate the amplitude dependence of resonance frequency and attenuation. To perform WRF, similar to the procedure introduced in [15, 16], a sliding window is used to capture the changing frequency content in the amplitude-decaying time signal. The window size is selected to encompass about 10 full cycles which amounts to 6 ms, with a step size of 0.6 ms (90% overlap between adjacent windows). Each window contains a decaying sinusoidal wave that can be described by an exponentially decaying sine function. Assuming constant frequency and damping within each window, the signal contained in the kth window is modeled as follows:

$$\begin{aligned} x_k \left( t \right) =A_k e^{-\theta _k t}\sin \left( {2\pi f_k t+\varphi _k } \right) k=1,2,\ldots , n \end{aligned}$$
(13)

where \(A_k \) denotes the max amplitude in each window, and can be used to calculate strain \(\varepsilon _k \) using Eq. (6), \(\theta _k \) is the damping factor which relates to the quality factor (\(Q_k )\) through \(\theta _k =\pi f_k /Q_k \), \(f_k \) and \(\varphi _k \) are the ‘local’ resonance frequency and phase shift, respectively. The curve fitting is accomplished using Levenberg-Marquardt algorithm. Having identified the parameter set (\(A_k ,\theta _k ,f_k ,\varphi _k )\) for each window, the hysteresis nonlinearity parameter \(\alpha _f\) can then be obtained by calculating the slope of normalized frequency shift \((f_k -f_n )/f_n\) versus \(\varepsilon _k \), where \(f_n \) corresponds to the resonance frequency of the signal within the last window (corresponding to a fixed amplitude of about 1 microstrain). We use the same window size throughout the analysis but the number of windows changes from sample to sample, depending on the attenuation.

4.2.3 Hilbert-Huang Transform (HHT)

An alternative method for analyzing the single-impact INRAS is Hilbert-Huang Transform (HHT) [44]. HHT combines the empirical mode decomposition (EMD) and the Hilbert spectral analysis (HSA) to generate a time-frequency representation of the signal. First, EMD decomposes the signal into a finite number of components, called intrinsic mode functions (IMF). Next, the analytic signalFootnote 1 corresponding to each IMF is calculated. The instantaneous frequency content \(\omega \left( t \right) \) of each IMF is calculated as the time derivative of the instantaneous phase \(\theta \left( t \right) \) of the corresponding analytic signal:

$$\begin{aligned} \omega \left( t \right) =\frac{d\theta (t)}{dt} \end{aligned}$$
(14)

Combining the instantaneous frequency contents for all the IMFs, an instantaneous time-frequency representation of the signal is attained. HHT is a more efficient tool for the analysis of non-stationary and nonlinear signals, because unlike FFT-based analysis (e.g., STFT or WRF), it does not use a set of stationary basis functions. HHT time-frequency analysis offers simultaneously high resolutions in both time and frequency domains. In comparison, the interdependent time and frequency resolutions of a STFT-spectrogram is restricted by Heisenberg uncertainty principle [45]. The main drawback of HHT analysis is the reduced accuracies of the extracted instantaneous frequencies at signal ends due to Gibb’s phenomenon (a.k.a. end effects).

4.3 Analysis of IDAET Data

The objective of IDAET data analysis is to determine the strain-induced changes in HF pulse velocities. The essential task here is to accurately calculate the time shift \(\tau \) between the unperturbed reference HF signal at time \(t_0, s({t-t_0 })\) and the signals recorded during and following the hammer impact at times \(t_j \), by cross-correlating the reference and perturbed signals:

$$\begin{aligned} C\left( {\tau ,t_j } \right) =\mathop \smallint \limits _0^\infty s\left( {t-t_0 } \right) s(t+\tau -t_j )dt \end{aligned}$$
(15)

The time shift \(\tau _{max} \left( {t_j } \right) \) corresponding to the maximum cross-correlation \(C_{max} \left( {t_j } \right) \)is further refined by fitting the cross-correlation function \(C\left( {-3+\tau :3+\tau ,t_j } \right) \) around its peak with a second-order polynomial function and registering the time lag corresponding to its maximum as the refined time shift \(\tau _{max} \left( {t_j } \right) \). The relative velocity change can then be expressed in terms of the calculated time shifts according to the following relationship:

$$\begin{aligned} \frac{\Delta c}{c_0 }\left( {t_j } \right) =-\frac{\tau _{max} \left( {t_j } \right) }{t_{ref} } \end{aligned}$$
(16)

where \(c_0 \) is the compressional wave velocity in the material at the unperturbed state and \(t_{ref} \) is the time of flight of the reference HF pulse (before the hammer strike). An example of the ultrasound pulse velocity variations with time \(\frac{\Delta c}{c_0 }\left( {t_j } \right) \) shortly before and after the hammer strike is shown in Fig. 4. Each point on this graph corresponds to one instance of velocity change measured by the probing transducer pair. The hammer strike results in an almost instantaneous sharp drop in measured velocities (often referred to as “offset” or “elastic softening”). This sudden elastic softening is followed by a slow recovery towards the unperturbed state (slow dynamics).

We extract two sets of parameters from the IDAET results. The first is the initial relative wave velocity drop \(\frac{\Delta c_{max} }{c_0 }\), which is related to the same microstructural features as those that influence the nonlinear hysteretic parameter \(\alpha \) [27]. As sketched in Fig. 3b, we further normalize this quantity by the maximum spatially averaged strain over the area of the probing transducers \(\left( {\frac{2\varepsilon _{max} }{3}} \right) \)to obtain:

$$\begin{aligned} \alpha _{DAET} =\frac{3\Delta c_{max} /c_0 }{2\varepsilon _{max} } \end{aligned}$$
(17)
Fig. 4
figure 4

Typical variations of relative ultrasound pulse velocity with time. \(\Delta c_{max} /c_0 \) is the initial relative wave velocity drop

Full size image

The second set of parameters includes the classical nonlinear parameters \(\beta \) and \(\delta \). To calculate \(\beta \) and \(\delta \), the velocity change \(\frac{\Delta c}{c_o }\left( {t_j } \right) \) is filtered using a high-pass filter with cutoff frequency of 600 Hz and related to the corresponding strain level. Figure 5a and b show examples of filtered \(\frac{\Delta c}{c_0 }\left( {t_j } \right) \) and the corresponding strain history. The strain at each time instance \(t_j \) is the estimated maximum strain within the specimen averaged over the time it takes for the HF pulse to travel from the emitter to the receiver. Having the strain and velocity change time histories, the wave velocity change versus average strain variation can be plotted (Fig. 5c). In this study, each set of testing is repeated three times, and all these three datasets were assembled together and used to estimate nonlinear parameter \(\beta \)and \(\delta \) by fitting the curve to Eq. (5). The rate of slow recovery (slow dynamics) could have been another parameter to extract from IDAET data. However, we were not able to obtain a reliable estimation of the recovery rate due to the contamination of a large of number of our measurements by low-frequency oscillations.

Fig. 5
figure 5

Examples of filtered strain and velocity time histories recorded during a typical IDAET: a the relative velocity change as a function of time, and b the strain amplitude as a function of time. Data contained within the specified window is used for plotting, c the relative velocity change as a function of strain amplitude

Full size image
Fig. 6
figure 6

Amplitude spectra for an air-entrained concrete sample (AE7) after: a 0, b 18, c 35, and d 55 FT cycles. Amplitude spectra for a non-air-entrained concrete sample (NonAE1) after: e 0, f 18, g 35, and h 55 FT cycles

Full size image

5 Results and Discussion

5.1 Multi-Impact INRAS

First, we analyze the data using the FFT procedure described in Sect. 4.2.1. Each multi-impact test consists of a series of 30 hammer strikes: 10 low, 10 medium, and 10 strong impacts. As noted previously, only impacts stronger than all the preceding ones are analyzed to avoid unwanted influences caused by conditioning and slow dynamics [24]. These effects will be discussed in detail in Sect. 5.2. Figure 6 shows the evolution of the FFT amplitude spectra for one air-entrained (AE7) and one non-air-entrained (NonAE1) specimens after 0, 18, 35, and 55 FT cycles. As expected, the resonance frequency shift for both samples is initially (0 FT cycles) very small while both samples are still intact (see Fig. 6a, e). In case of AE7, we observe no significant change in the resonance frequency shift with the increasing number of FT cycles (Fig. 6d). In contrast, the resonance frequency shift for NonAE1 is significant (Fig. 6h) even after 35 cycles, implying a gradual increase in the hysteretic nonlinearity of the sample. In addition, the main lobe of the spectra widens with increasing impact energy suggesting significant nonlinear damping in the damaged specimen. For a more quantitative comparison, the relative resonance frequency shift versus the maximum relative strain within the specimen at each impact level after 0, 18, 35, and 55 FT cycles for the two samples are compared in Fig. 7. For each damage level, the hysteresis nonlinear parameter \(\alpha _f \) is obtained through linear regression for a strain range of 1 to 15 microstrains. In case of AE7, the absolute value of \(\alpha _f \) increases only slightly from 162 to 193 after 55 FT cycles, whereas \(\alpha _f \) increased from 130 to 5340 for NonAE1. Similar results are observed on the other sample for both mixtures. \(\alpha _f \) increased from 149 to 214 for AE6, and from 124 to 4291 for NonAE2. We note that the (linear) resonance frequency \(f_0 \) also decreases with the increasing number of FT cycles, indicating a gradual reduction of the dynamic elastic modulus with increasing damage. A very similar trend (<1.5%) was found for the linear resonance frequencies measured following ASTM C215 (not shown). However, as compared in Fig. 8, the relative change in \(f_0 \) is two orders of magnitude smaller than that of \(\alpha _f \) confirming that the nonlinear parameter is far more sensitive to early damage than the standard linear measure.

Fig. 7
figure 7

Relative resonance frequency shift as a function of strain obtained using FFT for: a sample AE7; no significant change or trend is observed with the increasing number of FT cycles, b sample NonAE1; the slope changes dramatically with the increasing number of FT cycles

Full size image
Fig. 8
figure 8

A comparison between linear resonance frequency and hysteretic nonlinear parameter \(\alpha _f \) for an air-entrained (AE7) and a non-air-entrained sample (NonAE1). a Linear resonance frequency decreases by 33% (18%) after 55 FT (35FT) cycles for NonAE1 (NonAE2 respectively). b The absolute value of nonlinear parameter \(\alpha _f \) increases by 4010% (2800%) after 55 FT (35FT) cycles for NonAE1 (NonAE2 respectively). The respective changes for AE samples are negligible (of order 1 and 10% change for \(f_0 \) and \(\alpha _f \) respectively)

Full size image
Fig. 9
figure 9

a Relative resonance frequency shift as a function of strain obtained using WRF for: a sample AE7. The slope remains almost invariant to the increasing number of FT cycles (an enlarged version is included for better readability), b sample NonAE1. As the number of FT cycles increase, the slope changes dramatically

Full size image

5.2 Single-Impact INRAS

Next, we study the single-impact INRAS results using the previously described existing and proposed methods namely, WRF (4.2.2) and HHT (4.2.3). For each sample, the results pertaining to the strongest impact in the series (generating the widest range of strain) is presented here. Figure 9a and b show the relative frequency shift versus strain obtained using WRF for AE7 and NonAE1 after 0, 18, 35, and 55 FT cycles. Similar to FFT results, sample NonAE1 exhibits much larger frequency shift than sample AE7. However, unlike FFT results (Fig. 7), the relative frequency shift versus strain is not linear presumably due to conditioning and slow dynamics [24]. After a strong hammer strike, materials with hysteretic nonlinearity experience an immediate softening of dynamic elastic modulus, thus a sharp drop in resonance frequency (fast dynamics or conditioning). Once the impact force is removed, the dynamic elastic modulus slowly (time-logarithmic [48]) recovers. We believe that a combination of these two effects leads to the observed nonlinear dependence of relative frequency shift on strain. Similar observation has also been reported elsewhere [15,16,17].

Finally, we use HHT to obtain the resonance frequency shift versus strain relation. Figure 10 demonstrates the advantage of HHT over WRF. While the outcomes of WRF depend on the window size, HHT requires no window selection and a priori information about the signal. Figure 11 compares the outcomes of WRF and HHT when used to analyze single-impact INRAS of sample AE7 after 18 FT cycles. The corresponding STFT with the same window size as WRF is included for comparison. Despite their different principles, HHT and WRF yield fairly similar nonlinear relationships between the resonance frequency shift and strain. All methods reveal fluctuations in the resonance frequency–strain relationships. These fluctuations may be attributed to the presence of two very close frequencies in the response. If the cross section of the specimen slightly deviates from the nominal square, there would be two bending modes with too close resonance frequencies to be differentiated. We chose specimens of standard geometry to be able to directly compare our results to standard measures. Otherwise, in resonance testing, symmetry in the dimensions of the specimens should be avoided. Nevertheless, like multi-impact INRAS, single-impact INRAS using HHT can distinguish the concrete under different FT cycles as shown in Fig. 12.

5.3 Multi- Versus Single-Impact INRAS

A comparison between multi- and single-impact (the strongest impact strike in the series) INRAS is included in Fig. 11. The resonance frequency-strain curves corresponding to the multi-impact and single-impact testing resemble the loading and unloading phases of hysteretic constitutive relations. Conditioning and slow dynamics phenomena result in a different trajectory for the ‘recovery’ of the resonance frequency in the single-impact experiment. At the same time, we observe that the initial frequency drop in single-impact INRAS (corresponding to the hammer strike inducing a strain of about \(11 \times 10^{-6})\) does not match the resonance frequency reported for the same hammer strike in multi-impact INRAS. This discrepancy stems from the systematic error in the standard analysis of multi-impact INRAS [32], i.e., it suffers from the inherent limitations of FFT (4.2.1). Since FFT provides the frequency content averaged over the entire reverberation signal, it overestimates the resonance frequencies systematically. The higher the strain level, the larger are the associated errors. This in turn, leads to the systematic underestimation of the nonlinear parameter \(\alpha _f .\) One way to alleviate this error is to apply FFT to a short window capturing the onset of the reverberation signal and use the attained resonance frequencies to calculate \(\alpha _f \). Figure 13 presents a comparison between the standard FFT analysis and the suggested corrective approach, where resonance frequencies are calculated for a window over the beginning portion of the signal. Three single-impact measurements corresponding to high, medium, and low strength impacts are also included in this figure. In the next section, we explore whether the resonance frequency recovery trajectory and rate in single-impact INRAS carries additional information on the concentration of microscopic defects.

Fig. 10
figure 10

A comparison between WRF with different window sizes (10% overlapping for all) and HHT

Full size image
Fig. 11
figure 11

A comparison of relative frequency shift versus strain for single-impact INRAS obtained using four different analysis methods together with the results from multi-impact INRAS. The results shown are for sample AE7 after 18 FT cycles

Full size image
Fig. 12
figure 12

Comparisons between a NonAE1 and b AE7 of single-impact INRAS using HHT data analysis routine for single-impact INRAS

Full size image
Fig. 13
figure 13

Comparison between multi-impact INRAS (square markers), modified multi-impact INRAS (diamond markers), and single-impact INRAS (circular markers) at three different impact strength levels: high, medium, and low. The demonstrated results pertain to sample AE7 after 18 FT cycles

Full size image

5.4 Evolution of Recovery Rate \(\nu \) with Damage Progress in Single-Impact INRAS

We employ the soft ratchet model proposed by Vakhnenko et al. [36] to fit the progressive increase (recover) of resonance frequency after conditioning at high strains. To do so, we use the parameter \(\nu \) as described in Eq. (11) to monitor the recovery rate of concrete specimens with increasing levels of FT damage. Figure 14 shows an example of temporal recovery of resonance frequency (NonAE1 after 35 cycles). \(f_0 \) is chosen to match the resonance frequency recorded at the minimum strain level (\(\sim \)1 microstrain). As shown in Fig. 14, the model shows good agreement with the experimental data. Next, the model is applied to the single-impact INRAS data and the recovery rate \(\nu \) is extracted for samples undergoing increasing numbers of FT cycles. Figure 15 shows the revolution of this parameter for two samples: AE7 and NonAE1. Recovery rate clearly differentiates the two samples: it increases nearly 4 times after 55 FT cycles for sample NonAE1 whereas it remains almost unchanged for sample AE7.

Fig. 14
figure 14

Temporal relative frequency shift and its exponential fitting (Eq. (11)) for sample NonAE1 after 35 FT cycles

Full size image
Fig. 15
figure 15

The evolution of the recovery rate \(\nu \) for samples AE6, AE7 and NonAE1

Full size image
Fig. 16
figure 16

The initial velocity drop as a function of maximum strain amplitude for AE7 and NonAE1. \(\alpha _{DAET} \) is calculated as the slope of each line. Since all three impacts for sample NonAE1 after 35 FT cycles are relatively high strength impacts, we use average slope (instead of linear regression) for this sample

Full size image
Fig. 17
figure 17

Variation of wave velocity as a function of strain for a AE7 after 18 FT cycles. b AE7 after 35 FT cycles. c NonAE1 after 18 FT cycles. d NonAE1 after 35 FT cycles. The quantity 2\(\Delta \) c/c is represented on the y-axis, such that the fitted parameters directly correspond to \(\beta \) and \(\delta \) values, as described in Eq. (5)

Full size image

5.5 IDAET

First, we investigate how the initial relative velocity drop normalized by the linear wave velocity \(\frac{\Delta c_{max} }{c_0 }\) evolves with increasing damage. Figure 16 shows \(\frac{\Delta c_{max} }{c_0 }\) versus maximum strain \(\varepsilon _{max} \) for three separate impacts. This figure compares two select samples, AE7 and NonAE1, after 18 and 35 FT cycles. Based on the definition given in Eq. (17), the slope of each curve is \(\alpha _{DAET} \). By increasing the number of FT cycles from 18 to 35, \(\alpha _{DAET} \) does not change for sample AE7 whereas it increases by 122% for NonAE1. A comparison of \(\alpha _{DAET} \) and \(\alpha _f \) for sample NonAE1 suggests that \(\alpha _{DAET} \) and \(\alpha _f \) are not necessarily interchangeable; although both parameters increase with damage, \(\alpha _f \) increases approximately 3 times more than \(\alpha _{DAET} \). This difference can be explained by considering that \(\alpha _f \) is a global measurement of nonlinearity, weighted-averaged over the specimen volume material, whereas \(\alpha _{DAET} \) measures the nonlinearity locally. However, we refrain from overgeneralization of this observation considering the limited number of samples in the present study. A more definitive conclusion calls for an extensive future investigation on samples of simpler microstructure.

Next, we compare the classical nonlinear parameters \(\beta \) and \(\delta \) for the AE and Non-AE samples. Figure 17 illustrates the variations of wave velocity with strain amplitudes during the ring down for AE7 and NonAE1. The data points in different colors mark the data from repeated measurements. The quadratic and cubic nonlinear parameter \(\beta \) and \(\delta \) are obtained by simple polynomial curve fitting of all three sets of data. The results show that FT damage also leads to the rise of \(\beta \) (the absolute value) but not necessary \(\delta \). For sample AE7, absolute value of \(\beta \) increases from 22 after 18 FT cycles to 35 after 35 FT cycles (a 60% increase), whereas, for sample NonAE1, it increases more considerably from 15 to 54 (a 256% increase). In comparison, the absolute value of \(\delta \) decreases slightly for both AE7 (15%) and NonAE1 (25%) samples. These mixed results for \(\delta \) are attributed to the fact that the strain level is not exactly identical after 18 and 35 FT cycles. Indeed, previous studies in diverse rock samples [22, 26, 35] have shown that when DAET is performed at different strain levels on the same sample, the curvature (and therefore \(\delta )\) decreases dramatically with strain. The changes in \(\delta \) are therefore attributed to a combination of increasing damage and slightly different strain levels. On the other hand, the slope (and therefore \(\beta )\) typically changes by a factor 2 or 3 over 2 orders of magnitude in strain [22, 35]. Similarly, when log-log plots of “change in \(\Delta \)c/c at frequency f” versus “strain” are used, the slope is found to be nearly one for all samples (Fig. 5b–h of reference [26]), which indicates that \(\beta \) is rather strain invariant. Based on these observations, we are confident that the changes in \(\beta \) (60 and 256% increase) estimated over a small strain range (4–7 microstrains) can be attributed to increase in damage. We also note here that these rather small \(\beta \) and \(\delta \) values (or order 10–100 for \(\beta )\) should in theory be corrected for Poisson’s effect, as described in reference [35]. Because the sample dimensions and Poisson values are similar for all samples, this correction does not affect the observed evolution with damage.

To conclude, we acknowledge that using more controlled impacts and/or performing IDAET with multiple impacts covering at least an order of magnitude in strain would greatly simplify the interpretation of IDAET results, and would be essential to extend the use of this method to quantitative in-situ evaluation.

6 Conclusions

In this study, the results from multi-impact and single-impact INRAS are compared: in contrast to the multi-impact variant, the relative frequency shift–strain relation in single-impact INRAS is not linear presumably due to conditioning and slow dynamics. We propose to use HHT to calculate the instantaneous frequency content of the response. HHT is a more appropriate tool for analyzing non-stationary and nonlinear signals and provides instantaneous frequency estimations of higher resolution that are in agreement with the conventional analyses. This study confirms that material nonlinearity and level of damage can be inferred from a single-impact excitation. However, the extracted material parameters need to be carefully interpreted especially when compared to those from multi-impact INRAS or NRAS, where a low-to-high excitation is applied. In addition, we find that the post-impact ring-down signal can be adequately described by soft ratchet model and the extracted model parameters can be used to monitor FT damage in concrete. Finally, we introduce an impact version of DAET and demonstrate how to extract both classical and non-classical nonlinear parameters from the test results. Although measured independently, results from both IDAET and INRAS exhibit a manifold increase in the extracted nonlinear parameters for non-air-entrained samples (prone to FT damage) compared to the air-entrained ones (resistant to FT damage) confirming their suitability for early damage evaluation and monitoring.