Keywords

These keywords were added by machine and not by the authors. This process is experimental and the keywords may be updated as the learning algorithm improves.

12.1 Introduction

The durability of infrastructure materials, such as concrete, has direct impact on society because the productivity of many industries and safety of human beings depend on infrastructure condition, and further because maintenance of the infrastructure can represent a significant portion of a government’s budget. Thus the enhancement of concrete durability and improvement of infrastructure condition monitoring are significant concerns to the scientific community. The resonant frequency method has been traditionally used to assess the mechanical condition of concrete. Resonance frequencies of a solid body depend on test sample mass and dimensions, elastic properties, and boundary conditions. Resonance frequencies have been used to determine engineering properties such as the elastic moduli and material damping. The method is useful to assess the performance of materials within accelerated degradation durability test procedures, and to inspect quality of the products during manufacturing processes (pass/fail tests). Different testing standards and recommendations prescribe test configurations, and specific tests are recommended for different materials. A basic resonant frequency test requires a forced vibration system to set up mechanical resonances, and some system to sense the frequency content from the resonant vibration signals. For concrete-like materials, these specifications are given by ASTM C215 [1], wherein an impulsive impact event is applied to the test sample to excite the resonant frequencies and a small sensor is mounted on the surface of the test sample. From the impulsive impact vibration signals thus obtained, two standard parameters are usually derived: (1) the dynamic modulus, which depends on sample dimensions, mass, and the resonant frequency peak (f), and (2) the attenuation or damping capacity of the material. Figure 12.1a, b illustrates typical signals obtained from a single-impact vibration test, where the spectral (frequency domain) signal is computed from the time signal using a Fourier transform algorithm. The continuous reduction of the vibration signal amplitude with time during the signal “ring-down” is seen in the time domain signal. The resonant frequency and damping characteristics are extracted from the spectral signal in the region around the resonant frequency peak. The damping capacity of the material is determined from the quality factor (Q) (or inverse attenuation), which is defined as the ratio between the resonant frequency peak (f) and the bandwidth frequencies corresponding to a 50% reduction of vibration energy in the power frequency spectrum for a given vibration mode [2]. Meaningful application of the ASTM C215 test is found within other standard durability test methods [3, 4].

Fig. 12.1
figure 1

(a) Typical time domain acceleration signal obtained in impact vibration resonant tests, and (b) typical resonant spectrum, from which resonant frequency and quality factor can be evaluated

Full size image

It is important to note that standardized wave propagation and vibration test methods, such as ASTM C215, assume that the test material behaves in a linear elastic fashion, even after the material accumulates damage, and as such these methods are identified as “linear” test methods. The assumption of linearity implies, among other things, that the test results are independent of the mechanical energy level (e.g., maximum strain amplitude of the vibration motion) used in the measurement. However, infrastructure materials such as concrete are known to behave in a nonlinear and hysteretic fashion, especially at higher mechanical energy levels. It has been shown by many investigators that the nonlinear characteristics of the vibration signatures are very sensitive to the presence of damage and other microstructural characteristics within materials [5,6,7,8]. Because the nonlinear behavior is expected to be enhanced by increasing damage, considerable effort has been dedicated to develop nonlinear vibration techniques for improved damage content measurement. These nonlinear methods provide linear and nonlinear material characterization parameters. Different measurement modalities can be used to extract the nonlinear character, such as finite-amplitude and nonlinear wave mixing techniques [8,9,10]; some of these techniques are described elsewhere in this book. In nonlinear resonant frequency tests, the nonlinear and hysteretic behavior of concrete is exhibited by nonlinear harmonic mode generation and an apparent softening of the material with increasing vibration strain energy; as a result of the latter characteristic, the resonant frequency shifts downward and the attenuation shifts upward with increasing excitation amplitude [11, 12]. The nonlinear nature of the vibration response can be elicited by repeating the standard resonant frequency test configuration, but at varying vibration excitation amplitude through multiple acquisitions. The excitation amplitude can be changed by either changing the energy of the impulsive impact event or the driving voltage of an ultrasonic transmitter. Figure 12.2 illustrates the expected evolution of the amplitude dependent vibration resonant frequency (f) and attenuation (ξ) expressed with respect to those values at very low strain energy (linear) condition: fo and ξo.

Fig. 12.2
figure 2

(a) Expected behavior of the stress–strain behavior with increasing damage, (b) expected evolution of the resonant spectra with increasing damage, and amplitude dependence of the (c) resonant frequency, and (d) attenuation

Full size image

These phenomena have been leveraged by several researchers to measure nonlinear frequency and attenuation variation in a more simple and convenient manner by making use of the ring-down of a single forced vibration test. These types of approaches monitor instantaneous phase and attenuation information of the vibration as the amplitude of the signal naturally decreases during ring-down, and are referred as ring-down spectroscopies. The test configurations consist of either a burst excitation, wherein the signal is analyzed after switching off a monochromatic frequency burst [13], or a more straight-forward option that utilizes a single controlled impact event applied to the sample [14,15,16]. The latter approach enables implementation of standard test configurations and thus is less cumbersome when compared to other nonlinear measurement techniques, yet provides additional nonlinear material measurement characterization parameters.

In this chapter, different signal processing techniques that can be applied to investigate material nonlinearity derived from a single standard impact resonant frequency test are discussed. In addition, nonlinear multiple- and single-impact test approaches are compared, and the advantages and disadvantages of these techniques are discussed. Finally, some of the concerns related to impact resonant frequency tests, particularly those related to the investigation of the damage in cement-based materials, are addressed.

12.2 Background

Material degradation (D) is often defined using the dynamic modulus as

$$ D=1-\frac{E_{o,i}}{E_{o,p}} $$
(12.1)

where Eo,p is the modulus of elasticity in the pristine state and Eo,i is the modulus after an accelerated material degradation treatment. The subscript i may stand for a value indicating the number of cycles that imparted damage, the time of exposure in an aggressive environment, or another parameter characterizing the harshness of the treatment (e.g., the temperature, the concentration of a chemical solution, etc.). Usually, standard reference durability methods assume that the stress–strain relationship remains linear upon increasing damage, and hence the evaluation of damage depends on the variations of the linear resonant frequency. However, deviation from this assumption increases as the material damage level increases, and the material then behaves according to a nonlinear and hysteretic stress–strain relationship. The resulting nonlinear modulus (E) can be described as

$$ E={E}_o+H\left(\varepsilon, \dot{\varepsilon},\Delta \varepsilon \right), $$
(12.2)

where the function H(\( \varepsilon, \dot{\varepsilon},\Delta \varepsilon \)) describes a nonlinear and hysteretic departure from the linear elastic behavior, which in general depends on the strain (ε), the strain rate (\( \dot{\varepsilon} \)), and the dynamic strain amplitude (Δε). In resonant frequency experiments, this nonlinear and hysteretic behavior results in harmonic mode generation, increasing attenuation, and an apparent softening of the material manifested by changing resonant frequency and attenuation with increasing strain amplitude [17, 18]. The latter effects have been referred as the amplitude dependent internal friction [19], or the fast dynamic effect [20]. The relationship between frequency and attenuation shifts with the strain amplitude depends on the type of mechanical hysteresis involved [18, 21]. However, for most materials the resonant frequency was found to vary inversely and proportionately to the strain amplitude (Δε), within a certain level of strain amplitudes {Δεth, Δεupper} [22, 23] usually above 10−7 [24]. Therefore, the downward frequency shift experienced with respect to the linear elastic frequency value (fo) is expressed as

$$ \frac{\Delta f}{f_o}={\alpha}_f\cdotp \Delta \varepsilon, \kern1em \mathrm{and}\ \Delta \varepsilon \in \left\{\Delta {\varepsilon}_{th},\Delta {\varepsilon}_{\mathrm{upper}}\right\}. $$
(12.3)

The linear elastic frequency value (fo) is obtained for strain amplitude at and below the threshold value of the strain amplitude (Δεth). The proportionality constant αf is a measure of the hysteretic behavior. Analogously, the attenuation properties also become amplitude dependent, so the attenuation shifts from the attenuation in the linear strain regime (ξo) as

$$ \xi \left(\Delta \varepsilon \right)-{\xi}_0={\alpha}_{\xi}\cdotp \Delta \varepsilon, \kern1em \mathrm{and}\ \Delta \varepsilon \in \left\{\Delta {\varepsilon}_{\mathrm{th}},\Delta {\varepsilon}_{\mathrm{upper}}\right\}, $$
(12.4)

where αξ is the nonlinear attenuation parameter. Whenever a downward frequency shift is obtained, the attenuation properties are also shifted upward proportionately [25]. Thus, αf and αξ are proportional, which may indicate that both effects arise from the same physical mechanisms [8]: internal friction and rough contacts between unbounded interfaces. Furthermore, materials that exhibit amplitude dependent internal friction effects also reveal a time-dependent creep-like behavior which is referred as the slow dynamics effect [26]. Upon dynamic excitation, slow dynamics manifests in the material response as a progressive softening of the elastic modulus towards a new equilibrium state. Once the dynamic excitation ceases the material experiences a relaxation process whereby the modulus gradually restores to its initial value [26]. The two mechanisms (fast and slow dynamics) are thought to coexist during dynamic excitation, so the material is said to experience material conditioning [23].

The incorporation of a nonlinear hysteretic modulus into Eq. (12.1)—hence D(Δε) = 1 − Ei(Δε)/Ep(Δε)—reveals a damage parameter that depends on the strain amplitude. Alternately, the evolution of the nonlinear modulus upon material changes (i.e., degradation) can be described by including perturbation terms which reflect the variation of the linear and nonlinear elastic properties from those obtained in the pristine state (subscript p) as

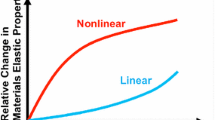
$$ {E}_i\left(\varepsilon, \dot{\varepsilon},\Delta \varepsilon \right)=\left({E}_{o,p}+\Delta {E}_o\right)+\left({H}_p\left(\varepsilon, \dot{\varepsilon},\Delta \varepsilon \right)+\Delta H\left(\varepsilon, \dot{\varepsilon},\Delta \varepsilon \right)\right). $$
(12.5)

Every perturbation term can be used in a relative basis for quantifying the evolution of nonlinear and linear parameters with increasing damage content. This idea is illustrated in Fig. 12.3, which shows expected evolution of the linear and nonlinear parameters with increasing damage in durability tests, say with increasing number of fatigue cycles or cycles of exposure in an aggressive medium. In most cases, the relative variations of the linear and nonlinear parameters exhibit a power-law behavior with increasing damage. The nonlinear parameters are able to detect the damage progression at early states, and vary with greater extent with increasing damage as compared with linear measurement parameters [6]. But at the same time, nonlinear parameters also exhibit significantly greater variability, which is not illustrated in Fig. 12.3. In some cases, the rise of material nonlinearity with damage can also reverse itself, which may correspond to crossovers between dominating mechanisms of energy dissipation, for example, viscous vs. dry friction attenuation. This effect can be especially observed in cases where the mechanism of degradation involves chemical reactions, for instance, the alkali-silica reaction in concrete [27]. This effect can also be observed during increase of moisture uptake during durability tests, see also Sect. 12.5.4. In other instances, a particular material degradation mechanism may lead to an apparent healing of the material, whereby the material nonlinearity decreases during accelerated durability tests. These cases include carbonation [28,29,30] and the degradation of particular fiber types in fiber reinforced concrete [31].

Fig. 12.3
figure 3

Conceptual illustration of the evolution of linear and nonlinear parameters with increasing damage, expressed in progressive cycles of damage, in durability tests

Full size image

12.3 Signal Processing for Single-Impact Vibration

Signal analysis techniques are used to investigate nonlinear behavior from single-impact vibration signals by extracting the instantaneous frequency and attenuation during the signal ring-down period. To achieve this, different time–frequency signal analysis techniques can be applied. Instead of providing an exhaustive review of time–frequency representations that are available, here we restrict our discussion to the Short-Time Fourier Transform, or “sliding window,” method and the time domain fitting method.

12.3.1 Sliding Window

The Fourier transform of a complete time signal provides a composite (average) response over the entire duration of the signal and thus does not permit time–frequency localization for certain time periods within the signal. However, the Short-Time Fourier Transform (STFT) allows for tracking the instantaneous frequency and amplitude variations during the signal ring-down using a sliding widow approach. For a given vibration time signal, the discrete Fourier transform is performed at overlapped time segments of the signal, which are weighted by a window function. Figure 12.4 schematically describes the signal processing technique. In Fig. 12.4b the spectral maxima for each windowed signal illustrates nonlinear softening (frequency reduction) with increasing vibration amplitude. The analysis can be stopped when the spectral amplitude at a given window position reaches a preset low threshold amplitude or a preset number of windows.

Fig. 12.4
figure 4

(a) Simulated vibration time signal. First and last positions of the sliding window are shown, (b) stacked spectra from each window wherein the red points show the maximum amplitude values

Full size image

The results depend on the signal analysis parameters, such as window length and window function type. Since the frequency resolution of the discrete Fourier transform depends on the signal length, there is a direct trade-off between time and frequency resolutions. Thus, shorter windows provide better time resolution but at the cost of poor frequency resolution. To improve frequency resolution, each signal for a given window position can be zero-padded to artificially increase the frequency step resolution [15]. However, when several modes are present in the signal, the frequency resolution decreases for higher frequency modes because the window length is kept constant. This does not pose a problem in standard test configurations (e.g., ASTM C215) because the test and the analysis of the resonant frequency are focused on only one resonant frequency mode. However, if the analysis of several modes is of interest, the resolution issue can be circumvented, for instance, through a wavelet analysis [32] or an adaptive window length approach [33], so that the frequency resolution can be kept constant along the time–frequency representation.

12.3.2 Time Domain Fitting

The analysis of single-impact vibration signals can be also conducted in the time domain. The time domain fitting method was first proposed by Van Den Abeele and De Visscher [13]. The method consists of fitting an exponentially decaying sine function

$$ {\left.y(t)\right|}_{\tau }={A}_{\tau}\cdot \exp \left(-{q}_{\tau}\cdot t\right)\cdot \sin \left(2\pi \cdot {f}_{\tau}\cdot t+{\varphi}_{\tau}\right), $$
(12.6)

to the entire signal using τ overlapped time segments of equal duration; in Eq. (12.6), Aτ is the signal amplitude, qτ is the decay parameter, fτ is the frequency, and φτ is the phase for each of the τ segments. The analysis then retrieves the values of A, f, q, and φ for each time segment τ, allowing investigation of the amplitude dependent internal friction effects. The experimental configuration proposed by Abeele and De Visscher used a loudspeaker to emit a low frequency long sinusoidal burst that matches the resonant frequency of the sample under investigation. The analysis of the signal was then performed during the ring-down of the reverberation signal after the burst excitation had been switched off. Such an experimental configuration and signal analysis was applied to analyze the material nonlinearity of concrete [13], titanium alloys [34], and carbon fiber reinforced polymer samples [35, 36].

In case of a single-impact excitation, it is expected that several vibration modes of the sample will be excited simultaneously. Hence, the model can be adapted by considering the superposition of M vibration modes as

$$ {\left.y(t)\right|}_{\tau }=\sum \limits_{m=1}^M{A}_{m,\tau}\cdot \exp \left(-{q}_{m,\tau}\cdot t\right)\cdot \sin \left(2\pi \cdot {f}_{m,\tau}\cdot t+{\varphi}_{m,\tau}\right) $$
(12.7)

where the subscript m stands for different vibration modes. One of the pitfalls of this technique is that the amplitude value corresponds to the maximum amplitude value within the measured time segment, while the frequency and decay parameter values are averaged (in the sense of least-squares) over the time segment. Also, the results depend on parameters such as the selected time segment length. Dahlén et al. [14] pointed out these concerns and proposed to fit the entire vibration signal to the model,

$$ y(t)=\sum \limits_{m=1}^{m=M}{A}_m\cdot \exp \left({\theta}_m(t)\right)\cdot \sin \left({\varphi}_m(t)\right), $$
(12.8)

where the functions θm(t) and ϕm(t) are time-dependent polynomial descriptions of the phase and attenuation of order Nm, and Km

$$ {\varphi}_m(t)=\sum \limits_{n=0}^{n={N}_m}{p}_{n,m}\cdot {t}^n,\kern1em \mathrm{and} $$
(12.9)
$$ {\theta}_m(t)=\sum \limits_{k=1}^{k={K}_m}{q}_{k,m}\cdotp \kern0.5em {t}^k, $$
(12.10)

where pn,m and qk,m are the coefficients of the polynomials corresponding to the vibration mode m. By fitting the entire signal, the instantaneous variations of signal amplitude can be precisely related to the instantaneous variations of frequency and attenuation; this approach is also called the global fitting method. It follows that the amplitude values are independent of the signal processing parameters (window length, window type, etc.), in contrast to the Fourier-based analysis or windowed fitting methods. The polynomial orders (Nm and Km) should be selected by finding an appropriate compromise between the residuals of the fit and the number of parameters included in the model. This is normally achieved through either the Akaike’s or the Bayesian Information Criteria. The latter favors the selection of parsimonious models, hence having lower polynomial orders. Two different algorithms to find the least-squares solution and polynomial order selection can be found in [14] and in [37].

The global fitting method becomes especially cumbersome when an increasing number of vibration modes coexist in the signal. Under certain circumstances, when the time-varying phase and attenuation exhibit non-monotonic variations with time, then higher order polynomials for the θm(t) and ϕm(t) functions are required. For instance, consider the case when the instantaneous frequency and attenuation appear to vary periodically. In this case, when the entire vibration signal is analyzed through a Fourier transform, the main resonant frequency peak may show a double hump or splitting of the resonant peak; this is further discussed in Sect. 12.5.3. In these cases, alternate functions θm(t) and ϕm(t) that are not polynomial in form can be considered in order to better describe the nonlinear behavior. Otherwise, a model-free method is preferred, such as the sliding window analysis described in Sect. 12.3.1.

12.4 Damage Quantification from a Single-Impact Response

Regardless of the feature extraction technique used to investigate the instantaneous characteristics of a single-impact vibration signal, the material nonlinearity can be detected by observing relationships between the signal amplitude and instantaneous frequency or attenuation. Unlike the nonlinear techniques that investigate the amplitude dependent internal friction by varying the excitation amplitude in consecutive runs, ring-down spectroscopies allow investigation of the material nonlinearity in a single run. Yet, experimental observations in damaged materials [35, 37] have revealed that the nonlinear behaviors extracted from single- and multiple-runs are substantially different, especially with increasing amount of damage within the sample. Figure 12.5a, b compares nonlinear multiple- and single-impact resonance results obtained from the same damaged concrete sample. Differences in frequency–amplitude dependence obtained from the two approaches are apparent by comparing the solid and dashed lines in Fig. 12.5b. The multiple-impact approach (Fig. 12.5a) analyzes the downward shift of the resonant frequency with successively increasing impact force for each event. In this case, the frequency decreases linearly with increasing spectral amplitude (see inset plot in Fig. 12.5a). The spectral amplitude is proportional to strain amplitude, but precise quantification of the hysteretic behavior through the slope of the frequency–amplitude relationship is limited by the arbitrary units of the spectral amplitude; recall that the Fourier spectral amplitude and frequency values are averaged over the duration of the ring-down signal. This is the main downside of the multiple-impact approach: it does not permit physical quantification, but rather a qualitative comparison between different damage states.

Fig. 12.5
figure 5

Investigation of the material nonlinearity of a concrete sample: (a) resonant spectra corresponding to multiple-impact events each with varying amplitude, where the inset figure shows the relationship between the relative frequency shift and the spectral amplitude; (b) instantaneous frequency–amplitude variation obtained during the ring-down of every single-impact event using the global time domain fitting method (continuous lines) where circle symbols represent the frequency values corresponding to the maximum amplitude for each individual impact and the dashed line fit to the maximum amplitude results match the linear trend found in (a)

Full size image

Considering now the single-impact approach, every impact vibration response from that same data set is analyzed individually, following the global time domain fitting method—see Sect. 12.3.2 for more detail. In contrast to the multiple-impact approach, analysis of ring-down of the single-impact signal enables the frequency shift to be related to signal amplitude using the physical units with which the signal was measured, thus enabling quantitative evaluation of the nonlinear behavior. The signal amplitude can then be translated to strain using analytical [38] or numerical approaches [39]. Moreover, the results shown in Fig. 12.5b demonstrate that the instantaneous frequency–amplitude dependences for every individual single-impact vibration signal are nonlinear, and that the response form depends on the impact force. Yet the frequency obtained at the maximum amplitude of every impact, indicated by circle symbols, reveals a linear relationship as ascertained from the Fourier transform of every impact signal (inset in Fig. 12.5a). These results illustrate the point that the frequency–amplitude dependences from both approaches differ substantially.

The dissimilarity between single- and multiple-impact method results can be attributed principally to the slow dynamics effect. In the multiple-impact method the slow dynamic effect is less significant assuming that the material is able to recover the resonant frequency to a reasonable amount between consecutive impacts. If sufficient recovery between impacts is achieved, then the variability of impact force on the resonant frequency is well represented by the strain amplitude and does not depend on the time lapse between consecutive impacts. In contrast, in the single-impact method, the frequency recovery during the ring-down signal depends not only on the strain amplitude, but also on the previous history of the dynamic load; the latter is represented in general form using the subscript “t-1,” to recognize that frequency shift resulting from the slow dynamics contribution lags with respect to the instantaneous strain amplitude. Then, the total (measured) frequency shift experienced during a ring-down signal (fo − f(Δε,Δεt-1)) can be considered as the superposition of two elastic subsystems: (1) one that depends on the instantaneous strain amplitude—or fast dynamics (fo − f(Δε))—having no memory of the load history, and (2) another that depends on the load history—or slow dynamics (fo − f(Δεmax,Δεt-1)). When expressed as a simple linear combination of effects, the expression for total frequency shift becomes

$$ \frac{f_0-f\left(\Delta \varepsilon, \Delta {\varepsilon}_{t-1}\right)}{f_0}={\left\langle \frac{f_0-f\left(\Delta \varepsilon \right)}{f_0}\right\rangle}_{\mathrm{fast}}+{\left\langle \frac{f_0-f\left(\Delta {\varepsilon}_{t-1},\Delta {\varepsilon}_{\mathrm{max}}\right)}{f_0}\right\rangle}_{\mathrm{slow}}. $$
(12.11)

Experimental observations in concrete suggest that fast and slow dynamics are coupled during dynamic excitation, as indicated by Eq. (12.11). This coupled effect has been referred as material conditioning [23, 40]. It follows that in order to decompose fast and slow dynamic contributions from the total, a priori knowledge is required about (1) the frequency–amplitude dependence set up by the fast dynamic behavior, and (2) the linear resonant frequency value fo. Thus, in the case of a linear relationship between frequency and strain amplitude (e.g., as shown in Fig. 12.5a for the case of spectral amplitude, which is proportional to the strain amplitude), the nonlinear hysteretic parameter can be extracted from the maximum value obtained from a single-impact response as

$$ {\alpha}_f=\frac{\left(\frac{f_0-{f}_{\Delta \varepsilon \max }}{f_0}\right)}{\Delta {\varepsilon}_{\mathrm{max}}}. $$
(12.12)

where fΔεmax is the frequency value obtained at the maximum strain amplitude (Δεmax). In this way, the frequency shift corresponding to the fast dynamic effect is proportional to the amplitude variation over the signal ring-down, and the slow dynamics contribution deviates away the proportional frequency shift behavior. Figure 12.6a, b illustrates conceptually the fast and slow dynamic contributions as a function of time and as a function of the strain amplitude for a general case where the frequency–amplitude dependence corresponding to the fast dynamic effect is assumed to be linear; note, however, that other nonlinear relationships can be also considered for the fast dynamics effect as the frequency–amplitude relationship depends on the type of mechanical hysteresis [21]. The linear combination of fast and slow dynamics expressed in Eq. (12.11) is illustrated in Fig. 12.6b, illustrating the relationship between frequency and amplitude obtained for both single- and multiple-runs. Note also that a similar decomposition can be derived for the amplitude dependent attenuation. The investigation of the nonlinear behavior through a single-impact approach contains the slow dynamic response (dotted lines in Fig. 12.6a, b), which in a multiple-impact approach may be avoided with sufficient material recovery time between impact events. The latter can be achieved by controlling the time lapse between impacts and by verifying that the resonant frequency has been restored to the value obtained in the linear strain regime (fo) between consecutive acquisitions.

Fig. 12.6
figure 6

Conceptual illustration of the resonant frequency shift during the signal ring-down and decomposed fast and slow dynamic contributions as a function of (a) time and (b) strain amplitude. The circular point indicates the maximum strain amplitude

Full size image

12.5 Sources of Variability and Systematic Errors

The measurement of linear and nonlinear elastic properties from resonant frequency tests is affected by different sources of variability. These sources of measurement variability are inherent to the specific feature extraction technique employed, to the particular test configuration employed, or to the ambient environmental conditions. Some of these effects are disregarded, or only vaguely addressed, in the test standards even though they may significantly affect the results or lead to misinterpretation of data. A good understanding of the following sources of variability would further enhance the robustness of linear and nonlinear resonance frequency evaluation for material characterization.

12.5.1 Errors in Nonlinear Parameter Estimation

The signal processing used to extract and quantify nonlinear behavior from the raw signal data affects the obtained parameter values and variability. In general, the signal processing must provide enough frequency resolution to reveal the small frequency variations that occur with changing excitation amplitude. Therefore, the smallest hysteretic parameter value that can be ascertained will depend on the frequency and amplitude resolutions of the signals. However, the accuracy of the hysteretic parameter depends on the precision with which the defined frequency in the linear strain regime, fo, is determined. The effects of incorrect selection of fo on the hysteretic parameter were previously discussed by Johnson et al. [41]. They identified the likely causes leading to incorrect estimation of fo are: (1) high material attenuation that can hinder the identification of fo, (2) insufficient frequency step resolution used in the signal analysis, and (3) the effect of material conditioning, meaning the fo value was not measured in the equilibrium state. Often, fo and ξo values are assumed to be the value obtained from the lowest excitation amplitude event, which depends on the sensitivity of the measurement excitation and sensing systems, rather than being ascertained at the true linear strain regime. Consideration of a pair Δεth, fo values that are above the true linear strain regime leads to an overestimation of the hysteretic parameter. Figure 12.7a shows synthetic data relating strain amplitude and frequency for αf = 103, Δεth = 10−7, and fo = 5000 Hz. Figure 12.7b shows the effects on the computation of the hysteretic parameter αf when slightly high values of Δεth and fo are assigned. Also, separate discussion is needed to consider the transformation from the dynamic response of the sample (acceleration, velocity, or displacement) to its internal dynamic strain amplitude. Although these conversions are appealing because the nonlinear behavior is defined by strain response (see Eq. (12.2)), the relations to conduct such a transformation presume linear elastic behavior [38]. With increasing material damage, these conversions will deviate from the linear elastic assumption; a comprehensive study addressing this issue is needed.

Fig. 12.7
figure 7

(a) Synthetic data representing the frequency variation of the resonant frequency as a function of the strain amplitude with a value αf = 1000, and whose true linear frequency fo is equal to 5000 Hz, and the true threshold strain amplitude Δεth equals 10−7, and (b) normalized frequency shift as a function of the strain amplitude, where the different curves represent normalized frequency shift obtained when the linear frequency is considered to be at higher values of strain amplitude than the true Δεth values

Full size image

12.5.2 Effect of Test Configuration

The test configuration that is employed may affect the obtained dynamic response results because of imperfect sample boundary conditions, varying mode excitation, or varying dynamic strain rate used in the dynamic excitation. Standard resonant frequency tests are normally performed on a sample assuming free boundary conditions. As such, samples are either supported on a foam mat, hung by elastic wires, supported on rods, or otherwise held at nodal positions. Some studies also have employed a cantilever configuration, however, non-ideal clamping conditions at the sample end may obscure the measurement of the material nonlinearity. For example, new sources of nonlinearity can be introduced to the overall system because of a loose clamp, while excessive torque on the clamped end can constrain the sample, leading to a mitigation of the nonlinear behavior [42]. Also, additional care must be taken with coupling transducers and excitation sources to the test sample to avoid nonlinear effects and spurious frequencies that are not inherent to the mechanical behavior of the material under inspection, but are associated with the test configuration itself. For example, rattling between transducers, rigs, etc. and the sample under inspection can lead to such spurious nonlinear system behaviors [43]. These spurious effects can be avoided, where possible, by the selection of test configurations that let the sample freely vibrate as much as possible.

Experimental observations have also revealed that different modes of vibration can exhibit distinct hysteretic behavior [39, 44], and so each may evolve in different ways with increasing damage. Therefore, a complete characterization of the nonlinear behavior should consider different vibration mode families (e.g., compressional, flexural, and torsional). Also, the effects of varying test strain rate may be significant, considering that strain rate does affect the nonlinear and hysteretic behavior as described in Eq. (12.2). In general, nonlinear and hysteretic behavior is enhanced with increasing dynamic strain rate [45, 46]. These observations suggest that shorter samples may enhance the nonlinear effects when compared to longer ones, as the same vibration mode will subject the shorter sample to a higher strain rate dynamic loading (higher frequency). To the authors’ knowledge, these issues have not yet been clearly addressed.

12.5.3 Double-Hump Effect

The resonant spectra of a standard flexural vibration test configuration may display closely spaced resonant frequencies mostly depending on the sample geometry, which are normally either prisms or cylinders. For samples that exhibit cross-sectional geometric symmetry, flexural modes in orthogonal directions appear at the same frequency value, and are said to be degenerate modes. If this symmetry is somehow disrupted, for example, because of imperfect geometry or the presence of an internal localized defect or density variation across the sample, the frequency of the degenerate modes separates. This effect has been dubbed as signal beating [47], double-hump effect [48], or splitting of degeneracies [49]. For concrete samples, in particular for imperfect cross-sectional geometry of the sample, the presence of a localized crack or honeycomb or chip within the material, non-uniform moisture distribution, or a density variation across the sample—for instance, because of bleeding of the concrete batch—may cause peak splitting. Also, in concrete durability tests, peak splitting effect may be enhanced as damage progresses in asymmetric fashion. Thus the double-hump effect can be observed upon increasing degradation, for example, with external chemical attack wherein the inward diffusion of aggressive chemical species can lead to a density variation across the sample, or in durability tests that subject the samples to thermal shocks or freezing-thawing cycles. In other cases, the peak splitting can be interpreted as a periodic variation of sample stiffness during opening and closing of an internal defect (e.g., a surface-breaking crack) upon dynamic motion [50, 51]. In other instances, a double-hump effect can be also caused by poorly attached sensors on the sample [27].

Figure 12.8a, b shows the vibration response in time and frequency domains corresponding to the flexural mode of a concrete sample containing a vertical surface-breaking crack at the mid-span. The presence of the crack disrupts the continuous amplitude ring-down of the signal (Fig. 12.8a). When the whole vibration signal is interpreted in the frequency domain, the resonant peak appears to split (Fig. 12.8b). When the instantaneous frequency is investigated (Fig. 12.8c), the resonant frequency appears to vary periodically, giving the appearance that the stiffness of the sample varies with dynamic excitation. Thus peak splitting may be leveraged to identify defective samples and detect damage where the span of the frequency split correlates with the size of the defect [49, 52, 53]. However, within the context of material characterization, where the goal of the resonant frequency test is to obtain engineering properties (elastic moduli, damping, or the hysteretic parameter), peak splitting may disrupt the analysis. In this case non-degenerate modes (e.g., from the longitudinal and torsional families of modes) should be selected to characterize the samples.

Fig. 12.8
figure 8

(a) Vibration signal corresponding to the flexural mode of a concrete sample containing a surface breathing crack, (b) resulting spectra showing splitting of the resonant peak, and (c) time–frequency representation; the inset plot shows the stacked spectra obtained through the sliding window method

Full size image

12.5.4 Environmental Factors: Internal Moisture and Temperature

The constitutive properties of porous materials such as concrete are affected by the internal moisture contained within the pore structure. In general, moisture in the internal pore structure exerts a buildup of internal (hydraulic) pressure, which results in an alteration of the apparent elastic properties. The way which moisture affects the linear and nonlinear elastic properties depends on the characteristics of the pore network [54]. For concrete-like materials, it has been shown that an increase of the apparent modulus and an increase of the apparent attenuation occur with increasing moisture content. The extent of variation of the dynamic properties with internal moisture variations depends, however, on the concrete properties and composition [55]. The increase of modulus with increasing moisture content appears to be controlled by capillary-sized porosity, which is usually in the pore size range of 10–0.01 μm [55, 56]. Loss of internal moisture can also produce tensile stresses leading to microcracking of brittle porous materials [57]. Hence, the hysteretic behavior of concrete can be enhanced after drying treatment because it can lead to shrinkage, cracking, and other microstructural modifications [56]. However, subsequent moisture uptake by the material can alleviate the mechanisms that give rise to the nonlinear behavior [37, 58]. These observations illustrate the important effect of moisture because it can obscure the presence of damage sensed by nonlinear parameters and lead to misinterpretations in durability tests. The elastic properties of materials depend also on the sample temperature [59]. The elastic modulus of different rock types exhibits hysteretic behavior during warming and cooling cycles [60]. These results may be also relevant for concrete-like materials. Environmental conditions (i.e., moisture and temperature) must be carefully maintained during durability test to avoid such misinterpretations.

12.5.5 Material Conditioning

Because of nonlinear hysteretic behavior exhibited by concrete, a memory effect may persist whereby the material temporarily “remembers” the previous load history [61]. As a consequence of this slow dynamics effect, the measured frequency and attenuation behavior may change if the standard resonant frequency test in concrete samples is repeated with short periods of rest in between [37, 62]. In other words, the resonant frequency and attenuation of a test may be affected by the previous impact test. Figure 12.9a shows the resonant frequency of concrete samples that underwent 100, 200, and 300 standard freezing-thawing cycles [3] and thus are expected to exhibit increasing amounts of distributed cracking damage. The resonant frequency test was repeated at a constant impact rate (1 Hz) and with a constant impact energy by using an automated impactor device. The results demonstrate that the resonant frequency decreases with accrued number of impacts for these types of tests, and that the amount of this change depends on the extent of internal damage. Yet, the initial resonant frequency can be eventually restored if enough rest time between subsequent tests is provided for the sample to recover the initial properties through the slow dynamics process (not shown in these data). Furthermore, the influence of the slow dynamic effect can be affected by the internal moisture content of the material. Figure 12.9b shows that the slow dynamic effect is modified by changing internal moisture content. Thus slow dynamic behavior arises from significant and separate contributions from internal moisture and internal damage levels, which can lead to misinterpretation of the obtained results if sufficient care is not taken. The influence of the slow dynamic effect on the measurement of the hysteretic parameters can be minimized by increasing the time lapse between consecutive acquisitions, that is by providing sufficient “rest” time between measurements by verifying that the elastic modulus has been restored to that obtained at linear strain amplitude excitation; however, “sufficient” rest time can require up to ten to thousands of seconds between consecutive acquisitions, depending on the material and ambient conditions [40].

Fig. 12.9
figure 9

(a) Repeated resonant frequency measurements in concrete samples that underwent 100, 200, and 300 freezing-thawing cycles, and (b) repeated resonant frequency measurements for varying moisture content in the concrete sample that underwent 300 cycles

Full size image

12.6 Concluding Remarks

This chapter describes the use of nonlinear single-impact resonant acoustic spectroscopy (NSIRAS) to quantify nonlinear material behavior of concrete, such as amplitude dependent internal friction effects. NSIRAS is a ring-down spectroscopic method where the data are collected using the standard impact resonant frequency test configuration (e.g., ASTM C 215). The NSIRAS approach offers a balance of sensitivity to material damage, when compared with linear vibration methods, and test simplicity in comparison to other nonlinear test methods such as nonlinear elastic wave spectroscopy or the dynamic acousto-elasticity test. Several different signal processing alternatives that extract nonlinear features, which arise from the nonlinear and hysteretic behavior of concrete, from the measurement signal were described. Multiple- and single-impact (ring-down spectroscopy) methods were compared. The single-impact method offers advantages in comparison to multiple-impact methods. For example, material nonlinearity can be investigated using the physical units of the signal amplitude, rather than the arbitrary units of spectral amplitude. Also, the single-impact method reduces the operating time and the number of impacts needed to carry out the test; multiple repeated impacts could lead to local damage in concrete samples, especially in durability tests as the distress progresses in the material. Some of the concerns and limitations related to impact resonant frequency tests are finally presented, particularly those related to the investigation of the durability of cement-based materials.