Correction of a High-Order Numerical Method for Approximating Time-Fractional Wave Equation

Abstract

A high-order time discretization scheme to approximate the time-fractional wave equation with the Caputo fractional derivative of order $\alpha \in (1, 2)$ is studied. We establish a high-order formula for approximating the Caputo fractional derivative of order $\alpha \in (1, 2)$. Based on this approximation, we propose a novel numerical method to solve the time-fractional wave equation. Remarkably, this method corrects only one starting step and demonstrates second-order convergence in both homogeneous and inhomogeneous cases, regardless of whether the data is smooth or nonsmooth. We also analyze the stability region associated with the proposed numerical method. Some numerical examples are given to elucidate the convergence analysis.

1 Introduction

Consider the following time-fractional wave equation, with $1< \alpha <2$,

$$\begin{aligned} \left\{ \begin{array}{ll} {^C _0}D^{\alpha }_t u + Au = f(t), &{} 0 \le t \le T,\\ u(0) = u_0, &{} \\ u'(0) = u_1, \end{array} \right. \end{aligned}$$

(1.1)

where ${{}^C _0}D^{\alpha }_t u$ stands for the Caputo fractional derivative of order $\alpha$ with respect to t defined by

$$\begin{aligned} {^C_0}D^{\alpha }_{t} u(t) = \dfrac{1}{\Gamma (2-\alpha )} \int _{0}^{t} ({t-s})^{1-\alpha }\ u''(s) \ \mathrm{{d}}s. \end{aligned}$$

Here $A = - \Delta$ with the definition domain $D(A) = H_0^1(\Omega ) \cap H^2(\Omega )$ and $\Delta$ stands for the Laplacian, where $H_{0}^{1}(\Omega )$ and $H^{2}(\Omega )$ denote the standard Sobolev spaces on a domain $\Omega \subset \mathbb {R}^d, d=1,2,3$. Furthermore, $u_{0}$ and $u_{1}$ are the initial values with $u_0, u_1 \in H$ where $H:= L^2(\Omega )$ is the Hilbert space of square integrable functions defined on $\Omega$ with the norm $\Vert \cdot \Vert$. Therefore for any $z \in \{z \ne 0: |\arg z| < \theta _{0}\}$ with $\pi /2< \theta _{0} < \pi /\alpha , \, \alpha \in (1, 2)$, the operator A satisfies the following resolvent estimates [6]

$$\begin{aligned} \Vert (z I + A)^{-1} \Vert \le C |z|^{-1}, \qquad \Vert (z^{\alpha } I + A)^{-1} \Vert \le C |z|^{-\alpha }. \end{aligned}$$

(1.2)

The time fractional wave equations are extensively used for modeling processes characterized by non-local effects, [1, 2, 5, 18]. The solution of the time fractional wave equation has a singularity near the origin. It is essential to identify efficient numerical methods for solving the time fractional wave equation while working within limited smoothness assumptions for the solutions.

Utilizing convolution quadratures as outlined in [10] and incorporating techniques from [11], Jin et al. [6] introduced two methods based on convolution quadrature in time. They established error estimates for both smooth and nonsmooth data in the context of time-fractional wave equations. Additionally, they corrected the initial steps of the BDF methods [7], resulting in high-order numerical methods for approximating the time-fractional wave equation with both smooth and nonsmooth data. A nonuniform $L2-1_{\sigma }$ Crank-Nicolson difference method was developed on a nonuniform temporal mesh [23] for solving time-fractional wave equation. In [12], convergence in the $H_{0}^{1}(\Omega )$-norm was derived for a low-order Petrov-Galerkin method with a nonsmooth source term. Li et al. [13] proposed a time-spectral method characterized by exponential decay in temporal discretization when the solution is smooth enough. Furthermore, in [14], they analyzed a space-time finite element method, showing that high-order temporal accuracy can still be achieved with appropriately graded temporal grids.

The time fractional wave equation can be written as an evolution equation with a positive-type memory term. Various numerical methods exist for dealing with evolution equations with such positive-type memory terms. McLean et al. [15, 16] introduced two positive definite quadratures specifically designed for the time fractional integral operator. Applying the convolution quadratures from [10] and using backward difference methods in time, Lubich et al. [3, 11] obtained the first and second-order time-stepping schemes. They derived optimal error estimates with nonsmooth initial data. Mustapha and McLean [17] proposed a novel class of algorithms by applying a discontinuous Galerkin method to address the challenges posed by the time fractional wave equation.

In more recent developments, the S2 and S3 formulae, both belonging to the S-type formula category, were introduced as means to approximate the Caputo fractional derivative. These formulae exhibit convergence orders of $O(k^{3-\alpha })$ and $O(k^{4-\alpha })$ for $\alpha \in (1, 2)$ [19]. The L3 formula, as presented in [21], has been formulated for approximating the Caputo derivative of order $\alpha \in (1, 2)$. This particular formula demonstrates second-order convergence and has been used in approximating solutions to the time-fractional wave equation.

Based on the ideas in [19, 21], in this paper, we introduce a new high-order time discretization scheme with the corrections on the starting steps. Using the discrete Laplace transform method, we prove that the proposed method has the optimal convergence order $O(k^{2})$ in both homogeneous and inhomogeneous cases with both smooth and nonsmooth data.

The paper is organized as follows. In Section 2, we introduce a high-order formula for approximating the Caputo derivative of order $\alpha \in (1, 2)$ with some specific weight corrections. Section 3 introduces the corrected numerical methods for approximating the time-fractional wave equation in both homogeneous and inhomogeneous cases. We establish optimal error estimates using the Laplace transform method. In Section 4, we consider the stability region of the proposed numerical method. Finally, Section 5 presents numerical results aimed at validating the theoretical findings and showing the robustness of the proposed numerical method.

Throughout this paper we denote C a generic constant independent of the step size k which could be different at different occurrences.

2 Time Discretization

Let $k = T/N$ and construct a partition over [0, T] as $0 =t_0< t_1<\cdots< t_n< \cdots < t_N = T$. We shall approximate the Caputo fractional derivative, with $\alpha \in (1, 2)$,

$$\begin{aligned} {^C_0}D^{\alpha }_t u(t_n)&= \dfrac{1}{\Gamma (2-\alpha )} \int _{t_0}^{t_n} (t_n-s)^{1-\alpha }\ u''(s) \ \mathrm{{d}}s, \nonumber \\&= \dfrac{1}{\Gamma (2-\alpha )} \sum _{j=1}^{n} \int _{t_{j-1}}^{t_j} (t_n-s)^{1-\alpha }\ u''(s) \ \mathrm{{d}}s. \end{aligned}$$

(2.1)

On the subintervals $[t_0, t_1]$ and $[t_1, t_2]$, we approximate u by the cubic interpolation polynomials $\Pi _{3,1} u$ and $\Pi _{3,2} u$ defined the nodes $(t_0, u(t_0)), (t_1, u(t_1)), (t_2, u(t_2)), (t_3, u(t_3))$, respectively. On the other subintervals $[t_{j-1}, t_j],\ 3\le j \le n$, we approximate u by $\Pi _{3,j} u$ defined on the nodes $(t_{j-3}, u(t_{j-3}))$, $(t_{j-2}, u(t_{j-2}))$, $(t_{j-1}, u(t_{j-1}))$, $(t_j, u(t_j))$. By setting

$$\begin{aligned}&\delta _t u_{j-\frac{1}{2}} = \dfrac{u_{j} - u_{j-1}}{k}, \quad \delta ^2_t u_{j} = \dfrac{\delta _t u_{j+\frac{1}{2}} - \delta _t u_{j-\frac{1}{2}}}{k},\\&\quad \delta ^3_t u_{j} = \dfrac{1}{k^2}(\delta _t u_{j+\frac{1}{2}} - 2\delta _t u_{j-\frac{1}{2}} + \delta _t u_{j-\frac{3}{2}}), \end{aligned}$$

we obtain, with $\delta ^3_t u_{j-\frac{3}{2}}: = \delta _{t}^{2} \big ( \delta _{t} u_{j-\frac{3}{2}} \big )$,

$$\begin{aligned} (\Pi _{3,j} u(t))'' = \delta ^2_t u_{j-2} + (t - t_{j-2}) \delta ^3_t u_{j-\frac{3}{2}}. \end{aligned}$$

Let $\Delta ^2 u_j = u_{j+2} - 2 u_{j+1} + u_j$ and similar as (2.10) in [21], we have, with $n \ge 3$,

$$\begin{aligned} {^C_0}D^{\alpha }_t u(t_n)&= \dfrac{1}{\Gamma (2-\alpha )} \Big ( \int _{t_0}^{t_1} (t_n-s)^{1-\alpha }\ (\Pi _{3,1} u(s))'' \ \mathrm{{d}}s + \int _{t_1}^{t_2} (t_n-s)^{1-\alpha }\ (\Pi _{3,2} u(s))'' \ \mathrm{{d}}s \nonumber \\&\quad + \sum _{j=3}^{n} \int _{t_{j-1}}^{t_j} (t_n-s)^{1-\alpha }\ (\Pi _{3,j} u(s))'' \ \mathrm{{d}}s \Big )= k^{-\alpha } \sum _{j=1}^{n-1} c_{n-1-j}^{(\alpha )} \ \Delta ^2 u_{j-1} + R^n, \end{aligned}$$

(2.2)

where $R^n = {O}(k^{2})$ and the coefficients $c_{l}^{(\alpha )}$ in (2.2) are defined by for $n \ge 3$,

$$\begin{aligned} c_{n-1-j}^{(\alpha )} =\frac{1}{\Gamma (3-\alpha )} \left\{ \begin{array}{ll} a_{n-3}^{(\alpha )} + 2 a_{n-2}^{(\alpha )} + 3a_{n-1}^{(\alpha )} - b_{n-1}^{(\alpha )} - b_{n-2}^{(\alpha )} - b_{n-3}^{(\alpha )}, &{} j = 1,\\ a_{n-4}^{(\alpha )} - a_{n-2}^{(\alpha )} - 2 a_{n-1}^{(\alpha )} + b_{n-1}^{(\alpha )} + b_{n-2}^{(\alpha )} + b_{n-3}^{(\alpha )} - b_{n-4}^{(\alpha )}, &{} j=2,\\ a_{n-j-2}^{(\alpha )} - b_{n-j-2}^{(\alpha )} + b_{n-j-1}^{(\alpha )}, &{} 3\le j \le \hspace{-1mm}n-2, \\ b_{n-j-1}^{(\alpha )}, &{} j=n-1, \end{array} \right. \end{aligned}$$

in which the coefficients $a_j^{(\alpha )}$ and $b_j^{(\alpha )}$ are defined by

$$\begin{aligned} a_j^{(\alpha )}&= (j+1)^{2-\alpha } - j^{2-\alpha }, \end{aligned}$$

(2.3)

$$\begin{aligned} b_j^{(\alpha )}&= \dfrac{1}{3-\alpha } \left( (j+1)^{3-\alpha } - j^{3-\alpha } \right) + (j+1)^{2-\alpha } - 2 j^{2-\alpha }. \end{aligned}$$

(2.4)

Then, we rewrite the L3 formula in (2.2) as

$$\begin{aligned} {^C_0}D^{\alpha }_t u(t_n) = k^{-\alpha } \sum _{j=0}^{n} w_{j, n} \ u(t_{n-j}) + R^n, \qquad n\ge 3, \end{aligned}$$

with the following coefficients

$$\begin{aligned} w_{j,n} = \left\{ \begin{array}{ll} c_{0}^{(\alpha )}, &{} j = 0,\\ c_{1}^{(\alpha )} - 2 c_{0}^{(\alpha )}, &{} j=1,\\ c_{j-2}^{(\alpha )} - 2 c_{j-1}^{(\alpha )} + c_{j}^{(\alpha )}, &{} j = 2, \ldots , n-2,\\ c_{n-3}^{(\alpha )} - 2 c_{n-2}^{(\alpha )}, &{} j=n-1,\\ c_{n-2}^{(\alpha )}, &{} j = n. \end{array} \right. \end{aligned}$$

(2.5)

Remark 2.1

When $\alpha \rightarrow 2$, the L3 formula reduces to the following scheme for approximating the second time derivative $u_{tt}(t_n)$ for $n \ge 3$, i.e.,

$$\begin{aligned} u_{tt}(t_n) \approx k^{-2} \Big (2 u(t_n) - 5 u(t_{n-1}) + 4 u(t_{n-2}) - u(t_{n-3}) \Big ), \end{aligned}$$

which has the second order convergence, that is

$$\begin{aligned} u_{tt}(t_n) - k^{-2} \Big (2 u(t_n) - 5 u(t_{n-1}) + 4 u(t_{n-2}) - u(t_{n-3}) \Big ) = O ( k^2), \quad \text{ as } \; k \rightarrow 0. \end{aligned}$$

Based on (2.5), we may define $w_j$ as follows

$$\begin{aligned} w_0&= \dfrac{1}{\Gamma (3-\alpha )} \Big (1 + \dfrac{1}{3-\alpha } \Big ), \nonumber \\ w_1&= \dfrac{1}{\Gamma (3-\alpha )} \Big ( 2^{2-\alpha } - 4 + \dfrac{1}{3-\alpha }(2^{3-\alpha } - 4) \Big ), \nonumber \\ w_2&= \dfrac{1}{\Gamma (3-\alpha )} \Big ( 6 - 2^{4 - \alpha } + 3^{2 - \alpha } + \dfrac{6}{3 - \alpha } - \dfrac{2^{5 - \alpha }}{3 - \alpha } + \dfrac{3^{3 - \alpha }}{3 - \alpha }\Big ),\nonumber \\ w_j&= \dfrac{1}{\Gamma (3-\alpha )} \Big ( (j+1)^{2-\alpha } + \dfrac{(j+1)^{3-\alpha }}{3-\alpha } - 4 j^{2-\alpha } - 4 \dfrac{j^{3-\alpha }}{3-\alpha } + 6 (j-1)^{2-\alpha } + 6 \dfrac{(j-1)^{3-\alpha }}{3-\alpha }\nonumber \\&- 4 (j-2)^{2-\alpha } - 4 \dfrac{(j-2)^{3-\alpha }}{3-\alpha } + (j-3)^{2-\alpha } + \dfrac{(j-3)^{3-\alpha }}{3-\alpha } \Big ), \qquad j = 3, 4, \ldots . \end{aligned}$$

(2.6)

Remark 2.2

In Eq. (2.5), the weights $w_{j, n}$ rely on the parameter n, whereas in Eq. (2.6), the weights $w_j$ are independent of n. In the subsequent section, we will employ the weights $w_j$, for $j=0, 1, 2, \dots$, from Eq. (2.6) to establish our numerical method. This selection is made in order to facilitate the application of the discrete Laplace transform method.

3 Error Analysis

In this section, we introduce the time discretization scheme for approximating (1.1). We proceed to derive error estimates for the schemes in both homogeneous and inhomogeneous cases, encompassing both smooth and nonsmooth data.

3.1 Homogeneous Case

In this subsection, we consider the time discretization of (1.1) with $f =0$, i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} {^C _0}D^{\alpha }_t u + Au = 0, &{} 0 \le t \le T,\\ u(0) = u_0, &{} \\ u'(0) = u_1. \end{array} \right. \end{aligned}$$

(3.1)

Let $V(t):= u(t) - u(0) - t u'(0)$ then (3.1) can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} {^C _0}D^{\alpha }_t V(t) + A V(t) = - A u(0) - A t u'(0), &{} 0 \le t \le T,\\ V(0) = 0, \qquad V'(0) = 0. \end{array} \right. \end{aligned}$$

(3.2)

Based on the idea in [7], we define the following corrected time discretization schemes for solving (3.2),

$$\begin{aligned} \begin{array}{ll} {k}^{-\alpha } \displaystyle \sum _{j=1}^{n} w_{n-j} V^j + A\ V^n = -A u_{0} - t_n A u_1 + a_1(-A u_{0}) + b_{1} k A u_1, &{}n=1, \\ {k}^{-\alpha } \displaystyle \sum _{j=1}^{n} w_{n-j} V^j + A\ V^n = -A u_{0} - t_n A u_1, &{} n \ge 2, \end{array} \end{aligned}$$

(3.3)

where the correction coefficients are $a_1 = \frac{1}{2}, b_1 = \frac{1}{12}$.

Lemma 3.1

([4, 7]) For $p \ne 1, 2, \ldots$, the polylogarithm function $Li_p(z) = \sum _{j=1}^{\infty } \dfrac{z^j}{j^p}$ is analytically continued in the split plane $\mathbb {C} \setminus [1, + \infty ]$ and satisfies the singular expansion

$$\begin{aligned} Li_p(e^{-z}) \sim \Gamma (1-p) z^{p-1} + \sum _{k=0}^{\infty } (-1)^k \xi (p-k) \dfrac{z^k}{k!} \quad \text {as} \quad z\rightarrow 0, \end{aligned}$$

(3.4)

in which $\xi$ is the Riemann zeta function.

Lemma 3.2

Let $\zeta = e^{-zk}, \, z \in \mathbb {C}$ and $1< \alpha <2$. Then, for some suitable constants $d_{1}, d_{2}$, we have

$$\begin{aligned} \tilde{w}(\zeta ) : = \sum _{j=0}^{\infty } w_j \zeta ^j = (zk)^{\alpha } - \frac{1}{3} (zk)^{2+\alpha } + d_1 (zk)^{4} + \frac{1}{3} (zk)^{3+\alpha } + d_{2} (zk)^{4 + \alpha } + \cdots , \quad \text{ as } \; zk \rightarrow 0. \end{aligned}$$

Proof

Note that

$$\begin{aligned} \tilde{w}(\zeta )&= \sum _{j=0}^{\infty } w_j \zeta ^j = \dfrac{1}{\Gamma (3-\alpha )} \left[ \zeta ^{-1} - 4 + 6 \zeta - 4 \zeta ^2 + \zeta ^3 \right] \Big ( \sum _{j=1}^{\infty } j^{2-\alpha } \zeta ^j \Big ) \\&\quad + \dfrac{1}{\Gamma (3-\alpha )} \left[ \dfrac{1}{3-\alpha } \zeta ^{-1} - \dfrac{4}{3-\alpha } + \dfrac{6}{3-\alpha } \zeta - \dfrac{4}{3-\alpha } \zeta ^2 +\dfrac{1}{3-\alpha } \zeta ^3 \right] \Big ( \sum _{j=1}^{\infty } j^{3-\alpha } \zeta ^j \Big ) \\&= \dfrac{1}{\Gamma (3-\alpha )} \left[ e^{zk} - 4 + 6 e^{-zk} - 4 e^{-2zk} + e^{-3zk}\right] Li_{\alpha -2} (\zeta ) \\&\quad + \dfrac{1}{\Gamma (3-\alpha )} \left[ \dfrac{1}{3-\alpha } e^{zk} - \dfrac{4}{3-\alpha } + \dfrac{6}{3-\alpha } e^{-zk} - \dfrac{4}{3-\alpha } {e^{-2zk}} +\dfrac{1}{3-\alpha } { e^{-3zk}} \right] Li_{\alpha - 3} (\zeta ). \end{aligned}$$

Utilizing (3.4) with $p = \alpha - 2, \alpha - 3$, we have

$$\begin{aligned} \tilde{w}(\zeta ) = (zk)^{\alpha } - \frac{1}{3} (zk)^{2+\alpha } + d_1 (zk)^4 + \frac{1}{3} (zk)^{3+\alpha } + d_2 (zk)^{4 + \alpha } + \cdots , \quad \text{ as } \; zk \rightarrow 0. \end{aligned}$$

for some suitable constants $d_1, d_2, \ldots$. $\square$

Lemma 3.3

Let $K(z) = z^{-1} (z^{\alpha } + A)^{-1} A$ and $z \in \Gamma _k$ where, for some $\theta \in (\pi /2, \pi )$,

$$\begin{aligned} \Gamma _k = \{ z \in \Gamma : |\Im z| \le \pi / k \}, \quad \Gamma = \{z\ne 0 : | \arg z| = \theta \}. \end{aligned}$$

(3.5)

We denote, with $\zeta = e^{-zk}, \, z \in \Gamma _{k}$,

$$\begin{aligned} z_k = \dfrac{\delta (\zeta )}{k}, \quad \delta (\zeta )=\tilde{w}(\zeta )^{1/\alpha }, \quad \mu (\zeta )=\delta (\zeta ) \Big (\dfrac{\zeta }{1 - \zeta } + a_1 \zeta \Big ). \end{aligned}$$

(3.6)

Then we have the following statements

$$\begin{aligned}&\mu (e^{-zk}) -1 = O((zk)^2), \quad \text {as} \; zk \rightarrow 0, \end{aligned}$$

(3.7)

$$\begin{aligned}&C|z| \le |z_k| \le C|z|, \end{aligned}$$

(3.8)

$$\begin{aligned}&\Vert K(z_k) - K(z) \Vert \le C k^{2} |z|, \end{aligned}$$

(3.9)

$$\begin{aligned}&\Vert \mu (\zeta ) K(z_k) - K(z) \Vert \le C k^{2} |z|, \end{aligned}$$

(3.10)

$$\begin{aligned}&k^{2} z_{k}^2 \Big ( \sum _{n=1}^{\infty } n ( e^{-zk})^n + b_{1} e^{-zk} \Big ) - 1 = O ( ( zk)^2 ), \quad \text {as} \; zk \rightarrow 0. \end{aligned}$$

(3.11)

Proof

By Lemma 3.2, we obtain

$$\begin{aligned} \mu (e^{-x}) - 1&= \Big ( \dfrac{e^{-x}}{1 - e^{-x}} + a_1 e^{-x} \Big ) \Big (\sum _{j=0}^{\infty } w_j (e^{-x})^j \Big )^{\frac{1}{\alpha }} -1 \\&=\Big ( \dfrac{e^{-x}}{1 - e^{-x}} + a_1 e^{-x} \Big ) (x^{\alpha } - \dfrac{1}{3} x^{2+\alpha } + d_1 x^4 + \dfrac{1}{3} x^{3+\alpha } +\cdots )^{\frac{1}{\alpha }} -1 \\&= (-\frac{1}{2} + a_1 ) x + c_1 x^2 +c_2 x^{4-\alpha } + c_3 x^3 + \cdots . \end{aligned}$$

By choosing $a_1 = \frac{1 }{2 }$, we get $\lim _{x\rightarrow 0} \frac{\mu (e^{-x}) - 1}{x^2} = C$ which implies (3.7).

We now turn to the proof of (3.8). We first show that there exists a constant $C>0$ such that

$$\begin{aligned} \frac{|z_{k}|}{|z|} \le C, \quad \text{ for } \; z \in \Gamma _{k}. \end{aligned}$$

(3.12)

Note that

$$\begin{aligned} \frac{|z_{k}|}{|z|} = \frac{| \delta (e^{-zk})|}{|kz|} = \frac{|\tilde{w} ( e^{-zk})^{\frac{1}{\alpha }}|}{|zk|}, \end{aligned}$$

and

$$\begin{aligned} \lim _{x \rightarrow 0} \frac{\tilde{w} ( e^{-x})^{\frac{1}{\alpha }}}{x} = \lim _{x \rightarrow 0} \frac{ ( \sum _{j=0}^{\infty } w_{j} ( e^{-x})^{j})^{\frac{1}{\alpha }}}{x} = \lim _{x \rightarrow 0} \frac{ ( x^{\alpha } - \frac{1}{3} x^{2+ \alpha } + d_{1} x^{4} + \frac{1}{3} x^{3+ \alpha } + \dots )^{\frac{1}{\alpha }}}{x} =1. \end{aligned}$$

Hence there exists $0< \delta _{1} < \frac{\pi }{\sin \theta }$ such that $\frac{|z_{k}|}{|z|} \le C, \, \text{ for } \, z \in \Gamma _{k}, \; |zk| < \delta _{1}.$ Since $\frac{\tilde{w} ( e^{-zk})^{\frac{1}{\alpha }}}{zk}$ is analytic for $z \in \Gamma _{k}, \, \delta _{1}< | zk| < \frac{\pi }{\sin \theta }$, we have $\Big | \frac{\tilde{w} ( e^{-zk})^{\frac{1}{\alpha }}}{zk} \Big | \le C$ for $z \in \Gamma _{k}, \, \delta _{1}< | zk| < \frac{\pi }{\sin \theta }$. Thus (3.12) follows.

We next show that there exists a constant $C>0$ such that

$$\begin{aligned} \frac{|z|}{|z_{k}|} \le C, \quad \text{ for } \; z \in \Gamma _{k}. \end{aligned}$$

(3.13)

Note that

$$\begin{aligned} z_k - z&= \dfrac{\delta (e^{-zk})}{k} - z = \dfrac{\delta (e^{-zk}) - zk }{k} = \dfrac{\Big (\sum _{j=0}^{\infty } w_j (e^{-zk})^j \Big )^{\frac{1}{\alpha }} - zk}{k} \\&= \dfrac{(zk) (1 - \frac{1}{3} (zk)^{2} +d_1 (zk)^{4-\alpha } + \cdots )^{\frac{1}{\alpha }} - zk}{k} = \dfrac{(zk) (1 - \frac{1}{3 \alpha } (zk)^{2} + \cdots ) - zk}{k} \\&= O(k^2 z^3), \quad \text{ as } \; kz \rightarrow 0. \end{aligned}$$

We see that there exists $0< \delta _{2} <1$ such that

$$\begin{aligned} | z- z_{k} | \le \frac{1}{2} | k^2 z^{3} |, \quad \text{ for } \, |zk |< \delta _{2}, \end{aligned}$$

which implies that

$$\begin{aligned} |z| \le | z- z_{k} | + |z_{k}| \le \frac{1}{2} |kz|^2 |z| + |z_{k}| \le \frac{1}{2} | z| + |z_{k}|, \quad \text{ for } \, |zk |< \delta _{2}. \end{aligned}$$

Thus we obtain

$$\begin{aligned} |z| \le 2 |z_{k}|, \quad \text{ for } \, z \in \Gamma _{k}, \; |zk |< \delta _{2}. \end{aligned}$$

(3.14)

Now we turn to the case for $z \in \Gamma _{k}, \; \delta _{2}< | zk| < \frac{\pi }{\sin \theta }$ for some $\theta \in (\frac{\pi }{2}, \pi )$ close to $\frac{\pi }{2}$.

Note that

$$\begin{aligned} | z_{k}^{\alpha } | = \Big | \frac{\tilde{w} ( e^{-zk})}{k^{\alpha }} \Big | = \Big | \frac{\tilde{w} ( e^{-zk})}{(zk)^{\alpha }} z^\alpha \Big | \ge \frac{ | \tilde{w} ( e^{-zk}) |}{ \big ( \frac{\pi }{\sin \theta } \big )^{\alpha } } |z|^{\alpha }, \quad z \in \Gamma _{k}, \; \delta _{2}< | zk| < \frac{\pi }{\sin \theta }. \end{aligned}$$

(3.15)

Assume at the moment that there exists a constant $c_{2}>0$ such that

$$\begin{aligned} | \tilde{w} ( e^{- zk}) | \ge c_{2}, \quad \text{ for } \; z \in \Gamma _{k}, \; \delta _{2}< | zk| < \frac{\pi }{\sin \theta }. \end{aligned}$$

(3.16)

We then get, by (3.15), there exists a constant $C>0$ such that

$$\begin{aligned} | z_{k}| \ge C |z|, \quad \text{ for } \; z \in \Gamma _{k}, \; \delta _{2}< | zk| < \frac{\pi }{\sin \theta }. \end{aligned}$$

Together this with (3.14) show (3.13).

It remains to show (3.16), that is, establishing a lower bound for $|\tilde{w} (e^{-zk})|$ when $z \in \Gamma _{k}$ and $\delta _{2}< |zk| < \frac{\pi }{\sin \theta }$. Due to the complexity of the expression for $\tilde{w} (e^{-zk})$, establishing a direct proof for (3.16) appears to be an exceedingly challenging task. Jin and Zhou [9, Lemma 5.4] have previously shown the existence of such a lower bound for the L1 scheme. Instead, we shall visually illustrate the existence of a constant $c_{2}$ satisfying (3.16) for some $\theta \in (\frac{\pi }{2}, \pi )$ close to $\frac{\pi }{2}$. To achieve this, we graphically present the complex function $\tilde{w} (e^{-w})$ for w in the range $[-1, 1] \times [\delta _{2}, \frac{\pi }{\sin \theta }]$ which contains the line $w \in \{ zk:, z \in \Gamma _{k},, \delta _{2}< | zk| < \frac{\pi }{\sin \theta } \}$. In Fig. 1, it is evident that $\tilde{w} (e^{-w})$ maintains a lower bound for $\delta _{2}=0.5, \theta =0.5, \alpha =\frac{\pi }{2}$. Table 1 provides the lower bounds for various combinations of $\delta _{2}$ and $\alpha$. Regardless of the specific values chosen, it is apparent that (3.16) remains valid. Thus, we have demonstrated the existence of the desired lower bound, supporting the conclusion that (3.16) holds true.

Fig. 1

Plot of the function $g(x, y) = |\tilde{w} (e^{-w})|$ for $w= x+ i y$ with $(x, y) \in [ -1, 1] \times [ \delta _{2}, \pi ]$ for $\alpha =1.1$ and $\delta _{2} =0.5$. The minimum value of g(x, y) on $[ -1, 1] \times [ \delta _{2}, \pi ]$ is 0.5

Table 1 The lower bounds $c_{2}$ of $|\tilde{w} (e^{-w})|$ in (3.16) on domain $w \in [ -1, 1] \times [ \delta _{2}, \pi ]$

Following the proof in [22, Lemma 2.2], and noticing $\Vert K'(z) \Vert \le C |z|^{-2}$, we get

$$\begin{aligned} \Vert K(z_k) - K(z) \Vert \le C |z|^{-2} k^2 |z|^{3} \le C k^2 |z|, \end{aligned}$$

which shows (3.9).

Now, using the fact that $\Vert K(z_k) \Vert \le C |z|^{-1}$, (3.10) follows from

$$\begin{aligned} \Vert \mu (\zeta ) K(z_k) - K(z) \Vert \le \Vert (\mu (\zeta ) - 1) K(z_k) \Vert + \Vert K(z_k) - K(z) \Vert \le |zk|^2 C |z|^{-1} + C k^2 |z| \le C k^2 |z|. \end{aligned}$$

It remains to prove (3.11). Note that, with $\delta$ defined by (3.6) and for some suitable constants $c_j, j=1, 2, \dots ,$

$$\begin{aligned}&\delta ^2(e^{-x}) \Big ( \sum _{n=1}^{\infty } n (e^{-x})^n + b_1 (e^{-x}) \Big ) -1 = \tilde{w}(e^{-x})^{\frac{2}{\alpha }} \Big ( \sum _{n=1}^{\infty } n (e^{-x})^n + b_1 (e^{-x}) \Big ) -1\\&= (x^{\alpha } - \frac{1}{3} x^{2+\alpha } +d_1 x^4 + \frac{1}{3} x^{3+\alpha } + \cdots ) \Big ( \dfrac{e^{-x}}{(1-e^{-x})^2} + b_1 e^{-x} \Big ) -1 \\&= c_1 x^2 + c_2 x^3 + c_3 x^4 + c_4 x^{4+ \alpha } + \cdots , \end{aligned}$$

we arrive at

$$\begin{aligned} \lim _{x\rightarrow 0} \dfrac{\delta ^2(e^{-x}) \Big ( \sum _{n=1}^{\infty } n (e^{-x})^n + b_1 (e^{-x}) \Big ) -1 }{x^2} = C, \end{aligned}$$

which completes the proof of (3.11). The proof of Lemma 3.3 is complete. $\square$

During the proof of the error estimate in Theorem 3.1 below, it is crucial to ensure the existence of $(z_k^{\alpha } + A)^{-1}$, where $z_k$ is defined in (3.6). In simpler terms, we need to demonstrate the existence of $\theta _0 \in (0, 2 \pi )$ such that $z_k^{\alpha } \in \Sigma _{\theta _0}$ for $z \in \Gamma _k$, with $\Gamma _k$ defined in (3.5). The theoretical proof of $z_k^{\alpha } \in \Sigma _{\theta _0}$ is generally challenging due to the complexity of the expression $z_k^{\alpha }$ [9]. Therefore, to address this issue, we will adopt the approach of visualizing the region of $z_k^{\alpha }$ through plots, similar to those presented in [20, Figures 4, 5, 6]. Note that

$$\begin{aligned} z_{k}^{\alpha } = \frac{\tilde{w} (\zeta )}{k^{\alpha }} =\frac{1}{k^{\alpha }} \sum _{j=0}^{\infty } w_{j} \zeta ^{j} =\frac{1}{k^{\alpha }} \sum _{j=0}^{\infty } w_{j} (e^{-k z})^{j} \approx \frac{1}{k^{\alpha }} \sum _{j=0}^{N} w_{j} (e^{-k z})^{j}, \; z \in \Gamma _{k}, \end{aligned}$$

(3.17)

where $z= |z| e^{i \theta } =\frac{y}{\sin \theta } e^{i \theta }$ for $y \in (0, \pi /k]$. Here we shall choose $\theta = \frac{257}{512} \pi$ in $\Gamma _{k}$, which is very close to $\pi /2$. In Figure 2, we choose $N=100$ in (3.17) and plot the region of $z_{k}^{\alpha }$ for the different $\alpha \in (1, 2)$. It is evident that for any $\alpha \in (1, 2)$, there exists a $\theta _{0} \in (0, 2 \pi )$ such that $z_{k}^{\alpha } \in \Sigma _{\theta _{0}}$ for all $z \in \Gamma _{k}$. Drawing from this observation, we put forward the following conjecture, which bears resemblance to the conjecture proposed in [20] for the subdiffusion problem with order $\alpha \in (0, 1)$.

Fig. 2

Plane graph of $z_{k}^{\alpha }$ for $\alpha =1.2, 1.4, 1.6, 1.8$

Conjecture 3.1

Let $\theta >\pi /2$ be sufficiently close to $\pi /2$ and $z_{k}$ be defined by (3.6). Then there exists $\theta _{0} \in (\pi /2, \pi )$ such that

$$\begin{aligned} z_{k}^{\alpha } \in \Sigma _{\theta _{0}}, \; \forall z \in \Gamma _{k}. \end{aligned}$$

To see the plane graphs of $z_{k}^{\alpha }$ when $\alpha \rightarrow 1$ and $\alpha \rightarrow 2$, in Fig. 3, we plot the plane graph for $\alpha =1.01$ and $\alpha =1.99$. It clearly show that there exist $\theta _{0} \in ( \pi /2, \pi )$ such that $z_{k}^{\alpha } \in \Sigma _{\theta _{0}}, \; \forall z \in \Gamma _{k}$.

Fig. 3

Plane graphs of $z_{k}^{\alpha }$ for $\alpha =1.01$ and $\alpha =1.99$

Theorem 3.1

Let $\alpha \in (1, 2)$ and let $V(t_n)$ and $V^n$ be the solutions of (3.2) and (3.3), respectively. Then

$$\begin{aligned} \Vert V(t_n) - V^n \Vert \le C k^{2} t_n^{-2} \Vert u_0\Vert + C k^{2} t_n^{-1} \Vert u_1\Vert . \end{aligned}$$

(3.18)

Proof

Taking the Laplace transform in both sides of (3.2) with respect to t, we obtain

$$\begin{aligned} \widehat{V}(z) = (z^{\alpha } + A)^{-1} (-A u_0 z^{-1} - A u_1 z^{-2}), \end{aligned}$$

and by the inverse Laplace transform, we get

$$\begin{aligned} V(t) = \dfrac{1}{2 \pi i} \int _{\Gamma } e^{zt} \left( (z^{\alpha } + A)^{-1} z^{-1} (-A u_0) + (z^{\alpha } + A)^{-1} z^{-2} (-A u_1) \right) \ \mathrm{{d}}z. \end{aligned}$$

On the other hand, taking the discrete Laplace transform in (3.3) leads to

$$\begin{aligned} \sum _{n=1}^{\infty } \Big (k^{-\alpha } \sum _{j=1}^{n} w_{n-j} V^j \Big ) \zeta ^n + \sum _{n=1}^{\infty } (A V^n) \zeta ^n&= (-A u_0) \Big (a_1 \zeta + \dfrac{\zeta }{1- \zeta } \Big ) \\&\quad + (-A u_1) \Big ( k b_1 \zeta + \sum _{n=1}^{\infty } t_n \zeta ^n \Big ). \end{aligned}$$

Using the equality

$$\begin{aligned} \sum _{n=1}^{\infty } \Big ( \sum _{j=1}^{n} w_{n-j} V^j \Big ) \zeta ^n = \Big (\sum _{j=0}^{\infty } w_j \zeta ^j \Big ) (V^1 \zeta + V^2 \zeta ^2 + \cdots ) = \tilde{w}(\zeta ) \tilde{V}(\zeta ), \end{aligned}$$

(3.19)

we obtain

$$\begin{aligned} \tilde{V}(\zeta ) = (k^{-\alpha } \tilde{w}(\zeta ) + A)^{-1} \left[ (-A u_0) \Big ( a_1 \zeta + \dfrac{\zeta }{1- \zeta } \Big ) + (-A u_1) \Big ( k \ b_1 \zeta + \sum _{n=1}^{\infty } t_n \zeta ^n\Big ) \right] , \end{aligned}$$

and we have

$$\begin{aligned} V^n =&-\dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} (A u_0) \Big ) \Bigg (z_k k \Big (a_1 {e^{-zk}} + \dfrac{{e^{-zk}} }{1- {e^{-zk}} } \Big ) \Bigg ) \ \mathrm{{d}}z \\&\quad -\dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} (A u_1) \Big ) \Bigg (z_k k^2 \Big ( b_1 {e^{-zk}} + \sum _{n=1}^{\infty } n {e^{-zk}} ^n \Big ) \Bigg ) \ \mathrm{{d}}z. \end{aligned}$$

Recalling (3.6), we get $V(t_n) - V^n = \textrm{I} + \textrm{II}$ therein

$$\begin{aligned} \textrm{I}&= \dfrac{1}{2 \pi i} \int _{\Gamma \setminus \Gamma _k} e^{z t_n} (z^{\alpha } + A)^{-1} z^{-1} (-A u_0) \ \mathrm{{d}}z \\&\quad + \dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-1} - (z_k^{\alpha } + A)^{-1} z_k^{-1} \mu (e^{-zk}) \Big ) (-A u_0) \ \mathrm{{d}}z := \textrm{I}_1 + \textrm{I}_2,\\ \textrm{II}&= \dfrac{1}{2 \pi i} \int _{\Gamma \setminus \Gamma _k} e^{z t_n} (z^{\alpha } + A)^{-1} z^{-2} (-A u_1) \ \mathrm{{d}}z \\&\quad + \dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-2} - (z_k^{\alpha } + A)^{-1} k^2 \big (\sum _{j=1}^{3} b_j \zeta ^j + \sum _{n=1}^{\infty } n \zeta ^n \big ) \Big ) (-A u_1) \ \mathrm{{d}}z \\ {}&:= \textrm{II}_1 + \textrm{II}_2. \end{aligned}$$

Noticing (1.2), $\Vert (z^{\alpha } + A)^{-1} A \Vert = \Vert I - z^{\alpha } (z^{\alpha } + A)^{-1} \Vert \le C,$ and then

$$\begin{aligned} \Vert \textrm{I}_1 \Vert&= \Vert \dfrac{1}{2 \pi i} \int _{\Gamma \setminus \Gamma _k} e^{z t_n} (z^{\alpha } + A)^{-1} z^{-1} (-A u_0) \ \mathrm{{d}}z \Vert \le C \int _{\frac{1}{k}}^{\infty } e^{-c t_n |z| } |z|^{-1} {|\mathrm{{d}}z|} \Vert u_0\Vert \nonumber \\&\le C \int _{\frac{1}{k}}^{\infty } e^{-c t_n |z| } |z|^{-2} |z| {|\mathrm{{d}}z|} \Vert u_0\Vert \le C k^{2} \int _{\frac{1}{k}}^{\infty } e^{-c t_n |z| } |z| {|\mathrm{{d}}z|} \Vert u_0\Vert \nonumber \\&\le C k^{2} t_n^{-2} \Vert u_0\Vert . \end{aligned}$$

(3.20)

Using (3.10), we obtain

$$\begin{aligned} \Vert \textrm{I}_2\Vert&= \Vert \dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-1} - (z_k^{\alpha } + A)^{-1} z_k^{-1} \mu (e^{-zk}) \Big ) (-A u_0) \ \mathrm{{d}}z \Vert \nonumber \\&\le C \Vert \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-1} A - (z_k^{\alpha } + A)^{-1} z_k^{-1} A \mu (e^{-zk}) \Big ) \ \mathrm{{d}}z \Vert \Vert u_0\Vert \nonumber \\&\le C k^{2} \int _{0}^{\infty } e^{-ct_n r} r \mathrm{{d}}r \Vert u_0\Vert \le C k^{2} t_n^{-2} \Vert u_0\Vert . \end{aligned}$$

(3.21)

(1.2) we obtain

$$\begin{aligned} \Vert \textrm{II}_1 \Vert&= \Vert \dfrac{1}{2 \pi i} \int _{\Gamma \setminus \Gamma _k} e^{z t_n} (z^{\alpha } + A)^{-1} z^{-2} (-A u_1) \ \mathrm{{d}}z \Vert \le C \int _{\frac{1}{k}}^{\infty } e^{-c t_n |z| } |z|^{-2} {|\mathrm{{d}}z|} \Vert u_1\Vert \nonumber \\&\le C k^{2} \int _{\frac{1}{k}}^{\infty } e^{-c t_n |z| } {|\mathrm{{d}}z|} \Vert u_1\Vert \le C k^{2} t_n^{-1} \Vert u_1\Vert . \end{aligned}$$

(3.22)

Finally, utilizing (3.9) and (3.11) we have

$$\begin{aligned} \Vert \textrm{II}_2 \Vert&= \Vert \dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-2} - (z_k^{\alpha } + A)^{-1} k^2 \big ( b_1 \zeta + \sum _{n=1}^{\infty } n \zeta ^n \big ) \Big ) (-A u_1) \ \mathrm{{d}}z \Vert \nonumber \\&\le C \Vert \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-2} A - (z_k^{\alpha } + A)^{-1} k^2 A \big (b_1 \zeta + \sum _{n=1}^{\infty } n \zeta ^n \big ) \Big ) \ \mathrm{{d}}z \Vert \Vert u_1\Vert \nonumber \\&\le C \Vert \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-2} A - (z_k^{\alpha } + A)^{-1} z_k^{-2} A \Big )\ \mathrm{{d}}z \Vert \Vert u_1\Vert \nonumber \\&\quad + C \Vert \int _{\Gamma _k} e^{z t_n} (z_k^{\alpha } + A)^{-1} A \Big ( z_k^{-2} - k^2 \big ( b_1 \zeta + \sum _{n=1}^{\infty } n \zeta ^n \big ) \Big ) \ \mathrm{{d}}z \Vert \Vert u_1\Vert \nonumber \\&\le C \int _{0}^{\infty } e^{-c t_n r} k^{2} \mathrm{{d}}r \Vert u_1\Vert \le C k^{2} t_n^{-1} \Vert u_1\Vert . \end{aligned}$$

(3.23)

The proof is completed by combining (3.20)–(3.23). $\square$

3.2 Inhomogeneous Case

In this subsection, we consider the time discretization of (1.1) with $f \ne 0$, i.e.,

$$\begin{aligned} \left\{ \begin{array}{ll} {^C _0}D^{\alpha }_t u + Au = f, &{} 0 \le t \le T,\\ u(0) = u_0, &{} \\ u'(0) = u_1. \end{array} \right. \end{aligned}$$

(3.24)

Let $V(t):= u(t) - u(0) - t u'(0)$ then (3.24) can be written as

$$\begin{aligned} \left\{ \begin{array}{ll} {^C _0}D^{\alpha }_t V(t) + A V(t) = - A u(0) - A t u'(0) + f(t), &{} 0 \le t \le T,\\ V(0) = 0, \qquad V'(0) = 0. \end{array} \right. \end{aligned}$$

(3.25)

Using the Taylor expansion and denoting the convolution of g and h by $g \times h$, we have

$$\begin{aligned} f(t) = f(0) + f'(0) t + R(t), \qquad R(t) = \dfrac{t^2}{2!} f''(0) + \left( \dfrac{t^2}{2!}\times f^{(3)}\right) (t). \end{aligned}$$

Following [22], we take the Laplace transform in both sides of (3.25) with respect to t and obtain

$$\begin{aligned} \widehat{V}(z) = (z^{\alpha } + A)^{-1} \Big ((-A u_0+f(0)) z^{-1} +( - A u_1 + f'(0)) z^{-2} +\widehat{R}(z) \Big ), \end{aligned}$$

and by the inverse Laplace transform, we obtain

$$\begin{aligned} V(t)&= \dfrac{1}{2 \pi i} \int _{\Gamma } e^{zt} \Big ( (z^{\alpha } + A)^{-1} z^{-1} (-A u_0+ f(0)) + (z^{\alpha } + A)^{-1} z^{-2} (-A u_1 + f'(0)) \nonumber \\&\quad + (z^{\alpha } + A)^{-1} \widehat{R}(z) \Big ) \ \mathrm{{d}}z. \end{aligned}$$

(3.26)

3.2.1 The Case for $f \in C^2([0,T]; L^2(\Omega ))$

In this subsection, we shall construct a corrected scheme for approximating (3.24) when $f \in C^2([0,T]; L^2(\Omega ))$ and prove the optimal error estimate.

Denoting $V^n$ as an approximation of the exact solution $V(t_n)$, we define the following corrected time discretization scheme for solving (3.25),

$$\begin{aligned} \begin{array}{ll} {k}^{-\alpha } \displaystyle \sum _{j=1}^{n} w_{n-j} V^j + A\ V^n = -A u_{0} - t_n A u_1 + f(t_n) + a_1(-A u_{0} + f(0) ) \\ \hspace{4.5cm} + b_{1} k ( A u_1 + f'(0) ), &{}n=1, \\ {k}^{-\alpha } \displaystyle \sum _{j=1}^{n} w_{n-j} V^j + A\ V^n = -A u_{0} - t_n A u_1 + f(t_n), &{} n \ge 2, \end{array} \end{aligned}$$

(3.27)

in which $w_j$ are defined by (2.6).

Lemma 3.4

For $\alpha \in (1, 2)$ and $z_k$ defined in (3.6), we have

$$\begin{aligned} \Vert (z^{\alpha } + A)^{-1} z^{-3} - (z_k^{\alpha } + A)^{-1} \Big ( k \sum _{n=1}^{\infty } \dfrac{t_n^2}{2!} \zeta ^n \Big ) \Vert \le C k^2 |z|^{-1-\alpha }. \end{aligned}$$

Proof

Following the proof of (3.9) and considering

$$\begin{aligned} \Vert 1 - z_k^3 k \big ( k \sum _{n=1}^{\infty } \dfrac{t_n^2}{2!} \zeta ^n \big ) \Vert {= O((zk)^2)}, \end{aligned}$$

we can write

$$\begin{aligned} \Vert (z^{\alpha }&+ A)^{-1} z^{-3} - (z_k^{\alpha } + A)^{-1} \Big ( k \sum _{n=1}^{\infty } \dfrac{t_n^2}{2!} \zeta ^n \Big ) \Vert \\&\le \Vert (z^{\alpha } + A)^{-1} z^{-3} - (z_k^{\alpha } + A)^{-1} z_k^{-3} \Vert + \Vert (z_k^{\alpha } + A)^{-1} z_k^{-3} \Big (1 - z_k^3 k \big ( k \sum _{n=1}^{\infty } \dfrac{t_n^2}{2!} \zeta ^n \big ) \Big ) \Vert \\&\le C {|z|^{-4-\alpha }} k^2 |z|^3 + C |z|^{-\alpha } |z|^{-3} k^2 |z|^2 \le C k^2 |z|^{-1-\alpha }. \end{aligned}$$

$\square$

Theorem 3.2

Let $\alpha \in (1, 2)$ and assume that $f \in C^2([0,t]; H)$ and $\int _{0}^{t_n} (t_n - s)^{\alpha } \Vert f^{(3)}(s)\Vert \mathrm{{d}}s < \infty$. Let $V(t_n)$ and $V^n$ be the solutions of (3.25) and (3.27), respectively,. Then we have

$$\begin{aligned} \Vert V(t_n) - V^n \Vert \le C k^{2}&\Big (t_n^{-2} \Vert u_0\Vert + t_n^{-1} \Vert u_1\Vert + t_n^{\alpha -2} \Vert f(0)\Vert + t_n^{\alpha - 1} \Vert f'(0)\Vert + t_n^{\alpha } \Vert f''(0)\Vert \\&+ \int _{0}^{t_n} (t_n - s)^{\alpha } \Vert f^{(3)}(s)\Vert \mathrm{{d}}s \Big ). \end{aligned}$$

Proof

Taking the discrete Laplace transform in (3.27), we get

$$\begin{aligned} \sum _{n=1}^{\infty } \Big (k^{-\alpha } \sum _{j=1}^{n} w_{n-j} V^j \Big ) \zeta ^n + \sum _{n=1}^{\infty } (A V^n) \zeta ^n&= (-A u_0 + f(0) ) \Big (a_1 \zeta + \dfrac{\zeta }{1- \zeta } \Big ) + \sum _{n=1}^{\infty } R(t_n) \zeta ^n \\&\quad + (-A u_1 + f'(0)) \Big ( k b_1 \zeta + \sum _{n=1}^{\infty } t_n \zeta ^n \Big ), \end{aligned}$$

and considering (3.19), we obtain

$$\begin{aligned} \tilde{V}(\zeta )&= (k^{-\alpha } \tilde{w}(\zeta ) + A)^{-1} \Big [(-A u_0 + f(0) ) \Big ( a_1 \zeta + \dfrac{\zeta }{1- \zeta } \Big ) +\sum _{n=1}^{\infty } R(t_n) \zeta ^n \nonumber \\&\quad + (-A u_1 + f'(0) ) \Big ( k \ b_1 \zeta + \sum _{n=1}^{\infty } t_n \zeta ^n\Big ) \Big ]. \end{aligned}$$

(3.28)

Therefore, we have

$$\begin{aligned} V^n =&-\dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} (A u_0 - f(0) ) \Big ) \Bigg (z_k k \Big (a_1 \zeta + \dfrac{\zeta }{1- \zeta } \Big ) \Bigg ) \ \mathrm{{d}}z \\&\quad -\dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} (A u_1 - f'(0)) \Big ) \Bigg (z_k k^2 \Big ( b_1 \zeta + \sum _{n=1}^{\infty } n \zeta ^n \Big ) \Bigg ) \ \mathrm{{d}}z \\&\quad -\dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} \Big ) \Big (-z_k k (\sum _{n=1}^{\infty } R(t_n) \zeta ^n) \Big ) \ \mathrm{{d}}z. \end{aligned}$$

With (3.6), we write $V(t_n) - V^n = \textrm{I} + \textrm{II} + \textrm{III}$ such that

$$\begin{aligned} \textrm{I}&= \dfrac{1}{2 \pi i} \int _{\Gamma \setminus \Gamma _k} e^{z t_n} (z^{\alpha } + A)^{-1} z^{-1} (-A u_0 + f(0) ) \ \mathrm{{d}}z \\&\quad + \dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-1} - (z_k^{\alpha } + A)^{-1} z_k^{-1} \mu (e^{-zk}) \Big ) (-A u_0 + f(0) ) \ \mathrm{{d}}z:= \textrm{I}_1 + \textrm{I}_2,\\ \textrm{II}&= \dfrac{1}{2 \pi i} \int _{\Gamma \setminus \Gamma _k} e^{z t_n} (z^{\alpha } + A)^{-1} z^{-2} (-A u_1 + f'(0)) \ \mathrm{{d}}z\\&\quad + \dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-2} - (z_k^{\alpha } + A)^{-1} k^2 \big (\sum _{j=1}^{3} b_j \zeta ^j + \sum _{n=1}^{\infty } n \zeta ^n \big ) \Big ) (-A u_1 + f'(0)) \ \mathrm{{d}}z\\ {}&:= \textrm{II}_1 + \textrm{II}_2. \\ \textrm{III}&= \dfrac{1}{2 \pi i} \int _{\Gamma } e^{z t_n} (z^{\alpha } + A)^{-1} z^{-1} (z \hat{R}(z)) \ \mathrm{{d}}z\\&\quad - \dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} (z_k k \sum _{n=1}^{\infty } R(t_n) \zeta ^n) \Big ) \ \mathrm{{d}}z:= \textrm{III}_1 + \textrm{III}_2. \end{aligned}$$

Utilizing (3.20) and (3.21), we may write

$$\begin{aligned} \Vert \textrm{I}_1 \Vert \le C k^2 t_n^{-2} \Vert u_0\Vert + C \int _{\frac{1}{k}}^{\infty } e^{-c t_n |z|} |z|^{-\alpha } |z|^{-1} {|\mathrm{{d}}z|} \Vert f(0)\Vert \end{aligned}$$

and $\Vert \textrm{I}_2 \Vert \le C k^2 t_n^{-2} \Vert u_0\Vert + C \Vert \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-1} - (z^{\alpha } + A)^{-1} z_k^{-1} \mu (e^{-zk}) \Big ) \mathrm{{d}}z\Vert \Vert f(0)\Vert$ where

$$\begin{aligned} C \int _{\frac{1}{k}}^{\infty } e^{-c t_n |z|} |z|^{-\alpha } |z|^{-1} {|\mathrm{{d}}z|} \Vert f(0)\Vert&= C k^2 \int _{\frac{1}{k}}^{\infty } e^{-c t_n |z|} |z|^{1-\alpha } {|\mathrm{{d}}z|} \Vert f(0)\Vert \le C k^2 t_n^{\alpha - 2} \Vert f(0)\Vert , \end{aligned}$$

and

$$\begin{aligned} C \Vert \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1}&z^{-1} - (z^{\alpha } + A)^{-1} z_k^{-1} \mu (e^{-zk}) \Big ) \mathrm{{d}}z\Vert \Vert f(0)\Vert \\&\le C k^2 \int _{0}^{\infty } e^{-c t_n |z|} |z|^{-\alpha } |z|^{-1} |z|^{2} {|\mathrm{{d}}z|} \Vert f(0)\Vert \le C k^2 t_n^{\alpha - 2} \Vert f(0)\Vert , \end{aligned}$$

which implies that $\textrm{I} \le C k^2 (t_n^{-2} \Vert u_0\Vert + t_n^{\alpha - 2} \Vert f(0)\Vert )$.

For $\textrm{II}$, employing (3.22) and (3.23) leads to

$$\begin{aligned} \Vert \textrm{II}_1 \Vert&\le C k^2 t_n^{-1} \Vert u_1 \Vert + C \Vert \int _{\Gamma \setminus \Gamma _k} e^{z t_n} (z^{\alpha } + A)^{-1} z^{-2} f'(0) \ \mathrm{{d}}z \Vert ,\\ \Vert \textrm{II}_2 \Vert&\le C k^2 t_n^{-1} \Vert u_1 \Vert + C \Vert \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1} z^{-2} - (z_k^{\alpha } + A)^{-1} z_k^{-2} \Big ) \ \mathrm{{d}}z \Vert \Vert f'(0)\Vert , \end{aligned}$$

in which

$$\begin{aligned}&C \Vert \int _{\Gamma \setminus \Gamma _k} e^{z t_n} (z^{\alpha } + A)^{-1} z^{-2} f'(0) \ \mathrm{{d}}z \Vert&\le C k^2 \int _{\frac{1}{k}}^{\infty } e^{-c t_n r} r^{-\alpha } {|\mathrm{{d}}z|} \Vert f'(0)\Vert \le C k^2 t_n^{\alpha -1} \Vert f'(0)\Vert , \end{aligned}$$

$$\begin{aligned} C \Vert \int _{\Gamma _k} e^{z t_n} \Big ( (z^{\alpha } + A)^{-1}&z^{-2} - (z_k^{\alpha } + A)^{-1} z_k^{-2} \Big ) \ \mathrm{{d}}z \Vert \Vert f'(0)\Vert \\&\le C \Vert \int _{\Gamma _k} e^{z t_n} (z_k^{\alpha } + A)^{-1} \Big ( z_k^{-2} - k^2 \big ( b_1 \zeta + \sum _{n=1}^{\infty } n \zeta ^n \big ) \Big ) \ {|\mathrm{{d}}z|} \Vert \Vert f'(0)\Vert \\&\le C \int _{0}^{\infty } e^{-c t_n r} k^{2} r^{-\alpha } \mathrm{{d}}r \Vert f'(0)\Vert \le C k^{2} t_n^{\alpha -1} \Vert f'(0)\Vert , \end{aligned}$$

which implies that $\textrm{II} \le C k^2 (t_n^{-1} \Vert u_1 \Vert + t_n^{\alpha -1} \Vert f'(0)\Vert )$.

Finally, we rewrite $R(t):= R_1(t) + R_2(t)$ with $R_1(t) = \frac{t^2}{2!} f''(0)$ and $R_2(t) = (\frac{t^2}{2!}* f^{(3)})(t)$ which leads to $\textrm{III} = \textrm{III}_1 + \textrm{III}_2$. Then, using Lemma 3.4 we have

$$\begin{aligned} \textrm{III}_1&\le C \Vert \int _{\Gamma \setminus \Gamma _k} e^{zt_n} (z^{\alpha } + A)^{-1} z^{-3} \mathrm{{d}}z\Vert \Vert f''(0)\Vert \\&\quad + C \Vert \int _{\Gamma _k} e^{zt_n} \Big ( (z^{\alpha } + A)^{-1} z^{-3} - (z_k^{\alpha } + A)^{-1} \big ( k \sum _{n=1}^{\infty } \dfrac{t_n^2}{2!} \zeta ^n \big ) \Big ) \mathrm{{d}}z\Vert \Vert f''(0)\Vert \le C k^2 t_n^{\alpha } \Vert f''(0)\Vert . \end{aligned}$$

Moreover, following [8, Lemma 3.7], we obtain $\textrm{III}_2 \le C k^2 \int _{0}^{t_n} (t_n - s)^{\alpha } \Vert f^{(3)}(s)\Vert \mathrm{{d}}s$ which completes proof. $\square$

3.2.2 The Case for $f \in C^1([0,T]; L^2(\Omega ))$

In this subsection, we shall construct a corrected scheme for approximating (3.24) when $f \in C^1([0,T]; L^2(\Omega ))$ and prove the optimal error estimate.

Following the idea in [7, (25)], we introduce $g = \partial _{t}^{-1} f$ in the time discretization scheme in order to to reduce the regularity requirements on f in the error estimates. To see this, we rewrite the scheme of (3.27) as

$$\begin{aligned} \begin{array}{ll} {k}^{-\alpha } \displaystyle \sum _{j=1}^{n} w_{n-j} V^j + A\ V^n = -A u_{0} - t_n A u_1 +\partial _{t} g(t_n) + a_1(-A u_{0} + f(0) ) \\ \hspace{4.5cm} + b_{1} k ( A u_1 + f'(0) ), &{}n=1, \\ {k}^{-\alpha } \displaystyle \sum _{j=1}^{n} w_{n-j} V^j + A\ V^n = -A u_{0} - t_n A u_1 + \partial _{t} g(t_n), &{} n \ge 2. \end{array} \end{aligned}$$

(3.29)

Since $g(0)=0$, then using Taylor expansion we have

$$\begin{aligned} g(t) = t \ \partial _{t} g({0}) + R_g(t) = t f({0}) + R_g(t), \qquad R_g(t) = \dfrac{t^2}{2!} \partial _{t}^2g(0) + \left( \dfrac{t^2}{2!}* \partial _{t}^3 g\right) (t). \end{aligned}$$

Replacing $f = \partial _{t} g$ in (3.25) and taking Laplace transform in both sides, we obtain

$$\begin{aligned} V(t) = \dfrac{1}{2 \pi i} \int _{\Gamma } e^{zt} (z^{\alpha } + A)^{-1}&z^{-1} (-A u_0 - A u_1 z^{-1}) \mathrm{{d}}z \nonumber \\&+ \dfrac{1}{2 \pi i} \int _{\Gamma } e^{zt} (z^{\alpha } + A)^{-1} \Big (z^{-1} f(0) + {z \widehat{R_g}(z)} \Big ) \ \mathrm{{d}}z. \end{aligned}$$

(3.30)

On the other hand, we take the Laplace transform in (3.29) and get

$$\begin{aligned} \sum _{n=1}^{\infty } \Big (k^{-\alpha } \sum _{j=1}^{n} w_{n-j} V^j \Big ) \zeta ^n + \sum _{n=1}^{\infty } (A V^n) \zeta ^n&= {(f(0) -A u_0)} \Big (a_1 \zeta + \dfrac{\zeta }{1- \zeta } \Big ) + { b_1 k f'(0) \zeta } \\&\quad -A u_1 \Big ( k b_1 \zeta + \sum _{n=1}^{\infty } t_n \zeta ^n \Big ) + \sum _{n=1}^{\infty } {(\partial _t R_g(t_n))} \zeta ^n, \end{aligned}$$

Therefore, we have

$$\begin{aligned} V^n =&-\dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} {(A u_0 - f(0))} \Big ) \Bigg (z_k k \Big (a_1 {e^{-zk}} + \dfrac{{e^{-zk}} }{1- {e^{-zk}} } \Big ) \Bigg ) \ \mathrm{{d}}z \nonumber \\&\quad -\dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} A u_1 \Big ) \Bigg (z_k k^2 \Big ( b_1 {e^{-zk}} + \sum _{n=1}^{\infty } n {e^{-zk}} ^n \Big ) \Bigg ) \ \mathrm{{d}}z \nonumber \\&\quad -\dfrac{1}{2 \pi i} \int _{\Gamma _k} e^{z t_n} \Big ( (z_k^{\alpha } + A)^{-1} z_k^{-1} \Big ) (-z_k k) \Big ( b_1 k {e^{-zk}} f'(0) + \sum _{n=1}^{\infty } R_g(t_n) {e^{-zk}} ^n) \Big ) \ \mathrm{{d}}z. \end{aligned}$$

(3.31)

Finally, we derive the error estimate for scheme (3.29) with lower regularity requirement. The proof of the Theorem 3.3 below runs along similar lines as in Theorem 3.2 with $g = \partial _{t}^{-1} f$ instead of f.

Theorem 3.3

Let $\alpha \in (1, 2)$ and assume that $f \in C^1([0,t]; H)$ and $\int _{0}^{t_n} (t_n - s)^{\alpha } \Vert f^{(2)}(s)\Vert \mathrm{{d}}s < \infty$. Let $V(t_n)$ and $V^n$ be the solutions of (3.25) and (3.29), respectively,. Then we have

$$\begin{aligned} \Vert V(t_n) - V^n \Vert \le C k^{2}&\Big (t_n^{-2} \Vert u_0\Vert + t_n^{-1} \Vert u_1\Vert + t_n^{\alpha -2} \Vert f(0)\Vert + t_n^{{\alpha -1}} \Vert f'(0)\Vert \\&+ \int _{0}^{t_n} (t_n - s)^{{\alpha -1}} \Vert f^{(2)}(s)\Vert \mathrm{{d}}s \Big ). \end{aligned}$$

4 Stability Region

In this section, we shall consider the stability region of the numerical method for solving the following test problem, with $\alpha \in (1, 2)$ and $\Re {\lambda } <0$,

$$\begin{aligned}&\, _{0}^{C}D_{t}^{\alpha } u(t) = \lambda u(t), \quad u(0) = u_{0}, \; u^{\prime } (0) = u_{1}, \end{aligned}$$

(4.1)

where $u_{0}$ and $u_{1}$ denote the values of u(t) and $u^{\prime } (t)$ at $t=0$, respectively.

Let $u^{n} \approx u(t_{n})$ be the approximate solution of $u (t_{n})$. We define the following numerical method to approximate (4.1),

$$\begin{aligned} k^{-\alpha } \sum _{j=0}^{n} w_{j} u^{n-j} = \lambda u^{n}, \end{aligned}$$

(4.2)

where $w_{j}, j=0, 1,,2, \dots$ are defined by (2.6).

Let $u^{n} = \xi ^{n}$ be the solution of (4.2). Then we have

$$\begin{aligned} \sum _{j=0}^{n} w_{j} \xi ^{n-j} = { k^{\alpha }} \lambda \xi ^{n}. \end{aligned}$$

(4.3)

The stability region consists of all complex values $z = k^{\alpha } \lambda$ that satisfy the following conditions: all roots $\xi _i$, with $i = 1, 2, \dots , n$, of the polynomial $\sum _{j=0}^{n} w_{j} \xi ^{n-j} = z \xi ^{n}$ must fulfill $|\xi _i| \le 1$, and only the single roots lie on the unit circle $|\xi _i| = 1$. To visualize the stability region, we employ the boundary locus method. In Fig. 4, we plot the values of z obtained by evaluating $z= \frac{\sum _{j=0}^{n} w_{j} \xi ^{n-j}}{\xi ^{n}}$ with $\xi = e^{i \theta }, \theta \in [0, 2 \pi ]$ for different $\alpha = 1.2, 1.4, 1.6, 1.8$. This enables us to visualize and determine the stability regions.

Fig. 4

Stability regions of the scheme (4.3) with $\alpha =1.2, 1.4, 1.6, 1.8$

Table 2 (Example 5.1) Numerical convergence orders of scheme (3.3)

5 Numerical Results

In this section, we shall consider some numerical examples to determine the convergence orders of the proposed numerical scheme (3.3) and (3.27) regarding the smooth and nonsmooth initial data.

Example 5.1

Consider the following fractional differential equation with $1<\alpha <2$,

$$\begin{aligned} \left\{ \begin{array}{ll} {^C _0}D^{\alpha }_t y(t) + y(t) = 0, &{} 0 \le t \le T,\\ y(0) = 0.5, \qquad y'(0) = 0, \end{array} \right. \end{aligned}$$

(5.1)

We aim to use the time discretization scheme (3.3) to solve (5.1). Let $T=1$, and $0< t_1< t_2< \cdots < t_n = T$ be a uniform mesh on [0, T] with the time step size k. First, we compute the reference solution $y_{ref}$ on a very small time step size, i.e. $k_{ref} = 2^{-10}$. For calculating the numerical solution at y(T) using the method (3.3), we choose $n = 2^3, 2^3, \ldots , 2^7$. The maximum error estimates and convergence orders are illustrated in Table 2. It has been demonstrated that the corrected numerical method exhibits the expected second-order convergence.

Example 5.2

Consider the following time-fractional wave equation with $1<\alpha <2$,

$$\begin{aligned} \left\{ \begin{array}{lll} {^C _0}D^{\alpha }_t u(x,t) {-} \dfrac{\partial ^2 u}{\partial x^2}(x,t)= f(x,t), &{} 0<x<1, &{} 0 \le t \le T,\\ u(0,t) = u(1,t) = 0 &{} &{} 0 \le t \le T,\\ u(x,0) = u_0(x), &{} 0\le x\le 1, &{}\\ u'(x,0) = u_1(x), &{} 0\le x\le 1, &{} \end{array} \right. \end{aligned}$$

(5.2)

where

• (a) $u_0(x) = x (1-x) \in H^2(\Omega ) \cap H_0^1(\Omega ), u_1(x) = 0$ and $f = 0$,

• (b) $u_0(x) = \chi _{[0,1/2]}(x), u_1(x) = 0$ and $f =0$,

• (c) $u_0(x) = 0, u_1(x) = \chi _{[0,1/2]}(x)$ and $f = t^{\beta } (\cos (t) + \sin (t))(1 + \chi _{[0,1/2]}(x))$, with $\beta = 0, 1.1$.

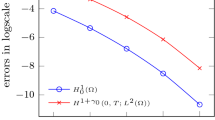
Let $0 = x_0<x_1< \cdots < x_m = 1$ be a uniform partition with space step size h. We compute the reference solutions (in each case) $u_{ref}$ at $T=1$ on a finer mesh with $h_{ref} = 2^{-7}$ and $k_{ref} = 2^{-10}$. For the cases (a) and (b), we consider the corrected numerical method (3.3) and finite difference method for the time and space discretizations, respectively. Then, we choose $n = 2^4, 2^5, \ldots , 2^8$ to obtain the numerical solutions at time T. In Table 3, the maximum error estimates and convergence temporal orders are presented which show the expected second-order convergence in time. In addition, numerical solution of case (a) with $\alpha = 1.5$ and $n = 2^4$ is shown in Fig. 5.

For the case (c), we consider the corrected numerical method (3.27) for the time discretization and finite difference method for the spatial variable. In this case, the problem has nonsmooth data in both initial condition and source term f. We choose $h = 2^{-6}$ and $n = 2^4, 2^5, \ldots , 2^8$ to obtain the numerical solutions which are listed in Tables 4 and 5 when $f \in C^2([0, T ], L^2(\Omega ))$ and $f \in C^1([0, T ], L^2(\Omega ))$, respectively. The illustrated convergence orders confirm the theoretical results.

Table 3 (Example 5.2 -cases (a) and (b)) Numerical temporal convergence orders of scheme (3.3) with $h = 2^{-7}$

Fig. 5

(Example 5.2) Numerical solutions using the scheme (3.3) with $\alpha = 1.5$ and $n = 2^{2}$ for case a (left) and case b (right)

Table 4 (Example 5.2 - case (c) - $\beta = 0$) Numerical temporal convergence orders of scheme (3.27) with $h = 2^{-6}$

Table 5 (Example 5.2 - case (c) - $\beta = 1.1$) Numerical temporal convergence orders of scheme (3.27) with $h = 2^{-6}$

6 Conclusion

In this paper, we have introduced a high-order formula for approximating the Caputo fractional derivative with an order $\alpha \in (1,2)$, which arises in the context of the time fractional wave equation. We have rigorously demonstrated the second-order convergence of the proposed method for both smooth and nonsmooth initial data. Furthermore, numerical examples have been provided to validate the reliability and effectiveness of our approach.