Time-fractional nonlinear evolution of dynamic wave propagation using the Burgers’ equation

Abstract

Fractional derivatives are crucial in diverse contexts, offering a means to extend classical derivatives to noninteger orders. This expansion of calculus enables a more detailed understanding of complex behaviors in scientific, engineering, and mathematical disciplines. In this study, we use theoretical and numerical analyses to thoroughly examine the time-fractional Burgers’ equation. Our main emphasis is on deriving time-decay estimates for solutions within a bounded domain. To determine optimal time-decay rates, we introduce a linear compact difference scheme by integrating an $L_1$ discretization formula for the Caputo derivative and compact difference operators with spatial derivatives. We provide a detailed analysis encompassing existence and uniqueness, and an error estimate of solutions under the $\Vert \cdot \Vert _{\infty }$ norm for the proposed scheme. Comprehensive numerical experiments highlight the efficiency and robustness of our approach, ensuring reliability for long-time simulations. Furthermore, numerical results are scrutinized to pinpoint the optimal time-decay rate. This work explores the asymptotic behavior of solutions to the time-fractional Burgers’ equation and the development of linear high-order accuracy difference methods for nonlinear time-fractional equations.

1 Introduction

The exploration of nonlinear evolution equations, particularly in shallow water equations and wave propagation in fluid dynamics, has attracted significant interest due to their ability to explain a diverse array of nonlinear wave phenomena with broad applications across various fields [1,2,3,4,5,6,7,8,9]. Shallow water equations are pivotal in understanding and predicting wave propagation behavior in coastal regions, estuaries, and lakes [10,11,12,13,14]. The wave equation and its solutions through partial differential equations (PDEs) are integral to numerous real-world applications. In coastal engineering, they inform the design of coastal protection structures and coastal erosion management [15,16,17]. Investigating wave propagation through shallow water equations contributes to advancing effective wave energy converters and tidal turbines [18,19,20], allowing researchers and engineers to develop innovative technologies for green energy generation. Furthermore, wind turbine design and placement can be optimized to maximize energy extraction while minimizing environmental impact by modeling the dynamics of wind waves using wave equations [20]. In ocean energy, studying wave propagation facilitates the design of efficient wave energy converters that capture and convert wave energy into electricity. This makes shallow water equations increasingly appealing to researchers and engineers seeking innovative solutions for environmental sustainability and green energy generation.

The Burgers’ equation, proposed by Bateman [21], is a simplified model integrating various fundamental aspects of fluid dynamics [22, 23] and is recognized for being a nonlinear partial differential equation (PDE). Despite its apparent simplicity, the Burgers’ equation combines linear diffusion with nonlinear convection terms, and the significance of both is crucial in elucidating behaviors exhibited by fluids. The equation is applied in diverse fields, including fluid mechanics [24], traffic flows [25], and gas dynamics [26]. Given its broad range of potential applications, The Burgers’ equation has been examined from various perspectives. A contemporary approach to studying a generalized version of the Burgers’ equation involves replacing the classical derivative with a fractional derivative. This fractional equation was employed to characterize the physical unidirectional propagation of weakly nonlinear acoustic waves within a gas-filled pipe and was a result of the cumulative effect of wall friction through a boundary layer [27, 28]. This paper investigates the behavior of solutions to the one-dimensional time-fractional Burgers’ equation

$$\begin{aligned} \frac{\partial ^\alpha }{\partial t^\alpha }u(x,t) + u(x,t)u_x(x,t) = u_{xx}(x,t) + f(x,t), ~ (x,t) \in \Omega \times (0,T], \end{aligned}$$

(1)

where $0< \alpha < 1$ and $\Omega = (0,L),$ with the boundary conditions

$$\begin{aligned} u(0,t) = u(L,t) = 0,\qquad 0 <t \le T, \end{aligned}$$

(2)

and the initial condition

$$\begin{aligned} u(x,0) = u_0(x),\qquad x\in \Omega , \end{aligned}$$

(3)

where f(x, t) and $u_0(x)$ are given smooth functions. Here, the Caputo fractional derivative of order $\alpha$ is defined by

$$\begin{aligned} \frac{\partial ^\alpha }{\partial t^\alpha }u(x,t) = \frac{1}{\Gamma (1-\alpha )} \int _{0}^{t} \frac{1}{(t-s)^{\alpha }}\frac{\partial u(x,s)}{\partial s}ds, \end{aligned}$$

(4)

where $\Gamma$ is the gamma function.

Numerous investigations into time-fractional PDEs have led to the application of diverse numerical techniques [29,30,31,32,33,34,35]. Researchers have employed a range of semi-analytical methods, including the Adomian decomposition method [36], homotopy analysis [37], generalized differential transform method and homotopy perturbation method [38]. Additionally, Yokus and Kaya [39] applied an expansion method and the Cole-Hopf transformation to obtain numerical solutions. In [40], two semi-implicit Fourier pseudo-spectral schemes were proposed based on fast Fourier transform and the $L_1$ discretization formula. Esen and Tasbozan [41] employed a collocation method with cubic B-spline basis functions. In [42], Yaseen and Abbas introduced a numerical technique utilizing a cubic trigonometric B-spline to address this problem. Oruc et al. [43] developed a unified method using a Chebyshev wavelet and the $L_1$ discretization formula. In [44], Wang et al. recommended the use of a weak Galerkin finite element method to solve this equation. Later, Hussein [45] proposed a continuous and discrete time-weak Galerkin finite element method to solve the two-dimensional time-fractional coupled Burgers’ equation. Recently, Zhang and Feng [46] used a local projection stabilization virtual element method on polygonal meshes in which the $L_1$ discretization formula was used to approximate a fractional term.

The finite difference method (FDM) plays a pivotal role in addressing intricacies posed by the time-fractional Burgers’ equation, emerging as a noteworthy numerical technique due to its effective solution strategies and its inherent advantages of simplicity, versatility, and computational efficiency. Li et al. [47] proposed a linear implicit finite difference scheme for solving the equation. The scheme was proven to be unconditionally stable globally and convergent with first-order in time and second-order in space. Qiu et al. [48] provided an implicit scheme which proved a stability and convergence analysis using an energy method to solve the time-fractional Burgers’ equation with second-order in space and $(2-\alpha )$-order in time. Recently, Qiao and Tang [49] proposed a nonlinear scheme with the $L_1$ discretization based on non-uniform meshes. The scheme provides the order of accuracy as $O\left( \tau ^{\min \{{2-\alpha , r\alpha }\}} + h^2\right)$. In the contemporary era, numerical schemes have been developed by incorporating valuable techniques from compact finite difference operators, aiming to enhance high-order accuracy in approximating derivatives. High-order compact difference schemes distinguish themselves with superior precision and have the advantage of considering a minimized set of neighboring grid points. They effectively reduce numerical dispersion and dissipation, resulting in a more accurate representation of solutions and allowing for larger time steps in time-dependent simulations. Li [50] utilized compact difference operators to devise a fourth-order compact difference scheme for the three-dimensional Rosenau-RLW equation. Wang et al. [51] introduced a novel fourth-order three-point compact operator for a nonlinear convection term. This operator was applied to a classical viscous Burgers’ equation, as detailed in [52, 53]. Several compact finite difference schemes have garnered attention in recent developments [54,55,56,57,58,59,60,61]. In the context of fractional derivative equations, Cui [62] introduced an implicit scheme using compact operators to address multi-term time-fractional mixed diffusion and diffusion wave equations. Zhang et al. [63] developed a nonlinear scheme for the time-fractional Burgers’ equation that enhanced a high order of accuracy in space by utilizing a compact difference operator. This approach achieved fourth-order accuracy in space while demonstrating both stability and convergence.

As previously discussed, the aforementioned research projects primarily focused on the advancement of numerical investigations of the time-fractional Burgers’ equation. While numerous numerical schemes have been proposed for solving the model, the long-term behavior of this equation has not been theoretically or numerically revealed. In fact, there have been scientific reports on the long-term behavior of time-fractional evolutionary and related equations. In [64], Dipierro et al. derived time-decay estimates for the $L_s$-norm of solutions to evolutionary equations with fractional time-diffusion. Furthermore, Smadiyeva and Torebek [65] have established time-decay rates for time-fractional evolutionary equations with time-dependent coefficients. Optimal decay rate estimates for solutions were also obtained in a linear case. Recently, D’Abbicco and Girardi [66] investigated decay estimates for a perturbed two-term space-time fractional diffusive problem. As a result, the existence of global-in-time solutions to corresponding nonlinear problems can be directly established under small initial data in $H^{s,m}$. A well-established observation of the Burgers’ equation is that the solution tends to zero as time t approaches infinity when zero boundary values are applied. Additionally, we know that the optimal decay rate based on theoretical results from large-time behavior of a solution to the classical Burgers’ equation [67, 68], is

$$\begin{aligned} \Vert u(\cdot ,t) \Vert _{L_2} \le C(1+t)^{-\frac{1}{4}}, \quad \quad \Vert u(\cdot ,t) \Vert _{L_\infty } \le C(1+t)^{-\frac{1}{2}} \end{aligned}$$

(5)

for all $t\ge 0$. In light of the findings presented in [67, 68] and the decay rate for evolutionary equations [64], we anticipate that the time-decay rates of solutions to the time-fractional Burgers’ equation will converge to zero at a rate comparable to that of the classical Burgers’ equation solution. This paper presents two primary contributions within the scope of our investigation.

• 1. The primary contribution of this paper is the implementation of a robust numerical scheme for solving the fractional Burgers’ equation based on compact difference operators and the $L_1$ discretization formula. It is worth noting that a considerable emphasis is placed on achieving order accuracy, involving the utilization of nonlinear schemes to achieve an accuracy of $(2-\alpha )$-order in the temporal domain [48, 62, 63]. To the best of the author’s knowledge, the use of linear compact schemes, maintaining a temporal convergence order of $2-\alpha$, remains notably infrequent in current research.

• 2. The second contribution of this paper is the determination of the time-decay rate for the fractional Burgers’ equation by implementing the approach proposed in [64]. Consequently, the proposed numerical scheme becomes imperative when examining an acquired theoretical decay rate and establishing the optimal decay rate.

Subsequent sections of this paper have been organized as follows. In the next section, we discuss preliminary lemmas and notations, presenting time decay rates of solutions for the time-fractional Burgers’ equation. Section 3 introduces a detailed compact finite difference scheme for the time-fractional Burgers’ equation. This section includes essential preliminary results as well as notations used in this paper and details the formulation of $L_1$ discretization. In Section 4, we demonstrate the existence and uniqueness of the proposed scheme and provide a stability and convergence analysis. Section 5 presents numerical results to validate the theoretical analysis and explore the long-time behavior of the time-fractional Burgers’ equation. Finally, the paper concludes with a discussion.

2 Decay estimate

In this section, we study the long-time behavior of the solutions of the time-fractional Burgers’ equation. We first start with introducing given notations; $L_p(\overline{\Omega })$ presents the Lebesgue integral space with the norm $\Vert \cdot \Vert _{L_p(\overline{\Omega })}$. Especially, $L_2(\overline{\Omega })$ is the sqare integral space with the norm $\Vert \cdot \Vert _{L_2(\overline{\Omega })}$. $H^k(\overline{\Omega })$ denotes the usual Sobolev spaces with the norms $\Vert \cdot \Vert _{H^k}(\overline{\Omega })$ and the seminorm $|\cdot |_{H^k(\overline{\Omega })}$. Moreover, we let $H^k_{0}(\overline{\Omega })=\left\{ u\in H^k(\overline{\Omega })\;| \; \frac{\partial ^i u}{\partial x^i }=0,\; \text {on} \;\partial \Omega ,\; i=0,1,\dots ,k-1 \right\}$. Let T and B be positive constants and a Banach space, respectively. $L_s(0,T;B)$ denotes the space of B-valued $L_s$-functions on [0, T].

Regrading to the results reported in [64], we are going to provide a preliminary decay estimate theorem based on the obtained results. Initiate the process, we assume that the initial condition $u_0$ does not vanish identically and lies in $L_q(\overline{\Omega })$, $q\in [1,\infty )$. We also suppose $u_0$ as a nonnegative and integrable function, this also logically assume u to be nonnegative and smooth. Additionally, we assume the structural condition ${\textbf {S1}}$, which will be required in the decay estimate

S1::

Let u be a solution of the homogeneous time-fractional Burgers’ equation (1)-(3). There exits a positive constant $C_0$, $s\in (1,+\infty ),$ and $\gamma \in (0,+\infty )$ such that

$$\begin{aligned} \Vert u(t)\Vert ^{s-1+\gamma }_{L_s(\overline{\Omega })}\le -C_0 \int _{\overline{\Omega }}u^{s-1}(x,t)u_{xx}(x,t)dx. \end{aligned}$$

(6)

Here, we recall the following lemma:

Lemma 1

[64, 69] Let $s>1$, $u:\overline{\Omega }\times [0,+\infty )\rightarrow \mathbb {R}$ and $u_0(x):=u(x,0)$. Let $v(t):=\Vert u(t)\Vert _{L_s (\bar{\Omega })}$ and suppose that $u_0\in L_s(\overline{\Omega })$, and for every $T>0$, that $u\in L_s((0,T),L_s(\overline{\Omega }))$. Then,

$$\begin{aligned} v^{s-1}(t) \frac{\partial ^\alpha }{\partial t^{\alpha } } v(t)\le \int _{\overline{\Omega }} u^{s-1}(x,t) \frac{\partial ^\alpha }{\partial t^{\alpha } } u(x,t)dx. \end{aligned}$$

Now, we already to proof the decay estimate results as follows

Theorem 2

Let $s>1$ and $u:\overline{\Omega }\times [0,+\infty )\rightarrow \mathbb {R}$ be a solution of the homogeneous time-fractional Burgers’ equation (1)-(3). Assume that $u_0\in L_s(\overline{\Omega })$, and for every $T>0$, that $u\in L_s((0,T),L_s(\overline{\Omega }))$. If the structural condition ${\textbf {S1}}$ holds, then

$$\begin{aligned} \frac{\partial ^\alpha }{\partial t^{\alpha } } \Vert u (t)\Vert _{L_s(\overline{\Omega })} \le -\frac{\Vert u (t)\Vert _{L_s(\overline{\Omega })}^{\gamma }}{C_0}. \end{aligned}$$

(7)

Moreover, there exists a positive constant $C_*$ such that

$$\begin{aligned} \Vert u (t)\Vert _{L_s(\overline{\Omega })} \le {C_*}{(1+t)^{-\alpha /\gamma }}. \end{aligned}$$

(8)

Proof

Let $v(t):=\Vert u(t)\Vert _{L_s(\bar{\Omega })}$. In relation to the argument presented in [64], by integrating the condition ${\textbf {S1}}$ and Lemma 1, we see that

$$\begin{aligned} v^{s-1}(t) \frac{\partial ^\alpha }{\partial t^{\alpha } } v(t)&\le \int _{\overline{\Omega }} u^{s-1}(x,t) \frac{\partial ^\alpha }{\partial t^{\alpha } } u(x,t) dx\\&= -\int _{\overline{\Omega }} u^{s-1}(x,t) \left( u_{xx}(x,t)-u(x,t)u_x(x,t)\right) dx\\&\le -\frac{1}{C_0} \Vert u(t)\Vert ^{s-1+\gamma }_{L_s(\overline{\Omega })} +\int _{\overline{\Omega }} u^{s}(x,t) u_x(x,t)dx. \end{aligned}$$

By applying the boundary conditions (2), we see that

$$\begin{aligned} {\int _{\overline{\Omega }}u^{s}(x,t) u_x(x,t)dx=\frac{1}{s+1}u^{s+1}(x,t)|_{\partial \Omega }=0,} \end{aligned}$$

which yields

$$\begin{aligned} v^{s-1}(t)\frac{\partial ^\alpha }{\partial t^{\alpha } } v(t) \le -\frac{1}{C_0} \Vert u(t)\Vert ^{s-1+\gamma }_{L_s(\overline{\Omega })}=-\frac{1}{C_0}v^{s-1+\gamma }(t). \end{aligned}$$

With the same argument used in [64, 70], we can conclude that

$$\begin{aligned} v^{s-1}(t)\frac{\partial ^\alpha }{\partial t^{\alpha } } v(t)=-\alpha \int _0^t \frac{v(\kappa )}{(t-\kappa )^{1+\alpha }} d\kappa -\frac{v(0)}{t^{\alpha }}\le 0, \end{aligned}$$

which gives Eq. (7). To prove Eq. (8), we consider the nonlinear fractional differential equation

$$\begin{aligned} \frac{\partial ^\alpha }{\partial t^{\alpha } } w(t)=-\frac{w^{\gamma }(t)}{C},\quad \quad w(0)=v(0). \end{aligned}$$

Based on the arguments in [64, 69, 71], we see that there exists a positive constant $\bar{C}_{0}$ such that

$$\begin{aligned} \Vert u (t)\Vert _{L_s(\overline{\Omega })} \le \frac{\bar{C}_{0}}{1+t^{\alpha /\gamma }}. \end{aligned}$$

By mean value theorem, we arrive at

$$\begin{aligned} \Vert u (t)\Vert _{L_s(\overline{\Omega })} \le {C_*}{(1+t)^{-\alpha /\gamma }}, \end{aligned}$$

where $C_*=\bar{C}_{0}\max \{1,\frac{\alpha }{\gamma }T^{{\alpha }/{\gamma }-1}\}$. This completes the proof. $\square$

We note that the condition ${\textbf {S1}}$ holds when $s=2$, $C_0=1$ and $\gamma =1$. In fact, we see that

$$\begin{aligned} -\int _{\overline{\Omega }}u(x,t)u_{xx}(x,t)dx= |u(t)|^2_{H^1(\overline{\Omega })}, \end{aligned}$$

(9)

where the boundary conditions (2) are used. Then, the condition ${\textbf {S1}}$ can be directly obtained by the Poincare inequality. As a result, we obtain the following corollary.

Corollary 3

Let u be a solution of the homogeneous one-dimensional time-fractional Burgers’ equation (1)-(3). Then, there exists a positive constant $C_*$ such that

$$\begin{aligned} \Vert u (t)\Vert _{L_2(\overline{\Omega })} \le {C_*}{(1+t)^{-\alpha }}. \end{aligned}$$

Remark 1

As $\alpha \rightarrow 1^-$, it is anticipated that the solution to the problem described by equations (1)-(3) converges toward the classical Burgers’ equation. In light of this observation, the time-decay rate derived from the aforementioned corollary may not be optimal, as suggested by findings in [67, 68]. To address this, we undertake a numerical investigation to determine the optimal time-decay rate. This investigation is facilitated by the implementation of a robust and efficient linear compact scheme, which will be presented in the next section.

3 Derivation of proposed scheme and theoretical results

In this section, we first describe the domain grid and its corresponding grid by letting that the solution is defined on the domain $[0,L]\times [0,T]$. Let N and J be positive integers and denote uniform partitions $\Omega _h=\{x_j~|~0\le j \le J\}$ and $\Omega _{\tau }=\{t_n~|~0\le n\le N\}$, where $x_j=jh$ with $h=L/J$, $t_n=n\tau$ with $\tau =T/N$. Therefore, the computational domain is defined as $\Omega _{h\tau } = \Omega _{h}\times \Omega _{\tau }$. For simplicity, we define the notations for any mesh function $u=\{u^n_j|0\le j\le J,~0\le n\le N\}$ on $\Omega _{h\tau }$ as shown below:

$$\begin{aligned}&\delta _x\left( u_{j}^{n} \right) =\frac{u_{j+1}^{n}-u_{j}^{n}}{h},{} & {} {{\delta _{\bar{x}}\left( u_{j}^{n} \right) }}=\frac{u_{j}^{n}-u_{j-1}^{n}}{h},{} & {} \delta _{\hat{x}}\left( u_{j}^{n} \right) =\frac{u_{j+1}^{n}-u_{j-1}^{n}}{2h},\\&\left( \bar{u}_{j}^n \right) =\frac{u_{j}^{n+1}+u_{j}^{n-1}}{2},{} & {} \delta _{\hat{t}}\left( u_{j}^n \right) =\frac{u_{{j}}^{n+1}-u_{j}^{n-1}}{2\tau },{} & {} {{{\delta ^{(2)}_{x\bar{x}}\left( u_{j}^{n} \right) }}}\\&{=\frac{u_{j+1}^{n}-2u^n_j+u_{j-1}^{n}}{h^2}}. \end{aligned}$$

The discrete $L_2$ inner product and the corresponding discrete $L_2$-norm can be defined by

$$\begin{aligned} \langle u,v\rangle =h \sum _{j=1}^{J-1}u_jv_j,\;\;\;\;\Vert u\Vert =\langle u,u\rangle ^{\frac{1}{2}}, \end{aligned}$$

respectively, and the discrete $L_\infty$-norm is defined by

$$\begin{aligned} \Vert u \Vert _\infty =\max _{1\le j \le J}|u_j |. \end{aligned}$$

The discrete solution space $V_h$ is defined by

$$\begin{aligned} V_{h}=\left\{ u=(u_j) | u=\left( u_0,u_1,\ldots ,u_J \right) , u_0=u_J=0\right\} . \end{aligned}$$

Before going though the implementation of the proposed scheme, we recall the following operators defined in [72] which will be useful to approximate the spatial derivative terms. Here, we let

$$\begin{aligned} \mathcal {A}_{x} (u_{j}^{n})&= \left( 1+\frac{h^2}{6}\delta ^{(2)}_{x\bar{x}}\right) u_j^n,\\ \mathcal {B}_{x} (u_{j}^{n})&= \left( 1+\frac{h^2}{12}\delta ^{(2)}_{x\bar{x}}\right) u_j^n, \end{aligned}$$

and the corresponding matrices representations

$$\begin{aligned} {\textbf{H}_{1}}= & {} \frac{1}{6}{{\left[ \begin{matrix} 4 &{} 1 &{} 0 &{} \ldots &{} 0 \\ 1 &{} 4 &{} 1 &{} \ldots &{} 0 \\ {} &{} \ddots &{} \ddots &{} \ddots &{} {} \\ 0 &{} \ldots &{}1 &{} 4 &{} 1 \\ 0 &{} \ldots &{} 0 &{} 1 &{} 4 \\ \end{matrix} \right] }_{(J-1)\times (J-1)}},\\ {\textbf{H}_{2}}= & {} \frac{1}{12}{{\left[ \begin{matrix} 10 &{} 1 &{} 0 &{} \ldots &{} 0 \\ 1 &{} 10 &{} 1 &{} \ldots &{} 0 \\ {} &{} \ddots &{} \ddots &{} \ddots &{} {} \\ 0 &{} \ldots &{} 1 &{} 10 &{} 1 \\ 0 &{} \ldots &{} 0 &{} 1 &{} 10 \\ \end{matrix} \right] }_{(J-1)\times (J-1)}}. \end{aligned}$$

To be specific, we denote $\mathcal {A}_{x}$ and $\mathcal {B}_{x}$ as a typical compact difference operator for the first-order and second-order derivatives, respectively. According to Taylor’s expansion, based on the compact difference operators [72, 73], we see that

$$\begin{aligned} u_{x}\arrowvert _{(x_j,t_n)}&=\mathcal {A}^{-1}_{x} \delta _{\hat{x}}(u_j^n)+\mathcal {O}(h^{4}), \\ u_{xx}\arrowvert _{(x_j,t_n)}&=\mathcal {B}^{-1}_{x} \delta _{x\bar{x}}^{(2)}(u_j^n)+\mathcal {O}(h^{4}). \end{aligned}$$

The following $L_1$ discretization [74] is recalled to approximate the Caputo fractional derivative defined by Eq.(4) as

$$\begin{aligned} \Delta ^{\alpha }_{t}g(t_n) = \frac{\tau ^{-\alpha }}{\Gamma (2-\alpha )}\left( g(t_n) - \sum _{k=1}^{n-1}\left( a_{n-k-1} - a_{n-k}\right) g(t_k) - a_{n-1}g(t_0) \right) , \end{aligned}$$

where $0< \alpha < 1$ and $a_k=(1+k)^{1-\alpha }-k^{1-\alpha }$.

Lemma 4

([74]) Let $0<\alpha <1$ and $(a_k)=(1+k)^{1-\alpha }-k^{1-\alpha }$. Then $(a_k)$ is a decreasing sequence, that is $a_0>a_1>\cdots >a_k\rightarrow 0$. Moreover, $a_{k}\ge \frac{1-\alpha }{(k+1)^2}$.

Lemma 5

([74]) Suppose $g(t) \in C^2[0,t_n]$. Let

$$\begin{aligned} R(g(t_n)) = \frac{1}{\Gamma (1-\alpha )}\int _{0}^{t_n} \frac{g'(s)}{(t_{n}-s)^{\alpha }}ds - \Delta ^\alpha _t g(t_n), \end{aligned}$$

then

$$\begin{aligned} |R(g(t_n))|\le \frac{1}{\Gamma (2-\alpha )}\left( \frac{1-\alpha }{12} + \frac{2^{2-\alpha }}{2-\alpha } - (1+2^{-\alpha })\right) \max _{0\le t \le t_n}|g''(t)|\tau ^{2-\alpha }, \end{aligned}$$

where $0< \alpha < 1$.

As is well-established, the time-fractional Burgers’ equation exhibits nonlinearity owing to the presence of the nonlinear convection term $uu_x$. Building upon insights from [47], the combination of the $L_1$ discretization formula with a direct approximation of the nonlinear term $uu_x$ at the point $(x_j,t_n)$ may induce nonlinearity in the scheme. An alternative approach to address this nonlinearity involves leveraging the previous profile of the numerical solution, as suggested in the literature as

$$\begin{aligned} uu_x|_{(x_j,t_n)}=u(x_j,t_{n-1})u_x(x_j,t_{n})+u(x_j,t_{n })u_x(x_j,t_{n-1}). \end{aligned}$$

Nevertheless, the linearity inherent in the scheme suggested in [47] aligns with a first-order accuracy in time. Specifically, the $L_1$ discretization formula yields an accuracy of $2-\alpha$ in time. Therefore, to archive our goal, we introduce the linearized formula to approximate the nonlinear convection term $uu_x$ at the point $(x_j,t_n)$ by

$$\begin{aligned} uu_x\arrowvert _{(x_j,t_n)} =\frac{1}{2}(u^2)_x\arrowvert _{(x_j,t_n)} = \frac{1}{2}\mathcal {A}_x^{-1}\delta _{\hat{x}}(\tilde{u}^n_j) + O(\tau ^2 + h^4), \end{aligned}$$

where $\tilde{u}^n_j=2u^{n-1}_j-u^{n-2}_j$, which provide a more accurate representation of the nonlinear term and enhancing the overall accuracy of the numerical scheme. Consequently, we introduce a compact linear scheme for solving the time-fractional Burgers’ equation (1)-(3) as

$$\begin{aligned} \Delta ^{\alpha }_{t}(u_j^n) + \frac{1}{2} \mathcal {A}_{x}^{-1}\delta _{\hat{x}} [(\tilde{u}^n_j )^2] - \mathcal {B}_{x}^{-1}\delta ^{(2)}_{x\bar{x}}(u_j^n) = f_j^n, ~~1\le j\le J-1,~~2\le n\le N,\nonumber \\ \end{aligned}$$

(10)

with boundary conditions

$$\begin{aligned} u_0^n=u_J^n=0,~~1\le n \le N, \end{aligned}$$

(11)

and the initial condition

$$\begin{aligned} u_{j}^{0}={{u}_{0}}\left( {{x}_{j}} \right) ,~~0\le j \le J. \end{aligned}$$

(12)

We note that Eq.(10) can be rewritten as

$$\begin{aligned} u_{j}^n - \frac{\mu }{h^2}\mathcal {B}_{x}^{-1}\left( u_{j+1}^n-2u_{j}^n+u_{j-1}^n\right) = - \frac{\mu }{4h} \mathcal {A}_{x}^{-1}[(\tilde{u}^n_{j+1} )^2-(\tilde{u}^n_{j-1} )^2 ]+ d_{j}^n,\nonumber \\ \end{aligned}$$

(13)

where $\mu = \tau ^{\alpha }\Gamma (2-\alpha )$ and

$$\begin{aligned} d^n_j = \sum _{k=1}^{n-1}\left( a_{n-k-1} - a_{n-k}\right) u^k_j - a_{n-1}u^0_j + \mu f^n_j. \end{aligned}$$

The vector form of the scheme (13) is

$$\begin{aligned} \left( \textbf{I} - \frac{\mu }{h^2}\mathbf {H_2^{-1}} \mathbf {A_2} \right) u^n = -\frac{\mu }{4h}\mathbf {H_1^{-1}} \mathbf {A_1}\text {diag}( {\tilde{u}^n} ) {\tilde{u}^n} + \mathbf {d_n}, \end{aligned}$$

(14)

where $\textbf{I}$ is the identity matrix, the matrices $\mathbf {A_1}$, and $\mathbf {A_2}$ are defined by

$$\begin{aligned} {\textbf{A}_{1}} ={{\left[ \begin{matrix} 0 &{} 1 &{} 0 &{} \ldots &{} 0 \\ -1 &{} 0 &{} 1 &{} \ldots &{} 0 \\ {} &{} \ddots &{} \ddots &{} \ddots &{} {} \\ 0 &{} \ldots &{} -1 &{} 0 &{} 1 \\ 0 &{} \ldots &{} 0 &{} -1 &{} 0 \\ \end{matrix} \right] }_{(J-1)\times (J-1)}},\\ {\textbf{A}_{2}} ={{\left[ \begin{matrix} -2 &{} 1 &{} 0 &{} \ldots &{} 0 \\ 1 &{} -2 &{} 1 &{} \ldots &{} 0 \\ {} &{} \ddots &{} \ddots &{} \ddots &{} {} \\ 0 &{} \ldots &{} 1 &{} -2 &{} 1 \\ 0 &{} \ldots &{} 0 &{} 1 &{} -2 \\ \end{matrix} \right] }_{(J-1)\times (J-1)}}. \end{aligned}$$

The vector $\mathbf {d_n}$ can be formulated as

$$\begin{aligned} \mathbf {d_n} = \sum _{k=1}^{n-1}\left( a_{n-k-1}-a_{n-k} \right) { u^k} + a_{n-1} {u^0} + \mu \mathbf {f_n}, \end{aligned}$$

where the vectors ${u^k}$, $\text {diag}( {\tilde{u}^n} ) {\tilde{u}^n}$, and $\mathbf {f_{n }}$ are expressed by

$$\begin{aligned} { {u^{k }} }={{\left[ \begin{matrix} u^k_1 \\ u^k_2 \\ \vdots \\ u^k_{J-2} \\ u^k_{J-1} \\ \end{matrix} \right] }},\qquad \text {diag}( {\tilde{u}^n} ) {\tilde{u}^n } ={{\left[ \begin{matrix} (\tilde{u}^n_1)^2 \\ (\tilde{u}^n_2)^2 \\ \vdots \\ (\tilde{u}^n_{J-2})^2 \\ (\tilde{u}^n_{J-1})^2 \\ \end{matrix} \right] }},\qquad \text {and}\qquad {\mathbf {f_{n }} }={{\left[ \begin{matrix} f^n_1 \\ f^n_2 \\ \vdots \\ f^n_{J-2} \\ f^n_{J-1} \\ \end{matrix} \right] }}, \end{aligned}$$

respectively.

Consequently, we can write the present scheme into a linear system as follow:

$$\begin{aligned} \textbf{W} {u^n} = \mathbf {b_n}, \end{aligned}$$

(15)

where

$$\begin{aligned} \textbf{W} = \textbf{I } - \frac{\mu }{h^2}\mathbf {H_2^{-1}} \mathbf {A_2}, \end{aligned}$$

and

$$\begin{aligned} \mathbf {b_n} = -\frac{\mu }{4h}\mathbf {H_1^{-1}} \mathbf {A_1} \text {diag}( {\tilde{u}^n} ) {\tilde{u}^n} + \mathbf {d_n}. \end{aligned}$$

It is noteworthy that the algorithm seems to achieve efficiency by solving the constant system $\textbf{W}$ as defined in Eq. (15) at each time step, leading to a significant reduction in computational time. Since the presented scheme is required the previous profile of ${u^0}, {u ^1},\dots , {u^n}$ to compute ${u^{n+1}}$; therefore, we need ${u^1}$ as known conditions. As a result, ${u^1}$ can be computed by using an available difference scheme such as [63].

Next, we delve into the existence and uniqueness of the solution and the convergence and stability of our numerical scheme. We first recall some lemmas, which will be used in this part.

Lemma 6

([75]) For any discrete functions $w,v\in V_{h}$, we have

• 1. $\langle \delta _{\hat{x}} w,v\rangle =-\langle w,\delta _{\hat{x}}v\rangle$.

• 2. $\langle \delta ^{(2)}_{x\bar{x}}w,v\rangle =\langle w,\delta ^{(2)}_{x\bar{x}}v\rangle =-\langle \delta _{ {x}}w,\delta _{ {x}}v\rangle$.

Moreover, we have

$$\begin{aligned} \langle \delta _{\hat{x}}w,w\rangle =0, \;\;\;\;\langle \delta ^{(2)}_{x\bar{x}}w,w\rangle =-\Vert \delta _{x} w \Vert ^2. \end{aligned}$$

Here, we let the matrices $\mathbf {R_1}$ and $\mathbf {R_2}$ be the Cholesky decomposition matrices of $\mathbf {H_1}$ and $\mathbf {H_2},$ respectively, which are defined by

$$\begin{aligned} \mathbf {H_1^{-1}}&= \mathbf {R_1^T} \mathbf {R_1} ,\\ \mathbf {H_2^{-1}}&= \mathbf {R_2^T}\mathbf {R_2} . \end{aligned}$$

The following lemma will be useful to derive the boundedness of the numerical solution.

Lemma 7

([50, 76]) For any discrete function $w \in V_h,$ we have

• 1. $\Vert w \Vert ^2 \le \langle \mathbf {H_1^{-1}} w,w \rangle = \Vert \mathbf {R_1}w \Vert ^2 \le 3\Vert w\Vert ^2$,

• 2. $\Vert w \Vert ^2 \le \langle \mathbf {H_2^{-1}} w,w \rangle = \Vert \mathbf {R_2}w \Vert ^2 \le \dfrac{3}{2}\Vert w\Vert ^2$.

Lemma 8

([57]) For any discrete functions $w,v \in V_h,$ we have

• 1. $\langle \mathbf {H_1 } w,v \rangle = \langle w,\mathbf {H_1 } v \rangle$ and $\langle \mathbf {H_2 } w,v \rangle = \langle w,\mathbf {H_2} v \rangle$.

• 2. $\langle \mathbf {H_1^{-1} } w,v \rangle = \langle w,\mathbf {H_1^{-1} } v \rangle$ and $\langle \mathbf {H_2^{-1} } w,v \rangle = \langle w,\mathbf {H_2^{-1}} v \rangle$.

Lemma 9

([75]) For any discrete function $w\in V_h$, we have

$$\begin{aligned} \Vert w \Vert \le \frac{L}{\sqrt{6}}\Vert \delta _xw \Vert \quad \quad \text {and}\quad \quad \Vert w \Vert _{\infty } \le \frac{\sqrt{L}}{2}\Vert \delta _x w \Vert . \end{aligned}$$

Lemma 10

(Discrete fractional Gronwall inequality [77]) Let $(\lambda _k)_{k=0}^{N-1}$ be a nonnegative sequence and $\lambda$ be a constant such that $\lambda \ge \sum _{k=0}^{N-1}\lambda _k$. Suppose that the discrete function $w^n$ satisfies

$$\begin{aligned} \Delta ^{\alpha }_{t} (w^n)^2\le \sum _{k=1}^{n}\lambda _{k-1}(w^k)^2 +w^n(\xi ^n+\eta ^n),\quad n\ge 1, \end{aligned}$$

(16)

where $\xi ^n$ and $\eta ^n$ are nonnegative sequences. If $\tau \le \root \alpha \of {\frac{1}{2\Gamma (2-\alpha )\lambda }}$, it holds that

$$\begin{aligned} w^n\le 2\left( w^0+ \max _{1\le k\le n}\sum _{l=1}^k P^{(k)}_{k-l}\xi ^l+ \omega _{1+\alpha }(t_n)\max _{1\ge k\le n} \eta ^k \right) E_{\alpha }(2\lambda t_n^{\alpha }), \quad 1\le n\le N, \end{aligned}$$

where $E_{\alpha }(x)=\sum _{k=0}^{\infty }\frac{x^k}{\Gamma (1+k\alpha )}$ is the Mittag-Leffler function and the discrete convolution kernel $P^{(s)}_{s-k}$ is defined by

$$\begin{aligned} P_{s-k}^{(s)}=\frac{1}{a_{0}^{(k)}}\left\{ \begin{matrix} 1, &{} k=s, \\ \sum \limits _{j=k+1}^{s}{(a_{j-k-1}^{(j)}-a_{j-k}^{(j)})P_{s-j}^{(s)},} &{} 1\le k\le s-1. \\ \end{matrix} \right. \end{aligned}$$

Furthermore, the boundedness condition (16) can be replaced by

$$\begin{aligned} \Delta ^{\alpha }_{t} w^n \le \sum _{k=1}^{n}\lambda _{k-1} w^k + \xi ^n+\eta ^n,\quad n\ge 1. \end{aligned}$$

Lemma 11

Let $u^k \in V_h$, for $k=0,1,2,\dots ,n$, we have

$$\begin{aligned} \left| \langle \Delta _t^{\alpha }u^n,\delta _{x\bar{x}}^{(2)} u^n \rangle \right| \ge \frac{1}{2} \Delta _t^{\alpha }\Vert \delta _xu^n\Vert ^2. \end{aligned}$$

Proof

By using the Cauchy-Schwarz inequality and Lemma 4, we see that

$$\begin{aligned}&\left| \langle \Delta _t^{\alpha }u^n, \delta _{x\bar{x}}^{(2)} u^n \rangle \right| \\&\quad =\frac{1}{\mu }\left| \langle u^n, \delta _{x\bar{x}}^{(2)} u^n \rangle - \sum _{k=1}^{n-1}\left( a_{n-k-1} - a_{n-k}\right) \langle u^k, \delta _{x\bar{x}}^{(2)} u^n \rangle - a_{n-1}\langle u^0, \delta _{x\bar{x}}^{(2)} u^n \rangle \right| \\&\quad \ge \frac{1}{\mu }\left[ \Vert \delta _xu^n\Vert ^2-\sum _{k=1}^{n-1}\left( a_{n-k-1} - a_{n-k}\right) |\langle \delta _x u^k, \delta _xu^n \rangle | - {a_{n-1}} |\langle \delta _xu^0, \delta _xu^n \rangle |\right] \\&\quad \ge \frac{1}{\mu }\left[ \Vert \delta _xu^n\Vert ^2-\sum _{k=1}^{n-1}\left( a_{n-k-1} - a_{n-k}\right) \Vert \delta _xu^k\Vert \Vert \delta _xu^n\Vert - {a_{n-1}} \Vert \delta _xu^0\Vert \Vert \delta _xu^n\Vert \right] \\&\quad \ge \frac{1}{2\mu }\left[ \Vert \delta _xu^n\Vert ^2-\sum _{k=1}^{n-1}\left( a_{n-k-1} - a_{n-k}\right) \Vert \delta _xu^k\Vert ^2- {a_{n-1}} \Vert \delta _xu^0\Vert ^2 \right] \\&\quad = \frac{1}{2} \Delta _t^{\alpha }\Vert \delta _xu^n\Vert ^2, \end{aligned}$$

which yields the desired result. $\square$

3.1 Existence and uniqueness

Theorem 12

(Uniquely Solvability) The compact difference scheme (10)-(12) is uniquely solvable.

Proof

Using mathematical induction, we can uniquely define $u^0$ with an initial condition and proceed to employ an available method for the computation of $u^1$. Therefore, we suppose that ${u}^0, {u}^1,\dots , {u}^{n}$ are solved uniquely. We let ${ {u}^{n+1}}$ and ${ {v}^{n+1}}$ be the solution of the sheme (10)-(12) and ${p}^{n+1} = { {u}^{n+1}} - { {v}^{n+1}}$. Therefore, ${p}^{n+1}$ can be obtained by solving the following equation

$$\begin{aligned} \left( \textbf{I } - \frac{\mu }{h^2}\mathbf {H_2^{-1}} \mathbf {A_2} \right) p^{n+1}= {\textbf {0}}. \end{aligned}$$

(17)

Taking inner product of Eq. (17) with $p^{n+1}$, we directly obtain

$$\begin{aligned} \Vert p^{n+1} \Vert ^2 + \mu \Vert \textbf{R}_2\delta _{x}p^{n+1}\Vert ^2= 0. \end{aligned}$$

This yields $\Vert p^{n+1} \Vert = 0$. Therefore, the compact difference scheme (10)-(12) is uniquely solvable. $\square$

3.2 A priori estimates

The essence of our analysis is to provide a priori estimates for the numerical solution. Here, we are going to show that the numerical solution of the proposed scheme is bounded, which will be useful in order to prove the convergence and stability of the present scheme.

Theorem 13

(Boundedness) Suppose $u_0 \in H^1_{0}(\overline{\Omega })$. Then, there exists a positive constant $\tau _1$ and $C_1$ such that, when $\tau \le \tau _1$, the numerical solution derived by the scheme (10)-(12) satisfies

$$\begin{aligned} \Vert \delta _{x}u^n \Vert \le C_1 \;\; \text {and}\quad \quad \Vert u^n \Vert _\infty \le C_1 \end{aligned}$$

for $n=0,1,2,\dots ,N.$

Proof

It follows from the $u_0 \in H^1_{0}(\overline{\Omega })$ that $\Vert u^0\Vert _{\infty }$ and $\Vert \delta _{x}u^0\Vert$ are bounded. For the first level, $u^1$ can be computed by a fourth-order method. Hence, the following estimates are gotten about $\Vert \delta _{x}u^1 \Vert \le C_1$ and $\Vert u^1 \Vert _\infty \le C_1$, for some positive constant $C_1$.

To prove the boundedness, by mathematical induction, we assume that there is a positive constant $C_1$ such that

$$\begin{aligned} \max _{0\le k\le n-1}\left\{ \max \{ \Vert \delta _{x}u^k\Vert , \Vert u^k\Vert _\infty \}\right\} \le C_1. \end{aligned}$$

(18)

Taking the inner product of Eq.(10) with $\delta ^{(2)}_{x\bar{x}}u^n$, we have

$$\begin{aligned} \frac{1}{2} \Delta _t^{\alpha }\Vert \delta _xu^n\Vert ^2 + \Vert \textbf{R}_2\delta ^{(2)}_{xx}u^n \Vert ^2 \le \frac{1}{2} \langle \mathcal {A}_{x}^{-1}\delta _{\hat{x}} (\tilde{u}^n )^2, \delta ^{(2)}_{x\bar{x}} u^n \rangle - \langle f^n,\delta ^{(2)}_{x\bar{x}}u^n \rangle , \end{aligned}$$

(19)

where Lemma 11 is used. Consider the inner product of the nonlinear term, using the Young’s inequality, Lemma 7, and Lemma 8, we see that

$$\begin{aligned} \frac{1}{2} \langle \mathcal {A}_{x}^{-1}\delta _{\hat{x}} (\tilde{u}^n )^2,\delta ^{(2)}_{x\bar{x}}u^n \rangle&=\frac{1}{2} \langle \delta _{\hat{x}}(\tilde{u}^n )^2,\mathcal {A}_{x}^{-1}\delta ^{(2)}_{x\bar{x}}u^n \rangle \\&=\frac{h}{2}\sum _{j=1}^{J-1} [\tilde{u}^n_{j+1}\delta _{\hat{x}}(\tilde{u}^n_j)+\tilde{u}^n_{j-1}\delta _{\hat{x}}(\tilde{u}^n_{j+1})] \mathcal {A}_{x}^{-1} \delta ^{(2)}_{x\bar{x}}u^n_j\\&\le \Vert \tilde{u}^n\Vert _{\infty }\Vert \delta _{\hat{x}}\tilde{u}^n\Vert \Vert \mathbf {H_{1}^{-1}} \delta ^{(2)}_{x\bar{x}} u^n\Vert \\&\le C_1\left( \frac{9C_1}{4}\Vert \delta _{\hat{x}}\tilde{u}^n\Vert ^2+\frac{1}{9C_1}\Vert \mathbf {H_{1}^{-1}} \delta ^{(2)}_{x\bar{x}} u^n\Vert ^2\right) \\&\le \frac{9C_1^2}{4}\Vert \delta _{\hat{x}}\tilde{u}^n\Vert ^2+\frac{1}{2} \Vert \delta ^{(2)}_{x\bar{x}} u^n\Vert ^2. \end{aligned}$$

Furthermore, we have

$$\begin{aligned} \langle f^n,\delta ^{(2)}_{x\bar{x}}u^n \rangle \le \frac{1}{2}\Vert f^n\Vert ^2+\frac{1}{2}\Vert \delta ^{(2)}_{x\bar{x}}u^n \Vert ^2. \end{aligned}$$

Here, we note that

$$\begin{aligned} \Vert \delta _{\hat{x}}\tilde{u}^n \Vert \le \Vert \delta _{x}\tilde{u}^n \Vert \le 2\Vert \delta _x u ^{n-1} \Vert + \Vert \delta _x u ^{n-2} \Vert , \end{aligned}$$

therefore, Eq. (19) can be rewritten as

$$\begin{aligned} \Delta _t^{\alpha }\Vert \delta _xu^n\Vert ^2 \le {54C_1^2} \Vert \delta _{x} {u}^{n-1}\Vert ^2+ {27C_1^2} \Vert \delta _{x} {u}^{n-2}\Vert ^2+ \Vert f^n\Vert ^2. \end{aligned}$$

Through the use of Lemma 10, if $\tau$ is sufficiently small such that $\tau \le \root \alpha \of {\frac{1}{162\Gamma (2-\alpha )C_1^2}}$, it holds that

$$\begin{aligned} \Vert \delta _xu^n\Vert ^2 \le 2\left( \Vert \delta _xu^0\Vert ^2+ \frac{t_n^{\alpha }}{\Gamma (1-\alpha )} \max _{1\le k\le n} \Vert f^n\Vert ^2 \right) E_{\alpha }(162C_1^2 t_n^{\alpha }). \end{aligned}$$

Finally, we complete the proof by applying Lemma 9. Hence, we can conclude that there is a positive constant $C_1$ such that $\Vert \delta _xu^n\Vert \le C_1$ and $\Vert u^n\Vert _{\infty } \le C_1$, provided that $\tau$ is sufficiently small.

$\square$

3.3 Error estimate

By the Taylor series expansion and Lemma 5, we provide the following truncation error, which is helpful to prove the convergence analysis of the present scheme.

Lemma 14

Let u(x, t) be the solution of the problem (1)-(3) such that $u(x,t) \in C^{6,2}\left( \overline{\Omega } \right)$ and $U^n_j = u(x_j,t_n)$. The local truncation error of the scheme (10)-(12) is

$$\begin{aligned} \Phi ^n_j=(\sigma _1)^n_j + (\sigma _2)^n_j + (\sigma _3)^n_j, \end{aligned}$$

where

$$\begin{aligned} (\sigma _1)^n_j&= \frac{1}{\Gamma (1-\alpha )}\int _{0}^{t_n} \frac{u'(s)}{(t_{n}-s)^{\alpha }}ds - \Delta ^\alpha _t U_j^n, \\ (\sigma _2)^n_j&= u_{xx}|_{(x_j,t_n)}-\mathcal {B}^{-1}_{x} \delta _{x\bar{x}}^{(2)}(U_j^n), \\ (\sigma _3)^n_j&= uu_{x}|_{(x_j,t_n)} - \frac{1}{2}{\mathcal {A}_{x}^{-1} \delta _{\hat{x}}(\tilde{U }_j^n )^2 } . \end{aligned}$$

Then there exists a constant $C_2$ such that $|\Phi ^n_j |\le C_2(\tau ^{2-\alpha } + h^4).$

Here, we introduce the standard error between the analytical solution and numerical solution as

$$\begin{aligned} e^n_j = u(x_j,t_n) - u^n_j = U^n_j - u^n_j. \end{aligned}$$

Therefore, the error equation can be written as

$$\begin{aligned} \Delta _t^{\alpha }e^n_j +\frac{1}{2} \mathcal {A}_{x}^{-1}\delta _{\hat{x}} [(\tilde{U}^n_j )^2]- \frac{1}{2} \mathcal {A}_{x}^{-1}\delta _{\hat{x}} [(\tilde{u}^n_j )^2] - \mathcal {B}_{x}^{-1}\delta ^{(2)}_{x\bar{x}}(e_j^n) = \Phi ^n_j. \end{aligned}$$

(20)

For simplicity, we denote that

$$\begin{aligned} \tau _2&=\root \alpha \of {\frac{2}{3\Gamma (2-\alpha )L(L+108)C_4^2}},\\ C_3&= \max _{(x,t)\in \overline{\Omega }\times (0,T]} \{|u(x,t)|, |u_x(x,t)| \}, \\ C_4&=3 (C_1 +C_3 ). \end{aligned}$$

Then we can obtain the following error estimate.

Theorem 15

Let u(x, t) be the solution of the problem (1)-(3) such that $u(x,t) \in C^{6,2}\left( \overline{\Omega } \right)$ and $u^n$ is the solution of the scheme (10)-(12). Denote

$$\begin{aligned} C_5= C_2\sqrt{ \frac{t_n^{\alpha }L}{2\Gamma (1-\alpha )} E_{\alpha }\left( \frac{3}{16}L(2L+27)C_4^2 t_n^{\alpha }\right) }. \end{aligned}$$

If $\tau$ sufficiently small such that $\tau <\min \{\tau _1,\tau _2\}$, then we have

$$\begin{aligned} \Vert U^n - u^n \Vert _{\infty }\le C_5(\tau ^{2-\alpha } + h^4). \end{aligned}$$

Proof

Taking inner product in Eq. (20) with $\delta ^{(2)}_{x\bar{x}}e^n$, we get

$$\begin{aligned}{} & {} \frac{1}{2}\Delta _t^{\alpha }\Vert \delta _x e^n\Vert ^2 + \Vert \textbf{R}_2\delta ^{(2)}_{x\bar{x}}e^n\Vert ^2 \nonumber \\{} & {} \quad = \frac{1}{2} \langle \mathcal {A}_{x}^{-1}\delta _{\hat{x}}[(\tilde{U}^n )^2 - (\tilde{u}^n )^2], \delta ^{(2)}_{x\bar{x}}e^n \rangle - \langle \Phi ^n,\delta ^{(2)}_{x\bar{x}}e^n\rangle , \end{aligned}$$

(21)

where Lemma 11 is used. Consider the inner product of the nonlinear term, by applying Lemma 8, we can rewrite as

$$\begin{aligned}&\frac{1}{2} \langle \mathcal {A}_{x}^{-1}\delta _{\hat{x}}[(\tilde{U}^n )^2 - (\tilde{u}^n )^2 ] , \delta ^{(2)}_{x\bar{x}}e^n\rangle \\&\quad =\frac{ h}{2}\sum _{j=1}^{J-1}\mathcal {A}_{x}^{-1}\delta _{\hat{x}}[ (\tilde{U}_j^n )^2 - (\tilde{u}_j^n )^2 ] \delta ^{(2)}_{x\bar{x}}(e_j^n)\\&\quad = \frac{ h}{2}\sum _{j=1}^{J-1} \delta _{\hat{x}}[\left( {e}_j^n \right) (\tilde{U}_j^n + \tilde{u}_j^n )] \mathcal {A}_{x}^{-1}\delta ^{(2)}_{x\bar{x}}(e_j^n)\\&\quad = \frac{ h}{2}\sum _{j=1}^{J-1} (\tilde{e}^n_{j+1})\delta _{\hat{x}} ( \tilde{U}_{j}^n + \tilde{u}_{j }^n )\mathcal {A}_{x}^{-1}\delta ^{(2)}_{x\bar{x}}(e_j^n) \\&\quad + \frac{ h}{2}\sum _{j=1}^{J-1} \delta _{\hat{x}}(\tilde{e}^n_{j+1}) ( \tilde{U}_{j-1}^n + \tilde{u}_{j-1}^n ) \mathcal {A}_{x}^{-1}\delta ^{(2)}_{x\bar{x}}(e_j^n). \end{aligned}$$

By utilizing Lemma 7, Lemma 9, and the Young’s inequality, we see that

$$\begin{aligned}&\frac{ h}{2}\sum _{j=1}^{J-1}(\tilde{e}^n_{j+1})\delta _{\hat{x}} ( \tilde{U}_{j}^n - \tilde{u}_{j}^n )\mathcal {A}_{x}^{-1} \delta ^{(2)}_{x\bar{x}}(e_j^n) \\&\quad \le \frac{1}{2} \Vert \tilde{e}^n\Vert _{\infty }\Vert \delta _{\hat{x}}(\tilde{U}^n + \tilde{u}^n)\Vert \Vert \textbf{H}_1^{-1}\delta ^{(2)}_{x\bar{x}}e^n\Vert \\&\quad \le C_4\left( \frac{9}{4}C_4\Vert \tilde{e}^n\Vert _{\infty }^2+\frac{1}{36C_4}\Vert \textbf{H}_1^{-1}\delta ^{(2)}_{x\bar{x}}e^n\Vert ^2\right) \\&\quad \le \frac{9C_4^2L }{16} \Vert \delta _x\tilde{e}^n\Vert ^2+\frac{1}{4 }\Vert \delta ^{(2)}_{x\bar{x}}e^n\Vert ^2, \end{aligned}$$

where the estimate $\Vert \delta _{\hat{x}}(\tilde{U}^n + \tilde{u}^n)\Vert \le \Vert \delta _{\hat{x}} \tilde{U}^n \Vert +\Vert \delta _{\hat{x}} \tilde{u}^n \Vert \le C_4$ is used.

In addition, we have

$$\begin{aligned}&\frac{ h}{2}\sum _{j=1}^{J-1} \delta _{\hat{x}}(\tilde{e}^n_{j+1}) ( \tilde{U}_{j-1}^n + \tilde{u}_{j-1}^n ) \mathcal {A}_{x}^{-1}\delta ^{(2)}_{x\bar{x}}(e_j^n)\\&\quad \le \frac{C_4}{6}\left( \frac{3C_4}{2}\Vert \tilde{e}^n\Vert ^2 +\frac{1}{6C_4}\Vert \textbf{H}_1^{-1}\delta ^{(2)}_{x\bar{x}}e^n\Vert ^2\right) \\&\quad \le \frac{ C_4^2L^2}{24}\Vert \delta _x\tilde{e}^n\Vert ^2+\frac{1}{4}\Vert \delta ^{(2)}_{x\bar{x}}e^n\Vert ^2. \end{aligned}$$

As a result, we obtain

$$\begin{aligned}&\frac{1}{2} \langle \mathcal {A}_{x}^{-1}\delta _{\hat{x}}[(\tilde{U}^n )^2 - (\tilde{u}^n )^2 ] , \delta ^{(2)}_{x\bar{x}}e^n\rangle \\&\quad \le \frac{ C_4^2L(2L+27)}{48}\Vert \delta _x\tilde{e}^n\Vert ^2+\frac{1}{2}\Vert \delta ^{(2)}_{x\bar{x}}e^n\Vert ^2\\&\quad \le \frac{ C_4^2L(2L+27)}{16}\left( 2\Vert \delta _x{e}^{n-1}\Vert ^2+\Vert \delta _x{e}^{n-1}\Vert ^2\right) +\frac{1}{2}\Vert \delta ^{(2)}_{x\bar{x}}e^n\Vert ^2. \end{aligned}$$

In addition, we note that

$$\begin{aligned} |\langle \Phi ^n ,\delta ^{(2)}_{x\bar{x}}e^n \rangle |&\le \Vert \Phi ^n\Vert \Vert \delta ^{(2)}_{x\bar{x}}e^n \Vert \le \frac{1}{2 }\Vert \Phi ^n\Vert ^2 + \frac{1}{2 }\Vert \delta ^{(2)}_{x\bar{x}}e^n\Vert ^2. \end{aligned}$$

Since $\Vert \delta ^{(2)}_{x\bar{x}}e^n \Vert \le \Vert \textbf{R}_2\delta ^{(2)}_{x\bar{x}}e^n \Vert$ and using Lemma 14, Eq. (21) gives

$$\begin{aligned} \Delta _t^{\alpha }\Vert \delta _x e^n\Vert ^2 \le \frac{ C_4^2L(2L+27)}{16}\left( 2\Vert \delta _x{e}^{n-1}\Vert ^2+\Vert \delta _x{e}^{n-2}\Vert ^2\right) + C_2^2\left( \tau ^{2-\alpha }+h^4\right) ^2.\nonumber \\ \end{aligned}$$

(22)

Hence, by applying Lemma 10, we obtain

$$\begin{aligned} \Vert \delta _xe^n\Vert ^2 \le 2 \frac{t_n^{\alpha }}{\Gamma (1-\alpha )} E_{\alpha }\left( \frac{3}{2}L(2L+27)C_4^2 t_n^{\alpha }\right) C_2^2\left( \tau ^{2-\alpha }+h^4\right) ^2, \end{aligned}$$

provided that $\tau$ is sufficiently small such that $\tau \le \root \alpha \of {\frac{8}{3\Gamma (2-\alpha )L(2\,L+27)C_4^2}}$. By utilizing Lemma 9, we have the error estimate in the $\Vert \cdot \Vert _{\infty }-$sense as

$$\begin{aligned} \Vert \delta _xe^n\Vert _{\infty }\le & {} \frac{\sqrt{L}C_2}{2}\sqrt{ 2 \frac{t_n^{\alpha }}{\Gamma (1-\alpha )} E_{\alpha }\left( \frac{3}{16}L(2L+27)C_4^2 t_n^{\alpha }\right) }\left( \tau ^{2-\alpha }+h^4\right) \\= & {} C_5\left( \tau ^{2-\alpha }+h^4\right) . \end{aligned}$$

The proof is finished. $\square$

Theorem 16

Under the conditions of Theorem 15, the solution $u^n$ of the finite difference scheme (10)-(12) is stable in the sense of $\Vert \cdot \Vert _{\infty }$.

4 Numerical experiments

In this section, the numerical results obtained from the finite difference method are computed to verify the effectiveness and correctness of our theoretical analysis in the previous section. Therefore, the efficiency of the present method is tested using the maximum error norm, which is defined by

$$\begin{aligned} \Vert \text {Error}^n \Vert _{\infty }&= \max _{j}|u(x_j,t_n)-u^n_j |, \end{aligned}$$

and the rate of convergence can be measured as following to the formula

$$\begin{aligned} \text {Rate}^x=\log _2\left( \frac{\text {Error}_h}{\text {Error}_{h/2}}\right) , \qquad \text {Rate}^t=\log _2\left( \frac{\text {Error}_\tau }{\text {Error}_{\tau /2}}\right) , \end{aligned}$$

where $\text {Error}_h$ and $\text {Error}_{h/2}$ are the norm errors with the grid sizes h and h/2, respectively. As the same in time which is grid sizes $\tau$ and $\tau /2$ are corresponding with $\text {Error}_\tau$ and $\text {Error}_{\tau /2}$, respectively. To demonstrate the effectiveness of our compact finite difference scheme, we present the following numerical example in order to ensure the robustness and accuracy of the proposed scheme and provide the reliability of the long-time behavior of the solution.

4.1 The non-homogeneous time-fractional Burgers’ equation [63]

$$\begin{aligned} \frac{\partial ^\alpha }{\partial t^\alpha }u(x,t) + u(x,t)u_x(x,t) = u_{xx}(x,t) + f(x,t), \end{aligned}$$

with the initial condition

$$\begin{aligned} u(x,0) =0, \end{aligned}$$

and the non-homogeneous as a term

$$\begin{aligned} f(x,t) = \frac{2t^{2-\alpha }\sin (\pi x)}{\Gamma (3-\alpha )} + 4\pi ^2t^2\sin (2\pi x) + 2\pi t^4\sin (2\pi x)\cos (2\pi x). \end{aligned}$$

It can be verified that the analytical solution the problem is

$$\begin{aligned} u(x,t) = t^2\sin (2\pi x). \end{aligned}$$

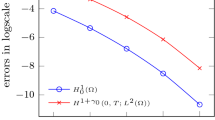
To validate the numerical solutions, the schemes included numerical testing across the computational domain $\Omega =(0, 1)$ for a final time $T=1$. In this illustration, we present our numerical results of a comparative analysis between the current scheme and the previously proposed nonlinear compact difference scheme in [63]. In this simulation, the Newton iterative method was used to compute a numerical solution to the nonlinear scheme. To demonstrate precision in both temporal and spatial aspects, we selected sufficiently small spatial and temporal step sizes, ensuring that the dominant error was influenced by only one factor. Specifically, for spatial accuracy, we set N to be adequately large based on $\alpha$. We chose $N=20000, 40000,$ and 60000 for $\alpha = 0.25, 0.50,$ and $\alpha = 0.75$, respectively. The spatial discretization involved four distinct J, namely, $J = 8, 16,$ and 32. Table 1 summarizes the performance of our linear scheme and the nonlinear scheme from [63], detailing error estimates and convergence rates. Both schemes consistently achieved fourth-order spatial convergence, with our linear scheme exhibiting slightly superior numerical accuracy. For temporal accuracy, we set $J=128$ and $N = 128, 256,$ and 512,  corresponding to $\alpha$ values of 0.25, 0.50, and 0.75 from Table 1. As shown in Table 2, after comparing the numerical results, we found that the nonlinear scheme [63] slightly outperformed our scheme. However, the error norms obtained by both schemes significantly decreased, aligning with the estimated $(2-\alpha )$-order convergence rates in time.

In Fig. 1, the numerical solution and its distribution, along with corresponding contour plots, have been presented for the case of $\alpha = 0.5$, $N = 40000$, and $J = 16$. The amplitude variations of the numerical solution, ranging from approximately $-1$ to 1, occurred across the domain and were consistent with those found in the exact solution. Additionally, Fig. 1b highlights the maximum error in the distribution, concentrated around points with extreme amplitudes. In Fig. 2, error plots are presented to illustrate how spatial and temporal step sizes affect error estimates for different values of $\alpha -$specifically, $\alpha = 0.25, 0.50$, and $\alpha = 0.75$. The simulation duration has been set at $T=1$. Our observations indicate that reducing the step size has a positive effect on error estimation, a finding in accordance with our theoretical expectations. Moreover, as $\alpha$ decreases, the error estimates exhibit consistent improvement, attributable to an $2-\alpha$ order of accuracy in time.

Table 1 The estimated errors and the order of convergence in space by using different J, N compared with the nonlinear scheme in [63]

Table 2 The estimated errors and the order of convergence in time by using $J=128$ and different N compared with the nonlinear scheme in [63]

Fig. 1

Numerical solutions and error distributions with their contours when $\alpha = 0.5, N= 40000$

Fig. 2

The $\Vert \cdot \Vert _\infty$-norm errors for different $\alpha$ with fixed time step sizes at the final time $T=1$

4.2 Long-time behavior

In this subsection, we study the long-time behavior of the homogeneous time-fractional Burgers’ equation

$$\begin{aligned} \frac{\partial ^\alpha }{\partial t^\alpha }u(x,t) - u_{xx}(x,t)+ u(x,t)u_x(x,t) = 0, \end{aligned}$$

(23)

with the initial condition

$$\begin{aligned} u(x,0) = u_0(x). \end{aligned}$$

(24)

Before conducting our simulations, a Gaussian initial function $u_0(x)=0.5e^{-8x^2}$ was set as the initial condition. At first, the computational domain was defined as $[-20,20]$, and the simulations extended to the final time $T=10$. Concurrently, we opted for $J=16$ and $N=100$. Figure 3 displays snapshots of the numerical solutions at different times, reflecting various values of $\alpha = 0.25, 0.50,$ and 0.75. The results highlight the influence of the parameter $\alpha$ on the amplitude of the numerical solutions. Notably, upon observation, the amplitude of the numerical solution decreased with increasing values of $\alpha$ as time progressed. In Fig. 4, we compare the numerical solutions obtained from time-fractional Burgers’ equations with different values of $\alpha$ (e.g., $\alpha =0.25,$ 0.5 and 0.75) to the numerical results derived from the classical Burgers’ equation. Notably, at the beginning of the simulation, the amplitudes sharply decreased, followed by a gradual decline. Moreover, it is evident that the amplitude of the numerical solution obtained from a classical equation decreases more rapidly and spreads out further compared to solutions with time-fractional derivatives.

Utilizing this insight, we plotted the values of $\Vert \cdot \Vert -$ and $\Vert \cdot \Vert _{\infty }-$norms to validate our observations and confirm Theorem 2 (and Corollary 3) (see Fig. 5). The findings illustrate that both $\Vert \cdot \Vert -$ and $\Vert \cdot \Vert _{\infty }-$norms exhibited a discernible decrease over time, aligning well with our observations and theoretical predictions. Furthermore, the decline in both norms became more noticeable with increasing values of $\alpha$.

Fig. 3

Numerical solutions with different $\alpha$ at selected times $T = 0, 5,$ and 10 while using $J=16$ and $N=100$

Fig. 4

Numerical solutions and their contours of the time fractional Burgers’ equation with different $\alpha$ and the numerical solution of the classical Bergers’ equation at $T=10$ using $J=16$ and $N=100$

Fig. 5

Maximum amplitude and $L_2$-norm of numerical solution with differrent $\alpha$ and compared with the numerical result of classical Burgers’ equation

To determine the optimal time-decay rate, we initiated our simulations by computing the decay rate proposed in [67, 68] for the classical Burgers’ equation and Corollary 3. To substantiate our suspicions, we introduced ratio rate functions, defined as follows:

$$\begin{aligned} F_0(t_n) = \Vert u^n\Vert (1+t_n)^{\frac{1}{4}}, \quad \quad R_0(t_n) = \Vert u^n \Vert _{\infty } (1+t_n)^{\frac{1}{2}}. \end{aligned}$$

The profiles of $F_0(t_n)$ and $R_0(t_n)$ are depicted in Fig. 6. The results reveal that the ratio functions $R_0(t_n)$ and $F_0(t_n)$ exhibit an increasing trend over time, with the exception of the classical case. This observation suggests that the decay rates in the time-fractional equation are sub-optimal, aligning with our earlier findings. It is noteworthy that, for $\alpha =0.75$, the ratio functions $R_0(t_n)$ and $F_0(t_n)$ nearly converge to constants; however, there is a slight increase observed around the time $T=10$.

The profiles of $F_0(t_n)$ and $R_0(t_n)$ are depicted in Fig. 6. The results reveal that the ratio functions $R_0(t_n)$ and $F_0(t_n)$ exhibited an increasing trend over time, with the exception of the classical case. This observation aligns with our earlier findings, suggesting that decay rates of time-fractional equations are sub-optimal,. It is noteworthy that for $\alpha =0.75$, the ratio functions $R_0(t_n)$ and $F_0(t_n)$ nearly converge to constants; however, a slight increase was observed around time $T=10$.

Fig. 6

The profiles (left) $F_0(t_n)$ and (right) $R_0(t_n)$

The next step involved verifying the time-decay rate obtained by Corollary 3. To achieve this, we introduced the following ratio rate function:

$$\begin{aligned} F_{\alpha }(t_n)=\Vert u^n\Vert (1+t_n)^{\alpha }. \end{aligned}$$

As displayed in Fig. 7, the profile of ratio function $F_{\alpha }(t_n)$ does not indicate an optimal time-decay rate. Again, this evidence suggests that the term $(1+t)^{\alpha }$ grows more rapidly than the norm $\Vert u^n\Vert$ shrinks over time. Similarly, as illustrated in Fig. 6, the terms $(1+t)^{1/4}$ and $(1+t)^{1/2}$ are not optimal functions. They cannot attain the desired time-decay rate for the time-fractional Burgers’ equation, as assessed using $\Vert \cdot \Vert -$ and $\Vert \cdot \Vert _{\infty }-$norms, respectively. However, under the condition ${\textbf {S}}_1$, a suggested ratio function in the $\Vert \cdot \Vert _s-$norm sense can be expressed as

$$\begin{aligned} F_{\alpha ,\gamma }(t_n)=\Vert u^n\Vert _s (1+t_n)^{\alpha /\gamma }. \end{aligned}$$

Following this approach, we reprocessed our simulations to determine which value of $\gamma$ achieves the optimal desired time-decay rate. For this purpose, we explored values of $\gamma$ set to 1, 2, 4,  and 8 for varying $\alpha$ values of 0.25, 0.5,  and 0.75. The profiles of $F_{\alpha ,\gamma }$ are depicted in Fig. 8 under the standard norm $\Vert \cdot \Vert$. Interestingly, the optimal decay rate appears to manifest when $\gamma =4$. This finding is consistent with the results presented in [67, 68] when $\alpha \rightarrow 1^-$. Moreover, the time-decay rate proposed by Theorem 2 is applicable to the $L_s-$norm. Consequently, we extended our simulations to investigate the long-term behavior of the solution. The simulations were conducted over the computational domain $[-60,60]$ and were run up to a final time of $T=500$. We maintained consistent spatial and temporal step sizes by setting $N=16$ and $J=100$, respectively. The values of $\alpha$ considered were 0.25, 0.50,  and 0.75. The characteristics of $F_{\alpha ,\gamma }$ with respect to the $\Vert \cdot \Vert _s-$norm ($s=2,4,6$) are presented in Fig. 9, illustrating the expected optimal time-decay rate.

Fig. 7

The profile $F_{\alpha }(t_n)$

Fig. 8

The profiles $F_{\alpha ,\gamma }(t_n)$ using $\Vert \cdot \Vert -$norm with $\alpha =0.25,0.5$, and 0.75

Fig. 9

The profiles $F_{\alpha ,\gamma }(t_n)$ using $\Vert \cdot \Vert _s-$norm for $s=2,4,$ and 6

Finally, we suggest the decay rates for the time-fractional Burgers’ equation in the sense of $\Vert \cdot \Vert _{\infty }$ corresponding to [67, 68] as

$$\begin{aligned} R_{\alpha }(t_n) = \Vert u^n \Vert _{\infty }(1+t_n)^{\frac{\alpha }{2}}. \end{aligned}$$

The ratio tends to stabilize as time progresses, ultimately reaching a steady-state behavior at larger time intervals as shown in Fig. 10.

Fig. 10

The maximum suggestion of decay rate when $T = 500$

5 Concluding remarks

This study undertook a theoretical and numerical examination of solution behavior in the context of the time-fractional Burgers’ equation. In the theoretical aspect, we established a time-decay estimate based on energy inequalities under curtain conditions. In the numerical realm, our introduction of a novel linear compact finite difference scheme designed for solving the time-fractional Burgers’ equation gave us further insights into long-term solution behavior and supported our theoretical findings. The present scheme was carefully designed, using an $L_1$ discretization formula for the Caputo derivative in time and compact difference operators in space. Stability and convergence analyses were performed with respect to a maximum norm through a rigorous analysis of its boundedness. To validate our main results, numerical simulations are presented in two main segments. In the initial segment, we illustrate the numerical solution by comparing it with a recently developed nonlinear scheme. The results highlight the superior numerical accuracy of our present scheme, achieving fourth-order accuracy in space and $(2-\alpha )$-order in time, comparable to a recent nonlinear scheme. Importantly, our scheme slightly outperforms its nonlinear counterpart when the temporal step size is sufficiently small, while the nonlinear scheme demonstrates resolution for rough temporal step sizes. It is worth noting that our primary contribution lies in the design of a linear compact scheme, resulting in computational advantages over a nonlinear alternative.

In addition, we monitored the long-term behavior of the time-fractional Burgers’ equation to validate our proposed theoretical results and determine the optimal time-decay rate. Our extensive simulations provide valuable insights into the decay rates of the time-fractional Burgers’ equation, revealing an interesting relationship with the parameter $\alpha$. This observation emphasizes the need for appropriate representation characterizing time-decay rates in the context of a time-fractional Burgers’ equation, aligning with results presented in [67, 68]. More precisely, the simulations suggest that the numerical solution has $O((1+t)^{-\alpha /4})$ and $O((1+t)^{-\alpha /2})$ decay as $t\rightarrow \infty$, in the sense of $\Vert \cdot \Vert -$ and $\Vert \cdot \Vert _{\infty }-$norms, respectively. The findings highlight the significance of understanding the long-term behavior of time-fractional Burgers’ equations and contribute significantly to the comprehension of time-decay estimates. However, there are several avenues for further exploration and improvement. It is recommended that future work delve deeper into theoretical support to gain a more comprehensive understanding of optimal time-decay rates. By continuing to explore numerical aspects, future studies have the potential to implement nonlinear PDEs with fractional terms. The development of linear compact schemes for high-dimensional time-fractional equations or multi-term fractional equations is another challenging topic.