Analysis of a New NFV Scheme Preserving DMP for Two-Dimensional Sub-diffusion Equation on Distorted Meshes

Abstract

In this paper, we describe a new nonlinear finite-volume scheme that preserves the discrete maximum principle (DMP) for the two-dimensional sub-diffusion equation on distorted meshes. One distinguishing feature of our method is its ability to uphold the DMP for the anisotropic sub-diffusion problems, thereby ensuring the absence of spurious oscillations in numerical solutions and maintaining the physical bounds of various quantities, such as concentration, temperature, and density. Notably, our scheme offers the advantage of being applicable to distorted meshes without stringent constraints. Numerical results demonstrate that our scheme successfully preserves maximum principle on various randomly distorted meshes.

1 Introduction

The sub-diffusion has been observed and validated in various interesting phenomena. It also referred as non-Gaussian. In this paper, we deal with the following sub-diffusion problem with a tensor diffusion coefficient $\kappa = \left( \begin{array}{cc} \kappa _{11}(x, t) &{} \kappa _{12}(x, t) \\ \kappa _{21}(x, t) &{} \kappa _{22}(x, t) \\ \end{array} \right)$:

$$\begin{aligned}{} & {} \partial _t^{\alpha }u-\nabla \cdot (\kappa (x, t)\nabla u)=f(x, t),\quad (x, t)\in \varOmega _T, \end{aligned}$$

(1.1)

$$\begin{aligned}{} & {} u(x, 0)=v(x),\quad x\in \bar{\varOmega }, \end{aligned}$$

(1.2)

$$\begin{aligned}{} & {} u(x, t)=\psi (x, t),\quad (x, t)\in \partial \varOmega \times (0, T], \end{aligned}$$

(1.3)

and

$$\begin{aligned} v(x)=\psi (x, 0), \quad x\in \partial \varOmega , \end{aligned}$$

(1.4)

where $\partial ^{\alpha }_tu =\int _0^t\frac{\partial u(\cdot , {\eta })}{\partial \eta }\frac{d\eta }{\varGamma (1-\alpha )(t-\eta )^{\alpha }}$, $0<\alpha <1$, $\varOmega _T\equiv \varOmega \times (0, T]$, $\varOmega$ is a connected bounded polygonal set of $\textrm{R}^2$ with boundary $\partial \varOmega$, f, v, $\psi$ are given functions. The tensor diffusion coefficient $\kappa$ is the positive definite, that is to say, there exists two constants $\mu _1>0$, $\mu _2>0$ such that the following conditions hold:

$$\begin{aligned} \mu _1\Vert \vartheta \Vert ^2\le \kappa (x, t)\vartheta \cdot \vartheta \le \mu _2\Vert \vartheta \Vert ^2, \quad {\;for \;}\ \ x\in \bar{\varOmega }, \ \ \vartheta \in \textrm{R}^2. \end{aligned}$$

(1.5)

For problem (1.1)–(1.4), a key feature is that the solution has an initial layer at $t=0$ and $\frac{\partial u}{\partial t}$ may blow up when $t \rightarrow 0$. In past decades, numerous authors have addressed this issue and proposed various schemes for linear and nonlinear sub-diffusion problems [1,2,3,4,5,6,7,8,9,10]. But all of the above works have focused on numerical schemes with high-order stability and convergence. There has been almost no consideration given to important properties, such as local conservation property, mass conservation property, monotonicity property, and DMP property.

Maximum principle (also known as extremum principle) is a crucial feature of sub-diffusion equations. Interesting theoretical studies on the maximum principle of equations (1.1)–(1.4) can be found in [11]. The DMP ensures non-negativity and eliminates non-physical oscillations in numerical solutions, making it a highly desirable property for numerical schemes. Jin et al. [12] provided the positivity property of problem (1.1)–(1.4) and proposed three numerical method, where non-negativity cannot be maintained for sufficiently small step, but after a certain threshold is reached, it may reappear. Ye et al. [13] provided a predictor-corrector method with a maximum principle (MP) for specified 1D fractional PDEs on a uniform grid. Jiang [14] established monotone properties of FDMs for 1D sub-diffusion equations on a uniform grid and developed a monotone FVM in [15]. In [16], Brunner presented a MP for sub-diffusion equation but did not include numerical simulations. It’s worth noting that all of the aforementioned methods preserve only the monotonicity, not the discrete maximum principle. Monotonicity refers to preserve non-negativity, which is a special case of the DMP. More recently, Du et al. [17, 18] established maximum principle-preserving (MPP) exponential time differencing schemes for semilinear parabolic equations. Liao et al. [19, 20] provided time-stepping MPP schemes for nonlocal nonlinear partial differential equations. These MPP schemes are designed for time-stepping on conforming spatial meshes and do not directly apply to randomly distorted spatial meshes.

This paper is the first in a series of papers on a nonlinear finite-volume (NFV) scheme that preserves DMP for the sub-diffusion problems with anisotropic diffusion coefficients on general polygonal meshes.

The primary contributions of this paper are as follows:

• We derive MP for a suitably defined solution for the first time and provide a proof that the discrete solution of the proposed scheme satisfies DMP.

• Using nonlinear weighted methods, we construct a conservative flux through a weighted combination of nonconservative fluxes.

• Furthermore, we offer a proof that the proposed scheme has local conservation property and relies solely on cell-centered unknowns.

The primary advantages of this method are as follows:

• It preserves local conservation property.

• It can be applied to general distorted meshes without imposing stringent mesh conditions.

• It preserves MP property even for problems with strongly anisotropic and heterogeneous full tensor coefficients.

The remainder of this article is organized as follows. The maximum principle properties of problem (1.1)–(1.4) is proved in Sect. 2. A new NFV scheme is constructed in Sect. 3. In Sect. 4, we prove DMP property of the proposed method. Five numerical examples are introduced in Sect. 5. A conclusion is presented in Sect. 6.

2 The Maximum Principle for (1.1)–(1.4)

Theorem 1

Suppose u(x, t) is the solution of (1.1)–(1.4) in $\varOmega _T$, $u(\cdot , t)\in C^{(\alpha )}([0, T])\equiv \{u|u\in C([0, T])$, $\partial _t^{\alpha }u \in C([0, T])\}$, $0<\alpha <1$. If $\frac{\partial ^2u}{\partial x_i\partial x_j}$, $\frac{\partial u}{\partial x_i}\in C(\bar{\varOmega }_T)$, $1\le i, j\le 2$, $\kappa$, $\frac{\partial \kappa }{\partial x_i} \in [L^{\infty }(\varOmega _T)]^{2\times 2}$, and $\kappa (x, t)$ is positive definite and satisfies the condition (1.5). Then

(1) If $f(x, t)\le 0$, $(x, t)\in \bar{\varOmega }_T$, then $u(x, t)\le \max \{0, M\}$,

where $M:= \max \left\{ \max \limits _{x\in \bar{\varOmega }}u(x, 0),\ \ \max \limits _{x\in \partial \varOmega , t\in [0, T]}u(x, t)\right\}$.

(2) If $f(x, t)\ge 0$, $(x, t)\in \bar{\varOmega }_T$, then $u(x, t)\ge \min \{0, m\}$,

where $m:= \min \left\{ \min \limits _{x\in \bar{\varOmega }}u(x, 0),\ \ \min \limits _{x\in \partial \varOmega , t\in [0, T]}u(x, t)\right\}$.

2.1 Two Preliminary Lemmas

To prove Theorem 1, we introduce two following results, which are the essential elements of our proof.

Lemma 1

[16, Lemma 3.3] Assume $f(t)\in C^{(\alpha )}([0, T])$ for $0<\alpha <1$. If there is some point $t_0\in (0, T)$ so that $f(t)\le f(t_0)$ for $t\in [0, t_0]$. Then

$$\begin{aligned} (\partial _t^{\alpha }f)(t_0)\ge 0. \end{aligned}$$

(2.6)

Lemma 1 was introduced by Luchko in [21, Theorem 1] under the stronger assumptions. We refer the reader to the work [16, 21] for the proof of the Lemma 1.

Lemma 2

[16, Lemma 3.4] Let a function $f=f(t)\in C^{(\alpha )}([0, T])$, satisfy

• (1) $f(t)\le f(t_0)$ for $0\le t\le t_0\le T$,

• (2) $(\partial _t^{\alpha }f)(t_0)=0$.

Then, for $0\le t\le t_0$, one gets

$$\begin{aligned} f(t)=f(t_0), \ \forall t\in [0, t_0]. \end{aligned}$$

(2.7)

2.2 Proof of Theorem 1

We only prove the maximum principle (1). Since the minimum principle (2) can be obtained if we substitute -u instead of u in the reasoning below.

Note that u(x, t) is continuous in $(x, t)\in \bar{\varOmega }\times [0, T]$. Then $\exists (x_0, t_0)$, $x_0\in \bar{\varOmega }$, $t_0\in [0, T]$ with following property

$$\begin{aligned} u(x_0, t_0) \ge u(x, t), \quad (x, t)\in \bar{\varOmega }_T. \end{aligned}$$

(2.8)

Now assume $0<u(x_0, t_0)$. The reason is that if $0 \ge u(x_0, t_0)$, maximum principle (1) is true.

Further, since $0<u(x_0, t_0)$, if $x_0\in \partial \varOmega$, $t_0\in [0, T]$ or $t_0=0$, the maximum point of u on $\bar{\varOmega }_T$ is $(x_0, t_0)$, i.e. $M=u(x_0, t_0)$. Obviously in this case the maximum principle (1) holds.

If $0<u(x_0, t_0)$, $x_0\in \varOmega$, $t_0\in (0, T]$, note that $u(x, t)\le u(x_0, t_0)$ in (2.8), then by using Lemma 1 we obtain the following relation

$$\begin{aligned} (\partial _t^{\alpha }u)(x_0, t_0)\ge 0, \end{aligned}$$

(2.9)

Also, the continuous function u has a maximum value, and its necessary condition is:

$$\begin{aligned} \frac{\partial u}{\partial x_{1}}(x_0, t_0)=\frac{\partial u}{\partial x_{2}}(x_0, t_0)=0, \end{aligned}$$

(2.10)

and Hessian matrix

$$\begin{aligned} \left[ \begin{array}{cc} \frac{\partial ^2u}{\partial x_1^2}&{} \frac{\partial ^2u}{\partial x_1\partial x_2} \\ \frac{\partial ^2u}{\partial x_2\partial x_1} &{} \frac{\partial ^2u}{\partial x_2^2} \\ \end{array}\right] _{(x_{0}, t_{0})} \end{aligned}$$

(2.11)

is a symmetric negative semidefinite.

Since $(\kappa _{ij})_{2\times 2}$ is positive definite, then we can find an invertible matrix $(Q(x, t))_{2\times 2}$ so that $\kappa (x, t)=Q^T(x, t)Q(x, t).$

Thus, by combining the condition (2.11), we have

$$\begin{aligned} \sum \limits _{i=1}^{2}\sum \limits _{j=1}^{2}\kappa _{ij}(x_{0}, t_{0})\frac{\partial ^2u}{\partial x_{i}\partial x_{j}}(x_{0}, t_{0})\le 0. \end{aligned}$$

(2.12)

Notice that $\nabla \cdot (\kappa \nabla u)=\sum \nolimits _{i=1}^{2} \sum \nolimits _{j=1}^{2}(\kappa _{ij}\frac{\partial ^2u}{\partial x_i\partial x_j}+\frac{\partial \kappa _{ij}}{\partial x_i}\frac{\partial u}{x_j})$, then by combining conditions (2.10) and (2.12) yield

$$\begin{aligned} \nabla \cdot (\kappa (x_{0}, t_{0})\nabla u(x_{0}, t_{0}))\le 0. \end{aligned}$$

(2.13)

Also, since $f(x_0, t_0)\le 0$, using (2.13), then Eq. (1.1) implies

$$\begin{aligned} (\partial _t^{\alpha }u)(x_0, t_0)=(\nabla \cdot (\kappa \nabla u))(x_0, t_0)+ f(x_0, t_0)\le 0. \end{aligned}$$

(2.14)

By combining (2.9) and (2.14), one has

$$\begin{aligned} (\partial _t^{\alpha }u)(x_0, t_0)= 0. \end{aligned}$$

Moreover, for all $0\le t\le t_0$, we have

$$\begin{aligned} u(x_0, t_0)\ge u(x_0, t). \end{aligned}$$

Thus, using the two equations above, the result in Lemma 2 implies that

$$\begin{aligned} u(x_0, t)= u(x_0, t_0), \ \forall t\in [0, t_0]. \end{aligned}$$

(2.15)

Further, using (2.15), we can get

$$\begin{aligned} u(x_0, t_0)= u(x_0, 0). \end{aligned}$$

(2.16)

We complete the proof.

3 The Construction of Discrete Scheme

3.1 Preliminaries

In order to deal with the weak singularity of the solution at initial time $t=0$, we first introduce a graded mesh subdivision of the temporal interval [0, T]. For a positive integer N, $0=t_0< \cdots <t_{N}=T$, assume $\tau _n = t_n -t_{n-1}$ and

$$\begin{aligned} \tau = \max _{1\le k\le N}\tau _k,\; t_n = T(n/N)^{r}, \quad r\ge 1,\quad n=0,\ldots , N. \end{aligned}$$

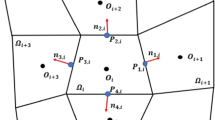
Next we will introduce notation on meshes and stencil (see Fig. 1) for spatial discretization. Assume $\mathscr {M}$ and $\mathscr {E}$ be a set of all cells and cell edges, respectively. The cell and cell-center are presented by K or L, the cell edge by $\sigma$, the boundary of K by $\partial K$, the midpoint of cell-edge by $M_i$, the cross point by $O_i$. $\mathscr {E}_{ext}$ and $\mathscr {E}_{int}$ the set of boundary and interior edges, respectively. Let $\mathscr {P}_{in}$ and $\mathscr {P}_{out}$ be the set of K in $\varOmega$ and $M_i$ on $\partial \varOmega$, respectively. Let $\vec {n}_{K\sigma }$/$\vec {n}_{L\sigma }$ be the unit outer normal on $\sigma$ of K/L, $\vec {t}_{KM_i}$/$\vec {t}_{LM_i}$ be the unit tangential vectors on $KM_i$/$LM_i$, $i=1,\dots$.

Fig. 1

Stencil of meshes and notation of stencil

We also define the angles

$$\begin{aligned}{} & {} \theta _{K_1}=(\overrightarrow{KM_1},\overrightarrow{KO_1}),\ \ \theta _{K_2}=(\overrightarrow{KO_1},\overrightarrow{KM_2}),\ \ \theta _{L_1}=(\overrightarrow{LM_3},\overrightarrow{LO_2}),\ \ \theta _{L_2}=(\overrightarrow{LO_2},\overrightarrow{LM_4}), \\{} & {} \theta _{K}=\theta _{K_1}+\theta _{K_2},\ \ \theta _{L}=\theta _{L_1}+\theta _{L_2}. \end{aligned}$$

From Fig. 1, we have

$$\begin{aligned}{} & {} \sin \theta _{K_{1}}\ge 0,\quad \sin \theta _{K_{2}}\ge 0,\quad \sin \theta _{L_{1}}\ge 0,\quad \sin \theta _{L_{2}}\ge 0,\nonumber \\{} & {} \sin \theta _{K}>0,\quad \sin \theta _{L}>0. \end{aligned}$$

(3.17)

3.2 Discretization

Let

$$\begin{aligned} \tilde{b}^{n,\alpha }_{j+1}=\frac{(t_n-t_{n-j-1})^{1-\alpha }-(t_n-t_{n-j})^{1-\alpha }}{\tau _{n-j}}, \ j=0,\ldots ,n-1, \end{aligned}$$

and

$$\begin{aligned} b^{n,\alpha }_{j} =\left\{ \begin{array}{lll} -\frac{(t_n-t_{0})^{1-\alpha }-(t_n-t_{1})^{1-\alpha }}{\tau _{1}}, &{} {j=0;}\\ \frac{(t_n-t_{j-1})^{1-\alpha }-(t_n-t_{j})^{1-\alpha }}{\tau _{j}} -\frac{(t_n-t_{j})^{1-\alpha }-(t_n-t_{j+1})^{1-\alpha }}{\tau _{j+1}}, &{} 1\le j\le n-1;\\ \frac{(t_n-t_{n-1})^{1-\alpha }}{\tau _{n}}, &{} j=n. \end{array} \right. \end{aligned}$$

(3.18)

Then, by the L1 scheme on graded meshes [5, Eq. (3.1)], one has

$$\begin{aligned} \partial _{t}^{\alpha }u(x,t_{n})= & {} D_{N}^{\alpha }u(x,t_{n})+R^{n}_{T,\alpha } \nonumber \\= & {} \frac{\sum \limits _{j=0}^{n-1}\tilde{b}^{n,\alpha }_{j+1}\triangle _tu(x,t_{n-j-1})}{\varGamma (2-\alpha )}+R^{n}_{T,\alpha } =\frac{\sum \limits _{j=0}^{n}b^{n,\alpha }_{j}u(x,t_{j})}{\varGamma (2-\alpha )}+R^{n}_{T,\alpha }, \end{aligned}$$

(3.19)

where $\triangle _tu(\cdot ,t_{n-j-1})=u(\cdot ,t_{n-j})-u(\cdot ,t_{n-j-1})$.

From [5, Lemma 5.2], one has

$$\begin{aligned} |R_{T,\alpha }^{n}|=|(D_{N}^{\alpha }- \partial _{t}^{\alpha })u(x,t_{n})| \le C n^{-\min \{2-\alpha ,r\alpha \}}. \end{aligned}$$

(3.20)

Noticing that $b^{n,\alpha }_{n}=\tau _n^{-\alpha }$, due to the monotonic increasing function $(t-s)^{-\alpha }$, it is easy to get the inequality

$$\begin{aligned} b^{n,\alpha }_{n}>0,\quad b^{n,\alpha }_{j}<0 \quad \hbox {for} \; j=0,1,\ldots ,n-1. \end{aligned}$$

(3.21)

Next we will construct a new weighted MPP NFV method for sub-diffusion problem (1.1)–(1.4).

To write down a NFV scheme for (1.1)–(1.4), for $1\le n\le N$, we first evaluate (1.1) at $t=t_n$ and integrate it over a cell K:

$$\begin{aligned} \int _{K}\partial _t^{\alpha }u(x,t_n)dx -\int _{K}(\nabla \cdot (\kappa \nabla u))(x,t_n) dx = \int _{K}f(x,t_n)dx. \end{aligned}$$

Applying the divergence equation, one has

$$\begin{aligned} \int _{K}\partial _t^{\alpha }u(x,t_n)dx -\int _{\partial K} ((\kappa \nabla u)(x,t_n))\cdot \vec {n}_{K,\sigma }dl = \int _{K}f(x,t_n)dx. \end{aligned}$$

From Fig. 1, since $((\kappa \nabla u))\cdot \vec {n}_{K,\sigma }=\nabla u\cdot (\kappa ^{T}\vec {n}_{K,\sigma })$, and then using the Gauss theorem to get

$$\begin{aligned} \int _{K}\partial _t^{\alpha }u(x,t_n)dx -\sum _{\sigma \in \mathscr {E}_K} \int _{\sigma }\nabla u(x,t_n)\cdot (\kappa ^{T}(x,t_n)\vec {n}_{K,\sigma })dl = \int _{K}f(x,t_n)dx, \end{aligned}$$

(3.22)

where $\mathscr {E}_K \subset \mathscr {E}$, $K\in \mathscr {M}$, $\kappa ^T$ is the transpose of $\kappa$.

Now let’s discretize equation (3.22) term by term.

By using (3.19) and (3.20), the first term of (3.22) can be designed as

$$\begin{aligned} \int _{K}\partial _t^{\alpha }u(x,t_n)dx =\frac{ m(K)}{\varGamma (2-\alpha )}\sum \limits _{j=0}^{n}b^{n,\alpha }_{j} u(K,t_{j}) +O({n}^{-\min \{2-\alpha ,r\alpha \}}), \end{aligned}$$

(3.23)

where m(K) is the area of K, and $u(K,t_j)m(K)\approx \int _{K}u(x,t_j)dx$.

Next, we will approximate the second term of (3.22).

Denote

$$\begin{aligned}{} & {} \tilde{\kappa }^n_K(x)=\kappa ^{T}(x,t_n)\vec {n}_{K,\sigma },\ 1\le n\le N, \end{aligned}$$

(3.24)

$$\begin{aligned}{} & {} \mathscr {F}_{K,\sigma }^n = -\int _{\sigma }\nabla u(x,t_n)\cdot (\kappa ^{T}(x,t_n)\vec {n}_{K,\sigma })dl= -\int _{\sigma }\nabla u(x,t_n)\cdot \tilde{\kappa }^n_Kdl. \end{aligned}$$

(3.25)

The key point is to construct a discrete approximation of the continuous flux $\mathscr {F}_{K,\sigma }^n$ for each edge $\sigma$ at time $t=t_n$.

From Fig. 1, since $KM_1$ (resp. $LM_{4}$) and $KM_2$ (resp. $LM_{3}$) are two edges of $\triangle KM_1M_2$ (resp. $\triangle LM_3M_4$), using (3.24), one has

$$\begin{aligned}{} & {} \tilde{\kappa }^n_K (x) =|\tilde{\kappa }^n_K(x) | \frac{\sin \theta _{K_{2}}}{\sin \theta _{K}}\vec {t}_{KM_{1}} +!`!`| \tilde{\kappa }^n_K (x)|\frac{\sin \theta _{K_{1}}}{\sin \theta _{K}}\vec {t}_{KM_{2}},\\{} & {} \tilde{\kappa }^n_L(x) =|\tilde{\kappa }^n_L(x)| \frac{\sin \theta _{L_{2}}}{\sin \theta _{L}}\vec {t}_{LM_{3}} +!`!`|\tilde{\kappa }^n_L(x)|\frac{\sin \theta _{L_{1}}}{\sin \theta _{L}}\vec {t}_{LM_{4}}, \end{aligned}$$

where $\tilde{\kappa }^n_L(x)= \kappa ^{T}(x,t_n)\vec {n}_{L,\sigma }$, $1\le n\le N$.

Combining (3.25) and the two equation above, one has

$$\begin{aligned} \mathscr {F}_{K,\sigma }^n= & {} -\int _{\sigma } |\tilde{\kappa }^n_K (x)| \left( \frac{\sin \theta _{K_{2}}}{\sin \theta _{K}}\nabla u^n(x)\cdot \vec {t}_{KM_{1}} +!`!`\frac{\sin \theta _{K_{1}}}{\sin \theta _{K}}\nabla u^n(x)\cdot \vec {t}_{KM_{2}}\right) dl \nonumber \\= & {} -|\tilde{\kappa }^n_K (K)||\sigma | \left( \frac{\sin \theta _{K_{2}}}{\sin \theta _{K}}\frac{u^n_{M_{1}}-u^n_{K}}{|KM_{1}|} +\frac{\sin \theta _{K_{1}}}{\sin \theta _{K}}\frac{u^n_{M_{2}}-u^n_K}{|KM_{2}|}\right) +C^n_{K,\sigma }h^2 \nonumber \\= & {} -\frac{|\kappa ^{T}(K,t_n)\vec {n}_{K,\sigma }|}{\sin \theta _{K}/|\sigma |} \left( \frac{\sin \theta _{K_{2}}}{|KM_{1}|}u^n_{M_{1}} +\frac{\sin \theta _{K_{1}}}{|KM_{2}|}u^n_{M_{2}} -\left( \frac{\sin \theta _{K_{2}}}{|KM_{1}|}+\frac{\sin \theta _{K_{1}}}{|KM_{2}|}\right) u^n_K\right) +C^n_{K,\sigma }h^2, \nonumber \\ \end{aligned}$$

(3.26)

where $h=(\sup _{K\in \mathscr {M}}m(K))^{1/2}$.

Likewise, one has

$$\begin{aligned} \mathscr {F}_{L,\sigma }^n= & {} -\int _{\sigma } |\tilde{\kappa }^n_L(x)| \left( \frac{\sin \theta _{L_{2}}}{\sin \theta _{L}}\nabla u^n(x)\cdot \vec {t}_{LM_{3}} +!`!`\frac{\sin \theta _{L_{1}}}{\sin \theta _{L}}\nabla u^n(x)\cdot \vec {t}_{LM_{4}}\right) dl \nonumber \\= & {} -|\tilde{\kappa }^n_L(L)||\sigma | \left( \frac{\sin \theta _{L_{2}}}{\sin \theta _{L}}\frac{u^n_{M_{3}}-u^n_{L}}{|LM_{3}|} +\frac{\sin \theta _{L_{1}}}{\sin \theta _{L}}\frac{u^n_{M_{4}}-u^n_L}{|LM_{4}|}\right) +C^n_{L,\sigma }h^2 \nonumber \\= & {} -\frac{|\tilde{\kappa }^n_L(L)|}{\sin \theta _{L}/|\sigma |} \left( \frac{\sin \theta _{L_{2}}}{|LM_{3}|}u^n_{M_{3}} +\frac{\sin \theta _{L_{1}}}{|LM_{4}|}u^n_{M_{4}} -\left( \frac{\sin \theta _{L_{2}}}{|LM_{3}|}+\frac{\sin \theta _{L_{1}}}{|LM_{4}|}\right) u^n_L\right) +C^n_{L,\sigma }h^2.\nonumber \\ \end{aligned}$$

(3.27)

We next can define the discrete normal flux:

$$\begin{aligned} \tilde{F}^n_{K,\sigma } =-\frac{|\kappa ^{T}(K,t_n)\vec {n}_{K,\sigma }|}{\sin \theta _{K}/|\sigma |} \left( \frac{\sin \theta _{K_{2}}}{|KM_{1}|}u^n_{M_{1}} +\frac{\sin \theta _{K_{1}}}{|KM_{2}|}u^n_{M_{2}} -\left( \frac{\sin \theta _{K_{2}}}{|KM_{1}|}+\frac{\sin \theta _{K_{1}}}{|KM_{2}|}\right) u^n_K\right) ,\nonumber \\ \end{aligned}$$

(3.28)

and

$$\begin{aligned} \tilde{F}^n_{L,\sigma } = -\frac{|\kappa ^{T}(L,t_n)\vec {n}_{L,\sigma }|}{\sin \theta _{L}/|\sigma |} \left( \frac{\sin \theta _{L_{2}}}{|LM_{3}|}u^n_{M_{3}} +\frac{\sin \theta _{L_{1}}}{|LM_{4}|}u^n_{M_{4}} -\left( \frac{\sin \theta _{L_{2}}}{|LM_{3}|}+\frac{\sin \theta _{L_{1}}}{|LM_{4}|}\right) u^n_L\right) .\nonumber \\ \end{aligned}$$

(3.29)

It is noted that (3.28) and (3.29) include cell-edge unknowns $u^n_{M_{i}}$ at the nodes $M_i$, we now should write down the cell-edge unknowns $u^n_{M_{i}}$ as functions of the cell-centered unknowns $u^n_{K}$ ($u^n_{L}$). For this purpose, by using following linear approximation [22], one has

$$\begin{aligned} u^n_{M_i} =\sum \limits _{j=1}^{J_{M_i,m}}\omega _{M_i,j}u^n_{K_{M_i,j}}+C_{M_i}^nh^2, \end{aligned}$$

(3.30)

where $u^n_{K_{M_i,j}}$, $1\le n\le N$, $i=1,2,\ldots$, is some neighboring cell-centered unknowns surrounding $M_i$, $J_{M_i,m}$ is the corresponding number of unknowns, $i=1,2,\ldots$, and $\omega _{M_i,j}$ is unknown coefficients, $j=1,2\ldots , n_{M_i}$, which satisfy

$$\begin{aligned} \left\{ \begin{array}{ll} \sum ^{J_{M_i,m}}_{j=1}\omega ^n_{M_i,j}=1,&{}\ \\ \omega ^n_{M_i,j}\ge 0.&{} \ \end{array} \right. \end{aligned}$$

(3.31)

For the detailed method determining these unknown weight coefficients $\omega ^n_{M_i,j}$ we refer the reader to the paper [22].

Thus, combining (3.28), (3.29) and (3.30), we have

$$\begin{aligned} \tilde{F}^n_{K,\sigma }= & {} -\frac{|\kappa ^{T}(K,t_n)\vec {n}_{K,\sigma }|}{\sin \theta _{K}/|\sigma |} \left( \frac{\sin \theta _{K_{2}}}{|KM_{1}|} \sum \limits _{j=1}^{J_{M_1,m}}\omega _{M_1,j}u^n_{K_{M_1,j}}+\frac{\sin \theta _{K_{1}}}{|KM_{2}|} \sum \limits _{j=1}^{J_{M_2,m}}\omega _{M_2,j}u^n_{K_{M_2,j}}\right. \nonumber \\{} & {} \left. -\left( \frac{\sin \theta _{K_{2}}}{|KM_{1}|}+\frac{\sin \theta _{K_{1}}}{|KM_{2}|}\right) u^n_K\right) +\widetilde{C}_K^nh^2, 1\le n\le N, \end{aligned}$$

(3.32)

$$\begin{aligned} \tilde{F}^n_{L,\sigma }= & {} -\frac{|\kappa ^{T}(L,t_n)\vec {n}_{L,\sigma }|}{\sin \theta _{L}/|\sigma |} \left( \frac{\sin \theta _{L_{2}}}{|LM_{3}|} \sum \limits _{j=1}^{J_{M_3,m}}\omega _{M_3,j}u^n_{K_{M_3,j}} +\frac{\sin \theta _{L_{1}}}{|LM_{4}|} \sum \limits _{j=1}^{J_{M_4,m}}\omega _{M_4,j}u^n_{K_{M_4,j}}\right. \nonumber \\{} & {} \left. -\left( \frac{\sin \theta _{L_{2}}}{|LM_{3}|}+\frac{\sin \theta _{L_{1}}}{|LM_{4}|}\right) u^n_L\right) +\widetilde{C}_L^nh^2. \end{aligned}$$

(3.33)

Further, we denote the discrete normal flux:

$$\begin{aligned} \tilde{\tilde{F}}^n_{K,\sigma }= & {} -\frac{|\kappa ^{T}(K,t_n)\vec {n}_{K,\sigma }|}{\sin \theta _{K}/|\sigma |} \left( \frac{\sin \theta _{K_{2}}}{|KM_{1}|} \sum \limits _{j=1}^{J_{M_1,m}}\omega _{M_1,j}u^n_{K_{M_1,j}}+\frac{\sin \theta _{K_{1}}}{|KM_{2}|} \sum \limits _{j=1}^{J_{M_2,m}}\omega _{M_2,j}u^n_{K_{M_2,j}}\right. \nonumber \\{} & {} -\left. \left( \frac{\sin \theta _{K_{2}}}{|KM_{1}|}+\frac{\sin \theta _{K_{1}}}{|KM_{2}|}\right) u^n_K\right) , 1\le n\le N, \end{aligned}$$

(3.34)

and

$$\begin{aligned} \tilde{\tilde{F}}^n_{L,\sigma }= & {} -\frac{|\kappa ^{T}(L,t_n)\vec {n}_{L,\sigma }|}{\sin \theta _{L}/|\sigma |} \left( \frac{\sin \theta _{L_{2}}}{|LM_{3}|} \sum \limits _{j=1}^{J_{M_3,m}}\omega _{M_3,j}u^n_{K_{M_3,j}} +\frac{\sin \theta _{L_{1}}}{|LM_{4}|} \sum \limits _{j=1}^{J_{M_4,m}}\omega _{M_4,j}u^n_{K_{M_4,j}}\right. \nonumber \\ {}{} & {} \left. - \left( \frac{\sin \theta _{L_{2}}}{|LM_{3}|}+\frac{\sin \theta _{L_{1}}}{|LM_{4}|}\right) u^n_L\right) ,\ 1\le n\le N. \end{aligned}$$

(3.35)

By using (3.27), (3.29), (3.30),(3.32) and (3.34), we have

$$\begin{aligned} \mathscr {F}_{K,\sigma }^n=\tilde{\tilde{F}}^n_{K,\sigma }+C_K^nh^2,\ 1\le n\le N, \end{aligned}$$

also, using (3.26), (3.28), (3.30),(3.33) and (3.35), we have

$$\begin{aligned} \mathscr {F}_{L,\sigma }^n=\tilde{\tilde{F}}^n_{L,\sigma }+C_L^nh^2,\ 1\le n\le N. \end{aligned}$$

Note that the normal flux component is continuous over the edge $\sigma$, one has

$$\begin{aligned} \tilde{\tilde{F}}^n_{K,\sigma }+ \tilde{\tilde{F}}^n_{L,\sigma }=C_0^nh^2. \end{aligned}$$

(3.36)

To make our proposed method to satisfy MP, we now rewrite (3.34) and (3.35) as our familiar form:

$$\begin{aligned} \tilde{\tilde{F}}^n_{K,\sigma }= & {} \tilde{\tilde{\tilde{F}}}^n_{K,\sigma }+(a^n_Ku_K^n-a^n_Ku_L^n), \end{aligned}$$

(3.37)

$$\begin{aligned} \tilde{\tilde{F}}^n_{L,\sigma }= & {} \tilde{\tilde{\tilde{F}}}^n_{L,\sigma }+(a^n_Lu_L^n-a^n_Lu_K^n), \end{aligned}$$

(3.38)

where $\tilde{\tilde{\tilde{F}}}^n_{K,\sigma }$ (resp. $\tilde{\tilde{\tilde{F}}}^n_{L,\sigma }$) does not include the term $u_K^n-u_L^n$ (resp. $u_L^n-u_K^n$).

By introducing a new factor

$$\begin{aligned} a^n=\min \{a^n_K,a^n_L\},\ 1\le n\le N, \end{aligned}$$

(3.37) and (3.38) can be rewritten as

$$\begin{aligned}{} & {} \tilde{\tilde{F}}^n_{K,\sigma }=\bar{F}^n_{K,\sigma }+(a^nu_K^n-a^nu_L^n),\\{} & {} \tilde{\tilde{F}}^n_{L,\sigma }= \bar{F}^n_{L,\sigma }+(a^nu_L^n-a^nu_K^n). \end{aligned}$$

Also

$$\begin{aligned} \bar{F}^n_{K,\sigma }= & {} \tilde{\tilde{F}}^n_{K,\sigma }+(a^nu_L^n-a^nu_K^n), \end{aligned}$$

(3.39)

$$\begin{aligned} \bar{F}^n_{L,\sigma }= & {} \tilde{\tilde{F}}^n_{L,\sigma }+(a^nu_K^n-a^nu_L^n). \end{aligned}$$

(3.40)

Thus, combining (3.36), (3.39) and (3.40), we have

$$\begin{aligned}{} & {} \bar{F}^n_{K,\sigma }+\bar{F}^n_{L,\sigma }=C_0^nh^2,\ 1\le n\le N,\nonumber \\{} & {} \tilde{\tilde{F}}^n_{K,\sigma }+ \tilde{\tilde{F}}^n_{L,\sigma }=C_0^nh^2,\ 1\le n\le N. \end{aligned}$$

To transform formulas (3.39) and (3.40) into a conservative scheme, the nonlinear combination technique will be used to define discrete fluxes on edge $\sigma$, we write

$$\begin{aligned}{} & {} F^n_{K,\sigma }=a^n(u_K^n-u_L^n)+\mu _1(u^n)\bar{F}^n_{K,\sigma }, \end{aligned}$$

(3.41)

$$\begin{aligned}{} & {} F^n_{L,\sigma }=a^n(u_L^n-u_K^n)+\mu _2(u^n)\bar{F}^n_{L,\sigma }, \end{aligned}$$

(3.42)

where $\mu _1(u^n)$ and $\mu _2(u^n)$ are nonnegative and nonlinear, which will be chosen below. We need the scheme to be conservative, then the following important fact should be satisfied:

$$\begin{aligned} F^n_{K,\sigma }+F^n_{L,\sigma }=0,\ 1\le n\le N, \end{aligned}$$

(3.43)

using (3.41)–(3.43), one has

$$\begin{aligned} \mu _1(u^n)\bar{F}^n_{K,\sigma }+\mu _2(u^n)\bar{F}^n_{L,\sigma }=0,\ 1\le n\le N. \end{aligned}$$

(3.44)

To make $\bar{F}^n_{K,\sigma }$ and $\bar{F}^n_{L,\sigma }$ to satisfy MP, we now turn to show how to choose the nonlinear coefficients $\mu _1(u^n)$ and $\mu _2(u^n)$. In this paper, we use the weighted combination of flux $\bar{F}^n_{K,\sigma }$ and $\bar{F}^n_{L,\sigma }$ to design a conservative flux.

Going back to (3.44), if $\bar{F}^n_{K,\sigma }\bar{F}^n_{L,\sigma }\ge 0$, we can take

$$\begin{aligned} \mu _1(u^n)=\mu _2(u^n)=0,\ 1\le n\le N. \end{aligned}$$

Then we insert the equation above into (3.41) and (3.42), a discrete conservative flux approximation of the continuous flux $\mathscr {F}_{K,\sigma }^n$ is written by

$$\begin{aligned}{} & {} F^n_{K,\sigma }=a^n(u_K^n-u_L^n),\ 1\le n\le N, \end{aligned}$$

(3.45)

$$\begin{aligned}{} & {} F^n_{L,\sigma }=a^n(u_L^n-u_K^n),\ 1\le n\le N. \end{aligned}$$

(3.46)

If $\bar{F}^n_{K,\sigma }\bar{F}^n_{L,\sigma }< 0$, we can take the nonlinear coefficients $\mu _1(u^n)$ and $\mu _2(u^n)$ by using the following weighted combination of nonconservative flux:

$$\begin{aligned} \mu _1(u^n)=\left( \frac{2\sqrt{|\bar{F}^n_{L,\sigma }|}}{\sqrt{|\bar{F}^n_{K,\sigma }|} +\sqrt{{|\bar{F}^n_{L,\sigma }|}}}\right) ^2,\ \mu _2(u^n)=\left( \frac{2\sqrt{|\bar{F}^n_{K,\sigma }|}}{\sqrt{|\bar{F}^n_{K,\sigma }|} +\sqrt{{|\bar{F}^n_{L,\sigma }|}}}\right) ^2,\ 1\le n\le N. \end{aligned}$$

Thus, inserting the equation above into (3.41) and (3.42), we can attain a discrete conservative flux approximation of the continuous flux $\mathscr {F}_{K,\sigma }^n$ on edge $\sigma$:

$$\begin{aligned}{} & {} F^n_{K,\sigma }=a^n(u_K^n-u_L^n)+ \left( \frac{2\sqrt{|\bar{F}^n_{L,\sigma }|}}{\sqrt{|\bar{F}^n_{K,\sigma }|} +\sqrt{{|\bar{F}^n_{L,\sigma }|}}}\right) ^2 \bar{F}^n_{K,\sigma }, \end{aligned}$$

(3.47)

$$\begin{aligned}{} & {} F^n_{L,\sigma }=a^n(u_L^n-u_K^n)+ \left( \frac{2\sqrt{|\bar{F}^n_{K,\sigma }|}}{\sqrt{|\bar{F}^n_{K,\sigma }|} +\sqrt{{|\bar{F}^n_{L,\sigma }|}}}\right) ^2\bar{F}^n_{L,\sigma }. \end{aligned}$$

(3.48)

If $\sigma \in \mathscr {E}_{ext}$, one can refer [23] and define

$$\begin{aligned} F^n_{K,\sigma }=\bar{F}^n_{K,\sigma },\quad F^n_{L,\sigma }=\bar{F}^n_{L,\sigma },\quad 1\le n\le N. \end{aligned}$$

(3.49)

At last, based on the temporal and spatial flux discretization, by using (3.19), (3.22), (3.23), (3.45)–(3.46) and (3.47)–(3.49), we can construct the following nonlinear finite volume method

$$\begin{aligned}{} & {} m(K)\sum \limits _{j=0}^{n}\frac{b^{n,\alpha }_{j}}{\varGamma (2-\alpha )} u_K^{j}+ \sum _{\sigma \in \mathscr {E}_K}F^n_{K,\sigma }=f^n_{K}m(K),\ \ 1\le n\le N,\ \ \forall K\in \mathscr {P}_{in}, \end{aligned}$$

(3.50)

$$\begin{aligned}{} & {} u^n_{M_{i}} = \psi ^n_{M_{i}},\ \ \forall M_{i}\in \mathscr {P}_{out},\ \ 1\le n\le N, \end{aligned}$$

(3.51)

$$\begin{aligned}{} & {} u^0_{K} = v(K),\ \ \forall K\in \mathscr {P}_{in}\cup \mathscr {P}_{out}, \end{aligned}$$

(3.52)

where $f^n_{K}=f(K,t_n)$.

4 Analysis of Discrete Maximum Principle

In this section, we first introduce feasible method for solving the nonlinear algebraic system (3.50)–(3.52), and then prove our numerical scheme satisfies the discrete maximum principle.

Let $J^n_{K,\sigma }$ (resp. $J^n_{L,\sigma }$) be the number of cell associated with K (resp. L) at time $t=t_n$. Going back to the expressions of discrete conservative flux (3.45)–(3.46) and (3.47)–(3.49), we can write the flux as the following equivalent form:

$$\begin{aligned}{} & {} F^n_{K,\sigma }=-\sum _{j=1}^{J^n_{K,\sigma }}A^n_{K,\sigma ,j}(u^n_{L_j}-u^n_K),\ 1\le n\le N, \end{aligned}$$

(4.53)

$$\begin{aligned}{} & {} F^n_{L,\sigma }=-\sum _{j=1}^{J^n_{L,\sigma }}A^n_{L,\sigma ,j}(u^n_{K_j}-u^n_L),\ 1\le n\le N. \end{aligned}$$

(4.54)

Set $A^n_{K,j}$ be the sum associated with $A^n_{L,\sigma ,j}$, $J^n_{K}$ is the number associated with cell K at time $t=t_n$. Then inserting (4.53) into (3.50), we have

$$\begin{aligned} \frac{ m(K)}{\varGamma (2-\alpha )}\sum \limits _{j=0}^{n}b^{n,\alpha }_{j} u_K^{j} -\sum _{j=1}^{J^n_{K}}A^n_{K,j}(u^n_{L_j}-u^n_K) =m(K)f^n_{K},\ \forall K\in \mathscr {P}_{in},\ 1\le n\le N. \nonumber \\ \end{aligned}$$

(4.55)

That is, the nonlinear system is as follows

$$\begin{aligned}{} & {} \frac{ m(K)}{\varGamma (2-\alpha )}b^{n,\alpha }_{n} u_K^{n} -\sum _{j=1}^{J^n_{K}}A^n_{K,j}(u^n_{L_j}-u^n_K) \nonumber \\{} & {} \quad =m(K)f^n_{K}-\frac{ m(K)}{\varGamma (2-\alpha )}\sum \limits _{j=0}^{n-1}b^{n,\alpha }_{j} u_K^{j},\ \ \forall K\in \mathscr {P}_{in},\ \ 1\le n\le N. \end{aligned}$$

(4.56)

From (3.21), we know that $b^{n,\alpha }_{n}>0$ and $-b^{n,\alpha }_{j}>0$, $n-1\ge j\ge 0$. Set $U^n$ be the unknowns solution vector, $A(U^n)$ be the corresponding coefficient matrix, and $F^n$ be corresponding right-hand term vector.

Thus our fully discrete nonlinear algebraic system (4.56) can be rearranged as the following matrix form:

$$\begin{aligned} A(U^n)U^n=F^n, \end{aligned}$$

(4.57)

where $1\le n\le N$, Picard nonlinear iteration can be used to process the above nonlinear system.

4.1 The Analysis of DMP

We now state that our algorithm (3.50)–(3.52) satisfies the following DMP.

Theorem 2

The NFV scheme (3.50)–(3.52) satisfies the DMP. That is,

(1) If function $f\le 0$, then the numerical solutions satisfy

$$\begin{aligned} u_K^{n,s}\le \max \{0,M^n\}, \forall K\in \mathscr {P}_{in}\cup \mathscr {P}_{out}, \forall n=0,1,2,\ldots , \end{aligned}$$

(4.58)

where

$$\begin{aligned} M^{n}:=\max \left\{ \max \limits _{K\in \mathscr {P}_{in}\cup \mathscr {P}_{out}}u_K^0,\ \ \max \limits _{K\in \mathscr {P}_{out}, 1\le \ell \le N, 0\le r \le s}u^{\ell ,r}_K\right\} . \end{aligned}$$

Namely, the positive maximum of function u can only be found at the boundary of the domain.

(2) If function $f\ge 0$, then the numerical solutions satisfy

$$\begin{aligned} u_K^{n,s}\ge \min \{0,m^n\}, \forall K\in \mathscr {P}_{in}\cup \mathscr {P}_{out}, \forall n=0,1,2,\ldots N, \forall s=0,1,2,\ldots , \end{aligned}$$

(4.59)

where

$$\begin{aligned}m^{n}:=\min \left\{ \min \limits _{K\in \mathscr {P}_{in}\cup \mathscr {P}_{out}}u_K^0,\ \ \min \limits _{K\in \mathscr {P}_{out}, 1\le \ell \le N, 0\le r \le s}u^{\ell ,r}_K\right\} .\end{aligned}$$

Namely, the negative minimum of function u can only be found at the boundary of the domain.

Proof

We only prove the maximum principle, i.e. the inequality (4.58). For the minimum principle (4.59), we only need to repeat the same arguments as the proof of inequality (4.58).

(1) If function $f\ge 0$. Assume

$$\begin{aligned} u_{K_0}^{n_0,s}= \max \{0,M^n\}, \ K_0\in \mathscr {P}_{in}\cup \mathscr {P}_{out},\ 0\le n_0\le N, s=0,1,2,\ldots . \end{aligned}$$

(4.60)

If $u_{K_0}^{n_0,s}\le 0$, then the inequality (4.58) follows directly.

We now consider the case $u_{K_0}^{n_0,s}> 0$.

For $\forall s=0,1,2,\ldots$, if $K_0\in \mathscr {P}_{out}, 1\le n_0\le N$ or $K_0\in \mathscr {P}_{in}\cup \mathscr {P}_{out},\ n_0=0,$ then the inequality (4.58) follows directly.

For $\forall s=0,1,2,\ldots$, if $K_0\in \mathscr {P}_{in},\ n_0\ne 0,$ using (3.19), we go back to (4.55), then

$$\begin{aligned} m(K_0)D_{N}^{\alpha }u_{K_0}^{n_0,s}= \sum _{j=1}^{J^{n_0}_{K_0}}A^{n_0,s}_{K_0,j}(u^{n_0,s}_{L_j}-u^{n_0,s}_{K_0}) +m(K_0)f^{n_0}_{K_0},\ K_0\in \mathscr {P}_{in},\ n_0\ne 0. \end{aligned}$$

(4.61)

Using formulas (3.17), and noting the important condition $\omega ^n_{M_i,j}\ge 0$ in (3.31), we have

$$\begin{aligned} A^{n_0,s}_{K_0,j} \ge 0,\ K_0\in \mathscr {P}_{in},\ n_0\ne 0, \ j=1,2,\ldots , J^{n_0}_{K_0}, s=0,1,2,\ldots , \end{aligned}$$

(4.62)

since (4.60), then for all $L_j\in \mathscr {P}_{in}\cup \mathscr {P}_{out}$, $j=1,2,\ldots , J^{n_0}_{K_0}$, we have

$$\begin{aligned} u^{n_0,s}_{L_j}-u^{n_0,s}_{K_0}\le 0, \ K_0\in \mathscr {P}_{in},\ n_0\ne 0, s=0,1,2,\ldots , \end{aligned}$$

(4.63)

noting that $f\le 0$, thus combining (4.61)–(4.63), we have

$$\begin{aligned} \sum _{j=1}^{J^{n_0}_{K_0}}A^{n_0,s}_{K_0,j}(u^{n_0,s}_{L_j}-u^{n_0,s}_{K_0}) +m(K_0)f^{n_0}_{K_0}\le 0,\ K_0\in \mathscr {P}_{in},\ n_0\ne 0,\ s=0,1,2,\ldots , \end{aligned}$$

that is

$$\begin{aligned} D_{N}^{\alpha }u_{K_0}^{n_0,s}\le 0,\ K_0\in \mathscr {P}_{in},\ n_0\ne 0,\ s=0,1,2,\ldots . \end{aligned}$$

(4.64)

Also, using (3.19), for $\forall s=0,1,2,\ldots$, we have

$$\begin{aligned} D_{N}^{\alpha }u_{K_0}^{n_0,s}= \frac{ 1}{\varGamma (2-\alpha )}\sum \limits _{j=0}^{n_0-1}\tilde{b}^{n_0,\alpha }_{j+1} (u_{K_0}^{n_0-j,s}-u_{K_0}^{n_0-1-j,s}),\ K_0\in \mathscr {P}_{in},\ n_0\ne 0, \end{aligned}$$

noticing (4.60), for all $n=0,1,2,\ldots ,N$, we can obtain

$$\begin{aligned} u^{n_0,s}_{K_0}-u^{n,s}_{K_0}\ge 0,\ \ \ K_0\in \mathscr {P}_{in},\ s=0,1,2,\ldots . \end{aligned}$$

(4.65)

Hence,

$$\begin{aligned} D_{N}^{\alpha }u_{K_0}^{n_0,s}\ge 0,\ K_0\in \mathscr {P}_{in},\ n_0\ne 0,\ s=0,1,2,\ldots . \end{aligned}$$

(4.66)

By combining (4.64) and (4.66), we obtain

$$\begin{aligned} D_{N}^{\alpha }u_{K_0}^{n_0,s}=0,\ K_0\in \mathscr {P}_{in},\ n_0\ne 0,\ s=0,1,2,\ldots . \end{aligned}$$

(4.67)

Further, we combine (4.65) and (4.67), then, for all $n=0,1,2,\ldots ,N$,

$$\begin{aligned} u^{n_0,s}_{K_0}-u^{n,s}_{K_0}= 0,\ \ \ K_0\in \mathscr {P}_{in},\ s=0,1,2,\ldots . \end{aligned}$$

Thus, we can take $n=0$, then the proof of the maximum principle inequality (4.58) is completed. $\square$

5 Numerical Example

We will give five numerical examples to display typical behaviour in this section. In our implementations, the temporal graded meshes is used with $r =\frac{2-\alpha }{\alpha }$ in all five examples. The $L_2^u$ is used to compute approximate errors for u: $L_2^u=(\sum \nolimits _{K\in \mathscr {M}}(u_K-u(K))^2\,m(K))^{1/2}$. The $L_2^F=$ is used to compute approximate errors for flux F: $L_2^F=(\sum \nolimits _{\sigma \in \mathscr {E}}(F_{K,\sigma }-\mathscr {F}_{K,\sigma })^2)^{1/2}$.

Example 1

Consider the tensor diffusion matrix $\kappa$ is anisotropic and homogeneous. For the sub-diffusion model (1.1)–(1.3), set $T=1$, $x_1\in [0,1]$, $x_2\in [0,1]$, and

$$\begin{aligned} \kappa ={x_2^2+\varepsilon x_1^2 \quad -(1-\varepsilon )x_1x_2 \atopwithdelims ()-(1-\varepsilon )x_1x_2 \quad \varepsilon x_2^2+x_1^2}, \end{aligned}$$

where $\varepsilon =1\times 10^{-3}$, $v(x_1,x_2)=0$, $\psi (x_1,x_2,t)=0$ and

$$\begin{aligned}f= {\left\{ \begin{array}{ll} 10, &{} {0<t<1, (x_1,x_2)\in [3/8,5/8]\times [3/8,5/8], }\\ 0, &{} \text {other}. \end{array}\right. } \end{aligned}$$

The exact solution $u(x_1,x_2,t)$ is unknown, but the principle of minimum values shows that it is non-negative. We test the problem on random quadrilateral meshes (RQMs) and random triangular meshes (RTMs) in Fig. 2, which is obtained by the random disturbance of mesh. That is $x_{1_{ij}}=\frac{i}{I}+\frac{{\rho }}{I}(R_{x_1}-0.5)$ and $x_{2_{ij}}=\frac{j}{J}+\frac{{\rho }}{J}(R_{x_2}-0.5)$ with random number $\rho \in [0,1]$. We consider ${\rho }=0.4$ in the example.

In Fig. 3, the numerical solutions are obtained on RTMs with $\alpha =0.8$, $\alpha =0.5$, $\alpha =0.2$. The minimum are 9.3951e$-$5, 7.9854e$-$5 and 6.7698e$-$5, respectively. The minimum 0 of the solution is reached on $\partial \varOmega$. The number of nonlinear iteration is 94, 184 and 236, respectively. Figure 4 shows the numerical solutions obtained on RQMs. The minimum are 3.3250e$-$6, 3.3415e$-$6 and 2.9352e$-$6, respectively. The minimum 0 is attained on $\partial \varOmega$. Figures 3 and 4 show that the proposed scheme have not non-physical oscillations while maintaining positivity.

Fig. 2

RTMs: $16\times 16\times 2$ (left) and RQMs: $24\times 24$ (right)

Fig. 3

Example 1: Numerical solutions of RTMS for $\alpha =0.2, 0.5, 0.8$ from left to right

Fig. 4

Example 1: Numerical solutions of RQMs for $\alpha =0.2, 0.5, 0.8$ from left to right

In the following example, we consider the problem which comes from Jiang and Xu [15]. We set the random number ${\rho }=0.6$ and $\alpha =0.5$ (Fig. 5).

Example 2

[15] Take $\kappa (x_1,x_2,t)=E$, $\varOmega =[0,1]\times [0,1]$,$T=1$, $v=0$, $f(x_1,x_2,t)=0$. $\psi (x_1,x_2,t)=(1+\frac{1-e^{10x_1x_2}}{2.20255\times 10^4})t^{2}$ is introduced in Example 4.2 of Jiang [15].

Fig. 5

RTMs: $20\times 20\times 2$ (left) and RQMs: $40\times 40$(right)

Fig. 6

Example 2: Numerical solution of distorted quadrilateral meshes ($40\times 40$)

Fig. 7

Example 2: Numerical solution of distorted triangular meshes ($20\times 20\times 2$)

The exact solution of this problem is unknown. In Figs. 6 and 7 we present the numerical results on RQMs and RTMs, respectively. The minimum and maximum in the domain are 0.1124 and 0.9571, respectively. The Figs. 6 and 7 affirm that the proposed scheme satisfy the DMP on distorted RMMs and RTMs. However, the finite difference scheme constructed in [15] can not satisfy the positivity of physical variables and has oscillations.

Example 3

Consider the model (1.1)–(1.3) with a non-smooth anisotropic solution. The domain is $\varOmega =(0, 1)\times (0, 1)\backslash [4/9, 5/9]\times [4/9, 5/9]$ with the hole width 2/9. That is $\partial \varOmega$ is formed by two disjoint parts: the interior and exterior boundary $\partial \varOmega _1$ and $\partial \varOmega _2$, respectively. We take $T=1$, $f= 0$, $\psi =1/5$ on $\partial \varOmega _1$, $\psi (x_1,x_2,t) = 1/5+t^{\alpha }$ on $\partial \varOmega _2$, the initial conditions $v(x_1,x_2)=1/5$, and $\kappa =RDR^\textrm{T}$, where

$$\begin{aligned} D={ 1+2x^2+y^2 \quad 0 \atopwithdelims ()0 \quad 1+x^2+2y^2},\qquad R={\cos \frac{5\pi }{12} \quad -\sin \frac{5\pi }{12} \atopwithdelims ()\sin \frac{5\pi }{12}\quad \cos \frac{5\pi }{12}}. \end{aligned}$$

We experiment the example on the RTMs and RQMs in the domain with the hole in Fig. 8) and consider ${\rho }=0.7$, and the number of cells are $18\times 18\times 2$ and $36\times 36$, respectively.

The numerical solutions are presented in Figs. 9 and 10 with $\alpha =0.5$, respectively. The minimum and maximum are 0.2 and 1.2, respectively. We find the proposed scheme satisfy the DMP on RTMs and RQMs.

Fig. 8

Random triangular meshes: $18\times 18\times 2$ (left) and random quadrilateral meshes: $36\times 36$(right)

Fig. 9

Example 3: Numerical solutions on random RTMs for $\alpha =0.5$

Fig. 10

Example 3: Numerical solutions on RQMs for $\alpha =0.5$

Example 4

[12] Consider (1.1)–(1.3) from [12]. Let $\varOmega =[0,1]\times [0,1]$, $\kappa =E$, $v=x_1(1-x_1)x_2(1-x_2)$, $\psi (x_1,x_2,t) =0$ and $f=0$.

Fig. 11

Example 4: Numerical solutions on RTMs for $\alpha =0.5, 0.75$ from left to right

Fig. 12

Example 4: Numerical solutions on RQMs for $\alpha =0.5, 0.75$ from left to right

The exact solution $u(x_1,x_2,t)$ is unknown. The main purpose is to compare preserving the minimum principle obtained by the proposed method with the all three methods, including SG method, LM method and FVE method, proposed by Jin et al. [12].

Taking ${\rho }=0.7$. In Figs. 11 and 12, we presented the numerical results on RTMs $40\times 40$ and RQMs $24\times 24\times 2$ with different $\alpha =0.5$, 0.75, respectively. The proposed method maintain the minimum of solution on RTMs and RQMs. But as Jin et al. [12] point out, the numerical solutions obtained by all three methods in [12] may produce negative values for small $\tau$.

Example 5

Consider (1.1)–(1.3) with $\varOmega =[0,1]\times [0,1]$, $\kappa =E$, $v=\sin (\pi x_1)\sin (\pi x_2)$, $\psi =0$, f is selected so that the solution is

$$\begin{aligned}u=(1+t^{\alpha }+t^{2+\alpha }+t^3)\sin (\pi x_1)\sin (\pi x_2), \ (x_1, x_2)\in \varOmega =[0,1]\times [0,1]. \end{aligned}$$

In this example, we take ${\rho }=0.7$ and mainly test the accuracy of proposed method. We always select $N = (\frac{1}{h})^{\frac{2}{2-\alpha }}$ so that the best convergence order $O(h^2+N^{-(2-\alpha )})=O(h^2)$ is reached in both time and space.

In Tables 1, 2, 3 and 4, we present the errors and convergence rates for solution u and flux F on random and uniform quadrilateral and triangular meshes, respectively. The proposed scheme obtains solution of second-order accuracy and first-order accuracy of flux for different $\alpha =0.2,0.5,0.7$, which verifies our theoretical results.

Table 1 Accuracy of schemes for Example 5 on random quadrilateral meshes

Table 2 Accuracy of schemes for Example 5 on uniform quadrilateral meshes

Table 3 Accuracy of schemes for Example 5 on random triangular meshes

Table 4 Accuracy of schemes for Example 5 on uniform triangular meshes

6 Conclusion

In this paper, we present the development of weighted NFV schemes that preserve the MP for the sub-diffusion problems on various distorted RTMs and RQMs. We prove the MP for a suitably defined solution for the first time and establish that the discrete solution satisfies the DMP. Using nonlinear weighted methods, we construct a conservative flux by combining nonconservative fluxes with appropriate weights. Furthermore, we demonstrate that the proposed scheme is local conservation and relies solely on cell-centered unknowns. It can be used to general distorted meshes without imposing stringent conditions on the mesh quality. The scheme preserves the MP for problems with strongly anisotropic and heterogeneous full tensor coefficients. Numerical results confirm that our scheme preserves the MP and achieves second-order accuracy for solutions and first-order accuracy for flux computations.