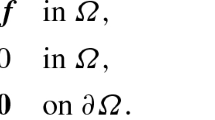Penalty-Free Any-Order Weak Galerkin FEMs for Linear Elasticity on Quadrilateral Meshes

Abstract

This paper develops a family of new weak Galerkin (WG) finite element methods (FEMs) for solving linear elasticity in the primal formulation. For a convex quadrilateral mesh, degree $k \ge 0$ vector-valued polynomials are used independently in element interiors and on edges for approximating the displacement. No penalty or stabilizer is needed for these new methods. The methods are free of Poisson-locking and have optimal order $(k+1)$ convergence rates in displacement, stress, and dilation (divergence of displacement). Numerical experiments on popular test cases are presented to illustrate the theoretical estimates and demonstrate efficiency of these new solvers. Extension to cuboidal hexahedral meshes is briefly discussed.

1 Introduction

This paper concerns finite element methods for linear elasticity formulated as

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle -\nabla \cdot \sigma = {\textbf{f}}({\textbf{x}}), \quad {\textbf{x}} \in \varOmega , \\ \displaystyle {\textbf{u}}|_{\varGamma ^D} = {\textbf{u}}_D, \quad \displaystyle (\sigma {\textbf{n}})|_{\varGamma ^N} = {\textbf{t}}_N, \end{array} \right. \end{aligned}$$

(1)

where $\varOmega \in {\mathbb {R}}^2$ is a bounded open and connected domain with a Lipschitz continuous boundary $\varGamma =\partial \varOmega$, ${\textbf{u}}$ is the solid displacement, $\varepsilon ({\textbf{u}}) = \frac{1}{2} \left( \nabla {\textbf{u}} + (\nabla {\textbf{u}})^T \right)$ is the strain tensor, $\sigma = 2\mu \varepsilon ({\textbf{u}}) + \lambda (\nabla \cdot {\textbf{u}}) {\mathbb {I}}$ is the stress tensor with ${\mathbb {I}}$ being the order-2 identity matrix, ${\textbf{f}}$ is a known body force, ${\textbf{u}}_D, {\textbf{t}}_N$ are Dirichlet and Neumann boundary data on the Dirichlet and Neumann boundaries $\varGamma ^D$ and $\varGamma ^N$, which form a non-overlapping decomposition of $\varGamma$. Furthermore, the Lamé constants

$$\begin{aligned} \displaystyle \lambda = \frac{E \nu }{(1+\nu )(1-2\nu )}, \quad \quad \mu = \frac{E}{2(1+\nu )} \end{aligned}$$

are defined by the elasticity modulus $E>0$ and the Poisson ratio $\nu \in (0,\frac{1}{2})$.

Development of efficient and robust numerical solvers for linear elasticity is an important task for scientific computing. Robustness is reflected as uniform convergence of such solvers with respect to the Poisson ratio $\nu$ when spatial meshes are refined. Some linear solvers are subject to the so-called Poisson-locking, which often appears as loss of convergence rates in displacement or spurious behaviors in stress or other quantities, when $\lambda \rightarrow \infty$. This corresponds to the case when the Poisson ratio $\nu \rightarrow \frac{1}{2}$. Namely, the elastic material becomes nearly incompressible. Such phenomenon is mainly caused by the fact that the approximation space cannot remain the optimal approximation under the incompressible constraint $\nabla \cdot {\textbf{u}} = 0$ [17, 18]. It is well known that the classical continuous Galerkin FEMs with linear or bilinear/trilinear shape functions on simplicial or 2d/3d-rectangular meshes are subject to Poisson-locking [13].

The mixed finite element methods based on the Hellinger-Reissner formulation are locking-free by design. In such formulation, the displacement vector field and the stress tensor field are approximated simultaneously. It is nontrivial to devise stable element pairs for displacement and symmetric stress. Some nice results can be found in [3, 26, 27]. However, the mixed FEMs need more unknowns and result in saddle-point problems.

Nonconforming finite elements for linear elasticity have been developed. In [27], the simplest nonconforming FEs were developed in the mixed formulation for rectangular grids of any dimension. In [12, 21], nonconforming FEs were investigated along with the introduction of pseudo-pressure.

Hybridizable discontinuous Galerkin (HDG) methods have been investigated for linear elasticity. The first HDG method was presented in [35], the HDG method for elasto-dynamics was introduced in [33], a priori error analysis was presented in [23], the HDG method for linear elasticity with strong symmetric stress was presented in [34].

Virtual element methods (VEMs) have also been developed for linear elasticity [7,8,9, 24]. High order linear and nonlinear VEMs were developed in [4, 5]. A detailed account of VEMs for linear elasticity can be found in [10].

The WG methodology was first introduced in [40]. The key characteristic of the WG methods is the use of weak functions and weak differential operators, which make the WG methods flexible and easy to construct. WG methodology has been applied to many problems, for instance, the elliptic problems [19, 39, 41], the Stokes flow [22], the Darcy flow [30, 31], the Maxwell equation [37], the div-curl systems [28], the Cahn-Hilliard equation [42], the poroelasticity problems [44], and the linear elasticity problems [16, 43].

There have been efforts on developing WG FEMs for linear elasticity in the primal formulation. In [38], WG FEMs were developed on polygonal and polyhedral meshes. Degree $k \ge 1$ polynomials were used in element interiors whereas degree $k-1$ polynomials were used on edges/faces. Their discrete weak gradient and discrete weak divergence were constructed as degree $k-1$ matrices and scalars, respectively. This requires a penalty term to handle the discrepancy between the shape functions in element interiors and on edges/faces. Lowest-order WG FEMs have been developed for linear elasticity on simplicial meshes [46] and 2d- or 3d- rectangular meshes [25]. These methods utilized the matrix version of the classical Raviart-Thomas spaces for constructing discrete weak gradients needed for approximation of strain in elasticity. The methods in [25] can be extended to quadrilateral and hexahedral meshes that are asymptotically parallelogram or parallelopiped [20].

For many finite element methods, penalty terms are needed to enforce weak continuity of shape functions. Such penalty terms may not have clear physical meaning but require additional efforts in implementation. However, for WG finite element methods, when shape functions and spaces for gradient reconstruction are properly chosen, no penalty term is needed [22, 32]. In this paper, we focus on development of penalty-free WG finite element schemes.

The Arbogast-Correa (AC) spaces (to be reviewed in Sect. 2) were first constructed in [1] and used for solving elliptic problems in the mixed finite element framework. The AC spaces are constructed as $H(\text{ div})$-subspaces on quadrilaterals. They inherit the spirit of the classical Raviart-Thomas spaces for 2d/3d-rectangles but apply to more general convex quadrilaterals. The local AC spaces has been incorporated with the WG methodology to develop penalty-free any order finite element methods for Darcy flow or elliptic boundary value problems that are efficient, easy-to-use, and respect important physical properties [32]. This paper continues the efforts in [32], aiming at development of a family of new WG finite methods for linear elasticity on general convex quadrilateral meshes in the primal formulation. These solvers are free of Poisson-locking and practically useful.

When a pure Dirichlet boundary condition is considered, we have $\varGamma ^N=\emptyset$. In this case, the grad-div PDE for elasticity reads [25, 46]

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle -\mu \varDelta {\textbf{u}} - (\mu +\lambda ) \nabla (\nabla \cdot {\textbf{u}}) = {\textbf{f}}, \quad {\textbf{x}} \in \varOmega , \\ \displaystyle {\textbf{u}}|_{\varGamma } = {\textbf{u}}_D. \end{array} \right. \end{aligned}$$

(2)

The rest of this paper is organized as follows. Section 2 discusses the local Arbogast-Correa spaces $AC_k$ and their bases. Based on that, Sect. 3 develops WG finite elements $(P_k^2,P_k^2;AC_k^2,P_k)$, which are then used for developing WG FEMs for linear elasticity in Sect. 4. Section 5 presents a rigorous analysis for these WG FEMs. Section 6 presents numerical experiments on popular test cases to demonstrate the accuracy and usefulness of these new methods. The paper is concluded with remarks in Sect. 7.

2 Arbogast-Correa Spaces $AC_k (k \ge 0)$ on Quadrilaterals

The $AC_k (k \ge 0)$ spaces for vector-valued functions on quadrilaterals were introduced in [1]. These spaces extend the Raviart-Thomas spaces $RT_{[k]}$ for rectangles [14] to general convex quadrilaterals. For a rectangle and the lowest order case, these two types of spaces agree, that is, $AC_0(E) = RT_{[0]}(E)$, when E is a rectangle. Otherwise, they are different. For example, when E is indeed a quadrilateral, $AC_k(E)$ contains rational vector-valued functions, but $RT_{[0]}(E)$ contains only polynomial vector-valued functions.

As discussed in [45], there are actually 3 types of Arbogast-Correa spaces on quadrilaterals.

• (i) The local space $AC_k(E)$ on an individual quadrilateral E;

• (ii) The broken space ${\mathcal {A}}{\mathcal {C}}_k({\mathcal {E}}_h)$ on a quadrilateral mesh ${\mathcal {E}}_h$, which is simply the Cartesian product of all local AC spaces;

• (iii) The global space $AC_k({\mathcal {E}}_h)$ is understood as ${\mathcal {A}}{\mathcal {C}}_k({\mathcal {E}}_h) \cap H(\text{ div },\varOmega )$, which implies normal continuity for the vector functions in $AC({\mathcal {E}}_h)$.

This paper uses the local AC spaces and their matrix version

Let E be a convex quadrilateral and ${\mathcal {F}}$ be the bilinear mapping from the unit square ${\hat{E}} = [0,1]^2$ to E. Let ${\textbf{J}}$ be the Jacobian matrix for this bilinear mapping and J be the Jacobian determinant. Then ${\mathcal {P}}_E = {\textbf{J}}/J$ is the Piola transformation, which maps a vector field on the unit square ${\hat{E}}$ to a vector field on the quadrilateral E via matrix–vector multiplication.

Let $({\hat{x}}, {\hat{y}}) \in {\hat{E}}$ and $(x,y) \in E$. We call $X=x-x_c, Y=y-y_c$ normalized coordinates [29], where $(x_c,y_c)$ is the geometric center of E.

For $k=0$, $\text{ dim }(AC_0(E)) = 4 = 2 + 1 + 1$ and one has

$$\begin{aligned} AC_0(E) = \text{ Span } \left\{ \left[ \begin{array}{r} 1\\ 0 \end{array} \right] , \left[ \begin{array}{r} 0\\ 1 \end{array} \right] , \left[ \begin{array}{r} X\\ Y \end{array} \right] , {\mathcal {P}}_E \left[ \begin{array}{r} {\hat{x}}\\ -{\hat{y}} \end{array} \right] \right\} . \end{aligned}$$

Similarly, for $k=1$, $\text{ dim }(AC_1) = 10 = 6 + 2 + 2$, and one could use the following ten (10) vector-valued functions as its local basis [32]:

$$\begin{aligned}{} & {} \left[ \begin{array}{c} 1\\ 0 \end{array} \right] , \; \left[ \begin{array}{c} X\\ 0 \end{array} \right] , \; \left[ \begin{array}{c} Y\\ 0 \end{array} \right] , \; \left[ \begin{array}{c} 0\\ 1 \end{array} \right] , \; \left[ \begin{array}{c} 0\\ X \end{array} \right] , \; \left[ \begin{array}{c} 0\\ Y \end{array} \right] , \\{} & {} \left[ \begin{array}{c} X^2\\ XY \end{array} \right] , \; \left[ \begin{array}{c} XY\\ Y^2 \end{array} \right] , \quad {\mathcal {P}}_E \left[ \begin{array}{c} 1-{\hat{x}}^2\\ 2{\hat{x}}{\hat{y}} \end{array} \right] , \; {\mathcal {P}}_E \left[ \begin{array}{c} 2{\hat{x}}{\hat{y}} \\ 1-{\hat{y}}^2 \end{array} \right] . \end{aligned}$$

In general, we have

$$\begin{aligned} AC_k(E) = {\mathbb {P}}_k(E)^2 + \widetilde{{\mathbb {P}}}_k(E) {\textbf{x}} + {\mathbb {S}}_k(E), \end{aligned}$$

(3)

where ${\mathbb {P}}_k(E)^2$ is the subspace of vector-valued polynomials with total degree at most k, $\widetilde{{\mathbb {P}}}_k(E)$ is the subspace of homogeneous scalar-valued polynomial with degree $=k$, and ${\mathbb {S}}_k(E)$ is the subspace of rational functions obtained via Piola transformation.

Roughly speaking, for a given vector field on a convex quadrilateral E,

• ${\mathbb {P}}_k(E)^2$ offers an approximation based on degree k polynomials;

• $\widetilde{{\mathbb {P}}}_k(E) {\textbf{x}}$ takes care of approximation for its divergence;

• ${\mathbb {S}}_k$ offers a divergence-free supplement.

Note that $\text{ dim }({\mathbb {P}}_k^2) = (k+1)(k+2)$, $\text{ dim }(\widetilde{{\mathbb {P}}}_k) = k+1$, but

$$\begin{aligned} s_k= & {} \text{ dim }({\mathbb {S}}_k) = \left\{ \begin{array}{lcl} 1 &{}&{} \text{ if } \;\; k=0; \\ 2 &{}&{} \text{ if } \;\; k \ge 1. \end{array} \right. \end{aligned}$$

(4)

$$\begin{aligned} \text{ dim }(AC_k(E))= & {} (k+1)(k+3) + s_k. \end{aligned}$$

(5)

One might have also noticed that

• (i) $(k+1)(k+3) = \text{ dim }(RT_k)$, the dimension of the Raviart-Thomas space for a triangle;

• (ii) whereas $s_k$ represents the additional degrees of freedom needed for augmenting the Raviart-Thomas space on a quadrilateral.

Furthermore, ${\mathbb {S}}_k = {\mathcal {P}}_E \hat{{\mathbb {S}}}_k$, where $\hat{{\mathbb {S}}}_k$ is defined on ${\hat{E}} = [0,1]^2$.

• For $k=0$, one has

  $$\begin{aligned} \hat{{\mathbb {S}}}_0 = \text{ Span } \{ {{\textbf {curl}}}({\hat{x}}{\hat{y}}) \}; \end{aligned}$$

  (6)

• For $k \ge 1$, there holds

  $$\begin{aligned} \hat{{\mathbb {S}}}_k = \text{ Span } \{ {{\textbf {curl}}}({\hat{x}}^{k-1}{\hat{y}}(1-{\hat{x}}^2)), \; {{\textbf {curl}}}({\hat{y}}^{k-1}{\hat{x}}(1-{\hat{y}}^2)) \}. \end{aligned}$$

  (7)

Lemma 1

Let E be a convex quadrilateral. For any ${\textbf{w}} \in AC_k(E)$,

• (i) $\nabla \cdot {\textbf{w}} \in P_k(E)$;

• (ii) $({\textbf{w}} \cdot {\textbf{n}})|_e \in P_k(e)$ for any edge e on the boundary of E.

Proof

These can be found in [1]. $\square$

The global AC spaces were used in [1] within the framework of mixed finite element methods for solving elliptic boundary value problems. This approach involves technical construction of global basis functions on the whole mesh. However, the AC spaces can also be utilized within the framework of WG FEMs for solving elliptic problems or Darcy flow [32]. The latter involves only local bases of the AC spaces in a much simpler way.

The local AC spaces were used in [45] for development of pressure-robust Stokes solvers. In this paper, we use them for developing locking-free solvers for elasticity problems.

3 WG$(P_k^2,P_k^2;AC_k^2,P_k)(k \ge 0)$ Finite Elements on Quadrilaterals

In this paper, we use the local AC spaces for developing new WG finite elements. What we need are actually local matrix spaces based on the AC spaces.

Let E be a convex quadrilateral. We use $AC_k^2(E) (k \ge 0)$ to denote the space of matrix-valued functions whose row vectors are in $AC_k(E)$.

We consider WG$(P_k^2,P_k^2)$-type vector-valued discrete weak functions defined on a convex quadrilateral E. Such a function ${\textbf{v}} = \{ {\textbf{v}}^\circ , {\textbf{v}}^\partial \}$ has two parts: ${\textbf{v}}^\circ$ is a vector-valued function defined in the element interior $E^\circ$, each component is a bivariate polynomial of total degree at most k; on the other hand, ${\textbf{v}}^\partial$ is a vector-valued function defined piecewise on each edge of the element boundary $E^\partial$ and each component is a univariate polynomial of degree at most k.

Similar to what has been discussed in [25], we define discrete weak gradients and discrete weak divergences for such vector-valued discrete weak functions.

Definition 1

(Discrete weak gradient). Let ${\textbf{v}} = \{ {\textbf{v}}^\circ , {\textbf{v}}^\partial \}$ be a WG$(P_k^2,P_k^2)$-type discrete weak function. We establish its discrete weak gradient $\nabla _w {\textbf{v}}$ in $AC_k^2(E)$ via integration by parts

$$\begin{aligned} \int _E (\nabla _w{\textbf{v}}) : W = \int _{E^\partial } {\textbf{v}}^\partial \cdot (W {\textbf{n}}) - \int _{E^\circ } {\textbf{v}}^\circ \cdot (\nabla \cdot W), \quad \forall W \in AC_k^2(E), \end{aligned}$$

(8)

where  :  is the standard colon product for matrices and ${\textbf{n}}$ is the outward unit normal vector on the element boundary $E^\partial$.

Clearly, one can utilize the aforementioned local basis functions for $AC_k(E)$ to construct a local basis for $AC_k^2(E)$. Then express $\nabla _w{\textbf{v}}$ as a linear combination of these basis functions. Such linear combination coefficients can be obtained by solving a small-size SPD linear system. This solving process is parallel in nature.

Definition 2

(Discrete weak divergence). Again let ${\textbf{v}} = \{ {\textbf{v}}^\circ , {\textbf{v}}^\partial \}$ be a WG$(P_k^2,P_k^2)$-type discrete weak function. We establish its discrete weak divergence $\nabla _w \cdot {\textbf{v}}$ in $P_k(E)$ via integration by parts

$$\begin{aligned} \int _E (\nabla _w \cdot {\textbf{v}}) w = \int _{E^\partial } {\textbf{v}}^\partial \cdot (w {\textbf{n}}) - \int _{E^\circ } {\textbf{v}}^\circ \cdot (\nabla w), \quad \forall w \in P_k(E). \end{aligned}$$

(9)

Similarly, this involves solving small-size SPD linear systems.

Now we define discrete weak strain as

$$\begin{aligned} \varepsilon _w({\textbf{v}}) = \frac{1}{2} \left( \nabla _w{\textbf{v}} + (\nabla _w{\textbf{v}})^T \right) , \end{aligned}$$

which will be used in the next section for establishing WG FEMs for linear elasticity.

4 WG FE Schemes for Linear Elasticity on Quadrilateral Meshes

Let ${\mathcal {E}}_h$ be a quadrilateral partition of $\varOmega$ and $\varGamma _h$ be the set of all edges in ${\mathcal {E}}_h$. Accordingly, $\varGamma ^D_h = \varGamma ^D \cap \varGamma _h$ and $\varGamma ^N_h = \varGamma ^N \cap \varGamma _h$. For any $E\in {\mathcal {E}}_h$, let $h_E$ be the diameter of the circumscribed circle of E and $h = \max _{E\in {\mathcal {E}}_h}h_E$ be the mesh size. For any $e\in \varGamma _h$, $h_{e}$ is the length of e. Define function spaces as follows.

$$\begin{aligned} \begin{aligned} {\textbf{V}}_h=&\{{\textbf{v}}=\{{\textbf{v}}^\circ ,{\textbf{v}}^\partial \}:{\textbf{v}}^\circ |_{E^\circ }\in P_k(E^\circ )^2,{\textbf{v}}^\partial |_{e}\in P_k(e)^2, \forall E\in {\mathcal {E}}_h, \forall e\in \varGamma _h\}, \\ {\textbf{V}}_h^0=&\{{\textbf{v}}\in {\textbf{V}}_h:{\textbf{v}}^\partial |_{\varGamma _h^D}={\textbf{0}}\}, \\ W_h=&\{q:q|_E\in P_k(E), \forall E\in {\mathcal {E}}_h\}, \\ W_h^0=&W_h\cap L^2_0(\varOmega ). \end{aligned} \end{aligned}$$

(10)

WG finite element scheme in the strain-div formulation. The weak Galerkin $(P_k^2,P_k^2;AC_{k}^2,P_k)$ scheme in the strain-div formulation for the linear elasticity problem (1) is formulated as: Seek ${\textbf{u}}_h \in {\textbf{V}}_h$ such that ${\textbf{u}}_h|_{\varGamma _h^D} = {\textbf{Q}}_h^\partial ({\textbf{u}}_D)$ and

$$\begin{aligned} {\mathcal {A}}_h^{SD}({\textbf{u}}_h,{\textbf{v}}) = {\mathcal {F}}_h^{SD}({\textbf{v}}), \qquad \forall {\textbf{v}} \in {\textbf{V}}_h^0, \end{aligned}$$

(11)

where

$$\begin{aligned} \begin{array}{l} \displaystyle {\mathcal {A}}^{SD}_h({\textbf{u}}_h,{\textbf{v}}) = 2\mu \sum _{E \in {\mathcal {E}}_h} (\varepsilon _{w}({\textbf{u}}_h), \varepsilon _{w}({\textbf{v}}))_E + \lambda \sum _{E \in {\mathcal {E}}_h} (\nabla _w \cdot {\textbf{u}}_h, \nabla _w \cdot {\textbf{v}})_E, \end{array} \end{aligned}$$

(12)

and

$$\begin{aligned} \displaystyle {\mathcal {F}}_h^{SD}({\textbf{v}}) = \sum _{E \in {\mathcal {E}}_h} ({\textbf{f}}, {\textbf{v}}^\circ )_{E^\circ } + \sum _{\gamma \in \varGamma ^N_h} \langle {\textbf{t}}_N, {\textbf{v}}^\partial \rangle _{\gamma }. \end{aligned}$$

(13)

WG finite element scheme in the grad-div formulation. The weak Galerkin $(P_k^2,P_k^2;AC_{k}^2,P_k)$ scheme in the grad-div formulation for the linear elasticity problem (2) is formulated as: Seek ${\textbf{u}}_h \in {\textbf{V}}_h$ such that ${\textbf{u}}_h|_{\varGamma _h^D} = {\textbf{Q}}_h^\partial ({\textbf{u}}_D)$ and

$$\begin{aligned} {\mathcal {A}}_h^{GD}({\textbf{u}}_h,{\textbf{v}}) = {\mathcal {F}}_h^{GD}({\textbf{v}}), \qquad \forall {\textbf{v}} \in {\textbf{V}}_h^0, \end{aligned}$$

(14)

where

$$\begin{aligned} {\mathcal {A}}_h^{GD}({\textbf{u}}_h,{\textbf{v}}) = \mu \sum _{E \in {\mathcal {E}}_h} (\nabla _w {\textbf{u}}_h, \nabla _w {\textbf{v}})_E + (\mu +\lambda ) \sum _{E \in {\mathcal {E}}_h} (\nabla _w \cdot {\textbf{u}}_h, \nabla _w \cdot {\textbf{v}})_E, \end{aligned}$$

(15)

and

$$\begin{aligned} \displaystyle {\mathcal {F}}_h^{GD}({\textbf{v}}) = \sum _{E \in {\mathcal {E}}_h} ({\textbf{f}}, {\textbf{v}}^\circ )_{E^\circ }. \end{aligned}$$

(16)

Remarks

Now we introduce a semi-norm on the weak function space ${\textbf{V}}_h$ by

$$\begin{aligned} |||{\textbf{v}}|||^2 := \sum _{E\in {\mathcal {E}}_h}\Vert \nabla _w{\textbf{v}}\Vert _{E}^2. \end{aligned}$$

(17)

• (i) No penalty term is needed for either of the above two WG FE schemes.

• (ii) Both schemes can be applied to general convex quadrilateral meshes. But analysis is performed for the grad-div scheme only.

Lemma 2

The semi-norm $|||\cdot |||$ is a norm on space ${\textbf{V}}_h^0$.

Proof

For any scalar-valued functions $v^\circ \in P_k(E^\circ )$ and $v^\partial \in P_k(E^\partial )$ satisfying $\int _{E^\circ }v^\circ = \int _{E^\partial } v^\partial$, we consider ${\textbf{q}}\in AC_k(E)$ satisfying

$$\begin{aligned} \nabla \cdot {\textbf{q}}= & {} v^\circ , \end{aligned}$$

(18)

$$\begin{aligned} {\textbf{q}}\cdot {\textbf{n}}= & {} v^\partial . \end{aligned}$$

(19)

Since $\nabla \cdot {\textbf{q}}\in P_k(E^\circ )$, ${\textbf{q}}\cdot {\textbf{n}}\in P_k(E^\partial )$, and $\text{ dim }(AC_k(E))=(k+1)(k+3)+1 \; \text{ or } \; 2$ is more than or equal to $\frac{(k+1)(k+2)}{2}+4*(k+1)-1$, which is the number of the independent equations in (18)-(19), we claim that Problem (18)-(19) has at least one solution. This implies that for any ${\textbf{v}}^\circ \in P_k(E)^2$, we have a $\tau _0\in AC_k^2(E)$ such that

$$\begin{aligned} \displaystyle \nabla \cdot \tau _0 = {\textbf{v}}^\circ - \overline{{\textbf{v}}^\circ }, \quad \quad \tau _0{\textbf{n}} = {\textbf{0}}, \end{aligned}$$

where $\overline{{\textbf{v}}^\circ } = \frac{1}{|E|} \int _{E^\circ } {\textbf{v}} ^\circ$ is the average of function ${\textbf{v}}^\circ$ on $E^\circ$. Assume that $|||{\textbf{v}}|||=0$ for ${\textbf{v}}=\{{\textbf{v}}^\circ ,{\textbf{v}}^\partial \}\in {\textbf{V}}_h^0$. Then

$$\begin{aligned} \begin{array}{l} \displaystyle 0 = (\nabla _w{\textbf{v}},\tau _0)_E = \langle {\textbf{v}}^{\partial },\tau _0{\textbf{n}} \rangle _{E^{\partial }}-({\textbf{v}}^\circ ,\nabla \cdot \tau _0)_{E^\circ } \\ \quad \displaystyle = -({\textbf{v}}^\circ ,{\textbf{v}}^\circ - \overline{{\textbf{v}}^\circ })_{E^\circ } = -\Vert {\textbf{v}}^\circ - \overline{{\textbf{v}}^\circ }\Vert ^2_{E^\circ }. \end{array} \end{aligned}$$

This implies that ${\textbf{v}}^\circ = \overline{{\textbf{v}}^\circ }$. Then we arrive at

$$\begin{aligned} 0=\langle {\textbf{v}}^{\partial },\tau {\textbf{n}} \rangle _{E^{\partial }}-({\textbf{v}}^\circ ,\nabla \cdot \tau )_{E^\circ }= \langle {\textbf{v}}^\partial -{\textbf{v}}^\circ ,\tau {\textbf{n}}\rangle _{E^{\partial }}, \end{aligned}$$

for any $\tau \in AC_k^2(E)$. By taking $\tau =\tau _1$ such that $\tau _1{\textbf{n}}={\textbf{v}}^\partial -{\textbf{v}}^\circ$ in the above equation, we obtain ${\textbf{v}}^{\partial }={\textbf{v}}^{\circ }$, which means that ${\textbf{v}}$ is a constant vector. Moreover, since ${\textbf{v}}^\partial |_{\varGamma _h^D} = {\textbf{0}}$, we get ${\textbf{v}} = {\textbf{0}}$. So $|||\cdot |||$ is a norm in ${\textbf{V}}_h^0$. $\square$

Lemma 3

(Coercivity). There exists a positive constant $\alpha _1$ such that

$$\begin{aligned} \alpha _1|||{\textbf{v}}|||^2 \le {\mathcal {A}}_h^{GD}({\textbf{v}},{\textbf{v}}), \quad \forall {\textbf{v}}\in {\textbf{V}}_h^0. \end{aligned}$$

Theorem 1

The weak Galerkin finite element scheme (14) in the grad-div formulation has a unique solution.

Proof

This follows from Lemma 3 and the Lax-Milgram Theorem [13]. $\square$

5 Analysis

For ease of presentation, we consider the finite element scheme in the grad-div formulation with a homogeneous Dirichlet boundary condition. We use $A \lesssim B$ to denote $A \le C B$ with C being a generic positive constant that is independent of h and $\lambda$. The $L^2$-norms of the errors of displacement and stress, namely, $\Vert {\textbf{u}}-{\textbf{u}}_h\Vert$ and $\Vert \sigma -\sigma _h\Vert$, are also considered in this section.

5.1 Projection Operators and Some Preliminary Results

Definition 3

(Local projection operators). Let $E \in {\mathcal {E}}_{h}$. We define

• (i) $Q_h$ as the $L^2$-projection from $L^2(E)$ to the space $P_k(E)$;

• (ii) ${\textbf{Q}}_h=\{{\textbf{Q}}_h^\circ , {\textbf{Q}}_h^\partial \}$, where ${\textbf{Q}}_h^\circ$ is the local ${\textbf{L}}^2$-projection from $L^2(E^\circ )^2$ to the space of $P_k(E^\circ )^2$ and ${\textbf{Q}}_h^\partial$ is the local ${\textbf{L}}^2$-projection from $L^2(E^\partial )^2$ to the space of $P_k(E^\partial )^2$;

• (iii) ${\mathbb {Q}}_h$ as the local $L^2$-projection from $L^2(E)^{2\times 2}$ to the space of $AC_k^2(E)$.

Lemma 4

(Commuting identities). Let $E \in {\mathcal {E}}_h$.

• (i) For any ${{\textbf {u}}} \in H^1(E)^2$, there holds $\nabla _{w}({{\textbf {Q}}}_h{{\textbf {u}}}) = {\mathbb {Q}}_h(\nabla {{\textbf {u}}})$;

• (ii) For any ${{\textbf {u}}} \in H^1(E)^2$, there holds $\nabla _{w} \cdot ({{\textbf {Q}}}_h{{\textbf {u}}}) = Q_h(\nabla \cdot {{\textbf {u}}})$.

Proof

Applying the definition of the discrete weak gradient, integration by parts, and the definitions of the projection operators, we obtain, for any $\tau \in AC_k^2(E)$,

$$\begin{aligned} \begin{aligned} (\nabla _w({\textbf{Q}}_h{\textbf{u}}), \tau )_E&= \langle {\textbf{Q}}_h^\partial {\textbf{u}}, \tau {\textbf{n}} \rangle _{E^\partial } - ({\textbf{Q}}_h^\circ {\textbf{u}}, \nabla \cdot \tau )_{E^\circ } \\&= \langle {\textbf{u}}, \tau {\textbf{n}} \rangle _{E^\partial } - ({\textbf{u}}, \nabla \cdot \tau )_{E^\circ } \\&= (\nabla {\textbf{u}}, \tau )_E \\&= ({\mathbb {Q}}_h(\nabla {\textbf{u}}), \tau )_E, \end{aligned} \end{aligned}$$

(20)

which implies the 1st identity (i). The 2nd identity can be proved similarly. $\square$

From the fact that $||| \cdot |||$ defines a norm on ${\textbf{V}}_{h}^{0}$, we know that the discrepancy between the interior and edge values of a discrete weak function is bounded by this norm. A more precise statement is expressed in the lemma below.

Lemma 5

The following property holds true

$$\begin{aligned} \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{v}}^\partial -{\textbf{v}}^\circ \Vert ^2_{E^\partial } \lesssim |||{\textbf{v}}|||^2, \quad \forall {\textbf{v}}\in {\textbf{V}}_{h}^{0}. \end{aligned}$$

(21)

Proof

Let $E \in {\mathcal {E}}_h$. We list the degrees of freedom for space $AC_k^2(E)$ as follows.

$$\begin{aligned} \begin{array}{ll} \displaystyle \langle \tau {\textbf{n}},{\textbf{v}} \rangle _e, &{} \quad \forall \, {\textbf{v}}\in P_k(e)^2, \; \forall e \subset \partial E, \\ \displaystyle (\tau ,\nabla {\textbf{w}})_E, &{} \quad \forall \, {\textbf{w}}\in P_{k}(E)^2, \\ \displaystyle (\tau ,\nu )_E, &{} \quad \forall \, \nu \in {\mathbb {B}}_k^2(E), \end{array} \end{aligned}$$

where ${\mathbb {B}}_k^2(E)$ is a space of matrix-valued functions whose row vectors are in the space ${\mathbb {B}}_k(E)$ consisting of divergence-free bubble functions, see [1] for details. Denote by $D_{E,k}(e)$ the subspace of $AC_k^2(E)$ such that all degrees of freedom vanish except $(\tau {\textbf{n}})|_e$. It is known that $D_{E,k}(e)$ is a dual of $P_k(e)^2$. It is also known that

$$\begin{aligned} \displaystyle \Vert {\textbf{v}}^\partial - {\textbf{v}}^\circ \Vert _e = \sup _{\tau \in D_{E,k}(e)} \frac{\int _{e} ({\textbf{v}}^\partial - {\textbf{v}}^\circ ) \cdot (\tau {\textbf{n}})}{\Vert \tau {\textbf{n}}\Vert _e}. \end{aligned}$$

(22)

For $\tau \in D_{E,k}(e)$, by the definition of discrete weak gradient, we have

$$\begin{aligned} \displaystyle \int _{E}(\nabla _w{\textbf{v}}):\tau = \int _{e} ({\textbf{v}}^\partial - {\textbf{v}}^\circ ) \cdot (\tau {\textbf{n}}). \end{aligned}$$

Combining the Cauchy-Schwarz inequality and (22) with the fact that $\Vert \tau \Vert _E\lesssim h^{\frac{1}{2}}\Vert \tau {\textbf{n}}\Vert _e$ (see [14] for the scaling argument), we have

$$\begin{aligned} \Vert {\textbf{v}}^\partial -{\textbf{v}}^\circ \Vert _e \lesssim \sup _{\tau \in D_{E,k}(e)} \frac{\Vert \nabla _w{\textbf{v}}\Vert _E\Vert \tau \Vert _E}{\Vert \tau {\textbf{n}}\Vert _e} \lesssim h^{\frac{1}{2}}\Vert \nabla _w{\textbf{v}}\Vert _E. \end{aligned}$$

Summing the above inequality over all edges $e \subset E^\partial$ and all elements $E\in {\mathcal {E}}_h$, we complete the proof. $\square$

Lemma 6

Let $E \in {\mathcal {E}}_h$ and ${\textbf{v}} \in {\textbf{V}}_h$.

• (i) For any matrix $W\in {AC}^2_k(E)$, there holds

  $$\begin{aligned} (W, \nabla _{w}{{\textbf {v}}})_E = (W, \nabla {\textbf{v}}^\circ )_{E^\circ } + \langle W{\textbf{n}}, {{\textbf {v}}}^\partial -{\textbf{v}}^\circ \rangle _{E^\partial }. \end{aligned}$$

  (23)

• (ii) For any scalar $w\in W_h$, there holds

  $$\begin{aligned} (w, \nabla _{w}\cdot {{\textbf {v}}})_E = (w, \nabla \cdot {\textbf{v}}^\circ )_{E^\circ } + \langle w{{\textbf {n}}}, {{\textbf {v}}}^\partial -{{\textbf {v}}}^\circ \rangle _{E^\partial }. \end{aligned}$$

  (24)

Proof

First apply the definition of discrete weak gradient or discrete weak divergence for the discrete weak function ${\textbf{v}}$. Then apply integration by parts for W or w. $\square$

Lemma 7

Assume ${\textbf{u}}\in H^1(\varOmega )^2$ and ${{\textbf {v}}} \in {\textbf{V}}_h$. Let $E \in {\mathcal {E}}_h$. Then

$$\begin{aligned} \begin{array}{l} \displaystyle (\nabla _w({\textbf{Q}}_h{\textbf{u}}), \nabla _w{\textbf{v}})_E = (\nabla {\textbf{u}}, \nabla {\textbf{v}}^\circ )_{E^\circ } + \langle ({\mathbb {Q}}_h(\nabla {\textbf{u}})) {\textbf{n}}, {\textbf{v}}^\partial - {\textbf{v}}^\circ \rangle _{E^\partial }, \\ (\nabla _w \cdot (Q_h{\textbf{u}}), \nabla _w\cdot {\textbf{v}})_E = (\nabla \cdot {\textbf{u}}, \nabla \cdot {\textbf{v}}^\circ )_{E^\circ } + \langle (Q_h(\nabla \cdot {\textbf{u}})) {\textbf{n}}, {\textbf{v}}^\partial - {\textbf{v}}^\circ \rangle _{E^\partial }. \end{array} \end{aligned}$$

(25)

Proof

Applying Lemma 4(i), the definition of discrete weak gradient, integration by parts, and properties of the projection operators, we obtain

$$\begin{aligned} \begin{aligned} (\nabla _w({\textbf{Q}}_h{\textbf{u}}), \nabla _w{\textbf{v}})_E&= ({\mathbb {Q}}_h(\nabla {\textbf{u}}), \nabla _w{\textbf{v}})_E \\&= \langle {\mathbb {Q}}_h(\nabla {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\partial \rangle _{E^\partial } - (\nabla \cdot {\mathbb {Q}}_h(\nabla {\textbf{u}}), {\textbf{v}}^\circ )_{E^\circ } \\&= \langle {\mathbb {Q}}_h(\nabla {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\partial - {\textbf{v}}^\circ \rangle _{E^\partial } + ({\mathbb {Q}}_h(\nabla {\textbf{u}}), \nabla {\textbf{v}}^\circ )_{E^\circ } \\&= \langle {\mathbb {Q}}_h(\nabla {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\partial - {\textbf{v}}^\circ \rangle _{E^\partial } + (\nabla {\textbf{u}}, \nabla {\textbf{v}}^\circ )_{E^\circ }. \end{aligned} \end{aligned}$$

(26)

Similarly, we use Lemma 4(ii), the definition of discrete weak gradient, integration by parts, and projection properties to obtain the 2nd equality. $\square$

5.2 Error Equation and Error Estimates

Lemma 8

(Error equation). Let ${\textbf{u}} \in H^{k+2}(\varOmega )^2$ be the exact solution of (2) and ${\textbf{u}}_h \in {\textbf{V}}_h$ be the numerical solution of (14). There holds

$$\begin{aligned} {\mathcal {A}}_h^{GD}({\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}},{\textbf{v}}) = \mu \, {\mathcal {G}}_1({\textbf{u}}, {\textbf{v}}) + (\mu +\lambda ) \, {\mathcal {G}}_2({\textbf{u}}, {\textbf{v}}), \end{aligned}$$

(27)

where

$$\begin{aligned} {\mathcal {G}}_1({\textbf{u}},{\textbf{v}}) = \sum _{E\in {\mathcal {E}}_h} \langle (\nabla {\textbf{u}}-{\mathbb {Q}}_h\nabla {\textbf{u}}) {\textbf{n}}, {\textbf{v}}^\partial - {\textbf{v}}^\circ \rangle _{E^\partial } \end{aligned}$$

(28)

and

$$\begin{aligned} {\mathcal {G}}_2({\textbf{u}},{\textbf{v}}) = \sum _{E\in {\mathcal {E}}_h} \langle (\nabla \cdot {\textbf{u}} - Q_h(\nabla \cdot {\textbf{u}})) {\textbf{n}}, {\textbf{v}}^\partial - {\textbf{v}}^\circ \rangle _{E^\partial }. \end{aligned}$$

(29)

Proof

Let ${\textbf{v}} = \{ {\textbf{v}}^\circ , {\textbf{v}}^\partial \} \in {\textbf{V}}_h$. Testing Equation (2) with ${\textbf{v}}$ on each $E \in {\mathcal {E}}_h$, we obtain

$$\begin{aligned} \begin{array}{l} \displaystyle ({\textbf{f}},{\textbf{v}}^\circ )_{E^\circ } = (-\mu \varDelta {\textbf{u}}-(\mu +\lambda )\nabla (\nabla \cdot {\textbf{u}}), {\textbf{v}}^\circ )_{E^\circ } \\ \quad \displaystyle = - \mu \langle (\nabla {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\circ \rangle _{E^\partial } + \mu (\nabla {\textbf{u}}, \nabla {\textbf{v}}^\circ )_{E^\circ } \\ \quad \quad \displaystyle -(\mu +\lambda ) \langle (\nabla \cdot {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\circ \rangle _{E^\partial } + (\mu +\lambda ) (\nabla \cdot {\textbf{u}}, \nabla \cdot {\textbf{v}}^\circ )_{E^\circ }. \end{array} \end{aligned}$$

(30)

We sum the above result over the whole mesh. We also make an assumption on normal continuity of the exact solution across edges. Then a combination with the homogeneous Dirichlet boundary condition implies

$$\begin{aligned} \sum _{E\in {\mathcal {E}}_h}\langle (\nabla {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\partial \rangle _{E^\partial } = 0, \quad \quad \sum _{E\in {\mathcal {E}}_h}\langle (\nabla \cdot {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\partial \rangle _{E^\partial } = 0. \end{aligned}$$

(31)

Thus

$$\begin{aligned} \begin{array}{l} \displaystyle \sum _{E\in {\mathcal {E}}_h}({\textbf{f}},{\textbf{v}}^\circ )_{E^\circ } = \sum _{E\in {\mathcal {E}}_h}\left( \mu \langle (\nabla {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\partial -{\textbf{v}}^\circ \rangle _{E^\partial } + \mu (\nabla {\textbf{u}}, \nabla {\textbf{v}}^\circ )_{E^\circ }\right. \\ \quad \quad \displaystyle \left. +(\mu +\lambda ) \langle (\nabla \cdot {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\partial -{\textbf{v}}^\circ \rangle _{E^\partial } + (\mu +\lambda ) (\nabla \cdot {\textbf{u}}, \nabla \cdot {\textbf{v}}^\circ )_{E^\circ }\right) . \end{array} \end{aligned}$$

(32)

Combing these together with (25), we arrive at

$$\begin{aligned} \begin{aligned} {\mathcal {A}}_h^{GD}({\textbf{Q}}_h{\textbf{u}},{\textbf{v}})&=\sum _{E\in {\mathcal {E}}_h}({\textbf{f}},{\textbf{v}}^\circ )_E -\mu \sum _{E\in {\mathcal {E}}_h}\langle (\nabla {\textbf{u}} -{\mathbb {Q}}_h\nabla {\textbf{u}}){\textbf{n}},{\textbf{v}}^\partial -{\textbf{v}}^\circ \rangle _{E^\partial } \\ \displaystyle&-(\mu +\lambda )\sum _{E\in {\mathcal {E}}_h}\langle (\nabla \cdot {\textbf{u}} -Q_h(\nabla \cdot {\textbf{u}})){\textbf{n}},{\textbf{v}}^\partial -{\textbf{v}}^\circ \rangle _{E^\partial }. \end{aligned} \end{aligned}$$

(33)

Subtracting (33) from (14), we get

$$\begin{aligned} \begin{array}{l} \displaystyle {\mathcal {A}}_h^{GD}({\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}},{\textbf{v}}) = \mu \sum _{E\in {\mathcal {E}}_h}\langle (\nabla {\textbf{u}}-{\mathbb {Q}}_h\nabla {\textbf{u}}){\textbf{n}}, {\textbf{v}}^\partial -{\textbf{v}}^\circ \rangle _{E^\partial } \\ [0.10in] \quad \displaystyle + (\mu +\lambda )\sum _{E\in {\mathcal {E}}_h}\langle (\nabla \cdot {\textbf{u}} -Q_h(\nabla \cdot {\textbf{u}})){\textbf{n}}, {\textbf{v}}^\partial -{\textbf{v}}^\circ \rangle _{E^\partial }, \end{array} \end{aligned}$$

(34)

which is the error equation stated in the lemma. $\square$

Lemma 9

Assume ${\textbf{u}}\in H^{k+2}(\varOmega )^2$ and ${{\textbf {v}}} \in {\textbf{V}}_h$. Then

$$\begin{aligned} \begin{array}{l} {\mathcal {G}}_1({\textbf{u}},{\textbf{v}})\lesssim h^{k+1}\Vert {\textbf{u}}\Vert _{k+2}|||{\textbf{v}}|||, \\ {\mathcal {G}}_2({\textbf{u}},{\textbf{v}})\lesssim h^{k+1}\Vert \nabla \cdot {\textbf{u}}\Vert _{k+1}|||{\textbf{v}}|||. \end{array} \end{aligned}$$

(35)

Proof

It follows from the Cauchy-Schwarz inequality, an inverse estimate, a trace inequality, a projection inequality, and (21) that

$$\begin{aligned} \begin{aligned}&{\mathcal {G}}_1({\textbf{u}},{\textbf{v}}) = \sum _{E\in {\mathcal {E}}_h} \langle (\nabla {\textbf{u}}-{\mathbb {Q}}_h\nabla {\textbf{u}}) {\textbf{n}}, {\textbf{v}}^\circ -{\textbf{v}}^\partial \rangle _{E^\partial } \\&\le \left( \sum _{E\in {\mathcal {E}}_h}h\Vert \nabla {\textbf{u}} -{\mathbb {Q}}_h\nabla {\textbf{u}}\Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \left( \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{v}}^\partial -{\textbf{v}}^\circ \Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \\&\lesssim \left( \sum _{E\in {\mathcal {E}}_h}(\Vert \nabla {\textbf{u}} -{\mathbb {Q}}_h\nabla {\textbf{u}}\Vert ^2_{E}+h^2\Vert \nabla (\nabla {\textbf{u}} -{\mathbb {Q}}_h\nabla {\textbf{u}})\Vert ^2_{E}\right) ^{\frac{1}{2}} \\&\quad \quad \left( \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{v}}^\partial -{\textbf{v}}^\circ \Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \\&\lesssim h^{k+1}\Vert {\textbf{u}}\Vert _{k+2}||| {\textbf{v}}|||. \end{aligned} \end{aligned}$$

(36)

Similarly, we have

$$\begin{aligned} \begin{aligned}&{\mathcal {G}}_2({\textbf{u}},{\textbf{v}}) = \sum _{E\in {\mathcal {E}}_h} \langle (\nabla \cdot {\textbf{u}}-Q_h(\nabla \cdot {\textbf{u}})) {\textbf{n}}, {\textbf{v}}^\circ -{\textbf{v}}^\partial \rangle _{E^\partial } \\&\le \left( \sum _{E\in {\mathcal {E}}_h}h\Vert \nabla \cdot {\textbf{u}} -Q_h(\nabla \cdot {\textbf{u}})\Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \left( \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{v}}^\partial -{\textbf{v}}^\circ \Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \\&\lesssim \left( \sum _{E\in {\mathcal {E}}_h}(\Vert \nabla \cdot {\textbf{u}} -Q_h(\nabla \cdot {\textbf{u}})\Vert ^2_{E}+h^2\Vert \nabla (\nabla \cdot {\textbf{u}} -Q_h(\nabla \cdot {\textbf{u}}))\Vert ^2_{E}\right) ^{\frac{1}{2}} \\&\quad \quad \left( \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{v}}^\partial -{\textbf{v}}^\circ \Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \\[0.10in]&\lesssim h^{k+1}\Vert \nabla \cdot {\textbf{u}}\Vert _{k+1}| ||{\textbf{v}}|||, \end{aligned} \end{aligned}$$

(37)

which concludes the proof. $\square$

We assume that the exact solution ${\textbf{u}}\in H^{k+2}(\varOmega )^2$ and satisfies the following regularity estimate [13]

$$\begin{aligned} \Vert {\textbf{u}}\Vert _{k+2} + \lambda \Vert \nabla \cdot {\textbf{u}}\Vert _{k+1} \lesssim \Vert {\textbf{f}}\Vert _{k}. \end{aligned}$$

(38)

Theorem 2

Let ${\textbf{u}}\in H^{k+2}(\varOmega )^2$ be the exact solution of (2) and ${\textbf{u}}_h \in {\textbf{V}}_h$ be the numerical solution obtained from the finite element scheme (14). Then

$$\begin{aligned} \displaystyle \mu \sum _{E \in {\mathcal {E}}_h} \Vert \nabla {\textbf{u}} - \nabla _{w} {\textbf{u}}_h\Vert _E^2 + (\mu +\lambda ) \sum _{E \in {\mathcal {E}}_h} \Vert \nabla \cdot {\textbf{u}} - \nabla _{w} \cdot {\textbf{u}}_h\Vert _E^2 \lesssim h^{2(k+1)} \Vert {\textbf{f}}\Vert _{k}^2. \end{aligned}$$

(39)

Proof

Apply Lemma 4 (the commuting identities), we decompose the elementwise errors into the projection errors and the discretization errors as follows

$$\begin{aligned} \Vert \nabla {\textbf{u}} - \nabla _{w}{\textbf{u}}_h\Vert _E \lesssim \Vert \nabla {\textbf{u}} - {\mathbb {Q}}_h (\nabla {\textbf{u}})\Vert _E + \Vert {\mathbb {Q}}_h(\nabla {\textbf{u}}) - \nabla _{w}{\textbf{u}}_h\Vert _E, \\ \Vert \nabla \cdot {\textbf{u}} - \nabla _{w} \cdot {\textbf{u}}_h\Vert _E \lesssim \Vert \nabla \cdot {\textbf{u}} - Q_h (\nabla \cdot {\textbf{u}})\Vert _E + \Vert Q_h (\nabla \cdot {\textbf{u}}) - \nabla _{w} \cdot {\textbf{u}}_h\Vert _E. \end{aligned}$$

The projection errors are determined by the approximation capacity of the spaces $AC_k^2$ and $P_k$, respectively. In other words, we have

$$\begin{aligned} \begin{array}{l} \displaystyle \sum _{E \in {\mathcal {E}}_h}\Vert \nabla {\textbf{u}} - {\mathbb {Q}}_h (\nabla {\textbf{u}})\Vert _E^2 \lesssim h^{2(k+1)} \Vert {\textbf{u}}\Vert _{k+2}^2, \displaystyle \\ \displaystyle \sum _{E \in {\mathcal {E}}_h}\Vert \nabla \cdot {\textbf{u}} - Q_h (\nabla \cdot {\textbf{u}})\Vert _E^2 \lesssim h^{2(k+1)} \Vert \nabla \cdot {\textbf{u}}\Vert _{k+1}^2. \end{array} \end{aligned}$$

(40)

For the discretization errors between the finite element solution and the projection, we set ${\textbf{v}}={\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}}$ in (27) and then apply (36) and (37) to obtain

$$\begin{aligned} \begin{array}{l} \displaystyle \mu \sum _{E \in {\mathcal {E}}_h} \Vert {\mathbb {Q}}_h(\nabla {\textbf{u}}) - \nabla _{w}{\textbf{u}}_h\Vert _E^2 + (\mu +\lambda ) \sum _{E \in {\mathcal {E}}_h} \Vert Q_h (\nabla \cdot {\textbf{u}}) - \nabla _{w}\cdot {\textbf{u}}_h\Vert _E^2 \\ \quad \displaystyle \lesssim h^{k+1} \left( \mu \Vert {\textbf{u}}\Vert _{k+2} + (\mu +\lambda ) \Vert \nabla \cdot {\textbf{u}}\Vert _{k+1} \right) \left( \sum _{E \in {\mathcal {E}}_h} \Vert {\mathbb {Q}}_h(\nabla {\textbf{u}}) - \nabla _{w}{\textbf{u}}_h\Vert _E^2\right) ^{\frac{1}{2}}. \end{array} \end{aligned}$$

(41)

Under the assumption (38) and the fact that $\mu$ is bounded, we obtain

$$\begin{aligned} \sum _{E \in {\mathcal {E}}_h} \Vert {\mathbb {Q}}_h(\nabla {\textbf{u}}) - \nabla _{w}{\textbf{u}}_h\Vert _E^2 \lesssim h^{2(k+1)} \Vert {\textbf{f}}\Vert _{k}^2. \end{aligned}$$

(42)

Plugging (42) into (41), we get

$$\begin{aligned} (\mu +\lambda ) \sum _{E \in {\mathcal {E}}_h} \Vert Q_h (\nabla \cdot {\textbf{u}}) - \nabla _{w}\cdot {\textbf{u}}_h\Vert _E^2 \lesssim h^{2(k+1)} \Vert {\textbf{f}}\Vert _{k}^2. \end{aligned}$$

(43)

With the help of the assumption (38), the desired error estimate in the theorem follows from combining (40) and (42)-(43) through a triangle inequality

$$\begin{aligned}\begin{array}{rl} \displaystyle \mu \sum _{E \in {\mathcal {E}}_h} \Vert \nabla {\textbf{u}} - \nabla _{w} {\textbf{u}}_h\Vert _E^2 \lesssim &{} h^{2(k+1)}\Vert {\textbf{f}}\Vert _{k}^2, \\ \displaystyle (\mu +\lambda ) \sum _{E \in {\mathcal {E}}_h} \Vert \nabla \cdot {\textbf{u}} - \nabla _{w} \cdot {\textbf{u}}_h\Vert _E^2 \lesssim &{} h^{2(k+1)}\Vert {\textbf{f}}\Vert ^2_{k}, \end{array} \end{aligned}$$

which concludes the proof. $\square$

5.3 Error Estimates in the $L^2$-norm

Next we establish an $L^2$-norm estimate using a standard duality argument.

Lemma 10

Let ${\textbf{u}} \in H^{k+2}(\varOmega )^2$ be the exact solution of the PDE problem (2) and ${\textbf{u}}_h \in {\textbf{V}}_h$ be the numerical solution obtained from the finite element scheme (14). Let ${\textbf{e}}_h={\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}}$. Then there holds

$$\begin{aligned} \Vert {\textbf{e}}_h^\circ \Vert _0\lesssim h^{k+1} \Vert {\textbf{f}}\Vert _{k}. \end{aligned}$$

(44)

Proof

Assume that $\varPhi$ is the solution of the dual problem

$$\begin{aligned} -\mu \varDelta \varPhi - (\mu +\lambda ) \nabla (\nabla \cdot \varPhi )= & {} {\textbf{e}}_h^\circ , \end{aligned}$$

(45)

$$\begin{aligned} \varPhi |_{\varGamma _h^D}= & {} {\textbf{0}}. \end{aligned}$$

(46)

The following dual solution regularity holds true

$$\begin{aligned} \Vert \varPhi \Vert _2+\lambda \Vert \nabla \cdot \varPhi \Vert _1\lesssim \Vert {\textbf{e}}_h^\circ \Vert _0. \end{aligned}$$

(47)

Using ${\textbf{e}}_h^\circ$ to test the dual equation, we obtain

$$\begin{aligned} \begin{array}{l} \displaystyle \Vert {\textbf{e}}_h^\circ \Vert ^2 = \sum _{E\in {\mathcal {E}}_h}(\mu \nabla \varPhi ,\nabla {\textbf{e}}_h^\circ )_E + \sum _{E\in {\mathcal {E}}_h}((\mu +\lambda ) \nabla \cdot \varPhi ,\nabla \cdot {\textbf{e}}_h^\circ )_E \\ \quad \quad \displaystyle - \sum _{E\in {\mathcal {E}}_h} \langle \mu \nabla \varPhi {\textbf{n}},{\textbf{e}}_h^\circ \rangle _{E^\partial } - \sum _{E\in {\mathcal {E}}_h} \langle (\mu +\lambda ) \nabla \cdot \varPhi ,{\textbf{e}}_h^\circ {\textbf{n}}\rangle _{E^\partial }. \end{array} \end{aligned}$$

(48)

It follows from the commuting identities that

$$\begin{aligned}{} & {} {\mathcal {A}}_h^{GD}({\textbf{e}}_h,{\textbf{Q}}_h\varPhi )=\sum _{E\in {\mathcal {E}}_h} (\mu \nabla {\textbf{e}}_h^\circ ,\nabla \varPhi )_E+\sum _{E\in {\mathcal {E}}_h} \mu \langle {\textbf{e}}_h^\partial -{\textbf{e}}_h^\circ ,{\mathbb {Q}}_h\nabla \varPhi {\textbf{n}}\rangle _{E^\partial } \\{} & {} \quad +\sum _{E\in {\mathcal {E}}_h}(\mu +\lambda )(\nabla \cdot {\textbf{e}}_h^\circ , \nabla \cdot \varPhi )_E+\sum _{E\in {\mathcal {E}}_h}(\mu +\lambda )\langle {\textbf{e}}_h^\partial -{\textbf{e}}_h^\circ ,Q_h(\nabla \cdot \varPhi ){\textbf{n}}\rangle _{E^\partial }. \end{aligned}$$

Together with Lemma 8, this implies that

$$\begin{aligned} \Vert {\textbf{e}}_h^\circ \Vert ^2= & {} \sum _{E\in {\mathcal {E}}_h} \mu \langle (\nabla {\textbf{u}}-{\mathbb {Q}}_h\nabla {\textbf{u}}) {\textbf{n}}, {\textbf{Q}}_h^\partial \varPhi - {\textbf{Q}}_h^\circ \varPhi \rangle _{E^\partial } \\{} & {} +\sum _{E\in {\mathcal {E}}_h}(\mu +\lambda ) \langle (\nabla \cdot {\textbf{u}} - Q_h(\nabla \cdot {\textbf{u}})) {\textbf{n}}, {\textbf{Q}}_h^\partial \varPhi - {\textbf{Q}}_h^\circ \varPhi \rangle _{E^\partial } \\{} & {} -\sum _{E\in {\mathcal {E}}_h}\mu \langle {\textbf{e}}_h^\partial -{\textbf{e}}_h^\circ ,({\mathbb {Q}}_h\nabla \varPhi -\nabla \varPhi ){\textbf{n}}\rangle _{E^\partial } \\{} & {} -\sum _{E\in {\mathcal {E}}_h}(\mu +\lambda )\langle {\textbf{e}}_h^\partial -{\textbf{e}}_h^\circ ,(Q_h(\nabla \cdot \varPhi )-\nabla \cdot \varPhi ){\textbf{n}}\rangle _{E^\partial }. \end{aligned}$$

It follows from the Cauchy-Schwarz inequality, a trace inequality, and a projection inequality that

$$\begin{aligned}{} & {} \sum _{E\in {\mathcal {E}}_h} \langle (\nabla {\textbf{u}}-{\mathbb {Q}}_h\nabla {\textbf{u}}) {\textbf{n}}, {\textbf{Q}}_h^\partial \varPhi - {\textbf{Q}}_h^\circ \varPhi \rangle _{E^\partial } \\{} & {} \quad \le \left( \sum _{E\in {\mathcal {E}}_h}h\Vert \nabla {\textbf{u}}-{\mathbb {Q}}_h\nabla {\textbf{u}}\Vert ^2_{E^\partial }\right) ^{\frac{1}{2}}\left( \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{Q}}_h^\circ \varPhi -\varPhi \Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \\{} & {} \quad \lesssim h^k\Vert {\textbf{u}}\Vert _{k+1}h\Vert \varPhi \Vert _2 \lesssim h^{k+1}\Vert {\textbf{u}}\Vert _{k+1}\Vert {\textbf{e}}_h^\circ \Vert _0. \end{aligned}$$

Similarly, we have

$$\begin{aligned}{} & {} \sum _{E\in {\mathcal {E}}_h} \langle (\nabla \cdot {\textbf{u}} - Q_h(\nabla \cdot {\textbf{u}})) {\textbf{n}}, {\textbf{Q}}_h^\partial \varPhi - {\textbf{Q}}_h^\circ \varPhi \rangle _{E^\partial } \\{} & {} \quad \le \left( \sum _{E\in {\mathcal {E}}_h}h\Vert \nabla \cdot {\textbf{u}} - Q_h(\nabla \cdot {\textbf{u}})\Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \left( \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{Q}}_h^\circ \varPhi -\varPhi \Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \\{} & {} \quad \lesssim h^k\Vert \nabla \cdot {\textbf{u}}\Vert _{k}h\Vert \varPhi \Vert _2 \lesssim h^{k+1}\Vert \nabla \cdot {\textbf{u}}\Vert _{k}\Vert {\textbf{e}}_h^\circ \Vert _0. \end{aligned}$$

Using the Cauchy-Schwarz inequality, a trace inequality, a projection inequality, and (47), we obtain

$$\begin{aligned}{} & {} \sum _{E\in {\mathcal {E}}_h}\langle {\textbf{e}}_h^\circ -{\textbf{e}}_h^\partial , ({\mathbb {Q}}_h\nabla \varPhi -\nabla \varPhi ){\textbf{n}}\rangle _{E^\partial } \\{} & {} \quad \le \left( \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{e}}_h^ \circ -{\textbf{e}}_h^\partial \Vert _{E^\partial }^2\right) ^{\frac{1}{2}} \left( \sum _{E\in {\mathcal {E}}_h}h\Vert {\mathbb {Q}}_h\nabla \varPhi -\nabla \varPhi \Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \\{} & {} \quad \lesssim |||{\textbf{e}}_h| ||h\Vert \varPhi \Vert _2 \lesssim h^{k+1}(\Vert {\textbf{u}}\Vert _{k+2}+(\mu +\lambda ) \Vert \nabla \cdot {\textbf{u}}\Vert _{k+1})\Vert {\textbf{e}}_h^\circ \Vert _0. \end{aligned}$$

Similarly, we have

$$\begin{aligned}{} & {} \sum _{E\in {\mathcal {E}}_h}(\mu +\lambda )\langle {\textbf{e}}_h^\circ -{\textbf{e}}_h^\partial ,(Q_h(\nabla \cdot \varPhi )-\nabla \cdot \varPhi ){\textbf{n}}\rangle _{E^\partial } \\{} & {} \quad \le \left( \sum _{E\in {\mathcal {E}}_h}h^{-1}\Vert {\textbf{e}}_h^\circ -{\textbf{e}}_h^\partial \Vert _{E^\partial }^2\right) ^{\frac{1}{2}}(\mu +\lambda ) \left( \sum _{E\in {\mathcal {E}}_h}h\Vert Q_h(\nabla \cdot \varPhi )-\nabla \cdot \varPhi \Vert ^2_{E^\partial }\right) ^{\frac{1}{2}} \\{} & {} \quad \lesssim |||{\textbf{e}}_h| ||h(\mu +\lambda )\Vert \nabla \cdot {\textbf{u}}\Vert _1 \\{} & {} \quad \lesssim h^{k+1}(\Vert {\textbf{u}}\Vert _{k+2}+(\mu +\lambda ) \Vert \nabla \cdot {\textbf{u}}\Vert _{k+1})\Vert {\textbf{e}}_h^\circ \Vert _0. \end{aligned}$$

Then we have

$$\begin{aligned} \Vert {\textbf{e}}_h^\circ \Vert _0 \lesssim h^{k+1} \Big ( \Vert {\textbf{u}}\Vert _{k+2}+(\mu +\lambda ) \Vert \nabla \cdot {\textbf{u}}\Vert _{k+1} \Big ). \end{aligned}$$

(49)

Combined with assumption (38), this finishes the proof. $\square$

Theorem 3

($L^2$-norm estimates for displacement and stress). Let ${\textbf{u}}$ be the exact solution of the PDE problem (2) and ${\textbf{u}}_h$ be the numerical solution obtained from the finite element scheme (14). Then

$$\begin{aligned} \begin{aligned} \displaystyle \Vert {\textbf{u}}-{\textbf{u}}_h^\circ \Vert _{L^2(\varOmega )}&\lesssim h^{k+1} \Vert {\textbf{f}}\Vert _{k}, \\ \Vert \sigma -\sigma _h\Vert&\lesssim h^{k+1} \Vert {\textbf{f}}\Vert _{k}, \end{aligned} \end{aligned}$$

(50)

where the numerical stress is computed as $\sigma _h=2\mu \varepsilon _w({\textbf{u}}_h)+\lambda (\nabla _w\cdot {\textbf{u}}_h){\mathbb {I}}$.

Proof

Applying the projection property and (44) with a triangle inequality, we arrive at

$$\begin{aligned} \Vert {\textbf{u}}-{\textbf{u}}_h^\circ \Vert _{L^2(\varOmega )}\le \Vert {\textbf{u}} -{\textbf{Q}}_h^\circ {\textbf{u}}\Vert _{L^2(\varOmega )}+\Vert {\textbf{Q}}_h^\circ {\textbf{u}} -{\textbf{u}}_h^\circ \Vert _{L^2(\varOmega )} \lesssim h^{k+1}\Vert {\textbf{f}}\Vert _{k}. \end{aligned}$$

From the definition of discrete weak divergence, we know that $\nabla _w\cdot ({\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}})\in L^2_0(\varOmega )$. There is a function $\zeta \in {\textbf{H}}_0^1(\varOmega )$ such that

$$\begin{aligned} \begin{array}{l} \nabla \cdot \zeta =\nabla _w\cdot ({\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}}), \\ \Vert \zeta \Vert _1\le \Vert \nabla _w\cdot ({\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}})\Vert . \end{array} \end{aligned}$$

Then from Lemma 8 and Lemma 9, we derive

$$\begin{aligned} \begin{array}{l} \displaystyle \lambda \Vert \nabla _w\cdot ({\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}})\Vert ^2 \\ \quad \displaystyle = \lambda \sum _{E\in {\mathcal {E}}_h}(\nabla _w\cdot ({\textbf{u}}_h -{\textbf{Q}}_h{\textbf{u}}),\nabla _w\cdot ({\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}}))_E \\ \quad \displaystyle = \lambda \sum _{E\in {\mathcal {E}}_h}(\nabla _w\cdot ({\textbf{u}}_h -{\textbf{Q}}_h{\textbf{u}}),Q_h(\nabla \cdot \zeta ))_E \\ \quad \displaystyle = \lambda \sum _{E\in {\mathcal {E}}_h}(\nabla _w\cdot ({\textbf{u}}_h -{\textbf{Q}}_h{\textbf{u}}),\nabla _w\cdot ({\textbf{Q}}_h\zeta ))_E \\ \quad \displaystyle \le {\mathcal {A}}_h^{GD}({\textbf{e}}_h,{\textbf{Q}}_h\zeta ) -\mu \sum _{E\in {\mathcal {E}}_h}(\nabla _w({\textbf{u}}_h -{\textbf{Q}}_h{\textbf{u}}),\nabla _w({\textbf{Q}}_h\zeta ))_E \\ \quad \displaystyle \lesssim h^{k+1}\Vert {\textbf{f}}\Vert _{k}\Vert \zeta \Vert _1. \end{array} \end{aligned}$$

Combining Theorem 2 with (40)(ii) and (38), we obtain

$$\begin{aligned} \begin{aligned} \displaystyle \Vert \sigma -\sigma _h\Vert&\lesssim \Vert \nabla {\textbf{u}}-\nabla _w{\textbf{u}}_h\Vert + \lambda \left( \Vert \nabla \cdot {\textbf{u}}-Q_h\nabla \cdot {\textbf{u}}\Vert + \Vert \nabla _w\cdot ({\textbf{u}}_h-{\textbf{Q}}_h{\textbf{u}})\Vert \right) \\ \displaystyle&\lesssim h^{k+1}\Vert {\textbf{f}}\Vert _{k}, \end{aligned} \end{aligned}$$

which finishes the proof. $\square$

6 Numerical Experiments

This section presents numerical experiments on three widely tested examples to demonstrate the convergence rates and usefulness of the WG finite element solvers developed in this paper.

Example 1

(Locking-free). This example is adopted from [12]. Similar problems have been tested in [15, 25]. Here $\varOmega =(0,1)^2$, $\lambda =1$ or $\lambda =10^6$, and $\mu =1$. A Dirichlet boundary condition is specified on the whole boundary using a known exact solution for the displacement

$$\begin{aligned} \displaystyle {\textbf{u}} = \left[ \begin{array}{r} -(1-\cos (2\pi x) )\sin (2 \pi y) \\ (1-\cos (2\pi y)) \sin (2 \pi x) \end{array} \right] + \frac{1}{1+\lambda } \left[ \begin{array}{c} \sin (\pi x) \sin (\pi y) \\ \sin (\pi x) \sin (\pi y) \\ \end{array} \right] . \end{aligned}$$

(51)

We solve the linear elasticity problem using the WG$(P_k^2,P_k^2;AC_k^2,P_k)$ methods with $k=0,1$ on a sequence of uniform rectangular meshes. The numerical results shown in Tables 1 and 2 clearly exhibit optimal order $(k+1)$ convergence rates in the $L^2$-norms of the errors in displacement, dilation, and stress. The convergence rates do not deteriorate for large $\lambda$ values.

Table 1 Example 1: Results of WG $(P_0^2,P_0^2;AC_0^2,P_0)$ solver on uniform rectangular meshes

Table 2 Example 1: Results of WG $(P_1^2,P_1^2;AC_1^2,P_1)$ solver on uniform rectangular meshes

Example 2

(Low regularity). This example is similar to [25] Example 2. Specifically, we have an L-shaped domain with vertices at (0, 0) , (1, 1) , (0, 2) , $(-2,0)$, $(0,-2)$, $(1,-1)$. A Dirichlet boundary condition is posed on the boundary of the whole domain using a known exact solution for displacement as shown below

$$\begin{aligned} {\textbf{u}} = \Big [ A\cos \theta - B\sin \theta , \; A\sin \theta + B\cos \theta \Big ]^T, \end{aligned}$$

(52)

where $(r,\theta )$ are the polar coordinates and

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle A = \frac{r^\alpha }{2\mu } \Big ( -(1+\alpha )\cos ((1+\alpha )\theta ) + C_1 (C_2-(1+\alpha )) \cos ((1-\alpha )\theta ) \Big ), \\ \displaystyle B = \frac{r^\alpha }{2\mu } \Big ( (1+\alpha ) \sin ((1+\alpha )\theta ) - C_1 (C_2-(1-\alpha )) \sin ((1-\alpha )\theta ) \Big ), \end{array} \right. \end{aligned}$$

(53)

with $\alpha , C_1, C_2$ being some constants. The most important constant is the critical exponent $\alpha \approx 0.544483$. More details about the analytical expressions for the dilation and stress can be found in [25]. It is known from [6, 46] that the exact solution has low regularity

$$\begin{aligned} {\textbf{u}} \in (H^{1+\alpha -\varepsilon }(\varOmega ))^2, \quad \quad \sigma \in (H^{\alpha -\varepsilon }(\varOmega ))^{2 \times 2} \end{aligned}$$

for any small $\varepsilon >0$. Furthermore, we have (for the same small $\varepsilon >0$)

$$\begin{aligned} {\textbf{u}}_D \in (H^{\alpha +\frac{1}{2}-\varepsilon }(\partial \varOmega ))^2. \end{aligned}$$

Other physical parameters take values $E = 10^5$ and $\nu = 0.3$.

Table 3 Example 2 ($\nu =0.3$): Results of WG$(P_0^2,P_0^2;AC_0^2,P_0)$ solver on quadrilateral meshes

The low regularity implies that, from an approximation theory viewpoint, there is really no need to use higher order finite elements. For numerical solutions, we use quadrilateral meshes that align with the domain boundary. So we are utilizing the AC spaces that are indeed different than the Raviart-Thomas spaces used in [25].

The numerical errors reported in Table 3 from applying the lowest-order WG$(P_0^2,P_0^2;AC_0^2,P_0)$ solver clearly demonstrate the 1st order convergence in displacement, since constant vectors are used in the WG scheme for approximating the displacement. The convergence rate for the errors in stress or dilation each approaches 0.544, which reflects the critical exponent or the regularity order of the exact solution. The corner singularity in stress is also faithfully captured by our new WG method, as demonstrated in Fig. 1. Since the exact solution has low regularity, there is no need for applying the higher order method WG$(P_1^2,P_1^2;AC_1^2,P_1)$.

Fig. 1

Example 2 with $\nu =0.3$: Profiles of numerical stress obtained from applying the WG$(P_0^2,P_0^2;AC_0^2,P_0)$ solver with $h=1/32$. Left: Numerical normal stress $\sigma ^h_{yy}$; Right: Numerical shear stress $\sigma ^h_{xy}$

Fig. 2

Example 3 illustration: a A plate with a circular hole; b The first quadrant of the plate

Example 3

(A square plate with a circular hole). Ideally, we should consider an infinite isotropic elastic plate with a circular hole at the center that has radius a. Assume a horizontal traction with magnitude S is posed on the far-left and far-right sides, whereas the top and bottom sides are traction-free. Due to symmetry, we consider only the first quadrant of this plate. See Fig. 2 for an illustration of the problem.

The exact solution for the displacement in the Cartesian coordinates is known as [47]

$$\begin{aligned} \begin{array}{l} \displaystyle u_1 = \frac{a}{8\mu } \left( \frac{r}{a}(\kappa +1)\cos \theta + 2\frac{a}{r} \Big ( {(}\kappa +1)\cos \theta + \cos (3\theta ) \Big ) - 2\frac{a^3}{r^3}\cos (3\theta ) \right) , \\ \displaystyle u_2 = \frac{a}{8\mu } \left( \frac{r}{a}(\kappa -3)\sin \theta + 2\frac{a}{r} \Big ({(}1-\kappa )\sin \theta + \sin (3\theta ) \Big ) - 2\frac{a^3}{r^3}\sin (3\theta ) \right) , \end{array} \end{aligned}$$

(54)

where $\kappa = 3-4\nu$. The exact solution for the stress in Cartesian coordinates is [10, 11]

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \sigma _{xx} = \frac{S}{2} \left( 2 - 3\frac{a^2}{r^2}\cos 2\theta +(-2\frac{a^2}{r^2}+3\frac{a^4}{r^4})\cos 4\theta \right) , \\ \displaystyle \sigma _{yy} = \frac{S}{2} \left( \quad - \frac{a^2}{r^2}\cos 2\theta +(2\frac{a^2}{r^2}-3\frac{a^4}{r^4})\cos 4\theta \right) , \\ \displaystyle \sigma _{xy} = \frac{S}{2} \left( \quad - \frac{a^2}{r^2}\sin 2\theta +(-2\frac{a^2}{r^2}+3\frac{a^4}{r^4})\sin 4\theta \right) . \end{array} \right. \end{aligned}$$

(55)

When expressed in the polar coordinates, the stress components are [36]

$$\begin{aligned} \left\{ \begin{array}{l} \displaystyle \sigma _{rr} = \frac{S}{2} \left( 1-\frac{a^2}{r^2} \right) + \frac{S}{2} \left( 1-4\frac{a^2}{r^2}+3\frac{a^4}{r^4} \right) \cos (2\theta ), \\ \displaystyle \sigma _{\theta \theta } = \frac{S}{2} \left( 1+\frac{a^2}{r^2} \right) - \frac{S}{2} \left( 1+3\frac{a^4}{r^4}\right) \cos (2\theta ), \\ \displaystyle \sigma _{r\theta } = - \frac{S}{2} \left( 1+2\frac{a^2}{r^2}-3\frac{a^4}{r^4} \right) \sin (2\theta ). \end{array} \right. \end{aligned}$$

(56)

Indeed, the mechanical quantities of interest decay fast as one moves away from the center of the hole, i.e., the origin [36, 47]. Far away from the hole (as $r \rightarrow \infty$), we have

$$\begin{aligned} \sigma _{rr} = S \cos ^2\theta , \quad \sigma _{\theta \theta } = S \sin ^2\theta , \quad \sigma _{r\theta } = -S \cos \theta \sin \theta . \end{aligned}$$

(57)

But on the rim of the circular hole, we have

$$\begin{aligned} \sigma _{rr} = 0, \quad \sigma _{\theta \theta } = S (1-2\cos (2\theta )), \quad \sigma _{r\theta } = 0. \end{aligned}$$

(58)

Clearly, as one travels on the rim from $\theta =0$ via $\frac{\pi }{4}$ to $\frac{\pi }{2}$, the stress $\sigma _{\theta \theta }$ changes from $-S$ via S to $3\,S$.

It is useful, especially for numerical experiments, to know the stress component conversion formulas between the Cartesian and polar coordinates, as shown below

$$\begin{aligned} \left[ \begin{array}{l} \sigma _{rr} \\ \sigma _{\theta \theta } \\ \sigma _{r\theta } \end{array} \right] = \left[ \begin{array}{rccrccr} \cos ^2\theta &{}&{}&{} \sin ^2\theta &{}&{}&{} \sin (2\theta ) \\ \sin ^2\theta &{}&{}&{} \cos ^2\theta &{}&{}&{} -\sin (2\theta ) \\ -\cos \theta \sin \theta &{}&{}&{} \cos \theta \sin \theta &{}&{}&{} \cos (2\theta ) \end{array} \right] \left[ \begin{array}{c} \sigma _{xx} \\ \sigma _{yy} \\ \sigma _{xy} \end{array} \right] . \end{aligned}$$

(59)

Fig. 3

Example 3: Quadrilateral meshes (numbers of partitions $N_r, N_\theta$) are used for numerical experiments

To apply FEMs, we restrict this quadrant to a square with side-length A. Furthermore,

• (i) No body force is presented to the system, i.e., ${\textbf{f}} = (0,0)$.

• (ii) There is a Neumann boundary condition ${\textbf{t}}_N = (1,0)$ on the right boundary.

• (iii) Due to symmetry of the problem, a partial Dirichlet boundary condition $u_1 = 0$ (for displacement ${\textbf{u}}=(u_1,u_2)$) is posed on the left boundary $x=0$; whereas a partial Dirichlet boundary condition $u_2 = 0$ is posed on the bottom boundary $y=0$.

• (iv) No boundary condition is posed on the rim or the top side of the plate.

For numerical experiments, we set $a=1$, $A = 10$, $S=1$, and $\nu =0.499$.

Fig. 4

Example 3 (circular hole radius $a=1$, Poisson ratio $\nu = 0.499$). Results by WG$AC_0$ with $N_r=N_\theta =32$: a Numerical displacement and dilation; b Exact stress $\sigma _{\theta \theta }$ and numerical stress $\sigma _{\theta \theta }^h$ on the rim

Fig. 5

Example 3 (circular hole radius $a=1$, Poisson ratio $\nu = 0.499$). Results by the WG$AC_0$ solver with $N_r=N_\theta =32$: a Numerical stress $\sigma _{\theta \theta }^h$ over the whole mesh; b Numerical stress $\sigma _{xx}^h$ over the whole mesh

Figure 4 shows results obtained from applying the WG$(P_0^2,P_0^2;AC_0^2,P_0)$ solver on a mesh with $N_r=N_\theta =32$. Panel (a) shows numerical displacement and dilation; Panel (b) shows the exact stress $\sigma _{\theta \theta }$ along with the numerical stress $\sigma _{\theta \theta }^h$ on the rim. From Panel (b), it is observed that the numerical stress approximates the exact stress very well. On the rim,

• When $\theta = 0$, the numerical stress $\sigma _{\theta \theta }^h$ approaches to $-1$.

• When $\theta = \frac{\pi }{2}$, the numerical stress $\sigma _{\theta \theta }^h$ approaches to 3.

• In between when $\theta = \frac{\pi }{4}$, the numerical stress $\sigma _{\theta \theta }^h$ approaches to 1.

These numerical results capture the features of the exact stress shown in (58).

Figure 5 shows numerical stresses in polar and Cartesian (calculated at element centers), respectively. It is clear from Panel (b) that $\sigma _{xx}^h$ is very close to the value 1 along the right side, reflecting the traction condition ${\textbf{t}}_N = (1,0)$.

7 Concluding Remarks

In this paper, we have developed a family of penalty-free any-order weak Galerkin finite element methods for linear elasticity on convex quadrilateral meshes. A complete account of rigorous analysis is presented to validate the locking-free property and optimal order convergence rates (in displacement, stress, and dilation) of the new methods. This claim is further supported by numerical experiments on several popular test examples.

It is clear that the methods in this paper are more efficient than those based on the WG$(Q_k^2,Q_k^2;RT_{[k]}^2,Q_k)$ elements [25], since the new methods use less degrees of freedom and apply to more general quadrilateral meshes.

Extension to cuboidal hexahedral meshes. The WG methods developed in this paper can be extended to 3-dim by utilizing the Arbogast-Tao spaces $AT_k (k \ge 0)$ constructed in [2]. Here we use $AT_0$ to briefly explain the main ideas. Let E be a cuboidal hexahedron. It is known that $\text{ dim }(AT_0)=6$. Shown below is a local basis for $AT_0$:

$$\begin{aligned} \left[ \begin{array}{c} 1\\ 0\\ 0 \end{array} \right] , \;\; \left[ \begin{array}{c} 0\\ 1\\ 0 \end{array} \right] , \;\; \left[ \begin{array}{c} 0\\ 0\\ 1 \end{array} \right] , \;\; \left[ \begin{array}{c} X\\ Y\\ Z \end{array} \right] , \;\; {\mathcal {P}}_E \left[ \begin{array}{c} {\hat{x}} \\ -{\hat{y}} \\ 0 \end{array} \right] , \;\; {\mathcal {P}}_E \left[ \begin{array}{c} 0 \\ {\hat{y}} \\ -{\hat{z}} \end{array} \right] , \end{aligned}$$

(60)

where X, Y, Z are the normalized coordinates, ${\hat{x}}, {\hat{y}}, {\hat{z}}$ are the coordinates for the reference element unit cubic, and ${\mathcal {P}}_E$ is the Piola mapping. Based on this, we define $AT_0^3$ as the space of all $3 \times 3$ matrices whose rows are in $AT_0$.

The finite element methods developed in this paper have been implemented in Matlab and the code modules are included in our package DarcyLite, which is publicly available at the 3rd author’s webpage. Efficient implementation of these methods on the deal.II platform is currently being investigated and will be reported in our future work.

Clearly, the WG discretization for linear elasticity developed in this paper can be combined with the WG solvers for Darcy flow investigated in [32] to develop penalty-free any order solvers for poroelasticity problems. This is currently under our investigation and will also be reported in our future work.