Consistent $\overline {\boldsymbol {C}}$ Element-Free Galerkin Method for Finite Strain Analysis

Abstract

We introduce both distinct quadrature and distinct polynomial degrees for the deviatoric and volumetric terms of the right Cauchy-Green tensor in the context of a Lagrangian-based element-free Galerkin (EFG) discretization. First and second derivatives of the mixed deformation gradient are made available. A finite element mesh is employed for quadrature purposes with the corresponding distribution of Gauss points. In terms of discretization, linear, quadratic, and cubic polynomials are combined, and support is determined from the number of pre-assigned nodes. Due to the adoption of a Lagrangian kernel, finite strain elastoplastic constitutive developments are based on the Mandel stress. These developments are found to be especially convenient from the implementation perspective, as EFG formulations for finite strain plasticity have been limited in terms of generality and amplitude of deformations in both compressible and quasi-incompressibility cases. Three benchmark tests are successfully solved, and it was found that a combination of cubic and quadratic bases provides superior results in the quasi-incompressible case. Besides absence of locking with selective interpolation, outstanding Newton convergence was observed regardless of strain levels.

1 Introduction

Simulations of engineering material processing technology are supported by elastoplastic analyses. Two constitutive requirements are important in this context: (1) the quality of the stress values present in the yield functions depends on the smoothness of the displacements and crucially on mesh distortion [1] and (2) quasi-incompressibility conditions in metal plasticity and polymers are difficult to satisfy with reasonable support sizes in meshless methods [2]. Compared with displacements, errors in stresses are a magnitude higher, even without accounting for incompressibility. High-order (quadratic and cubic) finite elements are typically not adopted in finite strain elastoplastic analysis due to well-known shortcomings:

• High-order elements are adversely impacted by mesh distortion. Convergence rate is changed by distortion [1]. Adaptive remeshing is required more often with high-order elements.

• Problems requiring high-order derivatives impose dedicated techniques or isogeometric formulations [3].

• Although stress quality improves with the order of the complete polynomial, in finite element methods, stresses are still discontinuous at inter-element boundaries [4]. Plasticity results are dependent on the quality of the stresses, which is compromised even in high-order finite elements.

• The use of finite elements for quasi-incompressible problems requires specialized techniques (see, for example, [5,6,7]).

Note that Rabczuk, Belytschko, and Xiao [8] proved that a Lagrangian kernel is required for stability,¹ but classical finite strain plasticity algorithms (e.g., [9, 10]) combined with EFG are based on configuration updating (see [11]). A comprehensive presentation of developments in meshless methods (including EFG) was recently published by J.-S. Chen et al. [12]. A related development combining partition of unity and least squares is described in Cai et al. [13]. Several remedies are described, in particular for boundary conditions. Therefore, meshless methods, in particular with quadratic and cubic bases and satisfying the Kronecker delta condition, perfectly fit these applications:

• Since no isoparametric mapping is used, mesh distortion sensitivity is attenuated with respect to finite elements.

• Stresses are continuous, as long as all terms participating in the shape functions are differentiable.

• Contact algorithms are relatively simplified.

• Quasi-incompressibility can be directly addressed by changing the polynomial basis.

• Strain localization problems can be directly addressed via strain-gradient methods.

Several applications have been published with meshless discretization for finite strain plasticity [11], but not at the same scale of finite elements. The reputation for difficult-to-impose boundary conditions still affects EFG, although developments in interpolation have resurrected interest in the question of the Kronecker delta property (see [14]). In contrast with finite strain plasticity, hyperelastic implementations of EFG are common, and recent papers report realistic results with high degree of continuity (see [15]). In this paper are the following:

A newly developed fully anisotropic elastoplastic framework based on the iteration for C _e [16] does not require the explicit form of the deformation gradient. This motivates a revisiting of the moving least squares/EFG approach. Another effect that is often reported in the context of EFG is the volumetric locking in quasi-incompressible applications, [11, 17]. This is addressed here by the following techniques:

• Selective quadrature for the right Cauchy-Green tensor C, with reduced quadrature in $\det \boldsymbol {C}$ and full quadrature in $\widehat {\boldsymbol {C}}=\det \left [\boldsymbol {C}\right ]^{-{1}/{3}}\boldsymbol {C}$

• Selective interpolation for these terms, with a higher-order polynomial being adopted for $\widehat {\boldsymbol {C}}$

In terms of discretization, this work adopts the following techniques:

• Ab initio definition of the shape functions and derivatives for the entire analysis.

• Parameterized quadrature and interpolation functions for the deviatoric and volumetric parts of the right Cauchy-Green tensor C.

• Quasi-singular weight functions (see [18,19,20]).

• Quadrature points are defined in tetrahedra.

• Lagrangian diffuse derivatives are adopted.

• Constitutive integration making use of the Mandel stress tensor and iteration on C _e [16].

Volumetric locking has been diagnosed in element-free Galerkin methods by Dolbow and Belytschko [21] where a mixed displacement-pressure formulation was proposed in the small strain case. Within the RKPM family of W.K. Liu’s group, a pressure projection method was proposed, where pressure is re-interpolated using fewer points and a specific patch [22]. Applications were made with incompressible hyperelasticity. More conventional F-bar formulations have been used in the context of particle methods with explicit integration by Wu et al. [23]. In the small strain case, Recio , Jorge and Dinis [24] have applied $\overline {B}$ and Enhanced strain techniques to an EFG formulation. For implicit integration, an incremental finite deformation version was adopted by Coombs et al. [25]. In neither of these papers the closed-form expressions for the equilibrium and Jacobian were presented in the finite strain case. In the incremental case (see [25]), expressions are significantly simplified, and results for moderate plastic deformations are shown in that paper. In Moutsanidis et al. [26], an F-bar implementation is presented for the conforming reproducing kernel method. Navas et al. [27], in order to avoid the locking involved in the fluid phase of the porous media, devised a B-bar algorithm.

This paper is organized as follows: Sect. 2 presents the interpolation, based on moving least squares and diffuse derivatives, as well as the algorithm to guarantee a sufficiently small support radius. Section 3 presents the discretization based on the total Lagrangian approach, including the partition of C with its first and second variations. This is followed by Sect. 4 where the constitutive integration, fitting the developments of Sect. 3, is described in detail. In Sect. 5, three benchmark tests are presented, and finally conclusions are drawn in Sect. 6.

2 Interpolation

2.1 General Approach for Moving Least Squares

Interpolation with a polynomial basis and least squares fitting was introduced by P. Lancaster and K. Salkauskas [18]. Herein, classical derivations are followed (see [19, 28, 29]). We introduce m as the number of terms in the polynomial basis, n as the number of supporting nodes, and D as support radius. For a given node K, , the distance to a given point with coordinates X is identified as $s_{K}\left (\boldsymbol {X}\right )$. Let us consider a q −tuple of nonnegative integers $\boldsymbol {\alpha }=(\alpha _{1},\ldots ,\alpha _{q})\in \mathbb {N}_{0}^{q}$. We write the absolute value as the sum $|\boldsymbol {\alpha |}=\sum _{i=1}^{q}\alpha _{i}.$ We consider the set of all polynomials of degree equal or less than p as:

$$\displaystyle \begin{aligned} \mathcal{P}_{p}=\left\{ p_{\alpha}\left(\boldsymbol{X}\right)=X_{1}^{\alpha_{1}}\cdots X_{q}^{\alpha_{q}}\,|\,|\boldsymbol{\alpha|}\leq p\right\} .{} \end{aligned} $$

(1)

We now introduce a polynomial basis as an array of elements of $\mathcal {P}_{p}$:

$$\displaystyle \begin{aligned} \boldsymbol{p}(\boldsymbol{X})=\{p_{1}\left(\boldsymbol{X}\right),p_{2}\left(\boldsymbol{X}\right),\cdots,p_{m}\left(\boldsymbol{X}\right)\}\quad p_{i}\in\mathcal{P}_{p}{} \end{aligned} $$

(2)

with $\#\boldsymbol {q}\left (\boldsymbol {X}\right )={\left (p+q\right )!}/{p!q!}=m$. We therefore use m elements of $\mathcal {P}$ for the polynomial basis. The direct form (2) is known to produce conditioning difficulties. Therefore, we adopt a normalized and shifted form using a complete basis:

$$\displaystyle \begin{aligned} \boldsymbol{p}\left(\boldsymbol{X}\right) & =\left\{ 1,\frac{\left(X_{1}-\overline{X}_{1}\right)}{D},\frac{\left(X_{2}-\overline{X}_{2}\right)}{D},\frac{\left(X_{3}-\overline{X}_{3}\right)}{D},\right.{}\\ & \frac{\left(X_{1}-\overline{X}_{1}\right)\left(X_{2}-\overline{X}_{2}\right)}{D^{2}},\frac{\left(X_{1}-\overline{X}_{1}\right)\left(X_{3}-\overline{X}_{3}\right)}{D^{2}},\frac{\left(X_{2}-\overline{X}_{2}\right)\left(X_{3}-\overline{X}_{3}\right)}{D^{2}}, \\ & \left.\frac{\left(X_{1}-\overline{X}_{1}\right)^{2}}{D^{2}},\frac{\left(X_{2}-\overline{X}_{2}\right)^{2}}{D^{2}},\frac{\left(X_{3}-\overline{X}_{3}\right)^{2}}{D^{2}},\cdots\right\} . \end{aligned} $$

(3)

We use $\overline {\boldsymbol {X}}$ as a centroid of the nodes within the D −radius of X. Given a point with coordinates X, the approximation weight of another point with coordinates X _I depends on the distance between the points $s_{I}\left (\boldsymbol {X}\right )=\left \Vert \boldsymbol {X}-\boldsymbol {X}_{I}\right \Vert .$ The notation $w\left [s_{I}\left (\boldsymbol {X}\right )\right ]$ is introduced to represent this weight function of X. From this basis, an m × n P Vandermonde matrix is defined by its elements as follows:

$$\displaystyle \begin{aligned} P_{iJ}=p_{i}\left(\boldsymbol{X}_{J}\right)\quad i=1,\ldots,m,\qquad J=1,\ldots,n{} \end{aligned} $$

(4)

The components of weight matrix, which is a function of the supporting points and the coordinates X, are given by:

$$\displaystyle \begin{aligned} W_{IJ}(\boldsymbol{X})=\delta_{IJ}w\left[s_{I}\left(\boldsymbol{X}\right)\right]\qquad I,J=1,\ldots,n{} \end{aligned} $$

(5)

Applying the traditional least squares arguments [28] leads to the following format for the n-dimensional shape function array $\boldsymbol {N}\left (\boldsymbol {X}\right )$:

$$\displaystyle \begin{aligned} \boldsymbol{N}\left(\boldsymbol{X}\right)=\boldsymbol{p}(\boldsymbol{X})\cdot\boldsymbol{A}^{-1}\left(\boldsymbol{X}\right)\cdot\boldsymbol{B}\left(\boldsymbol{X}\right){} \end{aligned} $$

(6)

where $\boldsymbol {A}\left (\boldsymbol {X}\right )$ is the m × m moment matrix $\boldsymbol {A}\left (\boldsymbol {X}\right )=\boldsymbol {B}\left (\boldsymbol {X}\right )\cdot \boldsymbol {P}^{T}$ and $\boldsymbol {B}\left (\boldsymbol {X}\right )$ is the m × n linear combination matrix $\boldsymbol {B}\left (\boldsymbol {X}\right )=\boldsymbol {P}\cdot \boldsymbol {W}\left (\boldsymbol {X}\right )$. We make use of the Q ⋅R decomposition of $\sqrt {\boldsymbol {W}\left (\boldsymbol {X}\right )}\cdot \boldsymbol {P}^{T}$:

$$\displaystyle \begin{aligned} \sqrt{\boldsymbol{W}\left(\boldsymbol{X}\right)}\cdot\boldsymbol{P}^{T}=\boldsymbol{Q}\left(\boldsymbol{X}\right)\cdot\boldsymbol{R}\left(\boldsymbol{X}\right){} \end{aligned} $$

(7)

where $\boldsymbol {Q}\left (\boldsymbol {X}\right )$ is an orthogonal matrix and $\boldsymbol {R}\left (\boldsymbol {X}\right )$ is an upper triangular matrix [30]. A classical Gram-Schmidt algorithm for the Q ⋅R decomposition is used (see [31]). For our application, only $\boldsymbol {R}\left (\boldsymbol {X}\right )$ is required. It is straightforward to obtain, from (6), the final form of the shape function array:

$$\displaystyle \begin{aligned} \boldsymbol{N}\left(\boldsymbol{X}\right)=\boldsymbol{p}(\boldsymbol{X})\cdot\boldsymbol{R}^{-1}\left(\boldsymbol{X}\right)\cdot\boldsymbol{R}^{-T}\left(\boldsymbol{X}\right)\cdot\boldsymbol{B}\left(\boldsymbol{X}\right).{} \end{aligned} $$

(8)

Therefore, this operation is relatively inexpensive since it consists of two triangular solves. Omitting the dependence on X, we have:

$$\displaystyle \begin{aligned} \boldsymbol{R}^{T}\cdot\boldsymbol{U} & _{1}=\boldsymbol{B}{} \end{aligned} $$

(9)

$$\displaystyle \begin{aligned} \boldsymbol{R}\cdot\boldsymbol{U}_{2} & =\boldsymbol{U}_{1}{} \end{aligned} $$

(10)

where U ₂ is a m × n matrix, which suffices to define the shape functions. Reintroducing the dependence on X, the result is:

$$\displaystyle \begin{aligned} \boldsymbol{N}\left(\boldsymbol{X}\right)=\boldsymbol{p}\left(\boldsymbol{X}\right)\cdot\boldsymbol{U}_{2}\left(\boldsymbol{X}\right).{} \end{aligned} $$

(11)

The interpolated value $\phi \left (\boldsymbol {X}\right )$ is obtained by linear combination of nodal values $\boldsymbol {\phi =}\left \{ \phi _{1},\phi _{2},\cdots ,\phi _{n}\right \}$ $\phi \left (\boldsymbol {X}\right )=\boldsymbol {N}\left (\boldsymbol {X}\right )\cdot \boldsymbol {\phi }$. In terms of components, Eq. (6) is written as:

$$\displaystyle \begin{aligned} N_{L}\left(\boldsymbol{X}\right)=p_{j}\left(\boldsymbol{X}\right)U_{2jL}\left(\boldsymbol{X}\right)\qquad L=1,\ldots,n;\quad j,k=1,\ldots,m{} \end{aligned} $$

(12)

First derivative of N _L(X) with respect to coordinates X _m, m = 1, 2, 3 is here denoted as:

$$\displaystyle \begin{aligned} N_{L}^{\prime}\left(\boldsymbol{X}\right)= & p_{j}^{\prime}\left(\boldsymbol{X}\right)U_{2jL}\left(\boldsymbol{X}\right) \\ - & p_{j}\left(\boldsymbol{X}\right)A_{jl}^{-1}\left(\boldsymbol{X}\right)A_{lp}^{\prime}\left(\boldsymbol{X}\right)U_{2pL}\left(\boldsymbol{X}\right) \\ + & p_{j}\left(\boldsymbol{X}\right)A_{jk}^{-1}\left(\boldsymbol{X}\right)B_{kL}^{\prime}\left(\boldsymbol{X}\right){} \end{aligned} $$

(13)

where:

$$\displaystyle \begin{aligned} B^{\prime}_{kL}\left(\boldsymbol{X}\right) & =P_{kJ}W^{\prime}_{JL}\left(\boldsymbol{X}\right){} \end{aligned} $$

(14)

$$\displaystyle \begin{aligned} A^{\prime}_{lp}\left(\boldsymbol{X}\right) & =B^{\prime}_{lL}\left(\boldsymbol{X}\right)P_{pL}.{} \end{aligned} $$

(15)

In terms of $p^{\prime }_{j}\left (\boldsymbol {X}\right )$ and $W^{\prime }_{JI}\left (\boldsymbol {X}\right )$, Eq. (13) can be written as a sum of two terms:

(16a)

where:

$$\displaystyle \begin{aligned} N_{L}^{\star}\left(\boldsymbol{X}\right)=p^{\prime}_{j}\left(\boldsymbol{X}\right)U_{2jL}\left(\boldsymbol{X}\right){} \end{aligned} $$

(16b)

and:

(16c)

It is a tradition to identify (16b) as the diffuse derivative (see Nayroles, Touzot, and Villon [32]).

2.2 Quasi-Singular Weight Function

Singular weight functions are known to produce an interpolation satisfying the Kronecker delta property [18]. Quasi-singular functions have been adopted to approximate this property [19]. The following quasi-singular weight function is introduced (see, for example, [19, 20]):

$$\displaystyle \begin{aligned} w\left[s_{I}\left(\boldsymbol{X}\right)\right]=\begin{cases} \left[{s_{I}^{2}\left(\boldsymbol{X}\right)}/{D^{2}}+\mbox{tol}^{2}\right]^{-1}-\left[1+\mbox{tol}^{2}\right]^{-1} & s_{I}\leq D\\ 0 & s_{I}>D \end{cases}{} \end{aligned} $$

(17)

where $\mbox{tol}\in \mathbb {R}^{+}$ is a tolerance parameter. The maximum value of $w\left [s_{I}\right ]$ is obtained as:

$$\displaystyle \begin{aligned} w[0]=1/(\mbox{tol}^{2}+\mbox{tol}^{4}).{} \end{aligned} $$

(18)

Here, we adopt tol = 1 × 10⁻³. The Kronecker delta property is approximately satisfied:

$$\displaystyle \begin{aligned} N_{I}\left(\boldsymbol{X}_{J}\right)\cong\delta_{IJ}.{} \end{aligned} $$

(19)

Derivatives of $w\left [s_{I}\right ]$ with respect to s _I are trivially given by

$$\displaystyle \begin{aligned} \frac{\mathrm{d} w\left[s_{I}\right]}{\mathrm{d} s_{I}} & =-\frac{2D^{2}s_{I}}{\left(D^{2}\mbox{tol}^{2}+s_{I}^{2}\right)^{2}}.{} \end{aligned} $$

(20)

Strong versions of this weighting are available (see M. Dehghan, [33]) but involve an intricate implementation.

3 Discrete Equilibrium Equations

In finite element technology, two papers introduced a consistent formulation for the so-called mean dilatation technique [6, 34] which was invented by Nagtegaal et al. [35]. A straightforward total Lagrangian implementation is followed (see, for example, [36]). We make use of the definition of the right Cauchy-Green tensor:

$$\displaystyle \begin{aligned} \boldsymbol{C}\left(\boldsymbol{X}_{h}\right)=\boldsymbol{F}^{T}\left(\boldsymbol{X}\right)\cdot\boldsymbol{F}\left(\boldsymbol{X}\right).{} \end{aligned} $$

(21)

A partition into volumetric and deviatoric parts is required for selective quadrature. Omitting the dependence on X _h, the derivatoric Cauchy-Green tensor follows from the Flory [37] decomposition:

$$\displaystyle \begin{aligned} \widehat{\boldsymbol{C}}=\det\left[\boldsymbol{C}\right]^{-{1}/{3}}\boldsymbol{C}.{} \end{aligned} $$

(22)

Introducing the variation symbol δ and taking advantage of the symmetry of C, the variation of $\widehat {\boldsymbol {C}}$ is calculated as (see also Appendix Section “First and Second Variations of $\det \left [\boldsymbol {C}\right ]$”):

$$\displaystyle \begin{aligned} \delta\widehat{\boldsymbol{C}}=\left(\det\left[\boldsymbol{C}\right]^{-{1}/{3}}\mathcal{I}-\frac{1}{3}\widehat{\boldsymbol{C}}\otimes\boldsymbol{C}^{-1}\right):\delta\boldsymbol{C}{} \end{aligned} $$

(23)

where $\mathcal {I}$ is the symmetric fourth-order identity tensor, i.e., . This variation will be required later in the formation of the weak form of equilibrium. Newton-Raphson iteration requires the second variation of $\widehat {\boldsymbol {C}}$. For the second variation of $\widehat {\boldsymbol {C}}$, we adopt the time derivative notation, which results in:

$$\displaystyle \begin{aligned} \delta\dot{\widehat{\boldsymbol{C}}}= & \left(\det\left[\boldsymbol{C}\right]^{-{1}/{3}}\mathcal{I}-\frac{1}{3}\widehat{\boldsymbol{C}}\otimes\boldsymbol{C}^{-1}\right):\delta\dot{\boldsymbol{C}} \\ + & \dot{\boldsymbol{C}}:\left(-\frac{1}{3}\det\left[\boldsymbol{C}\right]^{-{4}/{3}}\boldsymbol{C}^{-1}\otimes\mathcal{I}\right):\delta\boldsymbol{C} \\ + & \dot{\boldsymbol{C}}:\left(\frac{1}{9}\widehat{\boldsymbol{C}}\otimes\boldsymbol{C}^{-1}\otimes\boldsymbol{C}^{-1}-\frac{1}{3}\det\left[\boldsymbol{C}\right]^{-{1}/{3}}\mathcal{I}\otimes\boldsymbol{C}^{-1}\right):\delta\boldsymbol{C} \\ + & \dot{\boldsymbol{C}}:{\mathtt{T}}:\delta\boldsymbol{C}{} \end{aligned} $$

(24)

where T is a sixth-order tensor which is defined in terms of components as:

$$\displaystyle \begin{aligned} {\left[\mathsf{T}\right]}_{mnijkl}=\frac{1}{3}C_{km}^{-1}C_{nl}^{-1}\widehat{C}_{ij}.{} \end{aligned} $$

(25)

Given the decomposition, we assume an independent $\det \left [\boldsymbol {\overline {C}}\right ]$ which we denote as $\theta _{C}=\det \left [\boldsymbol {\overline {C}}\right ].$ In this case, we define a combined right Cauchy-Green tensor:

$$\displaystyle \begin{aligned} \boldsymbol{C}_{\star}=\left(\frac{\theta_{C}}{\det\left[\boldsymbol{C}\right]}\right)^{{1}/{3}}\boldsymbol{C}.{} \end{aligned} $$

(26)

Interpolation for $\overline {\boldsymbol {C}}$ makes use of a lower-order polynomial and/or fewer quadrature points. The specific form (26) was proposed by Simo et al. [6] with a clear significance: in the context of low-order finite elements, to replace an over-constrained imposition of $\det \left [\boldsymbol {C}\right ]\cong 1$ by an independent field θ _C. Here, $\overline {\boldsymbol {C}}$ can follow a distinct quadrature rule or a distinct interpolation. The first variation of C _⋆ is calculated as:

$$\displaystyle \begin{aligned} \delta\boldsymbol{C}_{\star}=\left(\frac{\theta_{C}}{\det\left[\boldsymbol{C}\right]}\right)^{{1}/{3}}\delta\boldsymbol{C}+\frac{1}{3}\left[\left(\boldsymbol{C}_{\star}\otimes\overline{\boldsymbol{C}}^{-1}\right):\delta\overline{\boldsymbol{C}}-\left(\boldsymbol{C}_{\star}\otimes\boldsymbol{C}^{-1}\right):\delta\boldsymbol{C}\right].{} \end{aligned} $$

(27)

Using the time derivative notation, an analogous form is obtained:

$$\displaystyle \begin{aligned} \dot{\boldsymbol{C}}_{\star}=\left(\frac{\theta_{C}}{\det\left[\boldsymbol{C}\right]}\right)^{{1}/{3}}\dot{\boldsymbol{C}}+\frac{1}{3}\left[\left(\boldsymbol{C}_{\star}\otimes\overline{\boldsymbol{C}}^{-1}\right):\dot{\overline{\boldsymbol{C}}}-\left(\boldsymbol{C}_{\star}\otimes\boldsymbol{C}^{-1}\right):\dot{\boldsymbol{C}}\right].{} \end{aligned} $$

(28)

The time derivative of δ C _⋆ is obtained from (27) as:

$$\displaystyle \begin{aligned} \delta\dot{\boldsymbol{C}}_{\star}= & -\dot{\theta}_{C}\frac{2}{9}\theta_{C}^{-{5}/{3}}\widehat{\boldsymbol{C}}\delta\theta_{C}-\frac{1}{3}\theta_{C}^{-{2}/{3}}\widehat{\boldsymbol{C}}\delta\dot{\theta}_{C}\\ + & \frac{1}{3}\theta_{C}^{-{2}/{3}}\left(\dot{\theta}_{C}\delta\widehat{\boldsymbol{C}}+\delta\theta_{C}\dot{\widehat{\boldsymbol{C}}}\right)+\theta_{C}^{{1}/{3}}\delta\dot{\widehat{\boldsymbol{C}}.} \end{aligned} $$

These expressions are error-prone to implement manually and therefore have been implemented in Mathematica [38] with the AceGen add-on, developed by Korelc [39]. The Mathematica sheets and corresponding Fortran 90 source codes are available in GitHub (see [40]). For a given point X _h with discrete support $\Omega _{\boldsymbol {X}_{h}}$, we have:

$$\displaystyle \begin{aligned} \boldsymbol{F}\left(\boldsymbol{X}_{h}\right)=\frac{\mathrm{d}\boldsymbol{x}_{h}}{\mathrm{d}\boldsymbol{X}_{h}}=\sum_{L\in\Omega_{\boldsymbol{X}_{h}}}\left(\frac{\mathrm{d} N_{L}\left(\boldsymbol{X}_{h}\right)\boldsymbol{x}_{L}}{\mathrm{d}\boldsymbol{X}_{h}}\right).{} \end{aligned} $$

(29)

In terms of components and omitting the dependence on X _h, we obtain the components of F as:

$$\displaystyle \begin{aligned} F_{ij}=\frac{\mathrm{d} N_{L}}{\mathrm{d} X_{j}}x_{iL}.{} \end{aligned} $$

(30)

Using the variation symbol, δ, we introduce the variation of F, in the equilibrium sense, as:

$$\displaystyle \begin{aligned} \delta F_{ij}=\frac{\mathrm{d} N_{L}}{\mathrm{d} X_{j}}\delta x_{iL}.{} \end{aligned} $$

(31)

Introducing the notation N _jL = dN _L∕dX _j for the shape function derivatives, the following results for C and its first and second variations are obtained:

$$\displaystyle \begin{aligned} C_{ij} & =N_{iK}N_{jL}x_{kK}x_{kL}\Rightarrow\\ \delta C_{ij} & =N_{iK}N_{jL}\left(x_{kL}\delta x_{kK}+x_{kK}\delta x_{kL}\right)\\ \dot{C}_{ij} & =N_{iK}N_{jL}\left(x_{kL}\dot{x}_{kK}+x_{kK}\dot{x}_{kL}\right)\\ \delta\dot{C}_{ij} & =N_{iK}N_{jL}\left(\dot{x}_{kL}\delta x_{kK}+\dot{x}_{kK}\delta x_{kL}\right). \end{aligned} $$

Note that besides the node indices K and L, the index k is also muted. Equilibrium is established in a weak form by the use of the second Piola-Kirchhoff stress S _⋆ and the spatial configuration variation δ x:

$$\displaystyle \begin{aligned} \frac{1}{2}\int_{\Omega_{0}}\boldsymbol{S}_{\star}:\delta\boldsymbol{C}_{\star}\,\mathrm{d}\Omega_{0}\,=\,\boldsymbol{f}_{\mbox{ext}}\cdot\delta\boldsymbol{x}{} \end{aligned} $$

(32)

where $\boldsymbol {S}_{\star }\equiv \boldsymbol {S}_{\star }\left (\boldsymbol {C}_{\star }\right )$ where C _⋆ was calculated as shown in (27). For the application of Newton-Raphson iteration, we require the first variation of (32). As discussed previously, to avoid confusion with the variation symbol δ, we use the time derivative to denote the variation of equilibrium. By taking this time derivative variation, the tangent modulus $\mathcal {C}$ is employed to read:

$$\displaystyle \begin{aligned} \frac{1}{2}\int_{\Omega_{0}}\boldsymbol{S}_{\star}:\delta\dot{\boldsymbol{C}}_{\star}\:\mathrm{d}\Omega_{0}+\frac{1}{4}\int_{\Omega_{0}}\delta\boldsymbol{C}_{\star}:\mathcal{C}:\dot{\boldsymbol{C}}_{\star}\;\mathrm{d}\Omega_{0}=\boldsymbol{f}_{\mbox{ext}}\cdot\delta\boldsymbol{x}\,-\,\frac{1}{2}\int_{\Omega_{0}}\boldsymbol{S}_{\star}:\delta\boldsymbol{C}_{\star}\,\,\mathrm{d}\Omega_{0}{} \end{aligned} $$

(33)

where f _ext is the external load vector and is the nodal velocity vector. Note that in the implementation, the second derivative of C _⋆ is required in $\delta \dot {\boldsymbol {C}}_{\star }$. In Voigt form (see [41]), we have the following internal force and tangent stiffness:

$$\displaystyle \begin{aligned} \boldsymbol{f}_{L} & =\int_{\Omega_{0}}\boldsymbol{B}_{L}^{T}\cdot I_{6}\cdot\hat{\boldsymbol{S}}_{\star}\:\mathrm{d}\Omega_{0}{} \end{aligned} $$

(34)

$$\displaystyle \begin{aligned} \boldsymbol{K}_{KL} & =\int_{\Omega_{0}}\boldsymbol{B}_{K}^{T}\cdot I_{6}\cdot\mathcal{C}\cdot I_{6}\cdot\boldsymbol{B}_{L}\:\mathrm{d}\Omega_{0}+\int_{\Omega_{0}}\boldsymbol{\check{S}}_{\star}\cdot I_{6}\cdot\boldsymbol{B}_{L}^{\star}\:\mathrm{d}\Omega_{0}.{} \end{aligned} $$

(35)

Matrices B and B ^⋆ are implemented in [40], and I ₆ is a diagonal matrix containing 1 for indices 11 and 22 and 33 and 2 for indices 44, 55, and 66. In contrast with advanced finite element formulations [42, 43], these are classical and direct derivations. In addition, shape functions and corresponding derivatives are calculated once, at the start of the solution process.

4 Hyperelasticity/Plasticity Using the Elastic Mandel Stress Tensor

4.1 Formulation

The Mandel stress tensor approach to finite strain plasticity is adopted [44, 45]. We make use of the Kröner-Lee decomposition [46,47,48]:

$$\displaystyle \begin{aligned} \boldsymbol{F}=\boldsymbol{F}_{e}\cdot\boldsymbol{F}_{p}.{} \end{aligned} $$

(36)

Using (36), the velocity gradient is determined by its definition and then partitioned as follows:

$$\displaystyle \begin{aligned} \boldsymbol{L}=\dot{\boldsymbol{F}}\cdot\boldsymbol{F}^{-1}=\boldsymbol{L}_{e}+\boldsymbol{F}_{e}\cdot\boldsymbol{L}_{p}\cdot\boldsymbol{F}_{e}^{-1}{} \end{aligned} $$

(37)

with $\boldsymbol {L}_{e}=\dot {\boldsymbol {F}}_{e}\cdot \boldsymbol {F}_{e}^{-1}$ the elastic velocity gradient and $\boldsymbol {L}_{p}=\dot {\boldsymbol {F}}_{p}\cdot \boldsymbol {F}_{p}^{-1}$ the plastic velocity gradient. The second Piola-Kirchhoff stress is a function of the elastic part of F by means of $\boldsymbol {C}_{e}=\boldsymbol {F}_{e}^{T}\cdot \boldsymbol {F}_{e}$ (cf. [49] page 166), the second Piola-Kirchhoff stress at the intermediate configuration is given by $\boldsymbol {S}_{e}\left (\boldsymbol {C}_{e}\right )$ (see [50]), from which energy consistency results in a specific form for the second Piola-Kirchhoff stress $\boldsymbol {S}=\boldsymbol {F}_{p}^{-1}\cdot \boldsymbol {S}_{e}\left (\boldsymbol {C}_{e}\right )\cdot \boldsymbol {F}_{p}^{-T}$. In the hyperelastic case, a strain energy density function $\psi \left (\boldsymbol {C}_{e}\right )$ exists such as:

$$\displaystyle \begin{aligned} \boldsymbol{S}_{e}\left(\boldsymbol{C}_{e}\right)=2\dfrac{\mathrm{d}\psi\left(\boldsymbol{C}_{e}\right)}{\mathrm{d}\boldsymbol{C}_{e}}.{} \end{aligned} $$

(38)

The Neo-Hookean model is used, with the following strain energy density function:

$$\displaystyle \begin{aligned} \psi(\boldsymbol{\mathbf{C}}_{e})=\frac{\mu}{2}\left[\mathrm{tr}\left(\boldsymbol{\mathbf{C}}_{e}\right)-3\right]-\mu\log\sqrt{\det\left(\boldsymbol{\mathbf{C}}_{e}\right)}+\frac{\lambda}{2}\left[\log\sqrt{\det\left(\boldsymbol{\mathbf{C}}_{e}\right)}\right]^{2}.{} \end{aligned} $$

(39)

The flow law follows similar arguments [45], with the initial plastic deformation gradient corresponding to the identity, $\left [\boldsymbol {F}_{p}\right ]_{0}=\boldsymbol {I}$. Agreeing with standard derivations on plasticity, a yield function ϕ is introduced, as well as a plastic multiplier $\dot {\gamma }$. Introducing the notation $\boldsymbol {Q}_{p}=\boldsymbol {F}_{p}^{-1}$, we summarize the constitutive system as:

$$\displaystyle \begin{aligned} \boldsymbol{S} & =\boldsymbol{Q}_{p}\cdot\boldsymbol{S}_{e}\left(\boldsymbol{C}_{e}\right)\cdot\boldsymbol{Q}_{p}^{T}{} \end{aligned} $$

(40)

$$\displaystyle \begin{aligned} \dot{\boldsymbol{Q}}_{p} & =-\dot{\gamma}\boldsymbol{Q}_{p}\cdot\boldsymbol{N}\left[\boldsymbol{T}_{e}\right]{} \end{aligned} $$

(41)

$$\displaystyle \begin{aligned} \left[\boldsymbol{Q}_{p}\right]_{0} & =\boldsymbol{I}{} \end{aligned} $$

(42)

$$\displaystyle \begin{aligned} \prec\phi\left(\boldsymbol{T}_{e}\right)+\dot{\gamma}\succ & -\dot{\gamma}=0{} \end{aligned} $$

(43)

with being the unit ramp function. In (41), the Mandel stress [44] T _e is given by:

$$\displaystyle \begin{aligned} \boldsymbol{T}_{e}=\boldsymbol{C}_{e}\cdot\boldsymbol{S}_{e}\left(\boldsymbol{C}_{e}\right).{} \end{aligned} $$

(44)

Assuming an associated flow law [48], we have the flow vector $\boldsymbol {N}\left (\boldsymbol {T}_{e}\right )$ determined from the derivative of $\phi \left (\boldsymbol {T}_{e}\right )$:

$$\displaystyle \begin{aligned} \boldsymbol{\boldsymbol{N}}(\boldsymbol{T}_{e})={\mathrm{d}\phi\left(\boldsymbol{T}_{e}\right)}/{\mathrm{d}\boldsymbol{T}_{e}}.{} \end{aligned} $$

(45)

When hardening is present, power equivalence provides the effective plastic strain rate $\dot {\varepsilon }_{p}$ as a function of the yield stress σ _y:

$$\displaystyle \begin{aligned} \dot{\varepsilon}_{p}=\dot{\gamma}\frac{\boldsymbol{T}_{e}:\boldsymbol{\boldsymbol{N}}(\boldsymbol{T}_{e})}{\sigma_{y}}.{} \end{aligned} $$

(46)

4.2 Constitutive Integration

For the constitutive integration, we use superscripts n and n + 1 to identify two consecutive time steps and Δt as the time step size. Applying the backward Euler method for $\dot {\boldsymbol {Q}}_{p}$ and $\dot {\gamma }$ results in:

$$\displaystyle \begin{aligned} \boldsymbol{Q}_{p}^{n+1} & =\boldsymbol{Q}_{p}^{n}\cdot\left.\underbrace{\left[\boldsymbol{I}+\Delta\gamma\boldsymbol{\widehat{N}}\left(\boldsymbol{C}_{e}^{n+1}\right)\right]^{-1}}_{\left[\Delta\widehat{\boldsymbol{Q}}\left(\boldsymbol{C}_{e}^{n+1},\Delta\gamma\right)\right]^{-1}}\right.{} \end{aligned} $$

(47)

$$\displaystyle \begin{aligned} \gamma^{n+1} & =\gamma^{n}+\underbrace{\dot{\gamma}^{n+1}\Delta t}_{\Delta\gamma}. \end{aligned} $$

(48)

We now define the elastic trial Cauchy-Green tensor as $\boldsymbol {C}_{e}^{\star }=\left [\boldsymbol {Q}_{p}^{n}\right ]^{T}\cdot \boldsymbol {C}^{n+1}\cdot \boldsymbol {Q}_{p}^{n}$. Introducing the function $\widehat {\boldsymbol {C}}_{e}^{\star }\left (\boldsymbol {C}^{n+1}\right )=\left (\boldsymbol {Q}_{p}^{n}\right )^{T}\cdot \boldsymbol {C}^{n+1}\cdot \boldsymbol {Q}_{p}^{n}$, the constitutive system for Δγ > 0 consists of the following equations:

$$\displaystyle \begin{aligned} \underbrace{\left[\Delta\widehat{\boldsymbol{Q}}\left(\boldsymbol{C}_{e}^{n+1},\Delta\gamma\right)\right]^{T}\cdot\boldsymbol{C}_{e}^{n+1}\cdot\left[\Delta\boldsymbol{\widehat{Q}}\left(\boldsymbol{C}_{e}^{n+1},\Delta\gamma\right)\right]-\widehat{\boldsymbol{C}}_{e}^{\star}\left(\boldsymbol{C}^{n+1}\right)}_{\boldsymbol{r}_{c}\left(\boldsymbol{C}_{e}^{n+1},\Delta\gamma,\boldsymbol{C}^{n+1}\right)} & =\boldsymbol{0}{} \end{aligned} $$

(49)

$$\displaystyle \begin{aligned} \phi_{\star}\left[\boldsymbol{C}_{e}^{n+1}\cdot\hat{\boldsymbol{S}}_{e}\left(\boldsymbol{C}_{e}^{n+1}\right)\right] & =0.{} \end{aligned} $$

(50)

Since $\boldsymbol {C}_{e}^{n+1}$ is symmetric, Voigt notation can be used, ${\mathbf {C}}_{e}^{n+1}=\mbox{Voigt}\left [\boldsymbol {C}_{e}^{n+1}\right ]$ and ${\mathbf {r}}_{c}\left ({\mathbf {C}}_{e}^{n+1},\Delta \gamma ,{\mathbf {C}}^{n+1}\right )=\mathrm {Voigt}\left [\boldsymbol {r}_{c}\left (\boldsymbol {C}_{e}^{n+1},\Delta \gamma ,\boldsymbol {C}^{n+1}\right )\right ]$. Omitting the function arguments for conciseness, the Newton-Raphson iteration for ${\mathbf {C}}_{e}^{n+1}$ (Voigt form) and Δγ is written as:

$$\displaystyle \begin{aligned} \underbrace{\left[\begin{array}{cc} \frac{\partial{{\mathbf{r}}_{c}}}{\partial{\mathbf{C}}_{e}^{n+1}} & \frac{\partial{{\mathbf{r}}_{c}}}{\partial\Delta\gamma}\\ \frac{\partial\phi}{\partial{\mathbf{C}}_{e}^{n+1}} & 0 \end{array}\right]}_{\boldsymbol{J}}\underbrace{\left\{ \begin{array}{c} \Delta{\mathbf{C}}_{e}^{n+1}\\ \Delta\Delta\gamma \end{array}\right\} }_{\Delta{\mathbf{Y}}}=-\underbrace{\left\{ \begin{array}{c} {\mathbf{r}}_{c}\left({\mathbf{C}}_{e}^{n+1},\Delta\gamma,{\mathbf{C}}^{n+1}\right)\\ \phi_{\star}\left[{\mathbf{C}}_{e}^{n+1}\cdot\hat{\mathbf{S}}_{e}\left({\mathbf{C}}_{e}^{n+1}\right)\right] \end{array}\right\} }_{\boldsymbol{\mathbf{r}}}{} \end{aligned} $$

(51)

with $\mathbf {Y}=\left \{ \begin {array}{cc} {\mathbf {C}}_{e}^{n+1}\quad & \Delta \gamma \end {array}\right \} ^{T}$ being the constitutive unknowns for this problem. Following ${\mathbf {C}}_{e}^{n+1},$ $\boldsymbol {Q}_{p}^{n+1}$ is determined by (47), and the second Piola-Kirchhoff stress at step n + 1 is given in tensor notation by:

$$\displaystyle \begin{aligned} \check{\boldsymbol{\boldsymbol{S}}}^{n+1}\left(\underbrace{\boldsymbol{\mathbf{C}}_{e}^{n+1},\Delta\gamma}_{\mathbf{Y}}\right)&=\boldsymbol{Q}_{p}^{n}\cdot\left[\Delta\boldsymbol{\widehat{Q}}\left(\boldsymbol{\mathbf{C}}_{e}^{n+1},\Delta\gamma\right)\right]^{-1}\cdot\hat{\boldsymbol{\boldsymbol{S}}}_{e}\left(\boldsymbol{\mathbf{C}}_{e}^{n+1}\right)\\&\quad \cdot\left\{ \left[\Delta\boldsymbol{\widehat{Q}}\left(\boldsymbol{\mathbf{C}}_{e}^{n+1},\Delta\gamma\right)\right]^{-1}\right\} ^{T}\cdot\left(\boldsymbol{Q}_{p}^{n}\right)^{T}.{} \end{aligned} $$

(52)

Stress sensitivity, the determination of the consistent modulus, with ${\mathbf {S}}^{n+1}={Voigt{\$\left [\boldsymbol {S}^{n+1}\right ]\$}}$, is determined as follows:

$$\displaystyle \begin{aligned} \frac{\mathrm{d}{\mathbf{S}}^{n+1}}{\mathrm{d}{\mathbf{C}}^{n+1}}=\frac{\partial\boldsymbol{\widehat{\mathbf{S}}}^{n+1}}{\partial{\mathbf{C}}_{e}^{n+1}}\cdot\frac{\mathrm{d}{\mathbf{C}}_{e}^{n+1}}{\mathrm{d}{\mathbf{C}}^{n+1}}+\frac{\partial\boldsymbol{\widehat{\mathbf{S}}}^{n+1}}{\partial\Delta\gamma}\frac{\mathrm{d}\Delta\gamma}{\mathrm{d}{\mathbf{C}}^{n+1}}.{} \end{aligned} $$

(53)

In (53), a single product dot ⋅ is adopted for double contraction of quantities in Voigt form. From (53), we can conclude that $\mathcal {C}$ is determined as a function of the solution of (51), since:

$$\displaystyle \begin{aligned} {\mathrm{d}\mathbf{Y}}/{\mathrm{d}\mathbf{C}{}^{n+1}}=-\boldsymbol{J}^{-1}\cdot\frac{\partial\mathbf{r}}{\partial{\mathbf{C}}^{n+1}}{} \end{aligned} $$

(54)

therefore, stress sensitivity is simply given by:

$$\displaystyle \begin{aligned} \frac{\mathrm{d}{\mathbf{S}}^{n+1}}{\mathrm{d}{\mathbf{C}}^{n+1}}=-\left({\mathrm{d}{{\widehat{\mathbf{S}}}}^{n+1}}/{\mathrm{d}\mathbf{Y}}\right)\cdot\left({\mathrm{d}\mathbf{Y}}/{\mathrm{d}\mathbf{C}{}^{n+1}}\right).{} \end{aligned} $$

(55)

The effective plastic strain rate follows the integration of (46):

$$\displaystyle \begin{aligned} \varepsilon_{p}^{n+1}=\varepsilon_{p}^{n}+\Delta\gamma\frac{\boldsymbol{T}_{e}:\boldsymbol{N}(\boldsymbol{T}_{e})}{\sigma_{y}}.{} \end{aligned} $$

(56)

4.3 Specific Yield Function

The nondimensional yield function is given by:

$$\displaystyle \begin{aligned} \phi_{\star}\left(\boldsymbol{T}_{e}\right)=\frac{\sigma_{\mbox{eq}}\left(\boldsymbol{T}_{e}\right)}{\sigma_{y}}-1{} \end{aligned} $$

(57)

where, as a prototype equivalent stress, a specific Hill48 criterion (1948 [51]) is adopted. The general form of the Hill48 equivalent stress σ _eq is written as:

$$\displaystyle \begin{aligned} \sigma_{\mbox{eq}}\left(\boldsymbol{T}_{e}\right) & =\left[F\left(T_{22}-T_{33}\right)^{2}+G\left(T_{33}-T_{11}\right)^{2}+H\left(T_{11}-T_{22}\right)^{2}\right.{} \end{aligned} $$

(58)

$$\displaystyle \begin{aligned} & +\left.2S_{1}\left(T_{4}^{s}\right)^{2}+2S_{2}\left(T_{5}^{s}\right)^{2}+2S_{3}\left(T_{6}^{s}\right)^{2}\right]^{{1}/{2}} \end{aligned} $$

(59)

where the subscript e of T _e is omitted for conciseness. In (58), the superscript s is adopted to indicate a symmetrized quantity. For example, $T_{6}^{s}={1}/{2}\left (T_{23}+T_{32}\right ).$ Introducing the yield ratios, y = {y ₁, …, y ₆} as constitutive data, we have for F, G, H, S _1,…,3:

$$\displaystyle \begin{aligned} F & =\frac{1}{2}\left({1}/{y_{2}^{2}}+{1}/{y_{3}^{2}}-{1}/{y_{1}^{2}}\right){}\\ G & =\frac{1}{2}\left({1}/{y_{1}^{2}}+{1}/{y_{3}^{2}}-{1}/{y_{2}^{2}}\right) \\ H & =\frac{1}{2}\left({1}/{y_{1}^{2}}+{1}/{y_{2}^{2}}-{1}/{y_{3}^{2}}\right) \\ S_{k} & ={3}/{2\left(y_{k+3}^{2}\right)}\quad k=3,\ldots,6. \end{aligned} $$

(60)

We note that many other yield criteria can be used, since any specific form of $\sigma _{\mbox{eq}}\left (\boldsymbol {T}_{e}\right )$ can inserted.

5 Numerical Tests

Numerical tests were performed with the code from the leading author, SimPlas [52], and the specific source code for $\overline {C}-$EFG was created using Mathematica [38] with the AceGen add-on [36, 39]. Source code for the equations in this work is available via GitHub [40].

5.1 Straight Cantilever Beam with Closed-Form Solution

We start with the Timoshenko and Goodier [53] cantilever beam in small strain elasticity. Two values of the Poisson coefficient are adopted: ν = 0.3 and ν = 0.49999. The quasi-incompressible case is here specified with a plane strain assumption. A comparison with the MINI element by D. Arnold [5] is performed. The beam is represented in Fig. 1.

Fig. 1

Timoshenko and Goodier cantilever beam [53] with fixed support

We use the first slope boundary condition by Timoshenko and Goodier [53] who obtained the solution for the displacement in the plane stress case:

$$\displaystyle \begin{aligned} \boldsymbol{u}\left(x,y\right)=\frac{P}{4c^{3}E}\left\{ \begin{array}{c} \frac{E}{G}\left(y^{3}-3c^{2}y\right)+3y\left(l-x\right)\left(l+x\right)-\nu y^{3}\\ \left(l-x\right)^{2}\left(2l+x\right)+3\nu xy^{2} \end{array}\right\} . \end{aligned}$$

Introducing this solution into the strain components and making use of Hooke’s law, we calculate the strain energy per unit thickness as:

$$\displaystyle \begin{aligned} U=\frac{1}{2}\int_{0}^{l}\left[\int_{-c}^{+c}\left(\varepsilon_{xx}\sigma_{xx}+\varepsilon_{yy}\sigma_{yy}+\gamma_{xy}\tau_{xy}\right)\mathrm{d} y\right]\mathrm{d} x.{} \end{aligned} $$

(61)

The plane strain case is obtained replacing E by E∕1 − ν ² and ν by ν∕1 − ν. Strain energy per unit thickness is given by:

$$\displaystyle \begin{aligned} U_{{plane{\$\:{strain}\$}}}=\frac{P^{2}\left[6c^{2}El+5Gl^{3}\left(1-\nu^{2}\right)\right]}{20c^{3}GE}. \end{aligned} $$

$$\displaystyle \begin{aligned} U_{{plane{\$\:{stress}\$}}} & =\frac{P^{2}\left(6c^{2}El+5Gl^{3}\right)}{20c^{3}GE}. \end{aligned} $$

Results are given in Table 1 for both cases. This table also shows the converged results for h = 0.005 obtained with a mixed finite element formulation [52]. Only the plane strain case will be addressed, since it is more demanding in terms of convergence.

Table 1 Closed-form and converged solutions for the cantilever beam

Displacement results as a function of the characteristic mesh size h are summarized in Table 2, with the following cases being considered:

• 1. ν = 0.3 with full quadrature (3 Gauss points per triangle for both C and $\overline {\boldsymbol {C}}$).

• 2. ν = 0.49999 with full quadrature.

• 3. ν = 0.49999 with selective quadrature (3 Gauss points per triangle for C and 1 Gauss point for $\overline {\boldsymbol {C}}$).

Table 2 Timoshenko and Goodier cantilever beam: numerical results for v(0)

The following notation is adopted for the polynomials:

• 1. 1 ≤ p ₀ ≤ 3 is the degree of polynomial adopted for $\overline {\boldsymbol {C}}$.

• 2. 1 ≤ p ₁ ≤ 3 with p ₁ ≥ p ₀ is the degree of polynomial adopted for C.

From the observation of Table 2, we conclude that:

• 1. For the compressible case, all formulations behave acceptably, with the exception of p ₀ = p ₁ = 1 which results in excessive displacements. In addition, with p ₀ = p ₁ = 2, we can conclude that results are non-monotonous.

• 2. Using full quadrature for the quasi-incompressible case, two combinations exhibit severe volumetric locking: p ₀ = p ₁ = 1 and p ₀ = 1, p ₁ = 2.

• 3. Using selective quadrature for the quasi-incompressible case only p ₀ = 1, p ₁ = 2 exhibits locking. Both p ₀ = p ₁ = 3 and p ₀ = 2 and p ₁ = 3 are acceptable formulations.

Tip displacement error convergence is shown in Fig. 2 for ν = 0.3 and ν = 0.49999. The latter is considered with full and selective quadrature. Energy error convergence is determined for both the compressible and quasi-incompressible cases in Table 3 for p ₀ = 2 and p ₁ = 3.

Fig. 2

Timoshenko-Goodier cantilever beam: tip displacement convergence for ν = 0.3 and ν = 0.49999. Results from the MINI element [5] are also included for comparison. (a) ν = 0.3, full quadrature. (b) ν = 0.49999, full quadrature. (c) ν = 0.49999, selective quadrature

Table 3 Timoshenko and Goodier cantilever beam: numerical results for U in the plane strain case with selective quadrature and p ₀ = 2 and p ₁ = 3

5.2 Billet Upsetting Test

We make use of the upsetting test reported by M.A. Puso and J. Solberg [54] in its two elastoplastic versions (linear and power hardening). Geometry, boundary conditions, and constitutive properties are shown in Fig. 3. Three uniform meshes are adopted for comparison, containing 535, 868, and 3616 nodes. Nodes are forced to remain above a horizontal plane by a non-penetration condition. Of the two cases reported in [54], the elastoplastic case described is the most demanding, and it was found that only their nodal integrated and stabilized UT4s provided stable and accurate results. Using a cubic basis (p ₀ = p ₁ = 3), Fig. 4 shows the very smooth contour plots for ε _p and hydrostatic σ _H. All three factors contribute to a more flexible behavior: finer meshes are less stiff, larger supports produce softer behavior, and quadratic basis produces results beneath the reaction displacement curve reported in [54]. Using uniform quadrature and uniform interpolation, Fig. 5 shows the results compared with the reported in [54]. We test three basis dimensions: linear, quadratic, and cubic with n = 25. In terms of quadrature, both 1 and 4 Gauss points are tested. Reduced quadrature produces exceedingly flexible results, as shown in Fig. 5. This conclusion leads us to favor either full quadrature (4 points in both terms) or selective quadrature (4 points for the deviatoric terms and 1 point for the volumetric term). Focusing on the polynomial bases, Fig. 6 shows the effect of p ₀ and p ₁ on the displacement-reaction behavior. The following conclusions are taken:

Fig. 3

Billet upsetting test: relevant data and notation

Fig. 4

Upsetting test: contour plots (ε _p, S ₃₃) for the power-law hardening case and 535 nodes

Fig. 5

Upsetting test, linear hardening, n = 25: effect of dimension of polynomial basis for uniform quadrature/uniform basis

Fig. 6

Upsetting test, n = 25, effect of selective polynomial basis for the deviatoric (p ₁) and volumetric (p ₀) terms. Reduced quadrature. (a) Linear and quadratic bases. (b) Quadratic and cubic bases. (c)

• In contrast with displacement-based finite elements, increasing the polynomial degree does not produce more flexible results.

• In contrast with finite elements, uniform reduced quadrature does not produce hourglassing/point instabilities. However, significant loss of stiffness is observed, which precludes its use in the quasi-incompressible case.

• The polynomial degree of the deviatoric term, p ₁, is important in terms of results.

Selective interpolation is now contemplated, with Fig. 7 showing the effect of combining distinct bases. We conclude that the deviatoric term p ₁ is crucial for the results.

Fig. 7

Upsetting test, n = 25, effect of selective polynomial basis for the deviatoric (p ₁) and volumetric (p ₀) terms. Full quadrature. (a) Linear and quadratic bases. (b) Quadratic and cubic bases

Combining selective quadrature with full interpolation, results show that significant differences exist by changing the basis (see Fig. 8). In terms of mesh convergence, excellent results are obtained, as Fig. 9 shows. In our experience, this is one of the advantages of meshless methods.

Fig. 8

Upsetting test, n = 25, effect of selective quadrature for uniform interpolation

Fig. 9

Effect of a number of nodes using full quadrature and selective interpolation

Finally, to complete the test of Puso and Solberg [54], the power-law hardening is tested in Fig. 10

Fig. 10

Results for power-law hardening

5.3 Tension Test

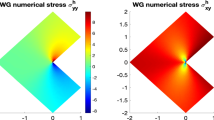
We apply the $\overline {C}$-EFG method to the tension test discussed by Simo and co-workers in the context of J ₂ plasticity [9] (see also the 1993 reference [55] where the test is described in detail). Geometry, boundary conditions, and material properties are summarized in Fig. 11, along with the two cases of nodal distribution, structured and unstructured, as this was found to have an effect on the results. The contour plot of the effective plastic strain, given by Eq. (56), is shown in Fig. 12 for two values of y. The specific yield stress σ _y is given by the hardening law shown in Fig. 11.

Fig. 11

Relevant dimensions and mesh for the Neo-Hookean/Hill48 tension test

Fig. 12

Tension test: deformed configurations for both yield functions ({1, 1, 1, 1, 1, 1} and {1, 0.8, 1, 0.9, 1, 1} with the corresponding effective plastic strain colors

Compared to mixed FE formulations, results are distinct. When compared with enhanced assumed strain hexahedra, specifically Simo and Armero [7, 55], both the initial plastic behavior and the post-localization behavior are different (see Fig. 13). We note that two significant differences exist: (1) Simo and Armero adopted a formulation based on the Kirchhoff stress tensor and radial-return mapping for J ₂ plasticity and (2) hexahedra tend to reproduce the incompressibility condition with sharper stretching. MINI elements (see, [5]) are also used for comparison, as Fig. 13 shows. When compared with the MINI runs, much coarser meshes are used in EFG for similar results. In contrast with the previous examples, finer node distributions result in a sharper localization region, with lower reactions for higher displacements. For the structured mesh with 3760 nodes, Fig. 14a shows the advantages of using p ₀ = 2 and p ₁ = 3 in terms of post-localization. When adopting an unstructured node distribution, a less pronounced post-localization behavior is exhibited (see Fig. 14b).

Fig. 13

Comparison with advanced finite element technology [7, 55] and effect of node density on the results

Fig. 14

Effect of selective interpolation and structured/unstructured node distribution. (a) Effect of selective interpolation. (b) Effect of structured/unstructured node distribution

6 Conclusions

In the context of $\overline {C}$ decomposition and by parameterizing the quadrature and the degree of the polynomial basis, we developed a discretization scheme with the following distinctive features:

• An initial perturbation of internal FE nodal positions is performed for efficiency reasons (low n).

• From linear up to cubic shape, functions are adopted for the volumetric and deviatoric terms of the right Cauchy-Green tensor. Lagrangian diffuse derivatives are defined ab initio for the entire analysis.

• A pre-established nodal support is imposed, and a tetrahedra integration with 1 or 4 quadrature points for C and $\overline {\boldsymbol {C}}$ is adopted.

• Constitutive integration makes use of the Mandel stress tensor and iteration on C _e [16].

Implementation is straightforward and was performed in SimPlas [52] with AceGen [39] and Mathematica [38]. Three benchmark tests were performed, which allow the following conclusions:

• Even with small supports and coarse meshes, results are highly competitive with established finite elements if either selective interpolation or selective quadrature are adopted. This holds for the quasi-incompressible case where special finite elements are adopted.

• Numerical testing shows that the ideal combination is p ₀ = 2 and p ₁ = 3 with either selective or full quadrature.

• Finite strain plasticity solutions are very robust, with large strains being possible without loss of convergence or instabilities.

• The finite strain formulation is simpler than with mixed finite elements and on par with displacement-based FEM. Source code is available at GitHub, cf. [40].

Appendices

Appendix

First and Second Variations of $\det \left [\boldsymbol {C}\right ]$

For the determinant of C, the following relations hold, which follow from established results and application of the chain rule:

$$\displaystyle \begin{aligned} \delta\det\left[\boldsymbol{C}\right] & =\det\left[\boldsymbol{C}\right]\boldsymbol{C}^{-1}:\delta\boldsymbol{C}{} \end{aligned} $$

(62)

$$\displaystyle \begin{aligned} \mathrm{d}\delta\det\left[\boldsymbol{C}\right] & =\mathrm{d}\boldsymbol{C}:\left(\det\left[\boldsymbol{C}\right]\boldsymbol{C}^{-1}\otimes\boldsymbol{C}^{-1}\right):\delta\boldsymbol{C} \\ & +\det\left[\boldsymbol{C}\right]:\mathrm{d}\delta\boldsymbol{C}-\mathrm{d}\boldsymbol{C}:\mathtt{S}:\delta\boldsymbol{C}{} \end{aligned} $$

(63)

where S is a fourth-order tensor with components $\mathtt {S}_{klij}=C_{ik}^{-1}C_{lj}^{-1}$. Given the n −th power of $\det \left [\boldsymbol {C}\right ]$, $\det \left [\boldsymbol {C}\right ]^{n},$ it follows that:

$$\displaystyle \begin{aligned} \delta\det\left[\boldsymbol{C}\right]^{n} & =n\det\left[\boldsymbol{C}\right]^{n-1}\delta\det\left[\boldsymbol{C}\right]{} \end{aligned} $$

(64)

$$\displaystyle \begin{aligned} \mathrm{d}\delta\det\left[\boldsymbol{C}\right]^{n} & =n(n-1)\det\left[\boldsymbol{C}\right]^{n-2}\delta\det\left[\boldsymbol{C}\right]\mathrm{d}\det\left[\boldsymbol{C}\right]+n\det\left[\boldsymbol{C}\right]^{n-1}\mathrm{d}\delta\det\left[\boldsymbol{C}\right]{} \end{aligned} $$

(65)

with $\delta \det \left [\boldsymbol {C}\right ]$ being given by (62) and $\mathrm {d}\delta \det \left [\boldsymbol {C}\right ]$ by (63). Given $\theta _{C}=\det \left [\overline {\boldsymbol {C}}\right ]$, similar expressions are obtained for δθ _C and dδθ _C.