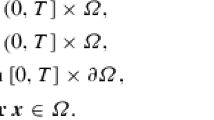Abstract
In this paper, a linear and decoupled Euler finite element scheme is proposed for solving the 3D incompressible Navier–Stokes equations with mass diffusion numerically by the mini element for the velocity equation and the \(P_2\) conforming element for the density equation. When the time step size \(\tau \) and the mesh size h both are sufficiently small, the proposed FEM algorithm is unconditionally stable at the full discrete level, which is a key issue in designing the efficient algorithm for the multi-physical field problem. Furthermore, optimal temporal-spatial error estimates are presented for the velocity in \(\mathbf{L} ^2\)-norm and the density in \(H^1\)-norm without any constraint of \(\tau \) and h by using the technique of error splitting.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
Let \(\Omega \subset \mathbf{R} ^3\) be a bounded and convex domain with the sufficiently smooth boundary \(\partial \Omega \) and [0, T] the time interval with some \(T>0\). We will use notations \(Q_T=[0, T]\times \Omega \) and \(\Sigma _T=[0, T]\times \partial \Omega \). In this paper, we consider the 3D incompressible Navier–Stokes equations with mass diffusion (or called the Kazhikhov–Smagulov model) in \(Q_T\), which can be deduced from the following 3D compressible Navier–Stokes equations:
In the above system (1.1–1.2), the unknows \(\rho : Q_T\rightarrow \mathbf{R} \) is the density of the fluid, \(\mathbf{v} : Q_T\rightarrow \mathbf{R} ^3\) is the velocity of the fluid and \(q: Q_T\rightarrow \mathbf{R} \) is the pressure which depends on the density \(\rho \). \(\mathbf{f} : Q_T\rightarrow \mathbf{R} ^3\) denotes the external force, \(\mu \) and \(\widetilde{\lambda }\) are two constants and present viscosity coefficients which are assumed to satisfy \(\mu >0\) and \(3 \widetilde{\lambda }+ 2\mu >0\). If the mass diffusion process obeys Fick’s law (cf. [12]), the velocity \(\mathbf{v} \) of the fluid can be decomposed into a potential part and an incompressible part:
where \(\lambda >0\) is the mass diffusion coefficient. Then the compressible Navier–Stokes equations (1.1–1.2) can be rewritten as
where \(P=q-\lambda \rho _t+\lambda (2\mu +\widetilde{\lambda })\Delta \ln \rho \). Eliminating the \(\lambda ^2\)-term in (1.4) and using the following relations:
we get the simplified model of (1.3–1.5) in \(Q_T\) which is described as
where \(p=P-\lambda \mathbf{u} \cdot \nabla \rho \). The above coupled system (1.6–1.8) are the incompressible Navier–Stokes equations with mass diffusion. It is clear that the system (1.6–1.8) reduce to the incompressible Navier–Stokes equations with variable density if \(\lambda =0\).
We complete (1.6–1.8) by the following boundary conditions
and the initial conditions
where \(\mathbf{n} \) denotes the outwards unit normal vector to \(\partial \Omega \). Furthermore, we assume that there have two positive constants m and M such that
which means that there has no vacuum state in \(\Omega \).
We recall some known results on the incompressible Navier–Stokes equations with mass diffusion. For the full model (1.3–1.5), Beirão da Veiga in [31] and Secchi in [29] established the local existence of the strong solution in terms of linearization and a fixed point method. Moreover, Secchi in [29] proved the eixstence and uniqueness of a global weak solution to 2D problem by imposing smallness on \(\lambda / \mu \) and established the asymptotic behavior towards a weak solution to the incompressible Navier–Stokes problem with variable density when the mass diffusion coefficient \(\lambda \rightarrow 0\). Guillén-González etc. in [15] proved the global existence of the strong solution for small initial data by means of an iterative method. When the mass diffusion coefficient \(\lambda \rightarrow 0\) and the viscosity coefficient \(\mu \rightarrow 0\), Araruna etc. in [4] studied the asymptotic behavior towards a solution to a inhomogeneous, inviscid and incompressible fluid governed by an Euler type system. For the numerical method of (1.3–1.5), Cabrales etc. in [6] proposed a fully discrete decoupled scheme by using a first-order time discretization and a \(C^0\) finite element approximation for all unknowns and proved some stability and convergences results.
For the simplified model (1.6–1.8), Kazhikhov and Smagulov in [21] proved the global existence of the weak solution and the local existence of the strong solution by means of the Galerkin method under the assumptions that the initial density \(\rho _0(x)\) satisfies (1.11) and the viscosity and mass diffusion coefficients satisfy \(\lambda <2\mu / (M-m)\). The global existence of the weak solution in the non-cylindrical domain was derived in [26]. Secchi in [28] studied the 3D Cauchy problem and established the local existence and uniqueness of the strong solution. The global existence of the strong solution to the 2D Cauchy problem and the 2D initial-boundary value problem were studied in [8, 9], respectively. For the numerical methods, there are not many works concerning numerical analysis of the simplified model (1.6–1.8). By using a first-order time discretization and a \(C^0\) finite element approximation for all unknowns, two decoupled numerical schemes were proposed for solving the 2D problem and the 3D problem in [16] and [17], respectively, where the stabilities of algorithms and the convergences of numerical solutions were investigated. Other numerical schemes can be found in [10] and [11, 27], where an hybrid finite volume-finite element scheme and spectral Galerkin schemes were studied, respectively. Furthermore, the stability and convergence of numerical algorithm were investigated in [10].
To our best knowledge, the first error analysis of finite element fully discrete scheme for the simplified model (1.6–1.8) was presented by Guillén-González and Gutiérrez-Santacreu in [18]. To describe error estimates derived in [18], we introduce some notations. Let \(0=t_0<t_1<\cdots <t_N=T\) be a uniform partition of the time interval [0, T] with the time step \(\tau =T/N\) and \(t_n=n\tau \). If \(\{\mathbf{v }^n\}_{n=1}^N\) is a given vector sequence with \(\mathbf{v} ^n\in X\) for a Banach space X, we introduce the following notations for the discrete-in-time norms:
Let \((\mathbf{u} _h^n, \rho _h^n)\) be the finite element approximations of \((\mathbf{u} (t_n), \rho (t_n))\) for \(1\le n\le N\). By using the mini-element (cf. [14]) for the approximation of velocity-pressure pair and the \(P_2\) element for the approximation of density, the authors in [18] proved that
under the weaker regularity assumptions on the exact solution. Concretely, the authors in [18] avoided using the assumption \(\mathbf{u} _{tt}\in L^2(0,T; \mathbf{L} ^{6/5}(\Omega ))\) which required that the data should satisfy an extra compatibility condition at \(t=0\).
In this paper, a decoupled numerical scheme is proposed by using the mini-element for the velocity-pressure pair and the \(P_2\) element for the density as that in [18]. Inspired by [22], this scheme is slightly different the scheme in [18] by introducing the post-processed velocity in the discretization of the density equation and the stable terms in the discretization of the Navier–Stokes type equation such that the proposed finite element scheme is unconditionally stable. The main result derived in this paper is the following optimal error estimate:
where \(h>0\) is the mesh size and \(C>0\) is some constant independent of h and \(\tau \). However, compared to [18], the higher regularities of the exact solution are assumed in this paper. The method of analysis is based on the technique of error splitting for the nonlinear parabolic problems proposed by Li and Sun in [23,24,25] and further developed in [2, 3, 7, 13, 32].
The rest of this paper is organized as follows. In Sect. 2, we state the proposed linear and decoupled Euler finite element scheme, present the stability of numerical scheme in Theorem 2.3 and the main result in Theorem 2.4. The proof of Theorem 2.4 is given in Sect. 3 by using the technique of error splitting. In particular, we firstly derive temporal error estimates and regularities of solutions to the time discrete scheme in Sect. 3.1, and then prove optimal spatial error estimates in Sect. 3.2.
2 Numerical Scheme and Main Result
2.1 Preliminaries
For the mathematical setting, we introduce the following notations. For \(k\in \mathbb N^+\) and \(1\le p\le +\infty \), we use \(W^{k,p}(\Omega )\) to denote the classical Sobolev space. The norm in \(W^{k,p}(\Omega )\) is denoted by \(\Vert \cdot \Vert _{W^{k,p}}\) defined by a classical way (cf. [1]). Denote \(W_0^{k,p}(\Omega )\) be the subspace of \(W^{k,p}(\Omega )\) where the functions have zero trace on \(\partial \Omega \). Especially, \(W^{0,p}(\Omega )\) is the Lebesgue space \(L^p(\Omega )\) and \(W^{k,2}(\Omega )\) is the Hilbert space which is simply denoted by \(H^k(\Omega )\). The boldface notations \(\mathbf{H} ^k(\Omega ), \mathbf{W} ^{k,p}(\Omega )\) and \(\mathbf{L} ^p(\Omega )\) are used to denote the vector-value Sobolev spaces corresponding to \(H^k(\Omega )^3, W^{k,p}(\Omega )^3\) and \(L^p(\Omega )^3\), respectively. We use \((\cdot ,\cdot )\) to denote the \(L^2\) or \(\mathbf{L} ^2\) inner product.
Introduce the following function spaces:
and
It is known that the norms \(\Vert \nabla \rho \Vert _{H^1}\) and \(\Vert \rho \Vert _{H^2}\) are equivalent to the seminorm \(\Vert \Delta \rho \Vert _{L^2}\) for \(\rho \in H_N^2(\Omega )\) and \(\rho \in H_{N,0}^2(\Omega )\), respectively.
Introduce the trilinear term \(a(\rho ; \mathbf{u} , \mathbf{v} )\) by
with
for any \(\rho \in L^\infty (\Omega )\) and \(\mathbf{u} , \mathbf{v} \in \mathbf{V} \). Under the condition (2.1), we can see that if \(\widetilde{m}\le \rho (x)\le \widetilde{M}\), then
The existence and uniqueness of weak solution to (1.6–1.8) are established by Kazhikhov and Smagulov in [21]. We recall it in the following theorem.
Theorem 2.1
Let \(\mathbf{u} _0\in \mathbf{H} \) and \(\rho _0\in W\) satisfying (1.11) and \(\mathbf{f} \in L^2(0,T; \mathbf{L} ^2(\Omega ))\). Suppose that the constants \(\lambda , \mu , m\) and M satisfies
Then there exists a unique weak solution \((\rho , \mathbf{u} )\) to (1.6–1.8) such that the solution satisfies
and the energy inequalities:
for all \(0<t\le T\), where \(\sigma (t)=\sqrt{\rho (t)}\) and \(\sigma _0=\sqrt{\rho _0}\).
Throughout this paper, we make the following assumptions on the prescribed data, the regularity of the solution to (1.6–1.10) and the domain \(\Omega \).
Assumption (A1): Assume that the prescribed data \(\mathbf{f} \), \(\mathbf{u} _0\) and \(\rho _0\) satisfy
Assumption (A2): Let \(\lambda , \mu , m, M\) satisfy (2.4) and \(\widetilde{m}, \widetilde{M}\) satisfy (2.1).
Assumption (A3): Assume that the solution \((\rho , \mathbf{u} , p)\) satisfies the following regularities:
Assumption (A4): Assume that the boundary \(\partial \Omega \) is sufficiently smooth such that the unique solution \(\phi \) of the Neumann problem
for prescribed \(g\in M\cap H^{k}(\Omega )\) satisfies
and the unique solution \((\mathbf{v} , q)\) of the Stokes problem
for prescribed \(\mathbf{g} \in \mathbf{L} ^p(\Omega )\) with \(1\le p\le 4\) satisfies
Remark 2.1
The verification of the regularity assumption \(\mathbf{u} _{tt} \in L^2(0,T; \mathbf{L} ^2(\Omega ))\) should involve an extra compatibility condition on the data at \(t=0\) which is not generally satisfied (see such condition for Navier–Stokes equations in [19]). We make this assumption merely to simplify the presentation. In [18], such assumption was avoided by using the technique of Euler integrator in the consistency error analysis.
2.2 Time Discrete Scheme
We first describe the time discrete scheme based on the backward Euler method. Let \(0=t_0<t_1<\cdots <t_N=T\) be a uniform partition of the time interval [0, T] with the time step \(\tau =T/N\) and \(t_n=n\tau \) with \(0\le n\le N\).
Given \(\rho ^0=\rho _0\) and \(\mathbf{u} ^0=\mathbf{u} _0\), we consider the following first-order Euler time discrete scheme for the simplified system (1.6–1.10).
Euler time discrete scheme:
Step I: For given \(\rho ^n\) and \(\mathbf{u} ^n\), we find \(\rho ^{n+1}\) by
with the boundary condition \(\partial _\mathbf{n} \rho ^{n+1}=0\) on \(\partial \Omega \), where
Step II: For given \(\rho ^n\), \(\mathbf{u} ^n\) and \(\rho ^{n+1}\) derived from (2.7), we find \((\mathbf{u} ^{n+1}, p^{n+1})\) by
with the boundary condition \(\mathbf{u} ^{n+1}=0\) on \(\partial \Omega \).
The weak form of (2.7–2.8) are described as follows. Find the weak solutions \(\rho ^{n+1}\in W\) and \((\mathbf{u} ^{n+1}, p^{n+1})\in \mathbf{V} \times M\), respectively, by
and
In the above form (2.10), we use
due to \(\nabla \cdot \mathbf{u} =0\) and \(\nabla \cdot ((\nabla \mathbf{u} )^t)=0\) and \(\mathbf{v} =0\) on \(\partial \Omega \).
From the assumption (A4) on the elliptic regularity, the well-posedness of solution to (2.7) was established in [17]. We recall it in the following lemma.
Lemma 2.1
For each \(0\le n\le N-1\), if
for some \(\kappa _1>0\) being independent of \(\tau \) and n, then for sufficiently small \(\tau \), the solution \(\rho ^{n+1}\) to (2.7) satisfies
for some \(\kappa _2>0\) being independent of \(\tau \) and n.
Remark 2.2
Although \(\mathbf{u} ^n\) in (2.7) replaces \(\mathbf{u} _h^n\) in [17], the proof of Lemma 2.1 follows immediately from the proof of Lemma 3.4 in [17] by noting the fact that \(\tau \displaystyle \sum _{n=1}^N\Vert \nabla \mathbf{u} ^n\Vert _{L^2}^2\le C\). Please see Appendix A in [17].
Next, we discuss the stability of the time discrete scheme (2.7–2.8). Setting \(\phi =2\tau \rho ^{n+1}\) in (2.9) gives
by using
Taking the sum gives
for all \(0\le n\le N-1\).
Suppose that
Setting \((\mathbf{v} , q)=2\tau (\mathbf{u} ^{n+1}, p^{n+1})\) in (2.10) and using (2.2), we have
where \(\sigma ^{n+1}=\sqrt{\rho ^{n+1}}\). Setting \(\phi =\tau |\mathbf{u} ^{n+1}|^2\) in (2.9) leads to
Then we obtain
Taking the sum gives
for all \(0\le n\le N-1\), where \(\sigma _0=\sqrt{\rho _0}\).
Thus, we get the following stable result of the time discrete scheme (2.7–2.8).
Theorem 2.2
Under the condition (2.11) and the assumptions on the time step \(\tau \) in Lemma 2.1, the solutions \(\rho ^{n+1}\) and \(\mathbf{u} ^{n+1}\) to (2.7) and (2.8) satisfy the following the discrete energy inequalities:
Remark 2.3
From the temporal error analysis in next section, we can see that the condition (2.11) holds for any \(0\le n\le N\). Thus, the above energy inequalities imply that the time discrete scheme (2.7–2.8) is unconditionally stable.
2.3 Finite Element Scheme
We give the finite element fully discretization of (2.7–2.8). Let \(\mathcal {T}_h = \{K_j\}_{j=1}^L\) be a quasi-uniform tetrahedral partition of \(\Omega \) with the mesh size \(h =\max _{1\le j\le L} \, \{diam \, K_j\}\). When \(\partial \Omega \) has a smooth curve, the element \(K_j\) adjacent to the boundary may represent a curved tetrahedron with a curved face. The definitions of finite element spaces on such a partition with curved elements can be dealt with that in [13, 25]. We use the mini element (\(P_1b-P_1\)) to approximate the velocity field \(\mathbf{u} \) and the pressure p, and use the piecewise quadratic Lagrange element (\(P_2\)) to approximate the density \(\rho \). The finite element spaces of \(\mathbf{V} , M\) and W are denoted by \(\mathbf{V} _h,\) \(M_h\) and \(W_h\), respectively. For this choice, the finite element spaces \(\mathbf{V} _h\) and \(M_h\) satisfy the discrete inf-sup condition. Further, we define the \(\mathbf{H} (\text{ div }, \Omega )\) conforming Raviart-Thomas finite element spaces of order 1 by
We denote by \(\mathbf{P} _{0h}\) the \(L^2\)-orthogonal projection operator from \(\mathbf{L} ^2(\Omega )\) to \(\mathbf{RT} _{0h}\) defined by
Start with \(\mathbf{u} _h^0=I_h\mathbf{u} _0\) and \(\rho _h^0=J_h\rho _0\), where \(I_h\) and \(J_h\) are the interpolation operators from \(\mathbf{V} \rightarrow \mathbf{V} _h\) and \(W \rightarrow W_h\), respectively, and satisfy
For \(1\le n\le N\), the finite element fully discrete approximations of (2.7–2.8) are described as follows.
Finite element fully discrete scheme:
Step I: For given \(\rho _h^n\in W_h\) and \(\mathbf{u} _h^n\in \mathbf{V} _h\), we find \(\rho ^{n+1}_h\in W_h\) such that
for all \(r_h\in W_h\).
Step II: For given \(\rho _h^n\in W_h\), \(\mathbf{u} _h^n\in \mathbf{V} _h\) and \(\rho _h^{n+1}\in W_h\) derived from (2.17), we find \((\mathbf{u} _h^{n+1}, p_h^{n+1})\in \mathbf{V} _h\times M_h\) such that
for all \((\mathbf{v} _h, q_h)\in \mathbf{V} _h\times M_h\).
Remark 2.4
In the above algorithm, the post-processed velocity \(\mathbf{P} _{0h}\mathbf{u} _h^n\) in (2.17) and the stabilized terms \( (D_\tau \rho _h^{n+1} , \mathbf{u} _h^{n+1}\cdot \mathbf{v} _h ) + (\nabla \cdot (\rho _h^n \mathbf{u} _h^{n+1}), \mathbf{u} _h^{n+1}\cdot \mathbf{v} _h) + \lambda (\nabla \rho _h^{n+1}, \nabla (\mathbf{u} _h^{n+1}\cdot \mathbf{v} _h))\) in (2.18) are used to preserve the unconditional stability of numerical scheme.
Taking \(r_h=2\tau \rho _h^{n+1}\) in (2.17), we get
by using
Taking the sum of (2.19) gives
for all \(0\le n\le N-1\).
Suppose that the following condition holds:
Taking \((\mathbf{v} _h, q_h)=2\tau (\mathbf{u} _h^{n+1}, p_h^{n+1})\) in (2.18) and using (2.2), we have
by using
where \(\sigma _h^{n+1}=\sqrt{\rho _h^{n+1}}\). Taking the sum of (2.21), we can get
for all \(0\le n\le N-1\), where \(\sigma _h^0=\sqrt{\rho _h^0}\).
Like that for the time discrete scheme (2.7–2.8), we get the following stable result of the fully discrete scheme (2.17–2.18).
Theorem 2.3
Under the condition (2.20), the solutions \(\rho _h^{n+1}\in W_h\) and \(\mathbf{u} _h^{n+1}\in \mathbf{V} _h\) to (2.17) and (2.18) satisfy the following the discrete energy inequalities:
Remark 2.5
From the temporal-spatial error analysis in next section, we can see that the condition (2.20) holds for sufficiently small h and \(\tau \). Thus, the above energy inequalities imply that the fully discrete scheme (2.17–2.18) is unconditionally stable. Furthermore, the discrete energy inequalities show the existence and uniqueness of solutions \(\rho _h^{n+1}\in W_h\) and \(\mathbf{u} _h^{n+1}\in \mathbf{V} _h\) when h and \(\tau \) are sufficiently small.
2.4 Main Result
We present the optimal error estimate in the following theorem. The proof will be given in Section 3. In the rest of this paper, we denote by C a generic positive constant, which is independent of n, h and \(\tau \), and C may be different at different places.
Theorem 2.4
Under the assumptions (A1)-(A4), there exist \(\tau _0>0\) and \(h_0>0\) such that when \(\tau <\tau _0\) and \(h<h_0\), the FE solutions \(\rho _h^{n+1}\) and \(\mathbf{u} _h^{n+1}\) to (2.17) and (2.18) satisfy
In the proof of Theorem 2.4, the following inverse inequalities and interpolation inequalities are frequently used (cf. [5]):
for any \(\mathbf{u} _h\in \mathbf{V} _h\) and \(\rho _h\in W_h\), and
Finally, we recall the discrete Gronwall’s inequality established in [20].
Lemma 2.2
Let \(a_k, b_k\) and \(\gamma _k\) be the nonnegative numbers such that
Suppose \(\tau \gamma _k<1\) and set \(\sigma _k=(1-\tau \gamma _k)^{-1}\). Then there holds:
Remark 2.6
If the sum on the right-hand side of (2.25) extends only up to \(n-1\), then the estimate (2.26) still holds for all \(k \ge 1\) with \(\sigma _k=1\).
3 Error Analysis
In this section, we will prove Theorem 2.4 by using the technique of error splitting. We first prove temporal errors in Sect. 3.1 and then prove spatial errors in Sect. 3.2. The finite element error estimates can be derived by combining temporal errors, projection errors and spatial errors.
3.1 Temporal Error Analysis
In this subsection, we will prove the optimal temporal errors. For \(0\le n\le N-1\), we take \(t=t_{n+1}\) in (1.6–1.8) to deduce that
and
where the truncation functions \(R_\sigma ^{n+1}\) and \(R_u^{n+1}\) are given by
Under the regularity assumption (A3), we have
For \(0\le n\le N\), we introduce temporal error functions by
Then error equations satisfied by \((\eta ^{n+1}, \mathbf{e} ^{n+1}, \epsilon ^{n+1})\) with \(0\le n\le N-1\) are
and
with \(\nabla \cdot \mathbf{e} ^{n+1}=0\) in \(\Omega \), where
Moreover, the weak formulations of (3.4) and (3.5) can be described as: find \(\eta ^{n+1}\in W \) such that
for all \(r\in W\), and find \((\mathbf{e} ^{n+1}, \epsilon ^{n+1})\in \mathbf{V} \times M\) such that
for all \((\mathbf{v} , q)\in \mathbf{V} \times M\).
We estimate \(\eta ^{n+1}\) and \(\mathbf{e} ^{n+1}\) in \(l^\infty (L^2)\)-norm and \(l^2(H^1)\)-norm in the following two lemmas.
Lemma 3.1
Under the regularity assumption (A3), there exists some \(C>0\) such that
for all \(0\le m \le N-1\).
Proof
Taking \(r=2\tau \eta ^{n+1}\) in (3.6) and using
it is easy to see that
Summing up the above estimate for n from 0 to m and using (3.3) and the discrete Gronwall’s inequality in Lemma 2.2, we complete the proof of (3.8). \(\square \)
Lemma 3.2
Under the assumptions (A2) and (A3), there exists some small \(\tau _1>0\) such that when \(\tau <\tau _1\), there holds
for all \(0\le m \le N-1\).
Proof
Setting \( (\mathbf{v} , q)=2\tau (\mathbf{e} ^{n+1}, \epsilon ^{n+1})\) in (3.7), we have
Multiplying (2.7) by \(\tau |\mathbf{e} ^{n+1}|^2\) and integrating over \(\Omega \), one has
where the integration by parts is used. Taking the sum of the above formulations, we get
Now, we suppose that
According to Lemma 2.1, we have
which with (2.2) and (3.10) gives
To close the mathematical induction (3.11), we need to prove that
The right-hand side of (3.13) can be estimated term by term as follows. It is easy to see that
By (A3) and (3.12), we have
and
where the Hölder inequality and the Young inequality are used. Taking into account the above estimates, we get from (3.13) that
where (3.8) in Lemma 3.1 and (3.12) are used. Summing up (3.15) for n from 0 to m, using (3.3), (3.8) and the discrete Gronwall’s inequality in Lemma 2.2, we derive (3.9) and complete the mathematical induction (3.14) by taking a sufficiently small \(\tau _1\) such that
\(\square \)
From the proof of Lemma 3.2, we can see that (3.14) holds for all \(0\le n\le N-1\). It follows from Lemma 2.1 that the solutions \(\rho ^{n+1}\) to (2.7) and \(\mathbf{u} ^{n+1}\) to (2.8) satisfy
for all \(0\le n\le N-1\). By (3.8) and (3.9), we get the following estimate for the density:
for \(0\le m \le N-1\). Furthermore, we can estimate \(\eta ^{n+1}\) in \(l^\infty (H^1)\)-norm and \(l^2(H^2)\)-norm as follows.
Lemma 3.3
Under the assumptions (A2) and (A3), when \(\tau <\tau _1\), where \(\tau _1\) is from Lemma 3.2, there exists some \(C>0\) such that
for all \(0\le m \le N-1\).
Proof
Multiplying (3.4) by \(-2\tau \Delta \eta ^{n+1}\) and integrating over \(\Omega \), we can prove that
Summing up the above estimate for n from 0 to m and using (3.18), we obtain
for \(0\le m \le N-1\). By noticing (3.18), again, we complete the proof of (3.19). \(\square \)
The error estimate (3.19) provides a uniform boundness of \(\rho ^{n+1}\) in \(H^2\)-norm. That is to say that there exists some \(C>0\) such that
Next, we estimate \(\mathbf{u} ^{n+1}\) in \(l^2(\mathbf{H} ^{2})\)-norm under the assumption (A4). To do this, we rewrite (2.8) as the Stokes type problem:
where
by using \(\nabla \cdot (\nabla \mathbf{u} ^{n+1} )^t=0\) due to \(\nabla \cdot \mathbf{u} ^{n+1}=0\). From (3.16) and
we have
where (3.9) is used. From (3.16), (3.17) and (3.20), one has
which with the assumption (A4) gives
From the Sobolev imbedding theorem \(\mathbf{W} ^{2, 3/2}(\Omega )\hookrightarrow \mathbf{W} ^{1, 3}(\Omega )\), we have
By (3.16), (3.17) and (3.20), again, we have
By the assumption (A4), again, we get
Thus, the numerical velocity \(\mathbf{u} ^{n+1}\) is uniformly bound in \(l^2(\mathbf{H} ^2)\)-norm. Based on the regularities (3.20) and (3.26), we can obtain the error estimate of \(\mathbf{e} ^{n+1}\) in \(l^\infty (\mathbf{V} )\)-norm and \(l^2(\mathbf{H} ^2)\)-norm stated in Lemma 3.4. To make this, we rewrite (3.5) as
with \(\nabla \cdot \mathbf{e} ^{n+1}=0\) in \(\Omega \).
Lemma 3.4
Under the assumptions (A2)-(A4), there exists some \(\tau _2<\tau _1\) such that when \(\tau <\tau _2\), there holds
for all \(0\le m \le N-1\).
Proof
Testing (3.27) by \(2\tau (\mathbf{e} ^{n+1}-\mathbf{e} ^n)\) leads to
The right-hand side of (3.29) can be estimated term by term by using the Hölder inequality and the Young inequality. From (3.16), it is easy to show that
and
A similar argument gives
Other terms can be bound, respectively, by
where we use the regularity assumption (A3) and (3.16). Substituting the above estimates into (3.29) leads to
Summing up (3.30) for n from 0 to m and using (3.9) and (3.19), we obtain
By (3.26) and the discrete Gronwall’s inequality in Lemma 2.2, we get
by using \( \Vert \nabla \eta ^{n+1}\Vert _{L^3}^2 \le C \Vert \eta ^{n+1}\Vert _{H^2}^2 \le C\tau \). On the other hand, from (3.27) and the regularity assumption (A4) of the solution to the Stokes problem, we have
Summing up (3.32) for n from 0 to m and using (3.19) and (3.31), we obtain
Taking a sufficiently small \(\tau _2<\tau _1\) such that \(C\tau _2<1\), we derive
which with (3.31) leads to
Thus, we complete the proof of Lemma 3.4. \(\square \)
From (3.28), we can see that
for some small \(\tau >0\). Thus, (3.14) holds and we close the mathematical induction.
The estimate (3.28) provides a uniform boundness of the time discrete solution \((\mathbf{u} ^{n+1}, p^{n+1)}\) in \( l^\infty (\mathbf{H} ^2)\times l^\infty (H^1)\)-norm, which means that there exists some \(C>0\) such that
In addition, the estimates (3.19) and (3.28) imply that
for all \(0\le n\le N-1\), if we notice the regularity assumption (A3).
Next, we estimate the time discrete solutions \((\rho ^{n+1}, \mathbf{u} ^{n+1}, p^{n+1)}\) in \(H^3\times \mathbf{W} ^{2,4}\times W^{1,4}\)-norm. We turn back to (2.7) and (3.21). In terms of (3.20) and (3.34), one has
and
From the regularity assumption (A4), we obtain
3.2 Spatial Error Analysis
In this subsection, we will prove the optimal spatial error estimate for the velocity in \(l^\infty (\mathbf{L} ^2)\)-norm and the density in \(l^\infty (H^1)\)-norm. The proof is based on the regularities of time discrete solutions derived in Sect. 3.1 and the following new projection operators.
For \(1\le n\le N\), we introduce three new projection operators \((\mathbf{R} _h^n, Q_h^n):\mathbf{V} \times M\rightarrow \mathbf{V} _h\times M_h\) and \(\Pi _h^n: W\rightarrow W_h\) defined by
and
where \(\rho ^n\) and \(\mathbf{u} ^{n-1}\) are the solutions to (2.7–2.8) and satisfy the point-wise inequality (3.16) and the regularity (3.34), respectively.
Then from the coercive property (2.2), and using a classical argument (cf.[5, 14]), the following approximations hold:
for any \((\rho , \mathbf{u} , p)\in H^2(\Omega )\cap \mathbf{H} ^2(\Omega )\cap \mathbf{V} \times H^1(\Omega )\). Furthermore, one has
if \((\rho , \mathbf{u} , p)\in W^{2,4}(\Omega )\cap \mathbf{W} ^{2,4}(\Omega )\cap \mathbf{V} \times W^{1,4}(\Omega )\).
We denote by \(\mathbf{P} _{1h}\) the standard Raviart-Thomas projection from \(\mathbf{H} (\text{ div },\Omega )\) onto \(\mathbf{RT} _h\), which satisfies the following properties (cf. [30]):
where \(P_1(\mathcal {T}_h)\subset H^1(\Omega )\) is the finite element space of functions which are the piecewise linear polynomials on each \(K\in \mathcal T_h\). For the time discrete solution \(\mathbf{u} ^n\), since \(\nabla \cdot \mathbf{u} ^n=0\) in \(\Omega \) and \(\mathbf{u} ^n\cdot \mathbf{n} =0 \) on \(\partial \Omega \), then
which implies that \(\mathbf{P} _{1h}\mathbf{u} ^n\in \mathbf{RT} _{0h}\). By noticing the definition of the \(L^2\)-projection \(\mathbf{P} _{0h}\), there holds that
Introduce spatial error functions by
where \((\rho _h^n, \mathbf{u} _h^n, p_h^n)\) and \((\rho ^n, \mathbf{u} ^n, p^n)\) are numerical solutions to (2.17–2.18) and (2.7–2.8), respectively. Moreover, we denote projection error functions by
From (3.37–3.41) and the regularities (3.20), (3.34) and (3.35), projection error functions satisfy
For \(0\le n\le N-1\), subtracting (2.17–2.18) from (2.9–2.10) with \((r, \mathbf{v} , q)=(r_h, \mathbf{v} _h, q_h)\) and noticing the definitions of projection operators \((\mathbf{R} _h^{n+1}, Q_h^{n+1})\) and \(\Pi _h^{n+1}\), we get the following error equations satisfied by \(\eta _h^{n+1}\) and \((\mathbf{e} _h^{n+1}, \epsilon _h^{n+1})\), respectively,
and
where we have noted \(\nabla \cdot \mathbf{u} ^n=0\) in \(\Omega \) and
by taking \(r=\mathbf{R} _h^{n+1}\mathbf{u} ^{n+1}\cdot \mathbf{v} _h\in W_h\) in (2.9).
We first estimate \(\eta _h^{n+1}\) and \(\nabla \eta _h^{n+1}\) in \(l^\infty (L^2)\)-norm in the following two lemmas.
Lemma 3.5
Under the assumptions (A1–A4), there exists some \(\tau _3<\tau _2\) such that when \(\tau <\tau _3\), there holds
for all \(0\le m\le N-1\).
Proof
Taking \(r_h=2\tau \eta _h^{n+1}\) in (3.48) leads to
by noticing
and
The right-hand side of (3.51) can be bound by using the Hölder inequality and the Young inequality. It follows from (3.43–3.45) that
For \(I_3^{n+1}\) and \(I_4^{n+1}\), we can prove that
Substituting the above estimates into (3.51), we obtain
Taking the sum from 0 to m and using the discrete Gronwall’s inequality in Lemma 2.2, we get the desired result (3.50) for some small \(\tau<\tau _3<\tau _2\). \(\square \)
Lemma 3.6
Under the assumptions (A1)-(A4), if
then there exists some \(C>0\) such that
for all \(0\le m\le N-1\).
Proof
Taking \(r_h=2 D_\tau \eta _h^{n+1}\) in (3.48) leads to
We estimate the right-hand side of (3.55) term by term according to the regularities derived in (3.20), (3.34), (3.36) and (3.36). From the Hölder inequality and the Young inequality, we have
where the inverse inequalities (2.23) is used, and
and
where the inverse inequalities (2.23) is used, and
Substituting the above estimates into (3.55) and taking the sum from 0 to m, we get
By the condition (3.53) and using the discrete Gronwall inequality in Lemma 2.2, we get the desired result (3.54). \(\square \)
Next lemma presents the estimate of \(\mathbf{e} _h^{n+1}\) in \(l^\infty (\mathbf{L} ^2)\)-norm and \(l^2(\mathbf{V} )\)-norm.
Lemma 3.7
Under the assumptions (A1–A4), there exists sufficiently small \(h_4>0\) and \(\tau _4<\tau _3\) such that when \(h<h_4\) and \(\tau <\tau _4\), the finite element scheme (2.18) admits a unique solution \((\mathbf{u} _h^{n+1}, p_h^{n+1})\in \mathbf{V} _h\times M_h\). Moreover, there holds
where \(C_0>0\) is independent of \(\tau \), h and m.
Proof
We will prove (3.56) by the method of mathematical induction.
\(\bullet \) Initialization \((m=0)\)
We first prove that (3.56) is valid for \(m=0\). Taking \(m=0\) in (3.50) and (3.54), we can get
by using
Furthermore, we get from the inverse inequality (2.23) and (3.57) that
Then there exists some sufficiently small \(h_4\) such that when \(h<h_4\), one has
which with (2.2) implies that the numerical scheme (2.18) with \(n=0\) admits a unique solution \((\mathbf{u} _h^1, p_h^1)\in \mathbf{V} _h\times M_h\). Taking \(n=0\) and \((\mathbf{v} _h, q_h)=2\tau (\mathbf{e} _h^1, \epsilon _h^1)\) in (3.49) and using (2.2) and \(\mathbf{e} _h^0=0\), we get
Due to \(\eta _h^0=0\), then from (3.43–3.45) and (3.35), one has
By (3.57) and (3.58), we estimate \((J_{4h}^{1}, \mathbf{e} _h^1)\) by
for sufficiently small \(h<h_4\). Using the integration by parts, we estimate \((J_{5h}^{1}, \mathbf{e} _h^1)\) by
Similarly, we can prove
From the definition of \(\Pi _h^1\), one has
where (3.57) is used. It is easy to see that
and
For \(J_{17h}\), we get from (3.57) that
Taking into account these estimates with (3.60), there exits some \(C_1>0\) independent of \(C_0\), h and \(\tau \) such that
Thus, (3.56) is valid for \(m=0\) by taking \(C_0\ge C_1\).
\(\bullet \) General step \((m\ge 1)\)
For \(0\le n\le N-1\), we assume that (3.56) is valid for \(m=n\), i.e.,
Then
Thus, the condition (3.53) is valid and the estimate (3.54) holds in Lemma 3.6.
By the inverse inequality (2.23), we have
which implies that
for sufficiently small \(h<h_4\) such that \((1+C_0)h^{1/2}_4\le 1\). From (3.50) in Lemma 3.5 and (3.63), one has
where we use the inverse inequality (2.23), (3.36) and
for sufficiently small \(h<h_4\). Then the finite element solution \(\rho _h^{n+1}\) satisfies
which with (3.16) implies that
for sufficiently small \(h<h_4\) such that
According to (2.2), the fully discrete scheme (2.18) admits a unique solution \((\mathbf{u} _h^{n+1}, p_h^{n+1})\in \mathbf{V} _h\times M_h\).
To close the mathematical induction, we need to prove that (3.56) is valid for \(m=n+1\). Setting \((\mathbf{v} _h, q_h)=2\tau (\mathbf{e} _h^{n+1}, \epsilon _h^{n+1})\) in (3.49), we get
Using the Hölder inequality, the Young inequality, the regularity results (3.34–3.36) derived in Sect. 3 and the projection approximations (3.43–3.47) and the induction assumptions (3.62–3.68), we estimate the right-hand side of (3.69) term by term as follows:
\(\bullet \) Estimate of \(2\tau (J_{1h}^{n+1}, \mathbf{e} _h^{n+1})\)
\(\bullet \) Estimate of \(2\tau (J_{2h}^{n+1}, \mathbf{e} _h^{n+1})\)
\(\bullet \) Estimate of \(2\tau (J_{3h}^{n+1}, \mathbf{e} _h^{n+1})\)
\(\bullet \) Estimate of \(2\tau (J_{4h}^{n+1}, \mathbf{e} _h^{n+1})\)
for sufficiently small \(h<h_4\) such that \(C(1+C_0)h_4^{1/2} < \mu _1/32\).
\(\bullet \) Estimate of \(2\tau (J_{5h}^{n+1}, \mathbf{e} _h^{n+1})\)
where the integration by parts is used.
\(\bullet \) Relation of \(2\tau (J_{6h}^{n+1}, \mathbf{e} _h^{n+1})\) and \(2\tau (J_{14h}^{n+1}, \mathbf{e} _h^{n+1})\)
where the integration by parts is used.
\(\bullet \) Estimate of \(2\tau (J_{7h}^{n+1}, \mathbf{e} _h^{n+1})\)
where the definition of \(\Pi _h^{n+1}\) is used.
\(\bullet \) Relation of \(2\tau (J_{8h}^{n+1}, \mathbf{e} _h^{n+1})\) and \(2\tau (J_{9h}^{n+1}, \mathbf{e} _h^{n+1})\)
by using the integration by parts.
\(\bullet \) Estimate of \(2\tau (J_{10h}^{n+1}, \mathbf{e} _h^{n+1})\)
by using the integration by parts.
\(\bullet \) Estimate of \(2\tau (J_{11h}^{n+1}, \mathbf{e} _h^{n+1})\)
by using the integration by parts.
\(\bullet \) Estimate of \(2\tau (J_{12h}^{n+1}, \mathbf{e} _h^{n+1})\)
\(\bullet \) Estimate of \(2\tau (J_{13h}^{n+1}, \mathbf{e} _h^{n+1})\)
by using the integration by parts and \(\nabla \cdot \mathbf{u} ^n=0\) in \(\Omega \).
\(\bullet \) Estimate of \(2\tau (J_{15h}^{n+1}, \mathbf{e} _h^{n+1})\)
\(\bullet \) Estimate of \(2\tau (J_{16h}^{n+1}, \mathbf{e} _h^{n+1})\)
\(\bullet \) Estimate of \(2\tau (J_{17h}^{n+1}, \mathbf{e} _h^{n+1})\)
Substituting these estimates for \(J_{1h}^{n+1}\) to \(J_{17h}^{n+1}\) into (3.69), we get
Taking the sum gives
where we used error estimates derived in Lemmas 3.5 and 3.6. From (3.36) (3.63) and (3.66), we have
and
Then (3.70) reduces to
Applying the discrete Gronwall’s inequality in Lemma 2.2, we derive
and
by using (3.68) and taking \(\sqrt{C\exp (CT)} \le C_0\). Thus, we prove that (3.56) is valid for \(m=n+1\) and finish the mathematical induction. \(\square \)
3.3 Proof of Theorem 2.4
By (3.9) in Lemma 3.2 and (3.56) in Lemma 3.7, it is easy to see that
where the uniform boundness (3.12) of \(\rho ^{n+1}\) is used. Thus, we get the optimal \(\mathbf{L} ^2\) error estimate for the velocity. To establish the optimal \(H^1\) error estimate for the density, we have
where (3.50) in Lemma 3.5 and (3.54) in Lemma 3.6 are used. Then,
Thus, we complete the proof of Theorem 2.4.
References
Adams, R.A.: Sobolev Spaces. Academic Press, New York (1975)
An, R.: Optimal error estimates of linearized Crank–Nicolson Galerkin method for Landau–Lifshitz equation. J. Sci. Comput. 69, 1–27 (2016)
An, R., Su, J.: Optimal error estimates of semi-implicit Galerkin method for time-dependent nematic liquid crystal flows. J. Sci. Comput. 74, 979–1008 (2018)
Araruna, F.D., Braz e Silva, P., Carvalho, R.R., Rojas-Medar, M.A.: On the behavior of Kazhikhov-Smagulov mass diffusion model for vanishing diffusion and viscosity coefficients. J. Math. Phy. 56, 061505 (2016)
Brenner, S., Scott, L.: The Mathematical Theory of Finite Element Methods. Springer (1994)
Cabrales, R.C., Guillén-González, F., Gutiérrez-Santacreu, J.V.: Stability and convergence for a complete model of mass diffusion. Appl. Numer. Math. 61, 1161–1185 (2011)
Cai, W.T., Li, B.Y., Li, Y.: Error analysis of a fully discrete finite element method for variable density incompressible flows in two dimsnsions. ESAIM: M2AN 55, S103–S147 (2021)
Cai, X.Y., Liao, L.W., Sun, Y.Z.: Global regularity for the initial value problem of a 2-D Kazhikhov–Smagulov type model. Nonlin. Anal. 75, 5975–5983 (2012)
Cai, X.Y., Liao, L.W., Sun, Y.Z.: Global strong solution to the initial-boundary value problem of a 2-D Kazhikhov–Smagulov type model. Dis. Contin. Dyn. Syst. S 7, 917–923 (2014)
Calgaro, C., Ezzoug, M., Zahrouni, E.: Stability and convergence of an hybrid finite volume-finite element method for a multiphasic incompressible fluid model. Commun. Pure Appl. Anal. 17, 429–448 (2018)
Damázio, P.D., Rojas-Medar, M.A.: On the convergence rate of semi-Galerkin approximations for the equations of viscous fluids in the presence of diffusion. Mat. Contemp. 15, 105–125 (1998)
Frank, D.A., Kamenetskii, V.I.: Diffusion and Heat Transfer in Chemical Kinetics. Plenum Press, New York (1969)
Gao, H.D.: Optimal error estimates of a linearized backward Euler FEM for the Landau–Lifshitz equation. SIAM J. Numer. Anal. 52(52), 2574–2593 (2014)
Girault, V., Raviart, P.A.: Finite Element Methods for Navier–Stokes Equations: Theory and Algorithms. Springer-Verlag, Berlin (1986)
Guillén-González, F., Damázio, P., Rojas-Medar, M.A.: Approximation by an iterative method for regular solutions for incompressible fluids with mass diffusion. J. Math. Anal. Appl. 326, 468–487 (2007)
Guillén-González, F., Gutiérrez-Santacreu, J.V.: unconditional stability and convergence of fully discrete schemes for 2D viscous fluids models with mass diffusion. Math. Comput. 77, 1495–1524 (2008)
Guillén-González, F., Gutiérrez-Santacreu, J.V.: Conditional stability and convergence of a fully discrete scheme for three-dimensional Navier–Stokes equations with mass diffusion. SIAM J. Numer. Math. 46, 2276–2308 (2008)
Guillén-González, F., Gutiérrez-Santacreu, J.V.: Error estimates of a linear decoupled Euler-FEM scheme for a mass diffusion. Numer. Math. 117, 333–371 (2011)
Heywood, J., Rannacher, R.: Finite element approximation of the nonstationary Navier–Stokes problem. I. regularity of solutions and second-order error estimates for spatial discretization. SIAM J. Numer. Anal. 19, 275–311 (1982)
Heywood, J., Rannacher, R.: Finite-element approximation of the nonstationary Navier–Stokes problem Part IV: error analysis for second-order time discretization. SIAM J. Numer. Anal. 27, 353–384 (1990)
Kazhikhov, A.V., Smagulov, S.: The correctness of boundary value problems in a diffusion model of an inhomogeneous fluid. Sov. Phys. Dokl. 21, 249–252 (1977)
Li, B.Y., Qiu, W.F.: A convergent post-processed discontinuous Galerkin method for incompressible flow with variable density. arXiv:2007.13292v1 (2020)
Li, B.Y., Sun, W.W.: Error analysis of linearized semi-implicit Galerkin finite element methods for nonlinear parabolic equations. Inter. J. Numer. Anal. Model. 10, 622–633 (2013)
Li, B.Y., Sun, W.W.: Unconditional convergence and optimal error estimates of a Galerkin-mixed FEM for incompressible miscible flow in porous media. SIAM J. Numer. Anal. 51, 1959–1977 (2013)
Li, B.Y., Gao, H.D., Sun, W.W.: Unconditionally optimal error estimates of a Crank–Nicolson Galerkin method for the nonlinear thermistor equations. SIAM J. Numer. Anal. 52, 933–954 (2014)
Salvi, R.: On the existence of weak solutions of boundary-value problems in a diffusion model of an inhomogeneous liquid in regions with moving boundaries. Portugaliae Math. 43, 213–233 (1986)
Gutiérrez-Santacreu, J.V., Rojas-Medar, M.A.: Uniform-in-time error estimates for spectral Galerkin approximations of a mass diffusion model. Math. Comput. 81, 191–218 (2012)
Secchi, P.: On the initial value problem for the equations of motion of viscous incompressible fluids in the presence of diffusion. Boll. Unione Mat. Ital. Sez. B 6, 1117–1130 (1982)
Secchi, P.: On the motion of viscous fluids in the presence of diffusion. SIAM J. Math. Anal. 19, 22–31 (1988)
Thomée, V.: Galerkin Finite Element Methods for Parabolic Problems. Springer-Verlag, New York (2006)
Beirão da Veiga, H.: Diffusion on viscous fluids. Eixstence and asymptotic properties of solutions. Annali della Scuola normale superiore di Pisa Classe di scienze 10, 341–355 (1983)
Wang, J.L.: A new error analysis of Crank–Nicolson Galerkin FEMs for a generalized nonlinear Schrödinger equation. J. Sci. Comput. 60, 390–407 (2014)
Acknowledgements
This work was supported by National Natural Science Foundation of China (No. 11771337) and Natural Science Foundation of Zhejiang Province (No. LY18A010021).
Author information
Authors and Affiliations
Corresponding author
Ethics declarations
Conflict of interest
Data sharing is not applicable to this article as no datasets were generated or analyzed during the current study.
Additional information
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
About this article
Cite this article
Li, Y., An, R. Unconditionally Optimal Error Analysis of a Linear Euler FEM Scheme for the Navier–Stokes Equations with Mass Diffusion. J Sci Comput 90, 47 (2022). https://doi.org/10.1007/s10915-021-01730-6
Received:
Revised:
Accepted:
Published:
DOI: https://doi.org/10.1007/s10915-021-01730-6
Keywords
- Kazhikhov–Smagulov model
- Navier–Stokes equations with mass diffusion
- Finite element discretization
- Unconditional stability
- Error estimates