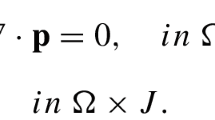Convergence analysis and error estimates for a second order accurate finite element method for the Cahn–Hilliard–Navier–Stokes system

Abstract

In this paper, we present a novel second order in time mixed finite element scheme for the Cahn–Hilliard–Navier–Stokes equations with matched densities. The scheme combines a standard second order Crank–Nicolson method for the Navier–Stokes equations and a modification to the Crank–Nicolson method for the Cahn–Hilliard equation. In particular, a second order Adams-Bashforth extrapolation and a trapezoidal rule are included to help preserve the energy stability natural to the Cahn–Hilliard equation. We show that our scheme is unconditionally energy stable with respect to a modification of the continuous free energy of the PDE system. Specifically, the discrete phase variable is shown to be bounded in $\ell ^\infty \left( 0,T;L^\infty \right)$ and the discrete chemical potential bounded in $\ell ^\infty \left( 0,T;L^2\right)$, for any time and space step sizes, in two and three dimensions, and for any finite final time T. We subsequently prove that these variables along with the fluid velocity converge with optimal rates in the appropriate energy norms in both two and three dimensions.

1 Introduction

In this paper, we prove error estimates for a fully discrete, second order in time, finite element method for the Cahn–Hilliard–Navier–Stokes (CHNS) model for two-phase flow. Let $\Omega \subset \mathbb {R}^d$, $d=2,3$, be an open convex polygonal or polyhedral domain. For all $\phi \in H^1(\Omega ), \mathbf{u}\in \mathbf{L}^2(\Omega )$, consider the energy

$$\begin{aligned} E(\phi , \mathbf{u}) = \int _{\Omega } \left\{ \frac{1}{4\varepsilon } \left( \phi ^2 - 1\right) ^2 + \frac{\varepsilon }{2} |\nabla \phi |^2 + \frac{1}{2\gamma } |\mathbf{u}|^2 \right\} d\mathbf {x}, \end{aligned}$$

(1.1)

where $\phi$ represents a concentration field, $\mathbf{u}$ represents fluid velocity, and $\varepsilon$ is a positive constant representing a non-dimensional interfacial width between the two phases. The CHNS system is a gradient flow of this energy [19, 20, 24, 27]:

$$\begin{aligned} \partial _t \phi + \nabla \phi \cdot \mathbf{u}= \varepsilon \nabla \cdot \left( M(\phi ) \nabla \mu \right) ,&\quad \text {in} \,\Omega _T, \end{aligned}$$

(1.2a)

$$\begin{aligned} \mu = \varepsilon ^{-1}\left( \phi ^3-\phi \right) -\varepsilon \Delta \phi ,&\quad \text {in} \,\Omega _T, \end{aligned}$$

(1.2b)

$$\begin{aligned} \partial _t \mathbf{u}- \eta \Delta \mathbf{u}+ \mathbf{u}\cdot \nabla \mathbf{u}+ \nabla p = \gamma \mu \nabla \phi ,&\quad \text {in} \, \Omega _T, \end{aligned}$$

(1.2c)

$$\begin{aligned} \nabla \cdot \mathbf{u}= 0,&\quad \text {in} \, \Omega _T, \end{aligned}$$

(1.2d)

$$\begin{aligned} \partial _n \phi =\partial _n \mu = 0, \mathbf{u}= \mathbf{0}&\quad \text {on} \, \partial \Omega \times (0,T), \end{aligned}$$

(1.2e)

where $M(\phi )>0$ is a mobility, $\eta = \frac{1}{Re}$ where Re is the Reynolds number, $\gamma = \frac{1}{We^*}$ where $We^*$ is the modified Weber number that measures relative strengths of kenetic and surface energies, and $\mu$ is the chemical potential:

$$\begin{aligned} \mu := \delta _\phi E = \frac{1}{\varepsilon } \left( \phi ^3 - \phi \right) - \varepsilon \Delta \phi . \end{aligned}$$

(1.3)

Here $\delta _\phi E$ denotes the variational derivative of (1.1) with respect to $\phi$. The equilibria are the pure phases $\phi = \pm 1$. The boundary conditions are of the following types: local thermodynamic equilibrium ($\partial _n\phi = 0$); no-flux ($\partial _n\mu =0$); and no-penetration/no-slip ($\mathbf{u} = \mathbf{0}$).

A weak formulation of (1.2a)–(1.2e) may be written as follows: find $(\phi ,\mu ,\mathbf{u},p)$ such that

$$\begin{aligned} \phi \in&\, L^\infty \left( 0,T;H^1(\Omega )\right) \cap L^4\left( 0,T;L^\infty (\Omega )\right) , \end{aligned}$$

(1.4a)

$$\begin{aligned} \partial _t \phi \in&\, L^2 \left( 0,T; {H_N^{-1}}(\Omega )\right) , \end{aligned}$$

(1.4b)

$$\begin{aligned} \mu \in&\, L^2 \left( 0,T;H^1(\Omega )\right) , \end{aligned}$$

(1.4c)

$$\begin{aligned} \mathbf{u}\in&\, L^2 \left( 0,T;\mathbf{H}^1_0(\Omega )\right) \cap L^\infty \left( 0,T; \mathbf{L}^2(\Omega )\right) , \end{aligned}$$

(1.4d)

$$\begin{aligned} \partial _t \mathbf{u}\in&\, L^2 \left( 0,T;\mathbf{H}^{-1}(\Omega )\right) , \end{aligned}$$

(1.4e)

$$\begin{aligned} p \in&\, L^2\left( 0,T;L^2_0(\Omega )\right) , \end{aligned}$$

(1.4f)

and there hold for almost all $t\in (0,T)$

$$\begin{aligned} \langle \partial _t \phi ,\nu \rangle + \varepsilon \,a\left( \mu , \nu \right) + b\left( \phi , \mathbf{u}, \nu \right)&= 0, \quad \forall \,\nu \in H^1(\Omega ), \end{aligned}$$

(1.5a)

$$\begin{aligned} \left( \mu , \psi \right) -\varepsilon \,a\left( \phi , \psi \right) - \varepsilon ^{-1}\left( \phi ^3-\phi , \psi \right)&= 0, \quad \forall \,\psi \in H^1(\Omega ), \end{aligned}$$

(1.5b)

$$\begin{aligned} \langle \partial _t \mathbf{u}, \mathbf{v}\rangle + \eta \, a\left( \mathbf{u}, \mathbf{v} \right) + B\left( \mathbf{u}, \mathbf{u}, \mathbf{v} \right) - c\left( \mathbf{v}, p \right) - \gamma \, b\left( \phi , \mathbf{v}, \mu \right)&=0, \quad \forall \, \mathbf{v}\in \mathbf{H}^1_0(\Omega ), \end{aligned}$$

(1.5c)

$$\begin{aligned} c\left( \mathbf{u}, q \right)&=0, \quad \forall \, q \in L^2_0(\Omega ), \end{aligned}$$

(1.5d)

where

$$\begin{aligned} a\left( u, v \right) := \left( \nabla u, \nabla v \right) , \quad b\left( \psi , \mathbf{v}, \nu \right) := \left( \nabla \psi \cdot \mathbf{v}, \nu \right) , \end{aligned}$$

(1.6)

$$\begin{aligned} c\left( \mathbf{v}, q \right) := \left( \nabla \cdot \mathbf{v}, q \right) ,\quad B\left( \mathbf{u}, \mathbf{v}, \mathbf{w} \right) := \frac{1}{2}\left[ \left( \mathbf{u}\cdot \nabla \mathbf{v}, \mathbf{w} \right) - \left( \mathbf{u}\cdot \nabla \mathbf{w}, \mathbf{v} \right) \right] , \end{aligned}$$

(1.7)

with the “compatible” initial data

$$\begin{aligned} \phi (0)&= \phi _0 \in H^2_N(\Omega ) := \left\{ v\in H^2(\Omega ) \,| \,\partial _n v = 0 \,\text{ on } \,\partial \Omega \right\} , \nonumber \\ \mathbf{u}(0)&= \mathbf{u}_0 \in \mathbf{V} := \left\{ \mathbf{v}\in \mathbf{H}^1_0(\Omega ) | \left( \nabla \cdot \mathbf{v}, q \right) = 0, \forall q \in L^2_0(\Omega )\right\} , \end{aligned}$$

(1.8)

and we have taken $M(\phi ) \equiv 1$. The consideration of non-constant mobility functions is reserved for future work. Observe that the homogeneous Neumann boundary conditions associated with the phase variables $\phi$ and $\mu$ are natural in this mixed weak formulation of the problem (in the sense that the boundary conditions do not have to be imposed via the spaces). We define the space $L^2_0$ as the subspace of functions of $L^2$ that have mean zero. Furthermore, we state the following definitions of which the first is non-standard: ${H_N^{-1}}(\Omega ) := \left( H^1(\Omega )\right) ^*$, $\mathbf{H}_0^1(\Omega ):= \left[ H_0^1(\Omega )\right] ^d$, $\mathbf{H}^{-1}(\Omega ) := \left( \mathbf{H}_0^1(\Omega )\right) ^*$, and $\langle \, \cdot \,, \, \cdot \, \rangle$ as the duality paring between ${H_N^{-1}}$ and $H^1$ in the first instance and the duality paring between $\mathbf{H}^{-1}(\Omega )$ and $\left( \mathbf{H}_0^1(\Omega )\right) ^*$ in the second. The notation $\Phi (t) := \Phi (\, \cdot \,, t)\in X$ views a spatiotemporal function as a strongly measurable map from the time interval [0, T] into an appropriate Banach space, X. We use the standard notation for function space norms and inner products. In particular, we let $\left\| u \right\| _{}:=\left\| u \right\| _{L^2}$ and $\left( u, v \right) := \left( u, v \right) _{L^2}$, for all $u,v\in L^2(\Omega )$.

The existence of weak solutions to (1.5a)–(1.5d) is well known. See, for example, [1, 30]. It is likewise straightforward to show that weak solutions of (1.5a)–(1.5d) dissipate the energy (1.1). In other words, (1.2a)–(1.2e) is a mass-conservative gradient flow with respect to the energy (1.1). Precisely, for any $t\in [0,T]$, we have the energy law

$$\begin{aligned} E(\phi (t), \mathbf{u}(t)) +\int _0^t \varepsilon \left\| \nabla \mu (s) \right\| _{}^2 + \frac{\eta }{\gamma } \left\| \nabla \mathbf{u}(s) \right\| _{}^2 ds = E(\phi _0, \mathbf{u}_0), \end{aligned}$$

(1.9)

and where mass conservation (for almost every $t\in [0,T]$, $\left( \phi (t)-\phi _0, 1 \right) = 0$) of the system (1.5a)–(1.5d) is shown by observing that $b\left( \phi , \mathbf{u}, 1 \right) = 0$, for all $\phi \in L^2(\Omega )$ and all $\mathbf{u}\in \mathbf{V}$.

Numerical methods for modeling two-phase flow via phase field approximation has been extensively investigated. See, for example, [6, 7, 10,11,12,13, 15, 16, 26,27,28, 30, 31, 33,34,35, 37,38,39], and the references therein. Of the most recent, Shen and Yang [35] proposed two new numerical schemes for the Cahn–Hilliard–Navier–Stokes equations, one based on stabilization and the other based on convex splitting. Their new schemes have the advantage of being totally decoupled, unconditionally energy stable, and adaptive in time. Additionally, the scheme which is based on stabilization is linear. They provide numerical experiments which suggest that their schemes are at least first order accurate in time. However, no rigorous error analysis was presented.

Abels et al. [2] introduce a thermodynamically consistent generalization to the Cahn–Hilliard–Navier–Stokes model for the case of non-matched densities based on a solenoidal velocity field. The authors demonstrate that their model satisfies a free energy inequality and conserves mass. The work of Abels et al. builds on the pioneering paper of Lowengrub and Truskinovsky [32] who use a mass-concentration formulation of the problem. Perhaps the fundamental difference between the approaches is that the model of Lowengrub and Truskinovsy end up with a velocity field that is not divergence free, in contrast with that of Abels et al. For this reason, and others, developing suitable numerical schemes for the model in [32] is a difficult task, but see the recent work of [17]. Garcke et al. [14] present a new time discretization scheme for the numerical simulation for the model in [2]. They show that their scheme satisfies a discrete in time energy law and go on to develop a fully discrete model which preserves that energy law. They are furthermore able to show existence of solutions to both the time discrete and fully discrete schemes. Again, however, no rigorous error analysis is undertaken for either of these schemes. Grün et al. [15, 16] provide another numerical scheme for the non-matched density model and they carry out an abstract convergence analysis for their scheme. Rigorous error analysis (with, say, optimal order error bounds) for models with non-matched densities seems to be a difficult prospect, but a very interesting line of inquiry for the future.

Most of the papers referenced above present first order accurate in time numerical schemes. Second order in time numerical schemes provide an obvious advantage over first order schemes by decreasing the amount of numerical error. On the other hand, second-order (in time) methods are almost universally more difficult to analyze than first-order methods. A few such methods have been developed in recent years [6, 20, 23, 25]. Most notably, Han and Wang [20] present a second order in time, uniquely solvable, unconditionally stable numerical scheme for the CHNS equations with match density. Their scheme is based on a second order convex splitting methodology for the Cahn–Hilliard equation and pressure-projection for the Navier–Stokes equation. The authors show that the scheme satisfies a modified discrete energy law which mimics the continuous energy law and prove that their scheme is uniquely solvable. However, no rigorous error analysis is presented and stability estimates are restricted to those gleaned from the energy law. The overall scheme is based on the Crank Nicolson time discretization and a second order Adams Bashforth extrapolation. Chen and Shen [6] have very recently refined the scheme of Han and Wang [20].

In this paper, we study a second-order in time mixed finite element scheme for the CHNS system of equations with matched densities. The method essentially combines the recently analyzed second-order method for the Cahn–Hilliard equation from [9, 18] and the pioneering second-order (in time) linear, Crank–Nicolson methodology for the Navier–Stokes equations found in [4]. The Cahn–Hilliard scheme from [9, 18] is based on a convex–concave decomposition of the energy and some key modifications of the Crank–Nicolson framework. More specifically, the contribution to the chemical potential from the convex part of the energy (1.1) is treated implicitly while that from the concave part is treated explicitly in the formation of the scheme. The mixed finite element version of the scheme was analyzed rigorously in [9]. The scheme herein is coupled, meaning the Cahn–Hilliard and Navier–Stokes equations must be solved simultaneously. But, the method is almost linear, with only a single weak nonlinearity present from the chemical potential equation. In particular, second order Adams-Bashforth extrapolations are used to linearize some terms and maintain the accuracy of the method, without compromising the unconditional energy stability and unconditional solvability of the scheme. The convergence analysis of a fully decoupled scheme, such as those in [6, 20] is far more challenging. The present work may be viewed as a first step towards analyzing such methods.

Theoretical justification for the convergence analysis and error estimates of numerical schemes applied to phase field models for fluid flow equations has attracted a great deal of attention in recent years. In particular, the recent work [8] provides an analysis for an optimal error estimate (in the energy norms) for a first-order-accurate convex splitting finite element scheme applied to the Cahn–Hilliard–Nonsteady–Stokes system. The key point of that convergence analysis is the derivation of the maximum norm bound of the phase variable, which becomes available due to the discrete $\ell ^2 (0,T; H^1)$ stability bound of the velocity field, at the numerical level. However, a careful examination shows that the same techniques from [8] cannot be directly applied to the second-order-accurate numerical scheme studied in this paper. The primary difficulty is associated with the 3 / 4 and 1 / 4 coefficient distribution in the surface diffusion for the phase variable, at time steps $t^{n+1}$, $t^{n-1}$, respectively. In turn, an $\ell ^\infty (0,T; H^2)$ estimate for the phase variable could not be derived via the discrete Gronwall inequality in the standard form.

We therefore present an alternate approach to recover this $\ell ^\infty (0,T; H^2)$ estimate for the phase field variable. A backward in time induction estimate for the $H^2$ norm of the phase field variable is applied. In addition, its combination with the $\ell ^\infty (0,T; L^2)$ estimate for the chemical potential leads to an inequality involving a double sum term, with the second sum in the form of $\sum _{j=1}^m (\frac{1}{3})^{m-j}$. Subsequently, we apply a novel discrete Gronwall inequality, namely Lemma 4.2 in Appendix 4, so that an $\ell ^\infty (0,T; H^2)$ bound for the numerical solution of the phase variable is obtained. Moreover, the growth of this bound is at most linear in time, which is a remarkable result.

It turns out that this stability bound greatly facilitates the second order convergence analysis in the energy norms for the numerical scheme presented in this paper. We point out that because of the $\ell ^\infty (0,T; H^2)$ bound for the discrete phase variable, we are able to carry out the analysis on the Navier–Stokes part of the system that is much in the spirit of that which appears in Baker’s groundbreaking paper [4]. Due to the increased complexity of numerical calculations and the appearance of the nonlinear convection terms, a few more technical lemmas are required for the analysis included in this paper compared to the work presented in [8] for the Cahn–Hilliard–Nonsteady–Stokes system. The use of these lemmas results in a numerical scheme which attains optimal convergence estimates in the appropriate energy norms: $\ell ^\infty (0,T; H^1)$ for the phase variable and $\ell ^2 (0,T; H^1)$ for the chemical potential. Moreover, such convergence estimates are unconditional: no scaling law is required between the time step size $\tau$ and the spatial grid size h.

The remainder of the paper is organized as follows. In Sect. 2, we define our second order (in time) mixed finite element scheme and prove that the scheme is unconditionally stable and solvable with respect to both the time and space step sizes. In Sect. 3, we provide a rigorous error analysis for the scheme under suitable regularity assumptions for the PDE solution. Finally, a few discrete Gronwall inequalities are reviewed and analyzed in Appendix 4.

2 A second-order-in-time, mixed finite element scheme

2.1 Definition of the scheme

Let M be a positive integer and $0=t_0< t_1< \cdots < t_M = T$ be a uniform partition of [0, T], with $\tau = t_{i+1}-t_{i}$ and $i=0,\ldots ,M-1$. Suppose ${\mathcal T}_h = \left\{ K \right\}$ is a conforming, shape-regular, quasi-uniform family of triangulations of $\Omega$. For $r\in \mathbb {Z}^+$, define $\mathcal {M}_r^h := \left\{ v\in C^0(\Omega ) \, | \,v|_K \in {\mathcal P}_r(K), \,\forall \,\, K\in \mathcal {T}_h \right\} \subset H^1(\Omega )$ and $\mathcal {M}_{r,0}^h:= \mathcal {M}_r^h \cap H_0^1(\Omega )$.

For a given positive integer q, we define the following:

$$\begin{aligned} S_h&:= \mathcal {M}_q^h, \\ \mathring{S}_h&:= S_h\cap L_0^2(\Omega ), \\ \mathbf{X}_h&:= \left\{ \mathbf{v}\in \left[ C^0(\Omega )\right] ^d \ | \ v_i \in \mathcal {M}_{q+1,0}^h, i = 1, \ldots , d \right\} , \\ \mathbf{V}_h&:= \left\{ \mathbf{v}\in \mathbf{X}_h\ | \ \left( \nabla \cdot \mathbf{v}, w \right) = 0, \forall w \in \mathring{S}_h\right\} . \end{aligned}$$

With the finite element spaces defined above, our mixed second-order energy stable scheme is defined as follows: for any $1\le m\le M$, given $\phi _h^{m}, \phi _h^{m-1} \in S_h, \mathbf{u}_h^m, \mathbf{u}_h^{m-1} \in \mathbf{X}_h, p_h^{m} \in \mathring{S}_h$ find $\phi _h^{m+1},\mu _h^{m+\frac{1}{2}} \in S_h, \mathbf{u}_h^{m+1} \in \mathbf{X}_h,$ and $p_h^{m+1} \in \mathring{S}_h$ such that

$$\begin{aligned}&\left( \delta _\tau \phi _h^{m+\frac{1}{2}}, \nu \right) + \varepsilon \,a\left( \mu _h^{m+\frac{1}{2}}, \nu \right) + b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \nu \right) = \, 0, \forall \, \nu \in S_h, \end{aligned}$$

(2.1a)

$$\begin{aligned}&\frac{1}{\varepsilon } \,\left( \chi \left( \phi _h^{m+1},\phi _h^m\right) , \psi \right) - \frac{1}{\varepsilon } \left( \tilde{\phi }_h^{m+\frac{1}{2}}, \psi \right) \nonumber \\&+ \varepsilon \,a\left( \check{\phi }_h^{m+\frac{1}{2}}, \psi \right) - \left( \mu _h^{m+\frac{1}{2}}, \psi \right) = \, 0, \forall \, \psi \in S_h, \end{aligned}$$

(2.1b)

$$\begin{aligned}&\left( \delta _\tau \mathbf{u}_h^{m+\frac{1}{2}}, \mathbf{v} \right) + \eta \, a\left( \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \mathbf{v} \right) + B\left( \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \mathbf{v} \right) - c\left( \mathbf{v}, \bar{p}_h^{m+\frac{1}{2}} \right) \nonumber \\&\quad - \gamma \, b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \mathbf{v}, \mu _h^{m+\frac{1}{2}} \right) = \, 0, \forall \, \mathbf{v}\in \mathbf{X}_h, \end{aligned}$$

(2.1c)

$$\begin{aligned}&c\left( \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, q \right) = \, 0, \forall \, q \in \mathring{S}_h, \end{aligned}$$

(2.1d)

where

$$\begin{aligned} \delta _\tau \phi _h^{m+\frac{1}{2}}&:= \frac{\phi _h^{m+1} - \phi _h^{m}}{\tau }, \quad \bar{\phi }_h^{m+\frac{1}{2}} := \frac{1}{2}\phi _h^{m+1} + \frac{1}{2}\phi _h^m, \quad \tilde{\phi }_h^{m+\frac{1}{2}} := \frac{3}{2} \phi _h^m - \frac{1}{2}\phi _h^{m-1}, \nonumber \\ \check{\phi }_h^{m+\frac{1}{2}}&:= \frac{3}{4} \phi _h^{m+1} + \frac{1}{4} \phi _h^{m-1}, \quad \chi \left( \phi _h^{m+1},\phi _h^m\right) := \frac{1}{2}\left( \left( \phi _h^{m+1}\right) ^2 + \left( \phi _h^{m}\right) ^2\right) \bar{\phi }_h^{m+\frac{1}{2}}. \end{aligned}$$

(2.2)

The notation involving the pressure and velocity approximations are similar. For initial conditions we take

$$\begin{aligned} \phi _h^0&:= R_h \phi _0, \ \phi _h^1 := R_h \phi (\tau ), \quad \mathbf{u}_h^0 := \mathbf{P}_h \mathbf{u}_0, \ \mathbf{u}_h^1 := \mathbf{P}_h \mathbf{u}(\tau ), \nonumber \\ p_h^0&:= P_h p_0,\ p_h^1 := P_h p(\tau ), \end{aligned}$$

(2.3)

where $R_h: H^1(\Omega ) \rightarrow S_h$ is the Ritz projection,

$$\begin{aligned} a\left( R_h\phi - \phi , \xi \right) = 0, \quad \forall \, \xi \in S_h, \quad \left( R_h \phi -\phi , 1 \right) =0, \end{aligned}$$

(2.4)

and $( \mathbf{P}_h, P_h) : \mathbf{V} \times L^2_0 \rightarrow \mathbf{V}_h\times \mathring{S}_h$ is the Stokes projection,

$$\begin{aligned} \eta \, a\left( \mathbf{P}_h \mathbf{u}- \mathbf{u}, \mathbf{v} \right) - c\left( \mathbf{v}, P_h p - p \right)&= 0, \quad \forall \, \mathbf{v}\in \mathbf{X}_h, \nonumber \\ c\left( \mathbf{P}_h \mathbf{u}- \mathbf{u}, q \right)&= 0, \quad \forall \, q \in \mathring{S}_h. \end{aligned}$$

(2.5)

It will be useful for our stability analyses to define the chemical potential at the $\frac{1}{2}$ time step via

$$\begin{aligned} \left( \mu _h^{\frac{1}{2}}, \psi \right) := \frac{1}{\varepsilon } \,\left( \chi \left( \phi _h^1,\phi _h^0\right) , \psi \right) - \frac{1}{\varepsilon } \left( \bar{\phi }_h^{\frac{1}{2}}, \psi \right) + \varepsilon \,a\left( \bar{\phi }_h^{\frac{1}{2}}, \psi \right) , \quad \forall \, \psi \in S_h. \end{aligned}$$

(2.6)

We also define the residual function $\rho _h^\frac{1}{2}\in S_h$ that solves

$$\begin{aligned} \left( \rho _h^{\frac{1}{2}}, \nu \right) := \left( \delta _\tau \phi _h^{\frac{1}{2}}, \nu \right) + \varepsilon \,a\left( \mu _h^{\frac{1}{2}}, \nu \right) + b\left( \bar{\phi }_h^{\frac{1}{2}}, \bar{\mathbf{u}}_h^{\frac{1}{2}}, \nu \right) , \quad \forall \, \nu \in S_h. \end{aligned}$$

(2.7)

While we do not expect the residual $\rho _h^\frac{1}{2}$ to be identically zero for finite $h,\tau > 0$, it will be stable in the relevant norms with the assumption of sufficiently regular PDE solutions.

Remark 2.1

We have assumed exact expressions for $\phi _h^1$ and $\mathbf{u}_h^1$. This is done to manage the length of the manuscript. We can employ a separate initialization scheme, but the analysis becomes far more tedious. See, for example, [9]. We point out that, because of the properties of the Ritz projection,

$$\begin{aligned} \left( \phi _h^0, 1 \right) = \left( \phi _h^1, 1 \right) , \end{aligned}$$

(2.8)

under the natural assumption that $\left( \phi (0), 1 \right) = \left( \phi (\tau ), 1 \right)$. Furthermore, note that this implies, $\left( \delta _\tau \phi _h^{\frac{1}{2}}, 1 \right) = 0$.

Proposition 2.2

Suppose that $\psi \in S_h$ and $\mathbf{v}\in \mathbf{V}_h$ are arbitrary. Then

$$\begin{aligned} b\left( \psi , \mathbf{v}, 1 \right) = 0. \end{aligned}$$

(2.9)

Proof

Using integration-by-parts, we get

$$\begin{aligned} b\left( \psi , \mathbf{v}, 1 \right) = \left( \nabla \psi , \mathbf{v} \right) = -\left( \psi , \nabla \cdot \mathbf{v} \right)&= -\overline{\psi }\left( 1, \nabla \cdot \mathbf{v} \right) -\left( \psi -\overline{\psi }, \nabla \cdot \mathbf{v} \right) \nonumber \\&= -\overline{\psi }c\left( 1, \mathbf{v} \right) -c\left( \psi -\overline{\psi }, \mathbf{v} \right) = 0. \end{aligned}$$

(2.10)

Observe that $c\left( 1, \mathbf{v} \right) =0$ by the divergence theorem, using $\mathbf{v}\cdot \mathbf{n}=0$ on $\partial \Omega$, and $c\left( \psi -\overline{\psi }, \mathbf{v} \right) =0$ since $\psi -\overline{\psi }\in \mathring{S}_h$ and $\mathbf{v}\in \mathbf{V}_h$. $\square$

Remark 2.3

The last result relies on the fact that $\psi -\overline{\psi }\in \mathring{S}_h$. In other words, the phase field space should be a subspace of the pressure space, which is restrictive but simplifies the analysis. If this does not hold, mass conservation is lost with the current scheme. On the other hand, if we define an alternate trilinear form

$$\begin{aligned} b(\psi ,{\mathbf{v}},{\nu }) := \left( \nabla \psi \cdot {\mathbf{v}}, \nu \right) \left( \nabla \cdot {\mathbf{v}}, \psi \nu \right) , \end{aligned}$$

we can decouple the pressure space from the phase space and still prove all of our results. The analysis of this case will be considered in a future work.

Remark 2.4

For the Stokes projection, if the family of meshes satisfy certain reasonable properties [5], we have

$$\begin{aligned} \left\| \mathbf{P}_h \mathbf{u}-\mathbf{u} \right\| _{} + h\left\| \nabla \left( \mathbf{P}_h \mathbf{u}-\mathbf{u}\right) \right\| _{} + h\left\| P_h p - p \right\| _{} \le C h^{s+1}\left( \left| \mathbf{u}\right| _{H^{s+1}} + \left| p\right| _{H^s}\right) , \end{aligned}$$

(2.11)

provided that $(\mathbf{u},p)\in \mathbf{H}_0^1(\Omega )\cap \mathbf{H}^{s+1}(\Omega )\times H^s(\Omega )$, for all $0\le s \le q+1$. In fact, for our analysis, we do not need the optimal case $s = q+1$. We only require that the sub-optimal case $s = q$ holds. In other words, we will only assume $(\mathbf{u},p)\in \mathbf{H}_0^1(\Omega )\cap \mathbf{H}^{q+1}(\Omega )\times H^q(\Omega )$. See Assumption 3.1.

Following similar arguments to what are given in [8], we get the following theorem, which we state without proof:

Theorem 2.5

For any $1\le m\le M-1$, the fully discrete scheme (2.1a)–(2.1d) is uniquely solvable and mass conservative, i.e., $\left( \phi _h^m-\phi ^0, 1 \right) {} = 0$.

2.2 Unconditional energy stability

We now show that the solutions to our scheme enjoy stability properties that are similar to those of the PDE solutions, and moreover, these properties hold regardless of the sizes of h and $\tau$. The first property, the unconditional energy stability, is a direct result of the convex decomposition.

Consider the modified energy

$$\begin{aligned} F(\phi , \psi , \mathbf{u}) := E(\phi , \mathbf{u}) + \frac{1}{4\varepsilon } \left\| \phi - \psi \right\| _{}^2 + \frac{\varepsilon }{8} \left\| \nabla \phi - \nabla \psi \right\| _{}^2, \end{aligned}$$

where $E(\phi , \mathbf{u})$ is defined as above.

Lemma 2.6

Let $(\phi _h^{m+1}, \mu _h^{m+\frac{1}{2}}, \mathbf{u}_h^{m+1}, p_h^{m+1}) \in S_h\times S_h \times \mathbf{X}_h\times \mathring{S}_h$ be the unique solution of (2.1a)–(2.1d), for $1\le m\le M-1$. Then the following energy law holds for any $h,\, \tau >0$:

$$\begin{aligned}&F\left( \phi _h^{\ell +1}, \phi _h^{\ell }, \mathbf{u}_h^{\ell +1} \right) + \tau \sum _{m=1}^\ell \left( \varepsilon \left\| \nabla \mu _h^{m+\frac{1}{2}} \right\| _{}^2 + \frac{\eta }{\gamma } \left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \right) \nonumber \\&\quad \quad + \sum _{m=1}^\ell \Bigg [ \frac{1}{4\varepsilon } \left\| \phi _h^{m+1} - 2 \phi _h^m + \phi _h^{m-1} \right\| _{}^2 + \frac{\varepsilon }{8} \left\| \nabla \phi _h^{m+1} - 2 \nabla \phi _h^m + \nabla \phi _h^{m-1} \right\| _{}^2 \Biggr ] \nonumber \\&\quad = F\left( \phi _h^1, \phi _h^0, \mathbf{u}_h^1 \right) , \end{aligned}$$

(2.12)

for all $1 \le \ell \le M-1$.

Proof

Setting $\nu = \mu _h^{m+\frac{1}{2}}$ in (2.1a), $\psi = \delta _\tau \phi _h^{m+\frac{1}{2}}$ in (2.1b), $\mathbf{v}= \frac{1}{\gamma } \bar{\mathbf{u}}_h^{m+\frac{1}{2}}$ in (2.1c), and $q = \frac{1}{\gamma } \bar{p}_h^{m+\frac{1}{2}}$ in (2.1d) gives

$$\begin{aligned} \left( \delta _\tau \phi _h^{m+\frac{1}{2}}, \mu _h^{m+\frac{1}{2}} \right) + \varepsilon \left\| \nabla \mu _h^{m+\frac{1}{2}} \right\| _{}^2 + b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \mu _h^{m+\frac{1}{2}} \right)&= 0, \end{aligned}$$

(2.13)

$$\begin{aligned} \frac{1}{\varepsilon } \,\left( \chi \left( \phi _h^{m+1},\phi _h^m\right) , \delta _\tau \phi _h^{m+\frac{1}{2}} \right) - \frac{1}{\varepsilon } \left( \tilde{\phi }_h^{m+\frac{1}{2}}, \delta _\tau \phi _h^{m+\frac{1}{2}} \right) \quad&\nonumber \\ + \, \varepsilon \,a\left( \check{\phi }_h^{m+\frac{1}{2}}, \delta _\tau \phi _h^{m+\frac{1}{2}} \right) - \left( \mu _h^{m+\frac{1}{2}}, \delta _\tau \phi _h^{m+\frac{1}{2}} \right)&= 0, \end{aligned}$$

(2.14)

$$\begin{aligned} \frac{1}{\gamma } \left( \delta _\tau \mathbf{u}_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right) + \frac{\eta }{\gamma } \, \left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 + \frac{1}{\gamma } B\left( \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right) \quad&\nonumber \\ - \, \frac{1}{\gamma } c\left( \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{p}_h^{m+\frac{1}{2}} \right) - b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \mu _h^{m+\frac{1}{2}} \right)&= 0, \end{aligned}$$

(2.15)

$$\begin{aligned} \frac{1}{\gamma } c\left( \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{p}_h^{m+\frac{1}{2}} \right)&= 0. \end{aligned}$$

(2.16)

Combining (2.13)–(2.16), using the following identities

$$\begin{aligned}&\left( \chi \left( \phi _h^{m+1},\phi _h^m\right) , \delta _\tau \phi _h^{m+\frac{1}{2}} \right) - \left( \tilde{\phi }_h^{m+\frac{1}{2}}, \delta _\tau \phi _h^{m+\frac{1}{2}} \right) \nonumber \\&\quad = \frac{1}{4\tau } \left( \left\| \left( \phi _h^{m+1}\right) ^2-1 \right\| _{}^2 - \left\| \left( \phi _h^{m}\right) ^2-1 \right\| _{}^2\right) \nonumber \\&\quad \quad + \frac{1}{4\tau } \left( \left\| \phi _h^{m+1} - \phi _h^m \right\| _{}^2 - \left\| \phi _h^{m} - \phi _h^{m-1} \right\| _{}^2\right) \nonumber \\&\quad \quad + \frac{1}{4\tau } \left\| \phi _h^{m+1} - 2 \phi _h^m + \phi _h^{m-1} \right\| _{}^2, \end{aligned}$$

(2.17)

$$\begin{aligned}&a\left( \check{\phi }_h^{m+\frac{1}{2}}, \delta _\tau \phi _h^{m+\frac{1}{2}} \right) = \, \frac{1}{2 \tau } \left( \left\| \nabla \phi _h^{m+1} \right\| _{}^2 - \left\| \nabla \phi _h^{m} \right\| _{}^2 \right) \nonumber \\&\quad \quad + \frac{1}{8 \tau } \left\| \nabla \phi _h^{m+1} - 2 \nabla \phi _h^m + \nabla \phi _h^{m-1} \right\| _{}^2 \nonumber \\&\quad \quad + \frac{1}{8 \tau } \left( \left\| \nabla \phi _h^{m+1} - \nabla \phi _h^m \right\| _{}^2 - \left\| \nabla \phi _h^{m} - \nabla \phi _h^{m-1} \right\| _{}^2 \right) , \end{aligned}$$

(2.18)

and applying the operator $\tau \sum _{m=1}^\ell$ to the combined equations, we get (2.12). $\square$

Before proceeding, we define the discrete Laplacian, $\Delta _h: S_h \rightarrow \mathring{S}_h$, as follows: for any $v_h\in S_h$, $\Delta _h v_h\in \mathring{S}_h$ denotes the unique solution to the problem

$$\begin{aligned} \left( \Delta _h v_h, \xi \right) = -a\left( v_h, \xi \right) , \quad \forall \, \,\xi \in S_h. \end{aligned}$$

(2.19)

In particular, setting $\xi = \Delta _h v_h$ in (2.19), we obtain

$$\begin{aligned} \left\| \Delta _h v_h \right\| _{}^2 = -a\left( v_h, \Delta _hv_h \right) . \end{aligned}$$

Furthermore, we make the following assumptions about the initial data.

Assumption 2.7

The initial data satisfy the following stabilities:

$$\begin{aligned} E\left( \phi _h^0, \mathbf{u}_h^0\right) \le C, \\ F\left( \phi _h^1, \phi _h^0, \mathbf{u}_h^1\right) = E(\phi _h^1, \mathbf{u}_h^1) + \frac{1}{4\varepsilon } \left\| \phi _h^1 - \phi _h^0 \right\| _{}^2 + \frac{\varepsilon }{8} \left\| \nabla \phi _h^1 - \nabla \phi _h^0 \right\| _{}^2 \le C, \\ \tau \left\| \nabla \mu _h^{\frac{1}{2}} \right\| _{}^2 + \tau \left\| \nabla \bar{\mathbf{u}}_h^{\frac{1}{2}} \right\| _{}^2 \le C, \\ \tau \left\| \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{{H_N^{-1}}}^2 + \tau \left\| \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{-1,h}^2 +\tau \left\| \mu _h^{\frac{1}{2}} \right\| _{}^2 \le C, \\ \tau \left\| \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}^2 + \left\| \mu _h^{\frac{1}{2}} \right\| _{}^2+ \left\| \rho _h^{\frac{1}{2}} \right\| _{}^2+\left\| \Delta _h \phi _h^0 \right\| _{}^2+\left\| \Delta _h \phi _h^1 \right\| _{}^2 \le C, \end{aligned}$$

where $C>0$ is independent of h and $\tau$.

See [3, 8, 31] for a definition of the norm $\left\| {\cdot } \right\| _{-1,h}$. We also need the following discrete Gagliardo–Nirenberg inequalities. See, for example, [21, 31].

Proposition 2.8

If $\Omega$ is a convex polygonal or polyhedral domain, and ${\mathcal {T}}_h$ is a globally quasi-uniform triangulation of $\Omega$, we have

$$\begin{aligned} \left\| \psi _h \right\| _{L^\infty } \le&\ C\left\| \Delta _h \psi _h \right\| _{}^{\frac{d}{2(6-d)}} \,\left\| \psi _h \right\| _{L^6}^{\frac{3(4-d)}{2(6-d)}} + C\left\| \psi _h \right\| _{L^6}, \quad \forall \, \psi _h \in S_h, \qquad d=2,3, \end{aligned}$$

(2.20)

$$\begin{aligned} \left\| \nabla \psi _h \right\| _{L^4} \le&\ C\left( \left\| \nabla \psi _h \right\| _{}+\left\| \Delta _h \psi _h \right\| _{}\right) ^{\frac{d}{4}} \left\| \nabla \psi _h \right\| _{}^{\frac{4-d}{4}}, \quad \forall \, \psi _h \in S_h,\quad d= 2,3, \end{aligned}$$

(2.21)

for some constant $C>0$ that is independent of h.

Remark 2.9

In the sequel, we will not track the dependences of the estimates on the interface parameter $\varepsilon >0$ or the viscosity $\eta >0$, though these may be important.

The next result follows from energy stability and Assumption 2.7. We omit the proof.

Lemma 2.10

Let $(\phi _h^{m+1}, \mu _h^{m+\frac{1}{2}}, \mathbf{u}_h^{m+1}, p_h^{m+1}) \in S_h\times S_h \times \mathbf{X}_h\times \mathring{S}_h$ be the unique solution of (2.1a)–(2.1d), for $1\le m\le M-1$. Then the following estimates hold for any $h,\, \tau >0$:

$$\begin{aligned} \max _{0\le m\le M} \left[ \left\| \nabla \phi _h^m \right\| _{}^2 + \left\| \left( \phi _h^m\right) ^2-1 \right\| _{}^2 + \left\| \mathbf{u}_h^m \right\| _{}^2 \right]&\le C, \end{aligned}$$

(2.22)

$$\begin{aligned} \max _{0\le m\le M}\left[ \left\| \phi _h^m \right\| _{L^4}^4 +\left\| \phi _h^m \right\| _{}^2 +\left\| \phi _h^m \right\| _{H^1}^2 \right]&\le C, \end{aligned}$$

(2.23)

$$\begin{aligned} \max _{1\le m\le M}\left[ \left\| \phi _h^m-\phi _h^{m-1} \right\| _{}^2 + \left\| \nabla \phi _h^m - \nabla \phi _h^{m-1} \right\| _{}^2\right]&\le C, \end{aligned}$$

(2.24)

$$\begin{aligned} \tau \sum _{m=0}^{M-1} \left[ \left\| \nabla \mu _h^{m+\frac{1}{2}} \right\| _{}^2 + \left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \right]&\le C, \end{aligned}$$

(2.25)

$$\begin{aligned} \sum _{m=1}^{M-1} \left[ \left\| \phi _h^{m+1} - 2 \phi _h^m + \phi _h^{m-1} \right\| _{}^2 + \left\| \nabla \phi _h^{m+1} - 2 \nabla \phi _h^m + \nabla \phi _h^{m-1} \right\| _{}^2 \right]&\le C, \end{aligned}$$

(2.26)

for some constant $C>0$ that is independent of h, $\tau$, and T.

We are able to prove the next set of a priori stability estimates without any restrictions on h and $\tau$.

Lemma 2.11

Let $(\phi _h^{m+1}, \mu _h^{m+\frac{1}{2}}, \mathbf{u}_h^{m+1}, p_h^{m+1}) \in S_h\times S_h \times \mathbf{X}_h\times \mathring{S}_h$ be the unique solution of (2.1a)–(2.1d), $1\le m \le M-1$. Then the following estimates hold for any $h,\, \tau >0$:

$$\begin{aligned}&\tau \sum _{m=0}^{M-1} \Bigg [ \left\| \delta _\tau \phi _h^{m+\frac{1}{2}} \right\| _{{H_N^{-1}}}^2 +\left\| \delta _\tau \phi _h^{m+\frac{1}{2}} \right\| _{-1,h}^2 \Bigg ] \le C, \end{aligned}$$

(2.27)

$$\begin{aligned}&\tau \sum _{m=0}^{M-1} \left\| \mu _h^{m+\frac{1}{2}} \right\| _{}^2 \le C (T+1), \end{aligned}$$

(2.28)

$$\begin{aligned}&\varepsilon \left\| \Delta _h \check{\phi }_h^{m+\frac{1}{2}} \right\| _{}^2 \le \left\| \mu _h^{m+\frac{1}{2}} \right\| _{}^2 + C, \quad \forall \ 1 \le m \le M-1, \end{aligned}$$

(2.29)

$$\begin{aligned}&\varepsilon \left\| \Delta _h \bar{\phi }_h^{\frac{1}{2}} \right\| _{}^2 \le \left\| \mu _h^{\frac{1}{2}} \right\| _{}^2 + C, \end{aligned}$$

(2.30)

$$\begin{aligned}&\tau \sum _{m=1}^{M-1} \Bigg [ \left\| \Delta _h \check{\phi }_h^{m+\frac{1}{2}} \right\| _{}^2 + \left\| \check{\phi }_h^{m+\frac{1}{2}} \right\| _{L^\infty }^{\frac{4(6-d)}{d}} \Bigg ] \le C (T+1), \end{aligned}$$

(2.31)

for some constant $C>0$ that is independent of h, $\tau$, and T.

The proof of Lemma 2.11 is very similar to proofs of [9, Lemma 2.7] and [8, Lemma 2.13]. We omit the details for the sake of brevity.

2.3 Unconditional $\ell ^\infty (0,T;L^\infty )$ stability of the discrete phase variable

Lemma 2.12

Let $(\phi _h^{m+1}, \mu _h^{m+\frac{1}{2}}, \mathbf{u}_h^{m+1}, p_h^{m+1}) \in S_h\times S_h \times \mathbf{X}_h\times \mathring{S}_h$ be the unique solution of (2.1a)–(2.1d), for $1\le m\le M-1$. Then the following estimates hold for any $h,\, \tau >0$:

$$\begin{aligned} \left\| \Delta _h \phi _h^{2m} \right\| _{}^2&\le \frac{8}{3} \sum _{k=1}^m \left( \frac{1}{3}\right) ^{k-1} \left\| \Delta _h \check{\phi }_h^{2k-\frac{1}{2}} \right\| _{}^2 + \left( \frac{1}{3}\right) ^m \cdot \left\| \Delta _h \phi _h^0 \right\| _{}^2, \end{aligned}$$

(2.32)

$$\begin{aligned} \left\| \Delta _h \phi _h^{2m+1} \right\| _{}^2&\le \frac{8}{3} \sum _{k=1}^m \left( \frac{1}{3}\right) ^{k-1} \left\| \Delta _h \check{\phi }_h^{(2k+1)-\frac{1}{2}} \right\| _{}^2 + \left( \frac{1}{3}\right) ^m \cdot \left\| \Delta _h \phi _h^1 \right\| _{}^2. \end{aligned}$$

(2.33)

Proof

Using the definition of $\check{\phi }_h^{m+\frac{1}{2}}$, for $1\le m\le M-1$, we have the following inequality:

$$\begin{aligned} \left\| \Delta _h \check{\phi }_h^{m+\frac{1}{2}} \right\| _{}^2= & {} \left\| \Delta _h \left( \frac{3}{4} \phi _h^{m+1} + \frac{1}{4} \phi _h^{m-1}\right) \right\| _{}^2 \nonumber \\= & {} \frac{9}{16} \left\| \Delta _h \phi _h^{m+1} \right\| _{}^2 + \frac{3}{8} \left( \Delta _h \phi _h^{m+1}, \Delta _h \phi _h^{m-1} \right) + \frac{1}{16} \left\| \Delta _h \phi _h^{m-1} \right\| _{}^2 \nonumber \\\ge & {} \frac{9}{16} \left\| \Delta _h \phi _h^{m+1} \right\| _{}^2 - \frac{3}{16} \left\| \Delta _h \phi _h^{m+1} \right\| _{}^2\nonumber \\&- \frac{3}{16} \left\| \Delta _h \phi _h^{m-1} \right\| _{}^2 + \frac{1}{16} \left\| \Delta _h \phi _h^{m-1} \right\| _{}^2 \nonumber \\= & {} \frac{3}{8} \left\| \Delta _h \phi _h^{m+1} \right\| _{}^2 - \frac{1}{8} \left\| \Delta _h \phi _h^{m-1} \right\| _{}^2. \end{aligned}$$

(2.34)

Its repeated use gives the result. $\square$

We are now ready to show the main result for this section.

Lemma 2.13

Let $(\phi _h^{m+1}, \mu _h^{m+\frac{1}{2}}, \mathbf{u}_h^{m+1}, p_h^{m+1}) \in S_h\times S_h \times \mathbf{X}_h\times \mathring{S}_h$ be the unique solution of (2.1a)–(2.1d), for $1\le m\le M-1$. Then the following estimates hold for any $h,\, \tau >0$:

$$\begin{aligned}&\tau \sum _{m=0}^{M-1} \left\| \delta _\tau \phi _h^{m+\frac{1}{2}} \right\| _{}^2 \le C (T+1), \end{aligned}$$

(2.35)

$$\begin{aligned}&\max _{0\le m\le M-1} \left\| \mu _h^{m+\frac{1}{2}} \right\| _{}^2 + \max _{1\le m\le M-1} \bigg [ \left\| \Delta _h \check{\phi }_h^{m+\frac{1}{2}} \right\| _{}^2 + \left\| \check{\phi }_h^{m+\frac{1}{2}} \right\| _{L^\infty }^{\frac{4(6-d)}{d}} \bigg ] \le C(T+1), \end{aligned}$$

(2.36)

$$\begin{aligned}&\max _{0\le m\le M} \bigg [ \left\| \Delta _h \phi _h^m \right\| _{}^2 + \left\| \phi _h^m \right\| _{L^\infty }^{\frac{4(6-d)}{d}} \bigg ] \le C(T+1), \end{aligned}$$

(2.37)

for some constant $C>0$ that is independent of h, $\tau$, and T.

Proof

The proof will be completed in two parts.

Part 1: ($m=1$) Subtracting (2.6) from (2.1b) with $m=1$, we obtain

$$\begin{aligned} \left( \mu _h^{\frac{3}{2}} - \mu _h^{\frac{1}{2}}, \psi \right)&= \varepsilon \,a\left( \check{\phi }_h^{\frac{3}{2}} - \bar{\phi }_h^{\frac{1}{2}}, \psi \right) - \frac{1}{\varepsilon } \left( \tilde{\phi }_h^{\frac{3}{2}}-\bar{\phi }_h^{\frac{1}{2}}, \psi \right) \nonumber \\&\quad + \frac{1}{\varepsilon } \left( \chi \left( \phi _h^2, \phi _h^1\right) - \chi \left( \phi _h^1, \phi _h^0\right) , \psi \right) \nonumber \\&=\, \varepsilon \, a\left( \frac{3}{4} \tau \delta _\tau \phi _h^{\frac{3}{2}} + \frac{1}{4} \tau \delta _\tau \phi _h^{\frac{1}{2}}, \psi \right) - \frac{1}{\varepsilon } \left( \tau \delta _\tau \phi _h^{\frac{1}{2}}, \psi \right) \nonumber \\&\quad + \frac{1}{\varepsilon } \left( \chi \left( \phi _h^2, \phi _h^1\right) - \chi \left( \phi _h^1, \phi _h^0\right) , \psi \right) . \end{aligned}$$

(2.38)

Additionally, we take a weighted average of (2.1a) with $m=1$ and (2.7) with the weights $\frac{3}{4}$ and $\frac{1}{4}$, respectively, to obtain,

$$\begin{aligned} \left( \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}}, \nu \right) =&\ - \varepsilon \, a\left( \frac{3}{4} \mu _h^{\frac{3}{2}} + \frac{1}{4} \mu _h^{\frac{1}{2}}, \nu \right) - \frac{3}{4} b\left( \tilde{\phi }_h^{\frac{3}{2}}, \bar{\mathbf{u}}_h^{\frac{3}{2}}, \nu \right) \nonumber \\&- \frac{1}{4} b\left( \bar{\phi }_h^\frac{1}{2}, \bar{\mathbf{u}}_h^{\frac{1}{2}}, \nu \right) + \frac{1}{4}\left( \rho _h^\frac{1}{2}, \nu \right) . \end{aligned}$$

(2.39)

Taking $\psi = \frac{3}{4} \mu _h^{\frac{3}{2}} + \frac{1}{4} \mu _h^{\frac{1}{2}}$ in (2.38), $\nu = \frac{3\tau }{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{\tau }{4} \delta _\tau \phi _h^{\frac{1}{2}}$ in (2.39), and adding the results yields

$$\begin{aligned}&\left( \mu _h^{\frac{3}{2}} - \mu _h^{\frac{1}{2}}, \frac{3}{4} \mu _h^{\frac{3}{2}} + \frac{1}{4} \mu _h^{\frac{1}{2}} \right) + \tau \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}^2 \\&\quad = - \frac{1}{\varepsilon } \left( \phi _h^1 - \phi _h^0, \frac{3}{4} \mu _h^{\frac{3}{2}} + \frac{1}{4} \mu _h^{\frac{1}{2}} \right) + \frac{1}{4 \varepsilon } \left( \chi \left( \phi _h^2, \phi _h^1\right) - \chi \left( \phi _h^1, \phi _h^0\right) , 3 \mu _h^{\frac{3}{2}} + \mu _h^{\frac{1}{2}} \right) \\&\quad \quad - \frac{3}{4} b\left( \tilde{\phi }_h^{\frac{3}{2}}, \bar{\mathbf{u}}_h^{\frac{3}{2}}, \frac{3\tau }{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{\tau }{4} \delta _\tau \phi _h^{\frac{1}{2}} \right) - \frac{1}{4} b\left( \bar{\phi }_h^\frac{1}{2}, \bar{\mathbf{u}}_h^{\frac{1}{2}}, \frac{3\tau }{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{\tau }{4} \delta _\tau \phi _h^{\frac{1}{2}} \right) \\&\quad \quad + \frac{1}{4}\left( \rho _h^\frac{1}{2}, \frac{3\tau }{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{\tau }{4} \delta _\tau \phi _h^{\frac{1}{2}} \right) \\&\quad \le \ \frac{1}{4} \left\| \mu _h^{\frac{3}{2}} \right\| _{}^2 + C \left\| \mu _h^{\frac{1}{2}} \right\| _{}^2 + C \left\| \phi _h^1 \right\| _{}^2 + C \left\| \phi _h^0 \right\| _{}^2 + C \left\| \chi \left( \phi _h^2, \phi _h^1\right) \right\| _{}^2 \\&\quad \quad + C \left\| \chi \left( \phi _h^1, \phi _h^0\right) \right\| _{}^2 \\&\quad \quad + \frac{3\tau }{4} \left\| \nabla \tilde{\phi }_h^{\frac{3}{2}} \right\| _{L^4} \left\| \bar{\mathbf{u}}_h^{\frac{3}{2}} \right\| _{L^4} \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}\\&\qquad + \frac{\tau }{4} \left\| \nabla \bar{\phi }_h^\frac{1}{2} \right\| _{L^4} \left\| \bar{\mathbf{u}}_h^{\frac{1}{2}} \right\| _{L^4} \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{} \\&\quad \quad + \frac{\tau }{4} \left\| \rho _h^{\frac{1}{2}} \right\| _{} \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{} \\&\quad \le \ C + \frac{1}{4} \left\| \mu _h^{\frac{3}{2}} \right\| _{}^2 + C \tau \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}}+ \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{} \left\| \nabla \bar{\mathbf{u}}_h^{\frac{3}{2}} \right\| _{} \left( \left\| \nabla \tilde{\phi }_h^{\frac{3}{2}} \right\| _{} + \left\| \Delta _h \tilde{\phi }_h^{\frac{3}{2}} \right\| _{}\right) \\&\quad \quad + C \tau \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}}+ \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{} \left\| \nabla \bar{\mathbf{u}}_h^{\frac{1}{2}} \right\| _{} \left( \left\| \nabla \bar{\phi }_h^{\frac{1}{2}} \right\| _{} + \left\| \Delta _h \bar{\phi }_h^{\frac{1}{2}} \right\| _{}\right) \\&\qquad + \frac{\tau }{6} \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{} \\&\quad \le \ C+ \frac{1}{4} \left\| \mu _h^{\frac{3}{2}} \right\| _{}^2 + \frac{3\tau }{6} \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}}+ \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}^2 + C \tau \left\| \nabla \bar{\mathbf{u}}_h^{\frac{3}{2}} \right\| _{}^2 + C \tau \left\| \nabla \bar{\mathbf{u}}_h^{\frac{1}{2}} \right\| _{}^2 \\&\quad \le \ C+ \frac{1}{4} \left\| \mu _h^{\frac{3}{2}} \right\| _{}^2 + \frac{\tau }{2} \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}}+ \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}^2 + C \tau \left\| \nabla \bar{\mathbf{u}}_h^{\frac{3}{2}} \right\| _{}^2, \end{aligned}$$

where we have used Young’s inequality, the embedding $H^1 \hookrightarrow L^6$, estimates (2.23) and (2.21) and Assumption 2.7. Again, considering Assumption 2.7 and considering estimate (2.25) and the following inequalities

$$\begin{aligned} \left\| \frac{3}{4} \delta _\tau \phi _h^{\frac{3}{2}} + \frac{1}{4} \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}^2 \ge&\ \frac{3}{8} \left\| \delta _\tau \phi _h^{\frac{3}{2}} \right\| _{}^2 - \frac{1}{8} \left\| \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}^2 \, \, (\text{ similar } \text{ to }\, (2.34)), \\ \left( \mu _h^{\frac{3}{2}} - \mu _h^{\frac{1}{2}}, \frac{3}{4} \mu _h^{\frac{3}{2}} + \frac{1}{4} \mu _h^{\frac{1}{2}} \right) =&\ \frac{3}{4} \left\| \mu _h^{\frac{3}{2}} \right\| _{}^2 - \frac{1}{2}\left( \mu _h^{\frac{3}{2}}, \mu _h^{\frac{1}{2}} \right) \\&\quad - \frac{1}{4} \left\| \mu _h^{\frac{1}{2}} \right\| _{}^2 \ge \frac{1}{2}\left\| \mu _h^{\frac{3}{2}} \right\| _{}^2 - \frac{1}{2}\left\| \mu _h^{\frac{1}{2}} \right\| _{}^2, \end{aligned}$$

we have,

$$\begin{aligned} \frac{1}{4} \left\| \mu _h^{\frac{3}{2}} \right\| _{}^2 + \frac{3\tau }{16} \left\| \delta _\tau \phi _h^{\frac{3}{2}} \right\| _{}^2 \le C \left\| \mu _h^{\frac{1}{2}} \right\| _{}^2 + \frac{\tau }{16} \left\| \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}^2 + C \tau \left\| \nabla \bar{\mathbf{u}}_h^{\frac{3}{2}} \right\| _{}^2 + C \le C. \end{aligned}$$

(2.40)

Now, using (2.29), (2.20), the embedding $H^1(\Omega ) \hookrightarrow L^6(\Omega )$, and (2.23), we have

$$\begin{aligned} \left\| \Delta _h \check{\phi }_h^{\frac{3}{2}} \right\| _{}^2 + \left\| \check{\phi }_h^\frac{3}{2} \right\| _{L^\infty }^{\frac{4(6-d)}{d}} \le C. \end{aligned}$$

Using Lemma 2.12, (2.20), the embedding $H^1(\Omega ) \hookrightarrow L^6(\Omega )$, and (2.23), we obtain

$$\begin{aligned} \left\| \Delta _h \phi _h^{2} \right\| _{}^2 + \left\| \phi _h^2 \right\| _{L^\infty }^{\frac{4(6-d)}{d}} \le C. \end{aligned}$$

Part 2: ($2 \le m \le M-1$)

For $2 \le m \le M-1$, we subtract (2.1b) from itself at consecutive time steps to obtain

$$\begin{aligned} \left( \mu _h^{m+\frac{1}{2}} - \mu _h^{m-\frac{1}{2}}, \psi \right)&= \varepsilon \,a\left( \check{\phi }_h^{m+\frac{1}{2}} - \check{\phi }_h^{m-\frac{1}{2}}, \psi \right) - \frac{1}{\varepsilon } \left( \tilde{\phi }_h^{m+\frac{1}{2}} - \tilde{\phi }_h^{m-\frac{1}{2}}, \psi \right) \nonumber \\&\quad + \frac{1}{\varepsilon } \left( \chi \left( \phi _h^{m+1}, \phi _h^m\right) - \chi \left( \phi _h^m, \phi _h^{m-1}\right) , \psi \right) \nonumber \\&= \varepsilon \,a\left( \frac{3}{4} \tau \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \tau \delta _\tau \phi _h^{m-\frac{3}{2}}, \psi \right) \nonumber \\&\quad - \frac{1}{\varepsilon } \left( \frac{3}{2} \tau \delta _\tau \phi _h^{m-\frac{1}{2}} - \frac{1}{2}\tau \delta _\tau \phi _h^{m-\frac{3}{2}}, \psi \right) \nonumber \\&\quad + \frac{1}{4 \varepsilon } \left( \omega ^m_h \left( \phi _h^{m+1} - \phi _h^{m-1}\right) , \psi \right) , \end{aligned}$$

(2.41)

for all $\psi \in S_h$, where

$$\begin{aligned} \omega ^m_h&:= \omega \left( \phi _h^{m+1}, \phi _h^m, \phi _h^{m-1}\right) := \left( \phi _h^{m+1}\right) ^2 + \left( \phi _h^{m}\right) ^2 + \left( \phi _h^{m-1}\right) ^2 \\&\qquad + \phi _h^{m+1} \phi _h^m + \phi _h^{m+1} \phi _h^{m-1} + \phi _h^m \phi _h^{m-1}. \end{aligned}$$

We note that using the $H^1(\Omega ) \hookrightarrow L^6(\Omega )$ embedding, we achieve the following bound,

$$\begin{aligned} \left\| \omega ^m_h \right\| _{L^3} =&\, \left\| \left( \phi _h^{m+1}\right) ^2 {+} \left( \phi _h^{m}\right) ^2 {+} \left( \phi _h^{m-1}\right) ^2 {+} \phi _h^{m+1} \phi _h^m + \phi _h^{m+1} \phi _h^{m-1} {+} \phi _h^m \phi _h^{m-1} \right\| _{L^3} \\ \le&\, C \left\| \phi _h^{m+1} \right\| _{L^6}^2 + C \left\| \phi _h^{m} \right\| _{L^6}^2 + C \left\| \phi _h^{m-1} \right\| _{L^6}^2 \\ \le&\, C \left\| \phi _h^{m+1} \right\| _{H^1}^2 + C \left\| \phi _h^{m} \right\| _{H^1}^2 + C \left\| \phi _h^{m-1} \right\| _{H^1}^2 \le C. \end{aligned}$$

Now, for all $2 \le m \le M-1$, we take a weighted average of the $m+\frac{1}{2}$ and $m-\frac{3}{2}$ time steps with the weights $\frac{3}{4}$ and $\frac{1}{4}$ of (2.1a), respectively, to obtain,

$$\begin{aligned} \nonumber \left( \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} {+} \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}}, \nu \right) =&\, - \varepsilon \, a\left( \frac{3}{4} \mu _h^{m+\frac{1}{2}} {+} \frac{1}{4} \mu _h^{m-\frac{3}{2}}, \nu \right) {-} \frac{3}{4} b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \nu \right) \\&- \frac{1}{4} b\left( \tilde{\phi }_h^{m-\frac{3}{2}}, \bar{\mathbf{u}}_h^{m-\frac{3}{2}}, \nu \right) , \, \, \forall \nu \in S_h. \end{aligned}$$

(2.42)

Taking $\psi = \frac{3}{4} \mu _h^{m+\frac{1}{2}} + \frac{1}{4} \mu _h^{m-\frac{3}{2}}$ in (2.41), $\nu = \tau \left( \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right)$ in (2.42), and adding the results yields

$$\begin{aligned}&\left( \mu _h^{m+\frac{1}{2}} - \mu _h^{m-\frac{1}{2}}, \frac{3}{4} \mu _h^{m+\frac{1}{2}} + \, \frac{1}{4} \mu _h^{m-\frac{3}{2}} \right) + \tau \left\| \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{}^2 \\&\quad = \, -\frac{\tau }{\varepsilon } \left( \frac{3}{2} \delta _\tau \phi _h^{m-\frac{1}{2}} - \frac{1}{2}\delta _\tau \phi _h^{m-\frac{3}{2}}, \frac{3}{4} \mu _h^{m+\frac{1}{2}} + \frac{1}{4} \mu _h^{m-\frac{3}{2}} \right) \\&\quad \quad + \frac{\tau }{4 \varepsilon } \left( \omega ^m_h \delta _\tau \phi _h^{m+\frac{1}{2}} , \frac{3}{4} \mu _h^{m+\frac{1}{2}} + \frac{1}{4} \mu _h^{m-\frac{3}{2}} \right) \\&\quad \quad + \frac{\tau }{4 \varepsilon } \left( \omega ^m_h \delta _\tau \phi _h^{m-\frac{1}{2}}, \frac{3}{4} \mu _h^{m+\frac{1}{2}} + \frac{1}{4} \mu _h^{m-\frac{3}{2}} \right) \\&\quad \quad - \frac{3\tau }{4} b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right) \\&\quad \quad - \frac{\tau }{4} b\left( \tilde{\phi }_h^{m-\frac{3}{2}}, \bar{\mathbf{u}}_h^{m-\frac{3}{2}}, \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right) \\&\quad \le \frac{3 \tau }{8 \varepsilon } \left\| \delta _\tau \phi _h^{m-\frac{1}{2}} \right\| _{} \cdot \left\| 3\mu _h^{m+\frac{1}{2}} + \mu _h^{m-\frac{3}{2}} \right\| _{} + \frac{\tau }{8 \varepsilon } \left\| \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{} \cdot \left\| 3 \mu _h^{m+\frac{1}{2}} + \mu _h^{m-\frac{3}{2}} \right\| _{} \\&\quad \quad + \frac{\tau }{16 \varepsilon } \left\| \omega ^m_h \right\| _{L^3} \Bigg ( \left\| \delta _\tau \phi _h^{m+\frac{1}{2}} \right\| _{} \cdot \left\| 3\mu _h^{m+\frac{1}{2}} + \mu _h^{m-\frac{3}{2}} \right\| _{L^6}\\&\qquad + \left\| \delta _\tau \phi _h^{m-\frac{1}{2}} \right\| _{} \cdot \left\| 3\mu _h^{m+\frac{1}{2}} + \mu _h^{m-\frac{3}{2}} \right\| _{L^6} \Bigg ) \\&\quad \quad - \frac{3\tau }{4} b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right) \\&\quad \quad - \frac{\tau }{4} b\left( \tilde{\phi }_h^{m-\frac{3}{2}}, \bar{\mathbf{u}}_h^{m-\frac{3}{2}}, \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right) . \end{aligned}$$

Now we bound the trilinear form $b(\, \cdot \,, \, \cdot \,, \, \cdot \, )$. Using (2.21), Hölder’s inequality, and (2.22), the following estimates are available:

$$\begin{aligned}&\left| b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right) \right| \nonumber \\&\quad \le \left\| \nabla \tilde{\phi }_h^{m+\frac{1}{2}} \right\| _{L^4}\left\| \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{L^4}\left\| \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{} \nonumber \\&\quad \le C \left\| \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{} \left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{} \left( \left\| \nabla \tilde{\phi }_h^{m+\frac{1}{2}} \right\| _{} + \left\| \Delta _h \tilde{\phi }_h^{m+\frac{1}{2}} \right\| _{}\right) \nonumber \\&\quad \le \frac{1}{2} \left\| \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{}^2 + C \left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 + C \left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \left\| \Delta _h \tilde{\phi }_h^{m+\frac{1}{2}} \right\| _{}^2 , \end{aligned}$$

(2.43)

and, similarly,

$$\begin{aligned}&\left| b\left( \tilde{\phi }_h^{m-\frac{3}{2}}, \mathbf{u}_h^{m-\frac{3}{2}}, \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right) \right| \nonumber \\&\quad \le \frac{1}{2} \left\| \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{}^2 + C \left\| \nabla \bar{\mathbf{u}}_h^{m-\frac{3}{2}} \right\| _{}^2 + C \left\| \nabla \bar{\mathbf{u}}_h^{m-\frac{3}{2}} \right\| _{}^2 \left\| \Delta _h \tilde{\phi }_h^{m-\frac{3}{2}} \right\| _{}^2, \end{aligned}$$

(2.44)

for any $2 \le m \le M-1$. Therefore, we arrive at

$$\begin{aligned}&\left( \mu _h^{m+\frac{1}{2}} - \mu _h^{m-\frac{1}{2}}, \frac{3}{4} \mu _h^{m+\frac{1}{2}} + \frac{1}{4} \mu _h^{m-\frac{3}{2}} \right) + \frac{\tau }{2} \left\| \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{}^2 \nonumber \\&\quad \le \, \frac{\tau }{8} \left\| \delta _\tau \phi _h^{m+\frac{1}{2}} \right\| _{}^2 + \frac{\tau }{32} \left\| \delta _\tau \phi _h^{m-\frac{1}{2}} \right\| _{}^2 + \frac{\tau }{32} \left\| \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{}^2\nonumber \\&\qquad + C \tau \left\| \mu _h^{m+\frac{1}{2}} \right\| _{H^1}^2 + C \tau \left\| \mu _h^{m-\frac{3}{2}} \right\| _{H^1}^2 \nonumber \\&\quad \quad + C \tau \left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 + C \tau \left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \left\| \Delta _h \tilde{\phi }_h^{m-\frac{1}{2}} \right\| _{}^2 \nonumber \\&\quad \quad + C \tau \left\| \nabla \bar{\mathbf{u}}_h^{m-\frac{3}{2}} \right\| _{}^2 + C \tau \left\| \nabla \bar{\mathbf{u}}_h^{m-\frac{3}{2}} \right\| _{}^2 \left\| \Delta _h \tilde{\phi }_h^{m-\frac{3}{2}} \right\| _{}^2, \, \, \forall \, 2 \le m \le M-1. \end{aligned}$$

(2.45)

Furthermore, we use Lemma 2.12 and (2.29) to derive the following inequalities:

$$\begin{aligned} \left\| \Delta _h \tilde{\phi }_h^{(2k+1)+\frac{1}{2}} \right\| _{}^2&\le C \left\| \Delta _h \phi _h^{2k+1} \right\| _{}^2 + C \left\| \Delta _h \phi _h^{2k} \right\| _{}^2 \nonumber \\&\le C \sum _{j=1}^k \left( \frac{1}{3} \right) ^{k-j} \left( \left\| \Delta _h \check{\phi }_h^{(2j+1)-\frac{1}{2}} \right\| _{}^2 + \left\| \Delta _h \check{\phi }_h^{(2j)-\frac{1}{2}} \right\| _{}^2 \right) + C \nonumber \\&\le C \sum _{j=1}^k \left( \frac{1}{3} \right) ^{k-j} \left( \left\| \mu _h^{(2j+1)-\frac{1}{2}} \right\| _{}^2 + \left\| \mu _h^{(2j)-\frac{1}{2}} \right\| _{}^2 \right) + C, \end{aligned}$$

(2.46)

$$\begin{aligned} \left\| \Delta _h \tilde{\phi }_h^{(2k)+\frac{1}{2}} \right\| _{}^2&\le C \left\| \Delta _h \phi _h^{2k} \right\| _{}^2 + C \left\| \Delta _h \phi _h^{2k-1} \right\| _{}^2 \nonumber \\&\le C \sum _{j=1}^k \left( \frac{1}{3} \right) ^{k-j} \left( \left\| \Delta _h \check{\phi }_h^{(2j)-\frac{1}{2}} \right\| _{}^2 + \left\| \Delta _h \check{\phi }_h^{(2j-1)-\frac{1}{2}} \right\| _{}^2 \right) + C \nonumber \\&\le C \sum _{j=1}^k \left( \frac{1}{3} \right) ^{k-j} \left( \left\| \mu _h^{(2j)-\frac{1}{2}} \right\| _{}^2 + \left\| \mu _h^{(2j-1)-\frac{1}{2}} \right\| _{}^2 \right) + C. \end{aligned}$$

(2.47)

Applying $\sum _{m=2}^{\ell }$ to (2.45) and using the following properties

$$\begin{aligned}&\left( \mu _h^{m+\frac{1}{2}} - \mu _h^{m-\frac{1}{2}}, \frac{3}{4} \mu _h^{m+\frac{1}{2}} + \frac{1}{4} \mu _h^{m-\frac{3}{2}} \right) = \, \frac{1}{2}\left( \mu _h^{m+\frac{1}{2}} - \mu _h^{m-\frac{1}{2}}, \mu _h^{m+\frac{1}{2}} + \mu _h^{m-\frac{1}{2}} \right) \\&\quad \quad + \frac{1}{4} \left( \mu _h^{m+\frac{1}{2}} - \mu _h^{m-\frac{1}{2}}, \mu _h^{m+\frac{1}{2}} - 2\mu _h^{m-\frac{1}{2}} + \mu _h^{m-\frac{3}{2}} \right) \\&\quad = \, \frac{1}{2}\left\| \mu _h^{m+\frac{1}{2}} \right\| _{}^2 - \frac{1}{2}\left\| \mu _h^{m-\frac{1}{2}} \right\| _{}^2 + \frac{1}{8} \left\| \mu _h^{m+\frac{1}{2}} - \mu _h^{m-\frac{1}{2}} \right\| _{}^2 \\&\quad \quad - \frac{1}{8} \left\| \mu _h^{m-\frac{1}{2}} - \mu _h^{m-\frac{3}{2}} \right\| _{}^2 + \frac{1}{8} \left\| \mu _h^{m+\frac{1}{2}} - 2 \mu _h^{m-\frac{1}{2}} + \mu _h^{m-\frac{3}{2}} \right\| _{}^2, \\&\left\| \frac{3}{4} \delta _\tau \phi _h^{m+\frac{1}{2}} + \frac{1}{4} \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{}^2 \ge \, \frac{3}{8} \left\| \delta _\tau \phi _h^{m+\frac{1}{2}} \right\| _{}^2 - \frac{1}{8} \left\| \delta _\tau \phi _h^{m-\frac{3}{2}} \right\| _{}^2 \, \, (\text{ similar } \text{ to }\,(2.34)), \end{aligned}$$

we conclude that

$$\begin{aligned}&\frac{1}{2}\left\| \mu _h^{\ell +\frac{1}{2}} \right\| _{}^2 + \ \frac{\tau }{16} \sum _{m=2}^{\ell } \left\| \delta _\tau \phi _h^{m+\frac{1}{2}} \right\| _{}^2 \nonumber \\&\quad \le \ \frac{1}{8} \left\| \mu _h^{\frac{3}{2}} - \mu _h^{\frac{1}{2}} \right\| _{}^2 + \frac{\tau }{32} \left\| \delta _\tau \phi _h^{\frac{3}{2}} \right\| _{}^2 + \frac{5 \tau }{32} \left\| \delta _\tau \phi _h^{\frac{1}{2}} \right\| _{}^2 \\&\quad \quad + C \tau \sum _{m=0}^{\ell }\left\| \mu _h^{m+\frac{1}{2}} \right\| _{H^1}^2 + C \tau \sum _{m=0}^{\ell }\left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \cdot \sum _{j=1}^m \left( \frac{1}{3} \right) ^{m-j} \left\| \mu _h^{j-\frac{1}{2}} \right\| _{}^2 \\&\quad \quad + C \tau \sum _{m=0}^{\ell }\left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \cdot \sum _{j=1}^m \left( \frac{1}{3} \right) ^{m-j} \left\| \mu _h^{j-\frac{3}{2}} \right\| _{}^2 + C \tau \sum _{m=0}^{\ell }\left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \\&\quad \le \, C (T+1) + C \tau \sum _{m=0}^{\ell }\left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \cdot \sum _{j=1}^m \left( \frac{1}{3} \right) ^{m-j} \left( \left\| \mu _h^{j-\frac{1}{2}} \right\| _{}^2 + \left\| \mu _h^{j-\frac{3}{2}} \right\| _{}^2 \right) , \end{aligned}$$

for any $2 \le \ell \le M-1$, where we have used Part 1, (2.28) and (2.25). Moreover, with an application of the discrete Gronwall inequality from Lemma 4.2 (with $\alpha = \frac{1}{3} < 1$), we arrive at

$$\begin{aligned} \frac{1}{2}\left\| \mu _h^{\ell +\frac{1}{2}} \right\| _{}^2 + \frac{\tau }{16} \sum _{m=2}^{\ell } \left\| \delta _\tau \phi _h^{m+\frac{1}{2}} \right\| _{}^2 \le&\ C (T+1) \cdot \exp \left( C A_\alpha \tau \sum _{m=0}^{\ell }\left\| \nabla \bar{\mathbf{u}}_h^{m+\frac{1}{2}} \right\| _{}^2 \right) \nonumber \\ \le&\ C ( T+1), \end{aligned}$$

(2.48)

where (2.25) has been repeatedly applied.

Now, using (2.29), (2.20), the embedding $H^1(\Omega ) \hookrightarrow L^6(\Omega )$, and (2.23), we get

$$\begin{aligned} \left\| \Delta _h \check{\phi }_h^{\ell +\frac{1}{2}} \right\| _{}^2 + \left\| \check{\phi }_h^{\ell +\frac{1}{2}} \right\| _{L^\infty }^{\frac{4(6-d)}{d}} \le C (T+1), \, \, \forall \, 2 \le \ell \le M-1. \end{aligned}$$

By Lemma 2.12, the following bound is available:

$$\begin{aligned} \left\| \Delta _h \phi _h^{\ell +1} \right\| _{}^2 \le C (T+1), \, \, \forall \, 2 \le \ell \le M-1. \end{aligned}$$

Using (2.20) again, the embedding $H^1(\Omega ) \hookrightarrow L^6(\Omega )$, and (2.23), we arrive at

$$\begin{aligned} \left\| \phi _h^{\ell +1} \right\| _{L^\infty }^{\frac{4(6-d)}{d}} \le C (T+1), \, \, \forall \, 2 \le \ell \le M-1. \end{aligned}$$

The proof is completed by combining Parts 1 and 2. $\square$

Remark 2.14

With a generic non-negative mobility, $M (\phi ) \ge 0$, the leading order energy stability analysis is still available. On the other hand, the $\ell ^\infty (L^\infty )$ estimate of the discrete phase variable $\phi _h$, given by Lemma 2.13, takes full advantage of the constant mobility assumption, $M (\phi ) \equiv 1$. As a consequence, the optimal convergence analysis presented in this article is based on such an assumption. Many of the stability results can be obtained straightforwardly in the non-degenerate case, where $M (\phi ) \ge M_0$, for some $M_0>0$. The analysis of the non-constant mobility case will be considered in a future paper.

3 Error estimates for the fully discrete scheme

For the CHNS system (1.2a)–(1.2e), the existence of a global-in-time weak solution, defined by (1.5a)–(1.5d), has been established in [30]. However, the regularity of the weak solutions stated in (1.4a)–(1.4f) is not sufficient to justify the optimal convergence analysis. To carry out such an error estimate, we need to seek a strong solution to the PDE system with higher order regularities. It was proven in [1] that unique strong solutions exist for the CHNS system (1.2a)–(1.2e), globally-in-time for 2D, and locally-in-time for 3D, with a constant mobility assumption ($M (\phi ) \equiv 1$). As a result, higher order regularities could be derived as follows: for any initial data $\mathbf{u}_0 \in H^m (\Omega )$, $\phi _0 \in H^{m+1} (\Omega )$, there is an estimate for $\Vert \mathbf{u}(t) \Vert _{H^m}$ and $\Vert \phi (t) \Vert _{H^{m+1}}$, $m \ge 1$, globally-in-time for 2D, and locally-in-time for 3D, under appropriate compatibility conditions between the initial data and boundary conditions [36]. In other words, we could always assume a smooth enough solution for the CHNS system (1.2a)–(1.2e), globally-in-time for 2D, and locally-in-time for 3D, so that the following regularity assumptions are reasonable. In any case, it is standard to assume that higher regularity solutions exist than are available from current PDE theory. See [29] for examples of this practice in the analysis of numerical methods for the Navier–Stokes equation.

Assumption 3.1

Weak solutions to the CHNS system (1.2a)–(1.2e) have the additional regularities

$$\begin{aligned}&\phi \in L^{\infty }(0,T;W^{1,6}(\Omega )) \cap H^1(0,T;H^{q+1}(\Omega ))\nonumber \\&\quad \cap H^2(0,T;H^{3}(\Omega )) \cap H^3(0,T;L^2(\Omega )), \end{aligned}$$

(3.1)

$$\begin{aligned}&\phi ^2 \in H^2(0,T;H^1(\Omega )), \end{aligned}$$

(3.2)

$$\begin{aligned}&\mu \in L^2(0,T;H^{q+1}(\Omega )), \end{aligned}$$

(3.3)

$$\begin{aligned}&\mathbf{u}\in H^{{3}}(0,T;\mathbf{L}^2(\Omega )) \cap {H^2 (0,T; \mathbf{H}^3 (\Omega ))}\nonumber \\&\quad \cap L^\infty (0,T;\mathbf{H}^{q+1}(\Omega )) \cap H^1(0,T;\mathbf{H}^{q+1}(\Omega )), \end{aligned}$$

(3.4)

$$\begin{aligned}&p \in {H^2}(0,T;H^q(\Omega ) \cap L^2_0(\Omega )) \cap L^\infty (0,T;H^{q}(\Omega )), \end{aligned}$$

(3.5)

where $q\ge 1$ corresponds to the finite element spaces defined at the beginning of Sect. 2. Furthermore, the initial data are sufficiently regular so that Assumption 2.7 is valid.

Remark 3.2

The norm bounds associated with the assumed regularities above are not necessarily global-in-time and therefore can involve constants that depend upon the final time T.

Remark 3.3

We also note that the higher order temporal derivative of the exact solution comes from its $L^\infty (0,T; H^m)$ estimate (for m large enough) since the higher order temporal derivatives could be converted into higher order spatial derivatives, indicated by a careful calculation of (1.5a)–(1.5d).

Now then, weak solutions $(\phi , \mu , \mathbf{u}, p)$ with the higher regularities (3.1)–(3.5) solve the following variational problem: for all $t\in [0,T]$,

$$\begin{aligned} \left( \partial _t \phi , \nu \right) + \varepsilon \,a\left( \mu , \nu \right) + b\left( \phi , \mathbf{u}, \nu \right)&= 0, \quad \forall \,\nu \in H^1(\Omega ), \end{aligned}$$

(3.6)

$$\begin{aligned} \left( \mu , \psi \right) -\varepsilon \,a\left( \phi , \psi \right) - \varepsilon ^{-1}\left( \phi ^3-\phi , \psi \right)&= 0, \quad \forall \,\psi \in H^1(\Omega ), \end{aligned}$$

(3.7)

$$\begin{aligned} \langle \partial _t \mathbf{u}, \mathbf{v}\rangle + \eta \, a\left( \mathbf{u}, \mathbf{v} \right) + B\left( \mathbf{u}, \mathbf{u}, \mathbf{v} \right) - c\left( \mathbf{v}, p \right) - \gamma \, b\left( \phi , \mathbf{v}, \mu \right)&=0, \quad \forall \, \mathbf{v}\in \mathbf{H}^1_0(\Omega ), \end{aligned}$$

(3.8)

$$\begin{aligned} c\left( \mathbf{u}, q \right)&=0, \quad \forall \, q \in L^2_0(\Omega ). \end{aligned}$$

(3.9)

We define the following: for any real number $m\in [0,M]$, $t_{m} := m \cdot \tau$, and $\psi ^{m} := \psi (t_{m})$. This definition applies to vector valued functions of time as well. Note that, in general,

$$\begin{aligned} \psi ^{m+\frac{1}{2}}:= \psi (t_{m+\frac{1}{2}}) \ne \frac{1}{2}\left( \psi ^{m}+\psi ^{m+1}\right) =:\bar{\psi }^{m+\frac{1}{2}}. \end{aligned}$$

An over-bar will always indicate a simple central average in time. Denote

$$\begin{aligned} {\mathcal {E}}_a^{\phi ,m}:= & {} \phi ^{m} - R_h \phi ^{m}, \quad {\mathcal {E}}_a^{\mu ,m} := \mu ^{m} - R_h \mu ^{m}, \quad {\mathcal {E}}_a^{\mathbf{u},m} := \mathbf{u}^{m} - P_h \mathbf{u}^{m},\nonumber \\ {\mathcal {E}}_a^{p,m}:= & {} p^{m} - P_h p^{m}. \end{aligned}$$

(3.10)

The following definitions are given for any integer $0\le m\le M-1$:

$$\begin{aligned} \delta _\tau \phi ^{m+\frac{1}{2}} :=&\ \frac{\phi ^{m+1} - \phi ^{m}}{\tau },&\quad \delta _\tau \mathbf{u}^{m+\frac{1}{2}} :=&\ \frac{\mathbf{u}^{m+1} - \mathbf{u}^{m}}{\tau }, \\ \sigma ^{\phi , m+\frac{1}{2}}_1 :=&\ \delta _\tau R_h \phi ^{m+\frac{1}{2}} - \delta _\tau \phi ^{m+\frac{1}{2}},&\quad \sigma ^{\mathbf{u}, m+\frac{1}{2}}_1 :=&\ \delta _\tau \mathbf{P}_h \mathbf{u}^{m+\frac{1}{2}} - \delta _\tau \mathbf{u}^{m+\frac{1}{2}}, \\ \sigma ^{\phi , m+\frac{1}{2}}_2 :=&\ \delta _\tau \phi ^{m+\frac{1}{2}} - \partial _t \phi ^{m+\frac{1}{2}},&\quad \sigma ^{\mathbf{u}, m+\frac{1}{2}}_2 :=&\ \delta _\tau \mathbf{u}^{m+\frac{1}{2}} - \partial _t \mathbf{u}^{m+\frac{1}{2}}, \\ \sigma ^{\phi , m+\frac{1}{2}}_3 :=&\ \bar{\phi }^{m+\frac{1}{2}} - \phi ^{m+\frac{1}{2}},&\quad \sigma ^{\mathbf{u}, m+\frac{1}{2}}_3 :=&\ \bar{\mathbf{u}}^{m+\frac{1}{2}} - \mathbf{u}^{m+\frac{1}{2}}, \\ \sigma _4^{\phi ,m+\frac{1}{2}} :=&\ \chi \left( \phi ^{m+1},\phi ^m \right) - \left( \phi ^{m+\frac{1}{2}}\right) ^3,&\quad \sigma ^{p, m+\frac{1}{2}}_3 :=&\ \bar{p}^{m+\frac{1}{2}} - p^{m+\frac{1}{2}}. \end{aligned}$$

Then the PDE solution, evaluated at the half-integer time steps $t_{m+\frac{1}{2}}$, satisfies

$$\begin{aligned}&\left( \delta _\tau R_h \phi ^{m+\frac{1}{2}}, \nu \right) + \varepsilon \, a\left( R_h \mu ^{m+\frac{1}{2}}, \nu \right) = \ \left( \sigma ^{\phi , m+\frac{1}{2}}_1 + \sigma ^{\phi , m+\frac{1}{2}}_2, \nu \right) \nonumber \\&\qquad - b\left( \phi ^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \nu \right) , \end{aligned}$$

(3.11a)

$$\begin{aligned}&\varepsilon \, a\left( R_h \bar{\phi }^{m+\frac{1}{2}}, \psi \right) - \left( R_h \mu ^{m+\frac{1}{2}}, \psi \right) = \ \varepsilon \, a\left( \sigma ^{\phi ,m+\frac{1}{2}}_3, \psi \right) + \left( {\mathcal {E}}_a^{\mu ,m+\frac{1}{2}}, \psi \right) \nonumber \\&- \frac{1}{\varepsilon } \left( \chi \left( \phi ^{m+1},\phi ^m\right) , \psi \right) + \frac{1}{\varepsilon }\left( \sigma _4^{\phi ,m+\frac{1}{2}}, \psi \right) \nonumber \\&+ \frac{1}{\varepsilon } \left( \phi ^{m+\frac{1}{2}}, \psi \right) , \end{aligned}$$

(3.11b)

$$\begin{aligned}&\left( \delta _\tau \mathbf{P}_h \mathbf{u}^{m+\frac{1}{2}}, \mathbf{v} \right) + \eta \, a\left( \mathbf{P}_h\bar{\mathbf{u}}^{m+\frac{1}{2}} , \mathbf{v} \right) \nonumber \\&- c\left( \mathbf{v}, P_h \bar{p}^{m+\frac{1}{2}} \right) {=} \ \eta \, a\left( \sigma ^{\mathbf{u},m+\frac{1}{2}}_3, \mathbf{v} \right) {+} \left( \sigma ^{\mathbf{u}, m+\frac{1}{2}}_1 {+} \sigma ^{\mathbf{u},m+\frac{1}{2}}_2, \mathbf{v} \right) {-} c\left( \mathbf{v}, \sigma ^{p,m+\frac{1}{2}}_3 \right) \nonumber \\&+ \gamma \, b\left( \phi ^{m+\frac{1}{2}}, \mathbf{v}, \mu ^{m+\frac{1}{2}} \right) - B\left( \mathbf{u}^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \mathbf{v} \right) , \end{aligned}$$

(3.11c)

$$\begin{aligned}&c\left( \mathbf{P}_h \bar{\mathbf{u}}^{m+\frac{1}{2}}, q \right) = c\left( \sigma ^{\mathbf{u},m+\frac{1}{2}}_3, q \right) , \end{aligned}$$

(3.11d)

for all $\nu , \psi \in S_h$, $\mathbf{v}\in \mathbf{X}_h$, and $q \in \mathring{S}_h$, for any $0\le m\le M-1$.

Restating the fully discrete splitting scheme (2.1a)–(2.1d), we have, for $1 \le m \le M-1$, and for all $\nu , \psi \in S_h$, $\mathbf{v}\in \mathbf{X}_h$, and $q \in \mathring{S}_h$,

$$\begin{aligned} \left( \delta _\tau \phi _h^{m+\frac{1}{2}}, \nu \right) + \varepsilon \, a\left( \mu _h^{m+\frac{1}{2}}, \nu \right)&= - b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \nu \right) , \end{aligned}$$

(3.12a)

$$\begin{aligned} \varepsilon \, a\left( \bar{\phi }_h^{m+\frac{1}{2}}, \psi \right) + \frac{\varepsilon }{4} \, a\left( \tau ^2 \delta _{\tau }^2\phi _h^m, \psi \right) - \left( \mu _h^{m+\frac{1}{2}}, \psi \right)&= - \frac{1}{\varepsilon } \left( \chi \left( \phi _h^{m+1}, \phi _h^m\right) , \psi \right) \nonumber \\&\quad + \frac{1}{\varepsilon } \left( \tilde{\phi }_h^{m+\frac{1}{2}}, \psi \right) , \end{aligned}$$

(3.12b)

$$\begin{aligned} \left( \delta _\tau \mathbf{u}_h^{m+\frac{1}{2}}, \mathbf{v} \right) + \eta \, a\left( \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \mathbf{v} \right) - c\left( \mathbf{v}, \bar{p}_h^{m+\frac{1}{2}} \right)&= \ \gamma \, b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \mathbf{v}, \mu _h^{m+\frac{1}{2}} \right) \nonumber \\&\quad - B\left( \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \mathbf{v} \right) , \end{aligned}$$

(3.12c)

$$\begin{aligned} c\left( \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, q \right)&= 0, \end{aligned}$$

(3.12d)

where $\delta _{\tau }^2\psi ^m := \frac{1}{\tau ^2}\left( \psi ^{m+1}-2\psi ^m+\psi ^{m-1}\right)$.

Now let us define the following additional error terms

$$\begin{aligned} {\mathcal {E}}_h^{\phi ,m}&:= R_h \phi ^{m} - \phi _h^{m}, \quad {\mathcal {E}}^{\phi ,m} := \phi ^{m} - \phi _h^{m}, \quad {\mathcal {E}}_h^{\mu ,m} := R_h \mu ^{m} - \mu _h^{m},\nonumber \\ {\mathcal {E}}_h^{\mathbf{u},m}&:= P_h \mathbf{u}^{m} - \mathbf{u}_h^{m}, \quad {\mathcal {E}}^{\mathbf{u},m} := \mathbf{u}^{m} - \mathbf{u}_h^{m}, \quad {\mathcal {E}}_h^{p,m} := P_h p^{m} - p_h^{m},\nonumber \\&\quad {\mathcal {E}}^{p,m} := p^{m} - p_h^{m}. \end{aligned}$$

(3.13)

We also define, for $1\le m\le M-1$,

$$\begin{aligned} \sigma _5^{\phi ,m+\frac{1}{2}}&:= \, \chi \left( \phi _h^{m+1},\phi _h^m \right) - \chi \left( \phi ^{m+1},\phi ^m \right) , \end{aligned}$$

(3.14)

$$\begin{aligned} \sigma _6^{\phi ,m+\frac{1}{2}}&:= \, \phi ^{m+\frac{1}{2}} - \tilde{\phi }_h^{m+\frac{1}{2}}, \end{aligned}$$

(3.15)

$$\begin{aligned} \sigma _6^{\mathbf{u},m+\frac{1}{2}}&:= \, \mathbf{u}^{m+\frac{1}{2}} - \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}. \end{aligned}$$

(3.16)

Subtracting (3.12a)–(3.12d) from (3.11a)–(3.11d), yields, for $1\le m\le M-1$,

$$\begin{aligned}&\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}}, \nu \right) + \varepsilon \, a\left( {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}, \nu \right) = \ \left( \sigma ^{\phi ,m+\frac{1}{2}}_1 + \sigma ^{\phi ,m+\frac{1}{2}}_2, \nu \right) \nonumber \\&\quad - b\left( \phi ^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \nu \right) \nonumber \\&\quad + b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \nu \right) , \end{aligned}$$

(3.17a)

$$\begin{aligned}&\varepsilon \, a\left( \bar{{\mathcal {E}}}_h^{\phi ,m+\frac{1}{2}} , \psi \right) + \frac{\varepsilon \tau ^2}{4} a\left( \delta _{\tau }^2{\mathcal {E}}_h^{\phi ,m}, \psi \right) \nonumber \\&\quad - \left( {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}, \psi \right) = \ \varepsilon \, a\left( \sigma _3^{\phi ,m+\frac{1}{2}}, \psi \right) + \left( {\mathcal {E}}_a^{\mu ,m+\frac{1}{2}}, \psi \right) \nonumber \\&\quad + \frac{1}{\varepsilon } \left( \sigma _5^{\phi ,m+\frac{1}{2}}, \psi \right) + \frac{1}{\varepsilon }\left( \sigma _4^{\phi ,m+\frac{1}{2}}, \psi \right) \nonumber \\&\quad + \frac{1}{\varepsilon } \left( \sigma _6^{\phi ,m+\frac{1}{2}}, \psi \right) + \frac{\varepsilon \tau ^2}{4} \, a\left( \delta _{\tau }^2\phi ^m, \psi \right) , \end{aligned}$$

(3.17b)

$$\begin{aligned}&\left( \delta _\tau {\mathcal {E}}_h^{\mathbf{u},m+\frac{1}{2}}, \mathbf{v} \right) + \eta \, a\left( \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \mathbf{v} \right) \nonumber \\&\quad - c\left( \mathbf{v}, \bar{{\mathcal {E}}}_h^{p,m+\frac{1}{2}} \right) = \ \left( \sigma ^{\mathbf{u},m+\frac{1}{2}}_1 + \sigma ^{\mathbf{u},m+\frac{1}{2}}_2, \mathbf{v} \right) + \eta \, a\left( \sigma _3^{\mathbf{u},m+\frac{1}{2}}, \mathbf{v} \right) \nonumber \\&\quad - c\left( \mathbf{v}, \sigma _3^{p,m+\frac{1}{2}} \right) +\gamma \, b\left( \phi ^{m+\frac{1}{2}}, \mathbf{v}, \mu ^{m+\frac{1}{2}} \right) \nonumber \\&\quad - B\left( \mathbf{u}^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \mathbf{v} \right) - \gamma \, b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \mathbf{v}, \mu _h^{m+\frac{1}{2}} \right) \nonumber \\&\quad + B\left( \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \mathbf{v} \right) , \end{aligned}$$

(3.17c)

$$\begin{aligned}&c\left( \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} , q \right) = c\left( \sigma _3^{\mathbf{u},m+\frac{1}{2}}, q \right) (= 0), \end{aligned}$$

(3.17d)

Setting $\nu = {\mathcal {E}}_h^{\mu , m+\frac{1}{2}}$ in (3.17a), $\psi = \delta _\tau {\mathcal {E}}_h^{\phi , m+\frac{1}{2}}$ in (3.17b), $\mathbf{v}= \frac{1}{\gamma } \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}$ in (3.17c), $q = \frac{1}{\gamma }\bar{{\mathcal {E}}}_h^{p,m+\frac{1}{2}}$ in (3.17d) and adding the resulting equations, we have

$$\begin{aligned}&\frac{\varepsilon }{2\tau } \left( \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 - \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2\right) + \frac{1}{2 \gamma \tau } \left( \left\| {\mathcal {E}}_h^{\mathbf{u},m+1} \right\| _{}^2 - \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2\right) \nonumber \\&\quad \quad + \varepsilon \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \frac{ \varepsilon \tau ^2}{4} \, a\left( \delta _{\tau }^2{\mathcal {E}}_h^{\phi ,m}, \delta _\tau {\mathcal {E}}_h^{\phi , m+\frac{1}{2}} \right) + \frac{\eta }{\gamma } \, \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 \nonumber \\&\quad = \left( \sigma ^{\phi ,m+\frac{1}{2}}_1 + \sigma ^{\phi ,m+\frac{1}{2}}_2, {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right) + \varepsilon \, a\left( \sigma _3^{\phi ,m+\frac{1}{2}}, \delta _\tau {\mathcal {E}}_h^{\phi , m+\frac{1}{2}} \right) \nonumber \\&\qquad + \left( {\mathcal {E}}_a^{\mu ,m+\frac{1}{2}}, \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \nonumber \\&\quad \quad + \frac{1}{\varepsilon } \left( \sigma _4^{\phi ,m+\frac{1}{2}} + \sigma _5^{\phi ,m+\frac{1}{2}} + \sigma _6^{\phi ,m+\frac{1}{2}} , \delta _\tau {\mathcal {E}}_h^{\phi , m+\frac{1}{2}} \right) + \frac{\varepsilon \tau ^2}{4} \, a\left( \delta _{\tau }^2\phi ^m , \delta _\tau {\mathcal {E}}_h^{\phi , m+\frac{1}{2}} \right) \nonumber \\&\quad \quad + \frac{1}{\gamma } \left( \sigma ^{\mathbf{u},m+\frac{1}{2}}_1 + \sigma ^{\mathbf{u},m+\frac{1}{2}}_2, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) + \frac{\eta }{\gamma } \, a\left( \sigma _3^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \nonumber \\&\qquad - \frac{1}{\gamma } c\left( \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} , \sigma _3^{p,m+\frac{1}{2}} \right) \nonumber \\&\quad \quad - b\left( \phi ^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right) + b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right) \nonumber \\&\quad \quad + b\left( \phi ^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \mu ^{m+\frac{1}{2}} \right) - b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \mu _h^{m+\frac{1}{2}} \right) \nonumber \\&\quad \quad - \frac{1}{\gamma } B\left( \mathbf{u}^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) + \frac{1}{\gamma } B\left( \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) , \end{aligned}$$

(3.18)

for all $1\le m\le M-1$. Expression (3.18) is the key error equation from which we will define our error estimates. Observe that the error equation is not defined for $m=0$.

The following estimates are standard and the proofs are omitted.

Lemma 3.4

Suppose that $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11d), with the additional regularities in Assumption 3.1. Then for all $t_m\in [0,T]$ and for any h, $\tau >0$, there exists a constant $C>0$, independent of h and $\tau$ and T, such that for all $0\le m\le M-1$,

$$\begin{aligned} \left\| \sigma ^{\phi ,m+\frac{1}{2}}_1 \right\| _{}^2&\le C\frac{h^{2q+2}}{\tau } \int _{t_m}^{t_{m+1}} \left\| \partial _s\phi (s) \right\| _{H^{q+1}}^2 ds, \end{aligned}$$

(3.19)

$$\begin{aligned} \left\| \sigma ^{\phi ,m+\frac{1}{2}}_2 \right\| _{}^2&\le \frac{\tau ^3}{640} \int _{t_m}^{t_{m+1}}\left\| \partial _{sss}\phi (s) \right\| _{}^2 ds, \end{aligned}$$

(3.20)

$$\begin{aligned} \left\| \nabla \Delta \sigma ^{\phi ,m+\frac{1}{2}}_3 \right\| _{}^2&\le \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \nabla \Delta \partial _{ss} \phi (s) \right\| _{}^2 ds, \end{aligned}$$

(3.21)

$$\begin{aligned} \left\| \nabla \sigma ^{\phi ,m+\frac{1}{2}}_3 \right\| _{}^2&\le \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \nabla \partial _{ss} \phi (s) \right\| _{}^2 ds, \end{aligned}$$

(3.22)

$$\begin{aligned} \left\| \frac{1}{2}\left( \phi ^{m+1}\right) ^2+\frac{1}{2}\left( \phi ^m\right) ^2 - \left( \phi ^{m+\frac{1}{2}}\right) ^2 \right\| _{H^1}^2&\le \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \partial _{ss} \phi ^2(s) \right\| _{H^1}^2 ds. \end{aligned}$$

(3.23)

In addition, for all $1\le m\le M-1$,

$$\begin{aligned} \left\| \tau ^2\nabla \Delta \delta _{\tau }^2\phi ^m \right\| _{}^2&\le \frac{\tau ^3}{3} \int _{t_{m-1}}^{t_{m+1}} \left\| \nabla \Delta \partial _{ss} \phi (s) \right\| _{}^2 ds, \end{aligned}$$

(3.24)

$$\begin{aligned} \left\| \tau ^2\nabla \delta _{\tau }^2\phi ^m \right\| _{}^2&\le \frac{\tau ^3}{3} \int _{t_{m-1}}^{t_{m+1}} \left\| \nabla \partial _{ss} \phi (s) \right\| _{}^2 ds, \end{aligned}$$

(3.25)

$$\begin{aligned} {\left\| \nabla \phi ^{m+\frac{1}{2}} - \nabla \left( \frac{3}{2} \phi ^m - \frac{1}{2}\phi ^{m-1}\right) \right\| _{}^2}&\le \frac{\tau ^3}{12} \int _{t_{m-1}}^{t_{m+1}}\left\| \nabla \partial _{ss}\phi (s) \right\| _{}^2 \, ds. \end{aligned}$$

(3.26)

Lemma 3.5

Suppose that $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11d), with the additional regularities in Assumption 3.1. Then for all $t_m\in [0,T]$ and for any h, $\tau >0$, there exists a constant $C>0$, independent of h and $\tau$ and T, such that for all $0\le m\le M-1$,

$$\begin{aligned} \left\| \sigma ^{\mathbf{u},m+\frac{1}{2}}_1 \right\| _{}^2&\le C\frac{h^{2q+2}}{\tau } \int _{t_m}^{t_{m+1}} \left\| \partial _s\mathbf{u}(s) \right\| _{H^{q+1}}^2 ds, \end{aligned}$$

(3.27)

$$\begin{aligned} \left\| \sigma ^{\mathbf{u},m+\frac{1}{2}}_2 \right\| _{}^2&\le \frac{\tau ^3}{640} \int _{t_m}^{t_{m+1}}\left\| \partial _{sss}\mathbf{u}(s) \right\| _{}^2 ds, \end{aligned}$$

(3.28)

$$\begin{aligned} \left\| \nabla \Delta \sigma ^{\mathbf{u},m+\frac{1}{2}}_3 \right\| _{}^2&\le \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \nabla \Delta \partial _{ss} \mathbf{u}(s) \right\| _{}^2 ds, \end{aligned}$$

(3.29)

$$\begin{aligned} \left\| \nabla \sigma ^{\mathbf{u},m+\frac{1}{2}}_3 \right\| _{}^2&\le \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \nabla \partial _{ss} \mathbf{u}(s) \right\| _{}^2 ds, \end{aligned}$$

(3.30)

$$\begin{aligned} \left\| \sigma ^{p,m+\frac{1}{2}}_3 \right\| _{}^2&\le \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \partial _{ss} p(s) \right\| _{}^2 ds. \end{aligned}$$

(3.31)

In addition, for all $1\le m\le M-1$,

$$\begin{aligned} \left\| \tau ^2\nabla \Delta \delta _{\tau }^2\mathbf{u}^m \right\| _{}^2&\le \frac{\tau ^3}{3} \int _{t_{m-1}}^{t_{m+1}} \left\| \nabla \Delta \partial _{ss} \mathbf{u}(s) \right\| _{}^2 ds, \end{aligned}$$

(3.32)

$$\begin{aligned} \left\| \tau ^2\nabla \delta _{\tau }^2\mathbf{u}^m \right\| _{}^2&\le \frac{\tau ^3}{3} \int _{t_{m-1}}^{t_{m+1}} \left\| \nabla \partial _{ss} \mathbf{u}(s) \right\| _{}^2 ds, \end{aligned}$$

(3.33)

$$\begin{aligned} {\left\| \nabla \mathbf{u}^{m+\frac{1}{2}} - \nabla \left( \frac{3}{2} \mathbf{u}^m - \frac{1}{2}\mathbf{u}^{m-1}\right) \right\| _{}^2}&\le \frac{\tau ^3}{12} \int _{t_{m-1}}^{t_{m+1}}\left\| \nabla \partial _{ss}\mathbf{u}(s) \right\| _{}^2 \, ds, \end{aligned}$$

(3.34)

$$\begin{aligned} \left\| \tau ^2\nabla \delta _{\tau }^2p^m \right\| _{}^2&\le \frac{\tau ^3}{3} \int _{t_{m-1}}^{t_{m+1}} \left\| \nabla \partial _{ss} p(s) \right\| _{}^2 ds. \end{aligned}$$

(3.35)

The following estimates are proved in [9].

Lemma 3.6

Suppose that $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11d), with the additional regularities in Assumption 3.1. Then, there exists a constant $C>0$ independent of h and $\tau$—but possibly dependent upon T through the regularity estimates—such that, for any $h, \tau >0$,

$$\begin{aligned} \left\| \nabla \sigma _4^{\phi ,m+\frac{1}{2}} \right\| _{}^2 \le&\, C\tau ^3 \int _{t_m}^{t_{m+1}} \left\| \nabla \partial _{ss} \phi (s) \right\| _{}^2 ds +C \tau ^3 \int _{t_m}^{t_{m+1}} \left\| \partial _{ss} \phi ^2(s) \right\| _{H^1}^2 ds, \end{aligned}$$

(3.36)

$$\begin{aligned} \left\| \nabla \sigma _5^{\phi ,m+\frac{1}{2}} \right\| _{}^2 \le&\, C \left\| \nabla {\mathcal {E}}^{\phi ,m+1} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}^{\phi ,m} \right\| _{}^2, \end{aligned}$$

(3.37)

where ${\mathcal {E}}^{\phi ,m} := \phi ^{m} - \phi _h^{m}$.

Lemma 3.7

Suppose that $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11d), with the additional regularities in Assumption 3.1. Then, there exists a constant $C>0$ independent of h and $\tau$ such that, for any $h, \tau >0$,

$$\begin{aligned} \left\| \nabla \sigma _6^{\phi ,m+\frac{1}{2}} \right\| _{}^2 \le&\ C \tau ^3 \int _{t_{m-1}}^{t_{m+1}}\left\| \nabla \partial _{ss}\phi (s) \right\| _{}^2 \, ds + C\left\| \nabla {\mathcal {E}}^{\phi ,m} \right\| _{}^2+ C\left\| \nabla {\mathcal {E}}^{\phi ,m-1} \right\| _{}^2, \end{aligned}$$

(3.38)

$$\begin{aligned} \left\| \nabla \sigma _6^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 \le&\ C \tau ^3 \int _{t_{m-1}}^{t_{m+1}}\left\| \nabla \partial _{ss}\mathbf{u}(s) \right\| _{}^2 \, ds + C\left\| \nabla {\mathcal {E}}^{\mathbf{u},m} \right\| _{}^2+ C\left\| \nabla {\mathcal {E}}^{\mathbf{u},m-1} \right\| _{}^2, \end{aligned}$$

(3.39)

where ${\mathcal {E}}^{\phi ,m} := \phi ^{m} - \phi _h^{m}$ and ${\mathcal {E}}^{\mathbf{u},m} := \mathbf{u}^m - \mathbf{u}_h^m$.

Proof

For $1\le m\le M-1$, using the truncation error estimate (3.26), we obtain

$$\begin{aligned} \left\| \nabla \sigma _6^{\phi ,m+\frac{1}{2}} \right\| _{}^2 \le 3\frac{\tau ^3}{12} \int _{t_{m-1}}^{t_{m+1}}\left\| \nabla \partial _{ss}\phi (s) \right\| _{}^2 \, ds + \frac{27}{4}\left\| \nabla {\mathcal {E}}^{\phi ,m} \right\| _{}^2 + \frac{3}{4}\left\| \nabla {\mathcal {E}}^{\phi ,m-1} \right\| _{}^2. \end{aligned}$$

(3.40)

Estimate (3.39) similarly follows. $\square$

The following technical lemma is proved in [8].

Lemma 3.8

Suppose $g \in H^1(\Omega )$, and $v \in \mathring{S}_h$. Then

$$\begin{aligned} \left| \left( g, v \right) \right| \le C \left\| \nabla g \right\| _{} \, \left\| v \right\| _{-1,h}, \end{aligned}$$

(3.41)

for some $C>0$ that is independent of h.

We use only some very basic estimates for the trilinear form B:

Lemma 3.9

Suppose $\mathbf{u}, \mathbf{v}, \mathbf{w}\in \mathbf{H}_0^1(\Omega )$. Then

$$\begin{aligned} \left| B\left( \mathbf{u}, \mathbf{v}, \mathbf{w} \right) \right| \le C \left\| \nabla \mathbf{u} \right\| _{} \left\| \nabla \mathbf{v} \right\| _{} \left\| \nabla \mathbf{w} \right\| _{}. \end{aligned}$$

(3.42)

If $\mathbf{u}\in \mathbf{L}^\infty (\Omega )$ and $\mathbf{v}, \mathbf{w}\in \mathbf{H}_0^1(\Omega )$, then

$$\begin{aligned} \left| B\left( \mathbf{u}, \mathbf{v}, \mathbf{w} \right) \right| \le C \left\| \mathbf{u} \right\| _{L^\infty } \left\| \nabla \mathbf{v} \right\| _{} \left\| \nabla \mathbf{w} \right\| _{}. \end{aligned}$$

(3.43)

If $\mathbf{u}\in \mathbf{L}^2(\Omega )$, $\mathbf{v},\mathbf{w}\in \mathbf{H}^1(\Omega )\cap \mathbf{L}^\infty (\Omega )$, then

$$\begin{aligned} \left| B\left( \mathbf{u}, \mathbf{v}, \mathbf{w} \right) \right| \le \left\| \mathbf{u} \right\| _{} \left( \left\| \nabla \mathbf{v} \right\| _{} \left\| \mathbf{w} \right\| _{L^{\infty }} + \left\| \nabla \mathbf{w} \right\| _{} \left\| \mathbf{v} \right\| _{L^{\infty }}\right) . \end{aligned}$$

(3.44)

We also recall some basic inverse inequalities

(3.45)

From this and the Gagliardo–Nirenburg and Poincaré inequalities it follows that [4]

$$\begin{aligned} \left\| \varphi _h \right\| _{L^\infty } \le C h^{\frac{1}{2} -\frac{d}{2}}\left\| \varphi _h \right\| _{ }^\frac{1}{2}\left\| \nabla \varphi _h \right\| _{ }^\frac{1}{2}, \quad d= 2,3, \end{aligned}$$

(3.46)

for all $\varphi _h\in \mathcal {M}_{r,0}^h$.

Lemma 3.10

Let $( \mathbf{P}_h, P_h) : \mathbf{V} \times L^2_0 \rightarrow \mathbf{V}_h\times \mathring{S}_h$ be defined as in (2.5) and suppose that $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11d), with the additional regularities in Assumption 3.1. Then, for any h, $\tau >0$ there exists a constant $C>0$, independent of h and $\tau$, such that, for $0 \le m \le M-1$,

$$\begin{aligned} \left\| \mathbf{P}_h \mathbf{u} \right\| _{L^\infty (0,T;L^{\infty }(\Omega ))} \le C, \end{aligned}$$

(3.47)

and, as a simple consequence,

$$\begin{aligned} \left\| {\mathcal {E}}_a^{\mathbf{u}} \right\| _{L^\infty (0,T;L^{\infty }(\Omega ))} \le C. \end{aligned}$$

(3.48)

Proof

Let $\mathbf{w}=\mathcal {I}_h \mathbf{u}\in \mathbf{X}_h$, the standard Lagrange nodal interpolant of $\mathbf{u}$. Following Baker’s unpublished paper [4] and using standard finite element approximations, including (2.11), inverse inequalities, and Sobolev’s embedding theorem, we have

$$\begin{aligned} \left\| \mathbf{P}_h \mathbf{u} \right\| _{L^\infty }&= \left\| \mathbf{P}_h \mathbf{u}- \mathbf{w}+ \mathbf{w}- \mathbf{u}+ \mathbf{u} \right\| _{L^\infty } \\&\le \left\| \mathbf{P}_h \mathbf{u}- \mathbf{w} \right\| _{L^\infty } + \left\| \mathbf{w}- \mathbf{u} \right\| _{L^\infty } + \left\| \mathbf{u} \right\| _{L^\infty } \\&\le C h^{-\frac{d}{2}} \left\| \mathbf{P}_h \mathbf{u}- \mathbf{w} \right\| _{} + \left\| \mathbf{w}- \mathbf{u} \right\| _{L^\infty } + \left\| \mathbf{u} \right\| _{L^\infty } \\&\le C h^{-\frac{d}{2}} \left( \left\| \mathbf{P}_h \mathbf{u}- \mathbf{u} \right\| _{} + \left\| \mathbf{u}- \mathbf{w} \right\| _{}\right) + \left\| \mathbf{w}- \mathbf{u} \right\| _{L^\infty } + \left\| \mathbf{u} \right\| _{L^\infty } \\&\le C \left( \left\| \mathbf{u}- \mathbf{w} \right\| _{L^\infty } + h^{-\frac{d}{2}}\left\| \mathbf{u}- \mathbf{w} \right\| _{}\right) + C h^{-\frac{d}{2}} \left\| \mathbf{P}_h \mathbf{u}- \mathbf{u} \right\| _{} + \left\| \mathbf{u} \right\| _{L^\infty } \\&\le \left\| \mathbf{u} \right\| _{L^\infty } + C h^{q+1-\frac{d}{2}} \left( \left| \mathbf{u}\right| _{H^{q+1}} + \left| p \right| _{H^{q}} \right) . \end{aligned}$$

Taking the $L^\infty$ norm over (0, T) and noting that $q \ge 1$, the proof is concluded. $\square$

We now proceed to estimate the terms on the right-hand-side of (3.18).

Lemma 3.11

Suppose that $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11d), with the additional regularities in Assumption 3.1. Then, for any h, $\tau >0$ and any $\alpha > 0$ there exist a constant $C=C(\alpha ,T)>0$, independent of h and $\tau$, such that, for $1 \le m \le M-1$,

$$\begin{aligned}&\frac{\varepsilon }{2\tau } \left( \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 - \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2\right) + \frac{1}{2 \tau \gamma } \left( \left\| {\mathcal {E}}_h^{\mathbf{u},m+1} \right\| _{}^2 - \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2\right) \nonumber \\&\qquad + \frac{\varepsilon \tau ^2}{4} \, a\left( \delta _{\tau }^2{\mathcal {E}}_h^{\phi ,m}, \delta _\tau {\mathcal {E}}_h^{\phi , m+\frac{1}{2}} \right) \nonumber \\&\qquad + \frac{3\varepsilon }{4} \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \frac{\eta }{2\gamma } \, \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 \le \ C \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2\nonumber \\&\qquad + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m-1} \right\| _{}^2 \nonumber \\&\qquad + C \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m-1} \right\| _{}^2 + \alpha \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 + C \mathcal {R}^{m+\frac{1}{2}}, \end{aligned}$$

(3.49)

where

$$\begin{aligned} \mathcal {R}^{m+\frac{1}{2}}&:= \frac{h^{2q+2}}{\tau } \int _{t_m}^{t_{m+1}} \left\| \partial _s\phi (s) \right\| _{H^{q+1}}^2 ds + \frac{h^{2q+2}}{\tau } \int _{t_m}^{t_{m+1}} \left\| \partial _s\mathbf{u}(s) \right\| _{H^{q+1}}^2 ds \nonumber \\&\quad \quad + \tau ^3 \int _{t_m}^{t_{m+1}}\left\| \partial _{sss}\phi (s) \right\| _{}^2 ds \nonumber \\&\quad \quad + \tau ^3 \int _{t_m}^{t_{m+1}}\left\| \partial _{sss}\mathbf{u}(s) \right\| _{}^2 ds + \tau ^3 \int _{t_m}^{t_{m+1}} \left\| \partial _{ss} \phi ^2(s) \right\| _{H^1}^2 ds\nonumber \\&\quad \quad + \tau ^3 \int _{t_{m-1}}^{t_{m+1}}\left\| \nabla \partial _{ss}\phi (s) \right\| _{}^2 \, ds \nonumber \\&\quad \quad + \tau ^3 \int _{t_{m-1}}^{t_{m+1}}\left\| \nabla \partial _{ss}\mathbf{u}(s) \right\| _{}^2 \, ds + \tau ^3 \int _{t_{m-1}}^{t_{m+1}} \left\| \nabla \Delta \partial _{ss} \phi (s) \right\| _{}^2 ds \nonumber \\&\quad \quad + \tau ^3 \int _{t_m}^{t_{m+1}} \left\| \partial _{ss} p(s) \right\| _{}^2 ds \nonumber \\&\quad \quad + h^{2q}\left| \mu ^{m+\frac{1}{2}} \right| _{H^{q+1}}^2 + h^{2q}\left| \phi ^{m+1} \right| _{H^{q+1}}^2 + h^{2q}\left| \phi ^{m} \right| _{H^{q+1}}^2 + h^{2q}\left| \phi ^{m-1} \right| _{H^{q+1}}^2 \nonumber \\&\quad \quad + h^{2q}\left| \mathbf{u}^{m+1} \right| _{H^{q+1}}^2 \nonumber \\&\quad \quad + h^{2q}\left| \mathbf{u}^{m} \right| _{H^{q+1}}^2 + h^{2q}\left| \mathbf{u}^{m-1} \right| _{H^{q+1}}^2 + h^{2q}\left| p^{m+1} \right| _{H^{q+1}}^2 + h^{2q}\left| p^{m} \right| _{H^{q+1}}^2\nonumber \\&\quad \quad + h^{2q}\left| p^{m-1} \right| _{H^{q+1}}^2. \end{aligned}$$

(3.50)

Proof

Define, for $1\le m\le M-1$, time-dependent spatial mass average

$$\begin{aligned} \overline{{\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}} := |\Omega |^{-1}\left( {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}, 1 \right) . \end{aligned}$$

(3.51)

Using the Cauchy–Schwarz inequality, the Poincaré inequality, with the fact that

$$\begin{aligned} \left( \sigma ^{\phi ,m+\frac{1}{2}}_1 + \sigma ^{\phi ,m+\frac{1}{2}}_2, 1 \right) = 0, \end{aligned}$$

and the local truncation error estimates (3.19) and (3.20), we get the following estimate:

$$\begin{aligned} \left| \left( \sigma ^{\phi ,m+\frac{1}{2}}_1 + \sigma ^{\phi ,m+\frac{1}{2}}_2, {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right) \right|&= \left| \left( \sigma ^{\phi ,m+\frac{1}{2}}_1 + \sigma ^{\phi ,m+\frac{1}{2}}_2, {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}-\overline{{\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}} \right) \right| \nonumber \\&\le \left\| \sigma ^{\phi ,m+\frac{1}{2}}_1 + \sigma ^{\phi ,m+\frac{1}{2}}_2 \right\| _{} \cdot \left\| {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}-\overline{{\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}} \right\| _{} \nonumber \\&\le C \left\| \sigma ^{\phi ,m+\frac{1}{2}}_1 + \sigma ^{\phi ,m+\frac{1}{2}}_2 \right\| _{} \cdot \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{} \nonumber \\&\le C\left\| \sigma ^{\phi ,m+\frac{1}{2}}_1 \right\| _{}^2 + C\left\| \sigma ^{\phi ,m+\frac{1}{2}}_2 \right\| _{}^2 + \frac{\varepsilon }{8} \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 \nonumber \\&\le C \frac{h^{2q+2}}{\tau } \int _{t_m}^{t_{m+1}} \left\| \partial _s\phi (s) \right\| _{H^{q+1}}^2 ds \nonumber \\&\quad \quad + C\frac{\tau ^3}{640} \int _{t_m}^{t_{m+1}}\left\| \partial _{sss}\phi (s) \right\| _{}^2 ds + \frac{\varepsilon }{8} \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2. \end{aligned}$$

(3.52)

Meanwhile, standard finite element approximation theory shows that

$$\begin{aligned} \left\| \nabla {\mathcal {E}}_a^{\mu ,m+\frac{1}{2}} \right\| _{} = \left\| \nabla \left( R_h \mu ^{m+\frac{1}{2}} - \mu ^{m+\frac{1}{2}}\right) \right\| _{} \le C h^q\left| \mu ^{m+\frac{1}{2}} \right| _{H^{q+1}}. \end{aligned}$$

Applying Lemma 3.8 and the last estimate, we have

$$\begin{aligned} \left| \left( {\mathcal {E}}_a^{\mu ,m+\frac{1}{2}}, \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right| \le&\, C \left\| \nabla {\mathcal {E}}_a^{\mu ,m+\frac{1}{2}} \right\| _{} \, \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h} \nonumber \\ \le&\, C h^q\left| \mu ^{m+\frac{1}{2}} \right| _{H^{q+1}} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h} \nonumber \\ \le&\, Ch^{2q}\left| \mu ^{m+\frac{1}{2}} \right| _{H^{q+1}}^2 + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2. \end{aligned}$$

(3.53)

Using Lemma 3.8 and estimate (3.21), we find

$$\begin{aligned} \varepsilon \, a\left( \sigma _3^{\phi ,m+\frac{1}{2}}, \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right)&= -\varepsilon \, \left( \Delta \sigma _3^{\phi ,m+\frac{1}{2}}, \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \nonumber \\&\le C \left\| \nabla \Delta \sigma _3^{\phi ,m+\frac{1}{2}} \right\| _{} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h} \nonumber \\&\le C \, \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \nabla \Delta \partial _{ss} \phi (s) \right\| _{}^2 ds + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2. \nonumber \\&\end{aligned}$$

(3.54)

Now, using Lemmas 3.6 and 3.8, we obtain

$$\begin{aligned} \varepsilon ^{-1}\left| \left( \sigma _4^{\phi ,m+\frac{1}{2}}, \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right| \le&\, C \left\| \nabla \sigma _4^{\phi ,m+\frac{1}{2}} \right\| _{} \, \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h} \nonumber \\ \le&\, C \left\| \nabla \sigma _4^{\phi ,m+\frac{1}{2}} \right\| _{}^2 + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 \nonumber \\ \le&\, C\tau ^3 \int _{t_m}^{t_{m+1}} \left\| \nabla \partial _{ss} \phi (s) \right\| _{}^2 ds \nonumber \\&{+} C \tau ^3 \int _{t_m}^{t_{m+1}} \left\| \partial _{ss} \phi ^2(s) \right\| _{H^1}^2 ds {+}s \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2. \end{aligned}$$

(3.55)

Similarly, using Lemmas 3.6 and 3.8, the relation ${\mathcal {E}}^{\phi ,m+1} ={\mathcal {E}}_a^{\phi ,m+1}+{\mathcal {E}}_h^{\phi ,m+1}$, and a standard finite element error estimate, we arrive at

$$\begin{aligned} \varepsilon ^{-1}\left| \left( \sigma _5^{\phi ,m+\frac{1}{2}}, \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right| \le&\, C \left\| \nabla \sigma _5^{\phi ,m+\frac{1}{2}} \right\| _{}^2 + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 \nonumber \\ \le&\, C \left\| \nabla {\mathcal {E}}^{\phi ,m+1} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}^{\phi ,m} \right\| _{}^2 + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 \nonumber \\ \le&\, C \left\| \nabla {\mathcal {E}}_a^{\phi ,m+1} \right\| _{}^2 +C \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_a^{\phi ,m} \right\| _{}^2 \nonumber \\&+C \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 \nonumber \\ \le&\, C h^{2q}\left| \phi ^{m+1} \right| _{H^{q+1}}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 + C h^{2q}\left| \phi ^{m} \right| _{H^{q+1}}^2 \nonumber \\&+ C \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2. \end{aligned}$$

(3.56)

Applying Lemmas 3.7 and 3.8, the relation ${\mathcal {E}}^{\phi ,m+1} ={\mathcal {E}}_a^{\phi ,m+1}+{\mathcal {E}}_h^{\phi ,m+1}$, and a standard finite element error estimate, we find that

$$\begin{aligned}&\varepsilon ^{-1}\left| \left( \sigma _6^{\phi ,m+\frac{1}{2}}, \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right| \le C \left\| \nabla \sigma _6^{\phi ,m+\frac{1}{2}} \right\| _{}^2 + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 \nonumber \\&\le C \tau ^3 \left( \int _{t_{m-1}}^{t_{m+1}}\left\| \nabla \partial _{ss}\phi (s) \right\| _{}^2 \, ds \right) + C\left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2\nonumber \\&\quad \quad +C \left\| \nabla {\mathcal {E}}_h^{\phi ,m-1} \right\| _{}^2 \nonumber \\&\quad \quad + C h^{2q}\left| \phi ^m \right| _{H^{q+1}}^2 {+} C h^{2q}\left| \phi ^{m-1} \right| _{H^{q+1}}^2 {+} \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2. \end{aligned}$$

(3.57)

The following inequality is a direct consequence of (3.24):

$$\begin{aligned} \frac{\varepsilon \tau ^2}{4} \, a\left( \delta _{\tau }^2\phi ^m, \delta _\tau {\mathcal {E}}_h^{\phi , m+\frac{1}{2}} \right) \le C \frac{\tau ^3}{3} \int _{t_{m-1}}^{t_m} \left\| \nabla \Delta \partial _{ss} \phi (s) \right\| _{}^2 ds + \frac{\alpha }{6} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2.\nonumber \\ \end{aligned}$$

(3.58)

Using Lemma 3.5, we also obtain

$$\begin{aligned} \left( \sigma ^{\mathbf{u},m+\frac{1}{2}}_1 + \sigma ^{\mathbf{u},m+\frac{1}{2}}_2, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \le&\, C \left\| \sigma ^{\mathbf{u},m+\frac{1}{2}}_1 \right\| _{}^2 + C \left\| \sigma ^{\mathbf{u},m+\frac{1}{2}}_2 \right\| _{}^2 + \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 \nonumber \\ \le&\, \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C\frac{h^{2q+2}}{\tau } \int _{t_m}^{t_{m+1}} \left\| \partial _s\mathbf{u}(s) \right\| _{H^{q+1}}^2 ds \nonumber \\&+ C \, \frac{\tau ^3}{640} \int _{t_m}^{t_{m+1}}\left\| \partial _{sss}\mathbf{u}(s) \right\| _{}^2 ds. \end{aligned}$$

(3.59)

Next, using (3.31),

$$\begin{aligned} -\frac{1}{\gamma } c\left( \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} , \sigma _3^{p,m+\frac{1}{2}} \right)\le & {} \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C \left\| \sigma ^{p,m+\frac{1}{2}}_3 \right\| _{}^2 \nonumber \\\le & {} \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \partial _{ss} p(s) \right\| _{}^2 ds,\nonumber \\ \end{aligned}$$

(3.60)

Now let’s consider the convection trilinear terms. Adding and subtracting the appropriate terms, for all $1 \le m \le M-1$,

$$\begin{aligned}&\left| - b\left( \phi ^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right) + b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right) \right. \nonumber \\&\quad \quad \left. +\, b\left( \phi ^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \mu ^{m+\frac{1}{2}} \right) - b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \mu _h^{m+\frac{1}{2}} \right) \right| \nonumber \\&\quad \le \ \left| b\left( \sigma _6^{\phi , m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, {\mathcal {E}}_h^{\mu , m+\frac{1}{2}}- \overline{{\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}} \right) \right| + \left| b\left( \sigma _6^{\phi , m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \mu ^{m+\frac{1}{2}} \right) \right| \nonumber \\&\quad \quad + \left| b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} - \sigma _3^{\mathbf{u},m+\frac{1}{2}}, {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}-\overline{{\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}} \right) \right| \nonumber \\&\qquad + \left| b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, {\mathcal {E}}_a^{\mu ,m+\frac{1}{2}} \right) \right| \nonumber \\&\quad \le \ \left\| \nabla \sigma _6^{\phi , m+\frac{1}{2}} \right\| _{} \left\| \mathbf{u}^{m+\frac{1}{2}} \right\| _{L^4} \left\| {\mathcal {E}}_h^{\mu , m+\frac{1}{2}}- \overline{{\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}} \right\| _{L^4}\nonumber \\&\quad \quad +\, \left\| \nabla \sigma _6^{\phi ,m+\frac{1}{2}} \right\| _{} \left\| \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{L^4} \left\| \mu ^{m+\frac{1}{2}} \right\| _{L^4} \nonumber \\&\quad \quad + \left\| \nabla \tilde{\phi }_h^{m+\frac{1}{2}} \right\| _{} \left\| \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} - \sigma _3^{\mathbf{u},m+\frac{1}{2}} \right\| _{L^4} \left\| {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}- \overline{{\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}} \right\| _{L^4} \nonumber \\&\quad \quad + \left\| \nabla \tilde{\phi }_h^{m+\frac{1}{2}} \right\| _{} \left\| \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{L^4} \left\| {\mathcal {E}}_a^{\mu ,m+\frac{1}{2}} \right\| _{L^4} \nonumber \\&\quad \le \ \frac{\varepsilon }{8} \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 \nonumber \\&\quad \quad + h^{2q}\left| \phi ^{m} \right| _{H^{q+1}}^2 + h^{2q}\left| \phi ^{m-1} \right| _{H^{q+1}}^2 + h^{2q}\left| \mathbf{u}^{m+1} \right| _{H^{q+1}}^2\nonumber \\&\qquad + h^{2q}\left| \mathbf{u}^{m} \right| _{H^{q+1}}^2 + h^{2q}\left| \mathbf{u}^{m-1} \right| _{H^{q+1}}^2 \nonumber \\&\quad \quad + h^{2q}\left| \mu ^{m+\frac{1}{2}} \right| _{H^{q+1}}^2 {+} C \tau ^3 \int _{t_{m-1}}^{t_{m+1}} \left\| \nabla \partial _{ss} \phi (s) \right\| _{}^2 ds {+} C \tau ^3 \int _{t_m}^{t_{m+1}} \left\| \nabla \partial _{ss} \mathbf{u}(s) \right\| _{}^2 ds, \end{aligned}$$

(3.61)

where we have used Lemmas 2.11, 3.4 and 3.7.

Additionally, after adding and subtracting the appropriate terms, for $1 \le m \le M-1$, we have

$$\begin{aligned}&\frac{1}{\gamma } \left| -B\left( \mathbf{u}^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) + B\left( \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \nonumber \\&\quad = \ \frac{1}{\gamma } \left| B\left( \sigma _3^{\mathbf{u},m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) - B\left( \frac{\tau ^2}{2} \delta _{\tau }^2\mathbf{u}^m, \mathbf{u}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right. \nonumber \\&\quad \quad +B\left( \tilde{\mathbf{u}}^{m+\frac{1}{2}}, \sigma _3^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) - B\left( \tilde{\mathbf{u}}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \nonumber \\&\quad \quad + B\left( \tilde{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) - B\left( \tilde{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{\mathbf{u}}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \nonumber \\&\quad \quad + B\left( \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) - B\left( \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \bar{\mathbf{u}}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \nonumber \\&\quad \quad \left. - B\left( \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| . \end{aligned}$$

(3.62)

This is the same basic decomposition considered in Baker’s paper [4]. We immediately see that the last term vanishes by anti-symmetry in the last two terms of B: $B\left( \tilde{\mathbf{u}}_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) =0$. We examine the other eight terms individually. Using estimate (3.42) of Lemma 3.9,

$$\begin{aligned}&\frac{1}{\gamma }\left| B\left( \sigma _3^{\mathbf{u},m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \le \ C \left\| \nabla \sigma _3^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \mathbf{u}^{m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \ \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \nabla \partial _{ss} \mathbf{u}(s) \right\| _{}^2 \, ds ; \end{aligned}$$

(3.63)

$$\begin{aligned}&\frac{1}{\gamma }\left| B\left( \frac{1}{2}\tau ^2 \delta _{\tau }^2\mathbf{u}^m, \mathbf{u}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \le \ C \left\| \nabla \tau ^2 \delta _{\tau }^2\mathbf{u}^m \right\| _{} \left\| \nabla \mathbf{u}^{m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \ \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + \frac{\tau ^3}{3} \int _{t_{m-1}}^{t_{m+1}} \left\| \nabla \partial _{ss} \phi (s) \right\| _{}^2 ds ; \end{aligned}$$

(3.64)

$$\begin{aligned}&\frac{1}{\gamma }\left| B\left( \tilde{\mathbf{u}}^{m+\frac{1}{2}} , \sigma _3^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \le C \left\| \nabla \tilde{\mathbf{u}}^{m+\frac{1}{2}} \right\| _{} \left\| \nabla \sigma _3^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C \left\| \nabla \sigma _3^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C \frac{\tau ^3}{96} \int _{t_m}^{t_{m+1}} \left\| \nabla \partial _{ss} \mathbf{u}(s) \right\| _{}^2 \, ds ; \end{aligned}$$

(3.65)

$$\begin{aligned}&\frac{1}{\gamma }\left| B\left( \tilde{\mathbf{u}}^{m+\frac{1}{2}} , \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \le C \left\| \nabla \tilde{\mathbf{u}}^{m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \ \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C h^{2q} \left( \left| \mathbf{u}^{m+1} \right| ^2_{H^{q+1}} + \left| \mathbf{u}^{m} \right| ^2_{H^{q+1}}\right) \nonumber \\&\quad \quad + C h^{2q} \left( \left| p^{m+1} \right| ^2_{H^{q}} + \left| p^{m} \right| ^2_{H^{q}} \right) ; \end{aligned}$$

(3.66)

$$\begin{aligned}&\frac{1}{\gamma }\left| B\left( \tilde{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{\mathbf{u}}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \le \ \left\| \nabla \tilde{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{\mathbf{u}}^{m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \ \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C h^{2q} \left( \left| \mathbf{u}^{m} \right| ^2_{H^{q+1}} + \left| \mathbf{u}^{m-1} \right| ^2_{H^{q+1}}\right) \nonumber \\&\quad \quad + C h^{2q} \left( \left| p^{m} \right| ^2_{H^{q}} + \left| p^{m-1} \right| ^2_{H^{q}} \right) . \end{aligned}$$

(3.67)

Using the stability estimate (3.48),

$$\begin{aligned}&\frac{1}{\gamma }\left| B\left( \tilde{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \le \ \left\| \tilde{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} \right\| _{L^\infty } \left\| \nabla \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \ C \left\| \nabla \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \ \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C h^{2q} \left( \left| \mathbf{u}^{m+1} \right| ^2_{H^{q+1}} + \left| \mathbf{u}^{m} \right| ^2_{H^{q+1}}\right) \nonumber \\&\quad \quad + C h^{2q} \left( \left| p^{m+1} \right| ^2_{H^{q}} + \left| p^{m} \right| ^2_{H^{q}} \right) ; \end{aligned}$$

(3.68)

and, with the estimate (3.44), the inverse-Sobolev inequality (3.46), the Poincaré inequality, and estimate (3.48) again,

$$\begin{aligned}&\frac{1}{\gamma }\left| B\left( \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \le \ C \left\| \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{L^\infty } \nonumber \\&\qquad + C \left\| \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} \right\| _{L^\infty } \nonumber \\&\le \ C \left\| \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} h^q (|\mathbf{u}|_{H^{q+1}} + |p|_{H^{q}}) h^{\frac{1-d}{2}} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad + C \left\| \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \ \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m-1} \right\| _{}^2; \end{aligned}$$

(3.69)

$$\begin{aligned}&\frac{1}{\gamma }\left| B\left( \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}}, \bar{\mathbf{u}}^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right) \right| \nonumber \\&\quad \le \ \left( \left\| \bar{\mathbf{u}}^{m+\frac{1}{2}} \right\| _{L^\infty } + \left\| \nabla \bar{\mathbf{u}}^{m+\frac{1}{2}} \right\| _{L^4} \right) \left\| \tilde{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \nonumber \\&\quad \le \ \frac{\eta }{22 \gamma } \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m-1} \right\| _{}^2. \end{aligned}$$

(3.70)

Combining the estimates (3.52)–(3.70) with the error equation (3.18), the result follows. $\square$

Lemma 3.12

Suppose that $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11b), with the additional regularities in Assumption 3.1. Then, for any $h, \tau >0$, there exists a constant $C>0$, independent of h and $\tau$, such that, for $1\le m\le M-1$,

$$\begin{aligned} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 \le&\, 2 \, \varepsilon ^2 \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 +C \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m-1} \right\| _{}^2 \nonumber \\&+ 5 \, C_2^2 \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C\mathcal {R}^{m+\frac{1}{2}}, \end{aligned}$$

(3.71)

where $C_2 = C_0^2 C_1$, $C_0$ is the $H^1(\Omega ) \hookrightarrow L^4(\Omega )$ Sobolev embedding constant, $C_1$ is a bound for $\max \limits _{0\le t \le T} \left\| \nabla \phi _h^m \right\| _{}$, and $\mathcal {R}^{m+\frac{1}{2}}$ is the consistency term given in (3.50).

Proof

Define $\mathsf {T}_h: \mathring{S}_h\rightarrow \mathring{S}_h$ via the variational problem: given $\zeta \in \mathring{S}_h$, find $\xi \in \mathring{S}_h$ such that $a\left( \mathsf {T}_h (\zeta ), \xi \right) = \left( \zeta , \xi \right)$ for all $\xi \in \mathring{S}_h$. Then, setting $\nu = \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right)$ in (3.17a) and combining, we have

$$\begin{aligned}&\left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 = \, - \varepsilon \, a\left( {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}, \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right) \nonumber \\&\quad + \left( \sigma ^{m+\frac{1}{2}}_1 + \sigma ^{m+\frac{1}{2}}_2, \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right) \nonumber \\&\quad - b\left( \phi ^{m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right) + b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{\mathbf{u}}_h^{m+\frac{1}{2}}, \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right) \nonumber \\&= \, - \varepsilon \, a\left( {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}}, \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right) + \left( \sigma ^{m+\frac{1}{2}}_1 + \sigma ^{m+\frac{1}{2}}_2, \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right) \nonumber \\&\quad - b\left( \sigma _6^{\phi ,m+\frac{1}{2}}, \mathbf{u}^{m+\frac{1}{2}}, \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right) \nonumber \\&\quad - b\left( \tilde{\phi }_h^{m+\frac{1}{2}}, \bar{{\mathcal {E}}}^{\mathbf{u},m+\frac{1}{2}} - \sigma _3^{\mathbf{u},m+\frac{1}{2}}, \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right) \nonumber \\&\le \, \varepsilon \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h} + \left\| \sigma ^{m+\frac{1}{2}}_1 + \sigma ^{m+\frac{1}{2}}_2 \right\| _{} \left\| \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right\| _{} \nonumber \\&\quad + \left\| \sigma _6^{\phi ,m+\frac{1}{2}} \right\| _{} \left\| \mathbf{u}^{m+\frac{1}{2}} \right\| _{L^4} \left\| \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right\| _{L^4} \nonumber \\&\quad + \left\| \tilde{\phi }_h^{m+\frac{1}{2}} \right\| _{L^\infty } \left\| \bar{{\mathcal {E}}}^{\mathbf{u},m+\frac{1}{2}} - \sigma _3^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right\| _{} \nonumber \\&\le \, \varepsilon ^2 \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \frac{1}{4} \left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 + C \left\| \sigma ^{m+\frac{1}{2}}_2 + \sigma ^{m+\frac{1}{2}}_1 \right\| _{}^2 \nonumber \\&\quad + C \left\| \sigma ^{m+\frac{1}{2}}_6 \right\| _{} \left\| \nabla \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right\| _{} + C_2 \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{} \left\| \nabla \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right\| _{} \nonumber \\&\quad + C \left\| \nabla \left( \bar{{\mathcal {E}}}_a^{\mathbf{u},m+\frac{1}{2}} - \sigma _3^{\mathbf{u},m+\frac{1}{2}}\right) \right\| _{} \left\| \nabla \mathsf {T}_h\left( \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right) \right\| _{} \nonumber \\&\le \, \varepsilon ^2 \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \frac{1}{2}\left\| \delta _\tau {\mathcal {E}}_h^{\phi ,m+\frac{1}{2}} \right\| _{-1,h}^2 +C \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m-1} \right\| _{}^2 \nonumber \\&\quad + \frac{5 C_2^2}{2} \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + C\mathcal {R}^{m+\frac{1}{2}}, \end{aligned}$$

(3.72)

for $1 \le m \le M-1$, where we have used Lemmas 3.4, 3.5, and 3.7. The result now follows. $\square$

Lemma 3.13

Suppose that $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11d), with the additional regularities described in Assumption 3.1. Then, for any h, $\tau >0$, there exists a constant $C>0$, independent of h and $\tau$, but possibly dependent upon T, such that, for any $1\le m\le M-1$,

$$\begin{aligned}&\frac{\varepsilon }{2\tau } \left( \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 - \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2\right) + \frac{1}{2 \tau \gamma } \left( \left\| {\mathcal {E}}_h^{\mathbf{u},m+1} \right\| _{}^2 - \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2\right) \nonumber \\&\quad + \frac{ \varepsilon \tau ^2}{4} \, a\left( \delta _{\tau }^2{\mathcal {E}}_h^{\phi ,m}, \delta _\tau {\mathcal {E}}_h^{\phi , m+\frac{1}{2}} \right) \nonumber \\&\quad + \frac{\varepsilon }{2} \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \frac{\eta }{4\gamma } \, \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 \le \, C \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 \nonumber \\&\quad + C \left\| \nabla {\mathcal {E}}_h^{\phi ,m-1} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m-1} \right\| _{}^2 + C \mathcal {R}^{m+\frac{1}{2}}. \end{aligned}$$

(3.73)

Proof

This follows upon combining the last two lemmas and choosing $\alpha$ in (3.49) appropriately. $\square$

Using the last lemma, we are ready to show the main convergence result for our second-order splitting scheme.

Theorem 3.14

Suppose $(\phi , \mu , \mathbf{u}, p)$ is a weak solution to (3.11a)–(3.11d), with the additional regularities described in Assumption 3.1. Then, provided that $0<\tau <\tau _0$, with some $\tau _0$ sufficiently small,

$$\begin{aligned}&\max _{1 \le m \le M-1} \left( \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 + \left\| {\mathcal {E}}_h^{\mathbf{u},m+1} \right\| _{}^2\right) +\, \tau \sum _{m=1}^{M-1} \left( \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2\right) \nonumber \\&\quad \le C(T)\left( \tau ^4+h^{2q}\right) , \end{aligned}$$

(3.74)

for some $C(T)>0$ that is independent of $\tau$ and h.

Proof

Using Lemma 3.13, we have

$$\begin{aligned} \frac{1}{2 \tau }&\,\left( \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} \right\| _{}^2 \!{-} \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 \right) {+} \frac{1}{2 \tau \gamma } \left( \left\| {\mathcal {E}}_h^{\mathbf{u},m+1} \right\| _{}^2 \!{-} \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2\right) {+} \frac{1}{4} \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2&\nonumber \\&+ \frac{\eta }{4\gamma } \, \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 + \frac{1}{8 \tau } \left( \left\| \nabla {\mathcal {E}}_h^{\phi ,m+1} - \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 - \left\| \nabla {\mathcal {E}}_h^{\phi ,m} - \nabla {\mathcal {E}}_h^{\phi ,m-1} \right\| _{}^2 \right) \nonumber \\ \le&\, C \left\| \nabla {\mathcal {E}}_h^{\phi , m+1} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi , m} \right\| _{}^2 + C \left\| \nabla {\mathcal {E}}_h^{\phi , m-1} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2 + C \left\| {\mathcal {E}}_h^{\mathbf{u},m-1} \right\| _{}^2 \nonumber \\&+ C\mathcal {R}^{m+\frac{1}{2}}. \end{aligned}$$

(3.75)

Now, applying $\tau \sum _{m=1}^\ell$ to (3.75), and observing that ${\mathcal {E}}_h^{\phi ,m}\equiv 0$ and ${\mathcal {E}}_h^{\mathbf{u},m}\equiv \mathbf{0}$, for $m = 0,1$, leads to

$$\begin{aligned}&\left\| \nabla {\mathcal {E}}_h^{\phi ,\ell +1} \right\| _{}^2 + \ \left\| {\mathcal {E}}_h^{\mathbf{u},\ell +1} \right\| _{}^2 + \frac{\tau }{2} \sum _{m=1}^{\ell } \left( \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2\right) \nonumber \\&\quad \le C_3\tau \sum _{m=1}^\ell \mathcal {R}^{m+\frac{1}{2}} + C_4\tau \sum _{m=2}^{\ell +1}\left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 + C_5\tau \sum _{m=2}^{\ell }\left\| {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2. \end{aligned}$$

(3.76)

If $0< \tau \le \tau _0:= \frac{1}{2C_4} < \frac{1}{C_4}$, since $1\le \frac{1}{1-C_4\tau } \le 2$, it follows from the last estimate that

$$\begin{aligned}&\left\| \nabla {\mathcal {E}}_h^{\phi ,\ell +1} \right\| _{}^2 + \left\| {\mathcal {E}}_h^{\mathbf{u},\ell +1} \right\| _{}^2 + \frac{\tau }{2} \sum _{m=1}^{\ell } \left( \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2\right) \nonumber \\&\quad \le \, \frac{C_3\tau }{1-C_4\tau }\sum _{m=1}^\ell \mathcal {R}^{m+\frac{1}{2}} + \frac{C_4\tau }{1-C_4\tau } \sum _{m=2}^{\ell }\left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 + \frac{C_5\tau }{1-C_4\tau } \sum _{m=2}^{\ell }\left\| \nabla {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2 \nonumber \\&\quad \le \, 2C_3C_6(\tau ^4+h^{2q}) + 2C_7 \tau \sum _{m=2}^{\ell }\left( \left\| \nabla {\mathcal {E}}_h^{\phi ,m} \right\| _{}^2 + \left\| \nabla {\mathcal {E}}_h^{\mathbf{u},m} \right\| _{}^2\right) , \end{aligned}$$

(3.77)

where we have used the fact that $\tau \sum _{m=1}^{M-1} \mathcal {R}^{m+\frac{1}{2}}\le C_6(\tau ^4+h^{2q})$ and where $C_7 := \max \left( C_4,C_5\right)$. Appealing to the discrete Gronwall inequality 4.1, it follows that, for any

$$\begin{aligned}&\left\| \nabla {\mathcal {E}}_h^{\phi ,\ell +1} \right\| _{}^2 + \left\| {\mathcal {E}}_h^{\mathbf{u},\ell +1} \right\| _{}^2 + \frac{\tau }{2} \sum _{m=1}^{\ell } \left( \left\| \nabla {\mathcal {E}}_h^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \left\| \nabla \bar{{\mathcal {E}}}_h^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2\right) \nonumber \\&\quad \le 2C_3C_6(\tau ^4+h^{2q})\exp (2C_7T), \end{aligned}$$

(3.78)

for any $1\le \ell \le M-1$. $\square$

Remark 3.15

From here it is straightforward to establish an optimal error estimate of the form

$$\begin{aligned}&\max _{1\le m \le M-1} \left( \left\| \nabla {\mathcal {E}}^{\phi ,m+1} \right\| _{}^2 + \left\| {\mathcal {E}}^{\mathbf{u},m+1} \right\| _{}^2 \right) + \tau \sum _{m=1}^{M-1} \left( \left\| \nabla {\mathcal {E}}^{\mu ,m+\frac{1}{2}} \right\| _{}^2 + \left\| \nabla \bar{{\mathcal {E}}}^{\mathbf{u},m+\frac{1}{2}} \right\| _{}^2 \right) \nonumber \\&\quad \le C(T)(\tau ^4+h^{2q}) \end{aligned}$$

(3.79)

using ${\mathcal {E}}^{\phi }= {\mathcal {E}}_a^{\phi }+ {\mathcal {E}}_h^{\phi }$, et cetera, the triangle inequality, and the standard spatial approximations. We omit the details for the sake of brevity.

Some discrete Gronwall inequalities

We will need the following discrete Gronwall inequality cited in [22, 29]:

Lemma 4.1

Fix $T>0$. Let M be a positive integer, and define $\tau \le \frac{T}{M}$. Suppose $\left\{ a_m\right\} _{m=0}^M$, $\left\{ b_m\right\} _{m=0}^M$ and $\left\{ c_m\right\} _{m=0}^{M-1}$ are non-negative sequences such that $\tau \sum _{m=0}^{M-1} c_m \le C_1$, where $C_1$ is independent of $\tau$ and M. Further suppose that,

$$\begin{aligned} a_\ell + \tau \sum _{m=0}^{\ell } b_m \le C_2 +\tau \sum _{m=0}^{\ell -1} a_m c_m, \quad \forall \, 1\le \ell \le M, \end{aligned}$$

(4.1)

where $C_2>0$ is a constant independent of $\tau$ and M. Then, for all $\tau >0$,

$$\begin{aligned} a_\ell +\tau \sum _{m=0}^{\ell } b_m \le C_2 \exp \left( \tau \sum _{m=0}^{\ell -1}c_m \right) \le C_2\exp (C_1), \quad \forall \, 1\le \ell \le M. \end{aligned}$$

(4.2)

Note that the sum on the right-hand-side of (4.1) must be explicit.

In addition, the following more general discrete Gronwall inequality is needed in the stability analysis.

Lemma 4.2

Fix $T>0$. Let M be a positive integer, and define $\tau \le \frac{T}{M}$. Suppose $\left\{ a_m\right\} _{m=0}^M$, $\left\{ b_m\right\} _{m=0}^M$ and $\left\{ c_m\right\} _{m=0}^{M-1}$ are non-negative sequences such that $\tau \sum _{m=0}^{M-1} c_m \le C_1$, where $C_1$ is independent of $\tau$ and M. Suppose that, for all $\tau >0$ and for some constant $0< \alpha < 1$,

$$\begin{aligned} a_\ell + \tau \sum _{m=0}^{\ell } b_m \le C_2 +\tau \sum _{m=0}^{\ell -1} c_m \sum _{j=0}^m \alpha ^{m-j} a_j, \quad \forall \, 1\le \ell \le M, \end{aligned}$$

(4.3)

where $C_2>0$ is a constant independent of $\tau$ and M. Then, for all $\tau >0$,

$$\begin{aligned} a_\ell +\tau \sum _{m=0}^{\ell } b_m \le ( C_2 + a_0 C_1) \exp \left( \frac{C_1}{1-\alpha }\right) , \quad \forall \, 1\le \ell \le M. \end{aligned}$$

(4.4)

Proof

We set $A_\alpha := \frac{1}{1-\alpha } > 1$. A careful application of induction, using (4.3), yields the following inequality:

$$\begin{aligned} a_\ell +\tau \sum _{m=0}^{\ell } b_m \le \prod _{m=1}^\ell d_{\ell ,m}, \quad \forall \, 1\le \ell \le M, \end{aligned}$$

(4.5)

where

$$\begin{aligned} d_{\ell ,m} = \left\{ \begin{array}{l@{\quad }l@{\quad }l} \prod _{k=0}^{m-1}\left( 1 + \tau \alpha ^k c_m \right) &{} \text{ if } &{} 1\le m\le \ell -1 \\ C_2 + a_0 \tau \sum _{k=0}^{\ell -1} c_k \alpha ^k &{} \text{ if } &{} m =\ell \end{array} \right. . \end{aligned}$$

(4.6)

Meanwhile, the following bound is available:

$$\begin{aligned} d_{\ell ,m} =&\ ( 1 + \tau c_m ) ( 1 + \alpha \tau c_m ) \cdots ( 1 + \alpha ^{m-1} \tau c_m ) \nonumber \\ \le&\ \exp ( \tau c_m ) \exp ( \alpha \tau c_k ) \cdots \exp ( \alpha ^{m-1} \tau c_m ) \nonumber \\ =&\ \exp \left( \tau ( 1 + \alpha + \cdots + \alpha ^{m-1} ) c_m \right) \le \exp \left( A_\alpha c_m \tau \right) , \quad \forall \, 1\le m < \ell -1, \end{aligned}$$

(4.7)

which in turn leads to

$$\begin{aligned} d_{\ell ,1} d_{\ell ,2} \cdots d_{\ell ,\ell -1} \le&\ \mathrm{e}^{A_\alpha c_1 \tau } \mathrm{e}^{A_\alpha c_2 \tau } \cdots \mathrm{e}^{A_\alpha c^{\ell -1} \tau } \nonumber \\ \le&\ \exp \left( A_\alpha \tau ( c_1 + c_2 + \cdots + c_{\ell -1} ) \right) \le \exp ( A_\alpha C_1 ). \end{aligned}$$

(4.8)

On the other hand, we also have

$$\begin{aligned} d_{\ell ,\ell }&= C_2 + a_0 \tau \left( c_0 + c_1 \alpha + \cdots + c_{\ell -1} \alpha ^{\ell -1} \right) \nonumber \\&\le \ C_2 + a_0 \tau \left( c_0 + c_1 + \cdots + c^{\ell -1} \right) \le C_2 + a_0 C_1. \end{aligned}$$

(4.9)

In turn, a substitution of (4.8) and (4.9) into (4.6) results in (4.4), the desired estimate. The proof of Lemma 4.2 is complete. $\square$