An enhanced flux continuity three-dimensional finite element method for heterogeneous and anisotropic diffusion problems on general meshes

Abstract

In this research, we present a novel enhanced flux continuity three-dimensional finite element method for heterogeneous and anisotropic (possibly discontinuous) diffusion problems on general meshes. We create a polygonal dual mesh $\mathcal {T}_h^*$ and its submesh $\mathcal {T}_h^{**}$ from a primal mesh $\mathcal {T}_h$ in such a manner that a set number of adjacent tetrahedral elements of $\mathcal {T}_h^{**}$ are united to form each dual control volume of $\mathcal {T}_h^*$, which corresponds to a primal vertex. The weak solution of the diffusion problem is approximated by the piecewise linear functions on the subdual mesh $\mathcal {T}_h^{**}$. In order to capture the local continuity of numerical fluxes across the interfaces, the proposed scheme gives the auxiliary face unknowns interpolated by the multi-point flux approximation. Moreover, the consistency, coercive, and convergence properties of the method are presented within a rigorous theoretical framework. Numerical results are carried out to highlight accuracy and efficiency.

1 Introduction

The three-dimensional heterogeneous and anisotropic diffusion problems arising in the wide range of fields have considerably drawn much attention from researchers in many scientific applications such as oil reservoir simulation, hydrogeology, semiconductor, biology model, and plasma physics. Particularly, we consider the following problem on an open bounded connected polyhedral domain $\Omega$ in ${\mathbb {R}}^3$:

$$\begin{aligned} -{\text {div}}(\Lambda \nabla u) = f \quad \text {in } \Omega , \end{aligned}$$

(1)

with the homogeneous Dirichlet boundary condition:

$$\begin{aligned} u = 0 \quad \text {on}~\partial \Omega . \end{aligned}$$

(2)

The source term f belongs to $L^2(\Omega )$. The tensor $\Lambda$ is piecewise Lipschitz continuous on $\Omega$, and satisfied symmetric, positive definite. Therefore, for almost every ${x}\in \Omega$, we have

$$\begin{aligned} {\underline{\lambda }} |\pmb {\xi }|^2 \le \Lambda ({x}) \pmb {\xi } \cdot \pmb {\xi } \le {\overline{\lambda }} |\pmb {\xi }|^2, \quad \forall \pmb {\xi } \in {\mathbb {R}}^3, \end{aligned}$$

(3)

where $\underline{\lambda }$ and ${\overline{\lambda }}$ are positive values.

The variational form of (1) can be represented as

$$\begin{aligned}&\text {Find } {\overline{u}} \in \mathcal {H}_0 := H^1_0(\Omega ) \text { such that } \nonumber \\&\int \limits _\Omega \Lambda ({x}) \nabla {\overline{u}}({x}) \cdot \nabla v({x}) d{x}= \int \limits _\Omega f({x}) v({x}) d{x},\quad \forall v \in H^1_0(\Omega ). \end{aligned}$$

(4)

For this problem, we developed a novel efficient method to accurately approximate the weak solution ${\overline{u}}$. When carrying out this work, we met the following two main difficulties: (i) the continuity of numerical fluxes regarding to the heterogeneous and anisotropic diffusion problems (possibly discontinuous) must be imposed on the numerical methods; (ii) they are designed to handle on general meshes. Note that the standard finite element method cannot pass two challenges (i) and (ii).

In the literature of numerical methods for the problem (1)–(2), the finite volume method is well known to find the approximate solutions of the heterogeneous and anisotropic problems (4) on admissible meshes. The two-point formula, which is used in this method to approximate the diffusion flux $- \int \nolimits _{\texttt {f}} \Lambda ({x}) \nabla {\overline{u}} ({x}) \cdot \textbf{n}_{K,\sigma } d {x}$ through any face f of each control volume K, guarantees the local conservation of the discrete fluxes. Note that the geometry of grid cells is admissible to ensure the consistency property of the two-point flux approximation. In [1], the authors proposed a cell-centered finite volume scheme which treats material discontinuities for three-dimensional diffusion equation. Its discrete normal flux is approximated by a linear combination of the directional flux along the line connecting cell centers and the tangent flux along the cell faces. However, the problem is only considered on a scalar diffusion coefficient.

Along with the cell-centered techniques, the potent hybrid techniques have been successfully used to polygonal and polyhedral meshes, both structured and unstructured, that include extra unknowns on the edges, faces, and vertices in order to approximate the solution ${\overline{u}}$. In particular, we first mention the mixed finite element method having the Raviart–Thomas basis functions. Its unknowns are the discrete fluxes and discrete gradients. This method demands high refined grids to apply for some highly heterogeneous and anisotropic cases. In [2], the authors introduced the mixed finite volume method (MFV) based on the original developments from the finite volume. This method can be carried out for any mesh type in arbitrary space dimension, and possesses the fluxes and the cell-centered unknowns. We also have the hybrid finite volume (HFV) methods [3] using both cell and edge unknowns. Giving another approach, the extensions of the discrete duality finite volumes (DDFV) method for applications to three-dimensional diffusion problems are the CeVeFE-DDFV [4], the CeVeDDFV-A [5], and the CeVeDDFV-B [6] methods. These methods are shown to be complicated when applied to solving many engineering problems with diffusion terms on a complex geometric computed domain. This is because the discrete gradient, the discrete divergence, the discrete duality property, and the kernel of the discrete gradient can be difficult to compute (e.g., volumes, faces) and describe for more complex geometries of the boundary faces, the primal, secondary, diamond cells (see [7, Remark 6], [6, Eq. (2)]). In addition, these schemes are limited to polyhedral cells whose faces have only three or four sides. According to the literature review, the numerical methods still have some mentioned drawbacks when applying to the three-dimensional heterogeneous and anisotropic diffusion problems. From the above drawbacks of the current schemes, our objective for this work is to investigate a novel enhanced flux continuity three-dimensional finite element method (EFC-3DFEM) for heterogeneous and anisotropic diffusion problems (4) on the general meshes. The EFC-3DFEM scheme includes the following advantages:

• 1. Given a general primal mesh, the method is suitable for constructing the dual and tetrahedral subdual meshes, ensuring that each dual control volume is indeed a macroelement, the union of a fixed number of adjacent tetrahedra from the subdual mesh $\mathcal {T}^{**}_h$ (see [8, pp. 497–498]). The approximate space for the solution ${\overline{u}}$ of (4) has piecewise linear basis functions on the tetrahedral subdual mesh $\mathcal {T}_h^{**}$;

• 2. In order to guarantee the local continuity of fluxes, the discrete gradient and fluxes are taken into account the anisotropic, heterogeneous tensor $\Lambda$ (potentially discontinuous) using the multi-point flux approximation approach;

• 3. With a mild assumption on geometry, the linear system is always symmetric and positive definite, this helps to reduce the computational cost by the iterative methods for solving linear systems;

• 4. The scheme provides the exact solution u of (1), if the tensor $\Lambda$ is piecewise constant in polygonal sub-domains and the exact solution u is affine in each of these sub-domains;

• 5. The scheme is demonstrated to achieve both strong dual consistencies and coercive properties. Consequently, the approximate solution converges to the weak solution ${\overline{u}}$ as the mesh size tends to 0, even for fully heterogeneous anisotropic (possibly discontinuous) diffusion problems;

• 6. The tetrahedral subdual mesh $\mathcal {T}_h^{**}$ is built as an improved primal mesh, which allows the scheme to provide greater precision at a same computational cost; and

• 7. Since the standard finite element programs which are based on tetrahedral meshes, thus they may be used directly, the algorithm is simple to implement.

The framework of this study is organized as follows: in Sect. 2, we describe in detail the construction of the dual mesh $\mathcal {T}_h^*$ and its subdual meshes $\mathcal {T}_h^{**}$. Section 3 presents the discretization of the EFC-3DFEM scheme to obtain a well-posed discrete variational problem. It evidences that the associated linear algebraic system is positive definite and symmetric, then it has the unique solution. In Sect. 4, the scheme is verified for strong, dual consistencies and coercive properties. With these properties, we can present the proof of the convergent results based on [3, Lemma 2.2]. Section 5 compares the results of numerical experiments [9] for the diffusion issue with the heterogeneous and anisotropic tensor (potentially discontinuous) and various mesh types. The paper is concluded in the last section.

2 Construction of meshes

In this part, we go through how to create a dual mesh from a given primal mesh, along with its submesh.

2.1 The primal mesh

Consider a discretization of $\Omega$ defined as a collection $\mathcal {D}= \left( \mathcal {T}_h,\mathcal {V},\mathcal {C},\mathcal {E}, \mathcal {F}\right)$ with

• a. $\mathcal {T}_h$ is a subset of $\Omega$ that is a family of non-empty, open, connected disjoint subsets such that

  $$\begin{aligned} \bigcup \limits _{K \in \mathcal {T}_h} {\overline{K}} = {{\overline{\Omega }}}. \end{aligned}$$

  For each $K \in \mathcal {T}_h$, we denote its volume by $m_K$, its circumscribed sphere’s diameter by $h_K$, and let $h = \max \{h_K, ~\forall K \in \mathcal {T}_h \}$.

• b. $\mathcal {V}$ is a set of all vertices of $\mathcal {T}_h$. We denote two sets of all vertices inside $\Omega$, and of all vertices on $\partial \Omega$ by $\mathcal {V}_{\Omega }$ and $\mathcal {V}_{\partial \Omega }$, respectively.

• c. $\mathcal {C}$ is a set of all mesh points of $\mathcal {T}_h$. Its elements are defined as follows: for each $K \in \mathcal {T}_h$, its associated mesh point ${x_K}$ is an interior point in K such that the segment $[{x_K},{x}]$ lies inside K for all points ${x}\in K$.

• d. $\mathcal {E}$ is a set of all edges of $\mathcal {T}_h$. Its two subsets $\mathcal {E}_{\Omega }$ and $\mathcal {E}_{\partial \Omega }$ contain interior edges and boundary edges, respectively. For each edge $\texttt {e}\in \mathcal {E}$, we denote the midpoint of $\texttt {e}$ by ${x_{\texttt {e}}}$ which is collected in the set $\mathcal {C}_{\mathcal {E}}$, and has two subsets $\mathcal {C}_{\mathcal {E}_{\Omega }} = \{{x_{\texttt {e}}}~|~ e \in \mathcal {E}_{\Omega } \}$ and $\mathcal {C}_{\mathcal {E}_{\partial \Omega }}= \{{x_{\texttt {e}}}~|~ e \in \mathcal {E}_{\partial \Omega } \}$.

• e. $\mathcal {F}$ is a set of all faces of $\mathcal {T}_h$ whose two subsets consist of $\mathcal {F}_{\Omega } = \{ \texttt {f}~|~\texttt {f}\text { inside } \Omega \}$ and $\mathcal {F}_{\partial \Omega } = \{ \texttt {f}~|~ \texttt {f}\text { on } \partial \Omega \}$. For each $\texttt {f}\in \mathcal {F}_{\Omega }$, there exist exactly two primal control volumes $K, L \in \mathcal {T}_h$ sharing the common face $\texttt {f}$. Supposed that a segment joining two points ${x_K}$ and ${x_L}$ intersects with $\texttt {f}$ at a point ${x_\texttt {f}}$ called the face point of $\texttt {f}$. For each $\texttt {f}\in \mathcal {F}_{\partial \Omega }$, a face point ${x_\texttt {f}}$ is an inner point of $\texttt {f}$ such that for any ${x}\in \texttt {f}$, $[{x_\texttt {f}},{x}] \in \texttt {f}$. These face points are collected in the set $\mathcal {C}_{\mathcal {F}} = \mathcal {C}_{\mathcal {F}_{\Omega }} \cup \mathcal {C}_{\mathcal {F}_{\partial \Omega }}$, where $\mathcal {C}_{\mathcal {F}_{\Omega }} = \{ {x_{\texttt {f}}} ~|~\texttt {f}\in \mathcal {F}_{\Omega }\}$ and $\mathcal {C}_{\mathcal {F}_{\partial \Omega }} = \{ {x_{\texttt {f}}} ~|~\texttt {f}\in \mathcal {F}_{\partial \Omega }\}$.

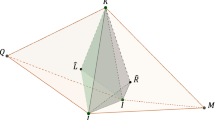
For the sake of simplicity, Fig. 1 introduces some symbols to points of these above sets.

Fig. 1

A primal vertex, the midpoint of a primal edge, the face point of a primal face, and the mesh point of a primal element are represented by the symbols in (A), (B), (C), and (D)

2.2 The dual mesh

The dual mesh is described as a collection $\mathcal {D}^* = \left( \mathcal {T}_h^*, \mathcal {V}^*, \mathcal {C}^*,\mathcal {E}^*, \mathcal {F}^*\right)$ with $\mathcal {T}_h^*, \mathcal {V}^*, \mathcal {C}^*,\mathcal {E}^*$, and $\mathcal {F}^*$ are the sets of the dual control volumes, dual vertices, dual mesh points, dual edges, and triangular dual faces, respectively. The dual mesh is later utilized to construct the tetrahedral submesh. To create the dual mesh $\mathcal {D}^{*}$ (see Algorithm 1), we apply the method described in [10, Section 2] (with minor adjustments).

Algorithm 1

The construction of the dual mesh

Next, we describe in detail the implementation of each step in Algorithm 1 as follows:

2.2.1 Constructing dual vertices

Step 1: The corresponding dual vertex of each primal element K in $\mathcal {T}_h$ is selected to represent the mesh point ${x_K}$ of K.

Step 2: Additionally, there are dual vertices at the face point ${x_{\texttt {f}}}$ of each primal boundary face $\texttt {f}$ in $\mathcal {F}\cap \partial \Omega$.

Step 3: The midpoint ${x_{\texttt {e}}}$ of each primal edge $\texttt {e}$ in $\mathcal {E}$.

Step 4: The primal boundary vertices ${x_V}$ in $\mathcal {V}\cap \partial \Omega$.

2.2.2 Constructing dual faces

Dual faces are formed by both primal edges and primal boundary vertices. We note that in our architecture, the “face” are often not ${\mathbb {R}}^3$ hyperplanes, but rather ${\mathbb {R}}^2$ surfaces combinations. We generate the corresponding triangular dual faces (Step 5) for each primal edge $\texttt {e}$ in $\mathcal {E}$ as follows:

Step 5 (a)::

If $\texttt {e}$ is inside of $\Omega$, we can begin to construct a “face” by progressively traversing all of its related primordial elements in a single direction. We get triangular dual faces by utilizing this “face” and attaching the midpoint ${x_{\texttt {e}}}$ (of $\texttt {e}$) to all of the vertices (see label A in Fig. 2).

Step 5 (b)::

There are two primordial boundary faces, $\texttt {f}_{\partial \Omega , \texttt {e}}^{1}$ and $\texttt {f}_{\partial \Omega , \texttt {e}}^{2}$ that share the edge $\texttt {e}$ if $\texttt {e}$ is on the boundary $\partial \Omega$. This allows us to also generate a “face” in this case. The algorithm begins at one of the two primal boundary faces, say $\texttt {f}_{\partial \Omega , \texttt {e}}^{1}$, and proceeds through the set $\mathcal {T}_{\texttt {e}}$ of all primal elements with $\texttt {e}$ as their edges until it reaches the other boundary face $\texttt {f}_{\partial \Omega , \texttt {e}}^{2}$, and then connects the midpoint of $\texttt {e}$ with the mesh point of $\texttt {f}_{\partial \Omega , \texttt {e}}^{1}$, the dual vertices ${x_K}$, for all K in $\mathcal {T}_{\texttt {e}}$ and the mesh point of $\texttt {f}_{\partial \Omega , \texttt {e}}^{2}$. Finally, the “face” is created by connecting the last mesh point of $\texttt {f}_{\partial \Omega , \texttt {e}}^{2}$ to the midpoint of $\texttt {e}$. The triangular dual faces are then formed by connecting the midpoint ${x_{\texttt {e}}}$ of $\texttt {e}$ to all vertices of this “face” (see labels B and C in Fig 2).

Fig. 2

Triangular dual faces correspond to multiple primordial edges that are either in the domain interior (A, four triangles), on a boundary edge (B, three triangles), or on a boundary edge (C, two triangles)

Step 6 (a)::

For each primal boundary vertex ${x_V}$ in $\mathcal {V}\cap \partial \Omega$, we designate $\mathcal {F}_{{x_V}}$ as a set of primal boundary faces, and $\mathcal {E}_{{x_V}}$ as a set of edges with ${x_V}$ as their vertex, in the same way. There are two edges $\texttt {e}_{\texttt {f},1}, \texttt {e}_{\texttt {f},2}$ in $\mathcal {E}_{{x_V}}$ that correspond to the boundary $\partial \texttt {f}$ for each $\texttt {f}$ in $\mathcal {F}_{{x_V}}$. The procedure for constructing the “face” corresponding to ${x_V}$ begins at the midpoint ${x_{\texttt {e}_{\texttt {f},1}}}$ for some $\texttt {f}\in \mathcal {F}_{{x_V}}$ and connects to the face point ${x_{\texttt {f}}}$ and the midpoint ${x_{\texttt {e}_{\texttt {f},2}}}$; continue until returning to the original point which is the midpoint ${x_{\texttt {e}_{\texttt {f},1}}}$.

Step 6 (b)::

By using this “face,” we connect the boundary vertex ${x_V}$ with all of its vertices to create triangular dual faces.

Obviously, the triangular dual face construction can be generated with the boundary $\partial \Omega$ by taking the intersection of multiple faces (see labels D, E, and F in Fig. 3). The aforementioned steps are designed to produce capping “face” that match to boundary primordial vertices, guaranteeing that the boundary $\partial \Omega$ is represented with the same accuracy in both the dual mesh and the primary mesh.

Fig. 3

Triangular dual faces (used for boundary capping) correspond to a number of primordial boundary vertices, including those on a boundary face (D), a 2-manifold boundary edge (E), and a corner point (F)

2.2.3 Creating dual control volumes corresponding to primal vertices

Polyhedrons M of the dual mesh $\mathcal {T}_h^*$ are constructed by gathering all the triangular dual faces corresponding to one primal vertex ${x_V}\in \mathcal {V}$ (Step 7). There are two cases:

Step 7 (a)::

If ${x_V}$ is in the interior of $\Omega$, then its related dual control volume $M_{{x_V}}$ is formed from all triangular dual faces associated with primal edges connected to ${x_V}$ (see label A in Fig. 4).

Step 7 (b)::

If ${x_V}$ is on the boundary $\partial \Omega$, $M_{{x_V}}$ is formed from the triangular dual faces of primal edges connected to ${x_V}$ and covered with the boundary triangular dual faces corresponding to ${x_V}$ (see labels B and C in Fig. 4).

Fig. 4

Dual polygons in dual mesh corresponding to a interior primal node (A, green), two boundary primal nodes (B, blue) and (C, yellow)

2.2.4 Creating mesh points of dual control volumes

Step 8: The mesh point ${x_M}$ associated with each dual control volume M in $\mathcal {T}_h^*$ will be identified with the primal vertex ${x_V}$ associated with M if ${x_V}$ in M, whereas the set $\mathcal {C}^*$ includes two subsets: $\mathcal {C}^*_{\Omega } = \{{x_M}~|~ {x_M}\in \Omega \}$ and $\mathcal {C}^*_{\partial \Omega } = \{{x_M}~|~ {x_M}\in \partial \Omega \}$.

Remark 1

[11, Algorithm 1] of the 3D-SC-FEM method can build triangular dual faces similarly to Algorithm 1 by connecting the vertices of its dual faces to the midpoints of primal edges and the boundary primal nodes. Hence, as mentioned in [11, Remark 3.2 ], constructing the dual mesh of the EFC-3DFEM method is feasible for real life, complex geometries, as demonstrated in [12, 13].

Remark 2

The dual mesh $\mathcal {T}^*_h$ is a non-overlapping partition of $\Omega$, which is different from the overlapping secondary mesh of the DDFV method (see [7, Remark 1]).

2.3 The subdual tetrahedral mesh

The subdual mesh collection, like the primal and dual meshes, is defined as $\mathcal {D}^{**} = \left( \mathcal {T}_h^{**}, \mathcal {V}^{**}, \mathcal {C}^{**}, \mathcal {E}^{**},\mathcal {F}^{**} \right)$, where $\mathcal {T}_h^{**}$ is a finite family of tetrahedrons T such that $\bigcup \limits _{T \in \mathcal {T}_h^{**}} { {\overline{T}}}= {{\overline{\Omega }}}$; $\mathcal {F}^{**}$, $\mathcal {E}^{**}$, and $\mathcal {V}^{**}$ are the faces, edges, and vertices of the mesh $\mathcal {T}_h^{**}$, respectively; $\mathcal {C}^{**}$ is the finite set of tetrahedrons mesh points T in $\mathcal {T}_h^{**}$. By connecting the mesh point ${x_M}$ of each control volume M in the dual mesh $\mathcal {T}_h^*$ with all of the vertices of its triangular dual faces to produce tetrahedrons (see Fig. 5), we may decompose each control volume M into tetrahedrons and produce the subdual mesh $\mathcal {D}^{**}$.

Remark 3

For actual complex geometries, as seen in [10, 14], the dual mesh $\mathcal {T}_h^*$ can be constructed. Additionally, piecewise linear approximations may be used on universal meshes, thanks to its tetrahedral subdual mesh $\mathcal {T}_h^{**}$.

Fig. 5

An illustration of creating tetrahedrons (of the subdual mesh) from a dual control volume: 24 tetrahedrons of the subdual mesh are created from the dual polygon (green) in Fig. 4

Remark 4

By construction of $\mathcal {T}_h^{**}$, we see that

• (a) The set $\mathcal {V}^{**}$ only consists of three subsets $\mathcal {C}$, $\mathcal {C}^*$, and $\mathcal {C}_{\mathcal {E}}$ containing mesh points of the primal mesh, mesh points of the dual mesh, midpoints of primal edges, respectively; $\mathcal {V}^{**} = \mathcal {V}^{**}_{\Omega } \cup \mathcal {V}^{**}_{\partial \Omega }$ with $\mathcal {V}^{**}_{\Omega } = \mathcal {C}\cup \mathcal {C}^*_{\Omega } \cup \mathcal {C}_{\mathcal {E}_{\Omega }}$, $\mathcal {V}^{**}_{\partial \Omega } = \mathcal {C}\cup \mathcal {C}^*_{\partial \Omega } \cup \mathcal {C}_{\mathcal {E}_{\partial \Omega }}$, and $\mathcal {C}_{\mathcal {E}} = \mathcal {C}_{\mathcal {E}_{\Omega }} \cup \mathcal {C}_{\mathcal {E}_{\partial \Omega }}$. Furthermore, for each $M \in \mathcal {T}_h^*$, the set $\mathcal {V}^{**}_{M}$ of its vertices is defined by

  $$\begin{aligned} \mathcal {V}^{**}_{M} = \mathcal {C}_M \cup \mathcal {C}_{\mathcal {E}_M}\cup \{{x_M}\}, \end{aligned}$$

  (5)

  where ${x_M}$ is the mesh point of M, $\mathcal {C}_M = \{{x_K}\in \mathcal {C}~|~{x_K}\text { is a vertex of } M \}$, $\mathcal {E}_M = \{e \in \mathcal {E}~|~ {x_M}\text { is a vertex of } \texttt {e}\}$, and $\mathcal {C}_{\mathcal {E}_M} = \{{x_{\texttt {e}}} \in \mathcal {C}_{\mathcal {E}} ~|~ \texttt {e}\in \mathcal {E}_M \}$.

• (b) The set $\mathcal {T}_h^{**}$ only has the following subsets:

  

  where $\mathcal {F}^{**}_T$ is a set of all triangular faces in T.

• (c) Each $T=({x_M}{x_K}{x_L}{x_{\texttt {e}}} ) \in \mathcal {T}^{**}_{\Omega }$ can be partitioned into two sub-tetrahedrons $T_K:= ({x_M}{x_K}{x_{\texttt {f}}}{x_{\texttt {e}}})$ and $T_L:= ({x_M}{x_L}{x_{\texttt {f}}}{x_{\texttt {e}}})$, where $\texttt {f}= \partial K \cap \partial L$, its face point ${x_{\texttt {f}}}$ is an intersecting point between a segment $[{x_K},{x_L}]$ and a face $\texttt {f}$.

Remark 5

Because the subdual mesh $\mathcal {D}^{**}$ is formed by decomposing each control volume M in $\mathcal {T}_h^*$, it satisfies

$$\begin{aligned} {\overline{M}} = \bigcup \limits _{T \in \mathcal {T}^{**}_{{x_M}}} {\overline{T}}, \end{aligned}$$

(6)

where ${x_M}$ is the mesh point of M, and $\mathcal {T}^{**}_{{x_M}} = \{T \in \mathcal {T}_h^{**}~|~{x_M}\text { is a vertex } T\}$. Moreover, for any two different dual elements $M, N \in \mathcal {T}_h^*$ with two mesh points ${x_M}, {x_N}$, we have

$$\begin{aligned} \mathcal {T}^{**}_{{x_M}} \cap \mathcal {T}^{**}_{{x_N}} = \emptyset . \end{aligned}$$

(7)

Remark 6

In [11], the staggered cell-centered finite element method (SC-FEM) presented the construction of dual and subdual meshes, where the vertices of its subdual mesh include in vertices and mesh points of the primal mesh. By this geometry, the SC-FEM scheme could not imposed the numerical flux continuity. Therefore, the mesh construction of the EFC-3DFEM scheme are absolutely different from the ones of the SC-FEM scheme.

Remark 7

From geometrical construction of the dual and subdual meshes, we observe that each dual control volume $M \in \mathcal {T}^*_h$ is indeed a macro-element-the union of some fixed number of adjacent tetrahedrons of the subdual mesh $\mathcal {T}^{**}_h$ (see [8, pp. 497–498]).

3 The EFC-3DFEM scheme

In this section, we construct the approximate space for the solution ${\overline{u}}$. On this space, we define the projection and the discrete gradient operators in two cases depending on the characteristics of the tensor $\Lambda$. Using these spaces and operators, we may express the discrete version of the problem (4) from which the corresponding linear algebraic systems are derived.

3.1 Spaces and discrete functional characteristics

In order to estimate the solution ${\overline{u}}$ of (4), the piecewise linear basis functions on the subdual mesh $\mathcal {T}_h^{**}$ and approximations $u_{P}$ in ${\mathbb {R}}$ of $u({x_P})$ at nodes ${x_P}$ in $\mathcal {V}^{**}$ are used. The values $\{u_{P}\}_{{x_P}\in \mathcal {V}^{**}}$ are elements of a vector $\textbf{u}_h$. This vector belongs to the following space:

$$\begin{aligned} \mathcal {H}_h = \{\textbf{u}_h:= (u_{P})_{{x_P}\in \mathcal {V}^{**}}, \quad u_{P} \in {\mathbb {R}} \}. \end{aligned}$$

(8)

Suppose $h^{**}:= \max \left\{ h_T = {\text {diam}}(T),~\forall T\in \mathcal {T}_h^{**}\right\}$ where $h_T$ is the circumscribed sphere’s diameter of the tetrahedral $T \in \mathcal {T}_h^{**}$, if $h \rightarrow 0$ then $h^{**} \rightarrow 0$.

Since we impose the homogeneous Dirichlet boundary condition (2) $(i.e.,~~u_{P} = 0$ with ${x_P}\in \mathcal {V}^{**}_{\partial \Omega }$) on the approximate solution, we need to deal with inner nodes by creating the following subset of $\mathcal {H}_h$

$$\begin{aligned} \mathcal {H}^0_h = \{\textbf{u}_h \in \mathcal {H}_h~~:~~ u_{P} = 0,\quad \forall {x_P}\in \mathcal {V}^{**}_{\partial \Omega } \}. \end{aligned}$$

(9)

This space has all basis vectors in $\left\{ \textbf{v}^{Q}_h \right\} _{{x_Q}\in \mathcal {V}^{**}_{\Omega }}$, where each element of a basis vector $\textbf{v}^{Q}_h:= \left( v^{Q}_{P}\right) _{{x_P}\in \mathcal {V}^{**}}$ is given by $v^{Q}_{P} = {\left\{ \begin{array}{ll} 1 &{} {x_P}= {x_Q},\\ 0 &{} {x_P}\ne {x_Q}, \end{array}\right. }$.

The discrete gradient $\nabla _{\Lambda }$ and the projection operator $\Phi$ must be defined in the following ways on the space $\mathcal {H}_h$ in order to construct the discrete version of (4):

To fulfill the continuity of fluxes across interfaces across primal control volumes, which are specified on each tetrahedron T in $\mathcal {T}_h^{**}$, must take into consideration the tensor $\Lambda$ (which may be discontinuous in the case where two different approximations of $\Lambda$ on T are $\Lambda _K$ on $T \cap K \ne \emptyset$, and $\Lambda _L$ on $T \cap L \ne \emptyset$, with $L, K \in \mathcal {T}_h$). As a result, their definitions are divided into the following two situations depending on the properties of $\Lambda$:

• Case 1. Homogeneous tensors ($\Lambda = \lambda \textbf{I}$, where $\textbf{I}$ is the 3D identity tensor, and $\lambda$ is a positive constant)

For any $\textbf{u}_h = (u_{P})_{{x_P}\in \mathcal {V}^{**}} \in \mathcal {H}^0_h$ ($i.e.~u_{P} = 0,~~ \forall {x_P}\in \mathcal {V}^{**}_{\partial \Omega }$), we define

$$\begin{aligned} \Phi \textbf{u}_h({x}) = {P_1 \textbf{u}_h({x}) :=} \sum \limits _{{x_P}\in \mathcal {V}^{**}_{\Omega }} u_{P} L_{1,P}({x}), \end{aligned}$$

(10)

where $L_{1,P}$ is the Lagrange basis function of degree 1 at ${x_P}$ in $\mathcal {V}^{**}_{\Omega }$.

Given that $\Phi \textbf{u}_h({x})$ is a piecewise polynomial of degree 1, the related discrete gradient $\nabla _{\Lambda } \textbf{u}_h$ on each T in $\mathcal {T}_h^{**}$ is constant. The restriction of the discrete gradient $\nabla _{\Lambda } \textbf{u}_h$ on each T in $\mathcal {T}_h^{**}$ may be written as

$$\begin{aligned} (\nabla _{\Lambda }\textbf{u}_h)_T&= \dfrac{-(u_{K} - u_{M}) \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})} - (u_{L} - u_{M}) \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})} - (u_{\texttt {e}} - u_{M}) \textbf{n}_{({x_M}{x_K}{x_L})}}{3m_T} \nonumber \\&= \dfrac{- u_{K}\textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})} - u_{L}\textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})} - u_{M}\textbf{n}_{({x_K}{x_L}{x_{\texttt {e}}})} - u_{\texttt {e}}\textbf{n}_{({x_M}{x_K}{x_L})}}{3m_T}, \end{aligned}$$

(11)

with $m_T$ is the volume of the tetrahedron $T = ({x_M}{x_K}{x_L}{x_{\texttt {e}}})$; $\textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})}$, $\textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})}$, $\textbf{n}_{({x_K}{x_L}{x_{\texttt {e}}})}$, and $\textbf{n}_{({x_M}{x_K}{x_L})}$ are four outward normal vectors of T at triangular faces $({x_M}{x_L}{x_{\texttt {e}}})$, $({x_M}{x_K}{x_{\texttt {e}}})$, $({x_K}{x_L}{x_{\texttt {e}}})$, and $({x_M}{x_K}{x_L})$, respectively. Their magnitudes are equal to the area of these faces $m_{({x_M}{x_L}{x_{\texttt {e}}})}$, $m_{({x_M}{x_K}{x_{\texttt {e}}})}$, $m_{({x_K}{x_L}{x_{\texttt {e}}})}$, and $m_{({x_M}{x_K}{x_L})}$, respectively.

• Case 2: Heterogeneous and anisotropic tensors.

Due to Remark 4.(b), two operators $\Phi$ and $\nabla _{\Lambda }$ will be defined on each $T \in \mathcal {T}^{**}_{\Omega }$ and $T \in \mathcal {T}^{**}_{\partial \Omega }$.

Let us first consider on each tetrahedron $T:= ({x_M}{x_K}{x_L}{x_{\texttt {e}}}) \in \mathcal {T}^{**}_{\Omega }$. By Remark 4.(c), the tetrahedron T has two sub-tetrahedrons $T_K = ({x_M}{x_K}{x_{\texttt {f}}}{x_{\texttt {e}}})$ and $T_L = ({x_M}{x_L}{x_{\texttt {f}}}{x_{\texttt {e}}})$ with $\texttt {f}\in \partial K \cap \partial L$ and its face point ${x_{\texttt {f}}}$. Remark that $T_K$, $T_L$ are inside two elements $K, L \in \mathcal {T}_h$, respectively, then the approximation values of $\Lambda$ on $T_K$ and $T_L$ are equal to $\Lambda _K$ and $\Lambda _L$, respectively, where $\Lambda _K = \frac{1}{m_K} \int _K \Lambda ({x}) d{x}$ and $\Lambda _L = \frac{1}{m_L} \int _L \Lambda ({x}) d{x}$. The piecewise linear function $\Phi \textbf{u}_h({x})$ on T must thus be determined by values at each of vertices of $T_K$ and $T_L$. To do this, we must propose an auxiliary unknown $u^{M}_{\texttt {f}}$ at ${x_{\texttt {f}}}$, as follows:

$$\begin{aligned} \Phi \textbf{u}_h({x}) = {\left\{ \begin{array}{ll} u_{M}, &{} {x}= {x_M},\\ u_{K}, &{} {x}= {x_K},\\ u_{L}, &{} {x}= {x_L},\\ u_{\texttt {e}}, &{} {x}= {x_{\texttt {e}}},\\ u^{M}_{\texttt {f}}, &{} {x}= {x_{\texttt {f}}}.\\ \end{array}\right. } \end{aligned}$$

(12)

and to define the restrictions of $\nabla _{\Lambda }\textbf{u}_h$ by

$$\begin{aligned}&\left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_K} = \dfrac{- u_{M} \textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})} - u_{K} \textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} - u_{\texttt {e}} \textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})} - u^{M}_{\texttt {f}} \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})}}{3m_{T_K }}{} & {} \text {on } T_K, \end{aligned}$$

(13)

$$\begin{aligned}&\left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_L} = \dfrac{- u_{M} \textbf{n}_{({x_L}{x_{\texttt {e}}}{x_{\texttt {f}}})} - u_{L} \textbf{n}^L_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} - u_{\texttt {e}} \textbf{n}_{({x_M}{x_L}{x_{\texttt {f}}})} - u^{M}_{\texttt {f}} \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})}}{3m_{T_L}}{} & {} \text {on } T_L, \end{aligned}$$

(14)

where $\textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}$ and $\textbf{n}^L_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}$ are the outward vectors of $T_K$ and $T_L$ at triangular face $({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})$.

In order to fulfill the local continuity of the numerical flux over the triangular face $({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})$ inside $\texttt {f}$, the auxiliary unknown $u^{M}_{\texttt {e}}$ is selected by

$$\begin{aligned} \Lambda _K (\nabla _{\Lambda }\textbf{u}_h)_{T_K} \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} + \Lambda _L (\nabla _{\Lambda }\textbf{u}_h)_{T_L} \cdot \textbf{n}^L_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} = 0. \end{aligned}$$

(15)

Substituting (13) and (14) in (15), it reads

$$\begin{aligned} \beta _{M} u_{M} + \beta _{K} u_{K} + \beta _{L} u_{L} + \beta _{\texttt {e}} u_{\texttt {e}} + \beta _{\texttt {f}} u^{M}_{\texttt {f}} = 0, \end{aligned}$$

(16)

with

$$\begin{aligned} \beta _{K}&= \dfrac{\left( \Lambda _K \textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{3m_{T_K}}, \quad \beta _{L} = \dfrac{\left( \Lambda _L \textbf{n}^L_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^L_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{3m_{T_L}},\\ \beta _{M}&= \dfrac{\left( \Lambda _K \textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{3m_{T_K}} + \dfrac{\left( \Lambda _L \textbf{n}_{({x_L}{x_{\texttt {e}}}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^L_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{3m_{T_L}},\\ \beta _{\texttt {e}}&= \dfrac{\left( \Lambda _K \textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{3m_{T_K}}+\dfrac{\left( \Lambda _L \textbf{n}_{({x_M}{x_L}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^L_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{3m_{T_L}},\\ \beta _{\texttt {f}}&= \dfrac{\left( \Lambda _K \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{3m_{T_K}}+\dfrac{\left( \Lambda _L \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})}\right) \cdot \textbf{n}^L_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{3m_{T_L}}. \end{aligned}$$

The above coefficients satisfy

$$\begin{aligned} \beta _{K} + \beta _{L} + \beta _{M} + \beta _{\texttt {e}} + \beta _{\texttt {f}} = 0. \end{aligned}$$

(17)

From (16), let us mention that all along the paper, we assume that $\beta _{\texttt {f}} \ne 0$. The linear combination of $u_{M}$, $u_{K}$, $u_{L}$ and $u_{\texttt {e}}$ is provided as the auxiliary unknown $u^{M}_{\texttt {f}}$:

$$\begin{aligned} u^{M}_{\texttt {f}} = {{\widetilde{\beta }}}^T_{M} u_{M} + {{\widetilde{\beta }}}^T_{K} u_{K} + {{\widetilde{\beta }}}^T_{L} u_{L} + {{\widetilde{\beta }}}^T_{\texttt {e}} u_{\texttt {e}}, \end{aligned}$$

(18)

with

$$\begin{aligned} {{\widetilde{\beta }}}^T_{K} = -\dfrac{\beta _{K}}{\beta _{\texttt {f}}},\quad {{\widetilde{\beta }}}^T_{L} = -\dfrac{\beta _{L}}{\beta _{\texttt {f}}},\quad {{\widetilde{\beta }}}^T_{M} = -\dfrac{\beta _{M}}{\beta _{\texttt {f}}},\quad {{\widetilde{\beta }}}^T_{\texttt {e}} = -\dfrac{\beta _{\texttt {e}}}{\beta _{\texttt {f}}}. \end{aligned}$$

(19)

As a consequence of (17), these above coefficients satisfy

$$\begin{aligned}&{{\widetilde{\beta }}}^T_{M} + {{\widetilde{\beta }}}^T_{K} + {{\widetilde{\beta }}}^T_{L} + {{\widetilde{\beta }}}^T_{\texttt {e}} = 1. \end{aligned}$$

(20)

Remark 8

Let us consider two tetrahedrons $T:= ({x_M}{x_K}{x_L}{x_{\texttt {e}}})$ and ${\widehat{T}}:= ({x_N}{x_K}{x_L}{x_{\texttt {e}}})$ in $\mathcal {T}_h^{**}$, see Fig. 6.

Fig. 6

Two tetrahedrons $T=({x_M}{x_K}{x_L}{x_{\texttt {e}}})$ and ${\widehat{T}}=({x_N}{x_K}{x_L}{x_{\texttt {e}}})$ have the common triangular face $({x_K}{x_L}{x_{\texttt {e}}})$

On the tetrahedrons T and ${\widehat{T}}$, the tensor $\Lambda$ is heterogeneous and anisotropic, then there exist two auxiliary unknowns given by

$$\begin{aligned} u^{M}_{\texttt {f}}&= {{\widetilde{\beta }}}^T_{M} u_{M} + {{\widetilde{\beta }}}^T_{K} u_{K} + {{\widetilde{\beta }}}^T_{L} u_{L} + {{\widetilde{\beta }}}^T_{\texttt {e}} u_{\texttt {e}}, \end{aligned}$$

(21)

$$\begin{aligned} u^{N}_{\texttt {f}}&= {{\widetilde{\beta }}}^{{\widehat{T}}}_{N} u_{N} + \widetilde{\beta }^{{\widehat{T}}}_{K} u_{K} + {{\widetilde{\beta }}}^{{\widehat{T}}}_{L} u_{L} + {{\widetilde{\beta }}}^{{\widehat{T}}}_{{\texttt {e}}} u_{\texttt {e}}. \end{aligned}$$

(22)

Note that ${{\widetilde{\beta }}}^{{\widehat{T}}}_{N} u_{N} \ne \widetilde{\beta }^T_{M} u_{M}$, thus $u^{M}_{\texttt {f}}$ may be different from $u^{N}_{\texttt {f}}$. Consequently, $\Phi \textbf{u}_h({x})$ is discontinuous at ${x_{\texttt {f}}}$.

Substituting (18) into (13) and (14), the discrete gradient $(\nabla _{\Lambda }\textbf{u}_h)_T$ depends on four nodal values $u_{M}$, $u_{K}$, $u_{L}$, and $u_{\texttt {e}}$ expressed by

$$\begin{aligned} \left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_K}&= \frac{- u_{M} {{\widetilde{\textbf{n}}}}^{{x_M}}_{T_K} - u_{K} {{\widetilde{\textbf{n}}}}^{{x_K}}_{T_K} - u_{L} {{\widetilde{\textbf{n}}}}^{{x_L}}_{T_K}- u_{\texttt {e}}\widetilde{\textbf{n}}^{{x_{\texttt {e}}}}_{T_K} }{3m_{T_K }}, \end{aligned}$$

(23)

$$\begin{aligned} \left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_L}&= \frac{- u_{M} {{\widetilde{\textbf{n}}}}^{{x_M}}_{T_L} - u_{K} \widetilde{\textbf{n}}^{{x_K}}_{T_L} - u_{L} {{\widetilde{\textbf{n}}}}^{{x_L}}_{T_L}- u_{\texttt {e}}{{\widetilde{\textbf{n}}}}^{{x_{\texttt {e}}}}_{T_L} }{3m_{T_L}}, \end{aligned}$$

(24)

where

$$\begin{aligned}&{{\widetilde{\textbf{n}}}}^{{x_M}}_{T_K} = \textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})} + {{\widetilde{\beta }}}^T_{M} \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})},{} & {} \widetilde{\textbf{n}}^{{x_K}}_{T_K} = \textbf{n}^{{x_K}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} + \widetilde{\beta }^T_{K} \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})},\\&{{\widetilde{\textbf{n}}}}^{{x_{\texttt {e}}}}_{T_K} = \textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})} + {{\widetilde{\beta }}}^T_{\texttt {e}} \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})},{} & {} \widetilde{\textbf{n}}^{{x_L}}_{T_K} = {{\widetilde{\beta }}}^T_{L} \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})},\\&{{\widetilde{\textbf{n}}}}^{{x_M}}_{T_L} = \textbf{n}_{({x_L}{x_{\texttt {e}}}{x_{\texttt {f}}})} + {{\widetilde{\beta }}}^T_{M} \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})},{} & {} \widetilde{\textbf{n}}^{{x_L}}_{T_L} = \textbf{n}^{{x_L}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} + \widetilde{\beta }^T_{L} \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})}, \\&{{\widetilde{\textbf{n}}}}^{{x_{\texttt {e}}}}_{T_L} = \textbf{n}_{({x_M}{x_L}{x_{\texttt {f}}})} + {{\widetilde{\beta }}}^T_{\texttt {e}} \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})},{} & {} \widetilde{\textbf{n}}^{{x_K}}_{T_L} = {{\widetilde{\beta }}}^T_{K} \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})}, \end{aligned}$$

and these vectors satisfy

$$\begin{aligned} {{\widetilde{\textbf{n}}}}^{{x_M}}_{T_K} + \widetilde{\textbf{n}}^{{x_K}}_{T_K} + {{\widetilde{\textbf{n}}}}^{{x_{\texttt {e}}}}_{T_K} + \widetilde{\textbf{n}}^{{x_L}}_{T_K} = \pmb 0, ~~~{{\widetilde{\textbf{n}}}}^{{x_M}}_{T_L} + \widetilde{\textbf{n}}^{{x_L}}_{T_L} + {{\widetilde{\textbf{n}}}}^{{x_{\texttt {e}}}}_{T_L} + \widetilde{\textbf{n}}^{{x_K}}_{T_L} = \pmb 0, \end{aligned}$$

(25)

due to (20).

In summary, for any $\textbf{u}_h \in \mathcal {H}_h$, the piecewise polynomial $\Phi \textbf{u}_h({x})$ of degree one and the piecewise constant function $\nabla _{\Lambda }(\textbf{u}_h)({x})$ are determined on each $T \in \mathcal {T}^{**}_{\Omega }$ as follows:

$$\begin{aligned} \Phi _T \textbf{u}_h({x})&= {\left\{ \begin{array}{ll} u_{M}, &{} {x}= {x_M},\\ u_{K}, &{} {x}= {x_K},\\ u_{L}, &{} {x}= {x_L},\\ u_{\texttt {e}}, &{} {x}= {x_{\texttt {e}}},\\ {{\widetilde{\beta }}}^T_{M} u_{M} + {{\widetilde{\beta }}}^T_{K} u_{K} + {{\widetilde{\beta }}}^T_{L} u_{L} + {{\widetilde{\beta }}}^T_{\texttt {e}} u_{\texttt {e}}, &{} {x}= {x_{\texttt {f}}},\\ \end{array}\right. } \end{aligned}$$

(26)

$$\begin{aligned} (\nabla _{\Lambda }\textbf{u}_h)_T ({x})&= {\left\{ \begin{array}{ll} \left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_K} &{} \forall {x}\in T_K, \\ \left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_L} &{} \forall {x}\in T_L , \\ \end{array}\right. } \end{aligned}$$

(27)

where $\left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_K}$, $\left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_L}$ are presented in (23), (24).

For each $T:= ({x_M}{x_K}{x_{\texttt {e}}}{x_{\texttt {f}}}) \in \mathcal {T}^{**}_{\partial \Omega }$, due to Remark 4.(b), T is inside $K \in \mathcal {T}_h$, as there is only an approximation $\Lambda _K$ of the tensor $\Lambda$ on T. Since there is only one approximation tensor $\Lambda _K$ for $\Lambda$ on T, the functions $\Phi _T \textbf{u}_h({x})$ and $\left( \nabla _{\Lambda } \textbf{u}_h\right) _T({x})$ can be determined by

$$\begin{aligned} \Phi _T(\textbf{u}_h)({x}) = \sum \limits _{{x_P}\in \mathcal {V}^{**}_T} u_{P} L_{1,P}({x}), \quad \left( \nabla _{\Lambda } \textbf{u}_h\right) _T({x}) = \sum \limits _{{x_P}\in \mathcal {V}^{**}_T} u_{P} \nabla L_{1,P}({x}), ~~\forall {x}\in T, \end{aligned}$$

(28)

where $\mathcal {V}^{**}_T$ is a set of all vertices of T.

Using the definitions (10), (11), (26), (27), and (28), we formulate the issue (4) in the following discrete form:

$$\begin{aligned}&\text { Finding} \textbf{u}_h := (u_{P})_{{x_P}\in \mathcal {V}^{*}}\in \mathcal {H}^0_h, \text { such that } \nonumber \\&\sum _{T\in \mathcal {T}^{**}_h} \int _T \left( \Lambda \nabla _{\Lambda } \textbf{u}_h\right) \cdot \nabla _{\Lambda } \textbf{v}_h~d{x}= \sum _{T\in \mathcal {T}^{**}_h} \int _T f({x}) \Phi (\textbf{v}_h) ~d{x}, \quad \forall \textbf{v}_h \in \mathcal {H}^0_h. \end{aligned}$$

(29)

And we introduce the following definition:

Definition 1

An approximate gradient discretization for the EFC-3DFEM scheme is defined by $(\mathcal {H}_h,h,\Phi ,\nabla _{\Lambda })$, where

• The set of discrete unknowns $\mathcal {H}_h$ is a finite-dimensional vector space presented in (8).

• The space step h is the maximum positive real circumscribed sphere’s diameter for all elements of $\mathcal {T}_h$.

• The mapping $\Phi : \mathcal {H}_{h} \rightarrow L^2(\Omega )$ has the definition of its restriction on each $T \in \mathcal {T}^{**}_h$ presented by (10) for homogeneous tensor $\Lambda$ case, and by (26) for anisotropic, heterogeneous tensor $\Lambda$ case.

• The mapping $\nabla _{\Lambda }: \mathcal {H}_{h} \rightarrow L^2(\Omega )^3$ has the definition of its restriction on each $T \in \mathcal {T}^{**}_h$ presented by (11) for homogeneous tensor $\Lambda$ case, and by (27) for anisotropic, heterogeneous tensor $\Lambda$ case.

3.2 The algebraic system of the EFC-3DFEM scheme

To construct the system of linear equations from the discrete problem (29), we continue by selecting its test vectors $\textbf{v}_h$ as basis vectors $\textbf{v}^{Q}_h$ of $\mathcal {H}^0_h$ with ${x_Q}$ in $\mathcal {V}^{**}_{\Omega }$ in two steps:

Step 1. :

For each ${x_M}\in \mathcal {C}^*_{\Omega } \subset \mathcal {V}^{**}_{\Omega }$, we take $\textbf{v}_h = \textbf{v}^{M}_h$ in (29). Due to Remark 5, two sets $\text {supp}\{\Phi (\textbf{v}^{M}_h)\}$, $\text {supp}\{\nabla _\Lambda \textbf{v}^{M}_h\}$ belong to M. Thus, (29) can be rewritten as

(30)

By (5), all unknowns in (30) consist only of $u_{M}$, $\{u_{K},~{{x_K}\in \mathcal {C}_M}\}$ and $\{u_{\texttt {e}},~{\texttt {e}\in \mathcal {E}_{M}}\}$. Therefore, the computational process can be expressed by the following system in matrix form:

$$\begin{aligned} \pmb {\mathscr {M}}\textbf{U}^* + \pmb {\mathscr {K}}^*\textbf{U}= \pmb {\mathscr {F}}^*, \end{aligned}$$

(31)

where $\textbf{U}^* = \left( u_{M}\right) _{{x_M}\in \mathcal {C}^*_{\Omega }} \in {\mathbb {R}^{\left|\mathcal {C}^*_{\Omega }\right|}}$, the notation $\left|\mathcal {C}^*_{\Omega }\right|$ represents the cardinality of set $\mathcal {C}^*_{\Omega }$, and $\textbf{U}= \left( u_{P}\right) _{{x_P}\in \left( \mathcal {C}\cup \mathcal {C}_{\mathcal {E}_{\Omega }} \right) } \in \mathbb {R}^d$. The diagonal matrix $\pmb {\mathscr {M}}\in {\mathbb {R}^{\left|\mathcal {C}^*_{\Omega }\right|\times \left|\mathcal {C}^*_{\Omega }\right|}}$ has each diagonal element equal to $\sum _{T\in \mathcal {T}^{**}_{{{x_M}}}} \int \limits _T \left( \Lambda \nabla _{\Lambda } \textbf{v}^{{M}}_h\right) \cdot \nabla _{\Lambda } \textbf{v}^{{M}}_h~d{x}$, with ${x_M}\in \mathcal {C}^*_{\Omega }$. The matrix $\pmb {\mathscr {K}}^* \in {\mathbb {R}^{\left|\mathcal {C}^*_{\Omega }\right|\times d}}$ has each component determined by $\sum _{T\in \mathcal {T}^{**}_{{x_M}}} \int \limits _T \left( \Lambda \nabla _{\Lambda } \textbf{v}^{{P}}_h\right) \cdot \nabla _{\Lambda } \textbf{v}^{{M}}_h~d{x}$, with $d = \left( \left|\mathcal {C}\right|+\left|\mathcal {E}_{\Omega }\right|\right)$, ${x_M}\in \mathcal {C}^*_{\Omega }$, and ${x_P}\in \mathcal {C}_{M} \cup \mathcal {C}_{\mathcal {E}_{M}}$. The vector $\pmb {\mathscr {F}}^*$ is equal to $\left( \sum _{T\in \mathcal {T}^{**}_{{x_M}}} \int _T f({x}) \Phi (\textbf{v}^{M}_h) ~d{x}\right) _{{x_M}\in \mathcal {C}^*_{\Omega }}$. The system (31) leads to

$$\begin{aligned} \textbf{U}^*= \pmb {\mathscr {M}}^{-1} \pmb {\mathscr {F}}^* - \pmb {\mathscr {M}}^{-1}\pmb {\mathscr {K}}^*\textbf{U}, \end{aligned}$$

(32)

which means that, for each ${{x_M}\in \mathcal {C}^*_{\Omega }}$, the unknown $u_{M}$ can be expressed as a combination of $\{u_{K}\}_{{x_K}\in \mathcal {C}_{M}}$, $\{u_{\texttt {e}}\}_{\texttt {e}\in \mathcal {E}_{\Omega }}$, and the source term f.

Step 2. :

For each ${x_K}\in \mathcal {C}\subset \mathcal {V}^{**}_{\Omega }$ and ${x_{\texttt {e}}} \in \mathcal {C}_{\mathcal {E}}\subset \mathcal {V}^{**}_{\Omega }$, by taking $\textbf{v}_h=\textbf{v}^{K}_h$ and $\textbf{v}_h = \textbf{v}^{{\texttt {e}}}_h$, (29) can be rewritten as

(33)

(34)

where

$$\begin{aligned}\mathcal {T}^{**}_{{x_K}}:= \left\{ T \in \mathcal {T}_h^{**}~|~ T \text { has a vertex } {x_K}\right\} ,\end{aligned}$$

$$\begin{aligned}\mathcal {T}^{**}_{{x_{\texttt {e}}}}:= \left\{ T \in \mathcal {T}_h^{**}~|~ T \text { has a vertex } {x_{\texttt {e}}} \right\} .\end{aligned}$$

Similar as Step 1, the computational process is also presented by the following matrix form as

$$\begin{aligned} \pmb {\mathscr {M}}^* \textbf{U}^* + \pmb {\mathscr {K}}\textbf{U}= \pmb {\mathscr {F}}, \end{aligned}$$

(35)

where ${d = (\left|\mathcal {C}\right|+\left|\mathcal {E}_{\Omega }\right|)}$, the vector $\pmb {\mathscr {F}}\in \mathbb {R}^d$, and two matrices $\pmb {\mathscr {M}}^* \in {\mathbb {R}^{d \times \left|\mathcal {C}^*_{\Omega }\right|}}$, $\pmb {\mathscr {K}}\in \mathbb {R}^{d \times d}$. Substituting (32) into (35), it implies

$$\begin{aligned} \textbf{A}\cdot \textbf{U}= \textbf{F}, \end{aligned}$$

(36)

with $\textbf{A}= \pmb {\mathscr {K}}- \pmb {\mathscr {M}}^* \pmb {\mathscr {M}}^{-1}\pmb {\mathscr {K}}^* \in \mathbb {R}^{d \times d}$, $\textbf{F}= \pmb {\mathscr {F}}- \pmb {\mathscr {M}}^* \pmb {\mathscr {M}}^{-1} \pmb {\mathscr {F}}^* \in \mathbb {R}^d$, $\textbf{U}= \left( u_{P}\right) _{{x_P}\in \left( \mathcal {C}\cup \mathcal {C}_{\mathcal {E}_{\Omega }} \right) } \in \mathbb {R}^d$. Note that the system (36) only depends on the unknowns of $\{u_{K}\}_{{x_K}\in \mathcal {C}}$ and $\{u_{\texttt {e}}\}_{\texttt {e}\in \mathcal {E}_{\Omega }}$, therefore the proposed scheme is called the edge-cell finite element scheme.

Remark 9

If the homogeneous Dirichlet boundary condition (2) is replaced by a Neumann or Robin boundary condition, the EFC-3DFEM scheme must have the additional unknowns $\{u_{\texttt {e}}\}_{\texttt {e}\in \mathcal {E}_{\partial \Omega }}$, $\{u_{\texttt {f}}\}_{\texttt {f}\in \mathcal {F}_{\partial \Omega }}$, and $\{u_{Q}\}_{{x_Q}\in \mathcal {C}^*_{\partial \Omega }}$.

It is now necessary to demonstrate the existence and originality of the solution for (36) where the stiffness matrix $\textbf{A}$ is a symmetric positive definite matrix. The exact claim reads as follows:

Proposition 1

The stiffness matrix $\textbf{A}$ in (36) is symmetric and positive definite.

Proof

When the tensor $\Lambda$ is isotropic, (10) and (11) show that the EFC-3DFEM is equivalent to the standard finite element on the tetrahedral subdual mesh $\mathcal {T}^{**}_h$. Thus, the stiffness matrix $\textbf{A}$ is always symmetric and positive definite.

For the heterogeneous and anisotropic tensor $\Lambda$ case, due to the Schur complement property (see [15, Theorem 1.12, p. 34]), it helps to notice that if the matrix $\textbf{S}= \left( {\begin{array}{*{20}{c}} {\pmb {\mathscr {M}}}&{}{\pmb {\mathscr {K}}^*}\\ {\pmb {\mathscr {M}}^*}&{}{\pmb {\mathscr {K}}} \end{array}} \right)$ is symmetric and positive definite, then the matrix $\textbf{A}:= \pmb {\mathscr {K}}- \pmb {\mathscr {M}}^* \pmb {\mathscr {M}}^{-1}\pmb {\mathscr {K}}^* \in \mathbb {R}^{d \times d}$ is also symmetric and positive definite.

Obviously, we verify that $\textbf{S}$ is symmetric, since we have the symmetric tensor $\Lambda$ and the following result for any $\textbf{u}_h = \left( u_{P}\right) _{{x_P}\in \mathcal {V}^{**}_{\Omega }}$, $\textbf{v}_h = \left( v_{P}\right) _{{x_P}\in \mathcal {V}^{**}_{\Omega }} \in \mathcal {H}^0_h$

$$\begin{aligned} {\widehat{\textbf{U}}}^T \textbf{S}{\widehat{V}} = \sum _{T\in \mathcal {T}^{**}_h}\int _T \Lambda \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{v}_h~d{x}= \sum _{T\in \mathcal {T}^{**}_h}\int _T \Lambda \nabla _{\Lambda } \textbf{v}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}= {\widehat{V}}^T \textbf{S}{\widehat{\textbf{U}}}, \end{aligned}$$

(37)

where ${{\widehat{\textbf{U}}}} = \left( \begin{array}{l} \textbf{U}^*\\ \textbf{U}\end{array} \right)$, ${{\widehat{V}}} = \left( \begin{array}{l} V^*\\ V \end{array} \right)$, $\textbf{U}^* = \left( u_{M}\right) _{{x_M}\in \mathcal {C}^*_{\Omega }}$, ${x_V}^* = \left( v_{M}\right) _{{x_M}\in \mathcal {C}^*_{\Omega }}$, $\textbf{U}= \left( u_{P}\right) _{{x_P}\in \left( \mathcal {C}\cup \mathcal {C}_{\mathcal {E}_{\Omega }} \right) }$ and ${x_V}= \left( v_{P}\right) _{{x_P}\in \left( \mathcal {C}\cup \mathcal {C}_{\mathcal {E}_{\Omega }} \right) }$. Note that $\mathcal {V}^{**}_{\Omega } = \left( \mathcal {C}^*_{\Omega } \cup \mathcal {C}\cup \mathcal {C}_{\mathcal {E}_{\Omega }} \right)$ due to Remark 4 (a).

To verify the positive definite property of $\textbf{S}$, we need to prove that

$$\begin{aligned} {\widehat{\textbf{U}}}^T \textbf{S}{\widehat{\textbf{U}}} = \sum _{T\in \mathcal {T}^{**}_h}\int _T \Lambda \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}> 0, \end{aligned}$$

(38)

for any $\textbf{u}_h \in \mathcal {H}^0_h$ such that $\textbf{u}_h \ne 0$.

From the property (3), the right-hand side of (38) can be estimated by

$$\begin{aligned} \sum _{T\in \mathcal {T}_h^{**}}\int _T \Lambda \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}\ge \underline{\lambda } \sum _{T\in \mathcal {T}^{**}_h}\int _T \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}, \end{aligned}$$

(39)

in which $\int _T \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}\ge 0$ for all $T \in \mathcal {T}_h^{**}$. Moreover, since $\textbf{u}_h \ne 0$ and $\textbf{u}_h \in \mathcal {H}^0_h$ ($i.e.,~ u_{P} = 0,~~\forall {x_P}\in \mathcal {V}^{**}_{\partial \Omega }$), we always have at least one tetrahedron $T_0$ satisfying one of the following two cases:

• Case 1. With $T_0:= ({x_M}{x_K}{x_{\texttt {e}}}{x_{\texttt {f}}}) \in \mathcal {T}^{**}_{\partial \Omega }$, we use (11) and values $u_{\texttt {e}} = u_{\texttt {f}} = 0$ at ${x_{\texttt {e}}}, {x_{\texttt {f}}} \in \partial \Omega$ to compute

  $$\begin{aligned}&\underline{\lambda } \int _{T_0} \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}\nonumber \\&\qquad = \dfrac{\underline{\lambda }}{9 m_T} \left[ \begin{aligned}&\left( u_{M} \textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})} + u_{K} \textbf{n}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} \right) ^2>0,{} & {} \text {if } u_{M}, u_{K} \ne 0, \\&\left( u_{M} \textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})} \right) ^2>0,{} & {} \text {if } u_{M} \ne 0, \\&\left( u_{K} \textbf{n}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} \right) ^2 >0,{} & {} \text {if } u_{K} \ne 0, \end{aligned} \right. \end{aligned}$$

  (40)

  where $\left( u_M \textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})} + u_K \textbf{n}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} \right) \ne \pmb 0$ if $u_{M}, u_{K} \ne 0$.

• Case 2. With $T_0:=({x_M}{x_K}{x_L}{x_{\texttt {e}}}) \in \mathcal {T}^{**}_{\Omega }$ having two sub-tetrahedrons $T_{0,K} = ({x_M}{x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})$ and $T_{0,L} =({x_M}{x_L}{x_{\texttt {e}}}{x_{\texttt {f}}})$, we use (27) to compute

  $$\begin{aligned}&\underline{\lambda } \int _{T_0} \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}= \frac{\underline{\lambda }}{9 m_{T_{0,K} }} \left( \pmb I^{(1)}_{T_0}\right) ^2 + \frac{\underline{\lambda }}{9 m_{T_{0,L} }}\left( \pmb I^{(2)}_{T_0}\right) ^2, \end{aligned}$$

  where

  $$\begin{aligned} \pmb I^{(1)}_{T_0}&= \left( u_{{M}} \widetilde{\textbf{n}}^{{{x_M}}}_{T_{{K}}} + u_{{K}} {{\widetilde{\textbf{n}}}}^{{{x_K}}}_{T_{{K}}} + u_{{L}} {{\widetilde{\textbf{n}}}}^{{{x_L}}}_{T_{{K}}}+ u_{{e}}\widetilde{\textbf{n}}^{{{x_{\texttt {e}}}}}_{T_{{K}}}\right) ,\\ \pmb I^{(2)}_{T_0}&= \left( u_{{M}} \widetilde{\textbf{n}}^{{{x_M}}}_{T_{{L}}} + u_{{K}} {{\widetilde{\textbf{n}}}}^{{{x_K}}}_{T_{{L}}} + u_{{L}} {{\widetilde{\textbf{n}}}}^{{{x_L}}}_{T_{{L}}}+ u_{{e}}\widetilde{\textbf{n}}^{{{x_{\texttt {e}}}}}_{T_{{L}}}\right) . \end{aligned}$$

  Obviously, the two vectors $\pmb I^{(1)}_{T_0}$ and $\pmb I^{(2)}_{T_0}$ are different from $\pmb 0$, since we have the property (25), and the set $\{u_{M}, u_{K}, u_{L}, u_{\texttt {e}} \}$ satisfies at most three non-zero elements and at least one element equal to 0. Therefore, we get

  $$\begin{aligned} \underline{\lambda } \int _{T_0} \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}> 0. \end{aligned}$$

  (41)

  Owning to (39)–(41), we obtain

  $$\begin{aligned} {\widehat{\textbf{U}}}^T \textbf{S}{\widehat{\textbf{U}}} \ge \underline{\lambda } \sum _{T\in \mathcal {T}^{**}_h}\int _T \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}\ge \underline{\lambda } \int _{T_0} \nabla _{\Lambda } \textbf{u}_h \cdot \nabla _{\Lambda } \textbf{u}_h~d{x}> 0. \end{aligned}$$

  (42)

This ends the proof of Proposition 1. $\square$

4 Convergence analysis

When applied to the isotropic tensor situation, the EFC-3DFEM method is similar to the traditional Finite Element Method (FEM) based on first-order Lagrange basis functions on $\mathcal {T}^{**}_h$, and convergence is always ensured.

We study here the convergence of the EFC-3DFEM method for the anisotropic and heterogeneous tensor situation (possibly discontinuous). This work begins by introducing the following two operators: $S_h: C^\infty _c(\Omega ) \rightarrow \mathbb {R}$ and $W_h: \left( C^{\infty }_c(\Omega ) \right) ^3 \rightarrow \mathbb {R}$ defined by

$$\begin{aligned}&S_{h}(\varphi ) = \left[ \Vert \Phi (\pmb {\varphi }_h) - \varphi \Vert ^{2}_{L^2(\Omega )} + \Vert \nabla _{\Lambda } \pmb {\varphi }_h - \nabla \varphi \Vert ^{2}_{L^2(\Omega )} \right] ^{{1}/{2}}, \\&\text {with }\varphi \in C^{\infty }_c(\Omega ), ~\pmb {\varphi }_h := \left( \varphi ({x_P})\right) _{{x_P}\in \mathcal {V}^{**}} \in \mathcal {H}^0_h, \nonumber \\ \text {and}\quad&W_{h}(\pmb {\varphi }) = \max \limits _{\textbf{v}_h \in \mathcal {H}_{h} \setminus \{\pmb 0\}} \frac{1}{\Vert \nabla _{\Lambda } \textbf{v}_h\Vert _{\left( L^2(\Omega )\right) ^3}} \int _{\Omega } \left[ \nabla _{\Lambda } \textbf{v}_h \cdot \pmb {\varphi }+ \Phi (\textbf{v}_h) {\text {div}}(\pmb {\varphi })\right] d{x}, \\&\text {with }\ \pmb {\varphi }\in \left( C^{\infty }_c(\Omega ) \right) ^{3}. \end{aligned}$$

As consequence of [16, Lemma 2.2 and Corollary 2.3], if the EFC-3DFEM scheme satisfies the strong consistency

$$\begin{aligned} \lim \limits _{h \rightarrow 0} S_{h}(\varphi )&= 0, \quad \forall \varphi \in C^\infty _c(\Omega ), \end{aligned}$$

(43)

the dual consistency

$$\begin{aligned} \lim \limits _{h \rightarrow 0} W_{h}(\pmb {\varphi })&= 0, \quad \forall \pmb {\varphi }\in \left( C^\infty _c(\Omega )\right) ^3, \end{aligned}$$

(44)

and the coercive property, i.e.,  there exists a positive constant C independent of h, such that

$$\begin{aligned} \Vert \Phi \textbf{v}_h \Vert _{L^2(\Omega )} \le C \Vert \nabla _{\Lambda } \textbf{v}_h \Vert _{\left( L^2(\Omega )\right) ^3},\quad \forall \textbf{v}_h \in \mathcal {H}_h, \end{aligned}$$

(45)

then its convergence is verified, and

$$\begin{aligned}&\left\| \nabla \overline{u}- \nabla _{\Lambda } \textbf{u}_h \right\| _{\left( L^2(\Omega )\right) ^3} \rightarrow 0, \quad \text {as } h \rightarrow 0, \end{aligned}$$

(46)

$$\begin{aligned}&\left\| \overline{u}- \Phi \textbf{u}_h \right\| _{L^2(\Omega )} \rightarrow 0, \quad \text {as } h \rightarrow 0. \end{aligned}$$

(47)

Next, rather than proving the strong, dual consistencies (43), (44) and the coercive property directly, this work simplifies the process by checking these properties for a variant form of the EFC-3DFEM scheme, referred to as the EFC-3DFEMb scheme. The description of this scheme is as follows:

$$\begin{aligned}&\text {Finding} \textbf{u}_h \in \mathcal {H}^0_h \text {such that } \nonumber \\&\sum _{T\in \mathcal {T}^{**}_h}\! \int _T \left( \Lambda \nabla _{\Lambda } \textbf{u}_h\right) \cdot \nabla _{\Lambda } \textbf{v}_h~d{x}= \! \sum _{T\in \mathcal {T}^{**}_h} \!\int _T f({x}) P_1 \textbf{v}_h ~d{x}, \quad \!\forall \textbf{v}_h \!:=\! (v_{P})_{{x_P}\in \mathcal {V}^{**}} \in \mathcal {H}^0_h, \end{aligned}$$

(48)

where the polynomial $P_1 \textbf{v}_h$ represents a first-order Lagrange basis function on the subdual mesh $\mathcal {T}^{**}_{h}$, with a value $P_1 \textbf{v}_h({x_P}) = v_{P}$ assigned at each point ${x_P}\in \mathcal {V}^{**}$.

In the purpose of presenting the proof for the convergence of the EFC-3DFEMb scheme, we need to introduce the following definitions and notations:

Definition 2

An approximate gradient discretization for the EFC-3DFEMb scheme is defined by $(\mathcal {H}_h,h,P_1,\nabla _{\Lambda })$, where

• The set of discrete unknowns $\mathcal {H}_h$ is a finite-dimensional vector space presented in (8).

• The space step h is the maximum positive real circumscribed sphere’s diameter for all elements of $\mathcal {T}_h$.

• the mapping $P_1: \mathcal {H}_{h} \rightarrow L^2(\Omega )$ is a first-order Lagrange basis functions on subdual mesh $\mathcal {T}^{**}_h$, with $\textbf{v}_h = (v_P)_{x_P \in \mathcal {V}^{**}} \in \mathcal {H}_h$, and a value $P_1 \textbf{v}_h(x_P) = v_P$ assigned at each point ${x_P}\in \mathcal {V}^{**}$.

• The mapping $\nabla _{\Lambda }: \mathcal {H}_{\mathcal {D}}: \mathcal {H}_{h} \rightarrow L^2(\Omega )^3$ has the definition of its restriction on each $T \in \mathcal {T}^{**}_h$ presented by (11) for homogeneous tensor $\Lambda$ case, and by (27) for anisotropic, heterogeneous tensor $\Lambda$ case.

The dual and strong consistencies for the EFC-3DFEMb scheme are evidenced by their properties measured through the following operators ${\widehat{S}}_{h}$ and ${\widehat{W}}_{h}$ as outlined below:

$$\begin{aligned} {\widehat{S}}_{h}(\varphi ) = \left[ \Vert P_1 \pmb {\varphi }_h - \varphi \Vert ^{2}_{L^2(\Omega )} + \Vert \nabla _{\Lambda } \pmb {\varphi }_h - \nabla \varphi \Vert ^{2}_{\left( L^2(\Omega )\right) ^3} \right] ^{{1}/{2}},&~\forall \varphi \in C^{\infty }_c(\Omega ), \end{aligned}$$

(49)

with $\pmb {\varphi }_h:= \left( \varphi ({x_P})\right) _{{x_P}\in \mathcal {V}^{**}} \in \mathcal {H}^0_h$, and for all $\pmb {\varphi }\in \left( C^{\infty }_c(\Omega )\right) ^3$

$$\begin{aligned} \hspace{-0.4cm}{\widehat{W}}_{h}(\pmb {\varphi }) = \max \limits _{\textbf{v}_h \in \mathcal {H}_{h} \setminus \{\pmb 0\}} \frac{1}{\Vert \nabla _{\Lambda } \textbf{v}_h\Vert _{\left( L^2(\Omega )\right) ^3}} \int _{\Omega } \left[ \nabla _{\Lambda } \textbf{v}_h \cdot \pmb {\varphi }+ P_1 \textbf{v}_h {\text {div}}(\pmb {\varphi })\right] d{x}. \end{aligned}$$

(50)

By utilizing the results presented in (70) and (71) from Proposition 2, along with Corollary 1, it can be demonstrated that the EFC-3DFEM scheme also satisfies the strong and dual consistency properties for the anisotropic and heterogeneous tensor situation (potentially discontinuous).

Let us now prove that the EFC-3DFEMb scheme satisfies the strong, dual consistency, and coercive properties. For given operators $\Phi$ and $\nabla _{\Lambda }$ specified on each tetrahedron T in $\mathcal {T}^{**}_h$ as described in Sect. 3, we need to define the following subsets of $\mathcal {T}^{**}_h$ in relation to the tensor $\Lambda$:

$$\begin{aligned} \mathcal {T}^{**}_{{\text {{const}}}}&= \left\{ T \in \mathcal {T}^{**}_h ~|~\Lambda ({x}) \text { is constant on } T \right\} ,\\ \mathcal {T}^{**}_{\Lambda }&= \left\{ T \in \mathcal {T}^{**}_h ~|~\Lambda ({x}) \text { is discontinuous on } T \right\} . \end{aligned}$$

Fig. 7

A tetrahedron $T = ({x_M}{x_K}{x_L}{x_{\texttt {e}}})$ with four vertices ${x_M}\in \mathcal {C}^*$, ${x_K}, {x_L}\in \mathcal {C}$, and an edge point ${x_{\texttt {e}}}$ with $e \in \mathcal {E}_{\Omega }$

For any tetrahedron $T:=({x_M}{x_K}{x_L}{x_{\texttt {e}}}) \in \mathcal {T}^{**}_h {\setminus } \mathcal {T}^{**}_{{\text {{const}}}}$, it has two sub-tetrahedrons $T_K:=({x_M}{x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})$ and $T_L:=({x_M}{x_L}{x_{\texttt {e}}}{x_{\texttt {f}}})$, see Fig. 7.

In addition, we need to introduce the following geometrical notations used in lemmas and theorems:

• (i) The sets $\mathcal {V}^{(1)}_T$, $\mathcal {V}^{(2)}_T$, and $\mathcal {V}^{(3)}_T$ contain pairs and triples of vertices that can be defined as

  $$\begin{aligned} \mathcal {V}^{(1)}_T&=\left\{ {x_M},{x_K}, {x_L}, {x_{\texttt {e}}}\right\} ,\\ \mathcal {V}^{(2)}_T&= \left\{ ({x_M},{x_K}), ({x_M},{x_L}), ({x_M},{x_{\texttt {e}}}), ({x_K},{x_L}), ({x_K},{x_{\texttt {e}}}), ({x_L},{x_{\texttt {e}}}) \right\} , \\ \mathcal {V}^{(3)}_T&= \left\{ ({x_M},{x_K},{x_L}), ({x_M},{x_L},{x_{\texttt {e}}}), ({x_M},{x_K},{x_{\texttt {e}}}), ({x_K},{x_L},{x_{\texttt {e}}}) \right\} . \end{aligned}$$

• (ii) For each pair $({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T$, the notation ${[{x_N}{x_Q}]}$ represents an edge, with its midpoint denoted as ${C}_{[{x_N}{x_Q}]}$ and its length as $m_{[{x_N}{x_Q}]}$.

• (iii) For each triple $({x_N}, {x_Q}, {x_R}) \in \mathcal {V}^{(3)}_T$, the notation $({x_N}{x_Q}{x_R})$ is a triangular face, with its centroid denoted as ${C}_{({x_N}{x_Q}{x_R})}$, and its area as $m_{({x_N}{x_Q}{x_R})}$.

• (iv) For a point ${x_N}\in \mathcal {V}^{(1)}_T$ and a triple $({x_Q},{x_R},x_S) \in \mathcal {V}^{(3)}_T$, $d^{{x_N}}_{({x_Q}{x_R}x_S)}$ is the distance from ${x_N}$ to the face $({x_Q}{x_R}x_S)$.

• (v) The point ${x_T}$ is the centroid of the tetrahedron T.

• (vi) The following notations

  $$\begin{aligned}&{\texttt {f}}_{[{x_M}{x_{\texttt {e}}}]} = \left( {x_T}, {C}_{[{x_M}{x_{\texttt {e}}}]}, {C}_{({x_M}{x_K}{x_{\texttt {e}}})}, {C}_{({x_M}{x_L}{x_{\texttt {e}}})}\right) ,\\&{\texttt {f}}_{[{x_K}{x_{\texttt {e}}}]} = \left( {x_T}, {C}_{[{x_K}{x_{\texttt {e}}}]}, {C}_{({x_M}{x_K}{x_{\texttt {e}}})}, {C}_{({x_K}{x_L}{x_{\texttt {e}}})}\right) , \\&{\texttt {f}}_{[{x_L}{x_{\texttt {e}}}]} = \left( {x_T}, {C}_{[{x_L}{x_{\texttt {e}}}]}, {C}_{({x_M}{x_L}{x_{\texttt {e}}})}, {C}_{({x_K}{x_L}{x_{\texttt {e}}})}\right) ,\\&{\texttt {f}}_{[{x_M}{x_K}]} = \left( {x_T}, {C}_{[{x_M}{x_K}]}, {C}_{({x_M}{x_K}{x_{\texttt {e}}})}, {C}_{({x_M}{x_K}{x_L})}\right) ,\\&{\texttt {f}}_{[{x_M}{x_L}]} = \left( {x_T}, {C}_{[{x_M}{x_L}]}, {C}_{({x_M}{x_L}{x_{\texttt {e}}})}, {C}_{({x_M}{x_K}{x_L})}\right) ,\\&{\texttt {f}}_{[{x_K}{x_L}]} = \left( {x_T}, {C}_{[{x_K}{x_L}]}, {C}_{({x_M}{x_K}{x_L})}, {C}_{({x_K}{x_L}{x_{\texttt {e}}})}\right) , \end{aligned}$$

  are six quadrangular faces constructed by connecting the centroid ${x_T}$ to centroids on boundary triangular faces and edges of T.

• (vii) Using the above faces, the vertices ${x_M}$, ${x_K}$, ${x_L}$, and ${x_{\texttt {e}}}$ involved in $\left\{ {\texttt {f}}_{[{x_M}{x_{\texttt {e}}}]}, {\texttt {f}}_{[{x_K}{x_{\texttt {e}}}]}, \right. \left. {\texttt {f}}_{[{x_L}{x_{\texttt {e}}}]} \right\}$, $\left\{ {\texttt {f}}_{[{x_M}{x_K}]}, {\texttt {f}}_{[{x_K}{x_{\texttt {e}}}]}, {\texttt {f}}_{[{x_K}{x_L}]} \right\}$, $\left\{ {\texttt {f}}_{[{x_M}{x_L}]}, {\texttt {f}}_{[{x_L}{x_{\texttt {e}}}]}, {\texttt {f}}_{[{x_K}{x_L}]} \right\}$, and $\left\{ {\texttt {f}}_{[{x_M}{x_{\texttt {e}}}]},\right. \left. {\texttt {f}}_{[{x_L}{x_{\texttt {e}}}]}, {\texttt {f}}_{[{x_K}{x_{\texttt {e}}}]} \right\}$ are connected in order to form the polygons $P_{{x_M}}$, $P_{{x_K}}$, $P_{{x_L}}$, and $P_{{x_{\texttt {e}}}}$, respectively. These polygons lie in the tetrahedron T and satisfy

  $$\begin{aligned} {\overline{T}} = {\overline{P}}_{{x_M}} \cup {\overline{P}}_{{x_K}} \cup {\overline{P}}_{{x_L}} \cup {\overline{P}}_{{x_{\texttt {e}}}}. \end{aligned}$$

• (viii) For each pair $({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T$, the polygon $P_{{x_N}}$ has the outward normal vector $\textbf{n}_{{x_N}{x_Q}}$ at ${\texttt {f}}_{[{x_N}{x_Q}]} \equiv {\texttt {f}}_{[{x_Q}{x_N}]}$. The vector $\textbf{n}_{{x_N}{x_Q}}$ has a magnitude $\left| \textbf{n}_{{x_N}{x_Q}}\right|$ equal to the area $m_{{\texttt {f}}_{[{x_N}{x_Q}]}}$ and also satisfies $\textbf{n}_{{x_N}{x_Q}} = - \textbf{n}_{{x_Q}{x_N}}$.

• (ix) For each pair $({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T$, $d_{{x_N}{x_Q}}$ is the distance from ${x_N}\in \mathcal {V}^{(1)}_T$ to the face ${\texttt {f}}_{[{x_N}{x_Q}]}$, and it satisfies $d_{{x_N}{x_Q}} = d_{{x_Q}{x_N}}$.

• (x) Besides, we introduce an operator $\Pi ^0_h$ defined on $\mathcal {H}_h$, specifically as follows: for any $\textbf{u}_h \in \mathcal {H}_h$, on each $T =({x_M}{x_K}{x_L}{x_{\texttt {e}}})$, $\Pi ^0_h(\textbf{u}_h)$ is a characteristic function such that

  $$\begin{aligned} \Pi ^0_h(\textbf{u}_h({x})) = {\left\{ \begin{array}{ll} u_{M} &{} \text {if } {x}\in P_{{x_M}}, \\ u_{K} &{} \text {if } {x}\in P_{{x_K}}, \\ u_{L} &{} \text {if } {x}\in P_{{x_L}}, \\ u_{\texttt {e}} &{} \text {if } {x}\in P_{{x_{\texttt {e}}}}. \\ \end{array}\right. } \end{aligned}$$

  (51)

• (xi) To estimate the convergence, $\mathcal {H}_h$ is endowed with the norm

  

  (52)

The next step is to examine the characteristics of the discrete gradient $\nabla _{\Lambda }$ as follows:

Lemma 1

For $\left( \mathcal {H}_h, h, P_1,\nabla _{\Lambda } \right)$ being a family of discretizations in the sense of Definition 2, which satisfies the below assumptions:   for any $T:=({x_M}{x_K}{x_L}{x_{\texttt {e}}}) \in \mathcal {T}^{**}_h {\setminus } (\mathcal {T}^{**}_{\Lambda }\cup \mathcal {T}^{**}_{{\text {{const}}}})$, there exists a positive constant $\delta$ independent of h, such that

Assumption A1

${\dfrac{\min \left\{ d^{{x_K}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}, d^{{x_L}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}, d^{{x_M}}_{({x_K}{x_L}{x_{\texttt {e}}})}, d^{{x_{\texttt {e}}}}_{({x_M}{x_K}{x_L})}\right\} }{\max \left\{ d^{{x_K}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}, d^{{x_L}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} \right\} } \ge \delta }$,

and

Assumption A2

${\frac{\min \left\{ |\textbf{n}_{{x_K}{x_{\texttt {e}}}}|,~ |\textbf{n}_{{x_M}{x_{\texttt {e}}}}|,~|\textbf{n}_{{x_L}{x_{\texttt {e}}}}|,~|\textbf{n}_{{x_K}{x_L}}|,~|\textbf{n}_{{x_M}{x_K}}|,~|\textbf{n}_{{x_M}{x_L}}|\right\} }{\max \left\{ \begin{array}{l} m_{({x_M}{x_K}{x_{\texttt {e}}})}, m_{({x_M}{x_L}{x_{\texttt {e}}})}, m_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})}, m_{({x_L}{x_{\texttt {e}}}{x_{\texttt {f}}})},\\ m_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})},~ m_{({x_M}{x_K}{x_{\texttt {f}}})},~ m_{({x_M}{x_L}{x_{\texttt {f}}})} \end{array} \right\} } \ge \delta }$.

Then, for any $T \in \mathcal {T}^{**}_h \setminus \mathcal {T}^{**}_{\Lambda }$, the discrete gradient $\nabla _{\Lambda } \textbf{u}_h$ is written as

$$\begin{aligned} m_T \left( \nabla _{\Lambda } \textbf{u}_h\right) _T&= (u_{K} - u_{M})(\textbf{n}_{{x_M}{x_K}} + \pmb \epsilon _{{x_M}{x_K}}) + (u_{L} - u_{M})(\textbf{n}_{{x_M}{x_L}} + \pmb \epsilon _{{x_M}{x_L}}) \nonumber \\&+ (u_{\texttt {e}} - u_{M})(\textbf{n}_{{x_M}{x_{\texttt {e}}}} + \pmb \epsilon _{{x_M}{x_{\texttt {e}}}}) + (u_{L} - u_{K})(\textbf{n}_{{x_K}{x_L}} +\pmb \epsilon _{{x_K}{x_L}}) \nonumber \\&+ (u_{\texttt {e}} - u_{K})(\textbf{n}_{{x_K}{x_{\texttt {e}}}} + \pmb \epsilon _{{x_K}{x_{\texttt {e}}}}) + (u_{\texttt {e}} - u_{L})(\textbf{n}_{{x_L}{x_{\texttt {e}}}} + \pmb \epsilon _{{x_L}{x_{\texttt {e}}}}), \end{aligned}$$

(53)

where the vectors $\left\{ \textbf{n}_{{x_N}{x_Q}}, \pmb \epsilon _{{x_N}{x_Q}} \right\} _{({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T}$ satisfy

$$\begin{aligned} \lim \limits _{h \rightarrow 0} \frac{|\pmb \epsilon _{{x_M}{x_K}}|}{|\textbf{n}_{{x_M}{x_K}}|} =&\lim \limits _{h \rightarrow 0} \frac{|\pmb \epsilon _{{x_M}{x_L}}|}{|\textbf{n}_{{x_M}{x_L}}|} = \lim \limits _{h \rightarrow 0} \frac{|\pmb \epsilon _{{x_M}{x_{\texttt {e}}}}|}{|\textbf{n}_{{x_M}{x_{\texttt {e}}}}|} = \lim \limits _{h \rightarrow 0} \frac{|\pmb \epsilon _{{x_K}{x_L}}|}{|\textbf{n}_{{x_K}{x_L}}|}\nonumber \\ =&\lim \limits _{h \rightarrow 0} \frac{|\pmb \epsilon _{{x_K}{x_{\texttt {e}}}}|}{|\textbf{n}_{{x_K}{x_{\texttt {e}}}}|} = \lim \limits _{h \rightarrow 0} \frac{|\pmb \epsilon _{{x_L}{x_{\texttt {e}}}}|}{|\textbf{n}_{{x_L}{x_{\texttt {e}}}}|} = 0. \end{aligned}$$

(54)

Proof

In the subdual mesh, each tetrahedron $T:=({x_M}{x_K}{x_L}{x_{\texttt {e}}}) \in \mathcal {T}^{**}_h {\setminus } \mathcal {T}^{**}_{\Lambda }$ can be separated into two tetrahedrons, each including sub-tetrahedrons $T_K$ and $T_L$. The tensor $\Lambda$ is approximated by $\Lambda _K$ and $\Lambda _L$, respectively. Thus, the discrete gradient $\left( \nabla _{\Lambda }\textbf{u}_h\right) _T$, which depends on $\Lambda _K$ and $\Lambda _L$, is presented in the following cases:

• Case 1. If $\Lambda _K = \Lambda _L$, the discrete gradient $\left( \nabla _{\Lambda } \textbf{u}_h\right) _T$ takes a form similar to (11). It is then computed as

  $$\begin{aligned} { m_T\left( \nabla _{\Lambda } \textbf{u}_h\right) _T}=&- ( u_{\texttt {e}}- u_{K})\frac{1}{4}\left[ \textbf{n}_{({x_M}{x_K}{x_L})} - \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})} \right] \nonumber \\&- ( u_{\texttt {e}}- u_{L})\frac{1}{4}\left[ \textbf{n}_{({x_M}{x_K}{x_L})} - \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})} \right] \nonumber \\&-( u_{\texttt {e}}-u_{M})\frac{1}{4}\left[ \textbf{n}_{({x_M}{x_K}{x_L})} - \textbf{n}_{({x_K}{x_L}{x_{\texttt {e}}})} \right] \nonumber \\&-(u_{L}-u_{K})\frac{1}{4}\left[ \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})} - \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})} \right] \nonumber \\&-(u_{K}-u_{M})\frac{1}{4}\left[ \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})} - \textbf{n}_{({x_K}{x_L}{x_{\texttt {e}}})} \right] \nonumber \\&-(u_{L}-u_{M})\frac{1}{4}\left[ \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})} - \textbf{n}_{({x_K}{x_L}{x_{\texttt {e}}})} \right] . \end{aligned}$$

  (55)

  Additionally, the geometrical properties of T (refer to Fig. 7) are as follows:

  $$\begin{aligned}&\textbf{n}_{{x_K}{x_{\texttt {e}}}} = -\frac{1}{4} \left[ \textbf{n}_{({x_M}{x_K}{x_L})} - \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})} \right] , \quad \textbf{n}_{{x_M}{x_{\texttt {e}}}} = -\frac{1}{4} \left[ \textbf{n}_{({x_M}{x_K}{x_L})} - \textbf{n}_{({x_K}{x_L}{x_{\texttt {e}}})} \right] , \nonumber \\&\textbf{n}_{{x_L}{x_{\texttt {e}}}} = -\frac{1}{4} \left[ \textbf{n}_{({x_M}{x_K}{x_L})} - \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})} \right] , \quad \textbf{n}_{{x_K}{x_L}} = -\frac{1}{4} \left[ \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})} - \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})} \right] , \nonumber \\&\textbf{n}_{{x_M}{x_K}} = -\frac{1}{4} \left[ \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})} - \textbf{n}_{({x_K}{x_L}{x_{\texttt {e}}})} \right] ,\quad \textbf{n}_{{x_M}{x_L}} = -\frac{1}{4} \left[ \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})} - \textbf{n}_{({x_K}{x_L}{x_{\texttt {e}}})} \right] . \end{aligned}$$

  (56)

  Substituting (56) into (55), we have

  $$\begin{aligned} m_T\left( \nabla _{\Lambda } \textbf{u}_h\right) _T =&(u_{\texttt {e}}-u_{K})\textbf{n}_{{x_K}{x_{\texttt {e}}}}+ (u_{\texttt {e}}-u_{L})\textbf{n}_{{x_L}{x_{\texttt {e}}}}+(u_{\texttt {e}}-u_{M})\textbf{n}_{{x_M}{x_{\texttt {e}}}} \nonumber \\ +&(u_{L}-u_{K})\textbf{n}_{{x_K}{x_L}}+(u_{K}-u_{M})\textbf{n}_{{x_M}{x_K}} +(u_{L}-u_{M})\textbf{n}_{{x_M}{x_L}}. \end{aligned}$$

  (57)

  It is noted that the formula (57) is equivalent to (53), where all vectors $\pmb \epsilon _{{x_K}{x_{\texttt {e}}}}$, $\pmb \epsilon _{{x_L}{x_{\texttt {e}}}}$, $\pmb \epsilon _{{x_M}{x_{\texttt {e}}}}$, $\pmb \epsilon _{{x_K}{x_L}}$, $\pmb \epsilon _{{x_M}{x_K}}$, and $\pmb \epsilon _{{x_M}{x_L}}$ are set to $\pmb {0}$.

• Case 2. If $\Lambda _K \ne \Lambda _L$ $\left( \text {such that}~\lim \limits _{h\rightarrow 0} \Vert \Lambda _K - \Lambda _L \Vert = 0\right)$, equation (27) for the discrete gradient $\left( \nabla _{\Lambda } \textbf{u}_h\right) _T$ is given as follows:

  • Case 2a. On $T_K = ({x_M}{x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})$, the discrete gradient $\left( \nabla _{\Lambda } \textbf{u}_h\right) _{T_K}$ is established as

    $$\begin{aligned} m_{T_K} \left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_K}&= ( u_{K} - u_{M})(\textbf{n}_{{x_M}{x_K}} {+} \pmb \epsilon ^K_{{x_M}{x_K}}) + (u_{L} {-} u_{M})(\textbf{n}_{{x_M}{x_L}} {+} \pmb \epsilon ^K_{{x_M}{x_L}}) \nonumber \\&+ (u_{\texttt {e}} - u_{M})(\textbf{n}_{{x_M}{x_{\texttt {e}}}} + \pmb \epsilon ^K_{{x_M}{x_{\texttt {e}}}}) + (u_{L} - u_{K})(\textbf{n}_{{x_K}{x_L}} + \pmb \epsilon ^K_{{x_K}{x_L}}) \nonumber \\&+ (u_{\texttt {e}} - u_{K})(\textbf{n}_{{x_K}{x_{\texttt {e}}}} + \pmb \epsilon ^K_{{x_K}{x_{\texttt {e}}}}) + (u_{\texttt {e}} - u_{L})(\textbf{n}_{{x_L}{x_{\texttt {e}}}} + \pmb \epsilon ^K_{{x_L}{x_{\texttt {e}}}}), \end{aligned}$$

    (58)

    Considering the assumptions A A1  and A A2, as $h \rightarrow 0$, the values in (17) obtain the following limits:

    $$\begin{aligned}&-\frac{\beta _{K}}{\beta _{\texttt {f}}} \rightarrow \frac{d^{{x_L}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{d^{{x_K}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}+d^{{x_L}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}},{} & {} -\frac{\beta _{M}}{\beta _{\texttt {f}}} \rightarrow 0, \\&-\frac{\beta _{L}}{\beta _{\texttt {f}}} \rightarrow \frac{d^{{x_K}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}}{d^{{x_K}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}+d^{{x_L}}_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})}},{} & {} -\frac{\beta _{e}}{\beta _{\texttt {f}}} \rightarrow 0. \end{aligned}$$

    The vectors in (58) satisfy the following convergences:

    $$\begin{aligned} \frac{|\pmb \epsilon ^K_{{x_K}{x_{\texttt {e}}}}|}{|\textbf{n}_{{x_K}{x_{\texttt {e}}}}|}&= \left| \left( - \frac{ m_{[{x_K}{x_L}]} }{ m_{[{x_K}{x_{\texttt {f}}}]}} \dfrac{\beta _{e}}{\beta _{\texttt {f}}} -1 + \frac{m_T}{m_{T_K }} + \frac{m_T}{m_{T_K }}\dfrac{\beta _{K}}{\beta _{\texttt {f}}} \right) \right| \frac{3 m_{({x_M}{x_K}{x_{\texttt {e}}})} }{ m_{({x_M}{x_L}{C}_{[{x_K}{x_{\texttt {e}}}]})} } \rightarrow 0, \nonumber \\ \frac{|\pmb \epsilon ^K_{{x_L}{x_{\texttt {e}}}}|}{|\textbf{n}_{{x_L}{x_{\texttt {e}}}}|}&= \left| \left( - \frac{ m_{[{x_K}{x_L}]} }{ m_{[{x_K}{x_{\texttt {f}}}]}} \dfrac{\beta _{e}}{\beta _{\texttt {f}}} +1 +\frac{m_T}{m_{T_K }}\dfrac{\beta _{L}}{\beta _{\texttt {f}}} \right) \right| \frac{3m_{({x_M}{x_K}{x_{\texttt {e}}})} }{m_{({x_M}{x_K}{C}_{[{x_L}{x_{\texttt {e}}}]})}} \rightarrow 0, \nonumber \\ \frac{|\pmb \epsilon ^K_{{x_M}{x_{\texttt {e}}}}|}{|\textbf{n}_{{x_M}{x_{\texttt {e}}}}|}&= \left| \frac{ m_{[{x_K}{x_L}]} }{ m_{[{x_K}{x_{\texttt {f}}}]}} \left( - \dfrac{\beta _{e}}{\beta _{\texttt {f}}} + \dfrac{\beta _{M}}{\beta _{\texttt {f}}}\right) \right| \frac{3m_{({x_M}{x_K}{x_{\texttt {e}}})} }{m_{({x_K}{x_L}{C}_{[{x_M}{x_{\texttt {e}}}]})} } \rightarrow 0, \nonumber \\ \frac{|\pmb \epsilon ^K_{{x_K}{x_L}}|}{|\textbf{n}_{{x_K}{x_L}}|}&= \left| \left( -1 -\frac{m_T}{m_{T_K }}\dfrac{\beta _{L}}{\beta _{\texttt {f}}} - 1 + \frac{m_T}{m_{T_K }} + \frac{m_T}{m_{T_K }}\dfrac{\beta _{K}}{\beta _{\texttt {f}}} \right) \right| \frac{3m_{({x_M}{x_K}{x_{\texttt {e}}})} }{ m_{({x_M}{x_{\texttt {e}}}{C}_{[{x_K}{x_L}]})} } \rightarrow 0, \nonumber \\ \frac{|\pmb \epsilon ^K_{{x_M}{x_K}}|}{|\textbf{n}_{{x_M}{x_K}}|}&= \left| \left( 1 - \frac{m_T}{m_{T_K }} - \frac{m_T}{m_{T_K }}\dfrac{\beta _{K}}{\beta _{\texttt {f}}} + \frac{ m_{[{x_K}{x_L}]} }{ m_{[{x_K}{x_{\texttt {f}}}]}} \dfrac{\beta _{M}}{\beta _{\texttt {f}}} \right) \right| \frac{3m_{({x_M}{x_K}{x_{\texttt {e}}})}}{ m_{({x_L}{x_{\texttt {e}}} {C}_{[{x_M}{x_K}]} )} } \rightarrow 0, \nonumber \\ \frac{|\pmb \epsilon ^K_{{x_M}{x_L}}|}{|\textbf{n}_{{x_M}{x_L}}|}&= \left| \left( -1 -\frac{m_T}{m_{T_K }}\dfrac{\beta _{L}}{\beta _{\texttt {f}}} + \frac{ m_{[{x_K}{x_L}]} }{ m_{[{x_K}{x_{\texttt {f}}}]}} \dfrac{\beta _{M}}{\beta _{\texttt {f}}} \right) \right| \frac{3m_{({x_M}{x_K}{x_{\texttt {e}}})}}{m_{({x_K}{x_{\texttt {e}}}{C}_{[{x_M}{x_L}]})}} \rightarrow 0, \end{aligned}$$

    (59)

    as $h \rightarrow 0$.

  • Case 2b.   On $T_L = ({x_M}{x_L}{x_{\texttt {e}}}{x_{\texttt {f}}})$, the results can be computed as in Case 2a, specifically as follows:

    $$\begin{aligned} m_{T_L} \left( \nabla _{\Lambda }\textbf{u}_h\right) _{T_L}&= ( u_{K} - u_{M})(\textbf{n}_{{x_M}{x_K}} + \pmb \epsilon ^L_{{x_M}{x_K}}) + (u_{L} - u_{M})(\textbf{n}_{{x_M}{x_L}} + \pmb \epsilon ^L_{{x_M}{x_L}}) \nonumber \\&+ (u_{\texttt {e}} - u_{M})(\textbf{n}_{{x_M}{x_{\texttt {e}}}} + \pmb \epsilon ^K_{{x_M}{x_{\texttt {e}}}}) + (u_{L} - u_{K})(\textbf{n}_{{x_K}{x_L}} + \pmb \epsilon ^L_{{x_K}{x_L}}) \nonumber \\&+ (u_{\texttt {e}} - u_{K})(\textbf{n}_{{x_K}{x_{\texttt {e}}}} + \pmb \epsilon ^L_{{x_K}{x_{\texttt {e}}}}) + (u_{\texttt {e}} - u_{L})(\textbf{n}_{{x_L}{x_{\texttt {e}}}} + \pmb \epsilon ^L_{{x_L}{x_{\texttt {e}}}}), \end{aligned}$$

    (60)

    whose vectors satisfy

    $$\begin{aligned}&\frac{|\pmb \epsilon ^L_{{x_N}{x_Q}}|}{|\textbf{n}_{{x_N}{x_Q}}|} \rightarrow 0, \quad \forall ({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T, \quad h \rightarrow 0. \end{aligned}$$

    (61)

  From (58)–(61), we obtain the formula $\left( \nabla _{\Lambda } \textbf{u}_h\right) _T$ as given in (53), where the vectors $\pmb \epsilon _{{x_N}{x_Q}}$ are determined by $\pmb \epsilon ^K_{{x_N}{x_Q}}$ and $\pmb \epsilon ^L_{{x_N}{x_Q}}$ on $T_K$ and $T_L$, respectively, for all $({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T$.

If $T: = ({x_M}{x_K}{x_{\texttt {e}}}{x_{\texttt {f}}}) \in \mathcal {T}^{**}_{{\text {{const}}}}$, the tensor $\Lambda$ has only one approximation $\Lambda _K$ on T, then $\left( \nabla _{\Lambda } \textbf{u}_h\right) _T$ is expressed as in (57):

$$\begin{aligned} { m_T\left( \nabla _{\Lambda } \textbf{u}_h\right) _T }&= (u_{\texttt {e}}-u_{K})\textbf{n}_{{x_K}{x_{\texttt {e}}}}+ (u_{\texttt {e}}-u_{\texttt {f}}^{M})\textbf{n}_{{x_L}{x_{\texttt {e}}}}+(u_{\texttt {e}}-u_{M})\textbf{n}_{{x_M}{x_{\texttt {e}}}} \nonumber \\&\quad +(u_{\texttt {f}}^{M}-u_{K})\textbf{n}_{{x_K}{x_{\texttt {f}}}}+(u_{K}-u_{M})\textbf{n}_{{x_M}{x_K}} +(u_{\texttt {f}}^{M}-u_{M})\textbf{n}_{{x_M}{x_{\texttt {f}}}}. \end{aligned}$$

(62)

$\square$

Lemma 2

Let $\left( \mathcal {H}_h, h, P_1,\nabla _{\Lambda } \right)$ be a family of discretizations in the sense of Definition 2 and let $\delta$ be a positive constant independent of h such that

Assumption A3

$$\begin{aligned}&\left| \dfrac{\left( \Lambda _K \textbf{n}_{({x_M}{x_K}{x_{\texttt {e}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{m_{T_K}}-\dfrac{\left( \Lambda _L \textbf{n}_{({x_M}{x_L}{x_{\texttt {e}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{m_{T_L}} \right| \nonumber \\&\qquad \ge \delta \max \left\{ \begin{array}{l} {\dfrac{\left( \Lambda _K \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{m_{T_K}} } + {\dfrac{\left( \Lambda _L \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{m_{T_L}}} ,\\ { \left| \dfrac{\left( \Lambda _K \textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{ m_{T_K} }-\dfrac{\left( \Lambda _L \textbf{n}_{({x_M}{x_L}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{ m_{T_L} } \right| } \end{array} \right\} , \end{aligned}$$

(63)

for any $T:= ({x_M}{x_K}{x_L}{x_{\texttt {e}}}) \in \mathcal {T}^{**}_{\Lambda }$.

On each sub-tetrahedron $T_K$ and $T_L$ of T, the discrete gradient $\nabla _{\Lambda } \textbf{u}_h$ is rewritten as

$$\begin{aligned} |T_K| (\nabla _{\Lambda } \textbf{u}_h)_{T_{K}}&= (u_{K} - u_{M})\pmb {\tau }^{T_K}_{{x_M}{x_K}} + (u_{L} - u_{M})\pmb {\tau }^{T_K}_{{x_M}{x_L}} + (u_{\texttt {e}} - u_{M})\pmb {\tau }^{T_K}_{{x_M}{x_{\texttt {e}}}} \nonumber \\&+ (u_{L} - u_{K})\pmb {\tau }^{T_K}_{{x_K}{x_L}} + (u_{\texttt {e}} - u_{K})\pmb {\tau }^{T_K}_{{x_K}{x_{\texttt {e}}}} + (u_{\texttt {e}} - u_{L})\pmb {\tau }^{T_K}_{{x_L}{x_{\texttt {e}}}}, \end{aligned}$$

(64)

$$\begin{aligned} |T_L| (\nabla _{\Lambda } \textbf{u}_h)_{T_{L}}&= (u_{K} - u_{M})\pmb {\tau }^{T_L}_{{x_M}{x_K}} + (u_{L} - u_{M})\pmb {\tau }^{T_L}_{{x_M}{x_L}} + (u_{\texttt {e}} - u_{M})\pmb {\tau }^{T_L}_{{x_M}{x_{\texttt {e}}}} \nonumber \\&+ (u_{L} - u_{K})\pmb {\tau }^{T_L}_{{x_K}{x_L}} + (u_{\texttt {e}} - u_{K})\pmb {\tau }^{T_L}_{{x_K}{x_{\texttt {e}}}} + (u_{\texttt {e}} - u_{L})\pmb {\tau }^{T_L}_{{x_L}{x_{\texttt {e}}}}, \end{aligned}$$

(65)

respectively, and

$$\begin{aligned}&|\pmb {\tau }^{T_K}_{{x_N}{x_Q}}|, ~|\pmb {\tau }^{T_L}_{{x_N}{x_Q}}| \le C_1|\textbf{n}_{{x_N}{x_Q}}|, \quad ({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T, \end{aligned}$$

(66)

where the positive constant $C_1$ depends on $\delta$.

Proof

Substituting (20) into the first equation in (27) yields

$$\begin{aligned}&(\nabla _{\Lambda }\textbf{u}_h)_{T_K} = - \dfrac{ \left[ \begin{array}{l} \left( u_{\texttt {e}} - u_{K} \right) \pmb {\tau }^{T_K}_{{x_K}{x_{\texttt {e}}}} + \left( u_{\texttt {e}} - u_{L} \right) \pmb {\tau }^{T_K}_{{x_L}{x_{\texttt {e}}}} + \left( u_{\texttt {e}}-u_{M}\right) \pmb {\tau }^{T_K}_{{x_M}{x_{\texttt {e}}}} + \\ \left( u_{L}-u_{K} \right) \pmb {\tau }^{T_K}_{{x_K}{x_L}}+ \left( u_{K} - u_{M} \right) \pmb {\tau }^{T_K}_{{x_M}{x_K}} +\left( u_{L}- u_{M}\right) \pmb {\tau }^{T_K}_{{x_M}{x_L}} \end{array} \right] }{3m_{T_K}}, \end{aligned}$$

(67)

with

$$\begin{aligned}&\pmb {\tau }^{T_K}_{{x_M}{x_K}} = \left( {{\widetilde{\beta }}}^T_{M} \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})} - {{\widetilde{\beta }}}^T_{K} \textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})}\right) ,{} & {} \pmb {\tau }^{T_K}_{{x_K}{x_L}} = \left( -{{\widetilde{\beta }}}^T_{L} \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}\right) ,\nonumber \\&\pmb {\tau }^{T_K}_{{x_M}{x_{\texttt {e}}}}= \left( -\textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})} + {{\widetilde{\beta }}}^T_{M} \textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})}\right) ,{} & {} \pmb {\tau }^{T_K}_{{x_M}{x_L}} = \left( -\widetilde{\beta }^T_{L}\textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})}\right) , \nonumber \\&\pmb {\tau }^{T_K}_{{x_K}{x_{\texttt {e}}}} = \left( {{\widetilde{\beta }}}^T_{K} \textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})} -{{\widetilde{\beta }}}^T_{e} \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})} \right) ,{} & {} \pmb {\tau }^{T_K}_{{x_L}{x_{\texttt {e}}}} = \left( {{\widetilde{\beta }}}^T_{L} \textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})} \right) . \end{aligned}$$

(68)

Regarding assumptions A A2  and A A3, the inequalities between the magnitudes of the aforementioned vectors and $\left\{ |\textbf{n}_{{x_N}{x_Q}}|\right\} _{({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T}$ are as follows:

$$\begin{aligned}&\left| \pmb {\tau }^{T_K}_{{x_M}{x_K}}\right| \le \max \left\{ |\widetilde{\beta }^T_{M}|,~|{{\widetilde{\beta }}}^T_{K}|\right\} (|\textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}| + |\textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})}|) \le \frac{\delta +3}{\delta ^2}|\textbf{n}_{{x_M}{x_K}}|, \\&\left| \pmb {\tau }^{T_K}_{{x_M}{x_L}} \right| \le \frac{1}{\delta ^2} |\textbf{n}_{{x_M}{x_L}}|,\\&\left| \pmb {\tau }^{T_K}_{{x_M}{x_{\texttt {e}}}} \right| \le \max \left\{ 1, \left| {{\widetilde{\beta }}}^T_{M}\right| \right\} (|\textbf{n}_{({x_K}{x_{\texttt {e}}}{x_{\texttt {f}}})}|+|\textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})}|) \le \frac{2(\delta +3)}{\delta ^2} |\textbf{n}_{{x_M}{x_{\texttt {e}}}}|,\\&\left| \pmb {\tau }^{T_K}_{{x_K}{x_L}} \right| \le \frac{1}{\delta ^2}|\textbf{n}_{{x_K}{x_L}} |, \\&\left| \pmb {\tau }^{T_K}_{{x_K}{x_{\texttt {e}}}} \right| \le \max \left\{ \left| {{\widetilde{\beta }}}^T_{K}\right| ,~\left| \widetilde{\beta }^T_{e}\right| \right\} \left( |\textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})}| + | \textbf{n}^K_{({x_M}{x_{\texttt {e}}}{x_{\texttt {f}}})} | \right) \le \frac{2}{\delta ^2} |\textbf{n}_{{x_K}{x_{\texttt {e}}}}|,\\ {}&\left| \pmb {\tau }^{T_K}_{{x_L}{x_{\texttt {e}}}} \right| \le \frac{1}{\delta ^2} |\textbf{n}_{{x_L}{x_{\texttt {e}}}}|, \end{aligned}$$

where the coefficients ${{\widetilde{\beta }}}^T_{M}$, $\widetilde{\beta }^T_{K}$, ${{\widetilde{\beta }}}^T_{L}$, and ${{\widetilde{\beta }}}^T_{e}$ are given in (19) and satisfy the following upper bounds:

$$\begin{aligned} \left| {{\widetilde{\beta }}}^T_{M} \right|&\le 1 + |\widetilde{\beta }^T_{K}| + |{{\widetilde{\beta }}}^T_{L}|+ | {{\widetilde{\beta }}}^T_{e}| \le 1 + \frac{3}{\delta },\\ \left| {{\widetilde{\beta }}}^T_{K} \right|&= \left| \dfrac{\left( \Lambda _K \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{3m_{T_K} \beta _{\texttt {f}}} \right| \le \dfrac{1}{\delta },\\ \left| {{\widetilde{\beta }}}^T_{e}\right|&= \left| \dfrac{\left( \Lambda _K \textbf{n}_{({x_M}{x_K}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{3m_{T_K} \beta _{\texttt {f}} }-\dfrac{\left( \Lambda _L \textbf{n}_{({x_M}{x_L}{x_{\texttt {f}}})}\right) \cdot \textbf{n}^K_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{3m_{T_L} \beta _{\texttt {f}}} \right| \le \frac{1}{\delta },\\ \left| {{\widetilde{\beta }}}^T_{L} \right|&= \left| \dfrac{\left( \Lambda _L \textbf{n}^L_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}\right) \cdot \textbf{n}^L_{({x_M}{x_{\texttt {e}}} {x_{\texttt {f}}})}}{3m_{T_L} \beta _{\texttt {f}}} \right| \le \dfrac{1}{\delta }. \end{aligned}$$

In this expression, the coefficient $C_1 = \frac{2(\delta + 3)}{\delta ^2}$ satisfies (66). $\square$

Proposition 2

Under the assumptions A A1–A A3, let $\left( \mathcal {H}_h, h, P_1,\nabla _{\Lambda } \right)$ be a family of discretizations in the sense of Definition 2. A positive constant $\delta$ independent of h satisfies the following conditions:

Assumption A4

$\quad {\frac{d_{{x_K}{x_{\texttt {e}}}}}{m_{[{x_K}{x_{\texttt {e}}}]}}, ~~\frac{d_{{x_L}{x_{\texttt {e}}}}}{m_{[{x_L}{x_{\texttt {e}}}]}}, ~~\frac{d_{{x_M}{x_{\texttt {e}}}}}{m_{[{x_M}{x_{\texttt {e}}}]}},~~\frac{d_{{x_K}{x_L}}}{m_{[{x_K}{x_L}]}},~~ \frac{d_{{x_K}{x_M}}}{m_{[{x_K}{x_M}]}},~~\frac{d_{{x_L}{x_M}}}{m_{[{x_L}{x_M}]}} \ge \delta }$,

Assumption A5

${\frac{\min \limits _{Q\in \{K,L\}}\left\{ \begin{array}{l} m_{\texttt {f}^{T_Q}_{({x_M}{x_K}{C}_{[{x_L}{x_{\texttt {e}}}]})}}, m_{\texttt {f}^{T_Q}_{({x_M}{x_L}{C}_{[{x_K}{x_{\texttt {e}}}]})}}, m_{\texttt {f}^{T_Q}_{({x_K}{x_L}{C}_{[{x_M}{x_{\texttt {e}}}]})}}, \\ m_{\texttt {f}^{T_Q}_{({x_K}{x_{\texttt {e}}}{C}_{[{x_M}{x_L}]})}}, m_{\texttt {f}^{T_Q}_{({x_L}{x_{\texttt {e}}}{C}_{[{x_M}{x_K}]})}} \end{array} \right\} }{\max \left\{ \begin{array}{l} m_{({x_M}{x_K}{C}_{[{x_L}{x_{\texttt {e}}}]})}, m_{({x_M}{x_L}{C}_{[{x_K}{x_{\texttt {e}}}]})}, m_{({x_K}{x_L}{C}_{[{x_M}{x_{\texttt {e}}}]})},\\ m_{({x_K}{x_{\texttt {e}}}{C}_{[{x_M}{x_L}]})}, m_{({x_L}{x_{\texttt {e}}}{C}_{[{x_M}{x_K}]})} \end{array} \right\} } \ge \delta }$,

where the planar parts $\texttt {f}^{T_Q}_{({x_M}{x_K}{C}_{[{x_L}{x_{\texttt {e}}}]})}$, $\texttt {f}^{T_Q}_{({x_M}{x_L}{C}_{[{x_K}{x_{\texttt {e}}}]})}$, $\texttt {f}^{T_Q}_{({x_K}{x_L}{C}_{[{x_M}{x_{\texttt {e}}}]})}$, $\texttt {f}^{T_Q}_{({x_K}{x_{\texttt {e}}}{C}_{[{x_M}{x_L}]})}$ and $\texttt {f}^{T_Q}_{({x_L}{x_{\texttt {e}}}{C}_{[{x_M}{x_K}]})}$ of the respective faces $({x_M}{x_K}{C}_{[{x_L}{x_{\texttt {e}}}]})$, $({x_M}{x_L}{C}_{[{x_K}{x_{\texttt {e}}}]})$, $({x_K}{x_L}{C}_{[{x_M}{x_{\texttt {e}}}]})$, $({x_K}{x_{\texttt {e}}}{C}_{[{x_M}{x_L}]})$, and $({x_L}{x_{\texttt {e}}}{C}_{[{x_M}{x_K}]})$ are within the tetrahedron $T_Q$ for each $Q \in \{K, L\}$.

Assumption A6

$\quad \frac{\rho _{T_K}}{h_T}, \frac{\rho _{T_L}}{h_T} \ge \delta ,$

Then, the EFC-3DFEMb scheme is coercive, meaning that there exists a positive constant $C_2$ independent of h such that

$$\begin{aligned} \Vert P_1 \textbf{v}_h \Vert _{L^2(\Omega )} \le C_2 \Vert \nabla _{\Lambda } \textbf{v}_h \Vert _{\left( L^2(\Omega )\right) ^2},\quad \forall \textbf{v}_h \in \mathcal {H}_h. \end{aligned}$$

(69)

The EFC-3DFEMb scheme also satisfies the following limits:

$$\begin{aligned}&\lim \limits _{h \rightarrow 0} {\widehat{S}}_{h}(\varphi ) = 0, \quad \forall \varphi \in C^\infty _c(\Omega ), \end{aligned}$$

(70)

$$\begin{aligned}&\lim \limits _{h \rightarrow 0} \widehat{W}_{h}(\pmb {\varphi }) = 0, \quad \forall \pmb {\varphi }\in \left( C^\infty _c(\Omega )\right) ^3, \end{aligned}$$

(71)

where the operators ${\widehat{S}}_{h}$ and ${\widehat{W}}_{h}$ are defined by (49) and (50), respectively.

Proof

We verify the existence of a positive constant $C_3$ depending on $\Omega$ and $\delta$ such that

$$\begin{aligned} \Vert \textbf{v}_h\Vert ^2_{1,\mathcal {T}^{**}_h} \le C_3 \Vert \nabla _{\Lambda } \textbf{v}_h \Vert ^2_{\left( L^2(\Omega )\right) ^2}, \quad \forall \textbf{v}_h \in \mathcal {H}_h, \end{aligned}$$

(72)

as follows: For any tetrahedron $T:=({x_M}{x_K}{x_L}{x_{\texttt {e}}}) \in \mathcal {T}^{**}_h$, the formula for $\nabla _{\Lambda } \textbf{v}_h$ in classifying T can be obtained by

• Case 1: If $T \in \mathcal {T}^{**}_{{\text {{const}}}}$, $(\nabla _{\Lambda } \textbf{v}_h)_T$ is then calculated as given in (57). This equation satisfies

  $$\begin{aligned}&v_{\texttt {e}} - v_{K} = (\nabla _{\Lambda } \textbf{v}_h)_T \cdot ({x_{\texttt {e}}} - {x_K}),{} & {} v_{\texttt {e}} -v_{L} =(\nabla _{\Lambda } \textbf{v}_h)_T \cdot ({x_{\texttt {e}}} - {x_L}),\\&v_{\texttt {e}} - v_{M} = (\nabla _{\Lambda } \textbf{v}_h)_T \cdot ({x_{\texttt {e}}} - {x_M}),{} & {} v_{L} - v_{K} = (\nabla _{\Lambda } \textbf{v}_h)_T \cdot ({x_L}- {x_K}), \\&v_{K} - v_{M} = (\nabla _{\Lambda } \textbf{v}_h)_T \cdot ({x_K}- {x_M}),{} & {} v_{L} - v_{M} = (\nabla _{\Lambda } \textbf{v}_h)_T \cdot ({x_L}- {x_M}), \end{aligned}$$

  Therefore,

  $$\begin{aligned}&\Vert (\nabla _{\Lambda } \textbf{v}_h)_T \Vert ^2 \ge \frac{\left| v_{\texttt {e}} - v_{K} \right| ^2}{m^2_{[{x_K}{x_{\texttt {e}}}]}}, \qquad \Vert (\nabla _{\Lambda } \textbf{v}_h)_T \Vert ^2 \ge \frac{\left| v_{\texttt {e}} - v_{L} \right| ^2}{m^2_{[{x_L}{x_{\texttt {e}}}]}},\nonumber \\&\Vert (\nabla _{\Lambda } \textbf{v}_h)_T \Vert ^2 \ge \frac{\left| v_{\texttt {e}} - v_{M} \right| ^2}{m^2_{[{x_M}{x_{\texttt {e}}}]}}, \qquad \Vert (\nabla _{\Lambda } \textbf{v}_h)_T \Vert ^2 \ge \frac{\left| v_{L} - v_{K} \right| ^2}{m^2_{[{x_K}{x_L}]}}, \nonumber \\&\Vert (\nabla _{\Lambda } \textbf{v}_h)_T \Vert ^2 \ge \frac{\left| v_{M} - v_{K} \right| ^2}{m^2_{[{x_K}{x_M}]}}, \qquad \Vert (\nabla _{\Lambda } \textbf{v}_h)_T \Vert ^2 \ge \frac{\left| v_{L} - v_{M} \right| ^2}{m^2_{[{x_L}{x_M}]}}. \end{aligned}$$

  (73)

  Additionally, $\frac{m_T}{m^2_{[{x_K}{x_{\texttt {e}}}]}} \ge \frac{\delta ^2}{3} \frac{|\textbf{n}_{{x_K}{x_{\texttt {e}}}}|}{ d_{{x_K}{x_{\texttt {e}}}}}$ from $m_T \ge m_{({x_K},{x_{\texttt {e}}},{\texttt {f}}_{[{x_K}{x_{\texttt {e}}}]})} = \frac{1}{3}d_{{x_K}{x_{\texttt {e}}}} |\textbf{n}_{{x_K}{x_{\texttt {e}}}} |$ and $d_{{x_K}{x_{\texttt {e}}}} \le m_{[{x_K}{x_{\texttt {e}}}]}$. In the same manner, it has

  $$\begin{aligned}&\frac{m_T}{m^2_{[{x_L}{x_{\texttt {e}}}]}} \ge \frac{\delta ^2}{3} \frac{|\textbf{n}_{{x_L}{x_{\texttt {e}}}}|}{ d_{{x_L}{x_{\texttt {e}}}}},{} & {} \frac{m_T}{m^2_{[{x_M}{x_{\texttt {e}}}]}} \ge \frac{\delta ^2}{3} \frac{|\textbf{n}_{{x_M}{x_{\texttt {e}}}}|}{ d_{{x_M}{x_{\texttt {e}}}}},{} & {} \frac{m_T}{m^2_{[{x_K}{x_L}]}} \ge \frac{\delta ^2}{3} \frac{|\textbf{n}_{{x_K}{x_L}}|}{ d_{{x_K}{x_L}}},\nonumber \\&\frac{m_T}{m^2_{[{x_K}{x_M}]}} \ge \frac{\delta ^2}{3} \frac{|\textbf{n}_{{x_K}{x_M}}|}{ d_{{x_K}{x_M}}},{} & {} \frac{m_T}{m^2_{[{x_L}{x_M}]}} \ge \frac{\delta ^2}{3} \frac{|\textbf{n}_{{x_L}{x_M}}|}{ d_{{x_L}{x_M}}},{} & {} \frac{m_T}{m^2_{[{x_K}{x_{\texttt {e}}}]}} \ge \frac{\delta ^2}{3} \frac{|\textbf{n}_{{x_K}{x_{\texttt {e}}}}|}{ d_{{x_K}{x_{\texttt {e}}}}}. \end{aligned}$$

  (74)

  From Eqs. (73) and (74), it follows that

  $$\begin{aligned}&m_T \Vert (\nabla _{\Lambda } \textbf{v}_h)_T \Vert ^2 \ge \frac{1}{6} m_T \left[ \begin{array}{l} \frac{\left| v_{\texttt {e}} - v_{K} \right| ^2}{m^2_{[{x_K}{x_{\texttt {e}}}]}} + \frac{\left| v_{\texttt {e}} - v_{L} \right| ^2}{m^2_{[{x_L}{x_{\texttt {e}}}]}} + \frac{\left| v_{\texttt {e}} - v_{M} \right| ^2}{m^2_{[{x_M}{x_{\texttt {e}}}]}} +\\ \frac{\left| v_{L} - v_{K} \right| ^2}{m^2_{[{x_K}{x_L}]}} + \frac{\left| v_{M} - v_{K} \right| ^2}{m^2_{[{x_K}{x_M}]}} + \frac{\left| v_{L} - v_{M} \right| ^2}{m^2_{[{x_L}{x_M}]}} \end{array} \right] \nonumber \\&\qquad \ge \frac{\delta ^2}{18} \left[ \begin{array}{l} \frac{|\textbf{n}_{{x_K}{x_{\texttt {e}}}}|}{d_{{x_K}{x_{\texttt {e}}}}} (v_{e}-v_{K})^2 +\frac{|\textbf{n}_{{x_L}{x_{\texttt {e}}}}|}{d_{{x_L}{x_{\texttt {e}}}}} (v_{e}-v_{L})^2+ \frac{|\textbf{n}_{{x_M}{x_{\texttt {e}}}}|}{d_{{x_M}{x_{\texttt {e}}}}} (v_{e}-v_{M})^2 + \\ \frac{|\textbf{n}_{{x_K}{x_L}}|}{d_{{x_K}{x_L}}} (v_{L}-v_{K})^2+\frac{|\textbf{n}_{{x_M}{x_K}}|}{d_{{x_M}{x_K}}} (v_{K}-v_{M})^2 + \frac{|\textbf{n}_{{x_M}{x_L}}|}{d_{{x_M}{x_L}}} (v_{L}-v_{M})^2 \end{array} \right] . \end{aligned}$$

  (75)

• Case 2: If $T \in \mathcal {T}^{**}_h \setminus \mathcal {T}^{**}_{{\text {{const}}}}$, $\nabla _{\Lambda } \textbf{u}_h$ is defined by (27). Considering $\nabla _{\Lambda }\textbf{v}_h$ on $T_K$, it has

  $$\begin{aligned}&v_{\texttt {e}} - v_{K} = (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \cdot ({x_{\texttt {e}}} - {x_K}),{} & {} v_{\texttt {e}} - v_{\texttt {f}}^{M} =(\nabla _{\Lambda } \textbf{v}_h)_{T_K} \cdot ({x_{\texttt {e}}} - {x_{\texttt {f}}}),\nonumber \\&v_{\texttt {e}} - v_{M} = (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \cdot ({x_{\texttt {e}}} - {x_M}),{} & {} v_{\texttt {f}}^{M} - v_{K} = (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \cdot ({x_{\texttt {f}}} - {x_K}), \nonumber \\&v_{K} - v_{M} = (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \cdot ({x_K}- {x_M}),{} & {} v_{\texttt {f}}^{M} - v_{M} = (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \cdot ({x_{\texttt {f}}} - {x_M}), \end{aligned}$$

  Therefore,

  $$\begin{aligned}&\Vert (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \Vert ^2 \ge \frac{\left| v_{\texttt {e}} - v_{K} \right| ^2}{m^2_{[{x_K}{x_{\texttt {e}}}]}},{} & {} \Vert (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \Vert ^2 \ge \frac{\left| v_{\texttt {e}} - v_{\texttt {f}}^{M} \right| ^2}{m^2_{[{x_{\texttt {f}}}{x_{\texttt {e}}}]}},\nonumber \\&\Vert (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \Vert ^2 \ge \frac{\left| v_{\texttt {e}} - v_{M} \right| ^2}{m^2_{[{x_M}{x_{\texttt {e}}}]}},{} & {} \Vert (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \Vert ^2 \ge \frac{\left| v_{\texttt {f}}^{M} - v_{K} \right| ^2}{m^2_{[{x_K}{x_{\texttt {f}}}]}}, \end{aligned}$$

  (76)
  $$\begin{aligned}&\Vert (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \Vert ^2 \ge \frac{\left| v_{M} - v_{K} \right| ^2}{m^2_{[{x_K}{x_M}]}},{} & {} \Vert (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \Vert ^2 \ge \frac{\left| v_{\texttt {f}}^{M} - v_{M} \right| ^2}{m^2_{[{x_M}{x_{\texttt {f}}}]}}. \end{aligned}$$

  (77)

  Then, the inequality is established as

  $$\begin{aligned} m_{T_K}\Vert (\nabla _{\Lambda } \textbf{v}_h)_{T_K} \Vert ^2&\ge \frac{1}{6} m_{T_K}\left[ \begin{array}{l} \frac{\left| v_{\texttt {e}} - v_{K} \right| ^2}{m^2_{[{x_K}{x_{\texttt {e}}}]}} + \frac{\left| v_{\texttt {e}} - v_{\texttt {f}}^{M} \right| ^2}{m^2_{[{x_{\texttt {e}}}{x_{\texttt {f}}}]}} + \frac{\left| v_{\texttt {e}} - v_{M} \right| ^2}{m^2_{[{x_M}{x_{\texttt {e}}}]}} +\\ \frac{\left| v_{\texttt {f}}^{M} - v_{K} \right| ^2}{m^2_{[{x_K}{x_{\texttt {f}}}]}} + \frac{\left| v_{M} - v_{K} \right| ^2}{m^2_{[{x_K}{x_M}]}} + \frac{\left| v_{\texttt {f}}^{M} - v_{M} \right| ^2}{m^2_{[{x_M}{x_{\texttt {f}}}]}} \end{array} \right] . \end{aligned}$$

  (78)

  In the same manner, the inequality on the tetrahedron $T_L$ can be obtained as

  $$\begin{aligned} m_{T_L}\Vert (\nabla _{\Lambda } \textbf{v}_h)_{T_L} \Vert ^2&\ge \frac{1}{6} m_{T_L}\left[ \begin{array}{l} \frac{\left| v_{\texttt {e}} - v_{L} \right| ^2}{m^2_{[{x_L}{x_{\texttt {e}}}]}} + \frac{\left| v_{\texttt {e}} - v_{\texttt {f}}^{M} \right| ^2}{m^2_{[{x_{\texttt {e}}}{x_{\texttt {f}}}]}} + \frac{\left| v_{\texttt {e}} - v_{M} \right| ^2}{m^2_{[{x_M}{x_{\texttt {e}}}]}} +\\ \frac{\left| v_{\texttt {f}}^{M} - v_{L} \right| ^2}{m^2_{[{x_L}{x_{\texttt {f}}}]}} + \frac{\left| v_{M} - v_{L} \right| ^2}{m^2_{[{x_L}{x_M}]}} + \frac{\left| v_{\texttt {f}}^{M} - v_{M} \right| ^2}{m^2_{[{x_M}{x_{\texttt {f}}}]}} \end{array} \right] . \end{aligned}$$

  (79)

  Besides, by the assumptions A A4-A A6, it holds that

  $$\begin{aligned}&\frac{m_T}{m^2_{[{x_K}{x_{\texttt {e}}}]}} \ge \frac{d_{{x_K}{x_{\texttt {e}}}}|\textbf{n}_{{x_K}{x_{\texttt {e}}}}|}{3m^2_{[{x_K}{x_{\texttt {e}}}]}} \ge \frac{\delta ^2}{3} \frac{|\textbf{n}_{{x_K}{x_{\texttt {e}}}}|}{ d_{{x_K}{x_{\texttt {e}}}}},\nonumber \\&\frac{m_{T_K}}{m^2_{[{x_M}{x_K}]}} \ge \frac{d_{{x_M}{x_K}} m_{\texttt {f}^{T_K}_{({x_L}{x_{\texttt {e}}}{C}_{[{x_M}{x_K}]})}}}{3m^2_{[{x_M}{x_K}]}} \ge \delta ^3 \frac{|\textbf{n}_{[{x_M}{x_K}]}|}{d_{[{x_M}{x_K}]}}, \nonumber \\&\frac{m_{T_L}}{m^2_{[{x_L}{x_{\texttt {e}}}]}} \ge \frac{1}{3} \frac{d_{{x_L}{x_{\texttt {e}}}} m_{\texttt {f}^{T_L}_{({x_M}{x_K}{C}_{[{x_L}{x_{\texttt {e}}}]})}}}{m^2_{[{x_L}{x_{\texttt {e}}}]}} \ge \delta ^3 \frac{|\textbf{n}_{[{x_L}{x_{\texttt {e}}}]}|}{d_{[{x_L}{x_{\texttt {e}}}]}}, \nonumber \\&\frac{m_{T_L}}{m^2_{[{x_M}{x_L}]}} \ge \frac{1}{3} \frac{d_{{x_M}{x_L}} m_{\texttt {f}^{T_L}_{({x_K}{x_{\texttt {e}}}{C}_{[{x_M}{x_L}]})}}}{m^2_{[{x_L}{x_{\texttt {e}}}]}} \ge \delta ^3 \frac{|\textbf{n}_{[{x_M}{x_L}]}|}{d_{[{x_M}{x_L}]}}, \nonumber \\&\frac{\min \left\{ m_{T_K}, m_{T_L} \right\} }{m^2_{[{x_K}{x_L}]}} \ge \delta \frac{d_{{x_K}{x_L}} m_{{\texttt {f}}_{[{x_K}{x_L}]}}}{m^2_{[{x_K}{x_L}]}} \ge \delta ^3 \frac{|\textbf{n}_{[{x_K}{x_L}]}|}{d_{[{x_K}{x_L}]}}, \nonumber \\&\frac{m_{T}}{m^2_{[{x_M}{x_{\texttt {e}}}]}} \ge \frac{1}{3} \frac{d_{{x_M}{x_{\texttt {e}}}}m_{{\texttt {f}}_{[{x_M}{x_{\texttt {e}}}]}}}{m^2_{[{x_M}{x_{\texttt {e}}}]}} \ge \delta \frac{|\textbf{n}_{[{x_M}{x_{\texttt {e}}}]}|}{d_{{x_M}{x_{\texttt {e}}}}},\nonumber \\&\frac{m_{T_K}}{m^2_{[{x_K}{x_{\texttt {f}}}]}} \ge \frac{m_{T_K}}{m^2_{[{x_K}{x_L}]}},\quad \frac{m_{T_L}}{m^2_{[{x_L}{x_{\texttt {f}}}]}} \ge \frac{m_{T_L}}{m^2_{[{x_K}{x_L}]}},\nonumber \\&\text { because of } m_{[{x_K}{x_L}]} \ge m_{[{x_K}{x_{\texttt {f}}}]},~ m_{[{x_L}{x_{\texttt {f}}}]}. \end{aligned}$$

  (80)

  Substituting (80) into the inequalities (78) and (79) yields:

  $$\begin{aligned}&6m_T \Vert \left( \nabla _{\Lambda } \textbf{v}_h \right) _T\Vert ^2 \nonumber \\&\quad \ge \left[ \begin{array}{l} \frac{m_{T_K}}{m^2_{[{x_K}{x_{\texttt {e}}}]}} \left( v_{\texttt {e}} - v_{K} \right) ^2 + \frac{m_{T_L}}{m^2_{[{x_L}{x_{\texttt {e}}}]}} \left( v_{\texttt {e}} - v_{L} \right) ^2 + \frac{m_{T_K}}{m^2_{[{x_M}{x_K}]}} \left( v_{K} - v_{M} \right) ^2 + \\ \frac{m_{T}}{m^2_{[{x_M}{x_{\texttt {e}}}]}}\left( v_{\texttt {e}} - v_{M} \right) ^2 + \frac{m_{T_L}}{m^2_{[{x_M}{x_L}]}} \left( v_{L} - v_{M} \right) ^2 +\\ {\frac{m_{T_K}}{m^2_{[{x_K}{x_{\texttt {f}}}]}}} \left( v_{\texttt {f}}^{M} - v_{K} \right) ^2 + {\frac{m_{T_L}}{m^2_{[{x_L}{x_{\texttt {f}}}]}}} \left( v_{\texttt {f}}^{M} - v_{L} \right) ^2 +\\ {\frac{m_{T}}{m^2_{[{x_M}{x_{\texttt {f}}}]}}} \left( v_{\texttt {f}}^{M} - v_{M} \right) ^2 + {\frac{m_{T}}{m^2_{[{x_{\texttt {e}}}{x_{\texttt {f}}}]}}} \left( v_{\texttt {f}}^{M} - v_{\texttt {e}} \right) ^2 \end{array} \right] \nonumber \\&\quad \ge \min \left\{ \frac{\delta ^3}{2},~ \delta \left( 1+\frac{1}{2 \delta } \right) \right\} \nonumber \\&\quad \left[ \begin{array}{l} \frac{|\textbf{n}_{[{x_K}{x_{\texttt {e}}}]}|}{d_{[{x_K}{x_{\texttt {e}}}]}} \left( v_{\texttt {e}} - v_{K} \right) ^2 + \frac{|\textbf{n}_{[{x_L}{x_{\texttt {e}}}]}|}{d_{[{x_L}{x_{\texttt {e}}}]}} \left( v_{\texttt {e}} - v_{L} \right) ^2 + \frac{|\textbf{n}_{[{x_M}{x_K}]}|}{d_{[{x_M}{x_K}]}} \left( v_{K} - v_{M} \right) ^2 + \\ \frac{|\textbf{n}_{[{x_M}{x_{\texttt {e}}}]}|}{d_{{x_M}{x_{\texttt {e}}}}} \left( v_{\texttt {e}} - v_{M} \right) ^2 + \frac{|\textbf{n}_{[{x_M}{x_L}]}|}{d_{[{x_M}{x_L}]}} \left( v_{L} - v_{M} \right) ^2 + \frac{|\textbf{n}_{[{x_K}{x_L}]}|}{d_{[{x_K}{x_L}]}} (v_{L} - v_{K}) ^2 \end{array} \right] . \end{aligned}$$

  (81)

From (75) and (81), we choose $C _3 = \frac{1}{\min \left\{ \frac{\delta ^3}{12},~ \frac{\delta }{6}\left( 1+\frac{1}{2 \delta } \right) , ~\frac{\delta ^2}{36} \right\} }$ to satisfy the inequality (72), which is the sum of (81) for all $T \in \mathcal {T}^{**}_h$.

Next, on each $T \in \mathcal {T}^{**}_h$, $P_1 \textbf{v}_h$ is written as

$$\begin{aligned} P_1 \textbf{v}_h ({x}) = {\left\{ \begin{array}{ll} \Pi ^0_h \textbf{v}_h ({x}) + \left. \nabla P_1 \textbf{v}_h \right| _T \cdot ({x}- {x_M}), &{} \text {if } {x}\in P_{{x_M}}, \\ \Pi ^0_h \textbf{v}_h ({x}) + \left. \nabla P_1 \textbf{v}_h \right| _T \cdot ({x}- {x_K}), &{} \text {if } {x}\in P_{{x_K}}, \\ \Pi ^0_h \textbf{v}_h ({x}) + \left. \nabla P_1 \textbf{v}_h \right| _T \cdot ({x}- {x_L}), &{} \text {if } {x}\in P_{{x_L}}, \\ \Pi ^0_h \textbf{v}_h ({x}) + \left. \nabla P_1 \textbf{v}_h \right| _T \cdot ({x}- {x_{\texttt {e}}}), &{} \text {if } {x}\in P_{{x_{\texttt {e}}}}, \end{array}\right. } \end{aligned}$$

(82)

where the restriction $\left. \nabla P_1 \textbf{v}_h \right| _T$ of $\nabla P_1 \textbf{v}_h$ on T is given as

$$\begin{aligned} m_T \left. \nabla P_1 \textbf{v}_h \right| _T =&(v_{e}-v_{K})\textbf{n}_{{x_K}{x_{\texttt {e}}}}+ (v_{e}-v_{L})\textbf{n}_{{x_L}{x_{\texttt {e}}}}+(v_{e}-v_{M})\textbf{n}_{{x_M}{x_{\texttt {e}}}} \nonumber \\ +&(v_{L}-v_{K})\textbf{n}_{{x_K}{x_L}}+(v_{K}-v_{M})\textbf{n}_{{x_M}{x_K}} +(v_{L}-v_{M})\textbf{n}_{{x_M}{x_L}}, \end{aligned}$$

(83)

and the operator $\Pi ^0_h$ is defined as given in (51).

The following result is obtained by applying the triangle inequality to (82)

$$\begin{aligned} \Vert P_1 \textbf{v}_h \Vert _{L^2(\Omega )} \le \Vert \Pi ^0_h \textbf{v}_h \Vert _{L^2(\Omega )} + h \Vert \nabla P_1 \textbf{v}_h \Vert _{\left( L^2(\Omega )\right) ^2}. \end{aligned}$$

(84)

By employing the Cauchy–Schwarz inequality in (83), we can continue estimating the terms $\Vert \nabla P_1 \textbf{v}_h \Vert _{\left( L^2(\Omega )\right) }$ and $\Vert \Pi ^0_h \textbf{v}_h \Vert _{L^2(\Omega )}$ as follows:

$$\begin{aligned}&\sum \limits _{T \in \mathcal {T}^{**}_h} m_T \vert \nabla P_1 \textbf{v}_h \vert \\&\quad \le \sum \limits _{T \in \mathcal {T}^{**}_h} \left[ \begin{array}{l} (v_{e}-v_{K})^2\frac{\vert \textbf{n}_{{x_K}{x_{\texttt {e}}}}\vert }{d_{{x_K}{x_{\texttt {e}}}}}+ (v_{e}-v_{L})^2\frac{\vert \textbf{n}_{{x_L}{x_{\texttt {e}}}}\vert }{d_{{x_L}{x_{\texttt {e}}}}}+(v_{e}-v_{M})^2\frac{\vert \textbf{n}_{{x_M}{x_{\texttt {e}}}}\vert }{d_{{x_M}{x_{\texttt {e}}}}} \\ +(v_{L}-v_{K})^2\frac{\vert \textbf{n}_{{x_K}{x_L}}\vert }{d_{{x_K}{x_L}}}+(v_{K}-v_{M})^2\frac{\vert \textbf{n}_{{x_M}{x_K}}\vert }{d_{{x_M}{x_K}}} +(v_{L}-v_{M})^2\frac{\vert \textbf{n}_{{x_M}{x_L}} \vert }{d_{{x_M}{x_L}}} \end{array} \right] \\&\left[ \sum \limits _{ {\begin{array}{l} T \in \mathcal {T}^{**}_h\\ T = ({x_M}{x_K}{x_L}{x_{\texttt {e}}}) \end{array}} } {\sum \limits _{({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T} \vert \textbf{n}_{{x_N}{x_Q}}\vert d_{{x_N}{x_Q}}} \right] . \end{aligned}$$

Taking note that $m_T = \frac{2}{3}\sum \limits _{({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T} \vert \textbf{n}_{{x_N}{x_Q}}\vert d_{{x_N}{x_Q}}$ and using the definition in (52), the above inequality can be rewritten as

$$\begin{aligned} \Vert \nabla P_1 \textbf{v}_h \Vert ^2_{\left( L^2(\Omega )\right) ^3} \le \frac{3}{2} m_{\Omega } ~\Vert \textbf{v}_h\Vert ^2_{1,\mathcal {T}^{**}_h}, \end{aligned}$$

(85)

where $m_{\Omega }$ represents the volume of $\Omega$.

According to [17, Lemma 5.3], there exists a positive constant $C_4$ independent of h such that

$$\begin{aligned} \Vert \Pi ^0_h \textbf{v}_h \Vert _{L^2(\Omega )} \le C_4 \Vert \textbf{v}_h\Vert ^2_{1,\mathcal {T}^{**}_h}, \quad \forall \textbf{v}_h \in \mathcal {H}_{h}. \end{aligned}$$

(86)

By combining (72) with (84)–(86), one can deduce

$$\begin{aligned} \Vert P_1 \textbf{v}_h \Vert _{L^2(\Omega )} \le \left( C_4 + \frac{3}{2} h m_{\Omega }\right) ~\Vert \textbf{v}_h\Vert ^2_{1,\mathcal {T}^{**}_h} \le C_3\left( C_4 + \frac{3}{2} h m_{\Omega }\right) ~ \Vert \nabla _{\Lambda } \textbf{v}_h \Vert ^2_{\left( L^2(\Omega )\right) ^3}. \end{aligned}$$

(87)

For a sufficiently small value of h, there exists a positive constant $C_2 > C_3\left( C_4 + \frac{3}{2} h m_{\Omega }\right)$ that is independent of h and satisfies the coercive property (69) for the EFC-3DFEMb scheme.

Next, we will prove that the EFC-3DFEMb scheme has the strong consistency property (70).

For any $\varphi \in C^{\infty }_c(\Omega )$, there exists a vector $\pmb {\varphi }_h$ such that the values of its elements are taken from $\left( \varphi ({x_P})\right) _{{x_P}\in \mathcal {V}^{**}} \in \mathcal {H}^0_h$. According to [17, Lemma 4.3], there exists a positive constant $C_5$ that is independent of h, and satisfies

$$\begin{aligned} \Vert \nabla _{\Lambda } \pmb {\varphi }_h - \nabla \varphi \Vert _{\left( L^2(\Omega )\right) ^3} \le C_5 h. \end{aligned}$$

(88)

Combining the result of [18, Lemma 3.1] with this, one can write

$$\begin{aligned} \Vert P_1 \pmb {\varphi }_h- \varphi \Vert _{L^2(\Omega )} \le h \Vert \nabla \varphi \Vert _{\left( L^2(\Omega )\right) ^3}. \end{aligned}$$

(89)

After establishing the strong consistency of the EFC-3DFEMb scheme, it is necessary to prove the dual consistency property (71) as follows:

For any $\pmb {\varphi }\in \left( C^{\infty }_c(\Omega )\right) ^3$, the operators I and $\{I_i\}_{i=\overline{1,3}}$ are defined by

(90)

Using the above operators, we can rewrite ${\widehat{W}}_{h}(\pmb {\varphi })$ as

$$\begin{aligned}&{\widehat{W}}_{h}(\pmb {\varphi }) = \max \limits _{\textbf{v}_h \in \mathcal {H}_{h}} \frac{1}{\Vert \nabla _{\Lambda } \textbf{v}_h \Vert } \int _{\Omega } \left[ \nabla _{\Lambda } \textbf{v}_h \cdot \pmb {\varphi }+ P_1 \textbf{v}_h {\text {div}}(\pmb {\varphi })\right] d{x}= \max \limits _{\textbf{v}_h \in \mathcal {H}_h} \frac{1}{\Vert \nabla _{\Lambda } \textbf{v}_h \Vert } I(\pmb {\varphi }). \nonumber \end{aligned}$$

In addition, based on Lemma 1, $I_1(\pmb {\varphi })$ can be rewritten as

$$\begin{aligned} I_1(\pmb {\varphi }) =&\sum \limits _{T \in \mathcal {T}^{**}_h \setminus \mathcal {T}^{**}_{\Lambda }}\left[ \begin{array}{l} (v_{K} - v_{M})(\textbf{n}_{{x_M}{x_K}} + \pmb \epsilon _{{x_M}{x_K}}) + (v_{L} - v_{M})(\textbf{n}_{{x_M}{x_L}} + \pmb \epsilon _{{x_M}{x_L}}) + \\ (v_{e} - v_{M})(\textbf{n}_{{x_M}{x_{\texttt {e}}}} + \pmb \epsilon _{{x_M}{x_{\texttt {e}}}}) + (v_{L} - v_{K})(\textbf{n}_{{x_K}{x_L}} + \pmb \epsilon _{{x_K}{x_L}}) +\\ (v_{e} - v_{K})(\textbf{n}_{{x_K}{x_{\texttt {e}}}} + \pmb \epsilon _{{x_K}{x_{\texttt {e}}}}) + (v_{e} - v_{L})(\textbf{n}_{{x_L}{x_{\texttt {e}}}} + \pmb \epsilon _{{x_L}{x_{\texttt {e}}}}) \end{array} \right] \cdot \pmb {\varphi }_T \nonumber \\&+ \sum \limits _{T \in \mathcal {T}^{**}_{\Lambda }} \left\{ \begin{array}{l} \left[ \begin{array}{l} (v_{K} - v_{M})\pmb {\tau }^{T_K}_{{x_M}{x_K}} + (v_{L} - v_{M})\pmb {\tau }^{T_K}_{{x_M}{x_L}} + (v_{e} - v_{M})\pmb {\tau }^{T_K}_{{x_M}{x_{\texttt {e}}}} \\ + (v_{L} - v_{K})\pmb {\tau }^{T_K}_{{x_K}{x_L}} + (v_{e} - v_{K})\pmb {\tau }^{T_K}_{{x_K}{x_{\texttt {e}}}} + (v_{e} - v_{L})\pmb {\tau }^{T_K}_{{x_L}{x_{\texttt {e}}}} \end{array} \right] \cdot \pmb {\varphi }_{T_K} + \\ \left[ \begin{array}{l} (v_{K} - v_{M})\pmb {\tau }^{T_L}_{{x_M}{x_K}} + (v_{L} - v_{M})\pmb {\tau }^{T_L}_{{x_M}{x_L}} + (v_{e} - v_{M})\pmb {\tau }^{T_L}_{{x_M}{x_{\texttt {e}}}} + \\ (v_{L} - v_{K})\pmb {\tau }^{T_L}_{{x_K}{x_L}} + (v_{e} - v_{K})\pmb {\tau }^{T_L}_{{x_K}{x_{\texttt {e}}}} + (v_{e} - v_{L})\pmb {\tau }^{T_L}_{{x_L}{x_{\texttt {e}}}} \end{array} \right] \cdot \pmb {\varphi }_{T_L} \end{array} \right\} , \end{aligned}$$

(91)

with $\pmb {\varphi }_T = \frac{1}{m_T} \int _T \pmb {\varphi }~d{x}$, $\pmb {\varphi }_{T_K} = \frac{1}{m_{T_K}} \int _{T_K} \pmb {\varphi }~d{x}$ and $\pmb {\varphi }_{T_L} = \frac{1}{m_{T_L}} \int _{T_L} \pmb {\varphi }~d{x}$.

By the Green expression, the operator $I_2(\pmb {\varphi })$ can be rewritten as

(92)

To estimate $I_1(\pmb {\varphi })$ and $I_2(\pmb {\varphi })$, we introduce the operators $R_i$ on the space $\left( C^{\infty }_c(\Omega )\right) ^3$, where i ranges from 1 to 3, as follows:

(93)

(94)

(95)

for any $\pmb {\varphi }\in \left( C^{\infty }_c(\Omega )\right) ^3$.

Using the above operators $R_i$ for i ranging from 1 to 3, and applying the Cauchy–Schwarz inequality, one obtains

$$\begin{aligned} |I_1(\pmb {\varphi }) + I_2(\pmb {\varphi })|^2 \le \Vert \textbf{v}\Vert ^2_{1,\mathcal {T}^{**}_h} \left[ R_1(\pmb {\varphi })+R_{2}(\pmb {\varphi })+R_{3}(\pmb {\varphi })\right] , \quad \forall \pmb {\varphi }\in \left( C^{\infty }_c(\Omega )\right) ^3. \end{aligned}$$

(96)

In (93) for $R_1(\pmb {\varphi })$, using the regularity of $\pmb {\varphi }\in \left( C^{\infty }_c(\Omega )\right) ^3$ yields the existence of $C_{\pmb {\varphi }} > 0$, which depends on $\pmb {\varphi }$, such that

$$\begin{aligned} \vert \pmb {\varphi }_{T} - \pmb {\varphi }_{{x_N}{x_Q}} \vert ^2 \le C_{\pmb {\varphi }} h^2, \quad \text {for each } ({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T. \end{aligned}$$

(97)

Combining the above result with the property (54) in Lemma 1, there exists a positive constant $C_6 > 0$ that is independent of h such that

$$\begin{aligned} \left| R_1(\pmb {\varphi }) \right| \le C_{6} m_{\Omega }h^2(1 + \pmb \epsilon (h)), \quad \text {with } \lim \limits _{h \rightarrow 0}\pmb \epsilon (h) = 0, \end{aligned}$$

(98)

where $m_{\Omega }$ represents the volume of the domain $\Omega$.

Hence,

$$\begin{aligned} |R_1(\pmb {\varphi })| \rightarrow 0, \quad \text {as } h \rightarrow 0. \end{aligned}$$

(99)

For $R_2(\pmb {\varphi })$, with property (54), one can obtain

$$\begin{aligned} \left| R_{2}(\pmb {\varphi }) \right| \rightarrow 0, \quad \text {as } h \rightarrow 0. \end{aligned}$$

(100)

For $R_3(\pmb {\varphi })$, using the Cauchy–Schwarz inequality, one can find that a positive constant $C_7$ depends on $\pmb {\varphi }$, such that

$$\begin{aligned}&\left( \frac{\pmb {\tau }^{T_K}_{{x_N}{x_Q}} \cdot \pmb {\varphi }_{T_K} + \pmb {\tau }^{T_L}_{{x_N}{x_Q}} \cdot \pmb {\varphi }_{T_L} -\textbf{n}_{{x_N}{x_Q}}\cdot \pmb {\varphi }_{{x_N}{x_Q}} }{|\textbf{n}_{{x_N}{x_Q}}|}\right) ^2 \nonumber \\&\quad =\left[ \begin{array}{l} \frac{\pmb {\tau }^{T_K}_{{x_N}{x_Q}} }{|\textbf{n}_{{x_N}{x_Q}}|}\cdot \left( \pmb {\varphi }_{T_K}-\pmb {\varphi }_{{x_N}{x_Q}}\right) + \frac{\pmb {\tau }^{T_L}_{{x_N}{x_Q}} }{{|\textbf{n}_{{x_N}{x_Q}}|}} \cdot \left( \pmb {\varphi }_{T_L} - \pmb {\varphi }_{{x_N}{x_Q}}\right) \\ \quad +\left( \frac{\pmb {\tau }^{T_K}_{{x_N}{x_Q}} }{|\textbf{n}_{{x_N}{x_Q}}|} + \frac{\pmb {\tau }^{T_L}_{{x_N}{x_Q}} }{{|\textbf{n}_{{x_N}{x_Q}}|}}-\frac{\textbf{n}_{{x_N}{x_Q}}}{{|\textbf{n}_{{x_N}{x_Q}}|}}\right) \cdot \pmb {\varphi }_{{x_N}{x_Q}} \end{array} \right] ^2 \nonumber \\&\quad \le 3 \left[ \begin{array}{l} \left( {\frac{|\pmb {\tau }^{T_K}_{{x_N}{x_Q}}| }{|\textbf{n}_{{x_N}{x_Q}}|}}\right) ^2 {\left( \pmb {\varphi }_{T_K}-\pmb {\varphi }_{{x_N}{x_Q}}\right) ^2} \\ \quad + \left( {\frac{|\pmb {\tau }^{T_L}_{{x_N}{x_Q}}| }{{|\textbf{n}_{{x_N}{x_Q}}|}}} \right) ^2 {\left( \pmb {\varphi }_{T_L} - \pmb {\varphi }_{{x_N}{x_Q}}\right) ^2 } \\ \quad + \left( {\frac{|\pmb {\tau }^{T_K}_{{x_N}{x_Q}}| }{|\textbf{n}_{{x_N}{x_Q}}|}} s+ {\frac{|\pmb {\tau }^{T_L}_{{x_N}{x_Q}}| }{{|\textbf{n}_{{x_N}{x_Q}}|}}}+1\right) ^2 |\pmb {\varphi }_{{x_N}{x_Q}}|^2 \end{array} \right] \le C_7, \quad \forall ({x_N},{x_Q}) \in \mathcal {V}^{(2)}_T. \end{aligned}$$

(101)

By applying (101) and utilizing $m_T =\frac{2}{3}\sum \nolimits _{({x_N},{x_Q})\in \mathcal {V}^{(2)}_T} d_{{x_N}{x_Q}}|\textbf{n}_{{x_N}{x_Q}}|$ in the formula (95), one can find that there exists a positive constant $C_8 > 0$, dependent only on $\pmb {\varphi }$, such that

$$\begin{aligned} \left| R_{3}(\pmb {\varphi }) \right| \le C_8 \sum \limits _{ T \in \mathcal {T}^{**}_{\Lambda }} m_T. \end{aligned}$$

(102)

According to [19, Theorem 3.8], it is established that

$$\begin{aligned} \sum \limits _{T \in \mathcal {T}^{**}_{\Lambda }} m_T \rightarrow 0, \quad \text {as } h \rightarrow 0, \end{aligned}$$

(103)

One can observe that the dimension of the zones where the tensor $\Lambda ({x})$ is piecewise Lipschitz continuous is one or two.

From Eqs. (102) and (103), it follows that

$$\begin{aligned} |R_{3}(\pmb {\varphi })| \rightarrow 0, \quad \text {as } h \rightarrow 0. \end{aligned}$$

(104)

Applying Holder’s inequality and utilizing (85) leads to

$$\begin{aligned} |I_3(\pmb {\varphi })| \le h \left\| \nabla P_1(\textbf{v}) \right\| _{\left( L^2(\Omega )\right) ^3} ~\left\| {\text {div}}(\pmb {\varphi }) \right\| _{L^2(\Omega )} \le h \sqrt{ \frac{3}{2}m_{\Omega }} ~\Vert \textbf{v}_h\Vert _{1,\mathcal {T}^{**}_h} \left\| {\text {div}}(\pmb {\varphi }) \right\| _{L^2(\Omega )}, \end{aligned}$$

(105)

and therefore

$$\begin{aligned} |I_3(\pmb {\varphi })| \rightarrow 0, \quad \text {as } h \rightarrow 0. \end{aligned}$$

(106)

Combining the inequalities (72), (96), (105) and for each $\pmb {\varphi }\in \left( C^{\infty }_c(\Omega )\right) ^3$, one can obtain

$$\begin{aligned} \frac{1}{\Vert \nabla _{\Lambda } \textbf{v}_h\Vert _{\left( L^2(\Omega )\right) ^3}}|I{(\pmb {\varphi })}|&\le \frac{\sqrt{C_3}}{ \Vert \textbf{v}_h \Vert _{1,\mathcal {T}^{**}_h}} \Vert \textbf{v}_h \Vert _{1,\mathcal {T}^{**}_h}\sqrt{(R_1(\pmb {\varphi })+R_{3}(\pmb {\varphi })+R_{2}(\pmb {\varphi }))} \nonumber \\&+ \frac{\sqrt{C_3}}{ \Vert \textbf{v}_h \Vert _{1,\mathcal {T}^{**}_h}} h \sqrt{ 3m_{\Omega }} ~\Vert \textbf{v}_h\Vert _{1,\mathcal {T}^{**}_h} \left\| {\text {div}}(\pmb {\varphi }) \right\| _{L^2(\Omega )}, \quad \forall \textbf{v}_h \in \mathcal {H}_h. \end{aligned}$$

(107)

Regarding the convergences of (99), (100), and (104) with the above inequalities, it can be concluded for each $\pmb {\varphi }\in \left( C^{\infty }_c(\Omega )\right) ^3$ that

$$\begin{aligned}&\frac{1}{\Vert \nabla _{\Lambda } \textbf{v}_h\Vert _{\left( L^2(\Omega )\right) ^3}}|I{(\pmb {\varphi })}| \rightarrow 0, \quad \text {as } h\rightarrow 0, \quad \forall \textbf{v}_h \in \mathcal {H}_h \setminus \{\pmb 0\}. \end{aligned}$$

As a result, the strong consistency property (71) has been proven. $\square$

Corollary 1

Let $\left( \mathcal {H}_h, h, \Phi ,\nabla _{\Lambda } \right)$ be a family of discretizations in the sense of Definition 1. If the EFC-3DFEMb scheme satisfies the coercive, dual, and strong consistency properties under the assumptions of Proposition 2, then the EFC-3DFEM scheme also satisfies the coercive, dual, and strong consistency properties.

Proof

For any $\textbf{v}_h \in \mathcal {H}_h$, with the definitions of $\Phi \textbf{v}_h$ in (26) and $P_1 \textbf{v}_h$ in (48), we get the following inequality:

$$\begin{aligned} \Vert \Phi \textbf{v}_h - P_1 \textbf{v}_h \Vert _{L^2(\Omega )} \le h \left( \Vert \nabla P_1\textbf{v}_h\Vert _{\left( L^2(\Omega )\right) ^3} + \Vert \nabla _{\Lambda } \textbf{v}_h \Vert _{\left( L^2(\Omega )\right) ^3}\right) . \end{aligned}$$

(108)

Substituting (72) and (85) into the above inequality, we get

$$\begin{aligned} \Vert \Phi \textbf{v}_h - P_1 \textbf{v}_h \Vert _{L^2(\Omega )} \le C_{9} h \Vert \nabla _{\Lambda } \textbf{v}_h \Vert _{\left( L^2(\Omega )\right) ^3} \end{aligned}$$

(109)

where $C_9$ is a positive constant independent of h.

By (109) and the coercivity (69) of $P_1$, a positive constant $C_{10}$ is defined and independent of h such that

$$\begin{aligned} \Vert \Phi \textbf{v}_h \Vert _{L^2(\Omega )}&\le \Vert \Phi \textbf{v}_h - P_1 \textbf{v}_h \Vert _{L^2(\Omega )} + \Vert P_1 \textbf{v}_h \Vert _{L^2(\Omega )} \le {C_{10}} \Vert \nabla _{\Lambda } \textbf{v}_h \Vert _{\left( L^2(\Omega )\right) ^3}, \end{aligned}$$

(110)

which means that the EFC-3DFEM scheme is coercive.

Let $\varphi \in C^{\infty }_c(\Omega )$, and consider a vector $\pmb {\varphi }_h$ whose elements are taken from $\left( \varphi ({x_P})\right) _{{x_P}\in \mathcal {V}^{**}} \in \mathcal {H}_h$. Utilizing the triangle inequality in (89) and (109), we estimate the error between $\Phi (\pmb {\varphi }_h)$ and $\varphi$ as follows:

$$\begin{aligned} \Vert \Phi \pmb {\varphi }_h - \varphi \Vert _{L^2(\Omega )}&\le \Vert \Phi \pmb {\varphi }_h - P_1\pmb {\varphi }_h \Vert _{L^2(\Omega )} + \Vert P_1\pmb {\varphi }_h - \varphi \Vert _{L^2(\Omega )}\nonumber \\&\le h \left[ C_{9} \Vert \nabla _{\Lambda } \pmb {\varphi }_h \Vert _{\left( L^2(\Omega )\right) ^3} + \Vert \nabla \varphi \Vert _{\left( L^2(\Omega )\right) ^3}\right] . \end{aligned}$$

(111)

Hence,

$$\begin{aligned} \Vert \Phi \pmb {\varphi }_h - \varphi \Vert _{L^2(\Omega )} \rightarrow 0, \quad \text {as } h \rightarrow 0. \end{aligned}$$

(112)

Combining the above with the convergence of (88), the EFC-3DFEM scheme satisfies the strong consistency property (43). From Proposition 1 and (109), it also satisfies the dual consistency (44). $\square$

5 Numerical experiments

In this section, three benchmark tests [9] are carried out to verify the numerical results for the convergence of EFC-3DFEM scheme with the following methods:

• FEM-T4 – The standard linear finite element method on a tetrahedral mesh [20];

• SUSHI – A scheme using stabilization and hybrid interfaces [21];

• CeVeFE-DDFV – A discrete duality finite volume scheme with cell/vertex/face+edge unknowns [22];

• VAG – The vertex approximate gradient scheme [23]; and

• MFD-GEN – The mimetic finite difference of generalized polyhedral meshes [24];

The above list includes the FEM-T4 method because the EFC-3DFEM method is equivalent to this approach on the tetrahedral subdual mesh $\mathcal {T}^{**}_h$ in the isotropic tensor situation. Except for the FEM-T4 method, the remaining methods satisfy the local conservativity of the fluxes, which is particularly essential for handling heterogeneous, anisotropic (possibly discontinuous) diffusion (e.g., Tests 2 and 3).

The relative errors on the subdual mesh $\mathcal {T}^{**}_h$ in $L^2$, $H^1$ semi-norm, and energy norm of proposed EFC-3DFEM scheme denoted by $\text {erl2}$, $\text {ergrad}$, and $\text {ener}$ are computed as follows:

$$\begin{aligned} \text {erl2}&= \left( \frac{\sum \limits _{T \in \mathcal {T}^{**}_h}\int _{T}\vert u_h - u \vert ^2 d{x}}{\sum \limits _{T \in \mathcal {T}^{**}_h}\int _{T}\vert u \vert ^2 d{x}} \right) ^{{1}/{2}}, \end{aligned}$$

(113)

$$\begin{aligned} \text {ergrad}&= \left( \frac{\sum \limits _{T \in \mathcal {T}^{**}_h}\int _{T} \vert \nabla _{\Lambda } u_h - \nabla u \vert ^2 d{x}}{\sum \limits _{T \in \mathcal {T}^{**}_h}\int _{T} \nabla u \vert ^2 d{x}} \right) ^{{1}/{2}}, \end{aligned}$$

(114)

$$\begin{aligned} \text {ener}&= \left( \frac{\sum \limits _{T \in \mathcal {T}^{**}_h}\int _{T}\left[ \Lambda \left( \nabla _{\Lambda } u_h - \nabla u \right) \right] \cdot \left( \nabla _{\Lambda } u_h - \nabla u \right) d{x}}{\sum \limits _{T \in \mathcal {T}^{**}_h}\int _{T}\left( \Lambda \nabla u \right) \cdot \nabla u ~ d{x}} \right) ^{{1}/{2}}, \end{aligned}$$

(115)

where u is the the exact solution and $\textbf{u}_h = (u_{P})_{{x_P}\in \mathcal {N}^{**}}$ is the numerical result $u_h$ at vertices of the subdual mesh $\mathcal {T}^{**}_h$. Besides, $\text {umin}$ and $\text {umax}$ are defined as the minimum and maximum values of the approximate solutions. Additionally, their rates of convergence are expressed for each number of mesh $i \ge 2$ as follows:

$$\begin{aligned} \text {ratiol2}&= -3 \frac{\log \left( {\text {erl2}(i)}/{\text {erl2}(i-1)}\right) }{\log \left( {\text {nu}(i)}/{\text {nu}(i-1)} \right) }, \end{aligned}$$

(116)

$$\begin{aligned} \text {ratiograd}&= -3 \frac{\log \left( {\text {ergrad}(i)}/{\text {ergrad}(i-1)}\right) }{\log \left( {\text {nu}(i)}/{\text {nu}(i-1)} \right) }, \end{aligned}$$

(117)

$$\begin{aligned} \text {ratioener}&= -3 \frac{\log \left( {\text {ener}(i)}/{\text {ener}(i-1)}\right) }{\log \left( {\text {nu}(i)}/{\text {nu}(i-1)} \right) }, \end{aligned}$$

(118)

with $\text {nu}$ denotes the number of unknowns in the linear system.

Additionally, four different fundamental mesh types of primal meshes are studied: the uniform tetrahedral mesh (Mesh 1), the checkerboard mesh (Mesh 2), the prism mesh with general bases (Mesh 3), and the locally refined mesh (Mesh 4) (see Fig. 8).

Fig. 8

Four types of primal meshes: (a) Mesh 1: uniform tetrahedral mesh, (b) Mesh 2: checkerboard mesh, (c) Mesh 3: prism mesh with general bases, and (d) Mesh 4: locally refined mesh

Test 1

Mild anisotropy.

Considering a constant, anisotropic permeability tensor $\Lambda _1$ and a regular solution $u_1$ determined on the unit cubic domain $\Omega$, a non-homogeneous Dirichlet condition on the domain boundary $\partial \Omega$ is as follows:

$$\begin{aligned} \Lambda _1(x,y,z)&= \left( {\begin{array}{*{20}{c}} {1}&{}{0.5}&{}{0}\\ {0.5}&{}{1}&{}{0.5}\\ {0}&{}{0.5}&{}{1} \end{array}} \right) , \end{aligned}$$

(119)

$$\begin{aligned} u_1(x,y,z)&= 1 + \sin (\pi x) \sin \left( \pi \left( y + \frac{1}{2}\right) \sin \left( \pi \left( z + \frac{1}{3} \right) \right) \right) . \end{aligned}$$

(120)

The minimum and maximum values of the solution $u_1$ on $\Omega$ are equal to 0 and 2, respectively. The primal meshes are Mesh 1 and Mesh 2.

Table 1 Convergence of the EFC-3DFEM scheme for Test 1 on Mesh 1

It can be observed in Table 1 that when the mesh is refined, the EFC-3DFEM delivers good convergence and the rate is of 1.9 in $L^2$-norm, nearly 0.9 in $H^1$-norm and energy norm. Besides, the EFC-3DFEM scheme is higher accurate than FEM-T4 in the relative errors as indicated in Fig. 9. On a finer mesh of the subdual mesh $\mathcal {T}^{**}_h$, the numerical results are really obtained.

From Table 2, the EFC-3DFEM delivers also good convergence and the rate increases to 1.98 in $L^2-$norm, 0.947 in $H^1-$norm and 0.949 in the energy norm. The EFC-3DFEM presents smaller errors in $L^2-$norm than VAG, CeVeFE-DDFV, and SUSHI schemes as shown Fig. 10 with the same primal mesh size.

Test 2

Heterogeneity and anisotropy.

On the cubic domain $\Omega$ of Mesh 3, a second test is considered with smoothly variable permeability tensor as

$$\begin{aligned} \Lambda _2(x,y,z) = \left( {\begin{array}{*{20}{c}} {y^2+z^2+1}&{}{-xy}&{}{-xz}\\ {-zy}&{}{x^2+z^2+1}&{}{-yz}\\ {-xz}&{}{-yz}&{}{x^2 + y^2 + 1} \end{array}} \right) . \end{aligned}$$

(121)

A regular solution $u_2$ is given as

$$\begin{aligned} u_2(x,y,z) = x^3y^2z + x\sin (2 \pi x z) \sin (2 \pi x y) \sin (2 \pi z), \end{aligned}$$

(122)

which implies a non-homogeneous Dirichlet condition on the boundary $\partial \Omega$. The minimum and maximum values are equal to $-0.862$ and 1.0487, respectively.

Fig. 9

The relative errors in $L^2$ norm (a), $H^1$ semi-norm (b), and energy norm (c) obtained by using the EFC-3DFEM and FEM-T4 schemes for Test 1 on Mesh 1

Table 2 Convergence of the EFC-3DFEM scheme for Test 1 on Mesh 2

Fig. 10

The relative errors in $L^2$ norm (a), $H^1$ semi-norm (b), and energy norm (c) obtained by using the EFC-3DFEM, VAG, CeVeFE-DDFV, MFD-GEN, and SUSHI schemes for Test 1 on Mesh 2

Table 3 Convergence results of the EFC-3DFEM scheme for Test 2 on Mesh 3

Fig. 11

The relative errors in $L^2$ norm (a), $H^1$ semi-norm (b), and energy norm (c) obtained by using the EFC-3DFEM, VAG, CeVeFE-DDFV, MFD-GEN, and SUSHI schemes for Test 2 on Mesh 3

Test 3

Strong discontinuous heterogeneous permeability.

The domain $\Omega$ partitioned into the following sub-domains ${{\overline{\Omega }}} = \bigcup \limits _{i = 1}^4 \overline{\Omega }_i$ is given by

$$\begin{aligned} \Omega _1&=[0,1]\times [0,0.5]\times [0,0.5],\\ \Omega _2&= [0,1]\times (0.5,1]\times [0,0.5],\\ \Omega _3&=[0,1]\times (0.5,1]\times (0.5,1],\\ \Omega _4&= [0,1]\times [0,0.5]\times (0.5,1]. \end{aligned}$$

The permeability tensor is defined as

$$\begin{aligned} \Lambda _3(x,y,z) = \left( {\begin{array}{*{20}{c}} {\alpha ^i_x}&{}{0}&{}{0}\\ {0}&{}{\alpha ^i_y}&{}{0}\\ {0}&{}{0}&{}{\alpha ^i_z} \end{array}} \right) , \end{aligned}$$

(123)

and the exact solution is as follows:

$$\begin{aligned} u_3(x,y,z) = \alpha _i\sin (2\pi x) \sin (2\pi y) \sin (2\pi z), \end{aligned}$$

(124)

for $(x,y,z) \in \Omega _i$, where the coefficient $\alpha _i$ is given in Table 4. The minimum and maximum values of $u_3$ on $\Omega$ are $-100$ and 100, respectively.

Table 4 The coefficients $\alpha ^i_x, \alpha ^i_y, \alpha ^i_z, \alpha _i$ for Test 3 on each sub-domain $\Omega _i$

The permeability tensor $\Lambda _3$ is discontinuous across the interfaces separating four sub-domains. The exact solution $u_3$ is designed to be continuous and ensures the conservation of the normal flux across such interfaces. Note that, the homogeneous Dirichlet boundary condition is imposed in this case.

Fig. 12

The relative errors in $L^2$ norm (a), $H^1$ semi-norm (b), and energy norm (c) obtained by using the EFC-3DFEM, VAG, CeVeFE-DDFV, MFD-GEN, and SUSHI schemes for Test 3 on Mesh 4

Table 5 Convergence results of the EFC-3DFEM scheme for Test 3 on Mesh 4

According to Fig. 11 and Table 3 of Test 2 on Mesh 3, Fig. 12 and Table 5 of Test 3 on Mesh 4, the EFC-3DFEM converges and the rates in $L^2$-norm is nearly 2; however, the $H^1$-norm and energy norm are nearly 1. Furthermore, with the same mesh size, the EFC-3DFEM offers less $L^2-$norm error than the VAG, CeVeFE-DDFV, and MFD-GEN schemes on Test 2; and than the VAG, MFD-GEN schemes on Test 3 as shown in Figs. 11 and 12.

Clearly, in the above numerical results, the convergence rate of EFC-3DFEM in $L^2$-norms, which is nearly 2, is greater than the rate estimated as 1 in (111).

6 Conclusion

The EFC-3DFEM is represented in this research for three-dimensional heterogeneous and anisotropic diffusion problems on generic meshes with discontinuities in the permeability tensor $\Lambda$. A primal mesh, a dual mesh, and a tetrahedral subdual mesh were used in the design. Based on the results in this study, the following conclusions can be drawn:

• The EFC-3DFEM possesses four important properties: (i) The stiffness matrix is symmetric and positive definite, (ii) The discrete unknowns are linear combinations at the center points and edge points of the primal mesh, (iii) It benefits from the local continuity of numerical fluxes, and (iv) Leveraging the ability to construct the dual mesh in complex geometric domains (see Remark 1), the subdual mesh is also constructed to align with real-world geometry.

• Within a rigorous theoretical framework, we demonstrate the convergence of the approximate solution for the full diffusion tensor (possibly discontinuous) and general polyhedral meshes.

• The construction of the dual and subdual meshes (see Remark 7) constitutes the core aspect of the macroelement technique [8]. This construction ensures stability by employing this technique when extended to address the three-dimensional Stokes, Oseen, Navier Stokes problems, including cases with variable viscosity, as demonstrated in the two-dimensional case [25].

• The numerical results indicate that the convergence rates are nearly 2 in the $L^2$-norm. In the cases of the $H^1$-norm and energy norm, the rates are close to 1, as expected.

• Furthermore, the method is facilitated for direct implementation in the conventional finite element codes based on tetrahedral meshes.